Time-of-flight PET image reconstruction using origin ensembles

Abstract

The origin ensemble (OE) algorithm is a novel statistical method for minimummean-square-error (MMSE) reconstruction of emission tomography data. This method allows one to perform reconstruction entirely in the image domain, i.e. without the use of forward and backprojection operations. We have investigated the OE algorithm in the context of list-mode (LM) time-of-flight (TOF) PET reconstruction. In this paper, we provide a general introduction to MMSE reconstruction, and a statistically rigorous derivation of the OE algorithm. We show how to efficiently incorporate TOF information into the reconstruction process, and how to correct for random coincidences and scattered events. To examine the feasibility of LM-TOF MMSE reconstruction with the OE algorithm, we applied MMSE-OE and standard maximum- likelihood expectation-maximization (ML-EM) reconstruction to LM-TOF phantom data with a count number typically registered in clinical PET examinations. We analyzed the convergence behavior of the OE algorithm, and compared reconstruction time and image quality to that of the EM algorithm. In summary, during the reconstruction process, MMSE-OE contrast recovery (CRV) remained approximately the same, while background variability (BV) gradually decreased with an increasing number of OE iterations. The final MMSE-OE images exhibited lower BV and a slightly lower CRV than the corresponding ML-EM images. The reconstruction time of the OE algorithm was approximately 1.3 times longer. At the same time, the OE algorithm can inherently provide a comprehensive statistical characterization of the acquired data. This characterization can be utilized for further data processing, e.g. in kinetic analysis and image registration, making the OE algorithm a promising approach in a variety of applications.

1. Introduction

In positron emission tomography (PET), the reconstruction of the large amount of noisy, low-count data to a high-quality estimate of the unobservable, true emission density remains a challenge. With data acquisition in PET having shifted in recent years to list mode (LM) (Barrett et al 1997), where each registered photon pair resulting from the annihilation of a tissue electron with a positron emitted during decay is stored individually, and the concomitant rise of data volumes, this challenge has been exacerbated. Storing coincidence events individually instead of per-channel accumulated counts, on the other hand, supports the time- of-flight (TOF) technique. In this technique, the arrival time difference of the annihilation photons is stored together with location information of the detector elements (Lewellen 1998). TOF PET reconstruction then exploits the relation of the arrival time difference to the relative event distance from the detector elements via the speed of light to inform the estimation of the event location (see figure 1).

Figure 1.

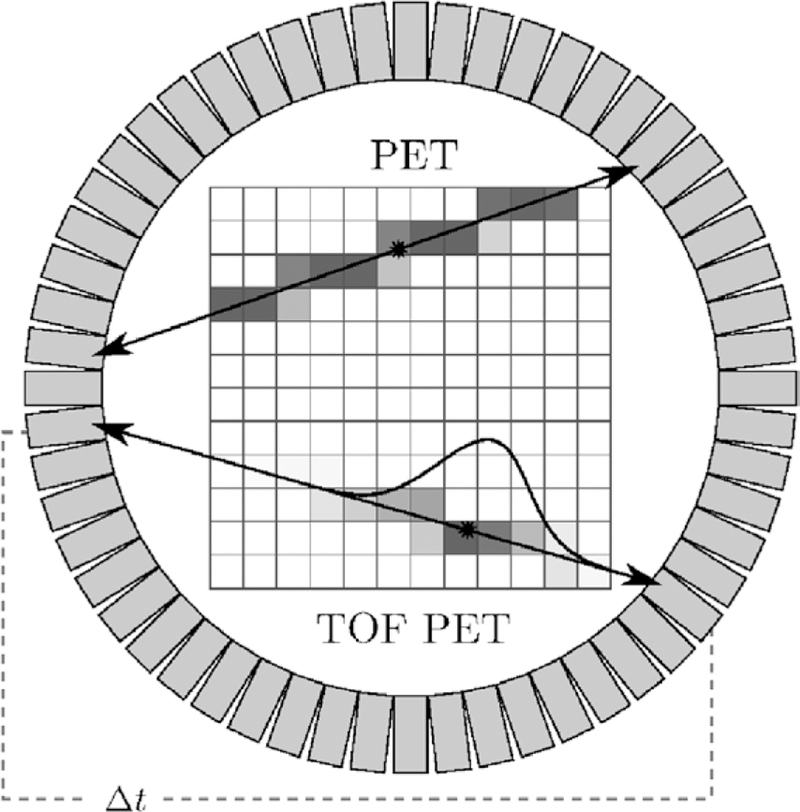
TOF PET principle (schematic drawing). When assuming perfect collinearity of annihilation photons, each registered coincidence event defines a line of response (LOR) connecting the two responding detectors. The gray value of each pixel encodes its probability to contain the origin of the registered event. In TOF PET, measurement of the arrival time difference of the annihilation photons (Δt) allows one to estimate the location of the registered event on its LOR much more accurately than in native PET, where the event is statistically spread over its entire LOR.

While analytical reconstruction techniques such as filtered backprojection (FBP) can be used for PET, statistically motivated iterative reconstruction algorithms are better suited for the LM-TOF data structure, and allow for an accurate incorporation of the statistical nature of photon counting noise (Leahy and Qi 2000). Most state-of-the-art reconstruction algorithms for LM-TOF data are based on expectation maximization (EM) (Dempster et al 1977), an iterative method for finding maximum likelihood (ML) or, when using a Bayesian interpretation, maximum a posteriori probability (MAP) estimates of the true radioactivity distribution (for an overview, refer to Defrise and Gullberg (2006)). A particularly popular example of this class is ordered-subset expectation-maximization (OSEM) reconstruction (Hudson and Larkin 1994), where, when applied to LM data, the event list is partitioned into equally sized subsets, resulting in a large reconstruction speed increase. This was initially traded off for convergence, but later modifications restored this property (Browne and Pierro 1996, Rahmim et al 2004). Statistical iterative reconstruction generally uses: (1) forward projection (FP) of the current image estimate to compute expected data in the projection domain, (2) difference or ratio comparison of the expected data to the acquired data to compute correction terms, and (3) backprojection (BP) of the correction terms to update the image estimate. Unfortunately, FP and BP operations are computationally expensive, and the FP/BP framework is not well suited for the incorporation of a priori information in the image domain.

We have previously described an alternative to FP/BP-driven algorithms that reconstructs the image entirely in the image domain, i.e. without the use of FP and BP operations: origin ensemble (OE) reconstruction (Sitek 2008, Sitek 2011, Sitek 2012, Sitek and Moore 2013). Its convergence to steady state and to a solution very close to that of EM was demonstrated in (Sitek 2008, Sitek 2011, Sitek 2012). OE reconstruction is based on computing the minimum-mean-square-error (MMSE) estimate for the number of events in each image element, e.g. in each voxel. The OE algorithm thus provides a different statistical characterization of the data compared to that delivered by ML and MAP reconstruction. In particular, OE reconstruction uses a Markov chain of origin ensembles, i.e. configurations of the registered coincidence events in the image domain. Starting with a random initial configuration of the registered events, during each OE update step, a randomly selected event is stochastically moved to a random new location along the line of sight. This is done with a transition probability that depends on the probability ratio of the states before and after the transition. When the Markov chain has reached equilibrium, the OE states are sampled, averaged, and normalized to form the OE image estimate.

This work aims to add two extensions to OE reconstruction that allow this promising approach to be used in practical applications: first, we show how to efficiently incorporate TOF information into the reconstruction process, and second, we examine the feasibility of a previously described approach to correct for random coincidences and scattered events (Sitek and Kadrmas 2011). Furthermore, we undertake the first extensive comparison of EM and OE reconstruction time and image quality. For this comparison, we use spherically symmetric, overlapping volume elements (so-called blobs (Matej and Lewitt 1996)) and the NEMA NU 2–2007 image quality evaluation protocol (National Electrical Manufacturers Association 2007, section 7).

The remainder of this paper is structured as follows: in section 2, we review the mathematical theory of OE reconstruction. This prepares for section 3, where after a brief introduction to the Metropolis-Hastings algorithm (Hastings 1970, Metropolis et al 1953) used to make OE reconstruction practicable (section 3.1), TOF information is incorporated to improve the OE update (section 3.2) and to formulate a better OE initial state (section 3.3). Section 3.4 discusses corrections for random coincidences and scattered events. In sections 4–6, we characterize the modified OE reconstruction scheme based on phantom measurements, and compare its runtime and image quality to that of the standard EM algorithm. A list of abbreviations used in this paper can be found in appendix A.

2. Theory

2.1. Minimum-mean-square-error PET reconstruction using origin ensembles

PET data can be modeled as a set of I × J independent Poisson numbers n = {n_ij} with expected values {λ_ij}, n_ij being the unobservable count of annihilation events in volume element i ∈ {1, …, I} registered by detector pair j ∈ {1, …, J} (Shepp and Vardi 1982). In the following, the set of volume elements (e.g. voxels or blobs) is referred to as the image domain, and the set of detector pairs as the projection domain. The statistical relationship between these domains is modeled by a system matrix {α_ij}, an element α_ij of which denotes the probability that an event in volume element i is registered by detector pair j. It is assumed that the system matrix elements are exactly known from the scanner geometry, and already contain information about the object-specific photon attenuation. Contributions of random coincidences and scattered events are initially neglected. We here adopt the notational system of Shepp and Vardi (1982).

According to the above statistical model, the probability that the scanner registers an event in volume element i altogether is

$${\epsilon }_i=\sum _j{\alpha }_{ij},$$ (1)

called the sensitivity of volume element i. Let further λ = {λ_i} denote the unknown discretized emission density in the image domain, normalized such that λ_i represents the total number of events that occurred in volume element i. The Poisson parameters λ_ij can thus be written as λ_ij = α_ij λ_i. Taking the complete data n into account, the likelihood of an estimate $\widehat{\mathbf{\lambda }}=\{\widehat{{\lambda }_i}\}$ for the emission density then reads as

$$\mathcal{L}(\widehat{\mathbf{\lambda }}|\text{n})={\mathcal{P}}_{\widehat{\mathbf{\lambda }}}\left(\text{n}\right)=\prod _{i,j}\frac{{\widehat{\lambda }}_{ij}^{n_{ij}}}{n_{ij}!}\hspace{0.17em}{\text{e}}^{-{\widehat{\lambda }}_{ij}},{\widehat{\lambda }}_{ij}={\alpha }_{ij}{\widehat{\lambda }}_i,$$ (2)

see Leahy and Qi (2000, equation (3)).

In a widely used class of statistical reconstruction techniques, one is now concerned with computing the ML estimate for the emission density λ from the acquired incomplete (projection) data $n^{*}\text{=}\left\{n_j^{*}\right\},$

$$n_j^{*}=\sum _i{n}_{ij}.$$ (3)

When stored in this format, the data are usually referred to as the sinogram. As indicated above, storage of the data in sinogram format proves impractical due the large number of detector pairs and measured event attributes. Therefore, ML reconstruction is also oftentimes performed for data in LM format, in which the data are stored as a raw list of registered coincidence events and their individual information. For both data formats, however, the final ML estimate

$${\widehat{\mathbf{\lambda }}}^{(\text{ML})}=\underset{\widehat{\mathbf{\lambda }}}{\arg \hspace{0.17em}\max }\mathcal{L}(\widehat{\mathbf{\lambda }}|{\text{n}}^{*})$$ (4)

is computed iteratively in practice, using e.g. an algorithm of the EM type, or a conjugategradient (CG) method (see Shepp and Vardi (1982) and Mumcuoğlu et al (1994), respectively). A particular characteristic of such techniques is their use of FP of the image estimate to the projection domain, which allows to compare the estimated projection data with the acquired projection data. In turn, BP of adequate correction terms is used to amend the image estimate accordingly. Successive FP and BP are repeated a certain number of times, or until a predefined convergence criterion is met.

In contrast to such FP/BP-driven improvement of the data fidelity in the projection domain, image reconstruction using origin ensembles relies on direct estimation of the number of registered events in each volume element,

$$n_i=\sum _j{n}_{ij}.$$ (5)

In particular, and as described in detail in this paper, the OE algorithm computes the MMSE estimate for the emission counts n_i. This is done entirely in the image domain, i.e. without accessing the projection domain. The MMSE estimate for the emission count of volume element i is given by

$$E\left[n_i|{\mathit{n}}^{*}\right]=\sum _{\widehat{n}\in \Theta }{n}_i\left(\widehat{\mathit{n}}\right)\mathcal{P}(\widehat{n}|{\mathit{n}}^{*}),$$ (6)

Jaynes (2003), where the sum extends over all sets of complete data n̂ consistent with the acquired data n^*. We call these sets of complete data the complete data domain Θ. Above, n_i (n̂) denotes the number of events in volume element i, as constituted by the particular set of complete data n̂. P (n̂|n*) is the posterior probability of complete data n̂, conditioned on the acquired data n^*.

Alongside other applications of the OE algorithm (see Sitek (2012) and Sitek and Moore (2013), for example), this method can be used to estimate the emission density λ in the following, conceptually straightforward manner. First, the MMSE estimate for each emission count n_i is computed. These estimates are corrected for event losses due to photon attenuation and varying scanner sensitivity. This is achieved by dividing the estimate E[n_i|n*] by the sensitivity ε_i, yielding the MMSE estimate for the number of events that actually occurred in volume element i. The final estimate for the emission density λ is then defined to be

$${\widehat{\lambda }}_i^{\left(\text{MMSE}\right)}=\{\begin{array}{cc}E\left[n_i|{\mathit{n}}^{*}\right]/{\epsilon }_i& \text{for}\hspace{0.17em}{\epsilon }_i>0,\\ 0& \text{for}\hspace{0.17em}{\epsilon }_i=0.\end{array}$$ (7)

We call the above procedure MMSE reconstruction.

In order to proceed with the OE algorithm, it is crucial to note that by assigning each registered event k to a single volume element i_k with a_ikjk > 0, a set of complete data n̂ϵΘ is constructed from the acquired data n^*. Here, j_k denotes the detector pair that registered event k. The condition a_ikjk > 0 thus implies that volume element i_k is in the line of sight for detector pair j_k. In other words, there is a chance that event k actually occurred in volume element i_k. In the remainder of this paper, the letter k is always used to index single events, while n represents emission counts. In general, regardless of whether the data are in sinogram or LM format, it is possible to represent any complete data n̂ϵΘ in the above way (see section 2.2 for further discussion). We call the arising configurations of registered events in the image domain origin ensembles (OEs). Let such OEs be represented by

$$\mathit{\omega =}\left\{\left(i,j\right),\hspace{0.17em}\dots ,\left(i_j,j_k\right),\hspace{0.17em}\dots \right\}\in \text{Ω,}$$ (8)

where Ω denotes the set of all possible OEs, called the OE domain. Note that an OE ω ∈ Ω contains more information than its corresponding set of complete data n̂(ω)∈Θ. This is due to the fact that ω not only constitutes the emission counts n̂_ij(ω), but also includes the presumed location of each registered event k. The basic idea of how to employ OEs for MMSE reconstruction can now be stated as follows.

Given an OE ω ∈ Ω, let n_i(ω) denote the number of events assigned to volume element i.

The MMSE estimate for emission count of volume element i then transforms to

$$\begin{array}{c}E\left[n_i|{\mathit{n}}^{*}\right]=\sum _{\widehat{n}\in \Theta }{n}_i\left(\widehat{\mathit{n}}\right)\mathcal{P}\left(\widehat{\mathit{n}}|{\mathit{n}}^{\text{*}}\right)=\sum _{\widehat{\mathit{n}}\in \Theta }{n}_i\left(\widehat{\mathit{n}}\right)\left\{\sum _{\omega \in \text{Ω}}\mathcal{P}\left(\widehat{\mathit{n}}|\mathit{\omega ,}{\mathit{n}}^{\text{*}}\right)\mathcal{P}\left(\mathit{\omega }|{\mathit{n}}^{\text{*}}\right)\right\}\\ =\sum _{\omega \in \text{Ω}}\left\{\sum _{\widehat{\mathit{n}}\in \Theta }{n}_i\left(\widehat{\mathit{n}}\right)\mathcal{P}\left(\widehat{\mathit{n}}|\mathit{\omega }\right)\right\}\mathcal{P}\left(\text{ω}|{\mathit{n}}^{\text{*}}\right)=\sum _{\omega \in \text{Ω}}{n}_i(\mathit{\omega })\mathcal{P}\left(\mathit{\omega }|{\mathit{n}}^{*}\right),\end{array}$$ (9)

see equation (6). Here, we used that P (n̂|ω, n*) = P (n̂|ω). This holds true since the acquired data n^* are included in the OE ω. Further, P (n̂|ω) = 1 if and only if n̂=n̂(ω), i.e. if the complete data n̂∈ Θ are consistent with the OE ω ∈ Ω. Finally, if n̂=n̂(ω), it is n_i (n̂) n_i (ω), also.

In summary, the MMSE estimate for the emission counts n_i can be obtained by weighted averaging over the OE domain Ω, instead of the complete data domain Θ. To use this approach for MMSE-OE reconstruction, we need: (1) an expression for the OE posterior P (ω|n*), and (2) an efficient way to compute the MMSE estimate (9).

2.2. Derivation of the origin-ensemble posterior

We derive an expression for the OE posterior P (ω|n*) by investigating the statistical connection between an OE ω ∈ Ω and its corresponding set of complete data n̂(ω)ϵΘ. To simplify the notation, we write n instead of n̂(ω), keeping in mind that such OE complete data are not to be confused with the actual, unobservable complete data. Furthermore, we denote by λ any potential emission density in the image domain. Such emission density is, yet again, not to be confused with the unobservable, true emission density.

By applying Bayes’ theorem and marginalizing λ out, the posterior probability of OE complete data n immediately transforms to

$$\mathcal{P}\left(\mathit{n}|{\mathit{n}}^{\text{*}}\right)=\frac{\mathcal{P}\left({\mathit{n}}^{*}|\mathit{n}\right)\mathcal{P}(\mathit{n})}{\mathcal{P}\left({\mathit{n}}^{*}\right)}=\frac{\mathcal{P}\left({\mathit{n}}^{*}|\mathit{n}\right)}{\mathcal{P}\left({\mathit{n}}^{*}\right)}\underset{\mathbf{\lambda }}{\int }{\mathcal{P}}_{\mathbf{\lambda }}(\mathit{n})\text{d}\mathcal{P}\left(\mathbf{\lambda }\right).$$ (10)

Here, P (n*|n) represents the probability to observe the acquired data n^* given complete data n, which is a certain event (in the stochastical sense), since n is constructed from n* through the OE ω. Ƥ_λ(n) represents the probability of complete data n conditioned on the particular emission density λ, as stated in equation (2). Ƥ (λ) represents prior information about the emission density, typically given in the image domain.

A decomposition of Ƥ_λ(n) into two separate factors φ and ψ, the first independent of, and the latter dependent on λ, now yields Ƥ_λ(n) =φ(n)ψ(λ, n), where

$$\phi (\mathit{n})=\prod _{i,j}\frac{{\alpha }_{ij}^{n_{ij}}}{n_{ij}!},$$ (11)

$$\psi \left(\mathbf{\lambda },\mathit{n}\right)=\prod _i{\lambda }_i^{n_i}{\text{e}}^{-{\epsilon }_i{\lambda }_i}.$$ (12)

By inserting φ and ψ into equation (10), we then obtain the proportional relationship

$$\mathcal{P}\left(\mathit{n}{|\mathit{n}}^{*}\right)\propto \phi (\mathit{n})\underset{\mathbf{\lambda }}{\int }\psi \left(\mathbf{\lambda },\mathit{n}\right)\text{d}\mathcal{P}\left(\mathbf{\lambda }\right).$$ (13)

The integral on the right-hand side of (13) is to be evaluated for the specific prior at hand. Three demonstrative examples can be found in Sitek (2012). In this work, we use a simple flat prior, Ƥ_f(λ) ≡ const. This leads to

$${\mathcal{P}}_{\text{f}}\left(\mathit{n}{|\mathit{n}}^{*}\right)\propto \phi (\mathit{n})\prod _i\frac{n_i!}{{\epsilon }_i^{n_i}},$$ (14)

where multiplication is performed over all i ∈ {i : ε_i > 0} (see Sitek (2012, appendices B and C)). The investigation of other priors is beyond the scope of this work.

At this junction, it is important to note that there are usually multiple OEs ω₁, …, ω_D that correspond to the same set of OE complete data n. We illustrate this by the following example. Consider the basic four-detector, four-voxel PET scheme depicted in figure 2. Here, three events k = 1, 2, 3 are registered during data acquisition, the first by detector pair j = 1, the latter two by detector pair j = 2. The observed incomplete data are thus ${\mathit{n}}^{*}=\left\{n_1^{*}=1,n_2^{*}=2,n_3^{*}=\cdots =n_6^{*}=0\right\}.$. For simplicity, we assume perfect collinearity of annihilation photons, hence α₁₅ = α₂₆ = α₃₁ = α₄₃ = 0. Consequently, event k = 1 could have occurred in any of the volume elements i = 1, 2, 4, and events k = 2, 3 in any of the volume elements i = 1, 2, 3, 4. There are, therefore, 3 × 4 × 4 = 48 possible OEs ω = {(i₁, j₁), (i₂, j₂), (i₃, j₃)}, where i₁, i₂, i₃ are the locations, and j₁, j₂, j₃ are the corresponding detector pairs of the registered events k = 1, 2, 3, respectively. Notably, one obtains two different OEs ω₁ and ω₂ by exchanging the locations of events k = 2 and k = 3. Such OEs are, however, deemed equiprobable, and correspond to the same set of complete data n. The 48 possible OEs thus correspond to 48/2 = 24 sets of complete data. The actual emission counts n = {n₁₁ = 1, n₁₂ = 1, n₁₃ = ··· = n₄₁ = 0, n₄₂ = 1, n₄₃ = ··· = n₄₆ = 0}, for example, are represented by the OEs ω₁ = {(1, 1), (1, 2), (4, 2)} and ω₂ = {(1, 1), (4, 2), (1, 2)}. Since ω₁ and ω₂ are deemed equiprobable, we conclude that Ƥ(ω₁|n*) = Ƥ(ω₂|n*) =1/2 Ƥ(n|n*).

Figure 2.

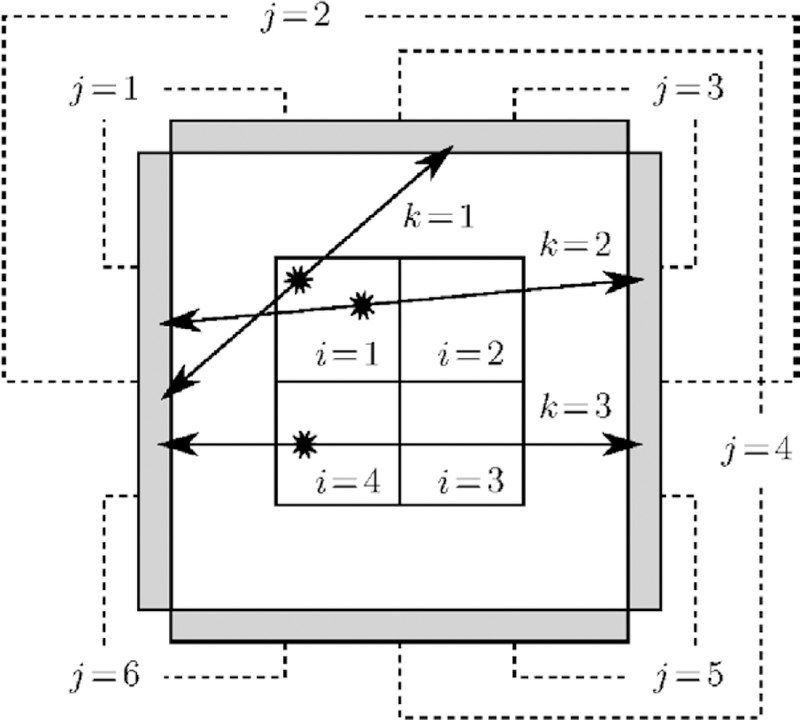
Four-detector, four-voxel PET system (schematic drawing). Three events k = 1, 2, 3 are detected during data acquisition, yielding incomplete data ${\mathit{n}}^{*}=\left\{n_1^{*}=1,n_2^{*}=2,n_3^{*}=\cdots =n_6^{*}=0\right\}.$ Perfect collinearity of annihilation photons is assumed, hence α₁₅ = α₂₆ = α₃₁ = α₄₃ = 0. Consequently, there are 48 possible OEs, and 24 sets of potential complete data. For example, the actual, unobservable emission counts n = {n₁₁ = 1, n₁₂ = 1, n₁₃ = ··· = n₄₁ = 0, n₄₂ = 1, n₄₃ = ··· = n₄₆ = 0} are represented by the OEs ω₁ = {(1, 1), (1, 2), (4, 2)} and ω₂ = {(1, 1), (4, 2), (1, 2)}.

It can be shown by similar, more general combinatorial considerations that for each set of potential complete data n ∈ Θ, there are

$$D=\prod _j\frac{n_j^{*}!}{\prod _i{n}_{ij}!}$$ (15)

equiprobable OEs ω₁, …, ω_D (see Sitek (2012, equation(10)). With this, we can state the fundamental statistical connection

$$\mathcal{P}\left({\mathit{\omega }}_1{|\mathit{n}}^{*}\right)=\cdots =\mathcal{P}\left({\mathit{\omega }}_D|{\mathit{n}}^{*}\right)=D^{-1}\cdot \mathcal{P}\left(\mathit{n}|{\mathit{n}}^{*}\right)$$ (16)

we sought to derive. Note that the computationally problematic terms n_ij! cancel each other out in the final equations (see equations (11), (13), (15) and (16)). For the flat prior, we obtain the particular relationship

$${\mathcal{P}}_{\text{f}}\left(\mathit{\omega }|{\mathit{n}}^{*}\right)\propto \prod _i\frac{n_i!}{{\epsilon }_i^{n_i}}\prod _j{\text{α}}_{ij}^{n_{ij}}.$$ (17)

As demonstrated below, this expression for the OE posterior is completely sufficient for MMSE-OE image reconstruction without a priori information.

3. Algorithmic methods

3.1. Origin-ensemble reconstruction via Metropolis-Hastings sampling

In practical applications, the number of registered events is typically on the order of 10⁶–10⁷, the number of volume elements being on the order of 10⁵–10⁶. Under such circumstances, the large number of possible OEs renders averaging over the entire OE domain Ω practically impossible. Markov chain Monte Carlo (MCMC) methods are a means to circumvent this technical barrier. In particular, they allow to leave out OEs with a low posterior probability in equation (9). In this way, it is possible to perform MMSE-OE reconstruction using a manageable number of OEs. In the following, the basic concept behind MCMC is recapitulated briefly, focusing on its application to the problem at hand. A general introduction to MCMC methods can be found in Andrieu et al (2003) and Brooks (1998).

In MCMC, an irreducible, aperiodic Markovian sequence is simulated on the underlying state space so that it asymptotically reaches a unique, predefined equilibrium distribution. We here consider a sequence of OEs

$${\mathit{\omega }}_0,{\mathit{\omega }}_1,{\mathit{\omega }}_2,\dots ,$$ (18)

and set the equilibrium distribution to be Ƥ (·|n*), i.e. the OE posterior. When the sequence (18) approaches equilibrium, the chance to find it in state ω ∈ Ω approaches P (ω|n*), likewise. In equilibrium, the states ω_s, s ϵ ℕ₀, can be treated as independent samples from the OE posterior. In combination, this yields

$$\frac{1}{S-S_0}\sum _{s=S_0}^S{n}_i\left({\mathit{\omega }}_s\right)\underset{S\to \infty }{\to }\mathbb{E}\left[n_i|{\mathit{n}}^{*}\right]$$ (19)

for every S₀ ϵ ℕ₀ and all i almost surely (in the stochastical sense), by the strong law of large numbers (see Brooks (1998, p 70) or Andrieu et al (2003, p 8)). The limit theorem (19) is the theoretical basis for MMSE-OE reconstruction via MCMC. In particular, we employ the left-hand side of (19) as an approximation to the MMSE estimate 𝔼 [n_i|n*]. The practical meaning of S₀ is explained in section 3.3.

Various strategies have been proposed for the simulation of the Markov chain (18). For the problem at hand, the Metropolis-Hastings technique (Metropolis et al 1953, Hastings 1970) is of particular interest. This technique requires the desired distribution Ƥ (·|n*) to be known only up to a multiplicative constant. This is convenient, since the large size of the OE domain usually renders a normalization of the OE posterior impracticable, as indicated above. Transitions of the Markov chain are here carried out in two steps. Based on the current state ω, a random new state ω′ ∈ Ω is first drawn from a proposal distribution

$$Q\left(\cdot |\mathit{\omega }\right):\text{Ω}\to \left[0,1\right],{\mathit{\omega }}^{\prime }\mapsto Q\left({\mathit{\omega }}^{\prime }|\mathit{\omega }\right).$$ (20)

Subsequently, the proposed state ω′ is stochastically accepted with an acceptance probability

$$A\left({\mathit{\omega }}^{\prime }|\mathit{\omega }\right)\in \left[0,1\right].$$ (21)

If the proposed state is rejected, the chain simply remains in its current state. In this work, we use the standard Metropolis acceptance probability

$$A\left({\mathit{\omega }}^{\prime }|\mathit{\omega }\right)=\min \left\{1,\frac{\mathcal{P}\left({\mathit{\omega }}^{\prime }|{\mathit{n}}^{*}\right)}{\mathcal{P}\left(\mathit{\omega }|{\mathit{n}}^{*}\right)}\cdot \frac{Q\left(\mathit{\omega }|{\mathit{\omega }}^{\prime }\right)}{Q\left({\mathit{\omega }}^{\prime }|\mathit{\omega }\right)}\right\}.$$ (22)

Here, Q (ω|ω′) denotes the probability to propose a transition to state ω when the Markov chain is in state ω′, while Q (ω′|ω) is the probability to propose a transition to state ω′ when the Markov chain is in state ω. The above choice of A ensures that Ƥ (·|n*) is an equilibrium distribution to the arising Markov chain, regardless of the choice of Q (see Brooks (1998, pp 72–3), for example). Equation (22) is the basis for the implementation used in this work, as detailed below.

State proposal and stochastical acceptance are typically repeated a certain number of times, to ensure that the Markov chain is aperiodic. This is usually necessary to decorrelate the samples (see below). Furthermore, the design of the proposal distribution Q should be so that any state of the OE domain can be reached via transitions of the Markov chain, i.e. so that the Markov chain is irreducible on Ω. Uniqueness of and convergence to the equilibrium distribution Ƥ (·|n*) are then guaranteed (Meyn and Tweedie 1994).

In this work, we generate random new states ω′ that differ from their predecessor ω solely

the location of a single event k. Let the respective event locations be i′ and i. For the flat prior, the ratio of state probabilities in equation (22) then simplifies to

$$\frac{{\mathcal{P}}_{\text{f}}\left({\mathit{\omega }}^{\prime }|{\mathit{n}}^{*}\right)}{{\mathcal{P}}_{\text{f}}\left(\mathit{\omega }|{\mathit{n}}^{*}\right)}=\frac{{\text{α}}_{i^{\prime }{j}_k}}{{\text{α}}_{i{j}_k}}\cdot \frac{{\epsilon }_i}{{\epsilon }_{i^{\prime }}}\cdot \frac{n_{i^{\prime }}(\mathit{\omega })+1}{n_i(\mathit{\omega })},$$ (23)

see equation (17). Further, it can easily be seen that an arbitrary state $\widehat{\omega }\in \text{Ω}$ can be reached from any other state ω ∈ Ω by moving each event k = 1, …, K from its location in ω to the location specified in ω̂. Therefore, we repeat state proposal and stochastical acceptance exactly K times, i.e. as often as there are registered events, to yield both aperiodicity and irreducibility of the Markov chain (18). We call one such pass a sweep of the OE algorithm.

For the purpose of MMSE-OE reconstruction, we propose the following two modifications to the original OE updating scheme of Sitek (2008, 2011, 2012) and Sitek and Moore (2013): (1) sequential updating of all event locations (so-called single-site updating) may be used. Such linear iteration over the events allows for a very fast data access, and is of minor impact on the behavior of the Markov chain (18) since all events can be treated as statistically and geometrically almost independent of one another (see Leahy and Qi (2000)). (2) We leave the proposal distribution Q as a free parameter of the algorithm, a potential choice of which is presented in section 3.2. Since in this work the proposal of volume elements depends solely on the considered event, and is independent of the current event location, Q_k(i′) shall denote the probability to propose volume element i′ as a possible new location for event k.

3.2. Including time-of-flight information into the origin-ensemble algorithm

As an example, we present our method in the setting of a two-dimensional, pixelized reconstruction area, where each detector pair j is characterized by an LOR connecting the two respective detectors. However, our approach can easily be applied in 3D settings as well, and works for more general volumes of response (VORs) and different types of volume elements in essentially the same way (see the comments at the end of this section).

Each line of response j is uniquely defined by its two endpoints $x_j^{\left(1\right)}$, $x_j^{\left(2\right)}\in {ℝ}^2$, and there-fore possesses the parametrized representation

$${\mathbf{\gamma }}_j:\left[0,1\right]\to {ℝ}^2,t\mapsto x_j^{\left(1\right)}+t\cdot \left\{x_j^{\left(2\right)}-x_j^{\left(1\right)}\right\}.$$ (24)

In the following, we concentrate on the system matrix elements α_ij, into which TOF information is included in statistical image reconstruction. These elements are computed on-the-fly in practice, since full storage of the very large and sparse system matrix is usually not practicable. The computation of a single matrix element α_ij is here based on determining the length of the segment of LOR j within pixel i, denoted by l_ij. In particular, one uses the proportional relationship

$${\text{α}}_{ij}\propto l_{ij}=\underset{{\mathbf{\gamma }}_j}{\int }{1}_i\text{ds,}$$ (25)

where 1_i is the indicator function of pixel i ⊂ℝ².

When TOF information is available, it can be incorporated into the reconstruction algorithm by introducing a TOF weight function ${\tilde{\mathcal{N}}}_k$ on the LOR of each event k. To account for measurement uncertainties, ${\tilde{\mathcal{N}}}_k$ is chosen to be approximatively Gaussian, i.e.

$${\tilde{\mathcal{N}}}_k\left({\mathbf{\gamma }}_{j_k}\left(t\right)\right)\approx \frac{1}{\sqrt{2\pi {\sigma }_k^2}}{\text{e}}^{-\frac{1}{2}{\left[\frac{t-{\mu }_k}{{\sigma }_k}\right]}^2}.$$ (26)

Note that γ_jk (t) can be mapped to t ∈ [0, 1], since γ_jk is injective. The mean μ_k ∈ [0, 1] determines the most likely position of event k on its LOR j_k. The standard deviation σ_k is attributed to both the individual length of LOR j_k and the TOF estimation accuracy of the scanner. Specifically, μ_k and σ_k can be precomputed based on the distance between $x_{j_k}^{\left(1\right)}$ and $x_{j_k}^{\left(2\right)}$, and the arrival time difference of the annihilation photons. Relation (25) then transforms to

$${\text{α}}_{i{j}_k}^{\left(\text{TOF}\right)}\propto l_{{}_{i{j}_k}}^{\left(\text{TOF}\right)}=\underset{{\mathbf{\gamma }}_{j_k}}{\int }\left(1_i\cdot {\tilde{\mathcal{N}}}_k\right)\text{ds},$$ (27)

see figure 3.

Figure 3.

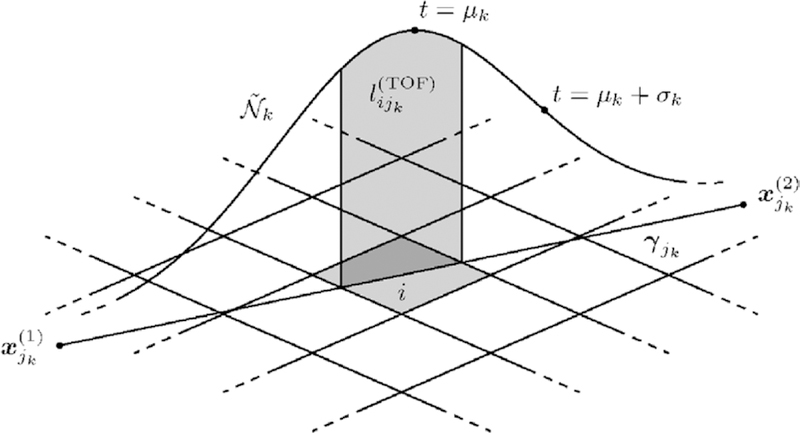
Incorporation of TOF information into the OE algorithm (schematic drawing). The shaded area under the TOF weight function ${\tilde{\mathcal{N}}}_k$ is directly proportional to the TOF-weighted system matrix element ${\text{α}}_{i{j}_k}^{\left(\text{TOF}\right)}$, as well as approximately equal to the probability to propose pixel i as a new location for event k, Q_k(i).

When inserting the ratio of OE posteriors in equation (23) into the acceptance probability A in step 6 of the OE algorithm, it becomes apparent that a sensible restriction to impose on the proposal distribution Q_k is

$$Q_k\left(i\right)\propto l_{i{j}_k}^{\left(\text{TOF}\right)}\propto {\text{α}}_{i{j}_k}^{\left(\text{TOF}\right)}.$$ (28)

Since relation (27) describes the dependence of ${\text{α}}_{i{j}_k}^{\left(\text{TOF}\right)}$ upon volume element i exclusively, relation (28) yields the cancellation of the proposal probabilities Q_k(i) and Q_k(i′) with the system matrix elements in the acceptance probability A, i.e.

$$\frac{{\text{α}}_{i^{\prime }{j}_k}^{\left(\text{TOF}\right)}}{{\text{α}}_{i{j}_k}^{\left(\text{TOF}\right)}}\cdot \frac{Q_k\left(i\right)}{Q_k\left(i^{\prime }\right)}=1.$$ (29)

This can reduce the computational expense of the OE algorithm significantly.

Condition (28) can in practice be met with sufficient accuracy in the following way: Considering an event k, a random number t ∈ [0, 1] is first drawn from a distribution as similar as possible to the TOF weight function ${\tilde{\mathcal{N}}}_k$. This yields a point γ_jk (t) on LOR j_k. Provided that the point γ_jk (t) lies inside the reconstruction area, the pixel i that contains γ_jk (t) is determined, and proposed as a new location for event k. The probability to propose pixel i as a new location for event k, Q_k(i), is then approximately equal to the integral on the right-hand side of equation (27). In this work, for example, we sample t directly from the Gaussian on the right-hand side of equation (26), and repeat random number generation if t ≠ ∈ [0, 1], or if γ_jk (t) does not lie inside the reconstruction area. Notably, in the above procedure, the system matrix elements are not evaluated explicitly.

To close this section, we elaborate how the presented approach can be used for different types of volume elements. For pixels/voxels, we find it advisable to scale, rotate, and translate the coordinate system so that all pixel/voxel coordinates are integers. This allows to determine the pixel/voxel that contains the generated point γ_jk (t) by simple rounding operations. In the case of overlapping volume elements, such as blobs, one oftentimes deals with multiple volume elements i₁, …, i_B containing the generated point γ_jk (t). In such situations, there are the following two options: either one determines all volume elements i₁, …, i_B that contain the generated point γ_jk (t), and randomly selects one of them according to their basis function values at γ_jk(t), or alternatively, one selects one of the volume elements i₁, …, i_B by sampling from the uniform distribution on the index set {1, …, B}. While the first method allows to completely avoid the evaluation of system matrix elements, the second method facilitates a fast selection of a new location for the considered event. Notably, in the second method, one has to evaluate the system matrix elements for the two event locations only, which can be computationally less expensive than sampling from a multinomial distribution, as is required in the first method.

Finally, note that the presented technique can be used as well if there is no TOF information available. In this case, the condition on Q_k is

$$Q_k\left(i\right)\propto l_{i{j}_k}\propto {\text{α}}_{i{j}_k},$$ (30)

and t can readily be drawn from the uniform distribution on [0, 1].

3.3. Generating the initial origin ensemble

When carried to convergence, the results of Metropolis-Hastings MCMC do not depend on the initial state of the underlying Markov chain, since this chain is constructed so that it eventually converges to its designated equilibrium distribution from any starting point with nonzero probability (Hastings 1970, Meyn and Tweedie 1994, Brooks 1998). In practice, however, only a limited number of MCMC samples is used. Since the incipient behavior of the Markov chain usually does not reflect the designated equilibrium distribution, a large number of samples is often discarded to avoid an inferential bias of the starting values (Brooks 1998, section 3.1). In many cases, the duration of this burn-in phase is heavily dependent upon the choice of starting values: if the initial state of the Markov chain lies in a region of low probability density (or probability mass, respectively), it can take a long time until the chain has reached equilibrium, and the subsequent sampling phase can be initiated. In section 3.1, we introduced the parameter S₀ in equation (19) to specify the duration of the burn-in phase. Since we are interested in keeping the burn-in period as short as possible, it is advisable to include all prior information available into the MCMC starting values.

We demonstrate our approach using LORs again, and note that a generalization to VORs is possible. As proposed by Sitek (2008, 2011, 2012) and Sitek and Moore (2013), it is sufficient to initially assign each event k = 1, …, K to an arbitrary volume element i with a_ijk > 0. However, this can result in a weak starting state of the OE Markov chain. When TOF information is available, it should be used to improve the starting state. In particular, we recommended to initially assign each event k to the volume element i that contains the TOF-estimated event location µ_k = γ_jk (µ_k), see figure 3, provided that this point lies inside the reconstruction area. As indicated in section 3.2, μ_k is the most likely position of event k on its LOR j_k. If μ_k does not lie inside the reconstruction area, we propose to trace the entire ray of event k in the image domain, and assign event k to the volume element i with the maximum TOF-weighted system matrix entry ${\text{α}}_{i{j}_k}^{\left(\text{TOF}\right)}$. The resulting initial state ω₀ is very likely to have a high posterior probability Ƥ_f (ω₀|n*). This is due to the fact that Ƥ_f (ω₀|n*) is directly proportional to the system matrix elements ${\text{α}}_{i{j}_k}^{\left(\text{TOF}\right)}$, see equation (17), and events are preferably assigned to volume elements with large system matrix elements in the above procedure.

There is no direct way to check whether the Markov chain (18) has reached equilibrium. We propose the state entropy

$$\mathcal{H}(\mathit{\omega })=-\sum _i\frac{n_i(\mathit{\omega })}{K}\log \frac{n_i(\mathit{\omega })}{K},$$ (31)

Shannon (1948), as an indicator of whether the MCMC sampling phase should be initiated (K is the total number of events in ω). The entropy ℋ is a measure of the disorder of events in the image domain: a low entropy indicates that the events are clustered in particular volume elements, whereas a large entropy suggests that the events are uniformly distributed over the image domain. Therefore, an OE of a high entropy is assumed to contain little information about the emission density, which is typically nonuniform. Hence, we recommend to initiate the sampling phase when the entropy has reached its minimum (see section 5.1).

3.4. Corrections for random coincidences and scattered events

Suppose that for each registered event k = 1, …, K we know the probability π_k that k is a true coincidence. There is then a 1 − π_k chance that k is a scattered event (a scatter), or a random coincidence (a random). There are 2^K possibilities to select a subset of the K registered events presumed to contain true events only. For example, if just three events k = 1, 2, 3 are detected, possible subsets are ∅, {1}, {2}, {3}, {1, 2}, {2, 3}, {1, 3}, and finally {1, 2, 3} (total of 2³ = 8 subsets). We can generally use the subset indicator χ = {χ_k} ∈ {0, 1}K to represent such subsets: χ_k = 1 indicates that k is a true event, whereas χ_k = 0 indicates that k is a scattered event or a random coincidence. Since all registered events are assumed to be statistically independent from one another (see section 3.1), we can assign the posterior probability

$$\mathcal{P}(\mathbf{\chi }|{\mathit{n}}^{*})=\prod _k{\pi }_k^{{\chi }_k}{\left(1-{\pi }_k\right)}^{\left(1-{\chi }_k\right)}$$ (32)

to each subset χ. The posterior Ƥ (χ|n*) is the probability that subset χ represents the true events of n^*. For instance, suppose that π₁ = 0.9, π₂ = 1 and π₃ = 0.99 in the above example. The chance that subset χ = {1, 1, 0} represents the true events is then Ƥ (χ|n*) = π₁·π₂· (1 − π₃) = 0.009.

A naive approach to correct for randoms and scatters in MMSE-OE reconstruction would be to compute the posterior expectation E[·|χ, n*] for each possible subset χ. The MMSE estimate for the number of true events in volume element i could then be obtained by weighted averaging of the form

$$\mathbb{E}[n_i|{\mathit{n}}^{*}]=\sum _{\mathbf{\chi }}\mathcal{P}(\mathbf{\chi }|{\mathit{n}}^{*})\mathbb{E}[n_i|\mathbf{\chi },{\mathit{n}}^{*}].$$ (33)

This approach, however, is obviously impracticable.

A different approach to random and scatter corrections is to switch between different event subsets while the OE algorithm is running. From a conceptional point of view, it is clear that the chance to draw a sample of subset χ should be approximately $\mathcal{P}(\mathbf{\chi }|{\mathit{n}}^{*})$ after burn in of the Markov chain. One such technique was first proposed by Sitek (2011), and later investigated superficially by Sitek and Kadrmas (2011). The procedure is very simple: each time an event k is considered by the OE algorithm, a Bernoullian trial is performed to decide whether k is a true event, or a random or scatter. Specifically, by chance π_k the event k is stochastically moved to a random new location, and by chance 1 − π_k it is temporarily removed from the OE. If an event has been removed from the OE, it is automatically re-added to its former location immediately before the next Bernoullian trial. We examine the feasibility of this approach in sections 4–6.

To close this section, we show how to precompute π_k for each event k. Given the estimated contributions of randoms (r _jk ), scatters (s _jk ), and true events (t _jk ) in detection bin j_k, the value of π_k can readily be calculated as

$${\pi }_k=1-\frac{\mathbb{E}\left[r_{j_k}+s_{j_k}|{\mathit{n}}^{*}\right]}{\mathbb{E}\left[r_{j_k}+s_{j_k}+t_{j_k}|{\mathit{n}}^{*}\right]}.$$ (34)

The contribution of randoms can be estimated e.g. using a delayed coincidence window technique (Rahmim et al 2004). The contribution of scatters can be estimated e.g. using Single Scatter Simulation (SSS), in which scatter sinograms are simulated and appropriately scaled using the outside-of-body scatter tail (Accorsi et al 2004, Watson 2007). The denominator in equation (34) can be estimated from the data n^*. Alternatively, it is possible to employ a fast reconstruction technique (OSEM, for instance) to reconstruct a prior image, which is then forward projected to the projection domain to obtain an estimate for the number of counts in each event detection bin.

4. Application to phantom data

4.1. Phantom and phantom measurement

A phantom scan was performed on a commercial TOF PET/CT scanner (GEMINI TF, Philips Medical Systems, Cleveland, Ohio). For this scan, the standard IEC NEMA Body Phantom (National Electrical Manufacturers Association 2007) was used (see figure 4). The phantom body was filled with 59.2 MBq of 18F-fluorodeoxyglucose (¹⁸F-FDG) dissolved in water. This was done 1329 s prior to the PET scan. To simulate hot lesions, the four smallest spheres were also filled with ¹⁸F-FDG dissolved in water, using four times the activity concentration of the background. The two largest spheres were filled with nonradioactive water for cold lesion imaging. The phantom was positioned on the patient table such that the centers of the spheres were located in the same transaxial plane. A conventional transmission image was then acquired using the CT. The phantom was moved further into the gantry, so that the sphere centers were located in the central plane of the PET unit. A single station of LM-TOF PET data with a total of 20.2 million coincidence events was then acquired during 1.5 min of scan time.

Figure 4.

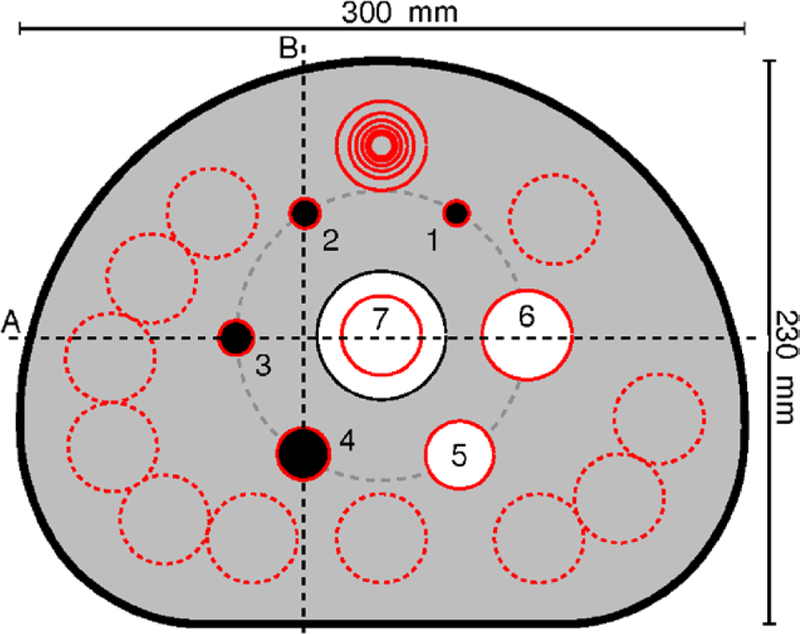
Transaxial cross section through the center of the spheres inside the IEC NEMA Body Phantom (schematic drawing). The four smallest spheres (1–4) represented hot lesions, the two largest spheres (5 and 6) cold lesions. For image quality assessment, a circular ROI was drawn on each sphere, the ROI diameter being as close as possible to the internal diameter of the sphere. A 30 mm circular ROI was drawn on the lung insert (7). Twelve ROIs of each size were drawn on the warm phantom background. Two profile lines (A and B) were drawn on the phantom.

4.2. Image reconstruction

3D LM-TOF PET reconstruction was performed using the OE algorithm, as well as 1000 iterations of the standard EM algorithm (Rahmim et al 2004). Reconstruction was performed with and without random and scatter corrections. CT-based attenuation correction (CTAC) was used in all reconstructions. Other corrections were for TOF timing variation, detector dead time, varying detector efficiency due to detector geometry and variations in crystal efficiency, and radioactive decay. Scattered event contributions were estimated using SSS (Accorsi et al 2004, Watson 2007). Random coincidence contributions were estimated using a delayed coincidence window technique (Rahmim et al 2004, section 4). Random and scatter contributions were included into the ML-EM algorithm as described in (Rahmim et al 2004, section 4.1). For demonstration purposes, the native ML-EM image was used to precompute the probability of each event being random or scattered, required for random and scatter corrections in the OE algorithm (see section 3.4). In particular, the native ML-EM image was forward-projected to each event detection bin, yielding the denominator on the right-hand side of equation (34). For random number generation in the OE algorithm, a Mersenne Twister pseudo random number generator (Matsumoto and Nishimura 1998) of type MT11213B was used.

The reconstruction area consisted of blobs (blob radius = 10 mm, blob center increment = 8.15 mm), arranged on a body-centered cubic (BCC) 75 × 75 × 26 grid (Matej and Lewitt 1995). In ML-EM reconstruction, on-the-fly computation of the system matrix elements was performed using LORs, as described in Matej and Lewitt (1996). In MMSE-OE reconstruction, single system matrix elements were computed in the same manner (see section 3.2, penultimate paragraph). Following reconstruction, the blob images were converted to 144 × 144 × 45 voxel images using a Kaiser-Bessel window function of shape parameter α = 8.3689 (see Matej and Lewitt (1996)). The voxel size in the final images was 4 × 4 × 4 mm³.

After each sweep of the OE algorithm, the entropy H defined in equation (31) was calculated to decide whether the sampling phase should be initiated (see section 3.3). Convergence of the MMSE-OE and ML-EM blob image was then studied in terms of the Euclidean metric

$${\Vert {\widehat{\mathbf{\lambda }}}^{\left(S\right)}-{\widehat{\mathbf{\lambda }}}^{\left(S-1\right)}\Vert }_2=\sqrt{\sum _i{\left[{\widehat{\lambda }}_i^{\left(S\right)}-{\widehat{\lambda }}_i^{\left(S-1\right)}\right]}^2,}$$ (35)

where λ̂^(S) denotes the blob image after drawing S samples from the OE Markov chain, and S iterations of the ML-EM algorithm, respectively.

4.3. Image quality measures

To evaluate and compare the image quality achieved by MMSE-OE and ML-EM reconstruction, the NEMA NU 2–2007 protocol for image quality assessment (National Electrical Manufacturers Association 2007, section 7) was used. The NEMA NU 2–2007 guidelines were designed to emulate whole-body ¹⁸F-FDG imaging in a clinical setting. Note that the above described experimental setup, as well as the scan parameters slightly differ from the NU 2–2007 guidelines (see Discussion). The NEMA NU 2–2007 image quality assessment comprises the evaluation of (1) contrast recovery (CRV), (2) background variability (BV), and (3) the residual count error in the lung insert. The residual count error in the lung insert is evaluated in order to examine the accuracy of random and scatter corrections (see National Electrical Manufacturers Association (2007, section 7.4.2)). For evaluations (1)–(3), the following preparations were made in MATLAB R2012a (The MathWorks Inc., Natick, Massachusetts).

In the transaxial slice through the centers of all spheres (see figure 4), a circular region of interest (ROI) was drawn on each sphere, such that the ROI diameter was as close as possible to the internal diameter of the sphere. In addition, a circular 30 mm ROI was drawn on the lung insert. Twelve circular ROIs of each size were then drawn on the phantom back-ground. These background ROIs were automatically replicated to transaxial slices ± 12 mm (equivalent to ± 3 voxels) and ± 24 mm (±6 voxels) away from the sphere centers. Thus, in total, 60 ROIs were drawn on the phantom background for each sphere diameter. The 30 mm ROI on the lung insert was automatically replicated to 10 transaxial slices in increments of 4 mm on both sides of the sphere centers. Finally, two profile lines were drawn on the phantom. CRV, BV, and residual count error in the lung insert were then evaluated in MATLAB R2012a as described by the National Electrical Manufacturers Association (2007, section 7).

For a better visual perception, all transaxial slice images shown below are scaled to 1000 × 1000 pixels, using bicubic interpolation. The emission density profiles correspond to these images. For evaluations (1)–(3), the images were also scaled to 1000 × 1000 pixels, but this time using nearest-neighbor interpolation. In this way, partial pixels could be taken into account, and ROI movements in increments of less than 1 mm were facilitated.

5. Results

5.1. Convergence and runtime

Figure 5 shows two transaxial images of the OE initial state, generated (a) without and (b) with TOF information. Note that the incorporation of TOF information into the OE initial state resulted in a state that better resembles the object. Even the shape of the phantom and its different components can be distinguished in the TOF initial state. When TOF information is not used, the events appear more evenly distributed over the image domain. Only the outer shape of the phantom remains vaguely perceivable.

Figure 5.

Transaxial slice through the centers of all spheres inside the IEC NEMA body phantom (magnified). OE initial state generated (a) without TOF information, and (b) with TOF information. The color encodes the number of registered events in each pixel.

Figure 6 shows the Shannon entropy of the MCMC OE states, calculated after each of 20 000 sweeps in both native MMSE-OE reconstruction and MMSE-OE reconstruction with random and scatter corrections. Note that the random and scatter corrected OE states present a consistently lower entropy than the native states. This is line with an expected higher contrast in the corrected MMSE-OE images. The qualitative evolution of the entropy, however, is the same in both runs: after an initial drop (≈ sweeps 1–50), the entropy declines with an approximately constant rate (≈ sweeps 50–500), and finally ceases to decline considerably (≈ sweeps 500–3000). In both runs, the entropy did not change more than 0.0005 after 3000 sweeps (figure 6, ×). At this point, sampling of the Markov chain was initiated.

Figure 6.

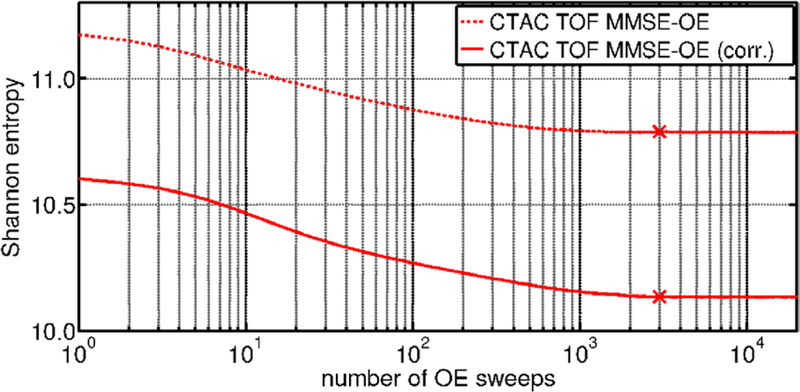
Shannon entropy of the MCMC OE states, calculated after each of 20 000 sweeps of the OE algorithm. Sampling of the Markov chain was initiated after 3000 sweeps in both native MMSE-OE reconstruction and MMSE-OE reconstruction with random and scatter corrections.

Figure 7 shows the difference of the blob image to its predecessor (see equation (35)) calculated each time after drawing a sample from the OE Markov chain, and after each iteration of the ML-EM algorithm, respectively. Note that the blob image difference defined in equation (35) does not depend on the number of registered events, but on the total number of events in the reconstructed images, which is ≈4.56 · 10⁹. We observe that the MMSE-OE images exhibit a much smoother convergence than the ML-EM images. This is due to the fact that MMSE-OE reconstruction is not governed by an objective function in the projection domain, as is the case in ML-EM reconstruction.

Figure 7.

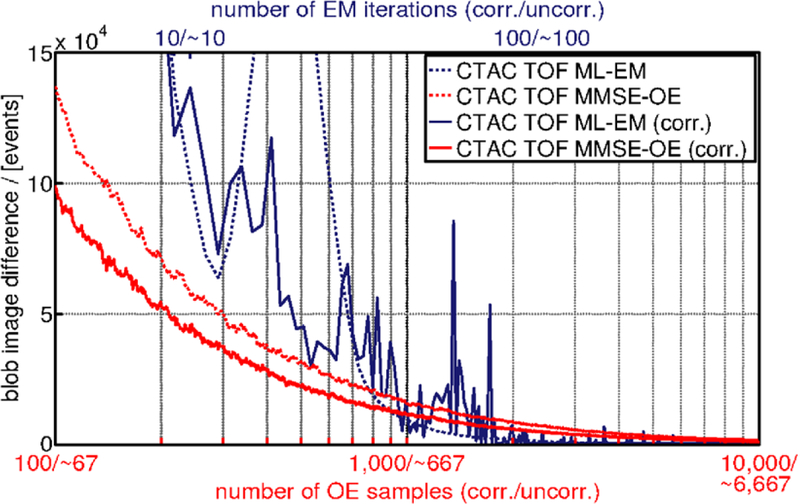
Difference of the blob image to its predecessor, measured each time after drawing a sample from the OE Markov chain, and after each iteration of the ML-EM algorithm, respectively. ML-EM iterations are scaled to MMSE-OE samples with respect to computing time.

In native MMSE-OE reconstruction, the blob image difference was <4500 events after drawing ≈2700 samples from the OE Markov chain. In MMSE-OE reconstruction with random and scatter corrections, this was achieved after drawing ≈2750 samples. When drawing another 1000 samples from the OE Markov chain, for example, this limits the blob image difference to

$${\Vert {\widehat{\mathbf{\lambda }}}^{\left(S+1000\right)}-{\widehat{\mathbf{\lambda }}}^{\left(S\right)}\Vert }_2⩽\sum _{S^{\prime }=1}^{1000}{\Vert {\widehat{\mathbf{\lambda }}}^{\left(S+S^{\prime }\right)}-{\widehat{\mathbf{\lambda }}}^{\left(S+S^{\prime }-1\right)}\Vert }_2<4.5\cdot {10}^6\text{events,}$$ (36)

which corresponds to ≈1‰ of the total number of events in the reconstructed images. Hence, the above convergence criterion is adequate for most practical applications, and can be used for runtime comparison. In ML-EM reconstruction, the above convergence criterion was met after 194 iterations when random and scatter corrections were enabled, and 57 iterations when corrections were disabled. Note that the above iteration/sample numbers are used for runtime comparison, but not for image quality assessment.

On a single CPU (Xeon E5150 @ 2.66 GHz, Intel, Santa Clara, California), the computing time for one sweep of the OE algorithm (total number of 20.2 million processed events) was 18 s on average when random and scatter corrections were disabled, and 12 s when random and scatter corrections were enabled. Note that random and scatter corrections accelerate MMSE-OE by ≈50% of the native reconstruction speed. This is due to the fact that the temporal removal of events from the OE is computationally much cheaper than their stochastical transition to a new location in the image domain. In terms of the number of OE samples, convergence speed remains approximately the same when random and scatter corrections are enabled.

On the same CPU, the computing time of one iteration of the ML-EM algorithm was 278 s on average when corrections were disabled, and 279 s when corrections were enabled. The total reconstruction time thus amounts to (3000 + 2750) × 12 s (=̂ 19 h and 10 min) in MMSE-OE reconstruction with random and scatter corrections, (3000 + 2700) × 18 s (28 h and 30 min) in native MMSE-OE reconstruction, 194 × 279 s (15 h and 2 min) in ML-EM reconstruction with random and scatter corrections, and 57 × 278 s (4 h and 24 min) in native ML-EM reconstruction. In conclusion, using the above convergence criterion, reconstruction time in MMSE-OE reconstruction was approximately 1.3 and 6.5 times longer than required by ML-EM reconstruction when random and scatter corrections were enabled and disabled, respectively.

5.2. Image quality

For image quality assessment, 1000 iterations of the EM algorithm and 10000 samples from the OE Markov chain were used. Figure 8 shows the reconstructed images of the emission density in the transaxial slice through the centers of all spheres inside the Body Phantom.

Figure 8.

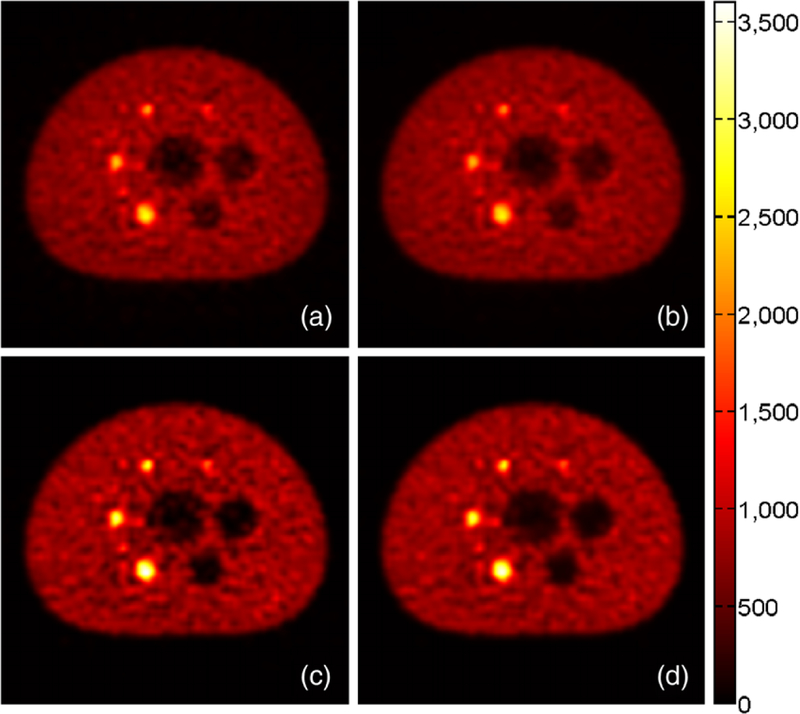
Transaxial slice through the centers of all spheres inside the IEC NEMA Body Phantom (magnified). Image reconstructed by (a) native CTAC TOF ML-EM with 1000 iterations, (b) native CTAC TOF MMSE-OE with 3000 sweeps to equilibrium and 10 000 subsequent samples, (c) CTAC TOF ML-EM with 1000 iterations and random and scatter corrections enabled, and (d) CTAC TOF MMSE-OE with 3000 sweeps to equilibrium, 10 000 subsequent samples, and random and scatter corrections enabled. The color encodes the reconstructed emission density in units of events per pixel.

The ML images (a) and (c) look remarkably similar to the corresponding MMSE images ((b) and (d), respectively). Even the noise speckles are of the same shape and in the same positions in all four images. Note that the native images (a) and (b) exhibit less contrast than the images (c) and (d), which are corrected for random coincidences and scattered events. This is particularly noticeable in the hot-sphere and cold-sphere image regions. In all four images, however, the smallest hot sphere can be distinguished from the warm phantom background.

Focusing on the differences between the ML and MMSE images, we can see that the MMSE images ((b) and (d)) exhibit less intensity variability than the corresponding ML images ((a) and (c), respectively). This is particularly shown by the more homogeneous depiction of the phantom background. The reduced intensity variability of the MMSE images can also be appreciated in the emission density profiles shown in figure 9. The emission density profiles further indicate that ML-EM reconstruction yielded a slightly better hot-sphere CRV than MMSE-OE reconstruction. Note that the OE algorithm slightly overestimated activity concentration in the cold regions of the phantom. This has previously been reported by Sitek (2011) and appears to be characteristic of MMSE-OE reconstruction.

Figure 9.

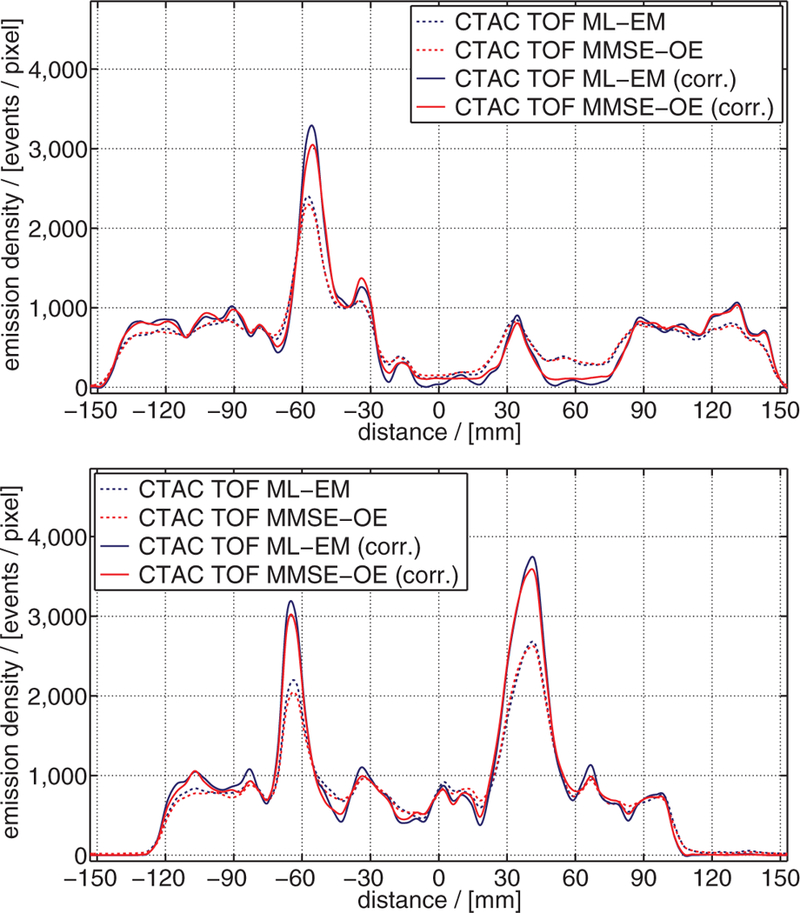
Emission density profiles through the reconstructed images of figure 8, as indicated in figure 4: (top) profile line A, (bottom) profile line B.

In figure 10, CRV, BV, and the residual count error in the lung insert are shown for all four reconstruction methods. Confirming the above observations, ML-EM reconstruction yielded a slightly better CRV than MMSE-OE reconstruction. In particular, ML-EM hot-sphere CRV was 2.5 ± 1.0%, and cold-sphere CRV 4.4 ± 1.6% higher than in MMSE-OE reconstruction. Note that the above-mentioned overestimation of activity concentration in cold regions slightly reduced the cold-sphere CRV in MMSE-OE reconstruction. It can further be seen that random and scatter corrections improved the CRV in ML-EM and MMSE-OE reconstruction to almost the same extent. This improvement becomes apparent especially in cold-sphere CRV (improvement of ≈30% in both ML-EM and MMSE-OE reconstruction). BV is consistently lower in the MMSE than in the ML images. In particular, the background exhibits 1.0 ± 0.2% less variability in the MMSE images than in the ML images. This quantitatively confirms the observed lower intensity variance in the MMSE images. Note that random and scatter corrections slightly increased BV in both the MMSE and the ML images. Finally, we can see that random and scatter corrections reduced the residual count error in the lung insert in all transaxial slices investigated. The residual count error was reduced by 6.3 ± 1.2% in ML-EM, and by 5.6 ± 1.2% in MMSE-OE reconstruction. The slightly better performance of random and scatter corrections in ML-EM reconstruction are, yet again, attributable to the overestimation of cold-region activity concentration in MMSE-OE reconstruction.

Figure 10.

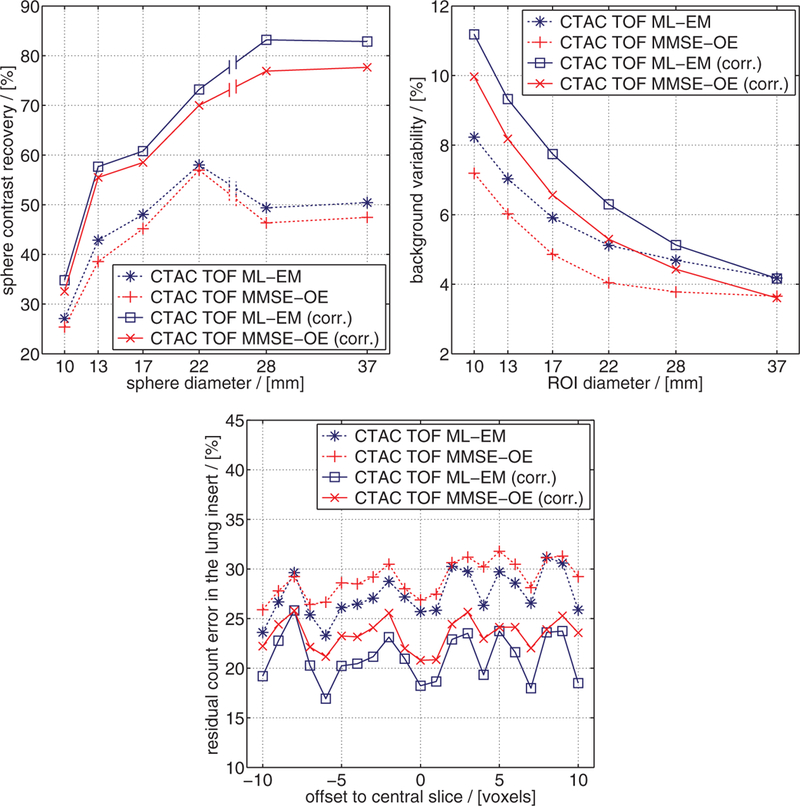
Results of the NEMA NU 2–2007 image quality assessment: (top left) CRV, (top right) BV, and (bottom) residual count error in the lung insert.

Figure 11 compares the trends in CRV and BV of the 13 mm hot sphere 2 (figure 4) and the 28 mm cold sphere 5 for both ML-EM and MMSE-OE reconstruction with an increasing number of EM iterations and OE samples, respectively. In ML-EM reconstruction, we observe the typical trade-off between CRV and BV in both cases: starting from relatively low values, both CRV and BV gradually increased during reconstruction, until convergence was attained. In MMSE-OE reconstruction, on the other hand, we observe a different behavior. Here, CRV remained approximately the same for both spheres, while BV gradually decreased as more and more samples were drawn from the OE Markov chain. Eventually, MMSE-OE reconstruction converged to a point nearby the respective CRV-BV curve of the EM algorithm. Very similar trends were obtained for all other sphere inserts inside the Body Phantom.

Figure 11.

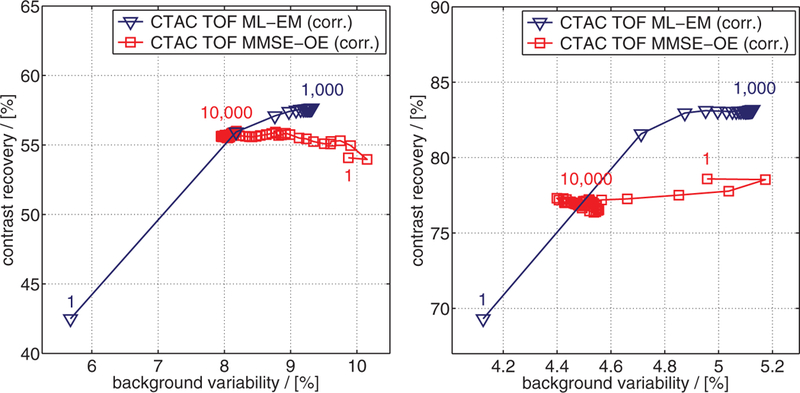
CRV/BV of (left) 13 mm hot sphere 2 and (right) 28 mm cold sphere 5, computed after 1, 5, 10, 15, …, 1000 EM iterations, and after drawing 1, 50, 100, 150, …, 10 000 samples from the OE Markov chain, respectively.

6. Discussion and outlook

The OE algorithm provides a novel view on statistical reconstruction in emission tomography. In this work, the OE approach was investigated in the context of image reconstruction. However, the OE algorithm further provides an approximation to the entire OE posterior (see sections 2.2 and 3.1). Hence, without significant additional computations, the OE algorithm can also be used to estimate the posterior variance of the emission counts in each image element, or in user-defined ROIs (see Sitek (2011) and Sitek and Moore (2013)). The OE algorithm therefore provides a complete statistical characterization of the data. This can be utilized for further data processing, e.g. in kinetic analysis and image registration. Such statistical characterization of the data is not easily obtainable with standard iterative ML methods, especially for LM data.

An important question beyond the scope of this work is how to parallelize the OE algorithm, or, alternatively, distribute the reconstruction task to multiple computation nodes. A great advantage of the common ML reconstruction methods is their inherent potential for parallelization. This potential is one of the reasons why EM and CG algorithms are the preferred reconstruction methods in PET today. Parallelization/distribution of Metropolis-Hastings MCMC is, on the other hand, not as straightforward, and various approaches exist. In the present case, a promising approach is the many-short-runs technique (see Brooks (1998, section 3.3)). In this technique, several independent Markov chains are run in parallel (the short runs). As compared to the one-long-run technique, the sampling phase in each short run is reduced, ideally by a factor on the order of the total number of short runs. This and other techniques for parallelization of MMSE-OE reconstruction poses an interesting topic for further research.

Due to the large variety of optimization strategies for Metropolis-Hastings MCMC, not all of the latter have been considered in this work. A frequently employed method to account for the autocorrelation of the MCMC Markov chain is called thinning (see Brooks (1998, section 3.2)). In this method, only every mth sample of the Markov chain is used, thereby ‘thinning out’ the correlated sample. We did not use thinning in this work, since the results in Sitek and Moore (2003, section 3.2) imply that MMSE-OE reconstruction does not benefit from this technique. On the contrary, thinning increases the computational cost of MCMC, and has previously been reported to reduce the accuracy of MCMC estimates (see Link and Eaton (2012), for instance). However, it is conceivable that other MCMC optimization strategies will prove beneficial for the runtime and performance of the OE algorithm.

Again, note that the experimental setup, as well as the scan parameters described in section 3 slightly differ from the NEMA NU 2–2007 guidelines. However, this is of minor impact on the image quality comparison in section 4.2, since all tests were performed with the same data. The particular protocol for image quality assessment (National Electrical Manufacturers Association 2007, section 7) was strictly followed. Small deviations in CRV, BV, and the residual count error in the lung insert due to small inaccuracies in e.g. ROI positioning or numerical rounding errors are negligibly small. Such deviations are, therefore, not depicted in figures 10 and 11.

The results of the image quality assessment demonstrate that the final MMSE images exhibit less BV, but also a slightly lower CRV than the corresponding ML images. As previously reported, the OE algorithm appears to slightly overestimate activity concentration in cold regions. However, the final MMSE-OE image quality is almost as good as that of ML-EM reconstruction. In ML image reconstruction, a spatial regularization technique is typically used to suppress noise artifacts in the reconstructed image (Leahy and Qi 2000). However, such regularization can over-smooth edges and small image details. In order to maintain lesion detection performance and activity concentration quantification accuracy of PET, a lot of effort has recently been put into developing adequate smoothing techniques (e.g. non-local regularization techniques, such as the method presented by Wang and Qi (2012)). Interestingly, in MMSE-OE reconstruction, one is faced with a different problem: the question that arises is how contrast can be increased without amplifying the noise in the image. One way to achieve this is through the use of a suitable prior (see section 2.2). In this work, we used a simple flat prior to ensure comparability of MMSE-OE and standard ML-EM reconstruction. We expect that other priors will enable us to increase the contrast while keeping noise amplification to a minimum. Note that for any such prior, a closed form of the OE posterior is required. Three priors for which a closed form of the OE posterior is available are the truncated flat prior, the conjugate prior, and the Jeffreys prior (see Sitek (2012)). Further research on how these and other priors affect the final image quality will have to be conducted.

In this work, MMSE-OE and ML-EM reconstruction were applied to phantom data with a total count number typically dealt with in clinical PET imaging (≈106–108 registered events). Another interesting question is how MMSE-OE reconstruction performs in low-count experiments (≈104–106 registered events). The results in Sitek (2012, section 5.1) suggest that the OE algorithm performs well in such situations in terms of CRV and BV. We expect that the MMSE-OE reconstruction time scales almost linearly with the total number of registered events. However, a thorough comparison between MMSE-OE and ML-EM image quality in low-count experiments is yet to be undertaken.

Finally, one of our main motivations in investigating MMSE-OE reconstruction is to include anatomical a priori knowledge into the reconstruction process. Such anatomical knowledge is usually obtained with CT or MRI, and can be incorporated into the reconstruction algorithm to improve image quality and activity concentration quantification accuracy (see Somayajula et al (2011) and Vunckx et al (2012), for example). We have recently employed the emerging Dixon MRI technique (Ma 2008) for fat-constrained whole-body ¹⁸F-FDG imaging, using the working hypothesis that adipose tissue metabolism is low in glucose consumption (see Prevrhal et al 2014a, 2014b). An interesting question for further research is how this and other approaches can be realized using MMSE-OE image reconstruction. In general, we expect the OE algorithm to pose an excellent framework for the inclusion of anatomical knowledge into the reconstruction process: adequate modifications to the MCMC transition kernel (see sections 2.2 and 3.1) can encourage or prevent event movements into particular volume elements. In this manner, it is possible to shift activity into particular image regions, without having to face a trade-off between data fidelity in the projection domain and bias in the image domain.

Appendix A. List of abbreviations

BCC

body-centered cubic

BP

backprojection

BV

background variability

CG

conjugate gradient

CPU

central processing unit

CRV

contrast recovery

CT

computed tomography

CTAC

CT-based attenuation correction

EM

expectation maximization

FBP

filtered backprojection

FDG

fluorodeoxyglucose

FP

forward projection

IEC

International Electrotechnical Commission

LM

list mode

LOR

line of response

MAP

maximum a posteriori probability

MCMC

Markov chain Monte Carlo

ML

maximum likelihood

MMSE

minimum mean square error

MRI

magnetic resonance imaging

NEMA

National Electrical Manufacturers Association

OE

origin ensemble

OSEM

ordered-subset expectation maximization

PET

positron emission tomography

ROI

region of interest

SD

standard deviation

SSS

Single Scatter Simulation

TOF

time-of-flight

VOR

volume of response