Alchemical Grid Dock (AlGDock) calculations in the D3R Grand Challenge 3: Binding Free Energies between Flexible Ligands and Rigid Receptors

Abstract

We participated in Subchallenges 1 and 2 of the Drug Design Data Resource (D3R) Grand Challenge 3. To prepare our submissions, we performed molecular docking with UCSF DOCK 6 and binding potential of mean force (BPMF) calculations — free energy calculations between flexible ligands and rigid receptors — using our open-source software package Alchemical Grid Dock (AlGDock). For each system, submissions were based on the minimum BPMF calculated for a selected set of crystal structures. In Subchallenge 1, our workflow performed poorly. Possible reasons for the poor performance include the neglect of cooperative ligands and limited sampling of ligand binding poses. In Subchallenge 2, our workflow led to some of most highly correlated submissions (Pearson R = 0.5) for vascular endothelial growth factor receptor 2. However, our results were poorly correlated for Janus Kinase 2 and Mitogen-activated protein kinase 14. Affinity prediction could potentially be improved by systematic selection of more diverse receptor configurations.

1. Introduction

As is evidenced by the existence of and participation in the Drug Design Data Resource (D3R) grand challenges, methods for predicting noncovalent binding poses and free energies for protein-ligand complexes remain an important goal in computer-aided molecular design. The most common approach to these types of predictions are based on molecular docking, in which a search for low-energy binding poses is followed by evaluating the poses with a scoring function.

Based on the D3R 2018 workshop presentations and evaluation results [1], it appears that the most successful methods in the D3R Grand Challenge 3 incorporated prior knowledge about binding poses and/or affinities. These types of calculations, however, have important limitations. First, knowledge-based scoring functions depend on the availability of applicable training data. Second, if scores are based on a single structure of a protein-ligand complex, they may not be able to realistically incorporate entropy. The lack of realistic entropy terms may impose an upper limit on their potential accuracy. Hence, the development of purely physics-based methods remains a worthy pursuit.

The majority of physics-based binding pose and affinity predictions in the D3R Grand Challenge 3 were based on molecular docking or the molecular mechanics/Poisson-Boltzmann surface area (MM/PBSA) method [2,3]. The latter method is based on simulations of the complex and, sometimes, the isolated binding partners. Normal modes analysis is sometimes used to estimate entropy changes. Unfortunately, large-scale calculations have shown that binding free energies estimated by MM/PBSA have only weak correlation with experiment [4]. Moreover, the accuracy of MM/PBSA is known to be dependent on the system and sensitive to parameters [5].

A more accurate (e.g. [6]) but computationally expensive class of physics-based methods are alchemical binding free energy calculations [7]. In these calculations, a ligand is transmuted between different variants (for relative binding free energies) or between a bound and unbound state (for absolute binding free energies) through a series of non-physical, or alchemical, thermodynamic states. Performing simulations in all these thermodynamics states is computationally costly. Likely for this reason, very few submissions to the D3R Grand Challenge 3 were based on alchemical binding free energy calculations.

Implicit ligand theory (ILT) [8,9] is a framework that has the potential to enable faster and more scalable binding free energy calculations. According to ILT, the standard binding free energy may be expressed as an exponential average of the binding potential of mean force (BPMF) — the binding free energy between a flexible ligand and rigid receptor configuration. If receptor configurations represent the unbound ensemble, then BPMFs may be used to compute absolute binding free energies [8]. If configurations are obtained from a bound ensemble, then BPMFs can be used to compute binding free energies relative to the ligand that defines the ensemble [9]. ILT-based free energy calculations have the potential to be faster and more scalable because they are based on BPMFs. BPMFs are faster than free energy calculations with a fully flexible receptor because they require sampling of significantly fewer degrees of freedom and because receptor-ligand interactions can be precomputed on a three-dimensional grid and subsequently interpolated [10–12]. Grid interpolation also makes BPMF calculations highly scalable; once the grid is computed, interpolation operations are largely independent of the size of the receptor.

We have developed an open-source computer program, Alchemical Grid Dock (AlGDock) [13,14], to compute protein-ligand BPMFs. As in many other free energy calculations, AlGDock uses Hamiltonian replica exchange [15–17]. It also treats protein-ligand interactions by interpolating a precomputed three-dimensional grid [10–12] in most intermediate thermodynamic states. (We have also developed algorithms to estimate BPMFs based on the fast Fourier transform [18]).

Prior to our participation in the D3R Grand Challenge 3, we had taken steps towards but had not successfully applied fully rigorous ILT-based binding free estimation to complex ligands and binding sites. We have successfully applied AlGDock to estimating binding free energies between a small hydrophobic cavity in the T4 lysozyme L99A mutant and 141 fragment-like organic molecules [19]. We have also computed BPMFs for the Astex Diverse Set, a curated subset of 85 protein-ligand complexes in the Protein Data Bank with pharmaceutical or agricultural relevance [20]. Some of these systems have complex ligands and binding cavities. BPMFs appeared to converge in a large fraction but not all of the systems. At this point, we still have not developed efficient methods for selecting appropriate receptor snapshots from molecular simulations or a set of crystal structures and properly weighting them to estimate binding free energies. Due to the combined factors of our incomplete methods development and the time limitations built into the challenge, we decided not to pursue rigorous binding free energy calculations based on multiple properly weighted BPMFs. Instead, we decided to assess how the minimum BPMF for multiple rigid receptor structures would fare in the blinded challenge.

With the available human and computational effort, we were able to complete and submit submissions to Subchallenge 1 and 2 of Grand Challenge 3. Subchallenge 1 consisted of pose and affinity prediction for ligands of Cathepsin S. Subchallenge 2 consisted of affinity prediction for ligands of vascular endothelial growth factor receptor 2 (VEGFR2), Janus Kinase 2 (JAK2), and Mitogen-activated protein kinase 14 (p38-α).

2. Methods

2.1. Structural Bioinformatics

For each protein, structures of highly homologous proteins available in the Protein Data Bank (PDB) were downloaded and analyzed. The observed binding poses in these structures were used to define the center and radius of a spherical binding site. Moreover, for Subchallenge 2 submissions, BPMFs were computed between each ligand and a subset of the downloaded structures.

MODELLER [21] 9.18 was used to identify protein sequences in the PDB with at least 90% homology to each template sequence. Template sequences for each receptor were UniProt [22] identifiers P25774 for Cathepsin S, P35968 for VEGFR2, O60674 for JAK2, Q16539 for p38-α. The number of structures downloaded for each receptor were 29, 34, 34, and 225, respectively. The specific structures downloaded are given in the “Homologous Structures” subsection of the “Supplementary Methods“ section in Online Resource 1.

To facilitate the binding site definition and selection of a representative subset, the homologous structures were aligned to an arbitrary template structure. These templates were 3IEJ (chain A) for Cathepsin S, 4ASE (chain A) for VEGFR2, 4IVA (chain A) for JAK2, and 3FMK (chain A) for p38-α. Each homologous structure was aligned to the template structure to minimize the root mean square deviation (RMSD) of α carbon atoms using ProDy [23] 1.8.2.

After the homologous structures were aligned, a spherical binding site was defined based on the observed ligand positions.

In AlGDock and other alchemical binding free energy calculations [7], it is common to define the binding site based on the ligand center of mass. Even if individual ligand atoms protrude outside of the site, a ligand is considered bound if its center of mass is within the binding site. To define this site, we first calculated the center of mass of each crystallographic ligand. The binding site radius was defined by computing the largest distance between a ligand center-of-mass and the binding site center (d_max) and rounding up to the nearest Ångstrom.

For example, in Cathepsin S, because the maximum ligand COM distance from the site center was 2.45 Å, the site radius was calculated as 3.0 Å. The binding site radius for JAK2, VEGFR2, and p38-α were calculated as 3, 6, and 8 Å, respectively. Because the calculated sizes were small for Cathespin S and JAK2 (likely due to limited diversity in crystallized ligands), we manually expanded the radius to 6 Å.

We attempted to select representative crystal structures based on clustering, but because of an indexing error we ended up with an essentially random subset of snapshots. Hierarchical clustering with complete linkage was performed based on the RMSD between coordinates of backbone atoms within the binding site. The indices of residues that fit this criterion are given in the “Binding Site Residues” subsection of the “Supplementary Methods“ section in Online Resource 1. The calculations were performed using scipy.cluster from scipy [24] 0.19.0.

2.2. System Preparation

Ligands were prepared using OpenEye Toolkits for Python, version 2.5.1.4. Starting from SMILES strings provided by D3R, ligand protonation states were assigned using the OEGetReasonableProtomer function in quacpac. Threedimensional conformations were generated using omega with 800 maximum conformers, an energy window of 15.0 kcal/mol, and minimum distance of 1.0 Å to distinguish conformers. Ligands were parameterized with the Generalized Amber Force Field [25] 2 in AmberTools 17 [26] and AM1BCC partial charges [27,28].

Protein protonation states were predicted with pdb2pqr 1.9.0 [29] at a pH of 7.0. They were parameterized with the AMBER ff14SB force field using AmberTools 17 [26]. In Subchallenge 1 Stage 1a and Subchallenge 2, the structures selected based on our attempted hierarchical clustering were prepared for docking and BPMF calculations. In Subchallenge 1 Stage 1b, the provided crystallographic structures were prepared. Due to time limitations and because most of the Cathepsin S structures were very similar, only a single structure, WCGQ (chain A), was prepared for Subchallenge 1 Stage 2. Although SO₄ and DMSO were present in some crystal structures for Subchallenge 1, we had no clear way to compare results between structures with and without these additional molecules. Therefore, they were removed from the structures and not considered.

2.3. Molecular Docking

Molecular docking was used to obtain preliminary binding poses and scores between each prepared receptor structure and ligands in the corresponding datasets. Docking was performed using UCSF DOCK 6.6 [30]. First, a molecular surface was generated with UCSF Chimera 1.11 [31]. Next, docking spheres were generated using sphgen, a program within UCSF DOCK 6, with default parameters. A subset of spheres within a half AlGDock grid edge length (see definition below) of the binding site center were retained. A box was generated using showbox, a program within UCSF DOCK 6 that shows the size and location of grids.

The box length was equal to the sum of the maximum distance between any ligand atom to the binding site center and the binding site radius. Docking was performed using the anchor and grow algorithm. Parameters for showbox and docking are given in the “Molecular Docking Parameters” subsection in the “Supplementary Methods“ section of Online Resource 1.

2.4. BPMF estimation

BPMFs were estimated using the version of AlGDock posted on GitHub [14] on Sep 3, 2017. The key algorithms behind AlGDock are described in a 2015 technical report [13]. In brief, BPMF calculations performed by AlGDock involve a thermodynamic cycle that can be divided into two stages: cooling and docking. In the former, the ligand is simulated by itself at different temperatures between the target temperature (300 K by default) and a high temperature (600 K by default). In the latter, the receptor-ligand interactions are gradually scaled in as the temperature is lowered from the high to target temperature.

The version of AlGDock used in this manuscript differs from that described in the technical report [13] in several important ways. As previously described [19], it automatically performs hydrogen mass repartitioning [32,33] and uses a power transformation during grid interpolation [12]. Furthermore, AlGDock now includes two options for treating solvation in intermediate thermodynamic states and an option to restrain ligands to a particular pose.

The two options for treating ligand solvation in intermediate thermodynamic states are Full and Desolvated:

1. In Full BPMF calculations, all thermodynamic states are bathed in generalized Born implicit solvent based on model 2 from Onufriev, Bashford, and Case (OBC) [34].

2. In Desolvated BPMF calculations, the OBC solvent around the ligand is sometimes scaled down and is not used in all thermodynamic states. For the unbound ligand at the target temperature, OBC is fully on. As the temperature of ligand increases, the strength of the implicit solvent is gradually scaled down to zero. Thermodynamic states used to sample the receptor-ligand complex do not include OBC solvent; the ligand is fully desolvated.

These options affect the sampling from thermodynamic states, but OBC solvent is still used for postprocessing in either case.

AlGDock also includes a new option for restraining a ligand to a particular binding pose. A harmonic restraint with a spring constant of 1000.0 kJ/(mol nm)⁻¹ is imposed on the center of mass and 1000.0 kJ/(mol radian)⁻¹ on three additional external degrees of freedom and a non-redundant set of flexible internal torsion angles. The restraint is scaled with a coefficient of a_r = tanh(16a²) as a function of a, which describes the progress of scaling the receptor-ligand interaction grid. We will refer to a BPMF calculated with restraints as a pose-specific BPMF.

AlGDock requires precomputed receptor-ligand interaction energy grids. van der Waals grids were calculated with a spacing of 0.25 Å spanning d_max in each dimension surrounding the binding site center. Electrostatic grids were produced by solving the linear Poisson-Boltzmann equation around the receptor molecule using the Adaptive Poisson-Boltzmann Solver, APBS [35] 1.4, with sequential focusing. Coarse grids were set to be at least 1.5 times larger than the range of the receptor molecule in each dimension. Fine grids were set to have the same size as the van der Waals grids and a spacing of 0.5 Å. Boundary conditions were based on the multiple Debye-Huckel model for the coarse grids and coarse-grid solutions for the fine grids. Both electrostatic grids were generated with the following parameters: chgm = spl4, swin = 0.3, pdie = 2.0, sdens = 10.0, sdie = 80.0, srad = 1.4, srfm = smol, and temp = 300.0.

At the beginning of cooling and docking, poses from UCSF DOCK 6 were minimized (without and with the receptor, respectively) to obtain an initial pose. The temperature was ramped from 20 K to the starting temperature in 30 stages of 1000 molecular dynamics steps. The thermalized pose was duplicated 50 times to generate a set of seeds for the initial thermodynamic state. Subsequent states were initialized using a thermodynamic speed of 25.0 during cooling and 0.25 during docking and randomly selecting 50 seeds from the previous thermodynamic state. From each seed, systems are initialized by 1000 steps of molecular dynamics.

After initialization, replica exchange was conducted for 10 cycles of cooling and 17 cycles of docking. Each cycle consists of 150 iterations of Hamiltonian Monte Carlo [36], external translation and rotation moves (for docking), and replica exchange. Hamiltonian Monte Carlo moves consist of initializing velocities from the Maxwell-Boltzmann distribution, 50 steps of velocity Verlet using a time step of 3.0 fs, and acceptance or rejection based on the Metropolis criterion.

Conformations of the unbound and fully bound states at the target temperature were postprocessed using the OBC model in NAMD [37] 2.10. BPMFs were estimated with a combination of statistical estimators as described [13].

2.5. Pose Prediction

Poses were predicted based on samples from the fully bound thermodynamic state. Ligand configurations from this state were clustered using hierarchical clustering from scipy [24] 0.19.0 with complete linkage and a threshold of 0.1 Å. The medoid was used to represent each cluster. Each cluster was scored by the mean interaction energy within the cluster. The interaction energy was calculated using the OBC model in NAMD [37] 2.10.

2.6. Submissions

We prepared up to three submissions for each stage in Subchallenge 1 and in Subchallenge 2. Two submissions, which we will refer to as the “Desolvated” and “Full” submissions, were based on BPMFs calculated using the corresponding ligand solvation options. If submissions were based on multiple receptor structures, then the lowest BPMF was used for both pose and free energy predictions. The third submission, which we will refer to as “Combination”, was based on pose-specific Desolvated BPMFs for poses predicted by Desolvated and Full BPMFs. The pose-specific BPMF with lowest energy among all receptor structures and both solvation options was submitted.

Subchallenge 1 had three stages. In Stage 1a, BPMFs were calculated between 24 ligands and the five representative Cathepsin S structures. In Stage 1b, they were calculated between the ligand and the provided crystallographic structures for each receptor. In Stage 1, we only submitted pose predictions. In Stage 2, Desolvated BPMFs were calculated between 136 ligands and one crystallographic structure. Poses from the given structures were not used. For six of the ligands, CatS 1, CatS 2, CatS 12, CatS 115, CatS 121, and CatS 122, no docking scores with the crystallographic structure were obtained. These ligands were labeled as “inact” in the submission. Because the lack of numerical values prevented their inclusion in correlation metrics, these submissions were considered to be partial sets on the D3R web page. For Stage 2, we only submitted binding affinity predictions based on Desolvated BPMFs. For Subchallenge 2, BPMFs were calculated between ligands and the representative crystal structures. We submitted three sets of binding affinity predictions based on the Full BPMFs, Desolvated BPMFs, and Combination.

3. Results and Discussion

3.1. Structural Bioinformatics

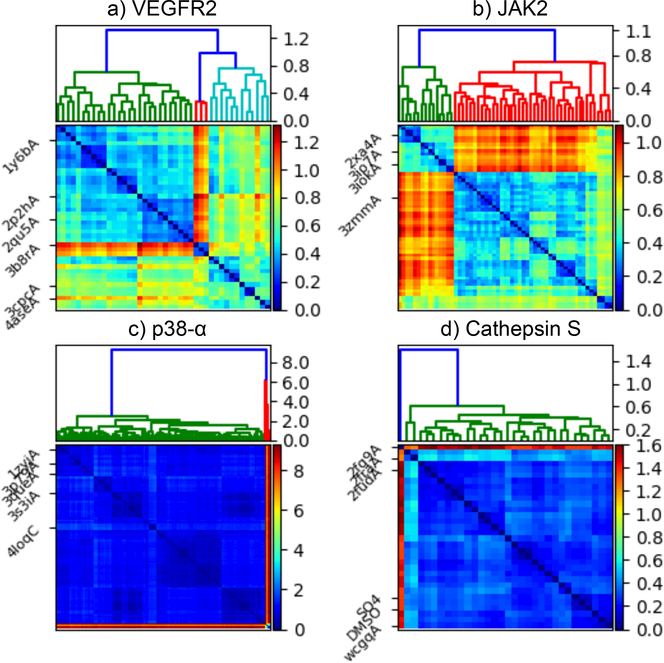
Existing PDB structures for the four receptors exhibit varying degrees of binding site variability (Figure 1). Most Cathepsin S binding sites are fairly similar, with RMSDs of about 0.6 Å or less from each other, but there is an outlier, 2FG9 (chain A), that differs from the others by a RMSD of up to 1.6 Å. VEGFR and JAK2 have similar levels of structural variability, in which several clusters of structures have RMSDs within about 0.5 Å. Most clusters within 0.8 Å of other cluster, but one cluster has an RMSD up to 1.2 Å from the others. p38-α is notable for a small group of structures with a very distinct binding site from the others.

Fig. 1. Analysis of homologous structures in the PDB.

Hierarchical clustering dendrograms (top) and binding site RMSD matrices (bottom) for (a) VEGFR2, (b) JAK2, (c) p38-α, and (d) Cathepsin S. Selected structures are labeled on the left of the RMSD matrices. Except for the SO₄ and DMSO labels for Cathepsin S, which denote the provided structures in complex with the respective ligands, the labels are PDB identifiers.

Due to an indexing error, the selected structures did not always adequately represent the configuration space of publicly available structures. The selected structures for Subchallenge 2 were: 1Y6B (chain A), 2P2H (chain A), 2QU5 (chain A), 3B8R (chain A), 3CPC (chain A), 4ASE (chain A) for VEGFR2; 2XA4 (chain A), 3IO7 (chain A), 3IOK (chain A), 3ZMM (chain A) for JAK2; and 1ZYJ (chain A), 3P79 (chain A), 3QUE (chain A), 3S3I (chain A), 4LOQ (chain C) for p38-α. In Subchallenge 1 Stage 1a, three Cathepsin S structures were selected: 2FQ9 (chain A), 2FRA (chain A), 2FUD (chain A). Additionally, the two provided structures (one with DMSO and one with SO₄) were also used for this stage. By luck, VEGFR2 structures appear to represent a diverse range of structures. However, for the other systems, large groups of known structures appear to be poorly represented. Unfortunately, the indexing error was not evident to us until after completion of the challenge.

3.2. Subchallenge 1

The performance of our workflow in subchallenge 1 was poor. In Stage 1a, the mean and standard deviation of the RMSD for the closest submitted pose for 22 ligands was 11.72 and 3.04 Å, respectively. The performance of pose prediction in Stage 1b was similar. For affinity rankings for 130 ligands in Stage 2 (receipt zfo0t), Kendall’s τ was −0.03 (0.06) and Spearman’s ρ was 0.03 (0.09), with the number in parentheses indicating the standard deviation of the correlation metric.

Several factors could have contributed to the poor results from our workflow. The most upstream factor may have been the neglect of DMSO and SO₄ in the receptor structure. Although we understood that these molecules form critical contacts with the ligands (Table 1), we did not have a procedure to compare results with and without these additional molecules. In the future, it should be possible to develop a binding theory that incorporates cooperativity between ligands and allows us to predict which will bind. Another confounding factor was limited ligand binding pose sampling. In Stage 1b, we only started with a near-native pose, with a RMSD of 3 Å or less from the crystal structure, among the top five DOCK 6 poses in 3 of 24 systems (Table 2). A pose between 3 and 6 Å was sampled but not among the top five for three other systems, CatS 20, CatS 8, and CatS 21. BPMF calculations did not enhance sampling of near-native poses and our submitted poses had an RMSD within 3 and 5 Å for only two (CatS 23 and CatS 17) and four (CatS 23, CatS 17, CatS 15, CatS 20) systems, respectively.

Table 1.

Minimum distances between cosolvent and ligand atoms, based on the 24 Cathepsin S crystallographic structures released by D3R.

PDB ID in D3R database	chain ID	cosolvent	ligand atom id	cosolvent atom id	distance (Å)
tjyg-CatS 2	A	SO4	F41	O1	5.1909
	B	SO4	F41	O2	5.6770
	C	SO4	F41	O3	5.5994
yquj-CatS 17	A	SO4	N80	O3	2.8678
	B	SO4	N80	O4	3.0679
uavh-CatS 20	A	SO4	C98	O1	2.9816
pbwz-CatS 22	A	SO4	N83	O1	2.5988
	B	SO4	N83	O4	2.6058
jjod-CatS 23	A	SO4	N87	O4	2.7566
	B	SO4	N87	O3	2.8651
	C	SO4	N87	O1	2.7855
	D	SO4	N87	O1	2.7641
yqqd-CatS 24	A	SO4	N85	O2	2.5900
gabj-CatS 14	B	DMSO	F46	O	3.3607

Table 2. Cathepsin S Pose Prediction Metrics for Stage 1b.

The RMSD and score for poses from molecular docking (DOCK 6) and Desolvated BPMF calculations (AlGDock). Scores are the grid score for DOCK 6 and mean interaction energy within the cluster for AlGDock. They are in units of kcal/mol.

Ligand ID	pose	AlGDock		DOCK 6
	#	RMSD (Å)	score	RMSD (Å)	Score
CatS 23	1	5.75	−262.79	12.54	−43.41
	2	13.73	−259.32	2.59	−42.16
	3	3.41	−256.04	11.47	−40.79
	4	1.80	−255.51	9.78	−39.71
	5	12.47	−254.91	11.93	−39.63
CatS 17	1	6.80	−157.92	14.26	−42.17
	2	14.73	−157.91	3.81	−41.15
	3	2.21	−123.97	3.07	−40.59
	4	1.91	−122.50	2.74	−40.22
	5	14.28	−121.10	2.23	−39.76
CatS 15	1	12.15	−38.38	1.80	−37.65
	2	12.31	−34.72	9.18	−37.55
	3	13.59	−32.92	10.93	−36.36
	4	3.17	−32.87	10.30	−35.99
	5	10.54	−31.88	9.95	−35.68
CatS 20	1	9.18	−168.10	14.33	−34.54
	2	15.88	−154.47	7.38	−34.01
	3	9.52	−150.43	7.10	−33.90
	4	8.42	−144.01	15.34	−33.71
	5	4.29	−142.85	6.22	−33.68
most native pose	9	–	–	3.36	−31.74
CatS 8	1	11.32	−38.00	11.14	−38.72
	2	5.35	−28.04	11.31	−38.29
	3	12.48	−24.72	11.26	−37.95
	4	10.50	−21.67	11.12	−37.81
	5	12.24	−18.98	10.70	−37.70
most native pose	24	–	–	5.57	−33.74
CatS 21	1	11.32	−40.55	10.62	−40.10
	2	11.39	−36.92	11.33	−35.93
	3	10.44	−10.09	12.81	−35.63
	4	10.24	−9.40	12.91	−34.30
	5	9.75	−8.28	10.09	−33.95
most native pose	29	–	–	4.01	−29.69

These two factors — cooperative ligands and pose sampling — are related, as the neglect of DMSO and SO₄ likely contributed to the limited sampling and poor scores of near-native poses. Even in three of the systems where a near-native binding pose was sampled (CatS 23, CatS 17, and CatS 20), the crystal structure shows a SO₄ within 3 Å from a ligand atom (Table 1). (The crystal structure for the fourth ligand, Cat 15, has no cosolvent in the ligand binding site.) The scores for these near-native poses could have been improved by inclusion of cosolvent in the model. We also could have selected molecular docking parameters to search ligand binding poses more thoroughly. In retrospect, the failure to find any suitable binding poses for some ligands with known affinity should have been a red flag indicating that a more exhaustive search was necessary. Finally, the use of only a single receptor structure may have affected the accuracy of Stage 2. However, because most the provided crystal structures had very similar binding site configurations, this was unlikely to be a major issue.

3.3. Subchallenge 2

For Subchallenge 2, our VEGFR2 results were among the most highly correlated submissions to the D3R. Our entry based on Desolvated BPMFs had the fourth best Kendall’s τ and Spearman’s ρ among 33 entries. Indeed, both the Kendall’s τ of 0.37 (0.09) and Spearman’s ρ of 0.52 (0.12) were within error bars of the entry with the highest correlation metrics; the best entry had a Kendall’s τ of 0.43 (0.09) and Spearman’s ρ of 0.61 (0.11). The performance of Full BPMFs was slightly worse (Table 3). If the minimum BPMF from Desolvated and Full BPMFs was used (this was not submitted), then correlation metrics were comparable.

Table 3. Affinity ranking metrics for Subchallenge 2.

In addition to our submissions to the grand challenge, metrics for other scores are included for comparison: the minimum of Desolvated and Full BPMFs (Minimum), the mean OBC interaction energy observed in BPMF calculations (mean Ψ), and grid scores from UCSF DOCK 6 (DOCK 6).

Receptor	Method	Score Type	Spearman’s ρ	Kendall’s τ	Pearson’s R	Entry ID
VEGFR2	BPMF	Desolvated	0.52(0.12)	0.37(0.09)	0.48(0.11)	0gmqd
		Full	0.42(0.14)	0.3(0.10)	0.49(0.13)	4qmwz
		Minimum	0.46(0.11)	0.31(0.09)	0.52(0.12)	–
	pBPMF	Combination	−0.08(0.15)	−0.06(0.10)	−0.12(0.13)	umw4e
	Mean Ψ	Desolvated	0.35(0.14)	0.22(0.10)	0.31(0.12)	–
	DOCK 6	–	0.43(0.14)	0.30(0.10)	0.41(0.12)	–
JAK2	BPMF	Desolvated	0.11(0.16	0.07(0.11)	0.11(0.14)	24ob4
		Full	−0.09(0.20)	−0.04(0.11)	0.06(0.21)	Jxdme
		Minimum	−0.00(0.20)	0.01(0.15)	0.08(0.20)	–
	pBPMF	Combination	−0.17(0.18)	−0.13(0.13)	−0.23(0.19)	zkt5d
	Mean Ψ	Desolvated	−0.00(0.17)	.01(0.11)	0.08(0.13)	–
	DOCK 6	–	0.04(0.19)	0.02(0.14)	0.04(0.19)	–
p38-α	BPMF	Desolvated	−0.18(0.19)	−0.12(0.14)	−0.24(0.18)	0nqfo
		Full	−0.25(0.18)	−0.16(0.13)	−0.26(0.15)	dzz7p
		Minimum	−0.23(0.19)	−0.15(0.15)	−0.27(0.15)	–
	pBPMF	Combination	−0.09(0.19)	−0.05(0.13)	−0.04 (0.20)	8h4d2
	Mean Ψ	Desolvated	0.01(0.19)	0.02(0.13)	−0.07(0.15)	–
	DOCK 6	–	−0.39(0.15)	−0.24(0.11)	−0.33(0.15)	–

Comparison with simpler affinity estimates suggests that consideration of entropy is an important factor in the strong performance of these entries. In particular, the performance of BPMFs was superior to the performance of mean interaction energies computed with the same force field and minimum interaction energies from the DOCK 6 grid score (Table 3). Neither of these calculations considers the loss of ligand entropy upon binding.

The poor performance of pose-specific BPMFs (“Combination” in Table 3) in VEGFR2 affinity prediction has several possible explanations. One explanation is that the top-scoring pose was not correctly identified or that multiple poses are necessary. The relatively reasonable performance of DOCK 6 scores is evidence against the latter option. Another possibility is that the harmonic restraint used to position the ligand was too strong, eliminating much of the residual entropy.

It is worth noting that all affinity rankings with comparably successful metrics were at least partly knowledge-based. Maxim Totrov’s group used ICM [38] with atomic property fields [39], which are three-dimensional potential energy terms specific to a particular receptor. Alexandre Bonvin used an VEGFR-specific prediction based on ligand similarity. Xiaoqin Zou’s group used a new version of ITScore [40], which is based on statistical potentials. As discussed in his presentation, Guo-wei Wei’s group used a potential based on machine learning. Finally, Carlos Camacho’s group used smina [41], which uses an empirical scoring function. In contrast, the only system-specific information that we used in our structure-based method (we incorrectly labeled entries 0gmqd and 4qmwz as ligand-based) was the size of the binding site. The performance of our method suggests that in ideal cases, physics-based scoring can be competitive with knowledge-based approaches.

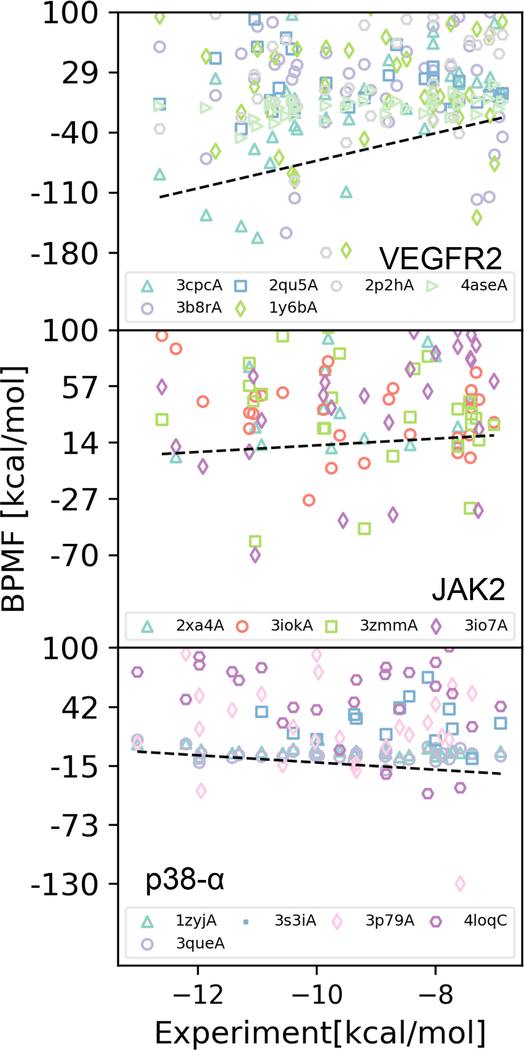
While our workflow worked well for VEGFR2, it was much less successful for JAK2 and p38-α. For these receptors, correlation metrics were weak and often even negative (Table 3). For many ligands, even the lowest BPMF among JAK2 structures was positive (Figure 2). Although most of the lowest BPMFs for p38-α ligands were negative, they were generally not as low as with VEGFR2. The most likely reason for these failures was the limited selection of receptor structures. For all of the receptors, a variety of structures led to the lowest BPMF; it was not the case that a single receptor structure bound all the ligands tightly. Thus, if a more diverse pool of receptor structures were selected, it is likely that at least one of them would bind tightly to a larger range of ligands.

Fig. 2.

Comparison of Desolvated BPMFs and experimental affinities for VEGFR (top), JAK2 (middle), and p38-α (bottom), excluding K_d’s > 10 μM. Marker shapes and color indicate the PDB identifier for the receptor structure with the lowest BPMF.

4. Conclusions

While our overall performance in D3R Grand Challenge 3 was not particularly impressive, we were able to derive a number of lessons that could improve our methodology and our performance in future challenges. From Subchallege 1, we learned that co-crystallizing ligands, especially if they are adjacent to the binding site, should be carefully considered. From Subchallenge 2, the importance of selecting receptor configurations that can bind a diverse set of ligands was evident. In the VEGFR2 dataset, where a representative set of structures was selected, our BPMF-based entries were among the best and competitive with knowledge-based approaches.