TICA: Transcriptional Interaction and Coregulation Analyzer

Abstract

Transcriptional regulation is critical to cellular processes of all organisms. Regulatory mechanisms often involve more than one transcription factor (TF) from different families, binding together and attaching to the DNA as a single complex. However, only a fraction of the regulatory partners of each TF is currently known. In this paper, we present the Transcriptional Interaction and Coregulation Analyzer (TICA), a novel methodology for predicting heterotypic physical interaction of TFs. TICA employs a data-driven approach to infer interaction phenomena from chromatin immunoprecipitation and sequencing (ChIP-seq) data. Its prediction rules are based on the distribution of minimal distance couples of paired binding sites belonging to different TFs which are located closest to each other in promoter regions. Notably, TICA uses only binding site information from input ChIP-seq experiments, bypassing the need to do motif calling on sequencing data. We present our method and test it on ENCODE ChIP-seq datasets, using three cell lines as reference including HepG2, GM12878, and K562. TICA positive predictions on ENCODE ChIP-seq data are strongly enriched when compared to protein complex (CORUM) and functional interaction (BioGRID) databases. We also compare TICA against both motif/ChIP-seq based methods for physical TF–TF interaction prediction and published literature. Based on our results, TICA offers significant specificity (average 0.902) while maintaining a good recall (average 0.284) with respect to CORUM, providing a novel technique for fast analysis of regulatory effect in cell lines. Furthermore, predictions by TICA are complementary to other methods for TF–TF interaction prediction (in particular, TACO and CENTDIST). Thus, combined application of these prediction tools results in much improved sensitivity in detecting TF–TF interactions compared to TICA alone (sensitivity of 0.526 when combining TICA with TACO and 0.585 when combining with CENTDIST) with little compromise in specificity (specificity 0.760 when combining with TACO and 0.643 with CENTDIST). TICA is publicly available at http://geco.deib.polimi.it/tica/.

Introduction

Transcription factors (TFs) are proteins involved in the initiation and regulation of gene transcription. DNA-binding domains present on TFs make them able to bind to specific DNA sequences, such as promoter sequences near transcription start sites (TSSs). Some bound TFs help to form the transcription initiation complex, while others bind distal regulatory regions to either stimulate or repress transcription of the targeted genes [1]. Transcriptional regulation is the most common form of gene control and the action of TFs allows for unique expression of each gene in different cell types and/or during different stages of cell development [1].

Members of TF families often require some interactions with other members from the same or even a different family [2]. These interactions can be of various nature, from protein dimerization and concurrent DNA binding to recruitment or suppression of other TFs’ binding in the proximity of a DNA-binding domain or site [3], [4]. Depending on the choice of partner, nature of the interaction, and cellular context, each interactor triggers a series of regulatory events, thus leading to a particular cellular fate [5]. The binding of TFs to their specific motifs in genomic regulatory regions has been the focus of extensive study; given that only a limited amount of TFs can be encoded in a genome, let alone be expressed at any given moment, combinatorial gene regulation strategies are required to generate diverse expression patterns [6]. Nevertheless, only some combinatorial regulatory effects are known, partially due to the intrinsic complexity of examining all combinations of a large number of TFs and partially due to the many confounding effects that influence TF DNA-binding and co-binding during in vivo confirmation experiments [7]. Thus computational methods provide a powerful supplement to wet-lab experiments in discovering co-regulation phenomena.

In this paper, we present the Transcriptional Interaction and Coregulation Analyzer (TICA), a computational method for in silico discovery of combinatorial TF interaction, based on ChIP-seq data. The “interactions” considered in this study include direct binding between TFs, presence of TFs in the same complex without direct contact between TFs, and blockage of another TF from binding its cognate partners. All three cases mentioned above exhibit co-located peaks in the regulatory region(s) of the cognate target genes of the TFs. Therefore, we look for significant co-located peaks in ChIP-seq datasets for the TFs studied. It is of note that we do not attempt to distinguish between the three kinds of aforementioned interactions or to decipher the regulatory effect of such interactions on the expression of cognate target genes.

We implemented TICA using the genometric query language (GMQL) [8], a high-level, interval-based query language for genomic datasets to support knowledge discovery across genomic repositories. GMQL extends the set of relational algebra operators with domain-specific ones, such as COVER, MAP, and JOIN, which were used to identify valid binding peaks and efficiently detect region hits in the neighbourhood of TF binding sites (TFBSs) and TSSs. Python was used for statistical testing (with modules pandas [9], NumPy [10], and scipy [11]). The TICA implementation is accessible as a web service at http://geco.deib.polimi.it/tica/.

Methods

Conceptual description

TICA combines ChIP-seq peak datasets from a list of TFs in a single cell line and generates interaction hypotheses, that is to say TF pairs that exhibit significant colocation based on experimental data.

Our model was built based on the assumption that interacting TFs must be enriched in co-locating peaks, and in the promoters of their cognate target genes, that is, if two binding sites from two different TFs are in the promoter region of the same TSS, then there is a chance that they regulate the expression of the splicing isoform defined by that TSS. Since physical interaction is directly linked with coregulation [12], we assume that the more such binding sites of two different TFs are found in the promoter region of the same TSS, the more likely these two TFs cooperate (or compete) for the regulation of the same gene. Therefore, TFs are predicted to be interacting if the distance distributions of the TF couples (defined as the number of base pairs intervening between the closest ends of the regions that form the couples) is significantly skewed toward to 0 when compared to those of random TF pairs.

Data pre-processing

Transcription factor binding sites

TICA requires genomic distances between TFBSs to be computed at precision levels close to single-digit base pair lengths, so the preferred format for TICA input data is ENCODE narrowPeak (https://genome.ucsc.edu/FAQ/FAQformat.html\#format12). When multiple samples are given for a single TF in a cell line, we consider as a binding site any region that is found in at least one of the original samples after merging overlaps.

Since TICA can in principle use any point-source binding information, we expect that some peaks in our input datasets could be artifacts or otherwise not significantly different from background noise. In addition, experimental evidence has suggested that TFs exhibit multiple binding sites clustered around target genes [13]. Based on the idea of binding clusters, we screen all binding events in the input dataset and filter out the binding events that do not reach a minimum amount of same binding events in a scanning area of 1 kb upstream and downstream of their boundary, which is set as 3 in our experiments.

Transcription start sites

Transcriptomics studies [14] suggest that not all spliced versions of a given gene are actively transcribed in every single cell line. Thus, TICA uses a two-step filter to select only TSSs that are active in a given cell. First, since TSSs that have a high amount of TF binding in their promoter region are more likely to be transcribed [15], we consider a TSS to be actively transcribed when the number of surrounding TFBSs is above a certain threshold, which is a parameter of the model. For our experiments, we consider a nominal value of 50 TFBSs to be sufficient. Promoter regions are standardized as spanning from −N bases upstream to +M downstream of the TSSs (also parameters of the model; Table 1). Second, evidence for active transcription is given by the presence of certain histone modifications upon or in the area surrounding a TSS, we thus use ChIP-seq broadPeak sequencing data (for reasons discussed in [16]) of the histone marks. These include H3K36me3 (found on the gene body of actively-transcribed genes [17], H3K4me1 (found in enhancer regions of actively-transcribed genes [18]), as well as H3K9ac and H3K4me3 (both found in promoter region of actively-transcribed genes [19]). A TSS is considered actively transcribed if at least one nucleotide base can be found in each of these regulatory regions with the relevant histone mark. GMQL queries for TFBS and TSS filtering are presented in File S1.

Table 1.

List of TICA parameters and related values

Class	Parameter	Chosen value	Category
Genomic dimensions	Gene body length	200 bp	Nominal
	Promoter length	2000 bp	Nominal
Metric constraints	Mindist couple max distance	2200	Computed
Tests and thresholds	Number of points in nulls	10,000	Tuned
	Test P value	0.2	Tuned
	Required number of rejected null hypotheses	1	Nominal
	Minimum number of mindist couples	1	Tuned
	Minimum fraction of mindist couples colocating in a shared promoter	0.01	Tuned

Note: Parameters are classified as nominal, tuned or computed. Nominal values are chosen as standard or reference while tuned values are set according to data analysis methods. The computed mindist couple max distance is defined to be the sum of one standardized promoter length and one standardized gene body length.

Minimal distance couple

We define two binding sites ${\stackrel{-}{x}}_1$ and ${\stackrel{-}{x}}_2$ of two different TFs, TF₁ and TF₂, to be a minimal distance couple (mindist couple) if:

$$d\left({\stackrel{-}{x}}_1,{\stackrel{-}{x}}_2\right)=\underset{x_i\in T_1}{\min }d\left(x_i,{\stackrel{-}{x}}_2\right)$$

AND

$$d({\stackrel{-}{x}}_1,{\stackrel{-}{x}}_2)=\underset{x_j\in T_2}{\min }d({\stackrel{-}{x}}_1,x_j)$$

where $T_1$ and $T_2$ refer to the sets of all binding sites available for TF₁ and TF₂, respectively, and $d(\_,\_)$ is the chromosome-wise base-pair distance on the genome (the distance between TFBSs on different chromosomes is assumed to be infinite). We define d as the mindist couple distance, and we observe that it is well defined for each mindist couple (due to the existence of the minimum of a finite set of numbers). To account for the localized nature of genomic interactions, we impose an upper bound on d, which equals to the sum of one standardized promoter length plus one standardized exon length (Table 1).

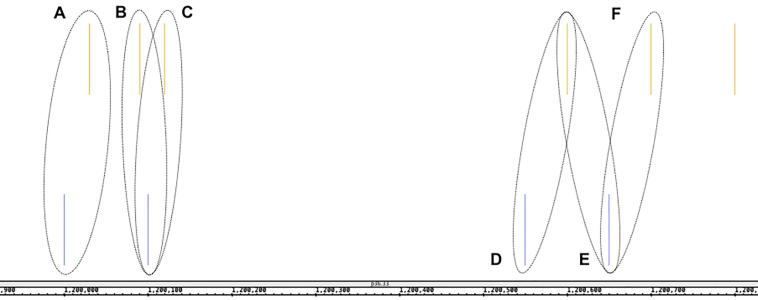
To compute the mindist couple distances, first we merge the lists of binding sites (filtered as described in Data pre-processing section) for the two TFs of interest, keeping track of the source. Then for each of the sorted binding sites (henceforth anchor), we check if two conditions are met: (1) at least one of the two adjacent binding sites belongs to a different (i.e., the other) TF; and (2) the distance from the anchor to at least one of the differently-labeled TFBS is below the aforementioned upper bound. Figure 1 exemplifies the process using synthetic data.

Figure 1.

Example of mindist couple extraction on synthetic TFBS data

The closest binding site fitting the criteria becomes paired with the anchor and forms a mindist couple, and their distance is defined as the couple distance accordingly. If both the adjacent binding sites are valid and tied for the closest, two different mindist couples with identical distance values are generated. If none of the two is valid, no couple is generated and the algorithm then proceeds to the next binding site. Note that a single binding site does not have to belong to only one couple, but any couple formed by the exact same binding sites (in any order) is only counted once. A. The TF2 binding sites (yellow) can only be associated to the first TF1 sample (blue), as the next one in the sorting has the same label. B. and C. TF1 is associated to both TF2 sites. These couples are found twice but only counted once. D. One of the two TF2 sites is out of admissible range for the TF1 site, so only one couple is found. E. and F. Both TF1 sites are equally distant to the anchor TF2 site, both generate a mindist couple.

Prediction algorithm

TICA requires two conditions for TF–TF interaction prediction. First, if two TFs are physically interacting while binding to the genome, their binding sites should generally be found close to each other. If not, their binding sites should be spread widely from one another. Second, most of the TF couples in a cell line are expected to be non-interacting [5]. Therefore, after pairing the closest binding sites between two TFs, interactors should exhibit a distribution significantly skewed toward 0 with respect to random, non-interacting TF couples (Figure 2 and Figure 3).

Figure 2.

Histograms of distance distribution for TF couple CTCF and Myc in HepG2

A. Distance distribution of the TF couple for CTCF and Myc, for which there is no evidence known to support the interaction behavior. B. Zoomed view of the distribution short and long tails. In both panels, blue columns denote the head of the distribution (couples with distance ranging 0–500 bp), red columns denote the short right tail of the distribution (distance >1000 bp), and orange columns denote the long right tail of the distribution (distance >500 bp). Note that the 500-bp tail and 1000-bp tail overlap for the distances >1000 bp. CTCF, CCCTC-binding factor.

Figure 3.

Histograms of distance distribution for TF couple MAX and Myc in HepG2

A. Distance distribution of the TF couple for MAX and Myc, which are well-known interacting TFs. B. Zoomed view of the distribution short and long tails. In both panels, blue columns denote the head of the distribution (couples with distance ranging 0–500 bp), red columns denote the short right tail of the distributions (distance >1000 bp), and orange columns denote the long right tail of the distribution (distance >500 bp). Note that the 500-bp tail and 1000-bp tail overlap for the distances >1000 bp. MAX, Myc-associated factor X.

Following these assumptions, we developed a two-fold test based on mindist couple distribution to predict interactions. Firstly, a deterministic rule excludes TF couples which do not present enough biological information in the datasets. Then, a combination of statistical tests that aggregate information from the distributions is evaluated to determine whether a couple is more skewed than the typical distribution in the same cell line.

Biological information thresholding

The more couples are found to co-locate in the promoter region of the same TSSs, the more likely they actually interact in order to regulate the same genes [20]. Hence, we hypothesize that TF pairs that do not co-locate in a large enough number of sites are unlikely to be interactors; also, if too few couples are found in promoters, the TFs are unlikely to be part of a regulatory module [21]. Therefore, we only consider as valid those predictions where candidates have a high enough amount of mindist couples, and for which the percentage of said couples that co-locate in the same promoter is also sufficiently high. Both these minimum levels are parameters of the algorithm and can be tuned by the users.

Statistical tests

Assuming two candidate TFs offer enough biological information, by pairing all their binding sites we determine their observed distance distribution. To infer whether a physical interaction occurs, we compute test statistics that describe the skewedness of the observed distribution toward zero. The chosen test statistics are median, median absolute deviation (MAD), average, and the long (right) tail size. Median, MAD, and average are well-known centrality measures, whereas the long tail size is to the best of our knowledge a novel contribution to the field (described below).

Right distribution tails

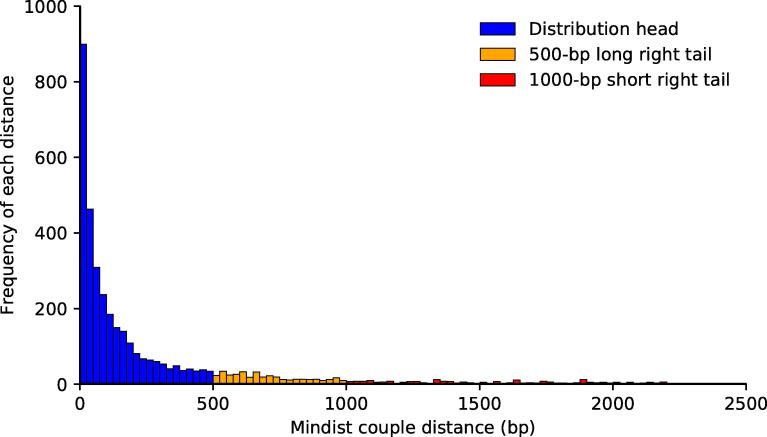
The concept of distribution right long tail can roughly be identified as the points of said distribution which are greater than or equal to a certain threshold value. The key observation is that if two TFs frequently co-locate close to each another, the number of mindist couple that has a large intracouple distance should be low. This is a complement of the reasoning of Jankowski and colleagues [22], [23]: physically interacting TFs show mindist couple distance distributions which are tightly packed around low values, e.g., Myc-associated factor X (MAX) and Myc (Figure 3), whereas randomly picked TF couples give rise to distributions which are significantly more spread out, e.g., CCCTC-binding factor (CTCF) and Myc in Figure 2. In our work, we consider the 1000-bp mark as the starting point for the right tail, whereas the 500-bp mark is more suited to the cases with a lower number of couples available. An example of the shape and size of the right tail for distance distributions is shown in Figure 4.

Figure 4.

Mindist couple distance right tails using TFs ARID3A and ATF1 on cell line HepG2Blue columns denote the head of the distributions, red columns denote the short right tail of distribution

(distance >1000 bp) and orange columns denote the long right tail of the distribution (distance >500 bp). Note that the 500-bp tail and 1000-bp tail overlap for the distances >1000 bp.

P values and null hypotheses

Each statistic is used to test whether or not a candidate couple is significantly different from the respective null distribution. P value for these tests is defined as the fraction of points in the null distribution corresponding to the respective test statistics which are closer to 0 in magnitude. Thus, we reject a certain null hypothesis $H_0$ at P value threshold $p^{\ast }$ (say, 0.05) for test statistic $\theta$ with respect to TF₁ and TF₂ if and only if $\mathit{P}\left({\theta }_0\le \theta \left({\mathit{TF}}_1,{\mathit{TF}}_2\right)\right)\le p^{\ast },$ where P is the empirical frequency measure and ${\theta }_0$ is a generic point in the null distribution generated b $\theta$.

Briefly, we build null distributions for each cell line by randomly sampling candidate couples from a list of background TFs, i.e., those with a TFBS count between the top 10% and bottom 10% marks after filtering (to remove the most extreme combinations) and extracting the mindist couples’ distance distribution (disregarding promoter colocation). We compute each of the four test statistics on such distribution: each of these is a point of the corresponding null distribution to be used in the final test. This process is repeated many times (usually at least 10,000), generating the required null distributions.

TICA tests the aforementioned null hypothesis for a subset of the aforementioned test statistics defined by the user and calls a candidate pair of TFs as interacting if and only if a minimum number of such hypotheses (also defined by the user) is rejected in this way. When testing on 3 out of 4 of the aforementioned statistics (baseline scenario), we selected a P value threshold of 0.20 for all tests associated (Table 1) and detailed reasons for this lax choice are given in File S2.

Validation

To the best of our knowledge, there is no single gold standard for the evidence of physical interactions and/or non-interactions. In particular, it is not clear how one should define a pair of TFs as non-interacting, given that most databases report only positive cases and are potentially incomplete. Nonetheless, two TFs that interact and have binding sites close to each other are expected to be part of the same protein complex. Thus, a positive prediction that is confirmed by a protein complex database is more likely to be correct with respect to one that isn’t.

To investigate this, we confront our predictions with CORUM [24], a catalog of protein complexes in mammalian organisms derived experimentally; we use human core complexes database released on July 2nd, 2017 (http://mips.helmholtz-muenchen.de/corum/#download). We also compared our prediction with a curated list of human protein–protein interactions in BIOGRID [25] as secondary evidence. Details are reported in File S2.

A pair of TFs can be considered as actually positive and supported by CORUM if its components are mentioned together in at least one CORUM complex. We assume that if a certain TF is not mentioned at all in the database then it is not an object of the involved study; therefore, all pairs containing that TF are discarded from the set of predictions that are searched for in the database. Finally, we define a pair of TF as negative if it is not positive and both its TFs cannot be discarded. We also restrict our interactions to complexes/interactions that contain TFs only.

Given the actually positive and negative sets defined above, we compute the recall/sensitivity and specificity measures, which remain invariant when the positive/negative proportion changes in the test data. This is important since we do not have a clear idea of how such positive/negative proportion changes when the databases get updated. We use the geometric mean performance $\mathit{GMP}\stackrel{\mathrm{def}}{=}\sqrt{\mathit{RS}}$ to combine recall and specificity, which works better when the positive:negative split is unbalanced [26].

We also compute the enrichment ratio, defined as recall divided by (1–specificity). The higher the enrichment, the more accurate we can expect the predictions to be. There are, however, some caveats. First, CORUM is incomplete, so the observed recall may be lower than actual when a predicted TF–TF interaction is co-operative or competitive in nature (hence not reported). Second, CORUM also includes complexes that are not involved in gene transcription, so the observed specificity may be lower than actual when a predicted non-interacting TF–TF pair is found as a co-complex pair. At the same time, the observed recall may be higher than actual when some predicted interacting pairs are actually non-interacting. However, since we restrict CORUM proteins to TFs in this study, the latter situation is minimized.

Finally, direct literature investigation allows us to be much more specific about the nature and contents of the evidence supporting a prediction. We perform manual investigation in published studies and literature that support our positive predictions by searching on public interfaces such as PubMed (http://www.ncbi.nlm.nih.gov/pubmed/) for published studies pertaining to a selected subset of interactors. We mark as “confirmed” a positive prediction when there is evidence in the literature, regardless of cell lines, that the two TFs physically bind to each other, bind to the same complex, or there is a statement that they are co-factors or that they compete for the same co-factors or target genes. As the process is time-consuming, we limit our manual checks only to a small subset of predictions for each cell line (Table S1).

Results

TICA parameter choice maximizes recall without sacrificing specificity

We performed several computational experiments using TICA on human ChIP-seq data from various immortalized cell lines to evaluate its performance. Three reference cell lines were tested, including HepG2 (liver carcinoma), K562 (chronic myelogenous leukaemia), and GM12878 (healthy blood cells). Data were downloaded from the ENCODE phase 2 (around 12% of samples) and 3 (around 88% of samples) repositories, using human genome assembly version 19 (hg19) as reference alignment. Table 2 reports the dataset cardinality for each cell line. We fitted our parameters using datasets from HepG2, a cell line with abundance of ChIP-seq libraries available in ENCODE and of gene expression [27], suitable for building null distributions and tuning parameters. Table 1 reports threshold values chosen for each parameter, including the minimal number of minimal distance couples (see Methods) and minimal percentage of TSS co-location. These values have been chosen to maximize recall, since tuning has shown that this choice does not significantly impact specificity.

Table 2.

Dataset cardinalities for all cell lines used in TICA computational experiments

Cell line	No. of available TFs	Total size (after filtering)	No. of active TSSs
HepG2	103	2.95 Gb	97,904
GM12878	102	6.4 Gb	122,854
K562	214	1.97 Gb	59,556

Note: Data are obtained from ENCODE phase 2 and 3 database, narrowPeak format. TSS, transcription start site.

We investigated whether the parameters fitted on HepG2 provide good results on other cell lines as well. To do this, we run TICA on two additional, well-studied cell lines (HEK293 and HeLa-S3) using the HepG2 parameters and ENCODE phase 3 datasets. A good performance was achieved on HeLa-S3 with respect to both databases (3% of possible interactors reported as a complex in CORUM and 8% as a PPI in BioGRID), on par with other cell lines (Table S2). For HEK293, we found out that only 13 TFs available in our ENCODE datasets are found in CORUM; on the other hand, while more than 150 ENCODE TFs are found in BioGRID, only 67 out of ca. 13,000 possible pairs are reported as PPIs (0.5%). We thus conclude that the reference datasets are not adequate enough to be used in validation for HEK293.

Type and number of TICA predictions

We compiled lists of candidate and background TFs for each cell line (Table S3). Candidate pairs are compiled using TFs for which narrowPeak data in the corresponding cell line are available in ENCODE at the time of writing. Due to the way binding sites are matched by TICA (see Methods), we cannot predict homotypic TF–TF interactions (i.e., interactions between TFs of the same kind). Thus, given N TFs for which experimental data are available and assuming the symmetry of interaction phenomena, we have up to N(N − 1)/2 possible tests. We computed all the statistics listed in Methods, requiring at least three of the corresponding tests to be rejected for a prediction to be called positive. Detailed listings of candidates and predicted interactions obtained by running TICA on all cell lines using the default parameters are reported in Table S4.

Enrichment with respect to CORUM is above 1 for all cell lines

Using FANTOM TF list for humans [28], we found 535 TFs out of 3601 proteins in CORUM complexes and 5709 couples of TF–TF interactions. Observing the confusion matrices with respect to CORUM, we note that the number of true negatives (e.g., 1079 in HepG2 data) is much higher than that of false positives (293), and even one to two orders of magnitude higher than that of false negatives (40), indicating that TICA shows very high specificity across all test scenarios.

In Table S2, we report recall, specificity, and enrichment analysis of TICA predictions with respect to CORUM and for all three cell lines and their intersections. We observe that enrichment ratio remains well above 1 for all test scenarios (minimum at 1.505, and almost always above 2.000).

We expect many of our predicted positives that could not be verified using CORUM (i.e., the presumed false positives) to be real positives, which awaits biological validation. For instance, out of the 42 (109–67) sampled positive predictions for HepG2 that were analyzed for CORUM (i.e., both TFs in each of these 42 couples were found in CORUM), 35 (32% of the total) are not reported to be co-complexed in CORUM (Table S5). Notably, 21 of these 35 predicted interactions have literature support. Thus, 32% of the current presumed false positives with respect to CORUM might turn out to be true positives. For K562, a similar calculation suggests 45 (54.2% of the total) of the current presumed false positives might turn out to be true positives.

TICA predictions are confirmed by manual literature investigation

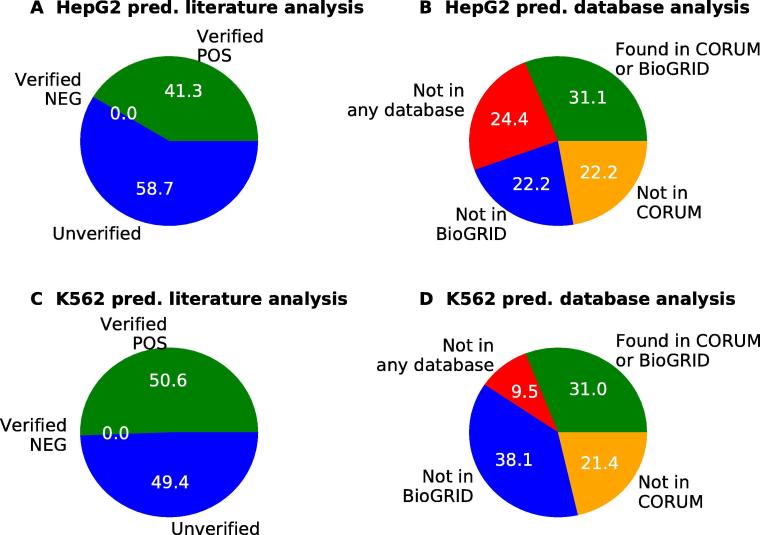
We performed manual literature investigation of selected predictions in tumor cell lines (HepG2 and K562) and classified the predictions according to whether they can be verified as positives or negatives with respect to literature, as described in Methods. As shown in Figure 5, about half of the predictions were confirmed in published literature. Notably, more than 50% of these prediction were also confirmed in one of the two databases (CORUM and BioGRID), suggesting a strong biological support for TICA predictions, irrespective of cell lines. A complete report of the literature investigation is given in Table S1.

Figure 5.

Summary of positive predictions supported by the literature

A. Literature analysis of the positive predictions for cell line HepG2. A positive prediction can be “Verified as POS” if interaction evidence is found in published literature (green); “Verified as NEG” if evidence is found that there is no interaction between members (red); or it can be “Unverified” if no evidence is found for either case (blue). B. Database cross-check of verified positive predictions for cell line HepG2. “Not in any database” (red) means that the predicted interactions are not found in either CORUM or BioGRID; blue indicates the number of positive predictions not found in BioGRID, whereas orange indicate the number of positive predictions not found in CORUM. Green slice indicates the number of predictions found in at least one of the two databases. C. Positive predictions literature analysis for cell line K562 (same color code as A). D. Database cross-check of verified positive predictions for cell line K562 (same color code as B). pred., predictions.

Cross-cell validation in the three cell lines shows TF predictions in healthy to be validated

We then investigated the amount of overlap between the sets of predicted positive interactions in different cell lines. To do so, we used the Jaccard Coefficient, defined as the ratio between the sizes of the intersection and of the union of the two sets. Moreover, we compared a single cell line with the combined predictions in the other two; when merging or intersecting predictions in different cells, we only consider those where both TFs are shared between the target cell lines. As shown in Table 3, GM12878 shares almost 50% of its positively-predicted interactions with HepG2 and the same with K562. This is consistent with the fact that GM12878 is derived from a healthy donor, and hence its TF–TF complexes should be basal in nature, unlike aberrant versions in tumor cell lines. 20% of positive TF–TF interaction predictions in GM12878 (on common TFs) are shared across all the three considered cell lines, further validating this hypothesis (Table S6).

Table 3.

Cross-cell comparison of positive TICA predictions

Cell line 1	Cell line 2	Positive predictions on shared TFs	Jaccard coefficient	Recall in cell line 1	Recall in cell line 2
HepG2	GM12878	46	0.146	0.177	0.426
HepG2	K562	89	0. 163	0.256	0.309
GM12878	K562	110	0. 186	0.460	0.237
HepG2	GM12878 ∪ K562	121	0.191	0.111	0.210
GM12878	HepG2 ∪ K562	142	0.186	0.181	0.276
K562	HepG2 ∪ GM12878	185	0.192	0.079	0.645
All cell lines (intersection)		14	0.186	0.089 / 0.206 / 0.130

Note: For the intersection of all three cell lines, the recall value is given for all cell lines, in order (viz., recall with respect to HepG2, GM12878, and K562). For comparisons involving all three cell lines, a TF in a prediction must be shared between all cell lines in order for it to be accepted as part of the combination / intersection.

Comparison with other TF-TF interactions prediction methods

To evaluate the improvement with respect to the state of art in TF–TF prediction, we compared TICA with three other methods for TF interaction prediction. These include TACO that predicts cell-specific TF dimers based on enrichment of motif complexes [23], CENTDIST that is a co-motif scanning algorithm ranking co-TF motifs based on their distribution around ChIP-seq peaks [29], and a computational method based on nonnegative matrix factorization (NMF) [30]. Results are tabulated in Table 4.

Table 4.

Comparison between TICA, TACO, CENTDIST, and NMF predictions

Predictor	Cell line	Recall	Specificity	Geometric mean performance	Enrichment
TICA	K562	0.421	0.807	0.583	2.181
TACO	K562	0.140	0.938	0.362	2.258
TICA ∪ TACO	K562	0.526	0.760	0.632	2.192
TICA	HepG2	0.278	0.857	0.488	1.944
CENTDIST	HepG2	0.390	0.720	0.530	1.393
TICA ∪ CENTDIST	HepG2	0.585	0.643	0.613	1.639
TICA	GM12878	0.424	0.611	0.509	NA*
NMF	GM12878	0.238	0.911	0.468	NA*
TICA	K562#	0.202	0.792	0.400	NA*
NMF	K562	0.214	0.835	0.423	NA*

Note: Union of predictors is defined as predicting a positive interaction if and only if it is predicted positive by at least one of TICA and TACO/CENTIDIST (respectively). An interaction is predicted negative if and only if it is predicted negative by both methods. Comparison was performed only on the cell lines indicated (K562 for TACO, HepG2 for CENTDIST, GM12878, and K562 for NMF [23]). ^* indicates that there is no software available for database-wide comparison. ^# indicates that only a subset of TFs predicted by NMF to be in complexes are used for comparison. NMF, nonnegative matrix factorization method by Giannopoulou and colleagues [30].

Using TACO, Jankowski et al. reported the top 10 best ranking predicted motif dimers using ChIP-seq data on cell line K562 (ibidem, Figure 4, page 6) [23]. We compiled the list of all TFs belonging to these dimers and intersected it with data available in ENCODE. This resulted into 28 relevant TFs and 378 candidate TF pairs. Data for these pairs were extracted and fed to TICA. The resulting predictions were compared with TACO’s original dimers. Note that if a TF pair is not reported in the aforementioned dimer list, we assume the corresponding TACO prediction to be negative. We observed that TICA has a 3-fold higher recall with respect to TACO on the 378 candidate list, with only 13% less specificity, resulting in a 1.6-fold increase in geometric mean performance.

We then selected 10 highly-conserved TFs from the list of ENCODE ChIP-Seq data available for HepG2 and submitted them to CENTDIST. Feeding the list of TFs and their CENTDIST-predicted partners to TICA resulted in 406 candidate predictions. It is of note that due to the assumptions and target heterotypic interactions, homotypic predictions in CENTDIST positive counts are not considered. As shown in Table 4, TICA has a much better enrichment ratio than CENTDIST with respect to CORUM/BioGRID, demonstrating better specificity but lower recall. However, comparison of recall rate is biased in favor of CENTDIST, since CENTDIST predictions were used to select the TFs for further consideration. It is also worth mentioning that CORUM complexes and CENTDIST’s co-motifs are not cell-line specific; hence some verified CENTDIST-only predictions may be false positives in the cell lines tested.

To compare our results with the NMF method [30], we extracted complexes on cell lines GM12878 and K562 reported previously (Figure 3 in [31]) and compared with TICA predictions on shared TFs. Validation was done using GeneMANIA [31], a gene network builder based on functional annotations that is used by Giannoupoulou et al. [30]. On GM12878, TICA shows improved recall but reduced specificity, resulting in greater geometric mean performance, but lower enrichment ratio with respect to the databases (Table 4 again); on K562, performance between the two methods with respect to proposed complexes is similar (Table 4). However, there is no report of the full list of predicted complexes [30]; so we expect that the comparison is skewed similarly to the CENTDIST comparison.

Discussion

In this study, we reported TICA, a new method for predicting interactions between TFs based on structural and positional information of their binding sites. By exploiting the expressive and distributed nature of the GMQL language together with simple statistics, TICA provides fast combinatorial analysis of interactions between TFs for detecting their potential physical interactions. Its main advantage lies in allowing users to do parallel pre-screening of possible novel interactions. TICA shows high specificity toward the commonly-used protein complexes (>80%), and thus can be exploited to weed out unlikely interactions.

The enrichment ratio of TICA's predictions with respect to CORUM ratio is above 1 in all scenarios, which indicates that it can effectively separate true TF–TF interactions and non-interactions. Of note is the fact that TICA reports fewer TF-TF interaction predictions on healthy cell line GM12878 as opposed to disease cell lines HepG2 and K562. Healthy generally have lower transcriptional activity than cancer cells [27], providing indirect evidence supporting the correctness of the prediction ratio.

The right tail size feature in TICA is (to the best of our knowledge) a novel introduction to the field. To investigate the relative impact of this feature, we computed all measures under three alternative conditions: using all four features (baseline scenario), using only the 1000-bp right tail size, and using all other three measures (i.e., without the right tail size). As reported in Table S7, incorporating the right tail size test consistently leads to improved geometric mean performance, irrespective of databases and/or cell lines considered. Using right tail size (with the baseline parameters) alone beats all other three measures in terms of geometric mean performance by a large margin in two out of the three cell lines examined. However, we detected lower database enrichment ratio when using the right tail size test alone compared to the baseline scenario. This might be due to a bias in the comparison: using the baseline P value (0.2) in the right tail size test results in laxer conditions for positive calling with respect to the three way test, leading to better recall but lower class separation power.

Novel interactions predicted are confirmed by manual investigation

We extracted lists of novel interactions predicted using TICA on the three aforementioned cell lines: we define an interaction as a novel prediction if evidence for it can be found in CORUM but not in PubMed. The combined support by TICA structural predictions and protein complexes/ functional interaction databases is a strong indicator that these interactions are likely to be real. A full list is provided in Table S8; henceforth we highlight some interesting examples.

SIN3A/TFAP4 in HepG2 is supported by the fact that efficient TFAP4 DNA binding is known to require another bHLH protein (http://www.genecards.org/cgi-bin/carddisp.pl?gene=TFAP4) and SIN3A contains paired amphipathic helix (PAH) domains, many of which contain basic regions close to the HLH motif (http://atlasgeneticsoncology.org/Educ/TFactorsEng.html). The interaction between CEBPB and NR2F2 in K562 is notable because there is evidence of a connection between these two TFs and the regulation of gonadotropin-releasing hormone (GnRH) [32]. Another interesting prediction is JUN/STAT1 in K562. Although we could not find up-to-date evidence of their interaction in vitro, JUN is known to interact with STAT3 [33] and STAT1 binds to its interacting partners at the same or very close to the binding sites of STAT3 [34], suggesting a potential interference scenario where tumor suppressor STAT1 could bind to JUN at STAT3′s binding sites and thus prevents the formation of JUN/STAT3 complexes in tumor cells. This speculation is supported by evidence of upregulation of c-JUN in mice with knocked-down STAT1 [35]. Finally, evidence has been found that cells transduced with a C-terminally truncated Runx1, which lacks important cofactor interacting sites, showed increased transcription of c-Myc [36], supporting the prediction of MYC/RUNX1 in K562.

Taking the union of multiple predictors leads to increased performance

Based on the comparison discussed in Results, we speculate that taking the union of TICA and TACO or CENTDIST in a given cell might produce an overall improved performance. To validate this possibility, we computed quality measures on the predictions resulting from taking the union of positive predictions from TICA and TACO or CENTDIST (Table 4). We notice a moderate drop in specificity (expected due to taking the union of two predictors) which is balanced by a sizeable increase in recall, leading to an overall increase in geometric mean performance and enrichment ratio, supporting our hypothesis.

Conclusions

TICA is a novel methodology that employs genomic positional information of TFBSs to predict physical interactions between TFs. The main advantages of TICA are three-fold. (1) TICA leverages novel, parallel computing techniques to efficiently scan ChIP-seq point-source (1 bp-sized) binding site datasets and extract high-confidence binding sites and active TSSs. (2) TICA does not require motif information for TFBSs, bypassing incompleteness of selected motif databases and related accuracy issues. (3) TICA demonstrates very high level of specificity even at the laxest levels of parameters, allowing users to weed out non-interacting TF–TF pairs with high levels of confidence before proceeding to experimental validation.

TICA has shown to be as reliable if not better than similar interaction prediction algorithms that rely on precise motif information, while allowing for significantly higher output rates (ranging 5000–22,000 predictions on available cell lines). Moreover, TICA appears complementary to alternative TF–TF interaction prediction approaches (viz., TACO and CENTDIST), and combining their predictions greatly improves sensitivity of the predictions at moderately-reduced specificity.

Finally, selected TF–TF pairs could be competing for the same cognate genes and interaction partners (competitive interactors) instead of being part of the same complex (cooperative interactors) Both interactions are interesting in the domain of gene expression regulation, and we plan to address their classification in future studies.

Authors’ contributions

SP designed the TICA methodology and analyzed the data. PP contributed to the algorithm’s construction and performed the code optimization. SC participated in the study design and result validation. LW conceived the study, contributed to the design of TICA, and validated the results. SP drafted the manuscript. All authors reviewed and approved the final manuscript.

Competing interests

The authors have declared no competing interests.

Handled by Jiang Qian

Supplementary material

The following are the Supplementary data to this article:

Supplementary File S1

GMQL queries for TICA data extraction and preprocessing

Supplementary File S2

Additional discussion on validation and P value threshold selection