Abstract
Recent studies suggest that the fast timescale motion of methyl-bearing side chains may play an important role in mediating protein activity. These motions have been shown to encapsulate the residual conformational entropy of the folded state that can potentially contribute to the energetics of protein function. Here, we provide an overview of how to characterize these motions using nuclear magnetic resonance (NMR) spin relaxation methods. The strengths and limitations of several techniques are highlighted in order to assist with experimental design. Particular emphasis is placed on the practical aspects of sample preparation, data collection, data fitting, and statistical analysis. Additionally, discussion of the recently refined “entropy meter” is presented and its use in converting NMR observables to conformational entropy is illustrated. Taken together, these methods should yield new insights into the complex interplay between structure and dynamics in protein function.
Keywords: protein dynamics, conformational entropy, NMR relaxation, dipolar relaxation, cross correlated relaxation, model-free analysis, dynamical proxy, isotopic labeling
1. Introduction
Nuclear magnetic resonance (NMR) spectroscopy offers an unparalleled ability to characterize molecular dynamics at atomic resolution. The range of accessible timescales is vast, spanning picoseconds to days and even longer. Accordingly, NMR has emerged as a powerful technique for elucidating the temporal changes in structure that mediate a diverse array of protein activities. Of notable interest are the fast picosecond-nanosecond timescale dynamics of protein side chains as these motions have been shown to reflect the considerable residual conformational entropy of folded proteins (Caro, Harpole, Kasinath, Lim, Granja, Valentine et al., 2017). While the role of conformational entropy is still being explored, recent studies suggest it contributes significantly to the free energy of several important protein functions including molecular recognition (Frederick, Marlow, Valentine, & Wand, 2007; Marlow, Dogan, Frederick, Valentine, & Wand, 2010; Takeuchi, Tokunaga, Imai, Takahashi, & Shimada, 2014; Tzeng, & Kalodimos, 2009) and allostery (Capdevila, Braymer, Edmonds, Wu, & Giedroc, 2017; Capdevila, Edmonds, Campanello, Wu, Gonzalez-Gutierrez, & Giedroc, 2018; Popovych, Sun, Ebright, & Kalodimos, 2006).
In this chapter we will review the experimental strategies and implementations used to comprehensively measure fast internal motion in proteins. We will cover isotopic labeling strategies that provide access to relaxation phenomena while maintaining the purity of the relaxation process under examination. The state-of-the-art pulse sequences will be summarized along with the analytical strategies designed to extract primary relaxation observables. The synthesis of primary relaxation data to local model-free and global tumbling parameters, their robustness, and achievable precision will be illustrated with various examples. Finally, how changes in internal motion can be related to fundamental thermodynamic variables will be described.
2. NMR Spin Relaxation Methods
2.1. The Relationship between Relaxation and Fast Timescale Dynamics
Traditionally, the fast timescale dynamics of proteins have been characterized by solution NMR spin relaxation experiments which provide exquisitely precise measures of the amplitude and timescale of motion. NMR relaxation rates are influenced by a variety of mechanisms including dipole-dipole interactions, chemical shift (shielding) anisotropy (CSA), quadrupolar interactions, and cross correlation. These relaxation mechanisms arise from the modulation of the effective local magnetic field and are therefore susceptible to time-dependent modulation by protein motion, thus providing a direct relationship between internal dynamics and relaxation. Relaxation mechanisms and their respective relationships to protein motion have been reviewed exhaustively elsewhere (Abragam, 1961; Cavanagh, Fairbrother, Palmer, Rance, & Skelton, 2007; Fischer, Majumdar, & Zuiderweg, 1998; Frueh, 2002; Igumenova, Frederick, & Wand, 2006; Jarymowycz, & Stone, 2006; Nicholas, Eryilmaz, Ferrage, Cowburn, & Ghose, 2010).
With respect to practical implementation, most relaxation experiments involve collecting a series of 2D or sometimes 3D spectra as a function of an incremented time delay wherein each cross peak arises from a single interaction vector (often oriented along a bond). In most cases, the relaxation parameter is defined through its explicit time dependence, which is often, though not always, a simple single exponential:
| (1) |
where I(t) is the peak height at delay time, t, I0 is the initial peak height, and R is the relaxation rate. In other cases, the relaxation time dependence is more complicated (e.g. cross correlated relaxation in methyl groups) or simply derived from a steady-state value (e.g. the heteronuclear NOE).
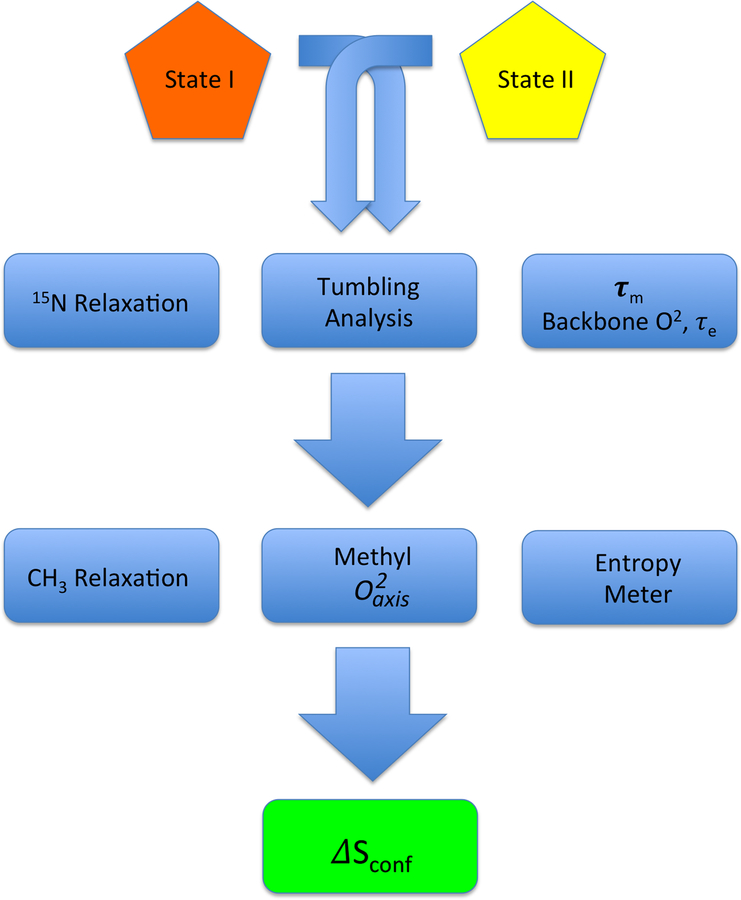
Relaxation parameters extracted from data fitting are directly related to a linear combinations of the spectral density, J(ω), where ω denotes a frequency. A variety of theoretical frameworks exist for doing this, though the so-called “model-free” formalism of Lipari and Szabo is employed most frequently (Lipari, & Szabo, 1982). The spectral density is related by real Fourier transform to the time domain correlation function defining the motion in the laboratory frame (Igumenova, et al., 2006). Accurate evaluation of the character of molecular reorientation is absolutely required for rigorous characterization of the internal motions. Typically, the molecular tumbling time is determined using 15N relaxation methods that probe the 15N-1H bond vectors of backbone amide groups. The idea is that the global tumbling dominates relaxation at rigid sites. Once the overall tumbling time of the molecule is known, the amplitude of internal motion can be determined for both backbone amide groups and side chains. Though a few notable exceptions have been reported (Jarymowycz, et al., 2006; Tzeng, et al., 2009), the internal dynamics of the backbone have largely been shown to be homogenously rigid and immutable upon change in functional state (Sharp, O’Brien, Kasinath, & Wand, 2015). As such, the backbone typically contains little entropic content. On the other hand, the internal motion of side chains, particularly those bearing methyl groups, has been shown to be heterogeneous and tunable (Caro, et al., 2017; Frederick, et al., 2007; Igumenova, et al., 2006; Kasinath, Sharp, & Wand, 2013; Marlow, et al., 2010), suggesting a rich entropic component. A simplified workflow for determining conformational entropy from NMR-derived measures of fast internal motion is shown in Figure 1.
Figure 1.
Simplified flow chart illustrating the key steps in determining protein conformational entropy from NMR relaxation measurements. Macromolecular tumbling is best characterized using relatively rigid components of the protein i.e. the backbone. Model-free analysis provides information about the dynamical character the backbone in addition to the appropriate tumbling model and parameters to employ subsequently. Methyl-relaxation is generally sufficient to carry through to an analysis of conformational entropy. Determination of absolute entropy is fraught with difficult (see text) and only differences in conformational entropy should determined, hence the requirement to compare two states (e.g. protein with and without ligand, etc.).
2.2. Measuring 15N Relaxation of Amide Groups
Overview
Quantification of backbone internal motion and determination of the overall molecular tumbling is traditionally performed using 15N relaxation experiments that probe the 15N-1H bond vectors of amide groups. Typically, three relaxation parameters are determined for each resolved amide bond vector: the longitudinal relaxation rate, R1, the transverse relaxation rate, R2, and the heteronuclear NOE, {1H}−15N HetNOE. Complete determination of the overall (global) molecular tumbling, local backbone order parameters, and local correlation times requires determination of R1, R2, and HetNOE values at two or more static field strengths to provide enough experimental observables for fitting (e.g. 2n local parameters + 1 global parameter for isotropic tumbling where n is the number of interaction vectors) as discussed in section 3.3. Sometimes, an additional local Rex parameter is also fit to obtain information about slower timescale dynamics arising from conformational exchange which increases the minimum number of necessary experimental observables to 3n+1 for the case of isotropic tumbling. So-called “lean” approaches (Gu, Hansen, Peng, & Bruschweiler, 2016) can be used to reduce data collection and a recent publication has provided a systematic and quantitative evaluation of using a reduced number of 15N relaxation observables in the quantification of internal motion (Jaremko, Jaremko, Ejchart, & Nowakowski, 2018). Alternative methods utilizing cross correlated relaxation have also been introduced but will not be discussed further here (Pelupessy, Espallargas, & Bodenhausen, 2003; Reif, Diener, Hennig, Maurer, & Griesinger, 2000; Weaver, & Zuiderweg, 2008; Weaver, & Zuiderweg, 2009). In our opinion, reducing the number of observables to the minimum value simply to save spectrometer time is ill-advised.
Sample Preparation
Sample preparation for 15N relaxation is straightforward and relatively cost effective. For smaller proteins with molecular weights < ~25 kDa, the entire suite of backbone relaxation experiments can be collected on uniformly 15N labeled samples without deuteration. For larger systems where sensitivity is degraded due to rapid transverse relaxation rates, uniform 2H, 15N labeling is required. In cases where deuteration is employed, care must be taken to adequately back exchange stably hydrogen bonded amide deuterons to protons through in vitro refolding or destabilization (Tugarinov, Kanelis, & Kay, 2006). Our laboratory has found that commercial protein refolding kits can greatly accelerate the identification of refolding conditions, even for large multi-domain proteins. More recently, we have developed a protocol for expression of proteins in E. coli during growth on H2O that results in extensive deuteration and does not require back-exchange (O’Brien, Lin, Fuglestad, Stetz, Gosse, Tommos et al., 2018). For quantitative backbone dynamics experiments, labeling schemes that place 13C adjacent to amide 15N should be avoided.
Pulse Sequences
The canonical pulse sequences for measuring 15N R1, 15N R2, and {1H}−15N HetNOE were introduced by Kay and co-workers (Farrow, Muhandiram, Singer, Pascal, Kay, Gish et al., 1994) nearly 25 years ago and are still commonly employed for measuring backbone dynamics today. In our experiences, these pulse sequences are appropriate for proteins with molecular weights < ~25 kDa at 25˚C. The 15N R1 and 15N R2 experiments are set up as separate series of 2D correlation experiments where a single delay time is incremented. The time-dependent decay of peak intensity is then fit to a single exponential to extract the relaxation rate. The {1H}−15N HetNOE experiment does not require fitting an exponential rate and consists of two 2D correlation experiments collected with and without proton saturation. The HetNOE value is then determined by taking the ratio of peak heights from the two spectra, Isat/I0. It should be noted that this experiment exhibits low intrinsic sensitivity. Moreover, the saturation period must be approximately 5x the amide proton T1 (1/R1) to ensure proper determination. For smaller, protonated proteins, a value of 5s is typically used. However, for larger proteins with longer amide proton T1 times, values of 10s-12s are not uncommon. Therefore, even though this experiment only consists of two spectra, it can be very time consuming or sometimes impossible to execute. Furthermore, the limiting effects of slow global tumbling begin to reduce the effectiveness of this parameter in subsequent analysis. Conversely, it should be pointed out that not having the hetNOE can lead to imprecision and bias in the determined tumbling parameters (Lee, & Wand, 1999).
For larger proteins with molecular weights > ~25 kDa, TROSY-sampling pulse sequences should be employed to ensure that the data quality is sufficiently high for quantitative analysis (Chill, Louis, Baber, & Bax, 2007; Lakomek, Ying, & Bax, 2012; Pervushin, Riek, Wider, & Wuthrich, 1997; Zhu, Xia, Nicholson, & Sze, 2000). Typically, the TROSY component is selected following the relaxation delay for read-out purposes only. Measurements of the relaxation rates of TROSY components have also been reported (Tugarinov, Muhandiram, Ayed, & Kay, 2002) but these rates are not usually used for downstream analysis of internal protein motion.
Systematic Errors
In recent years, it was reported that saturation of the water resonance can lead to systematic errors in R1 relaxation rates that greatly exceed the inherent precision of the experiments (Chen, & Tjandra, 2011). This effect was ascribed to a systematic decrease in the initial peak intensity due to NOE transfer or hydrogen exchange from the saturated water to the amide groups. The pulse sequences introduced by Kay and co-workers that are typically used today were designed to minimize saturation of the water resonance and are unlikely to yield spurious relaxation rates.
TROSY relaxation experiments may also be subject to systematic errors that arise from saturation of the water resonance—primarily originating from the use of non-selective 1H refocusing during the relaxation delay (Lakomek, et al., 2012). This effect is more acute in the case of TROSY experiments because deuteration results in a smaller 1H spin density and reduces the number of cross relaxation pathways available to return magnetization to thermal equilibrium. Bax and co-workers have introduced TROSY pulse sequences that largely eliminate these systematic errors (Lakomek, et al., 2012). The same report from Bax and co-workers also introduces a suite of optimized non-TROSY, HSQC pulse sequences for obtaining 15N relaxation parameters in smaller proteins.
R2 vs. R1ρ
The transverse relaxation rate of nuclei can be measured in both the laboratory (R2) and the rotating frame (R1ρ). With respect to the practice of determining relaxation parameters for the measurement of internal motion and molecular tumbling, there is no requirement that one approach be used over the other. R2 experiments that make use of CPMG pulse trains are subject to off-resonance effects that may compromise the determination of accurate relaxation parameters (Korzhnev, Tischenko, & Arseniev, 2000). Unfortunately, these effects cannot be readily corrected in a facile manner. Additionally, most common implementations of R2 experiments suffer from a first order phase distortion in the indirect dimension due to slight imperfections in the execution of the CPMG pulse train. The presence of phase errors can lead to small systematic errors in the quantification of peak heights which is necessary for extracting relaxation parameters. These distortions can be minimized or eliminated by modified phase cycling schemes (Yip, & Zuiderweg, 2004). R1ρ experiments make use of a spin lock pulse rather than a CPMG train which can readily be corrected for off-resonance effects according to the relation (Cavanagh, et al., 2007):
| (2) |
Where tan θ = ω/Ω, ω is the field strength of the spin lock field in Hz, and Ω is the cross peak’s resonance offset from the 15N carrier in Hz. This relation converts R1ρ to R2 which is required for downstream analysis. Similar to R2 experiments, R1ρ experiments can also exhibit a first order phase error in the indirect dimension, however, the effect can be minimized by adding adiabatic half passage pulses around the spin lock sequence (Lakomek, et al., 2012). We routinely use both experiments in our laboratory and a quantitative comparison of the two suggests that the extracted relaxation parameters are essentially identical (Lee, et al., 1999).
2.3. Measuring 2H Relaxation of Methyl Groups
Overview
Traditionally, fast dynamics in methyl-bearing side chains have been probed using 2H relaxation (Muhandiram, Yamazaki, Sykes, & Kay, 1995). The reasons for this are largely practical and originate from the relative ease of interpreting 2H relaxation which is essentially completely dominated by the quadrupolar interaction. 2H relaxation experiments typically utilize 13C-DH2 isotopic labeling of methyl groups to ensure purity of the relaxation mechanism and enable fitting with a single exponential. Minimally, longitudinal 2H R1 and transverse 2H R1ρ relaxation parameters are measured for downstream determination of side chain order parameters, though as many as five 2H relaxation rates can be determined for the 13C-DH2 isotopomer (Millet, Muhandiram, Skrynnikov, & Kay, 2002; Skrynnikov, Millet, & Kay, 2002). Four additional 2H relaxation rates can be measured for a 13C-D2H isotopomer using clever pulse sequences that prepare magnetization modes that relax as approximate single exponentials for large proteins (tumbling times > 9 ns) (Liao, Long, Li, Bruschweiler, & Tugarinov, 2012). It is unnecessary to collect all nine possible 2H relaxation rates for the determination of methyl order parameters. However, the availability of these additional rates provides an excellent self consistency test. Here, we focus only on the measurement of longitudinal 2H R1 and transverse 2H R1ρ relaxation.
Sample Preparation
Traditionally, 13C-DH2 labeled proteins are prepared using fractional deuteration and uniform 13C enrichment. This can be achieved using 50–65% v/v D2O in the growth medium and uniformly 13C-labeled glucose as the carbon source. This scheme will produce a mixture of 13C-DH2, 13C-D2H, and 13C-H3 isotopomers. The pulse sequences used to measure 2H relaxation select specifically for the isotopomer of interest (Muhandiram, et al., 1995). This effectively reduces the concentration of spin labels that contribute to the detectable signal and can be limiting for samples at low concentration.
Our laboratory typically does not combine this labeling with uniform 15N enrichment in order to avoid potential contamination from 15N-13C scalar couplings. Instead, we prefer to grow a separate uniformly 15N-labeled sample and combine it with 2H, 13C-labeled sample in an H2O buffer (Moorman, Valentine, & Wand, 2012). This way, a single sample can be used to measure both 15N relaxation for determination of the overall molecular tumbling and 2H relaxation for the determination of side chain order parameters.
Measurement of 13C-DH2 and 13C-HD2 relaxation can also be done on samples prepared using 3-13C1 pyruvate in 99.9% D2O minimal medium (Liao, et al., 2012). This labeling scheme leads to about equal populations of 13CHD2 and 13CH2D at Ileγ2, Valγ, Leuδ, Alaβ, and Metε methyl positions. Similar labeling patterns can be obtained using 1-13C1 glucose instead of pyruvate, though the incorporation is reduced by more than half (Liao, et al., 2012).
Methods for site-specific labeling of methyl groups have been introduced which enable complete incorporation of a single isotopomer, overcoming the potential sensitivity limitations introduced from isotopomer selection in fractionally deuterated samples (Tugarinov, et al., 2006). These methods have been reviewed extensively elsewhere and will only be briefly described here. Specific 13C-DH2 isotope labeled α-ketoacids are used in combination with uniformly 2H, 12C-labeled glucose and 99.9% D2O growth medium (Tugarinov, & Kay, 2005). This labeling approach is necessary for larger proteins which require high levels of deuteration. Unlike, the uniform 13C labeling approach, 15N labels can be safely incorporated in samples prepared using α-ketoacids for measurement of both backbone and side chain relaxation parameters in a single sample.
Pulse Sequences
Pulse sequences for measuring basic 2H spin relaxation parameters in methyl-bearing side chains were introduced by Kay and co-workers 20 years ago (Muhandiram, et al., 1995). Three relaxation experiments are collected: IzCz, IzCzDz, and IzCzDy (I=1H, C=13C, and D=2H) as series of 2D 13C-1H correlation spectra with variable incremented delay periods. Again, peak heights are fit to a single exponential function of the delay time in order to extract relaxation rates. The longitudinal 2H R1 and transverse 2H R1ρ rates are obtained by the relations:
| (3) |
| (4) |
Numerical simulations show that for a wide range of timescales and amplitudes of motion, the difference between the left and right sides of the above equations does not exceed ~3%, which is comparable to the inherent reproducibility of the measurements (Muhandiram, et al., 1995). Optimized pulse sequences have been introduced which allow ‘on the fly’ subtraction of the IzCz term, thus eliminating the need to acquire a third experiment (Millet, et al., 2002). Typically, since the bandwidth of the 2H spin lock pulse is wide, off resonance effects are negligible and
For high molecular weight proteins (> 25 kDa), the quality of 2H relaxation experiments degrades significantly. To overcome this limitation, Kay and co-workers have introduced TROSY versions of 2H relaxation experiments for 13C-DH2 and 13C-D2H isotopomers which have been validated on the 82 kDa protein, malate synthase G (Liao, et al., 2012; Tugarinov, & Kay, 2006). In the limit of slow tumbling, a single 2H relaxation parameter can be directly related to the methyl order parameter according to the relationship:
| (5) |
where QCC=e2 qQ/h, the quadrupolar coupling constant (167 ± 1 kHz). This bypasses the need to use the full model-free formalism. If the tumbling time of the protein is known, then methyl order parameters can be determined using a single experiment collected at a single static field strength. The quantitative accuracy of this approach has been exhaustively verified and it has been recently used to reveal the role of a dynamic hydrophobic core in mediating allostery in protein kinases (Kim, Ahuja, Chao, Xia, McClendon, Kornev et al., 2017).
2.4. Measuring 13C Relaxation of Methyl Groups
Overview
The use of 13C relaxation to probe motion in proteins has a long and extensive history. Unfortunately, due to intra-methyl cross correlated relaxation effects, the relaxation of 13CH3 groups is non-exponential and difficult to interpret. In order to simplify this interpretation, a wide variety of isotope labeling approaches have been introduced to produce 13C-HD2 isotopomers which will be described below. Though this labeling scheme eliminates complications due to intra-methyl cross correlated relaxation effects, the interpretation of 13C relaxation is still more complex than that for 2H relaxation. Unlike 2H relaxation, which is almost entirely dominated by the quadrupolar interaction, 13C relaxation arises from a mixture of several mechanisms. For Ile, Leu, and Val residues, over 70% of the relaxation rate derives from the 13C-1H dipolar interaction (Igumenova, et al., 2006). Additional non-negligible contributions to the observed relaxation rate come from intra-methyl 13C-2H dipolar interactions, 13C CSA, and remote dipolar interactions with 1H and 2H (Igumenova, et al., 2006). Proper interpretation of 13C relaxation therefore requires that a high-resolution structure of the protein is available so that remote dipolar interactions can be accounted for. The disadvantages introduced from the more complicated interpretation of 13C relaxation data are offset by the significant sensitivity boost 13C relaxation experiments offers over 2H relaxation which, on average, amounts to 3.3 fold for the 82 kDa protein, malate synthase G (Tugarinov, et al., 2005). Similar to 2H relaxation, longitudinal 13C R1 and transverse 13C R1ρ relaxation rates are measured using serially collected 2D correlation spectra that differ by the duration of an incremented time delay and rates are fit according to a single exponential decay.
Sample Preparation
In order to simplify the analysis of 13C relaxation, uniform 13C-13C scalar couplings must be removed from methyl groups and 13C-HD2 isotopomers must be present in the methyl groups of interest. A variety of methods exist for obtaining this type of labeling to various degrees of incorporation and these have been summarized elsewhere (Igumenova, et al., 2006). Today, 13C-HD2 isotopomers free of 13C-13C scalar couplings can be incorporated completely at Ile, Leu, and Val residues using specifically labeled α-ketoacids (Tugarinov, et al., 2006). These precursors are used in conjunction with 2H, 12C glucose and a 99.9% D2O growth medium to ensure high levels of protein deuteration at non-ILV methyl sites. Since the 13C label is confined to the methyl group, these samples can also be prepared with uniform 15N labeling so that tumbling times and methyl dynamics can be measured in a single sample, without the need to make separate samples with different labeling schemes.
Pulse Sequences
A variety of historical pulse sequences exist for probing 13C relaxation in proteins, specifically for longitudinal 13C R1, transverse 13C R1ρ, and {1H}−13C heteronuclear NOE which have been summarized elsewhere (Igumenova, et al., 2006). An early comparison of order parameters derived from 13C R1 and hetNOE relaxation parameters revealed a poor correlation with those derived from 2H relaxation methods (Lee, Flynn, & Wand, 1999). However, reasonable quantitative agreement between 13C and 2H derived order parameters could be obtained using 13C R1 and 13C R1ρ experiments, improved isotope labeling schemes combined with high levels of deuteration, and a structure-based analysis to account for remote dipolar contributions (Ishima, Petkova, Louis, & Torchia, 2001).
Further optimized 13C relaxation experiments for measuring 13C R1 and 13C R1ρ rates were presented by Kay and co-workers (Tugarinov, et al., 2005). These pulse sequences were shown to yield excellent data for high molecular weight proteins prepared using the α-ketoacid labeling scheme. In principle, these experiments are also suitable for use on smaller systems.
2.5. Measuring 1H-1H Dipolar Cross Correlated Relaxation of Methyl Groups
Overview
Relaxation measurements in 13C-H3 groups involves intra-methyl 13C-1H and 1H-1H cross correlated dipolar interactions (Kay, & Torchia, 1991; Kay, Bull, Nicholson, Griesinger, Schwalbe, Bax et al., 1992; Vold, & Vold, 1976; Werbelow, & Grant, 1977). Cross correlated relaxation can give rise to “forbidden” cross peaks in multiple quantum spectra that can be used to characterize molecular dynamics (Kay, & Prestegard, 1987; Muller, Bodenhausen, & Ernst, 1987) and form the basis for the so-called methyl-TROSY effect that results in significant sensitivity enhancement in the HMQC experiment for high molecular weight proteins (Ollerenshaw, Tugarinov, & Kay, 2003).
Intra-methyl cross correlated relaxation in highly deuterated, high molecular weight proteins can be exploited to characterize methyl dynamics (Tugarinov, & Kay, 2004; Tugarinov, & Kay, 2006; Tugarinov, Ollerenshaw, & Kay, 2006). In the slow tumbling limit (> 5 ns), the spectral density at zero frequency JCH,HH(0) dominates cross correlated relaxation rates, thus rendering them directly proportional to the order parameter, greatly simplifying the analysis. Additional experiments that rely on excitation of 1H double quantum and 1H triple quantum transitions were subsequently introduced and offer significant sensitivity gains relative to the original experiments (Sun, Kay, & Tugarinov, 2011). The 1H triple quantum transition experiment is the most sensitive and is preferred. The discussion below focuses on this experiment only.
Sample Preparation
Samples should be uniformly perdeuterated with 13C-H3 labeling confined to the methyl groups of interest. Branched methyl groups should only have one of the two methyl groups labeled to minimize effects of relaxation by remote protons. This can be obtained using the α-ketoacid precursors described above.
In recent years, a wide variety of more specific labeling schemes have been introduced which incorporate isolated 13C-H3 methyl groups in a deuterated background. These include pro-chrial stereo-specific labeling using acetolactate precursors (Gans, Hamelin, Sounier, Ayala, Dura, Amero et al., 2010) as well as approaches for specifically labeling leucine and valine using additional precursors (Miyanoiri, Takeda, Okuma, Ono, Terauchi, & Kainosho, 2013) or auxotrophic E. coli strains (Miyanoiri, Ishida, Takeda, Terauchi, Inouye, & Kainosho, 2016; Monneau, Ishida, Rossi, Saio, Tzeng, Inouye et al., 2016). These labeling schemes will prove useful and are often essential for characterizing large proteins with many methyl groups or proteins that exhibit crowded/overlapped methyl spectra which would compromise the accurate quantification of peak heights.
Pulse Sequences
The practical implementation of intra-methyl dipolar cross correlated relaxation experiments consists of collecting two relaxation series of 2D 13C-1H correlation spectra wherein each spectrum in a given series varies by an incremented delay time. The first “forbidden” experiment is a time-dependent build-up of 1H triple quantum coherences. The second “allowed” experiment is a decay of slow-relaxing 1H single quantum coherences. Both experiments are read out as conventional 2D 13C-1H HMQC. It should be noted that the “forbidden” experiment exhibits much lower sensitivity than the “allowed” experiment. In practice, both experiments are usually collected with a different number of scans and then the peak heights are corrected by linear scaling after processing.
Data are analyzed by taking the ratio of peak heights which is proportional to the cross correlated relaxation rate, η:
| (6) |
where δ is a fitted parameter that accounts for contributions from external protons. Values of δ must be negative to have physical meaning so fitting routines can be constrained to account for this (Tugarinov, Sprangers, & Kay, 2007). In practice, we have found that good data nearly always yield negative δ values, even without explicit constraint.
Downstream analysis is much simpler than that previously described for other relaxation methods. In the slow tumbling limit, fitted η values are directly proportional to the methyl order parameter:
| (7) |
Where μ0 is the vacuum permittivity constant, P2 is the second Legendre polynomial, θ is the angle between the methyl 3-fold axis and a vector connecting a pair of methyl 1H nuclei (90˚), γH is the gyromagnetic ratio of 1H, rHH is the inter-1H distance (1.813 Å) and τm is the molecular tumbling. The only unknown variable is which means that the system is over determined with data obtained at a single static field strength.
2.6. Ancillary Methods for Difficult Systems
Historically, highly quantitative characterization of internal motion in proteins has been limited to smaller systems with considerably long lifetimes. Though many of the advances described above reduce the amount of data required for analysis, several limitations persist.
Unstable and/or Dilute Samples
For unstable proteins with short lifetimes or samples that cannot be highly concentrated, time becomes the major limiting factor for characterizing internal motion. Non-uniform sampling (NUS) can help accelerate data collection and/or improve sensitivity. The basic premise is to reduce the experiment time by sampling the indirect dimension using non-uniform increments (dwell times) and reconstruct the sparse data in processing. If necessary, the time savings can be re-invested into signal averaging (Hyberts, Robson, & Wagner, 2013). There are a wide variety of NUS methods available that vary by sampling scheme and reconstruction method which have been discussed extensively elsewhere (Mobli, & Hoch, 2015). Historically, these methods did not provide quantitatively accurate peak heights and thus resulted in spurious relaxation rates (Hoch, 1985). The recent renaissance in NUS methods development, however, has shown that quantitatively accurate reconstructed peak heights can now be achieved under certain conditions (Hyberts, Takeuchi, & Wagner, 2010; Hyberts, Milbradt, Wagner, Arthanari, & Wagner, 2012). Unfortunately, it is difficult to predict whether or not quantitative accuracy can be achieved a priori. Moreover, we have found that the accurate reproduction of peak heights in one single plane of the relaxation series does not guarantee similar fidelity at different planes (Stetz, & Wand, 2016). Indeed, extensive characterization of NUS-derived relaxation rates suggests that there is high variability in the quantitative accuracy of these methods (Linnet, & Teilum, 2016).
Our laboratory has recently introduced a method to assess the quantitative accuracy of NUS relaxation data that relies on characterizing peak heights from a small set of reference data that can be collected prior to the relaxation suite (Stetz, et al., 2016). In brief, three planes of the relaxation series are collected with uniform sampling and then NUS. Alternatively, if many NUS schedules are to be tested, the uniformly sampled reference data can be re-sampled computationally. The non-linearity in peak height reconstruction is then calculated which is directly proportional to the error in relaxation rate. This method bypasses the need for a comprehensive understanding of the various underlying contributions that affect the reliability of NUS reconstruction and has been shown to be generally applicable to a wide variety of spectra (Stetz, et al., 2016).
Highly Overlapped Spectra
For highly overlapped 2D 1H-15N spectra, relaxation rates can be measured using 3D experiments, usually as an HNCO (Caffrey, Kaufman, Stahl, Wingfield, Gronenborn, & Clore, 1998; Chill, et al., 2007). This approach is not widely adopted due to the large increase in experiment time and data storage size associated with collecting a series of 3D experiments. Several approaches have been introduced to bypass this restriction, including collecting a reduced number of delay times (Chill, et al., 2007), reduced dimensionality (Tugarinov, Choy, Kupce, & Kay, 2004), and quantitatively accurate NUS (Gledhill, Walters, & Wand, 2009; Long, Delaglio, Sekhar, & Kay, 2015; Mayzel, Ahlner, Lundstrom, & Orekhov, 2017). Unfortunately, similar methods do not exist for characterizing side chain dynamics. We recommend that overlap in methyl spectra be addressed by collecting multiple data sets using different site-specific labeling schemes as discussed in the previous sections. Backbone sites can also be labeled site-specifically (Muchmore, McIntosh, Russell, Anderson, & Dahlquist, 1989), though we have found that the intrinsic dispersion of 15N chemical shifts in folded, globular proteins usually provides enough resolvable probes for the determination of global tumbling times.
3. Practical Aspects of Data Collection and Analysis
3.1. Guidelines for Setting up Experiments
Sample Concentration
In recent years, NMR studies have begun to focus more on challenging, biologically interesting systems rather than model systems. As such, sample preparation has become increasingly important and difficult since many biologically interesting samples cannot be concentrated highly. An empirical rule of thumb that we have developed to estimate the feasibility of performing relaxation experiments in a practical timeframe is if a signal-to-noise of approximately 100:1 can be obtained in the first FID of a 15N HSQC or 15N TROSY HSQC with 16 scans or fewer. We usually measure this across the entire amide envelope using the “sino” function in the TopSpin software for Bruker spectrometers. While this criterion will not guarantee success, interpretable and reproducible relaxation data are generally obtained when this criterion is met.
High Salt Samples
Many proteins are only stable in buffers that contain a relatively high concentration of salt (>100 mM) that compromises the sensitivity of cryoprobes and thus the reliability of relaxation experiments. Additionally, the increased pulse lengths required for “lossy” (i.e. conductive) samples may complicate proper execution of pulse sequences. A comprehensive inventory of low conductivity buffers has been reported which may assist with sample buffer optimization (Kelly, Ou, Withers, & Dotsch, 2002). Alternatively, specialized shaped tubes, 3 mm tubes, or Shigemi tubes can be used to reduce the total sample volume in the coil.
Sample Lifetime
Because relaxation measurements require extensive data collection, samples should be relatively stable and exhibit sufficient lifetimes to complete the measurements. Typically, samples should be stable for at least one week at the desired experimental temperature. Longer lifetimes are likely to be required if both backbone and side chain relaxation are to be collected on a single sample. In our experiences, many proteins are highly sensitive to cysteine oxidation which can result in sample aggregation or even precipitation. For proteins sensitive to cysteine oxidation, a suitable reducing agent must be added to the sample buffer. In most NMR applications, the reducing agent DTT is used. However, due to the relatively high pKa values of the two DTT thiols (~9.2 and ~10.1), only a small fraction of DTT molecules are redox active at the lower pH values used in typical NMR buffers. Moreover, DTT is rapidly oxidized by the air which makes it undesirable for long relaxation experiments. We have found that TCEP is a much better reducing agent for preserving samples. TCEP is highly active across a range of pH values and is not oxidized by the air.
Sample lifetime can also be affected by the presence of trace amounts of proteases. Though most commercial E.coli expression strains (B strains) are protease deficient (lon, ompT), samples can still become contaminated by other proteases. We recommend attempting to remove and/or inactive proteases before preparing the NMR sample through protein purification and the use of irreversible protease inhibitors such as phenylmethylsulfonyl fluoride (PMSF). In our experiences, adding commercially-available protease inhibitor cocktails directly to prepared NMR samples does not reduce protease activity over the long term as many of the inhibitors are reversible and/or exhibit short half lives in aqueous solutions. Proteolysis usually results in signature sharp resonances in the random coil region of 15N HSQC spectra and can therefore be easily identified. We recommended routinely collecting 15N HSQC spectra in between different relaxation experiments to monitor sample integrity.
Temperature Calibration
Protein dynamics can be quite sensitive to temperature (Lee, Sharp, Kranz, Song, & Wand, 2002; Song, Flynn, Sharp, & Wand, 2007). It is imperative that the temperature be calibrated using the appropriate standard sample. This is especially critical when data are collected at different field strengths/different spectrometers. For the commonly used temperature range of 25–37˚C, a 1D 1H spectrum of methanol is used for temperature calibration. The type of methanol sample will depend on whether or not data will be collected using a cryoprobe. For cryprobes, a sample of methanol-d4 is used and the chemical shift difference between the residual OH and CHD2 signals is determined which can be converted to temperature using a linear calibration curve (Findeisen, Brand, & Berger, 2007; Hoffman, 2006). For room temperature probes, a sample of neat methanol is used (Raiford, Fisk, & Becker, 1979). For high temperature work (> 37˚C), a sample of neat ethylene glycol is used (Raiford, et al., 1979). Modern versions of TopSpin software on Bruker spectrometers have automated analysis of temperature calibration spectra via the command “calctemp.”
Sampling Relaxation Decays
The duration of the relaxation delays will depend largely on the properties of the protein and the static field strength. For routine work, our laboratory often will empirically determine the longest delay time to be used by collecting the first FID of a relaxation experiment using different delay times and then quantifying the difference in peak height across the 1D signal envelope. We recommend that the longest delay time exhibit about 30% of the maximal signal (shortest delay) for single exponential relaxation. This can be quantified to reasonable accuracy using the “sino” function in the TopSpin software of Bruker spectrometers. The intermediate delay times can be calculated from the maximum delay time using the formula:
| (8) |
Where dn is the nth intermediate delay time you wish to determine, m is the total number of delays, and dmax is the longest delay time determined empirically.
3.2. Data Fitting and Error Analysis
Curve Fitting
Primary relaxation data is conventionally fit using least squares optimization (Press, 2007). This can be implemented in a variety of available software packages or using in-house scripts. Our laboratory uses in-house Python scripts which implement least squares optimization via the scientific computing library, SciPy. Regardless of the implementation, the routine will involve an iterative search of parameter space in the vicinity of an initial set of parameter guesses provided by the user in order to minimize the chi-squared, goodness of fit parameter (error function):
| (9) |
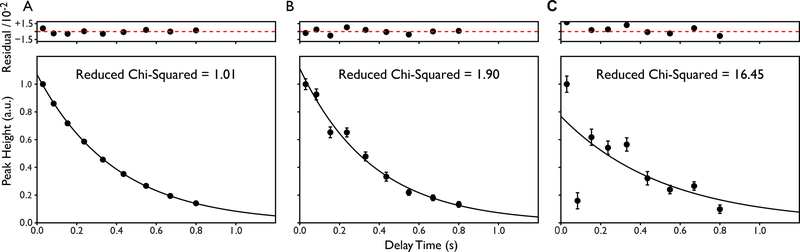
Where is the peak height at time calculated from the fit, is the experimentally measured peak height at time t, is the uncertainty in the peak height and N is the number of planes comprising the relaxation series. There are many algorithms that can be used to do carry out the minimization, however, we prefer Levenberg-Marquardt-type algorithms as these are usually able to find minima even when initial guesses are distant in parameter space. Example fits with a reduced chi-squared quality of fit parameter are shown in Figure 2.
Figure 2.
Example single exponential relaxation curves illustrating the effects of experimental noise on the fit statistics. (A) A well-determined single exponential with excellent fit statistics as determined by the reduced chi-squared value. The error bars are smaller than the data points. (B) A slightly noisy but well-determined single exponential with acceptable fit statistics. (C) A poorly-determined single exponential with unacceptable fit statistics. Residuals of the fit are shown above each relaxation curve and are scaled by a factor of 100.
Determining Uncertainties in Peak Height
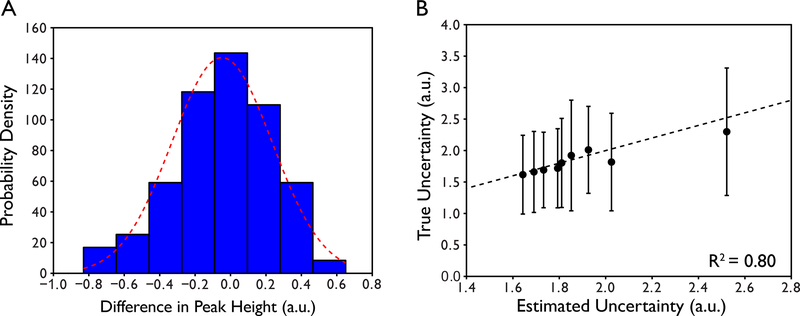
We have observed that the success of parameter optimization can be affected by improper definition of the uncertainty in peak height. These uncertainties are used as the error bars for each individual point in the relaxation decay or buildup. Our recommendation is to collect experimental replicates of 2–3 relaxation delays to determine a global estimate in peak height reproducibility. For example, in a typical experiment conducted in our laboratory, we will collect 9 unique delay times and duplicates of the 2nd, 5th, and 8th delays for a total of 12 sampled delays. One single uncertainty in peak height, which is applied to all peaks, is then estimated by taking the difference in peak height between duplicates, calculating the standard deviation of the differences, then scaling the standard deviation by (Skelton, Palmer, Akke, Kordel, Rance, & Chazin, 1993). A single global value must be determined over the entire set of peaks because the number of replicated planes is too small to obtain statistically meaningful per-residue uncertainties. These differences are typically normally distributed indicating random origin as shown in an example from a 15N R1 relaxation experiment on human ubiquitin in Figure 3a. This analysis is done for each pair of duplicated measurements and is typically applied to adjacent delay times that were not duplicated.
Figure 3.
Determination of the uncertainty in peak height. (A) Histogram of the differences in normalized peak heights between reference and duplicate spectra of a single plane of a 15N R1 relaxation series for the protein ubiquitin. The red dotted line is the best fit to a normalized Gaussian probability density function where the integrated area of the Gaussian is equal to 1. Note that the distribution is described well by a Gaussian function suggesting that uncertainties in peak height have a random origin. (B) Comparison of true uncertainty in peak height derived from 5 complete 15N R1 relaxation series and estimated uncertainty in peak height from replication of a subset of the data (see text).
We have found that this method of estimating uncertainties in peak height is an excellent approximation of the true experimental uncertainty in peak height derived from complete replication of the entire relaxation series. For ubiquitin, we have measured an entire 15N R1 relaxation experiment 5 times in order to estimate the true per-residue uncertainty in peak height. Typical uncertainties are < 1%. The mean experimental uncertainties in peak height largely agree with the estimated global uncertainties with an R2 = 0.80 as shown in Figure 3b. For less ideal systems, estimated uncertainties in peak height are larger but not egregiously so. For the 71 kDa lac repressor protein, peak height uncertainties estimated from two replicate delay times from a TROSY 15N relaxation series are typically below 5% with none exceeding 15%.
In cases where the uncertainties are < 1%, chi-squared values of the fit may be misleadingly high since the uncertainty is used in the denominator of the error function. This reduces the usefulness of the chi-squared value for determining goodness of fit. In these cases, we recommend scaling the uncertainties by a constant (usually a factor of 2) prior to fitting (Lee, et al., 1999).
Alternative methods of estimating the uncertainties in peak height utilize the RMS noise of the spectrum. This can be measured automatically in many data analysis programs. This value is then propagated to an uncertainty in peak height using the standard error propagation relation (Farrow, et al., 1994; Taylor, 1997). In our view, this generally underrepresents the uncertainty.
Determining Uncertainties in Fitted Parameters
Available fitting software packages will almost always report an uncertainty in the fitted parameter and/or some statistics about the goodness of fit. Since the minimization algorithms are mostly executed as matrix operations, uncertainties in fitted parameters can be obtained by taking the square root of the diagonal elements of the covariance matrix scaled by the reduced chi-squared value. Some newer routines in Python’s scientific computing library will do this automatically.
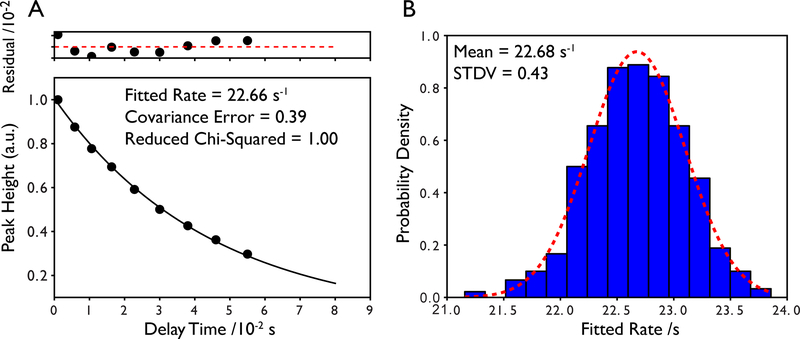
An alternative and perhaps more robust method for estimating the uncertainties in the fitted parameters is to use a bootstrap approach wherein Monte Carlo simulations are used to generate many simulated data sets where the data points have been randomly moved within the bounds of their error bars and then refit (Farrow, et al., 1994; Kamath, & Shriver, 1989). This is repeated many times and the standard deviation of the fitted values is taken to be the uncertainty in the fitted parameter. In the specific case of NMR relaxation, this would mean implementing a random sampling of the peak height within the uncertainty of the measurement as determined from replicate data or the RMS noise. Typically hundreds of simulated data sets are needed for convergence, however, this does not take much time on modern computers. We have found that Monte Carlo-derived errors are usually in good agreement with errors derived from the covariance matrix of the fitting routine as shown in for an example 15N R1ρ decay for the 42 kDa maltose binding protein in Figure 4.
Figure 4.
Estimation of the error in fitted relaxation parameters. (A) Example single exponential decay and error in fitted rate determined by scaling the diagonal elements of the covariance matrix by the reduced chi-squared value of the fit. Residuals of the fit are shown above the relaxation curve and are scaled by a factor of 100. The data is from a TROSY R1ρ experiment collected on the 42 kDa maltose binding protein. Error bars are smaller than the data points. (B) Error in the fitted rate determined from 500 Monte Carlo simulations using the uncertainty in peak height as the sampling bounds for each data point. The error is taken to be the standard deviation of the distribution. A fit to a normalized Gaussian probability density function is shown in the red dotted line where the integrated area of the Gaussian is equal to 1. Note the excellent agreement between the two methods.
3.3. Model-Free Formalism
The Spectral Density
The derivation of the model-free spectral density function has been described in detail elsewhere (Igumenova, et al., 2006; Lipari, et al., 1982). The Lipari-Szabo model-free spectral density is remarkably robust and capable of capturing even the most anisotropic motion anticipated even for methyl-bearing amino acid side chains (Frederick, Sharp, Warischalk, & Wand, 2008). In brief, the correlation functions for overall motion, C0(t), and internal motion CI(t) are assumed to be uncorrelated, which is generally guaranteed if they differ significantly in timescale. The spectral density is obtained by real Fourier transform of the correlation function yielding the functional from below for the case of isotropic molecular tumbling with a single correlation time:
| (10) |
Where Formally, 𝜏e is not a pure timescale constant but rather is defined as the area under the internal correlation function (Igumenova, et al., 2006; Lipari, et al., 1982). Since the spectral density is directly related to NMR-derived spin relaxation parameters, values of O2, τe, and τm can be extracted by numerical optimization. This is best accomplished using a grid search approach (Dellwo, & Wand, 1989) and various software packages for determining model-free parameters are currently available including software from our laboratory (Caro, et al., 2017). Once optimal model-free parameters have been determined, errors can be estimated using Monte Carlo methods. As a self consistency test, relaxation rates can be back-calculated from the model-free parameters. It is important to recognize that grid search methods may report “pegged” values when the numerical optimization fails. These will usually appear as the maximum value set in the search routine (for example = 1.0). It is therefore critically important to check the statistics of all fits prior to interpretation.
The functional form of J(ω) shown above is the simplest and most commonly used. However, an extended model-free spectral density which accounts for slower time scale motions has also been described (Clore, Szabo, Bax, Kay, Driscoll, & Gronenborn, 1990):
| (11) |
Where , and the “f’ and “s” subscripts refer to “fast” and “slow”, respectively. Since two additional local parameters must be determined, a total of 4n+1 experimental observables must be acquired to ensure a sufficiently determined system. In practice, if sufficient data are available, both models are employed then statistical tests are applied to identify the most appropriate (Mandel, Akke, & Palmer, 1995). A recent comprehensive comparison of the standard and extended model-free formalisms suggests that the extended model-free formalism may not be necessary in the vast majority of applications (Jaremko, Jaremko, Nowakowski, & Ejchart, 2015). Care must be taken when invoking the extended model free spectral density as apparent statistical justification arise from poor data.
While model-free has dominated the interpretation of NMR relaxation data, a competing formalism for describing internal motion has also been presented called the slowly relaxing local structure (SLRS) formalism (Freed, 1977; Polnaszek, & Freed, 1975; Tugarinov, Liang, Shapiro, Freed, & Meirovitch, 2001). Central to SLRS is the elimination of the requirement for complete uncoupling of internal and global motions which is a core assumption underlying model-free. The merits of this formalism relative to model-free have been discussed extensively (Frederick, et al., 2008; Halle, 2009; Meirovitch, Polimeno, & Freed, 2010; Meirovitch, Shapiro, Polimeno, & Freed, 2010). To date, the model-free spectral density prevails as the dominant formalism for the interpretation of NMR spin relaxation data and its robustness has been verified quantitatively (Frederick, et al., 2008).
Relating the Spectral Density to Relaxation Parameters
Relaxation parameters obtained from fitting NMR spin relaxation data are related to specific linear combinations of J(ω) evaluated at different frequencies, ω. The derivation of these relationships is involved (Abragam, 1961) and will not be described here. For 15N relaxation, the relationship between the commonly measured relaxation parameters, T1, T2, and NOE are given by:
| 12) |
| (13) |
| (14) |
Where constants d2 and c2 are defined as:
| (15) |
| (16) |
Where and are the gyromagnetic ratios of 1H and 15N nuclei, respectively, and are the Larmor frequencies of 1H and 15N, respectively, is the effective internuclear 1H-15N bond length, is the static field strength, and is the difference between the parallel and perpendicular components of an assumed axially symmetric 15N chemical shift tensor which is largely taken to be a uniform value of either −160 ppm (Hiyama, Niu, Silverton, Bavoso, & Torchia, 1988) or −170 ppm (Lee, et al., 1999). It is important to note that the effective N-H bond length shifted in the literature from 1.02 Å to 1.04 Å upon recognition of the effects of migration of the H on the obtained order parameter (Ottiger, & Bax, 1998) (see Equation 15 and discussion in (Igumenova, et al., 2006)).
For 2H relaxation, the relationship between the commonly measured relaxation parameters, T1 and T1ρ (Muhandiram, et al., 1995) are shown below:
| (17) |
| (18) |
Where is the quadrupolar coupling constant, which is typically taken to be 167 kHz (Mittermaier, & Kay, 1999).
For 13C relaxation, the relationship between the commonly measured relaxation parameters, T1 and T2 (Ishima, Louis, & Torchia, 1999) are shown below:
| (19) |
| (20) |
Constants , , and are defined as:
| (21) |
| (22) |
| (23) |
Where , , and are the gyromagnetic ratios of 1H, 13C, and 2H nuclei, respectively, , , and are the Larmor frequencies of 1H, 13C, and 2H, respectively, is the internuclear 1H-13C bond length and is the internuclear 2H-13C bond length, is the static field strength, and is the methyl 13C CSA. Methyl carbon CSA values are residue-type specific and average values are considerably smaller for Ile than for Leu and Val (17 vs. 25 ppm)(Tugarinov, Scheurer, Bruschweiler, & Kay, 2004), for example.
3.4. Characterization of Macromolecular Tumbling
Anisotropic Tumbling
Model-free analysis relies on the separation of timescales for the overall macromolecular tumbling and internal motions. In the completely general case of anisotropic tumbling, the analysis summarized above for isotropic tumbling must be modified such that the correlation function for overall rotational motion, C0(t) represents a linear combination of 5 different terms (Woessner, 1962):
| (24) |
Where the time constants, , and coefficients , depend on the principal components of the rotational diffusion tensor as well as the orientation of the diffusion tensor relative to the relaxation vector. In cases of symmetry, the number of terms can be reduced to 3 for axially symmetric diffusion and 1 for completely isotropic diffusion (the case illustrated in the previous sections). Precise knowledge of the rotational diffusion tensor is critical for the quantification of internal motions because motional anisotropy can be misinterpreted as slower timescale motions (Schurr, Babcock, & Fujimoto, 1994).
The determination of the rotational diffusion tensor requires collecting the conventional 15N relaxation parameters, R1, R2, and NOE and a high-resolution structure of the protein. Two approaches are typically used, one based on the calculation of local diffusion coefficients (Bruschweiler, Liao, & Wright, 1995; Lee, Rance, Chazin, & Palmer, 1997), and the other based on direct fitting of R2/R1 (T1/T2) ratios (Tjandra, Feller, Pastor, & Bax, 1995; Zheng, Czaplicki, & Jardetzky, 1995).
The local approach involves determining local tumbling times for each 1H-15N pair by fitting either the isotropic model-free spectral density function that also includes the part that reports on local motions (Bruschweiler, et al., 1995) or the T1/T2 ratios (Lee, et al., 1997). For fast, small-amplitude internal motions, the T1/T2 ratios depend essentially only on the spectral densities for overall molecular tumbling. For small anisotropies of the diffusion tensor, each local diffusion coefficient, , is determined using the relation:
| (25) |
These terms have a quadratic form and can be used to determine the tensor matrix in the molecular frame which can be diagonalized to yield the principal values of the diffusion tensor and the orientation of its principal axes relative to the molecular frame.
Determination of the diffusion tensor by direct fitting of its parameters to individual T1/T2 ratios has been reported (Tjandra, et al., 1995; Zheng, et al., 1995). This involves a least squares minimization of the error between experimental T1/T2 ratios and those calculated from the overall rotational diffusion coefficients and direction cosine terms. Additional computational methods have been introduced to determine rotational diffusion tensors of proteins based on a high-resolution structure (Bernado, de la Torre, & Pons, 2002; Bruschweiler, 2003; de la Torre, Huertas, & Carrasco, 2000; Korzhnev, Billeter, Arseniev, & Orekhov, 2001).
T1/T2 Ratio
For some proteins, it may only be feasible to collect a small set of 15N relaxation parameters, for example 15N R1 and R2 and a single static field strength. Though this is not enough observables to perform a full model-free analysis, it is a sufficient amount to determine local tumbling times using the T1/T2 ratio (Kay, Torchia, & Bax, 1989). In the limit that fast internal motion does not significantly influence R1 and R2, such is the case for relatively rigid backbone sites, the effects of τe can be ignored. Residue-specific values of the tumbling time can then be obtained using the expression:
| (26) |
Here, a simplified form of the model-free spectral density where only terms independent of τe are considered, can be used:
| (27) |
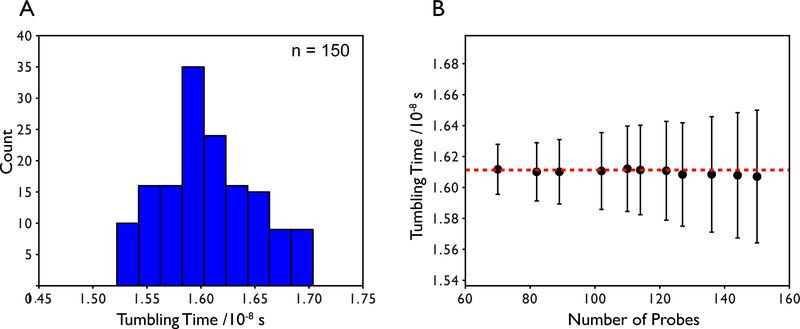
Note that the T1/T2 ratio is independent of the order parameter. Site-specific values of τm can then be obtained by least-squares fitting. Residues contaminated by conformational exchange should be excluded from the analysis. These residues can be identified through statistical filtering of the T1 and T2 values (Tjandra, et al., 1995) and/or analysis of the R1R2 product (Kneller, Lu, & Bracken, 2002). Once site-specific τm values are determined, they are typically averaged to obtain a single global τm. In our experiences, well structured, single domain proteins yield site-specific tumbling times that are normally distributed as shown in Figure 5a for TROSY R1 and R1ρ data collected on maltose binding protein. The mean is taken to be the global tumbling time and the standard deviation is taken to be the error in the tumbling time. Typically a 5–10% trimmed mean is used but for proteins with homogenous backbone dynamics, the mean value does not depend significantly on the number of probes that are trimmed as shown in Figure 5b. For multi-domain proteins, the approach can be applied separately for each domain. This approach has been useful for larger proteins > ~40 kDa (Bertelsen, Chang, Gestwicki, & Zuiderweg, 2009).
Figure 5.
(A) Distribution of local tumbling times derived from least squares fitting using the full 15N spectral densities for T1 and T2 and TROSY 15N R1 and R1ρ relaxation data collected on the 42 kDa maltose binding protein. Data exceeding 1.5 standard deviations from the mean have been filtered as well as any Rex outliers. (B) The average tumbling time and standard deviation as a function of the number of probes used in the calculation. The number of probes used in the calculation does not change the mean tumbling time by more than 0.4% indicating a well-determined global tumbling time. The largest standard deviation is approximately 2.7% of the mean.
TRACT
The TROSY for rotational correlation times (TRACT) method can provide reasonably quantitative estimates of the tumbling times of high molecular weight proteins (Lee, Hilty, Wider, & Wuthrich, 2006). Based on the TROSY method for improving the sensitivity and line widths of 1H-15N resonances, TRACT exploits cross-correlated relaxation between dipolar and CSA relaxation mechanisms to determine tumbling times. This renders the approach insensitive to effects from slower timescale dynamics resulting from conformational exchange processes.
The practical implementation of TRACT requires measuring the relaxation rates of both the α and β spin states, denoted as Rα and Rβ, respectively. These rates can be related to the dipole-dipole/CSA cross correlated relaxation rate, ηxy, which is proportional to the tumbling time, τm, via a linear combination of J(ω). In practice, rates are fit from collecting series of one-dimensional spectra that vary by an incremented time delay and integrating over the amide envelope. As such, the experiment is relatively fast and applicable to even very high molecular weight proteins. If the amide envelope is not homogenous across all peaks, such is the case with multi-domain proteins or proteins with intrinsically disordered regions, a two-dimensional version of the experiment can be run. While this method for determining the tumbling times of large proteins is widely used, it has been shown that TRACT-derived tumbling times may be subject to a systematic offset arising from the rigid body approximation (Nucci, Marques, Bedard, Dogan, Gledhill, Moorman et al., 2011).
3.5. Data Reproducibility
H2O vs D2O Solvent
Historically, backbone and methyl relaxation experiments have been measured using separate samples. The sample for backbone relaxation must be prepared in an H2O buffer to enable observation of exchangeable amide groups whereas the sample for methyl relaxation is usually prepared in a D2O buffer. The original reason for this was largely to eliminate complications arising from water suppression in methyl relaxation experiments. Today, D2O buffers are still typically used for measuring methyl dynamics because many of the modern methyl relaxation experiments require high levels of deuteration and D2O buffers eliminate exchangeable amide protons. In our laboratory, we have found that preparing two separate samples for relaxation experiments can be laborious and expensive, particularly when working with larger proteins that necessitate perdeuteration and site-specific methyl labeling. We have also found that buffer exchanging a single sample can lead to sample loss and inaccurate estimates of tumbling times due to changes in concentration.
To assess if methyl order parameters could be determined accurately in H2O buffers, we compared cross-correlated relaxation data for the 42 kDa maltose binding protein dissolved in both an H2O buffer and a D2O buffer. The tumbling time was determined by the T1/T2 ratio, using the H2O sample and TROSY-detected 15N relaxation experiments. The tumbling time was then scaled for the D2O sample according to the ratio of the solvent viscosities (Cho, Urquidi, Singh, & Robinson, 1999). The determined tumbling time of 16.1 ns ± 0.4 ns in H2O at 37˚C is within error with that previously published by Kay and co-workers (16.2 ± 1.0 ns) using different pulse sequences (Gardner, Zhang, Gehring, & Kay, 1998).
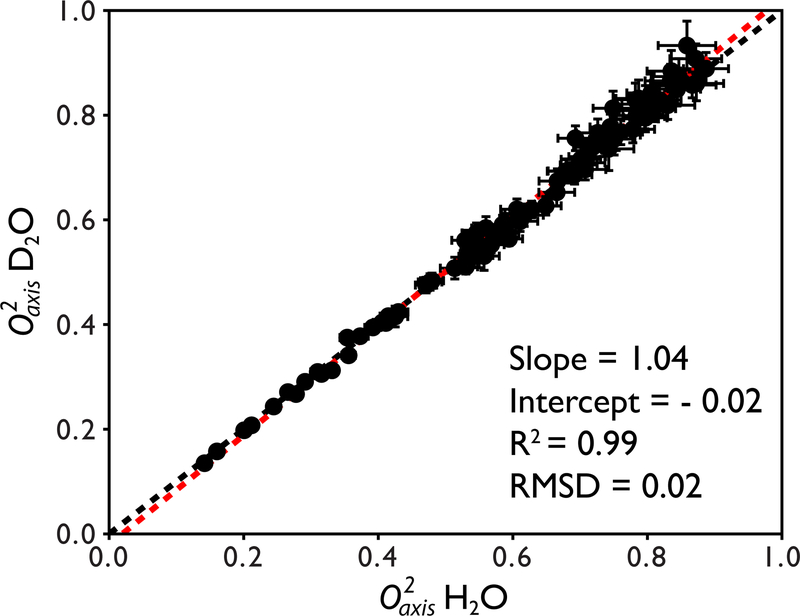
Methyl order parameters obtained from the H2O and D2O samples are in excellent agreement with an R2 = 0.99 as shown in Figure 6. Linear regression analysis of the order parameters yielded a best-fit line with a slope of 1.04 and an intercept of 0.02. The absolute pairwise RMSD is 0.02. The mean error between the two data sets is 2.34% which is on the order of the inherent reproducibility of the analysis based on the uncertainty in the tumbling time (~2.7%). All differences between H2O and D2O derived order parameters were <10% with the vast majority <5%. Water suppression was not an issue as the strong water resonance can be attenuated significantly using a selective shaped pulse or weak presaturation before the first 1H pulse.
Figure 6.
Quantitative comparison between O2axis values derived from cross correlated relaxation for the 42 kDa maltose binding protein prepared in H2O and D2O buffers. The x = y line is shown in black and the fitted line from linear regression analysis is shown in red. The equation of the fitted line as well as the correlation coefficient R2 and absolute pairwise RMSD are shown. On average, the values are within 2.5% of each other.
Intra-lab reproducibility
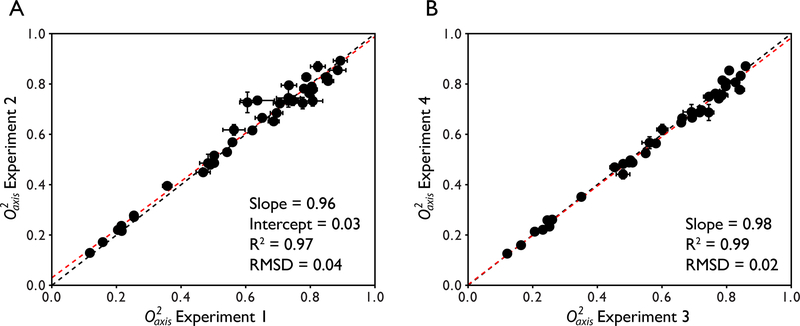
Our laboratory has also performed internal methyl order parameter reproducibility experiments for 2H relaxation using the protein ubiquitin. In total, 2 pairs of full backbone and methyl 2H relaxation experiments were performed. Full anisotropy tumbling analysis was used in the determination of methyl order parameters. Figure 7 shows the reproducibility of the measurement and analysis. For the first pair of data sets, linear regression analysis of the methyl order parameters yields a slope of 0.96 and intercept of 0.03. The R2 value is 0.97 and the absolute pairwise RMSD is 0.04. For the second pair of data sets, linear regression analysis of the methyl order parameters yields a slope of 0.98 and an intercept of 0.002. The R2 value is 0.99 and the absolute pairwise RMSD is 0.02. These reproducibility numbers are similar to those shown above for maltose binding protein in H2O and D2O buffers. This suggests that methyl order parameters are highly reproducible if the sample is appropriate for data collection.
Figure 7.
Intra-lab reproducibility of methyl order parameters for the protein ubiquitin derived using deuterium relaxation. Two separate pairs of experiments were collected for the analysis. The x = y line is shown in black and the fitted line from linear regression analysis is shown in red. The equation of the fitted line as well as the correlation coefficient R2 and absolute pairwise RMSD are shown.
Inter-lab reproducibility
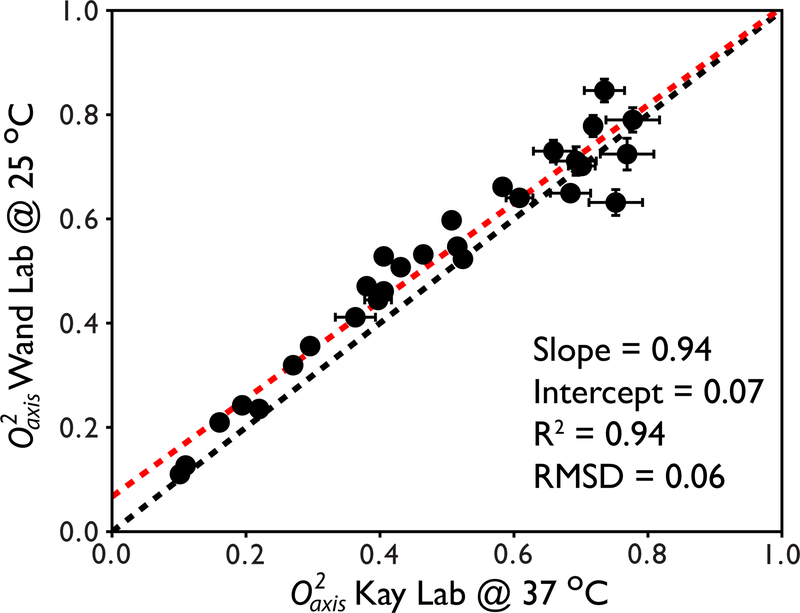
It can also be shown that methyl order parameters are highly reproducible across laboratories. We have compared methyl order parameters for the 82 kDa protein malate synthase G derived using our own implementation of the methyl cross correlated relaxation pulse sequences, our own estimation of the tumbling time, and our own method for sample preparation to those published by Kay and co-workers (Tugarinov, et al., 2007). The independently published methyl order parameters for Ile δ1 groups were reproduced to an astounding degree of precision (Figure 8). The R2 value was 0.94 and the slope and intercept determined from linear regression was 0.94 and 0.07, respectively. The absolute pairwise RMSD is 0.06. The differences largely reflect the fact that the two data sets were collected at different temperatures.
Figure 8.
Inter-lab reproducibility of methyl order parameters for Ile δ1 residues in the protein malate synthase G derived using cross correlated relaxation. The x = y line is shown in black and the fitted line from linear regression analysis is shown in red. The equation of the fitted line as well as the correlation coefficient R2 and absolute pairwise RMSD are shown. The slight uniform offset between the two data sets is consistent with the known temperature dependence of methyl order parameters (Lee, & Wand, 2001; Song, et al., 2007).
4. The Entropy Meter
In addition to being inherently important to protein function, internal protein motion offers a view into the underlying thermodynamics particularly in the context of conformational entropy. We are most concerned with those motions that express (expose) large contributions to protein conformational entropy i.e. motions that extensively sample the many states available to the folded native-state of the protein molecule. It has long been recognized from early simulations that the extremely fast soft-mode torsional oscillations of amino acid side chains contain significant entropy (Karplus, Ichiye, & Pettitt, 1987). NMR relaxation phenomena probe the interconversion of these states on the picosecond-nanosecond timescale. We have recently shown that it is possible to interpret changes in fast dynamics of protein side chains in terms of conformational entropy without debilitating assumptions (Caro, et al., 2017; Wand, & Sharp, 2018). The premise of the entropy meter is that fast (sub-ns) timescale motions report indirectly on the conformational states visited by a protein molecule and that these states reflect either directly or indirectly the overall conformational entropy (Akke, Bruschweiler, & Palmer, 1993; Caro, et al., 2017; Frederick, et al., 2007; Tzeng, & Kalodimos, 2012). Upon a change in functional state, such as the binding of a ligand, the populations of the various states of the ensemble will be redistributed. The importance of this redistribution is apparent from an alternate definition of the Lipari-Szabo squared generalized order parameter (Lipari, et al., 1982):
where Ω represents the various accessible states (here corresponding to orientational angles) and peq their probabilities. The connection between the population distributions of states and relaxation observables through the order parameter provides a basis for using motion as a proxy for entropy. Assumptions regarding the precise nature of the motion at a given site including the effects of correlated motion and limited sampling of motion (e.g. of methyl-bearing amino acid side chains only) are circumvented by empirically relating measures of motion to conformational entropy. It is important to note that absolute entropies will be difficult to access but estimateing changes in conformational entropy from NMR relaxation are predicted to be much more reliable (Lee, Sharp, Kranz, Song, & Wand, 2002; Li, Raychaudhuri, & Wand, 1996; Prabhu, Lee, Wand, & Sharp, 2003).
Theoretical considerations, molecular dynamics simulations and empirical experiment strongly suggest a generally linear relationship between side chain rotameric entropy and NMR relaxation (Caro, et al., 2017; Kasinath, et al., 2013; Wand, et al., 2018). Furthermore, coupling between methyl- and non-methyl-bearing amino acid side chains is sufficient for motion of the former to report on the disorder of the latter (Caro, et al., 2017; Kasinath, et al., 2013; Wand, et al., 2018). This means that conformational entropy is accessible using dynamical information from methyl relaxation only. For example, consider the physical origin of binding affinity. Formally, the Gibbs free energy of binding can be decomposed as follows
The entropy of solvent (ΔS0solvent) is perhaps the most familiar term and gives rise to the “hydrophobic effect,” which is relatively well understood. There is a loss in rotational-translational entropy (ΔS0rot-trans) when two molecules come together to form a single thermodynamic bound entity. The focus here is the change of internal conformational entropy of the protein (ΔS0conf), which is defined by the number of different microstates that the protein molecule explores in the “native” folded state. ΔS0ligand is the analogous quantity for the ligand. There are other potential contributions to the total binding entropy as well (e.g. H+ release) (incorporated into ΔS0other). Though they and solvent entropy may contribute to the total binding entropy they are not strongly coupled to a change in conformational entropy and will in general not interfere with accessing ΔS0conf. Using 28 protein-ligand complexes with known binding entropy and NMR dynamics changes, we solved for an empirical constant (sd) relating changes in motion between states with a change in the underlying conformational entropy.
| (27) |
where NχΔ<O2axis> is the NMR derived measure of the change in side chain dynamics between the two states being compared (Caro, et al., 2017; Wand, et al., 2018). There is a lot going on in this relationship but the overall point is that sd is defined with good precision. This now allows one to determine the change in conformational entropy (∆S0conf) that occurs upon a change in functional state of a protein (e.g. with and without a bound ligand) by measuring the change in dynamics using NMR relaxation methods and evaluating a simple relationship (Caro, Harpole, Kasinath, Lim, Granja, Valentine et al., 2017):
| (5) |
where Δ<O2axis> is the measured change in dynamics over the protein or protein region whose conformational entropy change, ΔS0conf, we wish to know. Nᵪ is the number of soft side chain degrees of freedom involved (i.e. torsion angles) and is directly determined from the covalent structure of the protein. Val and Thr have 1 torsion angle, Leu and Ile 2, and Met has 3. Ala, with zero, will be excluded from the entire calculation. The torsion angles of the ligand will similarly determine Nχligand. See (Caro, et al., 2017) for examples of how non-protein ligands can be handled.
The generality of the entropy meter means that its application has few requirements. Rigorous calculation of methyl O2axis values requires an explicit tumbling model. However, methyl assignments are not required since the entropy can be obtained from the difference of the averages of the two states of the protein being compared. However, when available, the average of side-chain specific changes in O2axis, or <∆O2axis> can provide deeper insight into the origins of the participation of conformational entropy. In some cases, the number of probes observed in the free and bound states may differ, and a discrepancy can be seen between the site-specific <∆O2axis> and the global ∆<O2axis>. The significance of this discrepancy can be evaluated with a bootstrap analysis to know how accurate the average values are. A bootstrap test randomly resamples the data hundreds of times and returns the value of interest (<O2axis> or <∆O2axis>). The stability of the value can be assessed by varying the size of the dataset, and the confidence interval can be extracted. As an example, we evaluate the binding of barnase to DNA. The ∆<O2axis> and <∆O2axis> values are −0.020 and −0.013, respectively. To evaluate if this difference is relevant, we perform a bootstrap analysis of the <O2axis> for the free and bound states and obtain for the free and bound states 0.668 ± 0.027 and 0.647 ± 0.028, respectively (Figure 9A). In addition, the 95% confidence interval of these average values are (0.615, 0.723) and (0.590, 0.699) for the free and bound states, respectively. The discrepancy between ∆<O2axis> and <∆O2axis> values is clearly larger than the accuracy of the values and is therefore not significant (Figure 9C). From this analysis it can be concluded that the <O2axis> values remain stable even when using just 20 data points.
Figure 9.
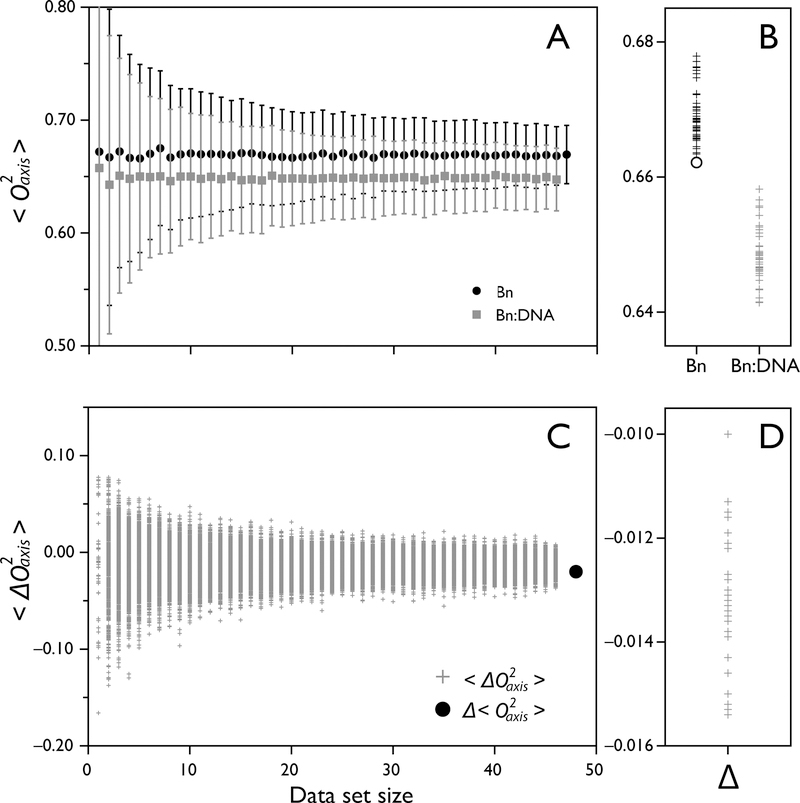
Sampling statistics of measured O2axis of barnase binding DNA. The O2axis values of free barnase and barnase bound to DNA are analyzed to determine the robustness of Δ<O2axis> and <ΔO2axis> values. (A) Bootstrap analysis of <O2axis> of barnase (black circles) and barnase-DNA (grey squares) as a function of dataset size, showing a narrow distribution of possible <O2axis> of 0.669 ± 0.026 and 0.647 ± 0.028, respectively. (B) Jackknife analysis of <O2axis> identifies the extra data point not measured in the barnase-DNA dataset by removing it and resulting in one of the extreme <O2axis> values using n-1 datapoints (open circle). (C) Bootstrap analysis of <ΔO2axis> of barnase binding DNA, yielding the value −0.013 ± 0.008. The value is well-determined even when only 20 datapoints are used. The global difference Δ<O2axis> is shown as a black circle. (D) Jackknife analysis of site-specific <ΔO2axis> shows a narrow distribution of possible values.
The response of the protein to a binding event can be quite heterogeneous, with some sites reporting much greater changes in O2axis than the average. These outliers form part of the global response of the protein and should be included to extract the ∆Sconf of binding. However, particular cases exist where caution should be taken not to introduce bias. Sites with high O2axis and fast relaxation properties can be particularly susceptible to poor spectral properties that can arise due to unusually large J-coupling constants that result in poor coherence transfer, and/or incomplete labeling. An unfortunate correlation between methyls with poor spectral properties and fast relaxation properties, and therefore high O2axis values, can introduce bias when analyzing global averages between two states of different molecular weights. This can be particularly troublesome when the molecular weight of the complex is significantly greater than that of the free molecule(s), since that methyl might only be observed in one of the two states. This sampling bias could lead to significant discrepancy between site-specific <∆O2axis> and global ∆<O2axis> values. The presence of bias can be evaluated with the help of a jackknife analysis, where the average value is recalculated exhaustively by omitting one data point at a time. When the dataset is large enough, the spread of values obtained should remain small. However, should one data point skew the average significantly, the jackknife analysis will highlight it as an outlier. In the case of barnase-DNA, the <O2axis> values obtained by omitting one data point vary by 0.016 and 0.017 for the free and bound states, respectively, which is smaller than the accuracy of the values. The same is true for the <∆O2axis> values, which can vary by 0.005 (Figure 9D). This indicates that no bias is present. But, as an exercise, when the largest O2axis value in barnase (0.974) is omitted, the jackknife average obtained is one of the extreme values (open circle, Figure 9B). Because this data point is not probed in the bound state, it could give rise to significant bias. Experimental strategies that mitigate this issue are to minimize overlap (individual protein labeling, higher statics fields), improve spectral quality (pulse sequence optimization), or by simply keeping a constant set of proxies between the two states.
5. Concluding Remarks
The characterization of fast internal side chain motion by solution NMR spectroscopy has matured greatly over the past decade. Here we have focused largely on approaches directed at measuring methyl-bearing amino acid side chain motion. Investigation of aromatic side chain motion has also seen considerable advances over the past decade (see Chapter by Weininger). The foundation provided by these advances in characterization of side chain motion have opened a path to probing entropic contributions to protein function in a variety of contexts (Wand, et al., 2018). The entropy meter provides a means to avoid many of the technical and theoretical barriers to using information about motion as a proxy for the underlying conformational entropy. Initial insights provided by the entropy meter demonstrate the richness of the role of conformational entropy in protein function and the importance of measuring this fundamental component of protein thermodynamics. The simplicity of the approach enables easy implementation for laboratories whose central focus is not NMR spectroscopy, and its generality promises novel information on a broad range of important biological interactions and mechanisms including allostery.
Table 1.
General guidelines for selecting the type of relaxation experiment suitable for a given protein system of interest. Based on our laboratory’s experiences and data collection at 25˚C
| Experiment | Molecular Weight | Sample Concentration | High Resolution Structure |
|---|---|---|---|
| Full Ansiotropy Analysis | < 25 kDa | > 0.5 mM | Required |
| 2H R1, R1ρ | < 25 kDa | > 0.5 mM | Not Required |
| TROSY 2H | > 25 kDa | > 0.5 mM | Not Required |
| 13C R1, R1p | Small or Large | > 0.1 mM | Required |
| 1H-1H Cross Correlated | > 25 kDa | > 0.2 mM | Not Required |
Acknowledgements
Our work in this area has been supported by the National Institutes of Health, the National Science Foundation and the G. Harold and Leila Y. Mathers Foundation. We are grateful to Kim A. Sharp for continuing discussion and collaboration.
References
- Akke M, Bruschweiler R and Palmer AG (1993). Nmr Order Parameters and Free-Energy - an Analytical Approach and Its Application to Cooperative Ca2+ Binding by Calbindin-D(9k). Journal of the American Chemical Society 115(21), 9832–9833. [Google Scholar]
- Bernado P, de la Torre JG and Pons M (2002). Interpretation of N-15 NMR relaxation data of globular proteins using hydrodynamic calculations with HYDRONMR. Journal of Biomolecular NMR 23(2), 139–150. [DOI] [PubMed] [Google Scholar]
- Bertelsen EB, Chang L, Gestwicki JE and Zuiderweg ER (2009). Solution conformation of wild-type E. coli Hsp70 (DnaK) chaperone complexed with ADP and substrate. Proc Natl Acad Sci U S A 106(21), 8471–8476. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bruschweiler R, Liao XB and Wright PE (1995). Long-Range Motional Restrictions in a Multidomain Zinc-Finger Protein from Anisotropic Tumbling. Science 268(5212), 886–889. [DOI] [PubMed] [Google Scholar]
- Bruschweiler R (2003). New approaches to the dynamic interpretation and prediction of NMR relaxation data from proteins. Current Opinion in Structural Biology 13(2), 175–183. [DOI] [PubMed] [Google Scholar]
- Caffrey M, Kaufman J, Stahl SJ, Wingfield PT, Gronenborn AM and Clore GM (1998). 3D NMR experiments for measuring N-15 relaxation data of large proteins: Application to the 44 kDa ectodomain of SIV gp41. Journal of Magnetic Resonance 135(2), 368–372. [DOI] [PubMed] [Google Scholar]
- Capdevila DA, Braymer JJ, Edmonds KA, Wu H and Giedroc DP (2017). Entropy redistribution controls allostery in a metalloregulatory protein. Proc Natl Acad Sci U S A 114(17), 4424–4429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Capdevila DA, Edmonds KA, Campanello G, Wu H, Gonzalez-Gutierrez G and Giedroc DP (2018). Functional role of solvent entropy and conformational entropy of metal binding in dynamically-driven allostery. J Am Chem Soc 140 (29), 9108–911929953213 [Google Scholar]
- Caro JA, Harpole KW, Kasinath V, Lim J, Granja J, Valentine KG, et al. (2017). Entropy in molecular recognition by proteins. Proc Natl Acad Sci U S A 114(25), 6563–6568. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Caro JA, Harpole KW, Kasinath V, Lim J, Granja J, Valentine KG, et al. (2017). Entropy in molecular recognition by proteins. Proc. Nat. Acad. Sci. USA 114(25), 6563–6568. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen K and Tjandra N (2011). Water proton spin saturation affects measured protein backbone 15N spin relaxation rates. J Magn Reson 213(1), 151–157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chill JH, Louis JM, Baber JL and Bax A (2007). Measurement of N-15 relaxation in the detergent-solubilized tetrameric KcsA potassium channel (vol 36, pg 123, 2006). Journal of Biomolecular NMR 38(1), 105–105. [DOI] [PubMed] [Google Scholar]
- Cho CH, Urquidi J, Singh S and Robinson GW (1999). Thermal offset viscosities of liquid H2O, D2O, and T2O. Journal of Physical Chemistry B 103(11), 1991–1994. [Google Scholar]
- Clore GM, Szabo A, Bax A, Kay LE, Driscoll PC and Gronenborn AM (1990). Deviations from the simple 2-parameter model-free approach to the interpretation of N-15 nuclear magnetic-relaxation of proteins. Journal of the American Chemical Society 112(12), 4989–4991. [Google Scholar]
- de la Torre JG, Huertas ML and Carrasco B (2000). HYDRONMR: Prediction of NMR relaxation of globular proteins from atomic-level structures and hydrodynamic calculations. Journal of Magnetic Resonance 147(1), 138–146. [DOI] [PubMed] [Google Scholar]
- Dellwo MJ and Wand AJ (1989). Model-Independent and Model-Dependent Analysis of the Global and Internal Dynamics of Cyclosporine-A. Journal of the American Chemical Society 111(13), 4571–4578. [Google Scholar]
- Farrow NA, Muhandiram R, Singer AU, Pascal SM, Kay CM, Gish G, et al. (1994). Backbone dynamics of a free and a phosphopeptide-complexed Src homology-2 domain studied by N-15 NMR relaxation. Biochemistry 33(19), 5984–6003. [DOI] [PubMed] [Google Scholar]
- Findeisen M, Brand T and Berger S (2007). A H-1-NMR thermometer suitable for cryoprobes. Magnetic Resonance in Chemistry 45(2), 175–178. [DOI] [PubMed] [Google Scholar]
- Fischer MWF, Majumdar A and Zuiderweg ERP (1998). Protein NMR relaxation: theory, applications and outlook. Progress in Nuclear Magnetic Resonance Spectroscopy 33(207–272. [Google Scholar]
- Frederick KK, Marlow MS, Valentine KG and Wand AJ (2007). Conformational entropy in molecular recognition by proteins. Nature 448(7151), 325–329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frederick KK, Sharp KA, Warischalk N and Wand AJ (2008). Re-evaluation of the model-free analysis of fast internal motion in proteins using NMR relaxation. J Phys Chem B 112(38), 12095–12103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Freed JH (1977). Stochastic-Molecular Theory of Spin-Relaxation for Liquid-Crystals. Journal of Chemical Physics 66(9), 4183–4199. [Google Scholar]
- Frueh D (2002). Internal motions in proteins and interference effects in nuclear magnetic resonance. Progress in Nuclear Magnetic Resonance Spectroscopy 41(3–4), 305–324. [Google Scholar]
- Gans P, Hamelin O, Sounier R, Ayala I, Dura MA, Amero CD, et al. (2010). Stereospecific isotopic labeling of methyl groups for NMR spectroscopic studies of high-molecular-weight proteins. Angewandte Chemie (International Edition) 49(11), 1958–1962. [DOI] [PubMed] [Google Scholar]
- Gardner KH, Zhang XC, Gehring K and Kay LE (1998). Solution NMR studies of a 42 KDa Escherichia coli maltose binding protein beta-cyclodextrin complex: Chemical shift assignments and analysis. Journal of the American Chemical Society 120(45), 11738–11748. [Google Scholar]
- Gledhill JM Jr., Walters BT and Wand AJ (2009). AMORE-HX: a multidimensional optimization of radial enhanced NMR-sampled hydrogen exchange. Journal of Biomolecular NMR 45(1–2), 233–239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gu Y, Hansen AL, Peng Y and Bruschweiler R (2016). Rapid Determination of Fast Protein Dynamics from NMR Chemical Exchange Saturation Transfer Data. Angew Chem Int Ed Engl 55(9), 3117–3119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Halle B (2009). The physical basis of model-free analysis of NMR relaxation data from proteins and complex fluids. J Chem Phys 131(22), 224507. [DOI] [PubMed] [Google Scholar]
- Hiyama Y, Niu CH, Silverton JV, Bavoso A and Torchia DA (1988). Determination of N-15 Chemical-Shift Tensor Via N-15-H-2 Dipolar Coupling in Boc-Glycylglycyl[N-15]Glycine Benzyl Ester. Journal of the American Chemical Society 110(8), 2378–2383. [Google Scholar]
- Hoch JC (1985). Maximum-Entropy Signal-Processing of Two-Dimensional Nmr Data. Journal of Magnetic Resonance 64(3), 436–440. [Google Scholar]
- Hoffman RE (2006). Standardization of chemical shifts of TMS and solvent signals in NMR solvents. Magnetic Resonance in Chemistry 44(6), 606–616. [DOI] [PubMed] [Google Scholar]
- Hyberts SG, Takeuchi K and Wagner G (2010). Poisson-Gap sampling and forward maximum entropy reconstruction for enhancing the resolution and sensitivity of protein NMR data. Journal of the American Chemical Society 132(7), 2145–+. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hyberts SG, Milbradt AG, Wagner AB, Arthanari H and Wagner G (2012). Application of iterative soft thresholding for fast reconstruction of NMR data non-uniformly sampled with multidimensional Poisson Gap scheduling. Journal of Biomolecular NMR 52(4), 315–327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hyberts SG, Robson SA and Wagner G (2013). Exploring signal-to-noise ratio and sensitivity in non-uniformly sampled multi-dimensional NMR spectra. Journal of Biomolecular NMR 55(2), 167–178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Igumenova TI, Frederick KK and Wand AJ (2006). Characterization of the fast dynamics of protein amino acid side chains using NMR relaxation in solution. Chemical Reviews 106(5), 1672–1699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ishima R, Louis JM and Torchia DA (1999). Transverse C-13 relaxation of CHD2 methyl isotopmers to detect slow conformational changes of protein side chains. Journal of the American Chemical Society 121(49), 11589–11590. [Google Scholar]
- Ishima R, Petkova AP, Louis JM and Torchia DA (2001). Comparison of methyl rotation axis order parameters derived from model-free analyses of H-2 and C-13 longitudinal and transverse relaxation rates measured in the same protein sample. Journal of the American Chemical Society 123(25), 6164–6171. [DOI] [PubMed] [Google Scholar]
- Jaremko L, Jaremko M, Nowakowski M and Ejchart A (2015). The Quest for Simplicity: Remarks on the Free-Approach Models. J Phys Chem B 119(36), 11978–11987. [DOI] [PubMed] [Google Scholar]
- Jaremko L, Jaremko M, Ejchart A and Nowakowski M (2018). Fast evaluation of protein dynamics from deficient (15)N relaxation data. J Biomolecular NMR 70(4), 219–228. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jarymowycz VA and Stone MJ (2006). Fast time scale dynamics of protein backbones: NMR relaxation methods, applications, and functional consequences. Chemical Reviews 106(5), 1624–1671. [DOI] [PubMed] [Google Scholar]
- Kamath U and Shriver JW (1989). Characterization of themotropic state changes in myosin subfragment-1 and heavy-meromyosin by UV difference spectroscopy. Journal of Biological Chemistry 264(10), 5586–5592. [PubMed] [Google Scholar]
- Karplus M, Ichiye T and Pettitt BM (1987). Configurational entropy of native proteins. Biophys. J 52(6), 1083–1085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kasinath V, Sharp KA and Wand AJ (2013). Microscopic insights into the NMR relaxation-based protein conformational entropy meter. J Am Chem Soc 135(40), 15092–15100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kay LE and Prestegard JH (1987). Methyl-Group Dynamics from Relaxation of Double Quantum Filtered NMR Signals - Application to Deoxycholate. Journal of the American Chemical Society 109(13), 3829–3835. [Google Scholar]
- Kay LE, Torchia DA and Bax A (1989). Backbone Dynamics of Proteins as Studied by N-15 Inverse Detected Heteronuclear Nmr-Spectroscopy - Application to Staphylococcal Nuclease. Biochemistry 28(23), 8972–8979. [DOI] [PubMed] [Google Scholar]
- Kay LE and Torchia DA (1991). The Effects of Dipolar Cross-Correlation on C-13 Methyl-Carbon T1, T2, and Noe Measurements in Macromolecules. Journal of Magnetic Resonance 95(3), 536–547. [Google Scholar]
- Kay LE, Bull TE, Nicholson LK, Griesinger C, Schwalbe H, Bax A, et al. (1992). The Measurement of Heteronuclear Transverse Relaxation-Times in Ax3 Spin Systems Via Polarization-Transfer Techniques. Journal of Magnetic Resonance 100(3), 538–558. [Google Scholar]
- Kelly AE, Ou HD, Withers R and Dotsch V (2002). Low-conductivity buffers for high-sensitivity NMR measurements. Journal of the American Chemical Society 124(40), 12013–12019. [DOI] [PubMed] [Google Scholar]
- Kim J, Ahuja LG, Chao FA, Xia Y, McClendon CL, Kornev AP, et al. (2017). A dynamic hydrophobic core orchestrates allostery in protein kinases. Sci Adv 3(4), e1600663. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kneller JM, Lu M and Bracken C (2002). An effective method for the discrimination of motional anisotropy and chemical exchange. Journal of the American Chemical Society 124(9), 1852–1853. [DOI] [PubMed] [Google Scholar]
- Korzhnev DM, Tischenko EV and Arseniev AS (2000). Off-resonance effects in 15N T2 CPMG measurements. J Biomolecular NMR 17(3), 231–237. [DOI] [PubMed] [Google Scholar]
- Korzhnev DM, Billeter M, Arseniev AS and Orekhov VY (2001). NMR studies of Brownian tumbling and internal motions in proteins. Progress in Nuclear Magnetic Resonance Spectroscopy 38(3), 197–266. [Google Scholar]
- Lakomek N-A, Ying J and Bax A (2012). Measurement of N-15 relaxation rates in perdeuterated proteins by TROSY-based methods. Journal of Biomolecular NMR 53(3), 209–221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee AL, Flynn PF and Wand AJ (1999). Comparison of H-2 and C-13 NMR relaxation techniques for the study of protein methyl group dynamics in solution. Journal of the American Chemical Society 121(12), 2891–2902. [Google Scholar]
- Lee AL and Wand AJ (1999). Assessing potential bias in the determination of rotational correlation times of proteins by NMR relaxation. Journal of Biomolecular NMR 13(2), 101–112. [DOI] [PubMed] [Google Scholar]
- Lee AL and Wand AJ (2001). Microscopic origins of entropy, heat capacity and the glass transition in proteins. Nature 411(6836), 501–504. [DOI] [PubMed] [Google Scholar]
- Lee AL, Sharp KA, Kranz JK, Song XJ and Wand AJ (2002). Temperature dependence of the internal dynamics of a calmodulin-peptide complex. Biochemistry 41(46), 13814–13825. [DOI] [PubMed] [Google Scholar]
- Lee AL, Sharp KA, Kranz JK, Song XJ and Wand AJ (2002). Temperature dependence of the internal dynamics of a calmodulin-peptide complex. Biochemistry 41(46), 13814–13825. [DOI] [PubMed] [Google Scholar]
- Lee D, Hilty C, Wider G and Wuthrich K (2006). Effective rotational correlation times of proteins from NMR relaxation interference. J Magn Reson 178(1), 72–76. [DOI] [PubMed] [Google Scholar]
- Lee LK, Rance M, Chazin WJ and Palmer AG (1997). Rotational diffusion anisotropy of proteins from simultaneous analysis of N-15 and C-13(alpha) nuclear spin relaxation. Journal of Biomolecular Nmr 9(3), 287–298. [DOI] [PubMed] [Google Scholar]
- Li Z, Raychaudhuri S and Wand AJ (1996). Insights into the local residual entropy of proteins provided by NMR relaxation. Protein Sci 5(12), 2647–2650. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liao X, Long D, Li DW, Bruschweiler R and Tugarinov V (2012). Probing side-chain dynamics in proteins by the measurement of nine deuterium relaxation rates per methyl group. J Phys Chem B 116(1), 606–620. [DOI] [PubMed] [Google Scholar]
- Linnet TE and Teilum K (2016). Non-uniform sampling of NMR relaxation data. Journal of Biomolecular NMR [DOI] [PubMed]
- Lipari G and Szabo A (1982). Model-free approach to the interpretation of nuclear magnetic-resonance relaxation in macromolecules 1. Theory and range of validity. Journal of the American Chemical Society 104(17), 4546–4559. [Google Scholar]
- Long D, Delaglio F, Sekhar A and Kay LE (2015). Probing invisible, excited protein states by non-uniformly sampled pseudo-4D CEST spectroscopy. Angewandte Chemie (International Edition) 54(36), 10507–10511. [DOI] [PubMed] [Google Scholar]
- Mandel AM, Akke M and Palmer AG 3rd (1995). Backbone dynamics of Escherichia coli ribonuclease HI: correlations with structure and function in an active enzyme. J Mol Biol 246(1), 144–163. [DOI] [PubMed] [Google Scholar]
- Marlow MS, Dogan J, Frederick KK, Valentine KG and Wand AJ (2010). The role of conformational entropy in molecular recognition by calmodulin. Nat Chem Biol 6(5), 352–358. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mayzel M, Ahlner A, Lundstrom P and Orekhov VY (2017). Measurement of protein backbone (13)CO and (15)N relaxation dispersion at high resolution. J Biomolecular NMR 69(1), 1–12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meirovitch E, Polimeno A and Freed JH (2010). Comment on “The physical basis of model-free analysis of NMR relaxation data from proteins and complex fluids” [J. Chem. Phys. 131, 224507 (2009)]. J Chem Phys 132(20), 207101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meirovitch E, Shapiro YE, Polimeno A and Freed JH (2010). Structural dynamics of bio-macromolecules by NMR: the slowly relaxing local structure approach. Prog Nucl Magn Reson Spectrosc 56(4), 360–405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Millet O, Muhandiram DR, Skrynnikov NR and Kay LE (2002). Deuterium spin probes of side-chain dynamics in proteins. 1. Measurement of five relaxation rates per deuteron in C-13-labeled and fractionally H-2-enriched proteins in solution. Journal of the American Chemical Society 124(22), 6439–6448. [DOI] [PubMed] [Google Scholar]
- Mittermaier A and Kay LE (1999). Measurement of methyl 2H quadrupolar couplings in oriented proteins. How uniform Is the quadrupolar coupling constant? J. Am. Chem. Soc 121(10608–10613. [Google Scholar]
- Miyanoiri Y, Takeda M, Okuma K, Ono AM, Terauchi T and Kainosho M (2013). Differential isotope-labeling for Leu and Val residues in a protein by E. coli cellular expression using stereo-specifically methyl labeled amino acids. J Biomolecular NMR 57(3), 237–249. [DOI] [PubMed] [Google Scholar]
- Miyanoiri Y, Ishida Y, Takeda M, Terauchi T, Inouye M and Kainosho M (2016). Highly efficient residue-selective labeling with isotope-labeled Ile, Leu, and Val using a new auxotrophic E-coli strain. Journal of Biomolecular Nmr 65(2), 109–119. [DOI] [PubMed] [Google Scholar]
- Mobli M and Hoch JC (2015). Nonuniform sampling and non-Fourier signal processing methods in multidimensional NMR. Progress in Nuclear Magnetic Resonance Spectroscopy 86–87(80–80. [DOI] [PMC free article] [PubMed]
- Monneau YR, Ishida Y, Rossi P, Saio T, Tzeng SR, Inouye M, et al. (2016). Exploiting E. coli auxotrophs for leucine, valine, and threonine specific methyl labeling of large proteins for NMR applications. J Biomolecular NMR 65(2), 99–108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moorman VR, Valentine KG and Wand AJ (2012). The dynamical response of hen egg white lysozyme to the binding of a carbohydrate ligand. Protein Sci 21(7), 1066–1073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muchmore DC, McIntosh LP, Russell CB, Anderson DE and Dahlquist FW (1989). Expression and nitrogen-15 labeling of proteins for proton and nitrogen-15 nuclear magnetic resonance. Methods Enzymol 177(44–73. [DOI] [PubMed] [Google Scholar]
- Muhandiram DR, Yamazaki T, Sykes BD and Kay LE (1995). Measurement of H-2 T-1 and T-1p Relaxation-Times in Uniformly C-13-Labeled and Fractionally H-2-Labeled Proteins in Solution. Journal of the American Chemical Society 117(46), 11536–11544. [Google Scholar]
- Muller N, Bodenhausen G and Ernst RR (1987). Relaxation-Induced Violations of Coherence Transfer Selection-Rules in Nuclear-Magnetic-Resonance. Journal of Magnetic Resonance 75(2), 297–334. [Google Scholar]
- Nicholas MP, Eryilmaz E, Ferrage F, Cowburn D and Ghose R (2010). Nuclear spin relaxation in isotropic and anisotropic media. Progress in Nuclear Magnetic Resonance Spectroscopy 57(2), 111–158. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nucci NV, Marques BS, Bedard S, Dogan J, Gledhill JM Jr., Moorman VR, et al. (2011). Optimization of NMR spectroscopy of encapsulated proteins dissolved in low viscosity fluids. Journal of Biomolecular NMR 50(4), 421–430. [DOI] [PMC free article] [PubMed] [Google Scholar]
- O’Brien ES, Lin DW, Fuglestad B, Stetz MA, Gosse T, Tommos C, et al. (2018). Improving yields of deuterated, methyl labeled protein by growing in H2O. J Biomolecular NMR [DOI] [PMC free article] [PubMed]
- Ollerenshaw JE, Tugarinov V and Kay LE (2003). Methyl TROSY: explanation and experimental verification. Magnetic Resonance in Chemistry 41(10), 843–852. [Google Scholar]
- Ottiger M and Bax A (1998). Determination of relative N-HN, N-C¢, CR-C¢, and CR-HR effective bond lengths in a protein by NMR in a dilute liquid crystalline phase. J. Am. Chem. Soc 120(12334–12341. [Google Scholar]
- Pelupessy P, Espallargas GM and Bodenhausen G (2003). Symmetrical reconversion: measuring cross-correlation rates with enhanced accuracy. Journal of Magnetic Resonance 161(2), 258–264. [DOI] [PubMed] [Google Scholar]
- Pervushin K, Riek R, Wider G and Wuthrich K (1997). Attenuated T2 relaxation by mutual cancellation of dipole-dipole coupling and chemical shift anisotropy indicates an avenue to NMR structures of very large biological macromolecules in solution. Proc Natl Acad Sci U S A 94(23), 12366–12371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Polnaszek CF and Freed JH (1975). Electron-Spin Resonance Studies of Anisotropic Ordering, Spin Relaxation, and Slow Tumbling in Liquid-Crystalline Solvents. Journal of Physical Chemistry 79(21), 2283–2306. [Google Scholar]
- Popovych N, Sun S, Ebright RH and Kalodimos CG (2006). Dynamically driven protein allostery. Nat Struct Mol Biol 13(9), 831–838. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prabhu NV, Lee AL, Wand AJ and Sharp KA (2003). Dynamics and entropy of a calmodulin-peptide complex studied by NMR and molecular dynamics. Biochemistry 42(2), 562–570. [DOI] [PubMed] [Google Scholar]
- Raiford DS, Fisk CL and Becker ED (1979). Calibration of Methanol and Ethylene-Glycol Nuclear Magnetic-Resonance Thermometers. Analytical Chemistry 51(12), 2050–2051. [Google Scholar]
- Reif B, Diener A, Hennig M, Maurer M and Griesinger C (2000). Cross-correlated relaxation for the measurement of angles between tensorial interactions. Journal of Magnetic Resonance 143(1), 45–68. [DOI] [PubMed] [Google Scholar]
- Schurr JM, Babcock HP and Fujimoto BS (1994). A Test of the Model-Free Formulas - Effects of Anisotropic Rotational Diffusion and Dimerization. Journal of Magnetic Resonance Series B 105(3), 211–224. [DOI] [PubMed] [Google Scholar]
- Sharp KA, O’Brien E, Kasinath V and Wand AJ (2015). On the relationship between NMR-derived amide order parameters and protein backbone entropy changes. Proteins 83(5), 922–930. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Skelton NJ, Palmer AG, Akke M, Kordel J, Rance M and Chazin WJ (1993). Practical aspects of 2-dimensional proton-detected N-15 spin relaxation measurements. Journal of Magnetic Resonance Series B 102(3), 253–264. [Google Scholar]
- Skrynnikov NR, Millet O and Kay LE (2002). Deuterium spin probes of side-chain dynamics in proteins. 2. Spectral density mapping and identification of nanosecond time-scale side-chain motions. Journal of the American Chemical Society 124(22), 6449–6460. [DOI] [PubMed] [Google Scholar]
- Song XJ, Flynn PF, Sharp KA and Wand AJ (2007). Temperature dependence of fast dynamics in proteins. Biophys J 92(6), L43–45. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stetz MA and Wand AJ (2016). Accurate determination of rates from non-uniformly sampled relaxation data. J Biomolecular NMR 65(3–4), 157–170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun H, Kay LE and Tugarinov V (2011). An optimized relaxation-based coherence transfer NMR experiment for the measurement of side-chain order in methyl-protonated, highly deuterated proteins. J Phys Chem B 115(49), 14878–14884. [DOI] [PubMed] [Google Scholar]
- Takeuchi K, Tokunaga Y, Imai M, Takahashi H and Shimada I (2014). Dynamic multidrug recognition by multidrug transcriptional repressor LmrR. Sci Rep 4(6922. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tjandra N, Feller SE, Pastor RW and Bax A (1995). Rotational diffusion anisotropy of human ubiquitin from N-15 NMR relaxation. Journal of the American Chemical Society 117(50), 12562–12566. [Google Scholar]
- Tugarinov V, Liang ZC, Shapiro YE, Freed JH and Meirovitch E (2001). A structural mode-coupling approach to N-15 NMR relaxation in proteins. Journal of the American Chemical Society 123(13), 3055–3063. [DOI] [PubMed] [Google Scholar]
- Tugarinov V, Muhandiram R, Ayed A and Kay LE (2002). Four-dimensional NMR spectroscopy of a 723-residue protein: chemical shift assignments and secondary structure of malate synthase g. J Am Chem Soc 124(34), 10025–10035. [DOI] [PubMed] [Google Scholar]
- Tugarinov V, Choy WY, Kupce E and Kay LE (2004). Addressing the overlap problem in the quantitative analysis of two dimensional NMR spectra: application to (15)N relaxation measurements. J Biomolecular NMR 30(3), 347–352. [DOI] [PubMed] [Google Scholar]
- Tugarinov V and Kay LE (2004). H-1, C-13-H-1, H-1 dipolar cross-correlated spin relaxation in methyl groups. Journal of Biomolecular Nmr 29(3), 369–376. [DOI] [PubMed] [Google Scholar]
- Tugarinov V, Scheurer C, Bruschweiler R and Kay LE (2004). Estimates of methyl C-13 and H-1 CSA values (Delta sigma) in proteins from cross-correlated spin relaxation. Journal of Biomolecular Nmr 30(4), 397–406. [DOI] [PubMed] [Google Scholar]
- Tugarinov V and Kay LE (2005). Quantitative C-13 and H-2 NMR relaxation studies of the 723-residue enzyme malate synthase g reveal a dynamic binding interface. Biochemistry 44(49), 15970–15977. [DOI] [PubMed] [Google Scholar]
- Tugarinov V, Kanelis V and Kay LE (2006). Isotope labeling strategies for the study of high-molecular-weight proteins by solution NMR spectroscopy. Nature Protocols 1(2), 749–754. [DOI] [PubMed] [Google Scholar]
- Tugarinov V and Kay LE (2006). Relaxation rates of degenerate H-1 transitions in methyl groups of proteins as reporters of side-chain dynamics. Journal of the American Chemical Society 128(22), 7299–7308. [DOI] [PubMed] [Google Scholar]
- Tugarinov V and Kay LE (2006). A 2H NMR relaxation experiment for the measurement of the time scale of methyl side-chain dynamics in large proteins. J Am Chem Soc 128(38), 12484–12489. [DOI] [PubMed] [Google Scholar]
- Tugarinov V, Ollerenshaw JE and Kay LE (2006). Dipolar dynamic frequency shifts in multiple-quantum spectra of methyl groups in proteins: correlation with side-chain motion. Magnetic Resonance in Chemistry 44(S122–S129. [DOI] [PubMed] [Google Scholar]
- Tugarinov V, Sprangers R and Kay LE (2007). Probing side-chain dynamics in the proteasome by relaxation violated coherence transfer NMR spectroscopy. J Am Chem Soc 129(6), 1743–1750. [DOI] [PubMed] [Google Scholar]
- Tzeng SR and Kalodimos CG (2009). Dynamic activation of an allosteric regulatory protein. Nature 462(7271), 368–372. [DOI] [PubMed] [Google Scholar]
- Tzeng SR and Kalodimos CG (2012). Protein activity regulation by conformational entropy. Nature 488(7410), 236–240. [DOI] [PubMed] [Google Scholar]
- Vold RR and Vold RL (1976). Transverse Relaxation in Heteronuclear Coupled Spin Systems - Ax, Ax2, Ax3, and Axy. Journal of Chemical Physics 64(1), 320–332. [Google Scholar]
- Weaver DS and Zuiderweg ERP (2008). eta(z)/kappa: A transverse relaxation optimized spectroscopy NMR experiment measuring longitudinal relaxation interference. Journal of Chemical Physics 128(15), [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weaver DS and Zuiderweg ERP (2009). Protein proton-proton dynamics from amide proton spin flip rates. Journal of Biomolecular Nmr 45(1–2), 99–119. [DOI] [PubMed] [Google Scholar]
- Werbelow LG and Grant DM (1977). Determination of Motional Asymmetry of Methyl Rotators from C-13 Spin Dynamics. Canadian Journal of Chemistry-Revue Canadienne De Chimie 55(9), 1558–1563. [Google Scholar]
- Woessner DE (1962). Nuclear Spin Relaxation in Ellipsoids Undergoing Rotational Brownian Motion. Journal of Chemical Physics 37(3), 647–&. [Google Scholar]
- Yip GN and Zuiderweg ER (2004). A phase cycle scheme that significantly suppresses offset-dependent artifacts in the R2-CPMG 15N relaxation experiment. J Magn Reson 171(1), 25–36. [DOI] [PubMed] [Google Scholar]
- Zheng ZW, Czaplicki J and Jardetzky O (1995). Backbone Dynamics of Trp Repressor Studied by N-15 Nmr Relaxation. Biochemistry 34(15), 5212–5223. [DOI] [PubMed] [Google Scholar]
- Zhu G, Xia Y, Nicholson LK and Sze KH (2000). Protein dynamics measurements by TROSY-based NMR experiments. J Magn Reson 143(2), 423–426. [DOI] [PubMed] [Google Scholar]