Fully Automatic Left Atrium Segmentation from Late Gadolinium Enhanced Magnetic Resonance Imaging Using a Dual Fully Convolutional Neural Network

Abstract

Atrial fibrillation (AF) is the most prevalent form of cardiac arrhythmia. Current treatments for AF remain suboptimal due to a lack of understanding of the underlying atrial structures that directly sustain AF. Existing approaches for analyzing atrial structures in 3D, especially from late gadolinium-enhanced (LGE)-MRIs, rely heavily on manual segmentation methods which are extremely labor-intensive and prone to errors. As a result, a robust and automated method for analyzing atrial structures in 3D is of high interest. We have therefore developed AtriaNet, a 16-layer convolutional neural network (CNN), on 154 3D LGE-MRIs with a spatial resolution of 0.625 mm × 0.625 mm × 1.25 mm from patients with AF, to automatically segment the left atrial (LA) epicardium and endocardium. AtriaNet consists of a multi-scaled, dual pathway architecture that captures both the local atrial tissue geometry, and the global positional information of LA using 13 successive convolutions, and 3 further convolutions for merging. By utilizing computationally efficient batch prediction, AtriaNet was able to successfully process each 3D LGE-MRI within one minute. Furthermore, benchmarking experiments showed that AtriaNet outperformed state-of-the-art CNNs, with a DICE score of 0.940 and 0.942 for the LA epicardium and endocardium respectively, and an inter-patient variance of <0.001. The estimated LA diameter and volume computed from the automatic segmentations were accurate to within 1.59 mm and 4.01 cm³ of the ground truths. Our proposed CNN was tested on the largest known dataset for LA segmentation, and to the best of our knowledge, it is the most robust approach that has ever been developed for segmenting LGE-MRIs. The increased accuracy of atrial reconstruction and analysis could potentially improve the understanding and treatment of AF.

I. INTRODUCTION

Atrial fibrillation (AF), leading to an irregular and rapid heart rate, is the most common sustained heart rhythm disturbance. AF is associated with substantial morbidity and mortality, causing 1 out of 5 strokes in people aged over 60 years [1]. The current overall prevalence of AF is about 2% in industrialized countries and is projected to more than double in the following couple of decades. Current clinical treatments for AF perform poorly due to a lack of basic understanding of the underlying atrial anatomical structure, which directly sustains AF in the human atria [2, 3].

AF, especially persistent AF, is driven by complex substrates, which are widely distributed throughout both atrial chambers [4]. Repeated episodes of AF also produce further changes in the structural properties of the atria, i.e., atrial structural remodeling (dilatation, myofiber changes and fibrosis) [5–7]. As a result, direct study of the atrial structure and its changes in patients with AF is vital to the understanding and treatment of AF.

Nowadays, gadolinium-based contrast agents are used in a third of all MRI scans to improve the clarity of the images of a patient’s internal structures including the heart, by improving the visibility of often disease-associated structures, such as fibrosis/scarring, inflammation, tumors, and blood vessels. Late gadolinium-enhanced magnetic resonance imaging (LGE-MRI) is widely used to study the extent and distribution of cardiac fibrosis/scarring [2, 8]. Clinical studies in AF patients using LGE-MRI suggest that the extent and distribution of atrial fibrosis (Utah stages I-IV) are reliable predictors of catheter ablation success rate and can be used for patient stratification for medical management [9, 10]. A large ongoing clinical trial, LGE-MRI Guided Ablation vs. Conventional Catheter Ablation of Atrial Fibrillation (DECAAF II), evaluates conventional catheter ablation treatment vs. catheter ablation guided by LGE-MRI which shows the area of fibrosis in the heart. Furthermore, left atrial (LA) diameter and volume computed from 3D LGE-MRIs provide reliable information for clinical diagnosis and treatment stratification [11].

Atrial segmentation is a crucial task for aiding medical management for AF patients based on structural analysis of the segmented 3D geometry and has led to many prior studies investigating algorithms for fully automatic atrial segmentation, especially for the LA. A benchmark study published by Tobon-Gomez et al. compared the performance of nine different algorithms for LA segmentation from non-gadolinium enhanced MRIs/CT and showed that methodologies combining statistical models with regional growing approaches were the most effective [13]. Similar techniques have also been proposed and further improved upon for segmenting the LA from LGE-MRIs in studies by Veni et al. [14], Zhu et al. [15] and Tao et al. [16]. Despite these recent efforts, most of the existing structural analysis studies, especially those that utilize clinical LGE-MRIs, are still based on labor-intensive and error-prone manual segmentation approaches [9, 10, 12]. This is mainly due to the limitations of current automated methodologies requiring supporting information which are often not available, such as shape priors for initialization [15, 17] or additional magnetic resonance angiography (MRA) sequences to aid the segmentation process [16]. The nine algorithms mentioned in the benchmarking study [13] were effective in segmenting the LA from non-gadolinium enhanced MRIs. However, they are also difficult to apply to the LGE-MRIs directly, as the (normal) atrial anatomy is more attenuated by the contrast agent and they are based on conventional approaches. There is, therefore, an urgent need for an intelligent algorithm that can perform fully automatic atrial segmentation directly from LGE-MRIs, particularly for LA, for accurate reconstruction and measurement of the atrial geometry for clinical usage.

Machine learning is a class of algorithms which learn from a given set of data and labels by creating their understanding in a process known as feature separation. Classification and segmentation are two typical problems solved with machine learning algorithms. In traditional machine learning classification algorithms such as support vector machines [18], random forests [19] and K-nearest neighbor [20], a set of features is generated manually from the raw data, and fed into a classifier. This requires domain expertise in the field of the task at hand, as a rigorous feature selection procedure is required to find the optimal feature combination for learning. Optimization is then performed on the features to minimize an objective function, which results in the linear separation of the data from different classes. However, despite the effectiveness of these algorithms over the years, the manual feature engineering and algorithm selection processes are major bottlenecks for improving the performance on classification tasks.

Neural networks [21] is a category of modern machine learning algorithms, and have been applied in many different fields including medicine and bioengineering. The effectiveness of neural networks lies in their ability to automate the feature extraction step. By eliminating the need for domain expertise when applying neural networks, the performance of these algorithms will only increase with the increasing amount of data available. Convolutional neural networks (CNNs) [22], which became popularized less than a decade ago, specialize in image processing, such as image classification [23], [24], [25], [26], object detection [27] and semantic segmentation [28], [29]. Thus, CNNs provide the ideal foundation for tackling the challenging task of atrium segmentation.

In this paper, we propose and evaluate a novel CNN for fully automatic LA segmentation. Our method is developed and validated on the largest 3D LGE-MRI dataset from 154 patients with AF from The University of Utah. This exciting development is a very important step towards patient-specific diagnostics and treatment.

II. METHODS

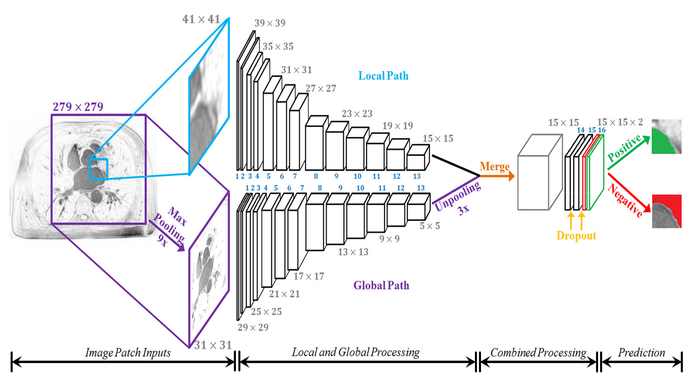
Direct LA segmentation from raw LGE-MRIs is challenging due to the massive imbalance between positive (thin wall LA) and negative (background) pixels. To overcome this, we propose a novel dual fully convolutional neural network (FCNN), with the alias AtriaNet (Fig. 1), that contains two parallel pathways to process both local and global information. The details of the configuration of AtriaNet are provided in Table. I. AtriaNet performs 2D patch-wise classification at every 15 × 15 region across each slice of a 3D LGE-MRI. The inputs into the network are a local 41 × 41 patch, and a global 279 × 279 patch, both centered on the 15 × 15 prediction region. The global pathway captures information about the position and gross structure of LA. To reduce the number of parameters used in the resultant AtriaNet, the large global patch is pooled to a smaller size. The local pathway captures the exact geometry of LA for every pixel within its small neighborhood. The two patches are separately convolved through 13 convolutional layers (conv 1 to conv 13) and are merged to combine the information by performing an element-wise sum. To maintain dimensional consistency, the last layer in the global path is unpooled to match the size of the local pathway with nearest neighbor interpolation. The network is then convolved two more times (conv 14 and conv 15) to further process the combined information where the output is produced in the final layer with 2 feature maps (conv 16). The Rectified Linear activation function is used for all layers apart from the last layer which uses a softmax activation function. Dropout is applied to convolutional layers 14 and 15 to reduce overfitting with a dropout rate of 50%. During testing, the network scans through each 15 × 15 region for every slice of a 3D LGE-MRI without overlapping, and feeds the corresponding 41 × 41 and 279 × 279 patches centered around it as input.

Fig. 1.

The architecture of the proposed dual fully convolutional neural network for atrial segmentation (AtriaNet). The size of the image at every second layer is shown, further details are in Table. I. The parallel (global and local) pathways process each MRI slice at different resolutions, which are combined at the end of the network. The final output has two feature maps, denoting the probability of a positive or negative pixel classification for each 15×15 patch respectively.

TABLE I.

The configurations of AtriaNet

Layer	Filter size	Stride	Feature Maps	Image Size (Local Path)	Image Size (Global Path)	Number of Parameters
Input	-	-	1	41 × 41	279 × 279	0
Pooling	9 × 9	9	1	-	31 × 31	0
Conv 1	3 × 3	1	64	39 × 39	29 × 29	3 × 3 × 1 × 64
Conv 2	3 × 3	1	64	37 × 37	27 × 27	3 × 3 × 64 × 64
Conv 3	3 × 3	1	128	35 × 35	25 × 25	3 × 3 × 64 × 128
Conv 4	3 × 3	1	128	33 × 33	23 × 23	3 × 3 × 128 × 128
Conv 5	3 × 3	1	256	31 × 31	21 × 21	3 × 3 × 128 × 256
Conv 6	3 × 3	1	256	29 × 29	19 × 19	3 × 3 × 256 × 256
Conv 7	3 × 3	1	256	27 × 27	17 × 17	3 × 3 × 256 × 256
Conv 8	3 × 3	1	512	25 × 25	15 × 15	3 × 3 × 256 × 512
Conv 9	3 × 3	1	512	23 × 23	13 × 13	3 × 3 × 512 × 512
Conv 10	3 × 3	1	512	21 × 21	11 × 11	3 × 3 × 512 × 512
Conv 11	3 × 3	1	512	19 × 19	9 × 9	3 × 3 × 512 × 512
Conv 12	3 × 3	1	512	17 × 17	7 × 7	3 × 3 × 512 × 512
Conv 13	3 × 3	1	512	15 × 15	5 × 5	3 × 3 × 512 × 512
Unpooling	3 × 3	3	512	-	15 × 15	0
Merge	-	-	512	15 × 15		0
Conv 14	1 × 1	1	128	15 × 15		3 × 3 × 512 × 128
Dropout 1	-	-	-	-		0
Conv 15	1 × 1	1	128	15 × 15		3 × 3 × 128 × 128
Dropout 2	-	-	-	-		0
Conv 16	1 × 1	1	2	15 × 15		3 × 3 × 128 × 2
Output	-	-	1	15 × 15		0
						Total: 15,448,896

*Conv layers did not contain padding

III. EXPERIMENTAL SETUP

A. LGE-MRI Patient Data

154 3D LGE-MRIs from 60 patients with AF prior to 3 to 27 months post clinical ablation were provided from the University of Utah [9]. The in vivo patient images were acquired at a spatial resolution of 0.625 mm × 0.625 mm × 1.25 mm using either a 1.5 Tesla Avanto or 3.0 Tesla Verio clinical whole-body scanner. Each 3D LGE-MRI scan contains 44 slices along the Z direction, each with an XY spatial size of 640 × 640 pixels or 576 × 576 pixels. The LGE-MRIs are in grayscale whereas the segmentation masks are in binary. The LA segmentations include the pulmonary vein regions, the mitral valve, and the left atrial appendage. Each 3D LGE-MRI patient data (both pre and post ablation) include two manually segmented masks of the LA epicardium and endocardium by experts [10], which were used as the ground truths in our study.

B. Pre-Processing

The 154 3D LGE-MRI dataset was randomly split into training (N = 110), validation (N = 22) and testing (N = 22) sets in our study (Table. II). Since each patient had multiple 3D LGE-MRIs for pre and post ablation, the data was split so that all scans from each unique patient were only in one of the training, validation or testing sets. Evaluation could, therefore, be performed to compare whether pre or post ablation impacts the segmentation accuracy. Training, validation, and testing for LA epicardium and endocardium segmentation were done separately. All individual raw 3D LGE-MRI data was normalized by using its mean and standard deviations of color intensity.

TABLE II.

The number of 3D late gadolinium-enhanced (LGE)-MRIs used for training, validation and testing.

	Number of Patients		Pre-Ablation	Post-Ablation	Total
Training Set #	40		40	70	110
Validation Set #	9		9	13	22
Testing Set #	11		11	11	22

Direct training on the entire LGE-MRI data was ineffective due to the small proportion of positive pixels per slice, which led to the data being very sparse and unbalanced. To alleviate this, smaller patches which contained a balanced number of positive and negative pixels were extracted from the training set. The same number of patches from the background were also sampled to match that of patches containing positive pixels used during training. Note that for every 15 × 15 label sampled (for evaluation during training), there was a need to generate a 41 × 41 local patch and a 279 × 279 global patch from original raw LGE-MRIs as inputs. Since the input patches of AtriaNet (41 × 41 and 279 × 279) were much larger than the 15 × 15 output patch, there were substantial overlaps when the input patches were sampled.

Data augmentation was also used to artificially increase the amount of data. Elastic deformations, affine transformations and warping were found to be effective in increasing the performance in previous studies [36]. The proportion of the training set to augment was tuned as to introduce a sufficient amount of new data but not cause overfitting.

C. Training

The adaptive moment estimation (ADAM) optimizer [37], a type of gradient descent algorithm, was used for optimization. The learning rate was kept constant at 0.0001 without adjustment and the exponential decay rates of the 1^st and 2^nd moment estimates were set to 0.9 and 0.999 respectively. During training, the accuracy was evaluated on the validation dataset after each iteration of all the training data through the network. This was repeated until the validation accuracy stopped increasing, and the best performing model was selected for evaluation on the test set. The network was developed in TensorFlow [38], an open-source deep learning library for Python, and was trained on an NVIDIA Titan X-Pascal GPU with 3840 CUDA cores and 12GB RAM. The training phase took approximately four hours and predictions on each 3D LGE-MRI took around one minute to compute.

D. Post Processing and Evaluation

Since atrial tissue is continuous and smooth, the raw segmentation output from AtriaNet was passed through a 3D Gaussian filter to enhance the segmented tissue mask. Isolated mask islands were removed automatically, keeping only the largest connected tissue in 3D as the final LA segmentation. Thresholding was applied to restrict the pixels to binary values, ensuring the atrial geometry was smooth and sharp.

Evaluation against the ground truths was done to evaluate the accuracy of AtriaNet for each 3D LGE-MRI data. Sensitivity, specificity, DICE and Hausdorff distance (HD) [39] measurements were used, as well as clinical relevant measurements (LA anterior-posterior diameter and 3D LA volume). The DICE score is calculated as

$$DICE=\frac{2N_{truepositive}}{2N_{truepositive}+N_{falsepositive}+N_{falsepositive}}$$ (15)

and was used during both validation and testing. The HD is defined as the greatest value of the distances from any point in one set to its corresponding closest point in another set. It is written as

$$HD(G,P)=\underset{g\in G}{max}\left\{\underset{p\in P}{\max }\left\{\sqrt{g^2-p^2}\right\}\right\}$$ (16)

for the two datasets of ground truth (G) and prediction (P).

The diameter and volume of the LA endocardium were evaluated to compare the potential measurement errors from the segmentation between the predictions and ground truths. The LA diameter, measured in millimeters, was calculated by finding the maximum distance from the anterior to the posterior of the LA endocardium. The LA volume, measured in cm³, was calculated by counting the total number of voxels within the endocardium and then scaling the sum by multiplying the original resolution of the LGE-MRI.

E. Hyper-Parameter Tuning

The proposed FCNN methodology consisted of multiple parameters which were carefully selected and validated through extensive experimentation. Various experiments were designed to evaluate the effects of different parameter values under controlled conditions on the validation and testing sets. The parameter values presented in Section II of this study were, therefore, the values which yielded the highest performance during these hyper-parameter tuning experiments.

Since the local and global input dimensions directly impacted the receptive field of AtriaNet, it was important to ensure that optimal values were selected so that AtriaNet was provided with sufficient information to efficiently capture the local and global features of the LA endocardium and epicardium. The input dimensions of the local and global path of AtriaNet were tuned by evaluating the network with a range of different combinations of local and global resolutions. These included local patch sizes ranging from 25 × 25 to 60 × 60 and global patches ranging from 252 × 252 to 306 × 306. During experimentation, all other parameters not being tuned were kept fixed to ensure fairness of comparison.

Single-step down-sampling was used in our network to minimize the computational burden of large input images. Comparisons were made between max-pooling and average pooling for this step. The pooling factor in the global pathway was also tuned to ensure that the network sufficiently retained the relevant global information while maintaining a low number of parameters. 5, 7, 9 and 11 sized filters were tested for pooling the global patch while the local patch remained fixed throughout the experiments. Since our proposed network required the dimensions of the global and local pathways to match during merging, the global input resolution was adjusted accordingly when testing different pooling factors. The unpooling layer was tested by comparing nearest neighbor, bi-linear and bi-cubic interpolation.

The sequence of values for the number of feature maps used for the convolutional layers throughout AtriaNet was tested and compared to ensure that the selected values produced the best segmentation performance without using excessive computation. Specifically, experiments were done comparing the proposed number of feature maps (Table I) with different versions of AtriaNet containing 0.25×, 0.5× and 2× the number of feature maps at each layer. This was expected to draw out the effects on the accuracy of segmentation with a network having significantly larger or smaller number of parameters. 3 × 3 filters were used for all convolutional layers due to their low computational costs and success in previously proposed literature [24, 26, 28, 29, 35, 40, 41].

Overfitting was a potential issue in larger neural networks due to the large number of parameters. To minimize this issue, dropout rates of 0%, 25%, 50% and 75% in AtriaNet were evaluated to find the most effective number of nodes to remove while still keeping enough nodes for sufficient feature learning.

F. Comparing Existing FCNNs for LA Segmentation

The robustness and superiority of AtriaNet was demonstrated by comparing its performance with current widely used CNN architectures for the task of LA endocardium segmentation using the same LGE-MRI dataset and same prior/post processing procedures. The networks investigated here included U-Net [35], Dilated U-Net [42], DeepOrgan [43] and V-Net [44], which are popular for medical image segmentation; and VGGNet [24], Inception [25] and ResNet [26] which have obtained state-of-the-art performances in image classification. Popular FCNNs for semantic segmentation such as FCN-8 [28], deconvolutional neural network (Deconv-Net) [29] and SegNet [45] were also investigated. Since the three classification networks were traditional CNNs, they were converted into FCNNs by replacing the fully connected layers at the end of the network with convolutional layers for pixel-wise segmentation prediction. The intermediate pooling layers were also removed to avoid significant losses in dimensionality. It should be noted that VGGNet with its fully connected layers removed, is the single-pathed version of our proposed FCNN, hence, the effect of having a dual-pathway was tested implicitly.

Since the mentioned architectures contained only one pathway, the impact of patch size equivalent to the local/global resolutions in AtriaNet was tested to evaluate its performance during the benchmark study. To ensure for a fair comparison of the different architectures, the same training, validation and testing datasets were used for LA endocardium segmentation. Due to the random initialization of the weight parameters, biases can be introduced in different training sessions where the accuracy can differ by a slight margin for the same network trained on the same data. To avoid this, each architecture was trained three times independently, and the results were averaged. All architectures were implemented using TensorFlow and trained from scratch to eliminate any source of bias from existing implementations. The default hyper-parameters, initializations and training schemes recommended by the original authors were used.

For further comparison, a previously proposed method for fully automatic LA segmentation was also compared with AtriaNet by executing an existing implementation of the algorithm on the testing data in our study and evaluating the generated segmented masks [15]. This allowed for a direct comparison of the effectiveness of our proposed method against a previous method used for the same task in terms of both the accuracy of segmentation and the computational efficiency.

IV. RESULTS

A. Optimal Hyper-Parameters

The results of the hyper-parameter tuning experiments are presented in this sub-section to validate the parameter choices used in our proposed AtriaNet. Table. III shows that in the case of a single path network, 41 × 41 was the optimal value for sufficiently capturing local information when used on its own. This also shows the importance of selecting the correct local patch as it significantly impacts the performance due to it being high resolution as opposed to the global patch which was pooled to a low-resolution input.

TABLE III.

DICE accuracies of AtriaNet with the single local pathway only, with different resolutions of input patches on 22 test data.

Local Patch Size	DICE Score
25 × 25	0.835
35 × 35	0.848
41 × 41	0.864
47 × 47	0.860
60 × 60	0.844

*All results shown are after data augmentation and post-processing

Table IV shows the performance of AtriaNet with different combinations of global and local input resolutions. It is important to note that due to the design of AtriaNet, only specific combinations of local and global resolutions are feasible such that they can merge together after conv 13. The results show that the proposed local (41 × 41) and global (279 × 279) resolutions produced the highest DICE score as it captured the local and global features more effectively than other values. These results demonstrate that using small inputs did not provide the network with enough information to sufficiently learn complex features, yet using large inputs was also problematic as they were more susceptible to overfitting.

TABLE IV.

The DICE accuracy on the 22 test data using AtriaNet with different local and global patch sizes.

Local Patch Size	Global Patch Size	DICE Score
32 × 32	252 × 252	0.930
35 × 35	261 × 261	0.932
41 × 41	279 × 279	0.942
44 × 44	288 × 288	0.938
47 × 47	297 × 297	0.933
50 × 50	306 × 306	0.926

*All results shown are after data augmentation and post-processing

Experimentation with max-pooling and average-pooling for the global pathway yielded no significant difference for the performance of AtriaNet. Experiments using nearest neighbor, bi-linear and bi-cubic interpolation also showed no significant difference for the unpooling layer. Results from tuning the pooling factors for the global pathway showed that 9 × 9 resulted in the best performance with a 0.942 DICE score. Filters deviating from this size performed worse as it either did not sufficiently capture enough global information, or important features were lost due to over down-sampling. This was reflected in the DICE scores from using 5 × 5, 7 × 7 and 11 × 11 pooling which were 0.913, 0.921 and 0.927 respectively.

Table V shows the performance of AtriaNet on the testing set with different numbers of feature maps in each layer. The DICE scores on the test data shows that the proposed values (Table I) produced the best segmentation performance. The models with a small number of feature maps did not contain a sufficient number of parameters to learn the complex features of the LA endocardium, while the models with a larger number of feature maps was more prone to over-fitting. Furthermore, increasing the number of feature maps significantly increased the computational expense, meaning that a model with a moderate number of feature maps was the most desirable.

TABLE V.

DICE scores for AtriaNet with different number of kernels at each layer from conv 1–13 for the 22 test data.

Number of Feature Maps per Layer	DICE Score
16–16-32–32-64–64-64–128-128–128-128–128-128	0.890
32–32-64–64-128–128-128–256-256–256-256–256-256	0.911
64–64-128–128-256–256-256–512-512–512-512–512-512	0.942
128–128-256–256-512–512-512–1024-1024–1024-1024–1024-1024	0.935

*All results shown are after data augmentation and post-processing

Hyper-parameter tuning of the dropout rates at the last layers of AtriaNet showed that 50% dropout provided the best balance between alleviating overfitting while still maintaining sufficient number of nodes in each layer for feature learning. This resulted in the 0.942 DICE score. Experiments showed that having no dropout produced the lowest DICE score of 0.927 and having 75% dropout resulted in a DICE score of 0.937 due to the excessive removal of parameters.

B. 3D Segmentation Results

Fig. 2 illustrates the segmentation and reconstruction results for the 3D LA epicardium for comparing the ground truth (1^st and 3^rd row) and the prediction segmentation by AtriaNet (2^nd and 4^th row) for 10 of 22 tested 3D LGE-MRIs (5 each for pre and post ablation). Overall, LA geometry was accurately reconstructed as the prediction captured both the general shape and the detailed curvature of the LA wall for each test 3D LGE-MRI scan (N = 22). The pulmonary veins were successfully captured as well, though the pulmonary veins segmented by AtriaNet was often smaller in diameter and did not extend out of the LA chamber as much as the ground truths. This was possibly due to the veins being relatively small and thin compared to LA, making it more difficult to predict.

Fig. 2.

The 3D reconstruction of the left atrial (LA) epicardium for pre (blue) and post (green) ablation for 10 test late gadolinium-enhanced (LGE)-MRIs out of 22. The 1^st and 3^rd rows are the ground truths and the 2^nd and 4^th rows are the segmentation results from AtriaNet. Each column contains LGE-MRI scans from the same patient.

The performance of AtriaNet was enhanced with data augmentation and post-processing. While elastic deformations and affine transformations did not prove to be particularly effective, warping 50% of the original data improved the model’s performance by 0.005. As a result, the training set was increased to 1.5 times its original size as the additional 50% consisted of randomly sampled augmented data. Post-processing improved the DICE score for both LA epicardium and endocardium segmentation by ~0.015. Table. VI shows the final evaluation metrics for both of the segmentation tasks grouped by pre and post ablation LGE-MRIs. The DICE segmentation accuracy was approximately equal for both the epicardium and endocardium (0.940 vs 0.942), however, the endocardium segmentation had a slightly higher sensitivity of 0.918, which implies that a slightly greater proportion of the positive pixels were successfully detected compared to that of the epicardium segmentation. The 0.999 specificity suggests that AtriaNet was extremely effective in detecting background pixels, and the >0.9 sensitivity shows AtriaNet was also very effective in detecting the positive pixels for accurate segmentation.

TABLE VI.

Evaluation metrics for left atrial (LA) epicardium (epi) and endocardium (endo) segmentation for the 22 test 3D late gadolinium-enhanced (LGE)-MRIs.

		DICE	Sensitivity	Specificity	Hausdorff Distance
LAEpi	Pre	0.943 ± 0.008	0.900 ± 0.045	0.999 ± 0.001	10.64 ± 2.08 mm
	Post	0.937 ± 0.019	0.902 ± 0.045	0.999 ± 0.001	10.76 ± 2.43 mm
	Overall	0.940 ± 0.014	0.901 ± 0.044	0.999 ± 0.001	10.70 ± 2.21 mm
LA Endo	Pre	0.945 ± 0.008	0.911 ± 0.035	0.999 ± 0.001	10.43 ± 2.29 mm
	Post	0.939 ± 0.019	0.926 ± 0.038	0.999 ± 0.001	10.07 ± 2.27 mm
	Overall	0.942 ± 0.014	0. 918 ± 0.036	0.999 ± 0.001	10.25 ± 2.24 mm

*All results shown are after data augmentation and post-processing

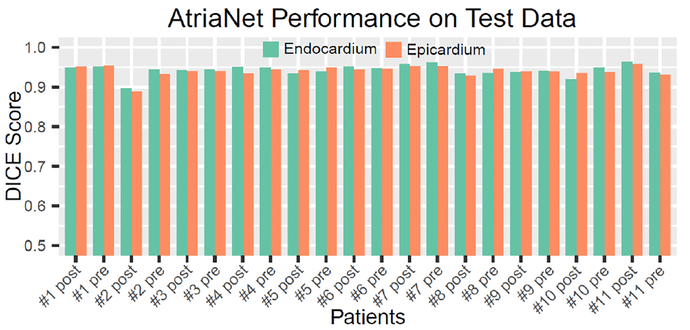
The DICE score for each test patient data is shown in Fig. 3. The results show that AtriaNet was very consistent in reconstructing both the LA epicardium and endocardium as seen from the small variation of the DICE scores across different patients. The standard deviation of the DICE scores for both epicardium and endocardium segmentation was 0.014. Table. VII shows the predicted and ground truth measurements for the LA diameter and volume, as well as their absolute and relative errors. The predicted masks were accurate within 1.59 mm and 4.01 cm³ of the ground truths on average for the diameter and volume measurements respectively. Overall, the segmentations for the pre-ablation patients were more accurate as seen from the higher DICE scores and lower relative errors of the estimated LA dimensions.

Fig. 3.

The DICE score for segmentation of the left atrial (LA) epicardium and endocardium for each of the 22 test 3D late gadolinium-enhanced (LGE)-MRIs.

TABLE VII.

The left atrial (LA) diameter and volume measurements and errors for the 22 test 3D late gadolinium-enhanced (LGE)-MRIs.

		Ground Truth Measurement	Predicted Measurement	Absolute Error	Relative Error
LA Diameter (mm)	Pre	40.85 ± 7.07	40.17 ± 7.59	1.36 ± 1.18	3.3 %
	Post	39.43 ± 7.22	39.78 ± 7.48	1.82 ± 2.23	4.6 %
	Overall	40.14 ± 7.01	39.97 ± 7.36	1.59 ± 1.75	3.9 %
LA Volume (cm3)	Pre	56.98 ± 19.73	58.50 ± 21.15	3.35 ± 2.91	5.9 %
	Post	50.56 ± 17.99	54.18 ± 20.71	4.67 ± 4.09	9.2 %
	Overall	53.77 ± 18.72	56.34 ± 20.55	4.01 ± 3.50	7.5 %

*All results shown are after data augmentation and post-processing

C. Error Analysis of Segmentation

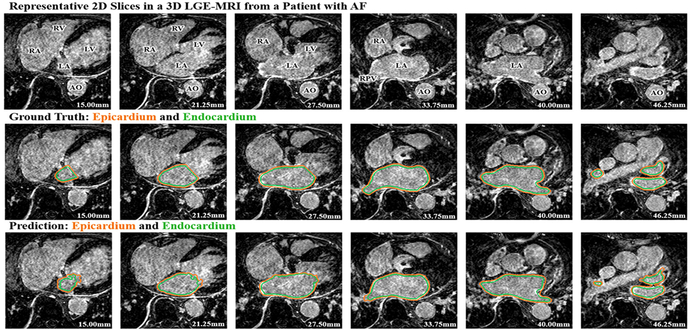
A detailed post analysis of the segmentation errors was performed for each test patient data to compare the predictions to the ground truths for each image slice throughout each 3D LGE-MRI. Fig. 4 illustrates the segmentation results for the LA epicardium and endocardium by AtriaNet compared with the ground truth for selected slices at the same depth for a test 3D LGE-MRI. The results shown are representative of the errors seen in other test LGE-MRIs. The relative depth of each slice from the bottom of the LGE-MRI scan is provided in millimeters.

Fig. 4.

The left atrial (LA) epicardium (orange) and endocardium (green) segmentation results from the proposed AtriaNet compared to the ground truth for representative slices on the same 3D late gadolinium-enhanced (LGE)-MRI for test patient #5 (pre-ablation). The 1^st row is the raw LGE-MRI scan, the 2^nd row is the ground truth and the 3^rd row is the segmentation produced by AtriaNet. Each column displays the same LGE-MRI slice. The depth of the MRI for each slice is shown in mm. AO, aorta; LV, left ventricle; RA, right atrium; RV, right ventricle; RPV, right pulmonary vein.

As seen from Fig. 4, at the depth of 27.5 mm to 40 mm (middle sections of the 3D atria), AtriaNet produced more accurate reconstructions of the LA geometry. AtriaNet was able to successfully capture the curvature of the LA tissue in detail, while also showing a clear gap between the epicardium and endocardium denoting the LA wall tissue. The pulmonary vein regions were the main sources of error within these slices, as the segmentation was less accurate as seen from the bottom left part of LA at 33.75 mm and the bottom right part of the LA at 40.00 mm, where the segmentation was non-smooth and the thickness of the vein was underestimated.

D. Comparative Evaluation with Other FCNNs

Table. VIII compares the performance of different network architectures with AtriaNet after data augmentation and post-processing for LA endocardium segmentation on the same 22 3D LGE-MRI test dataset. The metrics of all single pathway networks when using the local resolution as input are shown. Benchmarking experiments on the architectures using the global resolution (not shown) resulted in substantially lower performances for all single-path approaches (~0.1 lower DICE score) compared with using the local resolution. The superiority of the local resolution as input for single pathway networks was due to the ability to achieve sharp segmentations given the high resolution of the local patches, while the global resolution alone is inferior as the image is low in resolution due to pooling.

TABLE VIII.

The evaluation metrics between different network architectures using the same late gadolinium-enhanced (LGE)-MRI data for training, validation and testing.

Architectures	LA Endocardium Segmentation
	DICE	Sensitivity	Specificity	HD
U-Net35	0.642	0.596	0.756	21.74 mm
Dilated U-Net42	0.687	0.612	0.794	20.18 mm
VGGNet24	0.864	0.799	0.950	13.76 mm
Inception25	0.792	0.765	0.871	16.08 mm
ResNet26	0.804	0.783	0.883	15.80 mm
FCN-828	0.558	0.500	0.665	24.53 mm
Deconv-Net29	0.500	0.498	0.656	25.44 mm
SegNet45	0.656	0.601	0.764	20.73 mm
V-Net44	0.696	0.623	0.810	19.46 mm
DeepOrgan43	0.632	0.584	0.731	22.98 mm
Zhu et al.15	0.821	0.801	0.899	14.89 mm
AtriaNet	0.942	0.918	0.999	10.25 mm

*LA = left atrium; All results shown are after data augmentation and post-processing

The popular medical image segmentation architectures [35, 44] and the recent state-of-the-art image classification architectures [24–26] adapted for segmentation were all outperformed by AtriaNet in both DICE and HD evaluation. The single path version of AtriaNet, VGGNet, was the second-best performing architecture, and showed the use of an additional pathway in AtriaNet improved the performance by a DICE score of 0.078. The evaluation metrics indicated that the use of a dual pathway in AtriaNet resulted in a significantly more effective architecture for performing accurate LA segmentation compared to other existing neural networks.

Comparisons between AtriaNet and the previously proposed LA segmentation algorithm by Zhu et al. also showed significant improvements in the accuracy of the endocardium reconstruction [15]. Not only did our approach outperform the previous study by over 10% in DICE score, runtime experiments on the same computing hardware revealed that AtriaNet was significantly faster, 1 minute vs. 22 minutes, at segmenting each 3D LGE-MRI in the test dataset.

V. DISCUSSION

Direct segmentation of atrial chambers from 3D LGE-MRIs is a challenging task. This is due to a lack of distinguishing features on the LGE-MRIs that enable the separation of atrial tissue from non-atrial regions, in addition to the poor image quality of LGE-MRIs due to motion artifacts, noise interference and significant variations in image intensities.

Currently, our study is among the few that have attempted at direct automatic segmentation of the LA from LGE-MRIs [14, 46, 47]. Out of all existing attempts, most of the LGE-MRI studies, either in-vivo or ex-vivo, have relied heavily on manual segmentation [9, 48–50]. There are few studies that have attempted to automate the direct segmentation process. The study by Veni et al. proposed was a shape-driven approach in which the posterior probability of the LA surface was expressed via Bayesian equations [15]. Zhu et al. also proposed a shape model for segmenting the LA and was enhanced by variational regional growth [15]. However, the methodologies of both of these studies required a shape prior for initialization which was generated either manually or based on strong assumptions from observing the data to segment. This is undesirable as it would be more time consuming than a fully automated approach and is also more susceptible to large variations in the data. Tao et al., on the other hand, proposed an approach which used global multi-atlas segmentation followed by a local refinement algorithm [16]. In contrast to the three previous studies, our methods do not require any manual initialization or the use of any additional information apart from LGE-MRIs. Furthermore, benchmarking results of AtriaNet showed significant improvements in the accuracy of the LA endocardium reconstruction, as well as significant computational advantages.

In contrast to direct segmentation, indirect segmentation of LA from LGE-MRIs is a more popular approach that can be achieved by utilizing paired 3D MRA with the LGE-MRIs from the same patient. The 3D MRA images consists of image features that are more distinguishable than those in the LGE-MRIs, which enable the distinction between atrial tissue and background. As a result, the 3D MRA images are relatively easy to segment, for which comparably more studies have been conducted to develop automatic segmentation approaches [13, 15, 51, 52]. Although some alternative conventional approaches outlined in a segmentation benchmarking study [13, 52] and the multi-view CNN approach conducted by Mortazi et al. [51] have achieved good LA segmentation performances, a mapping/fusion approach was needed in addition to their indirect segmentation approach to map the segmented masks of MRA images to the LGE-MRIs. This could introduce additional errors which limit the accuracy of such approaches [52]. In addition, the use of MRA images in indirect segmentation of LGE-MRI means that an extra 3D MRA scan is needed for each patient, which is time consuming and rather costly. In comparison, direct segmentation of LGE-MRIs using our proposed CNN is much more straight forward, efficient and accurate.

Nowadays, CNNs are widely used for image classification and segmentation tasks. U-Net [35], dilated U-Net [42] and V-Net [44] have been successful in many medical segmentation tasks whereas VGGNet [24], Inception [25] and ResNet [26] have achieved state-of-the-art performances in image classification. However, due to the single scaled inputs/information utilized in these aforementioned architectures except Inception, all lack the ability to directly process multi-scaled information – an aspect AtriaNet excels at. The difficult task of LA segmentation from LGE-MRIs requires more input information to capture its complex geometry. In this aspect, AtriaNet can essentially process twice the amount of information due to its dual-pathway, resulting in its superior performance. Inception was the only architecture that contained multi-scale processing. However, it is done internally within only one image patch. This suggests that CNNs such as Inception [53], which uses internal multi-scale processing, learns substantially less information than explicit multi-scale processing, such as those used in AtriaNet. Furthermore, our experiments using various CNNs suggest that AtriaNet can generalize to many unseen patient data and produce robust segmentations, lessening the chance of over-fitting, compared with other CNN approaches.

Multi-scale processing has been explored in previous studies for enhancing the performance of neural networks in other research fields [54–56]. The CNNs proposed by Dou et al. for performing lung nodule classification [57] and by Kamnitsas et al. for brain lesion segmentation [58] both contained multiple pathways for different input resolutions. Despite the similarities of their designs and our proposed approach, AtriaNet contains a significantly greater number of layers and feature maps in each layer, allowing greater feature learning for segmenting more complex geometries such as the LA epicardium and endocardium. Furthermore, our experimental results showed that AtriaNet was able to perform high quality slice-by-slice 2D segmentation to achieve accurate 3D reconstruction of the atrial geometry, meaning it is effective for both 2D and 3D tasks.

The accuracy of AtriaNet could possibly be further improved by applying shape constraints which would be imposed on the either the intermediate layers or the output to control the generated 3D geometry. This would especially improve the segmentation at the mitral valve which connects the LA with the left ventricle as currently, this region is arbitrarily cut by a straight line in the ground truth masks. AtriaNet attempts to segment the mitral valve region with a smooth rounded shape, leads to a poor performance value when evaluated. This issue could potentially be alleviated by manually re-labelling the ground truths masks to improve the definition of the mitral valve, which in turn, will improve the quality of the samples provided to AtriaNet during training. The accuracy of the LA 3D reconstruction could also be improved by considering the 3D geometry and continuity between slices. A simple method to achieve this is to incorporate multiple slices as additional channels at the input of AtriaNet, however, our preliminary experiments showed that AtriaNet with three channeled or five channeled inputs performed worse and had substantially greater computational and memory costs. Further attempts at considering the continuity of the LA geometry in 3D warrant future investigation. In the future, we would like to apply AtriaNet for segmenting both atrial chambers and fibrosis since AF is a bi-chamber disease [4, 7, 59, 60]. We are currently progressing towards creating a dataset that contains manual segmentations of both atrial chamber masks, which could potentially be used to train AtriaNet.

VI. CONCLUSION

In this study, we have developed and evaluated a dual fully convolutional neural network for robust automatic LA segmentation from LGE-MRIs. Our algorithm enables the reconstruction of LA in 3D with a DICE accuracy of 94% as well as accurate estimates of key clinical measurements. The extensive evaluation of our pipeline demonstrates that it is superior to previously proposed state-of-the-art CNNs, setting a new benchmark for future studies. Our study may lead to the development of a more accurate and efficient atrial reconstruction and analysis approach, which can potentially be used for much improved clinical diagnosis, patient stratification and clinical guidance during ablation treatment for patients with AF.