Bayesian Latent Class Analysis Tutorial

Abstract

This article is a how-to guide on Bayesian computation using Gibbs sampling, demonstrated in the context of Latent Class Analysis (LCA). It is written for students in quantitative psychology or related fields who have a working knowledge of Bayes Theorem and conditional probability and have experience in writing computer programs in the statistical language R. The overall goals are to provide an accessible and self-contained tutorial, along with a practical computation tool. We begin with how Bayesian computation is typically described in academic articles. Technical difficulties are addressed by a hypothetical, worked-out example. We show how Bayesian computation can be broken down into a series of simpler calculations, which can then be assembled together to complete a computationally more complex model. The details are described much more explicitly than what is typically available in elementary introductions to Bayesian modeling so that readers are not overwhelmed by the mathematics. Moreover, the provided computer program shows how Bayesian LCA can be implemented with relative ease. The computer program is then applied in a large, real-world data set and explained line-by-line. We outline the general steps in how to extend these considerations to other methodological applications. We conclude with suggestions for further readings.

Overview

Bayesian data analysis is thriving in social and behavioral sciences, thanks in an important part to the rapid growth in introductory textbooks on practical analytic skills (e.g., Gelman and Hill (2007), M. D. Lee and Wagenmakers (2013), Kaplan (2014), McElreath (2016)). Syntax examples, such as those distributed with WinBUGS (Lunn, Thomas, Best, & Spiegelhalter, 2000), OpenBUGS (Lunn, Spiegelhalter, Thomas, & Best, 2009), JAGS (Plummer, 2003), and Stan (Stan Development Team, 2017), also help to put Bayesian analytics into immediate use with minimal requirements on understanding how the Markov Chain Monte Carlo (MCMC) simulations actually work. There are also programs that serve as shells for backend computations done in JAGS (blavaan package in R, Merkle and Rosseel (2016)) and Stan (rstanarm, Stan Development Team (2016)). Several commercial computer software packages popular among social scientists also support model fitting by Bayesian MCMC simulations (e.g., Mplus, Muthén & Muthén, 2011). It has never been easier to carry out Bayesian data analysis if all one wants to do is to find a practical solution for a statistical problem. A systematic review (Van de Schoot, Winter, Ryan, Zondervan-Zwijnenburg, & Depaoli, 2017) showed that accessible tutorials and software programs contributed to a proliferation of Bayesian analytics in psychology in the past 25 years. Indeed, why would non-specialists ever bother with the complex details in Bayesian computation when practical solutions abound?

We can offer several reasons. Coding a computer program facilitates a deeper understanding of Bayesian computation. A computer program has to be explicit and precise, thereby forcing the learner to understand the abstract Bayesian model with great specificity. Computer programming also complements clarity in theoretical expositions, as shown in introductory textbooks (e.g., Albert (2007), Lynch (2007), and Gelman and Hill (2007)) and an acclaimed textbook on rethinking Bayesian analytics (McElreath, 2016). Computer programming skills allow students and researchers to develop new methods and to invent new solutions not yet fully supported by commercial or open-source software programs (e.g., Neelon, O’Malley, and Normand (2011), Neelon, Zhu, and Neelon (2015), Neelon, Swamy, Burgette, and Miranda (2011), and Elliott, Gallo, Ten Have, Bogner, and Katz (2005)). The ability to code one’s own Bayesian computation promises other new possibilities, such as Bayesian nonparametric methods (e.g., Gershman and Blei (2012), Karabatsos and Walker (2009b), Karabatsos, Talbott, and Walker (2015), Karabatsos and Walker (2009a), Karabatsos (2006), Jara, Hanson, Quintana, Müller, and Rosner (2011)).

This tutorial shows how a non-technician can implement Bayesian computation, using Latent Class Analysis (LCA) as an illustrative example. We aim to demonstrate that abstract mathematics can be followed one simple step at a time by working out the simple calculations first and then by piecing them together to yield the full Bayesian model. The pedagogical plan is to follow a worked-out example step-by-step with mathematics kept at the most essential. It is about making Bayesian computation accessible to students who have never contemplated tackling such technically challenging topics. We also hope that instructors of Bayesian methods and/or advanced statistical modeling may use this tutorial as a teaching aid.

The intended readers are students involved in behavioral research who: 1) have a working knowledge of Bayes Theorem (e.g., Berry (1995) and Winkler (2003)); 2) have taken graduate-level statistics classes (e.g., regression and/or ANOVA; Gelman and Hill (2007), particularly Chapter 18 on Bayesian computation); 3) understand basic probability theory (e.g., Chapter 1 of P. M. Lee (2012); Lindley (1980); or a more accessible monograph by Rozanov (1977)); and 4) familiarity with computer programming in the statistical language R (e.g., Bayesian computation in Albert (2007)). Familiarity with computer programming is needed. However, the required programming skills are not much more advanced than the basics. This background may describe an advanced graduate student in quantitative psychology or a related field. More advanced knowledge in Bayesian statistical theory and MCMC simulation is helpful but not required.

Our ultimate goal is to illustrate how readers can go beyond the present example and begin exploring other Bayesian computation solutions. This necessitates a somewhat unique style. We have attempted, at the risk of being pedantic, to be extremely explicit in working through the details in the exposition and notation, much more specifically than what is typically available in elementary introductions. Graphics are used to visualize the general shapes of the parameters. Explanations and comments are added as we proceed. Detailed annotations are provided to connect the equations with the R code. At first, this tutorial may appear to require rigorous courses in mathematical statistics which most behavioral researchers have not taken. However, the worked-out examples should help make the equations more concrete and easier to follow.

This tutorial is organized as follows. We begin with an example on how Bayesian computation is typically described in methodology papers with a rigorous and succinct style that delves relatively rapidly into the conditional posterior distributions. The complex derivations can be hard to understand. Next, we provide an alternative to offer a more straightforward presentation without the loss in clarity and rigor. Each component of the LCA is explicitly described and mathematics carefully described. We then introduce a simple R program to carry out Gibbs sampling. The final section includes suggestions for further reading.

Hypothetical Example of LCA

The hypothetical LCA begins with a neuroscientist who sees cancer survivors with symptoms of mild cognitive problems. She gives a brief screening tool with 4 survey questions taken from the 48-item Multiple Abilities Questionnaire (MASQ) (Seidenberg, Haltiner, Taylor, Hermann, & Wyler, 1994), a self-reported symptom assessment for mild neurocognitive impairment. The 4 screening questions are:

• “After putting something away for safekeeping, I am able to recall its location,”

• “I can recall phone numbers that I use on a regular basis,”

• “I can keep my mind on more than one thing at a time,” and

• “I find it difficult to keep my train of thought going during a short interruption.”

The first three items are reverse-coded to screen for the presence of problems (1=‘present’ and 0=‘absent’).

Suppose the neuroscientist collects pilot screening data and analyzes the data with LCA looking specifically for a solution with three latent groups. The computer program outputs two sets of parameters: 1) the frequency distribution of the latent groups (in this case, the sample distribution is 50%, 30%, and 20% for latent class 1, 2, and 3, respectively); and 2) item response probabilities, or the probability of endorsing the 4 screening items among members of each of the latent groups (see Table 1).

Table 1.

Item response probability, the conditional probability that a person who is in one of the three latent classes will endorse the 4 screening items.

Profiles of Latent Classes	Items of Screening Tool
	1. misplace things	2. forget phone number	3. multitasking	4. train of thought
1 – ‘few or no symptoms’	0.20	0.20	0.10	0.10
2 – ‘memory lapses’	0.70	0.70	0.20	0.20
3 – ‘attention issues’	0.10	0.10	0.70	0.70

Table 1 shows how the neuroscientist describes the three latent groups. The first group is named the ‘few or no symptoms’ group based on the low item response probabilities of 0.20, 0.20, 0.10, and 0.10, for the 4 symptoms respectively. The second group is named the ‘memory lapses’ group because of the relatively higher probability of its members reporting memory problems (questions 1 and 2). And group 3 is named ‘attention issues’ because of the relatively more frequent endorsement of problems in attention. The ‘few or no symptoms’ group is the largest, accounting for 50% of the patients, with 30% in the ‘memory lapses’ group and the remaining 20% in the ‘attention issues’ group. These are latent groups (or ‘classes’) in the sense that they are not known a priori and not directly observable but their commonalities are revealed in how members of each latent group report neurocognitive problems. Throughout this tutorial they are called latent ‘groups’ or ‘classes’ interchangeably.

In the next section, we present the equations in the technical manner that is typical of many presentations, with a style that favors mathematical rigor and succinctness rather than detailed expositions. A beginner may find the derivations difficult to follow, complex, and impenetrable. However, we then show how these complex derivations can be made accessible to beginners. The rest of this paper provides a detailed didactic presentation, providing a step-by-step explanation of these equations. We recommend reading through this tutorial, paying close attention to how we substitute hypothetical numbers into these equations to demonstrate what they do, and then revisiting the technical steps section to reinforce the materials you have digested.

Bayesian Computation: Technical Steps

This section outlines Bayesian computation as typically described in an academic paper. The difficulties that arise, especially in the more technical steps, highlight the need to spend the rest of this tutorial going over them step by step with a concrete example.

Step 1: Likelihood Function.

The likelihood of observing the data vector y_i, as defined by Garrett and Zeger (2000), is a function of parameters π_j and p_jk,

$$f\left({\mathit{y}}_i;\mathit{\pi },\mathit{p}\right)=\sum _{j=1}^C{\pi }_j\prod _{k=1}^K{p}_{jk}^{y_{ik}}{\left(1-p_{jk}\right)}^{1-y_{ik}},$$ (1)

where π_j represents the distribution of latent class membership in the population (in the hypothetical case in Table 1, π_j = [π₁ = 0.50, π₂ = 0.30, π₃ = 0.20]). Also, p_jk represents the probability that a person in the jth latent group endorses the kth symptom. The overall likelihood is summed over latent classes c = 1,2,...,C.

As a result, the likelihood function of y_i always depends on c_i, typically written as

$$p\left({\mathit{y}}_i,c_{ij}|{\pi }_j,p_{jk}\right)=\prod _{j=1}^C{\left[{\pi }_{j}p\left({\mathit{y}}_i|p_{jk}\right)\right]}^{c_{ij}}.$$ (2)

Note that, for example, c_1j (for person 1) may take on the specific value of (1, 0, 0) (member of latent class 1), so that the exponents in Equation 2 produce a likelihood based solely on π₁ and p_1k because the likelihood is not affected by other latent groups (any number raised to a power of 0 yields the constant 1).

Step 2: Bayes’ Theorem.

Equation (2) is reversed by Bayes’ Theorem to find the joint posterior distribution of parameters π_j, p_jk given y_i and c_ij,

$$p\left({\pi }_j,p_{jk}|{\mathit{y}}_i,{\mathit{c}}_i\right)=\frac{p\left({\mathit{y}}_i,{\mathit{c}}_i|{\pi }_j,p_{jk}\right)p\left({\pi }_j,p_{jk}\right)}{p\left({\mathit{y}}_i,{\mathit{c}}_i\right)}=\frac{p\left({\mathit{y}}_i,{\mathit{c}}_i|{\pi }_j,p_{jk}\right)p\left({\pi }_j\right)p\left(p_{jk}\right)}{p\left({\mathit{y}}_i,{\mathit{c}}_i\right)},$$

The denominator, p(y_i, c_i), is a constant because its value is not affected by either π_j or p_jk.

The numerator contains three terms, the likelihood function p(y_i, c_i|π_j, p_jk) (which is just Equation (2)) and two priors, p(π_j) (prior for the latent class distribution) and p(p_jk) (prior for the response probabilities).

The denominator can be dropped because it does not affect the model. So the joint posterior distribution is proportional to the numerator, written with the ∝ symbol thusly

$$p\left({\pi }_j,p_{jk}|{\mathit{y}}_i,{\mathit{c}}_i\right)\propto p\left({\mathit{y}}_i,{\mathit{c}}_i|{\pi }_j,p_{jk}\right)p\left({\pi }_j\right)p\left(p_{jk}\right),$$

or for a simpler notation,

$$\left[{\pi }_j,p_{jk}|{\mathit{y}}_i,{\mathit{c}}_i\right]\propto \left[{\mathit{y}}_i,{\mathit{c}}_i|{\pi }_j,p_{jk}\right]\left[{\pi }_j\right]\left[p_{jk}\right].$$ (3)

We know what goes into [π_j, p_jk|y_i, c_i], which is Equation (2). However, what goes into the two priors?

Priors Resulting from Step 2.

At this stage of presentation, most academic articles invoke conjugate priors. They are aspects of theoretical distributions well known in Bayesian statistics and thus typically assumed understood. In keeping with the same style, we simply describe what they are. Details (and visual explanations) are provided in the next section, in which we make them more accessible to non-technicians.

Since p_jk are proportions derived from Bernoulli trials, their conjugate priors follow a Beta distribution with two parameters α and β; π_j is a categorical variable, thus its conjugate prior follows the Dirichlet distribution with parameters u_j. They are:

$$\begin{gathered} p\left({\pi }_j\right)~\text{Dirichlet}\left({\pi }_j;u_j\right)=\frac{\mathrm{\Gamma }\left(u_1+\dots +u_j\right)}{\mathrm{\Gamma }\left(u_1\right)\cdots \mathrm{\Gamma }\left(u_j\right)}{\pi }_1^{u_1-1}\cdots {\pi }_j^{u_j-1}\propto \prod _{j=1}^C{\pi }_j^{u_j-1}, \\ {p}_{jk}~\text{Beta}\left(p_{jk};\alpha ,\beta \right)=\frac{\mathrm{\Gamma }(\alpha +\beta )}{\mathrm{\Gamma }(\alpha )\mathrm{\Gamma }(\beta )}{p}_{jk}^{\alpha -1}{\left(1-p_{jk}\right)}^{\beta -1}\propto p_{jk}^{\alpha -1}{\left(1-p_{jk}\right)}^{\beta -1}. \end{gathered}$$

Incorporating these priors into Equation (3) yields a fully specified joint posterior distribution:

$$\begin{gathered} \left[{\pi }_j,p_{jk}|{\mathit{y}}_i,{\mathit{c}}_i\right]\propto \left[{\mathit{y}}_i,{\mathit{c}}_i|{\pi }_j,p_{jk}\right]\left[{\pi }_j\right]\left[p_{jk}\right] \\ =\prod _{i=1}^N\underset{\text{Equation}(2)}{\underbrace{\prod _{j=1}^C{\left[{\pi }_{j}p\left({\mathit{y}}_i|p_{jk}\right)\right]}^{c_{ij}}}}\underset{\text{Dirichlet}\text{prior}}{\underbrace{\prod _{j=1}^C{\pi }_j^{u_j-1}}}\underset{\text{Beta}\text{priors}}{\underbrace{\prod _{k=1}^K{p}_{jk}^{{\alpha }_{jk}-1}{\left(1-p_{jk}\right)}^{{\beta }_{jk}-1}}}. \end{gathered}$$ (4)

Steps 3 and 4: Joint Posterior and Gibbs Sampling.

Equation (4) is often further expanded in a typical technical presentation to include all details:

$$\begin{gathered} \left[{\mathit{y}}_i,{\mathit{c}}_i|{\pi }_j,p_{jk}\right]\left[{\pi }_j\right]\left[p_{jk}\right] \\ =\prod _{i=1}^N\prod _{j=1}^C{\left[{\pi }_{j}p\left({\mathit{y}}_i|p_{jk}\right)\right]}^{c_{ij}}\left[\frac{\mathrm{\Gamma }\left(u_1+\dots +u_j\right)}{\mathrm{\Gamma }\left(u_1\right)\cdots \mathrm{\Gamma }\left(u_j\right)}{\pi }_1^{u_1-1}\cdots {\pi }_j^{u_j-1}\right]\left[\frac{\mathrm{\Gamma }(\alpha +\beta )}{\mathrm{\Gamma }(\alpha )\mathrm{\Gamma }(\beta )}{p}_{jk}^{\alpha -1}{\left(1-p_{jk}\right)}^{\beta -1}\right], \end{gathered}$$

which makes the equations hard to follow even for an expert, not to mention for readers who are not familiar with the Beta and Dirichlet priors. These issues can easily take away a beginner’s confidence in going any further in understanding a technical paper. They will have to be addressed before we can complete steps 3 and 4. We now segue to a more didactic presentation to cover these fundamental concepts. The next two sections cover steps 3 and 4 in great detail. Equations are explained with concrete and specific examples. Hypothetical numeric values are plugged into these equations to show what they do. Afterwards, we will put everything together to work out the Gibbs sampling algorithm and thus complete the Bayesian exercise.

Priors in a Bayesian Analysis

This section provides more details on specific conjugate priors in LCA. In Bayesian theory, a prior is said to be conjugate of the posterior distribution if both are in the same distribution family (Raiffa & Schaifer, 1961). Conjugate priors are often preferred in Bayesian computation because they are much easier to implement. We use graphics to provide an intuitive understanding of conjugate priors in Bayesian LCA.

Beta Prior for Binary Item Response Probabilities.

The conjugate prior probability distribution for proportions is the Beta distribution. If, for example, our hypothetical neuroscientist asked 10 patients and 3 reported a specific memory problem, then this piece of prior information about the prevalence of this problem could be represented as a Beta(α = 3, β = 7) distribution where the α,β parameters can be thought of as the prior sample sizes for the number of patients reporting the symptom being present and absent, respectively.

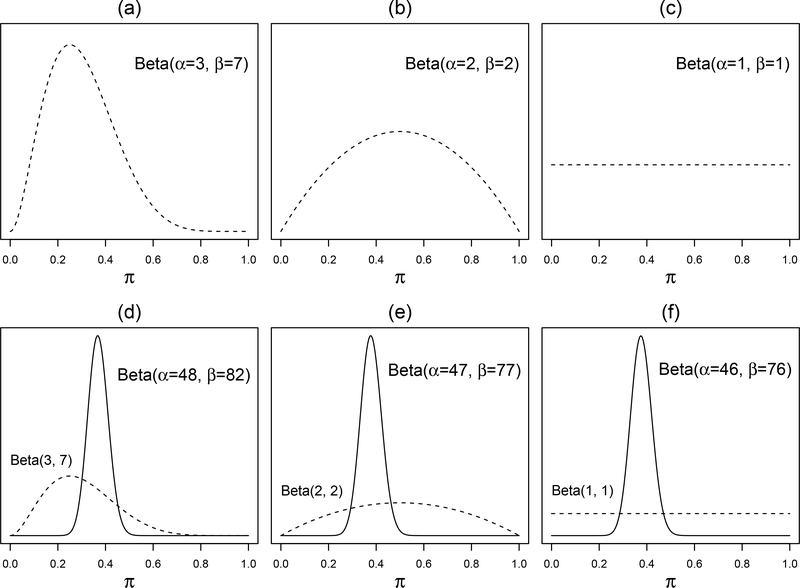
The shape of the Beta prior is determined by the prior data. Figure 1 shows some examples. Figure 1 (a) represents the Beta(α = 3, β = 7) prior above. This prior information comes with some uncertainty because of the somewhat small sample size of 10. The second example, in (b), represents a belief equivalent to 2 patients endorsing a cognitive problem out of a sample of 4. The uncertainty is greater because the sample is smaller still. The example in (c) represents a total lack of knowledge—the percentage can be any proportion in [0, 1] with equal possibility. This is what is often referred to as a flat, or non-informative, Beta prior. Non-informative priors are used throughout this tutorial, including the Beta(α = 1, β = 1) for p_jk.

Figure 1.

Examples of Beta distributions representing varying degrees of evidence strength over all possible values of the proportion. Subplot (a) shows a variable in which 3 of the 10 persons in the first latent group endorse the symptom; thus the peak is at around 30%. There is uncertainty because an observation of 3 out of 10 can still arise from an underlying probability of 50% (although much less likely). Subplot (b) is flatter, indicating a weaker evidence from 4 persons. Subplot (c) shows a flat Beta prior representing complete uncertainty about the proportion. Subplots (d) to (f) show how the priors above converge to posteriors of a similar shape if combined with a new, larger sample of 120 patients with 45 endorsing a symptom.

If the neuroscientist collected another, larger sample of 120 patients, and 45 endorsed this symptom, then the posterior could be calculated by combining the prior and the new data to yield a posterior Beta(α = 3 + 45, β = 7 + 75). This shift in the posterior distribution is shown in Figure 1 (d). The priors in (b) and (c), when combined with the new symptom data of (45 present, 75 absent), yield the Beta posteriors in (e) and (f), respectively. Note that, if the new dataset is large enough, it causes all three priors to converge to a posterior of a similar shape, despite the initial differences.

The density function of a Beta distribution is $\frac{\mathrm{\Gamma }(\alpha +\beta )}{\mathrm{\Gamma }(\alpha )\mathrm{\Gamma }(\beta )}{p}_{jk}^{\alpha -1}{\left(1-p_{jk}\right)}^{\beta -1}$, where Γ(α) = (α − 1)!, or simply as p_jk ~ Beta(p_jk; α,β).

Dirichlet Prior for Class Membership Distribution.

The Beta prior deals with a parameter with only two categories. If the parameter requires three or more categories, then the Beta distribution is no longer sufficient. The Dirichlet distribution is an extension of the Beta prior to three categories or more. The Dirichlet distribution is the conjugate prior for a categorical distribution. Figure 2 illustrates the Dirichlet distribution with three categories representing, for example, a sample of 20 divided into three latent classes, with 10, 6, and 4 in the three respective latent classes. This is represented mathematically as p_jk ~ Dirichlet(π_j; u_j).

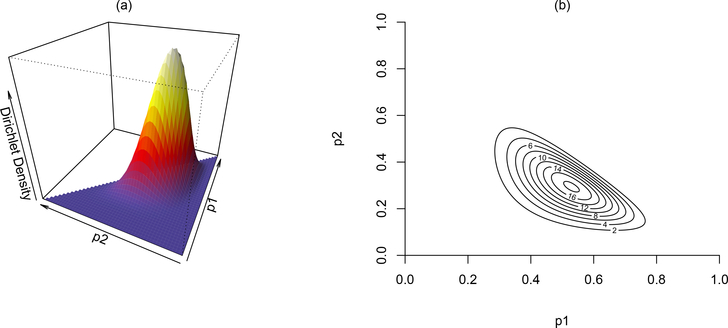
Figure 2.

A Dirichlet distribution for a multinomial variable with three categories. Subplot (a) shows the Dirichlet density in 3-dimensions, where the overall shape of the distribution is defined by the prior sample size u = [10, 6, 4], over the first and second percentages, labeled as p1 and p2, respectively. In (b), the contour of the 3-dimensional surface is plotted to visualize the mode of the distribution near (0.5, 0.3, 0.2).

The contour lines in (b) better illustrate where the peak of the distribution is, at $\left({\pi }_1^{*}=0.50,{\pi }_2^{*}=0.30,{\pi }_3^{*}=0.20\right)$, although ${\pi }_3^{*}$ is not plotted because ${\pi }_3^{*}$ is fixed once ${\pi }_1^{*}$ and ${\pi }_2^{*}$ are known. The plots show that the observed counts of 10, 6, and 4 out of a sample of 20 is most likely from an underlying probability distribution of 50% in the first category, 30% in the second category, and 20% in the third and last category, represented as $\left({\pi }_1^{*}=0.50,{\pi }_2^{*}=0.30,{\pi }_3^{*}=0.20\right)$.

It is important to note that other combinations of probabilities, such as $\left({\pi }_1^{*}=0.40,{\pi }_2^{*}=0.50,{\pi }_3^{*}=0.10\right)$ can also yield the same observed counts, although much less likely. We do not precisely know the underlying distribution of the latent groups, so we represent this uncertainty by the entire Dirichlet density surface covering all possible values of ${\pi }_1^{*}$, ${\pi }_2^{*}$ and ${\pi }_3^{*}$ that can yield the observed counts. The Dirichlet density is: $\frac{\mathrm{\Gamma }\left(u_1+\dots +u_j\right)}{\mathrm{\Gamma }\left(u_1\right)\cdots \mathrm{\Gamma }\left(u_j\right)}{\pi }_1^{u_1-1}\cdot \cdot \cdot {\pi }_j^{u_j-1}$, where the product of all category probabilities π_j raised to the power of their prior sample sizes u_j − 1. A flat, non-informative Dirichlet prior can be represented by setting all values to 1 in the prior sample size, π_j ~ Dirichlet(π_j; u_j = (1, 1, …, 1)).

It is worth highlighting that everything in Bayesian statistics is represented in a probability distribution, which better captures the uncertainty in the prior as well as in the posterior. Conjugate priors make the derivation of the posteriors easier to understand, which we will turn to next.

Worked-Out Examples for Better Accessibility

To better understand the technical steps, we will first put hypothetical numbers into the equations and work through the mathematics step by step to explain what the equations actually do. It is important to keep in mind that the actual Bayesian computation is more comprehensive than the simplified version here.

Suppose our neuroscientist sees a new patient, John, who responds to the four screening questions with ‘present’, ‘present’, ‘absent’, and ‘absent’, which yields the data vector y = (1, 1, 0, 0). The likelihood function in Equation (1) can be used to find the probability of observing y = (1, 1, 0, 0). First, we need to know which latent class John belongs to. There are 3 possibilities in our hypothetical 3-class solution. If John belongs to the ‘memory lapses’ group, then according to Table 1 the probability of observing y is 0.70 × 0.70 × (1 − 0.20) × (1 − 0.20), that is, a 0.70 probability of endorsing item 1, a 0.70 probability of endorsing item 2, a 1 − 0.20 probability of not endorsing item 3, and a 1 − 0.20 probability of not endorsing item 4. By assuming that these individual probabilities are independent given the model, they can be multiplied together to yield the probability of observing y. A more general way to write it is to follow the binomial probability formula to find (0.70¹0.30⁰)× (0.70¹0.30⁰)× (0.20⁰0.80¹)× (0.20⁰0.80¹) = 0.3136.

If the probability of an event is p_k, and the presence of an event is represented by 1 and 0 otherwise, then the overall probability of observing y = (1, 1, 0, 0) is $p_1^1{\left(1-p_1\right)}^0\times p_2^1{\left(1-p_2\right)}^0\times p_3^0{\left(1-p_3\right)}^1\times p_4^0{\left(1-p_4\right)}^1$, or generally as $\prod _{k=1}^4{p}_k^{y_k}{\left(1-p_k\right)}^{1-y_k}$, where y = (y₁ = 1, y₂ = 1, y₃ = 0, y₄ = 0) and the Greek upper-case letter Π represents the product of a series of numbers.

If, instead, John belongs to one of the other two latent groups, then his response probability is (0.20¹0.80⁰) × (0.20¹0.80⁰) × (0.10⁰0.90¹) × (0.10⁰0.90¹) = 0.0324 or (0.10¹0.90⁰)× (0.10¹0.90⁰)× (0.70⁰0.30¹)× (0.70⁰0.30¹) = 0.0009, respectively. Because John has a 50% probability of being in the ‘few or no symptoms’ group, 30% probability of being in the ‘memory lapses’ group, and a 20% probability of being in the ‘attention issues’ group, the overall probability of observing y = (1, 1, 0, 0) is a weighted average, using Equation (1),

$$\begin{gathered} f(\mathit{y};\mathit{\pi },\mathit{p})=0.50\times \left[\left({0.20}^1{0.80}^0\right)\times \left({0.20}^1{0.80}^0\right)\times \left({0.10}^0{0.90}^1\right)\times \left({0.10}^0{0.90}^1\right)\right]+ \\ 0.30\times \left[\left({0.70}^1{0.30}^0\right)\times \left({0.70}^1{0.30}^0\right)\times \left({0.20}^0{0.80}^1\right)\times \left({0.20}^0{0.80}^1\right)\right]+ \\ 0.20\times \left[\left({0.10}^1{0.90}^0\right)\times \left({0.10}^1{0.90}^0\right)\times \left({0.70}^0{0.30}^1\right)\times \left({0.70}^0{0.30}^1\right)\right] \\ =0.50\times 0.0324+0.30\times 0.3136+0.20\times 0.0009 \\ =0.0162+0.09408+0.00018=0.11046. \end{gathered}$$

Each row is the binomial probability of a response of y_i = (1, 1, 0, 0) for a specific latent class, weighted by the probability of the person belonging to that class. The overall probability of 0.11046 takes into account all three latent membership possibilities. Equation (1) may look intimidating to a beginner at first. However, a pattern emerges when the equation is unpacked with its components explicitly written down as above. It helps to follow the equation carefully and fill in appropriate numbers.

Now we turn to Equation (2). If we really want to be detailed in the notation, the probabilities summed above can be expressed as

$$\begin{gathered} p\left({\mathit{y}}_i=(1,1,0,0),{\mathit{c}}_i=(1,0,0)|{\pi }_j,p_{jk}\right)=0.01620, \\ p\left({\mathit{y}}_i=(1,1,0,0),{\mathit{c}}_i=(0,1,0)|{\pi }_j,p_{jk}\right)=0.09408,\text{and} \\ p\left({\mathit{y}}_i=(1,1,0,0),{\mathit{c}}_i=(0,0,1)|{\pi }_j,p_{jk}\right)=0.00018, \end{gathered}$$ (5)

where the c_i in bold represents a vector for the ith person’s specific latent class membership.

If a person’s class membership is known and fixed (e.g., in latent class 1), then his/her probability of response by Equation (2) gives [0.50 × 0.0324]¹· [0.30 × 0.3136]⁰·[0.20 × 0.0009]⁰ = [0.50 × 0.0324] ·1 · 1 = 0.01620, exactly the same as the value derived from Equation (1). Therefore, we can rewrite Equation (2) to incorporate these details:

$$\begin{gathered} p\left({\mathit{y}}_i,c_{ij}|{\pi }_j,p_{jk}\right)=\prod _{j=1}^C{\left[{\pi }_{j}p\left({\mathit{y}}_i|p_{jk}\right)\right]}^{c_{ij}} \\ =\prod _{j=1}^C{\left[{\pi }_j\prod _{k=1}^K{p}_{jk}^{y_{ik}}{\left(1-p_{jk}\right)}^{\left(1-y_{ik}\right)}\right]}^{c_{ij}} \\ =\prod _{j=1}^C\left[{\pi }_j^{c_{ij}}\prod _{k=1}^K{p}_{jk}^{y_{ik}{c}_{ij}}{\left(1-p_{jk}\right)}^{\left(1-y_{ik}\right)c_{ij}}\right], \end{gathered}$$ (6)

where the c_ij exponents outside the square brackets in the second line are distributed into the exponents of specific parameters in the third line.

Equations (5) and (6) give us three useful quantities, 0.01620, 0.09408, and 0.00018—the probabilities of the item responses arising from each of the three latent classes. They sum to 0.11046. Latent class 1 represents 14.7% of this sum (0.01620 ÷ 0.11046 = 0.14666). Latent classes 2 and 3 share 85.2% and 0.1%, respectively. A response of y_i = (1, 1, 0, 0) is most likely given by a patient in class 2, specifically at 85.2% probability. Intuitively, the ratio between each of the three proportions and the total sum defines the conditional probability of a person belonging to that specific latent class. The conditional probability of each person’s class membership is expressed as

$$p\left(c_{ij}|{\mathit{y}}_i,{\pi }_j,p_{jk}\right)=\prod _{j=1}^C{\left[\frac{{\pi }_{j}p\left({\mathit{y}}_i|p_{jk}\right)}{\sum _{j=1}^C{\pi }_{j}p\left({\mathit{y}}_i|p_{jk}\right)}\right]}^{c_{ij}},$$ (7)

where the denominator is the sum of all probabilities calculated from Equation (2). The purpose of explaining Equations (2) and (7) in such great detail is because they will be revisited later to complete the Bayesian analysis.

Technical Details Explained

Now we turn to Equation (4), to show how it arises naturally from Bayes’ Theorem, and to give details previously omitted. Recall, in step 2, we have

$$p\left({\pi }_j,p_{jk}|{\mathit{y}}_i,{\mathit{c}}_i\right)=\frac{p\left({\mathit{y}}_i,{\mathit{c}}_i|{\pi }_j,p_{jk}\right)p\left({\pi }_j,p_{jk}\right)}{p\left({\mathit{y}}_i,{\mathit{c}}_i\right)}=\frac{p\left({\mathit{y}}_i,{\mathit{c}}_i|{\pi }_j,p_{jk}\right)p\left({\pi }_j\right)p\left(p_{jk}\right)}{p\left({\mathit{y}}_i,{\mathit{c}}_i\right)},$$

where on the left side of the first equal sign we have the joint posterior distribution of the class membership distribution π_j and the item response probability p_jk. On the right we have the reverse in the numerator, the probability of observed responses y_i if the latent class membership c_i is also known and fixed, which we have already dealt with in Equation (5) and the more general Equation (2). Moreover, because π_j and p_jk are assumed independent, p(π_j, p_jk) = p(π_j)p(p_jk) and thus the final fraction.

We use square brackets below to make the equation easier to follow:

$$\left[{\pi }_j,p_{jk}|{\mathit{y}}_i,{\mathit{c}}_i\right]=\frac{\left[{\mathit{y}}_i,{\mathit{c}}_i|{\pi }_j,p_{jk}\right]\left[{\pi }_j\right]\left[p_{jk}\right]}{\left[{\mathit{y}}_i,{\mathit{c}}_i\right]}.$$ (8)

We have already seen examples of the quantities on the right side of this equation. Let us take a look at each of these in turn.

• [y_i, c_i|π_j, p_jk]: We have seen these in Equation (5), e.g., p(y_i = (1, 1, 0, 0), c_i = (1, 0, 0)|π_j, p_jk) = 0.01620, the probability of observing y_i when the class membership is known.

• [π_j]: The prior probability of class membership distribution. Our pilot sample of 20 (10 in group 1, 6 in group 6, and 4 in group 3) gives a prior of $\left[{\pi }_j\right]\propto \text{Dirichlet}\left({\pi }_{ic};u_{ic}\right)={\pi }_{i1}^{10-1}\times {\pi }_{i2}^{6-1}\times {\pi }_{i3}^{4-1}$, whose visual representation is in Figure 2.

• [p_jk]: The prior probability of item response probabilities in the 3 by 4 matrix in Table 1. We may choose to assign a flat prior to all 12 probabilities, [p_jk] ∝ Beta(p_jk; α = 1, β = 1), which is the flat prior in Figure 1.

• [y_i, c_i]: The probability of observing the raw data y_i, over all possibilities of c_i. We have already seen a simpler version of it, in the total probability in Equation (5).

Now the probability we seek is expressed in terms of quantities we can easily calculate. Also, the mathematics are explained in terms of quantities that make sense at a more intuitive level.

The last bullet point needs more explanation. Recall the total probability in Equation (5), its value is 0.11046 = (0.0162 + 0.09408 + 0.00018), identical in all cases of ci. The total probability in the denominator is the same in all three scenarios.¹ It serves as a scaling constant to convert the numerator vector [0.0162, 0.09408, 0.00018] into [0.1467, 0.8517, 0.0016] so that it sums to one. It has no effect on how the numerators are compared with one another. The unscaled numerator vector contains all the information we need. The distribution is said to be proportional to the numerator vector. and thus the notation:

$$\left[{\pi }_j,p_{jk}|{\mathit{y}}_i,{\mathit{c}}_i\right]\propto \left[{\mathit{y}}_i,{\mathit{c}}_i|{\pi }_j,p_{jk}\right]\left[{\pi }_j\right]\left[p_{jk}\right].$$

The cumbersome total probability can be dropped from the equation because the proportional to relationship still holds true.

Step 3: Joint Posterior of LCA

Pooling all relevant information, we add additional details to help understand the joint posterior [π_j, p_jk|y_i, c_i] and its components:

$$\begin{gathered} \left[{\pi }_j,p_{jk}|{\mathit{y}}_i,{\mathit{c}}_i\right]\propto \left[{\mathit{y}}_i,{\mathit{c}}_i|{\pi }_j,p_{jk}\right]\left[{\pi }_j\right]\left[p_{jk}\right] \\ =\prod _{i=1}^N\underset{\text{Equation}(2)}{\underbrace{\prod _{j=1}^C{\left[{\pi }_{j}p\left({\mathit{y}}_i|p_{jk}\right)\right]}^{c_{ij}}}}\underset{\text{Dirichlet}\text{prior}}{\underbrace{\prod _{j=1}^C{\pi }_j^{u_j-1}}}\underset{\text{Beta}\text{priors}}{\underbrace{\prod _{k=1}^K{p}_{jk}^{{\alpha }_{jk}-1}{\left(1-p_{jk}\right)}^{{\beta }_{jk}-1}}} \\ =\prod _{i=1}^N\underset{\text{Equation}(6)}{\underbrace{\prod _{j=1}^C\left[{\pi }_j^{c_{ij}}\prod _{k=1}^K{p}_{jk}^{y_{ik}{c}_{ij}}{\left(1-p_{jk}\right)}^{\left(1-y_{ik}\right)c_{ij}}\right]}}\prod _{j=1}^C{\pi }_j^{u_j-1}\prod _{k=1}^K{p}_{jk}^{{\alpha }_{jk}-1}{\left(1-p_{jk}\right)}^{{\beta }_{jk}-1} \\ =\prod _{i=1}^N\underset{\text{Dirichlet}\text{posterior}}{\underbrace{\prod _{j=1}^C{\pi }_j^{c_{ij}+u_j-1}}}\underset{\text{Beta}\text{posteriors}}{\underbrace{\prod _{k=1}^K{p}_{jk}^{y_{jj}{c}_{ij}+{\alpha }_{jk}-1}{\left(1-p_{jk}\right)}^{\left(1-y_{ij}\right)c_{ij}+{\beta }_{jk}-1}}}. \end{gathered}$$ (9)

Equation (9) defines the joint posterior probability distribution of the parameters by a Dirichlet posterior and Beta posteriors. The first two lines are described Equation (4). The third line replaces Equation (2) with the more detailed version found in Equation (6). We combine the likelihood of ${\pi }_j^{c_{ij}}$ with the Dirichlet prior of ${\pi }_j^{u_j-1}$ to form the posterior ${\pi }_j^{c_{ij}+u_j-1}$. Similarly, we combine $p_{jk}^{y_{ik}{c}_{ij}}$ with the matching part of the Beta prior to yield the Beta posterior $p_{jk}^{y_{ij}{c}_{ij}+{\alpha }_{jk}-1}$. Finally, we combine ${\left(1-p_{jk}\right)}^{\left(1-y_{ik}\right)c_{ij}}$ with the matching part of the Beta prior to yield ${\left(1-p_{jk}\right)}^{\left(1-y_{ij}\right)c_{ij}+{\beta }_{jk}-1}$. Thus, the Beta(1, 1) prior may be combined with, for example, a data likelihood of [45, 75] to yield a posterior of Beta(46, 76).

The Dirichlet posterior requires first calculating ${\pi }_j^{c_{ij}}$ based on each person’s known latent class and they are multiplied together, across the N respondents, to produce the data likelihood. The data likelihood is then multiplied by the prior to yield the posterior. Similarly, the Beta data likelihood also requires multiplication across the N respondents.

Before we move on to Step 4, we pause to reflect on two key concepts in Bayesian inference. They are easily missed in introductory tutorials that focus solely on practical analytic skills. First, conjugate priors simplify how priors are converted into posteriors (e.g., the parameters in the Dirichlet posterior are simply the prior parameters plus the data likelihood). Additionally, the algebraic derivations nicely demonstrate the second key concept we wish to highlight: “post is prior times likelihood” (P. M. Lee, 2012, section 2.1.2), the posterior density is prior density times the data likelihood.

Step 4: Gibbs Sampling

The essence of Gibbs sampling is to estimate the properties of the joint posterior distribution by simulation. Gibbs sampling is merely one of many Markov Chain Monte Carlo (MCMC) simulation techniques. What is MCMC simulation? The simple example of a coin toss offers an intuitive explanation. If we toss a coin many times, we expect the distribution of heads and tails to tell us whether or not the coin is biased. There is only one parameter, the proportion of heads. It gets complicated in problems involving many unknown parameters, such as in the LCA, where we know the joint posterior distribution of π_j, p_jk and c_i, but we cannot easily solve it (recall how we got stuck in Equation (4)).

We are now ready to sample π_j, p_jk, and c_i as per Equation (9). Let us take a look at these parameters in turn. To sample π_j, we treat all the other parameters in Equation (9) as fixed and known, and draw from the posterior Dirichlet distribution. For instance, if y_i = (1, 1, 0, 0), c_i = (1, 0, 0), p_jk are fixed at the values in Table 1, and the prior parameters are u = (u₁ = 10, u₂ = 6, u₃ = 4) and α = 1, β = 1, then Equation (9) gives

$$\begin{gathered} {\pi }_1^{1+10-1}\left({0.0324}^1\times {0.3136}^0\times {0.0009}^0\right)\text{for}\text{latent}\text{class}1, \\ {\pi }_2^{0+6-1}\left({0.0324}^1\times {0.3136}^0\times {0.0009}^0\right)\text{for}\text{latent}\text{class}2,\text{and} \\ {\pi }_3^{0+4-1}\left({0.0324}^1\times {0.3136}^0\times {0.0009}^0\right)\text{for}\text{latent}\text{class}3. \end{gathered}$$

Each of π₁, π₂, π₃ is weighted by the same constant 0.0324¹ × 0.3136⁰ × 0.0009⁰ that arises from the substitution of fixed values into the Beta posterior. The scaling constant does not affect the overall shape of the posterior distribution. Thus, the conditional posterior distribution for π_j becomes a Dirichlet distribution with sample sizes (1 + 10 − 1, 0 + 6 − 1, 0 + 4 − 1). Another person may have different responses, e.g., y_i = (1, 1, 1, 0) and c_i = (0, 1, 0), which yields a different distribution with parameters (0 + 10 − 1, 1 + 6 − 1, 0 + 4 − 1). Since π_j involves pooling memberships over people, the sampling from the posterior Dirichlet distribution also has to add up the posterior sample sizes over people,

$$\pi ~\text{Dirichlet}\left(\sum _1^N{\mathit{c}}_{i1}+u_1,\sum _1^N{\mathit{c}}_{i2}+u_2,\sum _1^N{\mathit{c}}_{i3}+u_3\right),$$

which provides a specific distribution, e.g., Dirichlet(50, 20, 30) in a 3-class solution, from which a new value of π may be randomly sampled. We will go into the detailed simulation later. For now, let’s assume that a new π_j has been drawn, and it happens to be (π₁ = 0.670, π₂ = 0.234, π₃ = 0.096).

The steps for sampling p_jk are more involved, partly because there are 12 values in the 3 by 4 matrix of p_jk. Again, we substitute all the fixed parameters into Equation (9), including the newly sampled π_j = (0.670, 0.234, 0.096), and allow the p_jk values to vary. Assuming fixed values in y_i = (1, 1, 0, 0), c_i = (1, 0, 0), and the newly sampled π_j = (0.670, 0.234, 0.096), we get

$$\begin{gathered} {0.670}^{1+10-1}[{(p_{11}^1{(1-p_{11})}^0)}^1\times {(p_{12}^1{(1-p_{12})}^0)}^1\times {(p_{13}^0{(1-p_{13})}^1)}^1\times {(p_{14}^0{(1-p_{14})}^1)}^1]\text{for}\text{class}1, \\ {0.234}^{0+6-1}[{(p_{21}^1{(1-p_{21})}^0)}^0\times {(p_{22}^1{(1-p_{22})}^0)}^0\times {(p_{23}^0{(1-p_{23})}^1)}^0\times {(p_{24}^0{(1-p_{24})}^1)}^0]\text{for}\text{class}2,\text{and}, \\ {0.096}^{0+4-1}[{(p_{31}^1{(1-p_{31})}^0)}^0\times {(p_{32}^1{(1-p_{32})}^0)}^0\times {(p_{33}^0{(1-p_{33})}^1)}^0\times {(p_{34}^0{(1-p_{34})}^1)}^0]\text{for}\text{class}3. \end{gathered}$$

The first line contains $p_{11}^1{\left(1-p_{11}\right)}^0$, the binomial probability of class 1 members endorsing symptom 1, raised to the power of the observed response (i.e., $p_{11}^1$ and (1 − p₁₁)⁰ because the person endorses item 1 in y_i = (1, 1, 0, 0)). This is subsequently raised to the power according to c_i = (1, 0, 0) and thus the power of 1 outside the parentheses in ${(p_{11}^1{(1-p_{11})}^0)}^1$. Latent classes 2 and 3 are raised to the power of 0. Note the pattern: the individual p_jk’s are first raised to the exponents according to the observed responses and then again raised to exponents according to the latent classes. The scaling constants, e.g., 0.670¹⁺¹⁰⁻¹, are ignored because they do not affect the overall shape of the Beta posteriors. Thus, the posterior distribution for p₁₁ is Beta(1 · 1 + 1, 0 · 1 + 1) = Beta(2, 1). This calculation is repeated 12 times, conditional on this person’s y_i and c_i. However, another person may get a different set of Beta posterior distributions, depending on that person’s responses.

Equation (9) shows that each of the twelve p_jk’s follows a Beta posterior distribution with the shape parameters ${\sum }_1^N{y}_{ij}{c}_{ij}+{\alpha }_{jk}-1$ and ${\sum }_1^N\left(1-y_{ij}\right)c_{ij}+{\beta }_{jk}-1$ summed across people. We need to: 1) work out the posterior Beta parameters for the twelve p_jk’s, one person at a time; and 2) sum the parameters across all N persons. This seems like a tedious task. Fortunately, it is easy to do with a computer programming language as will be shown later. Let us assume that we have worked out all these and added up all resulting Beta parameters across N people; then, we have 12 Beta posterior distributions from which we can draw a new sample of p_jk. Assume further that a draw for p₁₁ happens to yield a value of p₁₁ = 0.923. We repeat the same steps and (say) get a newly sampled $p_{jk}=\left(\begin{array}{cccc}0.923& 0.940& 0.237& 0.288\\ 0.277& 0.082& 0.790& 0.645\\ 0.397& 0.137& 0.149& 0.179\end{array}\right)$. We are now ready to update the latent class membership parameter based on the newly sampled π_j and p_jk.

In a three-class solution, each person’s class membership is a categorical variable, either (1, 0, 0), (0, 1, 0), or (0, 0, 1). Recalling the ‘divide-by-total’ formula in Equation (7), the probabilities of a response y_i = (1, 1, 0, 0) arising from latent classes (1, 0, 0), (0, 1, 0), or (0, 0, 1) are 0.1467, 0.8517, and 0.0016, respectively. Using Equation (7), y_i = (1, 1, 0, 0), and the newly updated π_j and p_jk, we get the revised multinomial probabilities (0.728, 0.272, 0.000). Let us assume that we draw an updated c_i for c_i = (1, 0, 0) from a three-category multinomial distribution.

Putting it All Together: Gibbs Sampling Algorithm

The details and worked-out example in the previous section can be succinctly summarized in an algorithm for Gibbs sampling (see also White and Murphy (2014)).

$${\pi }_j^{(t+1)}~\text{Dirichlet}({\pi }_j;c_{ij}^{(t)}+u_j)=\mathrm{Dirichlet}\left(\sum _{i=1}^N{c}_{i1}^{(t)}+u_1,\dots ,\sum _{i=1}^N{c}_{iC}^{(t)}+u_g\right),$$ (10)

$$\begin{gathered} p_{jk}^{(t+1)}~\text{Beta}(p_{jk};{\mathit{y}}_i{c}_{ij}^{(t)}+{\alpha }_{jk}-1,\left(1-{\mathit{y}}_i\right)c_{ij}^{(t)}+{\beta }_{jk}-1) \\ =\text{Beta}\left(\sum _{i=1}^N{\mathit{y}}_i{c}_{ij}^{(t)}+{\alpha }_{jk}-1,\sum _{i=1}^N\left(1-{\mathit{y}}_i\right)c_{ij}^{(t)}+{\beta }_{jk}-1\right), \end{gathered}$$ (11)

$${\mathit{c}}_i^{(t+1)}~\text{Multinomial}\left(1,\frac{{\pi }_1^{(t+1)}p\left({\mathit{y}}_i|{\mathit{p}}_1^{(t+1)}\right)}{{\sum }_{h=1}^J{\pi }_h^{(t+1)}p\left({\mathit{y}}_i|{\mathit{p}}_h^{(t+1)}\right)},\dots ,\frac{{\pi }_J^{(t+1)}p\left({\mathit{y}}_i|{\mathit{p}}_J^{(t+1)}\right)}{{\sum }_{h=1}^J{\pi }_h^{(t+1)}p\left({\mathit{y}}_i|{\mathit{p}}_h^{(t+1)}\right)}\right).$$ (12)

Here we use (t + 1) to indicate that these are the most recently sampled parameters ${\pi }_j^{(t+1)}$, $p_{jk}^{(t+1)}$, and ${\mathit{c}}_i^{(t+1)}$. Equation (10) samples the conditional posterior distribution for π_j. Recall that our prior Dirichlet distribution has parameters (10, 6, 4). Suppose that, in a new sample of 50 people, 20 belong to class 1, 18 to class 2, and the remaining 12 to class 3, then the posterior distribution follows a Dirichlet distribution with parameters (10 + 20, 6 + 18, 4 + 12)—the posterior sample size being simply the prior counts plus the newly simulated counts pooled across people. The summation $\sum _{i=1}^N{c}_{i1}^{(t)}$ is simply adding up, over the number of N people, the number of newly simulated counts in latent class 1.

Equation (11) shows that the conditional posterior distribution for the item response probabilities p_jk, like its prior, also follows a Beta distribution with the posterior sample size pooled over people. The posterior sample size is the sum of observed responses y_i weighted by the newly simulated latent class membership, plus the prior Beta parameters. Finally, Equation (12) simulates the posterior latent class membership. All is needed is to plug the newly simulated ${\pi }_j^{(t+1)}$ and $p_{jk}^{(t+1)}$ into Equation (7) to calculate the probabilities of a response arising from latent classes (1, 0, 0), (0, 1, 0), or (0, 0, 1). Then these probabilities are used to draw samples from a multinomial distribution.

In methodology papers the starting values are often named ${\pi }_j^{(0)}$, $p_{jk}^{(0)}$, and ${\mathit{c}}_i^{(0)}$, where the (0)’s index the order of iteration, not exponents. The next iteration increments the indices by 1 to get ${\pi }_j^{(1)}$, $p_{jk}^{(1)}$, and ${\mathit{c}}_i^{(1)}$. The simulation iterates through the loop, with the latest simulation results denoted as ${\pi }_j^{(t+1)}$, $p_{jk}^{(t+1)}$, and ${\mathit{c}}_i^{(t+1)}$; until a pre-specified number of iterations is reached. The starting values are used to begin the MCMC chain, and once the iteration loop begins, we only need to keep track of the values in iteration (t), the previous iteration, and the latest, (t + 1) iteration. This concludes all the necessary mathematical derivations in Bayesian LCA. The resulting algorithms are ready to go into a computer program for computation.

R Program to Carry Out Gibbs Sampling

Add Health Study (N = 6,504): a Real-World Dataset

The Gibbs sampling algorithm is applied to a large dataset, the publicly accessible Wave 1 data of the National Longitudinal Study of Adolescent to Adult Health (Harris et al., 2009, Add Health Study, N = 6,504), available at www.icpsr.umich.edu/icpsrweb/ICPSR/studies/21600.

We extracted data from 6 survey items probing problem behaviors of teenagers: 1) Lied to parents; 2) Loud/rowdy/unruly in a public place; 3) Damaged property; 4) Stolen from a store; 5) Stolen something worth < $50, and 6) Taken part in a group fight. The raw data counts are shown in Table 2.

Table 2.

Add Health study raw data.

	Lied	Publicly loud	Damaged property	Stolen from store	Stolen < $50	Group fight	(n)
1	0	0	0	0	0	0	1817
2	1	0	0	0	0	0	792
3	0	1	0	0	0	0	539
4	1	1	0	0	0	0	630
5	0	0	1	0	0	0	29
6	1	0	1	0	0	0	51
7	0	1	1	0	0	0	66
8	1	1	1	0	0	0	178
9	0	0	0	1	0	0	58
10	1	0	0	1	0	0	71
11	0	1	0	1	0	0	33
12	1	1	0	1	0	0	93
13	0	0	1	1	0	0	5
14	1	0	1	1	0	0	30
15	0	1	1	1	0	0	8
16	1	1	1	1	0	0	40
17	0	0	0	0	1	0	20
18	1	0	0	0	1	0	14
19	0	1	0	0	1	0	14
20	1	1	0	0	1	0	34
21	0	0	1	0	1	0	1
22	1	0	1	0	1	0	8
23	0	1	1	0	1	0	10
24	1	1	1	0	1	0	17
25	0	0	0	1	1	0	58
26	1	0	0	1	1	0	104
27	0	1	0	1	1	0	52
28	1	1	0	1	1	0	183
29	0	0	1	1	1	0	10
30	1	0	1	1	1	0	44
31	0	1	1	1	1	0	33
32	1	1	1	1	1	0	177
33	0	0	0	0	0	1	90
34	1	0	0	0	0	1	114
35	0	1	0	0	0	1	120
36	1	1	0	0	0	1	218
37	0	0	1	0	0	1	6
38	1	0	1	0	0	1	17
39	0	1	1	0	0	1	16
40	1	1	1	0	0	1	105
41	0	0	0	1	0	1	8
42	1	0	0	1	0	1	15
43	0	1	0	1	0	1	14
44	1	1	0	1	0	1	40
45	0	0	1	1	0	1	3
46	1	0	1	1	0	1	7
47	0	1	1	1	0	1	6
48	1	1	1	1	0	1	43
49	0	0	0	0	1	1	4
50	1	0	0	0	1	1	5
51	0	1	0	0	1	1	12
52	1	1	0	0	1	1	17
53	0	0	1	0	1	1	2
54	1	0	1	0	1	1	1
55	0	1	1	0	1	1	2
56	1	1	1	0	1	1	39
57	0	0	0	1	1	1	7
58	1	0	0	1	1	1	30
59	0	1	0	1	1	1	20
60	1	1	0	1	1	1	77
61	0	0	1	1	1	1	4
62	1	0	1	1	1	1	15
63	0	1	1	1	1	1	20
64	1	1	1	1	1	1	207

A subset of it was previously analyzed by Collins and Lanza (2010, Chapter 1, N = 2,087) to identify four latent classes of adolescent delinquent behaviors: 1) “Non-/Mild Delinquents” (49%), 2) “Verbal Antagonists” (26%), 3) “Shoplifters” (18%), and 4) “General Delinquents” (6%). In the example below, we replicate their four-class solution for comparative purposes.

R Program Line by Line

The R program to carry out Gibbs sampling is listed in Appendix A. Line numbers are added to facilitate the explanation below. The program can be divided into several logical steps: 1) line 1 defines the function called gibbs(); 2) lines 2 – 22 set up several variables that will be used throughout the simulation; 3) lines 23 – 30 prepare temporary variables to store the simulation results; 4) lines 31 – 38 define the Beta and Dirichlet priors; 5) lines 39 – 48 define the starting values; 6) lines 55 – 131 iterate through the Gibbs sampling; and 7) lines 132 – 143 perform post-simulation calculations. Each step is described below, under its own subsection heading. The most important lines are lines 61 – 87 to sample c_i as per Equation (12), line 94 to sample π_j as per Equation (10), and lines 99 – 100 to sample p_jk as per Equation (11).

Definition of gibbs().

Line 1 defines a function called gibbs() and the options it accepts. The options have to be clearly specified in the function. The user must supply the gibbs() function with a data matrix y and the number of latent classes G. By default, the simulation runs a total of 7,500 iterations (niter = 7500) with the first 2,500 iterations discarded (what are called ‘burn-in’ iterations, n.burn = 2500) and every 10th iteration kept (n. thin = 10). The burn-in discards the first few—possibly unstable—iterations. The sampling of every n-th iterate is called thinning where n is called the ‘thinning interval’ (Jackman, 2009, section 6.4). Consecutive values in a Gibbs sampling are highly correlated and contribute limited new information to the parameter estimates. By default this function thins by every 10th iterate. The function prints out a count of iterations so that the user knows that it is running (verbatim = TRUE).

Global Variables Used Throughout MCMC.

Lines 2 – 5 carry out rudimentary checks of obvious errors. Line 9 loads an additional R package gtools, where the rdirichlet() function for sampling the Dirichlet distribution is found. Lines 10 – 13 prepare a few global variables that will be used throughout the MCMC simulation, such as the variable G to define the number of latent groups (line 12), the number of items (K, line 10), and the number of observations (N, line 11).

Temporary Variables for Storing MCMC Results.

Lines 17 – 30 set up temporary variables for storing the MCMC results. For example, the MCMC simulation values for π_j are stored in a matrix called Pi with G columns and niter rows, so that the values are saved after each iteration. We generally name variables in a self-explanatory manner, like Pi for π_j. Similarly, the storages for p_jk and c_ij are called Pjk and Cij.

Beta and Dirichlet priors.

Line 35 shows the parameter values for a non-informative Dirichlet(1, 1, 1, 1) prior. Line 37 – 38 show the non-informative Beta(α = 1, β = 1) prior. Both priors are used throughout the simulation. These are convenient priors to make the program easier to follow. A user can (and should) change the parameter values to alter the priors used.

Starting Values.

Lines 40 – 48 set the starting values of π_j and p_jk, where they are drawn randomly from the Dirichlet and Beta priors. For example, the rdirichlet(n = 1, alpha = dirich.prior) draws one observation from the flat Dirichlet distribution. The rbeta() function draws one random sample of proportions per latent group from the flat Beta prior. The rdirichlet() function will be used again to draw from the posterior Dirichlet distribution.

Main Gibbs Sampling.

The main Gibbs sampling loop begins at line 58. Lines 61 – 76 follow Equation (6) to calculate each person’s probability of latent class membership. We need to carry out the calculations described in the worked-out examples in Equations (5) and (6). It may help to read these examples again to understand what is being done here. Recall that we need to calculate $p_{jk}^{y_{ik}{c}_{ij}}$ and ${\left(1-p_{jk}\right)}^{\left(1-y_{ik}\right)c_{ij}}$. It is easier to calculate them in several steps using simpler calculations. First, we get p_jk and (1 − p_jk) (lines 64 – 65). Next, we apply y_ik to the exponent of p_jk and (1 − y_ik) to the exponent of (1 − p_jk), respectively. This is done in line 67, using apply(y, MAR = 1, FUN = function(yv) { pr.p^yv * pr.q^(1-yv) }), where we take the raw data y one row at a time and apply it to p_jk and (1 − p_jk). An example of the detailed calculations can be found in the text describing Equation (5). Line 67 does the same calculation using apply() to loop over 6,504 rows in y. Here apply() takes a function, FUN = function(yv) { pr.p^yv * pr.q^(1-yv) }, and applies it over y one row at a time (the MAR = 1 option instructs R to apply the function over rows).

Next, lines 68 – 69 organize the results into a N by G by K array. Next, line 70 multiplies $p_{jk}^{y_{ik}}$ and ${\left(1-p_{jk}\right)}^{\left(1-y_{ik}\right)}$ over K, as described in Equation (6) and then the result is weighted by the latent class probability distribution in line 72. Lines 74 – 76 calculate the latent class membership probability by following Equation (7).

Then the sampling of ${\mathit{c}}_i^{(t+1)}$ from a multinomial distribution is done in lines 85–87. The sampled values, for example, may be [1, 0, 0, 0] for the first person and [0, 1, 0, 0] for the second person, etc. Equation (12) may appear intimidating, but its sampling is straightforward in R. Line 94 shows how the latent class distribution π^(t+1) is sampled from the posterior Dirichlet distribution, as per Equation (10), by pooling the prior sample sizes with the data. Note that the colSums() function adds the sample counts across latent classes. Lines 96 – 101 carry out the sampling of item response probabilities $p_{jk}^{(t+1)}$ from the posterior Beta distributions, as per Equation (11), one latent class at a time. The simulated values in the current iteration are then moved to the chain storages (lines 103 – 106).

Table 3 provides a side-by-side comparison between the most important Gibbs sampling steps in Equations (10) – (12) and the corresponding R commands. Note the close resemblance between the two. For example, sampling from a Dirichlet distribution in Equation (10) is done with the rdirichlet() function in R. The user feeds the R function with appropriate input parameters, in this case the sizes of latent classes summed over all observations in the dataset, and out come the samples of the posterior Dirichlet distribution. More generally, Gibbs sampling can be implemented by distilling complex equations into functions. All the user needs to do is to call the relevant functions from a library of ready-made functions and feed them with appropriate input parameters to sample the posteriors.

Table 3.

A comparison between the equations for Gibbs sampling and how they are implemented in R. The last column covers the primary R functions that carry out the sampling, which essentially involve feeding these functions the appropriate input parameters. For example, sampling from the Dirichlet posterior involve summing the number of people within each latent class and then combining the sums with the prior sample sizes.

Equation for Gibbs sampling	Line(s)	R function
${\pi }_j^{(t+1)}~\text{Dirichlet}\left({\sum }_{i=1}^N{c}_{i1}^{(t)}+u_1,\dots ,{\sum }_{i=1}^N{c}_{iC}^{(t)}+u_g\right)$ (10)	94	pi.tl <- rdirichlet(n = 1, alpha = colSums(Cl.tl) + dirich.prior)
$p_{jk}^{(t+1)}~\text{Beta}\left({\sum }_{i=1}^N{\mathit{y}}_i{c}_{ij}^{(t)}+{\alpha }_{jm},{\sum }_{i=1}^N\left(1-{\mathit{y}}_i\right)c_{ij}^{(t)}+{\beta }_{jm}\right)$ (11)	97 – 101	pkj.tl[g, ] <- rbeta(K, shapel = alpha + colSums(Cl.tl [, g] * y), shape2 = beta + colSums(Cl.tl [, g] * (1 - y) )
${\mathit{c}}_i^{(t+1)}~\text{Multinomial}\left(1,\frac{{\pi }_1^{(t+1)}p({\mathit{y}}_i|{\mathit{p}}_1^{(t+1)})}{{\sum }_{h=1}^J{\pi }_h^{(t+1)}p({\mathit{y}}_i|{\mathit{p}}_h^{(t+1)})},\dots ,\frac{{\pi }_J^{(t+1)}p({\mathit{y}}_i|{\mathit{p}}_J^{(t+1)})}{{\sum }_{h=1}^J{\pi }_h^{(t+1)}p({\mathit{y}}_i|{\mathit{p}}_h^{(t+1)})}\right)$ (12)	85 – 87	Cl.tl <- apply(Clp.tl, 1, function(prob) { rmultinom(n = 1, size = 1, prob = prob) })

The next block of commands (lines 108 – 116) addresses the label switching problem in the simulation which will be described below.

At the end of the burn-in, the program prints out a message (lines 121– 125). Lines 127 – 129 show a message every 500 iterations. Line 130 increments the iteration count by 1. The closing curly brace on line 131 loops the program back to line 59, where the while() loop began.

Output of gibbs().

Line 134 performs the thinning by extracting every n.thin value from the end of the burn-in (n.burn + 1) to the end of the iteration (niter). Lines 135 – 142 collect the results and return them as the final output of the gibbs() function.

Fitting Add Health Data by gibbs()

The commands below show how to run the gibbs() function. The first few lines import the downloaded Add Health raw data into R. The first row is removed because it contains all missing data. The original variables (e.g., H1DS3, H1DS15) are renamed to make them more readable. Our gibbs() function works with an input data matrix. Thus, we extract columns 2 to 7 from the raw data, convert them into a matrix called data for the gibbs() simulation. The set.seed(23) command is optional. It sets the seed for the random number generator so that the simulation results can be reproduced exactly. We supply the data, and ask gibbs() for a 4-class solution, overriding the default to run 12,000 iterations instead. The results are stored in gibbs.out.

> addhealth.dat <- read.csv(file = “addhealth.csv”, row.names = NULL)
> addhealth.dat <- as.data.frame(addhealth.dat)
> addhealth.dat <- addhealth.dat[−1, ] # removing first row, all missing
> attach(addhealth.dat)
> addhealth.dat <- data.frame(AID = AID, lied=H1DS3, publicly=H1DS15,
+ damaged=H1DS2, shoplift=H1DS4, stole50=H1DS13,
+ grpfight=H1DS14)
> data <- as.matrix(addhealth.dat[, 2:7]) - 1 # convert 2, 1 to 0, 1
> set.seed(23)
> gibbs.out <- gibbs(data, G = 4, niter = 12000)
iteration(s) completed:  1  500  1000  1500  2000
burn-in completed
2500  3000  3500  4000  4500  5000  5500  6000  6500  7000  7500
  8000  8500  9000  9500  10000  10500  11000  11500  12000
> gibbs.out$Pi.mean
[1] 0.48071825 0.08776944 0.13884230 0.29267001
> gibbs.out$Pjk.mean
	lied  publicly	   damaged   shoplift    stole50    grpfight
G1 0.2715719 0.1699331 0.006004635 0.02063179 0.008127299 0.04123363
G2 0.9185183 0.9676303 0.818434371 0.87509123 0.862129884 0.62657599
G3 0.7283306 0.5605000 0.257569880 0.94894426 0.705638879 0.20065908
G4 0.7282061 0.7747278 0.255566807 0.04994728 0.047320368 0.32502534

The π_j and p_jk estimates are found in gibbs.out$Pi.mean and gibbs.out$Pjk.mean, respectively. The simulation takes approximately 30 minutes on a 64-bit Linux computer with two quad-core Intel Xeon CPUs at 2.40GHz clock speed and 32GB of memory.

Results

LCA parameter estimates

A brief summary of the parameter estimates are provided in Table 4. Parameter estimates from SAS and the poLCA package in R are also included for comparison (both use EM). The latent class distribution parameter in our calculation above shows $\widehat{\pi }=[0.481,0.088,0.139,0.293]$. SAS shows $\widehat{\pi }=[0.479,0.086,0.140,0.295]$. Overall, our results agree well with those from SAS. We will not dwell on how to interpret these results and how to assign names to the latent classes which have already been covered elsewhere (Collins & Lanza, 2010). An observant reader will find that the results from poLCA show a different order. A careful inspection and explanation is provided below. The three sets of results are otherwise very similar.

Table 4.

Parameter estimates for the full Add Health sample (N = 6, 504) by different computation strategies.

Computation Strategy		Latent Classes
		Class 1		Class 2		Class 3		Class 4
gibbs() sampling	${\widehat{\mathit{\pi }}}_j$	0.481*	(0.016)†	0.088	(0.010)	0.139	(0.014)	0.293	(0.019)
	${\widehat{p}}_{jk}$
	Lied to parents	0.272	(0.013)	0.919	(0.020)	0.728	(0.021)	0.728	(0.019)
	Publicly loud/rowdy/unruly	0.170	(0.015)	0.968	(0.019)	0.561	(0.032)	0.775	(0.021)
	Damaged property	0.006	(0.003)	0.818	(0.046)	0.258	(0.028)	0.256	(0.016)
	Shoplifting	0.021	(0.005)	0.875	(0.021)	0.949	(0.035)	0.050	(0.024)
	Stolen something worth < $50	0.008	(0.003)	0.862	(0.024)	0.706	(0.043)	0.047	(0.014)
	Taken part in group fight	0.041	(0.006)	0.627	(0.037)	0.201	(0.025)	0.325	(0.017)
SAS PROC LCA	${\widehat{\mathit{\pi }}}_j$	0.479	(0.016)	0.086	(0.011)	0.140	(0.016)	0.295	(0.019)
	Lied to parents	0.270	(0.012)	0.922	(0.020)	0.731	(0.021)	0.726	(0.019)
	Publicly loud/rowdy/unruly	0.168	(0.014)	0.974	(0.023)	0.561	(0.033)	0.774	(0.022)
	Damaged property	0.005	(0.020)	0.822	(0.048)	0.260	(0.030)	0.253	(0.015)
	Shoplifting	0.020	(0.005)	0.879	(0.021)	0.964	(0.038)	0.043	(0.028)
	Stolen something worth < $50	0.008	(0.002)	0.862	(0.025)	0.695	(0.044)	0.052	(0.014)
	Taken part in group fight	0.040	(0.006)	0.631	(0.038)	0.202	(0.027)	0.324	(0.016)
poLCA() in R	${\widehat{\mathit{\pi }}}_j$	0.297	(0.019)	0.084	(0.010)	0.140	(0.015)	0.479	(0.016)
	Lied to parents	0.726	(0.018)	0.924	(0.020)	0.734	(0.020)	0.270	(0.012)
	Publicly loud/rowdy/unruly	0.773	(0.021)	0.978	(0.023)	0.565	(0.030)	0.167	(0.014)
	Damaged property	0.254	(0.015)	0.829	(0.045)	0.263	(0.028)	0.005	(0.004)
	Shoplifting	0.043	(0.028)	0.880	(0.021)	0.972	(0.042)	0.020	(0.005)
	Stolen something worth < $50	0.055	(0.015)	0.864	(0.025)	0.697	(0.045)	0.008	(0.002)
	Taken part in group fight	0.324	(0.016)	0.635	(0.036)	0.205	(0.025)	0.040	(0.006)

^*: Original parameter estimates without reordering the labels.

^†: posterior standard deviation.

MCMC diagnostics

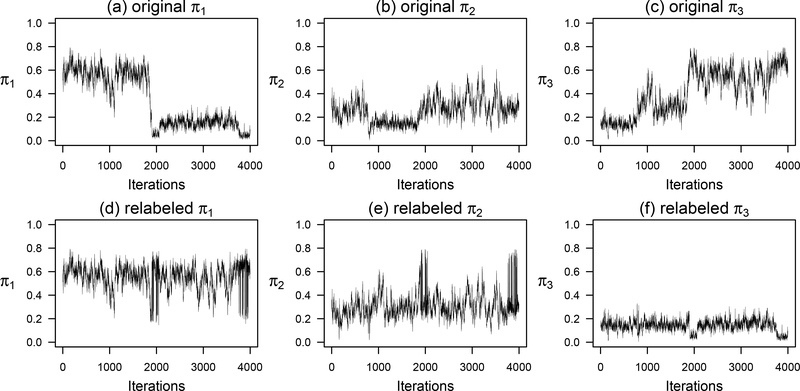
An important task to do is to inspect signs of problems in Bayesian computation. This is often done by visual inspection of the simulated values. Figure 3 provides an illustrative example of trace plots for π_j, using a randomly selected subset of n = 200 from the full Add Health data in a 3-class solution instead of 4. The much smaller subset of data and a 3-class solution was selected to make the problem more visible. Subplot (a) shows that the sampling of π₁ starts at around 0.60. However, it drifts downward to 0.15 as it approaches the 2,000th iteration. Then it stays around 0.15. Subplot (c) shows the opposite pattern, π₃ drifts upward to 0.60 at about the same position where π₁ drops to 0.15, an indication that π₁ and π₃ are swapped mid-simulation. The histograms for these posterior estimates may show more than one mode.

Figure 3.

Illustration of the label switching problem. Plotted here are MCMC simulation traces for π_j using a randomly selected subset of 200 observations from the full Add Health data. We fitted a simpler model with 3 latent classes instead of 4 to show a more visible pattern. Subplots (a) – (c) are the traces for the original MCMC chain. Subplots (d) – (f) are the relabeled chains. Signs of label switching are present in (a) where the chain first hovers around π₁ ≈ 0.60 and then it drifts to the proximity of 0.15 near the 2,000th iteration. This is corroborated by (c) where π₃ drifts up to ≈ 0.60 exactly when π₁ drifts down to ≈ 0.15, an indication that π₁ and π₃ switched labels during simulation. Similarly, signs of label switching are also visible in the π₂ chain, although not as pronounced. The relabeled MCMC chains in (d) – (f) show visibly improved simulation traces.

We need to repair the values swapped mid-simulation. For now, let us just see what the repaired trace plots look like. Plots 3(d) through 3(f) contain traces after a relabeling algorithm has been applied. The relabeled trace plots show no visibly switched peaks. Next we explain why π₁ and π₃ swap values mid-simulation, a phenomenon called “label switching”.

The Label Switching Problem Explained

Label switching is a common complication in Bayesian computation for models like LCA (Jasra, Holmes, & Stephens, 2005; Stephens, 2000; Richardson & Green, 1998; Celeux, Hurn, & Robert, 2000). A simplified, intuitive explanation is provided below. In the simplest LCA with two latent classes, Equation (1) can be written as

$$f\left({\mathit{y}}_i;\mathit{\pi },\mathit{p}\right)=\pi A+(1-\pi )B,$$

where $A={\prod }_{k=1}^K{p}_{1k}^{y_{ik}}{\left(1-p_{1k}\right)}^{1-y_{ik}}$ for j = 1 (following the item response probabilities for latent class 1) and B with the same form for j = 2. It is a weighted average between two quantities, weighted by π and its complement. However, the likelihood function can also be written in a different labeling scheme,

$$f\left({\mathit{y}}_i;\mathit{\pi },\mathit{p}\right)=(1-\pi )A+\pi B,$$

without changing anything else in the model. ² Since the true value of π is unknown, either labeling scheme represents exactly the same model. If the true value of π = 0.40, then 1 − π must be 0.60. However, nothing is changed if π = 0.60 by the second labeling scheme—either one is perfectly acceptable. As a result, two modes arise from the distribution of π with equal posterior probability. Similarly, in a 3-class solution, the latent classes can be arbitrarily labeled in any one of the 6 possible permutations. Because the order of the labels is not fixed, in one MCMC iteration the labeling may be 1–2-3, in the next 2–3-1. This adds difficulty in averaging across simulated results as is common in MCMC simulations. Interpretation of the results is equally problematic.

Table 4 shows that the R program poLCA gives comparable parameter estimates, except that latent classes 1 and 4 are swapped. The substantive interpretation of the results is not at all affected, seen in all three computer programs agreeing on the parameter estimates (barring slight differences due probably to decimal rounding). The switching of latent classes in this case is not exactly the label switching problem, although it is caused by the same underlying issue that the likelihood function is not uniquely defined. A full investigation of why poLCA switches latent classes deserves its own tutorial. The main message for now is that label switching refers to the problem occurring during MCMC simulation so that we get inaccuracies in Gibbs sampling when we average the raw chains.

Lines 107 – 116 in Appendix A provide a crude but pragmatic workaround for the label switching problem. Essentially, we compare how the N = 6,504 respondents are labeled between the first iteration post burn-in and each subsequent iteration. The idea is that respondents should be categorized into the same latent class throughout the simulation (Wyse & Friel, 2012). A comparable approach is reported in the R package BayesLCA (White & Murphy, 2014).

Discussion

This tutorial shows how Bayesian MCMC computation using Gibbs sampling is carried out using LCA as an illustrative example. We aim to provide a self-contained tutorial to help students understand the statistical modeling as well as the computer programming. Our primary goal is to address several difficulties in methodology papers in Bayesian statistics. Often the detailed derivations are omitted, assumed understood, or the notation is so complex that they are nearly impossible to follow. Our use of hypothetical data makes the calculations easier to work with. We also address the main challenge confronting non-technicians—how to transition from the mathematics and statistical modeling to computer programming. First, we must work out the statistical function that defines the joint conditional posterior distribution. Then, an essential Bayesian principle—posterior is prior times likelihood—guides the derivations for the marginal posterior distributions. The key is to carefully work out the mathematics to arrive at the convenient forms of the marginal posterior distributions. The subsequent sampling is relatively straightforward, by calling the rbeta() and rdirichlet() functions in R to carry out the sampling with appropriate parameters. The mathematics is no more than basic Bayes’ Theorem and summations of quantities. The computer programming is not trivial, but no more than writing loops to sample from statistical functions. The close resemblance between the computer program and the mathematics should aid the learning of both. Students willing to work through the step-by-step calculations may gain a deeper understanding of important concepts such as “thinning” and “burn-in”. We hope that readers will take away an important message. Complex notation can be tracked more easily with the help of a concrete example and computation tools. The approach outlined in this tutorial applies to other, more complex models.

We deliberately offer no model diagrams. Visual representations of statistical models, such as Directed Acyclic Graphs (DAG), often make complex mathematics easier to explain. However, DAGs cannot replace the need to precisely define what goes into the statistical functions. Our visual explanations focus on understanding what the statistical distributions look like and what statistical uncertainties they encapsulate, such as the Dirichlet and Beta priors, in the same style of other authors (e.g., Gelman, Carlin, Stern, and Rubin (2003, Section 18.4), P. M. Lee (2012, Section 9.2)), and Gelman and Hill (2007, Chapter 18)).

Our illustrative example in LCA should provide the foundation for a learner to move on to more complex models, such as the inclusion of baseline covariates and distal outcomes into LCA, which are supported by existing statistical packages or other sophisticated latent models (Elliott et al., 2005; Neelon, O’Malley, & Normand, 2011; Neelon et al., 2015) not supported by existing statistical packages. A fully Bayesian approach by MCMC simulation offers information not available in other computation approaches, e.g., the fit indices and probability of classifications above and other useful quantities such as the parameter standard errors by data augmentation (S. T. Lanza, Collins, Schafer, & Flaherty, 2005).

Limitations

There are nevertheless limitations that cannot be fully addressed within the scope of a tutorial. Below we direct the reader to the literature. For example, no R program yet includes a sophisticated and efficient way to address the labeling switching problem (Stephens, 2000; Jasra et al., 2005; Richardson & Green, 1998; Celeux et al., 2000; Papastamoulis, 2016). Simplifications in the priors are used whereas a production-ready tool should allow more sophisticated priors and hyper-priors (White & Murphy, 2014). Many statistical concepts are not covered. For instance, we have not covered nor tested the main assumption of local independence (Collins & Lanza, 2010, section 2.5.2). Item responses only depend on latent class membership and within the local latent class they are independent. This assumption allows us to multiply the independent probabilities in Equations (1) – (2). Also not covered are MCMC convergence diagnostics (Li & Baser, 2012, for a brief review) and Bayesian criteria for model comparison, such as the DIC (Spiegelhalter, Best, Carlin, & van der Linde, 2002) and the WAIC (Watanabe, 2010). Readers may find the comprehensive review by Gelman, Hwang, and Vehtari (2014) helpful.

These limitations notwithstanding, we hope this tutorial provides an accessible entry to one specific context of the vast Bayesian statistics literature. Others are welcome to improve upon the current R program to bring it up to production use comparable to what is available in commercial statistical software packages which is exactly the purpose of sharing the R code.

Suggestions for Further Reading

The suggested further readings are intended to help beginners to learn more, thus there is a preference on visual explanations and materials at an introductory level. The list is not exhaustive, and technical materials are not offered. They are more suitable after the reader has acquired greater independence and proficiency in Bayesian computing.

• Introductory Bayesian statistics

  • Berry (1995) is an introductory textbook on basic Bayesian concepts.
  • P. M. Lee (2012) provides beginners with the theoretical basics in Bayesian statistics.
  • Kaplan (2014) offers practical examples in regression and multilevel modeling using large databases in social sciences.
  • McElreath (2016) uses visual explanations extensively, with clear and succinct explanations accompanying these examples. Chapter 6 provides a clear and comprehensive exposition on model comparison metrics.
  • Gelman and Hill (2007) provides theoretical foundations and applications, with a focus in social and behavioral sciences.
  • Gelman et al. (2003) offers a comprehensive coverage of Bayesian statistics.

• Gibbs sampling

  It is said that the idea of solving complex problems by simulation was first proposed by the physicist Stanislaw Ulam in 1946, when he tried to calculate the chances of successful plays in the card game solitaire (Andrieu, De Freitas, Doucet, & Jordan, 2003). He realized that it would be much easier to lay out several games at random and then simply count the number of successful plays. Here lies the essence of MCMC simulation. A complex problem can be solved easily if we recast it as a much simpler problem of statistical simulation. Gibbs sampling is among the simplest MCMC techniques. As shown in Equation (9), the complex joint posterior distribution can be derived by sampling one parameter at a time while holding all the other parameters as fixed and known. A good approximation is obtained after a sufficiently large number of iterations. To explore what Gibbs sampling actually looks like, you can try the examples below. You can run the R code in Darren Wilkinson’s blog to see Gibbs sampling in action.

  • MacKay (2003, p.370) offers visual explanations of Gibbs sampling.
  • Gelman et al. (2003, Figure 11.3) shows how Gibbs sampling alternates between the conditional distributions.
  • Wilkinson (2011) is a blog on how Gibbs sampling can be done using several computer programming languages.
• Introduction in Bayesian computation

  • Albert (2007) offers beginners a good starting point on Bayesian computation.
• The label switching problem

  • Richardson and Green (1998) give a good illustration of the problem.
  • Jasra et al. (2005) provide an overview of various developments in fixing the problem. Celeux et al. (2000) provide another sophisticated method.
  • Papastamoulis (2016) summarizes the label.switching package in R.
  • Stephens (2000) offers a definitive guide (technical).
• Other Online Resources

  • Pennsylvania State University Methodology Center website at http://www.methodology.psu.edu/ra/lca
  • John Uebersax’s website at www.john-uebersax.com.

Appendix A

R code for Gibbs Sampling

1 gibbs <- function(y, G, dirich.prior = NULL, niter = 7500,
     n.burn = 2500, n.thin = 10, relabel = TRUE, verbatim = TRUE) {
2 if ( ! all(y == 0 | y == 1) )
3	stop(“y must be coded 0 or 1”)      # stop if y is not coded 0, 1
4 if ( niter <= n.burn )				# niter has to be > n.burn, error if not
5	stop(paste(“niter =“, niter, “, must be greater than n.burn =“, n.burn))
6 ###
7 # loading packages needed to run Gibbs sampling and basic settings
8 ###
9 require(gtools)	# rdirichlet()
10 K <- ncol(y)	# number of items
11 N <- nrow(y)	# number of respondents
12 G <- G	# number of latent groups
13 done.burn <- FALSE # burn.in is not yet done
14 ###
15 # MCMC basic setup, number of iterations and storages for chains
16 ###
17 Pi <- matrix(NA, nrow = niter, ncol = G) # storage for class membership
18 Pjk <- array(NA, dim = c(niter, G, K))	# storage for item resp prob
19 dimnames(Pjk) <- list(NULL, paste(“G”, 1:G, sep = ““), colnames(y))
20 Cij <- array(NA, dim = c(niter, N, G))	# storage for discrete classes
21 Cij.pr <- array(NA, dim = c(niter, N, G)) # storage for latent class prob
22 labelStor <- matrix(NA, nrow = niter, ncol = G) # storage for relabeling
23 #
24 ## Storages for simulated parameters pjk, C, at iteration t+1
25 #
26 pjk.t1 <- matrix(NA, nrow = G, ncol = K) # latest p_jk^(t+1) stored here
27 dimnames(pjk.t1) <- list(paste(“G”, 1:G, sep=““), colnames(y))
28 # N*G (people by group) matrix of each person’s class membership prob
29 Clp.t1 <- matrix(NA, nrow = N, ncol = G)
30 dimnames(Clp.t1) <- list(paste(“N”, 1:N, sep=““), paste(“G”, 1:G, sep=““))
31 ###
32 # Priors
33 ###
34 if ( is.null(dirich.prior) )
35	dirich.prior <- rep(1, G) # flat Dirichlet by default
36 # Beta prior, alpha=1 and beta=1 for a flat prior
37 alpha <- 1
38 beta <- 1
39 ###
40 # Starting values of pi and pjk, drawn randomly from Dirichlet, Beta priors
41 ###
42 start.pi <- rdirichlet(n=1, alpha = dirich.prior)
43 start.item.p <- matrix(NA, nrow = G, ncol = K)
44 for (g in 1:G)
45	{
46	start.item.p[g, ] <-
47		rbeta(K, shape1 = alpha, shape2 = beta)
48	}
49 ###
50 pi.t <- start.pi # membership distr [pi1=0.78, pi2=0.11, pi3=0.11]
51 pjk.t <- start.item.p # item response probability pjk on iteration t
52 # used later to address the label switch problem
53 perm <- gtools::permutations(n=G, r=G) # 24 total permutations when G=4
54 trace.num <- numeric(nrow(perm))	# trace of match between t0 and t+1 55 ################
56 # Main MCMC simulation
57 ################
58 iter <- 1			# begins with iteration number 1
59 while (iter <= niter)		# loop until niter is reached
60 {
61 # Each person’s class membership prob, using Eq (7)
62 #	[c|y,pi,p] = [pi * pr(y|p)] / [total probability]
63 # step 1: pr(y|p), first calcualte p and 1-p
64 pr.p <- t(pjk.t)	# transpose to K by G matrix for apply()
65 pr.q <- 1 - pr.p
66 # step 2: binomial item response probability per Eq (2)
67 A <- apply(y, MAR = 1, FUN = function(yv) { pr.p^yv * pr.q^(1-yv) })
68 A <- array(A, dim = c(K, G, N))
69 A <- aperm(A, c(3, 2, 1))	# reshape into N*G*K
70 eq2 <- apply(A, MARGIN = c(1, 2), prod)  # multiply across K, keeping N*G
71 # step 3: each binomial item resp prob weighted by class distr prob pi[j]
72 eq2 <- sweep(eq2, MARGIN = 2, STATS = pi.t, FUN = “*”)
73 # Calculate total probability for each person, per Eq (5)
74 p.total <- apply(eq2, MARGIN = 1, sum)
75 # finally, ‘divided-by-total’ yields latent class membership prob
76 Clp.t1 <- eq2/p.total
77 #
78 # Clp.t1 gives us the probability of each person’s latent class membership,
79 # e.g., person 1 has (0.30, 0.20, 0.15, 0.35) of being in class 1, 2, 3, and 4.
80 # So latest class membership can be c=[1,0,0,0] with 30% chance,
81 # c=[0,1,0,0] with 20% chance, c=[0,0,1,0] with 15% chance, and c=[0,0,0,1]
82 # with 35% chance. Next we use these probs to draw a single specific sample
83 # of c from any of the 4 possibilities above. Each person has one and only
84 # one class out of G latent classes.
85 Cl.t1 <- apply(Clp.t1, 1,
86 function(prob) { rmultinom(n = 1, size = 1, prob = prob) })
87 Cl.t1 <- t(Cl.t1)
88 ##
89 # Next, update pi (per Eq (10)) and pjk (per Eq (11)) using the newly
90 # calculated N*G matrix of discrete latent class membership
91 ##
92 # Sample $\pi_j^{(t+1)}$, percentages of latent classes in the population
93 # Eq (10) shows posterior = data by colSums(C.t) + prior sample sizes
94 pi.t1 <- rdirichlet(n = 1, alpha = colSums(Cl.t1) + dirich.prior)
95 # sample item response probability, one latent class at a time, sum over N
96 for (g in 1:G) # each column not guaranteed to add up to 1
97	{
98	# Eq (11) shows posterior beta(y*c + alpha, (1-y)*c + beta)
99	pjk.t1[g, ] <- rbeta(K, shape1 = alpha + colSums(Cl.t1[, g] * y),
100		shape2 = beta + colSums(Cl.t1[, g] * (1-y)) )
101	}
102 # simulated values in current iteration are added into chain storages
103 Pi[iter, ] <- pi.t1
104 Pjk[iter, , ] <- pjk.t1
105 Cij[iter, , ] <- Cl.t1
106 Cij.pr[iter, , ] <- Clp.t1
107 # ‘label switching’ problem to match latent classes at end of burn-in
108 if (relabel && done.burn)
109	{
110	match.tab <- t(Cl.t1) %*% Cl.0 # match between t+1 and t0 latent classes
111	for (l in 1:nrow(perm)) # across G! permutations, where matches are?
112		trace.num[l] <- sum(diag(match.tab[, perm[l, ]]))
113
114	relabel.ord <- perm[which.max(trace.num), ] # relabel by best match
115	labelStor[iter, ] <- relabel.ord
116	}
117 # Current simulated values will be used to draw the next iteration
118 pi.t <- pi.t1
119 pjk.t <- pjk.t1
120 # print a message if b.burn iterations done
121 if (iter == n.burn) {
122	done.burn <- TRUE
123	cat(“\nburn-in completed\n”)
124	Cl.0 <- Cl.t1 # latent classes immediately after burn-in
125	}
126 # verbatim can be set by the user to print iteration count every 500th iter
127 if (verbatim)
128	if (iter == 1) cat(“iteration(s) completed: “, iter, “ “)
129	if ( (iter %% 500) < 10^(−7) ) { cat(iter, “ “) }
130 iter <- iter + 1 # last thing before repeating is to incrememt iter by 1
131 }	# end while (iter <= niter)
132 cat(“\n”)
133 # Discard burn-in iterations, thin by n.thin
134 ti <- seq(from = n.burn+1, to = niter, by = n.thin)
135 Pi.chain <- Pi[ti, ]			# pi chain after burn-in and thinning
136 Pjk.chain <- Pjk[ti, ,]		# pjk after burn-in and thinning
137 labelStor <- labelStor[ti, ]
138 Pi.mean <- apply(Pi.chain, 2, mean) # average pi
139 Pjk.mean <- apply(Pjk.chain, c(2, 3), mean)  # average p[jk]
140 # put the results together in a list and return() the results
141 ans <- list(Pi.mean = Pi.mean, Pjk.mean = Pjk.mean, Pi.chain = Pi.chain,
		  Pjk.chain = Pjk.chain, Cpr.chain = Cij.pr, relabelOrd = labelStor)
142 return(ans)
143 }