Abstract
Environmental fate and transport processes are influenced by many factors. Simulation models that mimic these processes often have complex implementations, which can lead to over-parameterization. Sensitivity analyses are subsequently used to identify critical parameters whose uncertainties can be further reduced or better described and prediction variability minimized. In this study, a variance decomposition based global sensitivity analysis technique (Sobol’ method) is conducted based on estimated concentrations in vertical soil compartments using the Pesticide Root Zone Model (PRZM). Daily simulations are performed that explore the input parameter space. Estimated concentrations are compared to data collected over the course of a growing season from an experimental site in Georgia. Our results suggest that model sensitivity is conditional and should be examined at appropriate spatial and temporal resolution to avoid omitting important parameters. This approach can yield a better understanding about the interplay between sensitivity/uncertainty and model dynamics in non-monotonic, non-linear systems.
Keywords: Sobol’ sensitivity analysis, Global sensitivity analysis, Vertical transport, Fate and transport, Pesticides
1. Introduction
1.1. Overview of sensitivity analysis
Sensitivity analysis investigates how uncertainty in model outputs can be apportioned to different input sources (Saltelli et al., 2004, 2008) which usually focuses on the following aspects: 1) identifying parameters which are the most influential (contributing most to output variability) for the calibration process; 2) highlighting parameters which require additional research for strengthening the knowledge base; and 3) determining parameters which are insignificant and can be eliminated from the final model to avoid overparameterization (Hamby, 1994; Iman and Helton, 1988). Based on the type of analysis, it can be considered as qualitative or quantitative, whose major methods are listed in Fig. 1.
Fig. 1.
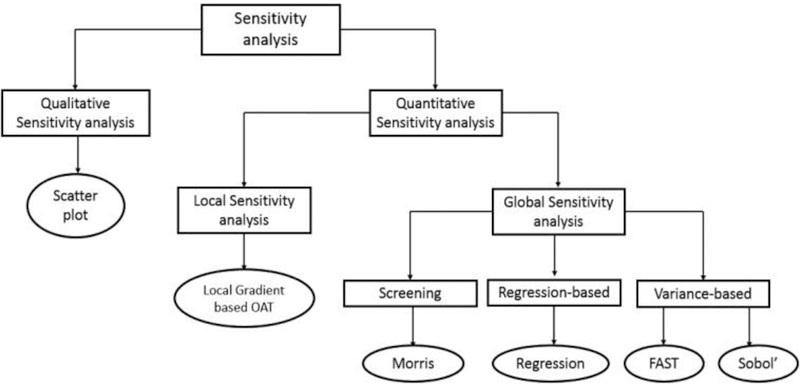
Category of commonly used sensitivity analysis methods.
As a representative of the qualitative sensitivity analysis method, scatter plot inspects the influence of individual inputs on an output visually (Cook and Weisberg, 2009; Frey and Patil, 2002). Although scatter plot does not provide quantitative rankings of inputs, it could depict the possible (non)linear or (non)monotonic dependence between an input and output (Cook and Weisberg, 2009). Thus, scatter plot is usually selected as the first step in the sensitivity analysis which allows for the identification of potentially complex dependencies and guides for the selection of quantitative sensitively analysis methods. A drawback of this approach is that interpretation of a scatter plot is subjective (Frey and Patil, 2002).
Quantitative sensitivity analysis methods are categorized into local or global approaches given the number of co-perturbed parameters. Local methods refer to analyses which characterize model inputs’ local gradients at a given point at a time, while other parameters usually are set to their nominal or mean values. Although with a low computational cost, the OAT method could contain biased results for non-linear models, since it assumes linearity between inputs and outputs (Nossent and Bauwens, 2012a; Saltelli et al., 2005). Global sensitivity analysis method searches the whole parameter space in a random or systematic approach. In addition, it allows all inputs to be varied simultaneously but has a high computational cost. However, with increasing computing capacity, global sensitivity analysis has become more prevalent since this makes exploring multi-dimensional parameter spaces are more feasible (Massmann and Holzmann, 2012; Reusser et al., 2011; Saltelli et al., 2005). Thus, local sensitivity analysis measures sensitivity information between a specific input value and the corresponding output space. While global analyses consider the whole input and output spaces which allows all inputs to be varied simultaneously (Saltelli et al., 2010).
1.2. Types of global sensitivity analysis
Global sensitivity analysis is a model independent technique, which means that the sensitivity analysis method does not require a specific type of relationship between inputs and model outputs (Baroni and Tarantola, 2014). When full coverage of parameter spaces are properly sampled, it can handle non-linearity, non-monotonicity and non-additivity models (Nossent and Bauwens, 2012a). There are three types of global sensitivity analysis methods (Fig. 1): screening methods, regression-based methods, and variance-based methods (Confalonieri et al., 2010).
The most common screening method, Morris method, captures not only the overall importance of a parameter, but also its interactions with other parameters. The Morris method is effective in identifying important parameters for a monotonic model at a reasonable computational cost. For non-monotonic models, Campolongo et al. (2007)improved Morris algorithms by considering absolute effective effects, which reduces the probability of not identifying important parameters (Type II error). Regression methods build linear equations between model inputs and outputs by sampling with Monte Carlo or Latin Hypercube techniques. When inputs are independent of each other, their standard regression coefficients (SRC), representing the effect of changing an input from its baseline value by a fixed fraction of the standard deviation, are used to rank inputs based on their impacts on model outputs (Confalonieri et al., 2010). However, parameters ranked by SRC are based on the linear regression model which is used to describe the target model, not directly on the target model (Saltelli et al., 1999). The performance of this method depends on coefficient of determination (R2) which captures the percentage of variance that can be explained by the proposed regression model (Confalonieri et al., 2010; Saltelli et al., 2005). The regression method is thus better suited to linear models (Saltelli et al., 1999, 2008).
Although computationally intensive, benefits associated to variance decomposition type of sensitivity analysis are significant, which are reliable for both linear and non-linear models, as well as monotonic and non-monotonic models. Global sensitivity analysis methods not only account for impacts from individual inputs, but also consider influences from interactions among inputs. Fourier Amplitude Sensitivity Test (FAST) developed by Cukier and his colleagues is considered to be the earliest variance-based method. FAST method adopts Fourier transformation function to sample input spaces in estimating their first-order sensitivity indices, which is also known as “main effect”, contribution of each input to the variance of the output (Cukier et al., 1975; Saltelli et al., 1999). Later, Saltelli et al. (1999) extended the original FAST method with the ability to compute total sensitivity indices for identified parameters (EFAST). However, the two main disadvantages for FAST and EFAST methods are that they fail to sample inputs directly from their distributions and results are not reliable when inputs are not continuously distributed (Confalonieri et al., 2010; Frey and Patil, 2002).
Sobol’ method estimates inputs’ first and higher order sensitivity indices by evaluating a multidimensional integral through a Monte Carlo simulation (Patelli et al., 2010). Sobol’ method has become the most powerful sensitivity analysis techniques since it directly samples parameter spaces, which is the main difference between FAST and Sobol’ method (Saltelli et al., 1999); and is capable of handling the case of dependent variables (Glen and Isaacs, 2012; Kucherenko et al., 2012; Li et al., 2013). Though Sobol’ method is straightforward to apply, it is computationally expensive. As a result, many researchers have developed optimized algorithms (Jansen, 1999; Saltelli, 2002; Saltelli et al., 2010; Sobol, 2001). A comparison of commonly applied sensitivity methods are listed in Table 1and an in-depth review are available from Matott et al. (2009) and Pianosi et al. (2016).
Table 1.
Comparison of commonly used sensitivity analysis methods.
| Criteria for comparison |
Scatter plots |
OAT | Morris | Regression based method |
FAST | Sobol’ |
|---|---|---|---|---|---|---|
| Local or global | N/A | Local | Global | Global | Global | Global |
| Discrete inputs | Yes | Yes | Yes | Yes | Yes | Yes |
| Model independence |
Yes | No | Yes | Yes | Yes | Yes |
| Non-linear | Yes | No | Yes | No | Yes | Yes |
| Non-monotonic | Yes | No | No | No | Yes | Yes |
| Consider parameter interactions |
No | No | Yes | No | No | Yes |
1.3. Study objective
The objective of this study is to apply Sobol’ sensitivity analysis on Pesticide Root Zone Model (PRZM), a compartment model that predicts the fate and transport of pesticides in unsaturated soil systems at plant root zone depths, to explore parameters’ impacts to the estimated pesticide soil concentrations. PRZM has been used by the USEPA as part of their risk assessment process for pesticide registration. We propose to evaluate those impacts spatially and temporally as suggested by recent studies (Guse et al., 2014; Herman et al., 2013a, 2013b; Massmann et al., 2014; Sieber and Uhlenbrook, 2005). The remaining parts are as follows: the second part of the paper introduces background of PRZM model and algorithms used to compute Sobol’ index; the third part presents results based on a field pesticide leaching study conducted in South Georgia (Jones and Russell, 2001). With this approach, we conditionally identify sensitive parameters over time and vertical depth. We use first order Sobol’ sensitivity indices to locate the high priority model inputs based on their relative ranking that directly influence estimated pesticide soil concentrations at different time periods and depths. In addition, we use low ranking total order indices, the sum of interaction terms with other varied parameters plus first order sensitivity index, to focus on excluding non-sensitive parameters based on their low first-order and parameter interaction contributions.
2. Method
2.1. PRZM model
PRZM is a heavily used, one-dimensional, dynamic compartment model capable of predicting the fate and transport of pesticides in unsaturated soil systems at plant root zone depths. PRZM is a finite difference model that uses a method of characteristics algorithm to solve partial difference equations that account for relevant climatic, chemical, and agronomic phenomena including soil temperature, volatilization, irrigation and cropping practices, solubility/sorption, and microbial transformation processes. Two major components in a PRZM model are hydrology and chemical transport. The hydrologic component estimates runoff, erosion, evapotranspiration, and water movement. The transport component distributes organic and inorganic chemicals in the soil.
PRZM has been applied in many environmental applications including pesticide leaching on agricultural lands (Banton and Villeneuve, 1989; Chang et al., 2008; Du et al., 2008; Jackson and Estes, 2007), construction of municipal landfills (Aivalioti and Karatzas, 2006), and assessing industrial emissions (Shin et al., 2011). When coupled with a geographic information system (GIS), PRZM can assess transport from multiple spatial locations (Akbar and Lin, 2010). For example, Akbar et al. (2011) developed a health risk map by spatially modeling bentazon leaching in Woodruff County, AK. Jackson et al. (2007) created PLUS, a PRZM and GIS-based tool which ranked the vulnerability caused by agricultural practices on over 8000 soil types and weather combinations. Similarly, Luo and Zhang (Luo and Zhang, 2009, 2010, 2011) employed a geo-referenced modeling system and simulated the spatiotemporal variations of pesticide transport at watershed scales. Another linkage used the Exposure Analysis Modeling System (EXAMS) to simulate impacts based on PRZM outputs. Within this framework, Chiovarou and Siewicki (2008) compared risk to resident biota in estuarine headwaters at two locations with varying pesticide application scenarios and storm intensities. Davis et al. (2007) estimated ecological risk to non-target aquatic organisms from applying six common mosquitocides used to control West Nile virus. Sabbagh et al. (2010) coupled the PRZM-EXAMS approach with a vegetated filter strip (VFS) model to evaluate performance on pesticide reductions. There have also been many verification studies testing whether predictions from PRZM are reliable in comparison to other models and/or field observations. PRZM has been compared to the Root Zone Water Quality Model (RZWQM) (Fox et al., 2006), the Leaching Estimation and Chemistry Model (LEACHP), the MACRO model (McQueen et al., 2007), and has also been validated against field data (Mamy et al., 2008).
As with other highly-dimensioned environmental models, PRZM’s inputs and outputs could contain is likely over-parameterized despite the fact that its inputs and outputs have significant uncertainty. The Federal Insecticide, Fungicide, and Rodenticide Act (FIFRA) Environmental Model Validation Task Force (FEMVTF) performed a model evaluation of PRZM by comparing model results against field measurements collected at 18 locations (Carbone, 2002; Carbone et al., 2002; Russell and Jones, 2002; Singh and Jones, 2002). As part of the validation process, FEMVTF conducted sensitivity analysis using Plackett and Burman’s approach to identify the most influential parameters (Carbone, 2002; Plackett and Burman, 1946; Warren-Hicks et al., 2002; Wolt et al., 2002). Although Plackett and Burman method is computational efficient, it only evaluates parameters at two fixed levels and finds 2-way interactions (Beres and Hawkins, 2001; Gan et al., 2014).
2.2. Sobol’ method
Let Equation (1) represent a model whose independent parameters are k elements in vector X, and its output is a scalar.
| (1) |
The essential concept behind Sobol’ method is that function f(X) can be decomposed into a series of factors and their interactions with increasing dimensionality (Kucherenko et al., 2009) (Eq. (2)):
| (2) |
where f0 can be treated as the expectation of Eq. (2), and subscripts i, j, k represents model parameters. In addition, if parameters of f(X) are independent and the individual terms are square-integrable and have zero mean over their domain, this decomposition is unique. As a result, the overall variance is expressed in Eq. (3) and it can be decomposed into Eq. (4) (Chan et al., 1997; Patelli et al., 2010):
| (3) |
| (4) |
where
| (5) |
The Sobol’ sensitivity index (Sobol, 2001) is the ratio between partial variance and total variance. The first order index (Eq. (6)) measures the proportion of the total model output variance explained by variations in parameter i; higher order index (Eq. (7)) captures this ratio between parameter interaction terms and total model output variance; while total order index (Eq. (8)) accounts for the proportion of total variance explained by parameter xi, as well as by interactions of xi and all other parameters. When the sum of all first-order indices (Si) is close to 1, a model’s inputs are more likely to be orthogonal, meaning less impact due to interactions among parameters (values calculated by Eq. (7) are quit low).
| (6) |
| (7) |
| (8) |
where Vari(Y) represent variance from parameter i; Vari,...,k(Y) is the variance from interaction terms; Var∼i(Y) represents total order variance which is total variance explained by all other parameters (except xi) on its own and also by all parameter combinations not including xi (Homma and Saltelli, 1996).
Researchers including Sobol’ have developed several Monte Carlo-based estimators to compute Eqs. (7) ; (8)). In this study, we adopt Saltelli et al.’s (2010) approach to quantify the first-order variance and compute the total order variance as developed by Jansen (1999) (Eq. (10)). These variance computations and their derivations are well-developed in the literature (Jansen, 1999; Saltelli, 2002; Saltelli et al., 2010; Sobol, 2001; Sobol et al., 2007).
| (9) |
| (10) |
where A and B are named sample and resample matrices, which are two independent matrices, based on inputs’ distributions with a dimension of N by k (N iterations, k variables), and j is a loop index from iteration 1 to N. Matrix ‘s columns are identical to Matrix A (sample matrix) except that the i-th column comes from Matrix B (resample matrix). Thus, if a model has k parameters, there should be k different AB matrices . Composition of Matrices A, B and are provide in Fig. 2.
Fig. 2.
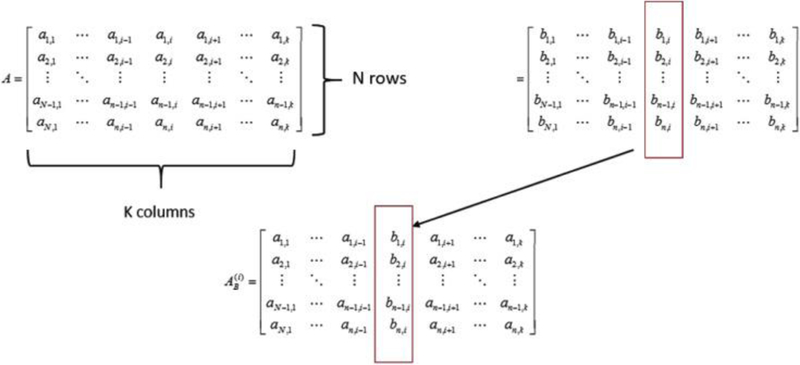
Composition of matrices A, B and .
2.3. Identifying sensitive parameters
The objective of our study is to identify the most sensitive PRZM parameters using global sensitivity techniques presented in Section 2.2. Essential steps included in this assessment are described as a flowchart in Fig. 3. The first step is to generate matrices A and B which are sometimes referred to as sample and re-sample matrices (Saltelli et al., 2010). To simplify, it is assumed that the total number of PRZM parameters to be evaluated is k (corresponding to k columns in Fig. 2), and these variables will be sampled N times from either already known or assumed statistical distributions; thus, the dimension for matrix A (or B) is N by k. To construct matrices , adopting a k-iteration loop is suggested in which matrix A’s i-th column is replaced by the corresponding column from the B matrices. Finally, matrices A, B and are vertically stacked into one “combined” matrix, P, which has N × (k+2) rows and k columns. The second step is to execute a Monte Carlo simulation with a total of N × (k+2) iterations and collect model outputs, which are time series of pesticide concentrations averaged over certain depth. Here, outputs are the predicted average pesticide soil concentrations across six depths (0–15 cm, 15–30 cm, 30–45 cm, 45–60 cm, 60–75 cm, 75–90 cm) for data collected over 140 consecutive days between Aug. 13, 1992 (Julian day 226) and Dec. 31, 1992 (Julian day 366). Thus, the dimension for the return matrix is 840 by N × (k+2), which contains f(A), f(B), and f(). The third and fourth steps apply Eqs. (6), (8), (9) ; (10) to quantify the first- and total order of sensitivity indices where higher first-order indices are used to highlight parameters with conditionally identifiable influences and remove those with persistently low total order indices over the entire simulation period as relatively unimportant PRZM inputs. As part of the post-processing, a small proportion of daily variable sensitivity index estimates for insensitive parameters that were slightly below zero due to numerical errors were set to zero. Further sampling did not diminish these negative values, which was verified by increasing the dimension of a sample matrix (A) to 15,000 rows, which took three days and 15 GB memory to evaluate the 195,000 simulations. Our convergence studies showed that additional further sampling and setting negative values to zero did not alter the sensitivity index probability distributions and the relative ranking of parameters. Therefore, post-processing of the estimates included setting all negative indices to zero. The procedures described above were implemented in R (R Core Team, 2013), where inputs were generated, passed to a compiled PRZM executable file, and model output was post-processed.
Fig. 3.
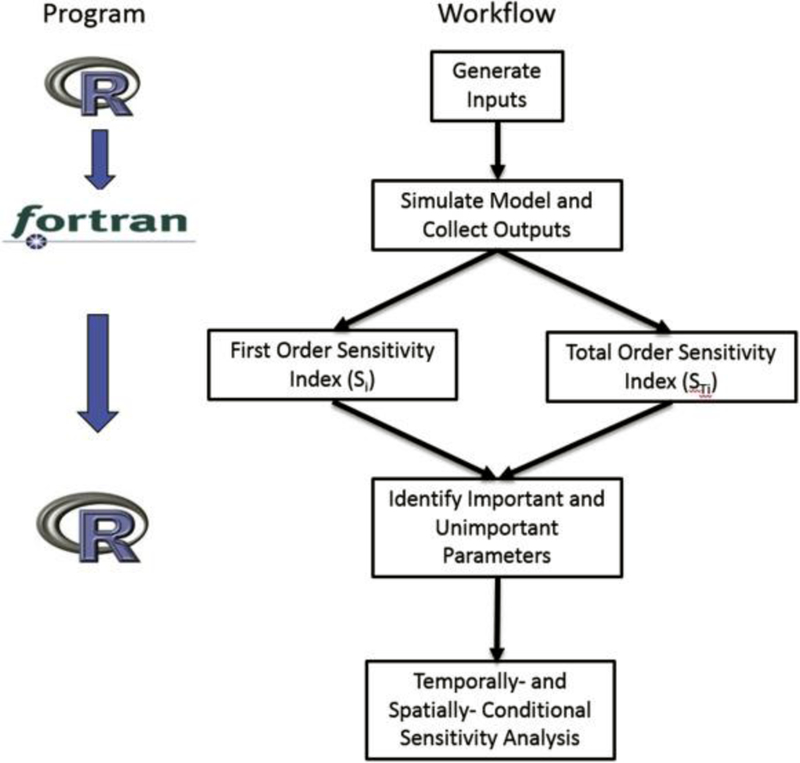
Essential steps involved to estimate global sensitivity index. We identified important parameters as those whose total sensitivity analyses were different than zero, then explored the conditional results for this subset of variables based on time and depth.
Based on a previous field pesticide leaching study in South Georgia (Jones and Russell, 2001; Wolt et al., 2002), 11 candidate PRZM parameters inputs were selected and sampled independently. Their influences on predicted pesticide soil concentrations across different depths were evaluated. The dimension of the sample (resample) matrix is 15,000 by 11, making the total evaluated PRZM functions 195,000 (15,000 × (11 + 2)). The justification for including these candidate parameters is based on a previous sensitivity analysis conducted by FEMVTF (Wolt et al., 2002). In addition, a rain intensity scalar parameter based on authors’ judgment is included to account for rainfall errors in measurement and extrapolation from the gauge location and also to allow for the assessment of the influence of the rainfall time series, a known sensitive parameter for vertical transport. A summary of ranges of inputs are presented in Table 2.
Table 2.
Inputs and distributions.
| Symbol | Meaning | Unit | Range (min, max)* |
Source |
|---|---|---|---|---|
| PLDKRT | Pesticide decay rate on foliage |
day−1 | (0, 6.60 × 10−1) |
Warren-Hicks et al. (2002) |
| AMXDR | Max rooting depth |
cm | (6.00 × 101, 1.20 × 102) |
Keller and Bliesner (2001) |
| CN_c | Runoff curve number (cropping) |
(6.20 × 101, 7.20 × 101) |
Estimate based on
Table 5–10 of Suárez (2005) |
|
| Kd_OC | Partitioning coefficient- organic component |
(1.00 × 10−2, 2.00) |
Authors judgment | |
| BD | Bulk density | g/cm3 | (1.00, 2.00) |
Estimate based
on Warren-Hicks et al. (2002) |
| PFAC | Pan factor | (6.00 × 10−1, 8.00 × 10−1) |
Estimate based on
Table 5–17 of Suárez (2005) |
|
| TAPP | Application rate |
kg ai/ha | (2.50 × 10−1, 7.50 × 10−1) |
Authors judgment |
| USLEC1 | Universal soil loss cover management factor (fallow) |
(5.90 × 10−1, 6.30 × 10−1) |
Warren-Hicks et al. (2002) |
|
| USLEC2 | Universal soil loss cover management factor (cropping) |
(2.20 × 10−1, 4.40 × 10−1) |
Warren-Hicks et al. (2002) |
|
| Decay Control | Pesticide decay rate in water and soil |
day−1 | (1.00 × 10−2, 1.00 × 10−1) |
Authors judgment |
| Rain | Rain intensity scalar |
(5.00 × 10−1, 1.50) |
Authors judgment |
Uniform distributions are assumed between the inputs’ minimums and maximums.
2.4. Normalized Nash-Sutcliffe efficiency
Normalized Nash-Sutcliffe efficiency (NNSE, Eq. (11)) is applied to evaluate the predictive power of PRZM simulations against field mean observations (Nash and Sutcliffe, 1970; Nossent and Bauwens, 2012b). The NNSE value ranges from 0 to 1, which represents very poor to perfect model performance. A NNSE of 0.5 indicates the performance of the dynamic model predictions is no better than a linear model fit through the mean of the observations. In addition, unlike the traditional Nash-Sutcliffe efficiency, the normalized coefficient can retain more accuracy in the estimated variance related terms (Nossent and Bauwens, 2012b).
| (11) |
where yo,t is the observation on day t, is the average across all the observations, and yi,t is the simulated value on day t from the ith Monte Carlo realization. We use NNSE to provide context for the performance of the simulations, it is not a required step in the process of applying the Sobol’ sensitivity analysis.
2.5. Conditional Pearson partial correlation coefficients
Conditional daily Pearson partial correlation coefficients (Lee Rodgers and Nicewander, 1988) between the sample matrix of 11 PRZM parameters and the model output, pesticide soil concentrations, were also run as a rough linear estimate of sensitivity. The partial correlation is a global (not local) method, but does not handle the non-linearity of the pesticide concentration output (or potential non-linearity of inputs) as Sobol’ can. However, despite the linearity limitations, the sign of the correlation coefficient (indicating positive or negative correlation between the input and the output) is information that is not provided by a Sobol’ analysis.
3. Results
3.1. Simulation of the pesticide soil concentration
Fig. 4 illustrates the mean (black solid), the 5th (green solid) and 95th (red solid) percentiles of the simulated pesticide soil concentrations (ppb) against the mean (black dashed), minimum (green dashed) and maximum (red dashed) field observations at depths of 0–15 cm and 15–30 cm. Simulated data presented in Fig. 4 are used for the following sensitivity analysis, and field observations are from a previous site-specific leaching study conducted by FEMVTF as part of the PRZM model calibration projects (Jones and Russell, 2001). Pesticide applications (purple bars) and rain events (orange bars) are also presented, with height representing magnitude (cm/day) of the event. As expected, the first soil compartment (0–15 cm depth) shows increases in pesticide concentrations that are positively associated with pesticide applications. Reductions in pesticide concentrations due to transfer of pesticides to deeper soil depths are associated with precipitation events. The magnitude of vertical pesticide concentration movement is positively linked to precipitation level. For instance, a significant precipitation event on Julian dates 277 and 278 (7.22 cm and 3.39 cm of rainfall) caused the greatest pesticide concentration movement during the simulation period. A source of pesticide concentration reduction is pesticide degradation, which was captured between Julian dates 294 and 306, an extended period with no new applications or rainfall events. Comparing simulated results and observed values shows similar trends over the observation period. In general, however, simulations overestimated pesticide soil concentrations.
Fig. 4.
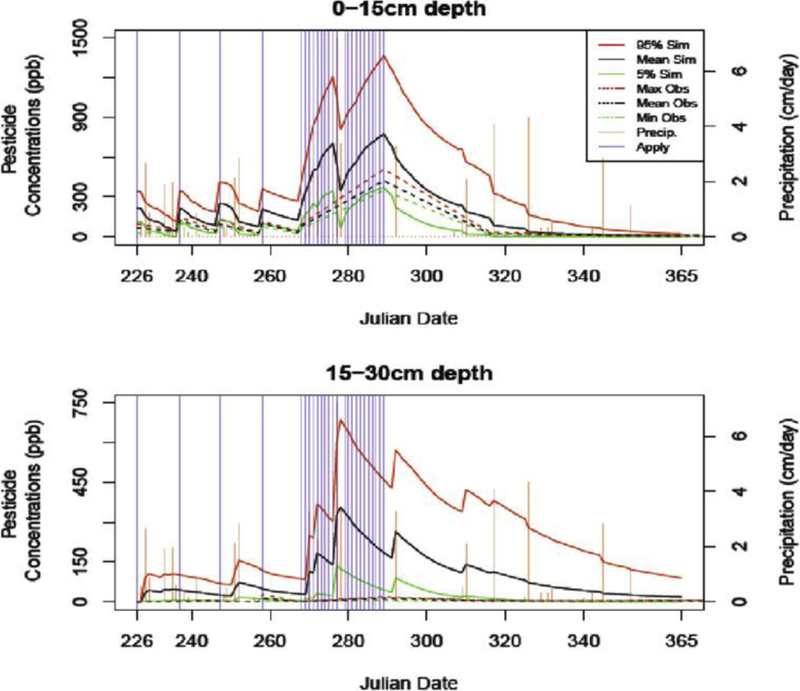
Pesticide soil concentrations.
For the second soil compartment (15–30 cm depth), magnitudes of simulated concentrations also decrease as a result of decay processes and loss to deeper compartments. Concentrations were relatively insensitive to timing of pesticide applications since time and rainfall are required for vertical transfer to greater depths. Pesticide concentrations in the second layer were positively correlated to rain events, while first soil compartment concentrations were negatively correlated. The simulated concentrations in the second compartment are consistently lower than simulated concentrations in the first compartment yet consistently above observed concentrations. Figure S1 of the supporting document includes the mean (black solid), the 5th (green solid) and 95th (red solid) percentiles of the simulated pesticide soil concentrations (ppb), as well as the timing of precipitation and pesticide application events for soil depths between 35 cm and 90 cm at increments of 15 cm. No field observation data are included in Figure S1 since few chemicals were detected in the soil below 35 cm. Patterns of pesticide concentrations among the four soil compartments are similar, since uniform soil conditions are assumed for those layers, including same soil parameters (e.g., bulk density, curve number, etc.) and depth attenuation effects.
Results of NNSEs show that for the first soil compartment (0–15 cm depth), the median performance of the model predictions is similar to the mean of field observations (45% of the 195,000 NNSEs are greater than 0.5). However, for the second soil compartment, less than 1% of the 195,000 NNSEs are greater than 0.5. These results echo those of FEMVTF (Carbone, 2002; Fox et al., 2006; Mamy et al., 2008; McQueen et al., 2007; Sabbagh et al., 2010), who found that adding a depth dimension to the decay parameters in PRZM and/or adding a supplemental model was necessary to coerce reasonable fits to pesticide concentrations at deeper depths. Although the proportions of NNSEs could be increased by a model calibration process, use of additional model for deeper depths, and/or by increasing the dimension of input parameters, we are interested in examining the sensitivity of the PRZM model across the full distributions of the default PRZM input parameters. The general trend of better model fits to observed data in the top soil compartment can visually be confirmed with Fig. 4, where field observations (black dashed) associated with the first soil compartment are closer to the simulations (solid lines) than those in deeper compartments.
3.2. Sensitivity indices
The first- (Si) and total order (STi) sensitivity indices are presented as box plots for the 11 candidate parameters and an additional box representing the summation of first-order indices (Fig. 5, another possible visualization is through a Circos plot (Kelleher et al., 2013; Pianosi et al., 2016)). Box plots are chosen to present the entire distribution of sensitivity indices for all relevant days. The first-order sensitivity index measures the influence of candidate parameters on predicted pesticide soil concentrations across all six soil compartments during the simulation period (Julian dates 226 to 365 for year 1992). Based on this index, parameters with a moderate influence only includes pesticide decay rate in water and soil (Decay Control), after comparing their median index value to the threshold (set to 0.2) (Shin et al., 2013; Van Werkhoven et al., 2009). If a parameter’s median index value is less than the threshold, it is considered as a non-important parameter (Vanrolleghem et al., 2015), including partitioning coefficient-organic component (Kd-OC), and application rate (TAPP), the rain intensity scalar (Rain), bulk density (BD), and pesticide decay rate on foliage (PLDKRT). The summation of first-order sensitivity indices for all parameters can be employed to evaluate main effects of the parameters on outputs, while a total sensitivity index considers impacts from parameter interactions (Saltelli, 2002; Saltelli et al., 2010). The sum of the first-order sensitivity indices suggests that 70% of the output variability can be explained by these first-order parameter contributions, while the remaining 30% is due to parameter interactions.
Fig. 5.
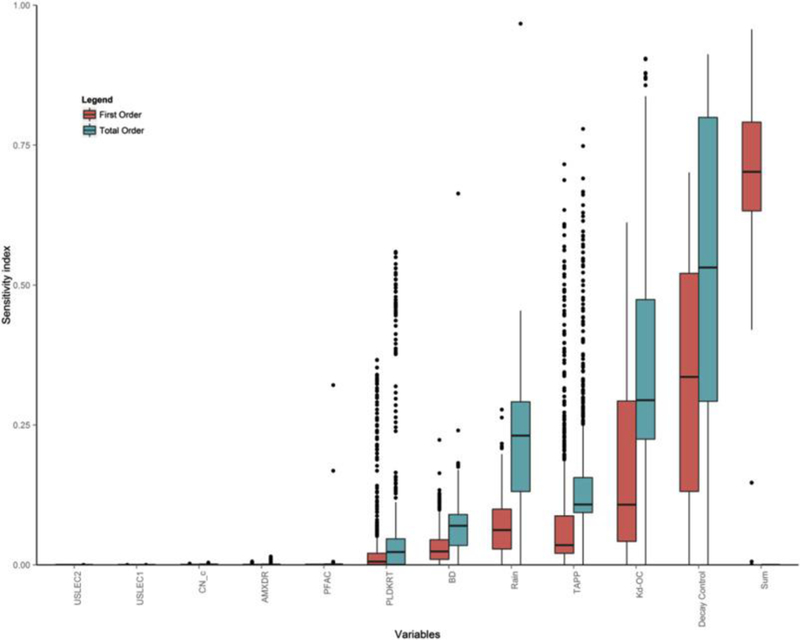
Boxplot of first (red) and total order (green) sensitivity indices.
Boxplots are generated based on sensitivity indices over the 140 day simulation period (Aug. 13, 1992 to Dec. 31, 1992). In terms of the boxplot, the band inside the box is always the second quartiles (the median); the bottom (top) of the box are always the first (third) quartiles; the lower (upper) whiskers represent values from the bottom (top) to the ones that are within 1.5 * IQR.
Therefore, the difference between the first order and the total sensitivity indices quantifies the joint effects of parameters on predicted pesticide concentrations. A parameter with a low total sensitivity index typically implies that it is unimportant since the total sensitivity index captures direct impacts of the variable on model outputs and also accounts for its interaction with other candidate parameters. From the perspective of the total sensitivity index, parameters including pan factor (PFAC), maximum rooting depth (AMXDR), cropping runoff curve number (CN_c), and management factors (USLECs) do not have a discernible impact on determining pesticide concentrations.
3.3. Conditional temporal analyses
Spatial and temporal sensitivity analyses are restricted to the six inputs whose total sensitivity indices are significantly different from zero. They can be roughly ranked as follows: Decay Control, Kd-OC, TAPP, Rain, BD, and PLDKRT. Changes of parameters’ first- and total order of sensitivity indices over time (Julian days 226–366) for the top six influential parameters identified previously are illustrated by Fig. 6. To capture the impact of parameters across depth, figures are generated for both the shallowest (0–15 cm, left panel) and the deepest (75–90 cm, right panel) soil compartments. Sensitivity indices for a given parameter can change significantly over the course of the simulation so we highlight changes in response to application and precipitation events (Fig. 6).
Fig. 6.
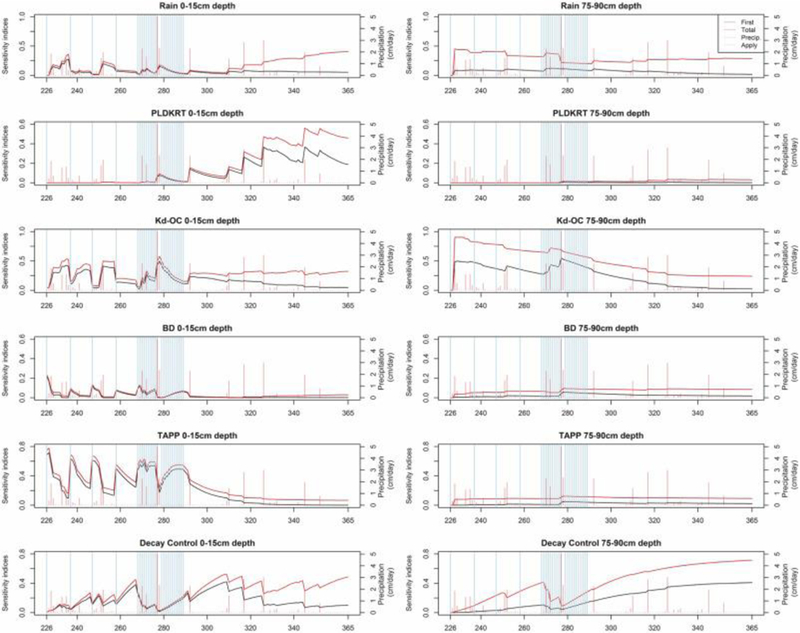
Time series plots of the first (black) and total order (red) sensitivity indices for the top six influential parameters at two soil compartments (0–15 cm and 75–90 cm).
The parameter for the pesticide decay rate in water and soil (Decay Control) are related to precipitation and pesticide application events. This is because the first order sensitivity index measures the proportion of total variance on model output (dissolved pesticide soil concentrations) that can be explained by a certain parameter. Thus, any events (e.g., precipitation, pesticide application) related to pesticide concentrations can have an influence on the calculated indices for pesticide decay process parameters. In the first soil compartment, precipitation events (orange bars) often trigger a sensitivity index decline during the event and is then followed by a significant rise in sensitivity in the days after the event. This is because precipitations have a more direct impact on changing the predicted pesticide concentrations than the decay effects. This phenomenon also can be observed from the lower half of Table 3 where the 5th percent of the first order sensitivity index for Decay Control estimated during the precipitation periods (0–15 cm, 3.72e-2; 75–90 cm, 2.39e-3) are smaller than those from dry periods (0–15 cm, 7.84e-2; 75–90 cm, 1.90e-2). Similarly, first order sensitivity index for Decay Control estimated during the pesticide application periods are smaller than the one calculated during pesticide free period (Table 3 and Fig. 7b). This is because, although pesticide applications provide mass for decay processes to operate on, the applied pesticide has a more direct impact on the model predicted pesticide soil concentration.
Table 3.
Summary of inputs’ first order sensitivity indices on external events.
| Depth | Parameters | Rain | PLDKRT | Kd-OC | BD | TAPP | Decay Control | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Pesticide Application |
Yes | No | Yes | No | Yes | No | Yes | No | Yes | No | Yes | No | |
| 0- 15 cm |
5% | 1.63E- 02 |
2.47E- 02 |
1.84E- 04 |
1.66E- 04 |
3.73E- 02 |
4.80E- 02 |
2.86E-03 | 0.00E+00 | 3.18E- 01 |
0.00E+00 | 3.52E- 02 |
7.78E- 02 |
| 50% | 6.16E- 02 |
6.01E- 02 |
1.16E- 02 |
1.07E- 01 |
1.71E- 01 |
1.45E- 01 |
5.55E-02 | 2.59E-03 | 4.92E- 01 |
1.00E-01 | 1.14E- 01 |
1.76E- 01 |
|
| 95% | 1.22E- 01 |
1.78E- 01 |
6.30E- 02 |
3.35E- 01 |
4.08E- 01 |
4.03E- 01 |
1.26E-01 | 5.92E-02 | 6.29E- 01 |
5.22E-01 | 2.42E- 01 |
4.64E- 01 |
|
| 75- 90 cm |
5% | 7.25E- 02 |
2.02E- 02 |
1.68E- 05 |
1.13E- 05 |
2.74E- 01 |
2.48E- 02 |
1.02E-02 | 5.68E-03 | 6.17E- 03 |
1.60E-03 | 2.04E- 02 |
5.63E- 03 |
| 50% | 1.01E- 01 |
7.27E- 02 |
3.54E- 04 |
2.79E- 03 |
4.17E- 01 |
1.87E- 01 |
1.90E-02 | 2.05E-02 | 1.25E- 02 |
2.41E-02 | 9.33E- 02 |
3.17E- 01 |
|
| 95% | 1.22E- 01 |
1.03E- 01 |
5.98E- 03 |
5.49E- 03 |
5.13E- 01 |
4.85E- 01 |
5.48E-02 | 4.08E-02 | 4.72E- 02 |
3.64E-02 | 1.63E- 01 |
5.06E- 01 |
|
| Depth | Precipitations | Yes | No | Yes | No | Yes | No | Yes | No | Yes | No | Yes | No |
| 0- 15 cm |
5% | 1.28E- 02 |
2.68E- 02 |
1.19E- 04 |
1.88E- 04 |
4.52E- 02 |
4.85E- 02 |
0.00E+00 | 0.00E+00 | 1.25E- 03 |
0.00E+00 | 3.72E- 02 |
7.84E- 02 |
| 50% | 7.05E- 02 |
5.93E- 02 |
1.16E- 02 |
8.06E- 02 |
1.58E- 01 |
1.39E- 01 |
2.73E-03 | 3.96E-03 | 1.67E- 01 |
1.50E-01 | 1.32E- 01 |
1.78E- 01 |
|
| 95% | 2.04E- 01 |
1.17E- 01 |
3.48E- 01 |
3.14E- 01 |
4.22E- 01 |
3.48E- 01 |
8.44E-02 | 6.91E-02 | 5.98E- 01 |
5.17E-01 | 4.77E- 01 |
4.45E- 01 |
|
| 75- 90 cm |
5% | 2.30E- 02 |
2.02E- 02 |
8.57E- 06 |
1.50E- 05 |
2.64E- 02 |
2.47E- 02 |
4.92E-03 | 1.01E-02 | 5.18E- 04 |
6.15E-03 | 2.39E- 03 |
1.90E- 02 |
| 50% | 8.28E- 02 |
7.63E- 02 |
3.41E- 04 |
3.23E- 03 |
3.24E- 01 |
2.32E- 01 |
1.93E-02 | 2.28E-02 | 1.37E- 02 |
2.48E-02 | 8.90E- 02 |
2.74E- 01 |
|
| 95% | 1.17E- 01 |
1.05E- 01 |
6.05E- 03 |
5.61E- 03 |
4.96E- 01 |
4.81E- 01 |
4.28E-02 | 5.14E-02 | 3.68E- 02 |
4.45E-02 | 4.95E- 01 |
5.06E- 01 |
|
External events refer to pesticide application (first half of the table) and precipitation (second half of the table).
Percentiles of the first order sensitivity index are estimated on days with (under column name “Yes”) and without (under column name “No”) external events.
Fig. 7.
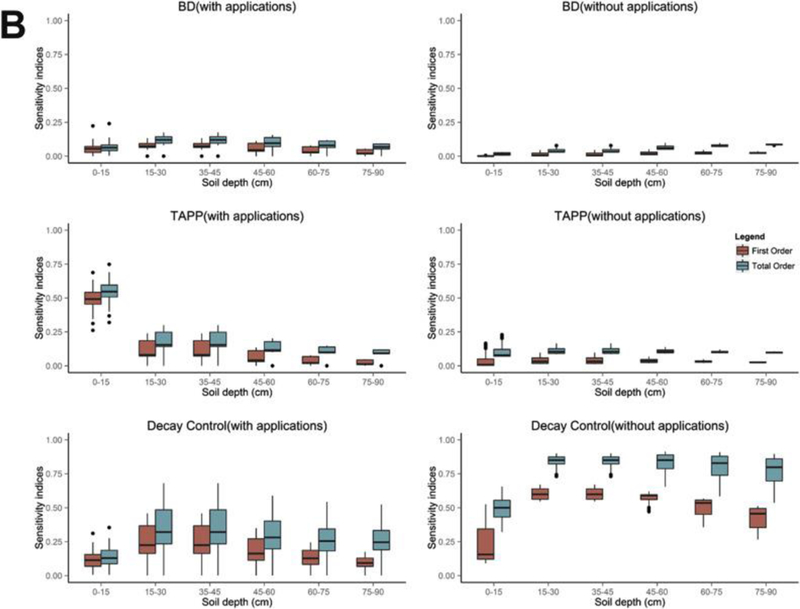
(a)Boxplots of first (red) and total order (green) sensitivity indices with and without pesticide applications. (7b) Boxplots of first (red) and total order (green) sensitivity indices with and without pesticide applications.
For the rain intensity scalar (Rain), increase in sensitivity indices is, not surprisingly, associated with precipitation events (higher percentiles of first order sensitivity indices in Table 3), however, the magnitude of increase is more significant within the pesticide application period (Julian days 226–299), which could due to the existence of higher pesticide concentrations. Interesting, during the same period, the relative importance of the rain intensity scalar has been diluted by the pesticide application events, which is because the proportion of model variability explained by other pesticide application related parameters has been increase. Also, the first and total sensitivity index lines diverge in the post-pesticide application period (Julian days 300–365), with total sensitivity increasing. This implies that residual chemical concentrations are driven by interaction effects with other parameters. At a deeper level, the rain sensitivity index is less sensitive to precipitation events since rainfall interacts with the top soil compartment more directly and attenuation over the vertical profile can reduce direct correlation. The divergence with depth between the first and total sensitivity indices also implies that deeper-level soil concentrations are determined by multiple interacting factors.
The temporal change in the first-order index for the pesticide decay rate on foliage (PLDKRT) in the first soil compartment is also positively associated with precipitation events after pesticide applications (higher percentiles under the column “No” in the first half of Table 3). Differences between the first and total sensitivity indices increase towards the end of the modeling period, indicating that residual concentrations are jointly determined by several parameters. As expected, both sensitivity indices in the deepest modeled soil compartment are essentially zero, suggesting that PLDKRT has little impact on deeper soil concentrations.
Sensitivity indices for the partitioning coefficient-organic component (Kd-OC) are impacted by pesticide application and precipitation events. Pesticide applications reduce Kd-OC’s sensitivity index since more pesticide mass is introduced into the soil system at the surface, having a larger impact on immediate first compartment concentrations than system partitioning processes. Precipitation events do not show a consistent upward or downward effect on Kd-OC sensitivity indices. Precipitation could increase Kd-OC’s sensitivity indices, which is because first rainfall caused vertical water flow lowers pesticide soil concentrations by transferring them to deeper depth. When this happened, Kd-OC determined internal partitioning process becomes more important. However, in the deepest simulated soil compartment, sensitivity indices of Kd-OC are not dependent on time or on events. Except the sensitivity curve shows a sharp peak at the beginning when the pesticide comes first into contact with the soil, because it is used for estimating the equilibrium concentrations of pesticide in the soil.
Sensitivity indices for bulk density (BD) are positively associated with pesticide applications and negatively related to precipitation in the upper compartments (higher percentiles under the column “Yes” in Table 3), however, these correlations change with depth. In the last soil compartment, indices are positively correlated only to precipitation and independent of pesticide applications. Although, reasons behind these phenomena are not very clear, it is true that high BD is an indicator of low soil porosity and soil compaction which impacts water infiltration (USDA, 2015).
The sensitivity curves for application rate (TAPP) show temporal dependence on events in shallow soil compartments. Indices increase when pesticides have been applied (higher percentiles under the column “Yes” in first half of Table 3) and decrease during high precipitation periods. In the deepest soil layer (75–90 cm) indices show no temporal dependence.
3.4. Conditional depth analyses
To further illustrate the differences in the first (red) and total (green) order of sensitivity indices at different depths conditional on pesticide applications, two sets of boxplots are conditionally generated based on whether the days are during the primary pesticide application period. Sensitivity indices on the left panels of Fig. 7a and b are based on periods with pesticide applications (25 application events between Julian Day 226 and 299), while the right panels represent days without pesticide applications (Julian Day 300–365). Within each figure, boxplots of sensitivity indices associated to six different depths are listed on the x-axis in ascending order. For the rain intensity scalar, the first order sensitivity index is for the most part depth independent, although indices are somewhat higher during the pesticide application period. The total sensitivity index of the rain intensity scalar is positively correlated to the soil depth with the exception of the first soil compartment during the no application period. This positive correlation suggests that rain intensity scalar and other parameters jointly determine pesticide soil concentrations in deeper compartments. The high total sensitivity index within the first 15 cm during the pesticide free period also indicates that the concentration in this area is jointly determined by several parameters. The pesticide decay rate on foliage (PLDKRT) parameter is not a sensitivity input during the pesticide application period, which is because other parameters during the applied pesticide period could have more direct impacts on determining pesticide soil concentration. While, PLDKRT can be identified as a sensitive input only in the first soil compartment during the pesticide free period, which is because PRZM assumes that rainfall caused pesticide loss only transferring applied pesticide from foliage to the first 4 cm of soil (Suárez, 2005). These findings demonstrate variability in the sensitivity of the parameters as a function of depth and pesticide application timing. During the pesticide application period, the first and total sensitivity indices of the partitioning coefficient-organic (Kd-OC) increase with depth. This implies that the partitioning coefficient has more influence on determining the pesticide soil concentrations at deeper depths, where pesticides are more likely not evenly distributed. However, when no pesticides are applied, the sensitivity indices of Kd-OC are depth-independent, likely because sufficient time has elapsed since the previous pesticide application to allow the soil concentration profile to be more uniformly distributed.
In Fig. 7b, when pesticide are not applied, soil bulk density (BD) is not an important model parameter based on its total sensitivity index. During the pesticide application period, sensitivity indices for the soil bulk density are positively correlated for the first two soil compartments but negatively correlated to the deeper components. This situation is likely due to pesticide concentrations decreasing dramatically in deeper zones, which reduces the influence of bulk density. Another good example to support the depth dependence of parameter sensitivity is the application rate parameter (TAPP). This parameter is highly influential in the first soil zone; however, this impact diminishes quickly as soil depth increases. Attenuation in soil prevents the applied pesticide from quickly being transported to deeper components, meanwhile other parameters and processes are needed to yield these concentrations at depth and therefore have higher sensitivity. As expected, during time periods when pesticides are not applied, pesticide soil concentrations are insensitive to the application rate. The importance of the pesticide decay rate in water and soil (Decay Control) parameter increases in the first two soil compartments, then, has little influence in the rest of the soil zones, demonstrating a pattern similar to soil bulk density. When pesticides are not applied, its first order index has a similar trend to the left panel of Fig. 7b, but with higher values. Therefore, during time periods of no pesticide inputs, decay rates play a relatively more important role at deeper depths. This can be viewed in the total sensitivity index plots since there is an increase in sensitivity from the first to the rest of the depth zones, which indicates pesticide decay rate has more power in determining pesticide soil concentrations in deeper areas due to interactions with other parameters.
3.5. Conditional Pearson correlation
Pearson correlation coefficients (daily), conditional on pesticide applications and precipitations, between the sample matrix of 11 PRZM parameters and the model output, pesticide soil concentrations. Results of correlation coefficients across modeling period as well as over iterations were aggregated into boxplots in Fig. 8. To highlight Figure’s conditional feature, five types of modeling periods were included: days with pesticide application (red), days without pesticide applications (light green), days with precipitation (green), days without precipitation (blue), and days including all conditions (purple). Based on the position of median correlation coefficients (the horizontal bar inside box), the parameters with moderate correlations to the outputs (pesticide application timing, partitioning coefficients, decay control, bulk density, and rainfall intensity) are similar to those identified by the Sobol’ analysis. However, the magnitudes of correlation coefficients vary based on external events, which highlights the importance of such conditional correlation analysis in absence of a global sensitivity analysis. For instance, pesticide decay rate in water and soil (Decay) has less correlations to the predicted pesticide soil concentrations during either pesticide application period (red) or precipitations (green), which is because the existences of those external events could have a direct impact on the pesticide soil concentration. Comparing to Sobol’ method, the sign of the correlation coefficient (indicating positive or negative correlation between the input and the output) is information. In this case significant negative correlations between output concentrations and both decay control and bulk density show that higher values for these parameters cause a decline in output concentrations within the estimated time series. Such conditional correlation analysis can also be applied to soil compartments at different depths. However, Pearson correlation coefficients were estimated based on the linear assumption between inputs and outputs. When a model’s response curve is not linear, it is possible that an input’s Pearson’s coefficient is close to zero but its first order sensitivity index is close to 1 (i.e., inputs and outputs has a U shape relationship). Under this situation, it is necessary to reply on more sophisticated sensitivity analysis method although it is more efficient to calculate correlation coefficients.
Fig. 8.
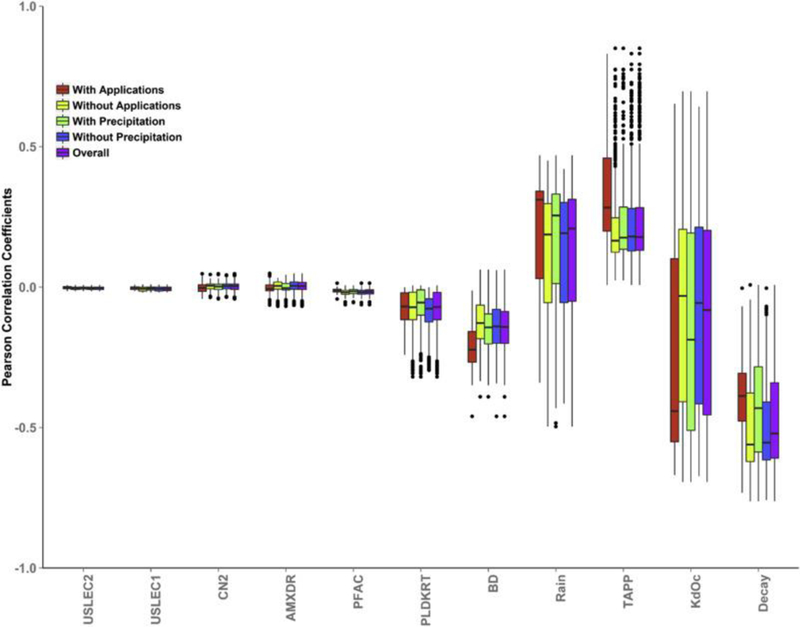
Boxplots of conditional Pearson correlation coefficients.
4. Discussion and conclusion
In this study, we apply a global sensitivity analysis technique, the Sobol’ method, on a widely adopted U.S. EPA exposure model, Pesticide Root Zone Model (PRZM), to conditionally identify sensitive parameters over time and vertical depth. We use high ranking first order sensitivity indices to locate the high priority model inputs based on their relative ranking that directly influence estimated pesticide soil concentrations at different time periods and depths. In addition, we use low ranking total order indices, the sum of interaction terms with other varied parameters plus first order sensitivity index, to focus on excluding non-sensitive parameters based on their low first-order and parameter interaction contributions. One of the most significant findings is that, for highly parameterized complex models (e.g., environmental fate and transport models), determining the most sensitive parameters depends on temporal, spatial, and event-driven conditions, since not all input parameters will have the same relative power in determining model output over the different model dimensions. Sensitivities can and do change when they are evaluated temporally, with depth, as well as taking other related conditions into account. Comparing to estimating time-varying averaged (averaging across a time window) or whole modeling period averaged sensitivity indices, this study computed daily sensitivity indices (the maximum time resolution based on inputs), which could better identify parameters whose impacts only last a short time period or under certain conditions (Herman et al., 2013b; Massmann et al., 2014).
In contrast, parameters identified using conditional global sensitivity methods can better capture influential parameters at key spatial locations and time points in the model, resulting in more accurate system behavior if parameterized and dimensioned correctly when used to estimate environmental conditions. Moreover, this information can guide the process of model calibration. For instance, to better predict pesticide residual concentration at shallow depths (0–15 cm), one should focus on pesticide application rates (TAPP), pesticide decay rate on foliage (PLDKRT) and rain intensity (Rain) have more impact on predicted pesticide concentrations. While in deeper soil compartments (>15 cm), more attention should be paid to the partitioning coefficient-organic component (Kd_OC), the decay rate in the soil and water (Decay Control), and the accuracy of the rainfall time series. When PRZM is applied to low precipitation areas, rates of pesticide applications and chemical decay rates in water and soil are drivers in determining model outputs, while these parameters become rain intensity and chemical decay rates on foliage at high precipitation areas.
These analyses present a more nuanced and robust assessment of the relative importance of model parameters over the course of the simulations. In dynamic spatial and temporal simulations, failing to capture variability provided by conditionally important input parameters during key time periods and/or locations can lead to suboptimal modeling in terms of overall goodness of fit to observations. This can happen early in the calibration process, when sensitivity analyses are used to reduce the number of uncertain parameters despite the fact that final parameter ranges have not yet been identified. In addition, when unconditional sensitivity analyses are used to jettison variables that are important under certain conditions, the overall dynamic features of the models may change. Therefore, examination of conditional sensitivity analyses is less likely to lead to incorrect or misleading behavior of the models that are used for environmental applications and decision-making. One straightforward approach to leveraging conditional sensitivity analyses would be to use a higher percentile.
In addition, use of the Sobol’ method can provide insight into significant parameter interactions. Most sensitivity analyses conducted are based on the assumption that input variables are independent (including the analysis conducted here). However, significant total order sensitivity index values (sum of the interaction terms plus first order sensitivity index) from the Sobol’ analyses conducted with independence assumptions can be used as one indication regarding whether parameter covariance is important. Capturing interactions between parameters can have significant effects on system dynamics that influence the estimation of model outputs and subsequent goodness of fit. These interactions can be captured in a Monte Carlo simulation (e.g., adding parameters for an input variance-covariance matrix) during a calibration/uncertainty analysis process. Although covariance in the Monte Carlo sampling can cause subsequent problems for both local and global sensitivity computation approaches (including Sobol), these difficulties are not insurmountable and the Sobol’ method is able to identify the significance of each possible interaction and can guide covariance decisions. If such variance-covariance matrix is not available, one can also partition inputs into distinct sets. The Sobol’ method is still valid as long as the groups are independent (inputs within each group can be correlated) (Glen and Isaacs, 2012). In this application, the 30% higher order interaction index sum indicates that estimation and calibration of such a matrix may capture some of the interaction variance with corresponding improvements in model fit. Candidate parameters in PRZM that may merit covariance parameters include pesticide decay rates for foliage and in water and soil (PLDKRT and Decay Control), management factors (USLEC1 and USLEC2), and soil properties (Bd and KdOC). Incorporation of additional covariance terms may address calibration difficulties in deeper depths where PRZM has traditionally labored for many applications.
Supplementary Material
Acknowledgments
The authors appreciate valuable discussion and inputs from Bertrand Iooss (a R package ‘sensitivity’ author). Thanks to Mike Cyterski for peer review and Fran Rauschenberg for manuscript review and edits. This research was supported in part by an appointment to the Postdoctoral Research Program at the USEPA Ecosystems Research Division, Athens, GA, administered by the Oak Ridge Institute for Science and Education through Interagency Agreement No. DW8992298301 between the U.S. Department of Energy and the U.S. Environmental Protection Agency. The views expressed in this article are those of the authors and do not necessarily represent the views or policies of the U.S. Environmental Protection Agency.
Footnotes
Software availability
Source code for the PRZM 3 model used for this manuscript is available from https://www.epa.gov/exposure-assessment-models/przm-version-index. R code, input data, results and binaries used for the analyses are available from a github repository located at https://github.com/puruckertom/hongpurucker2016.
References
- Aivalioti MV, Karatzas GP, 2006. Modeling the flow and leachate transport in the vadose and saturated zones of a municipal landfill. Environ. Model. Assess 11 (1), 81e87. [Google Scholar]
- Akbar TA, Lin H, 2010. GIS based ArcPRZM-3 model for bentazon leaching towards groundwater. Journal of Environmental Sciences-China 22 (12), 1854e1859. [DOI] [PubMed] [Google Scholar]
- Akbar TA, Lin H, DeGroote J, 2011. Development and evaluation of GIS-based ArcPRZM-3 system for spatial modeling of groundwater vulnerability to pesticide contamination. Comput. Geosci 37 (7), 822e830. [Google Scholar]
- Banton O, Villeneuve JP, 1989. Evaluation of groundwater vulnerability to pesticides: a comparison between the pesticide DRASTIC index and the PRZM leaching quantities. J. Contam. Hydrol 4 (3), 285e296. [Google Scholar]
- Baroni G, Tarantola S, 2014. A General Probabilistic Framework for uncertainty and global sensitivity analysis of deterministic models: a hydrological case study. Environ. Model. Software 51, 26e34. [Google Scholar]
- Beres DL, Hawkins DM, 2001. PlacketteBurman technique for sensitivity analysis of many-parametered models. Ecol. Model 141 (1e3), 171e183. [Google Scholar]
- Campolongo F, Cariboni J, Saltelli A, 2007. An effective screening design for sensitivity analysis of large models. Environ. Model. Software 22 (10), 1509e1518. [Google Scholar]
- Carbone JP, 2002. Predicting fate and transport: the pesticide root zone model. Environ. Toxicol. Chem 21 (8), 1533e1534. [PubMed] [Google Scholar]
- Carbone JP, Havens PL, Warren-Hicks W, 2002. Validation of pesticide root zone model 3.12: employing uncertainty analysis. Environ. Toxicol. Chem 21 (8), 1578e1590. [PubMed] [Google Scholar]
- Chan K, Saltelli A, Tarantola S, 1997. Sensitivity analysis of model output: variance-based methods make the difference. In: Proceedings of the 29th Conference on Winter Simulation IEEE Computer Society, pp. 261e268. [Google Scholar]
- Chang NB, Srilakshmi K, Parvathinathan G, 2008. Comparison of models of simazine transport and fate in the subsurface environment in a citrus farm. J. Environ. Manag 86 (1), 27e43. [DOI] [PubMed] [Google Scholar]
- Chiovarou ED, Siewicki TC, 2008. Comparison of storm intensity and application timing on modeled transport and fate of six contaminants. Sci. Total Environ 389 (1), 87e100. [DOI] [PubMed] [Google Scholar]
- Confalonieri R, Bellocchi G, Bregaglio S, Donatelli M, Acutis M, 2010. Comparison of sensitivity analysis techniques: a case study with the rice model WARM. Ecol. Model 221 (16), 1897e1906. [Google Scholar]
- Cook RD, Weisberg S, 2009. An Introduction to Regression Graphics. John Wiley & Sons. Cukier, R.I., Schaibly, J.H., Shuler, K.E., 1975. Study of sensitivity of coupled reaction systems to uncertainties in rate coefficients 3. Analysis of approximations. J. Chem. Phys 63 (3), 1140e1149. [Google Scholar]
- Davis RS, Peterson RKD, Macedo PA, 2007. An ecological risk assessment for insecticides used in adult mosquito management. Integrated Environ. Assess. Manag 3 (3), 373e382. [PubMed] [Google Scholar]
- Du Q, Chang NB, Yang CH, Srilakshmi KR, 2008. Combination of multispectral remote sensing, variable rate technology and environmental modeling for citrus pest management. J. Environ. Manag 86 (1), 14e26. [DOI] [PubMed] [Google Scholar]
- Fox GA, Sabbagh GJ, Chen WL, Russell MH, 2006. Uncalibrated modelling of conservative tracer and pesticide leaching to groundwater: comparison of potential Tier II exposure assessment models. Pest Manag. Sci 62 (6), 537e550. [DOI] [PubMed] [Google Scholar]
- Frey HC, Patil SR, 2002. Identification and review of sensitivity analysis methods. Risk Anal 22 (3), 553e578. [PubMed] [Google Scholar]
- Gan Y, Duan Q, Gong W, Tong C, Sun Y, Chu W, Ye A, Miao C, Di Z, 2014. A comprehensive evaluation of various sensitivity analysis methods: a case study with a hydrological model. Environ. Model. Software 51, 269e285. [Google Scholar]
- Glen G, Isaacs K, 2012. Estimating Sobol sensitivity indices using correlations. Environ. Model. Software 37, 157e166. [Google Scholar]
- Guse B, Reusser DE, Fohrer N, 2014. How to improve the representation of hydrological processes in SWAT for a lowland catchmentetemporal analysis of parameter sensitivity and model performance. Hydrol. Process 28 (4), 2651e2670. [Google Scholar]
- Hamby D, 1994. A review of techniques for parameter sensitivity analysis of environmental models. Environ. Monit. Assess 32 (2), 135e154. [DOI] [PubMed] [Google Scholar]
- Herman J, Kollat J, Reed P, Wagener T, 2013a. From maps to movies: highresolution time-varying sensitivity analysis for spatially distributed watershed models. Hydrol. Earth Syst. Sci 17 (12), 5109e5125. [Google Scholar]
- Herman J, Reed P, Wagener T, 2013b. Time-varying sensitivity analysis clarifies the effects of watershed model formulation on model behavior. Water Resour. Res 49 (3), 1400e1414. [Google Scholar]
- Homma T, Saltelli A, 1996. Importance measures in global sensitivity analysis of nonlinear models. Reliab. Eng. Syst. Saf 52 (1), 1e17. [Google Scholar]
- Iman RL, Helton JC, 1988. An investigation of uncertainty and sensitivity analysis techniques for computer models. Risk Anal 8 (1), 71e90. [Google Scholar]
- Jackson SH, Estes TL, 2007. Comparison of leaching predictions based on PRZM3.12, LEACHP, and RZWQM98 using standard scenario modeling. J. Agric. Food Chem 55 (13), 5194e5198. [DOI] [PubMed] [Google Scholar]
- Jackson SH, Hendley P, Cheplick M, 2007. PLUS: a regional groundwater assessment and ranking tool. J. Agric. Food Chem 55 (14), 5408e5415. [DOI] [PubMed] [Google Scholar]
- Jansen MJW, 1999. Analysis of variance designs for model output. Comput. Phys. Commun 117 (1e2), 35e43. [Google Scholar]
- Jones R, Russell M, 2001. Final Report of the FIFRA Environmental Model Validation Task Force [Google Scholar]
- Kelleher C, Wagener T, McGlynn B, Ward AS, Gooseff MN, Payn RA, 2013. Identifiability of transient storage model parameters along a mountain stream. Water Resour. Res 49 (9), 5290e5306. [Google Scholar]
- Keller J, Bliesner RD, 2001. Sprinkle and Trickle Irrigation. Blackburn Press. Kucherenko S, Rodriguez-Fernandez M, Pantelides C, Shah N, 2009 Monte Carlo evaluation of derivative-based global sensitivity measures. Reliab. Eng. Syst. Saf 94 (7), 1135e1148. [Google Scholar]
- Kucherenko S, Tarantola S, Annoni P, 2012. Estimation of global sensitivity indices for models with dependent variables. Comput. Phys. Commun 183 (4), 937e946. [Google Scholar]
- Rodgers Lee, Joseph Nicewander, Alan W, 1988. Thirteen ways to look at the correlation coefficient. Am. Statistician 42 (1), 59e66. [Google Scholar]
- Li L, Lu Z, Hao W, 2013. Importance analysis for models with correlated input variables using state dependent parameters approach. Mech. Syst. Signal Process 41 (1e2), 86e97. [Google Scholar]
- Luo YZ, Zhang MH, 2009. A geo-referenced modeling environment for ecosystem risk assessment: organophosphate pesticides in an agriculturally dominated watershed. J. Environ. Qual 38 (2), 664e674. [DOI] [PubMed] [Google Scholar]
- Luo YZ, Zhang MH, 2010. Spatially distributed pesticide exposure assessment in the Central Valley, California, USA. Environ. Pollut 158 (5), 1629e1637. [DOI] [PubMed] [Google Scholar]
- Luo YZ, Zhang MH, 2011. Environmental modeling and exposure assessment of sediment-associated pyrethroids in an agricultural watershed. PLoS One 6 (1). [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mamy L, Gabrielle B, Barriuso E, 2008. Measurement and modelling of glyphosate fate compared with that of herbicides replaced as a result of the introduction of glyphosate-resistant oilseed rape. Pest Manag. Sci 64 (3), 262e275. [DOI] [PubMed] [Google Scholar]
- Massmann C, Holzmann H, 2012. Analysis of the behavior of a rainfallerunoff model using three global sensitivity analysis methods evaluated at different temporal scales. J. Hydrol 475 (0), 97e110. [Google Scholar]
- Massmann C, Wagener T, Holzmann H, 2014. A new approach to visualizing time-varying sensitivity indices for environmental model diagnostics across evaluation time-scales. Environ. Model. Software 51, 190e194. [Google Scholar]
- Matott L Shawn, Babendreier, Justin E, Purucker S Thomas, 2009. Evaluating uncertainty in integrated environmental models: a review of concepts and tools. Water Resour. Res 45 (6). [Google Scholar]
- McQueen DAR, Farenhorst A, Allaire S, Cessna AJ, 2007. Automation and evaluation of three pesticide fate models for a national analysis of leaching risk in Canada. Can. J. Soil Sci 87 (2), 203e212. [Google Scholar]
- Nash J, Sutcliffe J, 1970. River flow forecasting through conceptual models part Ida discussion of principles. J. Hydrol 10 (3), 282e290. [Google Scholar]
- Nossent J, Bauwens W, 2012a. Multi-variable sensitivity and identifiability analysis for a complex environmental model in view of integrated water quantity and water quality modeling. Water Sci. Technol 65 (3), 539e549. [DOI] [PubMed] [Google Scholar]
- Nossent J, Bauwens W, 2012b. Optimising the convergence of a Sobol’sensitivity analysis for an environmental model: application of an appropriate estimate for the square of the expectation value and the total variance. In: Seppelt R, Voinov A, Lange S, Bankamp D (Eds.), International Environmental Modelling and Software Society (iEMSs) 2012 International Congress on Environmental Modelling and Software (Leipzig, Germany: ). [Google Scholar]
- Patelli E, Pradlwarter HJ, Schueller GI, 2010. Global sensitivity of structural € variability by random sampling. Comput. Phys. Commun 181 (12), 2072e2081. [Google Scholar]
- Pianosi F, Beven K, Freer J, Hall JW, Rougier J, Stephenson DB, Wagener T, 2016. Sensitivity analysis of environmental models: a systematic review with practical workflow. Environ. Model. Software 79, 214e232. [Google Scholar]
- Plackett RL, Burman JP, 1946. The design of optimum multifactorial experiments. Biometrika 33 (4), 305e325. [Google Scholar]
- R Core Team, 2013. R: a Language and Environment for Statistical Computing (Vienna, Austria: ). [Google Scholar]
- Reusser DE, Buytaert W, Zehe E, 2011. Temporal dynamics of model parameter sensitivity for computationally expensive models with the Fourier amplitude sensitivity test. Water Resour. Res 47 (7), W07551. [Google Scholar]
- Russell MH, Jones RL, 2002. Comparison of pesticide root zone model 3.12: leaching predictions with field data. Environ. Toxicol. Chem 21 (8), 1552e1557. [PubMed] [Google Scholar]
- Sabbagh GJ, Fox GA, Munoz-Carpena R, Lenz MF, 2010. Revised framework for pesticide aquatic environmental exposure assessment that accounts for vegetative filter strips. Environ. Sci. Technol 44 (10), 3839e3845. [DOI] [PubMed] [Google Scholar]
- Saltelli A, 2002. Making best use of model evaluations to compute sensitivity indices. Comput. Phys. Commun 145 (2), 280e297. [Google Scholar]
- Saltelli A, Annoni P, Azzini I, Campolongo F, Ratto M, Tarantola S, 2010. Variance based sensitivity analysis of model output. Design and estimator for the total sensitivity index. Comput. Phys. Commun 181 (2), 259e270. [Google Scholar]
- Saltelli A, Ratto M, Andres T, Campolongo F, Cariboni J, Gatelli D, Saisana M, Tarantola S, 2008. Global Sensitivity Analysis: the Primer. Wiley [Google Scholar]
- Saltelli A, Ratto M, Tarantola S, Campolongo F, 2005. Sensitivity analysis for chemical models. Chem. Rev 105 (7), 2811e2828. [DOI] [PubMed] [Google Scholar]
- Saltelli A, Tarantola S, Campolongo F, Ratto M, 2004. Sensitivity Analysis in Practice: a Guide to Assessing Scientific Models. Wiley [Google Scholar]
- Saltelli A, Tarantola S, Chan KPS, 1999. A quantitative model-independent method for global sensitivity analysis of model output. Technometrics 41 (1), 39e56. [Google Scholar]
- Shin HM, Vieira VM, Ryan PB, Detwiler R, Sanders B, Steenland K, Bartell SM, 2011. Environmental fate and transport modeling for perfluorooctanoic acid emitted from the Washington works facility in West Virginia. Environ. Sci. Technol 45 (4), 1435e1442. [DOI] [PubMed] [Google Scholar]
- Shin M-J, Guillaume JH, Croke BF, Jakeman AJ, 2013. Addressing ten questions about conceptual rainfallerunoff models with global sensitivity analyses in R. J. Hydrol 503, 135e152. [Google Scholar]
- Sieber A, Uhlenbrook S, 2005. Sensitivity analyses of a distributed catchment model to verify the model structure. J. Hydrol 310 (1), 216e235. [Google Scholar]
- Singh P, Jones RL, 2002. Comparison of pesticide root zone model 3.12: runoff predictions with field data. Environ. Toxicol. Chem 21 (8), 1545e1551. [PubMed] [Google Scholar]
- Sobol IM, 2001. Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates. Math. Comput. Simulat 55 (1e3), 271e280. [Google Scholar]
- Sobol IM, Tarantola S, Gatelli D, Kucherenko SS, Mauntz W, 2007. Estimating the approximation error when fixing unessential factors in global sensitivity analysis. Reliab. Eng. Syst. Saf 92 (7), 957e960. [Google Scholar]
- Suarez L, 2005. PRZM-3, a Model for Predicting Pesticide and Nitrogen Fate in the Crop Root and Unsaturated Soil Zones: Users Manual for Release 3.12. 2. US Environmental Protection Agency (EPA), Washington, DC. [Google Scholar]
- USDA, 2015. Soil Bulk Density/Moisture/Aeration.
- Van Werkhoven K, Wagener T, Reed P, Tang Y, 2009. Sensitivity-guided reduction of parametric dimensionality for multi-objective calibration of watershed models. Adv. Water Resour 32 (8), 1154e1169. [Google Scholar]
- Vanrolleghem PA, Mannina G, Cosenza A, Neumann MB, 2015. Global sensitivity analysis for urban water quality modelling: terminology, convergence and comparison of different methods. J. Hydrol 522, 339e352. [Google Scholar]
- Warren-Hicks W, Carbone JP, Havens PL, 2002. Using Monte Carlo techniques to judge model prediction accuracy: validation of the pesticide root zone model 3.12. Environ. Toxicol. Chem 21 (8), 1570e1577. [PubMed] [Google Scholar]
- Wolt J, Singh P, Cryer S, Lin J, 2002. Sensitivity analysis for validating expert opinion as to ideal data set criteria for transport modeling. Environ. Toxicol. Chem 21 (8), 1558e1565. [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


