Effects of cell morphology and attachment to a surface on the hydrodynamic performance of unicellular choanoflagellates

Abstract

Choanoflagellates, eukaryotes that are important predators on bacteria in aquatic ecosystems, are closely related to animals and are used as a model system to study the evolution of animals from protozoan ancestors. The choanoflagellate Salpingoeca rosetta has a complex life cycle with different morphotypes, some unicellular and some multicellular. Here we use computational fluid dynamics to study the hydrodynamics of swimming and feeding by different unicellular stages of S. rosetta: a swimming cell with a collar of prey-capturing microvilli surrounding a single flagellum, a thecate cell attached to a surface and a dispersal-stage cell with a slender body, long flagellum and short collar. We show that a longer flagellum increases swimming speed, longer microvilli reduce speed and cell shape only affects speed when the collar is very short. The flux of prey-carrying water into the collar capture zone is greater for swimming than sessile cells, but this advantage decreases with collar size. Stalk length has little effect on flux for sessile cells. We show that ignoring the collar, as earlier models have done, overestimates flux and greatly overestimates the benefit to feeding performance of swimming versus being attached, and of a longer stalk for attached cells.

1. Introduction

Protozoans play an important role in aquatic food webs and the carbon cycle [1–5]. Choanoflagellates, flagellated eukaryotes that are abundant in marine and freshwater habitats, are important predators on bacteria in aquatic ecosystems [6–8]. Not only are choanoflagellates important ecologically, but they are also of evolutionary interest, because they are the closest living relatives of the animals [9].

The first multicellular animals evolved more than 600 Ma from protozoan ancestors [10–12]. Comparative genomic and molecular phylogenetic analyses reveal a close relationship between animals and choanoflagellate protozoans [9]. We can make informed inferences about possible selective pressures on the protozoan ancestors of animals if we understand mechanisms responsible for performance differences that can affect fitness in choanoflagellates [13,14]. King developed the use of the choanoflagellate, Salpingoeca rosetta, which can be unicellular and can form multicellular colonies, as a model system to study the evolution of animal multicellularity [9,14,15].

1.1. Choanoflagellate life stages and morphology

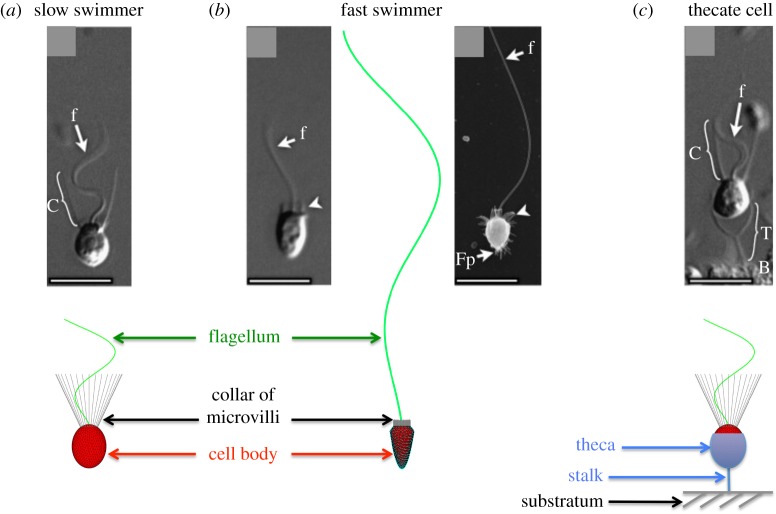
Salpingoeca rosetta has a complex life cycle with stages that have different morphotypes, some unicellular and some multicellular [16]. Unicellular forms are shown in figure 1. ‘Slow swimmers’ have an ovoid cell body that is pushed through the water by the waving of a single flagellum. The flagellum is surrounded by a collar of microvilli on which bacterial prey are captured [17]. Slow swimmers can be haploid or diploid, and the haploid slow swimmers can produce gametes (mating occurs when small flagellated cells fuse with larger flagellated cells with collars) [18,19]. ‘Fast swimmers’ have a single flagellum, a cell body that is slimmer and more pointed than that of slow swimmers, and a very short collar. They swim rapidly, aggregate in low pH, and are thought to be the dispersal phase of the S. rosetta life cycle [20]. ‘Thecate cells’ have the same morphology as slow swimmers, but the cell body is surrounded by an extracellular theca that is attached to the substratum by a stalk. When an attached thecate cell waves its flagellum, a water current is produced that carries bacterial prey to the collar [16,21]. Salpingoeca rosetta can also form multicellular colonies by cell division. Each cell in a colony has a morphology like that of a slow swimmer, and colonies can either be in the form of spherical rosettes or of chains [16,21]. The swimming and feeding performance of all of these life stages of choanoflagellates depends on their hydrodynamics.

Figure 1.

External morphology of the unicellular stages of the choanoflagellate Salpingoeca rosetta that we modelled: the slow swimmer (a) and fast swimmer (b) that locomote through the water, and the thecate cell (c) attached to a surface. The micrographs are reproduced with permission from fig. 1 in Dayel et al. [16] with permission from Elsevier. Scale bars, 5 mm. The dimensions of the components of the choanoflagellates used in our models are given in table 1. (Online version in colour.)

1.2. Hydrodynamics of choanoflagellates

Various approaches have been used to model the hydrodynamics of choanoflagellate feeding currents produced by the waving flagellum. Choanoflagellates are eukaryotes, so dynein-driven microtubule sliding produces waves of active bending that move along the flagellum. Early models of thecate cells represented the flagellar dynamics by a line of Stokeslets normal to a planar boundary [22] or by a helical arrangement of Stokeslets [23]. These models predicted the viscous eddies that were observed in laboratory experiments. The collar of microvilli was not explicitly represented in these models, but was accounted for by prescribing a pressure drop that depended upon an assumed collar geometry. Two more recent choanoflagellate models [21,24] that analysed the hydrodynamic implications of forming multicellular colonies did not include the effects of the collar on the fluid dynamics. Roper et al. [21] chose a minimal, point-force model of the choanoflagellate that resulted in a far-field flow that matched the flow fields measured around thecate S. rosetta attached to flat surfaces. Kirkegaard & Goldstein [24] modelled the choanoflagellate cell body as a sphere, and represented the effect of the oscillatory flagellum by applying either an averaged constant force or a constant velocity along a straight rod representing the flagellum. Most recently, Nielsen et al. [25] presented a detailed model of a sessile choanoflagellate encased in a lorica that forces all the water to flow through the collar. Their model included a representation of the cell body, the collar of microvilli and the undulatory flagellum. Their results suggested that a thin cylindrical flagellum could not account for experimentally measured water fluxes, and they proposed that the flagellum of this species has a broad vane [25]. Another earlier computational study of choanoflagellate hydrodynamics, using a regularized Stokeslet framework, modelled the effect on the flow of a lorica, a basket-like structure that is not present in the S. rosetta cells considered here [26].

1.3. Objectives of this study

The goal of this study is to explore how the morphological features of the different unicellular stages of S. rosetta affect two ecologically important aspects of their hydrodynamic performance: swimming speed of choanoflagellates in the water column, and flux of water carrying bacterial prey into the capture zone of the collar of both free-swimming and attached choanoflagellates. Using a three-dimensional computational fluid dynamic model that explicitly includes the cell body, collar and flagellar dynamics, we investigate how varying morphological features such as flagellar length and waveform, collar length and cell body shape change the swimming velocity and the flux of prey-carrying water into the capture zone of unattached cells. The effect of collar size is intriguing because collars with long microvilli may add to the drag on a swimmer, slowing it down so that it moves through less water per time, but collars also provide a larger surface area on which prey can be caught. We also explore the effect of stalk length on the flux of water to the collars of thecate cells, and compare their net flux with that of free-swimmers for collars of a range of sizes.

2. Methods

2.1. Morphological and kinematic features

We modelled the three unicellular stages in the life cycle of S. rosetta that are shown in figure 1: slow swimmers, fast swimmers and sessile thecate cells. The geometry of the cell body and microvilli, along with the kinematics of the flagellar waveform in the models are based on measurements we made by digitizing published micrographs of S. rosetta or our videos of living S. rosetta (table 1). As the images in figure 1 of a living fast swimmer and a thecate cell show, the microvilli of a S. rosetta do not appear to be bent significantly by the flow produced by the beating flagellum. Thus, for simplicity we have modelled collar microvilli as rigid structures. To determine the effect of the collar on the hydrodynamics of swimming and prey capture, we performed simulations for a range of collar lengths for each life stage. In addition, for the thecate cells, we also varied the length of the stalk connecting the cell to a wall.

Table 1.

Cell-body dimensions of S. rosetta and flagellar wave parameters (as in equation 2.1) used to construct our models.

life stage	feature	value (μm)	references
slow swimmer (ovoid cell)	cell length	4.4 μm	[27]
	cell width	3.4 μm	[27]
	microvilli length	5.8 μm (on average)	[27]
	number of microvilli	32	fig. 1,I-J [17]
	microvillus radius	0.046 μm	fig. 2,E [17]
	angle of collar	25°	fig. 1,E [16]
	wave parameter a	0.277	a
	wave parameter b	0.71 μm	b
	wavenumber k	0.68 rad μm−1	b
	frequency ω	24.3 Hz	[27]
	projected length L	10.4 μm (on average)	[27]
	flagellar arclength $\tilde{L}$	15.4 μm (on average)	b
	flagellar diameter	0.24 μm	[17]
	flagellar wavespeed 2πω/k	224.5 μm s−1	b
fast swimmer (slender cell)	cell length	4.4 μm	fig. 1,G [16]
	cell width	2.5 μm	fig. 1,G [16]
	microvilli length	0.6 μm (on average)	fig. 1,G [16]
	wave parameter a	0.13	c
	wave parameter b	0.61 μm	c
	wavenumber k	0.18 rad μm−1	c
	frequency ω	24.3 Hz	c
	projected length L	42.8 μm (on average)	c
	flagellar arclength $\tilde{L}$	47.8 μm (on average)	c
	flagellar wavespeed 2πω/k	848.2 μm s−1	c
	stalk length	3.0 μm (on average)	fig. 1,C [16]
thecate cell	cell body/wave parameters	same as slow swimmer

^aSee https://ib.berkeley.edu/labs/koehl/resint/multicellularity.html.^bModel parameters to roughly match with flagellar data in [27].^cModel parameters to roughly match with flagellar data from figure 1, G and H [16] and be consistent with the slow-swimmer data at [27].

The flagellum of S. rosetta beats in one plane [17]. To isolate the hydrodynamic consequences of the morphological features of the choanoflagellate (cell body and collar), we prescribed one of two flagellar waveforms. The first ‘slow-swimmer’ waveform is based upon the measurements made on high-speed videos (table 1) of the flagella of slow swimmers beating in the plane of the video that indicate a sinusoidal beat with increasing amplitude along the flagellum and a constant wavelength. Similar measurements made of flagella on rosette colonies showed that flagellar kinematics are the same for slow swimmers and cells in colonies of S. rosetta, and so we assume these kinematics for thecate cells, where experimental data are not available. The second ‘fast-swimmer’ waveform, which is based upon fig. 1G and H in Dayel et al. [16], has smaller curvature and a considerably longer flagellum than that of the slow swimmer.

For both waveforms, the specified kinematics is given by

$$\begin{array}{rl}x(s,t)& =s,\\ y(s,t)& =(as+b)\sin (ks-2\pi \omega t)\\ \mathrm{and}z(s,t)& =0,\end{array}\}$$ 2.1

where 0 ≤ s ≤ L and L is the projected flagellar length (the maximum extent in the x-direction). L is adjusted at each time t so that the initial flagellar arclength $\tilde{L}$ stays constant. The parameter values chosen for the prescribed waveforms are given in table 1. The choanoflagellate collar is made up of 32 rigid microvilli that are regularly spaced around the surface of a conical segment of a cone whose axis corresponds to the flagellar axis, and whose angle of opening is 25° (table 1).

One measure of the performance of a suspension-feeding flagellated organism is the volume of prey-carrying fluid that it can move into its capture zone during one beat cycle. The inward flux of fluid for the entire prey-capturing structure of an organism acts as a proxy measurement for the rate of bacterial capture. In the case of a choanoflagellate, the collar of microvilli is the prey-capturing structure. When we consider the water flow relative to the collar of a choanoflagellate, any bacterium that is carried along a streamline that moves within one bacterial radius from the collar could contact the collar and potentially be caught. We therefore define the capture zone of a choanoflagellate to be the conical surface around the collar that is one bacterial radius outside the collar (figure 2). For our calculations, we chose this bacterial radius to be 0.67 μm.

Figure 2.

Any bacterium carried by the flow relative to the collar of a choanoflagellate that touches the collar might be caught by the choanoflagellate. The streamlines are averaged over one flagellar cycle. Therefore, the capture zone of a choanoflagellate is the area of the surface around the collar that is one bacterium radius outside the collar. The capture zone defines a region of water around the collar and is not an actual surface that affects the flow. For our calculations, we used a bacterial prey of radius of 0.67 μm. (Online version in colour.)

The inward flux to the capture zone Q is computed as

$$Q=\rho {\int }_0^T{\int }_{\mathcal{S},\mathbf{v}\cdot \mathbf{n}>0}\mathbf{v}\cdot \mathbf{n}\hspace{0.17em}\mathrm{d}\sigma \hspace{0.17em}\mathrm{d}t,$$ 2.2

where ρ is the density of water, T is the duration of a flagellar beat (here T = 0.041 s), $\mathcal{S}$ is the conical surface of the capture zone (figure 2), v is the fluid velocity on the capture zone relative to the cell and n is the unit inward normal to the capture zone. Because we are resolving the time-dependent flagellar beat, these calculations do not impose a time-averaged velocity on a flagellar representation as in [21,24], but rather capture the highly oscillatory flow near the flagellum.

2.2. Fluid–choanoflagellate system

The surface of the choanoflagellate's cell body along with its microvilli and its actively beating flagellum support forces that are exerted on the viscous fluid in which the organism is immersed. These forces are not pre-set in our model, but are determined so that the prescribed kinematics of the flagellum are achieved, and so that the microvilli and the cell body remain rigid. For a free-swimming choanoflagellate, the total force and torque must be zero so that momentum and angular momentum are conserved. These six added constraints determine an instantaneous translational velocity and rotational velocity of the swimmer.

Because the length and velocity scales at the microscopic level are so small, inertial forces are negligible and the flow is well described by the incompressible Stokes equations:

$$\begin{array}{rl}& -\mathrm{\nabla }p+\mu \mathrm{\Delta }\mathbf{u}+\mathbf{F}(\mathbf{x},t)=0\\ & \text{and}\mathrm{\nabla }\cdot \mathbf{u}\hspace{0.17em}\mathbf{=}\mathbf{0.}\end{array}$$ 2.3

Here u is fluid velocity, p is pressure, μ is dynamic viscosity and F is a force density that represents the force of the choanoflagellate on the fluid. The fluid domain is taken to be either unbounded three-dimensional space (in the case of a free-swimmer) or three-dimensional space above a flat planar boundary with infinite extent.

We use the regularized Stokeslet method in three dimensions to compute the fluid flow due to the choanoflagellate's undulatory flagellum [28]. Forces are distributed on the surface of the cell body at discrete material points [29] as well as at discrete points along the centrelines of the flagellum and each of the microvilli [30]. The force density concentrated at one of these points x _k is: F_k = f_kψ_ε(x − x _k), where ψ_ε is a regularized three-dimensional Dirac delta function, with regularization parameter ε. For ε = 0, the regularized Stokeslet solution reduces to the classical singular Stokeslet [31]. When forces are distributed on a surface, the regularization parameter ε may be thought of as a numerical parameter that should be taken as small as possible. However, because we choose a distribution of forces only along the centrelines of the flagellum and microvilli, we regard the parameter ε as a physical parameter that is chosen to reflect the diameter of the slender filament [30,32,33]. Note that we chose different regularization parameters for forces applied at the flagellum, microvilli and the cell body surface.

For the case of the slow swimmer, the surface of the cell body was discretized by N_c = 700 material points using a spherical centroidal Voronoi tessellation [29]. This discretization is such that the average distance between neighbouring points on the surface is Δs_c = 0.27 μm and we choose a regularization parameter for forces on this surface to be ε_c = Δs_c. The centreline of the flagellum is discretized by N_f = 114 equally spaced points along its arclength so that Δs_f = 0.12 μm, and ε_f = 2Δs_f. This regularization parameter ε_f is approximately the diameter of a flagellum of an S. rosetta [17]. Each of the 32 microvilli is discretized by N_m = 127 equally spaced points so that for the average length of the microvilli (L_m = 5.8 μm), we have Δs_m = 0.05 μm, and ε_m = Δs_m. We include details about the implementation of this numerical method in the electronic supplementary material.

3. Results

3.1. Swimming performance

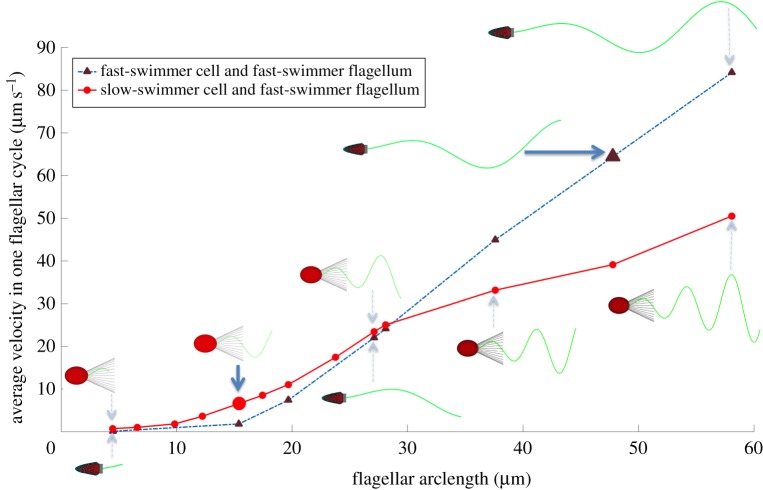
We studied the effects of collar size, cell shape and flagellar length and kinematics on the swimming speed of choanoflagellates. For the cell shapes of both the slow swimmer and the fast swimmer of S. rosetta, we computed the average swimming velocity of free-swimming cells, each with the same flagellar length and wave kinematics, and we varied the length of the collar of microvilli. We did this for the flagellum length and wave kinematics of both the fast swimmer and the slow swimmer. Figure 3 shows that the flagellar length and waveform dominates the difference in swimming speeds. We used the same beat frequency for the slow-swimmer and fast-swimmer flagella, thus the wavespeed of the sinusoidal undulation is greater for the fast swimmer because the wavelength of the fast swimmer is longer than that of the slow swimmer (table 1). Figure 3 also shows that for each cell shape the swimming velocity decreases monotonically with collar length. Although a slender cell body enhances swimming speed when the microvilli are very short, cell shape has little effect when collars are long. This holds true for both flagellar waveforms. In figure 3, the point on the black curve for the true fast swimmer and the point on the red curve for the true slow swimmer (values in table 1) are indicated by arrows. Our model shows that a number of features contribute to the ability of the fast swimmers of S. rosetta to move through the water more rapidly than the slow swimmers: fast swimmers have very short collars, cell bodies that are more slender than those of slow swimmers, and long flagella with longer sinusoidal wavelengths than those of slow swimmers.

Figure 3.

Swimming speed averaged over one flagellar beat cycle of unicellular choanoflagellates with ovoid cell bodies (red and green solid curves) and slender cell bodies (black and blue dashed curves), plotted as a function of the length of the microvilli of the collar when the cells were propelled by the slow-swimmer flagellum (two lower curves) and by the fast-swimmer flagellum (two upper curves). The morphologies of fast and slow swimmers of S. rosetta (table 1) are diagrammed and the arrows point to the swimming speeds of each of these morphologies. (Online version in colour.)

Beginning with the work of Taylor [34,35] the mathematical study of flagellar swimming due to sinusoidal oscillations of an infinite sheet or a filament in a viscous fluid is a classical problem in biological fluid dynamics. Higdon [36] later used slender body theory to examine the effect of flagellar length on swimming of finite filaments. While it is not our intention here to re-examine flagellar motility as a function of flagellar waveforms, we do wish to probe the effect of flagellar arclength on swimming velocity for the morphologies of the two motile unicellular of life stages of S. rosetta. Figure 4 shows the average swimming velocity as a function of flagellar arclength for (a) the slow swimmer with ovoid cell body and mean slow-swimmer collar length (table 1) using slow swimmer flagellar kinematics and (b) the fast swimmer with slender cell body and mean fast-swimmer collar length (table 1) using fast swimmer flagellar kinematics. The slow and fast swimmers that are assigned the typical wave kinematics and mean arclength for their life stage are indicated by arrows. Because the flagellar amplitude increases from head to tail, it is not surprising that the swimming speeds in both cases increase with flagellar arclength. We see that this increase becomes linear for the largest flagellar lengths that we simulated, where the drag from the cell body and the collar contributes less to overall performance. The slow swimmer waveform is taken to oscillate at a higher amplitude and at a smaller wavelength than that of the fast swimmer. For short flagella, including arclengths near the mean of the slow swimmer, the slow swimmer using the slow-swimmer waveform actually goes faster than the fast swimmer using the fast-swimmer waveform. Here the large amplitude and shorter wavelength of flagellar beating make up for the drag induced by the ovoid head and the collar. However, for larger flagellar arclengths, the fast swimmer outperforms the slower swimmer and this advantage increases as arclength increases. This cross-over in performance occurs near the flagellar arclength of 27 μm, where the swimming speed is nearly equal for the two flagellar waveforms. The eight plots in figure 5 compare the velocities of swimmers with two different cell body shapes, two different collar lengths and two different flagellar waveforms. We see that the high-amplitude, high-curvature waveform used by slow swimmers produces a faster swimming speed for all cell and collar morphologies than does the low-amplitude, low-curvature waveform that performs better when flagella are longer.

Figure 4.

Average velocity of the fast-swimmer cell and collar morphology and of the slow-swimmer cell and collar morphology, plotted as a function of the arclength of their respective prescribed flagellar waveforms. Solid blue arrows indicate the points that correspond to the real fast swimmer and slow swimmer (table 1). (Online version in colour.)

Figure 5.

Computed swimming velocities of eight swimmers with two different cell body shapes, two different collar lengths and two different flagellar waveforms. Flagellar arclength is fixed at 27 μm, and the flagellar waveform is varied for each combination. Note that in figure 4, the velocities of the slow swimmer and fast swimmer were nearly equal at this arclength. (Online version in colour.)

Our calculations of the motion of a cell as its flagellum undulates showed that a choanoflagellate wobbles from side to side during each beat cycle about the axis given by its swimming direction. We determined the amplitude of the change in angle of the long axis of a slow swimmer during one flagellar cycle to be 11.42° for a slow swimmer with microvilli length of 5.8 μm.

3.2. Feeding performance

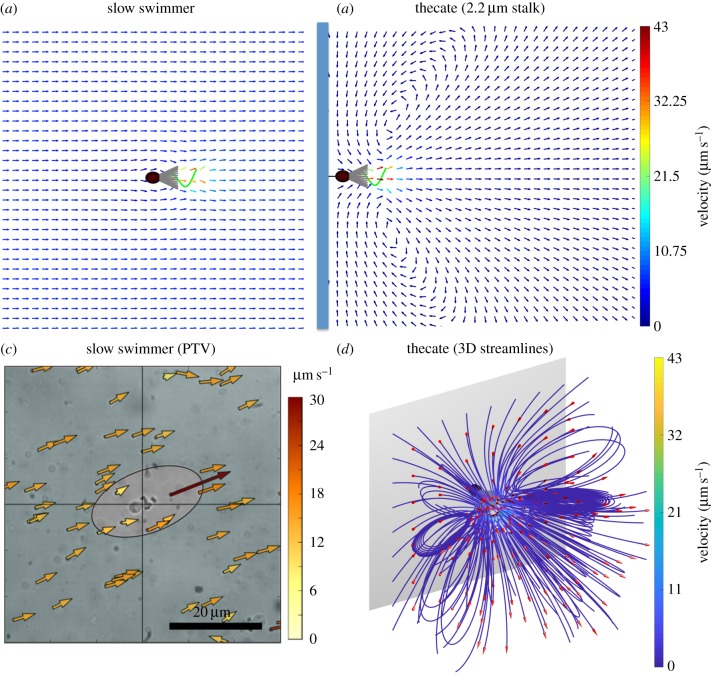
The water that moves relative to the collar of a choanoflagellate carries the bacterial prey that the choanoflagellate might catch if the prey contact the microvilli. Examples of the time-averaged flow fields relative to a slow swimmer when mid-water and to a thecate cell attached to a wall by a rigid stalk are shown in figure 6a,b. In both cases, the highest water velocities are in the region around the beating flagellum, and there is flow towards and along the collar. The velocity of the far-field flow relative to the slow swimmer is equal to the swimming speed of the swimmer, but opposite in direction, so the collar is continuously exposed to new samples of water as the choanoflagellate swims. Here, we compute the average velocity of the slow swimmer to be 6.6 μm s⁻¹. By contrast, eddies of recirculating water form around the thecate cell attached to a nearby wall (figures 6b,c and 7), as reported for other tethered microorganisms [37–39]. Therefore, the collar encounters water that it has already processed and that has then swept along the substratum as it moves back towards the thecate cell. Figure 6d shows a three-dimensional view of computed streamlines, demonstrating the toroidal eddies.

Figure 6.

Water flow relative to a choanoflagellate with a collar composed of cylindrical microvilli 5.8 μm long. (a,b) Average velocity vectors calculated relative to a choanoflagellate in the plane of flagellar beating for a slow swimmer (a), and for a thecate cell attached to a wall by a stalk 2.2 μm long (b). Velocities were averaged over one flagellar beat cycle. Size scale: cell body length = 4.4 μm. (c) Velocity vectors relative to a slow swimmer measured using particle-tracking velocimetry (PTV). Videos (Fastek Hi-Spec 1 camera, 100 fps) were made of S. rosetta viewed through a 63x Plan Apo oil immersion lens on a Leica DM 2500 compound microscope with interference contrast illumination. Velocities of 1 μm polystyrene beads relative to the swimming cell were calculated using in-house software written to use Python v. 2.7 bindings to the OpenCV v. 2.4 Computer Vision Library (https://opencv.org/). (d) A three-dimensional image of the streamlines around a simulated thecate cell, noting the toroidal eddies. (Online version in colour.)

Figure 7.

Streamlines averaged over a flagellar beat and colour contours of the fluid velocity magnitude in the plane of the flagellar beat (top row) and in a plane normal to the beat plane (bottom row). The resulting streamlines are the fluid velocities relative to the choanoflagellate averaged over one flagellar cycle. Left column: flow velocities relative to a free swimmer with collar composed of microvilli. Middle column: flow velocities around a thecate cell with collar composed of microvilli. Right column: flow velocities around a thecate cell with no collar. (Online version in colour.)

We zoom in on the flow characteristics closer to the choanoflagellate in figure 7. The first column shows the time-averaged streamlines of the flow relative to a slow swimmer mid-water, in both the plane of the flagellar beat (z = 0) and in a plane normal to the beat plane (y = 0), and the second column shows the time-averaged streamlines around a thecate cell attached to a wall with a stalk of length 2.2 μm, also in both planes. We see that this near-field flow is not axially symmetric for both slow swimmers and thecate cells.

To demonstrate the effect of the collar of microvilli on the flow features near the thecate cell, the third column of figure 7 shows the time-averaged streamlines and speed contours for a thecate cell with no collar. While fluid outside is drawn towards the capture zone, the colour contours indicate that when the collar alters the flow, the velocity of the water is very small as it comes into contact with the capture zone. By contrast, if we consider flow into a virtual capture zone in figure 2, but with no collar present (figure 7, column 3), the velocities near the virtual collar are much higher than when the collar is present. Thus, models that ignore the collar would considerably overestimate flow into the capture zone.

We explored the consequences of collar size on the feeding performance of thecate cells attached to a wall and for slow swimmers moving freely midwater. Using the localized flow computed on the surface of the capture zone, we evaluated the inward flux of water during one period of flagellar beating using equation (2.2). For slow swimmers, we used the water velocity relative to the free-swimming cell:

$$\mathbf{v}(\mathbf{x},\hspace{0.17em}t)=\mathbf{u}(\mathbf{x},\hspace{0.17em}t)-\mathbf{U}(t)-\mathbf{\Omega }(t)\times ({\mathbf{x}\mathbf{-}\mathbf{x}}_c),$$ 3.1

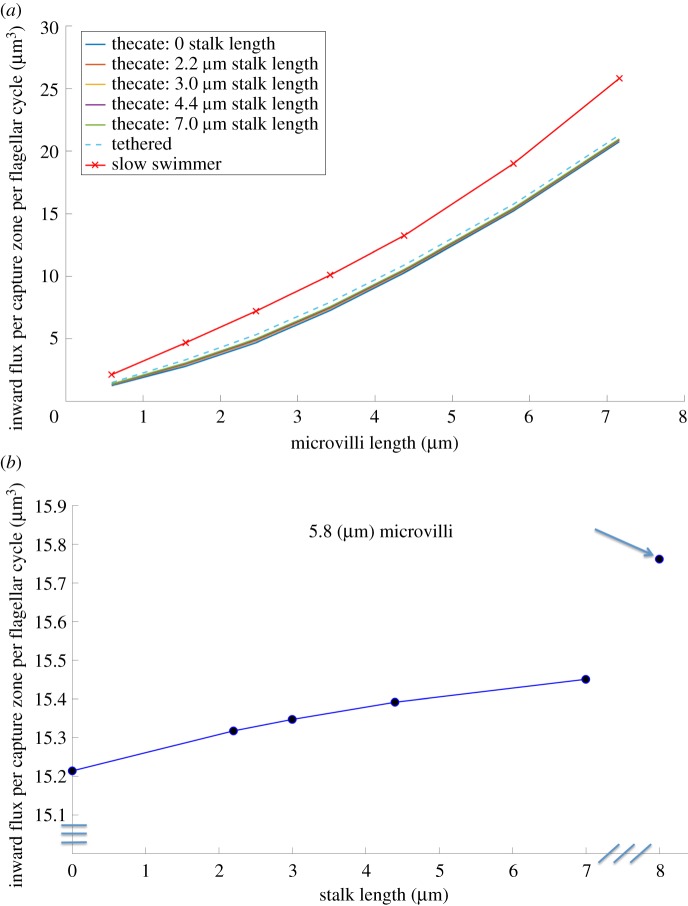
where x is the material coordinate of a point on the capture zone, x _c is the point connecting the cell body and the flagellum, U(t) is the instantaneous translational velocity and Ω(t) is the instantaneous rotational velocity of the swimmer. The collar of microvilli is the structure that captures bacteria, and the available surface area of the capture zone increases quadratically with microvillar length, due to the conical shape of the collar. However, we saw above that the morphology of the microvilli alters both the flow near the organism and the speed of swimming. Figure 8 shows the computed inward flux for both a slow swimmer when midwater and for a thecate cell with a stalk length of 3 μm, plotted as a function of microvillar length, and hence capture zone length. The bottom two curves in figure 8 correspond to flux calculated for the full coupled system where the morphology of the microvilli affects the local flow. We see that inward flux increases monotonically with capture zone length (governed by the increase in microvilli length) for both the thecate cell and the slow swimmer, and that the swimmer has a small advantage over its sessile counterpart. Even though the surface area of the capture zone increases with microvilli length, the speed of the slow swimmer, which contributes substantially to flux through the collar, decreases.

Figure 8.

Inward flux into the capture zone per flagellar cycle for a slow swimmer and a thecate cell calculated using the full model with microvilli affecting fluid dynamics (lower two curves) and using the reduced model with virtual microvilli that do not affect the flow (upper two curves). The thecate models have a stalk length of 3 μm. The capture zone (the area of a surface around the microvilli that is one bacterium radius outside the collar) is indicated by pale grey in the diagrams. The capture zone defines a region of water around the collar and is not an actual surface that affects the flow. The microvilli are shown in the lower diagram of cells with collars. A capture zone of similar size is shown in the upper diagram, which illustrates cells without microvilli. (Online version in colour.)

To evaluate the consequences of leaving the hydrodynamic effects of the collar out of the flow calculations, we also model the reduced system where the flow is unaffected by microvilli, so that increasing their length only changes the capture zone across which flux is calculated. The top two curves correspond to this reduced system, where (as in [24]), the microvilli are only virtual. The velocity of the free-swimmer in the topmost curve in figure 8 does not change with microvillar length, and is taken to be that of the organism without microvilli. This simplification greatly overestimates the inward flux into the capture zone. For instance, for slow swimmers with the typical microvillar length of 5.8 μm, ignoring the effect of the collar results in a flux that is 4.2 times that computed by the full model. In addition, ignoring the collar overestimates the advantage of the swimmers over thecate cells. The full model tells us that the flux into the capture zone of a swimmer is 24% more than that of a thecate cell, but the reduced model estimates this advantage at 51%.

Figure 9 shows how the inward flux into the capture zone is affected by the proximity of the wall to an attached thecate cell. Results are presented for different lengths of microvilli for thecate cells with a range of stalk lengths, from zero to 7 μm, and for a tethered cell in free-space (i.e. and infinitely long stalk). Again, we see that the inward flux increases with the length of the microvilli for all of the non-swimming cells (figure 9a). The inward flux for the corresponding slow swimmer moving freely midwater is higher than for the tethered cells at all lengths of microvilli (figure 9a). For the typical microvillar length of 5.8 μm, the inward flux per flagellar cycle increases with stalk length (figure 9b). A cell that is tethered but has no wall nearby (indicated by the arrow in figure 9b) enjoys an inward flux that is about 3.6% more than that of a thecate cell stuck to the wall. However, if we ignore the influence of the microvilli on the fluid flow, the increase of flux into the virtual capture zone by having no wall near a tethered cell is overestimated, and is computed to be about 9%, in line with the reduced model of [24].

Figure 9.

(a) Inward flux per period for thecate cells with different stalk lengths and a tethered cell (infinite stalk length) as well as the inward flux to a corresponding slow swimmer as a function of collar length. (b) For a thecate cell with typical microvilli collar length of 5.8 μm, inward flux as a function of stalk length. Also shown is the flux to a cell tethered midwater (infinite stalk length), indicated by the arrow. (Online version in colour.)

Figure 10 examines the ratio of inward flux of a tethered choanoflagellate to that of a corresponding freely moving slow swimmer for different lengths of microvilli, calculated for the full coupled-system where the microvilli affect the local flow. The freely swimming slow swimmer always outperforms the sessile cell, and this difference is more pronounced for cells with shorter collars (and hence faster swimming speeds). For all collar sizes, if we compare a slow swimmer midwater with a thecate cell attached to a wall by a stalk of 3 μm (figure 10, solid blue curve), the slow swimmer has a better feeding performance. Our calculations also show that when cells are midwater, if they are not allowed to move freely (i.e. if they are tethered in place, figure 10, dashed black curve) the flux into the capture zone is underestimated.

Figure 10.

Ratio of inward fluxes to capture zone during a flagellar beat of a thecate cell with stalk length of 3 μm to that of a free-swimming cell as the microvilli length increases (solid blue curve). Also shown is the ratio for cell tethered midwater (infinite stalk length) to a free-swimmer (dashed black curve). (Online version in colour.)

4. Discussion

4.1. Comparison of model predictions with data

The predictions of our model are consistent with measurements made of the performance of S. rosetta. The swimming speeds we calculated for slow and fast swimmers (figure 3) fall within the range of measured values [20,27]. Videos of S. rosetta slow swimmers show that the cells wobble from side to side with each beat of the flagellum at a mean amplitude of 20.4° (s.d. = 9.2) [27], so our calculated wobble amplitude of 11.42° falls within the range of measured values.

Our calculated flow velocities relative to S. rossetta (figure 7) are similar to velocities around living cells measured using particle-tracking velocimetry (PTV). The spatial resolution of PTV data is coarser than that of our model, but velocities at a few comparable positions relative to the choanoflagellates can be compared. Both measured (figure 6c) and calculated (figures 6a and 7, left column) fluid velocities relative to slow swimmers at positions greater than or equal to 5 μm lateral to the cell body are of order 10 μm s⁻¹, and at positions just behind the tip of the waving flagellum are about 25 μm s⁻¹. For thecate cells, calculated (figure 6b) and measured (fig. 2 in [21]) farfield flow fields are qualitatively similar, and flow velocities of order 10 μm s⁻¹ that were measured just rearward of the end of the collar at positions roughly 10 μm lateral to the cell's midline are similar to those we calculated (figure 7, middle column). The high velocities we calculated around the waving flagellum for both swimmers and attached cells (30–50 μm s⁻¹; figure 7) are not resolved in the PTV data.

For the flagellar kinematics of a typical S. rosetta choanoflagellate, we calculated the inward flux during one beat cycle to be approximately 19.01 μm³ for a slow swimmer and 15.76 μm³ for a thecate cell tethered mid-water, which produces clearance rates (volume flow rate through the capture zone) of 461.84 μm³ s⁻¹ and 383.01 μm³ s⁻¹, respectively, at the beat frequency of 24.3 Hz. These are at the low end of clearance rates reported for other species of choanoflagellates by Nielsen et al. [25], some directly measured and some estimated using published experimental data, between 400 μm³ s⁻¹ and 4400 μm³ s⁻¹.

4.2. Morphological features that affect performance

Our model enabled us to explore how specific morphological features affect the swimming speed of unicellular choanoflagellates when midwater. The slow swimmers of S. rosetta have long collars and ovoid cell bodies, while the fast swimmers have very short collars, cell bodies that are more slender and flagella that are greater in length with longer sinusoidal wavelengths than do slow swimmers (figure 1 and table 1). Our model showed that a longer flagellum increases speed, while longer microvilli reduce speed, and cell shape only affects speed when the collar is very short (figure 3). Although flagellum length and waveform have a bigger effect on swimming speed than do the other morphological features (figures 3 and 4), we found that if a fast swimmer has a flagellum the same length as the slow swimmer and undulates that flagellum using the fast-swimmer waveform, it travels through the water at a lower speed than the slow swimmer using the slow-swimmer waveform (figure 5). In more general terms, our work shows that a high-amplitude, small-wavelength, high-curvature flagellar waveform produces faster swimming if a flagellum is short, whereas a low-amplitude, long-wavelength, low-curvature waveform performs better if a flagellum is long, which is consistent with the earlier findings of Higdon [36].

We also used our model to assess how collar length affects the feeding performance of slow swimmers moving freely midwater and of attached thecate cells, which have similar cell shape and flagellar characteristics (figure 1 and table 1). The flux of prey-carrying water into the capture zone around the collar of a choanoflagellate (figure 2) is our measure of feeding performance. Bigger collars have a greater area for prey capture, thus flux into the capture zone increases with the length of the microvilli forming the collar for attached thecate cells (figures 8 and 9a). For slow swimmers, longer microvilli in the collar provide a greater area for prey capture, but drag on the collar also slows swimming, and much of the flux into the capture zone for slow swimmers is due to their motion relative to the water around them. In spite of this trade-off, flux into the capture zone of slow swimmers increases as collar length rises (figure 8). Our model assumed that all the microvilli of a collar were of equal length, but it would be interesting to explore the effects of non-uniform microvillar lengths on cell wobbling, swimming speed and feeding performance. Furthermore, the collars of S. rosetta appear to be stiff and were modelled as rigid structures, but future studies could explore the consequences of flexible microvilli on performance.

4.3. Effects of tethering and a nearby wall on feeding performance

Freely moving slow swimmers always experience a slightly greater flux into the capture zone than do tethered and thecate cells with the same collar length, but this difference decreases with the length of the collar (figures 9a and 10). This result is consistent with the data of Kreft [40], who found that the feeding rate on bacteria for swimming S. rosetta cells was higher than for thecate cells. However, the measured difference in feeding rate could also have been due to depletion of bacteria from the recirculating eddies in the water flow produced by the thecate cells attached to a nearby wall (figure 6), as has been suggested for other protozoans attached to walls [38]. However, such recirculation might not be a problem for cells in their natural estuarine habitats, where bacterial prey are not uniformly distributed. Concentrations of bacteria can be greater near the substratum, the flow produced by the thecate cell might sweep benthic prey up off the substratum and into the feeding current, and ambient flow can also sweep up prey and replace depleted water near a thecate cell with new bacteria-laden water [41]. These factors remain to be explored. Another mechanism could reduce depletion of prey in the eddies near sessile cells: if flagellar beating is modelled as a point force that turns on and off, this ‘blinking Stokeslet’ system produces chaotic flow [42] that can enhance mixing into the water near a tethered choanoflagellate [43]. Whether thecate S. rosetta cells periodically turn off their flagella should be studied.

The effects of tethering and proximity to a wall on the feeding performance of choanoflagellates were also examined. For a thecate cell attached to a nearby wall, inward flux per flagellar cycle increases slightly with stalk length. Even a cell with an infinitely long stalk produces an inward flux that is only 3.6% more than that of a thecate cell stuck directly to the wall (figure 9b). Since distance from the wall has a minor effect on flux into the capture zone, there is room for diversity in stalk length without performance consequences. We also found that when cells are midwater (i.e. no wall is nearby), flux is lower if they are tethered in place than if they can swim through the water. This suggests that models of the feeding currents of unattached protozoans midwater should not tether the cell in place.

We have assumed that the stalk of a thecate cell is completely rigid, and thus that the oscillating of the flagellum does not cause any deflection of the cell from its fixed position. By contrast, we allowed freely swimming cells to wobble from side-to-side as the flagellum beat, and found that this wobbling contributed to the inward flux of water. We believe that future models of the hydrodynamics of thecate choanoflagellates should explore the effects of the flexural stiffness of the stalk on feeding flux.

4.4. Comparison of model predictions with those of other models

As in early models, our model thecate cells attached to a planar wall do create viscous eddies of recirculating fluid near the choanoflagellate [22,23,37,39]. These far-field flow features are also captured by the minimal model of Roper et al. [21]. However, here our interest is in the near-field flow features that determine the feeding performance of the cell. The hydrodynamic effects of a collar of microvilli on the flux of water into the choanoflagellate's capture zone is twofold. The collar of microvilli affects the local flow at the capture zone as well as the overall swimming speed of the cell. Both of these effects are taken into account in our detailed hydrodynamic model. Moreover, we are able to quantify how ignoring the collar of microvilli in the hydrodynamic calculations affects both swimming and feeding performance. When we eliminate the collar of microvilli, our results on feeding performance as a function of stalk length for thecate cells agree closely with the model predictions of Kirkegaard & Goldstein [24], which do not account for the hydrodynamic effects of the collar. Furthermore, we find that ignoring the collar greatly overestimates the benefit both of swimming and of a longer stalk to feeding performance.

As described above, we calculated the volume flow rate through the capture zone (clearance rate) of a slow swimmer and of a thecate S. rosetta to be 461.84 μm³ s⁻¹ and 383.01 μm³ s⁻¹, respectively. Nielsen et al. [25] calculated the clearance rate for Diaphanoeca grandis, a choanoflagellate whose cell body and collar are surrounded by a lorica that forces the water pumped by the flagellum to move through the collar. In their CFD model, they held the cell stationary, thereby not including the contributions to inward flux of the swimming and the periodic rocking motion of the cell, which we found to be important for slow swimmers. However, their model of a tethered cell surrounded by a lorica can be compared to our model for a thecate cell tethered mid-water without a lorica. When Nielsen et al. [25] assumed a cylindrical flagellum, they calculated a clearance rate of 95 μm³ s⁻¹, which is lower than the clearance rates they measured for D. grandis (400–4400 μm³ s⁻¹) and than we calculated for S. rosetta with no lorica. They suggested that if the flagellum had sheet-like vanes (as have been observed on some choanoflagellates), it could generate an enhanced flow and produce a clearance rate of 898 μm³ s⁻¹.

5. Conclusion

Here we have examined the effect of morphological features on the swimming and feeding performance of different unicellular stages of the choanoflagellate S. rosetta. Unlike earlier studies, the collar of microvilli was explicitly represented in our model, and affected both the swimming speed of the cell and the local flux of fluid into the capture zone. We show that a longer flagellum increases swimming speed, longer microvilli reduce speed and cell shape only affects speed when the collar is very short. We also found that cells with short flagella swim faster if they use a high-amplitude, small-wavelength flagellar waveform, whereas cells with long flagella locomote more rapidly if they use a low-amplitude, long-wavelength waveform.

The flux of prey-carrying water into the collar capture zone is greater for swimming than sessile cells, but this advantage decreases with collar size. Stalk length has little effect on flux for sessile cells. We show that ignoring the hydrodynamic effects of the collar overestimates flux and greatly overestimates the benefit to feeding performance of swimming versus being attached, and of increasing the length of the stalk of attached cells.

Our model revealed the importance of the resistance of the collar to the swimming and feeding performance of choanoflagellates, which suggests future modelling directions. For example, models should explore the consequences of the accumulation of bacterial prey on the collar where the distribution of the prey and their size relative to the collar are taken into account. In addition, future models of the swimming and feeding of multicellular colonies should incorporate the hydrodynamic consequences of the collars to determine if a selective factor that might have favoured multicellularity in the ancestors of animals could have been enhanced feeding performance. Earlier models that addressed this question [21,24] did not account for the effects of the collars.

Data accessibility

Supporting data are posted at https://ib.berkeley.edu/labs/koehl/resint/multicellularity.html. Simulations and calculations were done in Matlab [44] and based on the method of regularized Stokeslets [28].

Authors' contributions

H.N., M.K. and L.F. contributed to model conceptualization, analysis of results and writing of the manuscript. M.K. provided empirical data and conceived biological questions to address. H.N. and L.F. developed the computational methodology and validated results. H.N. mentored two undergraduate students (C.O. and G.B.) on model development and implementation to generate simulation results. G.B. worked on calculating swimming speeds and flow-field generation around the choanoflagellate models, while C.O. worked on flux calculations of different models.

Competing interests

We declare we have no competing interests.

Funding

This research was supported by NSF grant nos. IOS-1147215 and IOS-1655318 to M.K., NSF grant no. DMS-1043626 to L.F., NSF grant no. DMS-1720323 to H.N., NSF grant no. DUE S-STEM 11553796 to C.O., and NSF grant no. MRI-ACI-1531594 to H.N. and C.O. M.K. and L.F. thank the Isaac Newton Institute for Mathematical Sciences for its hospitality during the Programme ‘Growth form and self-organisation’, which was supported by EPSRC grant no. EP/K032208/1.