Abstract
Many microorganisms secrete molecules that interact with resources outside of the cell. This includes, for example, enzymes that degrade polymers like chitin, and chelators that bind trace metals like iron. In contrast to direct uptake via the cell surface, such release strategies entail the risk of losing the secreted molecules to environmental sinks, including ‘cheating’ genotypes. Nevertheless, such secretion strategies are widespread, even in the well-mixed marine environment. Here, we investigate the benefits of a release strategy whose efficiency has frequently been questioned: iron uptake in the ocean by secretion of iron chelators called siderophores. We asked the question whether the release itself is essential for the function of siderophores, which could explain why this risky release strategy is widespread. We developed a reaction–diffusion model to determine the impact of siderophore release on iron uptake from the predominant iron sources in marine environments, colloidal or particulate iron, formed due to poor iron solubility. We found that release of siderophores is essential to accelerate iron uptake, as secreted siderophores transform slowly diffusing large iron particles to small, quickly diffusing iron–siderophore complexes. In addition, we found that cells can synergistically share their siderophores, depending on their distance and the size of the iron sources. Our study helps understand why release of siderophores is so widespread: even though a large fraction of siderophores is lost, the solubilization of iron through secreted siderophores can efficiently increase iron uptake, especially if siderophores are produced cooperatively by several cells. Overall, resource uptake mediated via release of molecules transforming their substrate could be essential to overcome diffusion limitation specifically in the cases of large, aggregated resources. In addition, we find that including the reaction of the released molecule with the substrate can impact the result of cooperative and competitive interactions, making our model also relevant for release-based uptake of other substrates.
Keywords: siderophores, secretion, public goods, iron uptake, diffusion
1. Introduction
Bacteria secrete massive amounts of metabolites and proteins into the environment, many of them involved in nutrient uptake. Examples include secreted exoproteases, chitinases or trace metal chelators like siderophores (chelating iron) or methanobactin (chelating copper). The secreted molecules transform their substrate (by degradation or chelation), which is then taken up by the bacterial cell. Release-based nutrient uptake strategies have been investigated as examples for cooperative behaviour in bacteria as well as probed for their stability to the ‘public goods dilemma’ [1,2], as the benefits gained by released metabolites, the transformed substrates, become available to cells not contributing to production. In addition, especially in well-mixed environments, generated substrates might be lost to the environment and not diffuse back to the producing cell. Nevertheless, release-based uptake strategies are widespread. We were thus interested in understanding what benefits are specifically generated by release, and investigated this in a prominent example: the uptake of iron by siderophores in the well-mixed ocean environment.
Bacterial metabolism requires iron and hence the limited availability of iron in many environments restrains bacterial growth and reproduction [3–6]. One common cause of iron limitation is simply low concentrations of iron such as in ocean surface waters [7,8]. In addition, other factors further limit the bioavailability of iron in seawater. First, as in all oxic, pH-neutral environments, iron is only poorly soluble [9,10]. Hence, iron mostly occurs in particles of different sizes, which are often operationally defined in the marine environment as soluble (less than 0.02 µm), colloidal (0.02–0.4µm) and particulate (greater than 0.4 µm) [7,8,11,12]. Second, the soluble and colloidal fractions of iron are largely complexed by organic ligands and are thus only available for uptake by bacteria by expressing the cognate transporter or by disassociating the iron from the ligand [13]. While the effects of the presence of organic ligands on bacterial iron uptake has received considerable attention [14,15], the impact of colloidal and particulate iron on bacterial growth is still poorly understood [8,12]. Nevertheless, these larger types of iron sources are prevalent throughout the ocean [11,16–18] and can constitute up to 85% of the accessible iron pools [19].
Many microbes have developed strategies to increase iron bioavailability. One particularly widespread and well studied such strategy is siderophore secretion [20]. Siderophores are chelators that bacteria release into the environment to bind iron. The resulting iron–siderophore complexes can then be taken up by the bacteria. An important consequence of secretion is that a cell might not recapture and hence benefit from the siderophores it produced itself, due to random diffusion of the siderophore molecules. In dilute, well-mixed environments, the probability of recapturing a siderophore once it is secreted is low, and a solitary bacterium thus has to produce a large number of siderophores in order to achieve sufficient uptake of iron [21]. Hence, siderophore secretion has been viewed as a strategy poorly adapted to the marine environment [22]. Also, released siderophores can be taken up by strains that do not contribute to siderophore production if these express the cognate receptor [23,24]. This can lead to a public goods dilemma, where non-producing genotypes can displace bacteria that produce siderophores [25]. Thus, it is not obvious why the release of siderophores is efficient, especially in the marine environment.
Different mechanisms have been suggested that could mitigate the negative effects of release. Amphiphilic siderophores—containing both a fatty-acid tail and a hydrophilic head group—can constitute a considerable fraction of siderophores isolated from seawater samples [26]. Such siderophores might stay attached to the cell membrane of the producing cell thanks to their fatty-acid side chain [27–29] or might be more easily retained due to lower diffusivity [30]. Furthermore, inorganic ferric iron can be acquired directly using ATP-binding cassette transporters that are frequently detected in marine bacterial genomes [31,32]. In addition, surface-associated reductases allow uptake from particulate iron [33–35], outer membrane receptors mediate uptake of iron bound to exogenous chelators like heme or transferrin [36], and ferric citrate can be taken up via transporters or porins [37].
Despite the existence of such alternative mechanisms that avoid the risk of siderophore loss, siderophore secretion is widespread in bacteria [38], and has been described as key for iron uptake in environments with low iron availability [39]. This suggests that the release itself of siderophores might be directly beneficial for their function. However, it is less clear what the possible benefits might be. Here, we were specifically interested in comparing the efficiency of bacterial iron uptake based on release of siderophores to a strategy avoiding release (e.g. mediated by membrane-associated amphiphilic siderophores). We developed a mathematical model to quantify the benefits of siderophore release in marine surface waters. We focus on the marine environment because of the wealth of data on iron distributions and because the efficiency of siderophore secretion in the ocean has been questioned before [21]. In contrast to this previous model, we take larger-sized particulate and colloidal iron as potential iron sources into account. Note that while the precise operational distinction between dissolved and colloidal iron has since shifted slightly, we here explicitly model the size-dependent mass transport properties of iron particles. Previous models (like the free ion activity model) assumed diffusion of iron sources to be instantaneous compared to uptake across the cytoplasmic membrane [40]. By contrast, we hypothesize that in order to understand benefits that lie in the release of siderophores, diffusion limitation is a key factor and needs to be taken into account, in line with previously voiced criticism for neglecting the role of diffusion in iron uptake [40–42].
We hypothesize that siderophores ‘scavenge’ iron from larger-sized iron sources that diffuse more slowly than soluble iron or iron–siderophore chelates, thus providing benefits beyond just releasing soluble iron from organic ligands [21]. Using a mathematical model for the diffusion and bacterial uptake of iron, we find that release of siderophores can be of key importance to overcome iron limitation in conditions where mass transfer limits iron uptake. Under these conditions, where iron uptake is slowed down due to diffusion limitation of large iron particles, only secreted siderophores, i.e. siderophores released from the cell, can accelerate iron uptake. Furthermore, we find that the production of siderophores in groups of cells increases the efficiency of siderophore-based iron uptake, concurrent with previous literature [21]. The secretion of siderophores by multiple cells acts synergistically, as long as the cells are sufficiently far apart. These results suggest that the act of ‘secreting’ siderophores itself has innate benefits to bacterial growth and could explain why even single marine cells engage in siderophore release.
2. Results
2.1. Modelling iron particle size as the number of contained iron ions
We investigate iron uptake with a focus on the effect of low iron solubility on diffusion limitation. A key consequence of low iron solubility is that the majority of iron is present in aggregates such as colloidal (less than 0.4 µm) and particulate iron (greater than 0.4 µm) [7,11,19]. The diffusion speed of a particle will depend on its size, and hence by modelling iron particles of varying size, we can capture the diffusion of such aggregated iron particles in marine environments.
We assume that the iron particles are spherical and increase in size with increasing number, k, of iron ions within. Soluble iron corresponds to the smallest iron ‘particle’, i.e. one iron ion surrounded by water molecules (k = 1). We consider iron particles from k = 1 up to k = 1012 iron ions (figure 1), with corresponding radii, rk, ranging from 0.1 nm to approximately the size of a cell, 1 µm, covering the range of colloid and particulate iron sizes present in marine environments; in open ocean waters, radii range from less than 10 nm up to at least 500 nm [8,11,12,19]. For reasons of mathematical tractability, we assume a homogeneous distribution of iron particles, i.e. all particles have the same k. By varying k, we can then isolate the effect of particle size on iron uptake.
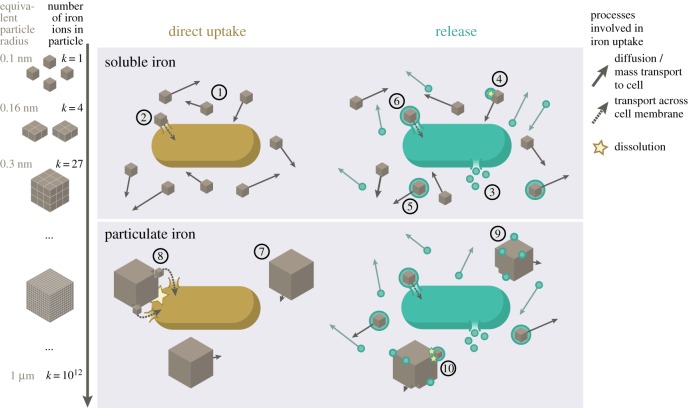
Figure 1.
Modelling the direct and siderophore-mediated uptake of soluble and particulate iron. This figure illustrates iron uptake in the two extreme cases of very strong iron aggregation or complete solubility. When iron is fully soluble and freely diffusing (1), non-secreting (yellow) cells must take up iron ions directly (2). Secreter cells (green) release siderophores (3) that themselves diffuse freely and encounter and bind soluble iron (4). The resulting iron–siderophore complexes also diffuse freely (5), and are subsequently taken up by the cell (6). In the presence of large particulate iron sources (7), non-secreter cells must first encounter a particle before extracting individual iron ions to take up (8) using surface-bound ligands or reductases. This activity is limited by the number of iron particles a cell encounters and can ‘hold on’ to, as well as the rate at which it actively dissolves the particulate iron. Siderophores bind to the surface of the particle (9), and subsequently disassociate from it as an iron–siderophore complex (10). This occurs at a distance from the cell, therefore alleviating the restrictions on how many particles can be actively dissolved simultaneously. We want to point out that in our model, iron sources are modelled as spheres, not cubes.
We want to highlight that this model implements several simplifications in order to single out the effect of diffusion limitation in the complex marine system. In reality, iron particles are generally polymorphous, containing iron as well as hydroxide or other groups. Over time, and depending on external conditions like pH, the particles can change in crystal structure and size [43,44], factors that also influence iron solubility [16]. Here, we assume that iron aggregates exclusively contain iron ions and only change when dissolved directly by cells or siderophores. We do not consider other dissolution processes, e.g. proton-promoted dissolution, that might be indirectly influenced when siderophores bind iron, e.g. by decreasing the solution saturation state [16]. We also do not consider the fact that the majority of dissolved iron is bound to ligands, some of which might be siderophores themselves [7]. While these factors are undoubtedly important for understanding the overall iron distribution in the ocean, they do not directly influence our investigation into the effects of diffusion limitation.
2.2. Low iron solubility strongly decreases the rate of direct iron uptake
To establish a baseline reference for the iron uptake rate, we first consider a single cell that relies on secretion-independent uptake by direct physical contact with iron particles, mediated, for example, by cell-attached siderophores or receptors (figure 1, top). The cell can only take up iron it encounters directly; in the absence of any ‘active’ motion, this can only be mediated by random diffusion. The uptake of iron can thus be described as a set of diffusing particles in three dimensions with the cell at the origin acting as an absorbing sphere (see Methods).
The likelihood of encounter between a cell and iron depends on the effective diffusion coefficient, which is the sum of the diffusion coefficient of the cell, DB, and of the iron, Dk. The more iron ions are contained in a particle (larger k), the larger the diameter of the particle and the smaller the diffusion coefficient, Dk ∼ k−1/3. As a consequence, the likelihood of encounter with the cell is smaller for larger particles (see Methods). Since generally Dk ≫ DB, the encounter rate of a k-particle for a single non-secreting cell with radius RB is approximately
| 2.1 |
where ρk = ρ0/k is the background concentration of iron particles and ρ0 is the total background concentration of iron. Before a cell can take up iron from a particle it encounters, it first needs to release iron ions from the particle. The detailed kinetics that describe such a bacterial-mediated dissolution of iron depends on the particular nature of the iron mineral (e.g. crystal structure) and the mechanism the bacteria employs to dissolve the mineral (surface ligands, reductases, etc.) [44,45]. Assuming cell-attached siderophores can bind to ions on the particle surface in a ligand exchange reaction and subsequently release iron ions from the crystal lattice at a rate κL, then the overall dissolution rate of a k-particle, ψk, will be proportional to the surface area of the particle, S(k) ∼ k2/3. The overall dissolution rate of the whole particle will then be ψk ∼ k−1/3, and based on geometric considerations can be approximated as (see Methods)
where κL is a pseudo-first-order rate constant and σ specifies the fraction of the surface area of the particle that a cell can sequester iron from. The balance between the encounter rate of new particles and their dissolution rate will determine whether cell-mediated dissolution can keep up with the influx of new iron.
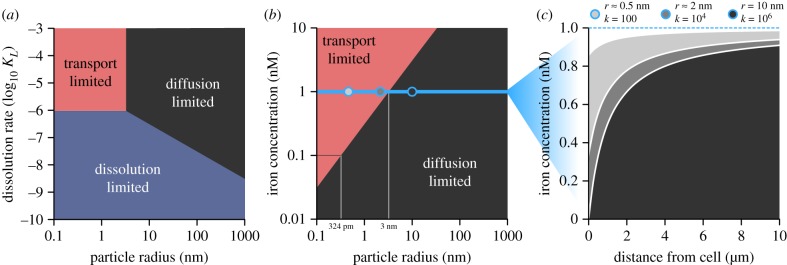
We distinguish between three environmental regimes that limit the iron uptake of a cell under direct encounter (figure 2a) that are the result of one of the three key processes involved in iron uptake becoming the limiting process (figure 1): (1) in a transport-limited environment, the cell is producing enough soluble iron in the proximity of the cell, but the overall uptake is limited by the amount of iron that can be processed by the transporters at the cell surface; (2) in a dissolution-limited environment, the cell encounters iron particles more rapidly than it can dissolve them; (3) in a diffusion-limited environment, the cell has enough transporter and dissolution ability, but the encounter rate with new particles is too low. Iron aggregation influences both the concentration of iron at the cell surface, as well as the rate at which the particles are dissolved, as a function of k1/3. Thus, depending on the dissolution rate, κL, the environment transitions from diffusion-limited when iron particles are large to either transport-limited (large κL) or dissolution-limited (small κL).
Figure 2.
The level of iron aggregation, i.e. particle size, influences what process iron uptake is limited by. (a) When iron particles are large, the environment is generally diffusion limited, but transitions to dissolution limited as the dissolution rate decreases. As the particle sizes decrease, the environment becomes either transport limited for high dissolution rates or dissolution limited for low dissolution rates. Here, the background concentration of iron is ρ0 = 1 nM. (b) The critical particle size for which the environment transitions from diffusion to transport limited (large κL) also depends on the background concentration of iron. As the size of iron sources increases at a given concentration, diffusion of iron slows down and eventually the iron at the cell surface is completely depleted. In this regime, all iron that arrives at the cell surface is immediately taken up, and the cell is limited by the amount of iron diffusing to the cell (diffusion limited, black area). The transition from transport-limited to diffusion-limited happens at increasing particle sizes as the background iron concentration increases (ca 324 pm for ρ0 = 0.1 nM and 3 nm for ρ0 = 1 nM). The blue line highlights the background concentration used for calculations leading to the data in (c) (0.1 nM). At this concentration, the threshold between the two types of limitation is at an aggregation level of k = 33. The radial iron concentrations at a background concentration of 1 nM (blue line) are shown for three particle sizes (blue circles) in (c). (c) The equilibrium iron concentrations as a function of the distance from the cell, with a background concentration of iron ρ0 = 1 nM. For small particles (low k), in the transport-limited regime (red areas in (a,b)), the iron concentration at the cell surface decreases with increasing particle size, due to increasingly slow diffusion of iron, but iron is never completely depleted. In the diffusion-limited regime (black areas in (a,b)), iron is completely depleted at the cell surface, and thus the steady-state concentrations do not depend on the particle size anymore.
At iron concentrations that are realistic for open ocean waters, ρ0 = 0.1–1 nM, diffusion limitation already occurs at particle sizes of r ≥ 0.3 nm to 3 nm, depending on the background iron concentration (figure 2b). We determined the equilibrium distribution of iron particles by solving the spherically symmetric diffusion process (see Methods and [21]). The distribution of particles at steady state (figure 1c) for ρ0 = 1 nM illustrates that in the transport-limited (or also dissolution-limited) regime, iron is never completely depleted at the cell surface, even though the iron concentration decreases towards the cell surface. By contrast, in a diffusion-limited regime, iron is completely depleted at the cell surface and only approaches background concentration levels at a distance of over four cell radii.
Under these conditions, the required time for a cell to encounter, dissolve, and take up sufficient iron to divide can reach up to days, for particles of size rk ≈ 1 nm, or months, for rk > 10 nm. The time to division increases further with decreasing dissolution rate, κL (see Methods; electronic supplementary material, figure S1). The generation time of marine bacteria has been estimated to generally be on the time scale of days [46,47], which is much faster than predicted by our model for a cell only using direct uptake. This suggests that other mechanisms, such as for example siderophore secretion, are necessary to reach environmentally realistic growth rates.
The extremely long iron acquisition times are due to two difficulties that cells face under direct iron uptake. First, the rate at which cells encounter iron particles is low due to the slow diffusion of the particles. Second, once cells encounter particles, larger particles are dissolved more slowly than smaller particles due to a lower surface-to-volume ratio (see Methods). Thus, although a cell will eventually ‘gather’ enough iron particles to reach a maximally possible uptake rate under the constraints set by the diffusion of the available iron, this maximum is only reached after extremely long time periods. For example, for particles of sizes around 5 nm, a cell starting from scratch would require over 4 years to reach the maximum uptake rate, although it would have already taken up enough iron to divide by around 6 months (see electronic supplementary material, figure S2). However, even if the cell were already taking up iron at its maximal rate—for example, by maintaining a reservoir of iron particles or by immediately dissolving the particles upon encounter (κL → ∞)—it would still require around a month to take up enough iron to divide. Thus, a main consequence of low iron solubility is that cells can suffer from strong diffusion limitation, even at high iron concentrations. Cells might face similar problems in the uptake of nutrients from other larger substrates, such as particulate carbon sources.
Transport limitation can be alleviated at the cell membrane, for example through more efficient or more numerous transporters. Dissolution limitation due to low rates can in part be alleviated at the cell level by increasing the dissolution activity of membrane-bound ligands or reductases. But, both diffusion limitation and dissolution limitation due to limited processing space around the cell can only be overcome by processing iron away from the cell. Secreted molecules like siderophores can modify iron sources and alter their transport properties to both increase diffusion and accelerate uptake when encountered by a cell (figure 1, bottom). In the following, we will hence quantify the effect of siderophore secretion on overcoming diffusion limitation—by increasing the diffusion speed of iron—and dissolution limitation—by increasing the number of iron particles that can be processed in parallel.
2.3. Secreted siderophores can transiently increase the uptake rate of iron from large particles by accelerating diffusion
We next investigated whether siderophore secretion could alleviate diffusion and dissolution limitation. In addition to the diffusion of iron, we accounted for free (unbound) siderophores that are produced at the cell surface and diffuse away from the cell, as well as the reaction of free siderophores with iron resulting in siderophore–iron complexes outside the cell (figure 1). These complexes diffuse freely and can be taken up by the cell upon an encounter. We model these processes using a set of reaction–diffusion equations that describe the radial concentrations of iron particles, F, free siderophores, X, iron–siderophore complexes, Y, and particle surface ions bound by siderophores, E (see Methods). In order to investigate the direct effects of iron uptake mediated by secreted iron chelators, we excluded the possibility that cells take up free, unbound iron in these calculations.
Because siderophore–iron complexes are smaller than most iron particles, their diffusion coefficients are generally larger than those of the particles. This leads to accelerated diffusion that could potentially mitigate the limitation caused by the slow movement of large iron particles. Furthermore, the scavenging of iron from particles by siderophores is not limited to direct contact of the cell with the iron source. Thus, siderophores are able to solubilize iron from a larger number of iron sources simultaneously.
The effects of secreting siderophores depend both on the size of the iron particle and whether the system is still in a transient phase or has already reached steady state. In the presence of large iron particles (rk > 10 nm; the colloidal range) siderophore secretion indeed results in an uptake rate that quickly surpasses that of direct uptake for extended periods of time (figure 3). As the cell starts to produce siderophores, these quickly diffuse and bind to the surface of slowly moving particles at distances around the cell of up to a few centimetres (electronic supplementary material, figures S4 and S5). This leads to an initial increase in the iron uptake rate, within the first seconds under our conditions (figure 3). These adsorbed siderophores then contribute to the dissolution of all the iron particles in a relatively large volume around the cell. Siderophore–iron chelates are released from particles over time and a fraction of these quickly diffuse back to the cell. The long-term direct uptake rate eventually approaches and even slightly surpasses the secretion uptake rate, but this only happens over extremely long time periods (months to years), as a cell using direct uptake must first accumulate a reservoir of particles to degrade. The transient increase thus likely comprises many bacterial generations [46,47]. Overall, siderophore secretion increases the iron uptake rate compared to direct uptake, however, only during a—potentially very long—transient phase, and this transient increase in the uptake rate directly results in a large increase in the amount of iron acquired (electronic supplementary material, figure S3).
Figure 3.
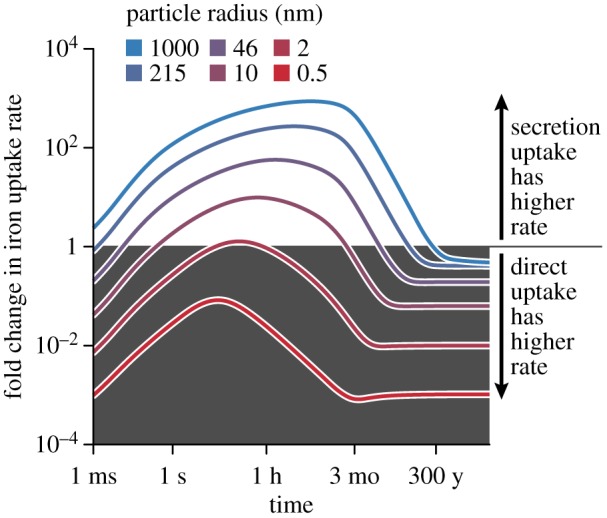
Siderophore secretion can strongly increase iron uptake over long time periods when iron is aggregated. The lines show the fold change in iron uptake rate for cells that secrete siderophores at a rate P = 4.5 × 10−2 amol h−1 compared to direct iron uptake. Iron particles are dissolved at a rate κ = 106 s−1. Secretion uptake is initially slower than direct uptake until the concentration of adsorbed siderophores builds up. For large particles, secretion uptake surpasses direct uptake, reaching 100–1000 fold increases in the iron uptake rate. Eventually, secretion uptake decreases to comparable levels as direct uptake. However, the increase in uptake speed can last days or years, depending on the particle size.
If iron is present in soluble form or as small particles (rk < 10 nm) the equilibrium uptake rate reached via siderophore secretion is mostly far below the direct uptake rate: releasing siderophores slows down iron acquisition. In this regime, the fast diffusion limit, the diffusion speed of iron is sufficiently high that the background concentration of iron can be assumed constant (see Methods, equation (4.15)). Secretion slows down uptake because of two factors. First, siderophores must encounter iron and bind it, introducing an additional step prior to uptake. Second, the diffusion speed of siderophore–iron complexes is lower than that of free iron for k < 1000, thus reducing the flux of bound iron towards the cell. For very small iron particles (highly soluble iron), siderophore secretion results in slower acquisition than direct uptake. Therefore, for particle sizes greater than 0.3 nm but smaller than 10 nm (at an iron concentration of 0.1 nM and a dissolution rate of κL = 106), the cell is diffusion-limited, but secretion of siderophores is not effective at overcoming this limitation.
To access poorly soluble iron, cells could also—instead of secreting siderophores—increase their own diffusion coefficient by engaging in swimming motility. However, in such cases, it would be unlikely that a cell could dissolve more than one particle at a time. The rate at which a cell first encounters and subsequently dissolves single particles is a function of both the rate at which a non-motile cell encounters iron particles, ϕk, and the rate at which it dissolves the particle, ψk, leading to an overall rate ϕkψk/(ψk + ϕk). An increase in cell motility can potentially increase the encounter rate of new particles, ϕk, but because ψk ≪ ϕk, further increases in the encounter rate will only have marginal effects on the compounded iron uptake rate.
2.4. The effect of siderophore secretion depends on siderophore production rate and particle size
The increased iron uptake rate achieved by secretion in the presence of large iron particles, although only transient, can shorten the time necessary until a cell has acquired enough iron to initiate cell division significantly, from over a year for direct uptake to a few weeks with siderophore secretion (assuming an iron content of 106 Fe atoms = 1.66 amol per cell [36]; see also electronic supplementary material for a detailed discussion). In addition, we find that the siderophore production rate has a strong influence on the parameter range in which secretion-based uptake is superior to direct uptake, and that very high production rates are necessary to overcome diffusion limitation efficiently (electronic supplementary material, figure S6). The cost of producing such a high number of siderophores is difficult to estimate, since the negative effect of siderophore production on growth, due to resources spent on production instead of cell division, likely depends on environmental parameters such as the level of resource limitation [48]. However, to obtain an estimate of the magnitude and efficiency of siderophore production, we calculated how many siderophore molecules need to be produced in order to take up one iron ion (a similar approach to Völker & Wolf-Gladrow [21]). For a low siderophore secretion rate of 0.045 amol h−1 and a particle size of rk = 100 nm, a secreter must release just under 28 000 siderophores to take up one iron ion, or a total of 47 femtomoles to divide. However, this seemingly high cost in terms of produced siderophores results in a significant reduction of the time necessary for acquiring enough iron to produce a daughter cell, from 354 days to 43 days at an iron concentration of ρ0 = 0.1 nM. Faster uptake is achieved through higher siderophore secretion rates, though this also implies that more siderophores per iron are secreted: a secretion rate of 4.5 amol h−1 results in a division time of 26 days, requiring around 180 000 secreted siderophores per iron taken up at an iron concentration of ρ0 = 0.1 nM and for rk = 100 nm.
2.5. Synergistic siderophore production between two neighbouring cells can occur over a wide range of parameters
High siderophore production rates likely require a substantial investment of cellular resources. One way to reduce the production effort is cooperative production of siderophores in groups of cells. Siderophore–iron chelates that never return to one secreter cell might still benefit a different neighbouring cell. Furthermore, if cells can share their siderophores, each cell might have to produce fewer siderophore molecules overall. The outcome of such interactions is not easily predictable, though, since any increase in benefit from additional siderophores might be offset by having to share the incoming iron-bound chelates.
Siderophore production in a group of cells has been shown to increase the efficiency of accessing iron-bound siderophores thanks to an accumulation of siderophores in the neighbourhood of the cells [21]. However, these results did not consider the effect of large colloidal and particulate iron sources. In our model (for details, see Methods; electronic supplementary material, figure S7), we observe that—especially in the case of large iron sources—siderophore production affects and alters the environment in a large neighbourhood around the cell. Iron-bound siderophore chelates build up at distances of several hundred micrometres (see electronic supplementary material, figure S4), thus potentially allowing for cooperative interactions between cells located at significant distances. Our model indicates that both costs and benefits are influenced by the size of iron sources. First, achieving fast uptake from large iron aggregates requires a high siderophore-to-iron expenditure ratio, indicating that an important proportion of siderophores is lost to the producer cell even if no other cell is present. Thus, direct costs of sharing may be minimal if iron is present in large particles. Second, the benefits of sharing siderophore production with a producing neighbour cell are influenced by the beneficial returns of increasing siderophore production rate (electronic supplementary material, figure S6b).
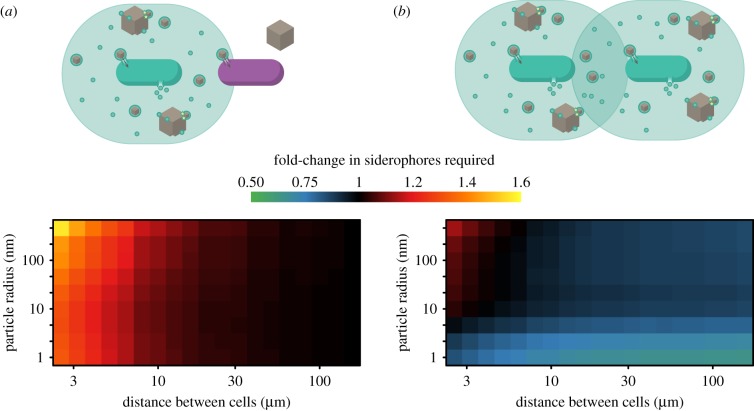
We investigated a first stage of growth in a group of cells by considering the interactions between two cells. We measured the average number of siderophores produced by a secreter cell per iron taken up during the uptake time. The net effect of growing in proximity to another cell depends on how much a cell suffers from competition for iron-bound siderophores compared to how much it benefits from the siderophores produced by its neighbour. If sharing siderophores is synergistic, i.e. more efficient in a group, a cell has to produce fewer siderophores to take up one iron ion when a producing neighbour is present. We first quantified how much a siderophore-secreting cell is negatively influenced by the presence of a second cell by implementing this cell as an iron–siderophore chelate sink (comparable to cheater cells in [1]). We assume that the second cell does not produce siderophores, but still can take up iron bound to siderophores (but not free iron). We measure the negative effect (or cost) in terms of how many more siderophores the secreter cell needs to produce on average to take up one iron, relative to a situation where no other cell were present. We find that, while the degree of iron aggregation does not strongly influence the interaction, the distance between the cells plays a key role (figure 4a). If the two cells were (hypothetically) at the exact same point in space, then all iron–siderophore chelates that arrive at the cells are shared evenly between the two, and the producing cell needs to produce many more siderophores, and increasingly so the larger the particles. As the distance between the two cells increases, the negative effect on the producer decreases (figure 4a). The loss of siderophores to the neighbouring cell at distances larger than 10 µm has a negligible effect on the producing cell (electronic supplementary material, figure S8). At the same time, at these distances, the non-producing cell is able to take up almost equivalent levels of iron as the secreting cell. Thus, siderophores can efficiently be taken up by the neighbouring cell at a very low cost to the producer, because the non-producer benefits from the siderophores that would likely be lost to the producer anyway.
Figure 4.
The length scale of competition for incoming iron–siderophore complexes is much shorter than the length scale of synergistic production of siderophores. (a) Only the secreter produces siderophores, the non-secreter consumes iron-bound siderophores, but does not contribute to production. The relative increase in the average number of siderophores that need to be produced to take up one iron, relative to if the secreter was alone, depends on the distance between the cells. When the two cells are close, the amount of siderophores required increases significantly (orange area). However, when cells are at distances of greater than 30 µm, the secreter does not need to produce additional siderophores (black area). The non-secreter generally acquires equal amounts of iron as the secreter. (b) Both cells produce siderophores. Secreters can increase the uptake rate of a neighbouring secreter at no or little additional cost, provided that the distance between cells is large enough. For small particles, the presence of an additional cell decreases the number of required siderophores by half, thereby alleviating the disadvantage of siderophore uptake for small particle sizes compared to direct uptake. The benefit is slightly reduced for larger aggregates, but remains synergistic and augments the benefit of secretion compared to direct uptake. Here, κL = 10−6, P = 0.045 amol h−1.
Because the benefits of siderophore secretion can be shared with neighbouring cells at relatively short distances without additional costs to the producing cell, we next examined how joint secretion may be synergistically beneficial for cells. We measure benefit here as a reduction in the amount of siderophores secreted to achieve uptake of one iron ion. Values smaller than 1 mean that both cells benefit from the presence of another producer, because they efficiently share siderophores. As a result, each cell has to secrete fewer siderophores to take up the same amount of iron.
Highly soluble and insoluble iron sources enable synergistic interactions, whereas medium-sized aggregates do not. Over a large range of separation distances (greater than 10 µm for P = 0.045 amol h−1), cells can share the benefits of secretion without an additional cost due to competition (blue-green areas in figure 4b), and cooperative effects are thus greater than competitive effects. The magnitude of the synergistic effect, however, depends on the marginal benefit of increased siderophore production rate (i.e. the slope in figure S6b in the electronic supplementary material). For production levels that only result in a small increase in iron uptake, the marginal benefit of an additional producer cell is small (black areas in figure 4b). The outcome of social interactions is therefore strongly influenced by the physical properties of iron, in particular the diffusion coefficient.
Overall, we find that at the majority of our conditions, siderophore secretion can lead to synergistic interactions between two neighbouring siderophore producing cells. This aids in making the secretion of siderophores a favourable strategy in a wide range of environments compared to direct uptake (figure 4b).
3. Discussion
The ubiquity of bacterial siderophore secretion despite the risk of siderophore loss and the evolutionary fragility it entails has stimulated a large body of research [1,49,50]. Here, we suggest that the release of siderophores is important for their function, potentially explaining why this uptake strategy is so widespread. We show that low iron solubility, present in many environments, can strongly slow down iron uptake if no siderophores are released, simply because the majority of iron sources occur in particles that diffuse slowly. Secreted siderophores solubilize iron and generate small chelates with significantly increased diffusion speed. When we estimate the beneficial effect of siderophores in the marine environment, we find that siderophore release can significantly increase iron uptake speed on a time scale of months. While our model is a highly simplified version of marine iron chemistry, we think that it can contribute to our understanding of beneficial effects that require release of siderophores, namely for the role of overcoming diffusion limitation.
Recently published data suggest that amphiphilic siderophores constitute the majority of siderophores in the ocean [26], which might appear contradictory to the predictions of our model. Amphiphilic siderophores are often viewed as the result of an evolutionary adaptation to the dilute marine environment that minimize diffusive loss by remaining associated with the producing cell rather than being secreted [28,30]. In this case, the maximal number of siderophores that can be produced by a cell is limited by the cell surface area, unlike secreted hydrophilic siderophores, which would strongly reduce the functionality of siderophores with respect to diffusion limitation for iron uptake. We suggest several explanations to address the apparent mismatch between the measurements of amphiphilic siderophores in the ocean and our model. First, quantitative data on the relative concentrations of hydrophilic compared to amphiphilic siderophores are limited and understanding the broad distributions of marine siderophore pools still requires further investigation. Second, amphiphilic siderophores need not represent a ‘non-secreter’ iron uptake strategy as we model it here. Chemical structures of amphiphilic siderophores vary considerably and as a result these siderophores do not necessarily stay associated with the cell. Aquachelins and marinobactins A–E, for example, are isolated from the supernatant of laboratory cultures rather than the pellet [27], suggesting that they are secreted by the cells. Thus, at least some of the amphiphilic siderophores measured in the oceans are likely also secreted siderophores. Third, hydrophilic, i.e. unambiguously secreted, siderophores have frequently been isolated from marine environments [26,51,52]. In reality, bacteria will likely employ a combination of different secreted and non-secreted iron uptake strategies to maximize iron acquisition.
Siderophores are also believed to be important drivers of competitive interactions between unrelated genotypes. The chemical diversity of siderophores allows siderophore-bound iron to often be ‘reserved’ for the siderophore producer and is only poorly accessible to other genotypes [53]. The biological basis is that uptake of siderophore-bound iron requires a transporter specific to the structure of the siderophore. In our model, we only consider the case where the ‘cheating’ genotype is able to access siderophore-bound iron (figure 4), as has previously been observed for marine bacterial communities [54]. Nevertheless, access to iron can be restricted once it is chelated to a siderophore and thus impede growth of competitors [55]. Successful ‘reservation’ of environmental iron is not possible if siderophores stayed attached to the cell, thus further contributing to the benefits of secretion. These effects with respect to competition do not preclude the benefits with respect to diffusion that we describe here, suggesting that siderophore secretion might fulfil multiple roles.
Siderophore secretion is often cited as one of the central examples for diffusible public goods in the study of the evolution of cooperation [1,25,56,57]. Secreted molecules, such as siderophores, are at risk of being ‘stolen’ by a cheater genotype that avoids the cost of production, but reaps the benefits. The current consensus is that cooperation by means of secreted public goods is stabilized by spatially structured environments, as this increases the probability of interactions between identical genotypes, and consequently decreases the probability of interactions between producers and cheats [56–59]. Only few of these studies, however, have considered the process of diffusion of the public good to the full extent [57,60–63]. More importantly, game-theoretical studies mostly model the diffusive public good itself as a carrier of some benefit [57,63]. In our study, we consider a more realistic view of the mechanism of siderophore-based iron uptake. A secreted siderophore per se is useless to the cell, and any neighbouring cell, until it encounters and chelates iron.
In addition to findings on the importance of siderophores for mediating diffusion limitation, our model also reveals that abiotic properties of the substrate, in this case the diffusivity of iron, can play an important role in social interactions between cells, and need be taken into account when considering cooperative dynamics. The same also applies to other secreted metabolites that interact with large slow substrates, such as chitinases secreted to degrade chitin, or other extracellular degrading enzymes (cellulase, exoprotease).
We suggest that when analysing microbial competition and cooperation in these release-based uptake strategies, it is important to consider two different length scales: (1) the length of competition, i.e. the distance between neighbouring producers at which they compete for the shared resource, in this case the iron-bound siderophores; and (2) the length of synergism, i.e. the distance at which the neighbouring producers synergistically use the siderophores produced. Our model shows that typically the length scale of competition is much shorter than the length scale of synergism. This allows neighbouring producer cells to jointly increase the global siderophore production without paying additional costs due to competition. Thus, the benefits of siderophore secretion increase with the number of cells, while the costs per cell stay constant, if the cells are sufficiently spaced. This could set the basis for successful cooperative interactions in the secretion of many compounds.
Marine particles are a specific environment that might favour secretion-based iron uptake in the ocean. Cells can attach and grow in groups, establishing the infrastructure for synergistic interactions. In addition, growth on a particle containing organic matter might provide plentiful resources that can be channelled into production of siderophores. Copiotrophic microorganisms, especially, might experience conditions that are highly favourable for siderophore secretion. Indeed, an increased capacity for siderophore production has previously been linked to copiotrophs [32,64].
Release-based nutrient uptake, such as the secretion of siderophores or enzymes, has stimulated intense research in evolutionary and environmental microbiology, because of the seemingly fragile efficacy: releasing a metabolite entails a risk of loss and can be considered an immense task of ‘environmental engineering’ as resources outside of the cell are transformed on a large scale. Here, we have focused on the specific prominent example of the secretion of siderophores in the ocean and showed that secretion conveys an especially large benefit if the nutrient of interest—in this case, iron—is hard to reach. However, because the benefits of secretion lie in modulating the diffusive properties of the resource, rather than the specific chemical interaction, we expect our results to apply to any secreted foraging strategy where cells and resource are physically separated. We suggest that the benefits of secretion in increasing the resource availability can outweigh these costs—especially in groups—and help us understand why bacteria frequently engage in release-based nutrient uptake.
4. Methods
4.1. Direct uptake
4.1.1. Encounter rate
If we assume a spherical cell with radius rB, then the probability that a spherical iron particle starting at a distance r from the cell encounters the cell before time t is just the hitting probability of a random walk [65,66]
| 4.1 |
with total radius and effective diffusion coefficient . The diffusion coefficient is D = kBT/6πhr, where kB ≈ 1.38 × 10−23 J K−1 is Boltzmann’s constant, T = 293 K is ambient temperature, h = 1.003 mPa s is the viscosity of water at ambient temperature, and r is the radius of the spherical particle in metres. By summing the diffusion coefficients to an effective diffusion coefficient, we fix the reference frame of the iron particle to the bacterium and subsume the movement of the bacterium into the movement of the iron particle. As a simplification, we assume that the cell is stationary in space, and thus the effective diffusion coefficient is . Note that generally iron diffusion is faster than diffusion of the cell, , so that in most cases is an acceptable approximation.
The total number of particles that have collided with the bacterium by time t is
where dn(r) is the number of particles at a distance r. If the concentration of iron is ρ and the iron particles are equally distributed in space, then . Thus the total number of particles becomes
We assume that all iron particles contain k Fe atoms and that the total concentration of iron is , where ρk is the concentration of particles of size k. The number of particles of size k that have collided with the bacterium at time t is
with and . The instantaneous encounter rate between a cell and iron particles is thus
| 4.2 |
At best, a bacterium can immediately take up a whole k-particle, such that maximum possible iron uptake is ϕk(t) = kφk(t), which for large t is ϕk ≈ 4πρ0 RB Dk.
4.1.2. Dissolution
Generally, a cell will not be able to absorb a complete k-particle, but will first need to dissociate iron ions from the aggregate. Kraemer [10] studied the ligand-controlled dissolution of iron minerals and derived that the overall dissolution rate is
where kL is a pseudo-first-order rate constant and [L] is the concentration absorbed ligands that are bound to surface ions. Thus, the dissolution rate of a whole particle depends on the exposed surface area and will change over time. We assume that the rate constant for cell-controlled dissolution of iron is similar in order of magnitude, κL ≈ 10−6 s−1.
For perfectly packed spherical particles of size k, a rough approximation of the number of ions that are on the sphere surface can be found as the ratio of the total sphere surface divided by the cross section of a single ion:
In reality, nS(k) will depend on precise shape or crystal structure of the iron mineral. The dissolution of iron particles by cells will likely be slower than free ligand-controlled dissolution because surface-bound ligands or reductases will only be able to react with a subset, σ, of the particle surface:
As the particle is continuously dissolved, the surface to volume ratio increases, affecting the dissolution rate [67]. The expected dissolution time of an idealized k-particle would be
Thus, an upper bound for the rate at which a cell might dissolve an aggregate for k ≫ 1 is thus
4.1.3. Uptake
We assume that a cell can maintain ‘hold’ of a reservoir of iron aggregates it encounters as it is dissolving them (figure 2). The amount of iron aggregates, Ik(t), that are currently being processed by the cell then is determined by the number of aggregates that arrived due to diffusion, φk(t), and the rate at which the aggregates are dissolved by the cell, ψk(t):
| 4.3 |
Assuming that the dissolved iron is fully sequestered by the cell, the total amount of iron that is taken up into the cell follows
Using the approximation that φk is constant through time, Ik(t) has a simple solution
and, hence, the actual flux of iron into the cell is
| 4.4 |
The exponential term implies that the cell may eventually reach an iron uptake rate that is the same as the influx of new iron, but depending on the dissolution rate of aggregates, ψk, this maximum is only reached slowly.
Note that the maximal uptake flux given by equation (4.4) can only be achieved if the cell is able to concurrently process the required amount, Ik(t), of iron particles, which requires physical attachment to the aggregate. Equation (4.3) implies that the maximum number of iron particles that are processed by the cell simultaneously is
Owing to spacial constraints, the maximum number of aggregates that can surround a cell of radius RB is roughly
Thus, under the assumption that cells can completely surround themselves with iron aggregates, the necessary background concentration of iron to saturate the cell’s dissolution ability is
where the iron uptake rate under dissolution saturation is
We say that the cell is iron-diffusion limited if the maximal flux is smaller than the maximally possible transport rate, i.e. lim t→∞αk(t) = ϕk < αT (figure 2b).
Finally, the total amount of iron that is actually taken up by the cell starting with A(0) = 0 is
| 4.5 |
and the time, τ, required to take up a set amount of iron, A0, is then the solution to A(τ) = A0.
4.1.4. Radial concentration
The concentration of iron aggregates, Fk(r, t), can be equivalently represented as a spherically symmetrical diffusion process:
| 4.6 |
with an absorbing boundary at r = Rk, a reservoir at infinity, lim r→∞ Fk(r, t) = ρk = ρ0/k, and initial concentration Fk(r, 0) = ρk. The general equilibrium solution to equation (4.6) with ∂t Fk(r, t) = 0 is . The constant c is found by the boundary condition at r = Rk. On the one hand we require Fk(Rk, t)≥0, and thus c≤Rkρk. On the other hand, the iron uptake is limited by the maximal transport or dissolution rate. For a fully absorbing boundary, the flux across the cell surface is
and thus the maximal flux for cmax = Rkρk is , the same as the asymptotic limit of equation (4.2) divided by absorbing surface area. Under transport or dissolution limitation, and , respectively.
4.2. Siderophore-mediated uptake
4.2.1. Reaction–diffusion equations
The iron uptake by a single secreting cell is modelled as a reaction–diffusion process for free iron, F, unbound siderophores, X, ligated surface ions, E, and bound siderophores, Y:
| 4.7 |
| 4.8 |
| 4.9 |
and
| 4.10 |
Here, E0 is total amount of ions at the surface of the iron aggregates, . When we only consider a single cell, the system is spherically symmetric, such that (see also [21]). When a free siderophore encounters an iron aggregate, it must first bind to an ion of iron at the aggregate surface,
where refers to an unligated surface ion. Kraemer [10] describes this reaction as an adsorption reaction by ligand-exchange that proceeds forward with a pseudo second-order rate constant, κX. For high-affinity siderophores, κX is generally much higher than the reverse reaction rate, such that we ignore the reverse reaction, and use κX = 106 M−1s−1. The pseudo-first-order rate constant, κL, describes the dissolution of the siderophore–iron complex from the crystal lattice, and is of the order of κL ∼ 10−2 h−1 ∼ 10−6 s−1. Initially, iron is equally distributed in space at a concentration of F(r, 0) = ρ0 and there are no siderophores present, X(r, 0) = 0. We assume that the concentration of free and bound siderophores tends to zero far away from the cell, lim r→∞ X(r, t) = Y(r, t) = 0, and the concentration of iron is constant far away from the cell, lim r→∞ F(r, t) = ρ0. The uptake rate of iron–siderophore complexes by the cell is then just equal to the flux of Y at r = RB:
with a maximal transport-limited rate of αT as in the direct uptake case.
The system of reaction–diffusion equations cannot be solved analytically, but can be integrated numerically. To gain some analytical understanding of the equilibrium distributions, we consider some limiting cases of the reaction–diffusion system.
4.2.2. No reaction
In the absence of any reaction of siderophores with iron, κX = 0. In this case, the equilibrium solution for the distribution of free siderophores is
where P is the excretion rate of siderophores from the cell. Here, R∞ is the upper bound of the considered volume. For an open system, R∞ → ∞,
| 4.11 |
4.2.3. Large aggregation, slow dissolution
When the level of aggregation is large, then the diffusion of free iron is much slower than the diffusion of free siderophores. Furthermore, the dissolution of the ligated surface ions is generally slow, such that the distribution of free siderophores, X(r), equilibrates with the bound surface iron, E. Assuming that the iron aggregates are stationary (Dk = 0), we can calculate the radial distribution of bound surface irons as the solution to
such that
| 4.12 |
From this we can derive a characteristic radius below which E(r) ≈ E0 when there is sufficient iron and above which E(r) declines towards zero. Solving ,
4.2.4. Large aggregation, immediate dissolution
When the level of aggregation is large, then the diffusion of free iron is much slower than the diffusion of free siderophores. But since the concentration of siderophores decreases with distance from the cell as a consequence of the spherical dilution, there exists a boundary at , where the influx of free siderophores completely reacts with the influx of free iron.
Let ΔX = ϕXΔt and ΔF = ϕFΔt be the amount of X and F that enters a finite small volume during time Δt. Then the amount that reacts will be ΔY = κΔFΔX. We are interested in the case where all iron ΔF reacts with all siderophores ΔX, kΔXΔF = ΔF and kΔXΔF = ΔX, and hence, ΔF = ΔX, or, .
Iron diffuses to from above, and siderophores diffuse to from below. Thus for , the distribution of free siderophores follows equation (4.11) with . Equivalently, the distribution of iron for follows that of freely diffusing iron, . The fluxes are then
and
These are equal at
| 4.13 |
This defines a boundary at a distance from the cell. Below this radius, there are enough siderophores to bind all free iron and thus there is no free iron. Above this radius, all the siderophores have been bound. Hence at equilibrium, siderophore–iron complexes are only produced at this radius.
The distribution of siderophore–iron complexes above then is
Below , , where ,
Finally, this results in a flux at the cell of
| 4.14 |
This converges to the maximal direct uptake flux, J = ρ0 DF/RB, for secretion rates P ≫ DFρ0.
4.2.5. Fast diffusion, immediate dissolution
If the diffusion speed of free iron is fast compared to the reaction speed of siderophores, then the background concentration of free iron can be assumed constant. The reaction–diffusion equations then become
with κ0 = κρ0. The equilibrium solutions to these equations for boundary conditions limr→∞X(r) = limr→∞ = 0, ϕX(RB) = −DX∂r X(r = RB) = P and Y(RB) = 0 are (see [21])
Here, is the characteristic diffusion–reaction length of siderophores with the background iron. The derivative of Y is
Hence, as derived in [21], the maximum iron uptake rate is
| 4.15 |
and the peak in the distribution is at a distance r, where
| 4.16 |
4.3. Numerical integration of the partial differential equations
With exception of the single cell direct uptake case, no analytical solutions to the reaction–diffusion equations are available. We therefore numerically integrated the equations using a finite-elements approach implemented in the FEniCS project v. 2018.1.0.6 [68]. The FEniCS software suite uses the variational formulation of the PDEs on meshes.
4.3.1. Single cell
For the single cell case, we exploited the spherical symmetry and used a linear expanding mesh between RB = 1 µm and R∞ = 10 m, and m = 400 mesh intervals:
where Δr = (R∞ − RB)/m. We solved the PDEs over discrete increasing time steps, with Δt0 = 10−4 s and Δtj+1 = 1.2Δtj, with a maximum time step of 1000 s (see also electronic supplementary material).
4.3.2. Two cells
In the two cell case, the system only has cylindrical symmetry along the axis that connects the two cells:
We generated two-dimensional (z, r)-meshes using the following procedure: we first created a circular domain of radius ρ1 = 100 µm. We then removed two circular ‘cells’, with radius RB and varying distance d from each other, from the domain. The domain was then converted to a mesh using FEniCS with a mesh size of 10, and subsequently refining all mesh elements within the circle ρ = ρ1/2. The mesh was finally expanded to a full radius of ρ∞ = 0.1 m, by adding concentric circles of m2 = 24 mesh points at increasing radii ρj+1 = ρj(1 + 2π/m2). Finally, we integrated the two-dimensional reaction–diffusion equations using an increasing time step, Δt0 = 10−2 s and Δtj+1 = 1.2Δtj, with a maximum time step of 1000 s.
Supplementary Material
Acknowledgements
We thank Thierry Sollberger for help with designing figures 1 and 4. We also thank Roman Stocker, Laura Sigg, Stephan Kraemer and Mak Saito for helpful discussions.
Data accessibility
All simulation code is available at https://bitbucket.org/gaberoo/IronDolfin.
Authors' contributions
All authors conceived the model, interpreted the results and wrote the paper. K.T.S. formulated the initial question and context. G.E.L. performed the simulations and mathematical calculations.
Competing interests
We declare we have no competing interests.
Funding
G.E.L. was supported by the Swiss National Science Froundation (162251) and the Human Frontier Science Program (LT000643/2016-L). K.T.S. and M.A. were supported by Eawag and ETH Zurich. K.T.S. was further supported by the Swiss National Science Foundation (grant no. PP2EZP3-162260).
References
- 1.Griffin AS, West SA, Buckling A. 2004. Cooperation and competition in pathogenic bacteria. Nature 430, 1024–1027. ( 10.1038/nature02744) [DOI] [PubMed] [Google Scholar]
- 2.Drescher K, Nadell CD, Stone HA, Wingreen NS, Bassler BL. 2014. Solutions to the public goods dilemma in bacterial biofilms. Curr. Biol. 24, 50–55. ( 10.1016/j.cub.2013.10.030) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Pakulski JD, Coffin RB, Kelley CA, Holder SL, Downer R, Aas P, Lyons MM, Jeffrey WH. 1996. Iron stimulation of Antarctic bacteria. Nature 383, 133–134. ( 10.1038/383133b0) [DOI] [Google Scholar]
- 4.Hutchins DA, DiTullio GR, Zhang Y, Bruland KW. 1998. An iron limitation mosaic in the California upwelling regime. Limnol. Oceanogr. 43, 1037–1054. ( 10.4319/lo.1998.43.6.1037) [DOI] [Google Scholar]
- 5.Cochlan WP. 2001. The heterotrophic bacterial response during a mesoscale iron enrichment experiment (IronEx II) in the eastern equatorial Pacific Ocean. Limnol. Oceanogr. 46, 428–435. ( 10.4319/lo.2001.46.2.0428) [DOI] [Google Scholar]
- 6.Paradkar PN, De Domenico I, Durchfort N, Zohn I, Kaplan J, Ward DM. 2008. Iron depletion limits intracellular bacterial growth in macrophages. Blood 112, 866–874. ( 10.1182/blood-2007-12-126854) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Boyd PW, Ellwood MJ. 2010. The biogeochemical cycle of iron in the ocean. Nat. Geosci. 3, 675–682. ( 10.1038/ngeo964) [DOI] [Google Scholar]
- 8.Tagliabue A, Bowie AR, Boyd PW, Buck KN, Johnson KS, Saito MA. 2017. The integral role of iron in ocean biogeochemistry. Nature 543, 51–59. ( 10.1038/nature21058) [DOI] [PubMed] [Google Scholar]
- 9.Braun V, Killmann H. 1999. Bacterial solutions to the iron-supply problem. Trends Biochem. Sci. 24, 104–109. ( 10.1016/S0968-0004(99)01359-6) [DOI] [PubMed] [Google Scholar]
- 10.Kraemer S. 2004. Iron oxide dissolution and solubility in the presence of siderophores. Aquat. Sci. 66, 3–18. ( 10.1007/s00027-003-0690-5) [DOI] [Google Scholar]
- 11.Wu J, Boyle E, Sunda W, Wen LS. 2001. Soluble and colloidal iron in the oligotrophic North Atlantic and North Pacific. Science 293, 847–849. ( 10.1126/science.1059251) [DOI] [PubMed] [Google Scholar]
- 12.Fitzsimmons JN, Boyle EA. 2014. Both soluble and colloidal iron phases control dissolved iron variability in the tropical North Atlantic Ocean. Geochim. Cosmochim. Acta 125, 539–550. ( 10.1016/j.gca.2013.10.032) [DOI] [Google Scholar]
- 13.Johnson KS, Gordon RM, Coale KH. 1997. What controls dissolved iron concentrations in the world ocean? Mar. Chem. 57, 137–161. ( 10.1016/S0304-4203(97)00043-1) [DOI] [Google Scholar]
- 14.Hassler CS, Schoemann V, Nichols CM, Butler ECV, Boyd PW. 2011. Saccharides enhance iron bioavailability to Southern Ocean phytoplankton. Proc. Natl Acad. Sci. USA 108, 1076–1081. ( 10.1073/pnas.1010963108) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Salmon TP, Rose AL, Neilan BA, Waite TD. 2006. The FeL model of iron acquisition: nondissociative reduction of ferric complexes in the marine environment. Limnol. Oceanogr. 51, 1744–1754. ( 10.4319/lo.2006.51.4.1744) [DOI] [Google Scholar]
- 16.Kraemer SM. 2005. Siderophores and the dissolution of iron-bearing minerals in marine systems. Rev. Mineral. Geochem. 59, 53–84. ( 10.2138/rmg.2005.59.4) [DOI] [Google Scholar]
- 17.Bergquist BA, Wu J, Boyle EA. 2007. Variability in oceanic dissolved iron is dominated by the colloidal fraction. Geochim. Cosmochim. Acta 71, 2960–2974. ( 10.1016/j.gca.2007.03.013) [DOI] [Google Scholar]
- 18.Fitzsimmons JN, Carrasco GG, Wu J, Roshan S, Hatta M, Measures CI, Conway TM, John SG, Boyle EA. 2015. Partitioning of dissolved iron and iron isotopes into soluble and colloidal phases along the GA03 GEOTRACES North Atlantic Transect. Deep Sea Res. Part 2 Top. Stud. Oceanogr. 116, 130–151. ( 10.1016/j.dsr2.2014.11.014) [DOI] [Google Scholar]
- 19.von der Heyden BP, Roychoudhury AN, Mtshali TN, Tyliszczak T, Myneni SCB. 2012. Chemically and geographically distinct solid-phase iron pools in the Southern Ocean. Science 338, 1199–1201. ( 10.1126/science.1227504) [DOI] [PubMed] [Google Scholar]
- 20.Hider RC, Kong X. 2010. Chemistry and biology of siderophores. Nat. Prod. Rep. 27, 637–657. ( 10.1039/b906679a) [DOI] [PubMed] [Google Scholar]
- 21.Völker C, Wolf-Gladrow DA. 1999. Physical limits on iron uptake mediated by siderophores or surface reductases. Mar. Chem. 65, 227–244. ( 10.1016/S0304-4203(99)00004-3) [DOI] [Google Scholar]
- 22.Hutchins DA, Rueter JG, Fish W. 1991. Siderophore production and nitrogen fixation are mutually exclusive strategies in Anabaena 712. Limnol. Oceanogr. 36, 1–12. ( 10.4319/lo.1991.36.1.0001) [DOI] [Google Scholar]
- 23.De Vos D, De Chial M, Cochez C, Jansen S, Tümmler B, Meyer JM, Cornelis P. 2001. Study of pyoverdine type and production by Pseudomonas aeruginosa isolated from cystic fibrosis patients: prevalence of type II pyoverdine isolates and accumulation of pyoverdine-negative mutations. Arch. Microbiol. 175, 384–388. ( 10.1007/s002030100278) [DOI] [PubMed] [Google Scholar]
- 24.West SA, Buckling A. 2003. Cooperation, virulence and siderophore production in bacterial parasites. Proc. R. Soc. Lond. B 270, 37–44. ( 10.1098/rspb.2002.2209) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Velicer GJ. 2003. Social strife in the microbial world. Trends Microbiol. 11, 330–337. ( 10.1016/S0966-842X(03)00152-5) [DOI] [PubMed] [Google Scholar]
- 26.Boiteau RM, Mende DR, Hawco NJ, McIlvin MR, Fitzsimmons JN, Saito MA, Sedwick PN, DeLong EF, Repeta DJ. 2016. Siderophore-based microbial adaptations to iron scarcity across the eastern Pacific Ocean. Proc. Natl Acad. Sci. USA 113, 14 237–14 242. ( 10.1073/pnas.1608594113) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Martinez JS, Zhang GP, Holt PD, Jung HT, Carrano CJ, Haygood MG, Butler A. 2000. Self-assembling amphiphilic siderophores from marine bacteria. Science 287, 1245–1247. ( 10.1126/science.287.5456.1245) [DOI] [PubMed] [Google Scholar]
- 28.Martinez JS, Carter-Franklin JN, Mann EL, Martin JD, Haygood MG, Butler A. 2003. Structure and membrane affinity of a suite of amphiphilic siderophores produced by a marine bacterium. Proc. Natl Acad. Sci. USA 100, 3754–3759. ( 10.1073/pnas.0637444100) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Xu G, Martinez JS, Groves JT, Butler A. 2002. Membrane affinity of the amphiphilic marinobactin siderophores. J. Am. Chem. Soc. 124, 13 408–13 415. ( 10.1021/ja026768w) [DOI] [PubMed] [Google Scholar]
- 30.Kümmerli R, Schiessl KT, Waldvogel T, McNeill K, Ackermann M. 2014. Habitat structure and the evolution of diffusible siderophores in bacteria. Ecol. Lett. 17, 1536–1544. ( 10.1111/ele.2014.17.issue-12) [DOI] [PubMed] [Google Scholar]
- 31.Hopkinson BM, Barbeau KA. 2012. Iron transporters in marine prokaryotic genomes and metagenomes. Environ. Microbiol. 14, 114–128. ( 10.1111/j.1462-2920.2011.02539.x) [DOI] [PubMed] [Google Scholar]
- 32.Hogle SL, Thrash JC, Dupont CL, Barbeau KA. 2016. Trace metal acquisition by marine heterotrophic bacterioplankton with contrasting trophic strategies. Appl. Environ. Microbiol. 82, 1613–1624. ( 10.1128/AEM.03128-15) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Shaked Y, Lis H. 2012. Disassembling iron availability to phytoplankton. Front. Microbiol. 3, 123 ( 10.3389/fmicb.2012.00123) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Kuhn KM, DuBois JL, Maurice PA. 2013. Strategies of aerobic microbial Fe acquisition from Fe-bearing montmorillonite clay. Geochim. Cosmochim. Acta 117, 191–202. ( 10.1016/j.gca.2013.04.028) [DOI] [Google Scholar]
- 35.Kranzler C, Kessler N, Keren N, Shaked Y. 2016. Enhanced ferrihydrite dissolution by a unicellular, planktonic cyanobacterium: a biological contribution to particulate iron bioavailability. Environ. Microbiol. 18, 5101–5111. ( 10.1111/1462-2920.13496) [DOI] [PubMed] [Google Scholar]
- 36.Andrews SC, Robinson AK, Rodriguez-Quiñones F. 2003. Bacterial iron homeostasis. FEMS Microbiol. Rev. 27, 215–237. ( 10.1016/S0168-6445(03)00055-X) [DOI] [PubMed] [Google Scholar]
- 37.Marshall B, Stintzi A, Gilmour C, Meyer JM, Poole K. 2009. Citrate-mediated iron uptake in Pseudomonas aeruginosa: involvement of the citrate-inducible FecA receptor and the FeoB ferrous iron transporter. Microbiology 155, 305–315. ( 10.1099/mic.0.023531-0) [DOI] [PubMed] [Google Scholar]
- 38.Sandy M, Butler A. 2009. Microbial iron acquisition: marine and terrestrial siderophores. Chem. Rev. 109, 4580–4595. ( 10.1021/cr9002787) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Miethke M, Marahiel MA. 2007. Siderophore-based iron acquisition and pathogen control. Microbiol. Mol. Biol. Rev. 71, 413–451. ( 10.1128/MMBR.00012-07) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Zhao CM, Campbell PG, Wilkinson KJ. 2016. When are metal complexes bioavailable? Environ. Chem. 13, 425–433. ( 10.1071/EN15205) [DOI] [Google Scholar]
- 41.Worms I, Simon DF, Hassler CS, Wilkinson KJ. 2006. Bioavailability of trace metals to aquatic microorganisms: importance of chemical, biological and physical processes on biouptake. Biochimie 88, 1721–1731. ( 10.1016/j.biochi.2006.09.008) [DOI] [PubMed] [Google Scholar]
- 42.Buffle J, Wilkinson KJ, Van Leeuwen HP. 2009. Chemodynamics and bioavailability in natural waters. Environ. Sci. Technol. 43, 7170–7174. ( 10.1021/es9013695) [DOI] [PubMed] [Google Scholar]
- 43.Cornell RM, Giovanoli R, Schneider W. 1989. Review of the hydrolysis of iron(III) and the crystallization of amorphous iron(III) hydroxide hydrate. J. Chem. Technol. Biotechnol. 46, 115–134. ( 10.1002/jctb.280460204) [DOI] [Google Scholar]
- 44.Schwertmann U, Friedl J, Stanjek H. 1999. From Fe(III) ions to ferrihydrite and then to hematite. J. Colloid Interface Sci. 209, 215–223. ( 10.1006/jcis.1998.5899) [DOI] [PubMed] [Google Scholar]
- 45.Melton ED, Swanner ED, Behrens S, Schmidt C, Kappler A. 2014. The interplay of microbially mediated and abiotic reactions in the biogeochemical Fe cycle. Nat. Rev. Microbiol. 12, 797–808. ( 10.1038/nrmicro3347) [DOI] [PubMed] [Google Scholar]
- 46.Jannasch HW. 1969. Estimations of bacterial growth rates in natural waters. J. Bacteriol. 99, 156–160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Kirchman DL. 2016. Growth rates of microbes in the oceans. Ann. Rev. Mar. Sci. 8, 285–309. ( 10.1146/annurev-marine-122414-033938) [DOI] [PubMed] [Google Scholar]
- 48.Brockhurst MA, Buckling A, Racey D, Gardner A. 2008. Resource supply and the evolution of public-goods cooperation in bacteria. BMC Biol. 6, 20 ( 10.1186/1741-7007-6-20) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Kümmerli R, Brown SP. 2010. Molecular and regulatory properties of a public good shape the evolution of cooperation. Proc. Natl Acad. Sci. USA 107, 18 921–18 926. ( 10.1073/pnas.1011154107) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Dumas Z, Kümmerli R. 2012. Cost of cooperation rules selection for cheats in bacterial metapopulations. J. Evol. Biol. 25, 473–484. ( 10.1111/jeb.2012.25.issue-3) [DOI] [PubMed] [Google Scholar]
- 51.Granger J, Price NM. 1999. The importance of siderophores in iron nutrition of heterotrophic marine bacteria. Limnol. Oceanogr. 44, 541–555. ( 10.4319/lo.1999.44.3.0541) [DOI] [Google Scholar]
- 52.Vraspir JM, Butler A. 2009. Chemistry of marine ligands and siderophores. Ann. Rev. Mar. Sci. 1, 43–63. ( 10.1146/annurev.marine.010908.163712) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Kloepper JW, Leong J, Teintze M, Schroth MN. 1980. Enhanced plant growth by siderophores produced by plant growth-promoting rhizobacteria. Nature 286, 885–886. ( 10.1038/286885a0) [DOI] [Google Scholar]
- 54.Cordero OX, Ventouras LA, DeLong EF, Polz MF. 2012. Public good dynamics drive evolution of iron acquisition strategies in natural bacterioplankton populations. Proc. Natl Acad. Sci. USA 109, 20 059–20 064. ( 10.1073/pnas.1213344109) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Schiessl KT, Janssen EML, Kraemer SM, McNeill K, Ackermann M. 2017. Magnitude and mechanism of siderophore-mediated competition at low iron solubility in the Pseudomonas aeruginosa pyochelin system. Front. Microbiol. 8, 1964 ( 10.3389/fmicb.2017.01964) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Kümmerli R, Griffin AS, West SA, Buckling A, Harrison F. 2009. Viscous medium promotes cooperation in the pathogenic bacterium Pseudomonas aeruginosa. Proc. R. Soc. B. 276, 3531–3538. ( 10.1098/rspb.2009.0861) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Allen B, Gore J, Nowak MA. 2013. Spatial dilemmas of diffusible public goods. Elife 2, e01169 ( 10.7554/eLife.01169) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Nadell CD, Foster KR, Xavier JB. 2010. Emergence of spatial structure in cell groups and the evolution of cooperation. PLoS Comput. Biol. 6, e1000716 ( 10.1371/journal.pcbi.1000716) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Julou T, Mora T, Guillon L, Croquette V, Schalk IJ, Bensimon D, Desprat N. 2013. Cell-cell contacts confine public goods diffusion inside Pseudomonas aeruginosa clonal microcolonies. Proc. Natl Acad. Sci. USA 110, 12 577–12 582. ( 10.1073/pnas.1301428110) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Vetter Y, Deming J, Jumars P, Krieger-Brockett B. 1998. A predictive model of bacterial foraging by means of freely released extracellular enzymes. Microb. Ecol. 36, 75–92. ( 10.1007/s002489900095) [DOI] [PubMed] [Google Scholar]
- 61.Allison SD. 2005. Cheaters, diffusion and nutrients constrain decomposition by microbial enzymes in spatially structured environments. Ecol. Lett. 8, 626–635. ( 10.1111/ele.2008.8.issue-6) [DOI] [Google Scholar]
- 62.Folse HJ III, Allison SD. 2012. Cooperation, competition, and coalitions in enzyme-producing microbes: social evolution and nutrient depolymerization rates. Front. Microbiol. 3, 338 ( 10.3389/fmicb.2012.00338) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Dobay A, Bagheri HC, Messina A, Kümmerli R, Rankin DJ. 2014. Interaction effects of cell diffusion, cell density and public goods properties on the evolution of cooperation in digital microbes. J. Evol. Biol. 27, 1869–1877. ( 10.1111/jeb.2014.27.issue-9) [DOI] [PubMed] [Google Scholar]
- 64.Bundy RM, Boiteau RM, McLean C, Turk-Kubo KA, McIlvin MR, Saito MA, Van Mooy BAS, Repeta DJ. 2018. Distinct siderophores contribute to iron cycling in the mesopelagic at station ALOHA. Front. Mar. Sci. 5, 61 ( 10.3389/fmars.2018.00061) [DOI] [Google Scholar]
- 65.Crank J. 1975. The mathematics of diffusion, 2nd edn Oxford, UK: Clarendon Press. [Google Scholar]
- 66.Frazier Z, Alber F. 2012. A computational approach to increase time scales in Brownian dynamics-based reaction-diffusion modeling. J. Comput. Biol. 19, 606–618. ( 10.1089/cmb.2012.0027) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Schwertmann U. 1991. Solubility and dissolution of iron oxides. Plant Soil 130, 1–25. ( 10.1007/BF00011851) [DOI] [Google Scholar]
- 68.Logg A, Mardal KA, Wells GN. 2012. Automated solution of differential equations by the finite element method. Berlin, Germany: Springer. [Google Scholar]
- 69.Alnæs M. et al. 2015. The FEniCS Project version 1.5. Arch. Numer. Softw. 3, 9–23. [Google Scholar]
- 70.Fgaier H, Eberl HJ. 2010. A competition model between Pseudomonas fluorescens and pathogens via iron chelation. J. Theor. Biol. 263, 566–578. ( 10.1016/j.jtbi.2009.12.003) [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
All simulation code is available at https://bitbucket.org/gaberoo/IronDolfin.