The foot is more than a spring: human foot muscles perform work to adapt to the energetic requirements of locomotion

Abstract

The foot has been considered both as an elastic mechanism that increases the efficiency of locomotion by recycling energy, as well as an energy sink that helps stabilize movement by dissipating energy through contact with the ground. We measured the activity of two intrinsic foot muscles, flexor digitorum brevis (FDB) and abductor hallucis (AH), as well as the mechanical work performed by the foot as a whole and at a modelled plantar muscle–tendon unit (MTU) to test whether these passive mechanics are actively controlled during stepping. We found that the underlying passive visco-elasticity of the foot is modulated by the muscles of the foot, facilitating both dissipation and generation of energy depending on the mechanical requirements at the centre of mass (COM). Compared to level ground stepping, the foot dissipated and generated an additional –0.2 J kg⁻¹ and 0.10 J kg⁻¹ (both p < 0.001) when stepping down and up a 26 cm step respectively, corresponding to 21% and 10% of the additional net work performed by the leg on the COM. Of this compensation at the foot, the plantar MTU performed 30% and 89% of the work for step-downs and step-ups, respectively. This work occurred early in stance and late in stance for stepping down respectively, when the activation levels of FDB and AH were increased between 69 and 410% compared to level steps (all p < 0.001). These findings suggest that the energetic function of the foot is actively modulated by the intrinsic foot muscles and may play a significant role in movements requiring large changes in net energy such as stepping on stairs or inclines, accelerating, decelerating and jumping.

1. Introduction

Steady-state human locomotion is characterized by spring-like mechanics and net zero mechanical work [1,2]. This spring-like function greatly improves locomotion economy, by using elastic elements such as long tendons in the legs to recycle mechanical energy [2–4]. The foot is a deformable structure that bends, stretches and recoils when the foot contacts the ground [2]. This foot-spring mechanism, enabled by the elastic plantar aponeurosis (PA), is reported to provide between 8 and 17% of the mechanical energy required for a stride [5,6]. However, this fundamental spring-like behaviour must be adapted when an acceleration or deceleration is required, via concentric or eccentric muscle contraction [7–10]. The ability to adapt mechanical function greatly enhances the versatility of human locomotion, but for the foot to adapt, it cannot be simply a passive spring.

The depiction of the foot as an elastic spring is based on in situ cadaveric observations of the PA straining in response to longitudinal arch (LA) compression and recoiling as the LA rebounds [6]. Recent in vivo evidence suggests that the energetic behaviour of the foot during constant speed locomotion is more akin to that of a viscous spring–damper system, rather than a purely elastic spring [11,12]. We have recently shown that a greater proportion of absorbed energy is dissipated by structures within the foot at higher running speeds [11]. When running at 2.2 m s⁻¹ approximately 30% of absorbed energy is dissipated. This number increases to 63% when running at 4.4 m s⁻¹, equating to 0.44 J kg⁻¹ of energy dissipated within the foot. Given the elastic nature of the PA, it is unlikely that this tissue has the capacity to dissipate such large magnitudes of energy [6,13]. The plantar fat pads of the heel and forefoot are known to have viscous damping properties and are likely to contribute to some energy dissipation within the foot [14,15]. However, these tissues operate near maximal deformation in locomotion, with the magnitude of energy dissipation limited to approximately 0.03 J kg⁻¹ [14], considerably less than that observed during running. It is therefore difficult to explain the amount of observed dissipation at the foot from passive structures alone.

An alternative explanation is that muscles acting on the foot can actively modulate energetic behaviour of the foot during locomotion. It has long been known that these muscles activate during various locomotor tasks [16–18]. Eccentric contractions could facilitate damping of energy during the rapid deceleration associated with the collision of the foot and the ground [19,20]. Furthermore, concentric actions may provide positive power for accelerations, in synergy with the ankle, knee and hip [7,9,21]. The plantar intrinsic foot muscles are a group of muscles with anatomical origins and insertions located within the foot. The largest of these muscles, abductor hallucis (AH) and flexor digitorum brevis (FDB), have muscle–tendon units (MTUs) that span the length of the LA and metatarsophalangeal (MTP) joints, coursing a parallel pathway to the PA [22]. The MTUs of AH and FDB actively lengthen and shorten during the stance phase, and thus have the capacity to perform negative and positive work at the foot [23,24]. While there is some indirect evidence to suggest that the energetic function of the foot is adaptable during locomotion [11,25], it remains unclear as to the specific role of the intrinsic foot muscles in mediating this function.

Therefore, the aim of this study was to test the hypothesis that the energetic function of the foot could be modulated from that of a spring, to a damper or motor, depending on the mechanical requirements of the locomotor task. In particular, because passive structures are unable to generate net positive work, a result showing the foot performing net positive work would definitively show that the foot muscles not only modulate an effective stiffness within the foot but also modify the energy of the body to achieve non-steady-state locomotor goals. To test this hypothesis, we had 10 healthy participants perform stepping tasks that required either net negative, net zero or net positive work to be performed at the centre of mass (COM). In order to quantify the energetic function of the foot and the contribution of the intrinsic foot muscles, we applied a series of modelling approaches to estimate work performed at the foot, the LA (hereon referred to as the foot arch) and MTP joints. The activation patterns of the FDB and AH were recorded to test whether changes in mechanical work at the foot corresponded to changes in muscle activation.

2. Material and methods

2.1. Participants

Eight male and two female subjects volunteered to participate in the study (age: 24.9 ± 5.8 years; height: 179 ± 7.0 cm; mass: 79.9 ± 13.0 kg), with written consent obtained from each participant. Selection criteria for participants required that they had no lower limb injury within the last six months and no known neurological impairments.

2.2. Experimental set-up

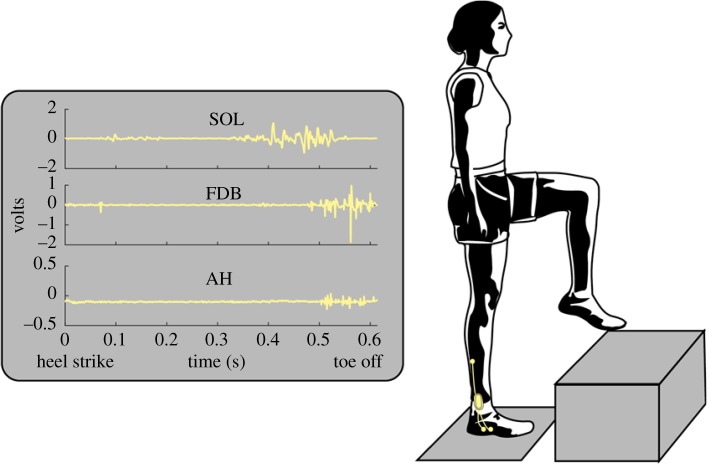
Participants performed three experimental conditions in a counter-balanced order, consisting of (1) level stepping, (2) stepping up and (3) stepping down. The experimental conditions were designed to induce a requirement for the COM to perform either positive work (step-ups) or negative work (step-downs). The level stepping condition was included as a control condition with close to net zero mechanical work being performed. Each condition began with participants standing stationary in a relaxed position on a walking track with two embedded in-ground force plates. For the level stepping task, participants started behind the first force plate, took a step with their right foot onto the first force plate and continued walking forwards over the second force plate. The speed at which they took the steps was self-selected and not constrained across conditions. The trial was completed when the participant was completely off both force plates, at which point they would return to their starting position. For the stepping up and stepping down trials, timber platforms (0.26 m height) were moved into place on one of the force plates. For the step-ups, participants started on the level ground behind both force plates, landed with their right foot on the force plate, then stepped up to the raised platform landing on their left foot, before coming to a rest with both feet on the raised platform. For the step-downs, participants started on the raised platform and then stepped down with their right foot before continuing forward and coming to a rest after moving over the second force plate. For all conditions, the stepping task was repeated over a 90-s period, resulting in 10–15 steps being recorded. For each condition, the analysis was conducted on the step in which only the right foot landed on a force plate. See figure 1 for an illustration of a subject stepping up.

Figure 1.

A depiction of a participant taking a step-up and representative EMG recording of the soleus (SOL), flexor digitorum brevis (FDB) and abductor hallucis (AH) during the stance phase of the right foot on the level ground during the stance phase of a step-up. Participants also took level steps and step-downs. For the step-downs, the step analysed was the step where the foot landed on the level force plate starting from the elevated position. (Online version in colour.)

2.3. Data collection and processing

2.3.1. Muscle activation measurements

Activation of the AH and FDB muscles was recorded during the stepping tasks using fine-wire electromyography (EMG), according to previously described techniques [26]. Fine-wire electrode insertions were performed under sterile conditions using ultrasound guidance (10 MHz linear array, SonixTouch, Ultrasonix, BC, Canada) in the right foot of each subject. All EMG signals were collected at 4 kHz, amplified 1000 times and recorded with a bandwidth of 30–1000 Hz (MA300, Motion Labs, LA, USA). Surface EMG data were also collected from the soleus (SOL) muscle in the right leg using Ag–AgCl electrodes with a 20 mm inter-electrode distance (Tyco Healthcare Group, Neustadt, Germany). In order to prevent movement artefacts, the fine-wire electrodes, connectors, cabling and pre-amplifiers were secured with a cohesive bandage around the distal part of the shank. A surface ground electrode of the same type and size was secured to the skin overlying the fibula head on the ipsilateral limb. See figure 1 for a representative trial of raw EMG data for SOL, FDB and AH.

All EMG signals were high-pass filtered using a recursive second-order Butterworth filter at 5 Hz to remove any unwanted low-frequency movement artefact. Following DC-offset removal, root mean square (RMS) signal amplitude was calculated using a moving window of 25 ms to generate an EMG RMS envelope for each step. The EMG envelope for each muscle was normalized to the peak RMS amplitude found across all conditions for the respective muscle, to provide a range of activation from 0 to 100%. The mean level of the activation during the first and final 50% of stance phase (in terms of time between foot contact and toe off) was used as a measure of overall activation to compare activation differences across conditions.

2.3.2. Motion and force data

An eight-camera three-dimensional optoelectronic motion capture system (Qualysis, Gothenburg, Sweden) was used to capture the three-dimensional motion of the right foot, shank, thigh and pelvis. Retro-reflective markers were placed on bony landmarks of the right foot in accordance with a previously described multi-segment foot model, developed to describe rearfoot and forefoot motion [23,27]. Additional markers were placed on the second and fourth toes for the purpose of building an MTU model for the intrinsic foot muscles [23]. Rigid clusters of four markers were adhered to the shank and thigh. Additional markers were placed on the medial and lateral malleolus and medial and lateral femoral epicondyles. During a standing calibration trial, markers located on the respective segment endpoints were used to generate a model of the shank and thigh. The pelvis was modelled and tracked by placing markers on the left and right anterior superior iliac spine and posterior superior iliac spines. Following the calibration trial, the medial and lateral knee markers were removed and the motion of the shank and thigh was tracked using the rigid marker cluster located on each segment. Markers were adhered with double-sided adhesive and further secured with a cohesive bandage, allowing secure positioning for all conditions. Markers were not removed between experimental trials.

Ground reaction force data were collected synchronously with the motion capture data, from two sequential in-ground force plates (OR 6-7, AMTI, MA, USA). Both force and motion data were low-pass filtered using a fourth-order Butterworth filter, with a cut-off of 30 Hz to preserve higher frequency collision dynamics during down steps. Stance phase was defined as the period in which the measured vertical force of the force plate exceeded 20 N, with the beginning and end of stance defined as foot contact and toe off, respectively.

2.3.3. Ground force assignments to foot segments

When the foot is flat on the ground, forces are distributed across the entire foot, making it difficult to quantify the magnitude of forces acting on individual foot segments (rearfoot, forefoot and toes). In order to overcome this technical limitation, we applied a weighted probability algorithm to instantaneously assign the relative proportion of the ground reaction force acting at each of the three foot segments (rearfoot, forefoot and toes) during the stepping cycle. This equation is described in detail in appendix A. Briefly, the amount of force assigned to each segment depended on the height of the segment and its proximity to the centre of pressure (COP). Additionally, the amount of the force assigned to the rearfoot after the COP had progressed past the MTP joint was set to zero, as the rearfoot was not in contact with the ground, and the weighting prior to that moment was rescaled such that there was no instantaneous jump in force.

2.3.4. Joint kinetics

An inverse dynamic solution was applied using custom software developed in Matlab (Mathworks, Nattick, MD, USA). Each of the four segments in the foot model (three in the right foot, one for the shank) were modelled as rigid bodies connected to each other by 6-DOF joints, which have been shown to help account for inaccurate joint-centre determination [20,28–30]. The mass of the entire foot was estimated using foot landmarks and data from cadavers as described previously [31], with 50% of the mass assigned to the rearfoot, 40% to the forefoot and 10% to the toes. The inertia of each segment was estimated by forming a truncated cone based on marker locations at the proximal and distal ends of the segment and assuming a uniform density distribution across the cone's volume. Joint moments and joint forces were calculated using the Newton–Euler equations, in which the only forces acting on a segment were assumed to be gravity, proximal and distal joints and contact forces with the ground for the three segments of the foot. Joint moments presented are those in the sagittal plane, which were much larger than the moments of the joints in the transverse and coronal planes. Joint power was calculated as the dot product of the joint torque and joint angular velocity, summed with the dot product of the joint force and relative velocity of the joint between the two segments. This measure of joint power estimates the total energetics of the joint in all three rotational planes in addition to translational components. To estimate the total work performed by the leg, we calculated COM work rate [32], taking the dot product of the ground reaction force under the measured leg and the COM velocity as measured by motion capture.

To estimate the energetic function of the foot, three different methods were implemented. Firstly, the individual joint powers generated at the MTP and foot arch were summed to represent a joint-level estimate of foot power. Secondly, using estimates for speed and force as described in the next section, the work performed by the plantar MTU was calculated. Thirdly, we applied a unified deformable segment analysis to quantify the instantaneous power of the foot as it interacts with the ground, as explained previously [11,12], termed the foot contact model.

2.3.5. Muscle–tendon unit kinematics and kinetics

The length of a plantar MTU was estimated in accordance with a previously described geometric model, based on foot segment motion [23]. The length of the plantar MTU was estimated as the distance between insertions on the calcaneus and phalanges, wrapped about a point slightly inferior to the MTP joint. The distance is the average between paths wrapped about the first and fourth metatarsal. The force of the plantar MTU was estimated as the foot arch joint moment divided by the distance between the foot arch joint and the insertion of the plantar MTU on the calcaneus. Only the portion of the foot arch moment orthogonal to the action of the plantar MTU was used in this calculation, because it would be impossible for the MTU to produce moments about the same axis through which it acts. Owing to the close anatomical proximity between the two tissues, the plantar MTU is a representation of a structure that incorporates the PA and intrinsic foot muscle MTU.

2.4. Statistics

A one-way repeated measures analysis of variance (ANOVA) was used to describe the effects of stepping mode on muscle activation, mechanical and energetic measures. Post hoc t-tests with Bonferroni corrections for multiple comparisons were used to compare between specific stepping mode (Down versus Level, Up versus Level, Down versus Up). Statistical significance was established at p ≤ 0.05. All numerical results are presented as mean difference ± the standard deviation.

3. Results

3.1. Muscle activation

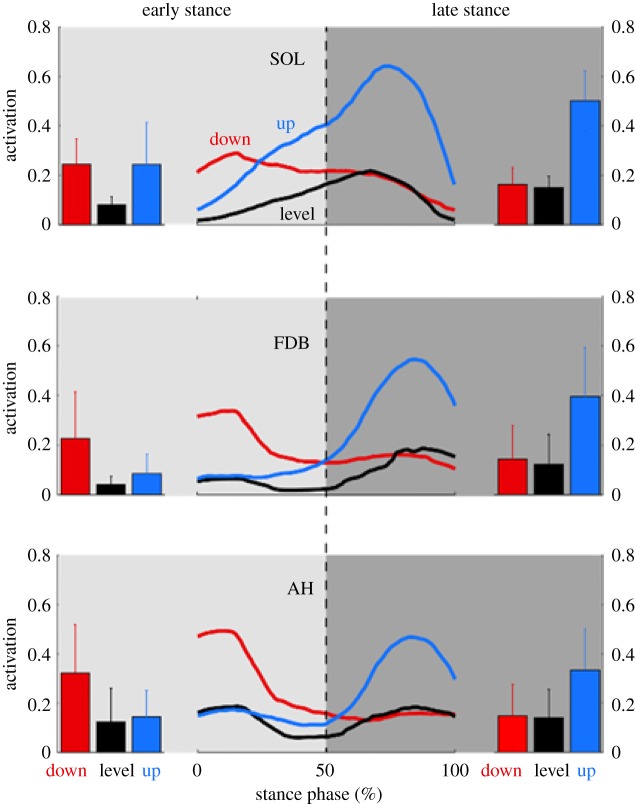
When stepping down, peak muscle activation was observed at the beginning of stance in SOL, FDB and AH. When stepping up, peak activation was observed in terminal stance, prior to propulsion, for all three muscles (figure 2). During the level stepping task, small peaks in muscle activation occurred in early and late stance for both AH and FDB, while SOL displayed a single activation peak in late stance. There was a significant effect of stepping mode on mean EMG RMS amplitude for all three muscles, during the first and the second half of stance phase (all p ≤ 0.05, table 1). During the first half of stance, SOL activation was significantly greater when stepping down, compared to level stepping (p ≤ 0.05), but not between stepping down and stepping up (p = 0.09), despite differences in the phasic pattern of activation. FDB and AH activity was greater when stepping down compared to level stepping and stepping up during the first half of stance (all p ≤ 0.05). During the second half of stance, mean activation was greater in the stepping up condition, compared to both the level stepping and stepping down conditions for all muscles (all p ≤ 0.05).

Figure 2.

Normalized activation of the soleus, flexor digitorum brevis (FDB) and abductor hallucis (AH) muscles during stance phase across 10 subjects. Normalized per subject by maximum activation during stance phase across all steps. Activation is compared between level ground steps (black), stepping down (red) and stepping up (blue). Bar plots on left-hand and right-hand side show mean and standard deviations of activations during the first and final 50% of stance phase, respectively. (Online version in colour.)

Table 1.

Mean ± standard deviation for muscle activation data.

				p-value
	down	level	up	D versus L	D versus U	L versus U
absorption phase
soleus (% max)	0.277 ± 0.11	0.0809 ± 0.038	0.222 ± 0.16	4 × 10−12	0.087	3 × 10−7
flexor digitorum brevis (% max)	0.254 ± 0.22	0.0416 ± 0.033	0.094 ± 0.068	9 × 10−11	6 × 10−7	0.22
abductor hallucis (% max)	0.353 ± 0.21	0.131 ± 0.15	0.143 ± 0.11	1 × 10−8	6 × 10−8	1
propulsion phase
soleus (% max)	0.186 ± 0.067	0.148 ± 0.045	0.505 ± 0.11	4 × 10−12	0.087	3 × 10−7
flexor digitorum brevis (% max)	0.157 ± 0.15	0.115 ± 0.11	0.443 ± 0.16	9 × 10−11	6 × 10−7	0.22
abductor hallucis (% max)	0.163 ± 0.14	0.147 ± 0.12	0.397 ± 0.13	1 × 10−8	6 × 10−8	1

*Denotes significant difference in pairwise comparisons between running speeds, p ≤ 0.05.

3.2. Joint mechanics

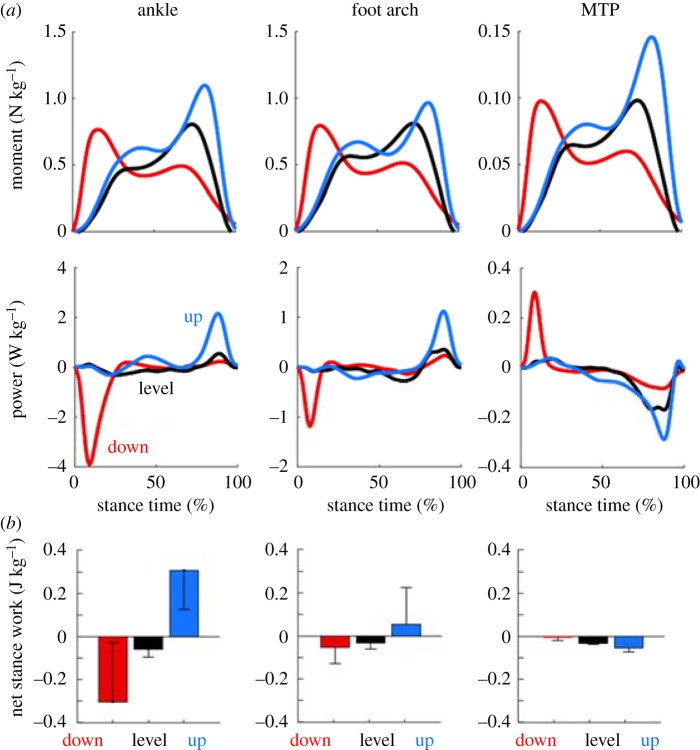
The moments generated about the ankle, foot arch and MTP joints were markedly similar, characterized by peaks in the extension moment in early and late stance (figure 3). When stepping down, the maximum extension moment occurred in early stance, following foot–ground collision. When stepping up, maximum extension moment occurred during late stance phase, prior to propulsion. While the general pattern of torque production was similar between joints, the magnitude of MTP moments was approximately 10% of the moments at the foot arch. There was a significant effect of stepping mode on peak joint moment for the ankle, foot arch and MTP joints (all p ≤ 0.05, table 2). Peak joint moment in level stepping was significantly less than the stepping up and stepping down tasks, for all joints (all p ≤ 0.05, table 2). Peak joint moment was similar between the stepping up and stepping down conditions, despite the differences in timing of the peak moment (figure 3).

Figure 3.

(a) Joint moments and powers of the foot averaged across 10 subjects. Positive and negative moments correspond to extension and flexion respectively. (b) Net joint work performed by each joint during the stance phase for each condition. (Online version in colour.)

Table 2.

Mean ± standard deviation for mechanics and energetics data.

				p-value
	down	level	up	D versus L	D versus U	L versus U
joint moments
ankle (Nm kg−1)	1.06 ± 0.25	0.85 ± 0.17	1.18 ± 0.23	1 × 10−4	0.046	1 × 10−9
foot arch (Nm kg−1)	1.09 ± 0.24	0.86 ± 0.12	1.03 ± 0.26	5 × 10−6	0.6	0.001
MTP (Nm kg−1)	0.13 ± 0.03	0.10 ± 0.01	0.14 ± 0.03	0.0004	0.008	3 × 10−10
joint work
ankle negative work (J kg−1)	−0.43 ± 0.23	−0.11 ± 0.03	−0.11 ± 0.06	2 × 10−15	6 × 10−15	1
ankle positive work (J kg−1)	0.10 ± 0.08	0.08 ± 0.0	0.39 ± 0.16	0.74	7 × 10−21	2 × 10−23
ankle net work (J kg−1)	−0.33 ± 0.19	−0.04 ± 0.03	0.29 ± 0.14	7 × 10−14	5 × 10−33	2 × 10−12
foot arch negative work (J kg−1)	−0.12 ± 0.04	−0.08 ± 0.02	−0.10 ± 0.14	0.29	1	0.06
foot arch positive work (J kg−1)	0.06 ± 0.03	0.06 ± 0.02	0.16 ± 0.06	1	5 × 10−14	5 × 10−16
foot arch net work (J kg−1)	−0.06 ± 0.03	−0.03 ± 0.02	0.06 ± 0.10	0.17	6 × 10−6	0.008
MTP negative work (J kg−1)	−0.02 ± 0.01	−0.04 ± 0.01	−0.06 ± 0.02	2 × 10−5	3 × 10−18	3 × 10−7
MTP positive work (J kg−1)	0.02 ± 0.01	0.01 ± 0.003	0.01 ± 0.01	4 × 10−14	2 × 10−7	0.009
MTP net work (J kg−1)	0.00 ± 0.01	−0.03 ± 0.01	−0.05 ± 0.02	6 × 10−20	2 × 10−29	4 × 10−4
leg negative work (J kg−1)	−1.15 ± 0.54	−0.43 ± 0.10	−0.18 ± 0.14	3 × 10−14	6 × 10−20	0.06
leg positive work (J kg−1)	0.21 ± 0.29	0.07 ± 0.03	0.68 ± 0.48	0.12	7 × 10−9	1 × 10−13
leg net work (J kg−1)	−0.94 ± 0.32	−0.36 ± 0.11	0.50 ± 0.47	8 × 10−9	8 × 10−34	1 × 10−18
MTU negative work (J kg−1)	−0.10 ± 0.05	−0.03 ± 0.01	−0.04 ± 0.01	2 × 10−14	3 × 10−14	1
MTU positive work (J kg−1)	0.06 ± 0.04	0.05 ± 0.01	0.11 ± 0.04	0.03	0.002	4 × 10−8
MTU net work (J kg−1)	−0.04 ± 0.05	0.01 ± 0.01	0.08 ± 0.04	1 × 10−10	3 × 10−44	2 × 10−14
contact negative work (J kg−1)	−0.34 ± 0.17	−0.14 ± 0.04	−0.16 ± 0.05	8 × 10−12	2 × 10−10	1
contact positive work (J kg−1)	0.13 ± 0.08	0.09 ± 0.06	0.21 ± 0.07	0.07	0.002	2 × 10−7
contact net work (J kg−1)	−0.21 ± 0.14	−0.04 ± 0.05	0.06 ± 0.06	4 × 10−19	7 × 10−37	0.0045

*Denotes significant difference in pairwise comparisons between running speeds, p ≤ 0.05.

3.3. Energetics

3.3.1. Centre of mass

The average forward speed of the COM for stepping down, level and up was 0.64 ± 0.08 m s⁻¹, 0.89 ± 0.08 m s⁻¹ and 0.73 ± 0.08 m s⁻¹, respectively. The leg acted on the COM to absorb energy during the stepping down task, generate mechanical energy during the stepping up task and maintain a relatively neutral level of energy during the level stepping task (table 2). The net negative work performed on the COM when stepping down was approximately 70% of the net positive work performed when stepping up. The magnitude of net work, negative work and positive work performed on the COM was significantly different between all conditions (all p ≤ 0.05, table 2).

3.3.2. Ankle and foot arch

The pattern of mechanical power generation within the ankle and foot arch was markedly similar, although the ankle displayed greater peaks in power absorption and generation. The ankle and foot arch performed net negative work during the step-downs and net positive work during the step-ups, while the level stepping condition was relatively energy neutral (figure 3). The magnitude of the net work performed at the foot arch and ankle was significantly different between all stepping conditions (all p ≤ 0.05, table 2). A greater amount of negative work was performed when stepping down, compared to the stepping up and level stepping, for the ankle and foot arch (all p ≤ 0.05). The magnitude of positive work was greater in the stepping up condition compared to level and down steps, for both the ankle and foot arch (all p ≤ 0.05).

3.3.3. The metatarsophalangeal joint

The MTP joint performed net negative work for all conditions, although the magnitude of work was generally much smaller than the ankle and foot arch. The pattern of power production at the MTP joint was in opposition to the ankle and foot, with a burst of positive power during early stance, followed by energy absorption in late stance, prior to propulsion (figure 3). Net work performed at the MTP joint decreased from the stepping down condition, to the level stepping and stepping up conditions (all p ≤ 0.05, table 2). More negative work was performed in the stepping up condition, compared to the level stepping and stepping down conditions (all p ≤ 0.05), while the largest magnitude of positive work was performed in the stepping down condition (all p ≤ 0.05).

3.3.4. Foot contact model

Net work performed at the foot was negative during the level stepping and stepping down conditions, with a transition to net positive work during the stepping up task. Net work performed at the foot was significantly different between all stepping conditions (all p ≤ 0.05). The magnitude of negative work was greater during the stepping down task, compared to both the level stepping and stepping up conditions (all p ≤ 0.05). A greater amount of positive work was performed during the stepping up condition compared to the level stepping and stepping down conditions (all p ≤ 0.05).

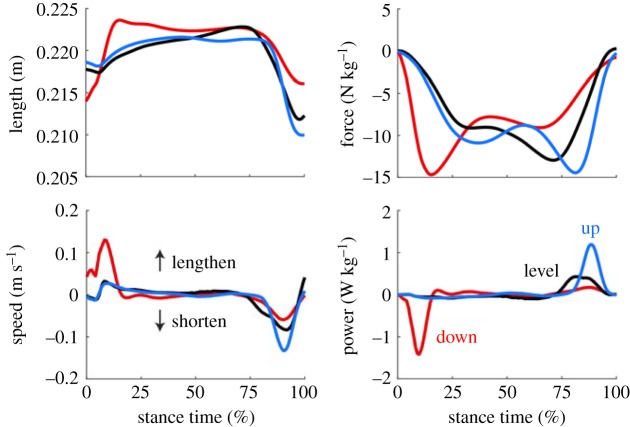
3.3.5. Plantar muscle–tendon unit

For all conditions, the MTU underwent an initial period of negative work, followed by positive work in late stance, prior to propulsion. Peak MTU length occurred in early stance during the stepping down task, while in the level stepping and stepping up tasks, it was observed in late stance. When stepping down, the plantar MTU was shorter at foot contact and underwent a rapid lengthening during collision. More negative work was performed by the MTU during this condition, compared to the level stepping and stepping up conditions (all p ≤ 0.05, figure 4 and table 2). In the stepping up condition, the MTU displayed a late burst of positive power, associated with a rapid shortening of the MTU. This burst of power was substantially greater than that observed in the level stepping and stepping down conditions (all p ≤ 0.05).

Figure 4.

Estimates of plantar MTU length and speed across subjects and conditions, based on motion capture data and estimates of MTU insertion points. Plantar MTU force is calculated by scaling the joint torque of the foot arch by the moment arm between the joint and the attachment of the MTU to the calcaneus. (Online version in colour.)

4. Discussion

Much of what we know about human foot function is based on steady-state locomotion. However, humans often accelerate, decelerate and walk up or down gradients. We know very little about how the human foot functions during such tasks that require the COM to perform net mechanical work. Here we provide evidence that the foot can dissipate, recycle and produce mechanical energy during locomotion. It is apparent that the intrinsic foot muscles have the capacity to actively modulate the energetic function of the foot, producing and dissipating mechanical energy when locomotor tasks require positive and negative work to be performed at the COM.

We present a clear relationship between the function of the intrinsic foot muscles and the mechanical energy requirements at the foot and COM, suggesting that these muscles may influence the dynamics of locomotion. Bursts of muscle activation were observed following foot contact when stepping down, occurring synchronously with energy absorption by the MTU. Conversely, when stepping up, the largest bursts of activation were observed prior to propulsion, while the MTU was generating mechanical power. Peak MTU length (figure 4) remained relatively constant across all conditions, suggesting that the contribution of the passive PA may also remain relatively constant. The most notable changes in plantar MTU dynamics were apparent in the MTU length at foot contact and propulsion during each task, as well as the associated velocity profiles. For example, the MTU was approximately 5 mm (2.5%) shorter at foot contact and 7 mm longer at propulsion, in the step-downs compared to the level stepping task, with a fast lengthening velocity immediately following foot contact. In this case, modulation of foot kinematics prior to foot contact presumably facilitates power attenuation, without excessively high peak strain in the MTU. Within the current experiment, we are unable to isolate the function of the contractile component of the MTU from the series elastic component. Further investigations may yield important insights into the muscle–tendon interactions within the foot and the strategies used to cope with energy dissipation and generation. However, these data provide important evidence that the intrinsic foot muscles modulate the energetic function of the foot, by altering foot kinematics prior to foot contact and at propulsion.

By comparing the changes in net work (in relation to level steps) of the entire foot as estimated by the contact method to the changes in net work at the plantar MTU, we see that the MTU performs 88% of the increase in net positive work for stepping up and only 38% of the increase in net negative work for stepping down (table 2). Since only muscles can actively produce net positive work in the body and the plantar MTU model captures the action of the predominant muscles of the foot, it makes sense that most of the net positive work performed by the foot must come from the MTU. By contrast, passive structures (such as the heel pads) can perform increased net negative work simply from changes in kinematics or rates of loading. Therefore, a much lower proportion of the negative work compensation at the foot is produced by the MTU, which would be desirable to reduce the energetic cost of eccentrically contracting the muscles of the foot.

Comparing the energetic function of the foot and the ankle reveals a close coupling in function between the ankle plantar flexors and the intrinsic foot muscles. Both muscle groups appear to possess similar phasic patterns of activation, associated with negative and positive work at the foot and ankle during each of the stepping tasks. Functionally, this makes sense as the action of both muscle groups produces force in similar directions (e.g. plantar flexion of the forefoot) and is active during similar periods of the gait cycle in locomotion. The foot's contribution to COM net mechanical work was relatively low (9–16%) compared with the ankle joint (30–42%), thus the importance of the intrinsic foot muscles' contribution to COM work remains unclear. Given the relatively small volume of contractile tissue within the foot [22], it may be that the contribution of the foot to COM work is limited during tasks that require large magnitudes of energy to be generated or attenuated.

In addition to the overall contribution of the intrinsic foot muscles to COM work, the capacity to provide ‘on-demand’ dissipation or generation of mechanical energy within the foot may also optimize the contractile dynamics of larger muscles within the lower limb. For example, dissipation of energy within the foot may help to prolong ground contact time, by reducing the resonance that may occur in a passive spring-like system [33]. Prolonging ground contact time might facilitate a longer period for the ankle and knee extensors to dissipate energy, reducing the magnitude of peak power attenuation and potentially the cost of dissipating mechanical energy [34,35]. The fat pads of the heel and forefoot also likely contribute to this function [36–38]. Similarly, positive power produced by the intrinsic foot muscles during accelerative tasks may help to stiffen the forefoot and enhance the leverage of the foot to apply ankle plantar flexion torques to the ground [39].

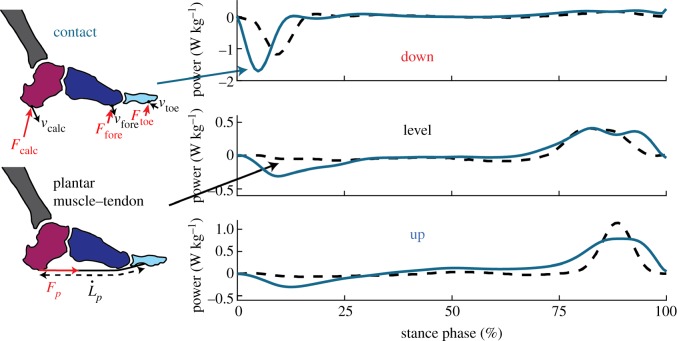
Our estimates of plantar MTU and foot contact work are in rough agreement with some differences in phasing and magnitude (figure 5). Most notably, the contact method estimates a larger amount of negative work during the collision phase in comparison to muscle–tendon estimate. This difference is likely due to compression of the fat pads of the heel and forefoot, as well as other soft tissue structures of the foot and lower leg, acting in directions that are orthogonal to the action of the MTU. For the level stepping condition, there is approximately 4.8 J (about 46% of the total negative work done by the foot) of dissipated energy that remains unaccounted for after removing the contribution of the MTU. This value is higher than the 1.5 J performed by the heel pads in walking [14,40], which makes sense because the measure would also capture the work performed by other soft tissues. Small errors in estimates of the velocity of the contact points, joint centres and insertion locations of the MTU may also explain some of this difference. Our estimate of foot contact work during the level stepping task is also in agreement with previous data using similar approaches to quantify the energetic function of the foot during locomotion [12]. The magnitude of energy absorbed by the plantar MTU (4.5 J) in level walking was similar but higher than that reported in running at 3.1 m s⁻¹ (3.1 J) [41]. Our methodology assumes all joint moment at the foot arch is produced by the plantar MTU which could lead to an overestimation of MTU work. By contrast, estimating work from mechanical properties of cadavers' feet may underestimate MTU work due to differences in dead and living tissue, differences in force profiles and, as we have seen, the intrinsic muscles which can actively perform work.

Figure 5.

A comparison of estimates for mechanical power of the foot. The plantar MTU estimate (black, dashed) is calculated from estimates of muscle–tendon force and length. The contact estimate (dark blue) is the external work performed by the contact of the foot with the ground on each of the three foot segments. (Online version in colour.)

In the current experiment, we report that the plantar MTU performs net positive work during the level stepping task, despite net negative work being performed by the foot. Recent experiments applying this same contact model during steady-state locomotion have also found the foot that behaves as an energy sink, with the proportion of absorbed energy dissipated by the foot increasing with locomotion speed [11,12]. We have speculated previously that the intrinsic foot muscles may potentially contribute to energy dissipation within the foot during level, constant speed locomotion [11]. However, based on the function of the plantar MTU observed in this study, it appears this may not be the case, at least at the low locomotion speeds encountered within this experiment. It may be advantageous to consider the function of the foot in two distinct paradigms: (1) a passive high frequency viscoelastic collision at the contact regions between the foot and ground which decelerates the leg during early stance and (2) lower frequency joint dynamics which are passively elastic due to the PA but actively modulated by the intrinsic muscles to generate or dissipate energy in conjunction with the ankle to meet the energetic requirements of the step.

4.1. Limitations

There are a few methodological limitations within our study that need to be acknowledged when considering these data. Our model of the plantar MTU is an estimate that combines the intrinsic foot muscle MTU and the PA into a single structure. We chose this method given the close proximity of the intrinsic foot muscles (FDB and AH) and the PA, with very similar origins, insertions and anatomical pathways. Given this approach, we were unable to parse the individual contributions of each tissue to the energetic function of the foot. However, given the passive elastic nature of the PA [6], we can assume the magnitude of stored energy in this tissue remained relatively constant across conditions, as the magnitude of peak MTU length (and strain) was relatively constant. Furthermore, the PA is unable to generate additional mechanical energy, and with a hysteresis of approximately 3% [6,13], it is unlikely that it can dissipate a great deal of mechanical energy. Therefore, we believe that the alterations in energetic function within the foot can be directly attributed to the function of the intrinsic foot muscles.

The measurement model of the MTU also makes other assumptions that likely introduce error. We assumed that there is a constant moment arm length of the plantar MTU, even though in other muscle groups that has been shown not to be the case [42]. While our method of estimating force distribution across the foot improves upon typical estimates using a single force plate (appendix A), it is a difficult problem and may also produce errors in the estimation of segmental forces and joint moments. Additionally, we assumed that all of the torque at foot arch is produced by the MTU, which likely overestimates MTU force. Estimates of Achilles tendon force based on joint torque measurements have been shown to overestimate the directly measured force in a variety of movements [43]. Accordingly, the MTU power data reported within this study should be considered estimate values and conclusions based on these data made in the context of these limitations.

The experiments were implemented such that the steps recorded are started from rest, and not steady-state walking, and step length and frequency were not controlled. The participants are accelerating from and decelerating to a standstill as opposed to maintaining a steady walking speed, which makes the data difficult to compare to data taken of steady-state walking at faster speeds. Nevertheless, the power production at the ankle during level steps is comparable to steady-state walking at a relatively slow speed of 0.9 m s⁻¹ [44], notably in that the amount of positive power generated during push-off is significantly lower than would be expected at faster walking speeds. Additionally, while we do not expect large differences in results between sex, having 80% male subjects may have introduced bias in the data that make the results more applicable to males as opposed to a general population.

In summary, we have shown that the plantar intrinsic foot muscles actively modulate the energetic function of the foot. The energetic function of the foot appears to be closely coupled to the ankle and is modulated to meet the mechanical requirements of the COM. The contribution of the foot to total mechanical work of the lower limb is generally less than 16%, considerably less than the other joints of the lower limb.

Appendix A

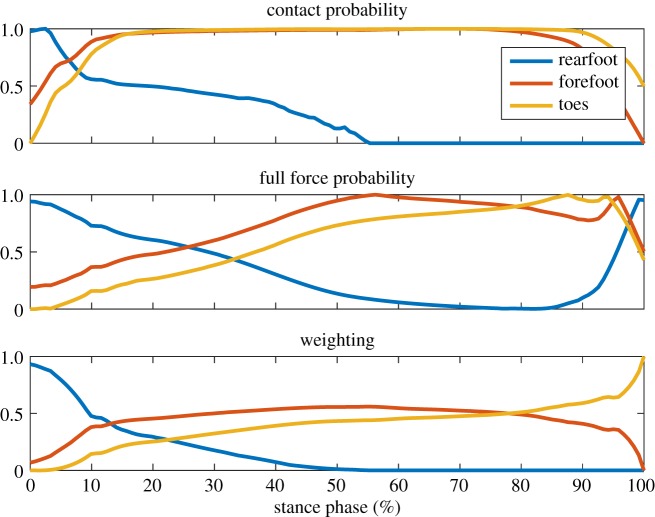
Estimating the contact forces across the foot from a single force plate is an underdetermined and difficult problem. Assigning force to the toes only once the COP has progressed past the MTP joint has been shown to be inaccurate compared with methods using multiple force plates and pressure insoles [45]. To account for this, a novel method of estimating contact forces was developed that assigns a weighting to each of the foot segments using a probability framework that takes into account the positioning of each segment in relation to the COP (figure 6).

Figure 6.

A representative trial showing force assignment to the three foot segments for a level step. (a) Probability of contact for each segment with the ground (normalized per segment). (b) Probability that the segment is supporting the full weight (normalized per segment). (c) Multiplying the contact and full force probabilities results in weighting for the ground force, which is normalized across all segments such that the sum of weights at each time during stance equals 1. (Online version in colour.)

The weighting assigned to each foot segment was calculated as follows:

$$W=p_{\mathrm{c}}{p}_{\mathrm{f}},$$

where p_c is the probability that the segment is in contact with the ground, and p_f is the probability that the segment is supporting the entire ground force.

The probability of contact p_c for each segment was estimated as the vertical height of the contact region of each segment, normalized to a range of zero to one by its maximum and minimum height during stance phase respectively. This results in a continuous normalized probability distribution of contact for each segment across the stance phase. However, this estimate of contact probability does not take into account the a priori knowledge that the rearfoot leaves the ground entirely at discrete points in time. To take this into account, when the COP of the total ground force passes through the MTP joint and towards the toes, the probability of rearfoot contact at all subsequent points was set to zero. To avoid a discrete jump in the probability distribution across time, the probability of contact prior to this moment is scaled such that there is a smooth transition from a finite probability to zero probability at the time the COP progresses past the MTP.

The probability that each segment is supporting the full contact force p_f is estimated as the distance between the COP and the segment contact point projected onto the ground and along the axial direction of the foot. Since at each point in time the sum of these probabilities across each segment must be equal to 1, the distributions were normalized by setting this sum equal to 1 at each point in time:

$$\sum _{i=1}^3{p}_{\mathrm{f}}^i=1.$$

See figure 6 for a representative weighting across the stance phase of level walking for a single step of one participant.

Data accessibility

Data from this study are available at https://www.dropbox.com/sh/drwmql75h8s5nhx/AADaGNVAIPVnBW4woBVexDIia?dl=0.

Authors' contributions

L.A.K. and D.J.F. designed the experiment. R.R., D.J.F. and L.A.K. collected data. R.R. performed data analysis. R.R. and L.A.K. drafted the manuscript. R.R., D.J.F. and L.A.K. edited and revised the manuscript.

Competing interests

We declare we have no competing interests.

Funding

L.A.K. is funded by a National Health and Medical Research Council Peter Doherty Fellowship (APP1111909).