Response of insect swarms to dynamic illumination perturbations

Abstract

Many animal species across taxa spontaneously form aggregations that exhibit collective behaviour. In the wild, these collective systems are unavoidably influenced by ubiquitous environmental perturbations such as wind gusts, acoustic and visual stimuli, or the presence of predators or other animals. The way these environmental perturbations influence the animals' collective behaviour, however, is poorly understood, in part because conducting controlled quantitative perturbation experiments in natural settings is challenging. To circumvent the need for controlling environmental conditions in the field, we study swarming midges in a laboratory experiment where we have full control over external perturbations. Here, we consider the effect of controlled variable light exposure on the swarming behaviour. We find that not only do individuals in the swarm respond to light changes by speeding up during brighter conditions but also the swarm as a whole responds to these perturbations by compressing and simultaneously increasing the attraction of individual midges to its centre of mass. The swarm-level response can be described by making an analogy to classical thermodynamics, with the state of the swarm moving along an isotherm in a thermodynamic phase plane.

1. Introduction

Many species of animals that form aggregations in the wild do so in a manner that can be described as collective, in the sense that the statistics of the group as a whole are distinguishably different from the aggregate statistics of individuals. It is commonly assumed that acting collectively is beneficial for social animals, enhancing their ability to react to external stimuli, evade predators or to solve specific tasks [1–3]. Understanding the nature of collectivity and quantifying its potential advantages has thus been the focus of significant interdisciplinary research interest over the past few decades, ranging from empirical studies of bird flocks [4], ants [5], fish schools [6] and insect swarms [7] to agent-based [8] and continuum [9] theoretical models to robotics applications [10]. Despite these substantial efforts, performance enhancements due to collectivity remain difficult to quantify or even identify in many animal systems, as it is often a priori unclear what kind of task is being optimized by the group [11] and because findings from one species are difficult to generalize to others. To circumvent the need to define tasks and to show an enhancement of individual capabilities, one can instead employ theoretical frameworks that directly describe the emergent group level rather than individual agents. Several approaches for quantitatively describing general collectives have recently been developed, and have shown that it can be advantageous to borrow methods from materials science and thermodynamics to describe collective systems as being analogous to bulk materials with well-defined, measurable properties at the group level [12–14]. Though such a description is agnostic as to the evolutionary basis of collective behaviour, it can provide a precise characterization of the nature of collective systems.

A key open question for illuminating the properties of collective systems is how they respond to external perturbations. In nature, animal groups constantly experience a wide array of transient, localized environmental perturbations such as sudden gusts of wind or changing visual cues or sounds, among others. How the collective behaviour is modified, whether on an individual or group level, by such external perturbations is not well understood. It is also unclear how collectivity may improve the ability of animals to cope with these perturbations. The variety of environmental perturbations that can occur in the wild is substantial. Thus, to quantitatively understand the impact of external perturbations on collective behaviour in general, it is beneficial to investigate singular, well-defined perturbations. This, in turn, argues for laboratory experiments, where one has the ability to precisely control applied perturbations and measure the response of the animals.

In this work, we focus on the midge species Chironomus riparius, which swarms as part of its mating ritual [15] and behaves collectively while doing so [7]. In the following, we use periodic light signals as a tool to investigate this species' response to external stimuli in a classical perturbation experiment. We apply both static and dynamic perturbations, and find that, while the midge behaviour is invariant under static perturbations (aside from a brief transient response), dynamic perturbations can produce new behavioural states. By quantifying the interplay between external perturbations and swarm response, our results help to clarify the group-level, macroscopic properties of swarms and help to lay the groundwork for a deeper understanding and potential control of engineered collective systems that are intended to solve actual tasks.

Below, we first describe our experimental set-up, including the midges themselves, the imaging technique and the experimental procedure we use to produce controlled light perturbations. We then investigate the kinematic statistics of the swarm under static light perturbations and contrast them with the response to dynamic light signals. Additionally, we analyse group-level statistics such as the volume, pressure and cohesion of the swarm under dynamic lighting.

2. Methods

In our laboratory, we maintain a self-sustaining colony of C. riparius, a non-biting midge species that predictably forms mating swarms at dusk and dawn, in a (122 cm)³ cubical acrylic enclosure. This midge species lives on a roughly two-week life cycle [16]. The first and longer part of that time is spent in the larvae and pupae stages, during which the insects burrow into a cellulose substrate placed (along with dechlorinated, oxygenated water) in eight 10 litre tanks inside the enclosure. During the last few days of their life cycle, the pupae mature and become flying adults. We enforce an artificial day–night cycle with a timed overhead lamp on top of the enclosure, with 16 h of daytime and 8 h of night-time, during which there is still some dim residual indirect background light. At dusk and dawn, males in the colony spontaneously form mating swarms above a visual feature placed on the bottom of the cubical enclosure [16], and wait for females to enter the swarm. In our experiment, we provide a black square as a ‘swarm marker' to nucleate the swarms. After mating, the females lay eggs in the breeding tanks, thus closing the life cycle. We observe the swarming behaviour during the artificial night using three hardware-synchronized Point Grey Flea3 1.3 MP cameras outside of the enclosure running at 100 frames per second. Each individual measurement consists of between 200 s and 40 min of data, with swarm sizes between 15 and 65 individuals. To illuminate the midges during this time, we use several arrays of infrared light-emitting diodes (LEDs), placed inside and on top of the enclosure; infrared light is invisible to the midges but can be captured by our cameras. We then use automated image processing and particle-tracking routines [17] to obtain the three-dimensional positions, velocities and accelerations of all the individual midges in the swarms. Further details of our experimental procedure can be found in [7].

In the experiments described below, we modulate the ambient light level using a 6500 K Luxeon Star LED array placed on top of the acrylic enclosure that provides white light. The array is driven by a Keysight 33210A function generator to produce time-dependent light signals with well-defined waveforms. The two distinct types of signal we use here are constant brightness levels and periodic square wave signals at a constant frequency. To quantify the light brightness in the laboratory, we measure the luminous flux per unit area in a corner of the laboratory furthest away from the acrylic tank. With this set-up, we are able to quantitatively investigate the influence of arbitrary light changes on the behaviour of swarming midges.

3. Results and discussion

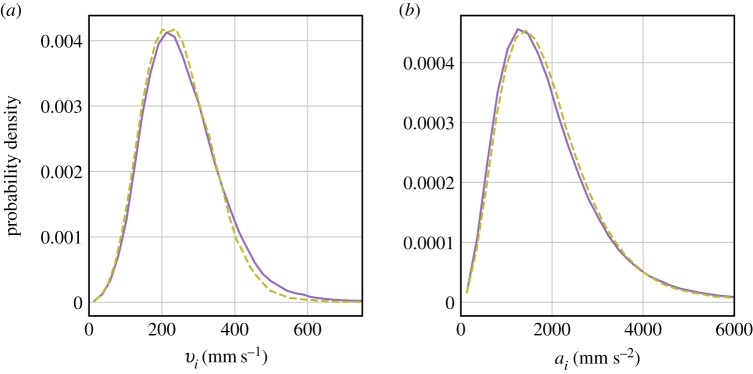
In general, swarms could potentially react to static perturbations such as different levels of ambient light, to dynamic perturbations such as periodically varying light signals, or possibly to combinations of both in a nonlinear way: swarms could be sensitive to both the absolute level of the light signal and its rate of change in potentially different ways. Our previous work on acoustic perturbations of C. riparius swarms showed that midges tend not to react to static, constant frequency noise but rather are sensitive to modulated, dynamic sound signals [18]. This finding is consistent with a common property of many biosensors, known variously as the fold-change detection mechanism or Weber's law, which makes responses independent of absolute sensory input levels [19] but rather sensitive to changes. To separate static from dynamic influences of light changes on the behaviour of our swarms, we first investigated the effect of different ambient light levels on the statistics of the swarming midges. Figure 1 shows the probability density functions (PDFs) of the velocity magnitude $v_i=\sqrt{v_{i,x}^2+v_{i,y}^2+v_{i,z}^2}$ and acceleration magnitude $a_i=\sqrt{a_{i,x}^2+a_{i,y}^2+a_{i,z}^2}$ of individual midges, where $v_{i,xyz}^{}$ and $a_{i,xyz}^{}$ are the Cartesian velocity and acceleration components, respectively, for midge i. Results are shown for both normal night-time lighting at 1.3lx and brighter conditions at 2.3lx. In both cases, the swarms had comparable numbers of midges. Both the velocity and acceleration PDFs are indistinguishable under the different lighting conditions, indicating that static light changes do not influence the behaviour of the swarm in a noticeable way, after an initial transient response that relaxes over the span of a few minutes.

Figure 1.

(a) PDFs of the velocity magnitude v_i of individual midges during ambient light levels of 1.3lx (solid line) and 2.3lx (dashed line). (b) PDFs of the acceleration magnitude a_i of individual midges for the same experiment. The statistics of both acceleration and velocity are nearly indistinguishable in the two different ambient light conditions. (Online version in colour.)

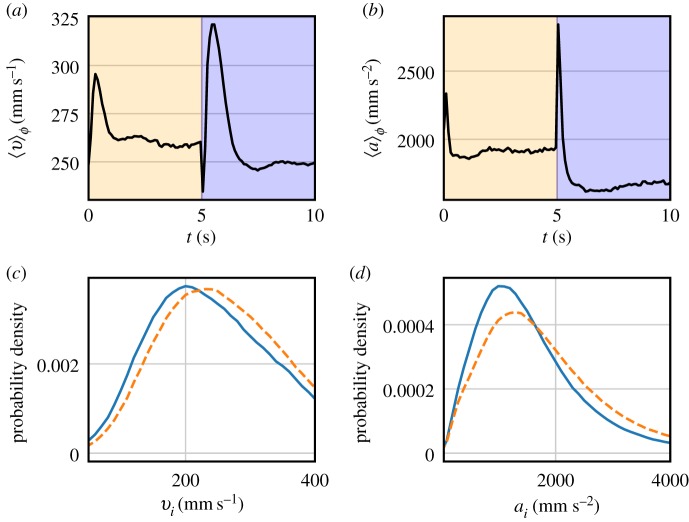
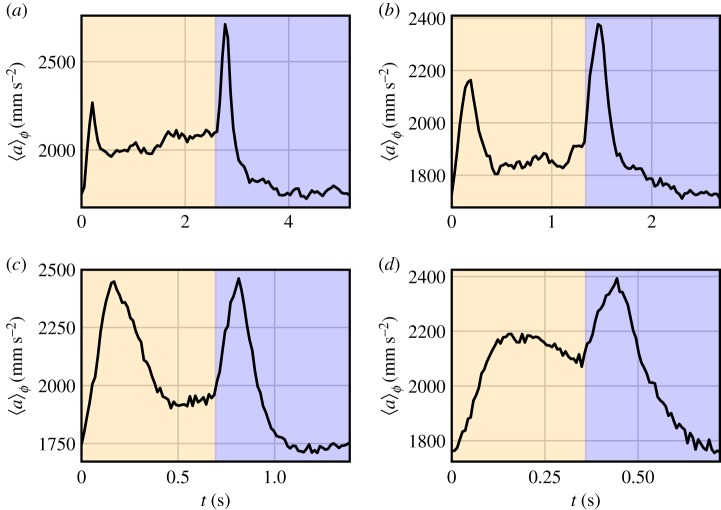
We also exposed the swarms to periodically varying lighting conditions that switched between the same two ambient levels as above but with a square-wave waveform at frequencies f between 0.1 Hz and 20 Hz. Figure 2a shows the phase-averaged velocity magnitude ${⟨v(t)⟩}_{\phi }=1/M{\sum }_{i=0}^{M-1}v(t+iT)$ over M full periods of length T. Here, the notation 〈 〉_φ denotes a phase average, rather than an ensemble average over all the midges in the swarm. In contrast to the static lighting perturbation, we observe a measurable response to this dynamic lighting perturbation. Every time the light switches between bright and dark (in either direction), midges in the swarm briefly ‘startle', exhibiting higher velocities before relaxing into a steady state. Note that this transient startle response is also typically evident immediately after switching between different static light levels. In contrast to the findings from static light changes, however, dynamic lighting changes produce two distinct steady states after the initial startle responses, with bright phases resulting in higher velocity levels and dark phases in lower velocity levels. Similar findings for the acceleration statistics can be seen in figure 2b, which shows the phase-averaged acceleration magnitude ${⟨a(t)⟩}_{\phi }=1/M{\sum }_{i=0}^{M-1}a(t+iT)$ for the same swarms. We observe a corresponding two-level response in the phase-averaged acceleration, though the startle response decays much more rapidly than in the velocity signal. We observe this two-level behaviour for a wide range of frequencies, as seen in figure 3. The phase-averaged acceleration also exhibits the startle responses that coincide with the switch from bright to dark and vice versa. This effect lasts for about 0.3 s and is independent of the driving frequency, suggesting that it stems from a spontaneous excited reaction midges perform whenever there is a rapid change in lighting conditions, consistent with a fold-change visual detection mechanism. When this change occurs on comparable time scales to the startle response of the swarm, there is not enough time for the swarm to return to a steady state between two subsequent lighting changes, as seen in figure 3d.

Figure 2.

(a) Phase-averaged velocity magnitude of midges under dynamic lighting conditions. The first 5 s of each period had a 2.3lx level of background light and the last 5 s had 1.3lx of background light. There is a strong ‘startle’ response immediately after the light switches in either direction with greatly increased velocities. After the startle response, midges in the swarm settle into two distinct levels of velocities, with bright phases corresponding to higher velocities. (b) Phase-averaged acceleration magnitude for the same experiment. The startle response is much narrower than for the velocities and the accelerations show a similar split into two distinct levels, with brighter phases resulting in higher accelerations. (c) PDFs of midge velocity magnitudes during the dark phase (solid line) and bright phase (dashed line). During bright phases, the PDF moves towards higher velocities. (d) PDFs of midge acceleration magnitude for the same experiment. Bright phases shift the PDFs to higher accelerations. (Online version in colour.)

Figure 3.

Phase-averaged acceleration of midges under periodic lighting at frequencies of 0.19 Hz (a), 0.37 Hz (b), 0.72 Hz (c) and 1.39 Hz (d). During the first half of the period, the ambient light was at 2.3lx and at 1.3lx during the second half. Similar to the 0.1 Hz frequency phase average in figure 2b, the swarms show a startle response lasting about 0.3 s independent of frequency after every light switch. The swarm retains a measurable two-level response separated from the startle response as long as the period of the light switches is longer than the startle response. For higher frequencies, as shown in (d), the distinct levels begin to disappear into the startle response. (Online version in colour.)

To separate the transient startle response from the more steady behaviour, we define dark and bright phases of the midge statistics by not including data within 1 s on either side of a lighting change in our statistics. Figure 2c,d shows the PDFs of individual midge velocities and accelerations in dark and bright phases separately. Comparing with figure 1, it is clear that, even though midges are not affected (in a steady-state sense) by static changes in ambient light, they are driven into different states under the influence of periodically changing lighting, with midges moving and accelerating more slowly in dark phases than in bright phases.

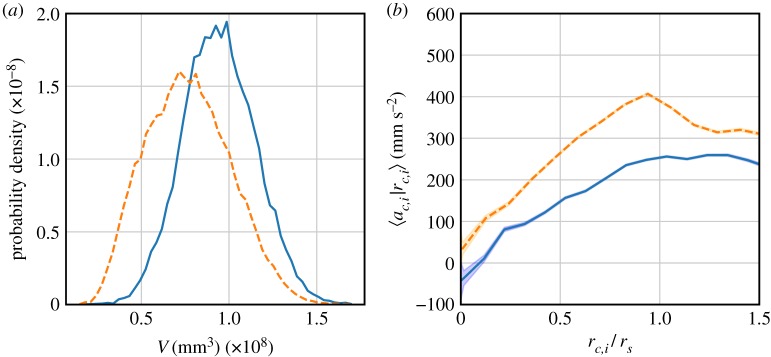
Our analysis up to this point shows a strong dependence of the individual statistics of swarming C. riparius on periodically changing lighting conditions. This observation, however, is not yet indicative of any collective response of the swarm as a whole, as these findings are based on aggregate statistics—that is, on simple averages over individuals. One approach to quantifying whether the swarm reacts collectively to periodic light changes is to investigate its geometric properties. Figure 4a shows the PDFs of the instantaneous volume V of the swarm for both the bright and dark phases for a measurement at an oscillation frequency of f = 0.1 Hz. We define the instantaneous volume of the swarm as the volume of the convex hull constructed from all the individual midges in the swarm at any given time. The volume PDFs from the two different phases are clearly distinguishable even though the number of midges in the swarm is virtually unchanged. Thus, the periodic light change not only affects the kinematic behaviour of individuals but also the global, collective properties of the swarm. Specifically, switching from the dark to the bright phase compresses the swarm, as seen in figure 5a, while switching from bright to dark dilates it. At the same time, the swarm also changes how tightly it is bound together during these transitions. As a measure of binding strength, we compute the conditional average of the acceleration of an individual 〈a_c,i|r_c,i〉 towards the centre of mass, ${\mathit{r}}_c=1/N{\sum }_1^N{\mathit{r}}_i,$ as a function of normalized distance from the centre of mass r_c,i/r_s as a proxy for a force [6]. Here, N is the number of midges in the swarm, r_c,i = |r_c − r_i| is the distance of an individual from the centre of mass, r_s = 〈r_i〉 is a linear measure of the swarm size, and $a_{c,i}={\mathit{a}}_i\cdot {\mathit{r}}_{c,i}/r_{c,i}$ is the acceleration component of the ith midge in the direction of the centre of mass. As shown in figure 4b, the attraction of the swarm to its centre of mass is much stronger during bright phases than during dark phases. In previous studies, it has been found that midges within the swarm behave as if they reside in a quasi-harmonic potential well, with an attraction to the swarm centre of mass that increases close to linearly with distance [7,20]. The centre of this effective potential is given by the position of the swarm marker. However, only midges close to the marker are strongly coupled to it, so the exact shape of the potential is determined by the midge–midge interactions [14,21]. A stronger attraction to the centre of mass can thus be interpreted as a change of shape in this effective potential due to the external light changes.

Figure 4.

(a) PDF of the swarm volume, separated by phase. Bright phases (dashed line) result in a more compact, compressed swarm. (b) Conditional acceleration of individual midges in the direction of the centre of mass as a measure of attraction strength and tightness of the swarm. Shaded areas indicate the standard error of the mean. During bright phases (dashed line), the swarm is noticeably more strongly attracted towards the centre of mass and thus more tightly bound to the centre than in the dark phases (solid line). (Online version in colour.)

Figure 5.

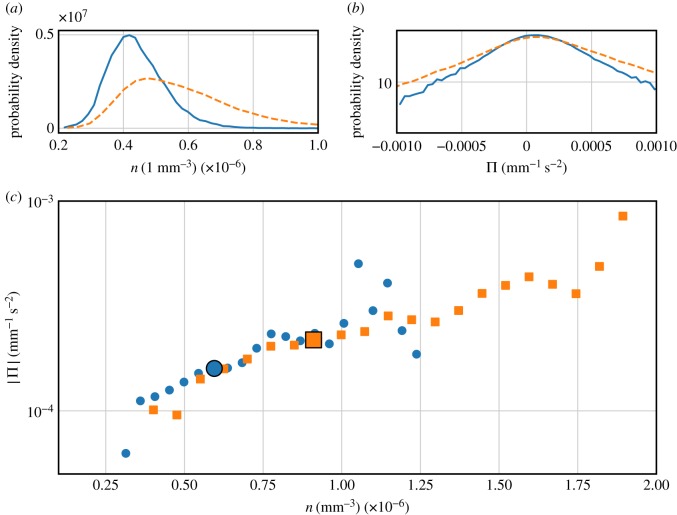
(a) PDF of the number density of the swarm, which differs noticeably for bright (dashed line) and dark (solid line) phases. Bright phases tend to display higher densities with a wider spread. (b) PDF of the pressure of the swarm. Bright phases result in more extreme events. (c) Pressure as a function of density for bright (squares) and dark (circles) phases. Large symbols denote the mean pressure and density in these phases. Even though the individual statistics of pressure and density differ between the phases, the functional relation remains the same. (Online version in colour.)

A quantitative physical understanding of this swarm response can be obtained by making an analogy to thermodynamics. We have previously shown that unperturbed C. riparius mating swarms behave similarly to equilibrium thermodynamic systems with well-defined global relations between volume, number density, pressure and chemical potential [13]. The behavioural response of the swarm under periodic light perturbations can be understood in a similar way. Figure 5a shows the PDFs of number density n = N/V during both light and dark phases for a measurement with a driving frequency of 0.1 Hz. Here, N is the number of midges in the swarm. The PDFs noticeably change shape, with dark phases corresponding to much more dilute swarms and bright phases to denser swarms with a higher density variability. We can define a microscopic pressure per unit mass via [13]

$$\mathrm{\Pi }=\frac{1}{NV}\sum _{i=1}^N\left(\frac{1}{3}(v_i^2+{\mathrm{a}}_i\cdot {\mathrm{r}}_i)\right),$$

which captures the work done by midges moving in the effective potential well of the swarm. Note that, unlike in an ideal gas, this microscopic pressure can be negative owing to the active nature of the midges. Figure 5b shows the PDFs of this swarm pressure for the light and dark phases. During light phases, the tails of this PDF are noticeably heavier than during the dark phases, meaning that higher pressures are much more likely to occur. Thus, both number density and pressure individually change their statistics in the two phases. Without prior knowledge of the relationship between these two quantities, this result could indicate that the swarm moves to some unspecified, new position in pressure–density space. Figure 5c shows the conditional average of the pressure as a function of number density in both the bright and dark phases. Note that, rather than separating the swarm into different regions as we did in our earlier work [13], we consider the entire swarm here. Although bright phases tend to be more dense than dark phases, the statistics of both lie on a single curve in pressure–density space regardless of the illumination state. That is, the swarm behaves as if the lighting changes drive it along an isotherm in a thermodynamic phase plane, maintaining a fixed functional relation between density and pressure. With this periodic lighting, we are able to move the swarm to a location in this phase space that is not explored by unperturbed swarms.

4. Conclusion

Our findings show that C. riparius swarms respond to dynamic light perturbations in a consistent, predictable way, both on an individual midge level as well as on the level of the swarm as a whole. Static light perturbations do not influence the behaviour of midges in a measurable way aside from a brief transient, indicating that the swarm is stable against a wide range of environmental conditions, leading to a preferred swarming behaviour in the absence of dynamic perturbations. Rather than relaxing into the ground state after the initial startle response, dynamic square-wave perturbations create a new stable behavioural state. These findings imply that there may exist many different steady states the swarm can be driven into, given the correct type and shape of dynamic perturbation. Future work could explore this hypothesis by combining different types of dynamic perturbations.

Data accessibility

The trajectory data are available under doi:10.6084/m9.figshare.6852800.v1.

Authors' contributions

M.S. and N.T.O. designed the research, M.S. and K.v.d.V. conducted the experiments and M.S. analysed the data. All authors interpreted the data and wrote the paper.

Competing interests

We declare we have no competing interests.

Funding

This research was sponsored by the Army Research Laboratory and accomplished under grant no. W911NF-16-1-0185. K.v.d.V. acknowledges support from an Early Postdoc.Mobility fellowship from the Swiss National Science Foundation and M.S. acknowledges support from the Deutsche Forschungsgemeinschaft under grant no. 396632606