A Selective Review on Random Survival Forests for High Dimensional Data

Abstract

Over the past decades, there has been considerable interest in applying statistical machine learning methods in survival analysis. Ensemble based approaches, especially random survival forests, have been developed in a variety of contexts due to their high precision and non-parametric nature. This article aims to provide a timely review on recent developments and applications of random survival forests for time-to-event data with high dimensional covariates. This selective review begins with an introduction to the random survival forest framework, followed by a survey of recent developments on splitting criteria, variable selection, and other advanced topics of random survival forests for time-to-event data in high dimensional settings. We also discuss potential research directions for future research.

1. Introduction

Survival analysis is an active area of research in biostatistics, which focuses on a time-to-event outcome that is typically censored [1–3]. Continuing advancement in data acquisition technology in recent years has made high dimensional or ultra-high dimensional data routinely available to researchers. This data deluge poses unprecedented challenges for analyzing survival data especially when the number of covariates (features, predictor variables) far exceeds the number of observations since standard survival analysis methods such as Cox’s proportional hazard regression [1,4] become inadequate in high dimensional settings. New methods are needed to deal with a large number of covariates for time-to-event data.

The most popular methods for high dimensional time-to-event data are those based on the Cox PH model. Current approaches include regularized Cox PH models [5–10], partial least squares [11,12], statistical boosting using Cox-gradient descent or Cox likelihood [13–15]. However, the assumptions underlying these methods such as the proportional hazards assumption are often violated in high-dimensional time-to-event data. To alleviate these problems, nonparametric and flexible methods such as survival trees and tree ensembles have been developed [16–19]. An excellent introduction to survival trees and forests methods can be found in [20] and a comprehensive review of statistical literature on this topic up to 2011 was provided by [21].

More recently, random survival forest (RSF) [22], a non-parametric method for ensemble estimation constructed by bagging of classification trees for survival data, has been proposed as an alternative method for better survival prediction and variable selection. Compared with regression based approaches, random survival forest has several advantages. First, it is completely data driven and thus independent of model assumptions. Second, it seeks a model that best explains the data and thus represents a suitable tool for exploratory analysis where prior information of the survival data is limited. Third, in case of high dimensional data, limitations of univariate regression approaches such as overfitting, unreliable estimation of regression coefficients, inflated standard errors or convergence problems do not apply to random survival forest [23]. Fourth, similar to survival trees, random survival forest is robust to outliers in the covariate space [24].

In this selective review, we aim to provide a survey of recent developments of random survival forests over the last decade relevant to bio-medical science and offer some guidelines on applying random survival forests in the context of high dimensional data. In Section 2, we give an introduction of the original random survival forest. In Section 3, we present several recently proposed splitting criteria for random survival forest, which are crucial to the performance of a survival forest. In addition to prediction, we also review its applications to variable selection in Section 4. Section 5 presents some further topics of random survival forest including transformations of covariates, competing risks, and dependent censoring. In section 6, we discuss the limitations of random survival forest and potential research directions for further research.

2. Basic Random Survival Forest

Denote the true survival time by a continuous random variable Y and the censoring time by a continuous variable C. Let T = min(Y, C) be the observation time and δ = I(Y≤C) be the right censoring indicator, where δ = 1 represents the observation is an event and δ = 0 represents the observation is censored. Let X = (x₁, x₂, ⋯, x_p) denote a p-dimensional covariate vector and D be the dataset containing n independent and identically distributed observations sampled from (X, T, δ), namely D = {(x_i, t_i, δ_i), i = 1,2, ⋯ , n}.

Before proceeding further, we first give a very brief introduction of survival trees, which serve as the building blocks of a random survival forest.

2.1. Survival tree

Tree-based approaches date back at least to [25] for classification and regression problems. However, it was the classification and regression tree (CART) algorithm developed by [26] that made decision trees a popular statistical learning tool. The CART paradigm has also been adopted by the first study containing all the elements of a standard survival tree for censored data [16] and by most survival trees [21].

Within the CART framework, construction of a survival tree usually contains the following three components:

• (a)Splitting. A tree is grown by splitting the data D recursively according to a splitting rule until a stopping criterion is met. Typical forms of splits include: splits of a single covariate, splits on linear combinations of predictors, and boolean combination splits [27]. In a basic binary splits using a single covariate, a potential split has the form X_j ≤s(j = 1, ⋯ , p) where s is a constant if X_j is continuous or ordinal, and the form X_j ∈{s₁, ⋯ , s_k} where s₁, ⋯ , s_k are possible values of X_j if X_j is categorical. Usually, a best split s* that maximizes some measure of improvement (splitting rule) is chosen. Common adopted splitting rules include logrank statistic, likelihood ratio statistic and martingale residuals [21,28].
• (b)
  Pruning. A fully grown trees tend to overfit the training data and often fail to generalize well on unseen test data. Hence, a large tree needs to be pruned to make a trade-off between misclassification error and the number of nodes in the pruned tree (the size of a tree). CART based pruning approaches utilize a cost-complexity measure for a tree A given by

  $$R_{\alpha }(A)=R(A)+\alpha \mid \tilde{A}\mid$$ (1)

  where R(A) is the sum of the resubstitution loss over the terminal nodes of A, |A| is the number of terminal nodes in A and α is a tuning parameter usually selected based on preferences of the tree size or cross-validation. After the pruning step, a sequence of nested pruned subtrees {A₀, A₁, ⋯ , A_M} is obtained, where A₀ is a fully grown tree and A_M is a root-only tree.
• (c)Selection. Once the pruned subtrees sequence has been obtained, we usually need to choose one single subtree for further exploration. The most popular methods are: the test set, cross-validation, bootstrap, AIC/BIC, and graphical (“kink” in the curve or elbow) [21]. Instead of choosing the tree with minimum loss, CART chooses the most parsimonious tree that performs substantially no worse than the ‘best’ tree according to the “one standard error rule” [29].

It is worth noting that tree pruning and tree selection are no longer necessary in random survival forests as the overfitting problem is greatly mitigated by constructing accurate but uncorrelated survival trees via bagging and random subspace [21,22].

2.2. Random survival forest

Several survival forest methods have been proposed in the literature [30,31]. Here we focus on the random survival forest (RSF) method of [22], which is the most closely related to the original random forest method [32]. The main output of this method is an estimated cumulative hazard function computed by averaging the Nelson-Aalen cumulative hazard function of each tree. The RSF algorithm consists of the following steps:

• (a)Drawing L bootstrap samples from a training dataset of size n. Namely, draw L random samples of size n with replacement from the original dataset. Theoretically speaking, the bootstrap sample contains about two-thirds of the original data. The remaining out-of-bag (OOB) observations will not appear in the bootstrap sample.
• (b)For each bootstrap sample, grow a full size survival tree based on a certain splitting criterion without pruning. At each internal node, randomly select mtry candidate covariates out of all p covariates. Candidate covariates, which minimize the risk within the nodes or maximize the separation between the nodes, are used for splitting. Stop growing until a certain stopping condition is met (e.g., when the number of observations within a terminal node is less than a preset value or when the node becomes pure). By default, $\mathit{mtry}=\sqrt{p}$ and the log-rank statistic is the splitting rule.
• (c)
  For each tree, a cumulative hazard function (CHF) is calculated. For a particular terminal node k at time point t, CHF is estimated by the Nelson-Aalen estimator.

  $${\widehat{H}}_h(t)=\sum _{t_{l,h^{\le t}}}\frac{d_{l,h}}{Y_{l,h}}$$ (2)

  where d_l,h and Y_l,h are the number of deaths and individuals at risk at time point t_l,h. Hence, all observations within the same node have the same CHF.
• (d)
  To predict the cumulative hazard of a new observation x, average over all CHFs from all the L trees to obtain the ensemble CHF of the forest:

  $${\widehat{H}}_E(t\mid x)=\frac{1}{L}\sum _{i=1}^L{\widehat{H}}_i(t\mid x)$$ (3)

  where H_i(t|x) denotes the CHF of the tree grown from the i-th bootstrap sample.

2.3. An Example

We illustrate the rationale of survival tree and random survival forest through a simple example. The dataset used here includes survival data for 137 patients with 9 censored observations from Veteran’s Administration Lung Cancer Trial [33]. In the trial, patients were randomized to receive either a standard chemotherapy or a test chemotherapy, and the event of interest here is the survival time in days since the treatment. A number of covariates which potentially affect survival time are provided: trt (type of lung cancer treatment: 1 for standard and 2 for test drug); celltype (type of cell involved: squamous, small cell, adeno and large); karno (Karnofsky score); diagtime (time between diagnosis and randomization); age (age in years); prior (any prior therapy, 0 for none and 10 for yes).

2.3.1. Cox proportional hazard model

We begin this analysis by presenting the results from the Cox proportional hazard model [4] in the following Table 1:

Table 1.

Cox proportional hazard model

Covariate	Coef	Exp (coef)	Se (coef)	z	p
trt	2.95E-01	1.34E+00	2.08E-01	1.42	0.1558
celltypesmallcell	8.62E-01	2.37E+00	2.75E-01	3.13	0.0017
celltypeadeno	1.20E+00	3.31E+00	3.01E-01	3.97	7.00E-05
celltypelarge	4.01E-01	1.49E+00	2.83E-01	1.42	0.1557
karno	−3.28E-02	9.68E-01	5.51E-03	−5.96	2.60E-09
diagtime	8.13E-05	1.00E+00	9.14E-03	0.01	0.9929
age	−8.71E-03	9.91E-01	9.30E-03	−0.94	0.3492
prior	7.16E-03	1.01E+00	2.32E-02	0.31	0.7579

The results suggest that among the six covariates examined in the study, cell type and Karnofsky score are significant predictors.

However, under different values of the Karnofsky, the log cumulative hazard functions are not parallel over time (Fig. 1), suggesting possible violations of the proportional hazards assumption. In this context, it is unrealistic to expect the reported coefficients to be satisfactory indicators of the actual covariate effects.

Fig. 1.

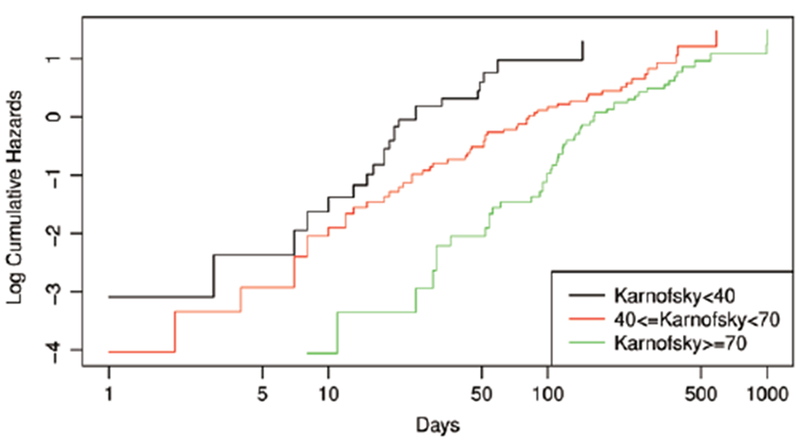
Plot of the estimated log cumulative hazard functions for different Karnofsky scores.

2.3.2. A CART survival tree

Next, we use a CART survival tree method (“rpart” R package) to analyze the same data. The corresponding tree plot is presented in Fig. 2 and in the plot, the first line in each node indicates the relative hazard rate within the group. From the entire sample of 137 patients, the first split is on Karnofsky score at 45 (with a hazard rate of 1), separating a group of 99 patients (with a hazard rate of 0.8) whose Karnofsky scores were greater than 45 from the rest whose scores were below that value (with a hazard rate of 2.5).

Fig. 2.

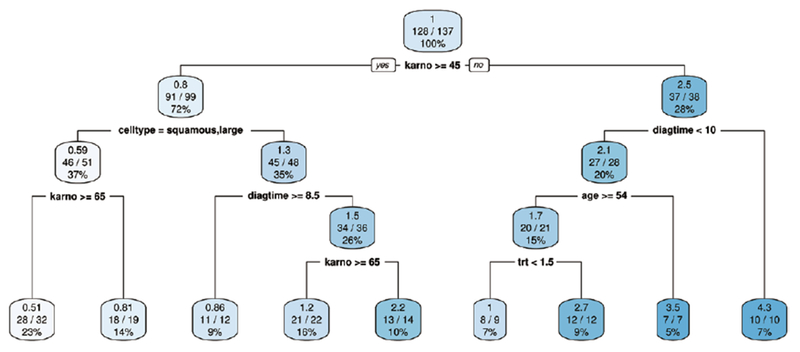
A CART survival tree.

From Fig. 2, one may observe that a patient with a Karnofsky score greater than 65 and a cell type of either squamous or large has the lowest risk (with a hazard rate of 0.51) while a patient who is older than 54 with a Karnofsky score less than 45 and a diagtime less than 10 has the highest risk (with a hazard rate of 3.5).

Note that in the final model, not all the covariates entering the computation will necessarily be selected. Only the covariates used as a best split in any of the tree nodes are chosen. This can be illustrated by an absence of covariate “prior” in the tree plot.

In CART survival trees, variable importance are generally computed based on the decrease of node impurity when the covariate in question is considered for the splitting. From variable importance scores produced by CART in Fig. 3, one can observe that the top two significant predictors indicated by CART are Karnofsky score and the time between diagnosis and randomization, which are different from the results obtained from the traditional Cox model.

Fig. 3.

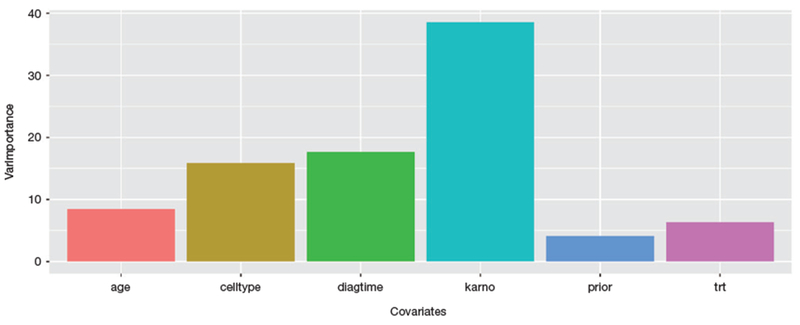
Variable importance scores by CART.

2.3.3. Random survival forest

Finally, we apply random survival forest to the above Veteran dataset. We use the program recently developed by [34], which is a fast implementation of random survival forests, particularly suited for high dimensional data. In our experiment, 500 bootstrap samples were generated. The default splitting rule (log-rank) and the default number of covariate randomly selected ($\sqrt{p}=2$) for each split were used. To illustrate a variety of methods available to calculate the variable importance scores in random survival forest, we use a different approach based on permutation methods here. In a permutation based approach, variable importance is based on the corresponding reduction of predictive accuracy when the covariate of interest is replaced with its random permutation value. The variable importance scores produced by random survival forest (Fig. 4) are different both from the results of Cox model and CART survival tree. The top two important covariates are the same with Cox model while the third covariate “age” is in similar ranking as in CART.

Fig. 4.

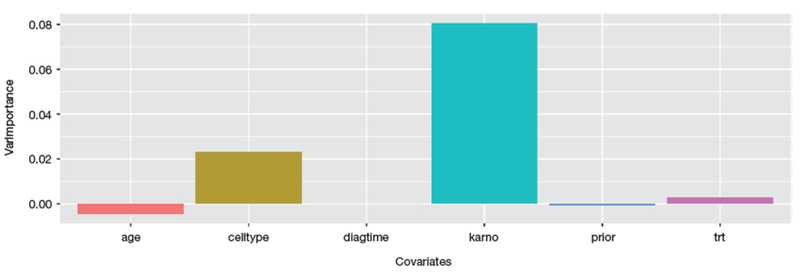
Variable importance scores by random survival forest.

As survival trees and random survival forests are generally used as risk prediction methods. In Fig. 5, we also report the predictive accuracy in term of C-index on the Veteran dataset by the above three approaches.

Fig. 5.

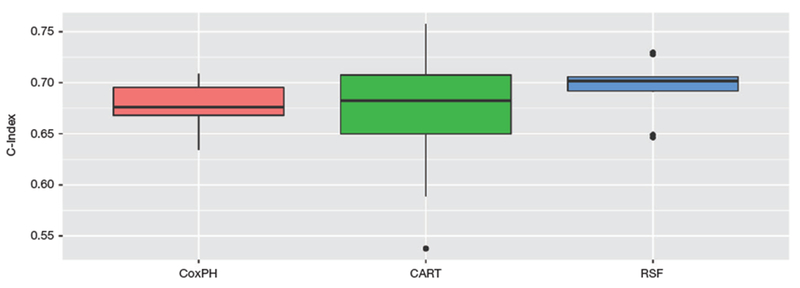
Performance comparison between Cox, CART and RSF.

It can be observed from Fig. 5 that in term of C-Index metric, random survival forest takes the first place, followed by CART and Cox model. However, the performance of CART survival tree is the most unstable. And this may justify the need and appropriateness of random survival forest in real applications.

Hence, when the underlying assumption for parametric or semi-parametric models (e.g. Cox models) are not satisfied, survival trees and random survival forests seem to perform better in prediction and can be used as effective alternatives [35–37].

3. Splitting Criteria

The splitting rule is an essential component of a survival tree and crucial to the performance of a survival forest [38]. There are a quite a few splitting criteria available for survival trees (see [28] for a comparison across nine splitting rules) but not all of them have been incorporated into the random forest framework. In the original random survival forests (RSF) [39], four distinct splitting methods, namely, a log-rank splitting rule, a conservation of events splitting rule, a log-rank score rule, and a fast approximation to the log-rank splitting rule were implemented. Besides these splitting rules, a few other new splitting criteria have also been proposed in the past decade [40–43], which are discussed below.

3.1. AUC splitting

Inspired by the concordance index [44], a new splitting criterion based on the area under the ROC curve (AUC) was proposed by [40]. In this AUC based splitting criterion, a possible split is made at value c for predictor x_j when a maximum value of

$$\mathit{AUC}(x_j,c)=\mid \frac{\Omega +0.5\beta +0.5\gamma }{\sum _{k,l\mid k<l}I(t_k<t_l){\sigma }_k}-0.5\mid$$ (4)

is reached, where Ω denotes the amount of all pairs where t_k < t_l, β the amount of all pairs where t_k < t_l and both values of x_kj, x_lj are smaller than or equal to the splitting value c, and γ the amount of all pairs where t_k < t_l and both values of x_kj, x_lj are greater than the splitting value c.

[40] presented a simulation study for the AUC-based criterion and suggested that in general AUC splitting outperforms the log-rank splitting only by a small margin. However, for datasets with lots of noise covariates or having a high censoring rate, AUC splitting performed much better than log-rank.

3.2. C-index splitting

[41] proposed a split criterion based Harrell’s concordance index(C-index) [45] which is defined by the following statistic

$$\mathrm{C}-\text{index}=\frac{\sum _{i,j}I(t_i>t_j)\cdot I({\eta }_j>{\eta }_i)\cdot {\delta }_j}{\sum _{i,j}I(t_i>t_j)\cdot {\delta }_j}$$ (5)

where the indices i and j refer to independent pairs of observations in the data, η_i and η_j are the respective predictions. Here δ_j discards pairs of observations that are not comparable because the smaller survival time is censored.

Assume that the observations in a tree node are split into two disjoint subnodes G₀ and G₁ by the threshold of a certain candidate covariate. In order to use the above C-index statistic for splitting, predictions η must be replaced by some appropriate values. They defined γ_i: = I(i ∈ G_i) ∈ {0,1} and estimated C-index statistic for splitting by

$$\begin{array}{cc}\hfill C& -\text{index}=\frac{\sum _{i,j}I(t_i>t_j)\cdot I(i\in G_0,j\in G_1)\cdot {\delta }_j}{\sum _{i\ne j}I(t_i>t_j)\cdot {\delta }_j}\hfill \\ \hfill & +\frac{0.5\cdot \sum _{i\ne j}I(t_i>t_j)\cdot I(i\in G_0,j\in G_0)\cdot {\delta }_j}{\sum _{i\ne j}I(t_i>t_j)\cdot {\delta }_j}\hfill \\ \hfill & +\frac{0.5\cdot \sum _{i\ne j}I(t_i>t_j)\cdot I(i\in G_1,j\in G_1)\cdot {\delta }_j}{\sum _{i\ne j}I(t_i>t_j)\cdot {\delta }_j}\hfill \end{array}$$ (6)

A large value of C-index indicates a better split and if a pair of observations fall into the same subnode, a value of 0.5 is assigned. They also showed that using different standardization and weighting schemes, both Harrell’s C-index and the log-rank statistic are special cases of the Gehan statistic [46].

Based on empirical studies using high dimensional simulated and real datasets, [41] identified three situations where C-index splitting might outperform log-rank statistic: when a high signal-to-noise ratio is present in the data; when the number of informative continuous covariates is large compared to the number of categorical covariates; when there is a high censoring rate in the data. Due to computational constraints caused by deeply grown survival trees, they recommended C-index splitting for small scale data and the log-rank splitting for large-scale studies.

They also pointed out that log-rank splitting is preferred over C-index in noisy scenarios. However, since C-index is regarded as a generalization of AUC [41,47,48], this finding is inconsistent with results obtained from [40] in which the author stated that AUC splitting performs much better than log-rank in case of lots of noise covariates.

3.3. L₁ splitting

By exploiting the test statistic proposed by [49] which has greater power than the log-rank test under a variety of situations, [42] came up with the splitting criterion based on the following so-called L₁ statistic

$$L_1=(n_L{n}_R){\int }_t\mid {\widehat{S}}_L(t)-{\widehat{S}}_R(t)\mid \mathit{dt}$$ (7)

where ${\widehat{S}}_L(t)$, ${\widehat{S}}_R(t)$, n_L and n_R denotes the Kaplan-Meier estimates and the number of observations in the left and right node, respectively.

To speed up computations in case of deeply grow trees, the also provided a simplification version of the L₁ statistic

$$L_1^{\ast }=\sqrt{(n_L{n}_R)}{\int }_t\mid {\widehat{S}}_L(t)-{\widehat{S}}_R(t)\mid \mathit{dt}$$ (8)

The performance of the above method was investigated through a simulation study of 30 scenarios and six real data sets. According to their results, compared to log-rank based random survival forest and Cox model, both versions provided good results but the L₁ criterion was slightly better. The authors pointed out their approaches can be potential competitors when the proportionality assumption is not satisfied.

3.4. Maximally selected rank splitting

More recently, [43] proposed a maximally selected rank statistics within the framework of conditional inference forests [30]. With maximally selected rank statistics, the optimal split variable is determined using a statistical test for binary splits and split variable selection bias is naturally reduced. To compare possible splits, they adopted the following score test statistic

$$T_{n\mu }=\frac{S_{n\mu }-E_{H_0}(S_{n\mu }\mid a,x)}{\sqrt{{\mathit{Var}}_{H_0}(S_{n\mu }\mid a,x)}}$$ (9)

where α is a log-rank score, x is a candidate covariate, S_nμ is the linear rank statistic for a split by a cutpoint μ, and E_H0(S_nμ|a, X), Var_H0 (S_nμ|a, X) are corresponding conditional expectation and variance as defined in [50].

The maximally selected rank statistic used in their study is defined as

$$M_n(a,x,{\epsilon }_1,{\epsilon }_2)=\underset{\mu \in [{\epsilon }_1,{\epsilon }_2]}{\max }(\mid T_{n\mu }\mid )$$ (10)

where ε₁, ε₂ correspond to quantiles of the distribution of x.

Instead of comparing such statistic values between split points on the same covariate and among all possible covariates in traditional random forest, they obtained p-values for the maximally selected rank statistic for each covariate and compare the covariates on the p-value scale. Since the exact distribution for the test statistic is unknown and no exact p-values can be derived, they proposed several techniques to approximate the p-values capable of dealing with large scaled datasets.

According to the results of simulation studies and three real datasets on breast cancer, they demonstrated that maximally selected rank splitting is effective in reducing split variable selection bias and is able to deal with non-linearity in the covariates. For example, their method performs better than random survival forest (log-rank splitting) if informative dichotomous covariates are combined with uninformative covariates with more categories and better than conditional survival forest if non-linear covariate effects are included. Lastly, this method is computationally efficient for large sample datasets such as genome-wide association studies.

4. Variable Selection

To handle high-dimensional or ultra-high dimensional survival data arising in modern biological and medical studies, variable selection plays a critical role and has become one of the hottest topics in survival analysis [8,51]. In additional to its general usage for survival prediction, random survival forest based methods have also been developed for variable selection in the past decade.

4.1. Variable hunting

[52] proposed a forward stepwise regularization based variable selection method called RSF-VH (variable hunting) in high-dimensional survival settings. They observed that in survival forests, covariates tending to split close to the root node have a strong effect on prediction accuracy and are deemed more important. Based on these facts, a dimensionless order statistic for trees called minimal depth of maximal subtrees is applied to calculate variable importance. By definition, minimal depth is also free of the choice of prediction error. In order to better regularize the forest, they discussed a weighted variable selection technique in a follow-up study [53].

The variable selection procedure in RSF-VH works as follows:

• (a)Randomly divide the data into training data and test data.
• (b)Train a random survival forest using a set of randomly chosen covariates, and select covariates using minimal depth thresholding.
• (c)The above selected covariates are used as an initial model. Covariates are then added to the initial model in order of minimal depth until the joint variable importance for the resulting nested models stabilizes.
• (d)Repeated the above steps several times. The most frequently appeared covariates in models with a size above average are finally selected and reported.

Results on different benchmark microarray data sets shows that RSF-VH yielded small gene lists consistently with low prediction error, compared to boosting, supervised principal components and other approaches.

The above approach was also extended to pathway analysis by [54] to account for important pathway of gene correlation and genomic interactions. Their result indicated that RSF pathway hunting algorithm is efficient in identifying signaling pathways from a high-dimensional genomic data with a relatively small sample size.

4.2. Iterative feature elimination

Different from most univariate approaches, [55] proposed a novel variable selection algorithm based on random survival forests to identify a set of prognostic genes in an iterative procedure. Their algorithm consists of the following five steps:

• (a)Train by a random survival forest model and rank all available covariates according to variable importance scores obtained by permutation.
• (b)Iteratively train a random survival forest model using the top most important covariates from the ranking list (default is 80%). And calculate the out-of-bag error rate in term of C-index.
• (c)Repeat the above step until the feature space contains only 2 covariates.
• (d)Find the set of covariates with the minimum number such that the out-of-bag error rate is within 1 standard error.

Unlike univariate selection, the above approach is able to incorporate multivariate correlations and does not require the user to set a cutoff for p-values. Experimental results on real high dimensional microarray datasets showed that their approach has the advantage of being able to identify a small set of genes while preserving the predictive accuracy for survival.

4.3. Topological index based on permutation

Different from using performance-based approaches, [56] proposed a strategy based on a testing procedure using a topological index which allows to select a basket of important variables in their iBST (improper Bagging Survival Tree) algorithm. Their variable selection procedure is iterated over the following steps:

• (a)Use the training data set to build a bagging survival forest. Compute the importance scores for all covariates using importance score obtained from the values of the splitting criterion at each split points or from tree depth (location) of the splitting and denote these scores by IIS_j(j=1, ⋯, p).
• (b)Similar to [57], train again a bagging survival forest and calculate the importance score for all covariates ${\mathit{IIS}}_j^0(j=1,\cdots ,p)$ based on the permutated data. And repeat this procedure Q times.
• (c)
  Compute the p-values for all competing variable x_j(j=1, ⋯, p)

  $$p_j=\frac{1}{Q}\sum _{q=1}^{Q}I\{{\mathit{IIS}}_{\mathit{jq}}^0>{\mathit{IIS}}_j\}$$ (11)
• (d)Given a global level α, variables satisfied the conditions that p_i < a/p are selected according to a Bonferroni procedure for multiple comparisons.

Stimulation and real data analysis showed that the above procedure is able to select the explanatory variables even in the presence of a high number of noise variables. However, since their procedure is permutation based, it could be computationally intensive.

5. Extensions of Random Survival Forests

Within the framework of random survival forests, a number of extensions or variants have also been developed. In this section, these developments will be presented in a thematic way. Transformation of covariates will be first discussed, followed by competing risks, dependent censoring and censoring unbiased transformations.

5.1. Transformation of covariates

Raw input covariates are not necessarily good predicator variables or features. Extracting good features via combinations, expansions and other kinds of transformation is one of the key steps to ensure the success of subsequent statistics or machine learning endeavors.

[35] proposed a random rotation survival forest (RRotSF) for analyzing high-dimensional survival data. The proposed methodology can be viewed as an extension of rotation forest from low dimensional data to high dimensional data. In their approach, the original variables is randomly split into K subsets (K is a parameter of the algorithm) and Principal Component Analysis (PCA) is applied to each data subset. Instead of keeping only a few major principal components for dimensional reduction, all principal components (rotation matrix) here are retained to preserve the variability information. Survival trees built on these rotated datasets make up a very competitive survival ensemble learning method.

In classification problems, prediction capability of a base learner usually improves when it is built from an extended variable space by adding new variables from randomly combination of two or more original variables. In their research, [36] investigated the plausibility of space extension technique, originally proposed for classification purpose, to survival analysis. By combing random subspace, bagging and extended space techniques, they developed a random survival forest with space extensions algorithm.

[58] gave a thorough analysis of the performance of random survival forests using feature extraction (e.g. the above mentioned transformation of covariates) and variable selection methods. And they concluded that feature extraction methods are a valuable alternative to variable selection methods if prediction is the main interest and if the training data is large enough such that the number of observations is sufficient to describe the underlying manifold. They suggested the use of embedded variable selection methods in case of small sample size data.

5.2. Competing risks

In bio-medical applications, a competing risk is an event that either hinders the observation of the event of interest or modifies the chance that this event occurs. For example, if the study aim is to estimate the time to death caused by dialysis, a patient may die of a kidney transplant. There have been quite a few extensions of survival trees to competing risks in the past decade [59–61]. However, extensions of random survival forests for competing risks have just been developed very recently.

[62] explored a novel extension of random survival forests to competing risks settings. Two news splitting rules for growing competing risk trees, namely log-rank splitting and the modified Gray’s splitting, were introduced to test the equality of the cause-specific hazard and the equality of the cumulative incidence function (CIF), respectively. They also defined several new ensemble estimators for competing risks such as ensemble CIF and event-specific estimates of mortality. To deal with high-dimensional problems and large data settings, they proposed that single competing risk tree is to be grown in each bootstrap sample and splitting rules are either event-specific, or combine event-specific splitting rules across all the competing events. Event-specific variable importance measures and minimal depth which is a non-event-specific by nature, can be used individually or simultaneously to identify variables specific to certain events or common to all events.

Instead of designing new splitting rules for competing risks, [63] proposed to replace the event status, which may be unknown due to right-censoring, by a jackknife pseudo-value on the basis of the marginal Aalen-Johansen estimator for the cumulative incidence function [64]. Then, machine learning tools such as random forests can be directly applied to the uncensored data. In their approach, node variance is chosen as split criterion for growing regression trees since the pseudoresponses take on values on a continuous scale. Due to the restriction of the pseudo random forests to a single cause of failure and few selected time points, their approach was computationally faster than that of the random survival forests in the high-dimensional setting.

5.3. Dependent censoring

The existing survival forest methods assume that given the covariates, the true time-to-event and the censoring times are independent. However, this assumption is not always satisfied as in the case of dependent censoring. In dependent censoring, both diseases may share common risk factors, but individuals dying not from the major cause are considered censored.

[65] was the first to explore survival forests in the dependent censoring context. They proposed different ways to build survival forests, by using a novel survival function estimator called copula-graphic estimator when aggregating the individual trees and/or by modifying the splitting rule. The main driver of the performance of this method is using an adequate value of Kendall’s τ to compute the copula-graphic estimator. They also propose a new method for building survival forests, called p-forest, that may be used not only when dependent censoring is suspected, but also as a new survival forest method in general. The results from a simulation study indicate that these modifications improve greatly the estimation of the survival function in situations of dependent censoring.

5.4. Censoring unbiased transformations

Different from relying on censoring-specific trees and forests, another alternative approach to model right censored data is to replace censored survival times with surrogate values using an appropriate censoring unbiased transformation, and then enter the imputed data into standard regression algorithms. More recently, [66] proposed a novel approach to build survival forest. By first extending the theory of censoring unbiased transformations, they constructed observed data estimators of full data loss functions in cases where responses can be right-censored. Two specific kinds of survival forests based on Buckley-James and doubly robust estimating equations are implemented. Compared to existing ensemble procedures such as random survival forests, conditional inference forests, and recursively imputed survival trees, their method demonstrated a better or competitive performance.

6. Discussion and Conclusion

Due to its high flexibility, built-in variable selection, and its nonlinear and nonparametric nature, the survival forests method has become an active research topic and a promising approach for high-dimensional survival data in many bio-medical applications. This paper provides only a partial survey of methodological developments of random survival forests in the past decade. There are many topics needing further investigations in this active area of research. For example, even though it is a nonparametric in nature, it does not mean that random survival forests can always be applied blindly to any type of survival data without caution. Recently, it was observed that random survival forest is inferior in identifying covariates with less ratio of population on a cardiovascular disease dataset due to its insensitivity to noise [67]. There is a need for a thorough investigation of the impact of noises variables with varying sample size for survival forests. Extending random survival forests to complex data structures such as interval-censored data, truncated data, joint modeling of longitudinal and time-to-event, is also warranted.