Abstract
Background
Many sensorimotor functions are intrinsically rhythmic, and are underlined by neural processes that are functionally distinct from neural responses related to the processing of transient events. EEG frequency tagging is a technique that is increasingly used in neuroscience to study these processes. It relies on the fact that perceiving and/or producing rhythms generates periodic neural activity that translates into periodic variations of the EEG signal. In the EEG spectrum, those variations appear as peaks localized at the frequency of the rhythm and its harmonics.
New method
Many natural rhythms, such as music or dance, are not strictly periodic and, instead, show fluctuations of their period over time. Here, we introduce a time-warping method to identify non-strictly-periodic EEG activities in the frequency domain.
Results
EEG time-warping can be used to characterize the sensorimotor activity related to the performance of self-paced rhythmic finger movements. Furthermore, the EEG time-warping method can disentangle auditory- and movement-related EEG activity produced when participants perform rhythmic movements synchronized to an acoustic rhythm. This is possible because the movement-related activity has different period fluctuations than the auditory-related activity.
Comparison with existing methods
With the classic frequency-tagging approach, rhythm fluctuations result in a spreading of the peaks to neighboring frequencies, to the point that they cannot be distinguished from background noise.
Conclusions
The proposed time-warping procedure is as a simple and effective mean to study natural non-strictly-periodic rhythmic neural processes such as rhythmic movement production, acoustic rhythm perception and sensorimotor synchronization.
Keywords: EEG, Frequency Tagging, Time Warping, Rhythm, Sensorimotor Synchronization, Anisochrony, Non-Stationarity
1. Introduction
Many sensorimotor functions are intrinsically rhythmic. This is the case for the perception of music, the production of gait movements, or the synchronization of complex motor performance to complex sensory stimulation as observed in dance or music playing.
It has been suggested that the neural processes underlying these rhythmic sensorimotor functions may at least partly differ from the sensorimotor processes underlying the processing and/or production of discrete transient events (Van Ede et al., 2018; Zoefel et al., 2018). For example, neural oscillations, which reflect rhythmic variations of excitability within a neural population (Buzsáki and Draguhn, 2004; Llinás, 1988), can be entrained to the frequency of a rhythmic process. By reinforcing phase and frequency specific information, this phenomenon could play a role in sensory selection (Schroeder and Lakatos, 2009), dynamic attention and temporal anticipation (Large and Jones, 1999), or the coupling of remote neural oscillators for multimodal integration (Lakatos et al., 2007).
EEG frequency tagging is a technique that is increasingly used to study rhythmic brain functions (Nozaradan, 2014). Classically, an event is repeated at a constant frequency such as to elicit a periodic and synchronized neural response, which can be measured in the spectrum of the recorded EEG signals at the frequency of stimulation and its harmonics. This “frequency-tagged” EEG activity can correspond to the periodic repetition of transient neural activities related to the processing of a periodic sequence of transient events. Furthermore, it may reflect the synchronized activity of neurons having the ability to entrain their activity to the periodic repetition or modulation of that stimulus, i.e. neurons that align the frequency and phase of their activity to the frequency and phase of the stimulus. A well-known example of this approach is the so-called “auditory steady-state evoked-potential”, which refers to the periodic EEG signal elicited by a sound whose intensity is modulated periodically over time (Galambos et al., 1981).
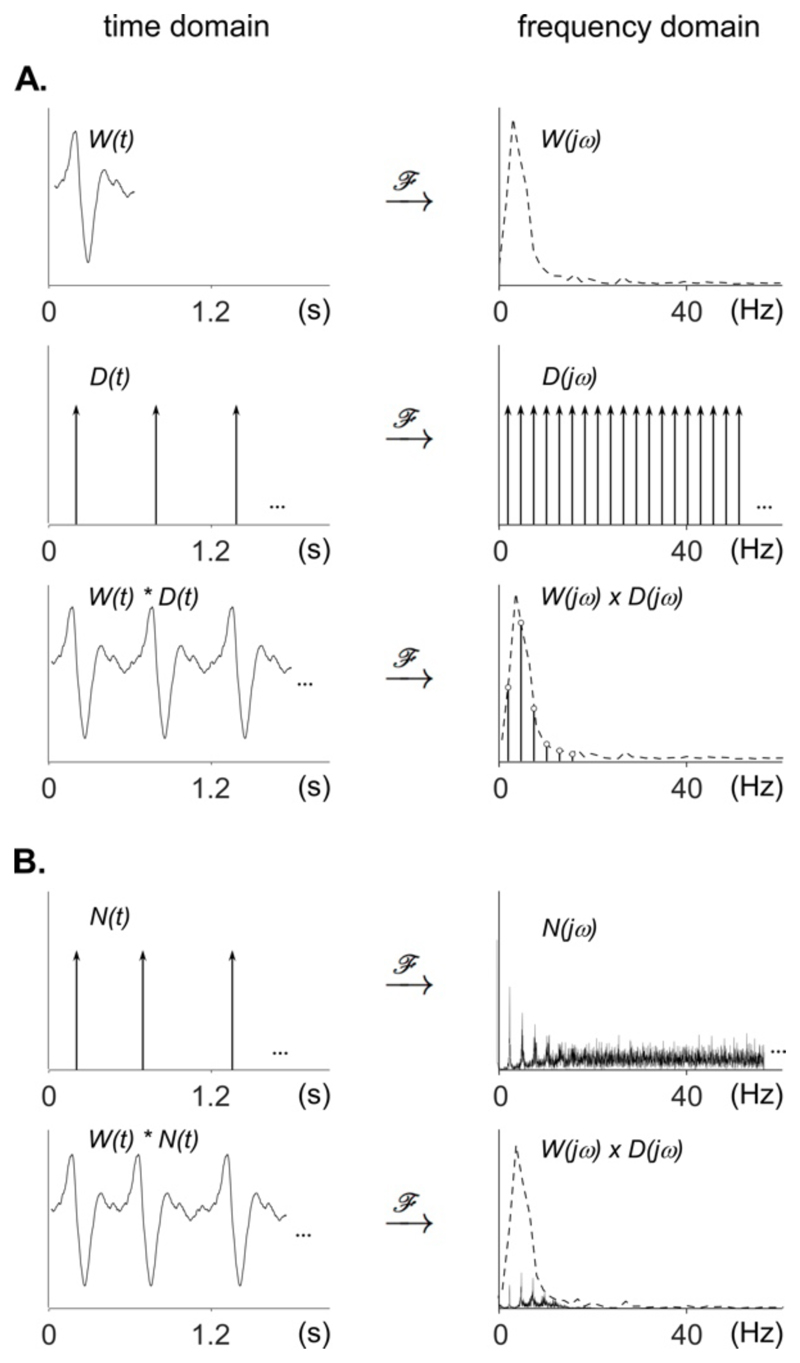
A periodic signal is a signal formed by a unitary waveform repeated at a regular interval, called the period. Mathematically, this periodic signal corresponds to the convolution of the unitary waveform with a periodic train of impulses, or Dirac comb (Fig. 1). The number of impulses per second corresponds to the fundamental frequency of the signal. When represented in the frequency domain, a pure sine wave appears as a single “peak”, at the fundamental frequency of the sine wave. When the unitary waveform is more complex, its spectrum consists of a set of peaks at the fundamental frequency and its harmonics. Mathematically, the spectrum of a periodic signal corresponds to the spectrum of the unitary waveform multiplied by the spectrum of the Dirac comb. Therefore, the amplitude of the peaks obtained at the different harmonics is determined by the frequency spectrum of the unitary waveform (Fig. 1; Collura, 1995; Zhou et al., 2016).
Figure 1. Time and frequency domain representation of periodic and non-strictly-periodic signals.
A. Time domain and frequency domain representations of a unitary waveform W(t), a periodic train of impulses (Dirac comb; D(t)), and a periodic signal corresponding to the convolution of W(t) and D(t) in the time domain, and the multiplication of W(jω) and D(jω) in the frequency domain. Note that the Fourier transform of the periodic signal has a spectrum that concentrates on the fundamental frequency and harmonics determined by the periodicity of the Dirac comb, with a relative amplitude distribution that is determined by the shape of the spectrum of the unitary waveform. B. Time domain and frequency domain representations of a non-strictly-periodic signal corresponding to the convolution of W(t) with a non-strictly-periodic train of impulses N(t). In contrast to the spectrum of the strictly-periodic Dirac comb D(jω), the frequency spectrum of the non-strictly-periodic train of impulses N(jω) is not constituted of isolated peaks at the fundamental frequency and harmonics. Instead, the energy of the signal spreads to surrounding frequencies, and the spectrum will become more and more random if the non-periodicity is increased. The spectrum of the non-strictly-periodic signal obtained by multiplying the spectrum W(jω) of the unitary waveform with the spectrum N(jω) of the non-strictly-periodic train of impulses, contains peaks having a lower amplitude as compared to the strictly-periodic signal.
Taking advantage of the spectral decomposition of periodic signals, the EEG frequency-tagging approach is able to isolate EEG signals elicited by periodic stimulation, even if it does not constitute sharp transients (e.g. EEG activity elicited by progressive sinusoidal modulation of stimulation amplitude) (Nozaradan et al., 2011). The frequency-tagging approach is also able to identify frequency-specific responses despite high inter-individual phase variability (Nozaradan et al., 2018). Importantly, several studies have shown that EEG frequency tagging can be used to tag cortical activity related to high-level perceptual processes such as the processing of musical rhythms (Chemin et al., 2014; Nozaradan et al., 2017, 2016a, 2016b, 2013, 2012, 2011), linguistic constituents (Buiatti et al., 2009) and face perception (Rossion, 2014; Rossion et al., 2015).
However, an important limitation of the EEG frequency-tagging approach comes from the fact that natural rhythms are not strictly periodic, i.e. their periodicity fluctuates over time (Chen et al., 1997; Goodwin, 1997; Repp, 2005). For example, when performing self-paced hand tapping movements, the variations in period duration reach approximately 4% of the average period (Semjen et al., 2000). Similarly, the subjective experience of a musical pulse is robust to period fluctuations, within a range of anisochrony evaluated to 8.6% of the mean period (Madison and Merker, 2002). The frequency-tagging approach implies to perform a Fourier transform on relatively long sequences of EEG signals, which is only valid under the assumption that the signal of interest is stationary, i.e., that its distribution parameters such as mean and variance do not change over time (Chatfield, 1989). As compared to the sharp peaks observed in the Fourier transform of a signal that is strictly periodic, the peaks observed in the Fourier transform of a fluctuating signal have lower amplitudes because each peak spreads out to neighboring frequencies (Fig. 1). In the case of EEG where the non-strictly-periodic signal is embedded within large-amplitude background activity, this reduction in peak amplitude and sharpness often renders their identification impossible.
In this paper, we propose a simple time-warping method to “render periodic” EEG signals related to activities that are not strictly periodic and, thereby, make it possible to “concentrate” non-strictly-periodic neural responses in the frequency domain. In other words, we propose to transform the signal in order to meet the assumption of stationarity that is necessary for the frequency-tagging approach.
The proposed time-warping method consists in stretching, i.e. contracting and dilating, the EEG signal such as to “accelerate” or “decelerate” it when the time interval between two events is respectively greater or smaller than the mean period of the non-strictly-periodic events. This time-warping procedure is fundamentally different from another method referred to as EEG “false-sequencing”, consisting in reconstructing a periodic signal by concatenating non-warped segments of the EEG signal having a constant length corresponding to the mean period (Quek and Rossion, 2017). The superiority of one approach over the other is actually dependent on the nature of the frequency-tagged EEG signal. If the waveform of the periodic EEG signal is independent of the period fluctuations, EEG false-sequencing should be superior to EEG time-warping, as compressing and dilating the EEG signal would distort the unitary waveform. Conversely, if the waveform of the periodic EEG signal is not invariant but is contracted or dilated as a function of the periodic fluctuations, EEG time warping could be superior to EEG false-sequencing, because compressing and dilating the EEG signal could actually enhance the unitary waveform similarity across repetitions.
To assess our time-warping method, we applied it to EEG signals recorded while participants performed self-paced and acoustic-paced periodic tapping movements of the hand, as well as simulated EEG data.
2. Methods
2.1. Participants
Nine right-handed healthy volunteers (6 females, 3 males; all right-handed; mean age = 28 years, SD = 4) took part in the experiment after providing written informed consent. All participants were familiar with EEG, but had no prior experience with the experimental setting. They had no history of hearing, neurological, or psychiatric disorder, and none were taking any medication at the time of the experiment. The experiment was approved by the local ethics committee.
2.2. Experimental design
The experiment contained three conditions, corresponding to three different tasks: (1) finger tapping synchronized to an acoustic beat, (2) finger tapping alone, and (3) passive listening to the acoustic beat (Fig. 2). The three conditions were presented in separate blocks, whose order of presentation was randomized across participants.
Figure 2. Experimental design of the EEG experiment.
The experiment was composed of three experimental conditions, presented in separate blocks, whose order was counterbalanced across participants. Each block started with up to five dummy trials of 16 s to allow the participant to become familiar with the task. Then, trials of 96 s (T) were repeated seven times, forming one block. The finger tapping synchronized to an acoustic beat task consisted in tapping the index finger in synchrony with an acoustic beat. The acoustic beat consisted in a 96 s sequence of 120 isochronous pure tones presented at an 800 ms inter beat interval. The finger tapping alone task consisted in tapping the right index against the table, at a rate as constant as possible. A short 6.4 s pacing acoustic sequence of eight isochronous beats (800 ms inter beat interval) was presented before each trial. The passive listening to the acoustic beat task consisted in listening to the 96 s sequence of 120 isochronous pure tones occurring at an 800 ms inter beat interval.
Finger tapping synchronized to an acoustic beat
The task consisted in tapping the right index finger against the table, in synchrony with an acoustic beat. The acoustic beat consisted in a 96 s sequence of 120 isochronous 990 Hz pure tones lasting 150 ms (7.5 ms rise time, 142.5 ms fall time), occurring with a period of 800 ms. The tapping consisted in a flexion of the metacarpophalangeal articulation of the right index, until the fingertip touched the table, followed by finger extension. Participants were instructed to synchronize their tapping to the acoustic rhythm such that the tapping of the index with the table coincided with the acoustic beats. A sequence of 96 s composed one trial, and the trial was repeated seven times to form one block.
Finger tapping alone
The task consisted in tapping the right index against the table, at a rate as constant as possible. A short 6.4 s pacing acoustic sequence of eight isochronous beats occurring with a period of 800 ms was presented before each trial. Participants were instructed to synchronize their tapping to this acoustic pacer, and to continue the tapping movements after the acoustic pacer stopped, keeping the tapping rhythm as constant as possible. The end of the trial was indicated by presenting a single tone. One trial lasted 96 s and was repeated 7 times to form one block.
Passive listening to the acoustic beat
In this condition, participants were requested to listen passively to the 800 ms periodic acoustic beat. Such as in the other blocks, each trial had a duration of 96 s and was repeated 7 times.
During the whole experiment, participants were seated comfortably in a chair, with their arms resting on a table and the right elbow placed on a cushion at wrist height. The right hand was attached to an orthosis used to record the movements performed in the finger tapping tasks (Fig. 3). The tapping hand was hidden from participants with a sheet of fabrics. Before the beginning of the experiment, participants could familiarize with the orthosis. Furthermore, each block was preceded by up to five dummy trials of 16 s in order to allow the participant to become familiar with the task. Before starting the actual EEG recording, the experimenter witnessed that the task was performed adequately.
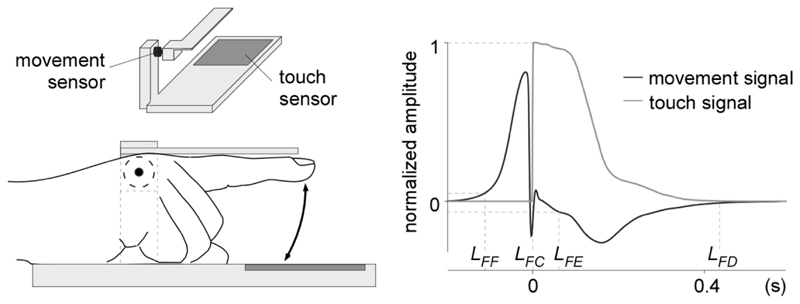
Figure 3. Finger movement recording.
Movements of the finger were recorded using an orthosis placed around the first two phalanges of participant’s right index (left panel). A movement sensor was mounted on the orthosis and a touch sensor was embedded in the surface onto which the finger tapped. The right panel shows the normalized amplitude of the two sensor signals, averaged across participants, conditions and taps. The point LFF corresponds to the initiation of the finger flexion. LFC corresponds to the time at which the fingertip touches the table. LFE corresponds to the initiation of finger extension. LFD corresponds to the time at which the finger returns to the default position. Note that the dynamics of finger flexion, measured by the time interval between LFF and LFC, was quite constant across participants and taps, whereas the dynamics of finger extension, measured by the time between LFE and LFD, was more variable. Those results are consistent with the fact that participants were requested to synchronize the tapping of the finger against the touch sensor.
In all conditions, the onset of each trial was initiated by the participant pressing a button. A random 1.5 to 3 s delay separated the button press from the onset of the trial. In order to encourage the participants to focus their attention to the task, at the end of each trial, they were asked to “rate” how much they paid attention to the task and how “precise” their tapping was. The instructions and questions were displayed on a computer screen, using MATLAB 2014a (The MathWorks, Natick, MA). The acoustic stimuli were presented binaurally using pneumatic earphone inserts (Etymotic ER1, Etymotic Research, Elk Grove, IL), and played using an externally-triggered zero latency audio stimulus generator (AUDIOFile, Cambridge Research System, Rochester, United Kingdom).
2.3. EEG recording
During the EEG recording, participants were instructed to relax, avoid any unnecessary head or body movement, and keep their eyes fixated on a point marked on a white surface in front of them. To avoid any visual feedback, the tapping hand was hidden from the participant using a sheet of fabric. The experimenter remained in the recording room with the participant at all times to monitor compliance to the procedure and instructions, as well as to monitor the EEG signals and, eventually, provide feedback to the participant in case of important eye or movement artifacts.
The EEG was recorded using 64 Ag-AgCl electrodes placed on the scalp according to the international 10-10 system (Waveguard64 cap, Cephalon A/S, Norresundby, Denmark). Electrode impedances were kept below 10 kΩ. The signals were amplified, low-pass filtered at 500 Hz, digitized using a sampling rate of 1,000 Hz, and referenced to an average reference (64-channel high-speed amplifier, Advanced Neuro Technologies, Enschede, The Netherlands). A trigger, produced by the audio stimulus generator was sent to the EEG amplifier at the beginning of each trial.
2.4. Finger-movements recording
Movements of the finger were recorded using a galvanometer (OSST8062, Sintec Optronics Pte Ltd, Singapore) mounted on an orthosis placed around the first two phalanges of participant’s right index, and a touch sensor (Makey Makey, MIT Media Lab's Lifelong Kindergarten, USA) placed on the table, in regard to the tapping finger (Fig. 3). The galvanometer generated a continuous signal proportional to the speed of the finger movement (range: ± 0.5 V; positive and negative values corresponding to finger flexion and extension, respectively) and the touch sensor measured the impedance between the finger and the touch pad. The signals generated by the galvanometer and the touch sensor were digitized at a sampling rate of 1,000 Hz using two auxiliary channels of the EEG system. Both signals were normalized such that, for the galvanometer signal, the unit corresponded to the maximal speed of the finger flexion, and for the touch sensor signal, the unit corresponded to the value at contact of the finger with the sensor.
For each movement (indexed by k) of the finger tapping trials, the onset of finger flexion movement (latency of finger flexion: LFF k) was arbitrarily defined as the moment when the normalized galvanometer signal became >0.05, and the time at which the fingertip came in contact with the table (latency of finger contact: LFC k) was defined as the moment when the touch signal passed from 0 to 1.
The two measures were used to compute, for each movement k, the duration of each finger flexion (DFF k = LFC k − LFF k) and the duration between the finger tap and the preceding finger tap (inter-tap-interval: ITIk = LFC k − LFF k−1).
2.5. EEG preprocessing
The continuous EEG signals recorded in each condition were segmented in epochs lasting 96 s, extending between 0 to 96 s relative to the onset of each task. A 50 Hz notch filter and a 0.1 Hz high-pass Butterworth zero-phase filter were applied to remove artifacts due to environmental noise as well as slow signal drifts. Artifacts produced by eye blinks or eye movements were removed from the EEG signal using a validated method based on an independent component analysis (Jung et al., 2000), using the runica algorithm (Bell and Sejnowski, 1995; Makeig, 2002). Those artifacts were identified visually based on their spatio-temporal distribution (waveform features typical of eye blinks, topographical distribution maximal at frontal electrodes).
2.6. Non-time-warped EEG signals
The 96 s preprocessed EEG epochs were further segmented to only keep the 2nd to the 106th event (i.e. from the second beat in the finger tapping synchronized on an acoustic beat task and the passive beat listening task, and the second finger tap in the finger tapping alone task). The EEG signal recorded during the first event was discarded to avoid contamination by the transient evoked potentials related to the onset of the task (e.g. Nozaradan et al., 2011). Especially in the finger tapping alone task, the number of tapping events varied from trial-to-trial. Across all trials, conditions and participants, the minimum number of tapping events was 106. Therefore, to perform the analyses on epochs having the same number of events across trials, conditions and participants, the EEG signals were segmented such as to include up to the 106th event. On average, we thus discarded 10 % of the 120 original events per trial. To ensure that the Fourier transform of these signals would yield discrete spectra with a frequency resolution respecting the alignment of the bins corresponding to the beat frequency and its harmonics, the final length of the epochs was set to a multiple of the beat period. In the tapping synchronized to the beat task and the passive beat listening task, this corresponded to 0.8 s x 105 events = 84 s. In the tapping alone task, the length of the different segments of 105 taps was not consistent across the epochs, because of the fluctuations of the tapping rate. The range of lengths spanned from 68.0 to 88.8 s.
2.7. Time-warped EEG signals
The 96 s EEG epochs recorded in the two finger tapping tasks were warped in the time domain to remove the fluctuations of the ITIs. The warping was performed by dilating or compressing each ITI segment of the EEG signals, using a linear interpolation, such as to obtain a constant number of bins for each ITI segment (800 bins corresponding to 0.8 s at a 1,000 Hz sampling rate). This procedure resulted in “accelerating” the EEG signals when the time interval between two touch onsets exceeded the 0.8 s target period, and in “decelerating” the EEG signal when the time interval between two touch onsets was shorter than the 0.8 s target period (Fig. 4, see Supplementary Material for algorithm and technical details). Such as for the original signals, the time-warped EEG signals were then segmented to only keep 105 events starting from the second event following the actual performance of the task. In all the conditions, the length of the epochs corresponded to 0.8 s x 105 events = 84 s.
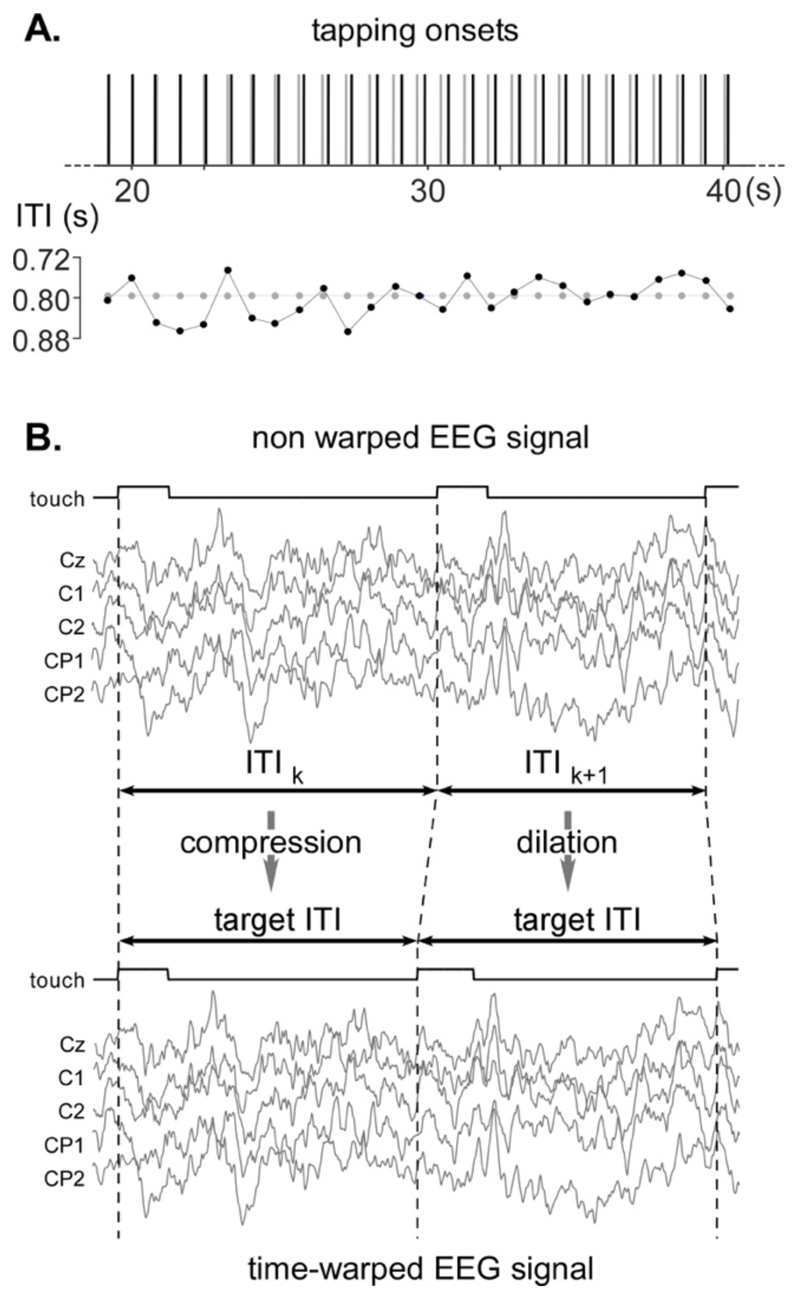
Figure 4. EEG time-warping procedure.
A. As shown in this representative trial of the finger-tapping to the beat task, the inter-tap interval (ITI) fluctuated from tap to tap, with a mean ITI of 800 ms. B. The time-warping procedure consists in compressing or dilating the EEG signals recorded within each ITI such as to scale it to a fixed target ITI of 800 ms. The compression and dilation of the EEG segments was computed by linear interpolation of the non-time-warped signals.
2.8. Frequency-domain analysis
The non-time-warped and time-warped EEG epochs were transformed in the frequency domain using a discrete Fourier transform (Frigo and Johnson, 1998). In the tapping synchronized to the beat and the passive beat listening conditions, the discrete Fourier transform yielded a frequency spectrum of signal amplitude (μV) ranging from 0 to 500 Hz with a frequency resolution of 0.0119 Hz (Bach and Meigen, 1999). In the tapping alone task, the frequency resolution ranged between 0.0113 Hz and 0.0147 Hz, because of the variations in epoch duration. Therefore, these frequency spectra were resampled using the nearest interpolation method such as to obtain a resampled resolution of 0.0119 Hz.
The periodic EEG activity related to beat perception and finger tapping can be expected to generate peaks in the EEG frequency spectra at the fundamental frequency (F=1.25 Hz) and harmonics (2F=2.5 Hz, 2F=3.75 Hz, etc.). To quantify these responses, the contribution of background noise was removed by subtracting, at each bin of the frequency spectra, the average amplitude measured at neighboring frequency bins (eight frequency bins ranging from −0.14 to −0.05 Hz and from +0.05 to +0.14 Hz relative to each frequency bin). The validity of this subtraction procedure relies on the assumption that, in the absence of a strong periodic signal, the signal amplitude at any given frequency bin should be similar to the signal amplitude of the mean of the surrounding frequency bins (Mouraux et al., 2011; Retter and Rossion, 2016). This subtraction procedure using neighboring frequency bins is important because background EEG noise is not equally distributed across scalp channels and, most importantly, is greater at lower frequencies as compared to higher frequencies (the power spectrum of background EEG typically follows a 1/f function; Freeman et al., 2003).
The noise-subtracted spectra were then averaged across epochs, for each condition and each individual. Within these averaged spectra and for each condition, we identified the frequencies at which the periodic EEG activity generated a significant increase in amplitude across individuals, by performing a t-test against zero of the amplitudes measured at the fundamental frequency (F=1.25 Hz) and the 23 first harmonics (from 2F=2.5 to 23F=30 Hz), averaged across all scalp channels (Fig. 5). The significance level was set at p < 0.05, corrected for multiple comparisons (Bonferroni). Finally, a summary measure of the amplitude of the periodic EEG response was computed by summing the noise-subtracted amplitudes at the fundamental frequency and harmonics that were significantly greater than zero (t-test against zero), and hemispheric lateralization was assessed by performing a paired-sample t-test between the average of the signals measured over the left and the right hemisphere.
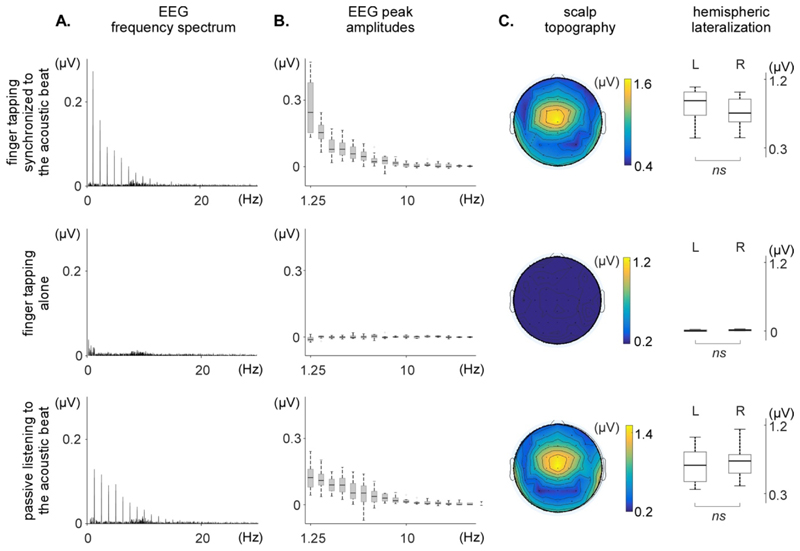
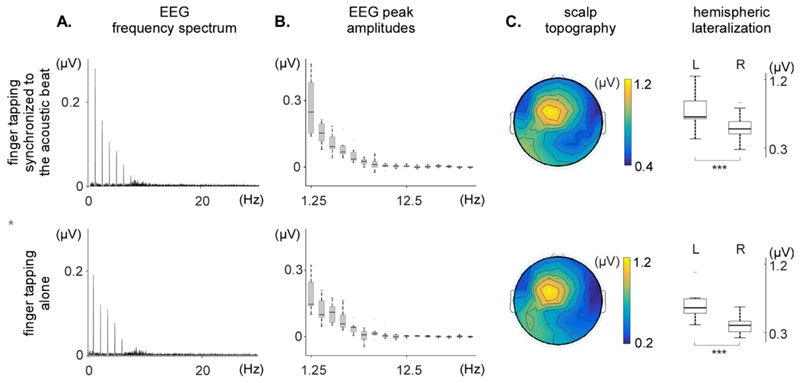
Figure 5. Frequency-domain analysis of the non-time-warped EEG signals obtained in each of the three conditions (finger tapping synchronized to the acoustic beat, finger tapping alone, and passive listening to the acoustic beat).
A. Frequency spectrum of the EEG signals, averaged across participants and across the 64 EEG channels. Note the clear peaks at beat frequency and harmonics in each of the EEG spectra, except for the EEG signals recorded in the finger tapping alone condition. B. Peak amplitude at the fundamental frequency and harmonics, across participants (median, lower/upper quartile and minimum/maximum values). C. Scalp topography and hemispheric lateralization of the periodic EEG response (sum of the spectrum amplitude at beat frequency and harmonics significantly greater than zero). The non-time-warped signals obtained in the finger taping synchronized to the acoustic beat and the passive listening conditions show similar scalp topographies, maximal over fronto-central electrodes, and symmetrically distributed over the two hemispheres (L: left; R: right). No significant activity is identified in the finger tapping alone condition.
2.9. Time-domain analysis
The non-time-warped and time-warped EEG signals of the tapping alone condition were segmented from -0.3 to +0.5 s relative to the latency of each contact of the fingertip with the table (LFC). The obtained segments were averaged across trials and across participants, in order to visualize and compare the shape of the unitary waveform in both the non-time-warped and the time-warped signals.
Additionally, the segments were categorized in two equal groups according to the length of the ITI. For each trial, segments were assigned to the short or long ITI group depending on whether the trial ITI was shorter or longer than the trial median ITI. Categorized segments were then averaged across trials and participants, in order to visualize and compare the shape of the unitary waveforms for long and short ITIs.
Estimation of similarity between non-time-warped and time-warped unitary waveforms, as well as short-ITI and long-ITI related waveforms, was made by computing, for each participant, the correlation coefficient between the two signals.
All EEG processing steps including the time warping procedure were carried out using Letswave 6 (Institute of Neuroscience, University of Louvain; www.letswave.org), an open-source MATLAB (The MathWorks, Natick, MA) toolbox. The EEG time-warping algorithm is available as supplementary material, and can be downloaded on the Github repository: github.com/BaptisteChemin/EEG-Time-Warping.
2.10. Control experiment: resting EEG signals
To examine whether the time-warping procedure could generate an artefactual enhancement of amplitude at the frequencies of interest due to the periodic compression or dilation of successive EEG segments, we conducted a control experiment in which resting EEG was recorded in nine healthy volunteers. During the experiment, participants were instructed to remain still, with their eyes open, during seven trials of 96 s. The signals were then processed using the same procedures as for the main experiment. Time-warping of the resting EEG signals was performed using the tapping latencies of the nine participants in the finger-tapping alone task.
2.11. Control analysis using simulated data
Time warping is likely to generate a certain quantity of signal distortion. Its ability to recover non-strictly-periodic EEG signals is likely to depend on the period duration, the amount of period fluctuation, and the shape of the unitary waveform. Most importantly, its depends on whether decreases/increases in period duration are associated with compression/dilation of the unitary EEG waveform, as would be expected if the period fluctuations are determined by neural processes reflected in the unitary waveform (Large and Jones, 1999).
To assess the influence of these factors, we generated simulated EEG data using as unitary waveform the group-level average unitary EEG waveform recorded at electrode Cz in the tapping alone condition. First, we generated a strictly-periodic 1.25 Hz signal by concatenating 105 unitary waveforms having a length of 0.684 s. Second, we generated a series of 1,000 non-strictly-periodic signals using the same unitary waveform separated by a fluctuating interval (normal distribution, mean interval = 0.8 s, controlled coefficient of variation (CV)). In this dataset, the shape of the unitary waveform was invariant. When the interval was greater than the length of the unitary waveform, the empty gap was replaced by a segment of ongoing EEG randomly taken from the resting EEG signals recorded in the control experiment. Conversely, when the interval was smaller than the length of the unitary waveform, the overlapping portions of the two consecutive unitary signals were summed. Third, we generated another series of 1,000 non-strictly-periodic signals in which the unitary waveform was contracted or dilated such as to adjust their length to the period duration, as could be expected if period fluctuations are determined by the temporal dynamics of the neural processes underlying the unitary waveform. All signals were band-passed using a 0.1 to 60 Hz Butterworth filter. Various amounts of period CV were tested, ranging between 0-30%, in steps of 0.5 %. After FFT transform, a measure of the amplitude of the periodic signal was obtained by summing the peaks at 1.25 Hz and the 9 following harmonics in the frequency spectrum of each signal. Finally, for both non-strictly-periodic datasets, an amplitude ratio was computed by dividing the amplitude of the periodic signal measured in the non-strictly-periodic dataset (averaged across the 1000 signals) by the amplitude of the periodic signal measured in the strictly-periodic signal. The Matlab toolbox developed to run these simulations is available on the GitHub repository.
3. Results
3.1. Finger tapping latencies
The ITIs between finger taps were normally distributed, with a narrower dispersion in the finger tapping synchronized to the acoustic beat condition (800 ± 46 ms; coefficient of variation: 5.7%) as compared to the finger tapping alone condition (779 ± 65 ms; coefficient of variation: 8.4%). The greater variability in ITI in the tapping alone task was expected, as in that condition, participants could not use the external acoustic pacer to improve their performance (Repp, 2005).
3.2. Frequency-domain analysis
3.2.1. Periodic EEG responses observed in the non-time-warped signals
The group-level average frequency spectra obtained in the finger tapping synchronized to an acoustic beat, the finger tapping alone and the passive beat listening conditions are shown in Figure 5.
In the finger tapping synchronized to the acoustic beat condition, clear peaks were observed in the EEG spectra at 1.25 Hz and harmonics. The noise-subtracted amplitudes at the beat frequency (1.25 Hz) and at the harmonic frequencies 2.5, 3.75, 5, 6.25, 7.5, 8.75, 10, 11.25, 12.5, 15, 18.75, 20, 22.5, 28.75 and 30 Hz were significantly greater than zero. The scalp topography of this periodic EEG response was maximal at fronto-central electrodes, and did not show any clear hemispheric lateralization relative to the tapping hand. This absence of lateralization was confirmed by the fact that the average of the signals measured over the left hemisphere (M=0.8461 μV, SD=0.2246 μV) was not significantly different from the average of the signals measured over the right hemisphere (M=0.778 μV, SD=0.197 μV); t(8)=2.30, p=0.0506.
In the finger tapping alone condition, no clear peaks were observed in the EEG frequency spectra, and only the noise-subtracted amplitude at 15 Hz was marginally greater than 0, amongst the 24 tested frequencies (t = 2.53, p = 0.035, uncorrected for multiple comparisons).
In the passive listening to the acoustic beat condition, clear peaks were observed in the EEG spectra, whose amplitudes were significantly greater than zero at 1.25, 2.5, 3.75, 5, 6.25, 7.5, 8.75, 10, 11.25, 12.5, 13.75, 15, 16.25, 17.5, 21.25, 22.5, 25, 26.25, and 27.5 Hz. The scalp topography of the response obtained during passive beat listening resembled closely the scalp topography of the response obtained in the finger tapping synchronized to the acoustic beat condition, being maximal at fronto-central electrodes and symmetrically distributed over the two hemispheres. The average of the signals measured over the left hemisphere (M=0.677 μV, SD=0.245 μV) was not significantly different from the average of the signals measured over the right hemisphere (M=0.703 μV, SD=0.229 μV; t(8)=-0.64, p=0.5424).
3.2.2. Periodic EEG responses observed in the time-warped signals
The group-level average frequency spectra of the time-warped EEG signals obtained in the tapping synchronized to the acoustic beat and tapping alone conditions are shown in Figure 6.
Figure 6. Frequency-domain analysis of the time-warped EEG signals in the frequency domain obtained in two of the three conditions (finger tapping synchronized to the acoustic beat and finger tapping alone conditions).
A. Frequency spectrum of the EEG signals, averaged across participants and across the 64 EEG channels. Note the clear peaks in both spectra. B. Peak amplitudes at the fundamental frequency and its harmonics, across participants (median, lower/upper quartile and minimum/maximum values). C. Scalp topography and hemispheric lateralization of the periodic EEG response (sum of the spectrum amplitudes at beat frequency harmonics significantly greater than zero). The time-warped EEG signals recorded in the finger tapping synchronized to the acoustic beat and finger tapping alone conditions show similar topographies, lateralized onto the (left) hemisphere contra-lateral to the tapping hand (L: left; R: right).
In the tapping synchronized to the beat condition, clear peaks were observed in the EEG spectra at 1.25 Hz and harmonics. The noise-subtracted amplitudes at the beat frequency (1.25 Hz) and at the harmonic frequencies 2.5, 3.75, 5, 6.25, 7.5, 16.25, and 17.5 Hz were significantly greater than zero. The scalp topography of this periodic EEG response was maximal over left central and parietal electrodes, and was thus clearly different from the scalp topography of the response observed in the non-time-warped EEG signals, which was symmetrical and maximal over fronto-central electrodes. This was confirmed by the fact that the average of the signals measured over the left hemisphere (M=0.798 μV, SD=0.261 μV) was significantly greater than the average of the signals measured over the right hemisphere (M=0.569 μV, SD=0.184 μV; t(8)=7.72, p<0.001).
In the tapping alone condition, clear peaks were observed in the EEG spectra of the time-warped signals at 1.25 Hz and harmonics. This was in striking contrast with the lack of any clear response in the EEG spectra of the non-time-warped signals of the same condition. The noise-subtracted amplitudes at the beat frequency (1.25 Hz) and at the harmonic frequencies 2.5, 3.75, 5, 6.25, 12.5, 13.75, 15, and 28.75 Hz were significantly greater than zero. The scalp topography of this periodic EEG response resembled closely the periodic EEG response obtained in the time-warped signals of the tapping synchronized to the acoustic beat condition, both being maximal over left central and parietal electrodes. The average of the signals measured over the left hemisphere (M=0.638 μV, SD=0.203 μV) was significantly greater than the average of the signals measured over the right hemisphere (M=0.385 μV, SD=0.119 μV); t(8)=7.53, p<0.001).
3.3. Time-domain analysis
3.3.1. Comparison of non-time-warped and time-warped EEG signals
The unitary waveforms obtained by averaging non-time-warped and time-warped EEG segments across ITIs are shown in Fig. 7A. Visual inspection of those waveforms showed very little differences between the non-time-warped and time-warped signals. The differences were mostly characterized by a smoothing of high-frequency components in the time-warped signals. The correlation coefficient between the two signals confirmed the high similarity between the two waveforms, across participants (R=0.971 +- 0.034).
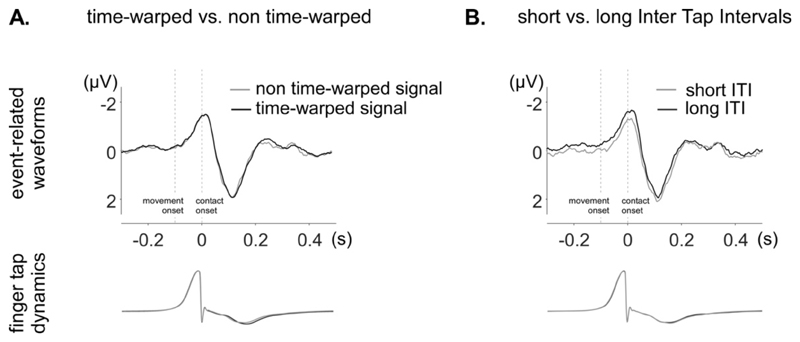
Figure 7. Time-domain analysis of the unitary EEG waveforms obtained in the tapping alone condition.
The average waveforms (electrode Cz) were obtained by aligning EEG segments to the onsets of the contact of the fingertip with the table. The finger tap dynamics recorded by the movement sensor are shown in the lower part of the figure, also averaged relative to contact onset. A. Average waveform of the non-time-warped EEG signal (grey) and the time-warped EEG signal (black). In both non-time-warped and time-warped signals, a clear EEG response is observed, time-locked to the contact onset, and consisting of a negative peak concomitant to the tapping, followed by a positive peak maximal approximately 110 ms after tapping. The non-time-warped and time-warped waveforms are highly similar, except for a slight smoothing of rapid activities in the time-warped signal. B. Waveforms obtained by averaging EEG segments separately for short ITIs (grey) and long ITIs (black). The period preceding contact onset was more negative for long ITIs as compared to short ITIs. Furthermore, the negative peak concomitant to the finger contact was broader.
3.3.2. Comparison of long and short ITI related EEG signals
The unitary waveforms obtained by averaging EEG segments separately for short and long ITIs are shown in Fig. 7B. The unitary waveforms obtained by averaging short ITI segments tended to differ from the unitary waveforms obtained by averaging long ITI segments (R=0.902 +- 0.062). Specifically, for long ITI segments, the period preceding contact onset was more negative and, most importantly, the negative peak concomitant to the finger contact was broader. Furthermore, the baseline preceding the negative peak was more negative for short ITIs.
3.4. Control experiment: time-warping of resting EEG signals
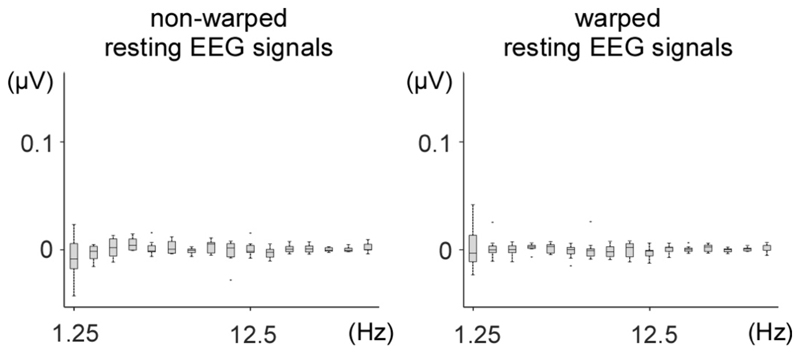
As shown in Fig. 8, the frequency spectra of the time-warped resting EEG signals recorded in the control experiment showed no significant enhancement of amplitude at 1.25 Hz and harmonics, indicating that the time-warping procedure did not introduce any artefactual enhancement of signal amplitude at the frequencies of interest.
Figure 8. Frequency-domain analysis of non-time-warped and time-warped resting EEG data.
The time-warping procedure was applied to resting EEG data using the tapping latencies of the nine participants in the finger-tapping alone task, with an average 800 ms ITI. The graphs show the peak amplitudes at the fundamental frequency and its harmonics, across participants (median, lower/upper quartile and minimum/maximum values). Time-warping did not introduce any artefactual enhancement of peak amplitude at those frequencies.
3.5. Control analysis using simulated data
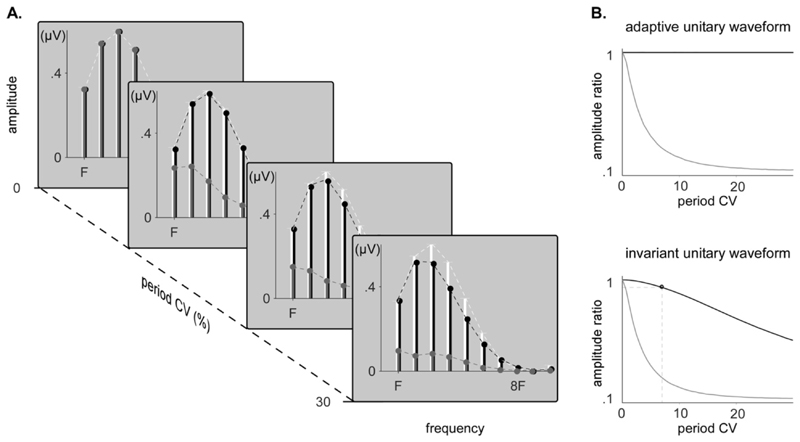
In both the invariant unitary waveform dataset and the adaptive unitary waveform dataset, increasing the period fluctuations led to a rapid decrease of the amplitude ratio when no time-warping was applied. When time-warping was applied to the non-strictly-periodic dataset constructed using an invariant unitary waveform, a slow decrease in amplitude ratio was observed, reaching 0.95 at a coefficient of variation of 5.5%. Expectedly, the amplitude ratio remained 1 independently of period fluctuations when the time-warping was applied to the non-strictly-periodic dataset constructed by contracting/dilating the unitary waveforms. The results are displayed in Fig. 9.
Figure 9. Amplitude recovery of original and tested synthetic signals.
A. Amplitude of the peaks measured in the spectra of strictly-periodic simulated EEG signals (white), non-strictly-periodic simulated EEG signals with a unitary waveform of invariant shape (grey) and time-warped non-strictly-periodic simulated EEG signals with a unitary waveform of invariant shape (black), for increasing coefficients of variation (CV) of the period fluctuation. B. Amplitude ratio between both time-warped (black) or non-time-warped (grey) non-strictly periodic signals and the strictly periodic signals, when the unitary waveform dynamically adapts to the period fluctuations or stays invariant and independent to the period fluctuations.
4. Discussion
Our results show that time-warping EEG signals is a simple and efficient method to concentrate non-strictly-periodic EEG signals in the frequency domain, such as the EEG activity elicited while performing self-paced periodic movements of the hand. Importantly, our results also show that the time-warping procedure does not generate any artefactual periodic response when it is applied to resting EEG signals.
Without time-warping, the EEG signals recorded when participants regularly tapped their right index against a table without any external synchronization cue showed almost no response in the frequency domain. In striking contrast, the same EEG signals showed clear responses in the frequency domain when they were time-warped using the tapping latencies. The scalp topography of these responses was maximal over the hemisphere contralateral to the tapping finger, compatible with activity originating predominantly from primary sensorimotor cortices. Most interestingly, when participants performed the hand tapping synchronized with an acoustic beat, the time-warping procedure was able to disambiguate, in the frequency domain, the periodic EEG signals related to processing the acoustic rhythm from the periodic EEG signals related to the performance of the finger tapping movement. In the non-time-warped EEG signals, the topography of the response was maximal over fronto-central electrodes, resembling closely the topography of the response recorded when participants listened passively to the acoustic beat, compatible with activity originating predominantly from auditory areas bilaterally (Nozaradan et al., 2011). In contrast, in the time-warped EEG signals, the topography of the response was maximal over the hemisphere contralateral to the tapping finger, resembling closely the response obtained in the tapping alone condition. This selective concentration of auditory- and movement-related activities was possible because each signal had a unique pattern of period fluctuations. In the non-time-warped signals, the activity related to processing the acoustic beat could be expected to be more periodic than the activity related to the fluctuating hand tapping movement. Hence, the peaks in the EEG frequency spectrum concentrated activity related to processing the acoustic beat. Conversely, in the timewarped signals, the activity related to processing the beat was rendered less periodic and the activity related to movement was rendered more periodic, leading to a stronger concentration of movement-related activity in the frequency domain.
Therefore, in the case of multiple response streams having the same average period but distinct period fluctuations, the time-warping method can be used to tease out different response streams by selectively concentrating the periodic activity of a specific response stream. The method does not allow to strictly isolate one stream from the other, but it does allow emphasizing one response stream over the others. An important advantage of time-warping over EEG false-sequencing, which concatenate segments of non-warped EEG signals (Quek and Rossion, 2016), is that false-sequencing cannot split coincident responses that are temporally overlapping. Hence, it cannot disentangle concurrent streams of sensory- and movement-related neural activities (Besle et al., 2009; Perez et al., 2013). Provided that the different streams originate from different brain areas and, therefore, project differently on the scalp, additional tools such as current source density analysis or blind source separation methods could be used to further disambiguate different response streams (Cohen and Gulbinaite, 2017; Ding et al., 2011).
The time-warping method assumes that the unitary waveform related to not-strictly periodic events dynamically adapts to the fluctuating inter-event-intervals. This seems to be at least partly the case for the periodic EEG signals elicited by self-paced rhythmic tapping movements. Indeed, the waveforms obtained by averaging separately the non-time-warped EEG segments corresponding to short and long inter-tap-intervals showed some dissimilarity: the negative wave occurring at tapping onset was broader for long ITIs as compared to short ITIs, indicating that its temporal dynamics are dependent on the period fluctuations.
The time-warping procedure was applied to nearly-periodic rhythms that fluctuated with an ecological coefficient of variation of 8.4% of the 0.8 s average period. The time-warping procedure could be used in future experiments to gain a better understanding of the mechanisms underlying neural entrainment to periodic stimuli. In the context of rhythm perception, Large & Jones (1999) proposed that the entrainment to a periodic rhythm emerges from the dynamics of neural systems acting as “internal oscillators” which can be entrained to nearly-periodic rhythms, and are tolerant to period fluctuations up to a certain amount (Madison and Merker, 2002). In this view, the neural processing of rhythms that are strongly non periodic would differ from the neural processing of periodic and nearly-periodic rhythms (Teki et al., 2011). Because the time-warping procedure can be used to cancel out the effects of period fluctuations on the frequency representation of non-strictly-periodic signals, the approach could be used to compare EEG responses elicited by rhythms fluctuating within or beyond the ecological range for rhythm perception. Furthermore, the contrasted effect of EEG time-warping and EEG false sequencing on the amplitude recovery of the signal of interest, given its dynamics at the single event level, could be further exploited in such experimental paradigms.
Finally, the EEG time-warping approach opens new perspectives in various research areas. For example, it could be used to compare EEG responses in participants displaying varying abilities to produce synchronized movements such as musicians vs. non-musicians, or healthy participants vs. motor-impaired patients. The approach could also be exploited to remove nearly-periodic movement-related artifacts, by concentrating these artifacts in the frequency domain, and filtering them out in the frequency domain (also see Gwin et al., 2010; Kline et al., 2015 for complementary approaches).
However, even after applying time warping, one should be cautious when comparing non-strictly-periodic EEG signals having different amounts of period fluctuations. If period fluctuations are associated with contractions/dilations of the unitary waveform, time warping will recover all the signal power, regardless of the amount of period fluctuations. In contrast, if the unitary waveform is invariant, the recovery will depend on the amount of period fluctuations. If the difference in the amount of periodic fluctuations is relatively small (lower than 5.5% of CV in our simulated EEG dataset), the difference in recovery will be negligible. However, if the difference in the amount of periodic fluctuations is very large, this will significantly affect recovery.
In conclusion, EEG time warping procedure is a simple and effective tool that makes it possible to use EEG frequency-tagging to study non-strictly-periodic neural processes related to rhythmic movement production, acoustic rhythm perception and, more generally, rhythmic sensorimotor synchronization.
Supplementary Material
Funding
BC is supported by the National Fund for Scientific Research for the French-speaking part of Belgium (FNRS-FRIA). AM is supported by the ERC starting grant PROBING-PAIN (336130). DM is a Research Fellow of the Fonds de la Recherche Scientifique - FNRS.
Footnotes
Author Contributions
BC designed the experiment. BC, GH and AM developed the time-warping function, written in Matlab 2016b and implemented in Letswave. Testing and data collection was performed by BC. BC analyzed the data. BC, DM and AM interpreted the results. BC and AM wrote the manuscript. All authors approved the final version of the manuscript for submission.
Declaration of Conflicting Interests
The authors declare that they have no conflicts of interest with respect to their authorship or the publication of this article.
References
- Bach M, Meigen T. Do’s and don’ts in Fourier analysis of steady-state potentials. Doc Ophthalmol. 1999;99:69–82. doi: 10.1023/A:1002648202420. [DOI] [PubMed] [Google Scholar]
- Bell AJ, Sejnowski TJ. An information-maximization approach to blind separation and blind deconvolution. Neural Comput. 1995;7:1129–59. doi: 10.1162/neco.1995.7.6.1129. [DOI] [PubMed] [Google Scholar]
- Besle J, Bertrand O, Giard MH. Electrophysiological (EEG, sEEG, MEG) evidence for multiple audiovisual interactions in the human auditory cortex. Hear Res. 2009;258:143–151. doi: 10.1016/j.heares.2009.06.016. [DOI] [PubMed] [Google Scholar]
- Buiatti M, Peña M, Dehaene-Lambertz G. Investigating the neural correlates of continuous speech computation with frequency-tagged neuroelectric responses. Neuroimage. 2009;44:509–519. doi: 10.1016/j.neuroimage.2008.09.015. [DOI] [PubMed] [Google Scholar]
- Buzsáki G, Draguhn A. Neuronal oscillations in cortical networks. Science. 2004;304:1926–9. doi: 10.1126/science.1099745. [DOI] [PubMed] [Google Scholar]
- Chatfield C. Non-linear and non-stationary time series analysis: M.B. Priestley, (Academic Press, London, 1988), £25.00, pp. 237. Int J Forecast. 1989;5:428–429. doi: 10.1016/0169-2070(89)90048-4. [DOI] [Google Scholar]
- Chemin B, Mouraux A, Nozaradan S. Body Movement Selectively Shapes the Neural Representation of Musical Rhythms. Psychol Sci. 2014 doi: 10.1177/0956797614551161. [DOI] [PubMed] [Google Scholar]
- Chen Y, Ding M, Kelso JAS. Long Memory Processes (1 / f α Type) in Human Coordination. Phys Rev Lett. 1997;79:4501–4504. doi: 10.1103/PhysRevLett.79.4501. [DOI] [Google Scholar]
- Cohen MX, Gulbinaite R. Rhythmic entrainment source separation: Optimizing analyses of neural responses to rhythmic sensory stimulation. Neuroimage. 2017;147:43–56. doi: 10.1016/j.neuroimage.2016.11.036. [DOI] [PubMed] [Google Scholar]
- Collura T. Human steady-state visual and auditory evoked potential components during a selective discrimination task. J Neurother. 1995 doi: 10.1300/J184v01n03_01. [DOI] [Google Scholar]
- Ding L, Ni Y, Sweeney J, He B. Sparse Cortical Current Density Imaging in Motor Potentials Induced by Finger Movement. J Neural Engeneering. 2011;8 doi: 10.1007/s10439-011-0452-9. Engineering. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Freeman WJ, Holmes M, Bruke B. Spatial spectra of scalp EEG and EMG from awake humans. Clin Neurophysiol. 2003;114 doi: 10.1111/ina.12046. [DOI] [PubMed] [Google Scholar]
- Frigo M, Johnson S. FFTW: an adaptive software architecture for the FFT. Proceedings of the 1998 IEEE International Conference on Acoustics, Speech and Signal Processing; 1998. pp. 1381–1384. [Google Scholar]
- Galambos R, Makeig S, Talmachoff PJ. A 40-Hz auditory potential recorded from the human scalp. Proc Natl Acad Sci U S A. 1981;78:2643–2647. doi: 10.1073/pnas.78.4.2643. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goodwin BC. Temporal organization and disorganization in organisms. Chronobiol Int. 1997;14:531–6. doi: 10.3109/07420529709001474. [DOI] [PubMed] [Google Scholar]
- Gwin JT, Gramann K, Makeig S, Ferris DP. Removal of Movement Artifact From High-Density EEG Recorded During Walking and Running. J Neurophysiol. 2010;103:3526–3534. doi: 10.1152/jn.00105.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jung TP, Makeig S, Westerfield M, Townsend J, Courchesne E, Sejnowski TJ. Removal of eye activity artifacts from visual event-related potentials in normal and clinical subjects. Clin Neurophysiol. 2000;111:1745–1758. doi: 10.1016/S1388-2457(00)00386-2. [DOI] [PubMed] [Google Scholar]
- Kline JE, Huang HJ, Snyder KL, Ferris DP. Isolating gait-related movement artifacts in electroencephalography during human walking. J Neural Engeneering. 2015;12:87–92. doi: 10.1088/1741-2560/12/4/046022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lakatos P, Chen CM, O-Connell MN, Mills A, Schroeder CE. Neuronal Oscillations and Multisensory Ineractions in Primary Auditory Cortex. Neuron. 2007;53:279–292. doi: 10.1016/j.neuron.2006.12.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Large EW, Jones MR. The Dynamics of attending; how people track time-varying events. Psychol Rev. 1999;106 [Google Scholar]
- Llinás RR. The intrinsic electrophysiological properties of mammalian neurons: Insights into central nervous system function. Science (80-. ) 1988;242:1654–1664. doi: 10.1126/science.3059497. [DOI] [PubMed] [Google Scholar]
- Madison G, Merker B. On the limits of anisochrony in pulse attribution. Psychol Res. 2002;66:201–207. doi: 10.1007/s00426-001-0085-y. [DOI] [PubMed] [Google Scholar]
- Makeig S. Response: event-related brain dynamics -- unifying brain electrophysiology. Trends Neurosci. 2002;25:390. doi: 10.1016/s0166-2236(02)02198-7. [DOI] [PubMed] [Google Scholar]
- Mouraux A, Iannetti GD, Colon E, Nozaradan S, Legrain V, Plaghki L. Nociceptive steady-state evoked potentials elicited by rapid periodic thermal stimulation of cutaneous nociceptors. J Neurosci. 2011;31:6079–6087. doi: 10.1523/JNEUROSCI.3977-10.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nozaradan S. Exploring how musical rhythm entrains brain activity with electroencephalogram frequency-tagging. Philos Trans R Soc Lond B Biol Sci. 2014;369:1–10. doi: 10.1098/rstb.2013.0393. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nozaradan S, Peretz I, Keller PE. Individual Differences in Rhythmic Cortical Entrainment Correlate with Predictive Behavior in Sensorimotor Synchronization. Sci Rep. 2016a;6 doi: 10.1038/srep20612. 20612. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nozaradan S, Peretz I, Missal M, Mouraux A. Tagging the neuronal entrainment to beat and meter. J Neurosci. 2011;31:10234–10240. doi: 10.1523/JNEUROSCI.0411-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nozaradan S, Peretz I, Mouraux A. Steady-state evoked potentials as an index of multisensory temporal binding. Neuroimage. 2012;60:21–28. doi: 10.1016/j.neuroimage.2011.11.065. [DOI] [PubMed] [Google Scholar]
- Nozaradan S, Schönwiesner M, Caron-Desrochers L, Lehmann A. Enhanced brainstem and cortical encoding of sound during synchronized movement. 2016b doi: 10.1016/j.neuroimage.2016.07.015. [DOI] [PubMed] [Google Scholar]
- Nozaradan S, Schönwiesner M, Keller PE, Lenc T, Lehmann A. Neural bases of rhythmic entrainment in humans: critical transformation between cortical and lower-level representations of auditory rhythm. Eur J Neurosci. 2018;47:321–332. doi: 10.1111/ejn.13826. [DOI] [PubMed] [Google Scholar]
- Nozaradan S, Schwartze M, Obermeier C, Kotz SA. Specific Contributions of Basal Ganglia and Cerebellum To The Neural Tracking of Rhythm. Cortex. 2017;95:156–168. doi: 10.1016/j.cortex.2017.08.015. [DOI] [PubMed] [Google Scholar]
- Nozaradan S, Zerouali Y, Peretz I, Mouraux A. Capturing with EEG the Neural Entrainment and Coupling Underlying Sensorimotor Synchronization to the Beat. Cereb Cortex. 2013 doi: 10.1093/cercor/bht261. [DOI] [PubMed] [Google Scholar]
- Perez O, Kass RE, Merchant H. Trial time warping to discriminate stimulus-related from movement-related neural activity. J Neurosci Methods. 2013;212:203–10. doi: 10.1016/j.jneumeth.2012.10.019. [DOI] [PubMed] [Google Scholar]
- Quek G, Rossion B. Predictability does not generate or modulate category-selective processes in fast periodic visual stimulation streams. J Vis. 2016;16:723. doi: 10.1167/16.12.723. [DOI] [PubMed] [Google Scholar]
- Quek GL, Rossion B. Category-selective human brain processes elicited in fast periodic visual stimulation streams are immune to temporal predictability. Neuropsychologia. 2017;104:182–200. doi: 10.1016/j.neuropsychologia.2017.08.010. [DOI] [PubMed] [Google Scholar]
- Repp BH. Sensorimotor synchronization: a review of the tapping literature. Psychon Bull Rev. 2005;12:969–992. doi: 10.3758/BF03206433. [DOI] [PubMed] [Google Scholar]
- Retter TL, Rossion B. Uncovering the neural magnitude and spatio-temporal dynamics of natural image categorization in a fast visual stream. Neuropsychologia. 2016;91:9–28. doi: 10.1016/j.neuropsychologia.2016.07.028. [DOI] [PubMed] [Google Scholar]
- Rossion B. Understanding individual face discrimination by means of fast periodic visual stimulation. Exp brain Res. 2014;232:1599–621. doi: 10.1007/s00221-014-3934-9. [DOI] [PubMed] [Google Scholar]
- Rossion B, Torfs K, Jacques C, Liu-Shuang J. Fast periodic presentation of natural images reveals a robust face-selective electrophysiological response in the human brain. J Vis. 2015;15 doi: 10.1167/15.1.18. 15.1.18. [DOI] [PubMed] [Google Scholar]
- Schroeder CE, Lakatos P. Low-frequency neuronal oscillations as instruments of sensory selection. Trends Neurosci. 2009;32:9–18. doi: 10.1016/j.tins.2008.09.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Semjen A, Schulze HH, Vorberg D. Timing precision in continuation and synchronization tapping. Psychol Res. 2000;63:137–147. doi: 10.1007/PL00008172. [DOI] [PubMed] [Google Scholar]
- Teki S, Grube M, Kumar S, Griffiths TD. Distinct neural substrates of duration-based and beat-based auditory timing. J Neurosci. 2011;31:3805–3812. doi: 10.1523/JNEUROSCI.5561-10.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Ede F, Quinn AJ, Woolrich MW, Nobre AC. Neural Oscillations: Sustained Rhythms or Transient Burst- Events? 2018 doi: 10.1016/j.tins.2018.04.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou H, Melloni L, Poeppel D, Ding N. Interpretations of Frequency Domain Analyses of Neural Entrainment: Periodicity, Fundamental Frequency, and Harmonics. Front Hum Neurosci. 2016;10 doi: 10.3389/fnhum.2016.00274. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zoefel B, ten Oever S, Sack AT. The Involvement of Endogenous Neural Oscillations in the Processing of Rhythmic Input: More Than a Regular Repetition of Evoked Neural Responses. Front Neurosci. 2018;12:1–13. doi: 10.3389/fnins.2018.00095. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.