Numerical cognition in honeybees enables addition and subtraction

Honeybees learn to add or subtract one item from a set using color cues and can interpolate operations to a novel number.

Abstract

Many animals understand numbers at a basic level for use in essential tasks such as foraging, shoaling, and resource management. However, complex arithmetic operations, such as addition and subtraction, using symbols and/or labeling have only been demonstrated in a limited number of nonhuman vertebrates. We show that honeybees, with a miniature brain, can learn to use blue and yellow as symbolic representations for addition or subtraction. In a free-flying environment, individual bees used this information to solve unfamiliar problems involving adding or subtracting one element from a group of elements. This display of numerosity requires bees to acquire long-term rules and use short-term working memory. Given that honeybees and humans are separated by over 400 million years of evolution, our findings suggest that advanced numerical cognition may be more accessible to nonhuman animals than previously suspected.

INTRODUCTION

Currently, there is considerable debate surrounding the ability of animals to have or learn complex number skills (1–5). A distinction is made between species that are able to use quantical (e.g., quantity discrimination) and numerical (exact, symbolic) cognition (2). While many species are able to use quantical cognition to forage, make decisions, and solve problems, it is debated whether any nonhuman or nonprimate animals could reach the level of numerical cognition, such as exact number and arithmetic operations, e.g., solving addition and subtraction problems (1, 2). Such a capacity would require complex management of quantities in both working memory and longer-term rule-based memory (6). There are studies which demonstrate that vervet monkeys (6), chimpanzees (7–9), orangutans (10), rhesus monkeys (11), one African gray parrot (12, 13), pigeons (14), spiders (15, 16), and human infants (17, 18) have the ability to add and/or subtract. Some studies show very sophisticated addition and subtraction abilities such as in the case of a chimpanzee and an African gray parrot that could both label the result of an addition sum using Arabic symbols or an English label, respectively, which would constitute exact numerical cognition (7, 12, 13). Other studies show that some species are able to perform addition and subtraction problems spontaneously, without training, in a more naturalized task, such as spiders that can count prey items and notice when prey is added or subtracted (15) and rhesus monkeys that choose to approach obscured food in the wild when a subtraction sum should result in food being present (11).

Honeybees are a model for insect cognition and vision (19, 20). Bees have demonstrated the ability to learn a number of rules and concepts to solve problems such as “left/right” (21), “above/below” (22), “same/different” (23), and “larger/smaller” (24–26). Honeybees have also shown some capacity for counting and number discrimination when trained using an appetitive (reward- only) differential conditioning framework (27–30). Recent advances in training protocols reveal that bees perform significantly better on perceptually difficult tasks when trained with an appetitive-aversive (reward-punishment) differential conditioning framework (31). This improved learning capacity is linked to attention in bees (31), and attention is a key aspect of advanced numerosity and spatial processing abilities in the human brain (32, 33). Using this conditioning protocol, honeybees were recently shown to acquire the numerical rules of “greater than” and “less than” and subsequently apply these rules to demonstrate an understanding that an empty set, zero, lies at the lower end of the numerical continuum (34). Thus, to inform the current debate on number skills in animals, research on insects with miniature brains enables valuable comparisons of what brains of different sizes and architectures can achieve.

The capacity of honeybees to learn complex rules and concepts (20) alongside evidence of their number sense (29, 34) suggests that they are a good model for testing numerical cognition. We trained bees to identify a salient color (blue or yellow) as a symbolic representation of whether to follow a rule based on addition (blue) or subtraction (yellow) and thus choose the correct result of an arithmetic operation.

In this study, honeybees were trained to enter a Y-maze and view a visual sample stimulus presented vertically containing a set of elements in isolation (Fig. 1). Bees would then fly through an opening into a decision chamber and choose between two possible options (Fig. 1). The sample stimulus could contain one, two, four, or five elements (one, two, or four elements if blue/addition; two, four, or five elements if yellow/subtraction). If the elements were blue, the bees would need to choose the stimulus option in the decision chamber which was one element greater than the sample; however, if the elements were yellow, the bees would need to choose the stimulus which contained one less element than the sample number (Fig. 1). The color of the elements, and thus the arithmetic problem to be solved, was randomly assigned per bee for each trial. Correct and incorrect options during experiments ranged from one to five elements, and the incorrect option could be higher or lower than the correct option (which also included the sample number as a possible incorrect option). The sample number of three elements was never shown during training and was only used as a novel sample number during testing. See Materials and Methods below for more information.

Fig. 1. Experimental apparatus used to train and test free-flying bees on their capacity to learn addition and subtraction.

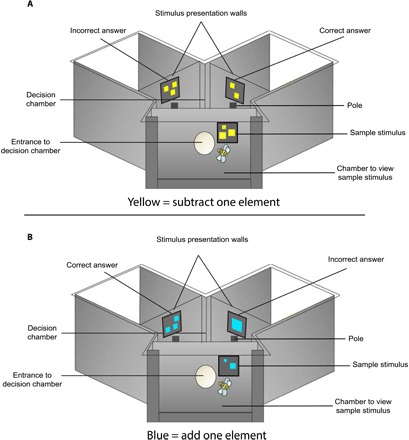
Apparatus setup for (A) subtraction and (B) addition trials. Diagram shows parts of the Y-maze and the stimuli positions. When the bees view a yellow sample stimulus (A), they must subtract one element from it, and when the bees view a blue sample stimulus (B), they must add one element to it. (Not visible in this diagram is the entrance wall into the first chamber).

RESULTS

Training phase

Over the course of 100 appetitive-aversive (reward-punishment) reinforced choices (31), honeybees were trained to add or subtract one element based on the color of a sample stimulus (fig. S1). Bees were provided with a 10-μl drop of either a 50% sucrose solution (CS+) or a 60 mM quinine solution (CS−) as rewarding or punishing outcomes for a correct or incorrect choice, respectively (see Materials and Methods). In this learning phase, there was a significant increase in the number of correct choices made over the 100 conditioned choices (z = 8.14, P < 0.001), demonstrating that bees learned to simultaneously add or subtract by one based on the color of the sample stimulus (Fig. 2A). Each individual bee appears to learn differently, possibly due to the random presentation of stimuli and by individual differences in cognitive abilities (Supplementary Materials, Methods, and Results and fig. S2).

Fig. 2. Results of the learning and testing phases.

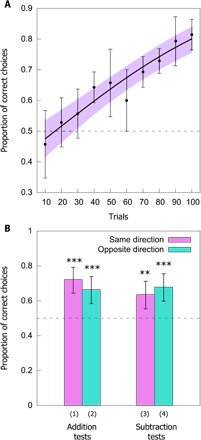
(A) Performance during the learning phase. Dashed line at 0.5 indicates chance level performance. Solid black line represents a function describing the learning phase of n = 14 bees as modeled by a generalized linear mixed-effect model (GLMM). Points (closed circles) along the curve indicate the observed mean ± 95% confidence intervals (CIs) (purple) of correct choices for the bees. Increase in performance during the learning phase was significant. (B) Performance during the testing phases for addition and subtraction. Pink columns (left) show results when the incorrect answer was in the same direction as the correct answer, and blue column (right) show results when the incorrect answer was in the opposite direction as the correct answer. Numbers under columns (1, 2, 3, and 4) correspond to the operations in the main text. Dashed line at 0.5 indicates chance level performance. Significance from chance level performance is indicated by *P < 0.05, **P < 0.01, and ***P < 0.001. Data shown are means ± 95% CI boundaries for all tests.

Testing phase

We subsequently tested the bees during nonreinforced tests (no reward or punishment) on their ability to interpolate the learned concepts of addition and subtraction to the novel sample stimulus of three elements (see Materials and Methods). We conducted four tests: two addition operations and two subtraction operations. Two of these four tests presented an incorrect option in the same numerical direction as the correct option, and the other two presented an incorrect option in the opposite numerical direction of the correct option:

1) Addition: Incorrect option in same numerical direction as correct option

Sample = 3, correct = 4, incorrect = 5

2) Addition: Incorrect option in opposite numerical direction as correct option

Sample = 3, correct = 4, incorrect = 2

3) Subtraction: Incorrect option in same numerical direction as correct option

Sample = 3, correct = 2, incorrect = 1

4) Subtraction: Incorrect option in opposite numerical direction as correct option

Sample = 3, correct = 2, incorrect = 4

In each of the four tests, the bees performed at a level that was significantly different from chance. In the addition (same direction) test, the bees chose the correct option of 4 in 72.1 ± 3.20% (mean ± SEM) of choices (z = 5.05, P < 0.001; Fig. 2B). In the other addition (opposite direction) test, the bees chose the correct option of 4 in 66.4 ± 2.69% of choices (z = 3.81, P < 0.001; Fig. 2B). In the subtraction (same direction) test, the bees chose the correct option of 2 in 63.6 ± 2.89% of choices (z = 3.17, P = 0.002; Fig. 2B). In the other subtraction (opposite direction) test, the bees chose the correct option of 2 in 67.9 ± 3.66% of choices (z = 4.13, P < 0.001; Fig. 2B). There was no significant difference between the performance of the bees in any of the four tests (z = −0.887, P = 0.375), demonstrating that the bees performed equally well on all tests.

DISCUSSION

Honeybees were able to use color as a symbolic representation of the addition and subtraction signs and learned, during 100 appetitive-aversive trials, to thus add or subtract one element from different samples. Furthermore, the bees could successfully interpolate the learned operations of addition and subtraction to an unfamiliar sample number and shape during tests.

Arithmetic operations such as addition and subtraction problems are known to involve complex cognitive processes as they require two levels of information processing. The first is the representation of numerical attributes, and the second is the mental manipulation of those representations in working memory (6). In the current study, the bees not only succeeded in performing these processing tasks but also had to perform the arithmetic operations in working memory as the number to be added or subtracted (one element) was not visually present, but rather an abstract concept that the bees had to resolve over the course of training. This important step in combining the arithmetic and symbolic learning abilities of an insect has identified numerous new areas for future research and also poses the question of whether these complex numeric understandings may be accessible to other species without large brains, such as the honeybee (35). While the posterior parietal cortex and the prefrontal cortex are key areas for numerical processing in primates (32), we have yet to determine where number representation and processing may occur in honeybee brains; however, we do show that the comparatively large and complex brain areas required in primates are not necessary for an insect to process number problems.

While the specific task of addition/subtraction may not be directly apparent in the honeybee’s natural environment, the skills and cognitive plasticity required for performing the arithmetic task are likely to be ecologically advantageous. For example, the ability of bees to acquire and manipulate learned information to make decisions using multiple memory phases (23) is useful in foraging to remember which flower traits (e.g., color, shape, and size) may provide essential resources and which flower traits may not (35). Thus, rule learning involving linking visual traits to reward quantification, such as in the arithmetic task, is likely to be beneficial to a honeybee’s foraging lifestyle.

Debates regarding a nonhuman animal’s capacity to demonstrate numerical cognition have thus far centered on arguments either that numerical skills are biologically evolved traits (1) or that animals have only limited quantical abilities and human culture is necessary for more complex numerical abilities (2, 4). However, these debates have inspired a third important argument: Verguts and Chen (5) suggest that, at the very least, we must consider the rapid evolution of individual learning of numerical cognition, which occurs during an animal’s lifetime. In this regard, the honeybee is a proficient learner of many tasks including sameness and difference judgments (23), mazes (21, 36), face stimuli (37), and spatial relationships (38), and the results of the current study demonstrate that honeybees are capable of learning and applying numerical cognition as individuals. Our results suggest the possibility that honeybees and other nonhuman animals may be biologically tuned for complex numerical tasks. These possibilities have important implications worth further exploration, particularly in insects.

Human infants with no language for number have demonstrated large-number addition and subtraction (18), and native speakers of Mundurukú from Brazil, a language that has no words for large numbers, can add large approximate numbers far beyond their naming range (39). While speakers of the Mundurukú language demonstrated exact arithmetic with small numbers (<4 and 5), they failed at exact arithmetic for large numbers (>4 or 5) but were able to use approximation to calculate solutions. These studies demonstrate that human language is not necessary for arithmetic operations such as addition and subtraction. Combined with the results from our current study, we propose that language and prior advanced numerical understanding are not a prerequisite necessary for the ability to calculate addition and subtraction solutions. In the current study, bees were tested only on the number range of 1 to 5 for their ability to add and subtract; thus, it would be valuable to examine bee performance on large number quantities to determine whether they could use approximation or exact arithmetic to solve similar large-number arithmetic problems.

MATERIALS AND METHODS

Study design

We aimed to determine whether free-flying honeybees could learn to add or subtract one element from an array of elements in a delayed matching-to-sample task. To address this question, we trained bees to use different colors (blue or yellow) as a prompt to perform either addition or subtraction. Bees were trained to use a Y-maze (described below; Fig. 1) to view a sample stimulus containing a certain number of colored elements on a gray background. Once they had viewed this stimulus, they could fly into a decision chamber to choose the correct option resulting from the arithmetic problem encountered (Fig. 1).

Study species

We used 14 free-flying honeybee (Apis mellifera) foragers for this experiment. All bees were marked with a colored dot on the thorax to identify individuals. An ad lib von Frisch–type gravity feeder providing ca. 10 to 30% sucrose was set up to maintain a regular number of bees.

Apparatus

Individual honeybees were trained to enter a Y-maze [as described in (22); Fig. 1]. Bees had to fly through an initial entrance hole to enter a chamber where they would view the sample stimulus. This stimulus would contain either blue or yellow elements on a gray background. Each bee could then fly through another hole into the decision chamber where it would be presented with two different options in each arm of the chamber. If the sample stimulus had been blue, then the bee would need to choose the stimulus with a number of elements, which was one more than the sample number; however, if the sample stimulus had been yellow, then the bee would need to choose the stimulus with a number of elements which was one less than the sample number (Fig. 1). This delayed matching-to-sample method using a Y-maze apparatus is the standard methodology for testing honeybee learning, and specifically quantity matching in honeybees (30), and has been validated through producing consistent learning outcomes to alternative apparatus (20).

The stimuli were presented on gray backgrounds located 15 cm away from the decision lines. Two stimuli, one correct and one incorrect, were presented simultaneously in each arm of the Y-maze on the gray plastic background (Fig. 1). A 10-μl drop of either a 50% sucrose solution (correct choice) or a 60 mM quinine solution (incorrect choice) was used as rewarding and punishing outcomes, respectively, during the training phase as this promotes enhanced visual discrimination performances in free-flying honeybees. Each stimulus had a gray landing pole located below it, which held the drop of either sucrose under the correct option or quinine under the incorrect option, so that the bees would learn to associate stimuli with either a reward or punishment. Poles were replaced when touched by a bee and cleaned with 20% ethanol to exclude olfactory cues. The sides of correct and incorrect stimuli were randomly changed between choices (38). If a bee made an incorrect choice and started to imbibe the quinine, then it was allowed to fly to the pole in front of the correct stimulus to collect sucrose to maintain motivation, but only the first choice was recorded for statistical analysis (38). Once the bee was finished imbibing the sucrose, it was allowed to fly back to the hive if satiated or make another decision by re-entering the maze. During the nonreinforced tests, a drop of water was placed on each of the poles placed in front of the stimuli. Ten choices (touches of the poles) were recorded for each of the four tests to enable statistical comparisons.

Stimuli

Each stimulus was a 6-cm by 6-cm gray square with either blue (addition) or yellow (subtraction) elements presented on it (fig. S1) and was covered with 80-μm Lowell laminate. The chosen colors were spectrally different and salient considering honeybee vision. Elements could be one of four shapes: square, diamond, circle, or triangle. Three of these shapes were used in training, and the other novel shape was used for testing to ensure that patterns and shapes were unfamiliar to the bees during tests. To control for surface area (SA), each pattern (cumulated SA of black elements) was 10 ± 0.3 cm² regardless of shape, pattern, or number of elements, and each element was above the minimum resolution threshold for honeybee vision as based on previous psychophysics findings (SA range: circle, 1 cm² to 9.95 cm²; square/diamond, 1 cm² to 6.32 cm²; triangle, 1 cm² to 10 cm²). There were 216 stimuli in total, 108 for addition and 108 for subtraction (fig. S1). Element size, line length, and convex hull for all stimuli were not consistently correlated with increasing or decreasing numbers of elements.

There were a total of 108 different patterns, comprising one to five elements of the four different shapes (square, diamond, circle, and triangle), which could be presented throughout the experiment, and this was done to control for the potential use of an associative mechanism by the bees to learn the outcomes of each stimulus. There were no low-level cues, which could be used to solve the problem, as the correct answer could be lower or higher than the original number depending on sample element color and the incorrect answer could be the same number as the sample or any (noncorrect) number above or below the sample. Thus, the correct answer was not predicted by visual similarity to the original sample number or numerical closeness to the sample number.

Training procedure

Bees were incrementally trained to enter the Y-maze and both arms of the apparatus over 30- to 60-min periods. Once each bee was able to fly into the entrance hole and the hole that led to the decision chamber and could find the poles in both Y-maze arms, the experiment began.

After entering the Y-maze, bees would be in the initial chamber where they could view the sample number. To solve the task, the bees were required to either add or subtract the value of one to this sample number depending on the color of the elements (Fig. 1). Bees would then fly through the next hole in the Y-maze and into the decision chamber where they could simultaneously view two stimuli in a dual choice test. If the sample number was blue, then the bee would need to choose the option that was one element greater than the sample stimulus to receive a reward, while if the sample number was yellow, then the bee would need to choose the option that was one element less than the sample number to receive a reward. The incorrect option was randomly selected and could be any number from 1 to 5, including the sample number itself that controlled for the bees choosing the correct option based on visual similarity, and incorrect choices were associated with a bitter tasting quinine solution.

Each bee thus completed 100 appetitive-aversive (31) reinforced trials presenting either addition or subtraction arithmetic problems. Whether a trial would involve adding or subtracting one element from the sample number was randomized.

Throughout the training, the numbers that could be used for the sample in the addition trials were 1, 2, and 4. Thus, correct answers could be 2, 3, and 5 and the incorrect answers could be 1, 2, 3, 4, and 5. During the subtraction trials, the numbers that could be used for the sample number were 2, 4, and 5. Thus, correct answers could be 1, 3, and 4 and the incorrect answers could be 1, 2, 3, 4, and 5. The number 3 was never shown as a sample number during training for any bee and was thus used as the sample number for all unreinforced tests to ensure the sample number was novel during tests.

Testing procedure

Once bees had completed the training, there were four tests of 10 unreinforced choices. Between each of the four tests, there were 10 refresher reinforced choices to maintain bee motivation. The sequence of these tests was randomized. These tests were nonreinforced (no reward or punishment) and used a 10-μl drop of water instead of quinine or sucrose to motivate the bees to land. We conducted four tests where two arithmetic operations were addition and two were subtraction. As the sample stimulus of three elements had never been presented during training, the bees had not previous received reinforcement on the number four for addition or two for subtraction trials. Two of these four tests presented an incorrect option in the same direction as the correct option, and the other two presented an incorrect option in the opposite direction of the correct option. Two of the tests required addition and two required subtraction using the novel sample number of three.

Two of the tests involved the incorrect answer being the same direction as the correct answer (addition: sample = 3, correct = 4, incorrect = 5; subtraction: sample = 3, correct = 2, incorrect = 1). Two of the tests involved the incorrect answer being in the opposite direction of the correct answer and thus also one element different from the sample (addition: sample = 3, correct = 4, incorrect = 2; subtraction: sample = 3, correct = 2, incorrect = 4).

Statistical analysis

To test for the effect of training on bee performance (number of correct choices), data from the learning phase of 100 choices were analyzed with a generalized linear mixed-effect model (GLMM) with a binomial distribution using the “glmer” package within the R environment for statistical analysis. We fitted a full model with trial number as a continuous predictor and subject as a random factor to account for repeated choices of individual bees.

To determine whether the bees were able to learn to follow additional and subtraction rules, we analyzed the test data by using a GLMM including only the intercept term as fixed factor and subject as a random term. The mean proportion of “correct” choices (MPCC) recorded from the tests were used as a response variable in the model. The Wald statistic (z) tested if the MPCC recorded from the learning test, represented by the coefficient of the intercept term, was significantly different from chance expectation, i.e., H₀: MPCC = 0.5.

A separate analysis was performed to determine whether there were any differences between the four tests regarding the performance of the bees. We analyzed the test data using a GLMM including only the intercept term as fixed factor and subject as a random term. The MPCC during the tests and the test type (addition test 1, addition test 2, subtraction test 1, and subtraction test 2) were used as a response variable in the model. The z statistic tested if the MPCC recorded from the tests differed on the basis of test type. All analyses were performed within the R environment for statistical analysis.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/5/2/eaav0961/DC1

Supplementary Materials, Methods, and Results

Fig. S1. The full set of stimuli used (n = 216) for the addition (blue; n = 108) and subtraction (yellow; n = 108) training and test phases.

Fig. S2. The Bayesian-determined bias for each of the bees, averaged over n_t = 10 trials (except for the first 10 experiments, which were evaluated with respect to all previous experiments).

Reference (40)