Biomechanical Comparison of the Temporalis Muscle Fascia, the Fascia Lata, and the Dura Mater

Abstract

The purpose of our research is to prove that elastic biomechanical characteristics of the temporalis muscle fascia are comparable to those of the fascia lata, which makes the temporalis muscle fascia adequate material for dural reconstruction in the region of the anterior cranial fossa. Fifteen fresh human cadavers, with age range from 33 to 83 years (median age: 64 years; mean age: 64.28 years), were included in the biomechanical study. Biomechanical stretching test with the comparison of elasticity among the tissues of the temporalis muscle fascia, the fascia lata, and the dura was performed. The samples were stretched up to the value of 6% of the total sample length and subsequently were further stretched to the maximum value of force. The value of extension at its elastic limit for the each sample was extrapolated from the force–extension curve and was 6.3% of the total sample length for the fascia lata (stress value of 14.61 MPa), 7.4% for the dura (stress value of 6.91 MPa), and 8% for the temporalis muscle fascia (stress value of 2.09 MPa). The dura and temporalis muscle fascia shared the same biomechanical behavior pattern up to the value of their elastic limit, just opposite to that of the fascia lata, which proved to be the stiffest among the three investigated tissues. There was a statistically significant difference in the extension of the samples at the value of the elastic limit for the fascia lata in comparison to the temporalis muscle fascia and the dura ( p  = 0.002; Kruskal–Wallis test). Beyond the value of elastic limit, the temporalis muscle fascia proved to be by far the most elastic tissue in comparison to the fascia lata and the dura. The value of extension at its maximum value of force for the each sample was extrapolated from the force–extension curve and was 9.9% of the sample's total length for the dura (stress value of 10.02 MPa), 11.2% for the fascia lata (stress value of 23.03 MPa), and 18.5% (stress value of 3.88 MPa) for the temporalis muscle fascia. There was a statistically significant difference in stress values at the maximum value of force between the dura and the temporalis muscle fascia ( p  = 0.001; Mann–Whitney U test) and between the dura and the fascia lata ( p  < 0.001; Mann–Whitney U test). Because of its elasticity and similarity in its mechanical behavior to the dura, the temporalis muscle fascia can be considered the most suitable tissue for dural reconstruction.

Introduction

Dural reconstruction in the region of the anterior cranial fossa is of paramount importance in skull base reconstruction. It is essential for restitution of an airtight and watertight barrier between the sterile brain and the contaminated sinonasal cavities. It also provides a strong mechanical support for intracranial structures, consequently preventing serious and possibly lethal postoperative complications. ^{1 2 3 4 5}

Biological materials have proved themselves to be superior to synthetic materials in terms of strength and elasticity, which is important for dural reconstruction in the region of the anterior cranial fossa. Furthermore, synthetic materials are prone to chronic inflammation and subsequent rejection by the host. ^{6 7} According to the available literature, the fascia lata nowadays is the preferred autologous material for the reconstruction of a postablative defect in the region of the anterior cranial fossa. ⁸

The purpose of our research is to prove that elastic biomechanical characteristics of the temporalis muscle fascia are comparable to those of the fascia lata, which is important for dural reconstruction in the region of the anterior cranial fossa. In this regard, we have analyzed and compared elastic biomechanical characteristic among the temporalis muscle fascia, the fascia lata, and the dura mater. In this way, we would have been able to determine which of the two materials (fascia lata and temporalis muscle fascia) resembles the most to the dura in terms of its biomechanical behavior.

Materials and Methods

All tested samples were harvested from 15 human cadavers at the University Hospital Centre Zagreb, with the approval of the Ethics Committee ( Fig. 1 ). Their age range was from 33 to 83 years (median age: 64 years; mean age: 64.28 years). After macroscopic inspection, inadequate samples were excluded from further research. The samples were tested within 24 hours after autopsy. They were stored in a 0.9% saline solution and at +7°C temperature until the time of their biomechanical testing. All materials from one cadaver were harvested at the same time and kept under the same environmental conditions (saline, temperature) until the time of their mechanical testing. This is important to notice because of the possible negative impacts of the saline on the material structure. All materials (temporalis muscle fascia, fascia lata, and dura) harvested from one cadaver were subsequently tested at the same time in the stretching session. The samples were tailored with a plastic template ( Fig. 2 ), with 30 mm in length and 15 mm in width, and placed in the testing machine grips with longitudinal orientation of collagen fibers in the direction of extension. ⁹ Additional 15 mm was added in length at each specimen end to facilitate the fixing of samples in the jaws of the testing machine. The additional sample edges were wrapped in sandpaper to prevent sample slippage. The thickness of each sample was measured by using a digital caliper with a resolution of 0.01 mm. All biomechanical tests were performed on the testing machine Stable Micro Systems TA.HD plus Texture Analyser with grips HD Tensile Grips (Stable Micro Systems Ltd.) and sample displacement rate of 0.05 mm/s ⁹ ( Fig. 3 ).

Fig. 1.

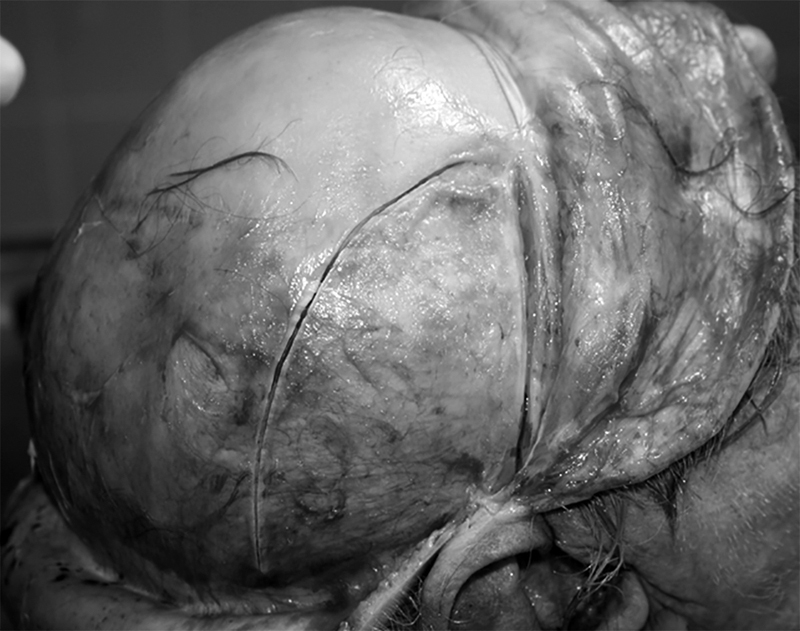
Harvesting technique. Anterior and posterior scalp skin flaps are developed in usual manner after bicoronal incision. The temporalis muscle fascia is anteriorly incised to protect the temporal branch of the facial nerve. Incision that follows temporal line and auricular circumference as far posteriorly as possible. After the fascial detachment from the muscle surface, horizontal incisions are posteriorly joined, which completes the harvesting procedure.

Fig. 2.

Plastic template was cut in dimensions of 60 mm (30 mm with additional 15 mm on both sides of the specimen to facilitate mounting in the grips of the testing machine) in length and 15 mm in width. Investigated material was placed on a flat surface, and tissue samples were cut following the templet edges, allowing maximal consistency in the dimensions of samples.

Fig. 3.

A tissue sample of the fascia lata in the grips of the testing machine. Additional 15-mm longitudinal sample length and sandpaper coverage increased grip friction force and added in the sample grip fixation, consequently preventing samples from slippage during their extension.

Fifteen samples of the temporalis muscle fascia, 10 samples of the fascia lata, and 14 samples of the dura (in total 39 samples) were subjected to a limited stretching test of 6% of their total sample length in five cycles, with breaks of 180 second This test was a simplification of biaxial stretching test published by Pancheri et al due to performances of our laboratory equipment. ⁹ Uniaxial loading was performed in our experimentation, taking into account the anisotropy of material but without influence of the force in perpendicular direction. On the contrary to biaxial loading, such approach is more clear for interpretation of the measured deformations. During the breaks, the samples were covered with the gauze soaked in 0.9% saline solution. The stress (MPa) was calculated for each sample according to the formula ¹⁰ :

σ = F / A , (1)

In the preceding equation, σ represents stress (MPa), F represents force (N), and A represents cross-section of the sample (mm ² ).

After the fifth cycle of extension to the stretching limit at 6% of total sample length, and appropriate tissue relaxation, all samples were subsequently stretched to their breaking point, and force–extension curves were generated. The force and elongation values at the elastic limit and maximum of force were extrapolated from the force–extension curves for each sample. The stress values were subsequently calculated using the previously described method.

Characteristic stress–strain curve of stretching test for all three investigated tissues are presented ( Figs. 4 5 6 ). Stress and strain were calculated from stretching force, cross-sectional area, and initial length and extension of each sample using machine software (Texture Exponent).

Fig. 4.

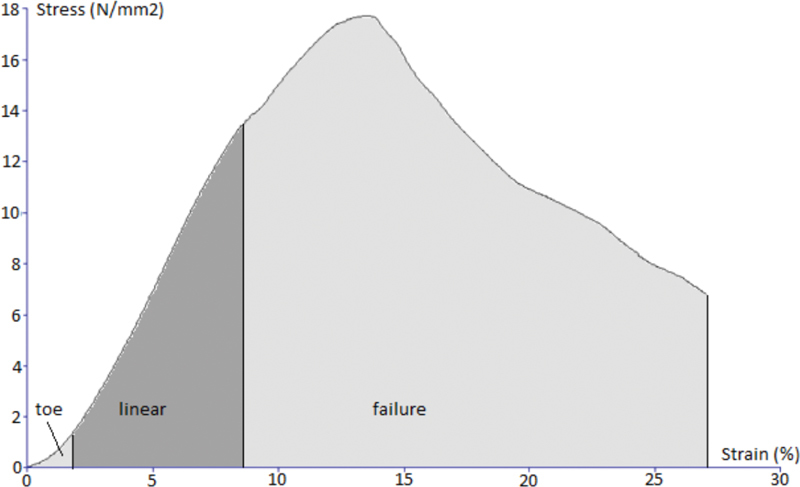
Characteristic stress–strain curve of the stretching test for the sample of the fascia lata.

Fig. 5.

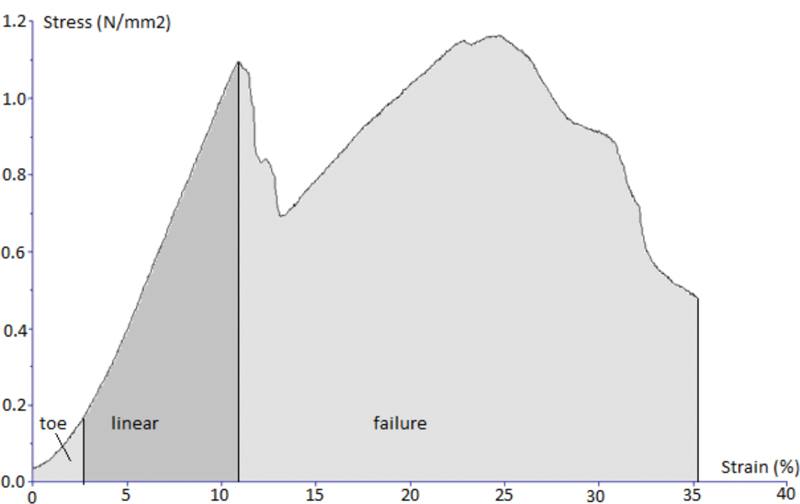
Characteristic stress–strain curve of the stretching test for the sample of the temporalis muscle fascia.

Fig. 6.

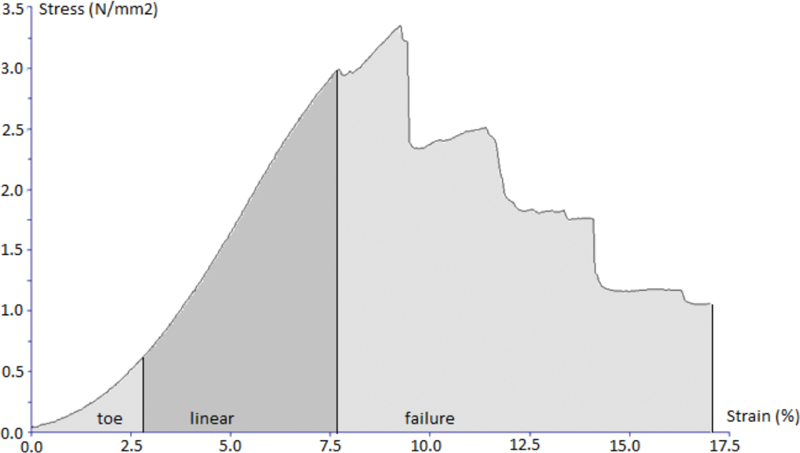
Characteristic stress–strain curve of the stretching test for the sample of the dura.

The intersample differences between the two independent groups were tested using the Mann–Whitney U test and those among the three independent groups were tested using the Kruskal–Wallis test. The intrasample differences were tested with the Friedman test.

The level of significance was set at α = 0.05. The program used for statistical analysis was SPSS (16.0, SPSS Inc., Chicago, Illinois, United States).

Results

The median (interquartile range) stress in the limited stretching test of 6% elongation of total sample length in five cycles was 1.67 (1.33–2.14) MPa for the temporalis muscle fascia, 13.58 (10.3–17.55) MPa for the fascia lata, and 5.28 (3.31–7.87) MPa for the dura. There was a statistically significant intersample stress difference at a limited extension of 6% of total sample length among the tissues for each stretching cycle ( p  < 0.001; Kruskal–Wallis test) ( Table 1 ).

Table 1. The values of median interquartile stress (in MPa) for the limited stretching test of 6% of the total sample length, in five cycles, for samples of the TMF, the FL, and the dura.

Cycle	Stress (in MPa) at limited extension of 6% of the total sample length						p -Value a
	TMF		FL		Dura
	Median (IQR b )	p -Value c	Median (IQR b )	p -Value c	Median (IQR b )	p -Value c
Cycle 1	1.3 (0.95–1.83)	0.385	12.98 (9.89–17.52)	<0.001	5.13 (2.65–7.28)	<0.001	<0.001
Cycle 2	1.55 (1.12–2.07)		13.48 (10.29–17.65)		5.5 (3.08–7.91)		<0.001
Cycle 3	1.62 (1.3–2.05)		13.62 (10.4–17.92)		5.39 (3.47–7.97)		<0.001
Cycle 4	1.65 (1.19–2.12)		13.51 (10.39–18.04)		5.5 (3.15–7.8)		<0.001
Cycle 5	1.67 (1.33–2.14)		13.58 (10.3–17.55)		5.28 (3.31–7.87)		<0.001

Abbreviations: FL, fascia lata; IQR, interquartile range; TMF, temporalis muscle fascia.

^aKruskal–Wallis test.

^bIQR: 25–75%.

^cFriedmanov test.

There was no statistically significant intrasample difference in stress among the stretching cycles for the temporalis muscle fascia ( p  = 0.385; Friedman test), whereas there was a statistically significant intrasample difference in stress among the stretching cycles for the fascia lata and the dura ( p  < 0.001; Friedman test) ( Table 1 ).

The median (interquartile range) extension of samples at their elastic limit extrapolated from the force–extension curve for the dura was 2.22 (2.07–2.78) mm, which was 7.4% of the total sample length. The same value for the temporalis muscle fascia was 2.42 (2.03–3) mm, which was 8% of the total sample length, and for the fascia lata, it was 1.91 (1.8–1.99) mm, which was 6.3% of the total sample length ( Table 2 ).

Table 2. Extension (in mm) of the samples at the values of elastic limit and the maximum of force in tensile test up to the maximum of force for the samples of the TMF, the FL, and the dura.

Sample	Extension at the elastic limit		Extension at the maximum of force
	Median (IQR a ) [mm]	p -Value b	Median (IQR a ) [mm]	p -Value b
TMF	2.42 (2.03–3)	0.002	5.56 (4.48–7.39)	<0.001
FL	1.91 (1.8–1.99)		3.36 (2.8–4.21)
Dura	2.22 (2.07–2.78)		2.98 (2.48–3.51)
TMF vs. dura		0.596 c	TMF vs. dura	<0.001 c
FL vs. dura		0.001 c	FL vs. dura	0.239 c

Abbreviations: FL, fascia lata; IQR, interquartile range; TMF, temporalis muscle fascia.

^aIQR: 25–75%.

^bKruskal–Wallis test.

^c Mann–Whitney U test.

There was no statistically significant difference in extension at the value of the elastic limit between samples of the dura and the temporalis muscle fascia ( p  = 0.596; Mann–Whitney U test). There was a statistically significant difference in the extension at the value of the elastic limit between samples of the dura and the fascia lata ( p  = 0.001; Mann–Whitney U test) ( Table 2 ).

There was a statistically significant difference in the extension of the samples at the value of the elastic limit for the fascia lata in comparison to the temporalis muscle fascia and the dura ( p  = 0.002; Kruskal–Wallis test) ( Table 2 ).

The median (interquartile range) extension of the samples at the maximum value of force extrapolated from the force–extension curve was 2.98 (2.48–3.51) mm for the dura, which was 9.9% of the sample's total length, 3.36 (2.8–4.21) mm for the fascia lata, which was 11.2% of the sample's total length, and 5.56 (4.48–7.39) mm for the temporalis muscle fascia, which was 18.5% of the sample's total length ( Table 2 ).

There was no statistically significant difference in extension at the maximum value of force between the dura and fascia lata samples ( p  = 0.239; Mann–Whitney U test). There was a statistically significant difference in extension at the maximum value of force between samples of the dura and the temporalis muscle fascia ( p  < 0.001; Mann–Whitney U test) ( Table 2 ).

The median (interquartile range) stress value at the elastic limit was 2.09 (1.59–2.94) MPa for the temporalis muscle fascia, 14.61 (10.35–18.76) MPa for the fascia lata, and 6.91 (2.79–7.87) MPa for the dura ( Fig. 7 ).

Fig. 7.

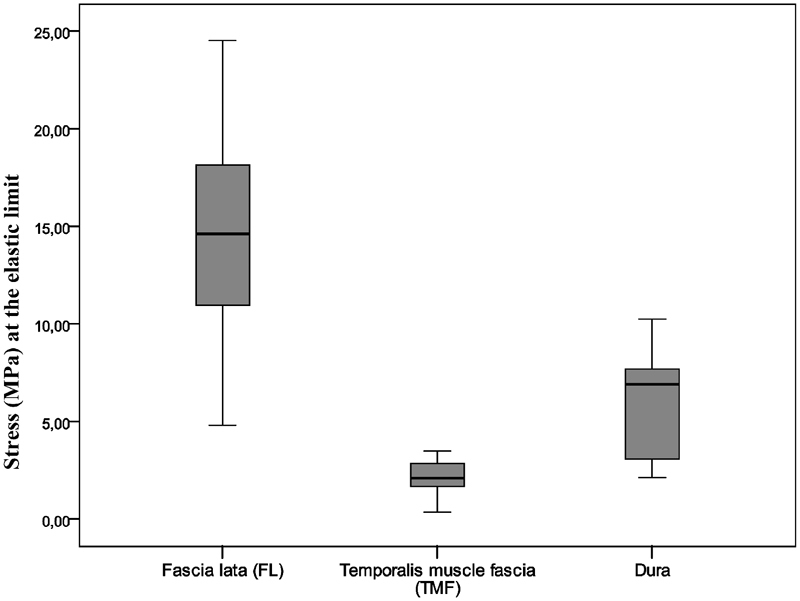
Median stress values (MPa) at the elastic limit for the samples of the fascia lata (FL), the temporalis muscle fascia (TMF), and the dura. Statistically significant intersample difference is present among all three groups of samples ( p  < 0.001; Kruskal–Wallis test); FL versus dura ( p  = 0.001; Mann–Whitney U test), and TMF versus dura ( p  < 0.001; Mann–Whitney U test).

There was a statistically significant difference in stress values at the elastic limit between the dura and the temporalis muscle fascia ( p  < 0.001; Mann–Whitney U test) and between the dura and the fascia lata ( p  = 0.001; Mann–Whitney U test) ( Fig. 7 ).

There was a statistically significant difference in stress value at the elastic limit for the temporalis muscle fascia in comparison to the fascia lata and the dura ( p  < 0.001; Kruskal–Wallis test) ( Fig. 7 ).

The median (interquartile range) stress values at the maximum value of force were 3.88 (2.27–4.85) MPa for the temporalis muscle fascia, 23.03 (17.4–32.71) MPa for the fascia lata, and 10.02 (4.33–12.75) MPa for the dura ( Fig. 8 ).

Fig. 8.

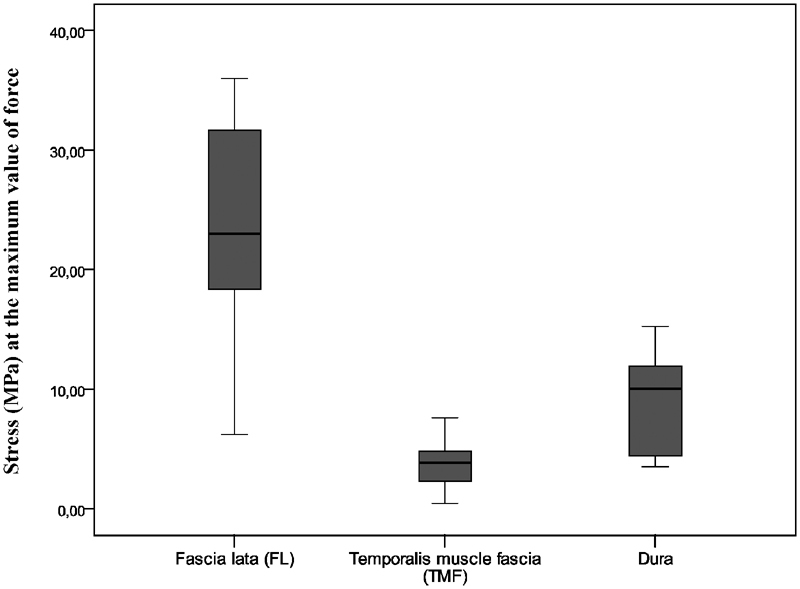
Median stress (MPa) at the maximum value of force for the samples of the fascia lata (FL), the temporalis muscle fascia (TMF), and the dura. Statistically significant intersample difference is present among all three groups of samples ( p  < 0.01; Kruskal–Wallis test), FL versus dura ( p  < 0.001; Mann–Whitney U test), and TMF versus dura ( p  = 0.001; Mann–Whitney U test). Intrasample differences among the stretching test are by far the lowest for the temporalis muscle fascia, both for the values of elastic limit and the maximum value of force, in comparison two other tissues, suggesting its biomechanical stability.

There was a statistically significant difference in stress values at the maximum value of force between the dura and the temporalis muscle fascia ( p  = 0.001; Mann–Whitney U test) and between the dura and the fascia lata ( p  < 0.001; Mann–Whitney U test) ( Fig. 8 ).

Discussion

The resection of anterior skull base tumors usually results in communication between the sterile area of the anterior cranial fossa and the contaminated space of the nose and paranasal sinuses. The purpose of reconstruction is to restitute the airtight and watertight barrier between the brain and the sinonasal cavity and to provide strong mechanical support to the intracranial structures. These are essential prerequisites in the prevention of serious and possibly lethal postoperative complications. Surgical techniques that meet these requirements provide patients with a good postoperative quality of life and an optimal functional and aesthetic outcome. ^{1 2 6 11 12 13} In this regard, dural reconstruction represents a paramount part of skull base reconstruction. The fascia lata nowadays is the golden standard biological material used for dural reconstruction following tumor ablation. ^{1 2 6 7 14 15}

In the past 15 years, our institution has been routinely and almost exclusively using the free temporalis muscle fascia graft for dural reconstruction. It was used in both endoscopic and open surgical procedures in the region of the anterior cranial fossa. The temporalis muscle fascia is soft, smooth, adaptable, and structurally similar to the dura. ¹⁶ Its harvesting is also, from the technical point of view, a straightforward procedure ( Fig. 1 ). According to our experience, it is large enough for effective and safe reconstruction of the most demanding dural defects. Donor-site morbidity is minimal or absent, and the incidence of intraoperative and postoperative donor site complications is minimal.

With this test of biomechanical properties, we have tried to validate the free temporalis muscle fascia graft in terms of its elasticity, which is an essential biomechanical property of any quality material in endoscopic dural reconstruction procedure and determines whether it is comparable in quality to those of the fascia lata.

Reconstructive material at the site of the dural defect is, with time, exposed to variable hydrostatic and hydrodynamic forces of the cerebrospinal fluid (CSF), which results in centripetal force at the edge of the postablative dural defect that tends to shift the material from the site of reconstruction. The more elastic the reconstructive material is, the more the hydrodynamic and hydrostatic load it takes on itself, which results in lower centripetal force at the edge of the dural defect.

In open procedures, it presents less of a problem because the reconstructive material is fixed in its place with sutures throughout the entire postablative defect circumference.

In endoscopic reconstruction, on the other hand, the reconstructive material is not fixed to the edge of the defect and is very prone to dislocation, which results in postoperative complications of CSF leakage and possible ascending infection in the region of cranial cavity. The only forces that keep the reconstructive material in its place are the pressure from the brain weight on the reconstructive material and the resulting adhesion force between the reconstruction material and surrounding bone. They are opposing centripetal forces at the edge of the dural defect, which is a result of CSF pressure to the surface of the reconstructive material.

The resulting force is the sum of all previously mentioned forces. Low resulting force at the borders of the postablative dural defect is responsible for stillness of the reconstructive material at the edge of the defect, which enables fast and adequate healing. The way to lower resulting force is either to reduce centripetal force or to increase pressure and adhesion at the edge of the defect. The only available maneuver to lower centripetal force is to increase the elasticity of the reconstructive material since permanent manipulations with the weight of the brain tissue and CSF pressure are not recommended or possible. The adhesion can be increased by tucking the reconstructive material more lateral to the edge of the defect (which has its technical limits), in that way increasing the contact surface between the reconstructive material and the bone. We can here conclude that the usage of the most elastic material available for reconstruction is the only maneuver that can lower centripetal force at the edge of the postablative dural defect and consequently ensure the best healing results.

We are positive that tissue, which resembles the most to the dura in terms of its biomechanical behavior and is the most elastic one, represents the best reconstructive material. To validate this claim, we have tested the biomechanical properties of the dura, the temporalis muscle fascia, and the fascia lata in terms of tissue elasticity by performing a stretching test for each tissue.

Typical biological tissue stress–strain curve in stretching test consists of three parts. Two of them are nonlinear (toe and failure part sections, at the beginning and the end of the curve) and in-between them is the linear part. When tissue is stretched, changes in its structure occur, which can be detected on the stress–strain curve. In the initial nonlinear section (toe section), collagen fibers are stretched from their initial curled state into the straight one. When all of the fibers are put in the straight position, they begin to take the load of stretching force in a linear manner, which can be seen as the linear section of the stress–strain curve. The elastic limit is the breaking point at which irreversible changes in tissue collagen microstructure occur, preventing tissue from returning to its original form after unloading. The elastic limit is defined as the maximum value point in the stress–strain curve at the end of the linear section, the limit beyond which begins the nonlinear (failure) part of the curve with the irreversible loss of tissue's elastic properties. Failure section ends at the point of maximum value of force, where tissue utterly deteriorates and eventually breaks. ^{17 18 19}

We have been able to determine the value of the elastic limit easily and precisely on the force–extension curve at the end of the linear portion of the curve.

According to the literature, relative extension of the sample at the value of elastic limit for the goat's (Capra hircus) fascia lata in uniaxial tension is in the range of 6%. ⁹ All biological tissues of mammals have similar mechanical behavior. ^{9 20} In this regard, goat and human fascia lata have a similar mechanical response in uniaxial extension in the direction of longitudinally oriented fibers in terms of stress, deformation, and relative extension. The results reported by Pancheri et al have implications for modeling the biomechanical behavior of the human fascia lata. ⁹ Consequently, we have set the stretching limit at the 6% of the total sample length and analyzed a tensile force for each tissue at that relative extension on the force–extension curve. With this maneuver, we have tried to investigate how the results of the stretching test for goat fascia lata can be compared with those of human fascia lata and how other two tissues behave in that conditions. After that, a stretching test for each sample was performed, and the values of elastic limit and the maximum force were extrapolated from the generated stress–strain curves.

After analyzing the results of our stretching tests, several interesting conclusions can be made. When the samples were stretched to the limited extent of 6% of the total sample length, we noticed a significant difference in stress between the stretching cycles for the dura and the fascia lata, but there was no difference in stresses between the stretching cycles for the temporalis muscle fascia. This implicates that the temporalis muscle fascia endures stress very well and biomechanically represents much more stable tissue in comparison to the dura and the fascia lata.

At a limited extension of 6%, which represents the value of elastic limit for goat fascia lata, the median stress of 12.98 to 13.62 MPa for the human fascia lata well corresponds to the extrapolated median stress of 14.61 MPa at the value of elastic limit from the force–extension curve on the stretching test to the maximum value of force.

On the other hand, the extrapolated median of extension at the elastic limit for the human fascia lata was 1.91 (1.8–1.99) mm, which is 6.3% of the sample's total length.

Therefore, we have confirmed that goat and human fascia lata have a similar biomechanical response in uniaxial extension in the direction of longitudinally oriented fibers in terms of stress, deformation, and relative extension. Moreover, we have double-checked the quality and reproducibility of our laboratory work and results.

When analyzing extrapolated extension of the samples at the elastic, limit which was 7.4% of the total sample length for the dura (stress value of 6.91 MPa), 8% for the temporalis muscle fascia (stress value of 2.09 MPa), and 6.3% for the fascia lata (stress value of 14.61 MPa), and knowing that the differences among the samples of the fascia lata in comparison to those of the temporalis muscle fascia and the dura were statistically significant ( p  = 0.002; Kruskal–Wallis test), we can conclude that the temporalis muscle fascia and the dura biomechanically behave almost identically as one material at a lower stress values up to their elastic limit. On the other hand, the fascia lata biomechanically behaves as a different material in comparison to the dura and the temporalis muscle fascia up to the value of its elastic limit.

At the maximum value of force, things look a little different. The median (interquartile range) extrapolated extension was 9.9% of the sample's total length for the dura (stress value of 10.02 MPa), 18.5% for the temporalis muscle fascia (stress value of 3.88 MPa), and 11.2% for the fascia lata (stress value of 23.03 MPa). The difference in extension at the maximum value of force between samples of the dura and the fascia lata was not statistically significant ( p  = 0.239; Mann–Whitney U test), whereas there was a statistically significant difference in extension at the maximum value of force between samples of the dura and the temporalis muscle fascia ( p  < 0.001; Mann–Whitney U test).

The dura and the fascia lata represent biomechanically stiffer materials in comparison to the temporalis muscle fascia, which far better tolerates higher stress values and consequently has the highest relative sample extension.

The extension of 11.2% of total sample length, which we have measured at the maximum value of force for the fascia lata, well corresponds to the previously published values of 10 to 18% for goat fascia lata ⁹ and 10% for human fascia lata. ²¹

Results of our work suggest that the temporalis muscle fascia represents the most elastic among the three investigated tissues. Its values of relative sample elongation were constantly the highest, and the values of stress were constantly the lowest throughout the whole investigation in comparison to the dura and the fascia lata. Furthermore, biomechanical properties of the dura and the temporalis muscle fascia were similar throughout the whole investigation as opposed to the fascia lata, which represents the stiffest and biomechanically completely different material. The values of stress for the temporalis muscle fascia were surprisingly low in comparison to two other materials ( Fig. 7 and 8 ), suggesting that the temporalis muscle fascia might be mechanically insufficient material for dural reconstruction in terms of resisting average CSF load. On the other hand, median stress value for the temporalis muscle fascia at the elastic limit of 2.09 (1.59–2.94) MPa and a maximum value of force of 3.88 (2.27–4.85) MPa are significantly higher than the normal intracranial pressure, which is reported to be in the range of 1.3 to 2 kPa (10–15 mm Hg) in healthy adults, depending on the movement and changes in body position. ²² These data prove that the temporalis muscle fascia should easily tolerate the daily CSF pressure load at the site of dural reconstruction in the long term and that it certainly has adequate security margins as the reconstructive material from the biomechanical point of view.

Because of its high elasticity, in comparison to fascia lata, the temporalis muscle fascia should far better tolerate sudden CSF pressure changes provoked by body movements and position changes. This consequently ends with much lower resulting centripetal forces at the borders of the postablative dural defect, which results in safe and quality reconstruction with low complication rate.

With respect to the biomechanical properties, which resembles the most to those of the dura, in combination with its high elasticity, the temporalis muscle fascia seems to be the most suitable tissue for dural reconstruction after ablative surgery in the region of the anterior cranial fossa.

That being said, the temporalis muscle fascia not only meets the biomechanical requirements for quality reconstructive material in endoscopic anterior cranial base surgery but also represents much better and safer reconstructive material in comparison to the fascia lata for that purpose.

Conclusion

The biomechanical behavior of the temporalis muscle fascia significantly exceeded our expectations. It proved to be superior to the fascia lata in terms of elasticity and stress tolerance. The temporalis muscle fascia, from a biomechanical perspective, represents a very stable tissue that is extremely resistant to stress. The biomechanical properties of the temporalis muscle fascia and the dura at lower stress up to the value of their elastic limit are very similar, and they behave almost identically as one tissue.

With this investigation, we have proved that the temporalis muscle fascia is the most elastic tissue in comparison to the dura and especially the fascia lata, which is the stiffest material of all three. With respect to its biomechanical properties, which resembles the most to those of the dura, and its elasticity, the temporalis muscle fascia seems to be the most suitable tissue for dural reconstruction after ablative surgery in the region of the anterior cranial fossa.