Explanation in mathematical conversations: an empirical investigation

Abstract

Analysis of online mathematics forums can help reveal how explanation is used by mathematicians; we contend that this use of explanation may help to provide an informal conceptualization of simplicity. We extracted six conjectures from recent philosophical work on the occurrence and characteristics of explanation in mathematics. We then tested these conjectures against a corpus derived from online mathematical discussions. To this end, we employed two techniques, one based on indicator terms, the other on a random sample of comments lacking such indicators. Our findings suggest that explanation is widespread in mathematical practice and that it occurs not only in proofs but also in other mathematical contexts. Our work also provides further evidence for the utility of empirical methods in addressing philosophical problems.

This article is part of the theme issue ‘The notion of ‘simple proof’ - Hilbert's 24th problem’.

1. Introduction

In Hilbert's 24th problem, he stresses the importance of simplicity in mathematics, proposing to give criteria for the simplicity of proofs in formal systems of mathematics. With his ideas on the subject largely under-developed, it is difficult to say why Hilbert placed so much value on simplicity, rather than, say, proposing to formalize the notion of a good proof, as others have done since [1,2].

The notion of simplicity in mathematics is of philosophical, as well as mathematical interest. Many writers associate simplicity with beauty: as Rüdiger Thiele observes, ‘It is widely believed among mathematicians that simplicity is a reliable guideline for judging the beauty … or elegance … of proofs’ [3, p. 5, internal citations omitted]. This is also a commonly held viewpoint among philosophers of mathematics [see [4], p. 89, for multiple examples]. However, a recent empirical study of how mathematicians actually use adjectives such as simple, beautiful, ingenious or fruitful, found no relationship between ‘beautiful’ and ‘simple’ [4]. Instead, ‘simple’ was seen as the opposite of dense, difficult, intricate, unpleasant, confusing, tedious, elaborate, non-trivial and obscure.

For that matter, Hilbert himself does not explicitly link simplicity to beauty, and elsewhere he relates simplicity to a lightening of cognitive load. He contrasts a simple problem statement with one which is convoluted, commenting of the latter: ‘confronted with them we would be helpless, or we would need some exertion of our memory, to bear all the assumptions and conditions in mind’ [3, p. 4]. Thiele writes ‘Hilbert himself possessed an uncanny ability to make things simple, to eliminate the unnecessary so that the necessary could be recognized’ [[3], p. 4, our italics] suggesting an increasing signal-to-noise ratio, to borrow a concept from engineering. The notion that a good proof involves simplicity is corroborated by Tim Gowers: in his identification of six features associated with good proofs, he talks about clarity (i), ease of understanding (ii, iii), reducing difficult problems to simple ones (v) and explanatoriness (vi) (but omits any talk of beauty) [1, p. 81 f.].

This suggests that our search for simplicity should move from aesthetic to epistemic criteria. But, what sort of epistemic criteria? There are several possible candidates. We could, for example, focus on mathematical understanding or mathematical clarity. However, if anything, these concepts are even more under-theorized than simplicity. By contrast, the nature of explanation in mathematics has long been a focus of philosophical enquiry. In this paper, we draw on accounts of explanation in mathematics and investigate them empirically. We hope that studying an aspect of mathematics that is so closely related to simplicity will help to lay the groundwork for a deeper understanding of Hilbert's 24th problem.

Although several competing theories of explanation have been proposed, they all have well-known limitations. A given account of explanation may work well for its devisor's chosen examples, but struggle to account for examples chosen by rivals. We maintain that this demonstrates the limitations of traditional philosophical methodology in solving such problems. Luckily, there are two recent developments which may be applied to the resolution of this old problem. Firstly, a variety of empirical methods have been applied to philosophical questions under the umbrella term experimental philosophy or ‘x-phi’. In the philosophy of mathematics, the emerging programme of using empirical data to investigate mathematical practice has come to be known as ‘Empirical Philosophy of Mathematics’ [5–7]. This programme has employed a diversity of data sources but not, we believe, the source on which we rely. This is a product of the second major recent development, the emergence of online collaborative mathematics projects [8–12]. These generate significant quantities of information on the process of mathematics, much of it publicly available, providing an invaluable but as yet comparatively neglected source of data for philosophical enquiry. In this paper, we show how an analysis of one such project can help reveal how explanation is used by mathematicians.

In §2, we propose six conjectures derived from some existing and novel theories of explanation applicable to mathematical practice. In §3, we introduce our specific case study, the online collaborative mathematics in Gowers and Tao's Mini-Polymath projects, 2009–2012. Section 4 introduces the methods we used to investigate our case study, §5 presents the data that we derived by these methods, and §6 assesses their implications for our conjectures. Finally, §7 states our conclusions and outlines some prospects for further work.

2. Six conjectures about mathematical explanation

In this section, we will introduce the conjectures which our empirical study tests. Mathematics poses two distinct problems for theories of explanation [13, p. 134]. Firstly, the existence of mathematical explanations in the natural sciences is difficult to reconcile with some theories of scientific explanation: not all such theories leave room for a physical observation to be explained by appeal to a mathematical fact. Secondly, explanation within mathematical practice is a hard case for many theories of explanation: the facts of mathematics do not appear to be related by either laws of nature or causation. Our concern is exclusively with the second problem, intramathematical explanation, although some of the theories devised to address it may also seek to address the first problem, extramathematical explanation.

One response to the difficulty of characterizing mathematical explanation would be to deny that there is any such thing. Michael Resnik & David Kushner claim that in actual mathematical practice, as opposed to a philosophical reflection on that practice, the explanation is ‘barely acknowledged’ [14, p. 151]; a similar view is expressed by Jeremy Avigad [15, p. 106]. But the most protracted critique of the existence of mathematical explanation is due to Mark Zelcer [16]. He reiterates these earlier claims that there is no tradition of explanation in mathematical practice and argues that, in the absence of such a tradition, mathematical explanation can only be understood by analogy with explanation in other sciences. He advances several reasons for rejecting such an approach to mathematical explanation, each of which turns on an aspect of scientific explanation (such as a relationship with predictions or a role in reducing surprise) that involves something mathematics allegedly lacks (predictions and surprise, respectively). However, as Zelcer acknowledges, the burden of proof is only on his side if he can sustain the empirical claim he shares with earlier authors: that there is no ‘implicit strand running through the history of mathematics that is most naturally interpreted as a search for what philosophers have been calling explanations’ [16, p. 180]. If support for such a strand can be found in mathematical practice, then the disanalogies Zelcer uncovers between scientific and mathematical explanation can no longer be read as evidence for the nonexistence of the latter.¹ This leads to our first conjecture.

Conjecture 2.1. —

There is such a thing as explanation in mathematics.

Bas van Fraassen developed one of the first theories of explanation that was not obviously inapplicable to mathematics, although it was not specifically developed with mathematics in mind. Van Fraassen argues that previous accounts of scientific explanation have ‘mislocate[d] explanation among semantic rather than pragmatic relations’ [18, p. 150]; that is, explanation is intrinsically contextual. His ‘pragmatic’ account proceeds from the claim that all explanations are answers to why-questions [18, p. 149]. Van Fraassen exploited the development of erotetic logic, the formal analysis of questions, to build a more nuanced theory which stresses the importance of context. Hence, his explanations are contrastive: in order to answer ‘Why A?’, we need to know the contrast class—is it ‘Why A rather than B?’ or ‘Why A rather than C?’? Specifically, van Fraassen analyses natural language why-questions in terms of abstract why-questions, Q = 〈P_k, X, R〉, where P_k is the topic, the proposition requiring explanation; X is the contrast class, a range of other propositions P_i; and R is a relevance relation that an answer A must bear to 〈P_k, X〉 in order to comprise a reason why P_k [19, p. 143].² Abstract why-questions are intended to remedy the characteristic ambiguity of natural language why-questions—in practice, for each such question there will be many, distinct candidates for Q, the choice to be determined by the broader context. Van Fraassen augments this descriptive account with a probabilistic system of evaluation, which we will set aside as obviously inapplicable to mathematical practice [21, p. 613]. However, David Sandborg has argued that why-question accounts in general are poorly suited for mathematics. For, he asks, if you don't understand a proof, how do you know which why-question to ask? For many proofs, knowing which why-question would elicit an explanatory answer is a large part of knowing that answer [21, p. 621]. Sandborg concludes that although ‘a theory of why-questions may aid the theory of explanation, the theory of explanation must go beyond it’ [21, p. 623]. Our second conjecture addresses the van Fraassen/Sandborg debate:

Conjecture 2.2. —

All explanations are answers to why-questions.

Mark Steiner was one of the first philosophers of mathematics to devise a theory of explanation for mathematics. For Steiner, proofs are explanatory if they turn on a ‘characterizing property’ of some entity, which he defines as ‘a property unique to a given entity or structure within a family or domain of such entities or structures’ [22, p. 143]. Hence characteristic properties deploy contrastive explanation, a device he shares with van Fraassen, to rehabilitate an Aristotelian appeal to essence. Several authors complain that Steiner's account of explanation is vulnerable to the charge that characterizing properties are often very difficult to find [[14], p. 149; [23], p. 240; [24], p. 206]. Steiner himself acknowledges a similar challenge from Solomon Feferman, but shows how Feferman's example of an explanatory proof apparently lacking a characterizing property may be transformed in such a way as to make the characterizing property explicit [22, p. 151]. However, as Resnik & Kushner observe, if a mathematician as experienced as Feferman cannot spot characterizing properties, it is hard to see how they can play much of a role in mathematical practice [14, p. 147].

Where Steiner's account is specifically tailored to mathematics, Philip Kitcher's is intended to be of wider application, although it shows the influence of Kitcher's work in the philosophy of mathematics. Kitcher contends that the key feature of explanatory proofs is that they unify. He uses this insight to characterize optimal explanation in terms of the knowledge base, K, of a scientific community and what he calls the ‘explanatory store’ of that knowledge base, E(K), which he defines as ‘the set of arguments acceptable as the basis for acts of explanation by those whose beliefs are exactly the members of K’ [25, p. 512]. The optimal explanatory store is then taken to be ‘the set of arguments that achieves the best tradeoff between minimizing the number of premises used and maximizing the number of conclusions obtained’ [26, p. 431]. Kitcher argues that this can be achieved by minimizing the number of ‘argument patterns’, distinctive forms of argument. Kitcher concludes by foreshadowing more recent empirical work, arguing for the need ‘to look closely at the argument patterns favoured by scientists and attempt to understand what characteristics they share’ [25, p. 530].

The problem with Kitcher's account is that it is easy to gerrymander because of its dependence on a ‘basic intuition, namely that unifying and explanatory power can be accounted for on the basis of quantitative comparisons alone’ [27, p. 170]. Johannes Hafner and Paolo Mancosu illustrate the problem with three proofs of the same theorem, drawn from a graduate textbook: they show that just totting up the numbers of schematic argument patterns actually misidentifies as most explanatory the proof the textbook authors found least explanatory. In general, what are sometimes called ‘nuclear flyswatter’ proofs,³ in which a single, disproportionately powerful technique is repeatedly applied, will be rated highly by Kitcher, whereas elegant combinations of several distinct but simple techniques will not. To remedy this, Kitcher needs an account of qualitative differences of the proof method, which he does not have.

A presupposition of both Steiner's and Kitcher's accounts of mathematical explanation is that they appeal to a higher level of generality: that is, both involve an abstraction away from the specific proof under consideration to some content that a key feature of the proof shares with such features in other proofs (and, perhaps, elsewhere). For Steiner, the higher level content is a ‘characteristic property’ that distinguishes a specific entity from other, related, entities; for Kitcher, the higher level content is a unifying feature, typically a shared argument pattern. On either account, it should be expected that a proffered explanation will appeal to a higher level, which leads to our next conjecture.

Conjecture 2.3. —

Explanation occurs primarily as an appeal to a higher level of generality.

One moral which may follow from this brief survey of the difficulties facing philosophical theories of mathematical explanation is the importance in any empirical study of having regard to the context of explanations. In particular, van Fraassen's relevance relation must be subject to some sort of contextual constraint, if it is to resist trivialization [20, p. 319]. Some progress in this direction may proceed from an unexpected source:

• (1)Trace explanations: ‘reveal the so-called execution trace, the sequence of inferences that led to the conclusion of the reasoning’;
• (2)Strategic explanations: ‘place an action in context by revealing the problem-solving strategy of the system used to perform a task’;
• (3)Deep explanations: ‘the system answers the question by using the knowledge base of the user, and not just that of the system […] the explainer must base the explanation on its understanding of what the explainee fails to understand’ [28, p. 73].

This distinction, presumed to be mutually exclusive, originates in the development of software for medical expert systems (whence it was retrieved by Douglas Walton, and applied to mathematics by Michel Dufour, [29, p. 6]). Researchers found it useful to distinguish three types of knowledge required for ‘understanding physicians’ explanations of their reasoning, as well as being a foundation for re-representing the knowledge' [30, p. 221]. These three kinds, structural, strategic and support knowledge, are distinct from the domain knowledge, such as facts about medicine. Structural knowledge indexes the domain knowledge into rules; strategic knowledge imposes a plan of how to apply these rules, in pursuit of which goals, and in which order; and support knowledge comprises the broader background which provides the justification for structural and strategic knowledge. Hence, a request for an explanation could be construed as a request for one of these three sorts of knowledge, which the system may meet by outputting a trace, strategic or deep explanation, respectively [31, p. 174]. That is, each of the three comprises a different contextual constraint on the relevance relation. By limiting that relation to independently motivated instances, Kitcher & Salmon's trivialization may be headed off. Indeed, van Fraassen's own discussion of relevance already draws distinctions that echo the trace/strategic/deep distinction. For example, ‘asking for a sort of reason that at least includes events-leading-up-to’ is naturally construed as a request for a trace explanation, whereas asking for a ‘motive’ would seem to be a request for a strategic (or perhaps deep) explanation [19, p. 143].

Perhaps surprisingly, explaining mathematical reasoning and explaining the output of an expert system are very similar activities. In both cases, the item requiring explanation is obtained as the end state of protracted ratiocination. This is quite unlike the characteristic situation in natural science, where the item requiring explanation is a naturally occurring phenomenon, not the product of a reasoning process. Following a reasoning process (trace explanation) or even learning why specific steps were chosen over others (strategic explanation) does not provide the same understanding of why the result is correct that ensues when it is connected to what is already understood (deep explanation). So trace, strategic and deep explanations do seem to arise in mathematical practice: for example, to request explanation of a particular mathematical result could be to seek clarification of specific steps in the proof that led to the result (trace); it could be to seek the rationale behind the choice of steps (strategic); it could be a more comprehensive attempt to ground the result in a secure knowledge base (deep). If this initial impression is born out by empirical observation, then the threefold trace/strategic/deep distinction would represent a well-motivated basis for constraining van Fraassen's relevance relation, and thereby rehabilitating his account of explanation, at least for mathematics. Thus, we make a further conjecture.

Conjecture 2.4. —

Explanations can be categorized as either trace explanations, strategic explanations or deep explanations.

A second, broader aspect of context salient to our enquiry is that we should be prepared for the context of mathematical explanation to exhibit both distinctive and generic features. That is, there may be contextual features of mathematical explanations that are similar to those of many other sorts of explanation, and there may be contextual features of mathematical explanations that are unique to mathematics. These two contextual questions led to our last two conjectures.

A concern for the generic aspects of context shared with non-mathematical explanation comports with the observation that ‘daily discourse is filled with explanations of behaviour in terms of the agent's purposes or intentions’ [32, p. 46]. As in Norman Malcolm's examples, ‘He is running to catch the bus’ or ‘He is climbing the ladder in order to inspect the roof’, the purposive elements can arise in the explanans; but purposive elements can arise in the explanandum too. For example, ‘She took her umbrella because she thought it would rain and she did not want to get wet; she thought it would rain because she had heard the weather forecast and she did not want to get wet because she was on her way to a party’. Here purposive elements arise in the explanans of the first clause, which is itself the explanandum of the second clause. Without endorsing any particular theory in the philosophy of mind, we may observe that the explanatory role of purposive elements is also foundational to Michael Bratman's belief/desire/intention (BDI) model of practical reasoning, which has itself been widely influential in the development of software agents [33]. Thus beliefs, goals, desires and like purposive elements may play a role in mathematical explanation too. That is,

Conjecture 2.5. —

Explanations in mathematics contain purposive elements.

The last conjecture, addressing the specifically mathematical aspects of context, recognizes Steiner's acknowledgement that this is an account not of ‘mathematical explanation, but explanation by proof ; there are other kinds of mathematical explanation’ [22, p. 147]. We therefore conjecture that proof will be only one mathematical context among many in which explanation may occur.

Conjecture 2.6. —

Explanations can occur in many mathematical contexts.

The last two conjectures are necessarily more exploratory than the others, if only in the sense that we did not prejudge the scope of their answers in advance of any analysis of our data. Rather, as described below in §4d, we developed sets of purposive elements and mathematical contexts on the basis of a pilot analysis of a subset of the data.

3. Online collaborative mathematics

To apply empirical methods to the study of mathematical explanation we looked for a suitable source of data which, ideally, would capture the live production of mathematics rather than the finished outcome in textbook or journal paper; would exhibit explanation in practice through capturing mathematical collaboration, and could be argued to comprise the activities of a representative subset of the mathematical community. The dataset we chose was the Mini-Polymath projects, online collaborations on a blog to solve problems drawn from International Mathematical Olympiads.

One of the popular myths about mathematics that does not survive the investigation of mathematical practice is that it is a solitary pursuit. Although there are celebrated incidents of ‘solo ascents’, such as Andrew Wiles's lengthy pursuit of the Taniyama–Shimura conjecture, successful mathematical practice is more characteristically collaborative: for example, single authored papers make up only 36% of the articles published in the leading research journal Annals of Mathematics between 2000 and 2010 [34, p. 11]. In recent years, the increasing ubiquity and reliability of online networking tools have facilitated the growth of remote collaboration between larger and more widely dispersed groups than has hitherto been practicable. In 2008, Tim Gowers and Terry Tao, both winners of the Fields medal, the mathematicians' Nobel Prize, set up the Polymath projects [35], in which mathematicians collaborate in public on a blog to solve leading-edge problems. An important aspect was that the activity was owned by the mathematical community, avoiding the supposed ‘bureaucracy’ of other sites [36], hence rules of engagement were collaboratively designed to foster openness, civility and inclusivity, for example encouraging participants to post remarks representing a ‘quantum of progress’ rather than doing lengthy pieces of work in isolation [35]. Some authors have argued that Polymath is potentially revolutionary, ‘the leading edge of the greatest change in the creative process since the invention of writing’ [37]: if the outcome to date is less dramatic, with around half the projects so far initiated leading to significant progress, most noticeably [38], it is nonetheless widely discussed and regarded by a number of leading mathematicians as significant, with ongoing reflection on how to refine the process [39].

Such sites provide a new and substantial corpus of data on mathematical practice. Online forums and blogs for informal mathematical discussion reveal some of the ‘back’ of mathematics: ‘mathematics as it appears among working mathematicians, in informal settings, told to one another in an office behind closed doors’ [40, p. 128].⁴ As Gowers has observed, Polymath is ‘the first fully documented account of how a serious research problem was solved, complete with false starts, dead ends, etc. It may be that the open nature of the collaboration was in the end more important than its size’ [43].⁵

It remains an open question how representative online behaviour is of other mathematical practices. Indeed, one should be careful not to assume that there is a ‘standard’ mathematical behaviour: recent empirical studies by Matthew Inglis and colleagues into whether there is agreement between mathematicians on proof validity and appraisal call into question what he calls an ‘assumption of homogeneity’.⁶ Diversity in mathematical practice is recognized by the series of recent conferences on mathematical cultures and practices [46], by the ethnomathematics community, by philosophical analyses of such notions as mathematical style [47], and so on.

The International Mathematical Olympiad (IMO) is an annual competition, in which around 500 high school students a year take part in national teams of six, with each individual tackling the same problem set, problems that have been carefully chosen (and translated into many languages), with the intention that each team is treated fairly, and all students gain from taking part. Nearly 17,000 people have competed since its inception in 1959, with many more involved through the significant training and development activities run by national organizations, which have been credited with building capacity and a wider cultural change in attitudes to mathematics [48]. Many of those taking part have gone on to mathematical careers, some at an outstanding level—14 of the 36 Fields medal winners between 1978 and 2014 were IMO participants. It seems reasonable to assume that the Olympiad ‘culture’ may be regarded as background for a significant fraction of the world's professional pure mathematicians. For example, Tao remarked of the Olympiad ‘the habits of problem-solving—taking special cases, forming a subproblem or subgoal, proving something more general and so on—these became useful skills later on’, while observing that ‘serious mathematical research involves other skills: acquiring an overview of a body of knowledge, getting a feeling for what sorts of techniques will work for a certain problem, putting in long and sustained effort to accomplish something’ (quoted in [48, p. 415]).

In 2009, Tao started a series of four annual experiments, designated Mini-Polymath, which extended the Polymath format to tackle the hardest question in four successive IMOs, each solved by just a few participants in the actual competition. It should be stressed that, whereas the participants in the IMO are high school students, participation in Mini-Polymath was open to all, but mostly drawn from readers of Tao's blog. Many participants were anonymous, but identifiable participants include graduate students, postdocs and faculty members in mathematics or related fields. The ground rules for the Mini-Polymath projects were again carefully designed [49]: people who knew the answer or had already attempted the problem were asked not to take part; participants were asked not to search the Internet or consult the mathematical literature; participants were encouraged to share ideas as soon as possible even if they were ‘frivolous’ or ‘failed’, as others might find them helpful or be able to repair them; and, unlike the actual IMO, participants were asked not to compete to be the quickest, but to view themselves as contributing to a team effort ‘to experimentally test the hypothesis that a mathematical problem can be solved by a massive collaboration’.

The first such experiment, Mini-Polymath 1, the ‘Grasshopper problem’, was solved by just 3 of the 565 participants in the 2009 IMO. The online experiment attracted 70 participants, who over a period of 35 hours made 258 posts to solve the problem (followed by 100 or so posts reflecting on the process), with just two posters accounting for 18% of the posts [34]. The four Mini-Polymath projects contain a total of around 750 posts. Alison Pease and Ursula Martin analysed the contributions to Mini-Polymath 3, the ‘Windmill Problem’, and strikingly found that a mere 14% of the posts represented proof steps, with the bulk referring to examples or counterexamples (33%), conjectures (20%) or concepts (10%) and the rest comprising miscellaneous comments for clarification or encouragement [10].

4. Method and procedure

In this section, we present the method we employed to test the conjectures we proposed in §2, with the results following in §5. Our study was intended to be sufficiently light in its methodological presuppositions as not to prejudge any account of explanation. We presumed only that explanation involves some sort of interaction between a comment and its social and mathematical context. We employed two related methods to test each of our conjectures:

• (1)Close content analysis (see [50]) of a complete search over four mathematical conversations, based on the presence of explanation indicators; and
• (2)Close content analysis of randomly selected excerpts from the same four mathematical conversations, based on the absence of explanation indicators.

Close content analysis is a qualitative methodology, common in social sciences, in which presence and meanings of concepts in rich textual data and relationships between them are systematically transformed into a series of results. The method proceeds by analysis design, application and narration of results. Analyses may be text-driven, content-driven or method-driven, depending on whether the primary motivation of the analyst is the availability of rich data, known research questions or known analytical procedures. Krippendorff [51] dates the method back to the early twentieth century and gives several examples of different disciplines using it to analyse their data, and social impact of results found in this way. These include content analyses being used in legal and political settings, including acceptance as evidence in court, monitoring other countries for adherence to nuclear policies, and analysing internal factors such as quality of life.

Validity is partially established via replicability, which involves both intra-annotator and inter-annotator agreement; known respectively as stability (the degree to which the method of analysis yields the same results, given the same data, at different times) and reproducibility (the extent of agreement between results achieved by different people applying the same method to the same data).

(a). Source material

Our source material is drawn from the online mathematical conversations described in §3. Specifically, we used all of the Mini-Polymath conversations to date [49,52–54]. Each project comprised a research thread, in which the problem was explored and a proof was collaboratively constructed; a discussion thread, in which meta-level issues were raised; and a wiki page in which progress was summarized. We analysed the comments on the research thread, 742 in total (see table 1 for details of the key times and numbers of comments and participants, and figure 1 for the timeline of the number of accumulated comments).

Table 1.

The data we used in our empirical investigation of explanation in mathematical practice.

year	IMO	timeline	comments/words (before solution)	participants
2009	Q6	Start: 20 July 2009 @ 6:02 am	356/32,430	81–100
		Solution: 21 July 2009 @ 11:16 am	(201)
		End: 15 August 2010 @ 3:30 pm
2010	Q5	Start: 8 July 2010 @ 3:56 pm	128/7099	28
		Solution: 8 July 2010 @ 6:24 pm	(75)
		End: 12 July 2012 @ 6:31 pm
2011	Q2	Start: 19 July 2011 @ 4:01 pm	151/9166	43–56
		Solution: 19 July 2011 @ 9:14 pm	(70)
		End: 17 October 2012 @ 3:25 pm
2012	Q3	Start: 12 July 2012 @ 10:01 pm	108/10,097	43–48
		Solution: 13 July 2012 @ 7:53 pm	(79)
		End: 22 August 2012 @ 3:27 pm
total			742/58,792	185–221

Figure 1.

Timeline of the number of accumulated comments for each MiniPolymath conversation.

(b). Methods

We formulated our six conjectures, or research questions, based on a review of the literature on explanation, as shown above. We then used problem-driven content analysis to explore our conjectures, motivated by the epistemic phenemena relating to explanation. In order to ascertain stable correlations, all three co-authors independently read a portion of the content and conducted (separately) analysis identifying factors related to explanation.

Each of us has a first degree in Mathematics; one of us has a PhD in Mathematics and over 10 years experience as a professional research mathematician; the other two have PhDs in other disciplines but each has more than 10 years experience studying mathematical reasoning. Our analyses were compared and we initially found inter-annotator disagreements between our intuitions as to whether a comment primarily played an explanatory or justificatory role in the conversation. We also found disagreement at the intra-annotator level, suggesting that ‘intuition’ for this schema was weak and unreliable. These disagreements resulted in a minor redesign of classificatory schemata: once we had settled on the schemata presented in this paper, we found that the disagreements disappeared and classification was reliable at both inter- and intra-annotator levels. The first author then performed a complete analysis in accordance with a discussion between all three. For each instance of a keyword, the surrounding context was carefully taken into consideration, in order to ensure that the close content analysis reflected the correct usage.

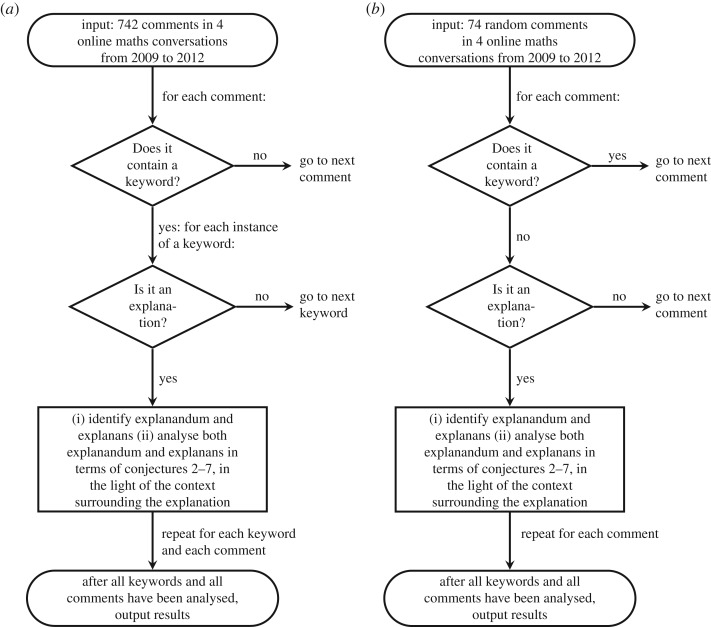
We used two approaches to investigate which explanations occur in informal mathematical conversations and in which contexts they arise. These procedures are represented schematically in figure 2.

• The Explanation-Indicator Approach (EIA). We used indicators which are associated with the explanation in order to identify possible instances of explanation (see §4c). We conducted an automated complete search for these indicators over the comments section of the four blogs on which the Mini-Polymath conversations were hosted (Stage 1, see §4c). For each occurrence of an indicator, we performed a close content analysis of the entire comment and comments around it, using cues from these to try to determine whether explanation played a role (Stage 2). We then performed close content analysis for each occurrence of a keyword which we categorized as an explanation (Stage 3). We made a number of contextual considerations. We looked at the sentence and comment in which the keyword occurred, identified the explanandum and the explanans (which may occur in different comments or may not both be present), considered the wider context of the explanation by looking at the other comments surrounding it and answered several questions about the nature of the explanation. For each keyword we considered whether there is a corresponding why-question (possibly implicit) (C2) and whether there was a clear difference of level (general or specific) between the explanandum and explanans which thus might be seen in terms of a characteristic property or unifying feature (C3). We also asked whether the keyword occurred in the context of object-level proof (i.e. concerned reasoning steps leading to a conclusion), or that of meta-level comment or meta-level proof (i.e. concerned a strategy employed), or in some other context (C4), what the context of the proof was, what sort of thing was being explained and what sort of explanation was offered (C5, C6). We give an example analysis to demonstrate our EIA method in figure 3 below.

• The Random Comment Approach (RCA). This approach was designed to pick out explanations which might not contain any of our explanation indicators. We analysed a random 10% of our corpora of 742 comments (§4a), which were found using a random number generator. The analysis followed similar stages to the Explanation-Indicator Approach: Select a comment at random and discard it if it contains an explanation indicator (Stage 1); use close content analysis to determine whether it involves an explanation (or multiple explanations) (Stage 2); and, if so, use close content analysis to analyse it according to our dimensions of explanation (Stage 3).

Figure 2.

The Explanation-Indicator Approach (a) and the Random Comment Approach (b).

Figure 3.

Analysis of the first (underlined) instance of underst* in the quoted passage, listing the questions we asked of each indicator-occurrence by our six conjectures, and possible answers (with our answers for this example shown in bold).

Why do we have two approaches? Firstly, to address the concern that the EIA may yield an unrepresentative sample. Secondly, so that our study may act as a pilot for the analysis of much larger datasets. Analysis of all 742 comments would have been onerous, but within the bounds of possibility; the same could not be said of datasets larger by an order of magnitude or more. Our two approaches are loosely inspired by the two methods employed by James Overton to investigate the occurrence of explanation in articles published in the journal Science [55, p. 1384]. However his focus on published work, almost none of it mathematics, led us to make substantial revisions.

(c). Choice of explanation indicators

The usefulness of indicator terms in recognizing arguments has long been known to the authors of textbooks: ‘The use of premise and conclusion indicators (words like “since”, “because”, “therefore”, “hence”, “it follows that” and so on) to help students identify the components of an argument is a standard part of most critical thinking textbooks and courses’ [56, p. 273]. For example, [57, p. 12] provides long lists of conclusion indicators and premise indicators . Even longer lists may be found elsewhere (for example [58]). There is little sign of any theoretical work underpinning the compilation of these lists. Nonetheless, it is usually at least acknowledged that these indicators can be ambiguous. In particular, authors often observe that ‘because’ can function as both premise indicator and explanation indicator (see, for example [58, TS 7]).⁷

In recent years, more attention has been paid to these indicators as a consequence of the emergence of ‘argument mining’, the use of automated search techniques to extract argumentational content from larger texts. The following lists were developed in this context:

• Indicators of premise after, as, because, for, since, when, assuming, …

• Indicators of conclusion therefore, in conclusion, consequently, … 

• Indicators of contrast but, except, not, never, no, … [60, p. 46]

Despite the lengthy lists of indicators compiled by some authors, in most corpora a small sample are disproportionately employed and the more obscure indicators seldom (if ever) occur. A brief exploratory analysis confirmed that this was also true of our corpus. Hence, our first stage comprised searching for the following indicators:

• —premise indicators: ‘since’; ‘because’; ‘, as’;
• —conclusion indicators: ‘thus’; ‘therefore’; ‘, so’;
• —explanation indicators: ‘expla*’; ‘underst*’.

Our search was performed over the comments section of the blogs (not including words in the problem itself). Both upper and lower case were included, and because of our search terms, stemming was automatically performed. Our annotated data can be found in [61].

(d). Close content analysis

A pilot analysis of a subset of our data allowed us to clarify how we would test C5 and C6. We developed two sets of categories, purposive and mathematical respectively, which we applied to the comments identified by each of the two processes, EIA and RCA.

With respect to C5, working from the abstracted examples below, we formulated associated keywords and constructed four categories of purposive element: abilities, knowledge, understanding and values or goals:

• Abilities (what can/can't we do). [Keywords: difficulty, hard, do] Examples: We can only almost do X; We can do X; We must be able to do X; X is always possible; X might not be the hardest bit; We can fix X in this way; The difficult bit might be X.

• Knowledge (what do/don't we know). [Keywords: know, plausible, mistake, wrong, assume, obvious, suppose] Examples: We don't know X; X is plausible; X is wrong; X is a mistake.

• Understanding (what do/don't we understand). [Keywords: understand] Examples: Why is this a contradiction?

• Values/goals (what do/don't we want). [Keywords: want, goal, need, help, problem, target, useful] Examples: X is a good idea; We want to do X; X will achieve our goal; We need to know X; X will help us in this way.

Once we had these categories, we then re-analysed the data and labelled both explanandum and explanans with whichever purposive categories applied (each example was labelled with between 0 and 4 categories).

With respect to C6, we performed a similar analysis of the mathematical contexts of explanations occurring in our corpus of comments. We found that they clustered into seven types: initial problem,⁸ proof, assertion, specific instance, argument, representation and property:

• Initial problem. Examples: The initial problem is harder if X; The initial problem is hardest when X; Condition X is necessary for the initial problem.

• Proof (approach). Examples: X is not a useful approach; Approaches X and Y might be the same; Approach X might not work; If we can do X then we have a complete proof.

• Assertions. Examples: There is only one of type X; x is not in set X; Y is a subset of X; If we do X then we'll get Y; There must always exist X that satisfies condition Y.

• Specific cases/instances. Examples: Things get harder in case X; There will always exist instance X that satisfies condition Y; The problem works in instance X; other cases X and Y are trivial; Case X might be a problem.

• Arguments. Examples: Let us suppose X. Then Y.

• Representation. Examples: there are many ways to write X; by reducing the problem to X.

• Property. Examples: X has this property; X might not be unique; X doesn't have this property; X might have this property.

Again, once we had these categories, we re-analysed the data and labelled both explanandum and explanans with whichever mathematical context categories applied (each example was labelled with between 0 and 7 categories).

Once we found these seven categories and the four above, we categorized each instance of explanandum and explanans with whichever applied. If more than one applied then we used multiple labels. We also considered the number of co-occurrences between different types of explanandum and explanans in the EIA.

Figure 3 gives an example of how the close content analysis process was applied, using the EIA. We list the questions we asked of each indicator-occurrence for our six conjectures, with their possible answers, with our categorizations for this example shown in bold.

5. Findings

(a). Explanation-indicator approach (EIA)

We found 243 instances of our indicator terms, of which we categorized 176 as connected to explanation. This gave an average of 0.3 indicators per comment, or 0.2 instances of explanation per comment. In general we found the explanation and premise indicators to be more reliable at indicating explanation than our conclusion indicators. The terms expla*, because, and underst* were especially reliable explanation indicators (with an aggregate reliability of 88%) and therefore was especially poor (only 45% reliable).

We show the total number of explanation indicators and the proportion of those that we rated as genuine explanation across the four conversations in table 2 and for each explanation-indicator keyword in order of reliability in table 3.

Table 2.

The number of explanation indicators in all four conversations, and the proportion of those that we rated as a genuine explanation.

year	number of comments	no. indicators found	indicators per comment	no. identified as explanation	% of indicators identified as explanation
2009	355	105	0.3	74	70%
2010	128	21	0.2	17	81%
2011	151	52	0.3	41	79%
2012	108	65	0.6	44	68%
total	742	243	0.3	176	72%

Table 3.

The type of explanation indicators across the four conversations, and the proportion of those that we rated as genuine explanation.

indicator type	keyword	number found	number identified as explanation	%
explanation	expla*	2	2	100
premise	because	25	23	92
explanation	underst*	22	18	82
premise	since	62	45	73
premise	, as	7	5	71
conclusion	, so	88	62	70
conclusion	thus	26	16	62
conclusion	therefore	11	5	45
total		243	176	72

(b). Random Comment Approach (RCA)

A pseudorandom number generator was used to select 74 comments—approximately 1 in 10—from the 742 comments in the corpus. Of these 74 comments, 13 were found to contain explanation indicators, and therefore discarded. Of the 61 remaining comments, we categorized 13 as relating to explanation. Thus, 21% (13/61) of the randomly selected indicator-free comments concerned explanation. We show the breakdown for each year in table 4.

Table 4.

Comments considered under the Random Comment Approach, by year.

year	number considered	number without indicator	number without indicator identified as explanation	% non-indicator comments classified as explanation
2009	22	20	4	20%
2010	18	16	2	13%
2011	16	13	5	38%
2012	18	12	2	17%
total	74	61	13	21%

Clearly results found via the EIA were far stronger in terms of evidential support. The low numbers involved in the RCA prevent us from forming conclusions based on these; rather results found by following this approach may suggest areas for further investigation.

(c). Close content analysis

The results of the close content analysis (§4d) for C2, C3 and C4 are summarized in table 5. Results for C5 and C6 are shown in tables 6–8, with the number of co-occurrences between mathematical and purposive types of explanandum and explanans in the EIA shown in figure 4.

Table 5.

Raw figures and percentages for our labellings for C2, C3, and C4 (given a total of 176 instances of explanation in the EIA and 13 instances of explanation in the RCA).

		raw		%
conjecture	labelling	EIA	RCA	EIA (%)	RCA (%)
C2	answers to why questions	174	13	99	100
	not answers to why questions	2	0	1	0
C3	primarily an appeal to a higher level	4	3	2	23
	not primarily an appeal to a higher level	172	10	98	77
C4	trace explanation	121	8	69	62
	strategic explanation	42	4	24	31
	deep explanation	11	1	6	8
	neither trace, strategic, nor deep	2	0	1	0

Table 6.

The breakdown of our purposive and mathematical context categories for each year, and the proportion of both of these.

year	no. labellings	purposive (%)	maths (%)	explanandum (%)	explanans (%)
2009	180	27	73	51	49
2010	47	26	74	49	51
2011	136	18	82	52	48
2012	122	20	80	52	48
total	485	23	77	51	49

Table 8.

Breakdown of our mathematics category.

	explanandum		explanans		total
	EIA (%)	RCA (%)	EIA (%)	RCA (%)	EIA (%)	RCA (%)
assertion	27	27	26	0	27	14
property	15	13	23	8	19	11
proof	23	33	12	0	18	18
example	16	7	18	46	17	25
representation	9	13	7	38	8	25
argument	2	0	10	8	6	4
initial problem	8	7	4	0	6	4

Figure 4.

Categorization of all explanandum/explanans pairs found via our EIA, with explananda shown in the rows and explanantia in the columns. Pa, Pk, Pu and Pv are from our purposive category (respectively—ability, knowledge, understanding, value); and Mip, Mproof, Mass, Meg, Marg, Mrep and Mprop are from our mathematics category (respectively—initial problem, proof, assertion, example, argument, representation and property). Darker shading indicates more occurrences.

6. Discussion

(a). Conjecture 1. There is such a thing as explanation in mathematics

True. On average, 33% of comments contained one indicator, of which we classified 72% as relating to explanation. This gives 23% of the whole conversation as relating to explanation. Of the remaining 67% of the conversation which did not contain an indicator, we classified 21% of a random sample as relating to explanation. This gives a further 14% of the whole conversation, for a combined total of 37% (23 + 14), thus providing strong empirical support for the conjecture that explanation does occur in mathematics.

We found that often a sentence seemed to play dual roles in explaining and justifying, while in a few cases it seemed clearly more one than the other. For instance, the keyword ‘since’ occurred in the following two comments (our boldface )—the first of which seems to be straightforward justification within a proof argument, and the second of which involved explanation.

Maybe some notation would help: if A is your set of possible steps, then say S(A) is the set of all possible positions you can end up on the way. So eg, if A = 2, 3, 5, S(A) = 0, 2, 3, 5, 7, 8, 10. Then the above is saying that for some a_i∈A where a_i∉M, there is an m_j∈M where m_j∉S(A − {a_i})—in which case you can reduce the problem to A′ = A − {a_i}, and m′∈M′ iff m′ + a_i∈M − {m_j}, and since S(A′)∉M′ we have an instance of the n − 1 case.

 Part of comment 59, by aj.

Some obvious points:

(1) Slot one will never have more than one coin.

(2) Slot two will never have more coins that slot three can have (since it can get the most coins through a swap with three).

 Comment by Mike — July 8, 2010 @ 5:05 pm

Such support raises a corresponding challenge for the accounts of philosophers who claim that explanation plays little role in mathematical practice. The disagreement here might be thought to be due to different interpretations of explanation and different types of mathematical practice, in addition to different methodologies for arriving at conclusions. The mathematical practice which we consider is drawn from the ‘back’ of mathematics [40]. This contrasts with the ‘front’ mathematical practice of public, polished proofs to which Resnik and Kushner, Avigad, and Zelcer apparently (if implicitly) restrict their attention. Nonetheless, since none of these philosophers invoke the front/back distinction themselves, this is at best a speculative suggestion as to how their view might be defended in the light of our data. Indeed, at least facially, their work suggests that they intend their argument to apply to both front and back. For example, whereas stating that explanation is ‘not an acknowledged goal of mathematical research’ [14, p. 151] might be thought to emphasize the front, commenting that ‘the term [explanation] is not so very often used in ordinary mathematical discourse’ [15, p. 106] might as readily refer to the back. It could also be objected that their definition of mathematical explanation was much narrower than ours, perhaps applying only to what we have called deep explanation: Zelcer, at least, might be read this way [16, p. 175]. But, although the deep explanation was the rarest of the varieties of explanation in our data, there were still enough examples to lend support to C1 even on this narrow construal.

Moreover, the all but exclusive focus by philosophers on proof in mathematical practice (sometimes acknowledged, as in [22, p. 147]) contrasts significantly with our findings, in which our corpus of mathematical practice includes many more activities. We give a fine-grained breakdown of the type of mathematical activity which we observed in the context of explanation in §6f: here proof only forms 18%. Zelcer grounds his dismissal of mathematical explanation, at least in part, on there being ‘no systematic analysis of standard and well-discussed texts illustrating any pattern of mathematical explanations’ [16, p. 180]. This may well have been correct—if only because there had been no systematic analysis of explanation in any mathematical texts! But our study reveals that some analyses of this sort do indeed exhibit a pattern of mathematical explanations.

(b). Conjecture 2. All explanations are answers to why-questions

True. 99% of explanations in the EIA approach could be read as answers to why-questions, and 100% in our random comment approach. In all but a handful of cases these were implicit why-questions, that is, a why-question could be envisaged, which the explanation would answer. For instance, in the following example, the parenthetical explanation flagged up by our ‘because’ indicator, can be rephrased as an answer to the why-question: ‘Why can we assume that it would be safe for the grasshopper to hop backwards to its previous point?’:

[…] If the grasshopper at any point finds itself unable to hop forward, it simply hops backwards to its previous point (which, because we are working iteratively is assumed to be safe). Of course it might find itself backtracking the whole path, but since we're not actually trying to construct an efficient algorithm this is fine. […]

Comment by Sarah — 20 July, 2009 @ 2:05 pm

Van Fraassen's claim that all explanations are answers to (implicit) why-questions must, presumably, have included the parenthesis—as it is otherwise clearly false (or else he thought that there were very few explanations). If this allowance is considered legitimate, then our findings provide extremely strong support for this aspect of van Fraassen's pragmatic account. Allowing the why-question to be implicit rather than explicit may also help to answer one of Sandborg's criticisms, that if the particular why-question is already known, then the need for an explanation is much reduced (someone who does not understand a proof is unlikely to know which why-question to ask). The issue here concerns van Fraassen's contrastive element, as in ‘Why P rather than Q?’ In the above example, the contrast class in the why-question is ambiguous: it could concern the assumption (‘why assume X rather than Y?’), the safety (‘why will it be safe rather than dangerous?’), the direction (‘why hop backwards rather than forwards?’) or the particular point (‘why hop to the previous point rather then another one before that?’). The explicit answer given to the implicit question—‘(which, because we are working iteratively is assumed to be safe)’—may resolve some of the ambiguity, although readings in which either iteratively or safe is emphasized would both make sense, thus some ambiguity remains. Thus, the contrast class may also be inherent in the question, as claimed by van Fraassen, but be unarticulated: a questioner may ask ‘Why P?’, with the answerer having to infer which contrast class Q the questioner requires. In the example above, Sarah is explaining to an imaginary person: the explainer both constructs and answers the why-question. This shows a way in which to reconcile Sandborg's objection with van Fraassen's contrastive element. We consider that van Fraassen's account of explanation as why-questions has been strongly corroborated, while agreeing with Sandborg's argument that a theory of explanation must go beyond a theory of why-questions: indeed we consider our work regarding the remainder of the conjectures as a step in that direction.

(c). Conjecture 3. Explanation occurs primarily as an appeal to a higher level of generality

False. Only 2% of the explanations found in our explanation-indicator approach had a clear difference of level of generality between the explanandum and explanans, and so could not be said to appeal to a higher level of generality. While we did find more examples in our random comment approach—here 23% of our explanations occurred as an appeal to a higher level of generality—in general we found that occurrences in which explanandum and explanans had a difference of level were extremely rare. (This is the area of greatest divergence between our two approaches: in some ways it is surprising that our findings under both approaches converge as much as they do.) Certainly, we have shown that for neither dataset is it true that explanation occurs primarily as an appeal to a higher level of generality. Those rare examples that did arise were typically in comments containing (or referring to) proofs. In particular, we found examples of case-split proofs (in which a case was proved because it was shown to be a special case of the general (proved) case) and inductive proofs (for instance, ‘why does a property hold in the case n = 5?’ (explanandum) ‘Because of the inductive argument that it holds for all natural n’ (explanans)).

For both Kitcher and Steiner, a difference in level of generality between explanandum and explanans would be a prerequisite for their theory. Since Kitcher is so narrowly focused on proof products, we would not expect to find examples of his type of explanation in our dataset, and we did not. However, the fact that it was so rare to find examples does have implications for Steiner's theory of characterizing properties. While the idea that explanations turn on what is distinctive about an object may be intuitively appealing, it was not representative of what we found. There is a sizeable body of work on whether proofs by case split or by induction are explanatory (for example, [62–64]); however, since they formed such a small proportion of our examples, we conclude that the lack of evidence that we found for Steiner's theory suggests that it does not apply to this context of mathematical practice.

(d). Conjecture 4. Explanations can be categorized as either trace explanations, strategic explanations or deep explanations

True. Of the 176 explanations in our explanation-indicator approach, we found that 69% occurred in the context of trace explanations, 24% as strategic explanations and 6% as deep explanations, with 1% classified as none of the three. This result was similar in our random comment approach: of 13 explanations, 62% were trace explanations, 31% were strategic explanations, and 8% were deep (the additional 1% comes from rounding errors). Thus almost all of our examples were covered by the three types of explanation.

An example of a trace explanation, describing object-level reasoning, is:

‘The remaining question is: can 2010^20102010 be written as 4*(x − 2k)? Clearly, by solving for k, we get k = x/2 − (2010^20102010)/8, which are integers, so the answer is affirmative.’

This is actually not needed, since we can simple swap $B_5\leftrightarrow B_6$ enough times to adjust the content of B₄.

Comment by SM — July 8, 2010 @ 7:16 pm

An example of a strategic explanation, explaining problem-solving strategy, is:

Come to think of it, it should be clear that 112 cannot be quite right, because it always chooses a_j as the final step. But we have examples where that isn't right (a_j was arbitrary so that $\sum _{i\ne j}{a}_i$ was not in M), so we know that the correct solution will have to account for the fact that there may be multiple a_j which satisfy that condition, some of which may not be part of a solving path.

Comment by Henry — July 20, 2009 @ 8:30 pm

An example of a deep explanation, explaining a particular misunderstanding, is:

Hi! I don't understand Tao's proof. More specifically, I don't get the last sentence ‘But this forces M to contain n distinct elements, a contradiction.’

 Can anyone elaborate the point a little further for me, please?

 Comment by Juan — 24 July, 2009 @ 7:53 am

We looked at proof #1 and have an additional suggestion to pietropc's suggestions in his post: in the last paragraph, one should chose i as the greatest element rather than smallest (or change a_i + a_n−j+1 + · s + a_n−1 to a_i + a_n−j+2 + · s + a_n ) to ensure that all the following numbers are distinct from each other.

 It might be nice to make the three groups of numbers that lie in M which are n numbers in total more explicit: 1. a_i + a_n−j+1 + · s + a_n for i∉I, 2. a_i + a_n−j+1 + · s + a_n−1 for i∈I and 3. for the biggest i∈I the numbers a_i + a_n−j+1 + · s + a_n − a_m.

 Comment by Alex and Ecki — 24 July, 2009 @ 7:57 am

Thanks, Alex & Ecki! Now I get it. It's a beautiful proof!

 Comment by Juan — 24 July, 2009 @ 8:16 am

The strategic explanations explained strategic reasoning about proofs at the object-level (24%), proofs at the meta-level (46%) and meta-level comments (29%).

There may be multiple reasons why there were fewer deep explanations than other kinds. Firstly, we analysed the data according to a narrow interpretation of the category. In particular, we considered whether the explainer had taken into account a particular perceived knowledge base of a particular person, as in the example above. Over the dialogue as a whole there was a perceived model of background mathematical common knowledge, as well as a dynamic, socially constructed collective knowledge base, which was the (implicitly or explicitly) agreed upon knowledge constructed over the course of the conversation. For instance, some explanations were given in terms of collected comments which had previously been agreed—we did not classify these as deep. Additionally there were some explanations addressed to a subset of the participants—a subset defined by their knowledge base: e.g. ‘to those who think the proof works…’. We likewise did not include this either as deep. For instance, we did not classify the comment below as deep, since there was nothing in it to indicate a particular insight into the questioner's knowledge base (note that this is unusual in that it is the same person asking and giving an explanation):

A question: Does the windmill process eventually form a cycle?

 Comment by Seungly Oh — July 19, 2011 @ 8:48 pm

I guess it should, since there are infinite many iterations and only finite options.

 Comment by Seungly Oh — July 19, 2011 @ 8:50 pm

A second reason for the comparative scarcity of deep explanation may be that, since the conversation is online, participants usually do not know each other; additionally many cues such as tone and body language are not represented, and so it is harder to build up a picture of individual knowledge bases. Thirdly, also due to the fact that the conversation occurs online in real-time, often with parallel threads, participants are under time-pressure, and therefore may not articulate lack of understanding as much as they would in a slower-moving conversation. The public nature of the conversation may also be a factor here.

There was no pattern as to mathematical context or purposive element in the deep explanations. An example of a deep explanation concerning a conceptual misunderstanding is below:

Ohhh…I misunderstood the problem. I saw it as a half-line extending out from the last point, in which case you would get stuck on the convex hull. But apparently it means a full line, so that the next point can be ‘behind’ the previous point. Got it.

 Comment by Jerzy — July 19, 2011 @ 8:31 pm

Yeah, so it's an infinite line extending in both directions and not just a ray. I'm thinking spirograph rather than the convex hull.

 Comment by Dan Hagon — July 19, 2011 @ 8:44 pm

That trace, strategic, and deep explanation appear to be exhaustive of the mathematical explanations we investigated supports our contention that they could provide an effective constraint on van Fraassen's relevance relation. It would seem that when mathematicians ask each other for explanations, they are almost always asking for one of these, so little will be lost if these are the only varieties available.

(e). Conjecture 5. Explanations in mathematics contain purposive elements

True. The EIA resulted in 485 labellings across conjectures 5 and 6 (an average of 2.8 labels per explanation (485/176), with 51% of the labels attached to the explanandum and 49% to the explanans. Of these, 23% of our labels were purposive-related and 77% were mathematics-related. The RCA resulted in 33 labellings (an average of 2.5 labellings per explanation), of which 15% concerned purposive and 85% concerned mathematics; with the explanandum/explanans split as 61%/39%. (Since the RCA produced such a small number of purposive-related labels, we made no further use of it in the assessment of conjecture 5.)

The EIA purposive labels were equally spread over explanandum and explanans, with value and understanding being the largest categories (34% and 32%, respectively) and ability and knowledge being smaller, but still significant categories (20% and 15%, respectively). We show the breakdown in table 7 above.

Table 7.

Breakdown of our purposive category using the EIA.

	explanandum (%)	explanans (%)	total (%)
value	37	30	34
understanding	30	34	32
ability	19	21	20
knowledge	14	15	15

(f). Conjecture 6. Explanations can occur in many mathematical contexts

True. As discussed in §6e, the EIA produced 485 labellings of which 77% were mathematics-related and the RCA produced 33 labellings of which 85% were mathematics-related. The labels resulting from both approaches clustered into seven types—assertion, property, proof, example, representation, argument and initial problem—shown in table 8 above.

There was some difference between those mathematics labels applying to the explanandum and explanans. On the EIA, assertion, example and representation applied in similar distributions to the explanandum and to the explanans, while the other labels had unequal splits across explanandum and explanans. On the RCA, there is essentially no agreement between explanandum and explanans. Taking the total of explanandum and explanans labels, on the EIA, the labels fell into three broad groups, with the largest category being assertion, then property, proof and example and the smallest representation, argument and initial problem. However, on the RCA, example and representation were most numerous, followed by assertion, property and proof , with argument and initial problem being least represented.

We also considered the number of co-occurrences between different types of explanandum and explanans in the EIA: our findings are shown in figure 4, where darker shading indicates more occurrences. This shows that the most common explanandum–explanans pairs are proof–proof, assertion–assertion, example–example and assertion–property. While this may not be surprising, it is not always the case that the diagonals in figure 4 have the darkest shading: an explanandum about an assertion is equally likely to be answered with an explanans about a property, as an assertion: it is also fairly likely to be answered with an explanans about an example or an argument. Likewise, an explanandum about a proof may well be answered with an explanans about an assertion or an example. In terms of the purposive elements, explananda about what one is able to do are most likely to receive an answer about what one is able to do, an assertion or a property. Explananda about what one knows are most likely to be answered with an assertion.

With such low numbers of explanation-labellings in the RCA, it did not make sense to break down the co-occurrence of explanandum–explanans pairs, but our most frequent combination was proof–representation (mathematics-related) and assertion–example (mathematics-related), both occurring 14% of the time.

7. Conclusion and future work

Our empirical investigation of mathematical practice shows that explanations are an essential component, largely driven by why-questions, embedded throughout the mathematical process, not just in proofs, and with a clear purposive element. While it is false that they appeal to a higher level of generality, they can be classified in terms of whether they explain reasoning at a trace or strategic level, and whether they take into account another's knowledge base. We have found a large, rich and diverse set of explanations in our investigation, taking place in a variety of dialogues.

One of the distinctive contributions of this paper is its methodology. Mathematicians are not constrained by philosophers' norms, so analyses of their practices should not preemptively narrow the range of accounts to the philosophically respectable. Our study is yet further evidence for the value of such a data-led approach in addressing philosophical problems. While we share this attitude with much recent work in x-phi, we have departed significantly from the survey-based techniques by which x-phi is best known. A corpus-based approach has been applied to the philosophical analysis of explanation before, notably in [55]. However, we differ from Overton in our emphasis on the process of mathematics in progress (the ‘back’) rather than the finished product (the ‘front’). This emphasis led us to a second innovation: whereas Overton's corpus consists of published articles, we studied a corpus derived from a community of mathematicians actively pursuing a solution to a problem. This also brought out the significance of collaborative work: contrary to the romantic image of the mathematician as solitary genius, much mathematical research is conducted interactively. We believe that the tools we have developed for these purposes (such as the RCA and the EIA) lend themselves to wider application to mathematical practice, such as a study of informal notions of simplicity (and perhaps beyond).⁹ There are other larger-scale projects to which they could be applied, including the original Polymath project and its successors. Results found using the methodology presented here could be usefully triangulated with participant interviews conducted once the conversation is considered to be finished, and/or with real-time observations in which a researcher observes a participant, using a think-aloud protocol, during the conversation.

The results of this paper have important lessons for the study of explanation in mathematics. We advanced six conjectures concerning intramathematical explanation. We found evidence to support five of them and to reject the sixth (C3). That conjecture, that explanation occurs primarily as an appeal to a higher level of generality, is presupposed by the two best-known accounts of mathematical explanation, those of Steiner and Kitcher. Hence, our study found little direct support for either of the two most influential positions, an important negative result. Our positive results are even more interesting. Contrary to some sceptical accounts, our findings confirmed the conjecture that explanation does indeed play a role in mathematics (C1). We also found support for the conjecture that all explanations can be framed as answers to why-questions (C2). Since this is a presupposition of van Fraassen's account of explanation, this provides some modest support for that account. We found that the neglected distinction between trace, strategic and deep explanations can be usefully applied to explanation in mathematics, which we suggest may usefully support van Fraassen's account (C4). We confirmed that explanations in mathematics contain purposive elements (C5), demonstrating their intimate connection to the intentions of the mathematicians who employ them. One of our most important results was that explanations are not confined to proofs: they can occur in the context of many different types of mathematical context (C6). This challenges the almost exclusive attention paid to proof in most philosophical treatments of mathematical explanation and also raises questions concerning Hilbert's 24th problem: can we formalize the notion of simplicity of a definition, a question, an example?

Our results open up numerous avenues for future research, both empirical and non-empirical. Space constraints prevent us from discussing more than a few of the most promising here. The support we found for the existence of mathematical explanation (C1) could be reinforced empirically in two ways: either by studying other mathematical corpora, transcripts of face-to-face collaborations between mathematicians, or digital archives of mathematicians' correspondence; or by contrasting mathematical corpora with non-mathematical corpora, whether of scientific practice, or of everyday language. Between them, our investigations of the conjectures C2, C3 and C4 suggest that van Fraassen's account of mathematical explanation may be better situated than its obvious rivals, the accounts of Steiner and Kitcher. However, this paper only presents a preliminary investigation: an empirical defence of van Fraassen would need to explore all the details of his picture. For example, the role of contrast classes would need to be investigated: is it possible to identify a contrast class for each implicit why-question? Perhaps the most exciting aspect of our study is the groundwork it undertakes for future philosophical accounts of mathematical explanation and related concepts, such as mathematical understanding, mathematical clarity or mathematical simplicity. It not only challenges current theories, it also identifies what should be the key features of a more empirically based successor. We hope to return to all of these issues in future papers.

Hilbert's 24th problem represents a challenge and an opportunity for researchers in automated reasoning; some of the implications that a formal notion of simplicity might have for automated theorem proving are teased out in [65]. Gowers' work on formalizing a good proof [1] was specifically written with computer proof in mind. Likewise, we see our work on explanation as being potentially relevant to automated reasoning. The importance of explanations in AI and Computing in general is now a research programme in its own right (now gaining traction under the banner of Explainable Artificial Intelligence (XAI)). The new EU General Data Protection Regulation (GDPR) introduces a ‘right to explanation’ of algorithmic decisions, making the topic especially pertinent. We anticipate that informal as well as formal and philosophical as well as computational interpretations of notions such as simplicity, explanation and understanding will gain new relevance as progress is made in bridging the gap between human and automated reasoning.

Data accessibility

https://github.com/alisonpease/Explanation-Data/releases/tag/v1.0 [61].

Competing interests

We declare we have no competing interests.

Funding

This work has been supported in part by the UK Engineering and Physical Sciences Research Council under grant nos EP/K040251/2 and EP/P017320/1, and the Future and Emerging Technologies (FET) programme within the Seventh Framework Programme for Research of the European Commission, under FET-Open grant no. 611553 (COINVENT).