Reactive and Nonreactive Scattering of HCl from Au(111): An Ab Initio Molecular Dynamics Study

Abstract

The HCl + Au(111) system has recently become a benchmark for highly activated dissociative chemisorption, which presumably is strongly affected by electron–hole pair excitation. Previous dynamics calculations, which were based on density functional theory at the generalized gradient approximation level (GGA-DFT) for the molecule–surface interaction, have all overestimated measured reaction probabilities by at least an order of magnitude. Here, we perform ab initio molecular dynamics (AIMD) and AIMD with electronic friction (AIMDEF) calculations employing a density functional that includes the attractive van der Waals interaction. Our calculations model the simultaneous and possibly synergistic effects of surface temperature, surface atom motion, electron–hole pair excitation, the molecular beam conditions of the experiments, and the van der Waals interaction on the reactivity. We find that reaction probabilities computed with AIMDEF and the SRP32-vdW functional still overestimate the measured reaction probabilities, by a factor 18 for the highest incidence energy at which measurements were performed (≈2.5 eV). Even granting that the experiment could have underestimated the sticking probability by about a factor three, this still translates into a considerable overestimation of the reactivity by the current theory. Likewise, scaled transition probabilities for vibrational excitation from ν = 1, j = 1 to ν = 2 are overestimated by the AIMDEF theory, by factors 3–8 depending on the initial conditions modeled. Energy losses to the surface and translational energy losses are, however, in good agreement with experimental values.

1. Introduction

Quantum and classical dynamics studies of dissociative chemisorption of molecules on transition-metal surfaces based on electronic structure calculations with density functional theory (DFT) have been remarkably successful at reproducing experimental results.^1,2 Examples include reactions of H₂ with Cu(111),³ Cu(100),⁴ Ru(0001),⁵ and Pt(111),⁶ of CH₄ with Ni(111),⁷ Pt(111),⁸ and Pt(211),⁸ and of N₂ with Ru(0001).⁹ In most of these examples, such a successful description was achieved by adopting a semiempirical approach called the specific reaction parameter approach to DFT (SRP-DFT).^3,10 However, as will be discussed below, the dissociation of HCl on Au(111) stands out as an example where theory has been remarkably unsuccessful with achieving agreement with experiment¹¹ with dynamics calculations based on a DFT description of the electronic structure.¹²⁻¹⁷ The HCl + Au(111) reaction has been suggested to represent an example of a dissociative chemisorption reaction that is strongly influenced by electronically nonadiabatic effects, such as electron–hole pair (ehp) excitation.^11,18 This adds special interest to this reaction: while experiments and calculations on nonreactive scattering of molecules from metal surfaces have revealed clear evidence of strong nonadiabatic effects,¹⁹⁻²⁵ persuasive evidence of a strong effect of ehp-excitation on reaction has so far been missing.²⁶⁻³³ (This statement is not applicable to laser-assisted surface reactions³⁴ when laser-light leads to the creation of hot electrons in the surface region which drive the chemistry as demonstrated, for instance, for the laser-induced recombinative desorption of molecular hydrogen from Ru(0001).³⁵⁻³⁸)

The HCl + Au(111) system has been studied also in the context of processes other than dissociative chemisorption. Both experimental^39,40 and theoretical⁴¹⁻⁴⁴ studies exist of the Eley–Rideal reaction of H with Cl on Au(111) leading to gaseous HCl. Rotationally inelastic scattering of HCl has been studied,^45,46 and experiments on vibrationally inelastic scattering⁴⁷⁻⁵¹ and on energy transfer to the surface⁴⁹ suggest evidence of electronically nonadiabatic scattering.^47−49,51 Experiments on the dissociative chemisorption of HCl on Au(111), which will be discussed further below, have only appeared recently.¹¹

The dissociative chemisorption of HCl on Au(111) was first studied theoretically by Zhang and co-workers with quantum dynamics,¹²⁻¹⁴ and this included predictions of the reactivity based on the PW91 functional,⁵² while later calculations¹⁵ were done with the RPBE functional.⁵³ However, these studies were based on the rigid surface approximation, which does not allow for energy transfers between the impinging molecule and the surface. The HCl + Au(111) system is one of a few systems^9,54,55 for which neural network potentials have been developed that can be used to assess the influence of phonon motion on scattering⁵⁴ and reaction.⁵⁵ Most importantly, the dissociation of HCl on Au(111) has been studied with ab initio molecular dynamics (AIMD)^16,17 and with MD with electronic friction (MDEF).¹⁷

The most striking result of the experiments on the dissociation reaction is that the reaction probability extracted from the measurements is quite low, that is, as low as only 2% at an incidence energy (E_i) of about 2.5 eV.¹¹ Both the predictive quantum dynamics calculations based on the PW91 functional^12,13 and AIMD calculations based on the PBE functional⁵⁶ and the more repulsive RPBE functional⁵³ dramatically overestimate the reaction probability extracted from the measurements, by more than 1 order of magnitude.¹⁷ The AIMD, MD, and MDEF simulations of ref (17) showed that (i) using a more repulsive functional than PW91 or PBE, such as the RPBE functional, (ii) including phonon motion, (iii) modeling the initial rotational state distribution in the molecular beam, and (iv) modeling ehp excitation within the independent atom approximation (IAA) of the local density friction approximation (LDFA)²⁷ all led to reductions of the reaction probability. In ref (17), these effects on the reaction probability were studied in isolation from one another, and additive or synergistic effects were not considered. The authors of ref (17) also suggested that the reaction probability extracted from the measurements could be underestimated by a factor 2–3 by a possibly erroneous calibration of the coverage of Au by Cl, as resulting from reaction (for the arguments, see ref (17)).

Of the other experiments on HCl + Au(111), the one most related to the sticking measurements arguably is the recent study of Geweke et al.⁵¹ on vibrationally elastic and inelastic scattering of (ν = 0, j = 1) and (ν = 1, j = 1) HCl. Interestingly, this study revealed not only a surface temperature-dependent component to the measured vibrational excitation probability, which was attributed to ehp excitation. In addition, a strong component was found which was independent of surface temperature and attributed to an electronically adiabatic mechanism. According to the authors,⁵¹ the adiabatic component most likely reflects trajectories sampling geometries near the late transition state, so that its energy dependence should yield information on the barrier height to reaction, as suggested also by studies on H₂ + Cu(111).⁵⁷⁻⁵⁹

The goal of the present paper is threefold. First, we aim to test how including the attractive van der Waals interaction between HCl and Au(111) might affect the reaction probability, by using a functional that incorporates a correlation functional due to Lundqvist and Langreth and co-workers.⁶⁰ It was argued that including this interaction might lead to a change in the transition-state geometry, in which H points obliquely down to the surface if a functional evaluated at the generalized gradient approximation (GGA) is used, such as PW91¹² or RPBE.¹⁷ Second, we aim to take into account possibly synergistic effects of using a functional incorporating van der Waals correlation, including phonon motion and ehp excitation, and modeling the initial rotational state distribution of the experimental molecular beam, by describing all of these effects at once in simulations using AIMD with electronic friction (AIMDEF).⁶¹⁻⁶⁴ Finally, we will also study vibrational excitation of HCl (ν = 1, j = 1) scattering from Au(111), under conditions where Geweke et al.⁵¹ found these probabilities to exceed 0.01, so that their study is accessible with AIMD. The main conclusion of our work is that our study employing a density functional including van der Waals interaction substantially overestimates the reaction probability and the vibrational excitation probability measured experimentally. This suggests that the barrier height to dissociative chemisorption should be substantially higher than obtained with GGA-DFT, whether or not the correlation functional is replaced with a van der Waals correlation functional, to achieve a quantitative description of experiment. We therefore suggest that an electronic structure method of which the accuracy is not adversely affected by charge transfer between the surface and the molecule, such as diffusion Monte-Carlo⁶⁵ or density functional embedded wave function theory,^66,67 should be used to investigate the reaction barrier height for HCl + Au(111). The latter has very recently been applied in the development of a six-dimensional PES for the O₂ + Al(111) system,⁶⁸ which has successfully captured the activated feature and steric effect that are observed experimentally but absent with GGA-DFT calculations.

This paper is organized as follows. Section 2 describes the method used. The computational set-up of the static DFT calculations (and to some extent also of the AIMD and AIMDEF calculations) is described in Section 2.1. Section 2.2 describes the details of the AIMD (Section 2.2.1) and AIMDEF (Section 2.2.2) dynamics calculations, also addressing the initial conditions used (Section 2.2.3) and the calculation of observables (Section 2.2.4). Section 3 provides and discusses the results. Section 3.1 deals with static aspects of the HCl–Au(111) interaction, such as transition states. Section 3.2 describes the dynamics results of the calculations on sticking and Section 3.3 on vibrationally inelastic scattering. In both these sections, a comparison is made with experimental results from the Wodtke group. Section 4 provides our conclusions and discusses ways in which progress can be made with theory for the HCl + Au(111) reaction in future.

2. Computational Methodology

We study dissociation of HCl on Au(111) with static DFT calculations, evaluating transition states and determining physisorption minima for several different functionals. We also perform dynamics calculations at normal incidence, using the AIMD and AIMDEF methods. These calculations are done at the level of the quasiclassical trajectory (QCT) method, that is, we always impart zero-point vibrational energy to HCl. For a motivation of the use of the QCT method for HCl + Au(111), the reader is referred to ref (17). For geometries of HCl relative to Au(111), we use the coordinate system depicted in Figure 1. The center-of-mass (COM) position is given either by the Cartesian coordinates (X, Y, Z) or the nonorthogonal coordinates (u, v, Z), where in each case Z measures the distance of the COM of HCl to the surface. The coordinate r measures the distance of H to Cl, θ is the polar angle that the Cl to H vector makes with the surface normal (see Figure 1), and ϕ the azimuthal angle made with the X axis.

Figure 1.

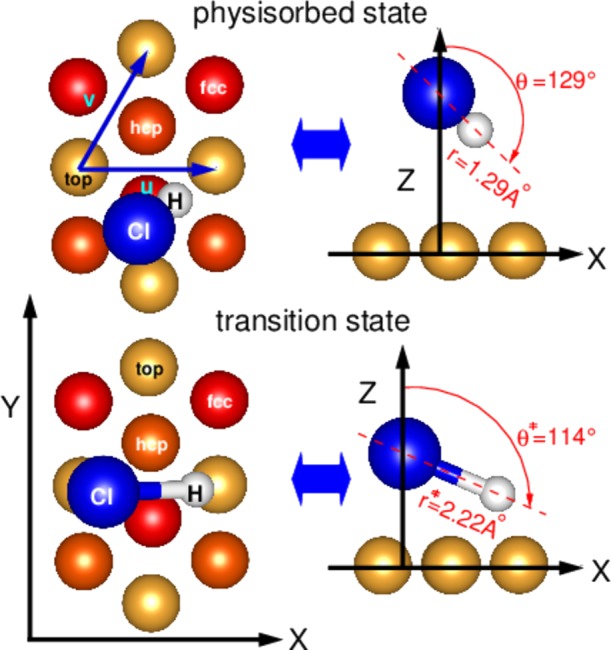
Coordinate system for HCl on Au(111) examplified for two specific geometries of HCl. In the upper panels, top (left) and side (right) views are drawn for HCl in the physisorption minimum. The lower panels show top (left) and side (right) views of the HCl geometry adopted at the transition state. The geometries were computed using the SRP32-vdW functional. First, second, and third layers of the Au slab are represented in gold, orange, and red, respectively. The Cl atom is shown in blue and the H atom in white. Indicated are the coordinates X, Y, Z of the COM, the interatomic distance r, the polar angle θ ∈ [0, π], and the skewed coordinates u and v. The azimuthal angle ϕ ∈ [0, 2π] (not shown) is the angle included between the X-axis and the lateral projection of the molecular axis.

2.1. Computational Setup

The static DFT calculations as well as the AIMD calculations were carried out using the VASP program version 5.3.5,⁶⁹⁻⁷² which uses periodic DFT. Previously,¹⁷ we carried out calculations using the GGA functionals PBE⁵⁶ and RPBE.⁵³ Here, we present the computational details for the static DFT calculations using several combinations of exchange functionals with the van der Waals correlation functional of Dion et al.,⁶⁰ and the new dynamics calculations presented here all rely on the SRP32-vdW functional⁷ successfully modeling dissociation of methane on group X metal surfaces.^7,8 Most computational details are identical to those of the earlier DFT and AIMD calculations,¹⁷ and here, we only provide the most important details of the computational setup.

The Au(111) surface is described using a four-layer slab with a (2 × 2) surface unit cell, using a vacuum gap of 16 Å between the periodically repeated slabs. We use a kinetic energy cut-off of 400 eV and an 11 × 11 × 1 Monkhorst–Pack k-point mesh centered on the Γ-point. The ion cores of the atoms are described by the projector-augmented wave method.^73,74 The optimization of bulk Au yields a lattice constant of 4.224 Å for the SRP32-vdW functional. Values obtained for the other functionals are presented in Table 1. Before computing the interaction of HCl with Au(111), we perform a relaxation calculation in which we optimize (through energy minimization) the interlayer distances in the slab. Before performing AIMD calculations, we expand the slab in the X and Y directions by taking into account the bulk expansion of Au with temperature. For the experimental surface temperature of 170 K,¹¹ this requires multiplying the bulk lattice constant with a factor ζ ≈1.0014, which was obtained in the same way and on the basis of the same experimental information⁷⁵ as used in ref (17).

Table 1. Listed are Bulk and Surface Lattice Constants, L_bulk and L, for the Au Bulk and Au(111) Surface Calculated at 0 K Using Different DFT Functionals.

	RPBE	RPBE-vdW	revPBE-vdW	SRP32-vdW
L/Lbulk [Å]	2.967/4.196	3.008/4.254	2.999/4.241	2.987/4.224
	PBE	optPBE-vdW	optB88-vdW	optB86b-vdW
L/Lbulk [Å]	2.938/4.155	2.955/4.179	2.941/4.159	2.914/4.121

2.2. Dynamical Simulations

2.2.1. AIMD Simulations

AIMD simulations are performed with the VASP code, using the SRP32-vdW functional. These calculations use the slab model and DFT setup discussed in Section 2.1. In AIMD, the forces are restricted to the electronically adiabatic forces resulting from the interactions between the H, Cl, and Au atoms (the Hellmann–Feynman forces). A time step of 0.5 fs is used, and the corresponding energy conservation is on average 10 meV. To determine sticking coefficients, we perform 500 trajectory calculations per energy point, ensuring a standard error ≤0.022 in the reaction probability. Absolute vibrational excitation probabilities are, however, obtained from 1000 trajectories. All trajectories start at 7 Å. A trajectory is considered reacted if r becomes larger than 2.58 Å or scattered if the molecule–surface distance becomes greater than 7 Å with the molecule moving away from the surface. Two types of simulations are performed: (i) simulations with the surface atoms remaining fixed at their equilibrium positions during the dynamics (the Born–Oppenheimer static surface or BOSS model) and (ii) simulations in which the surface atoms are allowed to move and are initially thermalized according to the experimental surface temperature (170 K).¹¹ All scattering trajectories were computed in the NVE (constant number of particles, volume, and energy) ensemble. An ensemble of 20 000 slab configurations was prepared to simulate a thermal surface, which taken together represent a macroscopic phase space configuration at T_s = 170 K. The procedure used is identical to that employed in ref (17), to which we refer for the details. As already noted in Section 2.1, the procedure used the static DFT bulk lattice constant multiplied with a factor ζ ≈ 1.0014. The thermalization was applied to the top three layers, while the bottom layer of the slab was kept fixed. From the kinetic and potential energies of the 20 slabs that were equilibrated to yield the 20 000 initial surface configurations, the resulting T_s was computed to be 177 ± 3 K (according to T_S = ⟨E_tot⟩/Nk_B, where ⟨E_tot⟩ is the averaged total energy of the system with N DOF and k_B is the Boltzmann constant).

2.2.2. AIMDEF Simulations

In the AIMDEF simulations, the forces acting on atom i of HCl (H or Cl) at position r_i = (x_i, y_i, z_i)^T are computed according to⁷⁶

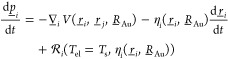1

Here, the first term on the rhs represents the adiabatic force resulting from the potential function V (the Hellmann–Feynman force), the second term is the velocity dependent friction force, and the third term is the randomly fluctuating force describing the nonadiabatic scattering of thermal electrons in the surface region from the adsorbate nuclei. Using eq 1, the effect of ehp’s is modeled with MDEF.⁷⁷ In eq 1, we use friction coefficients η_i obtained with the LDFA²⁷ in the IAA.²⁷ In eq 1, r_j is the position of the other atom of HCl, and R_Au denotes the positions of all the Au surface atoms. The friction coefficient of the H-atom depends on an impurity in jellium DFT-calculation and have been successfully employed to simulate the energy loss of several atomic particles interacting with metals and their surfaces.^23,78−80 The random fluctuating force is taken as Gaussian white noise with variance⁷⁶

2

to enable a description in which the molecule eventually becomes equilibrated to the surface according to the fluctuation–dissipation theorem.⁸¹

We only perform AIMDEF calculations in which the surface atoms (T_s) and the metal electrons (T_el) are thermalized according to the experimental surface temperature (T_s = T_el = 170 K)¹¹ and eq 2. The AIMDEF simulations sample the same initial conditions for HCl and the surface atoms as the thermal AIMD simulations. The AIMDEF simulations were performed with a user-modified version of the VASP code that allows to simultaneously treat ehp excitations and surface lattice motion in the dynamics simulation by computing the LDFA friction coefficients on-the-fly.^63,64 The electronic density needed to compute the friction coefficients was calculated from the self-consistent density of the entire HCl + Au(111) system with displaced Au atoms. Consistently with the IAA LDFA, the electronic densities due to the H and Cl atoms were subtracted from these densities using a Hirshfeld partitioning scheme.^63,64,82,83 The friction coefficients for the H and Cl atoms were obtained in the usual manner^84,85 by calculating the phase shifts of Kohn–Sham orbitals at the Fermi momentum for the proton embedded in a free electron gas for different values of the embedding electronic densities ρ_emb. The friction coefficients of the H-atoms depend on ρ_emb as described by eq 13 of ref (86). Following earlier work,⁶² we parameterized η according to

3

where r_s = (3/4πρ_emp)^1/3 is the Wigner–Seitz radius and B = 0 ℏ/a₀ for the H atom and B = 0.118158 ℏ/a₀ for the Cl atom. The remaining coefficients in eq 3 are listed in Table 2 for both species. The fitting functions reproduce the friction coefficients in the range r_s = 1–10a₀ for H and in the range r_s = 1–9.25a₀ for Cl. Friction forces only act on the H and the Cl atoms, and the computational details of the AIMDEF simulations are otherwise equal to those of the AIMD simulations.

Table 2. Parameters Entering the Functional Form Eq 3 To Represent Electronic Friction Coefficients in AIMDEF Simulations as Functions of the Wigner–Seitz Radius for H and Cl Atoms.

i	ai [ℏa0–(bi+2)]	bi	ci [a0–1]
H Atom
1	8.25494 × 10–8	1.00823 × 101	1.18939
2	6.51365 × 10–1	3.75934 × 10–1	0.60530
3	6.22390 × 10–4	–1.40174 × 101	–2.47727
Cl Atom
1	–4.99614 × 105	9.0063 × 10–1	5.40621
2	2.03582 × 102	–3.47537 × 100	1.01808
3	5.47567 × 105	1.02608 × 100	5.52931

2.2.3. Initial Conditions

To simulate the experiments on sticking of HCl to Au(111) at normal incidence,¹¹ the velocity of the molecule is sampled at random from the flux-weighted velocity distributions describing the experiments for the three different average incidence energies for which we perform calculations here. The stream velocities and width parameters describing these distributions have been provided in ref (11). The rotational and vibrational state is sampled randomly from the rovibrational state distribution of the incident beam as also specified by the experimentalists, taking the vibrational temperature T_vib equal to the nozzle temperature T_n, and the rotational temperature as¹⁷

4

In all other respects, the initial conditions were generated using a Monte-Carlo procedure and a procedure to “translate” the initial rovibrational state in initial coordinates and velocities of H and Cl as fully described in Section 2.3.3 of ref (17), to which we refer for the details.

For vibrational excitation calculations on nonreactive HCl molecules initially in the (ν = 1, j = 1) state, we compute 1000 AIMDEF trajectories for each energy point ⟨E_i⟩. We adopt the same Monte-Carlo procedure described above and in ref (17) to sample the ν = 1, j = 1 state for all possible m_j quantum numbers (m_j = {−1, 0, 1}). The flux-weighted velocity distributions of the corresponding molecular beams are given by

5

where A is a normalization constant. The experimental parameters α and ν₀ for the two beams considered here are given in Table 3. The AIMDEF simulations were performed at T_s = T_el = 900 and 575 K. Thermalized Au slabs were obtained by the NVE/NVT procedure described in ref (17). The expansion factor of the bulk lattice constant are ζ ≈ 1.0073 (575 K) and ζ ≈ 1.0126 (900 K), respectively.

Table 3. Parameters Describing the Velocity Distribution of the Two Different Molecular Beams of HCl (ν = 1, j = 1) Incident on Au(111) Considered in the Vibrational Excitation Calculations of This Work^a.

⟨Ei⟩ [eV]	v0 [m/s]	α [m/s]	Ts [K]
0.94	2210	188	575/900
1.06	2360	163	900

^aAlso specified are the considered surface temperatures T_s.

2.2.4. Calculations of Observables

Macroscopic observables ⟨O⟩ are computed as the average of the number of “microscopic measurements” N_t (number of trajectories) according to

6

In eq 6, ⟨O⟩ can be the (dissociative) sticking probability S₀, in which case o = 1 for a dissociatively adsorbed trajectory and o = 0 for a scattered trajectory. Alternatively, if the absolute vibrational excitation probability is computed for the transition from (ν = 1, j = 1) to ν = 2 (P(ν = 1, j = 1 → ν = 2)), o = 1 for scattered trajectories characterizable by the final vibrational state ν = 2, and 0 otherwise. We also compute scaled vibrational transition probabilities according to

7

with ν′ = 1 or 2, to enable comparison to the measured probabilities in the experiments on vibrationally inelastic scattering by Geweke et al.⁵¹ While the experimentalists referred to these quantities (the T_ν=1→ν′ defined in eq 6) as “absolute vibrational excitation probabilities”, from now on we refer to these quantities as vibrational transition probabilities because only the P(ν = 1, j = 1 → ν′ = 2) can truly be called “absolute” probabilities for vibrationally inelastic scattering. The latter ones are here computed as

8

where N_t is the total amount of AIMDEF trajectories computed for a certain reaction condition (here, typically N_t = 1000), and N_sc(ν′) is the amount of scattered trajectories with the final vibrational quantum number ν′.

To compute probabilities for vibrationally elastic or inelastic scattering, binning of the final rotational and vibrational state has to be performed. The final rotational quantum number j is evaluated from the final classical rotational angular momentum j_c according to

9

Next, j_q is binned to the nearest integer to obtain j. The vibrational state ν′ is then evaluated by computing the classical rovibrational energy of the molecule and comparing it to the quantum mechanical vibrational energies within the j-ladder. Next, ν′ is assigned by requiring that this classical energy is nearest to the energy of the (ν′, j) state in that ladder.

3. Results and Discussion

3.1. Static Properties of the HCl + Au(111) PES

Table 4 summarizes information regarding the interaction of HCl with Au(111), providing the energies and geometries computed for the physisorption state and the transition state toward dissociative adsorption for the PBE⁵⁶ and RPBE⁵³ GGA functionals, and several functionals combining GGA exchange with the nonlocal van der Waals correlation functional of Dion et al.⁶⁰ The latter include the SRP32-vdW functional successfully used for methane interacting with group X transition metals^7,8 and used in the present AIMD and AIMDEF simulations on HCl + Au(111). The PBE and RPBE functionals yield a barrier height of 0.76 and 1.05 eV. The SRP32-vdW functional yields a barrier height of 0.64 eV, that is, lower than the PBE barrier height of 0.75 eV.¹⁷ This suggests that the reaction probabilities computed with SRP32-vdW functional should be larger than obtained previously with PBE and should therefore be in worse agreement with the experimentally measured reactivity. However, note that the SRP32-vdW functional returns a barrier that is later (occurring at larger r-value) than the one obtained with PBE, and that the difference is considerable (0.3 Å). Whether the later barrier has a strong effect on the computed reactivity of the system remains to be shown by the dynamics calculations below. The original vdW functional of Dion et al.,⁶⁰ which used the revPBE exchange functional that is usually considered too repulsive,⁹¹ returns a barrier height of 0.80 eV, higher than the SRP32-vdW and PBE functionals, but lower than the RPBE value, and the same is true for RPBE-vdW. The other functionals containing vdW correlation (i.e., optPBE-vdW,⁹² optB88-vdW,⁹² and optB86b-vdW⁹³) all return barrier heights lower than or slightly higher than the SRP32-vdW value and lower than the PBE value. For all functionals tested (also for the GGA functionals), the dissociative chemisorption of HCl on Au(111) is endothermic (see also Figure 4 of ref (17)).

Table 4. DIMER⁸⁷⁻⁹⁰ Calculations on First-Order Saddle Points and Geometry Optimizations on the Physisorption Well Depth for HCl on Au(111) Using Different DFT Functionals^a.

DFT method	quantity	E [meV]	u [L]	v [L]	Z [Å]	r [Å]	θ [deg]	ϕ [deg]
RPBE17	Ephys	–6	0.651	0.541	4.40	1.29	123	29
RPBE17	E‡	1050	0.328	0.836	2.44	1.95	135	330
RPBE-vdW(*)	Ephys	–163	0.664	0.518	3.73	1.29	125	34
RPBE-vdW	E‡	818	0.199	0.984	2.45	2.20	115	0
revPBE-vdW	Ephys	–148	0.663	0.526	3.69	1.29	128	33
revPBE-vdW	E‡	800	0.196	0.982	2.45	2.21	115	0
SRP32-vdW(*)	Ephys	–217	0.689	0.487	3.45	1.29	129	37
SRP32-vdW	E‡	644	0.197	0.974	2.43	2.22	114	0
PBE17	Ephys	–30	0.498	0.821	3.87	1.29	129	330
PBE17	E‡	756	0.323	0.843	2.40	1.93	133	329
optPBE-vdW(*)	Ephys	–201	0.972	0.333	3.39	1.30	127	64
optPBE-vdW	E‡	661	0.342	0.829	2.43	1.92	133	330
optB88-vdW	Ephys	–219	0.024	0.276	3.24	1.30	127	60
optB88-vdW	E‡	550	0.340	0.830	2.38	1.89	132	330
optB86b-vdW(*)	Ephys	–221	0.02	0.260	3.20	1.30	126	60
optB86b-vdW	E‡	471	0.325	0.838	2.39	1.92	132	330

^aReaction barrier energies E^‡ and well depth E_phys are given relative to the classical minimum energy for HCl in the gas phase. Also listed are corresponding geometries. The lateral skewed coordinates u, v are given in units of the surface lattice constant L, reported in Table 1. The PBE and RPBE results are taken from ref (17). Normal mode analyses (NMA) show that physisorption wells marked by an asterisk are not local minima (NMA yield a small imaginary frequency along a single mode).

Concerning the physisorption well, there is a large difference between the GGA functionals (PBE and RPBE) and the functionals combining GGA exchange with vdW correlation. While the former put the well depth between 6 and 30 meV, the latter put the well depth between 148 and 221 meV, with the SRP32-vdW functional yielding a value of 217 meV (see Table 4). The latter values are in excellent agreement with the experimental estimate of 220 meV.⁴⁵ Of course, the PBE and RPBE functionals should not be expected to return a correct value of the van der Waals well depth, as their formulation precludes the evaluation of van der Waals dispersion energies. We also note that the SRP32-vdW functional returns a very similar barrier and physisorption geometries for the HCl molecule, see Figure 1. An antisteering effect induced by the presence of vdW interactions that would diminish sticking, as previously suggested in ref (17), seems therefore not likely.

3.2. Dynamics of the Dissociative Chemisorption

Figure 2 compares sticking probabilities computed with MD and the PBE functional within the static surface approximation¹⁷ with AIMD results obtained using the SRP32-vdW functional with the static surface approximation (for the highest ⟨E_i⟩) and modeling surface vibrational motion only. In both cases, the initial rovibrational population in the molecular beam and the velocity distribution of the beam were taken into account. Before drawing conclusions on the effect of using SRP32-vdW rather than PBE, we note that the PBE-MD results of ref (17) were in excellent agreement with the PBE-AIMD results of ref (17), showing that the neural network potential fit made of PBE data in that work was accurate. We also note that the static surface AIMD results on sticking obtained for the SRP32-vdW functional are quite similar to the SRP32-vdW AIMD results where the surface atoms were allowed to move and initially move according to the experimental surface temperature (170 K¹¹). A similar conclusion has previously been drawn regarding PBE-MD and PBE-AIMD results modeling surface atom motion for the range of incidence energies up to 2 eV, as shown in Figure 8 of ref (17). This justifies the following conclusion: the use of the SRP32-vdW functional leads to significantly lower sticking probabilities than the use of the PBE functional, in spite of the lower minimum energy barrier (0.64 eV for SRP32-vdW vs 0.76 eV for PBE, see Table 4). Even if this result might be surprising at first sight, it highlights that not only the energy barriers but the configurational space leading to dissociation rules the reaction probability, as also exemplified in other systems.^94,95 Thus, one might attribute the lower reactivity of the SRP32-vdW functional to the barrier being much later (at r = 2.22 Å vs 1.93 Å for PBE, see Table 4). It is also possible that other yet unknown factors regarding the topology of the SRP32-vdW HCl–Au(111) interaction act to reduce the reaction probability through dynamical effects as found using other functionals in refs.^12,13,96,97 We hope to address this aspect in future calculations.

Figure 2.

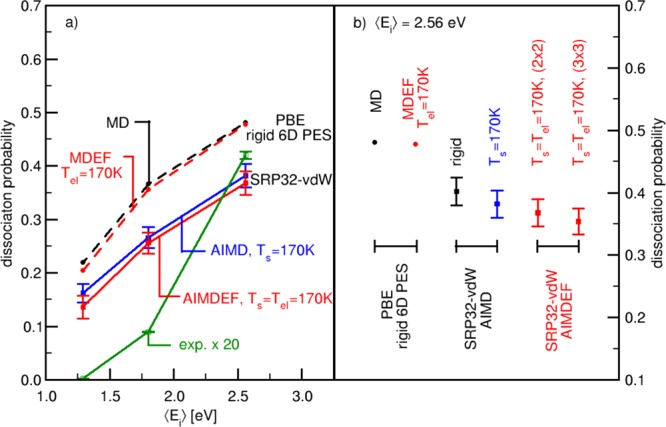
Dissociation probabilities S₀ for the HCl + Au(111) system. (a) S₀-values as functions of averaged translational incidence energies ⟨E_i⟩ computed using MD-BOSS simulations (black circles) and MDEF (red circles) simulations at T_el = 170 K performed on a 6D PBE-PES,¹⁷ AIMD(EF) simulations at T = 170 K (blue and red squares) using the SRP32-vdW functional. Experimental values¹¹ (green open squares) are multiplied by a factor 20. (b) Plotted are S₀-values computed at ⟨E_i⟩ = 2.56 eV using different methods and reaction conditions: MD and MDEF simulations on 6D PBE-PES as in panel (a) (black and red circle), AIMD simulations using the SRP32-vdW functional for a rigid Au(111) surface (black square) and for T_s = 170 K (blue square), AIMDEF simulations using the SRP32-vdW functional performed for T_s = T_el = 170 K and a (2 × 2) and a (3 × 3) supercell (red squares). Vertical lines represent error bars.

Figure 2a also compares AIMD and AIMDEF reaction probabilities computed with the SRP32-vdW functional with experimental sticking probabilities, where the latter have been multiplied by a factor 20. Three important points can be made regarding this figure and Table 5 where we collect the sticking probabilities computed in this work. The first point is that adding ehp excitation within the IAA to the LDFA only affects the computed sticking probability in a minor way, as previously found comparing MD and MDEF results for HCl + Au(111).¹⁷ Similar observations have been made in another independent study using a neural network potential energy surface which also includes surface atom DOFs.⁵⁵

Table 5. Computed Reaction Probabilities for HCl Incident on Au(111) As Obtained from MD(EF) and AIMD(EF) Trajectory Calculations at Different Simulated Reaction Conditions^a.

functional	method	Ts/Tel [K]	⟨Ei⟩ = 1.29 eV	⟨Ei⟩ = 1.80 eV	⟨Ei⟩ = 2.56 eV	Nt
SRP32-vdW	AIMD	170/0	0.162 ± 0.017	0.266 ± 0.020	0.382 ± 0.022	500
SRP32-vdW	AIMDEF	170/170	0.136 ± 0.021	0.256 ± 0.020	0.368 ± 0.022	500
SRP32-vdW	AIMDEF, (3 × 3)	170/170			0.354 ± 0.021	500
SRP32-vdW	AIMD, rigid	0/0			0.402 ± 0.022	500
revPBE-vdW	AIMD, rigid	0/0			0.370 ± 0.050	100
revPBE-vdW	AIMD	0/0			0.360 ± 0.050	100
PBE	MD, rigid	0/0	0.219	0.366	0.481	105
PBE	MDEF, rigid	0/170	0.204	0.356	0.478	105
Exp.11		170/170	(0.12 ± 0.07) × 10–3	(0.45 ± 0.04) × 10–2	0.021 ± 0.007

^aListed are sticking coefficients and corresponding standard deviations for different surface and electronic temperatures (T_s and T_el), and average incidence energies ⟨E_i⟩. Specified are also the amount of computed trajectories N_t.

The second point is concerned with the effect of using a larger surface unit cell (3 × 3 instead of 2 × 2). As seen from Table 5 and Figure 2b, this has little effect on the sticking probability, changing the AIMDEF result for this observable from 0.37 ± 0.02 to 0.35 ± 0.02 for the highest incidence energy investigated (2.56 eV). Using the (3 × 3) supercell, we also tested whether HCl recombines at larger interatomic distances and whether this affects the computation of the sticking probability. We therefore changed the r_diss-value from 2.58 to 4.1 Å at which we count dissociation to have occurred and continued the propagation of 177 trajectories on the (3 × 3) supercell already counted as adsorbed (S₀ = 0.354). We found only one trajectory that yielded a recombination process occurring at r > 2.58 Å followed by the backscattering of HCl. The resulting probability for recombination is only 0.002, and the effect on the computed sticking coefficient is small.

The third point concerns the agreement of the AIMDEF results with experiment. As Figure 2a shows, changing from the PBE functional to the SRP32-vdW functional and taking into account energy dissipation to surface atom motion and ehp excitation substantially improves the agreement between theory and experiment. Nevertheless, the present SRP32-vdW AIMDEF results still overestimate the published experimental sticking probability by a factor 18 at the highest ⟨E_i⟩ considered. As explained in the Introduction and more extensively in ref (17), this is reduced to a factor 6 if the experiment underestimated the sticking probability by a factor 3, as suggested. We suggest that this remaining discrepancy could be due to two factors playing a role in the theory. First, it is quite possible that with the present density functional we are underestimating the barrier height, or more generally, how repulsive the HCl–Au(111) interaction is. At the HCl–Au(111) TS, GGA-DFT leads to an electron transfer from the surface to the molecule of 0.3 electrons,¹⁷ and at this level of DFT, this could lead to an underestimate of the barrier height. We suggest using an electronic structure method of which the accuracy is not adversely affected by charge transfer between the surface and the molecule, such as diffusion Monte-Carlo⁶⁵ or density functional embedded wave function theory,^66,67 to investigate the reaction barrier height for HCl + Au(111). Second, it is possible that with the present IAA-LDFA theory, we are not yet quantitatively describing nonadiabatic effects on this reaction. This could be investigated using electronic friction theory with orbital dependent friction (ODF) coefficients^26,32,33,98 that goes beyond IAA, or additionally, using the independent electron surface hopping (IESH) method²¹ that can account for possible charge-transfer processes. However, it is not yet certain that these theories would give improved results for HCl + Au(111). For example, recent results for H₂ + Ag(111)³² and H₂ + Cu(111)³³ suggest that there may well be little effect of whether ODF or the LDFA is used when it comes to the computation of sticking coefficients. Nevertheless, it might be a worthwhile direction for future research on HCl + Au(111) to explore the use of ODF, but taking special care in using physically motivated broadening parameters that otherwise may lead to inaccurate results, as shown in ref (99). Regarding possible charge-transfer effects not included within electronic friction theories, HCl is intermediate between NO and H₂ in terms of where the ground-state neutral molecular potential and the ground state molecular anion potential cross, as already extensively discussed in ref (17). This might make it worthwhile to test the IESH method on HCl + Au(111), but we note that neither the IESH method nor the electronic friction method was successful at describing vibrational de-excitation of (ν = 3)NO, see ref (100). Finally, it is still possible that experimental data contain a larger uncertainty as discussed extensively in ref (17) and given the fact that all theoretical results significantly overestimate the initial sticking probability.

3.3. Vibrationally Elastic and Inelastic Scattering of (v′ = 1, j′ = 1) HCl

Scaled transition probabilities T_{ν=1,j=1→ν′} computed with AIMDEF for normal incidence are compared with experimental values⁵¹ in Table 6 and in Figure 3, and probabilities for vibrational excitation P_{ν=1,j=1→ν′=2} computed with AIMDEF are also shown in Figure 3, for the three initial conditions indicated. As can be seen, the computed T_{ν=1,j=1→ν′} exceed the experimental values by factors 3–8. The computed absolute probabilities P_{ν=1,j=1→ν′=2} are approximately 0.02–0.03. The computed P_{ν=1,j=1→ν′=1} were in the range 0.27–0.33, and the computed P_{ν=1,j=1→ν′=0} were in the range 0.24–0.26, in rough agreement with the experimental estimate⁵¹ that the latter should be less than 0.3. The values reported here on scaled and absolute transition probabilities may be affected by the binning procedure which can only approximately recover the quantum behavior from classical mechanics simulations. In ref (55), it was suggested that a Gaussian binning may be more accurate. This method needs, however, a large amount of trajectory calculations that can here not be provided by the computationally expensive AIMDEF simulations.

Table 6. AIMDEF Results on Vibrational Excitation for HCl (ν = 1, j = 1) Incident on Au(111) at Three Different Reaction Conditions (Varying Surface Temperature T_s and Average Translational Incidence Energy ⟨E_i⟩)^a.

⟨Ei⟩ [eV]	Ts [K]	Tν=1,j=1→ν′=1AIMDEF	Tν=1,j=1→ν′=2AIMDEF	Tν=1,j=1→ν′=2exp	S0	Elosssurf [meV]
0.94	575	0.925 ± 0.010	0.074 ± 0.010	0.009	0.349 ± 0.015	478 (50.9%)
0.94	900	0.935 ± 0.010	0.065 ± 0.010	0.018	0.390 ± 0.016	459 (48.8%)
1.06	900	0.910 ± 0.011	0.090 ± 0.011	0.028	0.427 ± 0.016	500 (47.2%)

^aFor each reaction condition, N_t = 1000 AIMDEF trajectories calculations are performed. Listed are sticking probabilities S₀, loss of classical total energy E_loss^surf (percentages are given with respect to ⟨E_i⟩), and scaled vibrational transition probabilities T_{ν=1,j=1→ν′} for ν′ = 1 and 2.

Figure 3.

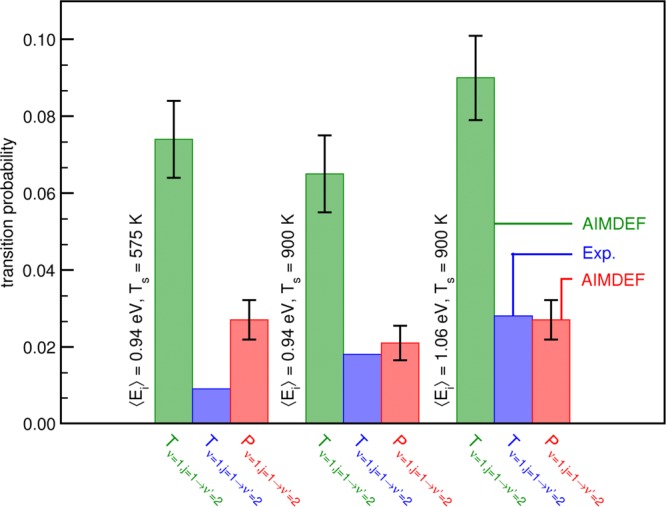
Absolute vibrational excitation and vibrational transition probabilities, P_{ν=1,j=1→ν′=2} (red) and T_{ν=1,j=1→ν′=2} (green and blue), respectively, for HCl scattering from Au(111). Shown are AIMDEF results (green and red) and results taken from experiments⁵¹ (blue). The AIMDEF results are based on 1000 trajectory calculations for each reaction conditions (different T_s and ⟨E_i⟩). Black vertical lines indicate error bars.

The computed T_{ν=1,j=1→ν′=2} exceed the calculated P_{ν=1,j=1→ν′=2} by a factor of about 3. The reason is that the sum of the probabilities for scattering to ν′ = 1 and ν′ = 2, by which P_{ν=1,j=1→ν′=2} is divided, takes on fairly small values, which lie in the range 0.30–0.36. In turn, these values are small not only because the computed P_{ν=1,j=1→ν′=0} are large, as noted above, but also because the computed dissociation probabilities S₀ are large for ν = 1 (in the range 0.35–0.43, see Table 6). We interpret the discrepancy in the computed and measured values of T_{ν=1,j=1→ν′} in the same way as the discrepancy for the sticking probabilities. First, the barrier to dissociation computed with SRP32-vdW is probably too low. As also discussed by Geweke et al., experiments on H₂ + Cu(111)^57,58 (but also calculations, see refs (59) and (101)) then suggest that the electronically adiabatic contribution to the vibrational excitation probability (P_{ν=1,j=1→ν′=2}) should be too high. Additionally, the computed probability for vibrational de-excitation (P_{ν=1,j=1→ν′=0}) and the reaction probability of (ν = 1)HCl should also be too high. In turn, this will then lead to a too small sum of P_{ν=1,j=1→ν′=1} and P_{ν=1,j=1→ν′=2}, by which the P_{ν=1,j=1→ν′=2} need to be divided to compute T_{ν=1,j=1→ν′=2}. Too low barriers can therefore lead to much too high T_{ν=1,j=1→ν′=2} for two reasons: on the one hand, the computed P_{ν=1,j=1→ν′=2} will be overestimated, and on the other hand, the probability for vibrationally elastic scattering P_{ν=1,j=1→ν′=1} will be underestimated because too low barriers also lead to too much vibrational de-excitation and too much dissociation. For a more direct and accurate comparison with experiment, it would be nice if P_{ν=1,j=1→ν′=2} could be measured directly. For instance, this could show whether the present discrepancy between the computed and measured transition probabilities is simply due to the computed probabilities for reaction and vibrational de-excitation being too high. This alternative explanation might apply to two of the three conditions for which results are shown in Figure 3, for which the computed vibrational excitation probabilities are close to the measured transition probabilities.

Second, it is possible that with the IAA-LDFA method we are not yet quantitatively describing the effect of nonadiabatic interactions on the vibrational transition probabilities. If nonadiabatic effects were larger than those predicted by IAA-LDFA, the vibrational excitation (ν = 1 → 2) probabilities and the reaction probabilities would be smaller, while it is not immediately clear how the probabilities for vibrational de-excitation should be affected. This might well result in improved transition probabilities T_{ν=1,j=1→ν′=2}, in the same way as discussed above for a higher barrier. Once again, this may be well worth investigating with ODF and with the IESH method. In this respect we also note that it should be important to use an accurate adiabatic interaction potential in combination with a theory for nonadiabatic interactions.¹⁰⁰

Considering trends, we note that for T_s = 900 K the computed value of T_{ν=1,j=1→ν′=2} increases with incidence energy, as found experimentally. On the other hand, for ⟨E_i⟩ = 0.94 eV, the computed value of T_{ν=1,j=1→ν′=2} decreases with surface temperature, whereas the measured value increases. One should not attach too much weight to these observations: with the small computed probabilities for vibrational excitation, the statistical errors in this probabilities are large as also indicated by the error bars in Figure 3 (throughout this manuscript, the error bars shown indicate 1σ error intervals), and as noted, the comparison is adversely affected by the sums of the computed probabilities for vibrational de-excitation and dissociative chemisorption being too high, and it is not entirely clear how this should affect the comparison between the scaled vibrational transition probabilities.

We can also compare the computed final energy in translational motion to experiments of Geweke et al.,⁵¹ albeit that we have to use computed final rotational state distributions to obtain “experimental values” that are final state-resolved with respect to ν. The equation we use to obtain the vibrational state-resolved final translational energy E_f is

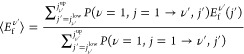10

In eq 10, the E_f^ν′(j′) were taken from Figure SI-3b of ref (51) to obtain experimental final average translational energies, whereas they were taken from AIMDEF calculations to obtain final computed average translational energies. In both cases, we used the computed P(ν = 1, j = 1 → ν′, j′), as no experimental values were available. The experimental results were obtained for an incidence energy of 1.06 eV and T_s = 673 K; assuming that surface temperature is less important than incidence energy in determining ⟨E_f⟩, the experimental translational energy loss that can be computed from ⟨E_f^ν′⟩, i.e., E_loss is best compared with the AIMDEF value obtained for ⟨E_i⟩ = 1.06 eV and T_s = 900 K. To take advantage of the published experimental values of the final translational energies (in Figure SI-3b of ref (51)), we use j_ν′=1^low = j_ν′=2 = 2 and j_ν′=1^up = 9 and j_ν′=2 = 7 to evaluate eq 10. We call this the ν′, j′-truncated case. In this way, we compute final vibrational state-resolved translational energy losses with AIMDEF that are in very good agreement with experiment (see Table 7). A caveat with the comparison is that the measured values correspond to a specific final scattering angle of 15°, whereas the computed probabilities are for scattering over all final angles. (The calculations are for normal incidence, and the experiment was performed for an incidence angle between 0° and 5° off normal; note that the vibrational transition probabilities were obtained by averaging over all final scattering angles as in the calculations.⁵¹)

Table 7. Total and Vibrational State Resolved Translational Energy Losses and Corresponding Rotational Energies Given in meV of HCl Scattered from Au(111) Computed From AIMDEF Simulations^a.

	ν′, j′-truncated		v′, j′-untruncated
	⟨Ei⟩ = 1.06 eV (Ts = 900 K)	⟨Ei⟩ = 1.06 eV, exp.51 (Ts = 673 K)	⟨Ei⟩ = 1.06 eV (Ts = 900 K)	⟨Ei⟩ = 0.94 eV (Ts = 575 K)	⟨Ei⟩ = 0.94 eV (Ts = 900 K)
Eloss(ν=1→ν′=1)	566.2 (53.4%)	590.2 (55.6%)	582.0 (54.9%)	574.6 (58.3%)	506.1 (53.8%)
Eloss(ν=1→ν′=2)	749.6 (70.7%)	769.9 (72.6%)	726.2 (68.5%)	701.6 (74.6%)	706.9 (75.2%)
Eloss	576.5 (54.3%)	598.9 (56.5%)	535.0 (50.5%)	505.4 (53.8%)	469.7 (50.0%)
⟨Erot⟩(ν′ = 1)	57.1		118.2	120.7	110.0
⟨Erot⟩(ν′ = 2)	32.9		87.7	95.0	90.1
⟨Erot⟩	55.7		175.2	167.3	159.4

^aThe experimental values are listed in the second column and are obtained using a mixed experimental theory approach, see text for details. Averaged rotational energies ⟨E_rot⟩ of scattered molecules are obtained using box-quantization. E_loss and ⟨E_rot⟩ are computed using either ν′, j′ untruncated (average over all scattered molecules) or truncated v′, j′-values (according to measured ν′, j′ values⁵¹), see text for details.

Also listed in Table 7 are theoretical translational energy losses for three different reaction conditions, which were computed by evaluating eq 10 over all scattered trajectories independent of their final ro-vibrational state. We call this the ν′, j′-untruncated case. The percentage translational energy losses (relative to the incidence translational energy) are in the range of 50–54%. This is in good agreement with the value of 55% measured by Cooper et al. for scattering of (ν = 0) HCl for incidence energies in the range 0.28–1.27 eV,⁴⁹ especially if one takes into account that this percentage of energy loss seems independent of the initial vibrational state of HCl (a similar percentage of energy loss was found for scattering of ν = 2,⁴⁸ as noted by Cooper et al.⁴⁹). The translational energy losses E_loss listed in Table 7 are somewhat larger than the total energy losses E_loss^surf provided in Table 6. This suggests that translational energy is preferentially transferred from the molecule to the surface during the scattering process, and—according to the law of energy conservation—that an additional amount of translational energy must also be converted to vibrational and rotational motion of scattered HCl. That energy redistribution takes place can be recognized by the average rotational energies of scattered molecules provided in Table 7, which are considerably larger than the rotational energy of ∼2.5 meV for incident (ν = 1, j = 1) HCl. The data show that considerable rotational excitation occurs for vibrationally elastic and inelastic scattering and that the effect is larger for molecules that scatter vibrationally elastically. Though, translational energy losses for inelastic scattering, E_loss, are larger than for the vibrationally elastic process, E_loss^{ν=1→ν′=1}, by about 200–250 meV. This energy difference makes up a large portion of the excitation energy of 330 meV to excite HCl from ν = 1 to ν = 2. Interestingly, a previous theoretical study⁵⁵ reported on total energy losses to the surface being larger for molecules scattering vibrationally elastically (ν = 0 → ν′ = 0) than for molecules scattering vibrationally inelastically (ν = 0 → ν′ = 1). Our results support the view that vibrational excitation is predominantly a T → V process as previously also suggested in ref (55).

The total energy losses to the surface (see Table 6) amount to about 460–500 meV and correspond to only 47–51% of the incidence translational energy. This is in good agreement with the theoretical value of 50%¹⁷ obtained with the simplistic Baule limit.¹⁰² Previous work using either AIMD trajectory calculations¹⁷ or dynamics simulations performed on a precalculated PES with surface atom motion⁵⁵ report on total energy losses of about 30% of the incidence translational energy for (ν = 0, j = 0) HCl scattering. For DCl scattering on Au(111), even larger percentage energy losses of up to 43% of ⟨E_i⟩ were computed using AIMD.¹⁶

4. Conclusion

We have performed AIMD and AIMDEF calculations employing a density functional that includes the attractive van der Waals interaction, to compute sticking coefficients and probabilities for vibrationally inelastic scattering of HCl from Au(111). The SRP32-vdW functional also used successfully to model dissociative chemisorption of methane on Ni and Pt surfaces is employed. The AIMDEF calculations used the IAA and the LDFA to obtain friction coefficients for HCl in the modeling of ehp excitation. Our calculations model the simultaneous and possibly synergistic effects of surface temperature, surface atom motion, ehp excitation, the molecular beam conditions of the experiments, and the van der Waals interaction on the reactivity. Comparison has been made to experimental data for dissociative chemisorption and vibrationally inelastic scattering obtained by Wodtke and co-workers.^11,51

The value we obtain for the physisorption well depth with the SRP32-vdW functional (≈220 meV) is in excellent agreement with experiment. Even though the minimum barrier height computed with the SRP32-vdW functional is lower than that obtained with the PBE functional (by about 100 meV), AIMD calculations with SRP32-vdW yield lower sticking probabilities than obtained with PBE. We attribute this to the barrier being much later with SRP32-vdW (by about 0.3 Å). The effect of changing the functional from PBE to SRP32-vdW is larger than the combined effect of modeling surface atom motion and ehp excitation with the LDFA. Using a van der Waals correlation functional may thus be important for obtaining improved agreement with experiment through shifting the barrier to larger values of r, thereby decreasing the reactivity. However, reaction probabilities computed with AIMDEF and the SRP32-vdW functional still overestimate the measured reaction probabilities,¹¹ by a factor 18 for the highest incidence energy at which measurements were performed (2.56 eV). Even granting that the experiment could have underestimated the sticking probability by about a factor three, this still translates into an overestimation of the reactivity by the current theory by about a factor 6. (The experiments may suffer from calibration problems for coverage of Au by Cl, as previously discussed.¹⁷)

Obviously, the overestimation of the reactivity obtained with the theory suggests that the barriers to reaction obtained with the SRP32-vdW functional might be too low. As discussed, this could be due to the SRP32-vdW functional containing GGA exchange, and there being substantial electron transfer from HCl to Au(111) at the transition state. Because GGAs favor electron delocalization,^103−105 this could lead to a too low barrier. We therefore suggest the application of electronic structure methods to the system which do not rely on ad hoc assumptions regarding the electron correlation, and of which the accuracy is not systematically affected if charge transfer occurs in a system. Two methods are of particular interest because they have been demonstrated to accurately describe gas–surface systems. For example, the most accurate semiempirical value of the reaction barrier for H₂ on Cu(111) has been reproduced to within an error of only 1.5 kcal/mol using quantum diffusion Monte-Carlo.⁶⁵ Also, the embedded correlation wave function method has been shown to be far more accurate in describing the O₂ + Al(111) system, which is affected by charge transfer, than standard DFT.⁶⁶⁻⁶⁸ The discussion about the importance of the electronic structure method and electronically nonadiabatic effects for the description of the reaction of HCl on Au(111) is therefore expected to benefit from calculations using these more sophisticated techniques. An additional improvement could be to replace the MDEF method with IAA-LDFA friction with different methods for dealing with nonadiabatic effects. Alternative methods to investigate are MDEF with ODF^26,32,33 or the IESH method which also can take charge-transfer effects into account.²¹

Scaled transition probabilities for vibrational excitation from ν = 1, j = 1 to ν = 2 are also overestimated by the AIMDEF theory relative to experimental values,⁵¹ by factors 3–8 depending on the initial conditions modeled. We explain this discrepancy with experiment in the same way as the discrepancy found for sticking. First, the barriers in the SRP32-vdW potential surface could be too low. On the one hand, this should lead to a too high electronically adiabatic contribution to vibrational excitation in the vicinity of the barrier to dissociative chemisorption. Additionally, it should also lead to a too small sum of probabilities (for vibrationally elastic scattering and for vibrational excitation) by which the probability of vibrational excitation is divided to obtain a scaled vibrational excitation probability in experiments.⁵¹ The reasons are that the too low barrier will lead to too much vibrational de-excitation (to ν′ = 0) and too much reaction of (ν = 1) HCl. As explained in detail in Section 3.3, it is worth to investigate whether alternative theories to deal with non-adiabatic effects (such as ODF-MDEF and the IESH method) could improve the agreement with experiments. In future, it would also be interesting to study contributions of the electronically adiabatic and the nonadiabatic components of the molecule–surface coupling to vibrational excitation in more detail. This could be done by developing a high-dimensional PES also describing the effects of surface atom motion similar to refs.^9,54,55 This PES could then be used in MD simulation on the one hand or MDEF simulations or MD simulations using the IESH method on the other hand to disentangle adiabatic and nonadiabatic effects on vibrational excitation of HCl scattering from Au(111). With these methods, it should be possible to run orders of magnitude more trajectories and compute vibrational excitation probabilities, as done in ref (55), with error bars small enough to determine whether one can reproduce the trends related to incidence energy and surface temperature seen experimentally in Figure 3.

We have also computed total energy losses to the surface and translational energy losses and compared these with experimental values for similar initial conditions. For the latter energy losses, good agreement is obtained of the AIMDEF calculations with experiment.

The authors declare no competing financial interest.