Abstract
Fatigue as a mode of failure becomes increasingly relevant with age in tissues that experience repeated fluctuations in loading. While there has been a growing focus on the mechanics of networks of collagen fibers, which are recognized as the predominant mechanical components of soft tissues, the network’s fatigue behavior has received less attention. Specifically, it must be asked (1) how the fatigue of networks differs from that of its component fibers, and (2) whether this difference in fatigue behaviors is affected by changes in the network’s architecture. In the present study, we simulated cyclic uniaxial loading of Voronoi networks to model fatigue experiments performed on reconstituted collagen gels. Collagen gels were cast into dog- bone shape molds and were tested on a uniaxial machine under a tension-tension cyclic loading protocol. Simulations were performed on networks modeled as trusses of, on average, 600 non-linear elastic fibers connected at freely rotating pin joints. We also simulated fatigue failure of Delaunay, and Erdős-Rényi networks, in addition to Voronoi networks,to compare fatigue behavior among different architectures. The uneven distribution of stresses within the fibers of the unstructured networks resulted in all three network geometries being more endurant than a single fiber or a regular lattice under cyclic loading. Among the different network geometries, for low to moderate external loads, the Delaunay networks showed the best fatigue behavior while at higher loads, the Voronoi networks performed better.
Keywords: fiber network mechanics, network fatigue, collagen gel fatigue
1. Introduction
Structures composed of fiber networks are extremely prevalent in our world. A number of consumer products, such as paper and open-cell foams, are composed of networks of polymeric elements with diameters on the order of micrometers. Networks composed of interconnected filaments or fibers are also a common occurrence in biology. These networks can form hierarchical structures ranging in size from a few micrometers, e.g., the actin filament network of the cytoskeleton33, to larger-scale structures on the order of millimeters, e.g., connective tissues such as the facet capsular ligament9, or the fibrin network in a clot52. Biopolymeric materials, such as collagen gels, are hydrated fibrous networks19. Electrospun materials, such as the scaffolds used in tissue engineering to mimic the mechanical properties of the native tissue, are networks composed of nano/microscale fibers10.
The literature on the mechanics of networks is vast, with a tremendous amount of work being done in particular on flexible macromolecular networks such as rubber. A major objective of such macromolecular materials science has been to derive constitutive equations governing the macroscale mechanics of the material 6,20,50. Analogous techniques have also been developed and used extensively in the study of other heterogeneous materials like metallic foams7. Due to their importance in various industries, several studies have focused on characterizing the pre-failure mechanics16, fatigue failure 31, and creep behavior of foams 5.
Recent advances in multiscale modeling have further motivated this research, guiding it in the direction of relating macroscale material behavior to parameters of the underlying microscale network1,8,40. For more information on the present understanding of mechanics of random networks, the reader is referred to the review by Picu37. The increasing use of synthetic materials with a fibrous microstructure in the manufacture of commercial products has also necessitated a better understanding and modeling of network failure and fatigue behavior, e.g., failure of electrospun scaffolds22.
More recently, network modeling has been used by the biological community to describe the behavior of various soft tissues and tissue analogs, e.g.,2,12,44,45,54. Network models have also been expanded to model catastrophic failure of tissues, e.g., 46,53. In spite of the advances made, fatigue failure of biological networks is still not well understood. Over the lifespan of a living being, tissues undergo many cycles of varying loads, e.g., tendons in the body experience fluctuating tensile stress during daily activities, the tissues of the lung expand and contract with breathing, and the aorta expands with every heartbeat to accommodate the flow of blood. While damage can be repaired as biological tissues remodel over time, fatigue can still become increasingly relevant in certain tissues with age as the collagen turnover rate slows down21,34. The tendency to fatigue can lead to injuries and a reduction in quality of life. For example, fatigue damage resulting from overuse can lead to tendinopathies4, fatigue failure is one of the major modes of failure of bioprosthetic heart valves27, and some forms of osteoarthrosis have been attributed to the fatigue of the collagen fiber network in articular cartilage51.
Obviously, the fatigue behavior of a fibrous network must depend on the properties of the individual fibers that constitute it. Given, however, that a network material’s pre-failure stress-strain behavior and tensile strength in a stretch-to-failure experiment depend on both the fiber properties and the network ar- chitecture37,43, one must ask whether the fatigue process is similarly affected. That is, if two networks are constructed of the same fibers but with different fiber connectivity, will the macroscopic fatigue behavior of the two networks differ, and if so, how? We examined that question in the context of different simulated networks subjected to cyclic uniaxial loading until failure,complemented by experiments on reconstituted collagen gels.
2. Modeling Approach
2.1. Network generation
Three-dimensional fiber networks were represented as trusses composed of non-linear elastic cylindrical members (fibers) connected by means of pin-joints (nodes) allowing free rotation. Initially, the networks were generated using a Voronoi49 tessellation. Voronoi networks have been shown to provide a close approximation to collagen gel mechanics35 and have been used in previous studies modeling the mechanics of collagenous connective tissues 54. Voronoi networks have also been used to model cellular solids e.g., sponges, foams38,39.
To construct Voronoi networks, three-dimensional space was divided among the initial seed points, forming polyhedral regions, such that every point inside a polyhedron was located closest to the seed point corresponding to that region and located within it. The edges of the Voronoi polyhedra calculated from the seed points represented fibers, and their vertices represented network nodes. Three-dimensional Voronoi cells were generated using the MATLAB function voronoin29.
Fiber networks generated using the above algorithm were isotropic and were trimmed to fit within a unit cube in the computational domain. The physical space represented by the computational domain was related to the dimensions of the fibers and their desired volume fraction within the network by the relation
| (1) |
where X is the conversion factor relating the physical and computational domains, r is the fiber radius, Σl is the total fiber length in the network within the computational domain, and ϕ is the fiber volume fraction. Every network had fibers of the same radius but a different length. In this work, we took r = 100nm23 and ϕ = 0.05. The total fiber length Σl was typically around 150 — 200, so the unit cube represented a physical domain of side X ≈ 10μm.
2.2. Single fiber mechanics and failure
Network fibers were modeled as one-dimensional nonlinear springs with the constitutive equation
| (2) |
where f is the force generated within the fiber, A is itscross-sectional area, E denotes fiber stiffness, B controls its non-linearity, and λ is the fiber stretch. At infinitesimal stretch, Equation 2 reduces to a linear material with Young’s modulus E. The constitutive equation was adapted from a previous structural model11 and has been used in multiscale modeling of the collagen microstructure in soft tissues.23,41 While the nonlinearity introduced by Equation 2 is not essential in understanding the fatigue behavior of networks, it is a more accurate model of collagenous tissue as it accounts for the lack of compression stiffness of the fibers. Similar non-linearity can also be added in the model in other ways, e.g., by assuming a linear elastic response for the fiber and introducing fiber waviness14, or by using bilinear fiber stiffness13.
Failure was introduced into the network by removing individual fibers, which was achieved in the model by reducing the small-strain modulus of a failed fiber (E in Equation 2) by several orders of magnitude (Table 1). Grossly reducing the magnitude of a failed fiber ensured that it did not contribute to the mechanical response of the network, while maintaining stability of the numerical approach used to model the network. Fiber failure occurred either due to a fiber stretching beyond a critical stretch or due to fatigue. As the network was stretched by an external cyclic loading, the stress experienced by individual fibers within the network changed from cycle to cycle since the stress within a network is distributed over many fibers, and this distribution changed as fibers failed and the network structure reorganized. A stress-life (SN) curve determined the fatigue behavior of the fibers by relating the number of cycles of repeated loading required to fail a fiber to the amplitude of the oscillating load applied to it. To account for the varying stress amplitudes experienced by a fiber, a damage fraction was calculated for each fiber, which measured the fraction of its life consumed by exposure to cycles at different stresses. Fatigue failure occurred when the value of this cumulative damage fraction exceeded 1 (Miner’s rule32). A fiber’s properties remained unchanged during the fatigue process until failure occurred. Additionally, it was assumed that the loading and unloading phases of the applied cyclic load on the network occurred instantaneously, so fiber fatigue failure was evaluated only at the peak of each loading cycle.
Table 1.
Values for the parameters of the constitutive equation (Equation 2) and the failure stretch of a fiber.
| Parameter | Meaning | Value |
|---|---|---|
| r | Fiber cross-section radius | 100 nm |
| E | Fiber stiffness | 10 MPa |
| B | Fiber non-linearity | 2.5 |
| λcritical | Failure stretch | 1.42 |
| Efailure | Stiffness value of failed fibers | 10−7 Pa |
2.3. Network mechanics and failure
Repeated loading to the same averaged network stress was applied to simulate the fatigue process. Since the properties of the network changed as fibers failed, the amount of displacement required to achieve the imposed stress changed during the course of the simulation. Thus, an iterative approach was used to apply the same stress at each cycle (Figure 1).
Fig. 1.
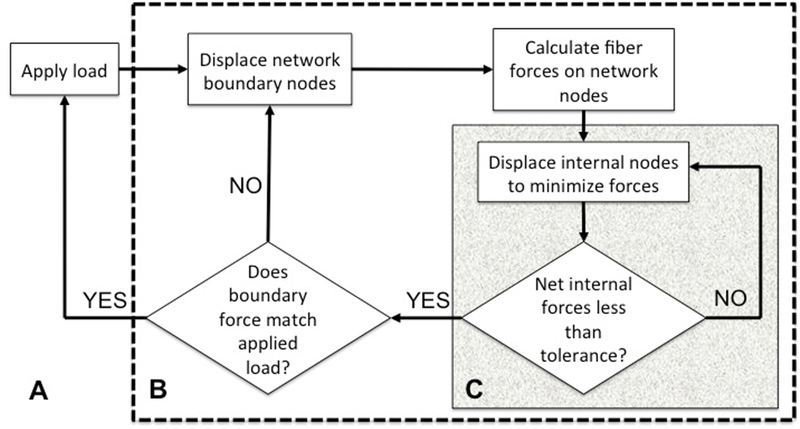
Basic outline of the force-controlled deformation model of a fiber network showing three loops. The outermost loop (A) specifies the desired loading cycle. The intermediate loop (B) adjusts the boundary displacements of the network so as to match the specified load. The innermost loop (C) calculates the equilibrium internal nodal positions for a boundary displacement specified by the intermediate loop. Upon convergence, the inner loop passes a stress value to the intermediate loop for comparison to the target stress
Uniaxial deformation of the network was simulated by imposing a displacement on all nodes lying on one face of the network while keeping the opposite face fixed in space. The surfaces facing in the other two principal directions were assumed to be stress-free. Network nodes were identified as either boundary nodes, which included all nodes lying on a network face and constrained to move with the network face, or internal nodes, which were free to move and equilibrate. Stretching of fibers due to the motion of the network boundary generated forces on all network nodes, boundary as well as internal. For a given network boundary displacement, however, the equilibrium solution of the boundary value problem had no net force on any internal node. The nodal positions corresponding to this equilibrium solution were calculated using Newton’s method by computing the Jacobian matrix J such that
| (3) |
where f is total force on a node, x is its position, and i and j are the unconstrained degrees of freedom of the network, i.e., every node had 3 degrees of freedom corresponding to translations in the 3 principal directions. Using the Jacobian, a displacement step was calculated for the internal nodes of the network
| (4) |
where Δx is the displacement step, and R is the vector of residual forces on the internal nodes. This calculation was performed iteratively until the net force on all internal nodes was less than a specified tolerance. The volume-averaged Cauchy stress in the network was obtained from the forces acting on nodes lying on the network boundary13:
| (5) |
where is the volume-averaged Cauchy stress on the network, xb is the nodal position of a boundary node, fb is the force acting on the node, and V is the volume of the network. The network deformation/equilibration cycle described above was performed iteratively using a bisection search to calculate a suitable network stretch such that the boundary forces matched the applied boundary loading. The initial stretches bounding the bisection search were selected such that the interval between the boundary force values generated by the network at these two stretches contained the external applied load. All computations were carried out through scripts written in MATLAB29.
Failure of the network was defined as no change in the volume-averaged stress for any further increase in network stretch. By this definition, a network was determined to have reached failure once the following condition was met
| (6) |
where and are the stress and stretch of the overall network respectively, measured in the direction of deformation, and . The slope was computed numerically by making a small displacement increment with no additional fatigue and recalculating the network stress. Ten Voronoi networks were subjected to a cyclic load-to-failure test to simulate fatigue and obtain an SN curve.
3. Collagen gel fatigue — experiments and model
3.1. Gel preparation and testing
Collagen gels were synthesized as described previously 24. Briefly, a 2 mg/mL collagen solution was prepared by combining the following (by volume fraction): 14.2% 1 M 4-(2-hydroxyethyl)-1-piperazineethanesulfonic acid (HEPES, ThermoFisher), 2.6% 1 M sodium hydroxide (NaOH, Sigma-Aldrich), 10% 10× Modified Eagle’s Medium (MEM, ThermoFisher), 6% fetal bovine serum (FBS, GE Healthcare), 0.1% penicillin-streptom-ycin, 0.1% fungizone, 1% L-glutamine (Invitrogen), and 66% 3 mg/mL rat-tail collagen I (ThermoFisher). All ingredients were mixed on ice in a centrifuge tube and then cast into acrylic dog-bone molds sealed at the bottom with vacuum grease to prevent leaking. The collagen solution was incubated in the molds for 3 hours at 37°C to facilitate polymerization. Polymerized gels were removed from the molds and immersed in a 1× phosphate buffered saline (PBS) bath prior to and during testing.
Uniaxial mechanical tests were performed on gels using a universal test machine with a 5N force transducer (TestResources, Shakopee, MN). First, five gels were tested in a displacement-controlled, uniaxial stretch- to-failure test to determine an average yield force for the gels, which was used to determine the load amplitudes in the subsequent fatigue tests. For stretch-to-failure tests, gels were stretched at a rate of 1 mm/min, and data were collected at 2 Hz. Next, load-controlled, uniaxial tension-tension fatigue tests were performed on collagen gels with the loading amplitudes varying cyclically between a lower limit of 10% and upper limit of 20–90% of the average yield force. For the fatigue tests, gels were stretched at a rate of 30 mm/min with a data sampling rate of 2 Hz; tests continued either until the sample failed from fatigue or until the duration of the test exceeded 30 minutes. The number of cycles at failure was recorded to obtain an SN curve.
3.2. Gel simulation.
The fatigue experiments described in Section 3.1 were simulated using the network model wherein Voronoi networks were used to represent collagen gels. The parameters for the fiber constitutive equation (Equation 2) in the network model were selected based on previous research modeling the mechanics of collagen fiber networks53 (Table 1). The fatigue behavior of a single fiber was defined by the SN curve of a human extensor digitorum longus (EDL) tendon, obtained from the literature 42:
| (7) |
where Snorm is the normalized load amplitude expressed as a percentage of the UTS and N is the number of cycles to failure. The high degree of collagen fiber alignment in the tendon made its fatigue behavior an acceptable approximation - and the closest one we could find - to that of a single collagen fiber.
The simulation of gel fatigue proceeded in a manner analogous to the procedure employed in testing the collagen gels. First, the simulated networks were stretched to failure to obtain an ultimate tensile strength (UTS) which was used to calculate the load amplitudes used in subsequent fatigue simulations. The cyclic loading applied to the simulated networks ensured that the networks always remained under tension. The upper load limit was equal to the external applied stress while the lower limit was 10% of the UTS.
4. Network architecture and fatigue
Having confirmed that (1) the network SN curve differs from that of an individual fiber, and (2) our network fatigue model showed a similar SN trend as that obtained from the collagen gel experiments, we investigated the effect of network geometry on its fatigue behavior. We compared the simulated SN curves obtained for three different network types with the same fiber properties.
4.1. Network generation and structure
In addition to the Voronoi networks generated previously, we also used networks created using the following two algorithms:
— Delaunay15: The initial randomly selected seed points formed the final nodes of the network. Connections were formed between those points such that the circumsphere of any tetrahedron formed by a set of four connected nodes did not contain any other network node. Networks were generated using the MATLAB function delaunay 29. Delaunay networks have been used in previous studies modeling fibrous tissues 3.
- — Erdős-Rényi18: For networks created using the Erdős-Rényi (ER) algorithm, seed points represented network nodes, and connections were formed randomly between pairs of nodes such that shorter connections were favored over longer ones. The probability distribution used to connect nodes varied inversely with the Euclidean distance between the pair of nodes and was given by
where p(i,j) is the probability of forming a connection between network nodes i and j, dist(i,j) is the Euclidean distance between nodes i and j, and max dist is the maximum Euclidean distance between two nodes calculated for the initial set of seed points. The average value of max dist was 1.4 units in the computational domain. ER networks were chosen to explore the space of possible networks more thoroughly.(8)
Networks generated using the above algorithms were also isotropic, and had the same network dimensions as the Voronoi networks detailed in Section 2.1. Networks were chosen to be isotropic as we wanted to elimi-nate any direction-dependent effects arising due to fiber anisotropy within the networks. Table 2 shows the average values of some measures of network topology obtained for each of the three network types - Delaunay, Voronoi, and ER.
Table 2.
Average network parameter values for the three different network types (n = 10 for each network type.)
| Network type | Total fiber length | Mean fiber length | Mean nodal degree | Number of nodes | Number of fibers | Physical dimension of network, μm (equation 1) |
|---|---|---|---|---|---|---|
| Delaunay | 127.90 | 0.23 | 15 | 397 | 560 | 8.90 |
| Voronoi | 68.40 | 0.11 | 4 | 430 | 612 | 6.50 |
| Erdős-Rényi | 366.38 | 0.60 | 74 | 590 | 660 | 15.10 |
Delaunay and Voronoi networks were generated from the same number of initial seed points, but the Voronoi networks, on average, had more nodes. The ER networks required a larger number of seed points to form a completely connected network, i.e., a network without any isolated clusters, conforming to the physical network size requirement, which resulted in the ER networks having a higher number of nodes. The internal nodes in the Delaunay and ER networks were highly connected while all the internal nodes in the Voronoi networks had a connectivity of 4 (Figure 2).
Fig. 2.
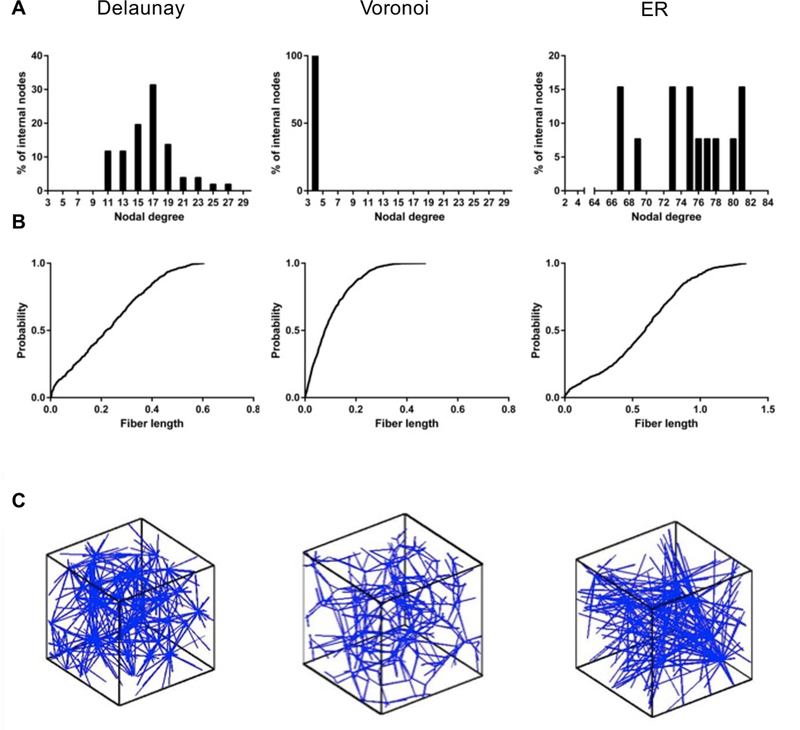
Histograms of nodal connectivity (A), cumulative probability distribution of fiber lengths in the computational domain (B), and representative images (C) of the three different network structures used — Delaunay, Voronoi, Erdős-Rényi
On average, the Voronoi networks were composed of a greater number of shorter fibers (Figure 2). The Delaunay networks showed a nearly uniform fiber distribution (linear CDF in Figure 2) of fibers with length 0 to 0.45 units and then a tail to about 0.6 units. The Voronoi networks, in contrast, showed a steady decrease in probability with length (concave down CDF) and had only one fiber above length 0.4 units. The ER networks showed considerably longer fibers, including some of length greater than 1.0 units. The mean fiber length was observed to be considerably longer in the ER net- works compared to the Delaunay and Voronoi geometries. The longer fibers spanning the ER networks resulted in a greater number of boundary nodes than internal ones when the network was trimmed to fit within the computational unit cube.
4.2. Fatigue simulation
Fatigue failure of the different networks was simulated to obtain an SN curve for each of the three network types. The parameters of the constitutive equation (Equation 2) governing the pre-failure behavior of an individual fiber remained unchanged from those noted in Table 1. Since the primary focus of this portion of the study was to compare the fatigue behaviors of different network geometries composed of the same fiber, any reasonable choice of fiber fatigue properties would have sufficed. The fiber SN curve used thus far (Equation 7) to model collagen gels required a large number of cycles to fatigue, especially at lower loads. Thus, to reduce simulation time, fibers were assigned an SN curve that was also an exponential, plus an offset, with parameters selected such that the fiber failed within a computationally acceptable number of cycles (Equation 9). The offset introduced a threshold value of stress, selected to be the stress generated in a fiber at a stretch of 1%, below which the fiber life was infinite.
| (9) |
Cyclic loading was simulated on 10 networks of each type and the amplitude of the oscillating load on the networks was varied to produce network fatigue between 1 to 30 cycles.
5. Results and Discussion
We begin this section by discussing the behavior of a representative network under cyclic loading, followed by a comparison of the fatigue behavior of collagen gels simulated using our model and that obtained experimentally. Finally, we examine the differences seen in the mechanics and fatigue of the different network types - Voronoi, Delaunay, and ER. Prior to simulating fatigue failure, however, the networks were confirmed to be sufficiently resolved, i.e., there was no change in the network stress-strain response with a further increase in the number of nodes and fibers. As seen in Figure 3, there was almost no change in the stress-stretch curve with change in number of fibers.
Fig. 3.
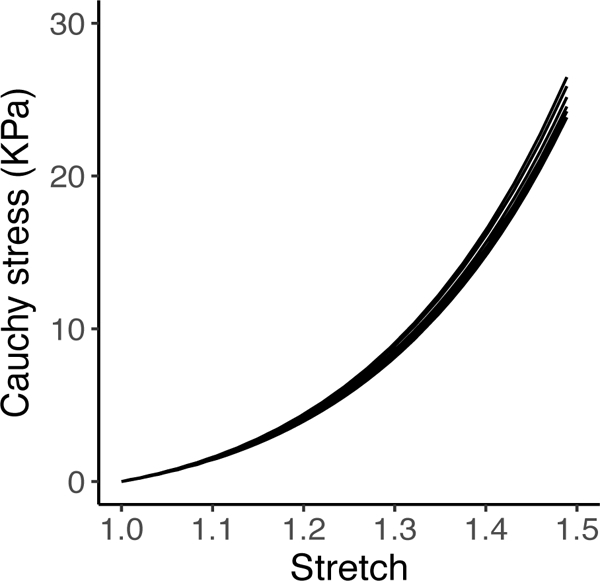
Stress-stretch plots for a network with 300, 400, 800, 1200, and 1600 nodes without fiber failure. The curves do not show any significant differences and overlap each other
5.1. Network response to cyclic loading
In the initial cycles with all fibers intact, the networks showed a non-linear stress-stretch response with overlapping loading and unloading phases, i.e., no hysteresis (path oao in Figure 4A). With the onset of fiber fatigue failure, however, the network became more compliant and stretched more at the peak load. The peak stretch then remained stable until additional fiber failure events led to further increases in network compliance (Figure 4A, locations (b-d)). The jumps seen in the stress-stretch curve at peak loads suggested a loss of elasticity of the material due to accumulation of fiber failure in the network similar to the stress-softening effects included in macroscale constitutive models for describing damage in soft tissues, e.g.,26,36.
Fig. 4.
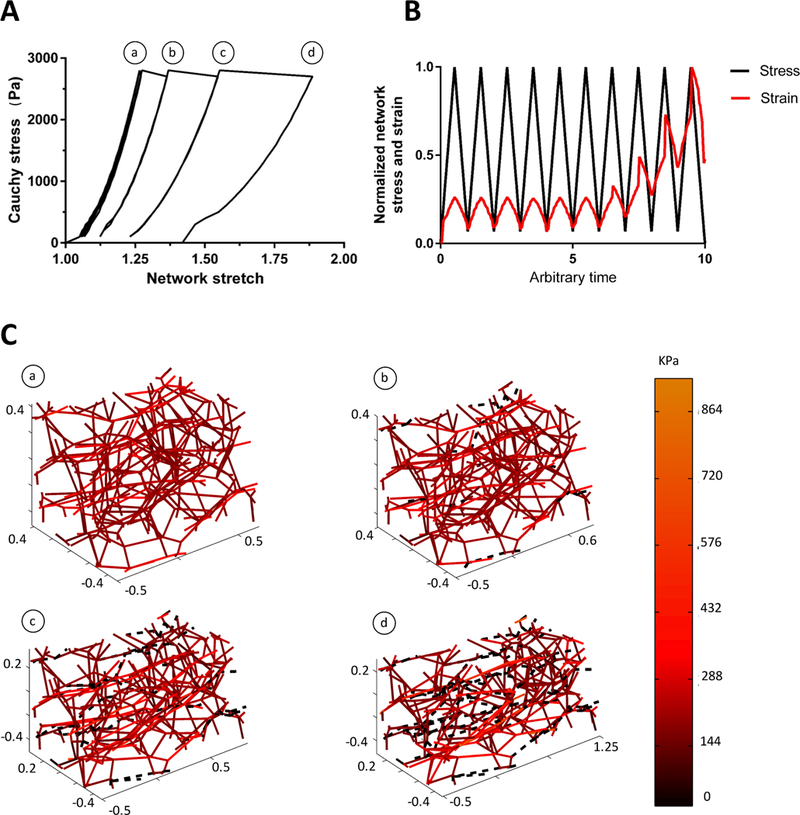
(A) A representative set of stress-stretch curves for a Voronoi network failing under fiber fatigue, (B) Evolution of network stress and strain with time, (C) Instantaneous snapshots of the network at the locations (a-d) indicated on the stress-stretch curve. The color bar shows the stress generated within each fiber and black dashed lines indicate failed fibers
The number of failed fibers within the network accumulated over time until the network lost integrity.This gradual accumulation of damage within the network through progressive failure of fibers is similar to that observed by Linka et al.25 in their study of soft tissue fatigue using a multiscale constitutive model. Figure 4B shows the evolution of network strain with time. While the applied stress remained the same over all the loading cycles, with the onset of fiber failure, a larger network strain was required for the network to support the applied load.
Because of the purely elastic fibers used in the model, the networks did not show any permanent deformation, or hysterises, prior to failure like that observed in fatigue tests on, e.g., bioprosthetic heart valves47, and included in more recent constitutive models of tissue fatigue26,28,36. Compared to these currently existing macroscale constitutive models, however, our model captured the non-affine nature of deformations within the network. At any given stretch, only a small number of fibers carried a majority of the load (Figure 4C); the load shifted as fibers failed and the remaining fibers reorganized.
5.2. Collagen gel fatigue
Figure 5A shows the average load-stretch curve for the collagen gel stretch to failure experiments. The large dot in Figure 5A shows the average failure stretch (19 ±1.7 % ) and ultimate tensile load (UTS, 0.06 ± 0.023 N)for all of the experiments (n = 6; mean ± 95% CI). Figure 5B shows the progressive increase in gel strain with time. Fatigue experiments on collagen gels were limited to a duration of 30 minutes (≈ 2000 cycles). Gels tested at peak loads greater than or equal to 40% of the UTS exhibited failure, as shown in Figure 5C. Also shown is the SN curve obtained from the fiber network model using fiber properties based on those of a tendon as reported by Schechtman et al.42. The model curve, with no fitting parameters, showed good agreement with the collagen gel data at the higher stresses. The deviation of the model from the experiments at lower stresses, however, suggests that the fatigue behavior of an individual collagen fiber is not well approximated by the fatigue properties of a tendon. These results also indicate that fiber rearrangement within a collagen fiber network increases fatigue life for a given normalized stress.
Fig. 5.
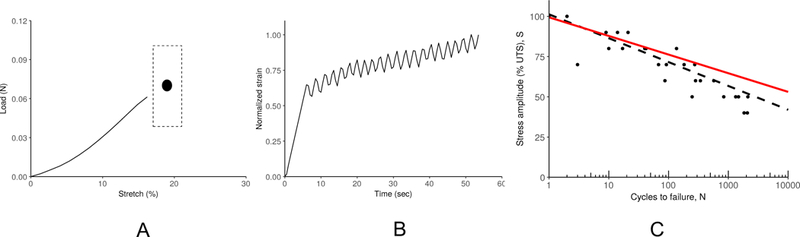
(A) Average load-stretch curve obtained for collagen gels. The dot indicates the mean failure load and stretch (n=6), with the box around the dot indicating the 95 % confidence interval. (B) The evolution of strain over time for a representative gel undergoing fatigue testing. Strain values were normalized to the strain at failure for that gel. (C) Fatigue behavior of collagen gels. Collagen gels (dots) showed a fatigue life similar to that reported previously for tendon (42, dashed line). A Voronoi network model (solid red line) assuming tendon properties for each fiber, showed a longer fatigue life than the tendon, suggesting that the network structure increased fatigue life at a given normalized stress.
5.3. Effects of network architecture
5.3.1. Pre-fatigue behavior
Networks of all three types showed a non-linear stress- stretch response with no hysteresis in the initial cycles. The distribution of load within all three network types was uneven, with only a small fraction of the fibers bearing a majority of the load. This skewed distribution is visualized in Figure 6 by plotting the cumulative probability distribution of fiber stresses. For example,at a low applied stress of 300 Pa, a majority of the fibers (≈50%) remained stress-free for all three network types. At a higher stress of 1500 Pa, however, the fraction of unloaded fibers in the Voronoi network dropped considerably (≈14%). The percentage of stress-free fibers in the other two network types did not vary as much with the external network load. The variation of the fraction of stress-free fibers with external load seen in the Voronoi networks was indicative of a prominent ‘toe- region’. A stability analysis of the truss-like networks provides a possible explanation for this variation. For large networks, the Maxwell criterion30 requires that the mean nodal degree be greater than 6 for a threedimensional truss to be stable. The Voronoi network, failing to satisfy this condition, possesses a larger number of nodal degrees of freedom, thus increasing the extent of fiber reorganization possible at lower loads and allowing a wider variation in the number of fibers aligning in the direction of stretch and supporting the applied force on the network.
Fig. 6.

Cumulative probability distribution of fiber stresses in the different network types at a network load of 300 Pa (dashed) and 1500 Pa (solid). Inset bar graphs show the percentage of total fibers that remain stress free for the two applied network loads
The Kolmogorov-Smirnoff (K-S) test for cumulative distribution functions further corroborates that the differences seen in the network behavior arise due to a fundamental difference in the architectures of the three network types. The high values of the K-S statistic (Table 3) demonstrate that the cumulative probability dis-tributions of fiber stresses within each network in Figure 6 are not drawn from the same underlying distribution (p < 0.05 for all comparisons).
Table 3.
Kolmogorov-Smirnoff statistic values comparing the cumulative probability distribution of fiber stresses for each network type prior to the onset of fiber fatigue failure. Rows and columns denote different network types, and the values indicate the K-S statistic for a comparison between the network type indicated by the row with that shown in the column. A lower value of the K-S statistic implies higher similarities in the distributions being compared.
| Delaunay | Voronoi | Erdős-Rényi | |
|---|---|---|---|
| Delaunay | - | 0.41 | 0.12 |
| Voronoi | 0.41 | - | 0.32 |
| Erdős-Rényi | 0.12 | 0.32 | - |
5.3.2. Whole-network-scale failure and fatigue
Prior to fatigue testing, a stretch-to-failure test was simulated on each network to obtain the UTS for the three network types (Figure 7). The failure stresses for the Voronoi and Delaunay networks did not differ significantly, however, the ER networks consistently showed a lower UTS.
Fig. 7.

Failure stresses obtained for each network type in a stretch-to-failure simulation showing the mean ± 95 % confidence intervals (n=10)
Semi-log plots of the mean SN data for all three network types are shown in Figure 8, with the stress offset by the network fatigue limit and normalized to the network UTS, i.e.,
| (10) |
where network face, σ∞ 1 is the fatigue limit, i.e., the network stress below which the network possesses infinite life, and σuts is the mean UTS for the network. Under this transformation, the SN curve for the fiber, i.e., Equation 9 would be a straight line on the semi-log plot, and any deviation from linearity in the SN curves of the networks would then indicate an effeect arising due to the network structure-induced non-linearity. The semi-log SN plots fit well to a line in the high stress-low cycle regime withslight deviation from linearity in the low stress-high cycle limit.
Fig. 8.
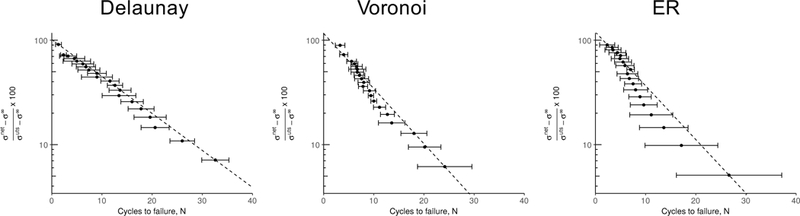
Stress-life (SN) plots obtained from simulations of the three different network structures (n = 10 for each network type) shown on a semi-log plot. Error bars indicate 95% confidence intervals. The stress indicated on the vertical axes is normalized to the ultimate tensile strength of the respective network type. The dashed lines are drawn passing through the first and last data points in each plot to show the deviation from linearity of the SN data, if any.
Exponential curve fits to the mean values of the SNdata were used to make a comparison between networks and fiber behavior (Figure 9). On account of the low fiber volume fractions, fibers experienced a magnitude of stress that was substantially larger than the volumeaveraged stress obtained for the network. To make a meaningful comparison between fiber and network fatigue properties, the fiber SN curve was scaled by a factor of . This scaling factor would make the fiber and network SN curves identical for a regular cubic lattice of fibers
Fig. 9.
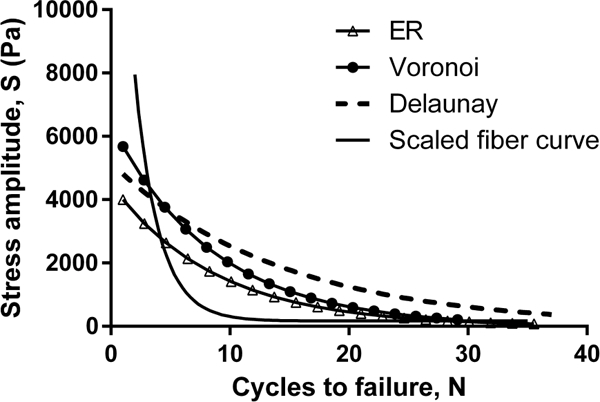
Comparison of the network and fiber SN plots. Network SN data for each network type was fit to an exponential curve
For all three network types tested, at low to moderate loads, the network structure was mechanically more endurant than the single fiber (Figure 9). As observed in Figure 4C, only a few fibers supported most of the applied load and thus only a fraction of fibers accumulated significant fatigue damage with each loading cycle that the network underwent. As those few loaded fibers eventually fatigued to failure, load was transferred to fresh fibers that could still endure multiple loading cycles, and so on. This geometric shielding effect occurring within the network allowed it to endure the repeated loading longer compared to an individual fiber.
At higher magnitudes of loading, however, in addition to fatigue, fibers also began to fail because of being overstretched. The network stretch generated to support the higher applied loads was sfficient to extend some fibers beyond their critical stretch value, especially in the highly connected Delaunay and ER networks, which resulted in fiber, and subsequently, network failure leading the fiber SN curve to cross over the network curves in the high-stress low-cycle region of Figure 9.
Among the different network geometries, the ER networks consistently performed worst on the fatigue tests. The longer average fiber length and high connectivity in the ER networks resulted in many fibers traversing between two opposite faces of the network in just a few connections. Thus, at a given network load, the in just a few connections. Thus, at a given network load, the fibers experienced larger stretches, and consequently larger stresses, compared to those in the other two network types, reducing the overall life of the ER networks.fibers experienced larger stretches, and consequently larger stresses, compared to those in the other two network types, reducing the overall life of the ER networks.
Over most of the range of loading simulated, the Delaunay networks outlasted the Voronoi. The short fiber lengths and well-connected nature of the Delaunay networks led to the uneven distribution of fiber stresses seen in Figure 6A with a large number of stress-free fibers. This distribution meant that the Delaunay networks had more backup fibers, i.e., fibers unstretched in the initial failure-free loading cycles, but which experienced gradually increased loading as network failure progressed over time and the network reorganized.
5.4. Limitations of the model and future research directions
The model described in this paper simulates fatigue failure of truss-like fiber networks undergoing cyclic loading. This study assumed that fatigue and failure occur only within the fibers themselves, and not in the connections between fibers. Although we consider this assumption to be reasonable for our choice of exible fiber networks, and a good first step in studying network fatigue behavior, we recognize that in many systems, e.g., in metallic foams31, fatigue and failure can also occur at fiber connections, requiring a different theoretical framework.
Additionally, the model analyzed network fatigue minus any growth, remodeling, and chemical efects that are present in biological tissues, e.g., mechanical overloading of collagen fibrils places them in a stable, denatured state48, potentially delaying failure. Denaturation of collagen can also lead to changes in the rest length of fibers, and affect the local stiffness of the tissue and its capacity to remodel17. Thus, the increase in fatigue life of a network compared to an individual fiber could be magnified in a tissue that can repair itself. Further research of long-term damage of fibrous tissues will need to address such mechanobiological efects of growth and remodeling of the network components.
6. Conclusions
The inhomogeneous distribution of load over fibers in an unstructured network has numerous mechanical consequences. For reasonable magnitudes of loads, an irregular fiber network structure can undergo more loading cycles than a single fiber or a regular fiber lattice. The network geometry enables an uneven distribution of stresses within the network fibers, with some fibers bearing higher loads than others. The nonuniform stress distribution leads to a gradual progression of fatiguewithin the network resulting in the network structure outlasting the individual fiber. This effect was observed in all network types that we studied.
Furthermore, a comparison of the fatigue failure behavior of networks having the same fiber mechanical properties but different network topologies suggests that geometric interactions between the fibers also affects the failure properties of the network. The three different network geometries simulated in this work — Delaunay, Voronoi, and Erdős-Rényi — showed different fatigue behaviors. The Delaunay network geometry showed the best low-stress, high-cycle behavior, so a Delaunay architecture might be preferable for fibrous structures undergoing repeated low to moderate loads.
Acknowledgements
The authors gratefully acknowledge financial support from the National Institutes of Health (R01- EB005813). We also thank the Minnesota Supercomputing Institute (MSI) for providing the computing resources used to carry out this work.
Footnotes
Conflict of interest The authors declare that they have no conflict of interest.
Contributor Information
Rohit Y. Dhume, Department of Mechanical Engineering, University of Minnesota, Minneapolis, MN 55455, dhume001@umn.edu
Elizabeth D. Shih, Department of Biomedical Engineering, University of Minnesota, Minneapolis, MN 55455, shih0031@umn.edu
Victor H. Barocas, Department of Biomedical Engineering, University of Minnesota, Minneapolis, MN 55455, baroc001@umn.edu
References
- 1.Abel J, Luntz J, Brei D (2013) Hierarchical architecture bof active knits. Smart Materials and Structures 22 [Google Scholar]
- 2.Abhilash AS, Baker BM, Trappmann B, Chen CS, Shenoy VB (2014) Remodeling of Fibrous Extracellular Matrices by Contractile Cells: Predictions from Discrete Fiber Network Simulations. Biophysical Journal 107(8):1829–1840, DOI 10.1016/j.bpj.2014.08.029 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Aghvami M, Billiar KL, Sander EA (2016) Fiber network models predict enhanced cell mechanosens- ing on fibrous gels. Journal of Biomechanical Engineering 138(10):101,006–11 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Andarawis-Puri N, Flatow EL (2011) Tendon fatigue in response to mechanical loading. Journal of Musculoskeletal and Neuronal Interactions 11:106–114 [PMC free article] [PubMed] [Google Scholar]
- 5.Andrews E, Gibson L, Ashby M (1999) The creep of cellular solids. Acta Materialia 47(10):2853–2863, DOI 10.1016/S1359-6454(99)00150-0,URL http://www.sciencedirect.com/science/article/pii/S13596454990 [DOI] [Google Scholar]
- 6.Arruda EM, Boyce MC (1993) A three dimensional constitutive model for the large stretch behavior of rubber elastic materials. J Mech Phys Solids 41:389–412 [Google Scholar]
- 7.Ashby M, Evans A, Fleck N, Gibson L, Hutchinson J, Wadley H (eds) (2000) Metal Foams:A Design Guide. Butterworth-Heinemann, Burlington, DOI 10.1016/B978-075067219-1/50010-6, URL http://www.sciencedirect.com/science/article/pii/B9780750672191500106 [DOI] [Google Scholar]
- 8.Ban E, Barocas VH, Shephard MS, Picu RC (2016) Softening in random networks of non-identical beams. Journal of the Mechanics and Physics of Solids 87:38–50, DOI 10.1016/j.jmps.2015.11.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Ban E, Zhang S, Zarei V, H Barocas V, Winkelstein B, R Picu C (2017) Collagen organization in facet capsular ligaments varies with spinal region and with ligament deformation. Journal of Biomechanical Engineering 139 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Barnes CP, Sell SA, Boland ED, Simpson DG, Bowlin GL (2007) Nano fiber technology: Designing the next generation of tissue engineering sca_olds. Advanced Drug Delivery Reviews 59(14):1413–1433, DOI 10.1016/j.addr.2007.04.022, intersection of Nanoscience and Modern Surface Analytical Methodology [DOI] [PubMed] [Google Scholar]
- 11.Billiar KL, Sacks M (2000) Biaxial mechanical properties of the native and glutaraldehyde-treatedaortic valve cusp: Part ii - A structural constitutive model. J Biomech Eng 122:327–335 [DOI] [PubMed] [Google Scholar]
- 12.Broedersz CP, MacKintosh FC (2014) Modeling semiexible polymer networks. arXiv:14044332 [cond-mat, physics:physics] ArXiv: 1404.4332 [Google Scholar]
- 13.Chandran PL, Barocas VH (2006) Affine versus non-affine fibril kinematics in collagen networks:teoretical studies of network behavior. Journal of Biomechanical Engineering 128:259–270 [DOI] [PubMed] [Google Scholar]
- 14.De Vita R, Slaughter WS (2007) A constitutive law for the failure behavior of medial collateral ligaments. Biomechanics and Modeling in Mechanobiology 6(3):189–197, DOI 10.1007/s10237-006-0054-x, URL 10.1007/s10237-006-0054-x [DOI] [PubMed] [Google Scholar]
- 15.Delaunay B (1934) Sur la sph_ere vide. Bulletin de l’Academie des Sciences de l’URSS, Classe des sciencesmath_ematiques et naturelles 6:793–800 [Google Scholar]
- 16.Deshpande VS, Fleck NA (2000) Isotropic constitutive models for metallic foams. J Mech Phys Solids 48:1253–1283 [Google Scholar]
- 17.Dittmore A, Silver J, Sarkar SK, Marmer B, Goldberg GI, Neuman KC (2016) Internal strain drives spontaneous periodic buckling in collagen and regulates remodeling. Proceedings of the National Academy of Sciences 113(30):8436–8441, DOI 10.1073/pnas.1523228113, URL http://www.pnas.org/content/113/30/8436, http://www.pnas.org/content/113/30/8436.full.pdf [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Erdős P, Rényi A (1959) On random graphs. Publicationes Mathematicae 6:290–297 [Google Scholar]
- 19.Flory PJ (1953) Principles of Polymer Chemistry. Cornell University Press, Ithaca, NY [Google Scholar]
- 20.Flory PJ, Rehner JJ (1943) Statistical mechanics of crosslinked polymer networks i. rubberlike elasticity. J Chem Phys 11:512 [Google Scholar]
- 21.Freeman MAR (1999) Is collagen fatigue failure a cause of osteoarthrosis and prosthetic component migration? a hypothesis. Journal of Orthopaedic Research 17:3–8 [DOI] [PubMed] [Google Scholar]
- 22.Koh C, Strange D, Tonsomboon K, Oyen M (2013) Failure mechanisms in _brous sca_olds. Acta Biomaterialia 9:7326–7334 [DOI] [PubMed] [Google Scholar]
- 23.Lai VK, Lake SP, Frey CR, Tranquillo RT, Barocas VH (2012) Mechanical behavior of collagen- _brin co-gels reects transition from series to parallel interactions with increasing collagen content. J Biomech Eng 134:011,004–9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Lake SP, Barocas VH (2012) Mechanics and kinematicsof soft tissue under indentation are determined by the degree of initial collagen fiber allignment. J Mech Behav Biomed Mater 13:25–35 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Linka K, Hillgrtner M, Itskov M (2018) Fatigue of soft _brous tissues: Multi-scale mechanics and constitutive modeling. Acta biomaterialia 71:398410, DOI 10.1016/j.actbio.2018.03.010, URL 10.1016/j.actbio.2018.03.010 [DOI] [PubMed] [Google Scholar]
- 26.Martin C, Sun W (2013) Modeling of long-term fatigue damage of soft tissue with stress softening and permanent set effects. Biomech Model Mechanobiol 12:645–655, DOI 10.1007/s10237-012-0431-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Martin C, Sun W (2014) Simulation of long-term fatigue damage in bioprosthetic heart valves: e_ects of leaet and stent elastic properties. Biomechanics and Modeling in Mechanobiology 13:759–770 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Martin C, Sun W (2014) Simulation of longterm fatigue damage in bioprosthetic heart valves: e_ects of leaet and stent elastic properties. Biomechanics and Modeling in Mechanobiology 13(4):759–770, DOI 10.1007/s10237-013-0532-x, URL 10.1007/s10237-013-0532-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.MATLAB (2013) version 8.0.2.701 (R2013b). The MathWorks Inc., Natick, Massachusetts [Google Scholar]
- 30.Maxwell JC (1864) L. on the calculation of the equilibrium and stiffness of frames. Philos Mag 27:294–299, DOI 10.1080/14786446408643668 [DOI] [Google Scholar]
- 31.McCullough KYG, Fleck NA, Ashby MF (1999) The stress-life fatigue behaviour of aluminium alloy foams. Fatigue Fract Engng Mater Struct 23:199–208 [Google Scholar]
- 32.Miner MA (1945) Cumulative damage in fatigue. Journal of Applied Mechanics 67:159–164 [Google Scholar]
- 33.Mitchison T, Cramer L (1996) Actin-based cell motility and cell locomotion. Cell 84(3):371–379, DOI 10.1016/S0092-8674(00)81281-7 [DOI] [PubMed] [Google Scholar]
- 34.Muir H (1973) Biochemistry. Adult Articular Cartilage p 118
- 35.Nachtrab S, Kapfer SC, Arns CH, Madadi M, Mecke K, Schrder-Turk GE (2011) Morphology and linear-elastic moduli of random network solids. Advanced Materials 23(22– 23):2633–2637, DOI 10.1002/adma.201004094, URL 10.1002/adma.201004094 [DOI] [PubMed] [Google Scholar]
- 36.Pena E (2011) Prediction of the softening and damage effects with permanent set in fibrous biological materials. J Mech Phys Solids 59:1808–1822 [Google Scholar]
- 37.Picu R (2011) Mechanics of random fiber networks a review. Soft Matter 7:6768–6785 [Google Scholar]
- 38.Roberts A, Garboczi E (2001) Elastic moduli of model random three-dimensional closed-cell cellular solids. Acta Materialia 49(2):189–197, DOI 10.1016/S1359-6454(00)00314-1 [DOI] [Google Scholar]
- 39.Roberts A, Garboczi E (2002) Elastic properties of model random three-dimensional open-cell solids. Journal of the Mechanics and Physics of Solids 50(1):33–55, DOI 10.1016/S0022-5096(01)00056-4 [DOI] [Google Scholar]
- 40.S SA, Picu CR (2004) Network model for the viscoelastic behavior of polymer nanocomposites. Polymer 45(22):7779–7790, DOI 10.1016/j.polymer.2004.08.060 [DOI] [Google Scholar]
- 41.Sander E, Stylianopoulos T, Tranquillo R, Barocas V (2009) Image-based multiscale modeling predicts tissue-level and network-level fiber reorganization in stretched cell-compacted collagen gels. Proc Natl Acad Sci USA 106:17,675–17,680 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Schechtman H, Bader DL (1997) In-vitro fatigue of human tendons. J Biomechanics 30:829–835 [DOI] [PubMed] [Google Scholar]
- 43.Shasavari A, Picu R (2012) Model selection forathermal cross-linked fiber networks. Phys Rev E Stat Phys 86:011–923 [DOI] [PubMed] [Google Scholar]
- 44.Stylianopoulos T, Barocas V (2007) Multiscale, structure-based modeling for the elastic mechanical behavior of arterial walls. J Biomech Eng 129:611–618 [DOI] [PubMed] [Google Scholar]
- 45.Suki B, Ito S, Stamenovic D, Lutchen KR, Ingenito EP (2005) Biomechanics of the lung parenchyma: critical roles of collagen and mechanical forces. Journal of Applied Physiology 98(5):1892–1899, DOI 10.1152/japplphysiol.01087.2004 [DOI] [PubMed] [Google Scholar]
- 46.Suki B, Jesudason R, Sato S, Parameswaran H, Araujo AD, Majumdar A, Allen PG, Bartolak-Suki E (2012) Mechanical failure, stress redistribution, elastase activity and binding site availability on elastin during the progression of emphysema. Pulm Pharmacol Ther 25(4):268–275, DOI 10.1016/j.pupt.2011.04.027 [DOI] [PubMed] [Google Scholar]
- 47.Sun W, Sacks M, Fulchiero G, Lovekamp J, Vyavahare N, Scott M (2004) Response of heterograft heart valve biomaterials to moderate cyclic loading. J Biomed Mater Res A 69:658–669 [DOI] [PubMed] [Google Scholar]
- 48.Veres SP, Harrison JM, Lee JM (2014) Mechanically overloading collagen fibrils uncoils collagen molecules, placing them in a stable, denatured state. Matrix Biology 33:54–59, DOI 10.1016/j.matbio.2013.07.003 [DOI] [PubMed] [Google Scholar]
- 49.Voronoi G (1908) Nouvelles applications des parametres continus _a la theorie des formes quadratiques. Journal fur die reine und angewandte Mathematik 133:97–102, DOI 10.1515/crll.1908.133.97 [DOI] [Google Scholar]
- 50.Wang MC, Guth E (1952) Statistical theory of networks of nongaussian exible chains. J Chem Phys 20:1144 [Google Scholar]
- 51.Weightman B, Chappell DJ, Jenkins EA (1978) A second study of tensile fatigue properties of human articular cartilage. Annals of the Rheumatic Diseases 37:58–63 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Weisel J, Nagaswami C (1992) Computer modeling of fibrin polymerization kinetics correlated with electron microscope and turbidity observations: Clot structure and assembly are kinetically controlled. Biophysical Journal 63(1):111–128, 199 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Witzenburg CM, Dhume RY, Shah SB, Korenczuk CE, Wagner HP, Alford PW, Barocas VH (2016) Failure of the porcine ascending aorta: Multidirectional experiments and a unifying microstructural model. Journal of Biomechanical Engineering DOI 10.1115/1.4035264 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Zhang L, Lake S, Lai V, Picu C, VH B, MS S (2013) A coupled fiber-matrix model demonstrates highly inhomogeneous microstructural interaction in soft tissues under tensile load. J Biomech Eng 135:011,008. [DOI] [PMC free article] [PubMed] [Google Scholar]


