Approaches for incorporating environmental mixtures as mediators in mediation analysis

Abstract

Mediation analysis offers an essential and rapidly expanding tool in environmental health studies to investigate the contribution of environmental factors towards observed associations between risk factors and health outcomes. When evaluating environmental factors, there may be particular interest in quantifying the impact of exposure to environmental mixtures on human health. In this context, evaluating the joint effect of multiple chemicals or pollutants, rather than individual examination, allows accurate identification of risk factors, assessment of interactions, and ultimately development of more targeted public health interventions. While mediation analysis has been extended to incorporate several methodological complexities specific to environmental factors, little attention has been given to integrating the analysis of environmental mixtures.

The aim of this review is to present some of the available methods for environmental mixtures, and discuss how these methods can be integrated within a mediation analysis framework. By incorporating these methods into a mediation framework, investigators will be able to evaluate the contribution of environmental mixtures as mediators of exposure-outcome associations, based on methodologies that are currently available.

While standard regression-based methods for multiple mediators can be used, these can easily become unstable as the number of mixture components increases. Summary and classification methods, or hierarchical modeling, can reduce the number of mediators by creating scores or possibly uncorrelated subgroups. This approach allows retrieving indirect effects due to the mixture or to a specific subgroup, but makes identification of component-specific effects and interactions complicated. Finally, one can use various approaches for analyzing mixtures in a two-stage fashion, selecting relevant mediators to be included in the final model.

We focused this review on techniques that have been presented to the environmental health community and that can be conducted with major statistical software. We encourage researchers to move beyond the evaluation of one environmental factor at a time to the assessment of the joint effects of environmental mixtures when a mediation model is of interest. Available methods target different aspects related to environmental mixtures and the choice of the suitable approach will depend on data structures and the research question of interest.

1. Introduction

Researchers are increasingly using mediation analysis to quantify the contribution of intermediate variables in explaining an exposure-outcome association (Baron & Kenny, 1986). Considerable methodologic developments have been presented in the last decades, and mediation analysis can now be conducted with several study designs and various types of outcomes. These methods also allow for methodological complexities, such as the presence of multiple mediators and interactions (VanderWeele, 2015).

Environmental health researchers may be interested in mediation analysis in several settings. So far, most research has focused on mediation techniques to investigate the mechanisms through which environmental factors generate health effects (Bind, Vanderweele, Coull, & Schwartz, 2016; Peng et al., 2016; Richmond, Timpson, & Sørensen, 2015). In this review we focus on those situations where environmental factors are instead evaluated as potential mediators of a given association, for example when environmental factors may contribute to explain the health effects associated with behavioral, social, and lifestyle characteristics (James-Todd, Chiu, & Zota, 2016; Mitchell & Popham, 2008; Seltenrich, 2015). There are three broad categories of environmental studies where this may be relevant. First, when a behavioral or lifestyle-related exposure is an established potential source of environmental chemicals. For example, studies investigating the health effects of dietary factors (such as fish) may want to a) disentangle the proportion of total effect that is due to contaminants present in the food (such as polychlorinated biphenyls (PCB)s) and b) quantify how the negative effects of these contaminants counterbalance the potentially positive effects of the dietary factor (Persky et al., 2001). Second, when the exposure of interest increases the risk of being overexposed to environmental hazards. This is a common scenario, for example, in studies focusing on occupational health or housing conditions, where higher exposures to chemicals or pollutants may partly explain differences in health status associated with specific job occupations or neighborhood/housing characteristics (Seals, Kioumourtzoglou, Gredal, Hansen, & Weisskopf, 2017). Finally, a third situation when environmental factors can be seen as potential mediators of given associations, is when they are potential determinants of health disparities, differences in health that affect disadvantaged groups of individuals such as specific racial/ethnic groups (Naimi, Schnitzer, Moodie, & Bodnar, 2016; Schulz & Northridge, 2004).

When evaluating environmental factors, there is a great interest in quantifying the impact of exposure to environmental mixtures on human health (Carlin, Rider, Woychik, & Birnbaum, 2013). People are often simultaneously exposed to a variety of potentially hazardous environmental factors (Aylward, Kirman, Schoeny, Portier, & Hays, 2013). In this context, evaluating the joint effect of multiple chemicals or pollutants, rather than single exposures, allows one to more accurately identify risk factors, assess interactions, and ultimately develop real-world public health interventions.

While mediation analysis has been used to incorporate several methodological complexities specific to environmental factors (Bind et al., 2016), little attention has been given to optimal approaches for integrating the analysis of environmental mixtures as mediators of a given association. However, as for the case of mixture analysis outside of a mediation context, it is more reasonable to hypothesize a contribution of the overall mixture to the mediation effect for a given exposure-outcome association. For example, if we had to evaluate the health effects of high-levels of fish consumption from a particular location known to have been contaminated with PCB, we may need to evaluate the contribution of PCB as a harmful set of chemicals for which fish is the main source of human exposure. In this situation, all the potentially harmful PCBs compounds that can be found in fish should be simultaneously incorporated to evaluate the potential mediation by PCBs in the association between high fish consumption from contaminated waters and a given outcome of interest.

A recent workshop held by the NIEHS reviewed the common limitations of classical statistical approaches for mixtures (i.e., multiple regression) and reviewed several methods that can be used to investigate chemical mixtures, broadly classifying them into: shrinkage methods, classification and prediction, variable selection, and exposure-response surface estimation (Taylor et al., 2016). Shrinkage and classification approaches mainly focus on data reduction, summarizing patterns of exposures with summary measures or scores, and may be preferred when the target is to evaluate the epidemiologic effects of being exposed to the mixtures, possibly accounting for high-dimensional matrixes of exposures. On the other hand, selection methods and approaches based on exposure-response surface estimation are often interested in disentangling the specific contribution of each component (eg one chemical, one pollutant) while taking into account that this is part of a mixture with potential interactions (Hamra & Buckley, 2018). As such, methods respond to different research questions and researchers often use different approaches to analyze the same data under different perspectives. Thus, no one mixtures method is the best for all questions. The limitations of classical regression approaches in evaluating mixtures remain valid in the context of mediation analysis, where regression-based approaches are the common modeling choice (VanderWeele, 2015). The aim of this review is to present some of the available methods for environmental mixtures, evaluating how these can be integrated into a mediation analysis framework to evaluate the contribution of environmental mixtures as mediators of a given exposure-outcome association.

2. Conceptual Model

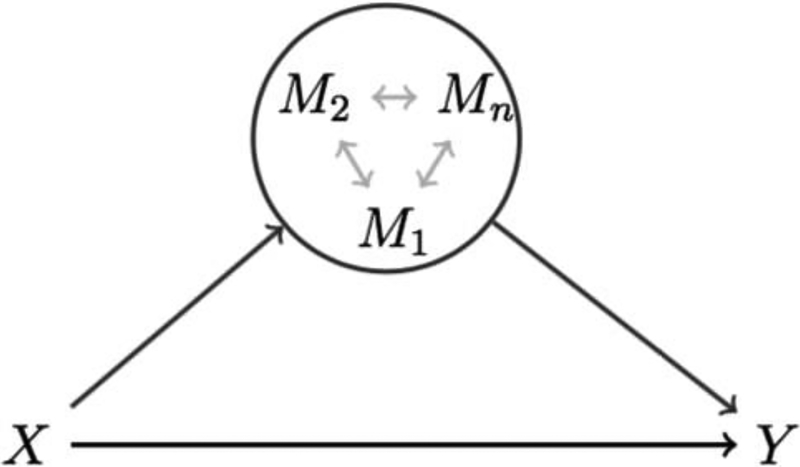
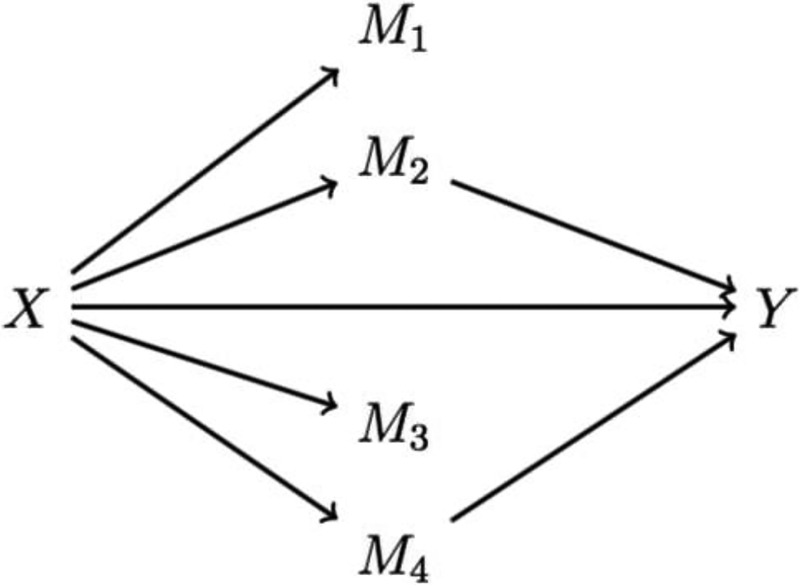
Figure 1 conceptualizes the situation of interest. Given an exposure X and an outcome Y, mediation analysis assumes that a certain proportion of the X-Y association may be mediated by a factor M. That is, the total effect of X on Y is decomposed into an indirect effect operating via M, and other pathways independent of M (direct effect). We focus here on the situation where M is a mixture of n environmental factors (M₁, M₂, …, M_n). In practical terms, we hypothesize that a proportion of the X-Y effect is explained by the fact that exposure to X increases the levels of several environmental hazards (e.g. chemicals, pollutants, contaminants), which in turn have an effect on the outcome Y. In such situations, evaluating the individual component contributions one at a time without adjusting for other correlated exposures would yield biased estimates (Correia & Williams, 2017), and it is therefore required to evaluate the joint contribution of the mixture components. The Table summarizes, without the claim of being exhaustive, several real world scenarios in which this conceptual model may be of interest.

Figure 1.

Decomposition of the total effect of a given exposure X on a health outcome Y into a direct effect of the exposure and an indirect effect operating through overexposure to a mixture M of environmental factors. Components of the mixture (M₁, M₂, …, M_n) are generally associated within each other and highly correlated.

Table.

Examples of known associations (X-Y) where a potential mediating role of a mixture of environmental factors (M) can be hypothesized from the literature.

Exposure (X)	Mediator (M)	Health outcome (Y)
Dietary factors (eg fish)	Contaminants (eg PCBs)	CVD
Neighborhood	Environmental pollutants	Lung cancer
Race/ethnicity	EDCs	Diabetes
Job occupation	Pesticides	Leukemia
Housing characteristics	Heavy metals	Neurological factors

Evaluating environmental mixtures introduces several analytical challenges. First, the components of the mixture are often inter-correlated (Figure 1) and may present synergistic or antagonistic interactions, requiring them to be simultaneously incorporated in the same statistical model (Taylor et al., 2016). On the other hand, an increasing number of covariates and interactions in a statistical model can easily lead to common modeling problems such as overfitting or multicollinearity. Moreover, in the specific setting presented in Figure 1, the mixture M will include components that are known to be associated with the exposure X, but this does not imply that they will all have the same effect on the outcome Y. We could observe, for example, that only one or few components of M have a substantial effect on the outcome of interest, or even that different components positively associated with X have opposite effects on Y (i.e. some harmful and some protective). On the other hand, components strongly associated with Y may have weaker associations with X. To take all these aspects into account, statistical approaches to evaluate the setting presented in Figure 1 should optimally be able to capture the overall indirect effect of the mixture M, as well as the independent contribution of each component of M. In the next section we revise several currently available approaches for environmental mixtures, discussing how and to what extent these methods can be included in a mediation model.

3. Mediation analysis with environmental mixtures

We assume for illustrative purpose that both X and Y are continuous and all relationships are linear. We also assume that the mixture has 4 components (M={M₁,M₂,M₃,M₄}), and that we want to adjust for a set of s confounders summarized in the vector Z={Z₁,…,Z_s}. The total effect (TE) of X on Y is calculated by estimating the effect of the exposure on the outcome in a statistical model that does not include the mediators of interest

$$E[Y|X=x,Z=z]={\beta }_0+{\beta }_{1}x+{\beta }^{\prime }z$$ (1)

with TE=β₁.

The next steps in mediation modeling require further adjusting model (1) for M, and estimating a model for M as a function of X. If we were to treat our four components of M one at a time, we would build four separate mediation models, one for each of the potential mediators. Formally, for each p=(1,2,3,4) we could estimate the following statistical models:

$$E[Y|X=x,M_p=m_p,Z=z]={\alpha }_0+{\alpha }_{1}x+{\alpha }_2{m}_p+a^{\prime }z$$ (2)

$$E\left[M_p|X=x,Z=z\right]={\gamma }_0+{\gamma }_{1}x+{\gamma }^{\prime }z$$ (3)

Assuming no interactions, we could estimate the indirect effect (IE) by combining coefficients of (1), (2), and (3), using the so-called difference or product methods.(Baron & Kenny, 1986) Specifically, for each of the components of M, its indirect effect will be estimated using the difference method, calculated using coefficients from (1) and (2) as IE_p=β₁- α_1. It can be shown that this indirect effect is mathematically equivalent in many contexts to the product α₂∙ γ₁. Mediation analysis can be conducted within the so-called counterfactual framework, where direct and indirect effects can be defined as natural or controlled. We refer to other papers for details on this distinction (VanderWeele, 2015). By placing mediation analysis within this framework one can define causal mediation effects and identify them under four assumptions: i) absence of unmeasured confounders of the exposure-outcome association; ii) absence of unmeasured confounders of the mediator-outcome association; iii) absence of unmeasured confounders of the exposure-mediator association; iv) absence of an effect of the exposure on a confounder of the mediator-outcome association. When multiple mediators are of interest, as in our setting, these assumptions should be verified for all exposure-mediator combinations (VanderWeele & Vansteelandt, 2014).

While this standard method can be used to provide the individual contribution of each mixture components, these are not jointly evaluated, and there is no way of estimating an overall contribution of the mixture. A first natural extension is to use a multiple regression approach for mixtures, incorporating all components (i.e. mediators) in the same statistical model.

3.1. Multiple regression

Inclusion of all components of M into the same statistical model would require defining the following single model:

$$E[Y|X=x,M=m,Z=z]={\alpha }_0+{\alpha }_{1}x+{\alpha }_2{m}_1+{\alpha }_3{m}_2+{\alpha }_4{m}_3+{\alpha }_5{m}_4+a^{\prime }z$$ (4)

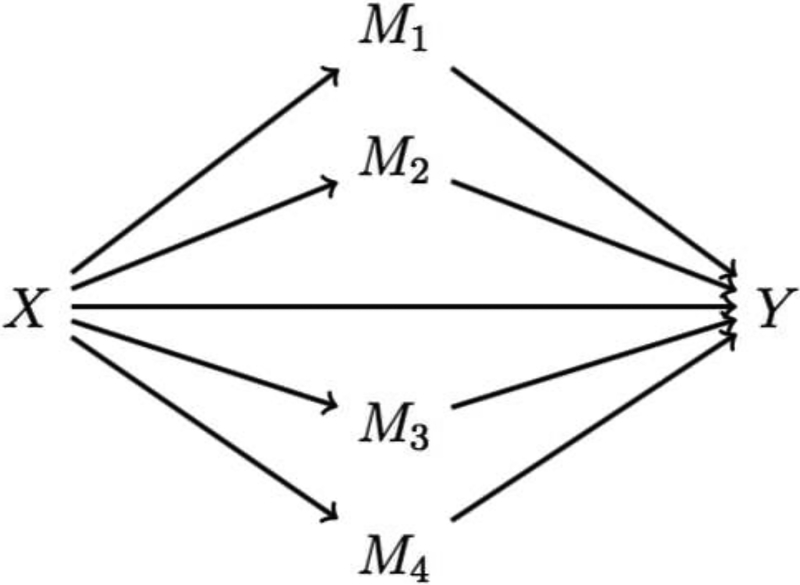
together with the 4 regression models shown in (3) for the each mediator as a function of the exposure. This formulation corresponds to assuming that the four components of M are nonsequential mediators (i.e. without a causal relationship within each other) of the X-Y association, as depicted in Figure 2.

Figure 2.

Mediation model where 4 components of a mixture M are evaluated as independent non-sequential mediators of the association between X and Y.

Direct and indirect effects can be estimated by using regression-based methods for multiple mediators (VanderWeele & Vansteelandt, 2014), combining coefficients estimated from models (4) and (3), the latter being estimated for each component of M. For example, the indirect effect due to M₁ will be estimated, using coefficients from (3) and (4) by γ₁∙ α_2. As recommended by Vanderweele and Vandsteelandt (VanderWeele & Vansteelandt, 2014), model (4) should be extended to incorporate all pairs of mediator-mediator interaction, thus providing a better interpretation to individual and overall indirect effects.

Pros and cons

Benefits of the multiple regression approach described above are that mediation analysis with multiple mediators can be conducted in several settings (eg time-varying coefficients, repeated measurements, non-linearities) (Daniel, De Stavola, Cousens, & Vansteelandt, 2015; Vansteelandt & Daniel, 2016), and this approach allows estimation of both mediator-specific and overall indirect effects (VanderWeele & Vansteelandt, 2014). Moreover, any pairwise or higher dimension interaction can be incorporated, and proportions due to mediated and interaction effects can be derived (Bellavia & Valeri, 2017). Nevertheless, this approach may rapidly become subject to problems such as overfitting or multicollinearity as the number of covariates and interactions increase. In such contexts, statistical approaches based on data reduction should be considered.

3.2. Reducing the mixture to a single mediator

A first intuitive approach to reduce the dimension of the mixture is to create a single score that summarizes the overall individual exposure to the mixture. One method for creating a mixture exposure index is the weighted quantile sum (WQS), which accounts for the specific contribution of each component while providing different weights to the components of the mixture (Czarnota, Gennings, & Wheeler, 2015). WQS regression constructs a weighted index estimating the effect of all predictor variables (i.e., the components of the mixture) on an outcome, and uses this weighted index in a regression model adjusted for relevant covariates to estimate the association of the index with the outcome. Weights are empirically determined through bootstrap sampling by splitting the dataset into training and validation. In a dataset with p covariates, weights are defined subject to the constraints ${\sum }_{i=1}^p{w}_i=1$ with 0 ≤ w_i ≤ 1, that is, the weight w_i, representing the weight for the ith exposure, is constrained to be between 0 and 1, and all weights sum to 1. The significance of the weighted index in all bootstrap samples is then tested, and the final estimate of the WQS is taken by only including the number of bootstrap samples where the weighted index was significant.

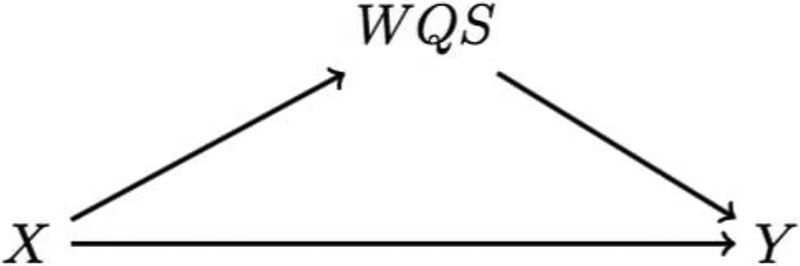
The WQS is then included in the statistical model of interest and estimated in the validation set, and the contribution of each individual predictor to the overall index effect may then be assessed by the relative strength of the weights the model assigns to each variable. WQS has been made available as a user-friendly package in the R statistical software (Renzetti et al., 2018). In the situation we are evaluating, we can use the WQS as a summary measure of the mixture, treating it as a mediator of the association between X and Y as presented in Figure 3.

Figure 3.

Mediation model in which the components of the mediating mixture are summarized to a single mediator using weighted quantile sum (WQS)

To assess the proportion of the total effect mediated by the mixture, as summarized by the WQS, we can fit the following statistical models:

$$\begin{gathered} E[Y|X=x,WQS=wqs,Z=z]={\alpha }_0+{\alpha }_{1}x+{\alpha }_{2}wqs+a^{\prime }z \\ E[WQS|X=x,Z=z]={\gamma }_0+{\gamma }_{1}x+{\gamma }^{\prime }z \end{gathered}$$

estimating direct and indirect effects as for the single mediator approach.

Using our previous example of PCBs exposures, researchers could use WQS to summarize all congeners generally measured in the blood, while taking into account the biological relevance of these congeners in the mixture.

Pros and cons

The main advantage of the WQS summary measure approach is that by reducing the mixture to a single score, a standard mediation model can be applied, thus avoiding any issue of overfitting and collinearity and allowing for all potential extensions of the simple mediation framework. Moreover, the use of WQS allows one to identify the contribution of each specific component of the mixture to the final score (Czarnota et al., 2015). On the other hand, by using a single predictor, one may not be able to detect potential interactions between mediators in predicting the outcome. The WQS is created based solely on the relationship between the mediators and the outcome, and does not take into account the potential dependencies of components of M on the exposure. As such, a formal mediation model that would yield valid inference for direct and indirect effects is not defined. Also, the method requires splitting the dataset in a training set, where weights are calculated, and a validation test, when the actual mediation model will be estimated. In addition, it is difficult to separate the contribution that these interactions provide to the indirect effect. Of interest, the score will not be an ideal summary in those situations where mixture components are expected to provide different, potentially opposite, effects on the outcome. For example, if a set of environmental factors associated with the exposure have both harmful and protective effects on the outcome, one may prefer to distinguish those types of components in more than one group. Thus, creating a single score for a multidimensional approach will represent a valuable approach if one is primarily interested in the overall contribution of a mixture and if similar contributions to the total effect can be hypothesized for all components.

3.3. Reducing the number of mediators

If it is unreasonable to assume that all mixture components might have the same behavior with respect to both exposure and outcome, classification methods can be applied to reduce dimensionality of the mixture while maintaining biologically meaningful groups. Groups can be defined a priori or by use of statistical methods, such as principal component analysis (PCA).

A priori classification

A priori classification may be used in contexts where specific components of the mixture are known to be highly correlated or behave in similar fashion. One common example is the analysis of phthalates, endocrine disruptors often grouped into high vs low molecular weight components. In this situation groups are generally summarized by calculating a summary measure for each of the subgroups (e.g. molar sum) (Braun et al., 2012).

Principal Component Analysis

Classification methods such as principal component analysis (PCA) can also be used to classify components of the mixture, thus reducing the number of mediators and overcoming limitations due to overfitting (Abdi Hervé & Williams Lynne J., 2010). PCA offers a valuable approach in the context of environmental mixtures, given the results are able to identify uncorrelated components. Starting from all components of the mixture of interest (which need to be rescaled to z-scores each with mean 0 and variance 1) in a matrix, a first score is identified as a linear combination of the mixture components, by maximizing the variance of the matrix. This scoring is done by calculating a loading factor that maximizes the variance of M, using this loading factor to assign the score t₁ that summarizes the individual values of this first subgroup. Further loading factors and score variables are then identified by maximizing the residual variance of M under the constraint of orthogonality (i.e. zero correlation) with the previous score. The choice of the number of subgroups is subjective and several selection criteria are available, depending on the goal of the study. A common criteria, among several available (Abdi and Williams, 2010), is to include a number of groups so that a substantial proportion of total variance is explained (generally around 80%, but the percentage can vary). Loading factors can be used to identify the contribution of each of the original mixture variables in the PCA score, possibly identifying biologically meaningful patterns of aggregation. For example, applications of PCA when evaluating mixtures of endocrine disruptors often identify groups that summarize exposure to chemicals with similar sources, or that share parent compounds, like metabolites of diethyl phthalate versus metabolites of non-diethyl phthalates.

Integrating subgroups in a multiple mediation model

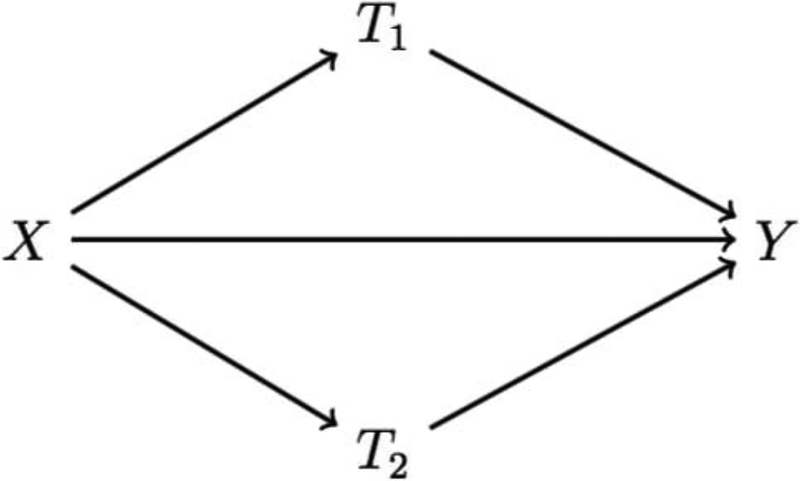
Several additional methods can be used to classify mixture components and derive subgroup-specific summary scores (Taylor et al., 2016). Let’s assume that 2 subgroups have been identified and that summary scores T₁ and T₂ (either molar sums, principal components, or others) have been estimated. Assuming the two score variables are not collinear, these can be integrated in a mediation context as presented in Figure 4:

Figure 4.

Mediation model in which components of the mediating mixture have been classified into 2 groups and summary scores for each group (T₁ and T₂) have been identified

Methods for multiple non-sequential mediators can be applied as presented in the multiple regression section, with T₁ and T₂ potential mediators of the X-Y associations, also including a possible interaction between them.

$$\begin{gathered} E[Y|X=x,T_1=t_1,T_2=t_2,Z=z]={\alpha }_0+{\alpha }_{1}x+{\alpha }_2{t}_1+{\alpha }_3{t}_2+{\alpha }_4{t}_1{t}_2+a^{\prime }z \\ E\left[T_1|X=x,Z=z\right]={\gamma }_0+{\gamma }_{1}x+{\gamma }^{\prime }z \\ E\left[T_2|X=x,Z=z\right]={\delta }_0+{\delta }_{1}x+{\delta }^{\prime }Z \\ E\left[T_1{T}_2|X=x,Z=z\right]={\eta }_0+{\eta }_{1}x+{\eta }^{\prime }z \end{gathered}$$

By combining coefficients from these models we can estimate the direct effect, DE=α₁, and the total indirect effect: IE=α₂∙ γ₁+α₃∙ δ₁+α₄∙ η₁, which is the sum of the specific contribution of T₁, T₂, and the additional combined contribution of the two mediators. By using a counterfactual approach for mediation analysis, the model can be extended to included exposure-mediator interactions (VanderWeele, 2015).

Pros and cons

Approaches presented in this subsection require the use of methods for multiple mediators as presented in the multiple regression approach. In the context of environmental mixtures, the obtained subgroups can generally be assumed to be non-sequential, thus substantially simplifying the estimation of path specific effects and the identification of the contribution of each of the subgroup (Daniel et al. 2015). If background information is available on the potential contribution of specific mixture components, chemicals that are expected to show similar behaviors can be forced to be grouped into the same category, thus overcoming one of the limitations of single mediator approaches (e.g. components with opposite expected effects could be separated). When mediators are highly correlated, a method such as PCA may be of great benefit, as it would produce orthogonal (i.e., uncorrelated) components. Classification approaches also provide a good amount of flexibility as they can be used to address different research questions. For example, methods like PCA or factor analysis may be helpful to identify and integrate in the mediation model patterns of exposures. On the other hand, when a specific hypothesis is well defined, other methods such as a priori classification may be preferred.

A major limitation of this approach is that subgroups may not have a simple interpretation. For example, a data reduction technique like PCA will combine components only based on their correlation structure, and without taking into account biological or chemical properties of the environmental factors. To simplify interpretation of results, one may prefer to use a priori defined subgroups. In addition, dimensionality reduction methods assure that only a certain proportion of the variance of the mixture is taken into account by the subgroups. Finally, one additional drawback is that deriving the specific contribution to the indirect effect of each mixture component is not straightforward. When a technique such as PCA is used, one can use the loading factors to identify individual contributions to the subgroup, but this does not directly translate into a contribution to the indirect effect due to that specific component of M. To identify component-specific indirect effects, and when a potential a priori classification into subgroups can be defined, hierarchical modeling procedures can represent a useful alternative approach (Correia & Williams, 2017; Greenland, 1993).

3.4. Hierarchical modeling

Given that it is possible to provide a plausible biological justification for identifying subgroups of the mixture, a hierarchical approach allows estimation of first-stage effects for each subgroup of environmental mixtures, as well as second-stage effects for specific mixture components. This method can handle multiple groups and the number of exposures or chemicals within each group can vary from one subgroup to the next, with no specific distributional assumptions. As an example, we may consider one subgroup to include parabens, another to include DEHP-related phthalate metabolites, and a third to include flame retardants. The approach would allow estimation of a main effect for each of these three subgroups of chemical exposures, and then individual deviations from their corresponding main effect. The assumption of this method is that the effect of each environmental factor on the outcome can be seen as the summation of the (fixed) effect of its group, and a residual effect that is specific to the individual component. If we assume, following the previous example, that 2 groups T₁ and T₂ have been identified, including respectively M₁-M₂ and M₃-M₄, the hierarchical model will estimate 2 first-stage effects for the subgroups, and 4 second-stage effects for the individual components of M. Assuming no interactions, model (4) can be modified as it follows:

$$E[Y|X=x,M\text{=}m\text{,}Z\text{=}z]={\alpha }_0+{\alpha }_{1}x+{\sum }_{j=1}^2\left({\alpha }_2+{\theta }_{M_j}{m}_j\right)+{\sum }_{j=1}^2\left({\alpha }_3+{\theta }_{M_{j+2}}{m}_{j+2}\right)+{\alpha }^{T}Z$$

From this model, α₂ and α₃ represent the first-stage effects for the groups T₁ and T₂, respectively. The 4 two-stage chemical-specific effects are estimated by α₂ + θ_M1, α₂ + θ_M2, α₃ + θ_M3, α₃ + θ_M4. Direct and indirect effects can be calculated by combining these coefficients and those from model (1) as presented in the context of mediation analysis for multilevel data (Bauer, Preacher, & Gil, 2006; Zhang, Zyphur, & Preacher, 2009).

Pros and cons

This method may offer the best option to retrieve both group- and chemical-specific effects, when data dimension makes difficult the use of multiple regression-based methods. However, mediator-mediator interactions cannot be easily incorporated, and biological assumptions to identified groups a priori are required. Moreover, implementation may also represent a challenge as random effects are easily calculated, but their standard errors are not (Correia & Williams, 2017), thus complicating the possibility of obtaining valid inference.

3.5. Two-stage approach: using a mixture method to select specific mediators

A final potential approach to evaluate mixtures of environmental factors as mediators of a given association is to proceed in a two-stage fashion by 1) focusing on the M-Y association to identify the components of the mixture with a stronger association with the outcome; and 2) develop a multiple (or even single) mediation model that only includes those environmental factors. This approach, depicted for example in Figure 5, has the main advantage that any of the several methods available for mixtures can be used, including techniques such as penalty methods (eg LASSO, elastic net) (Zou & Hastie, 2005) or regression tree (Breiman, 2017), for which a direct inclusion in regression-based mediation models would not be straightforward. Moreover, by using novel non-parametric methods such as Bayesian Kernel Machine Regression (BKMR), a flexible recently proposed approach that models the joint effect of chemicals using a kernel function, potential synergistic or antagonist effects, as well as non-linearity in the associations, could be easily identified (Bobb et al., 2014).

Figure 5.

Two-stage approach: the components of the mixture associated with the outcome are identified (M₂ and M₄ in this example) and subsequently included in the mediation model as independent mediators.

Nevertheless, a clear limitation of this approach is that mediators are selected based on the M-Y association alone. As such, components of M that have a strong association with X, but a weak association with Y, could be easily left out despite potentially providing an important contribution to the indirect effect. In addition, limitations of the specific approaches can be propagated when incorporating selected covariates in the mediation model. For example, LASSO is known to be subject to uncertain selection, and important components could be lost in the process. Also, when using BKMR, the choice of components and interactions to be included will only be based on subjective interpretation of the one-way and two-way dose-responses figures (Bobb et al., 2018). Finally, as for previous situations, subjectively choosing the components that are included in the mediation model may have an impact on the validity of estimated direct and indirect effects.

4. Final remarks

Mediation analysis is becoming an increasingly popular tool in the medical science and public health, and its application has also been growing in environmental epidemiologic studies. We examined the use of mediation analysis in environmental health studies in situations where the mediator of interest is a chemical mixture, a crucial topic in environmental health (Carlin et al., 2013). Several methods for mixture analysis have been developed over the last decades, and their advantages as compared to classical regression approaches have been presented to the environmental health community (Taylor et al., 2016). Since a joint effect of several chemicals with potential interactions is generally of greater interest than a set of independent individual effects, evaluating the contribution of environmental factors to a given X-Y association requires taking into account that mediators are components of a chemical mixture. We summarized in the Table a set of scenarios in which this conceptual model may be of interest in environmental health studies.

In this review we focused on methods for environmental mixtures currently available in the literature, describing how these can be integrated in mediation analysis to investigate mixtures of mediators. This can generally be accomplished with regression-based methods for multiple non-sequential mediators. However, this approach can easily become unstable as the number of mixture components increase. As such, classification and data reduction methods can be used to reduce the number of mediators by creating scores or possibly including uncorrelated subgroups. This second approach allows retrieving indirect effects due to the mixture or to a specific subgroup, but makes identification of component-specific effects and interactions complicated. If subgroups also present a plausible biological justification, hierarchical models can also be used to derive both group- and chemical-specific effects. Such methods provide considerable advantages when classifications are clearly identified, but including interaction terms may be challenging. Finally, one can use any potential mixture approach in a two-stage fashion, selecting relevant mediators to be included in the final model. While this approach allows for increased flexibility and the possibility of detecting antagonistic and synergistic effects, the selection is only based on one part of the mediation model.

As for the case of a standard mixture analysis, the pros and cons of the different approaches are largely due to the fact that different methods target different research questions (Hamra & Buckley, 2018). As such, the most suitable method will largely depend on the specific settings and aims of the study, and we recommend using different techniques to investigate the same research question under different perspectives (Hamra & Buckley, 2018; Stafoggia et al., 2017). The goal of this review was to present currently available approaches for environmental mixtures and discuss how and to what extent these methods can be included in a mediation model. By using methodologies that are currently available, and for which code for software implementation has been provided and made available online (Taylor et al., 2016), we provide an accessible framework for epidemiologist and environmental health researchers, who are interested in evaluating the mediation effect of chemical mixtures. At the same time, we found that in several settings (eg WQS, hierarchical modeling), the implementation of the methods into a mediation framework will easily provide point estimates for direct and indirect effects, but may be challenging in terms of deriving standard errors and obtaining valid inference, feature that is instead straightforward in classical regression-based approaches. Therefore, we recommend further methodological work for the development of statistical approaches that can incorporate environmental mixture into mediation models. Finally, we focused here on those situations where the chemical mixture is a potential mediator of a given association. It is important that future studies will investigate how to integrate methods for chemical mixtures when environmental factors are the exposures of interest, as well as complex settings in which mixtures are present both at the exposure and at the mediator level.

All approaches that we presented are mainly based on applications of multiple mediation models, and can be easily implemented in several settings and with all major statistical software (VanderWeele, 2015). We specifically focused attention to situations in which environmental factors are evaluated as mediators of the association, and implicitly assumed that these are assessed as continuous covariates. If binary mediators need to be evaluated (e.g. dichotomized biomarkers), alternative approaches for multiple mediators, such as the inverse odd ratio-weighted estimation should be sought (Nguyen et al., 2015; Tchetgen Tchetgen, 2013). In conclusion, in line with previous studies (Carlin et al., 2013; Taylor et al., 2016), we encourage researchers across the fields of environmental health to move beyond the evaluation of one environmental factor at the time. Instead, we suggests assessing the joint effects of environmental mixtures also when a mediation model is of interest. At the same time, this review shows the need of further methodological development to adequately incorporate mixtures in this context.

Highlights.

• Individuals are exposed to a mixture of environmental factors across their life.

• Several statistical approaches for evaluating environmental mixtures are available.

• The joint mixture effect should be assessed also when mediation is of interest.

• We review mixture methods and show how to integrate them in a mediation model.