Effects of Pulmonary Flow Heterogeneity on Oxygen Transport Parameters in Exercise

Abstract

Under resting normoxic conditions, the healthy lung has ample oxygen uptake capacity relative to oxygen demand, but during exercise, increased oxygen demand and utilization become increasingly dependent on ventilation-perfusion matching. A mathematical model is used to investigate the effect of pulmonary flow heterogeneity, as characterized by the coefficient of variation (CV) of capillary blood flow, on pulmonary oxygen uptake in exercise. The model reveals that any level of heterogeneity up to a CV of 3 is consistent with the observed level of arterial oxygen tension under resting conditions, but that such high levels of heterogeneity are incompatible with the levels of oxygen uptake observed during exercise. If a normal diffusing capacity is assumed, the best fit to literature data on arterial oxygen content of exercising humans under normoxic and hypoxic conditions is found with a relatively low CV of 0.48, suggesting that local flow regulation mechanisms such as hypoxic pulmonary vasoconstriction play an important role in ventilation-perfusion matching during exercise.

1. INTRODUCTION

The rate at which oxygen can be taken up into the bloodstream in the lung is a critical determinant of functional capacity, and can be affected not only by alterations in lung oxygen diffusing capacity but also by heterogeneity of pulmonary blood flow, leading to maldistribution and poor ventilation-perfusion matching. The capacity for oxygen transport of healthy individuals is higher than necessary to achieve high arterial oxygen saturation at rest under normoxic conditions, but saturation can become reduced under conditions of exercise, hypoxia, or disease either due to ventilation-perfusion $(\dot{V}/\dot{Q})$ mismatch, decreased gradients across the pulmonary-capillary membrane, or limitations in diffusing capacity.

The diffusing capacity of the lung for oxygen, a major determinant of the maximum rate of pulmonary oxygen uptake, can be defined as

$${\text{D}}_{\text{L}{O}_2}=\frac{{\dot{V}}_{O_2}}{P_A-\overline{P_b}}$$ (1)

where ${\dot{V}}_{O_2}$ is the oxygen uptake and P_A and $\overline{P_b}$ are alveolar and mean capillary ${\text{P}}_{O_2}$ We previously derived an estimate for this diffusing capacity in terms of the geometry of the pulmonary capillary and the diffusive mass transfer properties of the alveolar-capillary membrane, plasma and erythrocytes (Roy and Secomb, 2014). This value is independent of blood flows, ventilation, and oxygen tension and reflects the maximum theoretical diffusing capacity of the lung.

Heterogeneity in blood flow implies a distribution of flows through capillaries of the lung, which enter with the same venous oxygen content but leave with different values of arterial content. Vessels with higher flows may reach lower arterial saturation values than vessels with lower flows. Since vessels with higher flows are disproportionally represented in the flow- weighted average, flow heterogeneity has a significant potential to decrease the oxygen content of blood exiting the lung.

In order to quantify the effect of flow heterogeneity on pulmonary oxygen uptake, a mathematical model is utilized in this study. The model is used to estimate the degree to which increased heterogeneity in pulmonary blood flow affects values of arterial and venous oxygen levels under conditions of rest and exercise. Oxygen transport in the lung is dependent on the venous content, which is in turn affected by the systemic circulation. Likewise, the oxygen content in the systemic circulation is dependent on arterial oxygen content exiting the lung. For this reason, a combined pulmonary and systemic model is used in this study. A model for systemic oxygen consumption with Michaelis-Menten kinetics is included to account for the fact that consumption may be significantly less than oxygen demand, especially in extreme cases (e.g. high intensity exercise under hypoxic conditions). This model is used to investigate the hypothesis that high levels of heterogeneity would preclude the high oxygen uptake in the lung observed during exercise. The results are discussed in terms of the role of local active regulation of pulmonary capillary flow in reducing the heterogeneity of blood flow in the lung.

2. METHODS

A model reflecting the oxygen uptake and oxygen consuming characteristics of the human body is used to explore the hypothesis outlined above. Briefly, for given values of venous oxygen content, cardiac output and lung diffusing capacity, the model for pulmonary oxygen uptake is used to predict a value for arterial oxygen content. In simulations to test the effects of varying pulmonary flow heterogeneity, the arterial oxygen content is used as an input value for the model of systemic oxygen consumption to generate a value of venous oxygen content; this procedure is iterated to convergence to provide values of $P_a$ and $P_v$. The lung compartment, consisting of multiple identical capillary compartments with a distribution of flows, is connected with a non-perfused tissue compartment and two oxygen-consuming compartments arranged in parallel (Figure 1). The non-skeletal muscle compartment is assumed to have a fixed resting oxygen demand, whereas the skeletal muscle compartment isassigned a demand dependent on exercise intensity. Parameters used for resting conditions are selected from a range of commonly reported physiological values: cardiac output Q = 6 L min⁻¹, oxygen consumption ${\dot{V}}_{O_2}=245$ cm³ O₂ min⁻¹, arterial and venous oxygen tension $P_a=100$ and $P_v=40$ mmHg respectively, ${\text{P}}_{CO2}=40\text{mmHg}$, and respiratory quotient $R=0.8$ (Hall, 2015; Levick, 2013). Dissolved oxygen is taken into account in calculations of oxygen content and the Hill equation is used for calculations of hemoglobin oxygen saturation. In simulations to compare predicted arterial oxygen content with experimental values, venous oxygen content is set to measured values and the model for systemic oxygen consumption is not used.

Figure 1.

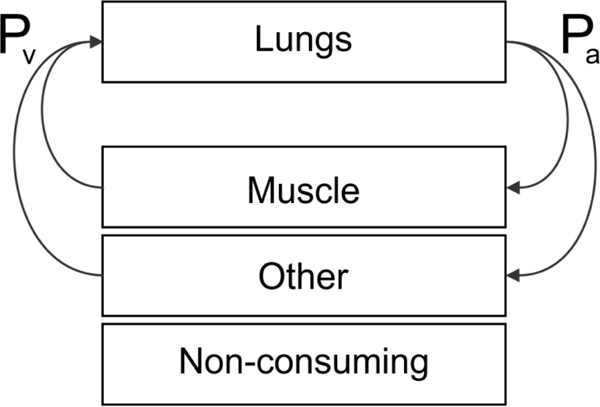
Model overview. A model for pulmonary oxygen uptake is coupled with a model for tissue oxygen utilization in which three compartments are considered: (i) a non-oxygen consuming compartment (9.2 kg); (ii) a skeletal muscle compartment (10.8 kg) with oxygen consumption dependent on exercise intensity; (iii) a non-skeletal (“other”) muscle compartment (50 kg) with oxygen consumption fixed at resting values.

2.1. Pulmonary model

To represent the heterogeneity of perfusion in pulmonary capillaries, cardiac output is non-uniformly divided among 101 otherwise identical capillary compartments arranged in parallel in accordance with a lognormal distribution of blood flow corresponding to a specified coefficient of variation. Example flow distributions are shown in Figure 2. In other studies (Beck et al., 2012; Rice et al., 1999), heterogeneity of pulmonary perfusion and ventilation have been discussed in terms of the quantity LogSD, defined as the standard deviation of the logarithm (base 10) of the quantity in question. The relationship between CV and LogSD is shown in the inset to Figure 2.

Figure 2.

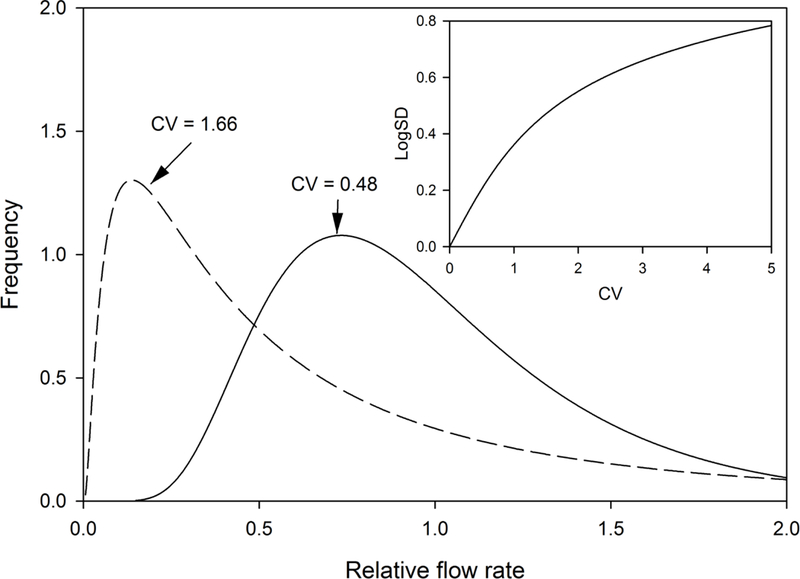
Examples of lognormal flow distributions. A CV of 1.66 corresponds to a LogSD of 0.5. The inset shows the relationship between CV and LogSD.

All capillaries are assumed to have an identical diffusing capacity, corresponding to a total pulmonary diffusing capacity ${\text{D}}_{\text{L}{O}_2}=102{\text{cm}}^3{\text{O}}^2{\text{min}}^{\mathrm{-1}}{\text{mmHg}}^{\mathrm{-1}}$ as calculated previously (Roy and Secomb, 2014). Oxygen loading in the lung is simulated by assuming that the entire cardiac output Q passes through parallel compartments of length L_cap with total length L_tot (Wagner, 1996). In each capillary i, the flow is (Q_cap)_i, and conservation of mass gives:

$${\left(Q_{cap}\right)}_i{C}_0\frac{dS\left(P_b\right)}{dx}=\frac{{\text{D}}_{\text{L}{O}_2}}{L_{tot}}\left(P_A-P_b\right)$$ (2)

where x is position along the capillary $(0\le x\le L_{cap})$ and P_b represents the blood ${\text{P}}_{O_2}$ as a function of x. The oxygen carrying capacity of whole blood $C_0=C_{Hb}\times H_D$ is assumed to be proportional to the hematocrit H_D (see Table 1) and is approximately 0.2 cm³ O₂ (cm³ blood)⁻¹ under normal conditions. Alveolar ${\text{P}}_{O_2}(P_A)$ is computed as a function of the ambient partial pressure of oxygen, reported values of the respiratory quotient R, and alveolar ${\text{P}}_{{C\mathrm{O}}_2}$ (assumed to be the same as arterial ${\text{P}}_{{CO}_2}$ from the alveolar gas equation (Story, 1996). Values of P_A thus range from 99.7 mmHg under normoxic conditions to 57.0 and 35.6 mmHg at 15% and 12% oxygen respectively. The average flow in each capillary $\overline{Q_{cap}}$ is equal to $Q/N_{cap}$. Setting $t=x/L_{cap}$ and using the fact that $L_{tot}/L_{cap}=Q/\overline{Q_{cap}}=N_{cap}$ (the total number of capillaries), we obtain:

$$\frac{d{P}_b}{dt}=\frac{\overline{Q_{cap}}}{{\left(Q_{cap}\right)}_i}\frac{D_{\text{L}{O}_2}\left(P_A-P_b\right)}{Q{C}_0{S}^{\prime }\left(P_b\right)}$$ (3)

independent of the number and length of pulmonary capillaries, where $S\text{'}(P_b)$ represents the slope of the oxyhemoglobin dissociation curve at $P_b$. This equation is integrated from $t=0$ to $t=1$, with $P_b\left(0\right)\text{=}{P}_v$ to obtain $P_a\text{=}{P}_b(1)$. The flow-weighted average of the oxygen content from each capillary compartment is used to calculate the arterial saturation, which is then used as the input to the systemic model.

Table 1.

Parameter values.

Parameter	Value	Units	Reference
P50	26.3	mmHg	(Hsia, 1998)
n	2.7	-	(Hsia, 1998)
CHb	1.39	cm3 O2/g	(McGuire and Secomb, 2001)
HD	14.39	g/dL	(McGuire and Secomb, 2001)
Sh	2.5	-	(Heliums et al., 1996)
Kpl	8.3 × 10−10	(cm2 s−1)(cm3 O2 cm−3 mmHg−1)	(Heliums et al., 1996)
DLO2	102	cm3 O2 min−1 mmHg−1	(Roy and Secomb, 2014)
P0	10.5	mmHg	(Golub and Pittman, 2012)
rc	2.5	μm	(Roy and Secomb, 2014)
NA(c,f)skel	1288	mm−2	[Calculated]
NA(c,f)nonskel	308	mm−2	(Pasarica et al., 2009)
Kt	9.4 × 10−10	(cm2 s−1)(cm3 O2 cm−3 mmHg−1)	(Bentley et al., 1993)
Dt	2.41 × 10−5	cm2 s−1	(Bentley et al., 1993)
αt	3.89 × 10−5	cm3 O2 cm−3 mmHg−1	(Bentley et al., 1993)
CMb	3.83 × 10−7	mol cm−3	(Meng et al., 1993)
DMb	1.73 × 10−7	cm2 s−1	(Jurgens et al., 1994)

2.2. Systemic model

In the systemic model, cardiac output is divided between two compartments (Figure 1). For a body mass of 70 kg, the non-skeletal muscle (“other”) compartment is assigned a mass of 50 kg and the muscle compartment is assigned a mass of 10.8 kg. For each compartment, the oxygen uptake characteristics are predicted using a Krogh cylinder model with geometrical parameters appropriate to each compartment (Table 1). In this model, blood flows through a capillary surrounded by a cylindrical tissue region with radius dependent on capillary density. Blood enters with a specified P_a and the oxygen level falls along the capillary as oxygen is consumed in each slice of the cylinder. Intracapillary resistance is characterized by the Sherwood number Sh, assumed to be 2.5 in this study (see Table 1). Michaelis-Menten oxygen kinetics are used to calculate the oxygen consumption based on the assigned oxygen demand in each compartment, resulting in radial gradients of oxygen in the tissue cylinder. This assumption means that local oxygen consumption is less than oxygen demand. In cases when the consumption is prescribed according to observed values, the value of oxygen demand is not known a priori, but must be calculated to correspond to the prescribed consumption. The P₅₀ of blood is assumed to remain constant along the length of the capillary. The oxygen demand of the non-skeletal compartment is fixed at its rest value, whereas the demand of the skeletal muscle compartment is varied with exercise intensity. Facilitated diffusion by myoglobin is taken into account in the tissue compartment (McGuire and Secomb, 2001). As noted above, the actual consumption in the muscle compartment may fall significantly below the level of demand under hypoxic conditions. Since the oxygen demand of each compartment is not known a priori, the following procedure is utilized to calculate the parameters appropriate for each case (rest, moderate, and maximal exercise): (i) The blood flow and oxygen consumption of the non- skeletal compartment are calculated under resting conditions based on its mass fraction. (ii) The oxygen demand for the non-skeletal compartment is calculated to be consistent with its consumption obtained from the calculation above assuming a value for its capillary density (see Table 1). (iii) An oxygen demand of 80 cm³ O₂ cm⁻³ min⁻¹ (corresponding to conditions of ${\dot{V}}_{O_2\max }$) is used to calculate a value for the capillary density of the skeletal muscle compartment (McGuire and Secomb, 2003). (iv) The blood flow and oxygen consumption for the skeletal muscle compartment are calculated for each case (rest, moderate, and maximal exercise) by subtracting the resting non-skeletal compartment blood flow and oxygen consumption values obtained in (i) from the measured values in each case. The demand for the skeletal muscle compartment is then calculated based on this value of the consumption in conjunction with the capillary density calculated in (iii).

Once these parameters for the systemic model have been derived, they are used to explore the effect of pulmonary perfusion heterogeneity in the combined model. The flow- weighted oxygen content from both compartments is used as the mixed venous input to the pulmonary circulation. The simulation of pulmonary and systemic oxygen transport is repeated iteratively until convergence of $P_a$ and is $P_{\overline{v}}$ achieved.

3. RESULTS

The model was initially used to investigate the impact of CV on arterial ${\text{P}}_{O_2}$ and saturation (Figure 3). Under resting conditions, the CV was found to have little effect on calculated arterial ${\text{P}}_{{\mathrm{O}}_2}$ values, which are seen to be consistent with typical observed levels of approximately 90 to 100 mmHg (Rice et al., 1999) for CV values from zero up to approximately 3. In this range of ${\text{P}}_{O_2}$, arterial saturation is close to 1 and shows only slight changes with varying CV. Due to this low sensitivity, the actual perfusion heterogeneity under resting conditions cannot be reliably estimated from comparisons of predicted and observed arterial oxygen content.

Figure 3.

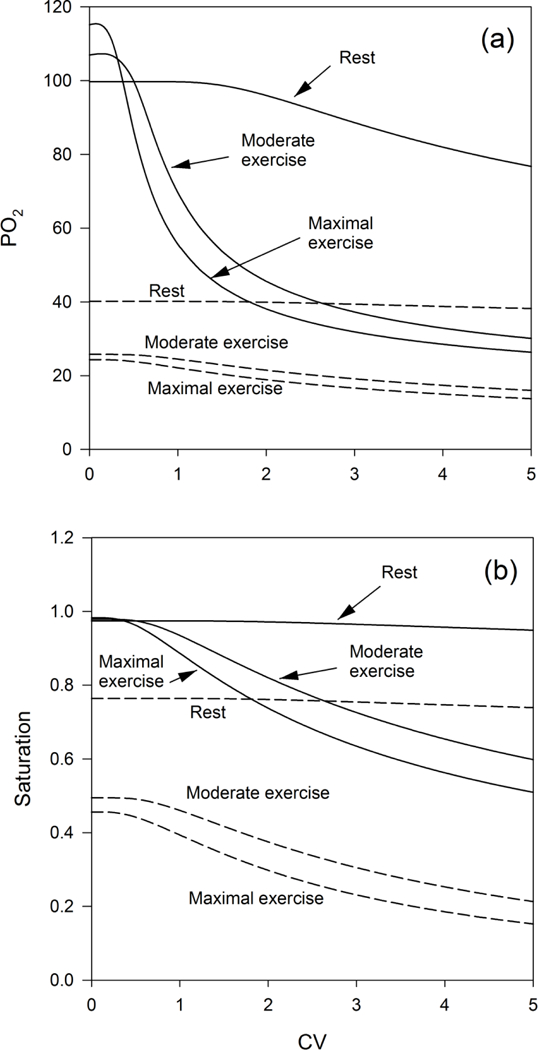
(a) Calculated values of arterial ${\text{P}}_{O_2}$ (solid lines) and venous ${\text{P}}_{O_2}$ (dashed lines) for simulated conditions of rest, moderate, and maximal exercise as a function of the CV of pulmonary blood flow. (b) Calculated values of arterial saturation (solid lines) and venous saturation (dashed lines) for conditions of rest, moderate, and heavy exercise as a function of the CV of pulmonary blood flow. The results imply that in exercise, the CV has to be in the range of 0.5 to 1 to maintain adequate tissue oxygen supply and to support the observed arteriovenous saturation differences.

Under conditions of moderate or heavy exercise, the predicted arterial and venous ${\text{P}}_{O_2}$ values for values of CV exceeding 1 are not consistent with reported values. In experiments under normoxic conditions, the observed arterial ${\text{P}}_{O_2}$ remains above 90 mmHg, with venous values in the range of 20–30 mmHg (Roca et al., 1989). Although the predicted venous values are similar, the predicted arterial ${\text{P}}_{O_2}$ drops dramatically at values of CV greater than 1, suggesting that a degree of heterogeneity above this would lead to an inability to maintain arterial ${\text{P}}_{O_2}$ and to sustain the observed levels of oxygen demand. The corresponding panel illustrating the drop in arterial and venous saturation demonstrates that the arteriovenous decrease in oxygen content declines substantially over the range of CV investigated in the cases of moderate exercise (from 0.48 to 0.39) and maximal exercise (from 0.53 to 0.36). These changes are directly proportional to the predicted declines in systemic oxygen consumption resulting from increasing CV of pulmonary capillary blood flow. The results imply that flow regulation in the lung plays a major role in maintaining oxygen consumption relative to demand. In order to obtain a specific estimate of CV in exercise, aggregated data from five experimental studies were used to estimate the CV that yielded the best fit to observations of arterial saturation in exercise under conditions of normoxia and hypoxia. All five studies used cycle ergometry and included measurements of arterial and mixed or femoral venous ${\text{P}}_{O_2}$ at a range of work rates. In each case, measured values of FiO2, cardiac output, oxygen consumption and respiratory quotient were used. Observed venous ${\text{P}}_v$ were used and the pulmonary model was used to predict corresponding arterial ${\text{P}}_{O_2}$ and saturation values. The predicted values of ${\text{P}}_a$ were compared to the observed values by regression through the origin on values of ${(1-S_a)}_{\text{calc}}\text{vs}.{(1-S_a)}_{\text{meas}}$. When a value of CV = 0 was used, the slope was found to differ substantially from the line of identity (Figure 4A). The difference in slope from 1 was used as a basis to adjust CV until convergence to a slope of 1 was achieved. With the assumption of a normal diffusing capacity, the best fit overall to aggregated data from five studies was found with a CV of 0.48 (Figure 4B), corresponding to a LogSD of 0.2, lower than the values of 0.3 to 0.6 reported at rest (Beck et al., 2012) and the values of 0.33 to 0.64 reported in young healthy subjects (Wagner et al., 1974).

Figure 4.

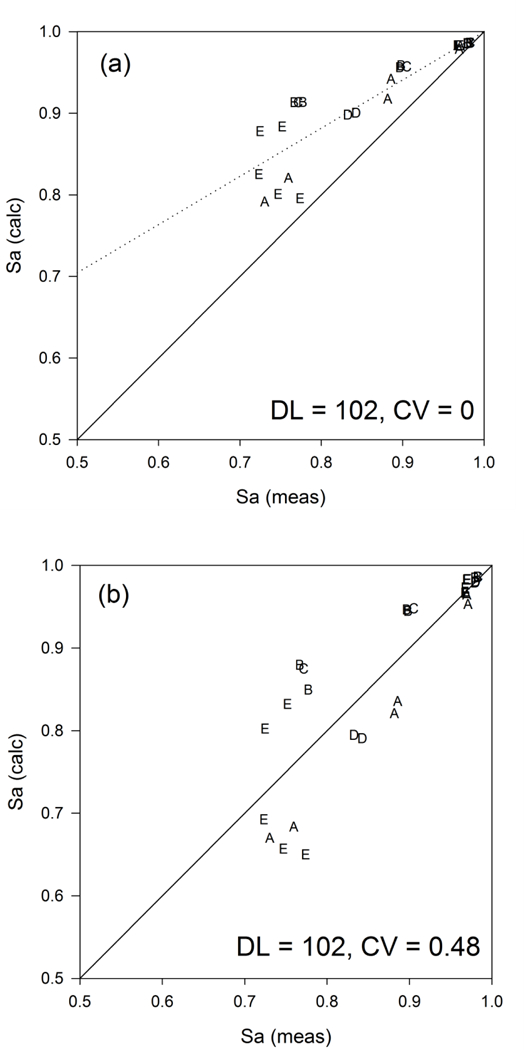
Calculated vs. reported values of arterial oxygen saturation based on data obtained under conditions of exercise and hypoxia from a number of studies based on D_LO2 = 102 cm³ O₂ min⁻¹ mmHg⁻¹. Regression lines (dashed) shown compared to lines of identity. (a) CV = 0; (b) CV = 0.48. Letters corresponding to references: A (Roca et al., 1989); B (Roca et al., 1992); C (Cardus et al., 1998); D (Schaffartzik et al., 1993); E (Knight et al., 1992).

4. DISCUSSION

Heterogeneity is inherent in microcirculation of all tissues, including systemic and pulmonary (Duling and Damon, 1987; Pries et al., 2009; Pries et al., 1995; Rice et al., 1999). In the lung, heterogeneity of ventilation also exists (Beck et al., 2012; West, 1969). It has long been understood that heterogeneity in $\dot{V}/\dot{Q}$ matching can impair oxygen uptake in the lung (Wagner, 1992; West, 1969). Many theoretical studies of pulmonary oxygen transport consider a single homogeneous oxygen exchanging compartment or a small number of homogeneous compartments or zones. However, the relationship between heterogeneity and oxygen transport characteristics is not fully understood. There is a lack of quantitative information on the effects of heterogeneity at the microvascular level on overall oxygen transport characteristics of the lung, both at rest and under conditions of physiologic stress. In a study of the contributions of perfusion and ventilation heterogeneity in $\dot{V}/\dot{Q}$ matching (Wilson and Beck, 1992), it was found that inhomogeneities in flow contribute approximately two-thirds and inhomogeneities in ventilation contribute approximately one-third of the variance to the heterogeneity of the $\dot{V}/\dot{Q}$ distribution.

The model developed herein for exploring the effect of perfusion heterogeneity in the lung involves several simplifying assumptions. In reality, both ventilation and perfusion exhibit heterogeneity, but in the model the heterogeneity is attributed to perfusion and alveolar ${\text{P}}_{O_2}$ is assumed to be uniform within the lung. The results obtained here may approximately represent the behavior in the presence of heterogeneous ventilation, if the CV in the present model is interpreted as representing the distribution of deviations of capillary blood flows from ideal matching with alveolar ventilation. The model for systemic oxygen transport uses a Krogh cylinder model for both the muscle and non-muscle compartments, and does not include the effects of heterogeneity in systemic blood flow.

Our results show a striking difference between rest and exercise with regard to the effects of heterogeneity. In contrast to the minimal effect of pulmonary flow heterogeneity at rest, in exercise the degree of flow heterogeneity must be much lower in order to maintain oxygen uptake and tissue oxygenation. At rest, the levels of oxygen uptake required to maintain observed values of arterial ${\text{P}}_{O_2}$ are consistent with values of CV of approximately 3, whereas in exercise we find that the CV needs to be below 1 with a value of 0.48 estimated from experimental data. This is consistent with measurements of the perfusion distribution width obtained by open-circuit wash-in during rest and exercise in humans (Beck et al., 2012; Wilson and Beck, 1992), in which the LogSD of the perfusion is noted to fall from a value of 0.47 at rest to approximately 0.33 during heavy exercise, corresponding to values of CV of approximately 1.5 at rest and 0.9 during heavy exercise.

The implication of these results is that for sufficient uptake in exercise, relatively tight regulation of blood flow is needed, whereas at rest a high degree of heterogeneity can be tolerated. Hypoxic vasoconstriction is an important mechanism for local regulation of pulmonary blood flow. For vessels with high flows, leading to inadequate blood oxygenation, the effect of hypoxic vasoconstriction (HPV) is to reduce flow in these vessels, thereby increasing the saturation of the exiting blood. In this way, HPV reduces the heterogeneity in $\dot{V}/\dot{Q}$ matching. At rest, high saturations are achieved in virtually all capillaries despite heterogeneity, so this mechanism is not activated. However, HPV has been shown to be active at the low levels of venous oxygen tension seen in exercise and hypoxia (Sylvester et al., 2012). Our results suggest that intact HPV is necessary to achieve moderate or maximal exercise.

Highlights.

• A theoretical model is used to investigate effects of pulmonary flow heterogeneity

• The normal lung can tolerate a high degree of pulmonary flow heterogeneity at rest

• Pulmonary flow heterogeneity decreases arterial oxygen saturation during exercise

• Observed arterial oxygen levels in exercise imply limits on flow heterogeneity

• Flow regulation must mitigate ventilation-perfusion mismatch during exercise