Abstract
Next generation sequencing (NGS) technologies have led to a ubiquity of molecular sequence data. This data avalanche is particularly challenging in metagenetics, which focuses on taxonomic identification of sequences obtained from diverse microbial environments. Phylogenetic placement methods determine how these sequences fit into an evolutionary context. Previous implementations of phylogenetic placement algorithms, such as the evolutionary placement algorithm (EPA) included in RAxML, or PPLACER, are being increasingly used for this purpose. However, due to the steady progress in NGS technologies, the current implementations face substantial scalability limitations. Herein, we present EPA-NG, a complete reimplementation of the EPA that is substantially faster, offers a distributed memory parallelization, and integrates concepts from both, RAxML-EPA and PPLACER. EPA-NG can be executed on standard shared memory, as well as on distributed memory systems (e.g., computing clusters). To demonstrate the scalability of EPA-NG, we placed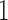 
billion metagenetic reads from the Tara Oceans Project onto a reference tree with 3748 taxa in just under 
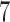h, using 2048 cores. Our performance assessment shows that EPA-NG outperforms RAxML-EPA and PPLACER by up to a factor of 
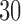in sequential execution mode, while attaining comparable parallel efficiency on shared memory systems. We further show that the distributed memory parallelization of EPA-NG scales well up to 2048 cores. EPA-NG is available under the AGPLv3 license: https://github.com/Pbdas/epa-ng.
Keywords: Metabarcoding, metagenomics, microbiome, phylogenetics, phylogenetic placement
In the last decade, advances in genetic sequencing technologies have drastically reduced the price for decoding DNA and dramatically increased the amount of available DNA data. The Tara Oceans Project (Sunagawa et al. 2015), for example, has generated hundreds of billions of environmental sequences. Moreover, sequencing costs are decreasing at a significantly higher rate than computers are becoming faster according to Moore’s law. Therefore, state-of-the art bioinformatics software is facing a grand scalability challenge.
A common metagenetic data analysis step is to infer the microbiological composition of a given sample. This can be done, for instance, by determining the best hit for each query sequence (QS) in a database of reference sequences (RSs), using sequence similarity measures, and by subsequently assigning the taxonomic label of the chosen RS to the QS. However, approaches based on sequence similarity do not use or provide phylogenetic information about the QS. This can decrease identification accuracy (Koski and Golding 2001), especially when the QSs are only distantly related to the RSs, for example, when more closely related QS are simply not available.
Phylogenetic placement algorithms alleviate this problem by placing a QS onto a reference tree (RT) inferred on a given set of RSs. This allows for identifying QSs by taking the evolutionary history of the sequences into account. Maximum likelihood-based phylogenetic placement algorithms have previously been implemented by Matsen et al. (2010) (PPLACER) and Berger et al. (2011) (RAxML-EPA). These tools have been successfully employed in a number of studies, for instance, to correlate bacterial composition with disease status (Srinivasan et al. 2012) as well as in diversity studies (Findley et al. 2013; Sunagawa et al. 2013). More recently, we used phylogenetic placements to study protist diversity in rainforest soils (Mahé et al. 2017). In this study, we experienced significant throughput and scalability limitations with PPLACER and RAxML-EPA. To address them, we re-implemented and parallelized RAxML-EPA from scratch using libpll-2 (Flouri et al. 2017), a state-of-the-art library for phylogenetic likelihood computations.
Materials and Methods
The general algorithm for phylogenetic placement as implemented in EPA-NG, which we call the placement procedure, is described in the original article by Berger et al. (2011). Our Supplementary Text available on Dryad at https://doi.org/10.5061/dryad.kb505nc also contains a description of the general algorithm.
Like other phylogenetic placement software, EPA-NG operates in two phases: it first quickly determines a set of promising candidate branches for each QS (preplacement), and subsequently evaluates the maximum placement likelihood of the QS into this set of candidate branches more thoroughly via numerical optimization routines (thorough placement). The user can choose to treat every branch of the tree as a candidate branch, however, this induces a significantly higher computational cost. Consequently, by default, EPA-NG dynamically selects a small subset of the available branches via preplacement. Using preplacement heuristics typically reduces the number of thoroughly evaluated branches from thousands (depending on the RT size) to often less than ten (depending on the query and reference data).
EPA-NG also offers a second heuristic called masking that is similar to the premasking feature in PPLACER. It effectively strips the input multiple sequence alignments (MSAs) of all sites that are unlikely to contribute substantially to the placement likelihood score. Such sites consist entirely of gaps either in the reference or in the query alignment. Additionally, for each individual QS, only the core part of the alignment is used to compute the likelihood of a placement. The core of an aligned QS is the sequence with all leading, and trailing gaps discarded. Note that PPLACER also discards all gap sites within an individual sequence, including gaps in the core. We opted not to implement this, as our experiments showed that computing these per-site likelihoods, rather than omitting the computations, was more efficient in our implementation.
Parallelization
EPA-NG offers two levels of parallelism: MPI to split the overall work between the available compute nodes, and OpenMP to parallelize computations within the compute nodes. Such hybrid parallelization approaches typically reduce MPI related overheads and yield improved data locality (Rabenseifner et al. 2009).
In hybrid mode, EPA-NG splits the input QS into parts of equal size, such that each MPI-Rank has an equal number of QS to place on the tree. No synchronization is required to achieve this, as each rank computes which part of the data it should process from its rank number and the overall input size. An illustration of this scheme can be found in the Supplementary Text available on Dryad.
For within-node parallelization, we use OpenMP. Here, each thread works on a subset of QS and branches.
Evaluation
We used three empirical data sets to evaluate and verify EPA-NG, the neotrop data set (Mahé et al. 2017), the bv data set (Srinivasan et al. 2012), and the tara data set (Sunagawa et al. 2015). We compared EPA-NG against PPLACER and RAxML-EPA under different settings: with/without masking (not implemented in RAxML-EPA), with/without preplacement. Details on the command line parameters for these distinct settings, as well as full descriptions of the data sets, are provided in the Supplementary Text available on Dryad. In the Supplementary Text available on Dryad, we compare the single-node parallel performance parallel efficiency (PE) of the tested programs and also provide a sequential runtime comparison.
Verification
In Berger et al. (2011) and Matsen et al. (2010), the authors verify the placement accuracy of their algorithms via simulation studies and leave-one-out tests on empirical data. As there already exist two highly similar and well-tested evolutionary placement tools, we compare the results of EPA-NG to the RAxML-EPA and PPLACER results via the phylogenetic Kantorovich–Rubinstein (PKR) metric (Evans and Matsen 2012) to verify that our implementation works correctly.
The PKR is analogous to the earth-movers distance for calculating the distance between two distributions. The earth-movers distance is the minimum amount of work required to transform one distribution into the other, that is, mass transported times the distance over which it needs to be carried.
The result of a QS placement is a set of placement branches on the RT, each with an associated likelihood weight ratio (LWR) (Berger et al. 2011). In the PKR method, these LWRs are interpreted as a distribution over the RT. The PKR distance is then simply the minimum amount of work required to transform one placement distribution into the other by moving the LWR mass along the branches of the RT.
We computed the pairwise median PKR-distance between the three programs PPLACER, RAxML-EPA, and EPA-NG, for three distinct data sets in two different modes. Both, the bv and tara data sets were used as described in the Supplementary Text available on Dryad, with 15,060 and 10,000 QS, respectively. For the neotrop data set, we sub-sampled 10,000 QS to roughly match the other two data set sizes. Sub-sampling allowed us to directly compare the runtimes of the different modes, as the non-heuristic settings can increase the runtime by up to three orders of magnitude.
Two different modes were tested: the thorough setting with all heuristics disabled and the preplacement setting with heuristics enabled, but premasking disabled for better comparability with RAxML-EPA which does not implement premasking.
The results are shown in Table 1. They include a measure denoted by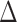 
that summarizes the PKR-values for a given data set and mode. 
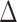is the ratio by which the distance between RAxML-EPA and PPLACER is greater than the average distance between EPA-NG to either of them. In other words, 
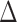quantifies the proximity of our results to those of RAxML-EPA and PPLACER. We observe an average 
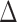-value of 
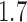for the preplacement mode, and of 
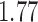for the thorough mode. This means, that under comparable settings, EPA-NG produces results that are on average 70–77% closer to RAxML-EPA and PPLACER, than RAxML-EPA and PPLACER are to each other. Overall, the absolute PKR values are very small. Thus, we are confident that our implementation is correct and yields qualitatively and quantitatively highly similar results to existing placement tools.
Table 1.
Median PKR-distances between placement implementations.
| Mode | Data | EPA-ng to RAxML | EPA-ng to pplacer | RAxML topplacer |
|
|---|---|---|---|---|---|
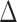
| preplacement | neotrop | 0.162 | 0.045 | 0.115 | 1.11 |
| bv | 0.009 | < 0.001 | 0.010 | 2.11 | |
| tara | 0.064 | 0.013 | 0.072 | 1.87 | |
| thorough | neotrop | 0.113 | 0.024 | 0.108 | 1.57 |
| bv | 0.010 | 0.002 | 0.011 | 1.83 | |
| tara | 0.060 | 0.013 | 0.070 | 1.92 |
The ratio by which the distance between the two older implementations RAxML-EPA and PPLACER is greater than the average distance between either of them to EPA-NG is denoted by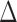 
.
Sequential Performance
We assessed the speed of EPA-NG, RAxML-EPA, and PPLACER, under a combination of settings including or excluding preplacement and premasking heuristics. When placing 50,000 sequences from the neotrop data set, we observe a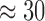 
-fold performance improvement for EPA-NG over PPLACER when both heuristics are enabled. This corresponds to an absolute sequential runtime of 207s for EPA-NG compared with 5775s for PPLACER. Note that aligning the queries to the reference MSA for this data set required 
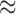30,000s using PaPaRa (Berger and Stamatakis 2011) in sequential mode. This shows that QS alignment currently constitutes the major performance bottleneck in placement analyses. More details are available in the Supplementary Text available on Dryad.
Parallel Performance
We tested the scalability of EPA-NG under three configurations. First, with preplacement and masking heuristics disabled (thorough test). Secondly, with only the preplacement heuristic enabled. Lastly, we tested masking in conjunction with preplacement. This corresponds to the default settings (default test).
As runs under these configurations exhibit large absolute runtime differences, we used three distinct input sizes (number of QS) for each of them. The smallest input size for each configuration was selected, such that a respective sequential run terminates within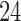 
h. We chose subsequent sizes to be 
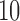and 
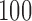times, larger, representing medium and large input sizes for each configuration. All scalability tests were based on a set of one million (
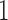M) aligned QSs from the neotrop data set. To obtain the desired input sizes, we either sub-sampled (10k, 100k) or replicated (10M, 100M, 1B) the original set of 1M sequences. We assess parallel performance via the parallel efficiency measure. We compute the efficiency 
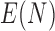as
 |
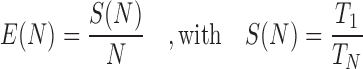(1) |
where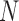 
is the number of cores used, 
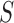is the parallel speedup, 
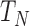is the execution time of the program using 
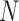cores, and 
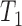is the fastest sequential execution time.
As the parallel speedup and the PE are calculated based on the fastest sequential execution time, we performed a separate run using the sequential version of EPA-NG (see Section Sequential Performance). For each configuration, we performed a sequential run for the small input volume. As the larger input volumes could not be analyzed sequentially within reasonable times, we multiplied the sequential runtime by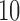 
and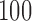 
, for the medium and large input sizes, respectively.
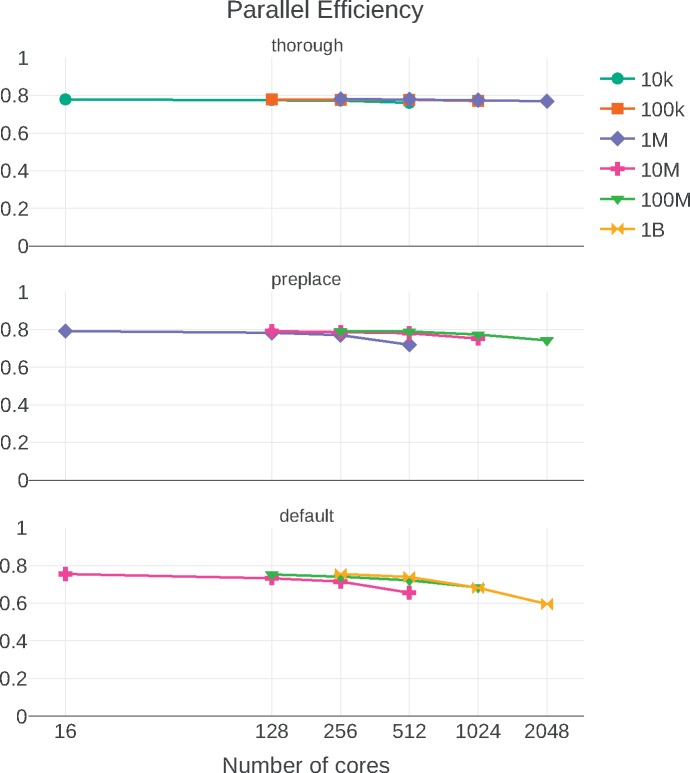
The results are displayed in Figure 1. We observe that the thorough test preserves the single-node efficiency (16 cores,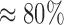 
PE) consistently for all core counts and input data sizes. The preplace test behaves similarly, but PE tends to decrease with increasing core count. This is because the response times are becoming so short, that overheads (e.g., MPI initialization and some pre-computations) start dominating the overall runtime according to Amdahl’s law. This is most pronounced for the 1M QS / 512 cores data point, where PE noticeably declines. The response time in this case was only 83 s, compared with 30,542 s of the corresponding sequential run.
Figure 1.
Weak scaling parallel efficiency plot of EPA-NG on a medium-sized cluster. Input files with sizes ranging from ten thousand (10K) to one billion (1B) query sequences. Three different configurations are shown: thorough, meaning no preplacement of masking heuristic was employed, preplace where only the preplacement heuristic was used, and default where both masking and preplacement were employed.
These effects become even more prominent in the default run, which shows a PE of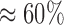 
on 2048 cores. This is primarily due to the increased processing speed when using masking that accelerates preplacement by an additional factor of 
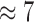. As a consequence, operations such as I/O, MPI startup costs, or data pre-processing functions have a more pronounced impact on PE.
Real-World Showcase
We performed two tests to showcase the improved throughput of EPA-NG and to demonstrate how this enables larger analyses in less time.
Placing One Billion Metagenomic Tara Ocean Sequences
We performed phylogenetic placement of one billion metagenomic fragments (pre-filtered to the 16S rDNA region) against a 3748 taxa RT. Using 2048 cores (128 compute nodes), we were able to complete this analysis in under 7 h.
Extrapolating Total Reduction in Analysis Time of the Neotropical Soils Study
We used a representative sample of the neotrop data from Mahé et al. (2017) to obtain runtimes for both, EPA-NG and RAxML-EPA, using the same settings as in the original study. With this runtime data, we extrapolated the total placement time of the study for both programs. We find that EPA-NG would have required less than half the overall CPU time (RAxML-EPA: 2173 core days, EPA-NG: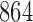 
core days) under the same heuristic settings (no heuristics). Further, using EPA-NG’s novel heuristics, the placement could have been completed in 
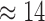core hours (roughly a 3700-fold runtime reduction).
Our distributed parallelization also improves usability. That is, the user does not have to manually split up the query data (i.e., split the data into smaller chunks which can complete within say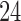 
h on a single node) for circumventing common cluster wall time limitations.
Conclusions and Future Work
In this work, we presented EPA-NG, a highly scalable tool for phylogenetic placement. We showed that it is up to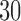 
times faster than PPLACER and RAxML-EPA when executed sequentially, while yielding qualitatively highly similar results. Moreover, EPA-NG is the first phylogenetic placement implementation that can parallelize over multiple compute nodes of a cluster, enabling analysis of extremely large data sets, while achieving high PE and short response times. Our showcase test was executed on 2048 cores, and placed 
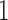billion metagenomic query sequences (QSs) from the Tara Oceans project, on a RT with 3748 taxa, requiring a total runtime of under 
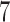h.
We plan to more tightly integrate EPA-NG with upstream and downstream analysis tools, such as programs for aligning the QS against a reference MSA (Berger and Stamatakis 2011), respective placement post-analysis tools (Matsen et al. 2010; Czech and Stamatakis 2017), and methods using the EPA such as SATIVA (Kozlov et al. 2016). In addition, we plan to explore novel approaches for handling increasingly large RTs, such as, for instance, trees comprising all known bacteria.
Acknowledgments
The authors would like to thank Frederick A. Matsen IV for his advice and valuable input, and for hosting Pierre Barbera for a one month period in early 2016 in his lab at the Fred Hutchinson Cancer Research Center in Seattle, USA. We further would like to thank Micah Dunthorn and Frédéric Mahé for supplying the Neotrop data set, Colomban de Vargas and Laura Rubinat-Ripoll for helping with the Tara Oceans data set and supplying a suitable reference tree, and Sujatha Sunagawa for making the BV data set publicly available.
Supplementary Material
Data available from the Dryad Digital Repository: http://dx.doi.org/10.5061/dryad.kb505nc.
Funding
This work was financially supported by the Klaus Tschira Stiftung gGmbH in Heidelberg, Germany.
References
- Berger S.A., Krompass D., Stamatakis A.. 2011. Performance, accuracy, and web server for evolutionary placement of short sequence reads under maximum likelihood. Syst. Biol. 60:291–302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berger S.A., Stamatakis A.. 2011. Aligning short reads to reference alignments and trees. Bioinformatics 27:2068–2075. [DOI] [PubMed] [Google Scholar]
- Czech L. and Stamatakis A.. 2017. genesis—A toolkit for working with phylogenetic data. http://genesis-lib.org. [Google Scholar]
- Evans S.N., Matsen F.A.. 2012. The phylogenetic Kantorovich-Rubinstein metric for environmental sequence samples. J. R. Stat. Soc. Series B Stat. Methodol. 74:569–592. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Findley K., Oh J., Yang J., Conlan S., Deming C., Meyer J.A., Schoenfeld D., Nomicos E., Park M., NIH Intramural Sequencing Center Comparative Sequencing Program, Kong H.H., Segre J.A.. 2013. Topographic diversity of fungal and bacterial communities in human skin. Nature 498:367–370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Flouri T., Darriba D., Kozlov A., Holder M.T., Morel B., Stamatakis A.. 2017. libpll—The phylogenetic likelihood library. https://github.com/xflouris/libpll-2. [Google Scholar]
- Koski L.B., Golding G.B.. 2001. The Closest BLAST Hit Is Often Not the Nearest Neighbor. J. Mol. Evol. 52:540–542. [DOI] [PubMed] [Google Scholar]
- Kozlov A.M., Zhang J., Yilmaz P., Glöckner F.O., Stamatakis A.. 2016. Phylogeny-aware identification and correction of taxonomically mislabeled sequences. Nucleic Acids Res. 44:5022–5033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mahé F., de Vargas C., Bass D., Czech L., Stamatakis A., Lara E., Singer D., Mayor J., Bunge J., Sernaker S., Siemensmeyer T., Trautmann I., Romac S., Berney C., Kozlov A., Mitchell E.A.D., Seppey C.V.W., Egge E., Lentendu G., Wirth R., Trueba G., Dunthorn M.. 2017. Parasites dominate hyperdiverse soil protist communities in Neotropical rainforests. Nat. Ecol. Evol. 1:91. [DOI] [PubMed] [Google Scholar]
- Matsen F.A., Kodner R.B., Armbrust V.E.. 2010. pplacer: linear time maximum-likelihood and Bayesian phylogenetic placement of sequences onto a fixed reference tree. BMC Bioinformatics 11:1–16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rabenseifner R., Hager G., Jost G.. 2009. Hybrid MPI/OpenMP parallel programming on clusters of multi-core SMP nodes. In: Baz D.E.,, Spies F.,, Gross T., editors. 200917th Euromicro International Conference on Parallel, Distributed and Network-based Processing. Weimar, Germany: Computer Society Press; p. 427–436. [Google Scholar]
- Srinivasan S.,, Hoffman N.G.,, Morgan M.T.,, Matsen F.A.,, Fiedler T.L.,, Hall R.W.,, Ross F.J.,, McCoy C.O.,, Bumgarner R.,, Marrazzo J.M.,, Fredricks D.N. 2012. Bacterial communities in women with bacterial vaginosis: high resolution phylogenetic analyses reveal relationships of microbiota to clinical criteria. PLoS One 7:1–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sunagawa S.,, Coelho L.P.,, Chaffron S.,, Kultima J.R.,, Labadie K.,, Salazar G.,, Djahanschiri B.,, Zeller G.,, Mende D.R.,, Alberti A.,, Cornejo-castillo F.M.,, Costea P.I.,, Cruaud C.,, Ovidio F.,, Engelen S.,, Ferrera I.,, Gasol J.M.,, Guidi L.,, Hildebrand F.,, Kokoszka F.,, Lepoivre C.,, D’Ovidio F.,, Engelen S.,, Ferrera I.,, Gasol J.M.,, Guidi L.,, Hildebrand F.,, Kokoszka F.,, Lepoivre C.,, Lima-Mendez G.,, Poulain J.,, Poulos B.T.,, Royo-Llonch M.,, Sarmento H.,, Vieira-Silva S.,, Dimier C.,, Picheral M.,, Searson S.,, Kandels-Lewis S.,, Bowler C.,, de Vargas C.,, Gorsky G.,, Grimsley N.,, Hingamp P.,, Iudicone D.,, Jaillon O.,, Not F.,, Ogata H.,, Pesant S.,, Speich S.,, Stemmann L.,, Sullivan M.B.,, Weissenbach J.,, Wincker P.,, Karsenti E.,, Raes J.,, Acinas S.G.,, Bork, P. 2015. Structure and function of the global ocean microbiome. Science 348:1–10. [DOI] [PubMed] [Google Scholar]
- Sunagawa S., Mende D.R., Zeller G., Izquierdo-Carrasco F., Berger S.A., Kultima J.R., Coelho L.P., Arumugam M., Tap J., Nielsen H.B., Rasmussen S., Brunak S., Pedersen O., Guarner F., de Vos W.M., Wang J., Li J., Doré J., Ehrlich S.D., Stamatakis A., Bork P.. 2013. Metagenomic species profiling using universal phylogenetic marker genes. Nat. Methods 10:1196. [DOI] [PubMed] [Google Scholar]