The entropy of the life table: A reappraisal

Abstract

The life table entropy provides useful information for understanding improvements in mortality and survival in a population. In this paper we take a closer look at the life table entropy and use advanced mathematical methods to provide additional insights for understanding how it relates to changes in mortality and survival. By studying the entropy (H) as a functional, we show that changes in the entropy depend on both the relative change in life expectancy lost due to death (e^†) and in life expectancy at birth (e₀). We also show that changes in the entropy can be further linked to improvements in premature and older deaths. We illustrate our methods with empirical data from Latin American countries, which suggests that at high mortality levels declines in H (which are associated with survival increases) linked with larger improvements in e₀, whereas at low mortality levels e^† made larger contributions to H. We additionally show that among countries with low mortality level, contributions of e^† to changes in the life table entropy resulted from averting early deaths. These findings indicate that future increases in overall survival in low mortality countries will likely result from improvements in e^†.

1. Introduction

The life table is perhaps the most useful tool in mortality analyses, as it summarizes the mortality experience of a population at a given point in time into a set of simple indicators (Preston et al., 2000). For example, life expectancy, a by-product of the life table, has been used extensively and widely as a measure of population health in national and international contexts (United Nations, 2012). Other life table measures such as the life table entropy, however, have received much less attention, although the entropy could also be considered an equally useful indicator for understanding improvements in mortality and survival in a population (Wilmoth and Horiuchi, 1999).

In this paper we take a closer look at the life table entropy and provide additional insights for understanding how it relates to changes in mortality and survival. Unlike previous work that relied on univariate calculus (e.g., Demetrius, 1974, 1975, 1976, 1978, 1979; Goldman and Lord, 1986; Keyfitz, 1977), we provide a more rigorous development and a further description of the life table entropy using the calculus of variations. This approach has previously been used in demographic research (Arthur, 1984; Beltrán-Sánchez and Soneji, 2011; Preston, 1982), and as we show, it provides us with additional tools to deepen our understanding of the population entropy and overall population survival. We focus, in particular, on a widely used measure of mortality improvement - life expectancy at birth (which represents the average length of life in the survival curve of a population) - and an additional measure called e^† that has recently been proposed as a marker of lifespan inequality (Zhang and Vaupel, 2009). For example, averting deaths at younger ages (premature deaths) is associated with reductions in lifespan inequality (Zhang and Vaupel, 2008). Recent evidence from 40 countries shows a negative correlation between life expectancy (e₀) and lifespan disparity (e^†) from 1840 to 2009, with most of the increase in life expectancy resulting from improvements in premature deaths (Vaupel et al., 2011). The authors conclude that improvements in life expectancy at birth can also be accompanied by reductions in lifespan disparity (e^†). In this paper we provide a mathematical foundation for these empirical findings by linking changes in the life table entropy, life expectancy at birth, and lifespan disparity. We demonstrate, mathematically and empirically, that changes in the entropy depend on both the relative change in life expectancy lost due to death (e^†) and in life expectancy at birth (e₀). We also show that changes in the entropy can be further linked to averting premature and older deaths. These results provide important implications for understanding current and future changes in the overall survival of a population. For instance, using data from Latin American countries for 1950–2005, we show that at low mortality levels changes in e^† contributed the most to overall survival, indexed by the entropy, which resulted from improvements in premature deaths. This implies that in these countries future increases in overall survival will likely come from changes in e^† and that these improvements are likely to reduce lifespan inequality as a result of averting early deaths (Zhang and Vaupel, 2008, 2009).

The paper is organized as follows. We begin in Section 2 with a brief overview of the mathematical definitions of the mortality and survival functions, and the life expectancy and entropy (for the interested reader, Appendix A.1 contains a brief literature review of the entropy). We then review how the entropy is used to measure relative changes in life expectancy in Section 2.1, and discuss the functional nature of the entropy in Section 2.2. We present our main results in Sections 2.3‒2.4, where we use the calculus of variations (reviewed in Appendix B) to show that changes in the entropy depend on both the relative change in life expectancy lost due to death (e^†) and in life expectancy at birth (e₀) - c.f. (2.5) - and also provide a new way to describe the effect of changes in the mortality function on the population entropy (c.f. Proposition 2). In Section 3 we further link changes in the entropy with improvements in premature and older deaths in relation to e₀ and e^†. Section 4 applies our results to mortality data from 18 Latin American countries from about 1950 to 2008. Therein we discuss our finding that at high mortality levels declines in H (which are associated with survival increases) linked with larger improvements in e₀, whereas at low mortality levels e^† made larger contributions to H. We end with concluding remarks in Section 5.

2. The entropy

The life table entropy is commonly used throughout demography to study the relative changes in life expectancy associated with changes in age-specific mortality rates. In this section we review the construction of the entropy due to Keyfitz (1977) (see Appendix A.1 for a brief history), and then present our main analytical results.

2.1. The demographic motivation for introducing the entropy

Let μ(x) be the force of mortality at age x. The probability of surviving from birth to age x is then

$$S(x)=e^{-{\int }_0^x\mu (s)ds},$$ (2.1)

so that life expectancy at age x is given by

$$e(x)={\int }_x^{\infty }{e}^{-{\int }_0^a\mu (s)ds}da.$$

In many of the situations of interest to us in this paper, x is fixed and μ(s) may vary. For instance, we may be interested in studying changes in life expectancy at birth (which implies that x = 0). We therefore introduce the following notation to reflect these cases:

$$S_x[\mu (s)]=e^{-{\int }_0^x\mu (s)ds},e_x[\mu (s)]={\int }_x^{\infty }{e}^{-{\int }_0^a\mu (s)ds}da.$$ (2.2)

Consider now a relative increase ϵ > 0 in μ - that is, a proportional increase in μ at all ages - similar to that proposed by Keyfitz (1977). Then the new mortality function is (1 + ϵ)μ(s) (note that Δμ = ϵ μ, so that Δμ/μ = ϵ), the new probability of surviving from birth to age x is

$$\begin{gathered} S_x[(1+ϵ)\mu (s)]=e^{-{\int }_0^x(1+ϵ)\mu (s)ds}={\left(e^{-{\int }_0^x\mu (s)ds}\right)}^{1+ϵ} \\ ={\left(S_x[\mu (s)]\right)}^{1+ϵ}, \end{gathered}$$

and the new life expectancy at age x is

$$e_x[(1+ϵ)\mu (s)]={\int }_x^{\infty }S{(a)}^{1+ϵ}da.$$

Without loss of generality, let us specialize to the most studied case of life expectancy—life expectancy at birth:

$$e_0[(1+ϵ)\mu (s)]={\int }_0^{\infty }S{(a)}^{1+ϵ}da.$$

We expect the relative increase in mortality to cause a relative decrease in life expectancy. To measure this decrease, Keyfitz and Caswell (2005, sec. 4.3.1) calculate de₀/dϵ|_ϵ=0 and then consider ϵ to be finite but small to arrive at the approximation

$$\frac{\Delta e_0}{e_0}\approx \left(\frac{{\int }_0^{\infty }S(x)\ln (S(x))dx}{{\int }_0^{\infty }S(x)dx}\right)ϵ.$$ (2.3)

Since 0 ≤ S(x) ≤ 1 (this follows from (2.1)), the ratio in the parentheses is negative, confirming our expectation that a relative increase in mortality should result in a relative decrease in life expectancy. Accordingly, the negative of the expression in parentheses is known as the entropy of the life table, and is customarily denoted by H. More formally, we make the following definition.

Definition 1. Given a survival function S(x), the quantity defined by

$$H[S(x)]=-\frac{{\int }_0^{\infty }S(x)\ln (S(x))dx}{{\int }_0^{\infty }S(x)dx}$$ (2.4)

is called the entropy of the population.

We will explain the bracket notation in the next section, but for now let us note that the approximation in (2.3) suggests the following interpretation for H (Goldman and Lord, 1986): a small proportional increase ϵ in the death rate at all ages results in a proportional decrease in life expectancy of approximately H times ϵ. For example, for H = 1 “when the death rates at all ages increase by 1 percent, the expectation of life diminishes by 1 percent Keyfitz and Caswell (2005, Sec. 4.3.1)”. Thus, H measures how relative changes in the mortality function affect the relative change in life expectancy of a population. In other contexts H has other interpretations (see Appendix A.2), but it is commonly known to be “in general highly sensitive to variations in age-specific mortality” Demetrius (1979) (Appendix A.3 contains a more thorough discussion of this point), which makes it a useful tool for characterizing a population’s survivorship.

2.2. Understanding the life table entropy (H) as a functional of the survival function (S) and the force of mortality (μ)

The preceding analysis described the effect on H of a specific change in the mortality function μ(x) (and consequently, by (2.2), in S(x)). This suggests that we view H as a functional—a quantity whose input is a function and whose output is a real number. Indeed, as (2.4) makes clear, H is a functional of S(x), since it takes as input a survival function S(x) and outputs a real number (this is why we have used the H[S(x)] notation). Similarly, H can also be seen as a functional of μ(x), in which case we write H[μ(x)].

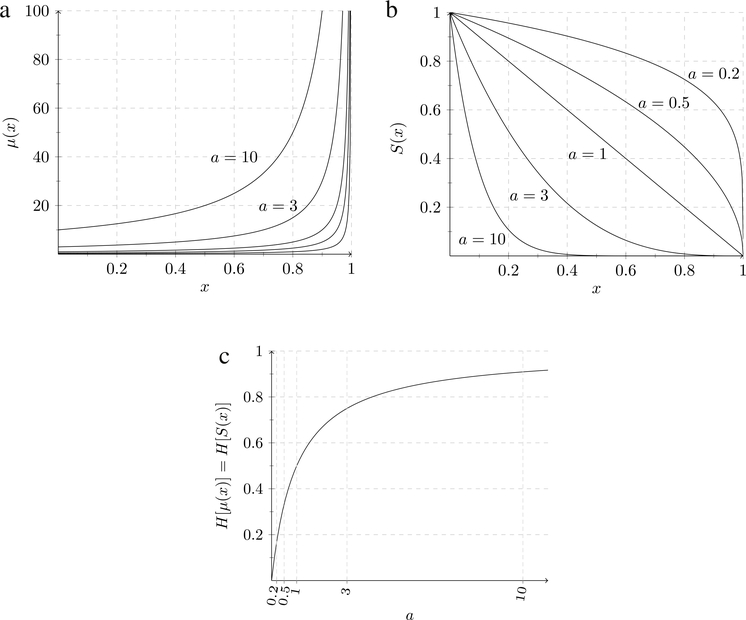
Functionals are similar to functions, except that the “independent variable” is now a function. To better see this important distinction (and also the functional nature of H), consider the so-called hyperbolic mortality example, where

$$\begin{gathered} \mu (x)=\frac{a}{s_0-x},S(x)={\left(1-\frac{x}{s_0}\right)}^a, \\ H[\mu (x)]=H[S(x)]=\frac{a}{a+1}. \end{gathered}$$

For simplicity, set s₀ = 1 so that we can uniquely identify a curve in the family of mortality and survival curves, μ(x) = a/(1 − x) and S(x) = (1 − x)^a, by the parameter a. Since H = a/(a + 1), it follows that H assigns to each function μ(x) = a/(1 − x) (or, equivalently, S(x) = (1 − x)^a) one number a/(a + 1), clearly illustrating the functional nature of H. A plot of μ(x) and S(x) for various a-values is shown in Fig. 1 panels (a) and (b), respectively, and the corresponding plot of the entropy H is shown in Fig. 1(c).

Fig. 1.

Plots of (a) μ(x) = a/(1 − x) for a = 0.2, 0.5, 1, 3, 10 (the a-values decrease as one moves from upper-left to lower-right), (b) S(x) = (1 − x)^a for a = 0.2, 0.5, 1, 3, 10, and (c) the entropy H[μ(x)] = H[S(x)] = a/(a + 1).

A closer look at panels (b) and (c) reveals two more characteristics of H as a functional of S(x). Firstly, it detects the degree of concavity (also called convexity) in an S(x) function. Secondly, decreasing H values signal changes in the survival curve toward greater survivorship. (Appendix A.3 contains a discussion of these two general features of H.) By the same token, panels (a) and (c) also indicate similar characteristics of H as a functional of μ(x) but in this case decreasing H values signal changes in the force of mortality curve toward lower mortality. Because the survival function is bounded, 0 ≤ S(x) ≤ 1, changes in S(x) have “less room” to operate and this leads to different dynamics when studying changes in H as a functional of S(x) versus when H is a functional of μ(x)—which, at least theoretically, is unbounded. Thus, the entropy H would express differential effects in response to changes in the survival function (S(x)) or to changes in the force of mortality (μ(x)), and calculus of variations offers a unique opportunity to study these changes. We study these two cases in Sections 2.3 and 2.4, respectively.

2.3. A theorem concerning the entropy as a functional of the survival function

Changes in functions are described by calculus, while changes in functionals are described by the calculus of variations. (Appendix B contains a brief review of the subject, as well as the notation we will use throughout the remainder of the paper.) Importantly, calculus of variations allow us to look at variations in the entire survival function S(x) and their link with changes in H (as in Fig. 1), as opposed to univariate calculus in which changes are localized at a given point in the survival function. In this section we focus our attention on δH and δ²H - the analogues of the first and second derivatives of a single-variable function, respectively - and what they can tell us about changes in the survival function. To begin, let us note that the denominator of (2.4) is just e₀[S(x)] (recall (2.2)). Moreover, Goldman and Lord (1986) and Vaupel (1986) have shown that the numerator of (2.4) - which includes the minus sign - can be re-expressed as

$${\int }_0^{\infty }\mu (x)S(x)e(x)dx,$$

which has been traditionally denoted by e^† (Vaupel, 1986). Therefore,

$$e^{†}[S(x)]=-{\int }_0^{\infty }S(x)\ln (S(x))dx,$$

so that the entropy (2.4) then becomes

$$H[S(x)]=\frac{e^{†}[S(x)]}{e_0[S(x)]}.$$

Now, denote by S(x; ϵ) a family of smooth “varied curves”: curves that are small perturbations of S(x) but have the same endpoint values as S(x) (i.e., for all ϵ, S(0; ϵ) = S(0) and S(x; ϵ) → 0 as x → ∞).¹ The difference S(x; ϵ) − S(x) is called the variation of S(x) and is traditionally denoted by δS (c.f. Appendix B). We can now prove the following theorem.

Proposition 1.

Let δS be a variation of the survival function S(x). Then:

1. The relative change in H[S(x)] is

   $$\frac{\delta H[S(x)]}{H[S(x)]}=\frac{\delta e^{†}[S(x)]}{e^{†}[S(x)]}+\frac{-\delta e_0[S(x)]}{e_0[S(x)]},$$ (2.5)

   where the first variations of e^†[S(x)] and e₀[S(x)] are given by

   $$\delta e^{†}[S(x)]=-\delta e_0[S(x)]-{\int }_0^{\infty }\ln (S(x))v(x)dx,$$ (2.6)

   $$\delta e_0[S(x)]={\int }_0^{\infty }v(x)dx,$$ (2.7)

   and where δS(x) has been expanded to first-order in ϵ: δ S(x) = ϵv(x), with v(x) a smooth function that vanishes at zero and as x → ∞.
2. The second variation δ²H[S(x)] is

   $$\begin{gathered} {\delta }^{2}H[S(x)]=-\frac{1}{e_0}[{\int }_0^{\infty }\frac{{(v(x))}^2}{S(x)}dx \\ +2\{\delta e_0\delta H+\left({\int }_0^{\infty }w(x)dx\right)(H+1) \\ +{\int }_0^{\infty }w(x)\ln (S(x))dx\}], \end{gathered}$$ (2.8)

   where δ S(x) has been expanded to second-order in ϵ: δ S(x) = ϵv(x) + ϵ²w(x), where v(x) and w(x) are smooth functions that vanish at zero and as x → ∞.

The proof of Proposition 1 can be found in Appendix C.

Eq. (2.5) decomposes the relative change in H into the sum of the relative changes in e^† and e₀. Therefore, this equation shows that changes in overall survival, indexed by H, depend on improvements in both e^† and in e₀. In addition, Eq. (2.6) shows that e₀ and e^† change in opposite directions in response to a variation in the survival function, since for small variations in S(x), where v(x) → 0, the first variations of e₀ and e^† would be the exact opposites of each other.

We end this section by noting that when ϵ is finite but small we can use the first and second variation to approximate H[S + δS] to second order in ϵ (see also (B.8)):

$$H[S(x)+\delta S(x)]\approx H[S(x)]+ϵ\delta H[S(x)]+\frac{{ϵ}^2}{2}{\delta }^{2}H[S(x)].$$ (2.9)

2.4. The entropy as a functional of the mortality function

Let us now return to the problem of studying the effect on H of varying μ(x). The following theorem is the analogue of Proposition 1.

Proposition 2.

Let δμ be a variation of the mortality function μ(s). Then the relative change in H[μ(s)] is given by

$$\frac{\delta H[\mu (s)]}{H[\mu (s)]}=\frac{\delta e^{†}[\mu (s)]}{e^{†}[\mu (s)]}+\frac{-\delta e_0[\mu (s)]}{e_0[\mu (s)]},$$ (2.10)

where the first variations of e^†[μ(x)] and e₀[μ(x)] are given by

$$\begin{gathered} \delta e^{†}[\mu (s)]=-\delta e_0[\mu (s)] \\ -{\int }_0^{\infty }{S}_x[\mu (s)]\ln \left(S_x[\mu (s)]\right)\ln \left(S_x[v(s)]\right)dx, \end{gathered}$$ (2.11)

$$\delta e_0[\mu (s)]={\int }_0^{\infty }{S}_x[\mu (s)]\ln \left(S_x[v(s)]\right)dx,$$ (2.12)

with $S_x[v(s)]=e^{-{\int }_0^{x}v(s)ds}$, and where δμ(s) has been expanded to first-order in ϵ: δμ(s) = ϵv(s), with v(s) a smooth function that vanishes at zero and as s → ∞.

The proof of Proposition 2 can be found in Appendix C.

Although (2.10) is a direct analogue of (2.5), note that the equations identifying the first variations of δe^†[S(x)] and δe₀[S(x)] ((2.6) and (2.7)) are very different from those shown above in (2.11) and (2.12). The extra terms shown in the latter case come from the non-linear link between the force of mortality and average years of life (δe^† and δe₀). These equations highlight the differential effect on the entropy H resulting from changes in the survival function (S(x)) versus changes in the force of mortality (μ(x)).

Similar to Eq. (2.6), Eq. (2.11) shows that there is a negative association between the first variation of e^†[μ(x)] and that of e₀[μ(x)]—when one increases the other one decreases. Moreover, for very small variations (δμ(s) close to zero) the second term in (2.11) becomes negligible (because S_x[v(s)]|_v(s)≈0 → 1 and ln(S_x[v(s)]) → 0), and the two variations become negatives of each other.

2.5. Reproducing the Keyfitz result with Propositions 1 and 2

As a quick application of Propositions 1 and 2, let us show that the calculation performed by Keyfitz and Caswell (2005, Sec. 4.3.1) and reviewed in Section 2.1 is indeed an investigation of the change in the functional H under the variation δμ = ϵμ(s) of the mortality function (Beltrán-Sánchez and Soneji, 2011).

To begin, note that the new mortality function (1 + ϵ)μ(s) in that calculation can be written

$$(1+ϵ)\mu (s)=\mu (s)+ϵ\mu (s)=\mu (s)+\delta \mu (s).$$

In the language of Proposition 2, this means that v(s) = μ(s), so that (2.12) immediately gives

$$\frac{\delta e_0}{e_0}=\frac{{\int }_0^{\infty }S(x)\ln (S(x))dx}{{\int }_0^{\infty }S(x)dx}.$$ (2.13)

If we now consider ϵ to be finite but small, applying (B.7) yields

$$\frac{\Delta e_0}{e_0}\approx ϵ\frac{\delta e_0}{e_0}=\left(\frac{{\int }_0^{\infty }S(x)\ln (S(x))dx}{{\int }_0^{\infty }S(x)dx}\right)ϵ,$$

which verifies the entropy result of Keyfitz and Caswell (2005, sec. 4.3.1) (Eq. (2.3)).

We can also derive (2.13) (and therefore again reproduce (2.3)) using Proposition 1 as follows. The variation in the mortality function causes a variation in the survival function S(x) of

$$\begin{gathered} \delta S(x)=S{\left(x\right)}^{1+ϵ}-S(x)=S(x)\left(S{(x)}^{ϵ}-1\right)=S(x)\left(e^{ϵ\ln (S(x))}-1\right) \\ =S(x)\left(ϵ\ln (S(x))+{ϵ}^2\frac{{(\ln (S(x)))}^2}{2}+\cdots \right). \end{gathered}$$

(The terms in parentheses in the last equation come from Taylor-expanding e^{ϵ ln(S(x))} − 1.) Therefore, to first-order in ϵ, the variation in the mortality function results in a variation δS = ϵS(x) ln(S(x)) in the survival function. Then, using (B.6) to compute the first variation of e₀[S(x)] we arrive at

$$\begin{gathered} \delta e_0[S(x)]={\left[\frac{\partial }{\partial ϵ}{e}_0\{S(x)+ϵS(x)\ln (S(x))\}\right]}_{ϵ=0} \\ ={\int }_0^{\infty }S(x)\ln (S(x))dx. \end{gathered}$$

Dividing this equation by e₀ then yields (2.13).

Analytical expressions for the entropy are also known for other special scenarios. In Appendix D we consider a few of these special cases and apply Propositions 1 and 2 to again verify the results found in the literature.

3. Early deaths from late deaths

Propositions 1 and 2 allow us to study changes in the life table entropy (H) associated with improvements in the survival and mortality functions across all ages. These propositions can also be used to provide additional insights to link premature and older deaths with life table entropy, and to inform about changes in lifespan disparity. For instance, an important property of e^† as a measure of life disparity is that there is a unique threshold age, a^†, that separates early from late deaths (Zhang and Vaupel, 2009). The importance of this age for overall survival is that improvements in reducing early (premature) deaths reduces variation in lifespans (overall survival), while improvements in late (older) deaths increases variation in lifespans (Vaupel et al., 2011). An age a^† separates early from late deaths if 0 = e^†(a^†)−e₀(a^†)[1 −Λ(a^†)], where $\Lambda \left(a^{†}\right)={\int }_0^{a^{†}}\mu (s)$ is the cumulative hazard function (Zhang and Vaupel, 2009).

Proposition 1 can be re-expressed to incorporate a given threshold age a^†. The result is (Appendix E):

$$\begin{gathered} \frac{\delta H[S(x)]}{H[S(x)]}=\left\{\frac{\delta e^{†}[S(x|x<a^{†})]}{e^{†}[S(x)]}+\frac{-\delta e_0[S(x|x<a^{†})]}{e_0[S(x)]}\right\} \\ +\left\{\frac{\delta e^{†}[S(x|x\ge a^{†})]}{e^{†}[S(x)]}+\frac{-\delta e_0[S(x|x\ge a^{†})]}{e_0[S(x)]}\right\}, \end{gathered}$$ (3.1)

where the first conditional variations of e^†[S(x)] and e₀[S(x)] are given by

$$\delta e^{†}[S(x|x<a^{†})]=-\delta e_0[S(x|x<a^{†})]-{\int }_0^{a^{†}}\ln (S(x))v(x)dx,$$ (3.2)

$$\delta e^{†}[S(x|x\ge a^{†})]=-\delta e_0[S(x|x\ge a^{†})]-{\int }_{a^{†}}^{\infty }\ln (S(x))v(x)dx,$$ (3.3)

$$\delta e_0[S(x|x<a^{†})]={\int }_0^{a^{†}}v(x)dx,$$ (3.4)

$$\delta e_0[S(x|x\ge a^{†})]={\int }_{a^{†}}^{\infty }v(x)dx,$$ (3.5)

where v(x) is a smooth function that vanishes at zero and as x → ∞.

Eq. (3.1) shows that relative changes in the entropy can be decomposed as the sum of relative changes in e^†[S(x)] and e₀[S(x)] associated with early and late deaths. In addition, Eqs. (3.2)–(3.5) highlight the interplay between e^†[S(x)] and e₀[S(x)] in determining overall survival when early and/or late deaths are averted. Proposition 2 can also be written in analogous form to (3.1) with its respective conditional variations in e^†[μ(s)] and e₀[μ(s)] (Appendix E).

Note that the above equations are general in the sense that they work with any threshold age. For instance, one may be interested in investigating changes in the entropy associated with mortality improvements below and above the mean, median, mode² or any other moment of the survival probability function or the force of mortality (Appendix E).

4. Application to Latin American mortality data

In this section we describe the results of applying Proposition 1 to assess changes in the entropy, H, and their corresponding link with changes in e₀ and e^†.

4.1. Data and methods

We use period mortality data from 18 countries in Latin America from about 1950 to 2008 from the Latin American Mortality Database (Palloni et al., 2014) (Table 1).This data covers the period when major improvements in mortality took place in the region, with particularly fast declines in infant mortality and sizeable increases in life expectancy at birth (Palloni and Wyrick, 1981; Palloni and Pinto, 2011).

Table 1.

Latin American countries with available period mortality data by age and sex.

Country	Years
Argentina	1953,1965, 1975, 1985, 1996, 2005
Brazil	1985,1995, 2005
Chile	1956,1965, 1976, 1987, 1997, 2006
Colombia	1957,1968, 1979, 1989, 1999, 2008
Costa Rica	1956,1968, 1978, 1992, 2005
Cuba	1961,1975, 1991, 2006
Dominican Republic	1955,1965, 1975, 1987, 1997, 2006
Ecuador	1956,1968, 1978, 1986, 1995, 2005
El Salvador	1955,1966, 1981, 1999, 2008
Guatemala	1957,1968, 1977, 1987, 1998, 2005
Honduras	1955,1967, 1981, 1989
Mexico	1955,1965, 1975, 1985, 1995, 2005
Nicaragua	1956,1967, 1983, 2000, 2007
Panama	1955,1965, 1975, 1985, 1995
Paraguay	1956,1967, 1977, 1987, 1997, 2006
Peru	1966,1976, 1987, 2000, 2008
Uruguay	1969,1980, 1990, 2000, 2007
Venezuela	1955,1966, 1976, 1985, 1995, 2006

Source:Latin American Mortality Database (LAMBdA).

We focus here on age 0, that is, life expectancy at birth (e₀) with its corresponding life expectancy lost due to death (e^†) and life table entropy (H). To highlight the usefulness of Proposition 1 for studying changes in overall survival, we also provide an application decomposing changes in H associated with improvements in early vs. late deaths. Because population data typically comes in discrete form, we use standard techniques to estimate e(0), e^†(0), and H at time t (life table notation) - see Appendix F.1 - and also use the discrete versions of the first variations in Proposition 1 - see Appendix F.2.

4.2. Results

As a first application of Proposition 1, for each country in Table 1 we compare the observed change in H between two consecutive time periods t₁ and t₂ (H[S(x, t₂)] − H[S(x, t₁)]) to the predicted change in H (δH[S(x, t₁)]).³ Using advanced numerical integration techniques (Appendix F.2), we find that in each country the average percentage error in the estimation across all periods is <0.16%⁴

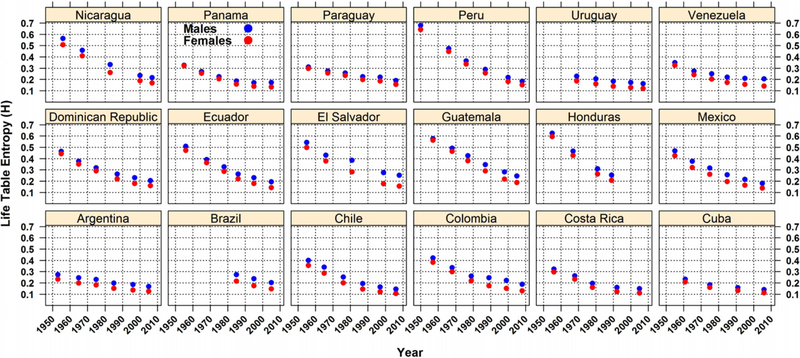
Next, Fig. 2 shows estimates of the life table entropy, H, for all countries included in the analyses for males and females (see Appendix Table 2 for specific values). Results indicate a decline in H over time suggesting improvements in overall survival in all these countries since the 1950’s. Interestingly, there is a different pattern in H between countries that had an early demographic transition and those with a late transition. For instance, countries with an early demographic transition (e.g., Argentina, Costa Rica, Cuba, and Uruguay) start at lower levels in H in the 1950’s and show slower pace of decline over time; the opposite is true for countries with a late demographic transition (e.g., El Salvador, Guatemala, Honduras and Nicaragua). This result reflects the fact that countries with an early demographic transition had already attained relatively low mortality levels in the 1950’s (Palloni and Pinto, 2011); thus, their corresponding life table entropy early on is lower than that of countries with a late demographic transition. In addition, improvements in overall survival tend to be larger when starting at high mortality levels, suggesting that H would show faster declines for countries with a late demographic transition.

Fig. 2.

Life table entropy by country, year and gender.

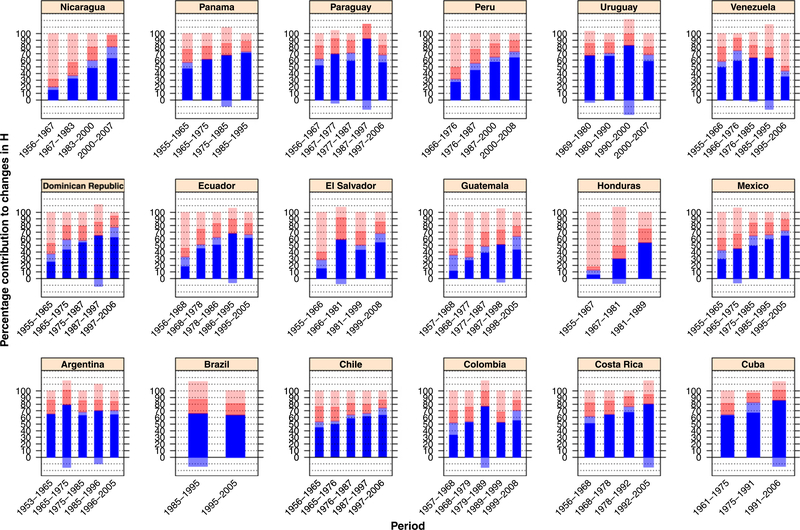
As a second application of Proposition 1 - and (2.5) specifically - we now decompose changes in H over time to assess whether increases in overall survival in Latin America in the second part of the 20th century are due to larger improvements in e^† vs. e₀.

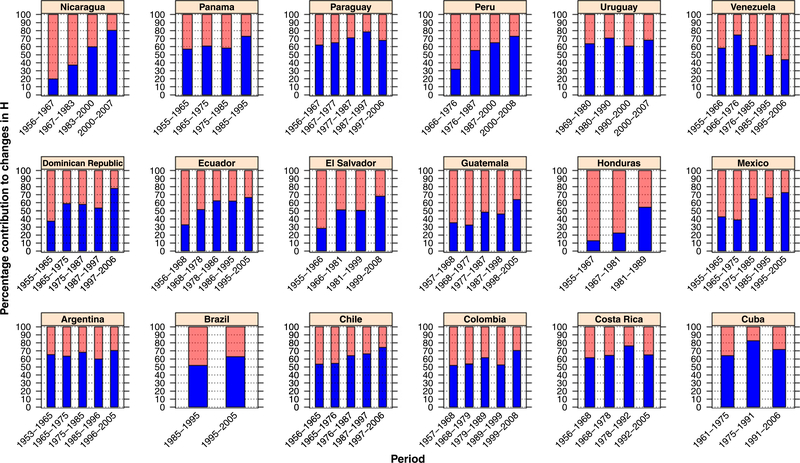
The percentage contribution of e^† and e₀ to the change in H between two consecutive periods for each country for males and females is shown in Figs. 3 and 4, respectively (Appendix Table 3). Results clearly indicate a differential contribution of e₀ and e^† to changes in H over time. Improvements in e₀ show larger contributions to increasing overall survival at high mortality levels (e.g., before 1990), but improvements in e^† contributed the most as the mortality level declines. For instance, for males in El Salvador, Guatemala, Honduras and Nicaragua, increases in e₀ contributed about 60% of the change in H before 1980, but after 2000, a similar percentage contribution is due to improvements in e^†. On the other hand, increases in survival for males in countries with low mortality levels (e.g., Argentina, Cuba and Uruguay) were mostly due to improvements in e^†. There is a similar pattern for females, but in this case, e^† made larger contributions to overall survival because females tend to experience lower mortality rates than males.

Fig. 3.

Contribution of e^† (blue) and e₀ (pink) to changes in Male Life Table Entropy by Country and Period. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

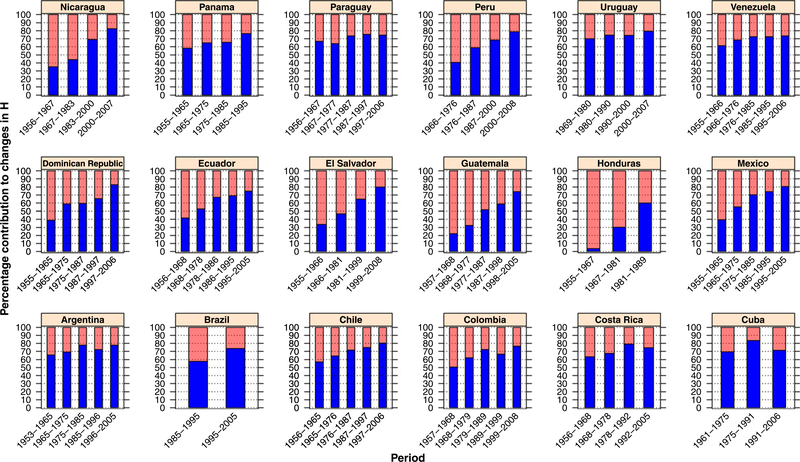
Fig. 4.

Contribution of e^† (blue) and e₀ (pink) to changes in Female Life Table Entropy by Country and Period. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

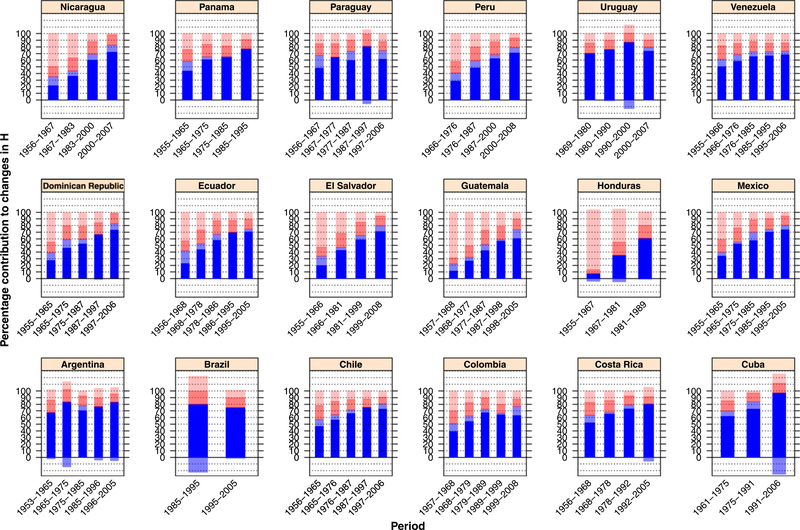
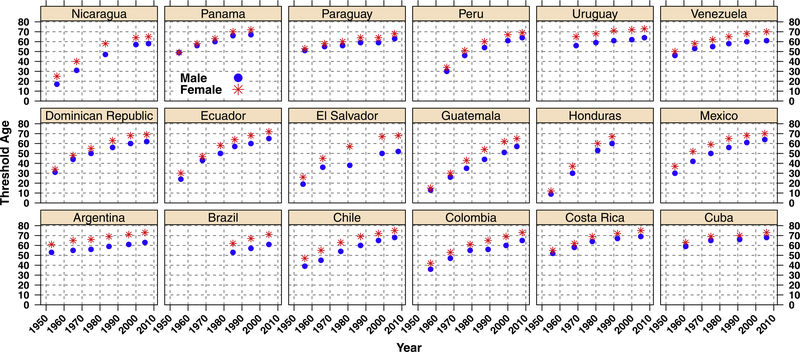
Importantly, there was a different age pattern of mortality decline in Latin America since the 1950’s between countries with early and late demographic transitions (Palloni and Wyrick, 1981). For the latter countries, declines in infant and childhood mortality are likely responsible for the bulk of overall survival, but for the former countries, declines in adult and older adult mortality are the most likely contributors (Palloni and Pinto, 2011). Thus, as a third application of Proposition 1, we estimate the age separating early (premature) from late (older) deaths (a^†, Appendix Table 2) and further decompose changes in H over time associated with averting premature and older deaths using Eqs. (3.1)–(3.5) (Appendix Table 4).

Due to space limitations we only show results for males (Fig. 5); results for females are shown in the Appendix Fig. 6. Results for the age separating premature from older deaths show that in countries with a late demographic transition, a^† starts at lower values and increases at a faster pace over time relative to countries with a late demographic transition (Appendix Table 4, Appendix Fig. 7). This time trend corresponds to a faster mortality reduction over time among the former countries.

Fig. 5.

Contribution of changes in premature (blue for e^† and pink for e₀) and older (light blue for e^† and light pink for e₀) deaths to changes in male life table entropy by country and period. Negative values in older e^† (light blue) indicate that there was an increase over the period in average years of life lost due to death at older ages. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Fig. 6.

Contribution of changes in premature (blue for e^† and pink for e₀) and older (light blue for e^† and light pink for e₀) deaths to changes in female life table entropy by country and period. Negative values in older e^† (light blue) indicate that there was an increase over the period in average years of life lost due to death at older ages. Source: Authors’ calculations using data from LAMBdA (Palloni et al., 2014) and Eqs. (3.1)-(3.5). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

Fig. 7.

Threshold age, a^†, separating premature and older deaths for males and females by country and period.

Source: Authors’ calculations using data from LAMBdA (Palloni et al., 2014) and formula 0 = e^† (a^†) − e₀(a^†)[1 − Λ(a^†)], where $\Lambda \left(a^{†}\right)={\int }_0^{a^{†}}\mu (s)ds$ is the cumulative hazard function (Zhang and Vaupel, 2009).

Fig. 5 shows results decomposing changes in the male entropy due to improvements in premature and older deaths. In countries with a late demographic transition (e.g., El Salvador, Guatemala, and Honduras), increases in overall survival are mainly due to increases in e₀ resulting from improvements in older deaths (light pink). As the mortality level declines in these countries there is a larger contribution to overall survival from premature deaths (pink). On the contrary, in countries with an early demographic transition (e.g., Argentina, Cuba, and Uruguay), increases in overall survival are due to improvements in e^† resulting from averting premature deaths (dark blue). In some of these countries, for example in Argentina, Cuba and Uruguay, males at older ages experienced worsening rather than improving average years of life lost due to death—hence the negative contribution to overall survival in the figure. Nonetheless, premature deaths made large enough contributions to overall survival that they offset the mortality deterioration at older ages.

5. Concluding remarks

In this paper we provide a demographic interpretation of changes in the life table entropy by studying this concept from the functional viewpoint. This approach allow us to provide additional insights for understanding changes in overall survival in a population. In particular, we find that changes in the entropy depend on the relative changes in both life expectancy lost due to death (e^†) and in life expectancy at birth (e₀), with the exact relationship given by (2.5). Our results also provide a new way to describe the effect of changes in the mortality function on the population entropy (c.f. Proposition 2). These are well-studied demographic concepts that now have a natural and consistent link to a population’s entropy and changes in its mortality and survival functions.

When we apply our methods to period mortality data in Latin American countries since the 1950’s, we obtain an especially useful description of the interplay between e₀ and e^† in determining changes in overall survival of a population. We show that, in these countries, declines in H - which are associated with increases in overall survival - are driven by faster improvements in e₀ in high mortality regimes, and by e^† in low mortality regimes. This insight reinforces the interpretation of e^† as an indicator of life disparity (Vaupel et al., 2011; Shkolnikov et al., 2011). Thus, in countries experiencing a low-mortality regime, improvements in overall survival will increasingly depend on reducing disparities in length of life in adulthood.

Moreover, we show that changes in the survival function produce changes in opposite direction between e^† and e₀ (see Eq. (2.11)). In fact, for very small changes in the survival function, e.g. those currently experienced in low-mortality countries, e^† and e₀ are direct opposites. Thus, our equation helps elucidate previous research that shows a negative correlation between e^† and e₀ among low-mortality countries, why this correlation is higher in recent times, and why countries with low life disparity (e^†) tend to have higher values in life expectancy at birth (e₀) (Vaupel et al., 2011).

For Latin American countries, our decomposition of changes in the entropy due to averting premature and older deaths shows that improvements in overall survival (i.e., declines in H) are associated with averting premature deaths. The implication of this result is that countries in Latin America are likely reducing lifespan inequality, which is a consequence of averting early deaths (Zhang and Vaupel, 2009, 2008).

Our methods and the substantive results have immediate applications for envisioning future changes in overall survival in other countries. For instance, it is likely that most increases in survival in high-income countries will result from improvements in e^†, while in low- and middle-income countries e₀ is likely to still play an important role in determining overall survival of the population. Our methods also provide additional insights for linking changes in the life table entropy with improvements in premature and older deaths. Our formulas are general in the sense that they work with any threshold age. For instance, one may be interested in investigating changes in the entropy associated with mortality improvements below and above the mean, median, and mode.

The results we have achieved have been made possible by casting the problems we have studied within the domain of the calculus of variations. The examples considered in Appendix D further showcase how demographic questions, like the change in a population’s life expectancy given a relative change in their overall mortality, can be answered with variational calculus. These tools have already proven useful in the field (see e.g., Arthur, 1984; Beltrán-Sánchez and Soneji, 2011; Preston, 1982; Engelman et al., 2014), and we would like to further advocate their use, especially given the potential insights - such as those contained in Proposition 1 and the applications of it we have discussed - that may surface as a result of their usage.

Source: Latin American Mortality Database (LAMBdA).

Appendix A. Origin and interpretations of the entropy

A.1. A brief history of the origin of the life table entropy

The concept of entropy was initially proposed in the physical sciences as a measure of the level of disorder in a system. A similar concept in population studies - population entropy or life table entropy - was independently developed by Demetrius and Keyfitz in the 1970’s using different principles. The first approach, developed by Demetrius (1974, 1975, 1976, 1978), is a direct analogue of the entropy of physical systems. Demetrius considers a population to be a system of n interacting age classes that can be represented by a lattice system. This system has a phase space with an associated set of (invariant) probability measures. Thus, given a finite partition of the lattice system there is a Kolmogorov entropy which, in an equilibrium state (i.e., a state that maximizes the entropy for a fixed mean energy), corresponds to “the variability of the contribution of the different age classes to the stationary age distribution (Demetrius, 1974)”.

Table 2.

Estimates of life expectancy at birth (e₀), life expectancy lost due to death (e^†), entropy of the life table (H), and the age separating early from late deaths (a^†) for males and females for 18 countries in Latin America.

Year	Males				Females
	e0	e†	a†	H	e0	e†	a†	H
Argentina
1953	59.6	16.1	53.0	0.27	64.7	15.1	61.0	0.23
1965	61.8	15.1	55.0	0.24	68.0	13.4	65.0	0.20
1975	63.2	14.5	56.0	0.23	69.9	12.6	66.0	0.18
1985	66.1	13.1	59.0	0.20	72.4	10.9	69.0	0.15
1996	67.6	12.6	61.0	0.19	74.3	10.2	71.0	0.14
2005	69.5	11.7	63.0	0.17	75.6	9.5	73.0	0.13
Brazil
1985	60.6	16.6	53.0	0.27	66.5	14.2	62.0	0.21
1995	64.4	15.2	57.0	0.24	70.9	12.4	67.0	0.17
2005	67.7	13.7	61.0	0.20	73.9	10.8	71.0	0.15
Chile
1956	51.6	20.6	39.0	0.40	56.3	20.0	47.0	0.36
1965	55.3	18.8	45.0	0.34	61.0	17.7	55.0	0.29
1976	61.9	15.7	54.0	0.25	67.7	13.6	63.0	0.20
1987	67.0	13.1	60.0	0.20	72.9	10.6	69.0	0.15
1997	70.3	11.5	65.0	0.16	75.8	9.1	72.0	0.12
2006	72.4	10.5	68.0	0.14	77.6	8.2	75.0	0.11
Colombia
1957	50.9	21.4	36.0	0.42	54.0	20.8	42.0	0.39
1968	56.1	18.7	47.0	0.33	60.0	18.1	53.0	0.30
1979	61.9	16.2	55.0	0.26	66.4	14.4	61.0	0.22
1989	63.4	15.6	56.0	0.25	69.9	12.3	65.0	0.18
1999	66.0	14.7	60.0	0.22	72.9	11.0	69.0	0.15
2008	69.1	12.9	65.0	0.19	75.2	9.8	73.0	0.13
Costa Rica
1956	58.6	19.0	52.0	0.33	60.8	18.2	55.0	0.30
1968	62.8	16.6	58.0	0.26	65.8	15.3	62.0	0.23
1978	68.5	13.5	64.0	0.20	72.4	11.5	69.0	0.16
1992	71.6	11.5	67.0	0.16	75.7	9.4	72.0	0.12
2005	73.1	10.9	69.0	0.15	77.6	8.6	75.0	0.11
Cuba
1961	64.6	15.1	59.0	0.23	67.3	14.3	63.0	0.21
1975	69.4	12.7	65.0	0.18	72.2	11.5	69.0	0.16
1991	71.0	11.2	66.0	0.16	74.3	9.8	70.0	0.13
2006	73.3	10.3	68.0	0.14	76.8	8.7	73.0	0.11
Dominican Republic
1955	49.0	22.8	31.0	0.47	50.9	22.7	34.0	0.44
1965	54.8	20.8	44.0	0.38	57.4	20.3	48.0	0.35
1975	58.3	18.7	50.0	0.32	61.5	18.1	55.0	0.29
1987	62.7	16.6	56.0	0.26	67.6	14.9	63.0	0.22
1997	66.1	15.4	60.0	0.23	71.5	13.0	68.0	0.18
2006	67.8	14.0	62.0	0.21	72.9	11.7	69.0	0.16
Ecuador
1956	46.9	23.9	24.0	0.51	49.7	23.7	30.0	0.48
1968	54.3	21.3	43.0	0.39	56.7	20.7	47.0	0.36
1978	58.8	19.2	50.0	0.33	62.6	17.9	58.0	0.29
1986	63.2	16.7	57.0	0.26	67.5	14.8	64.0	0.22
1995	66.0	15.3	60.0	0.23	71.2	12.9	68.0	0.18
2005	69.5	13.5	65.0	0.19	74.7	10.8	72.0	0.15
El Salvador
1955	44.0	23.9	19.0	0.54	47.2	23.7	26.0	0.50
1966	50.7	21.9	36.0	0.43	54.9	20.9	45.0	0.38
1981	53.4	20.6	38.0	0.39	62.3	17.7	57.0	0.28
1999	61.2	16.9	50.0	0.28	70.8	12.5	67.0	0.18
2008	62.9	15.9	52.0	0.25	72.5	11.3	68.0	0.16
Guatemala
1957	42.4	24.4	13.0	0.58	42.6	24.0	15.0	0.56
1968	46.5	22.9	26.0	0.49	48.4	22.5	30.0	0.47
1977	50.9	21.6	35.0	0.43	54.4	20.8	43.0	0.38
1987	55.9	19.4	44.0	0.35	60.7	17.8	54.0	0.29
1998	61.3	17.4	51.0	0.28	67.1	14.6	62.0	0.22
2005	64.2	15.8	57.0	0.25	69.4	13.1	65.0	0.19
Honduras
1955	39.6	24.8	9.0	0.63	40.7	24.3	12.0	0.60
1967	48.5	22.6	30.0	0.47	51.4	22.0	37.0	0.43
1981	60.6	18.8	53.0	0.31	64.5	17.0	60.0	0.26
1989	65.4	16.7	60.0	0.26	69.6	14.6	67.0	0.21
Mexico
1955	48.5	22.8	30.0	0.47	51.7	22.1	37.0	0.43
1965	54.2	20.5	42.0	0.38	59.3	19.1	52.0	0.32
1975	59.3	18.9	50.0	0.32	64.3	16.9	59.0	0.26
1985	63.4	16.3	56.0	0.26	69.1	13.6	65.0	0.20
1995	66.8	14.4	61.0	0.22	72.1	11.8	68.0	0.16
2005	69.8	12.6	64.0	0.18	74.3	10.3	70.0	0.14
Nicaragua
1956	42.5	24.0	17.0	0.56	47.0	24.0	25.0	0.51
1967	49.0	22.7	31.0	0.46	52.9	22.0	40.0	0.42
1983	57.7	19.4	47.0	0.34	63.8	16.8	58.0	0.26
2000	64.7	15.3	57.0	0.24	69.5	13.1	64.0	0.19
2007	65.8	14.2	58.0	0.22	70.8	12.0	65.0	0.17
Panama
1955	57.4	18.8	49.0	0.33	58.6	19.0	49.0	0.32
1965	61.7	16.7	56.0	0.27	63.7	16.3	58.0	0.26
1975	65.7	14.8	60.0	0.23	67.9	14.1	63.0	0.21
1985	70.0	13.1	66.0	0.19	72.9	11.6	70.0	0.16
1995	71.4	12.3	67.0	0.17	74.9	10.6	72.0	0.14
Paraguay
1956	58.6	18.2	51.0	0.31	60.5	18.2	53.0	0.30
1967	61.2	16.8	55.0	0.27	63.4	16.3	58.0	0.26
1977	62.6	16.2	56.0	0.26	65.3	15.4	60.0	0.24
1987	65.0	14.6	59.0	0.23	68.1	13.5	64.0	0.20
1997	65.2	14.5	59.0	0.22	69.1	12.9	64.0	0.19
2006	68.1	13.0	63.0	0.19	71.9	11.2	68.0	0.16
Peru
1966	48.1	22.9	30.0	0.48	50.9	22.9	34.0	0.45
1976	55.6	20.4	46.0	0.37	58.5	19.7	51.0	0.34
1987	61.0	17.6	54.0	0.29	64.4	16.5	60.0	0.26
2000	66.3	14.5	61.0	0.22	70.4	12.8	67.0	0.18
2008	69.2	12.7	64.0	0.18	73.0	11.0	69.0	0.15
Uruguay
1969	63.0	14.5	56.0	0.23	68.8	12.8	65.0	0.19
1980	65.4	13.5	59.0	0.21	71.6	11.5	68.0	0.16
1990	67.5	12.5	61.0	0.19	73.9	10.3	71.0	0.14
2000	68.8	12.1	62.0	0.18	75.3	9.6	72.0	0.13
2007	70.2	11.5	64.0	0.16	76.3	9.1	73.0	0.12
Venezuela
1955	55.6	19.5	46.0	0.35	58.5	19.1	50.0	0.33
1966	60.8	16.8	53.0	0.28	64.5	15.6	58.0	0.24
1976	62.1	15.7	55.0	0.25	67.6	13.9	62.0	0.21
1985	65.1	14.4	58.0	0.22	70.5	12.2	65.0	0.17
1995	66.5	14.0	60.0	0.21	72.3	11.3	68.0	0.16
2006	67.3	13.9	61.0	0.21	74.2	10.4	70.0	0.14

Source: Authors’ calculations using data from LAMBdA (Palloni et al., 2014).

Contrary to Demetrius, Keyfitz (1977) uses demographic principles to derive an analogous formula of population entropy. Keyfitz develops his concept while searching for an alternative indicator to assess changes in life expectancy associated with fractional declines in age-specific mortality rates. Both approaches lead to similar entropy formulations, although their focus is rather different as Demetrius (1979) emphasizes the net maternity function while Keyfitz (1977) focuses on changes in the mortality schedule.

A.2. Other interpretations of the entropy

While the entropy of a physical system has the same meaning regardless of the context - the higher the entropy the higher the disorder in the system - the many applications in human and non-human populations of the population entropy have resulted in a variety of context-specific interpretations. For example, population entropy has been associated with the fitness of an age-structured population (Demetrius, 1974), the life-history of a population (e.g., populations that only reproduce once have zero entropy—semelparous populations) (Demetrius, 1975), the rate of convergence of a population to its stable equivalent age distribution (Tuljapurkar, 1982, 1993), the general shape of the survival function (e.g., entropy = 0 if all mortality concentrates at one age or entropy = 1 if mortality is the same at all ages) (Demetrius, 1978; Keyfitz and Caswell, 2005), and the “degree” of concavity of the survival function, such that increasing concentration of deaths at some age corresponds to lower entropy values (e.g., low entropy in high-income countries as deaths concentrate at older ages) (Wilmoth and Horiuchi, 1999; Nagnur, 1986).

Table 3.

Contribution to changes in the life table entropy (H) due to changes in life expectancy at birth (e₀) and in life expectancy lost due to death (e^†) for males and females for 18 countries in Latin America.

Period	Males						Females
	Change in H		Overall cont		% cont		Change in H		Overall cont		% cont
	Observed	Predicteda	$\frac{\delta e^{†}}{e^{†}}$	$-\frac{\delta e_0}{e_0}$	$\frac{\delta e^{†}}{e^{†}}$	$\frac{\delta e_0}{e_0}$	Observed	Predicteda	$\frac{\delta e^{†}}{e^{†}}$	$-\frac{\delta e_0}{e_0}$	$\frac{\delta e^{†}}{e^{†}}$	$\frac{\delta e_0}{e_0}$
Argentina
1953–1965	−0.026	−0.028	−0.018	−0.010	65.2	34.8	−0.036	−0.035	−0.023	−0.012	65.5	34.5
1965–1975	−0.015	−0.016	−0.010	−0.006	63.6	36.4	−0.018	−0.017	−0.012	−0.005	69.1	30.9
1975–1985	−0.032	−0.033	−0.022	−0.010	68.2	31.8	−0.029	−0.029	−0.023	−0.006	77.9	22.1
1985–1996	−0.012	−0.011	−0.007	−0.005	59.9	40.1	−0.014	−0.014	−0.010	−0.004	72.3	27.7
1996–2005	−0.018	−0.017	−0.012	−0.005	70.3	29.7	−0.011	−0.011	−0.009	−0.002	77.7	22.3
Brazil
1985–1995	−0.038	−0.035	−0.018	−0.017	51.9	48.1	−0.039	−0.034	−0.019	−0.014	57.5	42.5
1995–2005	−0.033	−0.032	−0.020	−0.012	62.9	37.1	−0.028	−0.028	−0.020	−0.007	73.6	26.4
Chile
1956–1965	−0.058	−0.062	−0.033	−0.029	53.4	46.6	−0.066	−0.069	−0.039	−0.030	57.0	43.0
1965–1976	−0.087	−0.090	−0.049	−0.041	54.6	45.4	−0.088	−0.090	−0.058	−0.032	64.4	35.6
1976–1987	−0.058	−0.058	−0.037	−0.021	64.0	36.0	−0.056	−0.055	−0.039	−0.015	71.7	28.3
1987–1997	−0.031	−0.029	−0.019	−0.010	66.4	33.6	−0.025	−0.023	−0.017	−0.006	75.1	24.9
1997–2006	−0.019	−0.019	−0.014	−0.005	74.3	25.7	−0.015	−0.014	−0.011	−0.003	80.5	19.5
Colombia
1957–1968	−0.087	−0.090	−0.047	−0.043	51.9	48.1	−0.084	−0.087	−0.044	−0.043	50.6	49.4
1968–1979	−0.072	−0.075	−0.040	−0.035	53.6	46.4	−0.084	−0.085	−0.053	−0.032	62.2	37.8
1979–1989	−0.016	−0.016	−0.010	−0.006	61.4	38.6	−0.041	−0.041	−0.030	−0.011	72.4	27.6
1989–1999	−0.024	−0.022	−0.011	−0.010	52.7	47.3	−0.025	−0.022	−0.015	−0.008	66.5	33.5
1999–2008	−0.036	−0.035	−0.025	−0.010	70.4	29.6	−0.021	−0.021	−0.016	−0.005	76.6	23.4
Costa Rica
1956–1968	−0.060	−0.061	−0.038	−0.024	61.4	38.6	−0.067	−0.067	−0.043	−0.025	63.5	36.5
1968–1978	−0.068	−0.068	−0.044	−0.024	64.5	35.5	−0.073	−0.072	−0.049	−0.023	67.7	32.3
1978–1992	−0.037	−0.037	−0.028	−0.009	76.2	23.8	−0.035	−0.035	−0.028	−0.007	79.2	20.8
1992–2005	−0.011	−0.010	−0.006	−0.003	65.0	35.0	−0.013	−0.013	−0.010	−0.003	74.7	25.3
Cuba
1961–1975	−0.050	−0.048	−0.031	−0.017	64.2	35.8	−0.054	−0.051	−0.036	−0.016	69.6	30.4
1975–1991	−0.025	−0.025	−0.021	−0.004	82.6	17.4	−0.027	−0.028	−0.023	−0.004	83.7	16.3
1991–2006	−0.017	−0.018	−0.013	−0.005	71.6	28.4	−0.018	−0.016	−0.011	−0.005	71.4	28.6
Dominican Republic
1955–1965	−0.086	−0.089	−0.033	−0.056	37.4	62.6	−0.091	−0.093	−0.036	−0.057	39.0	61.0
1965–1975	−0.058	−0.058	−0.034	−0.024	58.8	41.2	−0.060	−0.061	−0.036	−0.025	58.9	41.1
1975–1987	−0.057	−0.057	−0.033	−0.024	57.7	42.3	−0.074	−0.073	−0.043	−0.025	59.4	40.6
1987–1997	−0.032	−0.030	−0.016	−0.014	53.4	46.6	−0.038	−0.036	−0.024	−0.013	65.6	34.4
1997–2006	−0.026	−0.027	−0.021	−0.006	77.5	22.5	−0.021	−0.021	−0.018	−0.004	82.8	17.2
Ecuador
1956–1968	−0.117	−0.121	−0.040	−0.081	32.9	67.1	−0.113	−0.116	−0.048	−0.067	41.9	58.1
1968–1978	−0.065	−0.066	−0.034	−0.032	51.3	48.7	−0.078	−0.079	−0.041	−0.038	52.5	47.5
1978–1986	−0.064	−0.065	−0.041	−0.025	62.3	37.7	−0.067	−0.068	−0.046	−0.022	67.1	32.9
1986–1995	−0.032	−0.031	−0.019	−0.012	61.9	38.1	−0.039	−0.039	−0.027	−0.012	68.9	31.1
1995–2005	−0.037	−0.036	−0.024	−0.012	66.4	33.6	−0.035	−0.035	−0.026	−0.009	74.8	25.2
El Salvador
1955–1966	−0.113	−0.117	−0.033	−0.084	28.4	71.6	−0.120	−0.123	−0.042	−0.082	33.8	66.2
1966–1981	−0.046	−0.047	−0.024	−0.023	51.2	48.8	−0.098	−0.097	−0.046	−0.051	47.0	53.0
1981–1999	−0.111	−0.113	−0.057	−0.056	50.5	49.5	−0.106	−0.109	−0.071	−0.038	64.8	35.2
1999–2008	−0.023	−0.023	−0.016	−0.007	68.1	31.9	−0.022	−0.022	−0.017	−0.004	79.9	20.1
Guatemala
1957–1968	−0.083	−0.086	−0.030	−0.056	35.2	64.8	−0.098	−0.099	−0.022	−0.077	22.3	77.7
1968–1977	−0.067	−0.069	−0.022	−0.047	32.4	67.6	−0.084	−0.085	−0.027	−0.057	32.4	67.6
1977–1987	−0.077	−0.081	−0.039	−0.042	48.5	51.5	−0.089	−0.092	−0.048	−0.044	51.8	48.2
1987–1998	−0.065	−0.063	−0.029	−0.034	46.2	53.8	−0.076	−0.074	−0.043	−0.031	58.6	41.4
1998–2005	−0.037	−0.037	−0.024	−0.013	63.9	36.1	−0.029	−0.029	−0.021	−0.008	74.0	26.0
Honduras
1955–1967	−0.160	−0.163	−0.021	−0.142	12.9	87.1	−0.169	−0.163	−0.006	−0.157	3.6	96.4
1967–1981	−0.155	−0.150	−0.034	−0.116	22.6	77.4	−0.164	−0.156	−0.047	−0.108	30.3	69.7
1981–1989	−0.055	−0.053	−0.029	−0.024	54.2	45.8	−0.055	−0.053	−0.032	−0.021	60.0	40.0
Mexico
1955–1965	−0.091	−0.096	−0.041	−0.055	42.7	57.3	−0.105	−0.104	−0.041	−0.063	39.5	60.5
1965–1975	−0.059	−0.058	−0.022	−0.035	38.9	61.1	−0.061	−0.060	−0.033	−0.027	55.1	44.9
1975–1985	−0.063	−0.063	−0.041	−0.022	64.6	35.4	−0.065	−0.066	−0.046	−0.020	70.1	29.9
1985–1995	−0.040	−0.040	−0.027	−0.014	66.0	34.0	−0.033	−0.034	−0.025	−0.009	74.2	25.8
1995–2005	−0.035	−0.035	−0.026	−0.010	72.4	27.6	−0.026	−0.026	−0.021	−0.005	80.6	19.4
Nicaragua
1956–1967	−0.102	−0.107	−0.021	−0.086	19.8	80.2	−0.094	−0.099	−0.035	−0.064	35.2	64.8
1967–1983	−0.127	−0.130	−0.048	−0.082	37.0	63.0	−0.152	−0.153	−0.067	−0.086	43.9	56.1
1983–2000	‒0.099	−0.102	−0.061	−0.041	59.7	40.3	−0.074	−0.076	−0.052	−0.023	69.1	30.9
2000–2007	−0.021	−0.021	−0.017	−0.004	80.2	19.8	−0.020	−0.020	−0.017	−0.004	82.5	17.5
Panama
1955–1965	−0.057	−0.057	−0.032	−0.025	56.8	43.2	−0.067	−0.067	−0.039	−0.028	58.3	41.7
1965–1975	−0.045	−0.044	−0.027	−0.017	60.7	39.3	−0.049	−0.049	−0.032	−0.017	65.1	34.9
1975–1985	−0.039	−0.036	−0.021	−0.015	58.2	41.8	−0.047	−0.044	−0.029	−0.015	65.5	34.5
1985–1995	−0.014	−0.014	−0.010	−0.004	73.0	27.0	−0.019	−0.018	−0.014	−0.004	76.5	23.5
Paraguay
1956–1967	−0.035	−0.036	−0.023	−0.014	62.0	38.0	−0.043	−0.043	−0.029	−0.014	67.0	33.0
1967–1977	−0.017	−0.018	−0.012	−0.006	64.8	35.2	−0.022	−0.022	−0.014	−0.008	64.1	35.9
1977–1987	−0.033	−0.033	−0.023	−0.010	71.1	28.9	−0.037	−0.038	−0.028	−0.010	73.5	26.5
1987–1997	−0.003	−0.004	−0.003	−0.001	78.2	21.8	−0.012	−0.012	−0.009	−0.003	75.5	24.5
1997–2006	−0.032	−0.030	−0.021	−0.010	67.8	32.2	−0.030	−0.030	−0.022	−0.008	74.6	25.4
Peru
1966–1976	−0.108	−0.110	−0.035	−0.075	31.9	68.1	−0.113	−0.114	−0.046	−0.068	40.7	59.3
1976–1987	−0.078	−0.079	−0.044	−0.035	55.3	44.7	−0.081	−0.082	−0.049	−0.034	58.9	41.1
1987–2000	−0.070	−0.071	−0.046	−0.025	64.9	35.1	−0.074	−0.075	−0.051	−0.024	68.3	31.7
2000–2008	−0.036	−0.036	−0.026	−0.010	72.9	27.1	−0.031	−0.031	−0.025	−0.007	78.7	21.3
Uruguay
1969–1980	−0.023	−0.024	−0.015	−0.009	63.6	36.4	−0.026	−0.025	−0.017	−0.007	70.2	29.8
1980–1990	−0.022	−0.022	−0.016	−0.006	70.7	29.3	−0.021	−0.020	−0.015	−0.005	74.6	25.4
1990–2000	−0.010	−0.010	−0.006	−0.004	60.7	39.3	−0.011	−0.010	−0.008	−0.003	74.1	25.9
2000–2007	−0.012	−0.011	−0.008	−0.004	68.1	31.9	−0.008	−0.008	−0.007	−0.002	79.3	20.7
Venezuela
1955–1966	−0.076	−0.079	−0.046	−0.033	58.2	41.8	−0.084	−0.086	−0.053	−0.033	61.3	38.7
1966–1976	−0.023	−0.023	−0.017	−0.006	74.6	25.4	−0.038	−0.037	−0.026	−0.012	68.4	31.6
1976–1985	−0.030	−0.031	−0.019	−0.012	61.5	38.5	−0.031	−0.031	−0.023	−0.009	72.5	27.5
1985–1995	−0.011	−0.010	−0.005	−0.005	49.3	50.7	−0.017	−0.016	−0.012	−0.004	72.4	27.6
1995–2006	−0.005	−0.004	−0.002	−0.002	43.8	56.2	−0.016	−0.016	−0.012	−0.004	73.4	26.6

^aPredicted values are estimated as: $\delta H\left[S\left(x,t_1\right)\right]\approx H\left[S\left(x,t_1\right)\right]\left(\frac{\delta e^{†}[S(x)]}{e^{†}\left(0,t_1\right)}-\frac{\delta e_0[S(x)]}{e\left(0,t_1\right)}\right)$(see Appendix F.2); ‘cont’, contribution.

Source: Authors’ calculations using data from LAMBdA (Palloni et al., 2014) and formulas from Proposition 1.

Table 4.

Contribution to changes in the life table entropy (H) due to changes in early (premature) and late (older) deaths in life expectancy at birth (e₀) and in life expectancy lost due to death (e^†) for males and females for 18 countries in Latin America.

Period	Males									Females
		Overall contribution				% contribution					Overall contribution				% contribution
	Pred	δe†/e†		−δe0/e0		δe†/e†		δe0/e0		Pred	δe†/e†		−δe0/e0		δe†/e†		δe0/e0
	Δ in Ha	Early	Late	Early	Late	Early	Late	Early	Late	Δ in Ha	Early	Late	Early	Late	Early	Late	Early	Late
Argentina
1953–1965	−0.028	−0.018	0.000	−0.006	−0.004	64.4	0.9	20.5	14.3	−0.035	−0.023	0.001	−0.006	−0.005	67.5	−2.0	18.7	15.8
1965–1975	−0.016	−0.012	0.002	−0.003	−0.002	78.9	−15.3	22.0	14.4	−0.017	−0.014	0.002	−0.003	−0.002	83.1	−14.0	18.7	12.2
1975–1985	−0.033	−0.021	−0.002	−0.005	−0.005	62.8	5.4	16.5	15.3	−0.029	−0.021	−0.002	−0.004	−0.002	70.1	7.8	14.3	7.8
1985–1996	−0.011	−0.008	0.001	−0.002	−0.003	69.9	−10.0	15.5	24.5	−0.014	−0.011	0.001	−0.002	−0.002	76.2	−4.0	13.0	14.8
1996–2005	−0.017	−0.011	−0.001	−0.002	−0.003	63.7	6.6	13.4	16.3	−0.011	−0.009	0.001	−0.001	−0.001	82.8	−5.0	12.6	9.7
Brazil
1985–1995	−0.035	−0.023	0.005	−0.007	−0.010	65.7	−13.9	21.1	27.0	−0.034	−0.027	0.008	−0.007	−0.008	79.7	−22.2	19.7	22.7
1995–2005	−0.032	−0.020	0.000	−0.006	−0.006	63.4	−0.4	17.3	19.8	−0.028	−0.021	0.000	−0.004	−0.003	74.7	−1.2	14.7	11.7
Chile
1956–1965	−0.062	−0.027	−0.006	−0.014	−0.015	44.4	9.0	22.7	23.9	−0.069	−0.032	−0.007	−0.014	−0.015	46.2	10.8	20.8	22.2
1965–1976	−0.090	−0.044	−0.005	−0.018	−0.022	49.6	5.0	20.6	24.8	−0.090	−0.050	−0.007	−0.018	−0.014	56.1	8.3	19.6	16.0
1976–1987	−0.058	−0.034	−0.003	−0.010	−0.011	58.2	5.8	17.1	18.9	−0.055	−0.036	−0.003	−0.008	−0.007	65.9	5.8	15.2	13.0
1987–1997	−0.029	−0.018	−0.002	−0.004	−0.006	61.1	5.2	13.6	20.1	−0.023	−0.017	0.000	−0.003	−0.003	75.3	−0.2	12.3	12.6
1997–2006	−0.019	−0.012	−0.002	−0.002	−0.003	63.0	11.3	11.8	13.9	−0.014	−0.010	−0.001	−0.001	−0.001	72.5	8.0	9.9	9.6
Colombia
1957–1968	−0.090	−0.030	−0.017	−0.016	−0.027	33.1	18.9	18.2	29.9	−0.087	−0.034	−0.010	−0.017	−0.026	38.7	11.9	19.2	30.2
1968–1979	−0.075	−0.039	−0.001	−0.016	−0.019	52.2	1.4	21.5	24.9	−0.085	−0.046	−0.007	−0.017	−0.015	53.9	8.3	19.7	18.0
1979–1989	−0.016	−0.013	0.003	−0.004	−0.003	76.7	−15.3	22.2	16.4	−0.041	−0.028	−0.002	−0.007	−0.005	66.9	5.5	16.6	11.0
1989–1999	−0.022	−0.011	0.000	−0.003	−0.007	52.3	0.3	15.2	32.1	−0.022	−0.014	−0.001	−0.003	−0.005	63.8	2.7	12.9	20.6
1999–2008	−0.035	−0.019	−0.005	−0.005	−0.005	55.0	15.4	14.8	14.8	−0.021	−0.013	−0.003	−0.002	−0.003	62.6	14.0	10.9	12.5
Costa Rica
1956–1968	−0.061	−0.031	−0.007	−0.013	−0.011	50.6	10.8	20.4	18.2	−0.067	−0.035	−0.008	−0.013	−0.012	52.0	11.5	19.1	17.4
1968–1978	−0.068	−0.043	−0.001	−0.013	−0.010	63.7	0.8	20.0	15.5	−0.072	−0.047	−0.002	−0.013	−0.011	65.0	2.7	17.7	14.6
1978–1992	−0.037	−0.025	−0.003	−0.006	−0.003	67.2	8.9	15.0	CO CO*	−0.035	−0.025	−0.002	−0.005	−0.003	72.7	6.5	13.0	7.9
1992–2005	−0.010	−0.008	0.001	−0.001	−0.002	80.0	−15.0	14.3	20.7	−0.013	−0.010	0.001	−0.001	−0.002	80.1	−5.4	11.1	14.2
Cuba
1961–1975	−0.048	−0.030	−0.001	−0.008	−0.009	62.5	1.6	16.9	19.0	−0.051	−0.032	−0.004	−0.008	−0.008	61.7	7.9	15.2	15.2
1975–1991	−0.025	−0.017	−0.004	−0.003	−0.001	66.7	15.9	13.4	4.0	−0.028	−0.020	−0.003	−0.004	−0.001	72.5	11.2	12.7	3.6
1991–2006	−0.018	−0.015	0.002	−0.003	−0.002	85.5	−13.9	15.1	13.3	−0.016	−0.015	0.004	−0.002	−0.002	97.0	−25.6	14.2	14.4
Dominican Republic
1955–1965	−0.089	−0.022	−0.011	−0.014	−0.042	25.1	12.3	15.6	47.0	−0.093	−0.025	−0.011	−0.015	−0.042	27.2	11.8	16.0	45.0
1965–1975	−0.058	−0.025	−0.009	−0.012	−0.012	43.3	15.6	21.0	20.2	−0.061	−0.028	−0.008	−0.013	−0.013	45.8	13.1	20.5	20.6
1975–1987	−0.057	−0.031	−0.002	−0.012	−0.012	53.9	3.7	21.1	21.2	−0.073	−0.038	−0.005	−0.014	−0.016	52.2	7.2	18.7	21.9
1987–1997	−0.030	−0.020	0.003	−0.006	−0.008	64.8	−11.4	20.1	26.5	−0.036	−0.024	0.000	−0.006	−0.006	66.7	−1.1	17.1	17.3
1997–2006	−0.027	−0.017	−0.004	−0.004	−0.002	62.0	15.5	16.7	5.8	−0.021	−0.016	−0.002	−0.003	0.000	73.1	9.6	15.0	2.2
Ecuador
1956–1968	−0.121	−0.022	−0.018	−0.015	−0.066	18.1	14.8	12.7	54.4	−0.116	−0.026	−0.022	−0.017	−0.050	22.7	19.2	14.8	43.3
1968–1978	−0.066	−0.030	−0.004	−0.015	−0.017	45.0	6.3	23.0	25.7	−0.079	−0.034	−0.007	−0.016	−0.021	43.5	9.0	20.5	27.0
1978–1986	−0.065	−0.033	−0.008	−0.013	−0.011	50.7	11.6	20.5	17.2	−0.068	−0.039	−0.007	−0.014	−0.009	57.4	9.7	20.2	12.8
1986–1995	−0.031	−0.021	0.002	−0.007	−0.005	68.0	−6.1	20.9	17.2	−0.039	−0.027	0.000	−0.007	−0.005	69.7	−0.7	17.8	13.3
1995–2005	−0.036	−0.022	−0.002	−0.006	−0.006	60.5	5.9	16.4	17.2	−0.035	−0.025	−0.002	−0.005	−0.004	70.5	4.3	14.6	10.6
El Salvador
1955–1966	−0.117	−0.018	−0.016	−0.013	−0.071	15.0	13.5	11.3	60.3	−0.123	−0.024	−0.018	−0.017	−0.065	19.5	14.3	13.4	52.8
1966–1981	−0.047	−0.028	0.004	−0.015	−0.008	58.7	−7.6	32.8	16.0	−0.097	−0.041	−0.004	−0.020	−0.031	42.3	4.6	20.9	32.1
1981–1999	−0.113	−0.049	−0.008	−0.023	−0.033	43.0	7.5	20.3	29.2	−0.109	−0.064	−0.007	−0.022	−0.016	58.4	6.4	20.0	15.2
1999–2008	−0.023	−0.013	−0.003	−0.004	−0.003	54.2	13.9	17.1	14.8	−0.022	−0.015	−0.002	−0.003	−0.001	70.9	8.9	14.1	6.1
Guatemala
1957–1968	−0.086	−0.010	−0.021	−0.008	−0.048	11.2	24.0	9.0	55.8	−0.099	−0.011	−0.011	−0.009	−0.068	11.5	10.8	8.8	68.8
1968–1977	−0.069	−0.019	−0.003	−0.013	−0.034	27.4	5.0	18.2	49.4	−0.085	−0.023	−0.005	−0.014	−0.043	26.5	5.8	16.6	51.0
1977–1987	−0.081	−0.031	−0.008	−0.017	−0.025	38.6	9.9	21.2	30.3	−0.092	−0.039	−0.009	−0.019	−0.025	42.1	9.7	20.7	27.5
1987–1998	−0.063	−0.032	0.003	−0.014	−0.020	51.4	−5.3	21.7	32.1	−0.074	−0.042	−0.002	−0.015	−0.016	56.4	2.2	20.1	21.3
1998–2005	−0.037	−0.016	−0.008	−0.005	−0.008	43.2	20.7	14.7	21.4	−0.029	−0.017	−0.004	−0.004	−0.003	60.3	13.7	15.3	10.8
Honduras
1955–1967	−0.163	−0.009	−0.012	−0.008	−0.134	5.4	7.5	4.6	82.4	−0.163	−0.012	0.006	−0.010	−0.147	7.3	−3.7	5.9	90.5
1967–1981	−0.150	−0.045	0.011	−0.028	−0.088	30.1	−7.5	18.8	58.6	−0.156	−0.054	0.007	−0.031	−0.078	34.8	−4.5	19.8	49.9
1981–1989	−0.053	−0.029	0.000	−0.011	−0.013	54.1	0.1	20.6	25.2	−0.053	−0.032	0.000	−0.010	−0.011	60.8	−0.8	19.3	20.7
Mexico
1955–1965	−0.096	−0.027	−0.013	−0.017	−0.038	28.6	14.0	17.9	39.4	−0.104	−0.035	−0.006	−0.020	−0.043	33.7	5.8	19.2	41.3
1965–1975	−0.058	−0.026	0.004	−0.012	−0.023	45.2	−6.4	21.6	39.6	−0.060	−0.031	−0.002	−0.013	−0.014	52.2	2.9	21.1	23.8
1975–1985	−0.063	−0.031	−0.010	−0.012	−0.010	48.9	15.7	18.9	16.5	−0.066	−0.038	−0.009	−0.012	−0.008	57.2	12.9	18.0	11.9
1985–1995	−0.040	−0.024	−0.003	−0.007	−0.007	58.6	7.5	17.7	16.2	−0.034	−0.023	−0.001	−0.005	−0.003	69.9	4.3	15.8	10.0
1995–2005	−0.035	−0.023	−0.003	−0.006	−0.004	64.3	8.1	16.0	11.6	−0.026	−0.019	−0.002	−0.003	−0.002	73.6	7.0	13.4	6.0
Nicaragua
1956–1967	−0.107	−0.016	−0.005	−0.012	−0.074	14.8	4.9	11.6	68.6	−0.099	−0.021	−0.014	−0.015	−0.049	21.4	13.8	14.9	49.9
1967–1983	−0.130	−0.041	−0.007	−0.025	−0.057	31.6	5.4	19.1	43.9	−0.153	−0.054	−0.013	−0.029	−0.056	35.5	8.4	19.2	36.8
1983–2000	−0.102	−0.049	−0.012	−0.020	−0.021	47.8	11.9	19.7	20.6	−0.076	−0.045	−0.007	−0.014	−0.009	59.7	9.4	18.6	12.4
2000–2007	−0.021	−0.013	−0.004	−0.003	−0.001	62.5	17.7	16.7	3.1	−0.020	−0.015	−0.002	−0.003	0.000	71.9	10.5	15.2	2.4
Panama
1955–1965	−0.057	−0.027	−0.006	−0.011	−0.014	47.0	9.8	19.1	24.1	−0.067	−0.029	−0.010	−0.012	−0.016	43.2	15.0	17.3	24.4
1965–1975	−0.044	−0.027	0.000	−0.009	−0.009	61.1	−0.4	19.7	19.6	−0.049	−0.030	−0.002	−0.009	−0.008	60.5	4.6	18.5	16.5
1975–1985	−0.036	−0.024	0.003	−0.006	−0.009	67.4	−9.3	17.7	24.1	−0.044	−0.028	−0.001	−0.007	−0.008	64.2	1.3	15.4	19.0
1985–1995	−0.014	−0.010	0.000	−0.002	−0.002	70.5	2.5	15.2	11.8	−0.018	−0.014	0.000	−0.003	−0.002	76.9	−0.4	14.1	9.5
Paraguay
1956–1967	−0.036	−0.019	−0.004	−0.007	−0.007	51.7	10.3	19.7	18.3	−0.043	−0.020	−0.008	−0.007	−0.007	47.6	19.4	17.5	15.6
1967–1977	−0.018	−0.013	0.001	−0.004	−0.002	69.6	−4.8	22.8	12.4	−0.022	−0.014	0.000	−0.004	−0.004	64.5	−0.4	19.9	16.0
1977–1987	−0.033	−0.019	−0.004	−0.006	−0.004	58.7	12.4	17.8	11.2	−0.038	−0.022	−0.005	−0.006	−0.004	59.2	14.3	16.4	10.1
1987–1997	−0.004	−0.004	0.001	−0.001	0.000	92.5	−14.2	21.7	0.0	−0.012	−0.010	0.001	−0.002	−0.001	80.9	−5.4	18.0	6.5
1997–2006	−0.030	−0.017	−0.004	−0.004	−0.005	56.2	11.7	14.4	17.7	−0.030	−0.018	−0.004	−0.004	−0.004	61.4	13.2	13.1	12.3
Peru
1966–1976	−0.110	−0.029	−0.006	−0.019	−0.056	26.6	5.4	17.1	51.0	−0.114	−0.032	−0.014	−0.019	−0.048	28.2	12.5	17.0	42.3
1976–1987	−0.079	−0.035	−0.008	−0.016	−0.019	44.7	10.6	20.9	23.8	−0.082	−0.040	−0.009	−0.017	−0.017	48.3	10.6	20.6	20.5
1987–2000	−0.071	−0.041	−0.006	−0.014	−0.011	57.0	7.9	19.8	15.2	−0.075	−0.046	−0.005	−0.014	−0.010	61.9	6.4	18.9	12.7
2000–2008	−0.036	−0.023	−0.003	−0.006	−0.004	63.6	9.3	16.1	11.0	−0.031	−0.022	−0.003	−0.005	−0.002	70.5	8.2	14.6	6.7
Uruguay
1969–1980	−0.024	−0.016	0.001	−0.004	−0.005	67.3	−3.7	17.6	18.8	−0.025	−0.017	0.000	−0.004	−0.004	70.3	−0.2	14.9	14.9
1980–1990	−0.022	−0.015	−0.001	−0.003	−0.003	66.1	4.6	15.4	13.9	−0.020	−0.016	0.000	−0.003	−0.002	75.9	−1.3	13.7	11.7
1990–2000	−0.010	−0.008	0.002	−0.002	−0.002	82.4	−21.7	16.9	22.4	−0.010	−0.009	0.001	−0.001	−0.001	87.1	−13.0	13.5	12.4
2000–2007	−0.011	−0.007	−0.001	−0.001	−0.002	58.1	10.0	11.5	20.4	−0.008	−0.006	0.000	−0.001	−0.001	73.3	6.0	10.6	10.1
Venezuela
1955–1966	−0.079	−0.039	−0.008	−0.017	−0.016	48.7	9.5	21.3	20.5	−0.086	−0.043	−0.010	−0.017	−0.016	50.1	11.2	20.2	18.5
1966–1976	−0.023	−0.014	−0.004	−0.004	−0.002	58.4	16.2	18.6	6.7	−0.037	−0.022	−0.004	−0.006	−0.006	58.2	10.1	16.5	15.1
1976–1985	−0.031	−0.020	0.001	−0.006	−0.006	63.6	−2.1	18.5	20.0	−0.031	−0.020	−0.002	−0.005	−0.004	65.0	7.5	15.1	12.3
1985–1995	−0.010	−0.006	0.001	−0.002	−0.003	63.2	−13.9	15.6	35.0	−0.016	−0.011	−0.001	−0.002	−0.002	66.2	6.2	12.9	14.7
1995–2006	−0.004	−0.001	0.000	0.000	−0.002	34.7	9.1	7.0	49.2	−0.016	−0.011	−0.001	−0.002	−0.002	68.1	5.3	12.2	14.4

^aPredicted change in H (Pred Δ in H) is estimated as: $\delta H\left[S\left(x,t_1\right)\right]\approx H\left[S\left(x,t_1\right)\right]\left\{\left[\frac{\delta e^{†}[S(x|x<a^{†})]}{e^{†}[S(x)]}+\frac{-\delta e_0|S(x|x<a^{†})]}{e_0[S(x)]}\right]+\left[\frac{\delta e^{†}[S(x|x\ge a^{†})]}{e^{†}[S(x)]}+\frac{-\delta e_0[S(x|x\ge a^{†})]}{e_0[S(x)]}\right]\right\}$(see Appendix F.2); Δ, change. The age that separates premature from older deaths, a^†, is shown in the Appendix Table 2.

Source: Authors’ calculations using data from LAMBdA (Palloni et al., 2014) and Eqs. (3.1)-(3.5).

In demography, most of the studies about population entropy follow Keyfitz’s principle by studying the relative change in life expectancy associated with changes in age-specific mortality rates. These studies have elucidated important properties of the entropy. For instance, Goldman and Lord (1986), Mitra (1979, 1978) and Vaupel (1986) re-expressed the entropy using life table notation as the weighted average of life expectancies at age x, which can be further described as the average years of future life that are lost by the observed deaths (Goldman and Lord, 1986), the proportional increase in life expectancy at birth if everyone’s first death were averted (Mitra, 1979; Vaupel, 1986), or alternatively, life expectancy lost due to death among those surviving to a given age (Vaupel and Canudas Romo, 2003; Zhang and Vaupel, 2009). This last definition, called e-dagger (e^†), was first coined by Vaupel (1986). This indicator has been further developed elsewhere (Vaupel and Canudas Romo, 2003; Zhang and Vaupel, 2009) and shown to be a useful indicator of life disparity (Vaupel et al., 2011; Shkolnikov et al., 2011).

A.3. The effect of changes in age-specific mortality on H

A population’s entropy also detects changes in age-specific mortality. To see this, consider first the case of constant mortality, where μ(s) = μ is constant⁵ and taken positive, for the moment. Then S(x) = e^−μx, and after inserting this into the formula for H (the negative of the parenthetical term in (2.3)) a straightforward calculation yields H = 1. The case when μ(s) = 0 - the zero mortality case⁶ - leads to S(x) = 1, ln S(x) = 0, and thus H = 0.⁷ Thus, we conclude that if the mortality function is constant across age, H = 0, 1. The contrapositive of this statement is that if H ≠ 0, 1 then the mortality function is non-constant across age. One more example further illustrates this point. Let us refer to this as the almost-constant mortality case, wherein

$$\mu (s)=\{\begin{array}{ll}{\mu }_1,\hfill & s\in {ℝ}_{\ge 0}-[a,b],\hfill \\ {\mu }_2,\hfill & s\in [a,b],\hfill \end{array}$$ (A.1)

where 0 < a < b and μ₁, μ₂ ≠ 0. We envision b − a to be small, so that the force of mortality is the constant μ₁ for most of the ages s, and only different (yet still constant) for a small subset of ages. The corresponding survival function is

$$S(x)=e^{(b-a)\left({\mu }_1-{\mu }_2\right)-{\mu }_{1}x},$$

and the corresponding entropy is

$$H=1-(b-a)\left({\mu }_1-{\mu }_2\right).$$

In the limit of b → a, the force of mortality becomes constant and H → 1, which verifies our earlier results of the constant mortality case. But when b ≠ a, the change across age in the force of mortality in (A.1) is detected by H. To summarize, for a given population, values of H ≠ 0, 1 immediately tell us that the population’s mortality function varies across age. Moreover, the almost-constant mortality case also highlights the sensitivity of H: no matter how small the difference b − a is, H detects the change in mortality, suggesting that H is “in general highly sensitive to variations in age-specific mortality” Demetrius (1979).

Because mortality is related to the survival function via (2.1), these results suggest that a population’s entropy may be a useful tool in characterizing its survivorship (in the cases when mortality is not constant across age). Indeed, in the literature H is often referred to as the “simple parameter” that can “characterize the shape of [survival] curves” Demetrius (1979). Often the “shape” refers to the degree of concavity (also convexity) of the survival curve, and we find several references agreeing that “H is a convenient summary of the degree of concavity in an l(x) column” Keyfitz and Caswell (2005, Sec. 4.3.2). We see clearly that as the concavity of the survival curves in Fig. 1(a) changes, the entropy H in Fig. 1(b) changes as well. Moreover, we note that decreasing H values - given by decreasing a-values - leads to increased survivorship.

Appendix B. Introduction to the calculus of variations

Consider the following calculus problem. Given a real-valued function y(x) of a real variable x that is differentiable on a given interval (a, b), approximate the change in y due in a small change ϵ in x from an initial point x₀ ∈ (a, b).

This problem can be solved easily by using differentials as follows. The assumed differentiability of y guarantees the existence of y′(x₀), defined by

$$y^{\prime }\left(x_0\right)=\underset{ϵ\to 0}{\lim }\frac{y\left(x_0+ϵ\right)-y\left(x_0\right)}{ϵ}.$$ (B.1)

The infinitesimal change dy in y due to an infinitesimal change dx in x is then defined by

$$dy=y^{\prime }\left(x_0\right)dx.$$

If we now suppose that the change in x is finite but small, we may drop the equality in (B.1) and use the approximation

$$y^{\prime }\left(x_0\right)\approx \frac{y\left(x_0+ϵ\right)-y\left(x_0\right)}{ϵ},\mathrm{or}\mathrm{equivalently},\Delta y\approx y^{\prime }\left(x_0\right)ϵ,$$ (B.2)

where Δy = y(x₀ + ϵ) − y(x₀). The last approximation in (B.2) has a simple interpretation: the change in input Δx = ϵ produces an approximate change in the function’s values given by the derivative y′(x₀) multiplied by Δx = ϵ. Moreover, from (B.2) we also see that the relative change in y, given by dy/y, is y′(x₀) multiplied by the relative change dx/x:

$$\begin{gathered} \frac{dy}{y}=y^{\prime }\left(x_0\right)\frac{dx}{x},\text{or},\mathrm{for}\mathrm{a}\mathrm{finite}\mathrm{but}\mathrm{small}\mathrm{change}\Delta x=ϵ, \\ \frac{\Delta y}{y}\approx y^{\prime }\left(x_0\right)\frac{ϵ}{x}. \end{gathered}$$ (B.3)

The related problem of approximating the change in a differentiable multivariable function y(x) in the direction of a vector v can be treated similarly. The analogue of y′(x₀) is the directional derivative y′(x₀) defined by

$$y^{\prime }\left({\mathbf{x}}_0\right)=\underset{ϵ\to 0}{\lim }\frac{y\left({\mathbf{x}}_0+ϵ\mathbf{v}\right)-y\left({\mathbf{x}}_0\right)}{ϵ}.$$ (B.4)

The approximate change in y in the direction v is then given by (B.2), with y′(x₀) replaced by y′(x₀).

Now, if the object of interest is not a function but instead a functional, the derivative (B.4) has an analogue. To describe it let us consider the simplest example of a functional: the familiar Riemann integral

$$I[y(x)]={\int }_a^{b}y(x)dx.$$ (B.5)

Given a function y(x) that is Riemann integrable over the interval [a, b], the functional I[y(x)] produces a number—the net signed area between a and b under the graph of y(x). We can now ask the same question as before: what is the approximate change in I[y(x)] due to a change in y(x)?

The answer to this question is an exercise in the calculus of variations. Following Sagan (1992) one first defines a variation of y(x) - denoted by δy(x) - by ϵv(x), where v(a) = v(b) = 0. (Intuitively, the curve y(x)+δy(x) in general closely resembles y(x) but is not equal to it.) Then, the first variation of a functional

$$J[y(x)]={\int }_a^{b}F(x,y(x))dx,$$

where F is a smooth function defined as follows.

Definition 2. Let v(x) and y(x) be two functions differentiable on a domain A, with v satisfying v(a) = v(b) = 0. Then the first variation δJ[y(x)] is defined by

$$\begin{gathered} \delta J[y(x)]=\underset{ϵ\to 0}{\lim }\frac{J[y(x)+\delta y(x)]-J[y(x)]}{ϵ} \\ ={\left[\frac{\partial }{\partial ϵ}J[y(x)+\delta y(x)]\right]}_{ϵ=0} \\ ={\left[\frac{\partial }{\partial ϵ}J[y(x)+ϵv(x)]\right]}_{ϵ=0} \end{gathered}$$ (B.6)

whenever the limit exists.

As in (B.4), this can be thought of as the derivative of J[y(x)] “in the direction of v(x)”.

In practice, the process of calculating δJ begins in one of two ways. In the first, one is given a family of varied curves parameterized by some parameter ϵ. In this case (B.6) is calculated by Taylor expanding these varied curves in powers of ϵ. For example, for the functional (B.5) let us consider the effect of the variations e^(1+ϵ)x of the function e^x on I[e^x]. Here y(x) + δy(x) = e^(1+ϵ)x, and to calculate (B.6) we Taylor expand the varied curves:

$$e^{(1+ϵ)x}=e^x{e}^{ϵx}=e^x\left(1+ϵx+{ϵ}^2\frac{x^2}{2!}+\cdots \right).$$

Then (B.6) gives

$$\begin{gathered} \delta I\left[e^x\right]={\left[\frac{\partial }{\partial ϵ}{\int }_a^b{e}^{(1+ϵ)x}dx\right]}_{ϵ=0} \\ ={\left[\frac{\partial }{\partial ϵ}{\int }_a^b{e}^x\left(1+ϵx+{ϵ}^2\frac{x^2}{2!}+\cdots \right)dx\right]}_{ϵ=0}={\int }_a^{b}x{e}^{x}dx. \end{gathered}$$

To interpret this last result, we note that as in (B.2) we may write (Theorem 1.5 Sagan, 1992)

$$\Delta J[y(x)]=J[y(x)+\delta y(x)]-J[y(x)]\approx ϵ\delta J[y(x)]$$ (B.7)

when ϵ is small. For example, if we choose a = 0 and b = 1 in the e^x example and consider the variation to be y(x) + δy(x) = e^(1.01)x, then

$$\Delta I\left[e^x\right]=I\left[e^{(1.01)x}\right]-I\left[e^x\right]\approx (0.01){\int }_0^{1}x{e}^{x}dx=\mathrm{0.01.}$$

This compares well with the actual increment I[e^(1.01)x] − I[e^x] = 01004.

In the second approach to calculating the first variation δJ one is given the variation δy. For example, for the functional (B.5) we have δy = ϵv(x)

$$\begin{gathered} \delta I[y(x)]=\underset{ϵ\to 0}{\lim }\frac{I[y(x)+\delta y(x)]-I[y(x)]}{ϵ} \\ =\underset{ϵ\to 0}{\lim }\frac{{\int }_a^b(y(x)+ϵv(x))dx-{\int }_a^{b}y(x)dx}{ϵ}={\int }_a^{b}v(x)dx. \end{gathered}$$

Using (B.7), we then have

$$\Delta I[y(x)]\approx ϵ{\int }_a^{b}v(x)dx,$$

which tells us that for small enough ϵ, changing the integrand y(x) to y(x) + ϵv(x) changes the net signed area by approximately ϵ multiplied by the net signed area of v(x), a conclusion made even more clear by drawing a few example graphs.

The preceding development has focused on the analogue of the first derivative in the calculus of variations. But as in the case with functions, where higher-order derivatives can be defined, we can also define higher-order variations of functionals.

Definition 3. Let y(x; ϵ) be a family of smooth varied curves for the function y(x) such that for all ϵ we have y(a; ϵ) = y(a) and y(b; ϵ) = y(b). Define δy(x) = y(x; ϵ) − y(x) and let

$$\delta y(x)=ϵv(x)+{ϵ}^2{w}_1(x)+\cdots +{ϵ}^n{w}_{n+1}(x)+\cdots$$

be the Taylor expansion in powers of ϵ of δy(x). Then the nth variation δⁿJ[y(x)] is defined by

$${\delta }^{n}J[y(x)]={\left[\frac{{\partial }^n}{\partial {ϵ}^n}J[y(x)+\delta y(x)]\right]}_{ϵ=0}$$

whenever the derivative exists.

We note that in the case of n = 1 this definition reduces to definition (B.6).

For instance, continuing with the e^x example, we have

$$\begin{gathered} {\delta }^{2}I\left[e^x\right]={\left[\frac{{\partial }^2}{\partial {ϵ}^2}{\int }_a^b{e}^x\left(1+ϵx+{ϵ}^2\frac{x^2}{2!}+\cdots \right)dx\right]}_{ϵ=0} \\ ={\int }_a^b{x}^2{e}^{x}dx. \end{gathered}$$

We can then extend (B.7) to second order in ϵ (Theorem 1.8.1 Sagan, 1992):

$$J[y(x)+\delta y(x)]-J[y(x)]\approx ϵ\delta J[y(x)]+\frac{{ϵ}^2}{2}{\delta }^{2}J[y(x)]$$ (B.8)

when ϵ is small. For example, choosing a = 0 and b = 1 in the e^x example and again considering the variation to be y(x) + δy(x) = e^(1.01)x, then

$$\begin{gathered} I\left[e^{(1.01)x}\right]-I\left[e^x\right]\approx (0.01){\int }_0^{1}x{e}^{x}dx+\frac{{(0.01)}^2}{2}{\int }_0^1{x}^2{e}^{x}dx \\ =0.0100359, \end{gathered}$$

which is an even better approximation to the actual increment I[e^(1.01)x ] − I[e^x] = 0.01004.

Finally, motivated by (B.3), we make the following definition.

Definition 4. The relative change of a functional J[y(x)] is defined by

$$\frac{\delta J[y(x)]}{J[y(x)]}$$

everywhere J[y(x)] is nonzero.

Appendix C. Proofs of propositions

Proof of Proposition 1.

Let δS(x) = ϵv(x) be a variation of S(x), i.e. v(x) is a smooth function that vanishes at zero and as x → ∞.

• 1To show: $\frac{\delta H}{H}=\frac{\delta e^{†}}{e^{†}}-\frac{\delta e_0}{e_0}.$

Proof. We begin with the observation that H[S + δS] = e^†[S + δS]/e₀ [S + δS] can be written as

$$\begin{gathered} 0=H[S+\delta S]e_0[S+\delta S]-e^{†}[S+\delta S] \\ =H[S+ϵv]e_0[S+ϵv]-e^{†}[S+ϵv]. \end{gathered}$$

Now, taking the derivative with respect to ϵ yields

$$\begin{gathered} \frac{\partial H}{\partial ϵ}[S+ϵv]e_0[S+ϵv]+H[S+ϵv]\frac{\partial e_0}{\partial ϵ}[S+ϵv] \\ -\frac{\partial e^{†}}{\partial ϵ}[S+ϵv]=0, \end{gathered}$$ (C.1)

Setting ϵ = 0 now gives

$$\delta H[S]e_0[S]+H[S]\delta e_0[S]-\delta e^{†}[S]=0.$$ (C.2)

Solving for δH[S] yields

$$\begin{gathered} \delta H=\frac{\delta e^{†}-H\delta e_0}{e_0}\Rightarrow \frac{\delta H}{H}=\frac{e_0}{e^{†}}\left(\frac{\delta e^{†}}{e_0}-\frac{e^{†}}{e_0}\frac{\delta e_0}{e_0}\right) \\ =\frac{\delta e^{†}}{e^{†}}-\frac{\delta e_0}{e_0}. \end{gathered}$$

We now show that δe^† and δe₀ are given by (2.6). By (B.6) we have

$$\begin{gathered} \frac{\partial e^{†}}{\partial ϵ}[S(x)+ϵv(x)] \\ =-\frac{\partial }{\partial ϵ}\left[{\int }_0^{\infty }(S(x)+ϵv(x))\ln (S(x)+ϵv(x))dx\right] \\ =-{\int }_0^{\infty }v(x)[\ln (S(x)+ϵv(x))+1]dx. \end{gathered}$$

Evaluating this expression at ϵ = 0 yields

$$\begin{gathered} \delta e^{†}[S(x)]=-{\int }_0^{\infty }v(x)[\ln (S(x))+1]dx \\ =-{\int }_0^{\infty }v(x)dx-{\int }_0^{\infty }\ln (S(x))v(x)dx, \end{gathered}$$

which is the first equation in (2.6). Lastly,

$$\begin{gathered} \frac{\partial e_0}{\partial ϵ}[S(x)+ϵv(x)]=\frac{\partial }{\partial ϵ}\left[{\int }_0^{\infty }(S(x)+ϵv(x))dx\right] \\ ={\int }_0^{\infty }v(x)dx. \end{gathered}$$

Thus,

$$\delta e_0[S(x)]={\int }_0^{\infty }v(x)dx,$$

reproducing the second equation in (2.6). □

• 2
  To show: The second variation

  $$\begin{gathered} {\delta }^{2}H=-\frac{1}{e_0}[2\{\delta e_0\delta H+\left({\int }_0^{\infty }w(x)dx\right)(H-1) \\ -{\int }_0^{\infty }w(x)\ln (S(x))dx\}-{\int }_0^{\infty }\frac{{(v(x))}^2}{S(x)}dx]. \end{gathered}$$

Proof. For ease of writing, let S(x) + δS(x) = S(x; ϵ) be a family of varied curves, where S(x; 0) = S(x), S(0; ϵ) = 0, and S(x; ϵ) → 0 as x → ∞. Expand S(x; ϵ) in an ϵ series:

$$S(x)+\delta S(x)=S(x)+ϵv(x)+{ϵ}^{2}w(x)+\cdots .$$

Now, differentiate (C.1) with respect to ϵ twice to arrive at

$$\begin{gathered} H^{\prime \prime }[S(x;ϵ)]e_0[S(x;ϵ)]+2H^{\prime }[S(x;ϵ)]e_0^{\prime }[S(x;ϵ)] \\ +H[S(x;ϵ)]e_0^{\prime \prime }[S(x;ϵ)]-{\left(e^{†}\right)}^{\prime \prime }[S(x;ϵ)]=0, \end{gathered}$$

where the primes denote derivatives with respect to ϵ. Setting ϵ = 0 then yields

$$\begin{gathered} H^{\prime \prime }[S(x;0)]e_0[S(x;0)]+2H^{\prime }[S(x;0)]e_0^{\prime }[S(x;0)] \\ +H[S(x;ϵ)]e_0^{\prime \prime }[S(x;0)]-{\left(e^{†}\right)}^{\prime \prime }[S(x;0)]=0. \end{gathered}$$ (C.3)

To calculate the quantities in this equation, we begin with $e_0[S(x;ϵ)]={\int }_0^{\infty }S(x;ϵ)dx$. Then

$$\begin{gathered} e_0^{\prime }[S(x;0)]={\int }_0^{\infty }v(x)dx=\delta e_0[S(x)], \\ {e}_0^{\prime \prime }[S(x;0)]=2{\int }_0^{\infty }w(x)dx. \end{gathered}$$ (C.4)

Similarly,

$$\begin{gathered} e^{†}[S(x;ϵ)]=-{\int }_0^{\infty }S(x;ϵ)\ln (S(x;ϵ))dx \\ \Rightarrow {\left(e^{†}\right)}^{\prime }[S(x;0)]=-{\int }_0^{\infty }{S}^{\prime }(x;0)[\ln (S(x;0))+1]dx \\ \Rightarrow {\left(e^{†}\right)}^{\prime \prime }[S(x;0)]=-{\int }_0^{\infty }(S^{\prime \prime }(x;0)(\ln (S(x;0))+1) \\ +\frac{{\left(S^{\prime }(x;0)\right)}^2}{S(x;0)})dx. \end{gathered}$$

Therefore,

$$\begin{gathered} {\left(e^{†}\right)}^{\prime \prime }[S(x;0)]=-2{\int }_0^{\infty }w(x)(\ln (S(x))+1)dx \\ -{\int }_0^{\infty }\frac{{(v(x))}^2}{S(x)}dx. \end{gathered}$$ (C.5)

Finally, substituting (C.4)–(C.5) into (C.3) gives

$$\begin{gathered} \left({\delta }^{2}H\right)e_0+2(\delta H)\left(\delta e_0\right)+(2H)\left({\int }_0^{\infty }w(x)dx\right) \\ +2{\int }_0^{\infty }w(x)(\ln (S(x))+1)dx+{\int }_0^{\infty }\frac{{(v(x))}^2}{S(x)}dx=0. \end{gathered}$$

Solving for δ²H reproduces (2.8). □

Proof of Proposition 2.

Proof. Let δμ(s) = ϵv(s) be a variation of the mortality function μ(s), and suppose that v(0) = 0 and v(s) → 0 as s → ∞. Then

$$\begin{gathered} e_0[\mu +\delta \mu ]={\int }_0^{\infty }{e}^{-{\int }_0^x(\mu (s)+ϵv(s))ds}dx \\ ={\int }_0^{\infty }{e}^{-{\int }_0^x\mu (s)ds}{e}^{-ϵ{\int }_0^{x}v(s)ds}dx \\ ={\int }_0^{\infty }{e}^{-{\int }_0^x\mu (s)ds}\left(1-ϵ\left({\int }_0^{x}v(s)ds\right)+\text{h}.\text{p}.\text{e}.\right)dx \\ =e_0[\mu ]-ϵ\left[{\int }_0^{\infty }S[\mu (s)]\left({\int }_0^{x}v(s)ds\right)dx\right]+\text{h}.\text{p}.\text{e}., \end{gathered}$$

where the abbreviation h.p.e. stands for “higher powers in epsilon”. Therefore,

$$\begin{gathered} \delta e_0[\mu (s)]=\underset{ϵ\to 0}{\lim }\frac{e_0[\mu +\delta \mu ]-e_0[\mu ]}{ϵ} \\ =-{\int }_0^{\infty }S[\mu (s)]\left({\int }_0^{x}v(s)ds\right)dx. \end{gathered}$$ (C.6)

Now, since $S[v(s)]=e^{-{\int }_0^{x}v(s)ds}$, then $\ln (S[v(s)])=-{\int }_0^{x}v(s)ds$. Therefore, (C.6) can be written as in (2.12). Similarly, we have that

$$\begin{gathered} e^{†}[\mu +\delta \mu ]=-{\int }_0^{\infty }{e}^{-{\int }_0^x(\mu (s)+ϵv(s))ds} \\ \times \left[-{\int }_0^x(\mu (s)+ϵv(s))ds\right]dx \\ ={\int }_0^{\infty }{e}^{-{\int }_0^x\mu (s)ds}\left(1-ϵ\left({\int }_0^{x}v(s)ds\right)+\text{h}.\text{p}.\text{e}\right) \\ \times \left({\int }_0^x\mu (s)ds+ϵ{\int }_0^{x}v(s)ds\right)dx \\ =e^{†}[\mu ]-ϵ[{\int }_0^{\infty }S[\mu (s)]\left({\int }_0^{x}v(s)ds\right) \\ \times \left(\left({\int }_0^x\mu (s)ds\right)-1\right)dx]+\text{h.p.e.} \end{gathered}$$

It follows that

$$\begin{gathered} \delta e^{†}[\mu ]=\underset{ϵ\to 0}{\lim }\frac{e^{†}[\mu +\delta \mu ]-e^{†}[\mu ]}{ϵ} \\ =-{\int }_0^{\infty }S[\mu (s)]\left({\int }_0^{x}v(s)ds\right)\left(\left({\int }_0^x\mu (s)ds\right)-1\right)dx \\ =-{\int }_0^{\infty }S[\mu (s)](-\ln (S[v(s)]))(-\ln (S[\mu (s)])-1)dx \\ =-{\int }_0^{\infty }S[\mu (s)]\ln (S[v(s)])(\ln (S[\mu (s)])+1)dx \\ =-{\int }_0^{\infty }S[\mu (s)]\ln (S[v(s)])dx \\ -{\int }_0^{\infty }S[\mu (s)]\ln (S[v(s)])\ln (S[\mu (s)])dx \\ =-\delta e_0[\mu (s)]-{\int }_0^{\infty }S[\mu (s)]\ln (S[\mu (s)])\ln (S[v(s)])dx, \end{gathered}$$

which reproduces (2.11). □

Appendix D. More applications of Propositions 1 and 2

In Appendix D.1 we reproduce the results of constant mortality case of Appendix A.3 as a basic illustration and check of Proposition 1. In Appendix D.2 we illustrate a particular case assuming a Gompertz force of mortality, i.e. μ(x) = a e^bx and $S(x)=e^{a/b}{e}^{-(a/b)e^{bx}}$, and evaluate the change in H when there is a proportional change in S(x) at all ages (similar to that shown by Keyfitz (1977)).

D.1. Reproducing the constant mortality case results

Let μ be a positive real number and S(x) = e^−μx, and consider a variation δS that produces the new survival curve S + δS = e^−(μ+ϵ)x, where ϵ > 0. To illustrate the results of Proposition 1, we first Taylor expand S + δS in powers of ϵ:

$$\begin{gathered} S+\delta S=e^{-(\mu +ϵ)x}=e^{-\mu x}{e}^{-ϵx}=e^{-\mu x}\left(1-ϵx+\frac{{(ϵx)}^2}{2!}+\cdots \right) \\ =S+e^{-\mu x}\left(-ϵx+\frac{{(ϵx)}^2}{2!}+\cdots \right). \end{gathered}$$

From the last equation we see that

$$\delta S=ϵ\left(-x{e}^{-\mu x}\right)+{ϵ}^2\left(x^2{e}^{-\mu x}/2\right)+\cdots .$$

Thus, comparing with the expansion δS(x) = ϵv(x) + ϵ²w(x) we see that v(x) = −xe^−μx and w(x) = x²e^−μx/2. From (2.6) we then have

$$\begin{gathered} \delta e^{†}[S(x)]={\int }_0^{\infty }[1-\mu x]\left(-x{e}^{-\mu x}\right)dx=-\frac{1}{{\mu }^2}, \\ \delta e_0[S(x)]={\int }_0^{\infty }\left(-x{e}^{-\mu x}\right)dx=-\frac{1}{{\mu }^2}. \end{gathered}$$ (D.1)

Now, since

$$\begin{gathered} e^{†}\left[e^{-\mu x}\right]=-{\int }_0^{\infty }(-\mu x)e^{-\mu x}dx=\frac{1}{\mu }, \\ {e}_0\left[e^{-\mu x}\right]={\int }_0^{\infty }{e}^{-\mu x}dx=\frac{1}{\mu }, \end{gathered}$$

we see that δe^†/e^† = −1/μ = δe₀/e₀. Therefore, according to (2.5) we have that δH = 0. This suggests that, for example, the survival functions S₁(x) = e^−2x and S₂(x) = e^−2.01x both have the same H value. This is confirmed by the fact that H = 1 for the constant mortality case (c.f. Appendix A.3).

To illustrate (2.8) we make use of the following facts:

$${\int }_0^{\infty }{x}^2{e}^{-\mu x}dx=\frac{2}{{\mu }^3},{\int }_0^{\infty }{x}^2{e}^{-\mu x}(-\mu x)dx=-\frac{6}{{\mu }^3}.$$

Using these, along with the fact that H[S(x)] = 1, Eq. (2.8) gives

$${\delta }^{2}H[S(x)]=-\mu \left[\frac{2}{{\mu }^3}+\left\{0+\frac{2}{{\mu }^3}(1+1)-\frac{6}{{\mu }^3}\right\}\right]=0.$$

Therefore, to second order in ϵ we have, according to (2.9),

$$H[S+\delta S]\approx 1+0\cdot ϵ+0\cdot {ϵ}^2=1.$$

These calculations are again in accordance with our results from the constant mortality example of Appendix A.3.

To illustrate Proposition 2, note that the mortality function here is μ(s) = μ, and that the variation δμ(s) = ϵ. Thus, v(s) = 1 and (2.12) gives⁸

$$\delta e_0[\mu (s)]={\int }_0^{\infty }{e}^{-\mu x}\ln \left(e^{-{\int }_0^{x}1ds}\right)dx={\int }_0^{\infty }\left(-x{e}^{-\mu x}\right)dx,$$

matching (D.1). Similarly, (2.11) gives

$$\delta e^{†}[\mu (s)]=-{\int }_0^{\infty }\left(-x{e}^{-\mu x}\right)dx-{\int }_0^{\infty }{e}^{-\mu x}(-\mu x)(-x)dx,$$

again matching (D.1). Since e^†, e₀, δe^†, δe₀ all have the same values as before, (2.10) leads to the same δH = 0 conclusion.

D.2. Proportional changes in S and their effect on H

Suppose that we consider a small proportional increase in S(x) to kS(x), where k > 1 is close to one. We can then write

$$kS(x)=(1+k-1)S(x)=S(x)+(k-1)S(x)=S(x)+\delta S(x),$$

where δS(x) = ϵS(x), with ϵ = k − 1 > 0 but close to zero. Note that v(x) = S(x) and w(x) = 0. From (2.6) we then have

$$\begin{gathered} \delta e^{†}[S(x)]=-{\int }_0^{\infty }[1+\ln (S(x))]S(x)dx, \\ \delta e_0[S(x)]={\int }_0^{\infty }S(x)dx. \end{gathered}$$ (D.2)

Notice that the relative change in life expectancy δe₀/e₀ = 1, whereas the relative change in the average years of future life that are lost by observed deaths is

$$\begin{gathered} \frac{\delta e^{†}[S(x)]}{e^{†}[S(x)]}=\frac{{\int }_0^{\infty }[1+\ln (S(x))]S(x)dx}{{\int }_0^{\infty }S(x)\ln (S(x))dx} \\ =\frac{{\int }_0^{\infty }S(x)dx+{\int }_0^{\infty }S(x)\ln (S(x))dx}{{\int }_0^{\infty }S(x)\ln (S(x))dx}=-\frac{e_0}{e^{†}}+1, \end{gathered}$$

So that (2.5) gives

$$\begin{gathered} \frac{\delta H[S(x)]}{H[S(x)]}=\left(-\frac{e_0}{e^{†}}+1\right)-1=-\frac{e_0}{e^{†}} \\ =-\frac{1}{H[S(x)]}\Rightarrow \delta H[S(x)]=-1. \end{gathered}$$ (D.3)

Thus, we conclude that since δH[S(x)] < 0 the survival curves S(x) must be changing shape toward increased survivorship, which is true since we have assumed that k > 1.

For the second variation, using (D.2) and (D.3) in (2.8) yields

$$\begin{gathered} {\delta }^{2}H[S(x)]=-\left[\frac{1}{e_0}{\int }_0^{\infty }\frac{{(S(x))}^2}{S(x)}dt+2\{(1)(-1)+0+0\}\right] \\ =-\left[\frac{1}{e_0}{e}_0-2\right]=1. \end{gathered}$$

From (2.9) it follows that

$$\begin{gathered} H[kS(x)]\approx H[S(x)]+ϵ\delta H[S(x)]+\frac{{ϵ}^2}{2}{\delta }^{2}H[S(x)] \\ =H[S(x)]+(k-1)(-1)+\frac{{(k-1)}^2}{2}(1) \\ =H[S(x)]+(1-k)+\frac{{(k-1)}^2}{2}. \end{gathered}$$ (D.4)

We note that analogous calculations can be carried out for the k < 1 case.

Let us now compare these approximations to the exact results one obtains in the Gompertz case. Let μ(x) be the force of mortality at age x and assume it follows a Gompertz curve, i.e. μ(x)= a e^bx. It follows that the corresponding survival function at age x is given by $S(x)=C{e}^{-(a/b)e^{bx}}$, where $C=e^{a/b}$, and that

$$H[S(x)]=\frac{a}{b}\frac{{\int }_0^{\infty }{e}^{-(a/b)e^{bx}}{e}^{bx}dx}{{\int }_0^{\infty }{e}^{-(a/b)e^{bx}}dx}-\ln (C).$$ (D.5)

To calculate H[kS(x)] we first note that $kS(x)=kC{e}^{-(a/b)e^{bx}}$, so that we can simply replace C by kC in (D.5). Therefore,

$$\begin{gathered} H[kS(x)]=\frac{a}{b}\frac{{\int }_0^{\infty }{e}^{-(a/b)e^{bx}}{e}^{bx}dx}{{\int }_0^{\infty }{e}^{-(a/b)e^{bx}}dx}-\ln (kC) \\ =\frac{a}{b}\frac{{\int }_0^{\infty }{e}^{-(a/b)e^{bx}}{e}^{bx}dx}{{\int }_0^{\infty }{e}^{-(a/b)e^{bx}dx}}-\ln (k)-\ln (C) \\ =H[S(x)]-\ln (k). \end{gathered}$$ (D.6)

Since we have assumed that k > 1 but close to one, writing ln k = ln (1 + (k − 1)) we can then Taylor expand ln(1 + (k − 1)) to express (D.6) as

$$\begin{gathered} H[kS(x)]=H[S(x)]-\left((k-1)-\frac{{(k-1)}^2}{2}+\cdots \right) \\ =H[S(x)]+(1-k)+\frac{{(k-1)}^2}{2}-\cdots . \end{gathered}$$ (D.7)

From this we see that the second-order approximation (D.4) matches the actual result (D.7) exactly (to second order).

Appendix E. Early and late deaths

E.1. Reworking of Proposition 1

Given a threshold age a^†, we can break up the first variations of e₀[S(x)] and e^†[S(x)] as follows:

$$\begin{gathered} \delta e_0[S(x)]={\int }_0^{a^{†}}v(x)dx+{\int }_{a^{{}^{†}}}^{\infty }v(x)dx \\ =:\delta e_0[S(x|x<a^{†})]+\delta e_0[S(x|x\ge a^{†})], \end{gathered}$$ (E.1)

$$\begin{gathered} \delta e^{†}[S(x)]=-\left(\delta e_0[S(x|x<a^{†})]+\delta e_0[S(x|x\ge a^{†})]\right) \\ -\left({\int }_0^{a^{†}}\ln (S(x))v(x)dx+{\int }_{a^{†}}^{\infty }\ln (S(x))v(x)dx\right) \\ =\left\{-\delta e_0[S(x|x<a^{†})]-{\int }_0^{a^{†}}\ln (S(x))v(x)dx\right\} \\ +\left\{-\delta e_0[S(x|x\ge a^{†})]-{\int }_{a^{†}}^{\infty }\ln (S(x))v(x)dx\right\} \\ =:\delta e^{†}[S(x|x<a^{†})]+\delta e^{†}[S(x|x\ge a^{†})], \end{gathered}$$ (E.2)

where v(x) is a smooth function that vanishes at zero and as x → ∞.

Thus, Proposition 1 can be written as:

$$\begin{gathered} \frac{\delta H[S(x)]}{H[S(x)]}=\left\{\frac{\delta e^{†}[S(x|x<a^{†})]}{e^{†}[S(x)]}+\frac{-\delta e_0[S(x|x<a^{†})]}{e_0[S(x)]}\right\} \\ +\left\{\frac{\delta e^{†}[S(x|x\ge a^{†})]}{e^{†}[S(x)]}+\frac{-\delta e_0[S(x|x\ge a^{†})]}{e_0[S(x)]}\right\}. \end{gathered}$$ (E.3)

E.2. Reworking of Proposition 2

Similarly, given a threshold age a^†, we can break up the first variations of e^†[μ(s)] and e₀[μ(s)] as follows:

$$\begin{gathered} \delta e_0[\mu (s)]={\int }_0^{a^{†}}{S}_x[\mu (s)]\ln \left(S_x[v(s)]\right)dx \\ +{\int }_{a^{†}}^{\infty }{S}_x[\mu (s)]\ln \left(S_x[v(s)]\right)dx \\ =:\delta e_0[\mu (s|x<a^{†})]+\delta e_0[\mu (s|x\ge a^{†})], \end{gathered}$$ (E.4)

$$\begin{gathered} \delta e^{†}[\mu (s)]=-\left(\delta e_0[\mu (s|x<a^{†})]+\delta e_0[\mu (s|x\ge a^{†})]\right) \\ -{\int }_0^{a^{†}}{S}_x[\mu (s)]\ln \left(S_x[\mu (s)]\right)\ln \left(S_x[v(s)]\right)dx \\ -{\int }_{a^{†}}^{\infty }{S}_x[\mu (s)]\ln \left(S_x[\mu (s)]\right)\ln \left(S_x[v(s)]\right)dx \\ =(-\delta e_0[\mu (s|x<a^{†})] \\ -{\int }_0^{a^{†}}{S}_x[\mu (s)]\ln \left(S_x[\mu (s)]\right)\ln \left(S_x[v(s)]\right)dx) \\ +(-\delta e_0[\mu (s|x\ge a^{†})] \\ -{\int }_{a^{†}}^{\infty }{S}_x[\mu (s)]\ln \left(S_x[\mu (s)]\right)\ln \left(S_x[v(s)]\right)dx) \\ =:\delta e^{†}[\mu (s|x<a^{†})]+\delta e^{†}[\mu (s|x\ge a^{†})], \end{gathered}$$ (E.5)

where $S_x[v(s)]=e^{-{\int }_0^{x}v(s)ds}$.

Thus, Proposition 2 can be written as:

$$\begin{gathered} \frac{\delta H[\mu (s)]}{H[\mu (s)]}=\left\{\frac{\delta e^{†}[\mu (s|x<a^{†})]}{e^{†}[\mu (s)]}+\frac{-\delta e_0[\mu (s|x<a^{†})]}{e_0[\mu (s)]}\right\} \\ +\left\{\frac{\delta e^{†}[\mu (s|x\ge a^{†})]}{e^{†}[\mu (s)]}+\frac{-\delta e_0[\mu (s|x\ge a^{†})]}{e_0[\mu (s)]}\right\}. \end{gathered}$$ (E.6)

Appendix F. Discrete approximations

F.1. Life table notation

One can use the following approximation formulas to estimate e(0), e^†(0), and H at time t (life table notation):

$$e(0,t)={\int }_0^{\infty }S(a,t)da\approx \frac{1}{l(0,t)}\sum _{x=0}^{\omega }L(x,t)$$ (F.1)

$$\begin{gathered} e^{†}(0,t)=-{\int }_0^{\infty }S(a,t)\ln (S(a,t))da \\ \approx \frac{1}{l(0,t)}\sum _{y=0}^{\omega -1}d(y,t)\left[\frac{e(y,t)+e(y+1,t)}{2}\right] \end{gathered}$$ (F.2)

$$H(t)=\frac{e^{†}(0,t)}{e(0,t)}$$

where l(0, t), L(x, t), d(x, t), and e(x, t) correspond to the following life table values at age x, time t: radix at age 0, person-years lived, deaths, and life expectancy.

F.2. Discrete version of Proposition 1

One can use the following approximation formulas to estimate the first variations shown in Proposition 1:

$$\begin{gathered} \delta e_0[S(x)]\approx \frac{1}{l(0)}\sum _{x=0}^{\omega }\left[L\left(x,t_2\right)-L\left(x,t_1\right)\right] \\ \delta e^{†}[S(x)]=\left[e\left(0,t_1\right)-e\left(0,t_2\right)\right]-\left[e^{†}\left(0,t_1\right)-e^{†,*}\left(0,t_2\right)\right] \end{gathered}$$

where the approximation formulas for e(0, t) and e^†(0, t) are shown in Eqs. (F.1) and (F.2), respectively. The estimation of e^†,*(0, t₂) can be carried out using Eq. (F.2) with d(y) replaced by d*(y); the latter corresponds to counterfactual life table deaths at age y estimated with mortality at time t₁ and life table survivors at time t₂.

To derive the two formulas above, let δS(x) = S(x, t₂) − S(x, t₁) be a variation of the survival function between times t₁ and t₂. Thus, v(x) = S(x, t₂) − S(x, t₁). The first variation of e₀ is then given by:

$$\begin{gathered} \delta e_0[S(x)]={\int }_0^{\infty }v(x)dx \\ ={\int }_0^{\infty }\left[S\left(x,t_2\right)-S\left(x,t_1\right)\right]dx \\ ={\int }_0^{\infty }S\left(x,t_2\right)-{\int }_0^{\infty }S\left(x,t_1\right)dx \\ =e\left(0,t_2\right)-e\left(0,t_1\right) \end{gathered}$$

$$\delta e_0[S(x)]\approx \frac{1}{l(0)}\sum _{x=0}^{\infty }\left[L\left(x,t_2\right)-L\left(x,t_1\right)\right],$$

where l(0, t₁) = l(0, t₂) = l(0).

The first variation of e^† is given by:

$$\begin{gathered} \delta e^{†}[S(x)]=-\left[{\int }_0^{\infty }v(x)dx+{\int }_0^{\infty }\ln \left(S\left(x,t_1\right)\right)v(x)dx\right] \\ =-[\delta e_0[S(x)]+{\int }_0^{\infty }\ln \left(S\left(x,t_1\right)\right)S\left(x,t_2\right)dx \\ -{\int }_0^{\infty }\ln \left(S\left(x,t_1\right)\right)S\left(x,t_1\right)dx] \\ =-\left[\delta e_0[S(x)]-e^{†,*}\left(0,t_2\right)+e^{†}\left(0,t_1\right)\right] \\ \delta e^{†}[S(x)]=\left[e\left(0,t_1\right)-e\left(0,t_2\right)\right]-\left[e^{†}\left(0,t_1\right)-e^{†,*}\left(0,t_2\right)\right] \end{gathered}$$ (F.3)

where

$$\begin{gathered} e^{†,*}\left(0,t_2\right)=-{\int }_0^{\infty }\ln \left(S\left(a,t_1\right)\right)S\left(a,t_2\right)da \\ ={\int }_0^{\infty }{\int }_0^a\mu \left(x,t_1\right)S\left(a,t_2\right)dxda \\ ={\int }_0^{\infty }\mu \left(x,t_1\right){\int }_x^{\infty }S\left(a,t_2\right)dadx \\ ={\int }_0^{\infty }\mu \left(x,t_1\right)l\left(x,t_2\right)e\left(x,t_2\right)dx \\ {e}^{†,*}\left(0,t_2\right)={\int }_0^{\infty }{d}^{*}(x)e\left(x,t_2\right)dx \end{gathered}$$

d*(x) represents counterfactual life table deaths at age x estimated with mortality at time t₁ and life table survivors at time t₂. From Eq. (F.2), the discrete approximation of the above equation is given by:

$$e^{†,*}\left(0,t_2\right)\approx \frac{1}{l(0)}\sum _{y=0}^{\omega -1}{d}^{*}(y)\left[\frac{e\left(y,t_2\right)+e\left(y+1,t_2\right)}{2}\right],$$ (F.4)

where l(0, t₁) = l(0, t₂) = l(0). Thus, a discrete approximation of δe^†[S(x)] (Eq. (F.3)) uses formulas (F.1), (F.2) and (F.4) corresponding to e(0, t), e^†(0, t) and e^†,*(0, t), respectively.

The preceding discretizations imply that (2.5) can be discretized as

$$\begin{gathered} \delta H\left[S\left(x,t_1\right)\right]\approx H\left[S\left(x,t_1\right)\right]\left(\frac{\delta e^{†}[S(x)]}{e^{†}\left(0,t_1\right)}-\frac{\delta e_0[S(x)]}{e\left(0,t_1\right)}\right) \\ \approx H\left[S\left(x,t_1\right)\right](\frac{e\left(0,t_1\right)-e\left(0,t_2\right)-\left(e^{†}\left(0,t_1\right)-e^{†,*}\left(0,t_2\right)\right)}{e^{†}\left(0,t_1\right)} \\ -\frac{\left(e\left(0,t_2\right)-e\left(0,t_1\right)\right)}{e\left(0,t_1\right)}) \\ =H\left[S\left(x,t_1\right)\right]\left(\frac{e\left(0,t_1\right)-e\left(0,t_2\right)+e^{†,*}\left(0,t_2\right)}{e^{†}\left(0,t_1\right)}-\frac{e\left(0,t_2\right)}{e\left(0,t_1\right)}\right) \\ =\left(\frac{e^{†}\left(0,t_1\right)}{e\left(0,t_1\right)}\right)\left(\frac{e\left(0,t_1\right)-e\left(0,t_2\right)+e^{†,*}\left(0,t_2\right)}{e^{†}\left(0,t_1\right)}-\frac{e\left(0,t_2\right)}{e\left(0,t_1\right)}\right). \end{gathered}$$ (F.5)

Discretization of equations relating H with early and late deaths.

We use a similar discretization of Eqs. (3.1)–(3.5) as shown above, except that now we have intervals for age (i.e., [0, a^†] or [a^†, ∞)).

Using these discretizations in practice requires numerical integration for some calculations (e.g., (2.4)). To reduce the calculation errors we use more advanced techniques from the theory of numerical integration. In particular, we fitted a third degree monotone cubic spline using Hyman filtering (Hyman, 1983) to the quinquennial S(x) column of the life table to produce single-year survival probabilities. We then estimated the area under this curve using trapezoids, which simplifies the numerical integration because the length of the intervals is one unit long.