Automatic Detection and Classification of Ca²⁺ Release Events in Line- and Frame-Scan Images

Abstract

Analysis of Ca²⁺ signals obtained in various cell types (i.e., cardiomyocytes) is always a tradeoff between acquisition speed and signal/noise ratio of the fluorescence signal. This becomes especially apparent during fast two- or three-dimensional confocal imaging when local intracellular fluorescence signals originating from Ca²⁺ release from intracellular Ca²⁺ stores (e.g., sarcoplasmic reticulum) need to be examined. Mathematical methods have been developed to remedy a high noise level by fitting each pixel with a transient function to “denoise” the image. So far, current available analytical approaches have been impaired by a number of constraints (e.g., inability to fit local, concurrent, and consecutive events) and the limited ability to customize implementation. Here, we suggest a, to our knowledge, novel approach for detailed analysis of subcellular micro-Ca²⁺ events based on pixel-by-pixel denoising of confocal frame- and line-scan images. The algorithm enables spatiotemporally overlapping events (e.g., a Ca²⁺ spark occurring during the decaying phase of a Ca²⁺ wave) to be extracted so that various types of Ca²⁺ events can be detected at a pixel time level of precision. The method allows a nonconstant baseline to be estimated for each pixel, foregoing the need to subtract fluorescence background or apply self-ratio methods before image analysis. Furthermore, by using a clustering algorithm, identified single-pixel events are grouped into “physiologically relevant” Ca²⁺ signaling events spanning multiple pixels (sparks, waves, puffs, transients, etc.), from which spatiotemporal event parameters (e.g., full duration at half maximal amplitude, full width at half maximal amplitude, amplitude, wave speed, rise, and decay times) can be easily extracted. The method was implemented with cross-platform open source software, providing a comprehensive and easy-to-use graphical user interface enabling rapid line-scan images and rapid frame-scan image sequences (up to 150 frames/s) to be analyzed and repetitive Ca²⁺ events (Ca²⁺ sparks and Ca²⁺ puffs) originating from clusters of Ca²⁺ release channels located in the sarcoplasmic reticulum membrane (ryanodine receptors and inositol 1,4,5-trisphosphate receptors) of isolated cardiomyocytes to be examined with a high level of precision.

Introduction

Ca²⁺ microdomain signals occur in many different cell types. Microdomain Ca²⁺ plays a fundamental role in complex intracellular regulatory functions in excitable and nonexcitable cells and is the requirement that a single second messenger, such as Ca²⁺, can act as an intracellular signaling ion in many versatile ways. The underlying microscopic small and subcellular elementary Ca²⁺ signaling events occur from coordinated openings of individual or clustered Ca²⁺ release channels (e.g., ryanodine receptors (RyRs), inositol 1,4,5-triphosphate receptors (InsP₃Rs)) located in the sarcoplasmic reticulum (SR) membrane or in the membrane of other intracellular Ca²⁺ stores. However, those Ca²⁺ events are the building blocks of complex global Ca²⁺ signals, such as Ca²⁺ waves and whole-cell Ca²⁺ transients. Various Ca²⁺ signaling events have been characterized in organelles, cells, and tissues, and each has its own “signature” in terms of spatial and temporal features. In response to the expanded collection of Ca²⁺ signaling events, an ever-growing nomenclature of Ca²⁺ events has been developed (1, 2).

There are currently numerous methods to analyze Ca²⁺ sparks and other elementary and general Ca²⁺ signals obtained from confocal line-scan images (e.g., 3, 4, 5, 6). These employ various approaches: noise thresholding (5), wavelet transform (7), etc.

Recently, Tian et al. (8) suggested a method in which the fluorescence time-trace image in each pixel was fitted. Although this pixel-by-pixel method provided a practically noise-free approximation of the original fluorescence data, several limitations made it impractical for use in the detection of Ca²⁺ release events.

In this study, we extended and optimized this method in several ways. The resulting, to our knowledge, new approach allows Ca²⁺ release events to be classified on the basis of pixel-by-pixel denoising of the original signal recording. This allows various types of local and global Ca²⁺ release events to be analyzed in greater detail; i.e., repetitive, combined, or overlapping events of different nature (e.g., “Ca²⁺ sparks” and “Ca²⁺ puffs”). Ultimately, our method was coded using the Python programming language (Python Software Foundation, Wilmington, DE) and includes a user-friendly graphical interface. The software is available for download on Bitbucket at the following links: https://bitbucket.org/ardoi/juicer/downloads/juicer_100718_MacOs.zip (MacOS version) or https://bitbucket.org/ardoi/juicer/downloads/juicer_040718_win.zip (Windows version). The installation instructions can be found here: https://bitbucket.org/ardoi/juicer/src/default/install.md. For additional information, e.g., the user guide, see: https://bitbucket.org/ardoi/juicer/src/default/. The source code is available from Zenodo (https://zenodo.org/record/1303452), and for citation, the following DOI can be used: 10.5281/zenodo.1303452.

Methods

Confocal Ca²⁺ imaging

Rapid confocal line-scan images were obtained using an Olympus FluoView 1000 confocal microscope (Olympus, Tokyo, Japan). Ca²⁺ changes in the SR were obtained by using the low-affinity Ca²⁺ dye Fluo-5N (9). Cells were incubated in a modified Tyrode solution containing Fluo-5N cell-permeable acetoxymethyl ester (44 μmol/L) at 37°C for 3 h. Subsequently, myocytes were permeabilized with saponin to remove the excess Fluo-5N from the cytosol. To record the cytosolic Ca²⁺ changes, 25 μmol/L Rhod-2 (tripotassium salt) was used as a high affinity Ca²⁺ indicator. The [Ca²⁺]_free in the internal permeabilization solution was adjusted to 100 nmol/L. For frame-scan (x-y-t) Ca²⁺ imaging, cardiomyocytes were incubated with 50 μmol/L Fluo-3 cell-permeable acetoxymethyl ester (Biotium, Fremont, CA) and plated on extracellular matrix-gel- (Sigma, St. Louis, MO) coated glass coverslips. Cells were superfused with 1.8 mmol/L [Ca²⁺] modified Tyrode solution. To standardize the SR-Ca²⁺ content, the cells were electrically stimulated using field stimulation (1 Hz, 10 s, pulse duration 0.25 ms). Rapid two-dimensional confocal full-frame imaging (512 × 64 pixels, pixel size 130 nm, 150 fps) of cardiomyocytes was performed using a diode laser (Coherent 488-50; Coherent, Santa Clara, CA) with a multibeam confocal scanner (VT-infinity; VisiTech International, Sunderland, UK) mounted on an inverted microscope (Nikon, Tokyo, Japan) equipped with a 60× A/1.20WI objective lens (0.13 × 0.13 μm/pixel) and a Hamamatsu electron multiplying charge-coupled device digital camera system (Hamamatsu, Hamamatsu City, Japan).

Cell isolation

Cardiomyocytes were isolated from adult male C57BL6 mice. Animals were euthanized by means of cervical dislocation. Acute cardiac myocyte isolation was performed by the Langendorff perfusion technique as described earlier (9) (collagenase type II, 160 U/mL and protease type XIV, 0.21 U/mL for 15 min). Cardiomyocytes were kept in modified Tyrode solution, and [Ca²⁺]₀ was slowly increased to 1.8 mmol/L. All experiments were performed at room temperature and approved by the State Veterinary Office of the Canton of Bern (Veterinärdienst, Bern, Switzerland) and in keeping with the provisions of the Federal Act of 16 December 2005 on the Welfare of Animals (AniWA, SR 455).

Solutions are as follows. Modified Tyrode solution: 140 mmol/L NaCl, 5 mmol/L KCl, 1 mmol/L MgCl₂, 1 mmol/L Na₂HPO₄, 5 mmol/L Hepes, 10 mmol/L D-glucose (pH 7.4) (adjusted with NaOH); the saponin-containing permeabilization solution: K-Asp 100 mmol/L, KCl 20 mmol/L, MgCl₂ 3.7 mmol/L, EGTA 1 mmol/L, Hepes 10 mmol/L, and saponin 0.005% mmol/L (pH 7.2), adjusted with KOH; saponin-free internal solution: K-Asp 120 mmol/L, K₂ATP 3 mmol/L, MgCl₂ 3 mmol/L, EGTA 0.1 mmol/L, phosphocreatine 10 mmol/L, Hepes 10 mmol/L, creatine phosphokinase 5 U/L, and dextran 40 K 4% mmol/L (pH 7.2), adjusted with KOH.

Computational

The detection algorithm is presented in detail in the Results.

Results

Pixel-by-pixel event classification

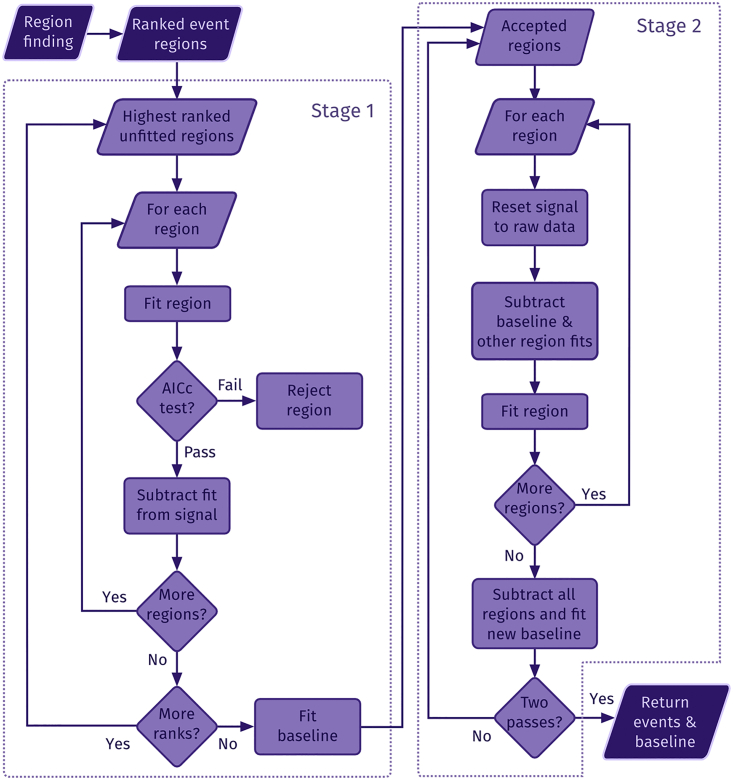
The algorithm is presented schematically in Fig. 1. Each subroutine is explained in detail below.

Figure 1.

Diagram. A diagram depicting the procedure used to estimate event parameters and overall baseline in detected regions is shown.

Region detection

Regions of interest showing potential local Ca²⁺ event activity must be detected and selected first in the confocal image before a fluorescence signal in each pixel can be fitted with a transient function. For this reason, we modified a continuous wavelet transform-based peak detection algorithm developed by Du et al. (10). Whenever the original algorithm provides the location of the peak, we extended it to also yield the width of the peak.

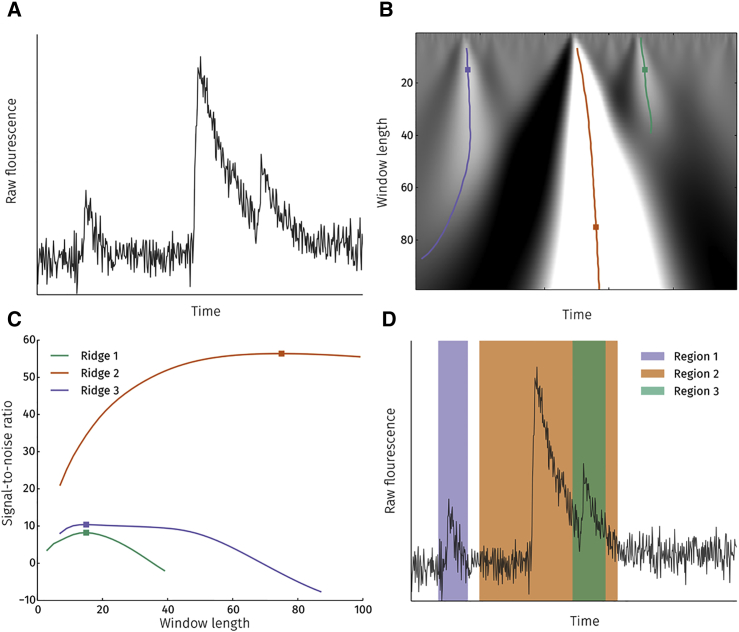
The original algorithm works by calculating a wavelet transform of the Ca²⁺ signal (example shown in Fig. 2 A) for increasing window lengths (Fig. 2 B). Ridge lines along local maxima on the surface correspond to peaks if they satisfy certain criteria (length of the ridge, signal/noise ratio (SNR), etc.; see (10) for details). In our extension, the width of the peak is obtained by determining the first maximum of the wavelet transform values along the ridge line (Fig. 2 C). The left and right edges of the region are taken, respectively, as

$$\left[pea{k}_{center}-1.5\times width,pea{k}_{center}+2\times width\right].$$

Figure 2.

Detecting regions with potential events. (A) An example of a raw fluorescence signal from a single pixel for which event regions are detected. (B) Continuous wavelet transform is performed on the raw signal with varying wavelet widths. Colored lines indicate ridge lines along maxima at changing window length values. Squares denote the first maxima on each ridge line. (C) Signal-to-noise ratio (SNR) of the continuous wavelet transform along each ridge line. (D) Detected event regions (regions 1–3; raw fluorescence signal from (A)) are marked in blue, orange, and green. Only the region 2 shows an overlap with a region having a lower peak SNR, i.e. with region 3.

Region estimation provides a ranked list of potential event regions. The rank of a region is defined as the total number of potential regions minus the number of regions with a lower peak SNR that overlap with it. For example, region 1 and 3 in Fig. 2 D have rank 3 because neither overlaps with a region having a lower peak SNR. Region 2 has a rank of 2 as it overlaps with region 3, which has a lower peak SNR. Ranking regions is necessary to ensure overlapping signals are fitted in the right order during the fitting stage.

Signal fitting

Fitting function for transients

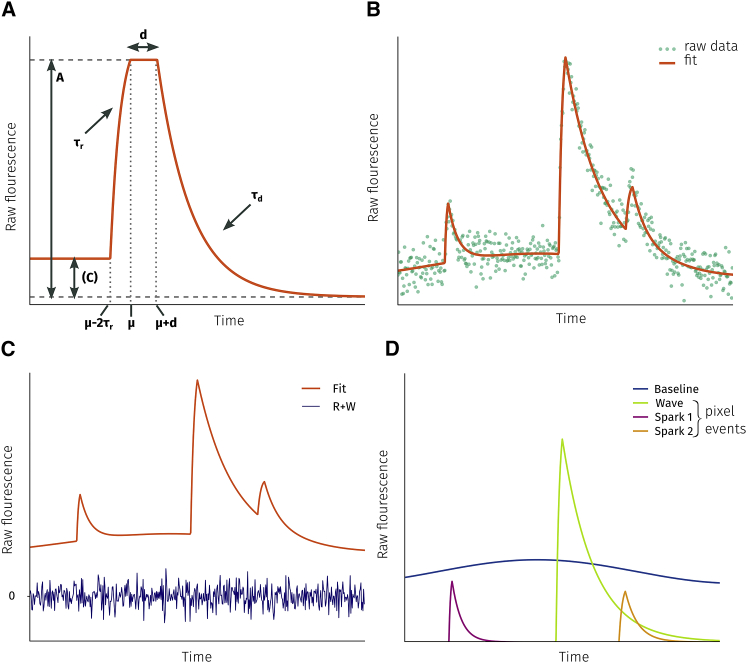
The function used to fit Ca²⁺ release events is shown in Fig. 3 A. The shape of the function is described by four parameters: amplitude (A), rise and decay time constants (τ_r, τ_d), and plateau duration (d). An additional parameter (μ) determines the time when the maximum is reached. The piecewise function describing a transient is

$$g\left(A,d,{\tau }_d,{\tau }_r,\mu ,t\right)=A\times \{\begin{array}{ll}ll1-\text{exp}\left(-\frac{t-\mu }{{\tau }_r}\right)\times \text{exp}\left(-2\right)\hfill & \mu -2{\tau }_r\le t<\mu \hfill \\ 1-\text{exp}\left(-2\right)\hfill & \mu \le t<\mu +d\hfill \\ \text{exp}\left(-\frac{t-\mu -d}{{\tau }_d}\right)\times \left(1-\text{exp}\left(-2\right)\right)\hfill & t\ge \mu +d\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}.$$ (1)

Figure 3.

Fitting function. (A) The fitting function for transients given by Eq. 1. (B) The result of fitting raw fluorescence data with the combined fitting function. (C) The raw signal is the sum of the fit, noise (W), and residual (R). (D) The fit is a superposition of the baseline and pixel events.

The transient consists of four phases: zero level before the onset of the transient, an exponential increase with time constant τ_r starting when t = μ − 2τ_r, a plateau phase of duration d starting at t = μ, and an exponential decay with time constant τ_d starting at t = μ + d.

To improve the performance of the optimizer when fitting, the function used for fitting should be continuously differentiable. With this in mind, the transient function is convolved with a zero-mean Gaussian G(σ) to yield the actual fitting function:

$$f\left(A,d,{\tau }_d,{\tau }_r,\mu ,t,\sigma \right)=g\times G.$$

For notational purposes, we shall represent the fit function parameters by

$$\mathbf{p}=\left[\begin{array}{lllll}A\hfill & d\hfill & {\tau }_d\hfill & {\tau }_r\hfill & \mu \hfill \end{array}\right].$$

Such a p vector is sufficient to describe an event. The parameter vector for the k-th event in the i-th pixel is denoted as p_{i, k}. The smoothing parameter σ will be fixed for all pixels and treated as a global variable rather than being specific to each event. Using this notation, the k-th event in the i-th pixel is represented by f(p_{i, k}, t).

The entire raw fluorescence signal for the i-th pixel can be represented as

$$F_i\left(t\right)=b\left({\mathbf{q}}_i,t\right)+\sum _{k=0}^{m}f\left({\mathbf{p}}_{i,k},t\right)+W\left(t\right)+R\left(t\right).$$

Here, b is an n-th order polynomial, with q_i being the polynomial coefficients for the i-th pixel. The polynomial describes the baseline fluorescence in the pixel signal. Allowing it to be a low-order polynomial allows it to capture slow dynamics in the background fluorescence. The next component sums up all events in the i-th pixel. Lastly, W represents noise in the signal, and R is the remaining residual that neither the baseline nor events capture. An example of raw signal F(t) is shown in Fig. 3 B together with the fit (i.e., F(t) − W(t) − R(t)). Ideally, R = 0, but achieving this is limited by the accuracy of the event region detection (we cannot fit what we do not detect) and whether or not our fitting function is general enough to be able to approximate various types of events. We can consider W(t) + R(t) to be the overall residual noise. This is shown together with the fit in Fig. 3 C. The individual m events are depicted in Fig. 3 D. Notice that all events start from and decay to zero. Any deviations from zero are due to the baseline polynomial.

Because initially it is not known which part of the signal is the event and which is the baseline, the first fit step requires estimation of the baseline properties. The signal in the candidate region is fitted with an extended fit function (Fig. 3) that also depends on relaxation baseline B and baseline offset C. The C parameter allows for the possibility of an elevated (or depressed) background fluorescence level before the release event.

Iterative fitting

Fitting of potential event regions is performed iteratively. The algorithm is depicted in Fig. 2.

First, the highest-ranked regions are fitted with the extended fit function. After parameter optimization with the signal in the region, the region is fitted with a linear model. For both models, the corrected Akaike Information Criterion (AICc; 11) is calculated, and the region is taken to contain an event only if the AICc for the fit function is less than the AICc for a linear fit. This ensures that the fit obtained with the fit function is good enough to justify the use of the more complicated model. After this, the fit is subtracted from the original signal. This allows the lower-ranked regions to be fitted with reduced interference from higher-ranking regions. When all regions have been fitted and their fits subtracted from the signal, the remaining signal is fitted with a polynomial function b(q_i, t) to approximate the baseline fluorescence.

In the second stage, signals from approved regions (i.e., those where the AICc value warranted the use of the event function) are fitted again. Before performing the fit for each region, the baseline and previously obtained fits for other regions are subtracted from the raw signal. This allows the simpler fit function to be used because the subtraction eliminates the need for the extra baseline parameters (B and C). Once all regions have been fitted in this manner, the results are subtracted from the raw signal to estimate the baseline again. The second fitting stage is repeated once to improve the quality of the fits.

The result of the fitting procedure n are baseline vectors (n = n_x × n_y is the total number of pixels in the image), an n_x × n_y matrix N containing the number of detected events in each pixel, and a set of event parameter vectors, i.e.,

$$\sum _{\mathit{i}=0}^{{\mathit{n}}_{\mathit{x}}}\sum _{\mathit{j}=0}^{{\mathit{n}}_{\mathit{y}}}{\mathit{N}}_{\mathit{j},\mathit{i}}.$$

Approximating the original image

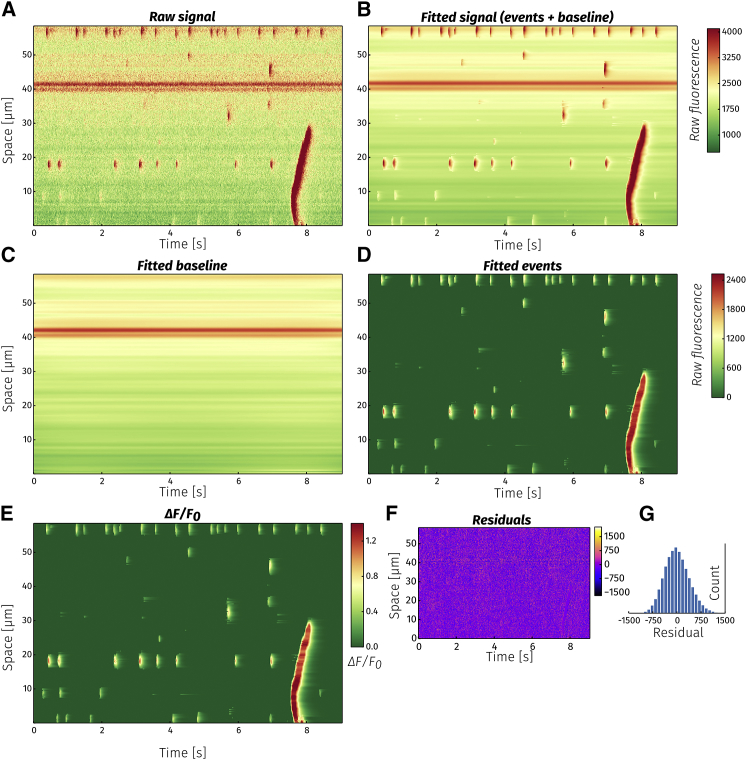
Having detected events from all the pixels, it is possible to combine all fitted pixels into an approximation of the original image with a reduced level of noise. The results of applying the denoising algorithm to a line-scan image, in which one pixel corresponds to one horizontal line (Fig. 4 A), are presented in Fig. 4 B. The fitted image is obtained by adding the baseline image (Fig. 4 C) and fitted pixel events (Fig. 4 D). Separating the baseline and events into separate images allows us to easily calculate the standard ΔF/F₀ image of the line scan (Fig. 4 E). Subtracting the fitted image from the original data yields the noise and residual (W + R). The histogram of the unfitted portion of the signal is symmetric around zero and Gaussian.

Figure 4.

Fitting a line-scan image. (A) The raw fluorescence signal. (B) Each horizontal line along the temporal axis was fitted with the fitting algorithm. The fitted signal in the denoised image is a sum of fitted events (C) and baseline (D). ΔF/F₀ image (E) is obtained by dividing the event image (C) with the baseline (D). Because the fitted baseline is a function of time, the ΔF/F₀ image is automatically corrected for temporal changes in background fluorescence (e.g., bleaching). (F) The residual signal obtained when subtracting the fitted image from raw data. (G) A histogram of the residual values.

Shape and location parameters

Each pixel event is characterized by the parameters p. Four of these (A, d, τ_d, τ_r) determine the shape of the μ event and the location in time. To completely characterize a pixel event, we also need to know the pixel’s spatial location. This would require one or two spatial coordinates, respectively, for line or frame scans. Hence, a pixel event is completely defined by two vectors: the shape parameter vector p^s = [A, d, τ_d, τ_r] and the position parameter vector p^p = [μ, x, y]. The separation of shape and position parameters for events is necessary in the next clustering step.

Clustering

Having determined the events in each pixel, we can then use the event vectors to reconstruct the image with reduced noise levels. However, this will not tell us anything about the features of actual release events (e.g., spark or wave numbers or properties) because the actual macroscopic events are comprised of several pixel events from nearby pixels. The elementary events from various pixels need to be combined into resolved Ca²⁺ release events.

This is achieved by applying the DBSCAN clustering method (12). The DBSCAN algorithm works in the parameter space and finds clusters of arbitrary shape based on the density of events. In contrast to many other clustering methods (e.g., k-nearest neighbors, spectral clustering), the number of clusters found is not determined in advance. The number of clusters found depends on the data and two parameters: the minimal number of events in a cluster and the maximal distance from a cluster to be included in it. This feature is very beneficial in our case because we do not know in advance how many release events are present on an image.

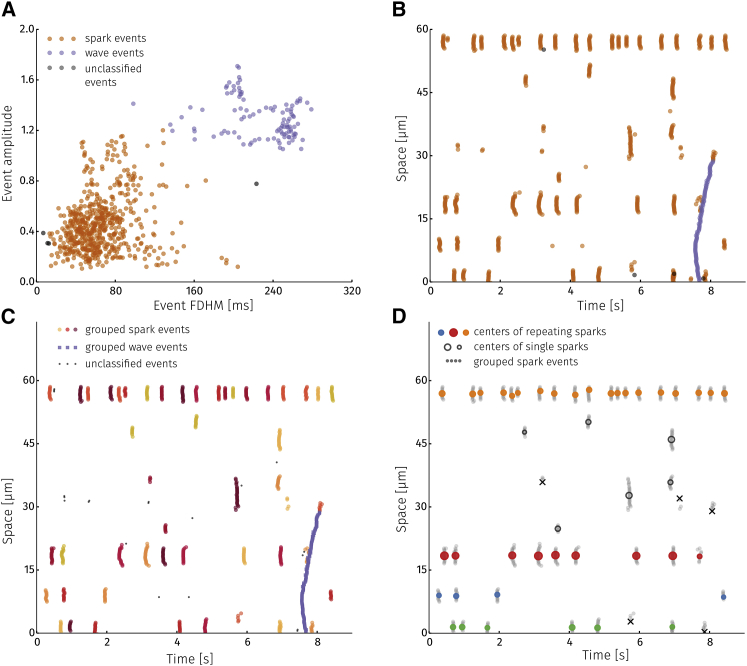
Clustering is performed in two steps. First, pixel events are distributed into groups according to their shape, i.e., clustering is done on the shape vectors p^s. Although the function used to fit various release events (e.g., sparks or waves) is the same, the shape parameters of an event approximating a spark are likely to be more similar to other spark events rather than to wave events. This is clearly visible in Fig. 5 A, in which amplitudes and full duration at half maximal amplitude (FDHM) for all events detected on the line scan from Fig. 3 A are plotted. The DBSCAN algorithm has detected two separate groups of events together with a small set of events that did not belong to any group (colored as orange, purple, and black, respectively). Pixel events depicting sparks have lower amplitude and smaller FDHM values and are well separated from wave pixel events. It should be noted that the clustering algorithm by itself is unaware of the existence of sparks or waves. The DBSCAN algorithm merely detects distinct groups of events. It is up to us to categorize them as phenomena of interest (see Discussion).

Figure 5.

Classifying detected events. (A) A density-based clustering algorithm is used to classify pixel events into categories based on their shape. Colors represent event categories. Black signifies events that could not be categorized. (B) Categories obtained from clustering by shape plotted according to event location. (C) In the second step of classification, each shape category is clustered further based on location. Groups of pixel events are obtained that make up a Ca²⁺ release event (in this case, sparks and a wave). (D) All detected sparks visualized according to their center (location of colored circle) and amplitude (color of the circle). Events marked with a black x were not symmetric and not classified as sparks. Circle color shows sparks originating from the same 2 μm segment. Empty circles are sparks without nearby sparks.

Having determined the different types of events, the second clustering step groups each event type by location. Fig. 5 B shows the spatiotemporal location of all pixel events. Applying the DBSCAN clustering algorithm to these data, we obtain the results shown in Fig. 5 C. Spatiotemporally close pixel events can be interpreted as being from the same underlying Ca²⁺ signaling event. Pixel events making up a single Ca²⁺ spark are depicted in the same shade of orange. A single Ca²⁺ wave is shown in blue. Events that failed to be classified are black. Events that fail to be classified in either the shape or positional clustering steps are essentially filtered out as invalid events.

With this two-step approach, release events of various types consisting of elementary Ca²⁺ signaling events from multiple pixels are obtained.

Algorithm parameters

As mentioned above, the DBSCAN method used for grouping pixel events requires two parameters to be provided: the minimal number of events in a cluster and the maximal distance for an event to be considered as part of a cluster. Because the parameter values are specific to the types of events present in the data and experimental conditions, it is not reasonable to provide preset values for the parameters. In practical use of the algorithm, these parameters can be specified by the user while performing the analysis. The graphical user interface of the analytical software allows the user to choose the parameters that provide a sensible separation of different event types. Chosen values can be saved as presets and applied to images recorded under similar conditions to ensure that the same settings are used throughout.

Event characterization

From line scans, local Ca²⁺ release events (e.g., Ca²⁺ sparks) can be characterized by mean fluorescence amplitude (ΔF/F₀), full width at half maximal amplitude (FWHM), FDHM, rise time (τ_r), decay time (τ_d), and the spatial location. Global Ca²⁺ release events (e.g., Ca²⁺ waves) are typically described by the average wave (amplitude) profile, the wave speed, and the spatial distribution. Ca²⁺ release event characterization from frame scans is similar; the additional spatial dimension enables a more sophisticated analysis (e.g., FWHM_x vs. FWHM_y of Ca²⁺ sparks and/or Ca²⁺ puffs). For Ca²⁺ waves, for example, the wave maximal time (i.e., time point) can be specified on the region of interest (x-y map).

Sensitivity analysis

Pixel trace

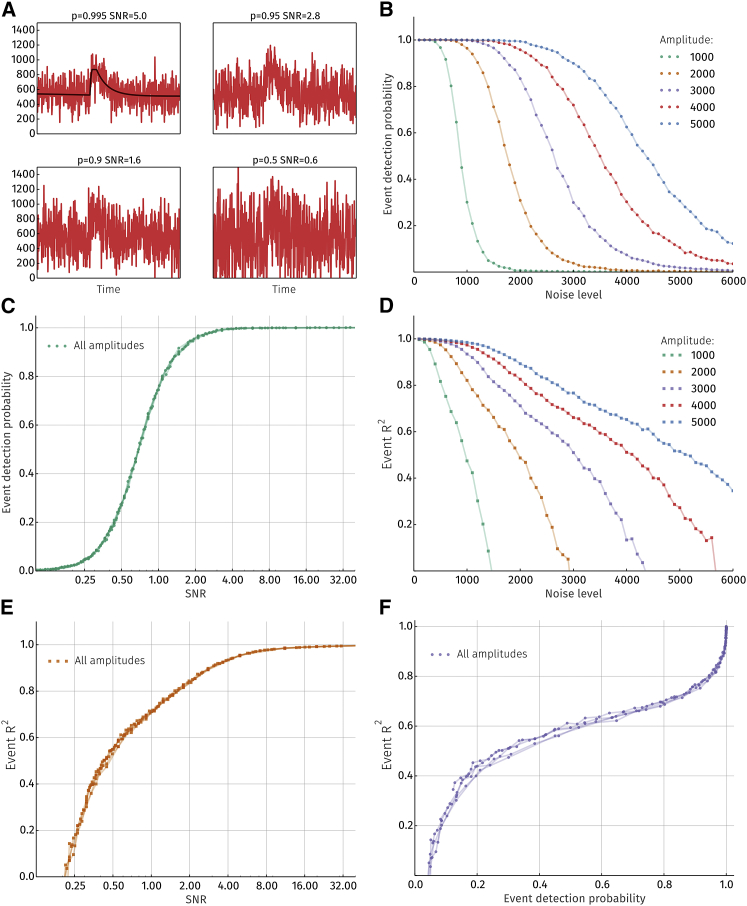
As the amount of noise in the signal increases, the performance of the event detection algorithm should decrease. The sensitivity of the method to noise was explored by estimating both the probability of detecting an event in a noisy signal and the accuracy of the fit. A synthetic signal to be fitted was generated from the fitting function for five different amplitudes. Different levels of normally distributed noise were added to this signal (noise level is the SD of the noise distribution). Some examples of this process are shown in Fig. 6 A.

Figure 6.

Sensitivity and accuracy of the algorithm. (A) Four versions of the same original signal (shown in black on the top left panel) with different levels of added noise. The title for each plot indicates detection probability and the SNR for each respective signal. (B) Detection probabilities as a function of noise level for signals with various amplitudes. (C) Detection probabilities as a function of SNR are no longer dependent on signal amplitude. (D) R² value for detected events as a function of noise level for signals with various amplitudes. (E) R² value as a function of SNR. (F) A combination of (C) and (E) to show the relationship between detection probability and fit accuracy is given.

Fig. 6 B shows the probability of detecting the event in the signal as a function of noise level. Increasing the event amplitude shifts the event detection probability curve toward higher noise levels and vice versa. It is more informative to look at the relationship between detection probability and the SNR of the event. This is calculated as

$$SNR=\frac{{\int }_a^{b}f{\left(t\right)}^{2}dt}{\left(t_b-t_a\right){\sigma }_n^2},$$

where t_a and t_b are times before and after the peak, respectively. When the fluorescence is at half of its peak value (i.e., t_b − t_a = FDHM), f(t) is the raw event signal and σ_n the SD of the noise (i.e., noise level). The resulting plot is depicted in Fig. 6 C, and it can be seen that detection probability is only dependent on the SNR. For visual comparison, the appearance of four events with different SNR and detection probabilities are shown in Fig. 6 A. The signal on the top right has an SNR of 5.0, and the algorithm is typically able to detect such signals with 99.5% probability. As the SNR decreases, so does the detection probability, i.e., lowering to 50% when SNR is 0.6.

In Fig. 6 D, the accuracy of the fit compared to the original event is estimated for various amplitudes and noise levels as the R² value. Predictably, the R² value decreases as the amount of noise increases. Similar to detection probabilities, R² curves calculated for different amplitudes overlap when plotted as a function of SNR. Combining data from Fig. 6, C and E, the relationship between the probability of finding an event and the accuracy of the fit can be obtained.

Biological examples

Ca²⁺ event detection

Locations of individual Ca²⁺ sparks can be precisely estimated once the clustering steps are approached (see Figs. 4 and 5). The fluorescence image for each Ca²⁺ spark is reconstructed from all its pixel events. A Gaussian function is fitted to the spatial profile of the spark at the time of maximal fluorescence. The spatial location and FWHM are obtained from the fit parameters.

Ca²⁺ waves in the cytosol and SR

When analyzing the time course of Ca²⁺ waves in cardiomyocytes, it is customary to deskew them (13) before averaging the signal in the spatial dimension. This requires us to detect the half maximal fluorescence along each pixel and then straighten the skewed wavefront in the line scan. This approach can be problematic for noisy images or when a single image contains several waves.

Now, with the suggested algorithm, deskewing the line scan is no longer necessary. The peak time for each pixel event composing the wave will be known from fitting and can be used to calculate the average wave profile and wave speed.

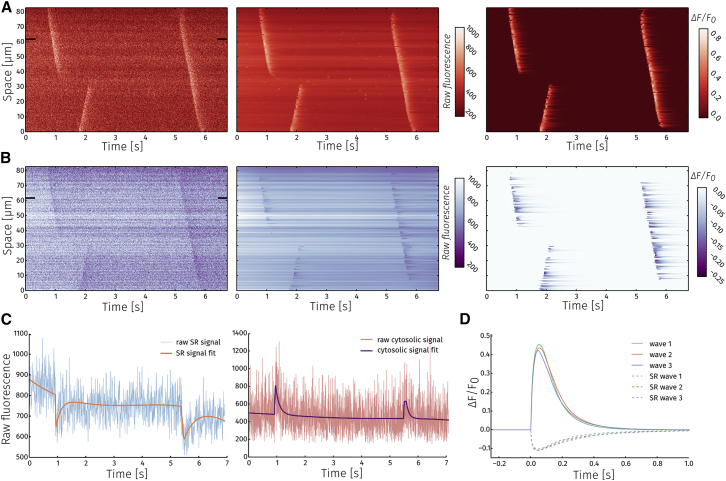
As shown in Fig. 7, it is also possible to use detected cytosolic wave events to analyze Ca²⁺ waves in the SR (9). The SR signal has a lower SNR than the cytosolic signal, which makes it difficult to apply the fitting algorithm directly. Assuming that a decrease in the SR signal is accompanied by increased fluorescence in the cytosol, the first step of the algorithm—region detection—can be skipped, and the regions detected in the cytosol can be reused for analysis in the SR.

Figure 7.

Dual channel line-scan analysis. (A) and (B) show, from left to right, the raw signal, fitted signal, and ΔF/F₀ for cytosolic and SR measurements, respectively. (C) Raw data with the fit for a time trace from a single pixel (indicated by black rectangles on (A) and (B)) for SR (left) and cytosolic (right) signals are shown. (D) Average wave profiles for the three detected waves in the SR and the cytosol.

Frame-scan analysis

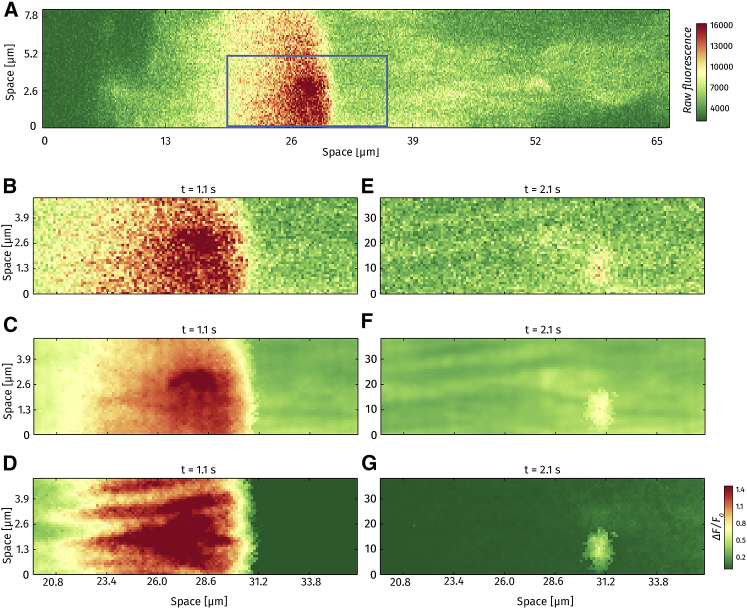
Despite having focused on analyzing line scans so far, the method can be readily applied to the analysis of frame scans (x-y images) as well. Figs. 8 and 9 show the results for frame-scan analysis, comparing raw, fitted, and ΔF images from the same 139 × 33 pixel area (X × Y μm). For each case, three different time points are presented: a wave, a weak spark, and a strong spark.

Figure 8.

Frame-scan analysis. (A) A snapshot of a 512 × 64 pixel frame scan at t = 1.1 s after initiation of recording. Rectangle shows the in-focus region analyzed in subsequent panels. (B–D) Raw image, pixel-by-pixel fitted image, and ΔF/F₀, respectively, for a Ca²⁺ wave. (E–G) Raw image, pixel-by-pixel fitted image, and ΔF/F₀, respectively, for a Ca²⁺ spark.

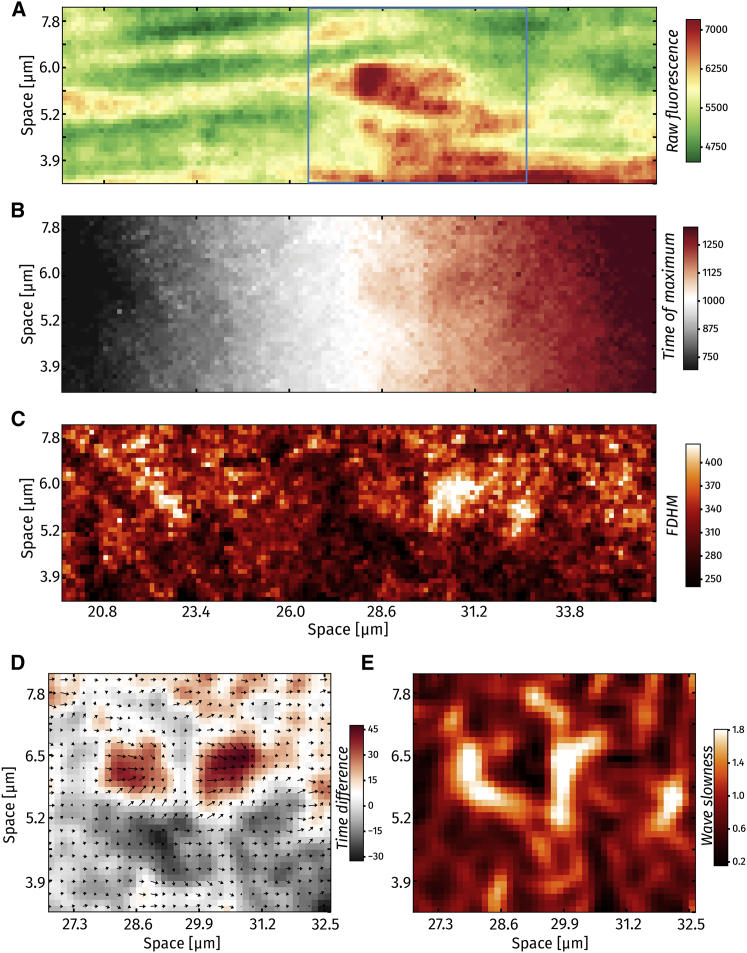
Figure 9.

Detailed frame-scan analysis. (A) Baseline fluorescence (dye distribution) in the zoomed-in region from Fig. 8. (B) A map showing wave peak time. (C) A map showing wave FDHM. (D) Time difference between actual time of wave maximum and expected time. Arrows indicate the gradient of wave peak time. (E) Wave “slowness,” i.e., highest resistance to wave traversal.

Event clustering for frame-scan images is performed in a similar fashion to line-scan images, with the exception of two spatial dimensions used for release event grouping.

The information provided by the method can be used to construct parameter maps for release events. In Fig. 9, four examples of such maps are represented. Fig. 9 A shows the zoomed area from Fig. 8 A for which the subsequent analyses are performed. Wave maximal time in Fig. 9 B shows the time when the fluorescence reaches its maximal value in every pixel. This is given by the μ parameter of the fitting function. FDHM in Fig. 9 C reveals the FDHM amplitude, which can be calculated from the fit parameters as

$$FDHM=d+{\tau }_d\times ln\left(2\right)-{\tau }_r\times \left[1+\frac{1}{2}\left(\frac{1+e^2}{2}\right)\right].$$

Thus, Fig. 9 B presents the relative time point for a given location when wave fluorescence reaches its maximum. In contrast, Fig. 9 D shows the difference in milliseconds between the expected and actual maximal fluorescence time in the area outlined in Fig. 9 A. In dark red regions, it takes ∼45 ms longer to reach its maximum. In dark gray regions, however, the maximum is reached up to 30 ms earlier than expected. The gradient of the wave maximal time, shown with arrows in Fig. 9 D, shows the directions from which wave progression is slower. The arrows are longest in the red regions and shortest in the gray regions. The length of the gradient vectors is shown in Fig. 9 E as wave “slowness” (rather than speed because in the gray regions, the wave appears to move instantaneously). For both red regions in Fig. 9 D, we can see from Fig. 9 E that it is the leading left edges of the regions that cause the slowdown of wave progression.

Discussion

The main advantage of the presented approach is the ability to make maximal use of the information hidden in the raw fluorescence data (e.g., line- or frame-scan images). This enables us to analyze local Ca²⁺ events in a sophisticated manner (e.g., the examination of repetitive or combined events). In consideration of the advantages of the pixel-wise fitting approach reported by Tian et al., i.e., minimal compromises in the signal amplitude and/or time course compared to traditional methods such as signal averaging, filtering, and smoothing of data (8), we extend this method for local Ca²⁺-release-event classification. By extension, our approach allows us to analyze repetitive events such as Ca²⁺ sparks, Ca²⁺ puffs, and Ca²⁺ waves. We successfully analyzed combined events (i.e., local Ca²⁺ release events on top of other local or global Ca²⁺ release events), e.g., when a Ca²⁺ spark occurs within the time window of a Ca²⁺ puff (14).

Within the multiparametric approach of density-based spatial clustering, the ability to extract and classify (pixel-by-pixel and local) events is very useful. Different fitted parameters such as amplitude, FDHM, FWHM, τ_r, and τ_d are considered and included in the algorithm. Threshold values for suitable parameters can be identified and are available for subsequent analysis. Even though several parameters from different types of local Ca²⁺ release events (e.g., Ca²⁺ sparks and Ca²⁺ puffs) may overlap, the combination of several parameters may be sufficient for a precise event classification. A differentiated analysis of global Ca²⁺ release events such as Ca²⁺ waves, including wave speed and wave profile characteristics, is also feasible.

Using confocal imaging techniques under experimental conditions, the difference between various types of Ca²⁺ release events can be very marginal and can occur with high variability. The pixel-by-pixel denoising of confocal frame- and line-scan images allows for a more accurate identification and separation of different “types” of local Ca²⁺ release events. The clustering algorithm per se does not consider or provide biologically relevant information; in terms of a specific receptor type (e.g., RyR versus InsP₃R) as a potential source for the Ca²⁺ release event—and very similar events may not unequivocally be classified at first glance (e.g., Ca²⁺ spark versus Ca²⁺ puff). However, consideration of empirical threshold values for selected parameters (e.g., FDHM) is a suitable way to integrate additional and experimentally verified criteria, which was demonstrated recently (14).

A potential source of difficulty in the separation and classification of different types of Ca²⁺ release events (Ca²⁺ sparks versus Ca²⁺ puffs) arises from the very low number of Ca²⁺ puffs occurring in cardiomyocytes. Ca²⁺ puffs are virtually hidden in the large number of Ca²⁺ sparks. Firstly, conventional Ca²⁺ spark analysis tools (e.g., Sparkmaster) (5) are not sufficient and sensitive enough and fail to identify rare and/or very similar Ca²⁺ events in the total mass of Ca²⁺ events occurring. Secondly, pharmacological separation by selective inhibition of RyRs and/or InsP₃Rs alone may also not be sufficient to separate and classify Ca²⁺ events. This strategy is associated with a high level of misclassification. In other words, “pharmacology-driven” criteria for event separation are highly limited (15). The pixel-by-pixel denoising algorithm was successfully applied to fluorescence full-frame confocal images to largely solve that challenging problem. We were able to examine local, functional interactions of Ca²⁺ sparks and Ca²⁺ puffs in atrial myocytes with great precision (14). When combined with pharmacological tools, the multiparametric approach of density-based spatial clustering is a very powerful tool for studying subcellular Ca²⁺ signaling.

Author Contributions

All experiments were performed at the Department of Physiology, University of Bern, Bern, Switzerland. M.E. and E.N. conceived and designed the study. A.I. developed and programmed the analysis tools and designed the interface. M.W. and M. F.-T. collected and analyzed the experimental data. A.I., M.W., M.E., and E.N. drafted and revised the article. All authors approved the final version for publication.

Editor: Valentin Nagerl.

Appendix: Image Preprocessing

The only preprocessing step used is convolving the image with a (2n + 1) × (2n + 1) kernel in which the center element is 1/(n + 1) and the k-th layer surrounding the center is made up of values 1/8k × (n + 1). For example, when n = 1, the kernel would be: $\left(\begin{array}{l}1/161/161/16\\ 1/161/21/16\\ 1/161/161/16\end{array}\right)$.

Convolving the image with this kind of kernel reduces the noise while retaining more of the original signal than simple averaging. Contributions from the i-th layer around the center will have the same weight as the central pixel. In this work, we use the kernel with (n = 1).