Magnetic Entropy as a Proposed Gating Mechanism for Magnetogenetic Ion Channels

Abstract

Magnetically sensitive ion channels would allow researchers to better study how specific brain cells affect behavior in freely moving animals; however, recent reports of “magnetogenetic” ion channels based on biogenic ferritin nanoparticles have been questioned because known biophysical mechanisms cannot explain experimental observations. Here, we reproduce a weak magnetically mediated calcium response in HEK cells expressing a previously published TRPV4-ferritin fusion protein. We find that this magnetic sensitivity is attenuated when we reduce the temperature sensitivity of the channel but not when we reduce the mechanical sensitivity of the channel, suggesting that the magnetic sensitivity of this channel is thermally mediated. As a potential mechanism for this thermally mediated magnetic response, we propose that changes in the magnetic entropy of the ferritin particle can generate heat via the magnetocaloric effect and consequently gate the associated temperature-sensitive ion channel. Unlike other forms of magnetic heating, the magnetocaloric mechanism can cool magnetic particles during demagnetization. To test this prediction, we constructed a magnetogenetic channel based on the cold-sensitive TRPM8 channel. Our observation of a magnetic response in cold-gated channels is consistent with the magnetocaloric hypothesis. Together, these new data and our proposed mechanism of action provide additional resources for understanding how ion channels could be activated by low-frequency magnetic fields.

Introduction

Genetically encoded ion channels that open in response to magnetic fields—“magnetogenetics”—constitute a potentially powerful approach to discover the relationship between cell activity and behavior. Because magnetic fields can freely penetrate bone and tissue, cells that express these magnetogenetic proteins could be activated or inactivated throughout the brain of freely moving animals without the need for any implanted probes. Compared to other noninvasive brain stimulation techniques like ultrasound (1) and transcranial magnetic (2) or electric fields (3, 4), magnetogenetics could target cells of a specific genetic identity. Although cell-specific modulation can be achieved with existing techniques such as opto- (5), thermo- (6), and chemogenetics (7), magnetogenetics would provide an important complement by enabling high temporal resolution as well as deep tissue penetration. Additionally, because optical and magnetic stimuli do not strongly interfere with one another, magnetogenetics could be used simultaneously with existing optogenetic or fluorescent techniques with little or no cross talk.

Thermo-, chemo-, and optogenetics were created based on naturally occurring proteins that respond to temperature, chemical, or optical stimuli; however, there are no known natural genes that produce magnetic sensitivity when expressed in a host cell or organism. A major challenge in identifying the genetic basis of natural magnetoreception is the absence of a scientific consensus regarding the biophysical mechanism except in the case of magnetotactic bacteria (8). Without a natural magnetic field receptor, scientists are forced to engineer synthetic proteins that respond to magnetic fields.

One approach to create magnetically sensitive ion channels is to use chemically synthesized magnetic nanoparticles that can be heated by relaxation losses in the presence of high-frequency alternating magnetic fields (AMFs) (9). These synthetic nanoparticles can be injected into an organism, where they associate with temperature-sensitive ion channels to create magnetically sensitive cells (10, 11). For heat to be produced by this mechanism, the frequency of the magnetic field must be near the nanoparticle’s Néel relaxation frequency, which is typically 100–500 kHz.

Although exogenous chemically synthesized nanoparticles can effectively create magnetically sensitive cells, a method that did not require delivery of synthetic nanoparticles and relied on low-frequency magnetic fields would have a number of advantages. Generating high-frequency AMFs of sufficient amplitude to stimulate cells in vivo requires magnetic field generators that cost thousands of dollars and consume 5–15 kW of power (12). Low-frequency magnetic field generation consumes much less power and can even be achieved using a permanent magnet. Additionally, using genetically encoded nanoparticles would eliminate the need for nanoparticle injections and greatly simplify the implementation of magnetogenetics, particularly in small model organisms like flies and worms.

Recently, two independent labs have reported completely genetically encoded magnetogenetic protein assemblies based on the iron-binding protein ferritin (13, 14); however, no established biophysical mechanisms can explain the observed magnetic responses (15, 16). In each case, the reported magnetogenetic constructs were based on tethering genetically encoded iron nanoparticles assembled within a 24-mer ferritin cage to ion channels of the TRP-family (17). For example, the “Magneto2.0” construct is a chimeric ferritin with improved assembly and iron-loading properties fused to the truncated C-terminus of the mechano- and thermosensitive TRPV4 channel (18). Several experiments show that this channel can be activated by steady magnetic fields (13, 14). Although the authors suggested that this response may be mediated by the mechanical force between adjacent nanoparticles, these forces are at least eight orders of magnitude weaker than the pN-scale forces required to activate mechanoreceptors (15). Magnetically induced eddy currents responsible for transcranial magnetic stimulation also fail to account for the observed magnetic response because transcranial magnetic stimulation requires voltage-gated ion channels (19), and the TRPV4 channel used in Magneto2.0 (13) has negligible voltage sensitivity (Fig. S5).

To understand how these TRP-ferritin assemblies could be activated by low-frequency magnetic fields, we designed an experiment to isolate the pathways in TRPV4 required for a magnetic response. Specifically, we probed the mechanical and thermal activation pathways of the magnetogenetic assembly and discovered that magnetic sensitivity depended on the heat-sensing pathway. Based on these results, we propose a mechanism of action based on changes in the magnetic entropy of ferritin nanoparticles, in which the TRP channel is activated by heat generated via the magnetocaloric effect. This magnetocaloric effect also predicts that heat will be absorbed during demagnetization, which could cool the associated ion channel. Cooling is unique to the magnetocaloric effect compared to previously reported relaxation losses in AMFs, which are only expected to generate heat (20, 21). To test this magnetocaloric hypothesis, we designed and tested a magnetogenetic protein (MagM8) based on the cold-gated TRPM8 channel. We found a significant magnetic response of the MagM8 channel, which is consistent with our proposed magnetocaloric mechanism. We hope that presenting these data and our proposed mechanism of action will help guide new theory and experiments to understand the conditions under which low-frequency magnetic fields could activate ion channels.

Methods

Cell culture and molecular biology

HEK293 cells obtained from ATCC (Manassas, VA) were cultured in Dulbecco’s modified Eagle’s medium (DMEM; Lonza, Basel, Switzerland) supplemented with 10% fetal bovine serum (lot #1750106; Gibco, Waltham, MA) and 1% penicillin-streptomycin (Lonza). pcDNA3.0-Magneto2.0-p2A-mCherry, pcDNA3.0-TRPV4-p2A-ferritin-p2A-mCherry, and pEGFP-TRPM8 were obtained from Addgene, Watertown, MA (#74308, #74309, and #64879, respectively). Sequences were assembled using NEBuilder HiFi DNA Assembly, and mutations were performed with the Q5 Site-Directed Mutagenesis Kit (New England Biolab, Ipswich, MA). Cells were transfected 4 days before recording, using Lipofectamine 2000 (Invitrogen, Carlsbad, CA) following manufacturer’s recommendations. Cells were replated on sterile coverslips (Azer Scientific Cover Glass, No. 1, Circle, 12 mm; Azer Scientific, Morgantown, PA) 48 h before recording to obtain a confluency of 60–70%.

Electrophysiology

The cells were placed in electrophysiology extracellular buffer (145 mM NaCl, 5 mM KCl, 3 mM MgCl₂, 10 mM HEPES, and 1 mM CaCl₂ (pH 7.2); adjusted to 320 mOsm with sucrose). Glass patch pipettes with a resistance of 3–5 MΩ were filled with intracellular buffer (140 mM KCl, 10 mM HEPES, and 0.5 mM EGTA (pH 7.2); adjusted to 320 mOsm with sucrose) and brought into contact with the cell membrane to generate seals ≥1 GΩ. A negative pressure of −70 mmHg was applied inside the pipettes to gain access to the whole cell configuration. An Axopatch 700 A amplifier (Molecular Devices, San Jose, CA) was used to monitor currents under voltage clamp conditions. The current was filtered at 10 kHz and digitized at 2 kHz using a Digidata 1550 (Molecular Devices).

Calcium imaging

All calcium recordings were performed in an imaging extracellular buffer (iECB; 119 mM NaCl, 5 mM KCl, 10 mM HEPES, 2 mM CaCl₂, 1 mM MgCl₂ (pH 7.2); 320 mOsm). Cells are incubated with 2 μM Fluo-4 AM (Thermo Fisher Scientific, Waltham, MA) in culture media for 30 min and rinsed in DMEM for 10 min. For (−)Mech conditions, the cells were further incubated in the presence of 25 μM of 4-bromophenacyl bromide (pBPB) for 15 min before recording. For depleting intracellular calcium stores, after being incubated with Fluo-4, the cells were further incubated 30 min with 1 μM thapsigargin (Sigma Aldrich, St. Louis, MO) diluted in DMEM. The coverslip with the cells was then transferred to the recording chamber, covered with iECB, and equilibrated at room temperature for 5 min before recording. Cells with Fluo-4 were imaged on a Nikon Eclipse inverted microscope with a 20× objective (Nikon S Fluor, numerical aperture NA = 0.75; working distance WD = 1 mm; Nikon, Tokyo, Japan). For fluorescence excitation, we used an LED with a center wavelength of 470 nm (M470L3; ThorLabs, Newton, NJ). The LED output was filtered with neutral density filters to ∼0.2 mW/mm² (PM100D; Thorlabs). Images were collected with a Zyla sCMOS Camera (Andor, Belfast, UK) through a GFP Filter Cube Set (Nikon) and analyzed with MATLAB.

Magnetic stimulation

The magnetic stimulation was delivered by a 1 inch × 1 inch cylindrical neodymium rare-earth permanent magnet (grade N48; Apex Magnet, Petersburg, WV) on a computer-controlled translation stage (Thorlabs). The sham magnet is made of copper and is of similar size and weight as the permanent magnet. The magnet was covered with adhesive black felt to prevent light reflection or diffraction. Additionally, protective black felt was positioned above the sample to avoid optical artifacts from the magnet moving close to the sample. To collect a baseline fluorescence value, no magnetic stimulation was performed for the first 30 s of imaging. After the initial 30 s of imaging, the magnet was brought within ∼8 mm of the coverslip at a frequency of 0.08 Hz. At that distance, the magnetic field is predicted to be 275 mT based on manufacturer’s specifications and measured in excess of 200 mT (GM-2 gaussmeter; AlphaLab, Salt Lake City, UT). The periodic magnetic stimulation was applied for 270 s, and the imaging and magnet movements were synchronized using Axopatch (Molecular Devices). For each coverslip, a recording was first performed in the absence of magnetic stimulation (“No Stim”), and the microscope was then moved to a different field of view (FOV) for magnetic stimulation (“0.08 Hz Stim”). This approach ensured that for each experiment, the cells were exposed to the same illumination conditions and exposed only once to the magnetic stimulation protocol. After magnetic stimulation, the coverslip was discarded. The experiments were performed at 23–25°C, and recordings occurred within 30 min of the cell being removed from the incubator.

Mechanical and thermal stimulation

Mechanical and thermal responses were measured via calcium imaging of cells under constant fluid flow in a microfluidic chamber. The recording chamber consisted of a central chamber (∼100 μL), three inlet ports, and one outlet port. Coverslips with adherent cells were placed into the chamber, and a 4α-phorbol 12,13-didecanoate lid provided a watertight seal and thermal insulation during perfusion. The three inlet ports were connected to valve-controlled reservoirs, allowing a gravity-driven exchange of the buffer at 2 mL/min. For each coverslip, calcium activity was monitored during the perfusion of 320 mOsm iECB at 23°C for 30 s. 240 mOsm iECB (mechanical stimulation) or heated 320 mOsm iECB (thermal stimulation) were then perfused for 60 s, followed by a return to 320 mOsm iECB at 23°C for 30 s.

For thermal stimulation, iECB was heated with an in-line heater (Warner Instrument, Hamden, CT) to yield the appropriate temperature in the recording chamber (measured via thermocouple). Upon perfusion of heated iECB, a small decrease in Fluo-4 intensity was consistently observed in all samples. This stimulation artifact is believed to be due to a temperature-dependent Fluo-4 extrusion (22) or decrease in F_max (23). For cold stimulation of MagM8, an in-line heater maintained the bath temperature at 40°C, and an in-line cooler delivered the cooled buffer. The cells were maintained at 40°C for 5 min before being exposed to a lower temperature for 1 min by switching the gravity-driven flow from the in-line heater to the in-line cooler set at the appropriate temperature.

Image processing and analysis

Calcium data were analyzed using custom algorithms developed in MATLAB (The MathWorks, Natick, MA). First, transfected cells were identified based on mCherry expression, and regions of interest corresponding to individual transfected cells were automatically selected via our segmentation algorithm. We then calculated the percent change in fluorescence (ΔF/F₀) for each region of interest based on the average fluorescence value divided by the average fluorescence value of the first captured image, F₀. Rarely, sample movement or focal shifts would accompany magnet movement resulting in periodic artifacts in the imaging data. The motion artifacts were small compared to the magnetic field induced changes in fluorescence.

Data availability

All the recordings used to generate the figures presented in this manuscript, as well as the MATLAB script written to analyze these .tif files, are available at: https://figshare.com/projects/Magnetic_entropy_as_a_proposed_mechanism_for_gating_of_magnetogenetic_ion_channels/38582.

Results

Magnetic stimulation of the channel Magneto2.0 under different conditions

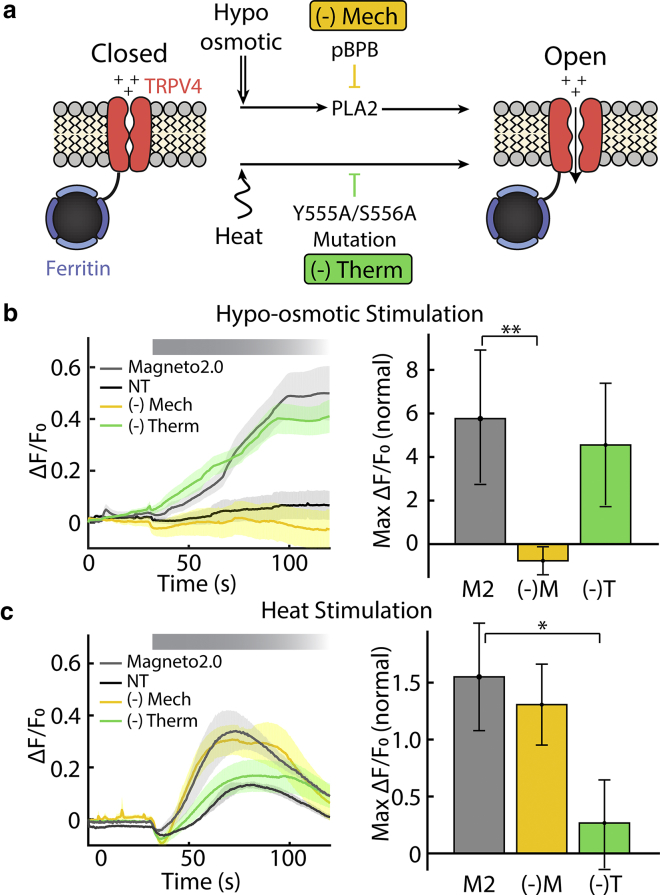
One reason that the magnetic activation pathway of TRP fusion proteins is difficult to ascertain is the fact that the TRPV4 channel in Magneto2.0 is known to be activated by both thermal and mechanical stimuli (24). To better understand how magnetic fields can activate Magneto2.0, we designed experiments to selectively inhibit either the thermal or mechanical sensitivity. Before attempting to selectively inhibit these different activation pathways, we first confirmed that despite a truncated C-terminal segment and the association to ferritin, Magneto2.0 retains the dual sensitivity to mechanical and thermal stimulation reported for TRPV4 (13) (Fig. 1; Fig. S6).To reduce the mechanical sensitivity of Magneto2.0, we used a PLA2 inhibitor, pBPB (24, 25). This condition, referred to as (−)Mech, showed reduced sensitivity to hypoosmotic shock but normal temperature sensitivity as measured by calcium-sensitive fluorescence imaging in transfected HEK cells (Fig. 1, b and c, (−)Mech). Similarly, we created a version of Magneto2.0 with reduced thermal sensitivity by mutating the YS domain in the third transmembrane domain (Y555A/S556A) (24). In TRPV4, this mutation also impairs the activation by 4αPDD, suggesting a common activation mechanism between that agonist and heat at the protein level. Importantly, channel gating by mechanical stimulation is unchanged in the mutated TRPV4 (24) and Magneto2.0 (Fig. 1 b). This variant, referred to as (−)Therm, showed normal response to hypoosmotic shock but reduced sensitivity to temperature (Fig. 1, b and c, (−)Therm).

Figure 1.

Inhibition of distinct activation pathways in Magneto2.0. (a) Schematic depicting independent pathways by which TRPV4 responds to stimuli. pBPB inhibits the PLA2-dependent mechanical response of TRPV4 (24). We refer to this condition as (−)Mech. The mutation Y555A/S556A inhibits the thermal response of TRPV4 (24). We refer to this condition as (−)Therm. (b) Calcium-sensitive fluorescence imaging shows that (−)Mech (and not (−)Therm) has reduced sensitivity to hypoosmotic stimulation compared to wild-type Magneto2.0 (non-transfected (NT), n = 6 separate cell cultures with a total of 3473 cells; Magneto2.0, n = 6 separate cell cultures with a total of 660 cells; (−)Mech, n = 7 separate cell cultures with a total of 711 cells; (−)Therm, n = 5 separate cell cultures with a total of 338 cells). (c) Calcium-fluorescence imaging shows that (−)Therm has a significantly reduced response to thermal stimulation (40°C perfusion) compared to (−)Mech and Magneto2.0. The brief decrease in fluorescence observed upon perfusion of warm buffer is due to the heat deformation of the coverslip that results in a change in focus (NT, n = 3 separate cell cultures with a total of 1482 cells; Magneto2.0, n = 5 separate cell cultures with a total of 395 cells; (−)Mech, n = 4 separate cell cultures with a total of 578 cells; (−)Therm, n = 6 separate cell cultures with a total of 343 cells). Bold lines in ΔF/F₀ versus time represent mean values, and shaded regions represent mean ± standard error (SE) based on the number of independent cell cultures recorded. Bar plots represent the maximal ΔF/F₀ normalized to the maximal ΔF/F₀ for NT cells. The error bars show the mean ± SE of the ratios, calculated from the standard deviation (SD) of the maximal averages used in each ratio and based on the number of independent cell cultures recorded. Except for NT, data are obtained only from mCherry⁺ (transfected) cells. The significances are assessed with a two-tailed unpaired Student’s t-test, (^∗p < 0.05, ^∗∗p < 0.01).

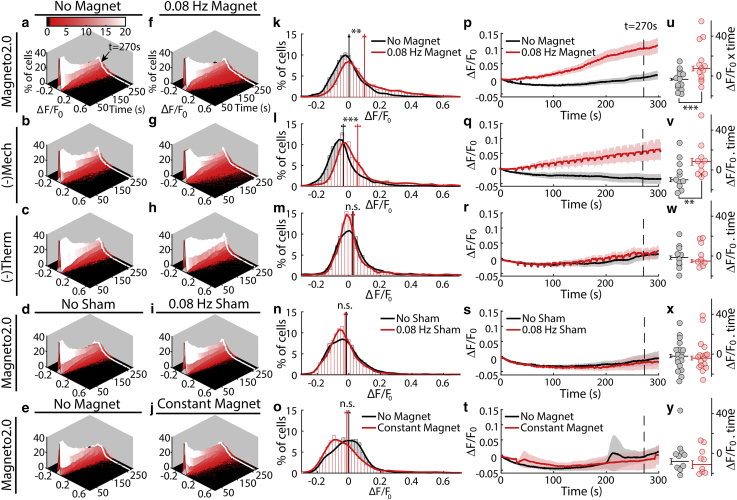
An additional challenge for understanding the activation pathway for Magneto2.0 is the low intensity and low probability of the magnetic response. To overcome this challenge, we recorded calcium activity in large numbers of individual cells using calcium-sensitive fluorescent imaging, which allows us to better determine the statistical significance of any weak magnetic responses. For each experimental condition, we recorded the calcium activity of over 1000 transfected cells from 14 independent cell cultures (Fig. 2). These experiments show that Magneto2.0-expressing cells (and cells in the (−)Mech group) display a statistically significant calcium response to low-frequency magnetic stimulation compared to our control groups (Fig. 2). The cells in the (−)Therm group showed no statistically significant calcium response to the same magnetic stimulation (Fig. 2).

Figure 2.

Magnetic activation of Magneto2.0 is thermally mediated. (a–j) Distribution of intracellular calcium levels over time based on calcium-sensitive fluorescence imaging (ΔF/F₀) is shown. In the absence of stimulation (a–e), distribution broadens over time but remains centered near zero. Under periodic magnetic stimulation (275 mT, 0.08 Hz, beginning at t = 30 s), a small percentage of cells (seen in red tail of the distribution) show an increase in calcium-sensitive fluorescence for Magneto2.0 (f) and (−)Mech (g), shifting the mean of the distribution. This is not the case for (−)Therm (h) and Magneto2.0 exposed to a sham magnet (i) or to a constant magnetic field (j). (k–o) Histograms taken from the data in (a)–(j) show the distribution of fluorescence values at t = 270 s with no magnetic stimulation (black) and with magnetic stimulation (red) (bin size 0.02 ΔF/F₀). These histograms correspond to the white lines in (a)–(j). Vertical red and black lines represent the mean value of these distributions with and without magnetic stimulation, respectively. Error bars show the mean ± SE for each histogram. (p–t) Plotting the mean value of ΔF/F₀ over time shows statistically significant responses for Magneto2.0 (p) and (−)Mech (q) in response to magnetic stimulation but not for (−)Therm (r) or Magneto2.0 exposed to a sham magnet (s) or to a constant magnetic field (t). ΔF/F₀ values from each cell culture are averaged using a 20 s sliding window. The resulting average and mean ± SE (calculated using n = number of independent cell cultures) are shown as a solid line and a shaded region, respectively. The periodic artifacts most visible in (q) and (r) result from a small reversible movement of the microscope stage that sometime accompanied magnet movement. Equal numbers of “No Stimulation” and “Magnetic Stimulation” experiments were performed for each condition. (u–y) Each dot represents the area under the curve of the calcium activity calculated for a given cell culture. The average area under the curve for all cell cultures is shown as a horizonal bar with error bars indicating the corresponding mean ± SE, calculated using n = number of independent cell cultures. The significance of the increase in calcium activity was assessed using the left-tailed Wilcoxon test. This nonparametric test is used because the increased cell activity is not necessarily normally distributed. ^∗p < 0.1; ^∗∗p < 0.05; ^∗∗∗p < 0.01. The total number of cells measured from separate cell cultures are (indicated as total number of cell/number of separate cell cultures) Magneto2.0, n = 1573/14 (no stimulation), n = 1510/14 (magnetic stimulation); (−)Mech, n = 1290/11 (no stimulation), n = 1587/11 (magnetic stimulation); (−)Therm, n = 1724/10 (no stimulation), n = 1073/10 (magnetic stimulation); Sham Stimulation, n = 2759/19 (no stimulation), n = 2970/19 (sham stimulation); Constant Magnet, n = 1536/12 (no stimulation), n = 1692/12 (magnetic stimulation). Note that prior studies of magnetogenetic channels often calculate mean ± SE with n representing the number of cells. In that case, the error bars would be significantly smaller than the error bars shown here.

We tested the magnetic sensitivity of Magneto2.0, (−)Mech, and (−)Therm by stimulating transfected HEK cells with a magnetic field of ∼275 mT at a frequency of 0.08 Hz for 270 s. This stimulation protocol is similar to that reported for HEK cells in Wheeler et al. (13), which gave us the opportunity to compare our results to reported data. Although our data were gathered from a larger number of cells, the response amplitude and kinetics are comparable to the results reported by Wheeler et al. For each cell culture grown on a coverslip, we performed one experiment as a control and a second experiment with a magnet or sham magnet stimulation. For the control, we imaged calcium activity from one FOV in the absence of external stimuli. For the second experiment, we imaged a new FOV on the same coverslip during stimulation by a magnet or sham magnet. 10–20 FOVs from independent cell cultures were recorded for each condition, yielding ≥1000 cells per condition. When calculating statistical significance, we considered both individual cells (Fig. 2, a–o; n > 1000 cells per condition) and independent cell cultures (Figs. 2, p–y and 5; n ≥ 10 cell cultures) as the number of replicates and report the statistical significance using both methods. To control for variations that might be introduced by the experimental setup (temperature, movement of the mechanical stage, time dependence, etc.), we performed control experiments on independent cell cultures using a sham magnet of identical weight, size, and coating to the real magnet. The recording chamber was also covered in all recordings to prevent artifacts from changes in the image background or illumination conditions. To measure the temperature sensitivity of the ion channels (Figs. 1 and S6), we imaged changes in intracellular calcium concentration using the calcium-sensitive fluorescence dye Fluo-4. Because the baseline fluorescence F₀ depends on the initial intracellular calcium concentration as well as the loading efficiency of Fluo-4, the change in fluorescence is normalized to F₀ to yield quantitative measures of the change in calcium. Note that because overexpression of constitutively active TRP channels could raise the baseline calcium, we waited 4 days after transfection to allow cells to achieve homeostasis with elevated calcium levels.

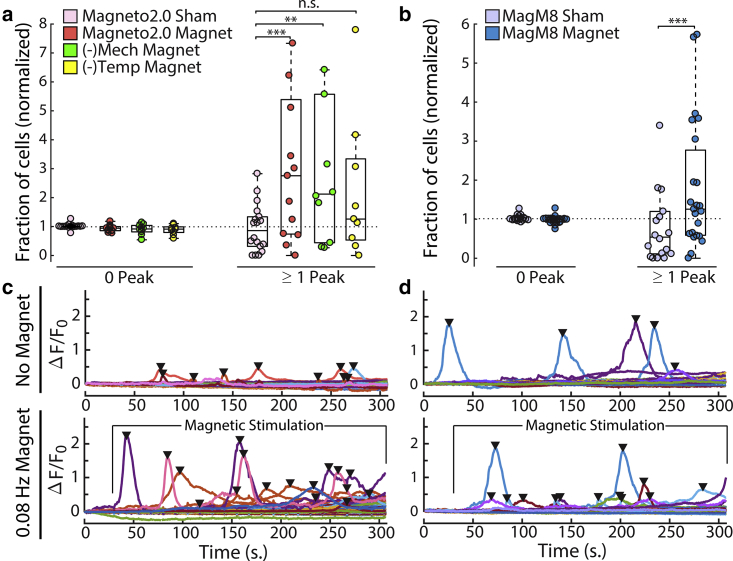
Figure 5.

Identifying responding cells based on calcium peaks: the calcium activity of transfected cells is monitored by fluorescence intensity (Fluo-4), and the resulting ΔF/F₀ traces are analyzed to detect calcium peaks, as shown in (c and d). The presence or absence of calcium transients allows us to separate the recorded cells in each cell culture between “responding” cells (one or more calcium peak) and “nonresponding” cells (no calcium peak detected). For each cell culture, one FOV is recorded with no exposure to the magnet or to the sham magnet, followed by a measurement of another FOV in the same culture during stimulation by a magnet or the sham magnet at a frequency of 0.08 Hz. For each cell culture, the percentage of responding transfected cells during exposure to the magnet or the sham is divided by the percentage of responding cells observed in the control group (no stimulation). These normalized fractions of responding cells are plotted for each cell culture (circles in (a) and (b)). The significance of the increase in calcium activity between the population exposed to a real magnet and the population exposed to a sham magnet is assessed using the left-tailed Wilcoxon test (non-normal distribution). The significance of the difference between the condition is indicated as ^∗p < 0.1; ^∗∗p < 0.05; ^∗∗∗p < 0.01.

We then quantified the cumulative change in the calcium concentration in each cell as the average ΔF/F₀ over time (Figs. 2, u–y and 4, i and j) and as the area under the ΔF/F₀ curve for each cell culture (Figs. 2, u–y and 4, k and l). Because the calcium-sensitive fluorescence is computed from the transfected cells in 10 or more independent cell cultures, yielding recordings from over 1000 cells per condition, we also plotted the distribution of ΔF/F₀ values in individual cells to show the variance in the data. We also plotted this distribution over time to show how it is affected by the magnetic stimulus (Fig. 2, a–j). We then plotted a snapshot of this distribution 270 s after the start of the experiment (Fig. 2, k–o). Representative ΔF/F₀ cell traces can be seen in Fig. 5 and Fig. S8. Moreover, the data and the script used to generate these plots are available online on Figshare. Note that the increase in calcium observed in the population average during magnetic stimulation (Fig. 2, p and q) does not represent an increase in the baseline calcium of each cell but rather an increase in calcium spikes in which the ensemble average results in a slow monotonic increase (see Fig. 5 c). Our ability to measure small changes in calcium influx is the result of averaging over many cells that each express a large number of ion channels. Because the dynamics of each channel is independent, the average baseline calcium influx into each cell as well as the magnetic response of each cell scales with the number of channels per cell (N_ch). The variance of Magneto2.0 activation scales as 1/N_ch, meaning that the signal/noise ratio of the magnetic response increases with increasing channel number. We further reduce the noise in our measurements by averaging over many cells, which reduces the variance of our measure of intracellular calcium with the number of cells (N_cells) as 1/N_cells. This averaging over many cells, each expressing many channels, allows the population to report small changes in the average ion channel activation even if this change is small compared to the thermal variance of any individual channel (Supporting Materials and Methods).To quantify the increase in calcium activity in the presence of Magneto2.0 and magnetic stimulation, we also computed the number of “responding” cells per cell culture by counting the number of calcium peaks or transient increases in calcium in each cell (Fig. 5, c and d). We defined a cell as “responding” when we detect one or more calcium peaks. For each cell culture, we determined the proportion of responding cells to total transfected cells in the absence and presence of the magnetic stimuli, respectively. We then calculated for each cell culture the ratio of proportion of responding cells during magnetic stimulation over the proportion of responding cells in the absence of stimulation (Fig. 5, a and b). The ratio of cells displaying calcium peaks was significantly greater in magnetically stimulated cultures and is consistent with calcium-induced calcium-released (CICR) initiated by the calcium influx through TRP channels or, in this case, Magneto2.0 (26, 27, 28, 29, 30, 31). In addition to the number of peaks per cell and cell culture, we have investigated the amplitudes of the calcium transients.

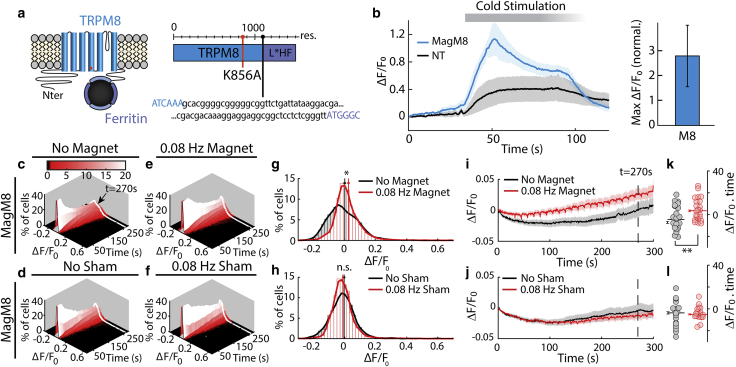
Figure 4.

Magnetic activation of MagM8. (a) TRPM8 is mutated (K856A, in orange) and fused to the chimeric ferritin (L^∗H-Ferritin) by a 23 residues linker to create MagM8. (b) Intracellular calcium level in transfected (blue) and NT (black) cells is reported as ΔF/F₀ and shows that MagM8 responds to cooling stimulation (40–15°C). The shaded region and error bars show the mean ± SE based on n = 4 independent cell cultures (slides), containing a total of 1066 transfected cells and 545 NT cells. (c–f) Distribution of intracellular calcium levels over time (as ΔF/F₀) is shown. In the absence of stimulation (c and d), the distribution broadens over time but remains centered near zero. Under periodic magnetic stimulation (275 mT, 0.08 Hz, beginning at t = 30 s), a small percentage of cells (seen in red tail of the distribution) show an increase in calcium-sensitive fluorescence for MagM8 stimulated with a magnet (e) but not for MagM8 exposed to the sham magnet (f). (g and h) Histograms taken from the data in (c)–(f) show the distribution of fluorescence values at 270 s with no magnetic stimulation (black) and with magnetic stimulation (red) (bin size 0.02 ΔF/F₀). These histograms correspond to the white lines in (c)–(f). Vertical red and black lines represent the mean value of these distributions with and without magnetic stimulation, respectively. Error bars show the mean ± SE for each histogram. At 270 s, p = 0.07 for n = slides, p < 0.001 for n = cells for magnetic stimulation; p = 0.53 for n = slides and 0.88 for n = cells for sham stimulation. (i and j) Plotting the mean value of ΔF/F₀ over time shows that MagM8 exposed to a magnetic field displays a statistically significant response to magnetic stimulation, whereas MagM8 exposed to a sham magnet does not. The periodic artifacts in (i) and (j) result from small reversible movement of the microscope stage that sometimes accompanied magnet movement. Shaded regions are mean ± SE calculated with n = independent cell cultures recorded. (k and l) The area under the curve of the calcium activity was calculated for each cell culture. The resulting value for each cell culture is shown as a dot, and the average is shown as a horizonal bar with error bars indicating the corresponding mean ± SE. The significance of the difference between the conditions is indicated as ^∗p < 0.1; ^∗∗p < 0.05; ^∗∗∗p < 0.01. The total number of cells measured from separate cell cultures are (indicated as total number of cells/number of separate cell cultures) with magnet, n = 5184/23 (no stimulation), n = 5372/23 (magnetic stimulation); with sham magnet, n = 2237/18 (no stimulation), n = 2283/18 (sham stimulation). The significance of the increase in calcium activity was assessed using the left-tailed Wilcoxon test. This nonparametric test is used because the increased cell activity is not necessarily normally distributed.

The normalized distribution of the peak prominence did not significantly differ between the recording conditions. To control for potential confounding effects of imaging the same group of cells multiple times, we performed each recording only once per FOV and normalized all data to experiments on the same coverslip. We used a similar normalization for the nonresponding transfected cells (“0 Peak”). The averages for the different conditions as well as the individual values for each slide are plotted in Fig. 5, a and b, respectively. No significant difference in transfection efficiency or RFP fluorescence between the high- and low-responding cell cultures was measured (Fig. 2, u–y). These data suggest that multiple factors—including membrane trafficking of the Magneto2.0 channel, the availability, assembly, and iron loading of ferritin oligomers, and cell health—may affect the magnetic response. Ferritin assembly and loading in particular is difficult to control in live cells because ferritin expression is dynamically regulated by intracellular iron levels and oxidative stress via the iron response element (32).

Based on the average ΔF/F₀ (Fig. 2), the area under the curve, and the number of responding cells (Fig. 5), we found that the (−)Mech variant of Magneto2.0 is activated by magnetic stimulation, whereas the (−)Therm variant is not, suggesting that magnetic sensitivity to slowly varying fields is indeed a thermally mediated process as predicted by our magnetocaloric hypothesis. This response to magnetic stimulation observed in Magneto2.0 is similar to the data reported by Wheeler et al. in transfected HEK cells (13) and is not observed for non-transfected cells (Fig. S7). To confirm that calcium activity is due to the applied magnetic field, we repeated our experiment after replacing the magnet with a sham magnet of identical size, weight, and coating (but with no permanent magnetic moment). We found that stimulation with the sham magnet did not produce significant calcium activity in Magneto2.0-transfected cells (Fig. 2). Moreover, the fraction of cells showing calcium peaks (responding cells) was also significantly higher during stimulation with the magnet compared to stimulation with the sham magnet (Fig. 5). We also saw no significant increase in calcium activity when we applied a constant 275 mT magnetic field for 270 s (Fig.1, bottom row), suggesting that the process of magnetization (and not steady magnetic fields) give rise to the calcium signal, which is expected for the magnetocaloric effect.

Magnetocaloric theory

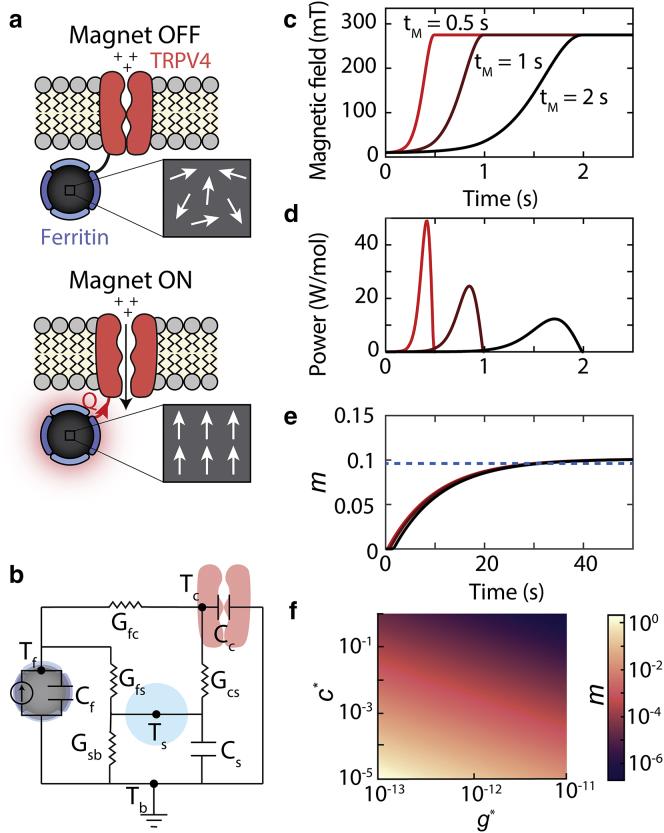
Although relaxation losses used for prior magnetothermal experiments (11, 14, 33) are not predicted to generate heat during the low-frequency stimulation used in our experiments, a fundamentally different mechanism, the magnetocaloric effect, may explain our observed thermally mediated magnetic response. The magnetocaloric effect describes the relationship between the magnetic entropy and the temperature change of a magnetic material within a magnetic field (20). Under conditions described below, the temperature change generated by a reduced entropy during magnetization may be sufficient to gate nearby thermoreceptors. In the absence of a magnetic field, both paramagnetic and superparamagnetic materials have randomly oriented magnetic domains. In the case of paramagnetic materials, many magnetic domains randomly orient (Fig. 3 a) within a single particle, whereas in the case of superparamagnetic materials, each particle has a single domain that randomly fluctuates over time. Thus, no net magnetic moment is observed if measurements are made over periods of time longer than the relaxation time (34), which is expected to be on the order of nanoseconds for small particles like ferritin (35). For either paramagnetic or superparamagnetic materials, when a magnetic field is applied, the moments align while the field is present, thereby reducing the magnetic entropy (Fig. 3 a). This decrease in entropy produces heat in the ferritin nanoparticle (Q_f) given by (20)

$$Q_f=\underset{0}{\overset{B}{\int }}T{\left(\frac{\partial M}{\partial T}\right)}_{B}dB.$$ (1)

Figure 3.

The magnetocaloric gating mechanism: (a) schematic shows how the magnetocaloric effect in ferritin can activate nearby temperature-sensitive ion channels (e.g., TRPV4). An applied magnetic field will align the magnetic moments within paramagnetic ferritin nanoparticles, which will reduce the magnetic entropy. The reduced magnetic entropy generates heat (Q) via the magnetocaloric effect that can activate a nearby temperature-sensitive ion channel. Here, we have depicted ferritin as a paramagnet, but the calculations are equivalent for superparamagnetic particles. (b) The equivalent circuit model used to estimate heat transfer between the ferritin particle and ion channel is shown. T_f, T_c, T_s, and T_b represent the temperature of the ferritin, channel, water shell around ferritin, and bath, respectively. C_f, C_c, and C_s represent the heat capacities of the ferritin, channel, and near-water shell, respectively. G_fc, G_fs, G_cs, and G_sb represent the thermal conductances between the ferritin and channel, ferritin and water shell, channel and water shell, and water shell and bath, respectively. (c) The applied magnetic field as a function of time for three different magnetization times (t_m = 0.5, 1, and 1.5 s) is shown. (d) The power generated in a mole of ferritin particles because of magnetocaloric effect for the magnetic field profiles in (c) is shown. (e) The number of additional openings per channel (m) caused by the magnetocaloric effect based on (d) and Eq. 5 is shown. The dashed blue line indicates the maximal percentage of channels that open as derived by the analytical expression for m in Eq. 8. Note that the total number of channels that open depends on the maximal value of the magnetic field and not the rate of magnetization. Calculations assume T_b = 25°C, c^∗ = 10⁻⁵, and g^∗ = 10⁻¹². (f) The fraction of channels that respond depends on the value of c^∗ (heat capacity scaling factor) and g^∗ (thermal conductance scaling factor), which can vary by orders of magnitude depending on the biophysical mechanism that triggers temperature-dependent channel gating. We expect that the m values near 10⁻⁵ and greater would yield a physiological response.

B is the applied field, T is the temperature of the bath, and M is the magnetization of ferritin. The magnetization of ferritin is modeled using a Langevin function along with a linear field component to describe the predominant antiferromagnetically ordered phase of the ferrihydrite component (36); the Langevin function applies to the uncompensated spins on the surface of the ferritin and the linear contribution to the antiferromagnetic core.

$$M=M_0\left[\coth \left(\frac{{\mu }_{p}B}{kT}\right)-\frac{1}{\left(\frac{{\mu }_{p}B}{kT}\right)}\right]+{\chi }_{1}B$$ (2)

μ_p is the average magnetic moment for each ferrihydrite particle, M₀ is the saturation magnetization, χ₁ is the susceptibility of the antiferromagnetic core, and k is the Boltzmann constant. Both M₀ and χ₁ are temperature dependent (36) (see Supporting Materials and Methods for values).

Using the small angle approximation for the Langevin function in Eq. 2 and considering the temperature dependence of M₀ and χ₁ (see Supporting Materials and Methods), we can evaluate the integral in Eq. 1 to calculate the total heat generated by an applied magnetic field:

$$Q_f=\left[\left|{\left(\frac{\partial M_0}{\partial T}\right)}_B\right|\frac{{\mu }_p}{3k}+M_0\frac{{\mu }_p}{3kT}+T\left|{\left(\frac{\partial {\chi }_1}{\partial T}\right)}_B\right|\right]\frac{B^2}{2}.$$ (3)

Based on Eq. 3, we calculate that a 275 mT magnetic field will generate heat of 6 J/mol of ferritin at room temperature (25°C). Prior work questioning the biophysics of magnetogenetic channel gating (e.g., (15)) calculated heat due to relaxation losses, which is a different mechanism than the entropic heating produced by the magnetocaloric effect. Relaxation losses are primarily observed when the magnetic spins oscillate at radio frequencies and are negligible at the frequencies of less than 1 Hz that were used for our experiments.

Although 6 J/mol is small compared to the ambient thermal energy (kT), animals are known to be sensitive to temperature differences of 1 mK (37). The energy needed to raise the channel temperature by 1 mK is only 0.2 kT (at room temperature). An animal’s ability to sense changes in thermal energy less than kT can be explained by population averaging. The temperature of a single channel has an SD equal to 1 K, but the average temperature of an ensemble of channels has an SD that scales as 1/√N where N is the number of channels (38) (see Supporting Materials and Methods). Thus, we expect an SD of 0.01 μK for an ensemble of 160,000 ion channels in a neuron sampled over ∼ms channel response time (see Supporting Materials and Methods). In this case, the addition of 6 J/mol because of the magnetocaloric effect shifts the mean of the Boltzmann distribution of channel energy by 1000 times the SD. In the case of Magneto2.0, this shift in the mean of the thermal energy distribution increases the number of channel openings. Although most literature suggests that ferritin is superparamagnetic (35, 39), our calculation for the heat produced by the magnetocaloric effect gives identical results for superparamagnetic or paramagnetic materials. There have also been reports of a magnetite-maghemite component in ferritin contributing to the magnetization in the form of an additional Langevin term with magnetic moment of 640 μ_B, which would add 1.5 J/mol to the above calculation (40). We expect less than a 1% change in the ferritin temperature, and thus we can accurately estimate Q_f using the isothermal approximation in Eq. 3 (see Supporting Materials and Methods).

The fraction of thermal energy that is absorbed by the channel depends primarily on the heat capacity of the channel, ferritin, and the water as well as the thermal conductance across the interfaces between materials. We model this heat transfer process as an equivalent circuit shown in Fig. 3 b. The thermal conductance will depend on the interfacial heat transport at the nanometer scale, which is known to deviate significantly from bulk heat transfer laws. Indeed, temperature in the immediate vicinity of iron oxide nanoparticles has been reported by independent sources to reach several orders of magnitude higher than predicted by bulk heat transport equations (10, 41, 42, 43, 44, 45). Although these findings are not universally accepted, one explanation for this increased temperature is a decrease in the thermal conductance of the water surrounding the nanoparticles, which we can include in our equivalent circuit model. In this case, the thermal conductance of the water shell around the nanoparticle can be written as g^∗ G, where G is the macroscopic thermal conductance and g^∗ is a scaling factor. Several experiments from multiple laboratories report the temperature surrounding iron oxide nanoparticles heated by AMFs, which allows us to estimate the value of g^∗ (see Table S1). These experiments using thermolabile linkers (41, 42) or thermo-responsive optical probes (10, 43, 44, 45) report heat dissipation rates of 10⁻²–10⁻³ s⁻¹, leading to an estimated g^∗ of 10⁻¹³ for nanoparticle suspensions (see Supporting Materials and Methods). Some of these experiments also suggest that the temperature decays rapidly from the nanoparticle surface with a decay length of ∼1–2 nm from the nanoparticle surface, consistent with our water shell model (42). Based on these reports, we hypothesize that the thermal conductance measured around other iron oxide nanoparticles will be similar for ferritin, and we model the slow thermal decay rates by assuming a water shell of ∼1.5 nm thickness around the particles with a thermal conductance reduced by a factor of g^∗ (Supporting Materials and Methods). This water shell model is also supported by recent experiments (33) showing that nanoparticles attached to the surface of cells, where heat can transfer more easily to lipids or transmembrane proteins, have faster dissipation rates of ∼0.1 s⁻¹, giving g^∗ values of ∼10⁻¹².

The heat capacity of the channel may also be affected by local nanoscale heating. For example, delivering thermal energy to some protein domains may drive channel gating more effectively than heating the channel uniformly. In this case, the effective change in temperature at the critical protein domain can be written as ΔT/c^∗, where c^∗ is a heat capacity scaling factor. For TRP channels, we estimate c^∗ to be between 10⁻⁵ and 1, where the upper bound of the effective heat capacity represents uniform heating of the channel with heat distributed evenly to all degrees of freedom (see Supporting Materials and Methods). The lower bound corresponds to all heat being absorbed locally by a single degree of freedom, such as the breaking of a hydrogen bond or the rotation of a protein side chain before the protein reaches thermal equilibrium (see Supporting Materials and Methods). One possibility for how local heating can more efficiently gate TRPV4 stems from reports that a single hydrogen bond between residue L596 in the S4–S5 linker and residue W733 in the TRP domain functions as a “latch” that stabilizes the protein in the closed and inactivated state (46, 47). This hydrogen bond is estimated to be only about ∼2.5 nm from the ferritin binding site based on the recently solved structure of TRPV4 (48), raising the interesting possibility that heating this bond directly can activate the channel more effectively than uniform channel heating.

To estimate the heat transfer between the ferritin and the channel, we use an equivalent circuit model for heat transport, in which current, voltage, capacitance, and electrical conductance represent thermal power, temperature, heat capacity, and thermal conductance, respectively (Fig. 3 b). The equivalent circuit is based on four primary components: ferritin (f), water shell around the ferritin (s), channel (c), and the bath (b). It is possible to estimate the local temperature change (ΔT) due to the magnetocaloric effect using this circuit and estimated values of thermal conductances, which in turn determines the channel response. Using the equivalent circuit and the value of g^∗, we obtain the following equation for the temperature change (ΔT_c) of the channel (see Supporting Materials and Methods for details):

$$\frac{d\Delta T_c}{dt}=\frac{\frac{d{Q}_f}{dt}-g^{\ast }{G}_{sb}\left(T_c-T_b\right)}{C},$$ (4)

where G_sb is the macroscopic thermal conductance of a water shell of thickness 1.5 nm, C is the sum of heat capacities of the water shell, ferritin, and channel. Using a value of g^∗ = 10⁻¹², the temperature decay rate (g^∗G_sb/C) is 10⁻¹ s⁻¹, which matches recent measurements of thermal decay rates for nanoparticles attached to a cell surface (33). The effective temperature at the critical protein domain can then be written as ΔT_c^∗ = ΔT_c/c^∗.

To estimate the number of channels activated by magnetocaloric heating, we can model channel gating using the open-close two-state thermodynamic model often used to describe the temperature response of thermoreceptors (see Supporting Materials and Methods) (49). Although TRP channels are expected to have more than two states, a simple model with a single closed and open state reproduces the functional form of the temperature sensitivity of the channel and is useful for estimating the channel open probability (P_open). TRPV4 channels can be activated by moderate temperatures (>24°C) and are known to exhibit constitutive activity at physiological temperatures (50). We have confirmed the temperature-dependent gating of Magneto2.0 from 15 to 40°C (Fig. S6). Previous work has shown that the temperature sensitivity of the TRPV4 channel results from temperature-dependent changes in the opening rate (α) and the closing rate (β) (49), both of which are continuous functions of the temperature. To determine whether the temperature change caused by the magnetocaloric effect is sufficient to gate TRP thermoreceptors, we can estimate the number of additional openings per channel (m) caused by magnetocaloric heating. To calculate this value, we integrate the change in number of openings per channel per unit time, which is the product of the temperature-dependent channel open rate (α) and the probability that a channel is in a closed and activatable state (P_close):

$$m=\underset{t_0}{\overset{\infty }{\int }}\left[\alpha \left(t\right)P_{close}\left(t\right)-\alpha \left(t_0\right)P_{close}\left(t_0\right)\right]dt,$$ (5)

where t₀ is the start of the magnetization. Note that we are assuming that the heat dissipation time (t_d, expected to be less than 10 s) is fast enough to neglect any adaptation by the cell to a change in temperature. This adaptation typically involves transcriptional regulation of calcium pumps and ion exchangers on the timescale of tens of minutes (51, 52). However, the heat dissipation time is much slower than the time it takes for the population of channels to reach the steady-state value (t_s). Although the population response time is not well characterized for TRPV4, we can set a limit for the time constant based on the channel response times of similar channels (such as TRPV1), which is in the order of a few μs to a few ms (49).

We can then rewrite Eq. 5 based on the change in the effective channel temperature (ΔT_c^∗). Because t_s ≪ t_d, we can assume that at each time point, P_close is equal to the steady-state value. At steady state, α/β = P_open/P_close, and so αP_close can be replaced by βP_open. By assuming that the initial temperature of the channel is equal to the initial bath temperature (T_b), we can write β(t) P_open(t) at any given time according to the change in effective temperature of the channel (T_b + ΔT^∗_c(t)).

$$m=\underset{t_0}{\overset{\infty }{\int }}\left[\beta \left(T_b+\mathit{\Delta }{T}_c^{\ast }\left(t\right)\right)P_{open}\left(T_b+\mathit{\Delta }{T}_c^{\ast }\left(t\right)\right)-\beta \left(T_b\right)P_{open}\left(T_b\right)\right]dt$$ (6)

Equation 6 is solved numerically to evaluate m for different magnetization rates. Fig. 3 e plots the cumulative number of additional openings per channel (m) integrated between the start of the magnetic stimulation and time t. The asymptotic value of m corresponds to the total number of additional openings per channel accumulated as a result of the heat generated by the magnetocaloric effect. This total number of additional openings per channel depends on the total heat generated by the magnetocaloric effect and not the rate of heat generation (i.e., the rate of magnetization). For a single magnetic stimulation, this asymptotic value of m is reached when ferritin has been magnetized and the associated heat has dissipated (at the rate determined by g^∗). At this point, we expect no additional channel openings as a result of the magnetocaloric effect. To obtain a closed form expression for m, Eq. 6 can be further simplified as follows. Because we expect the magnetocaloric effect to produce small changes in the temperature of ferritin and the channel, we can expand P_open and β using a Taylor series and take only the terms of the first order to write m as a product of the temperature sensitivity of the channel and the time-averaged change in temperature:

$$m={\frac{d\left(\beta P_{open}\right)}{dT}|}_{T_b}\underset{t_0}{\overset{\infty }{\int }}\mathit{\Delta }{T}_c^{\ast }\left(t\right)dt.$$ (7)

Next, because we expect heat from the ferritin to dissipate much slower (∼10 s) compared to the magnetization time used in our experiments (∼1 s), we can assume instantaneous heating at t = 0 and thereby replace dQ_f/dt with Q_fδ(t), where δ(t) is the Dirac δ function. Substituting this in Eq. 4 and using ΔT_c^∗ = ΔT_c/c^∗ gives the following simplified expression for ΔT_c^∗:

$$\mathit{\Delta }{T}_c^{\ast }\left(t\right)=\frac{Q_f}{c^{\ast }C}{e}^{-\frac{g^{\ast }{G}_{sb}}{C}t}.$$ (8)

Integrating Eq. 8 with respect to time and using Eq. 3 for Q_f and inserting in Eq. 7, we can write the final form of m in terms of the applied magnetic field (B) and the scaling factors g^∗ and c^∗:

$$m=\kappa \frac{1}{c^{\ast }{g}^{\ast }}{\frac{d\left(\beta P_{open}\right)}{dT}|}_{T_b}{B}^2,$$ (9)

where κ represents the heating due to the magnetocaloric effect and is defined as

$$\kappa \equiv \frac{1}{2G_{sb}}\left[\left|{\left(\frac{\partial M_0}{\partial T}\right)}_B\right|\frac{{\mu }_p}{3k}+M_0\frac{{\mu }_p}{3kT}+T\left|{\left(\frac{\partial {\chi }_1}{\partial T}\right)}_B\right|\right].$$ (10)

To calculate m from Eq. 9, we must evaluate the derivative d(βP_open)/dT, which we can approximate using experimental data and our two-state kinetic model (see Fig. 3 f; Supporting Materials and Methods). The value of m obtained from the closed form solution in Eq. 9 is equal to the maximal value of m obtained by solving Eq. 6 numerically, as shown in Fig. 3 e, and does not depend on the rate of magnetization.

Even with a small number of channels activated by the magnetocaloric effect, these gatings can affect neuronal activity because of the large ionic conductance of TRPV4. Based on the values of channel currents, rheobase of neurons, and the number of channels expressed in a transfected neuron, we find that m values in the range of 10⁻⁶–10⁻³ are sufficient to elicit action potentials in neurons (see Supporting Materials and Methods). These values fall well within the range of our theoretical predictions of m for Magneto2.0 and MagM8 (Figs. 3 f and S2). For example, TRPV4 channels have a conductance of 60 pS (53), and the activation of a single ion channel with conductances of 60–70 pS has been shown to trigger action potentials in neocortical and hippocampal neurons. Transfected hippocampal neurons can express between 160,000 and 1,000,000 heterologous functional TRPV1 channels (54), and thus we can expect magnetic responses with m values as low as 10⁻⁶.

Transfected HEK cells are expected to express ∼1000 exogenous ion channels (55). Given the high conductance of TRPV4 channels, ∼10⁵ Ca²⁺ ions enter the cell per channel opening, which is near the minimal detection limit for Fluo-4 (see Supporting Materials and Methods). This signal could be amplified by secondary calcium signals that originate from intracellular calcium stores through CICR mechanisms. These CICR mechanisms have previously been observed in response to TRP channels gating (26, 27, 28, 29, 30, 31). Therefore, m values of 10⁻³ are sufficient to see a calcium response in each cell. With repeated stimuli and the fact that not all cells need to respond for us to measure a magnetic response from the population, m values as small as 10⁻⁵ can yield detectable calcium responses.

Overall, our model predicts that a combination of low thermal conductance at nanoscale distances and local heat absorption by the channel protein can produce weak physiological responses, which is consistent with previous reports (13, 14) and our own data (Fig. 2).

Magnetic stimulation of the cold-responsive channel MagM8

Unlike previous magnetothermal experiments based on relaxation losses (11, 14, 33), the magnetocaloric effect predicts that the demagnetization should cool magnetic nanoparticles, which should allow them to gate associated cold-activated ion channels. To test this prediction of the magnetocaloric theory, we fused the cold-activated TRPM8 protein to the chimeric ferritin previously used to construct Magneto2.0. The C-terminus domain of TRPM8 was not deleted because it has been implicated in temperature sensing (56), but we mutated the S4–S5 linker region (K856A) to shift the temperature response curve to higher temperatures and allow the channel to be active at room temperature (57) (Fig. 4 a). The resulting protein, named MagM8, was effectively gated by lowered temperature (40–14°C; Fig.4 b). We calculate m values for MagM8 that are in the same range as for Magneto2.0 (see Fig. S2; Supporting Materials and Methods).

Using the same magnetic stimulation protocol as we did for Magneto2.0 (0.08 Hz for 270 s), we found that magnetic stimulation of MagM8 increased the calcium activity and the number of responding cells. Over the course of the recording, the stimulated transfected cells displayed a significant increase of the average calcium-dependent fluorescence compared to the nonstimulated cells, and such an effect was not observed when the cells were exposed to the sham magnet (Fig. 4, c and d). Moreover, a significantly higher number of MagM8-transfected cells displayed calcium transients during stimulation with the magnet than when exposed to the sham stimulation (Fig. 5, c and d). As predicted by our theory, only a small amount of the MagM8 channels were activated during each demagnetization, which explains the weak response observed in our experiments. Nevertheless, these data support the activation of MagM8 by ferritin demagnetization, which is consistent with our magnetocaloric hypothesis.

Discussion

Thermal conductance and absorption

Our data suggest that previous reports of activation of TRP-ferritin fusion proteins by low-frequency AMFs could be thermally mediated and that the mechanism of action could be the conversion between magnetic entropy and heat via the magnetocaloric effect. This proposed mechanism relies on extremely favorable conditions at the surface of the nanoparticles, and more work is needed to confirm this effect. In particular, our model relies on decreased thermal conductance (g^∗) and local heat absorption (c^∗) because of the nanoscale separation distance between the ferritin nanoparticle and channel protein. Although numerous direct and indirect measures of temperature surrounding synthetic magnetic nanoparticles support g^∗ in the range of 10⁻¹¹–10⁻¹³ (10, 41, 42, 43, 44, 45), similar experiments with ferritin along with improved theoretical understanding of heat transport at the nanoscale will help constrain the estimates of g^∗. Although these corrections to bulk thermal transport are extreme, such dramatic changes to the rate of physical processes is not unprecedented at the nanoscale. For example, the Raman signal from molecules within a few nanometers of a metal surface can be increased by 7–14 orders of magnitude (58), establishing that nanoscale separation distances can significantly modify physical processes.

Frequency dependence of magnetocaloric gating

The magnetocaloric hypothesis predicts that magnetic particles heat during magnetization and cool during demagnetization. In the case of a slowly varying field, a nonlinear response of the cell and/or channel is required to produce a net physiological change over time. For example, during cycles of magnetization, the calcium influx produced by heating TRPV4 must be larger than the net calcium efflux produced during cycles of demagnetization that cool TRPV4. We expect that three mechanisms might contribute to such asymmetric responses: 1) secondary messengers and/or calcium itself can trigger the release of calcium from intracellular calcium stores (31, 59, 60, 61); 2) the local depolarization can trigger voltage-gated ion channels in neurons and, to a lesser extent, in nonexcitatory cells (62); and 3) TRPV4 activity can be amplified by positive feedback through phosphorylation of key residues and calcium-dependent membrane recruitment of TRPV4 (or in this case, Magneto2.0) (63, 64, 65). Any of these mechanisms could give rise to a net calcium influx over time instead of the oscillating levels that might result if the calcium levels precisely followed the cycles of magnetocaloric heating and cooling. Similarly, in the case of MagM8, the calcium influx produced by cooling TRPM8 during demagnetization must be larger than the net calcium efflux produced during cycles of magnetization that heat TRPM8. Increasing the stimulation frequency above 0.1 Hz in our experiments is not expected to increase the value of m. Because the heat dissipates at the rate of 0.1 s⁻¹ (as determined by g^∗), at higher frequencies, the ferritin nanoparticles are cooled by demagnetization before they can completely dissipate the heat generated by magnetization and are therefore not expected to increase the response (see Fig. S3; Supporting Materials and Methods). In the case of rapidly switching fields (e.g., hundreds of kHz), the field switches much faster than these nonlinear effects. In that case, the channel response is determined by the average channel temperature per cycle, which decays based on the thermal relaxation rate of 0.1 s⁻¹. Thus, we expect that the application of a radio frequency (RF) magnetic field would raise the temperature surrounding the nanoparticle for a brief period of time before it decays back to the bath temperature. Therefore, an RF magnetic field would cause magnetocaloric heating that would dissipate within seconds (Fig. S4). Note that our predictions suggest that the magnitude of response is independent of the duration of the RF magnetic stimulus. The data in Stanley et al. show that the physiological response increases for longer stimulus periods, suggesting the magnetocaloric effect may not explain these results. The giant thermal resistance values (1/g^∗) required for our theory (and supported by multiple experiments (10, 41, 42, 43, 44, 45)) may also have implications for high-frequency magnetic stimulation of ferritin-TRP assemblies. Although the specific absorption rate of ferritin in AMFs may be too small to produce significant temperature changes in a volume of fluid (66), the lowered thermal conductance may produce local temperature changes sufficient to gate nearby thermoreceptors, which is consistent with recent reports of ferritin-TRP fusion proteins that respond to high-frequency AMFs (14). Importantly, unlike RF heating, magnetocaloric heating depends only on the magnetic moment and not on the magnetic anisotropy of the particle. Additionally, the absence of measurable bulk RF heating using ferritin nanoparticles does not imply a lack of local magnetocaloric heating.

Utility, optimization, and future work

Based on the experimental data, we can estimate the value of m, assuming that each peak recorded results from the gating of a single channel and that transfected cells express an average 1000 exogenous ion channels (53). Taking the difference between the average number of peaks per transfected cell with and without magnetic stimulation and assuming that transfected cells express an average of 1000 exogenous ion channels, we estimate m values of 1.5 × 10⁻⁴ ± 2 × 10⁻⁴ for Magneto2.0 and 3.5 × 10⁻⁵ ± 1.2 × 10⁻⁴ for MagM8, which is on the lower end of the spectrum of values predicted by the magnetocaloric theory (Fig. 3 f; Fig. S2). Based on the measured temperature sensitivities of Magneto2.0 and MagM8 (Fig. S6), we would expect MagM8 to show a stronger response to the magnetic stimulation compared to Magneto2.0 because of a shallower temperature sensitivity and thus a high dP_open/dT at room temperature. Our theoretical calculations also predict larger values of m for MagM8 compared to Magneto2.0 (Figs. 3 f and S2). However, unlike Magneto2.0, we created only a single version of the fusion protein and performed no screening to determine the optimal location of the ferritin fusion site. Thus, the weaker magnetic sensitivity observed for MagM8 may be due to inefficient heat transfer from the ferritin to the temperature-sensitive domains in MagM8.

It is important to emphasize that our data show that magnetic stimulation of Magneto2.0 and MagM8 produces a weak population response as measured by the average calcium level increases. This effect is qualitatively different from optogenetic stimulation, which produces precisely timed action potentials in each cell expressing the transgene. The stimulation observed in our experiments appears to be more similar to neuromodulation, in which the application of a magnetic field would bias neural activity but not necessarily produce specifically timed action potentials on demand. Considering magnetic fields do not scatter like optical stimuli, this neuromodulation may prove particularly useful to uniformly modulate diffuse cell populations throughout the brain. As a result, magnetogenetics might prove to be most useful as a minimally invasive method to shift the excitability of select neuronal populations distributed throughout the brain.

Previous experiments showed that strong and dependable magnetic activation of cells is possible in vitro and in vivo using TRP channels associated to artificial iron oxide NPs and high-frequency AMFs (11, 14, 33, 67); however, this method requires the injection of NPs inside the brain—multiple times for long-term experiments—which can also affect off-target cells. Moreover, large amounts of power (typically between 5 and 15 kW) are needed to generate the RF magnetic fields used for these applications. For these reasons, a purely genetic manipulation of the target cells and a low-frequency (low-power) magnetic stimulus would provide several advantages to the scientists and engineers who hope to use magnetogenetics for basic science and clinical applications. Our experimental results show that low-frequency magnetic stimulation of TRP-ferritin fusion proteins like Magneto2.0 and MagM8 can generate small but statistically significant calcium responses, highlighting the need to improve the strength of this magnetic sensitivity to understand the mechanism of action. For example, single-channel electrophysiology would provide a more detailed description of channel activity, but this approach is prohibitively laborious if less than 1% of channels are activated by the magnetic stimuli, as is predicted for Magneto2.0 and MagM8. Additionally, stronger calcium or voltage responses would allow researchers to study quantitative differences between stimulation protocols that would help refine the underlying activation mechanism. In addition to better magnetogenetic constructs, better biophysical understanding of the thermal gating mechanisms of TRP channels will further improve our estimates of number of channels that respond to heating by the magnetocaloric effect.

Perhaps the most exciting outcome of the magnetocaloric hypothesis is a rational approach to improve the magnetic response. For example, we predict that improving the heat transfer efficiency or the thermal sensitivity of Magneto2.0 will improve the magnetic sensitivity. Overall, the magnetocaloric hypothesis presented here could account for our data and the data presented in previous reports of magnetogenetics. To validate this hypothesis, more work is needed to fully understand the reports of frustrated thermal transport at the surface of magnetic nanoparticles. Nevertheless, our proposed mechanism provides both a potential explanation for the recently reported magnetogenetic proteins and a potential approach for developing new, more sensitive constructs that respond to low-frequency magnetic stimuli.

Author Contributions

G.D., S.P., and J.T.R. conceived and designed the experiments. A.M.B., G.D., and C.N.T. collected the data. E.D.A., B.W.A., and G.D. designed the analysis tools. E.D.A., G.D., S.P., and C.N.T. performed the analysis. A.M.B., G.D., S.P., and J.T.R. wrote the manuscript. A.M.B., S.P., and J.T.R. developed the theory. J.T.R. supervised the research.

Editor: Vasanthi Jayaraman.

Supporting References

References (54, 55, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81) appear in the Supporting Material.