A New Computational Method for Membrane Compressibility: Bilayer Mechanical Thickness Revisited

Abstract

Because lipid bilayers can bend and stretch in ways similar to thin elastic sheets, physical models of bilayer deformation have utilized mechanical constants such as the moduli for bending rigidity $\left({\kappa }_C\right)$ and area compressibility (K_A). However, the use of these models to quantify the energetics of membrane deformation associated with protein-membrane interactions, and the membrane response to stress is often hampered by the shortage of experimental data suitable for the estimation of the mechanical constants of various lipid mixtures. Although computational tools such as molecular dynamics simulations can provide alternative means to estimate K_A values, current approaches suffer significant technical limitations. Here, we present a novel, to our knowledge, computational framework that allows for a direct estimation of K_A values for individual bilayer leaflets. The theory is based on the concept of elasticity and derives K_A from real-space analysis of local thickness fluctuations sampled in molecular dynamics simulations. We explore and validate the model on a large set of single and multicomponent bilayers of different lipid compositions and sizes, simulated at different temperatures. The calculated bilayer compressibility moduli agree with values estimated previously from experiments and those obtained from a standard computational method based on a series of constrained tension simulations. We further validate our framework in a comparison with an existing polymer brush model and confirm the polymer brush model’s predicted linear relationship with proportionality coefficient of 24, using elastic parameters calculated from the simulation trajectories. The robustness of the results that emerge from the method allows us to revisit the origins of the bilayer mechanical (compressible) thickness and in particular its dependence on acyl-chain unsaturation and the presence of cholesterol.

Introduction

Cells exhibit a wide variety of morphologies, ranging from discoid or spherical shapes (e.g., erythrocytes and staphylococcus bacteria, respectively) to branched formations with multiple highly curved and flat elongated segments (e.g., nerve axons in the brain, microvilli in the intestines, and rod cells in the retina of the eye). A cell’s ability to take on distinct shapes is directly dependent on the flexibility of its bounding plasma membrane (PM), and thus, maintaining a certain level of flexibility of the PM is essential to both cell and human physiology. A prominent example of the consequences of deficits in PM flexibility is sickle cell anemia, a disease characterized by a drastic change in the shape and stiffness of red blood cells that leads to their accumulation on vessel walls and blockage of blood flow (1, 2, 3, 4, 5, 6).

The PM has two layers, or leaflets, composed of a mixture of various types of amphiphilic lipid molecules, each type with its own set of structural and thermodynamic properties. Despite this complexity, the PM’s flexibility has been successfully modeled quantitatively as a simple elastic sheet with characteristic bending and compressibility constants (7). Although measurements of PM’s elastic properties have been performed directly on live cells, the interpretation of such measurements is still challenging because of the complexity and nonuniformity of the cellular membrane environment (8, 9). Instead, experiments on less complex, compositionally symmetric model membranes have been utilized to characterize the bilayer’s bending rigidity (κ_C) and area compressibility (K_A) moduli as a function of lipid composition. These mechanical constants quantify, respectively, the energetic cost associated with bending the membrane and stretching/compressing its area and have thus been used to make successful predictions about biological phenomena, e.g., of the changes in shape of closed lipid vesicles under stress (10, 11, 12). Because the proper function and organization of transmembrane proteins are often regulated by membrane deformations near the protein (e.g., local bilayer bending and thinning or thickening), K_A and κ_C also appear as important parameters in theoretical models quantifying the energetics of protein-membrane interaction (13, 14, 15). All these approaches directly link the elastic properties of membranes to bilayer shape and the sorting of both lipids (e.g., into distinct lipid domains) and proteins (e.g., into local clusters or oligomers) on the surface of a heterogeneous membrane such as the PM.

Various methods exist for measuring κ_C both in vitro and in silico (16, 17, 18), but the equally important compressibility modulus K_A is less well studied. It quantifies the response of membrane area to tension, which under physiological conditions may arise from various perturbations, such as changes in osmolarity across the membrane or the addition of lipids or other molecules to only one of the membrane’s leaflets. Several experimental approaches have been developed to measure K_A in model membranes, and these methods rely on extracting the compressibility modulus from a relationship between systematically varied tension and the resulting bilayer area expansion. Perhaps the most commonly used technique utilizing this approach is the micropipette aspiration of giant unilamellar vesicles (GUVs), which has supplied the largest set of bilayer K_A data available currently (19, 20, 21). The procedure involves imaging a single GUV while applying incremental amounts of suction pressure to it with a micropipette. The tension exerted on the bilayer is calculated directly from the applied pressure, whereas the resulting changes in the bilayer area are inferred from geometrical considerations of the corresponding changes in GUV shape. In an alternative approach, pressure is applied to extruded unilamellar vesicles through osmotic imbalance between the vesicles’ interior and exterior due to solutes such as salt or sugar (22, 23, 24). The ensuing trends in the bilayer structure are monitored from the vesicle diameter measured with techniques such as light scattering or electron microscopy. NMR alone (25) or in combination with x-ray diffraction (26) has also been used to measure K_A of bilayers at low hydration by relating changes in bilayer area to changes in the osmotic pressure of a polymer (e.g., polyethylene glycol) solution. Unfortunately, experimental data on the behavior of many lipids, including lipid mixtures, are still scarce, and the availability of the resources needed to make the measurements is often limited. In that respect, a combination of rigorous physics-based simulation and well-calibrated computational tools holds great promise for enabling an otherwise impossible elasticity-based analysis of membrane systems that remain elusive to experimental methods.

With the feasibility of more extensive molecular dynamics (MD) simulations, the area compressibility modulus has been estimated from trajectories of (on average) flat lipid bilayer patches. The classical computational approach is based on the same principle as the experimental methods, i.e., that for small changes in area per lipid (A_lip), tension is linear with direct area expansion. To calculate the bilayer K_A, a series of constrained-area (or tension) simulations is performed, and the value emerges from the slope of the best-fit line through the data of ln(A_lip) versus surface tension. Although the estimated moduli are typically in good agreement with experimental estimates, the analysis of one lipid composition requires multiple simulations, which makes this approach very expensive computationally. An alternative computational strategy that circumvents this requirement uses the equilibrium thermal fluctuations of the bilayer at constant zero tension instead. In this spirit, K_A is estimated from a single simulation trajectory utilizing the equilibrium expression $K_A=\langle A_{box}\rangle /\langle \delta A_{box}^2\rangle k_{B}T$, where A_box represents the lateral area of the simulation box, k_B is the Boltzmann constant, T is temperature, and $\langle \cdot \rangle$ denotes ensemble average (see Methods below). Because the analysis is directly related to the fluctuations of the simulation box, the modulus exhibits a strong dependency on the thermodynamic phase behavior of the bilayer (which is directly related to the relaxation rate of its lateral area), system size, and the corresponding length of the simulation trajectory. Importantly, no existing computational or experimental method allows for calculation of K_A of individual bilayer leaflets, which is a prerequisite for the quantification of the energy of local leaflet distortions in an asymmetric bilayer.

Here, we report a, to our knowledge, novel computational methodology that overcomes the aforementioned shortcomings in the calculation of area compressibility and obtains the K_A moduli of a bilayer and of each of its leaflets from a single MD trajectory. Like the existing methods, we take advantage of thermal fluctuations but express the compressibility modulus as a function of leaflet thickness instead of bilayer area. After our recent success in calculating each leaflet’s bending rigidity from real-space analysis of local splay fluctuations (18), we base our method for K_A estimation on sampling the leaflet thickness locally. The data are then used to estimate the corresponding probability distribution and potential of mean force (PMF) profile as a function of changes in thickness. Finally, the K_A is extracted from a quadratic fit of a small region of the PMF around the global minimum, according to the elastic energy of stretching (see Methods). We show that for a large set of single and multicomponent bilayers, the resulting compressibility moduli are in excellent agreement with the ones reported from experiments in vitro or calculated with alternative computational approaches. We find that the K_A values obtained with our framework are less sensitive to bilayer size and simulation length because of the local nature of the analysis. We further validate our approach by reproducing the linear relationship between bilayer thickness, K_A, and κ_C in the polymer brush model (PBM) (20), using mechanical constants calculated from the simulation trajectories. This analysis lets us revisit the definition of the bilayer mechanical thickness and clarify observed discrepancies reported in the literature with respect to the PBM’s predictions (17, 27, 28).

Methods

Here, we present the theoretical framework and details of the method for the calculation of the area compressibility moduli of a bilayer and each of its leaflets, based on the analysis of trajectories from MD simulations. Compressibility Modulus from Area Fluctuations contains an overview of compressibility calculation from area fluctuations, followed by the formulation for the calculation of individual local leaflet moduli. In Compressibility Modulus from Thickness Fluctuations, we re-express the theory in terms of local leaflet thicknesses to address some of the challenges presented by using area in the formulation developed in the previous section, and provide a detailed methodological description of the new computational framework. Simulations and Analysis presents details of the simulation trajectories used for the application of the method, as well as a summary of the corresponding analysis.

Compressibility modulus from area fluctuations

Bilayer compressibility

Following Helfrich’s formalism (29), we treat the bilayer as a two-dimensional (2D) elastic sheet with mechanical constants describing its modes of deformation. For small equilibrium fluctuations around the free-energy minimum, each deformation mode is associated with an elastic energy that is approximated by a quadratic function of the relevant deformation, analogous to Hooke’s law. For changes in area, the elastic energy E of stretching/compressing a bilayer patch with equilibrium area a₀ is given as (see Eq. 1 in (30))

$$E=\frac{1}{2}{K}_A{a}_0{\left(\frac{a-a_0}{a_0}\right)}^2,$$ (1)

where a is the deformed area and K_A is the bilayer area compressibility modulus. Assuming that bilayer area stretching/compression are independent degrees of freedom in the context of the full energy functional describing bilayer mechanics (cf. bending or tilt), K_A can be obtained from the bilayer’s thermally excited area fluctuations (31). Specifically, from the equipartition theorem $\langle E\rangle =\left(1/2\right)k_{B}T$ where k_B is Boltzmann constant and T is temperature, it follows that

(2)

This is the expression commonly used to obtain K_A from MD simulations of a bilayer by sampling fluctuations in the lateral area of the simulation box A_box (17, 31, 32). Because E is the energy of a deformed state described by Δa/a₀ = (a − a₀)/a₀, from statistical mechanics, it also follows that the probability of this state can be written as

$$p\left(\mathit{\Delta }a/a_0\right)=C{e}^{-\frac{E}{k_{B}T}},$$ (3)

where C is a constant. Rearrangement of Eq. 3 leads to an alternative equality from which K_A can be calculated, provided the probability distribution of the deformed states is known:

$$\ln p\left(\frac{\mathit{\Delta }a}{a_0}\right)=-\frac{1}{2k_{B}T}{K}_A{a}_0{\left(\frac{\mathit{\Delta }a}{a_0}\right)}^2+\ln C,$$ (4)

which can be written as

$$-\frac{2k_{B}T}{a_0}\ln p\left(\frac{\mathit{\Delta }a}{a_0}\right)=K_A{\left(\frac{\mathit{\Delta }a}{a_0}\right)}^2+C^{\text{'}}.$$ (5)

Although both Eqs. 2 and 5 are equivalent upon sufficient sampling of area fluctuations, Eq. 2, in which K_A is inversely proportional to the mean-square area fluctuations, is more sensitive to outliers and deviations from the elastic regime (see Eqs. 12 and 13 and discussion afterwards) when used for K_A estimation. In contrast, Eq. 5 relies on the distribution of deformations around the mean and can thus provide a more robust approximation of the area compressibility modulus.

Leaflet compressibility

The area compressibility modulus of a bilayer quantifies the total energy of membrane stretching/compression and can be used to infer the energetics of deforming individual bilayer leaflets in symmetric bilayers whose two leaflets are assumed to behave in the same way. However, in an asymmetric membrane, the two leaflets can have very different lipid compositions with potentially different energetic costs for stretching/compression that cannot be simply inferred from the elastic properties of the bilayer. To enable the analysis of these more general (and physiologically relevant) systems, we sought a formulation that would yield the area compressibility modulus of each leaflet of the membrane independently. Specifically, the goal was to obtain leaflet compressibility from area fluctuations in the spirit of the above-described theory (Eqs. 2, 3, 4, and 5).

Globally (e.g., considering the entire simulated bilayer patch), the area fluctuations of the two leaflets are identical and equal to the area fluctuations of the whole bilayer. Therefore, the apparent leaflet compressibility moduli calculated from area fluctuations at that scale would always appear the same, masking any potential differences in the inherent mechanical properties of the leaflets. To extract these differences and find the effective local leaflet moduli, we perform the analysis on a length scale much smaller than the global bilayer area. In particular, we view each leaflet as a collection of more than one parallel elastic blocks that are made of the same material (i.e., have the same compressibility modulus). Within a leaflet, it is assumed that all blocks have the same average area (e.g., the average area of a lipid) but can have different instantaneous areas, and their area fluctuations are weakly coupled. Because of its elastic nature, the deformation energy of a block has the same form as Eq. 1, and its compressibility modulus (which is the effective local leaflet modulus) can be obtained accordingly from its area fluctuations through Eqs. 2 or 5.

To relate the effective local leaflet moduli to the bilayer’s compressibility, we express the energy of bilayer stretching/compression as a function of the stretching/compression of the individual leaflet blocks. If we denote the instantaneous global areas of the two leaflets with A_x and A_y and the instantaneous and average local areas of their elastic blocks with a_xi, a_yi and a_x0, a_y0, respectively (i being the identity of the block), the second-order approximation of the bilayer energy can be written as

$$E=\sum _i{K}_A^x{a}_{x0}{\left(\frac{a_{xi}-a_{x0}}{a_{x0}}\right)}^2+\sum _i{K}_A^y{a}_{y0}{\left(\frac{a_{yi}-a_{y0}}{a_{y0}}\right)}^2+\sum _{i\ne j}{K}_{xx}{a}_{x0}\left(\frac{a_{xi}-a_{x0}}{a_{x0}}\right)\left(\frac{a_{xj}-a_{x0}}{a_{x0}}\right)+\sum _{i\ne j}{K}_{yy}{a}_{y0}\left(\frac{a_{yi}-a_{y0}}{a_{y0}}\right)\left(\frac{a_{yj}-a_{y0}}{a_{y0}}\right)+\sum _{i\ne j}{K}_{xy}\sqrt{a_{x0}{a}_{y0}}\left(\frac{a_{xi}-a_{x0}}{a_{x0}}\right)\left(\frac{a_{yj}-a_{y0}}{a_{y0}}\right).$$ (6)

The first two terms in Eq. 6 represent summations over the deformation energies of the individual elastic blocks in the two leaflets, the next two terms are the corresponding interblock correlations within each leaflet, and the last term quantifies the correlations between blocks from different leaflets. Each term has its characteristic modulus, and $K_A^x$ and $K_A^y$ in particular are the effective local leaflet compressibility moduli.

Because the bilayer area A is A = A_x = A_y = (A_x + A_y)/2, $A_x={\sum }_i{a}_{xi}$ and $A_y={\sum }_i{a}_{yi}$, we can express the variance of A as a sum over variances and covariances of the local areas:

$${\sigma }^2\left(A\right)=\frac{{\sum }_i{\sigma }^2\left(a_{xi}\right)+{\sum }_i{\sigma }^2\left(a_{yi}\right)}{2}+\frac{{\sum }_{i\ne j}{\sigma }^2\left(a_{xi},a_{xj}\right)+{\sum }_{i\ne j}{\sigma }^2\left(a_{yi},a_{yj}\right)+W}{2},$$ (7)

where $W=\sum _{i,j}{\sigma }^2\left(a_{xi},a_{yj}\right)$. Because the global areas of the two leaflets are constrained to be the same, their variances are the same, and consequently, the sum of the interleaflet correlations is 0, i.e., W = 0.

In addition, ${\sigma }^2\left(a_{xi}\right)=a_{x0}{\sigma }^2\left(\left(a_{xi}-a_{x0}\right)/a_{x0}\right)$, and at the same time ${\sigma }^2\left(a_{xi}\right)=1/K_A^x$ (because in the second-order approximation of the energy, the multivariate Boltzmann distribution becomes the multivariate normal distribution). If n denotes the number of blocks, Eq. 7 then simplifies to

$$\frac{1}{K_A}=\frac{1}{2}\left(\frac{1}{K_A^x}+\frac{1}{K_A^y}\right)+Q,$$ (8)

where Q is the average sum of the interblock correlations within each leaflet:

$$Q=\frac{{\sum }_{i\ne j}{\sigma }^2\left(a_{xi},a_{xj}\right)+{\sum }_{i\ne j}{\sigma }^2\left(a_{yi},a_{yj}\right)}{2n}.$$ (9)

Although these interblock correlations within a leaflet can generally deviate from 0, when the local areas (elastic blocks) are small, the correlations can be both positive and negative (representing the fact that the blocks can undergo stretching/compression deformations in two dimensions), and we find that they cancel each other out in the respective sums (see Supporting Materials and Methods). As a result, we assume Q ≈ 0 and arrive at the final relationship between the bilayer K_A and the local compressibility moduli, $K_A^x$ and $K_A^y$, of the two leaflets:

$$\frac{1}{K_A}=\frac{1}{2}\left(\frac{1}{K_A^x}+\frac{1}{K_A^y}\right).$$ (10)

Note that the derivation above assumes that the two leaflets have the same number of elastic blocks; however, Eq. 10 holds even in the general case when these numbers are different (as for membranes with asymmetric lipid composition; see Supporting Materials and Methods for the extended derivation).

It is important to note that in our formulation, a local leaflet K_A in a symmetric bilayer has the same magnitude as the bilayer K_A and therefore should be treated differently from the global leaflet compressibility moduli often referred to in the literature as 1/2 the bilayer K_A (33). The latter are based on a model in which the global area changes in the two leaflets are the same because of the constraints on the bilayer geometry but are uncoupled, and thus the elastic energy (and consequently, the K_A) of deforming each leaflet is half the energy (K_A) of deforming the bilayer. In contrast, $K_A^x$ and $K_A^y$ capture the local properties of the leaflets, which are affected by the global constraint on area only indirectly and thus reveal features that are more specific of the leaflets themselves. From Eqs. 6, 7, 8, and 9 to 10, it further follows that the harmonic mean of the local leaflet moduli gives the bilayer K_A, which, as we show in Results and Discussion, quantitatively matches experimentally measured bilayer moduli for various membrane systems.

Compressibility modulus from thickness fluctuations

The theoretical formulation presented in the previous section allows for the calculation of an effective local leaflet compressibility modulus from area fluctuations. To capture the individual leaflet properties when calculating $K_A^L$ (where L can be x or y), given the outlined considerations (e.g., the cancelation of the Q term in Eq. 8), we chose to analyze the fluctuations of the smallest local unit area that is characteristic for leaflet L, that is, the average area per lipid in the leaflet. In this way, the two leaflets in a symmetric bilayer will have the same local unit area, as expected, whereas in an asymmetric bilayer, they may be different. We thus seek a local description of instantaneous leaflet area that would allow for ample sampling of area fluctuations while treating each leaflet independently from the other leaflet.

Because the definition and calculation of local leaflet areas is rather challenging (31, 34), we assume volume conservation to relate deformations in local area to deformations in local thickness and then estimate the coefficients from thickness fluctuations. Specifically, let a^L and t^L be the instantaneous local area and thickness of a leaflet, and $a_0^L$ and $t_0^L$ are their corresponding equilibrium values. Assuming that $a_0^L{t}_0^L=a^L{t}^L=V$, where V is a constant, we can express the energy of stretching/compressing leaflet L, E^L, as a function of characteristic changes in thickness instead of relative changes in area:

$$E^L=\frac{1}{2}{K}_A^L{a}_0^L{\left(\frac{a^L-a_0^L}{a_0^L}\right)}^2=\frac{1}{2}{K}_A^L{a}_0^L{\left(\frac{V/t^L-V/t_0^L}{V/t_0^L}\right)}^2=\frac{1}{2}{K}_A^L{a}_0^L{\left(\frac{t_0^L-t^L}{t^L}\right)}^2.$$ (11)

Consequently, Eqs. 2 and 5 become

(12)

and

$$-\frac{2k_{B}T}{a_0^L}\ln p\left(\frac{t_0^L-t^L}{t^L}\right)=K_a^L{\left(\frac{t_0^L-t^L}{t^L}\right)}^2+C^{\text{'}}.$$ (13)

Although both Eqs. 12 and 13 can be used to obtain $K_A^L$ in theory, practical (numerical) considerations render Eq. 13 more suitable (see Supporting Materials and Methods for comparison between the two approaches). Our formal framework is therefore centered on extracting $K_A^L$ from Eq. 13 through the following steps:

• 1)Calculate local leaflet thicknesses at different chain depths within the bilayer.
• 2)From all possible definitions of leaflet thickness, identify the one that is suitable for the calculation of $K_A^L$.
• 3)Use Eq. 13 to obtain $K_A^L$.

In the following, we present details of the above three stages in our algorithm.

Calculating local leaflet thicknesses from simulations

Over the course of a simulation trajectory, the thickness of each bilayer leaflet is laterally inhomogeneous and fluctuates around its equilibrium value $t_0^L$ as a result of thermal motions. To construct the probability distribution of thickness changes in Eq. 13, p(Δt/t^L), by sampling local fluctuations, we take a grid-based approach and calculate the leaflet thickness at different grid points on the leaflet surface. In a continuum representation, a leaflet can be viewed as a stack of layers with each layer being a surface made of a particular lipid atom (ς), e.g., a phosphate surface (ς = P), a first glycerol carbon surface (ς = C1 using CHARMM36 atom naming scheme), a first sn-1 carbon surface (ς = C21), a first sn-2 carbon surface (ς = C31), and so on (see Fig. S1). To calculate the leaflet thickness at a grid point (x, y), we first find the height of each of these surfaces at this grid point by performing interpolation on the corresponding atomic z-coordinates as follows:

$$h_{\varsigma ,\left(x,y\right)}=\frac{{\sum }_i\frac{z_{\varsigma ,i}}{d_{i,\left(x,y\right)}^n}}{{\sum }_i\frac{1}{d_{i,\left(x,y\right)}^n}},$$ (14)

where h_{ς, (x, y)} is the height of the ς-surface (i.e., the surface made of atom type ς at grid point (x, y)), z_{ς, i} is the z-coordinate of atom i, d_{i, (x, y)} is the 2D distance between atom i and (x, y), n is interpolation order, and the summations are done over all leaflet atoms i of type ς (note that the atoms on individual lipid chains have unique atom names; thus, each lipid has at most one atom of type ς). Because a lipid can have multiple chains and the heights in Eq. 14 are calculated separately for each carbon atom on each chain, we simplify the analysis by averaging the corresponding surface heights across all lipid chains:

$$h_{\varsigma ,\left(x,y\right)}=\frac{1}{N_{sn}}\sum _{ch=1}^{N_{sn}}{h}_{\varsigma \left(ch\right),\left(x,y\right)},$$ (15)

where h_{ς(ch), (x, y)} is the height of the surface calculated from the ς carbon on the ch chain and N_sn is the number of lipid chains. Eq. 15 can also be extended to lipids whose chains have different lengths (see Supporting Materials and Methods). Thus, a single “average chain” is created at each grid point and used in the subsequent analysis. Although this approach works well for most bilayers, we found that for lipids like SAPE (see simulation details below for lipid name abbreviations), which has one fully saturated and one highly unsaturated chain, this averaging can become problematic for the subsequent analysis that is based on correlations of the resulting heights (described in the next section). Empirically, we found that the problem is alleviated when before the averaging in Eq. 15, each double bond and its preceding carbon are represented by a single data point with an instantaneous height equal to the average interpolated height across the three carbons. Thus, each double bond effectively reduces the unsaturated chain length (or the number of surfaces defining the unsaturated chain) by two carbons. As this procedure is more general and at the same time does not affect the results for the bilayers for which Eq. 15 can be applied, it was integrated in the methodological framework.

The leaflet thickness at the level of the ς-surface, denoted τ_ς, is defined as the difference between the height of the ς-surface and the height of the lowest-situated surface at the grid point (usually, the surface of the terminal methyl carbons):

$${\tau }_{\varsigma ,\left(x,y\right)}=h_{\varsigma ,\left(x,y\right)}-\min \left(h_{\left(x,y\right)}\right).$$ (16)

The interpolation order n in Eq. 14 determines the contribution to h_{ς, (x, y)} of the atoms closest to (x, y) relative to those that are further apart, i.e., the higher the n, the larger the effect from nearby atoms, and the lower the n, the larger the effect from all atoms. Hence, n is related to the effective number of atoms (lipids) that are being averaged and consequently to the equilibrium area $a_0^L$ in Eq. 13 (i.e., the area whose thickness fluctuations are effectively being analyzed).

Because atoms are weighted differently in the interpolation, we estimate $a_0^L$ by first using the denominator in Eq. 14 to approximate the effective number of lipids being averaged, and then multiplying this number by the average area per lipid in the leaflet, $A_{lip}^L$. When n = 2, the denominator in Eq. 14 is ∼1, conveniently setting $a_0^L\sim A_{lip}^L$, and we therefore use n = 2 and $a_0^L=A_{lip}^L$ in the subsequent analysis (see Supporting Materials and Methods for the derivation and Fig. S2 for a demonstration of the invariability of the results with n). As described in the Supporting Materials and Methods, the interpolated thicknesses (Eq. 16) preserve the product of local area and thickness (i.e., the assumption underlying Eq. 11), which further establishes their suitability for the calculation of $K_A^L$.

Identifying the relevant thickness for fluctuations analysis

The first step of the method described above allows us to calculate local thicknesses at different surfaces (i.e., different depths) within the leaflet. Naturally, surfaces at heights near the water/hydrocarbon interface fluctuate less because of interfacial tension, whereas those further down into the leaflet fluctuate more because of the increased fluidity of the lipid chains around the bilayer midplane. The height (and consequently thickness) fluctuations in a leaflet therefore fall roughly into two categories: ones that are relatively suppressed and ones that are dominated by relatively unconstrained motion of the lipid chains. The former would tend to overestimate $K_A^L$, whereas the latter would tend to underestimate it. The fluctuations of the surface lying at the intersection of these two regimes will thus be the most suitable from the elasticity considerations to obtain a reliable estimate of $K_A^L$. We term the thickness at the level of this surface the relevant thickness for $K_A^L$ and proceed to identify its location within a bilayer leaflet.

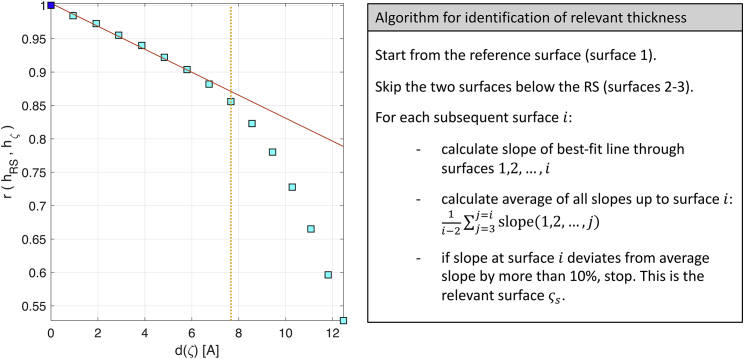
The location of the atomic surface corresponding to the relevant thickness may differ in different membranes because of various degrees of bilayer fluidity. We have therefore developed a general algorithm for identifying the surface relevant for $K_A^L$ calculations for an arbitrary lipid membrane. Specifically, we examine the correlation between the height fluctuations of a particular surface ς and those of a reference surface (RS) close to the water-hydrocarbon interface (in our case, the RS is the surface of the first acyl-chain carbon atom that is not connected to oxygen). Fig. 1 shows a typical behavior of this correlation, r(ς) = r(h_RS, h_ς) (here, for the top leaflet of a DPPC bilayer) as the distance, d(ς), between a surface ς and the RS increases ($d\left(\varsigma \right)=\left|\breve{h_{RS}}-\breve{h_{\varsigma }}\right|$, where $\breve{h}$ denotes median of the distribution of local heights). At small d(ς), the correlation drops slowly and linearly with distance (Fig. 1, red solid line), implying a regime of suppressed thickness fluctuations (i.e., fluctuations of the atoms in this segment of the chain are strongly coupled to one another). At larger d(ς) distances, the r(ς) vs. d(ς) profile strongly deviates from the initial linear behavior because d(ς) increases more slowly, whereas r(ς) decreases more rapidly, characteristic of the more fluid region of the bilayer in which the lipid chains exhibit greater flexibility and intercalate with the chains of the opposing leaflet. Given the two well-defined regimes, we choose the first point outside of the linear regime (Fig. 1, yellow dashed line) to represent the leaflet whose thickness fluctuations can be used to extract $K_A^L$. We identify this surface ς_s following the algorithm outlined on the right hand side box in Fig. 1. For DPPC, the surface ς_s is at the 10th carbon (shown in yellow in Fig. S1). Interestingly, for this and all other bilayers that we examined, ς_s appears to be located right around the region within the leaflet where the density of the opposing leaflet vanishes (i.e., just outside the interleaflet interdigitation zone, see Fig. S3).

Figure 1.

Identification of relevant thickness for calculation of $K_A^L$. (left) The correlation of the height fluctuations of a surface ς with the height fluctuations of a reference surface (RS) is plotted as a function of distance from RS for the top leaflet of a DPPC membrane (the first acyl chain carbon atom not attached to oxygen is indicated as the square symbol at position (0,1) on the plot and corresponds to the top layer in Fig. S1). The solid red line shows the corresponding best-fit line through all points preceding ς_s. A sample representation of the relevant surface can be seen in Fig. S1. (right) An outline of the algorithm used to identify the relevant surface ς_s from the data (denoted by a dotted line on the plot). To see this figure in color, go online.

Calculating $K_A^L$ from LTFs

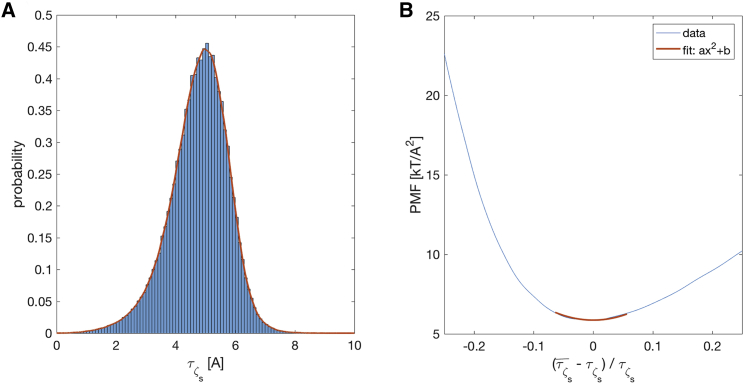
Having identified ς_s, we calculate the local thickness fluctuations (LTFs), τ_ς, at every grid point in every frame of the trajectory and estimate its probability distribution using kernel density estimation (Fig. 2 A). From this distribution, we estimate t₀ (defined here and throughout as the most probable thickness, i.e., at the peak of the distribution), and the left-hand side of Eq. 13, i.e., the PMF, as shown in Fig. 2 B. The characteristic asymmetric shape of the PMF is consistent with the free energy versus area per molecule profile predicted by Ben-Shaul from theoretical considerations of lipid chain packing (35) and arises from the relative ease of deforming the membrane upon thickness contraction (area expansion, increase in entropy) compared to thickness expansion (area contraction, decrease in entropy). To find the leaflet compressibility, we identify a small region around t₀ (between 5 and 7% of t₀) where the PMF is closest to a normal distribution. We then fit a quadratic function to the PMF in this region and obtain $K_A^L$ from the quadratic coefficient in the best fit (see Supporting Materials and Methods for a step-by-step outline of the procedure). Errors are calculated with a 2D bootstrapping approach over both time and space as described in the Supporting Materials and Methods.

Figure 2.

Calculation of $K_A^L$ from LTFs. (A) Probability distribution of the relevant thickness, τ_ς, constructed from the time evolution of the local interpolated thicknesses for the top leaflet of a DPPC bilayer (bar graph). The distribution is smoothed for subsequent analysis by using a kernel density (solid line). (B) The left-hand side of Eq. 13 is plotted as a function of characteristic changes in the local thickness (thin line). The PMF in the region of thicknesses within 6% of the mean thickness is fitted to a function of the form y ∼ ax² + b (see text for details). $K_A^L$ is obtained from the quadratic coefficient a = 238 mN/m of the best fit (shown as the thick line segment). To see this figure in color, go online.

Simulations and analysis

Simulation details

Table S1 lists information for all simulated bilayers. The following lipid names are abbreviated as shown in the parentheses: 1,2-dilauroyl-sn-glycero-3-phosphocholine (DLPC, di12:0), 1,2-dimyristoyl-sn-glycero-3-phosphocholine (DMPC, di14:0), 1,2-palmitoyl-sn-glycero-3-phosphocholine (DPPC, di16:0), 1,2-dilinoleoyl-sn-glycero-3-phosphocholine (DLiPC, di18:2), 1,2-dioleoyl-sn-glycero-3-phosphocholine (DOPC, di18:1(cis)), 1-stearoyl-2-oleoyl-sn-glycero-3-phosphocholine (SOPC, 18:0,18:1), 1,2-dielaidoyl-sn-glycero-3-phosphocholine (DEPC, di18:1(trans)), 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC, 16:0,18:1), 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphoethanolamine (POPE, 16:0,18:1), 1-stearoyl-2-diarachidonoyl-sn-glycero-3-phosphoethanolamine (SAPE, 18:0,20:4), 1,2-dioleoyl-sn-glycero-3-phospho-(1′-rac-glycerol) (DOPG, di18:1(cis)), 1′,3′-bis[1,2-dioleoyl-sn-glycero-3-phospho]-sn-glycerol (TOCL, tetra18:1), N-palmitoyl-D-erythro-sphingosylphosphorylcholine (PSM), and cholesterol (Chol). As indicated in Table S1, some of the bilayers were taken from (18). All remaining bilayers were constructed with CHARMM-GUI (36, 37, 38) and simulated with NAMD (39) using the CHARMM36 force field (40, 41). Initial equilibration was carried out with CHARMM-GUI’s protocols. After equilibration, the simulations were performed with a 10–12 Å cutoff for nonbonded and short-range electrostatic interactions and particle mesh Ewald with grid spacing of 1 Å for long-range electrostatics. Van der Waals force switching was turned on. Temperature was controlled with a Langevin thermostat while constant pressure was maintained with NAMD’s Langevin piston Nose-Hoover method with a 200 fs period and 50 fs decay. All simulations were run with a time step of 2 fs and rigidbonds set to all, and both atomic coordinates and velocities were output every 20 ps.

Simulation analysis and method implementation

All bilayer properties were estimated from the last segments of the trajectories over which the lateral area of the simulation box was considered converged, as determined with a method based on maximizing the number of effectively uncorrelated data points (42). Table S1 lists the total simulation time for each system and the length of the trajectory segments used for the analysis. All trajectories were centered before analysis such that the mean z-position of the terminal methyl carbons on all lipids was set to 0.

The interpolated heights, as described in step 1 of the calculation of leaflet compressibility from thickness fluctuations, were calculated for each leaflet with a modified version of VMD’s MEMBPLUGIN (43) and sampled on an 8 × 8 Å² square grid. All subsequent analysis (outlined step by step in Supporting Materials and Methods) was performed with MATLAB (The MathWorks, Natick, MA). Number density profiles were calculated with the Density Profile tool in VMD (44), and acyl-chain order parameter profiles were obtained with in-house Tcl and MATLAB scripts. All code for calculation of the area compressibility moduli is available upon request.

Lateral pressure profile calculation

Lateral pressure profiles were calculated from the last ∼100 ns of the centered simulation trajectories. The calculation was done with NAMD 2.11 using stored instantaneous atomic coordinates and velocities. Each system was divided into slabs of ∼0.8 Å thickness and lateral area equal to the area of the simulation box (all slabs in a given frame of the trajectory have equal volume). The total lateral pressure in each slab was the sum of the independently obtained Ewald and non-Ewald pressure contributions. The x, y, and z dimensions of the grid size used for calculating the Ewald contribution were all equal and less than half the (x, y) dimension of the simulation box (typically, 30 Å). Because of the known limitations of the Harasima algorithm with Particle Mesh Ewald electrostatics implemented in NAMD for the discretized pressure calculation, the normal component of the pressure tensor in each slab, p_N, was set to $p_N=L_N^{-1}\int dz{p}_L\left(z\right)$, where L_N is the length of the simulation box in the direction of the bilayer normal and p_L(z) is the lateral (or tangential) pressure in slab z (45, 46). The total pressure in slab z was then calculated as p(z) = p_L(z) − p_N.

Treatment of Chol-containing membranes

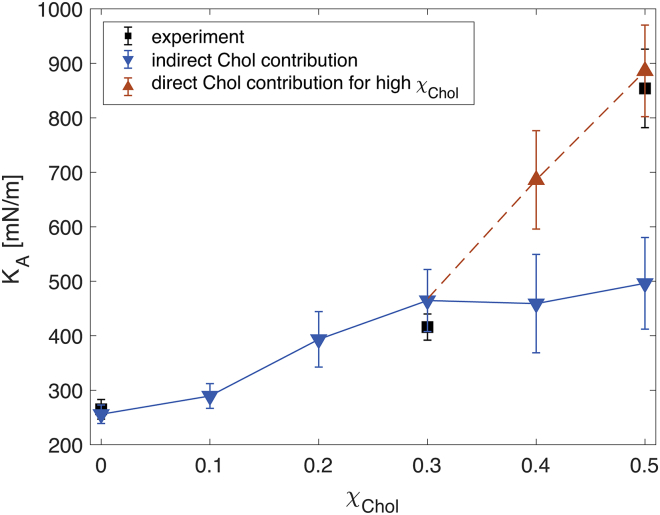
At relatively small mole fractions (up to 0.3–0.35) of Chol in the bilayers, the expected effect of Chol on the bilayer structural properties (average area and volume per lipid) is mainly a condensing effect on the non-Chol lipids (34, 47). It is reasonable, therefore, to assume that Chol’s effect on the area compressibility modulus at such small Chol mole fractions will be indirect and captured in the K_A calculated from the non-Chol components only, as detailed in Supporting Materials and Methods. However, as shown (see, for example, (47)), at higher mole fractions (above 0.35), the distribution of Chol’s tilt angles becomes narrower and moves closer to zero, indicating that its motion is more restricted and the molecule is more parallel to the bilayer normal. In this regime, Chol is likely to contribute directly to the leaflet compressibility (i.e., compression of the bilayer would involve compression of the Chol molecules themselves), and its effect needs to be considered explicitly. This is achieved by assuming that the ratio of the area compressibility calculated by considering only the non-Chol components $\left(K_a^{L\left(nonCh\right)}\right)$ and all components $\left(K_a^L\right)$ is the same as the fraction (s_f) of the surface area occupied by the non-Chol lipids, i.e., $K_a^{L\left(nonCh\right)}/K_a^L=s_f$ (where $s_f={\chi }_{nonCh}{a}_{0\left(nonCh\right)}^L/a_0^L$). From here, $K_a^L=K_a^{L\left(nonCh\right)}/s_f$. This correction to $K_a^L$ is used only for bilayers with Chol mole fractions >0.35 and is found to produce a gradual increase in the bilayer compressibility modulus, consistent with experimental measurements (see Fig. 3 and discussion below).

Figure 3.

Bilayer area compressibility for DOPC/Chol mixtures with increasing amount of Chol. The bilayer K_A was calculated either by considering only the non-Chol lipids for all Chol mole fractions χ_Chol or the non-Chol lipids for χ_Chol ≤ 0.3 (triangles pointing downward). The direct contribution of Chol to the bilayer compressibility for χ_Chol > 0.3 is indicated with triangles pointing upward (see Simulations and Analysis for details). Experimentally determined compressibility moduli are shown as squares. The dashed and solid lines are guides to the eye to the respective data points. Error bars represent errors on the bilayer K_A propagated from the respective uncertainties on the two leaflet moduli calculated as described in Supporting Materials and Methods. To see this figure in color, go online.

Results and Discussion

Validation of the new method for quantifying compressibility moduli from LTFs

The canonical method for calculating bilayer area compressibility from MD simulations involves performing a series of NPγT simulations (e.g., (31)). In each simulation, a nonzero tension γ is applied in the x-y plane, and the bilayer K_A is obtained by analyzing the linear relationship between the applied tension and the resulting area expansion (31). Because this methodology directly mimics the micropipette aspiration technique (48), it is expected to closely reproduce the experimental results, provided that the properties of the simulated bilayers are correctly captured by the underlying force field. Table 1 shows the calculated moduli from NPγT simulations of several single-component lipid membranes and the corresponding experimental measurements (see also Table S2). There is indeed a very good agreement between the two, verifying that the simulations are well-converged and able to reproduce the known values of K_A using standard techniques. Therefore, these and other single and multicomponent symmetric bilayers served as controls for the validation of our, to our knowledge, new LTF method.

Table 1.

Area Compressibility of Compositionally Symmetric Single-Component Bilayers Calculated with Different Methods: LTF, Constrained Tension Simulations, and Box Area Fluctuations

Bilayer	LTF			Exp	Constrained Tension (NPγT) Simulations	Box Area Fluctuations
	Top	Bottom	Bilayer
DLPC	258 ± 28	214 ± 22	234 ± 17	–	–	213 ± 20
DMPC	236 ± 20	236 ± 22	236 ± 15	234a ± 23	235 [172, 297]	263 ± 23
DPPC	238 ± 34	274 ± 34	255 ± 24	231b ± 20	223 [188, 257]	183 ± 20
DLiPC	200 ± 26	202 ± 22	201 ± 17	247a ± 21	237 [189, 285]	261 ± 23
DOPC (full)	240 ± 20	274 ± 28	256 ± 17	265a ± 18, 310c ± 20	253 [211, 295]	246 ± 20
DOPC (part)	266 ± 32	260 ± 26	263 ± 21			313 ± 33
DOPC rep 1	246 ± 24	256 ± 26	251 ± 18			223 ± 31
DOPC rep 2	272 ± 28	272 ± 68	272 ± 37			274 ± 26
SOPC	260 ± 24	232 ± 32	245 ± 21	235a ± 14, 290c ± 6	–	236 ± 21
DEPC (full)	212 ± 24	214 ± 22	213 ± 16	229a ± 12	–	204 ± 18
DEPC (part)	240 ± 38	186 ± 42	210 ± 30			321 ± 53
POPC 1	206 ± 32	168 ± 20	185 ± 18	255d ± 75	214 [134, 293]	220 ± 17
POPC 2	236 ± 26	186 ± 28	208 ± 20			172 ± 30
POPC 3	258 ± 28	234 ± 32	245 ± 22			250 ± 23
POPC 4	214 ± 38	198 ± 36	206 ± 26			236 ± 22
POPE	242 ± 28	218 ± 15	229 ± 30	233e	285 [260, 310]	291 ± 261
SAPE	230 ± 12	208 ± 20	218 ± 25	–	–	265 ± 14
DOPG	236 ± 13	230 ± 14	233 ± 19	–	–	220 ± 26
TOCL	224 ± 8	238 ± 7	231 ± 11	–	–	254 ± 20
PSM	344 ± 20	286 ± 20	312 ± 29	–	324 [251, 396]	499 ± 42

If available, experimentally measured moduli are shown (Exp) with references to the respective literature sources. All moduli are given in units of mN/m. The LTF bilayer K_A was calculated with Eq. 10. LTF errors for the leaflets were calculated with a 2D bootstrap method as described in Supporting Materials and Methods and propagated to obtain the error on the bilayer K_A. The 95% confidence interval for the values obtained from a linear fit of tension versus area expansion in NPγT simulations (Table S2) are shown in brackets. For lipid name abbreviations, see Simulations and Analysis in the text. DOPC rep one and DOPC rep two represent two independently constructed and simulated replica trajectories of the DOPC bilayer. The four POPC bilayers labeled one to four differ in their size, simulation temperature, and salt concentration, as shown in Table S1.

^aSee Rawicz et al. (20).

^bSee Nagle and Tristram-Nagle (62).

^cSee Rawicz et al. (21).

^dSee Binder and Gawrisch (49).

^eSee Rand and Parsegian (63).

Tables 1 and 2 list the compressibility moduli for each leaflet and for the bilayer obtained from LTF analysis of the equilibrated trajectories (see Table S1 for a detailed description of all simulated bilayers). The bilayer K_A values obtained from the LTF method are in excellent agreement with those measured experimentally or obtained from NPγT simulations (Table 1), indicating that our approach reproduces the accuracy of existing methods when applied to symmetric bilayers. We note, however, that although the confidence intervals associated with the linear fits from the NPγT simulations are large, the LTF errors calculated with a 2D bootstrapping algorithm (as described in Supporting Materials and Methods) are much smaller and comparable to the experimental uncertainties. (The experimental uncertainty for POPC is notably larger than the rest because the measurement was obtained with a different infrared linear-dichroism-based method (49)).

Table 2.

Area Compressibility of Compositionally Symmetric Multicomponent Bilayers Calculated with Three Different Methods

Bilayer	LTF Methoda			Expa	Box Area Fluctuationsa
	Top	Bottom	Bilayer
POPC/Chol 70/30	862 ± 92	676 ± 126	757 ± 87	673b	562 ± 87
DOPC/Chol 90/10	276 ± 36	306 ± 24	290 ± 23	–	260 ± 27
DOPC/Chol 80/20	466 ± 62	340 ± 68	393 ± 51	–	338 ± 34
DOPC/Chol 70/30	544 ± 74	406 ± 76	465 ± 57	416b ± 24	532 ± 75
DOPC/Chol 60/40	804 ± 118	598 ± 120	686 ± 90	–	829 ± 76
DOPC/Chol 50/50	956 ± 140	826 ± 102	886 ± 84	854b ± 72	1011 ± 99
DPPC/Chol 80/20	2916 ± 364	3368 ± 436	3126 ± 281	–	1968 ± 208
POPE/POPG 70/30	194 ± 22	228 ± 28	210 ± 17	–	193 ± 19
POPC/POPS 70/30	350 ± 40	318 ± 34	333 ± 26	–	360 ± 43
POPE/POPS 70/30	366 ± 40	332 ± 50	348 ± 33	–	322 ± 69
DMPC/POPC 10/90	238 ± 22	188 ± 32	210 ± 22	–	258 ± 19
DMPC/POPC 43/57	264 ± 26	230 ± 32	246 ± 21	–	224 ± 19
DMPC/POPC 75/25	282 ± 24	244 ± 38	262 ± 24	–	250 ± 19

For lipid name abbreviations, see Simulations and Analysis in the text.

^aAs described in the caption of Table 1.

^bSee Evans et al. (19).

Table 1 also lists the corresponding compressibility moduli calculated from the same equilibrated portions of the trajectories but from lateral bilayer area fluctuations using Eq. 2. Although these values are also in reasonable agreement with published results from the same method (17, 38), there is a large variability among the resulting K_A values. For example, for PSM simulated at 48–55°C, Lee et al. (38) calculated a value of 456 ± 65 mN/m, which is similar to the one we obtained from the bilayer area fluctuation analysis (499 ± 42 mN/m), but Venable et al. (17) reported 310–350 mN/m, which is very similar to the moduli we obtained from NPγT simulations and with the LTF method. This variability seems more likely for high-melting lipids (PSM, DMPC, DPPC) whose dynamics 5–10°C above their melting temperatures are generally slower compared to low-melting temperature lipids, suggesting that the underlying reason for the divergent results is likely an insufficient sampling of the lateral area fluctuations. Indeed, in the analysis of box fluctuations each frame of the simulation trajectory represents a single data point, which makes proper sampling highly dependent on the length of the simulation and the size of the bilayer patch (the latter is closely related to the amplitude of the fluctuations (50)). To illustrate this point, we compare in Table 1 the K_A values for DOPC and DEPC (two fluid bilayers of the same size) calculated from either the full equilibrated trajectories of 517 and 680 ns respectively or only from the last 100 ns of the simulation runs. The K_A moduli obtained with bilayer area fluctuation analysis vary from 246 ± 20 to 313 ± 33 mN/m for DOPC and from 204 ± 18 to 321 ± 53 mN/m for DEPC, whereas those calculated with the LTF method do not show such variability. The reproducibility of the LTF moduli can also be seen from the analysis of replica simulations of DOPC, i.e., systems with identical size and lipid composition that were constructed and simulated independently from one another (Table 1).

For bilayers with up to 200 lipids, the results from our method are only weakly dependent on bilayer size: For POPC membranes with 128 and 200 lipids, we calculated K_A values of 245 ± 22 and 208 ± 20 mN/m, respectively (Table 1). For a larger POPC bilayer with 416 lipids, the K_A was 185 ± 18 mN/m, which may indicate a potential challenge for the analysis of larger systems, although the result is within the error of one of the smaller bilayers. Notably, because larger size of the simulated systems generally leads to larger undulations (50), the results might be affected by the assumption inherent in our method that the bilayer normal is the same throughout the bilayer surface (along the z axis of the simulation box). Because thicknesses are calculated by interpolation on the z positions of all atoms in the leaflet (see Methods), using the LTF method with the single bilayer normal assumption would tend to underestimate the apparent K_A when large-scale undulations are present in the system. Introducing local normal vectors in the LTF formulation would, however, require complex numerical calculations that would be unlikely to have a significant effect on the resulting moduli. This is indicated by the results for a leaflet’s bending rigidity modulus obtained from a similarly local-in-nature analysis of real-space fluctuations of lipid splay angles, which produced very similar results with and without the implementation of local normal vectors (51). Instead, we sought to circumvent the problem by constraining the radius of interpolation, R_int. We reasoned that because large-scale bilayer undulations are known to appear on length scales larger than the bilayer thickness (t_pp), setting R_int to a length slightly larger than t_pp could help alleviate the size dependence of K_A. Indeed, using R_int that is 10% larger than t_pp produced a bilayer K_A of 241 ± 23 mN/m for the larger POPC bilayer with 416 lipids, the same as calculated for the smaller systems.

Table 1 shows that the bilayer K_A varied between 230 and 260 mN/m for most single-component bilayers we studied. This nearly constant K_A across the bilayers is consistent with the idea that the bilayer compressibility is mostly influenced by the interfacial energy density, which arises from the common-to-all-bilayers hydrocarbon-water interactions at the leaflet-solvent interface (20). In that respect, the somewhat higher compressibility of PSM (312 ± 29 mN/m) could be explained with the formation of intra- and intermolecular hydrogen bonds, characteristic for sphingomyelin molecules (52, 53, 54). Interestingly, we found TOCL to have a compressibility modulus of 231 ± 11 mN/m, in contrast to a previously reported modulus of 342 mN/m obtained from a rather poor linear fit of tension versus area expansion in a set of constrained tension simulations (Fig. 4 in (55)). The similarity of TOCL’s compressibility to that of a DOPG membrane (233 ± 19 mN/m) is particularly interesting because TOCL’s bending rigidity modulus was found to be twice that of DOPG (18). (Note that chemically, TOCL resembles two DOPG lipids with linked headgroups).

Application of the LTF method to mixed lipid systems

Interestingly, we found that binary mixtures of 30 mol% 1-palmitoyl-2-oleoyl-sn-glycero-3-phospho-L-serine (POPS) with 70 mol% POPC or POPE at 20 and 25°C (respectively) have higher K_A values compared to most single-component bilayers. This is consistent with the combination of their large phosphate-to-phosphate thicknesses (40.1 and 42.8 Å) and small areas per lipid (60.9 and 55 Ų). Similarly, when increasing amounts of DMPC are added to POPC at 25°C, the bilayer K_A increases gradually: from 210 ± 22 mN/m for 10 mol% DMPC to 262 ± 24 mN/m for 75 mol% DMPC, which is accompanied by a systematic decrease in the average bilayer thickness (from 38.6 to 36.6 Å) and area per lipid (from 63.8 to 61.4 Ų). Indeed, as shown in Fig. S4, we found a strong correlation (0.965) between the bilayer K_A and the ratio of bilayer thickness/area per lipid for all fluid multicomponent bilayers we studied, with the exception of the 8:2 DPPC/Chol membrane, which is under gel-like conditions (see Table 2).

Chol has a large effect on membrane compressibility (see Refs. in Table 2), and this is captured successfully by the LTF analysis, as shown by the good agreement with experimental data (see Fig. 3; Table 2). Indeed, the addition of Chol to DOPC at low concentrations (10 mol%) has a negligible effect on K_A, but from ∼20 mol% and higher, the K_A value starts to increase gradually (see Fig. 3 and the discussion on the effect of Chol on bilayer mechanical thickness below). In agreement with results from experiments, we also find that Chol has a larger effect on the compressibility of POPC compared to DOPC: at 30 mol% Chol, POPC/Chol has a K_A of 757 ± 87 mN/m, whereas DOPC/Chol has a K_A of 465 ± 57 mN/m. Interestingly, the large K_A of the highly ordered 8:2 DPPC/Chol bilayer at 25°C (3126 ± 281 mN/m) is similar to the one reported for a 1:1 SM/Chol bilayer at 15°C (3327 ± 276 mN/m) (21).

Ideal conditions for calculating area compressibility moduli with the LTF method

The accurate calculation of the area compressibility moduli relies on the equilibration of the bilayer area fluctuations. Thus, convergence of the bilayer lateral area must be ensured. One of the advantages of the LTF method is that because of its local nature, it does not require long simulation times for analysis and also is not sensitive to system size. We recommend performing the analysis on at least 100–150 ns of equilibrated trajectory (or 5000–10,000 frames), depending on bilayer size and thermodynamic state (e.g., smaller bilayers with a total of less than 150 lipids may need longer simulation times to obtain better statistics). If the chosen sampling is insufficient, this will result in larger errors on the K_A that could be reduced by extending the simulation time.

Notably, in its current formulation, the LTF method assumes relatively small fluctuations in the membrane shape so that the local thicknesses can be obtained simply from the z-coordinates of the relevant groups of atoms (see Calculating Local Leaflet Thicknesses from Simulations). This assumption may not hold if the bilayer is large and develops strong undulations. In that case, it may be necessary to specify a radius of interpolation for calculating local heights. Because the typical wavelength of such undulations appears on length scales larger than the bilayer thickness, this correction may need to be applied only on simulated bilayers whose thickness is much smaller than half the length of the simulation box (when utilizing periodic boundary conditions).

As described in the Methods, we applied the LTF method to all-atom trajectories. This framework could be used directly for analysis of some lower resolution models as well, e.g., united-atom representation in which each carbon and its associated hydrogen atoms are grouped together. However, the method’s application to models in which multiple carbon atoms are grouped into a single “bead” may require modification of the algorithm used to identify the relevant thickness for K_A shown in Fig. 1. Importantly, the premise of the LTF method is that the compressibility of a leaflet can be obtained from the local fluctuations in leaflet thickness. As a result, the accuracy of the recovered K_A values will depend on how well the underlying model captures the structural features of the lipid molecules. An atomic representation designed to reproduce experimentally measured ensemble properties at the expense of instantaneous structural details may lack the resolution required for describing the depth-specific dynamics of leaflet thickness from which the leaflet K_A emerges. In such cases, it is possible that only the bilayer K_A can be obtained, e.g., from the thermally excited bilayer area fluctuations (Eq. 2).

Compression-bending relationship and the role of chain unsaturation

Another aspect of the validation of our method relates to the reproducibility of known relationships among the mechanical properties of the membrane. One basic principle of the mechanical properties of elastic sheets is that the compression (K_A) and bending (κ_C) moduli are related to one another through the sheet’s thickness t_el up to some constant C, i.e., $K_A=C{\kappa }_C/t_{el}^2$. Because the elastic moduli of a lipid bilayer are calculated by assuming that the bilayer behaves as an elastic sheet, we tested whether the same compression-bending relationship holds for our systems. Using experimentally measured K_A, κ_C, and phosphate-to-phosphate thickness of a number of phosphatidylcholine bilayers, this relation was initially demonstrated using in vitro data by treating each leaflet as a collection of freely jointed polymer chains (20). The proposed simple model is referred to as the PBM, which derives a proportionality constant C of 24 and thus gives

$$K_A\approx \frac{24{\kappa }_C}{t_m^2}\to \sqrt{\frac{{\kappa }_C}{K_A}}\approx t_m\sqrt{\frac{1}{24}},$$ (17)

where t_m is the mechanical thickness of the bilayer (i.e., the “deformable” thickness corresponding to t_el in the above elastic sheet analogy). Because bilayer thickness is often measured as the average distance between the phosphate atoms of the two leaflets (t_pp), t_m can be expressed as t_pp − t_inc, where t_inc is some incompressible part within the length of the membrane. Notably, if t_pp is the true mechanical thickness of the bilayer, then t_inc = 0, and in a plot of t_pp vs. $\sqrt{{\kappa }_C/K_A}$, according to Eq. 17 above, all data points would lie on a line with slope $\sqrt{1/24}$ and x-intercept 0. However, t_inc was found to be nonzero (20) and equal to 10 Å, implying that t_m was 10 Å shorter than t_pp. This difference was proposed to reflect the fact that the deformable thickness of a bilayer is limited to its hydrocarbon thickness, and because 5 Å represents the approximate vertical separation between the phosphorus atoms from the hydrocarbon acyl chains on either side of the bilayer, t_m is 10 Å shorter than t_pp, explaining the nonzero t_inc. The only bilayers described as deviating from this behavior were polyunsaturated membranes (20), which appeared to have shorter mechanical thicknesses than expected.

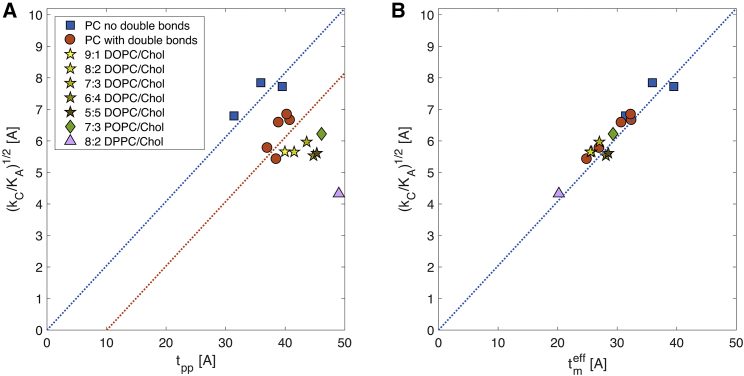
We were able to test the relation between compression and bending and the applicability of the PBM to the membrane systems we studied by taking advantage of the ability to calculate all three bilayer properties: bending rigidity (18), area compressibility, and phosphate-to-phosphate thickness (Table S3) from our trajectories. Fig. 4 A shows the results for all single-component phosphatidylcholine (PC) bilayers together with the data for the binary mixtures of PC and Chol. Notably, the relationship between bending, compression and thickness could be explained with the PBM model (each dotted line has a slope of $\sqrt{1/24}$) for all single-component bilayers. However, based on the results in Fig. 4 A, the membranes can be roughly divided into two categories with different mechanical thicknesses (x-intercepts): PC lipids with fully saturated acyl chains for which t_m ≈ t_pp (DLPC, DMPC, DPPC, shown as squares) and lipids with one or more double bonds for which t_m ≈ t_pp − 10 Å (POPC, SOPC, DEPC, DOPC, DLiPC, shown as circles in Fig. 4). We find that the data in Fig. 4 A cannot be explained by the rationale for t_inc given in (20) because the distance between the phosphates and the hydrocarbon chains on either side of the bilayer, proposed to be the origin of t_inc, is independent of the saturation of the lipid chains (e.g., the average distance between the phosphates and the first carbons on the acyl chains is 4.7 Å for DPPC, 5.0 Å for POPC, 4.6 Å for DOPC, and 4.6 Å for DLiPC). Instead, our result suggests an alternative model in which the double bonds are the ones responsible for reducing the deformable thickness.

Figure 4.

Application of the polymer brush model (PBM) to simulated bilayers suggests a new definition of bilayer mechanical thickness. (A) The ratio from Eq. 17 of the bilayer bending rigidity (calculated from real-space analysis of splay fluctuations (18)) and area compressibility (calculated with the LTF method) is shown as a function of phosphate-to-phosphate distance, t_pp, for all single-component fully saturated (squares) and unsaturated (circles) PC bilayers (Table 1), and for binary mixtures of PC and Chol (stars, diamond, and a triangle, Table 2). All dotted lines have been drawn with the PBM’s slope of $\sqrt{1/24}$ and different x-intercepts. A nonzero x-intercept indicates a deviation of the bilayer mechanical thickness, t_m, from t_pp, as explained in the text. (B) The ratio of the mechanical constants of the same bilayers in (A) is plotted against the effective mechanical thickness of the bilayers $t_m^{eff}$, which is assumed to be equal to 1) t_pp for all fully saturated PCs, 2) the difference between t_pp and the length of the region around the double bonds for single-component unsaturated PCs and 9:1 DOPC/Chol, 3) the difference between t_pp and the length of Chol’s ring body for all remaining binary mixtures of DOPC and Chol and POPC and Chol, and 4) the difference between t_pp and the full length of Chol for DPPC/Chol (Table S3). See text for more details. To see this figure in color, go online.

To evaluate this alternative model, we tested whether double bonds lead to relatively incompressible regions in the bilayer and decrease t_m by increasing t_inc. We first examined how pressure was distributed in tension-free bilayers with varying degrees of saturation (Fig. S5). An increase in the number of double bonds in the lipid chains led to an increase in the pressure in the region around the double bonds. This observation prompted us to further investigate the relationship between pressure and compressibility in the context of lipid chain unsaturation. To do so, we calculated the compressibility factor, which is a correction factor in statistical mechanics that relates pressure, volume, and number of particles (see below) and quantifies the deviation of the behavior (in particular, the compressibility) of a real gas from that of an ideal gas (or some other model matter with a defined equation of state) (56). Although the membrane is not an ideal gas (or a gas at all), the pressure at any given depth within the bilayer can be calculated in a slab with a defined volume that contains a certain number of atoms (see Simulations and Analysis in Methods), and hence the local state variables are well defined. Thus, we hypothesized that the double bonds may have an influence on compressibility that would be observable through this approximate model.

In our analysis, we use the van der Waals equation of state that is often employed in the study of fluids:

$$\left(P+\frac{n^{2}a}{V^2}\right)\left(V-nb\right)=nRT,$$ (19)

where a describes attractive interactions between atoms in the fluid and b describes the excluded volume (i.e., the volume occupied by the atoms that is excluded from the total volume) (56), n is the number of atoms, and P, V, R, and T are the usual state variables. We can write the pressure as a quadratic function of n:

$$P=\left(\frac{RT}{V-nb}\right)n-\frac{n^{2}a}{V^2},$$ (20)

which reveals a strictly positive component that is a function of excluded volume and a strictly negative component that is a function of strength of the attractive interactions. In the DPPC saturated bilayer (Fig. S6, row 1), we observe a negative relationship between P and n, which suggests that the inter- and intramolecular bonds and interactions present in the bilayer make the dominant contribution to the pressure. However, when analyzing membranes with varying degrees of unsaturation, we find that upon adding double bonds, a regime of positive slope occurs (Fig. S6, rows 2–4). This observation can be explained by the dominance of the first term in Eq. 20 due to the increase in excluded volume caused by the presence of double bonds, which limit the space that can be sampled by the lipid chains. Indeed, a comparison between the van der Waal’s constants for ethylene (C₂H₄, b = 0.05821 L/mol), ethane (C₂H₆, b = 0.06499 L/mol), and hydrogen (H₂, b = 0.02651 L/mol) (56, 57) clearly shows that a double bond increases the b term (i.e., $b_{C_2{H}_4}>b_{C_2{H}_6}-b_{H_2}$). Further comparison of the corresponding a terms (C₂H₄, a = 4.612 bar L²/mol²; C₂H₆, a = 5.570 bar L²/mol²; H₂, a = 0.2453 bar L²/mol²) suggests that a double bond also decreases the attractive interactions between atoms (i.e., $a_{C_2{H}_4}<a_{C_2{H}_6}-a_{H_2}$), which would further contribute to the dominance of the first term in Eq. 20.

To investigate the expected change in compressibility due to the additional double bonds, we interpreted the data in Fig. S5 in the context of the compressibility factor. When quantifying the deviation from a van der Waals fluid, the compressibility factor is defined as

$$Z=\frac{V}{V-nb}-\frac{an}{RTV}.$$ (22)

When Z > 1, the volume is greater than expected for a given pressure due to its incompressibility. In the regime in which the excluded volume term dominates (i.e., when there are double bonds present), Z becomes large and positive, indicating the membrane is less compressible. This analysis thus confirms that the addition of double bonds to lipid chains leads to relatively incompressible regions that decrease t_m by increasing t_inc.

Motivated by the effect of the double bonds on the chain-order parameter profile of the lipids, we used a simple heuristic approach to approximate the length of the perturbed region around the double bonds, t_DB, for the unsaturated PC bilayers from Fig. 4 A: namely, the perturbed region extends four carbons above and below the midpoint of all double bonds for DOPC and DLiPC and two carbons above and below the midpoint of the double bonds for POPC, SOPC, and DEPC (see Fig. S7; Table S3). Remarkably, after subtracting t_DB from t_pp and replotting the data in Fig. 4 B, all data points moved to the line with x-intercept at 0, confirming our hypothesis regarding the nature and source of the incompressibility and suggesting that the bilayer mechanical thickness for unsaturated lipids can be defined as the phosphate-to-phosphate thickness excluding the regions around the double bonds. We note that this result also explains the observation in (20) that polyunsaturated bilayers have shorter mechanical thicknesses because the perturbed region around their double bonds would be larger, and consequently, t_m would be smaller.

Although DLiPC (di18:2 PC) has two more double bonds per molecule than DOPC (di18:1 PC), we find that both DLiPC and DOPC bilayers have similar mechanical thicknesses. This result is consistent with the nearly identical chain stress distributions in monolayers of these two lipids predicted by Cantor (58). As illustrated by the analysis in (58), the effect of the double bonds on monolayer properties (and very likely bilayer properties) depends on both the number and the location of the double bonds.

Note that in the validation of the PBM described in (20), the mechanical thickness of DMPC was found to be 10 Å shorter than t_pp, like the rest of the examined bilayers. However, the reported DMPC’s bending rigidity modulus measured by micropipette aspiration (13.2 kT) was much lower than the one obtained with flicker spectroscopy (31.1 kT (59)) and also with our computational method (34.7 kT (18)). The low value of κ_C reported in (20) is most likely due to the difficulties of applying the micropipette aspiration technique to higher-melting-temperature lipids, as discussed in (18). If a higher κ_C had been used instead in the PBM analysis, DMPC’s mechanical thickness would likely have been predicted to be much closer to t_pp, consistent with the data in Fig. 4.

The effect of Chol on bilayer mechanical thickness

As illustrated by the analysis above, the effective mechanical thickness of a bilayer, $t_m^{eff}$, can be expressed as the phosphate-to-phosphate distance excluding the length of any region that resists compression. In this respect, it is interesting to investigate the behavior of lipid bilayers containing Chol because the sterol contains a rigid and relatively incompressible set of rings (47). Fig. 4 A shows the mechanical properties of various lipid mixtures with Chol, including a set of DOPC/Chol bilayers with varying amounts of Chol tested against PBM. Most of these bilayers exhibit a larger deviation from either of the dotted lines, indicating a larger t_inc than the non-Chol membranes. To determine t_inc for the DOPC/Chol and POPC/Chol membranes, we first used the same heuristic approach as for the unsaturated lipids described above and calculated $t_m^{DB}=t_{pp}-2t_{DB}$. With this definition, all DOPC/Chol data points from Fig. 4 A shifted to the line with an x-intercept at 0, but for the POPC/Chol bilayer, $t_m^{eff}$ was shorter than $t_m^{DB}$ (Fig. S8 A). Given the larger effect of Chol on POPC compared to DOPC and the relatively incompressible and rigid nature of the sterol ring structure as discussed above, we reasoned that in the POPC/Chol membrane, t_inc would be better approximated by the length of Chol’s ring region, t_Chol. To test this hypothesis, we calculated t_Chol as the average distance between the C3 and C17 atoms of Chol (using CHARMM36 notation) projected onto the z axis and found it to be 8.4 Å (Table S3). Remarkably, plotted as a function of $t_m^{Ch}=\left(t_{pp}-2t_{Chol}\right)$, the PBM data point for POPC/Chol fell on the line with x-intercept at 0 (Fig. S8 B), indicating that $t_m^{Ch}\approx t_m^{eff}$.

We then tested how well $t_m^{Ch}$ approximates $t_m^{eff}$ in the DOPC/Chol mixtures. In light of the results in Fig. 3 showing that Chol has an effect on the bilayer K_A only at 20 mol% or higher, we expected that t_inc ≈ 2t_Chol for these Chol bilayers but not for the 9:1 DOPC/Chol membrane. Indeed, as shown in Fig. S8 B, $t_m^{eff}\approx t_m^{Ch}$ for the 20–50% DOPC/Chol mixtures, and $t_m^{eff}>t_m^{Ch}$ for the 10% DOPC/Chol bilayer.

Three different regimes are required to describe the effect of Chol on the structural properties of bilayers, corresponding to low, intermediate, and high Chol mole fractions (47, 60). The results presented above and summarized in Figs. 3 and 4 suggest that this is also the case for the Chol effects on bilayer mechanical thickness and compressibility. Thus, our analysis shows that at 10 mol%, Chol does not have an effect on either $t_m^{eff}$ or K_A; at 20 and 30 mol%, Chol affects $t_m^{eff}$ and increases K_A indirectly through its condensing effect on DOPC; and at 40 and 50 mol%, Chol affects $t_m^{eff}$ and increases K_A directly, i.e., its contribution to K_A must be considered explicitly (Fig. 3). These regimes are consistent with the reduction in the translational and rotational entropy for Chol with increasing concentration: at low mole fractions, Chol adopts relatively large tilt angles with respect to the bilayer normal, and thus relatively random orientations (large tilt angles result in larger degeneracy of rotational states (18, 61)). This increased orientational freedom can alleviate any potential stress from compressing the bilayer’s thickness. At higher concentrations, Chol’s conformational freedom gradually decreases because Chol molecules tend to align parallel to the bilayer normal (61). Bilayer compression under such conditions likely involves compression of the Chol molecules.

We also investigated the applicability of the PBM to a fully saturated DPPC/Chol bilayer with 20 mol% Chol. The bilayer was simulated at 25°C and is in a very ordered gel-like state, as indicated by its small area per lipid and large elastic moduli (Tables 2, S1, and S3). The PBM comparison for this system, shown in Fig. 4 A, indicates that the mechanical thickness of the membrane is significantly smaller than t_pp. Interestingly, we found that for this bilayer, the Chol tail was more rigid than in the other membranes (Fig. S9 A) and comparable in its tilt distribution to the ring body of Chol in the 7:3 DOPC/Chol bilayer (Fig. S9 B). This result suggested that Chol’s tail in this bilayer was harder to compress and that the mechanical thickness of the membrane could exclude the sterol tail as well because of the high order in the system. Indeed, considering in the calculations the full length of Chol—including its ring and tail regions—we were able to successfully recover $t_m^{eff}$ of the DPPC/Chol bilayer (Fig. 4 B). Both Chol concentration and the temperature determine the thermodynamic phase behavior of the bilayer and thereby the degree of Chol’s conformational freedom. Therefore, it remains to be investigated whether Chol affects the mechanical properties of other fully saturated lipids in a similar way and how the observed relationships vary with temperature.

Revised definition of bilayer mechanical thickness clarifies conflicting reports on the PBM’s applicability

As illustrated by our analysis, the effect of double bonds and Chol on bilayer’s mechanical thickness has not been systematically characterized before. Therefore, we sought to examine the relation of our findings to published observations from both in vitro and in silico work. We found that our results resolve some contradictory reports in the literature regarding the validity of the PBM for different bilayers. Indeed, since the PBM was first introduced, the model has been experimentally tested in a number of studies by assuming that t_m = t_pp − 10 Å, yielding conflicting results (17, 27, 28). In 2008, Pan et al. found a good agreement between their results and the PBM’s predictions for DOPC (27), but in 2009, they reported that the theory was incapable of describing the relationship between the mechanical constants in Chol-containing bilayers (28). In a comprehensive review of bilayer mechanical properties from MD simulations published more recently, Venable et al. found a relatively good agreement between the simulation results and the PBM for POPC and DOPC, but there was a bigger deviation for DMPC and DPPC (see Fig. 11 (17)). These conflicting observations can be consolidated in light of our finding that the presence of Chol and/or acyl-chain unsaturation can affect the mechanical thickness of the bilayers. Not surprisingly, the PBM was successfully applied to lipids with one or two double-bonded tails such as DOPC and POPC both in the experimental and computational studies because for those lipids, t_m can indeed be approximated by t_pp − 10 Å. However, according to our analysis, the incompressible body of Chol has a length of ∼8.3 Å, effectively decreasing t_m by an additional 6 Å (3 Å from each leaflet), i.e., t_m ≈ t_pp − 16 Å. Thus, if the hydrocarbon thickness 2D_C (used as a proxy to t_pp − 10 Å) in Eq. 6 in (28) is substituted with (2D_C − 6 Å), the ratio between predicted and actual κ_C for SOPC and DOPC in the presence of 30 mol% Chol becomes 1.0 and 1.36, respectively, indicating a good agreement with the theory contrary to the stated conclusion in (50). Similarly, because DMPC and DPPC are fully saturated and hence t_m ≈ t_pp, the use of t_pp − 10 Å for their mechanical thickness in (17) explains the larger deviation of their calculated bending moduli from the PBM’s predictions.

Together, all these results are consistent with the notion that bilayer mechanical thickness depends on lipid composition and cannot be simply taken as the bilayer hydrocarbon thickness. Our analysis illustrates a simple but general principle of bilayer mechanics, whereas the assumption for elastic material behavior holds only for the regions within the membrane that are equally compressible. In particular, the presence of both acyl-chain unsaturation and Chol produce nonuniform compressibility in the membrane hydrocarbon core that needs to be taken into account when quantifying the deformable membrane thickness.

Conclusions

We have presented a, to our knowledge, new computational framework for calculating area compressibility moduli of lipid bilayers and their individual leaflets from all-atom MD simulations. The approach is based on sampling LTFs from an MD simulation trajectory in which these properties are sufficiently converged. We show that the method overcomes a number of limitations of existing computational approaches and yields elastic moduli values that are in agreement with available experimental data for both single and multicomponent bilayers composed of saturated and unsaturated lipids and Chol and simulated at several temperatures. Importantly, because it is free from the need to sample global lateral bilayer fluctuations, our method is uniquely capable of analyzing the area compressibility of bilayers under tension (i.e., simulated in an NPAT [constant temperature, pressure and lateral surface area] ensemble). We note that it should also allow, in principle, future applications for the calculation of the spatial variability in leaflet compressibility moduli in the presence of transmembrane inclusions.

The data presented show that the mechanical properties of the simulated bilayers, and the relation between specific parameters representing their properties, are consistent with an elastic sheet model and consonant with a PBM. However, the application of the PBM is shown to require a significant modification of the canonical definition of the membrane mechanical thickness considered as simply the hydrocarbon region of the bilayer. Indeed, we demonstrated the specific considerations that are necessary to determine the appropriate mechanical thickness required to calculate unknown elastic moduli. These include the quantitative accounting for acyl-chain unsaturation and Chol concentration, both of which introduce relatively incompressible regions within the bilayer that decrease the effective mechanical thickness.

Although all of the bilayers we have examined have the same lipid composition and the same number of lipids in their two leaflets, the physical model underlying Eq. 10 is general enough to allow for analysis of the great variety of compositionally asymmetric bilayers that are physiologically relevant because their local leaflet K_A values could be different. This aspect of the method continues to be the subject of our ongoing computational studies. Systematic experimental measurements of the compressibility moduli of asymmetric bilayers, especially ones whose leaflets are expected to have significantly different mechanical properties, would greatly benefit the validation and/or refinement of the theoretical predictions from the harmonic mean relationship between the bilayer K_A and the local leaflet moduli (Eq. 10).

Author Contributions

M.D., G.K., M.V.L., and H.W. designed the research and wrote the manuscript. M.D. performed all simulations and computational analysis.

Editor: Ana-Suncana Smith.