Reconnection scaling in quantum fluids

Significance

Superfluid helium exhibits topological defects in the form of line-like objects called quantum vortices. Reconnection occurs when two vortices collide and recoil by exchanging tails. We observe such a reconnection for nearly isolated conditions and find that the intervortex separation for a certain range scales closely as the square root of the time after reconnection and that the prefactor in the square-root law shows an analytical dependence on the reconnection angle. Reconnection is important because it provides a mechanism for energy dissipation which otherwise does not occur in the zero-temperature limit. The kinematics of reconnections are similar in systems of classical vortices, cosmic strings, magnetic flux tubes in plasmas, liquid crystals, and even DNA.

Abstract

Fundamental to classical and quantum vortices, superconductors, magnetic flux tubes, liquid crystals, cosmic strings, and DNA is the phenomenon of reconnection of line-like singularities. We visualize reconnection of quantum vortices in superfluid ⁴He, using submicrometer frozen air tracers. Compared with previous work, the fluid was almost at rest, leading to fewer, straighter, and slower-moving vortices. For distances that are large compared with vortex diameter but small compared with those from other nonparticipating vortices and solid boundaries (called here the intermediate asymptotic region), we find a robust 1/2-power scaling of the intervortex separation with time and characterize the influence of the intervortex angle on the evolution of the recoiling vortices. The agreement of the experimental data with the analytical and numerical models suggests that the dynamics of reconnection of long straight vortices can be described by self-similar solutions of the local induction approximation or Biot–Savart equations. Reconnection dynamics for straight vortices in the intermediate asymptotic region are substantially different from those in a vortex tangle or on distances of the order of the vortex diameter.

Reconnections are collisions of two line-like topological defects which subsequently recombine by exchanging each other’s tails (1). These changes in topological configuration occur in magnetic flux tubes (2), cosmic strings (3), polymers, liquid crystals (4), superconductors (5), and DNA (6) and are common in quantum (7) as well as classical vortices (8). Reconnections are crucial in redistributing and dissipating energy (kinetic or magnetic) in turbulence, astrophysical plasmas, and fusion devices (2).

Here, we study reconnection of quantized vortices in superfluid ⁴He. Superfluid helium can be modeled as a mixture of a viscous normal component and an inviscid superfluid component. Vorticity in the superfluid fraction is constrained to quantum vortices (9), which are phase singularities and topological defects in the order parameter describing the superfluid. The circulation of the quantized vortices is constrained to be the quantum of circulation $\kappa =h/m$, where $h$ is Planck’s constant and $m$ the mass of the helium atom. The tangle of quantum vortices that forms when the superfluid is driven far from equilibrium is called quantum turbulence (10). Reconnections are thought to be central to the decay of quantum turbulence (11), which lacks viscosity as a dissipative mechanism in the zero-temperature limit (12). Reconnections are understood to excite a cascade of kelvin waves (13) leading to energy dissipation via emissions of phonons (14) and possibly rotons (15). Reconnection of quantized vortices has been visualized in superfluid helium (7) and in Bose–Einstein condensates (16). Unlike in classical fluids (8, 17), quantized vortices and their reconnections are well-defined concepts because the vorticity does not diffuse. In the present work, the vortex core $a_0\approx 10^{-10}$ m, while the vortex length $l\simeq 1$ mm. This work focuses on reconnection in the intermediate asymptotic state where the vortices are straight and distances are large compared with the vortex diameter and small compared with those from the next nonparticipating vortices or the walls of the apparatus.

The first person to address reconnection analytically was Crow (18) with his work on trailing vortices (in classical fluids). Schwarz (19) introduced numerical techniques based on the Biot–Savart equation and studied the problem quantitatively. Other works (20, 21) are based on the nonlinear Schrödinger equation, also known as the Gross–Pitaevksii (GP) equation. In classical fluids, reconnection has been studied experimentally (22, 23) and numerically (24, 25). The first experimental study of reconnection in superfluid helium was by Bewley et al. (7), who used a technique previously developed in ref. 26 to visualize the vortex position by means of micrometer-sized solid hydrogen tracers trapped on vortex cores. Later studies by Paoletti et al. (27, 28) included some 20,000 reconnection events and found that the intervortex distance $\delta$ scales as $A\sqrt{\kappa t_a}\left(1+c{t}_a\right)$, where $t_a=|t-t_0|$ and $t_0$ is the time of reconnection, $A$ is a dimensionless prefactor, and $c$ is a correction factor. This was a necessary modification of the $\delta \propto \sqrt{\kappa t_a}$ scaling deduced from dimensional analysis, assuming that the only relevant quantity in reconnecting vortices is the quantum of circulation, and with previous numerical simulations in an ideal fluid by ref. 29. The numerical work using the GP equation yields, for scales close to the vortex core, deviations from the 1/2 scaling, with different exponents for advancing and receding vortices (30, 31), although such deviations have not been observed in similar calculations in ref. 32.

Compared with these previous experimental studies we use a visualization technique that uses frozen air tracers which are much finer, described briefly in Materials and Methods and in detail in ref. 33. The technique, previously used to visualize kelvin waves (34), uses submicrometer particles injected directly in the superfluid phase, permitting the visualization of longer and straighter vortices. While the studies by Paoletti et al. (27, 28) inferred the reconnection events indirectly from rapid separations of particle pairs, we observe reconnection events when many particles are visible on both vortices along their length. However, the number of events is smaller by a factor of 1,000 (20 events vs. 20,000 events) for two reasons. First, we worked in a quiet system, at a temperature around 1.9 K, in which there was no imposed heat flux (velocity of the normal component $\sim 0.01$ mm/s) and the vortices had enough time to relax to almost straight configurations; this is in contrast to refs. 27 and 28 in which reconnections were excited in large numbers by pulsing a heat flux that drove a counterflow and created vortex tangles. Second, we looked for events in which both vortices are fully decorated with particles and both branches lie within the narrow laser sheet, which is only 150 $\mathrm{\mu }$m thick. These stringent selection criteria greatly reduce the number of observable events but this choice of conditions has the benefit of eliminating the projection effect of out-of-plane vortices.

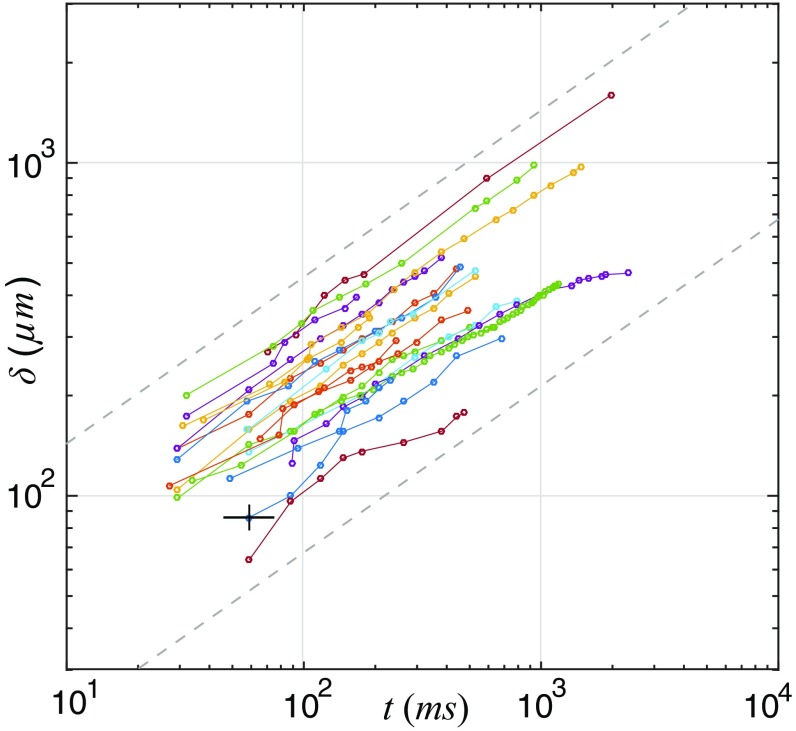
When two straight vortices approach each other, they locally reconfigure into antiparallel configuration (19, 23, 35, 36). However, on the larger separation scale considered here, two approaching straight vortices are always in a parallel configuration and there exists a self-similar evolution for which the vortex asymptotes form a global angle $\theta$ (Fig. 1). This self-similar evolution is what we observe in our experimental visualizations (Fig. 1). We first note that the intervortex distance $\delta$ follows the 1/2 scaling, $\delta \propto \sqrt{\kappa t_a}$, quite well (Fig. 2). To measure $\delta$ we considered the closest intervortex distance by manually interpolating the position of neighboring particles. We estimate a line vortex density of $\sim 10^6$ m⁻²which corresponds to an average intervortex spacing in the whole system of $\sim$1 mm.

Fig. 1.

(Left) The first frame of images shows the experimentally observed vortices within $t_a=t-t_0=30$ ms of the time or reconnection $t_0$, the second frame those within the next 30 ms, and the last frame those after 240 ms. (Right) The vortices at the time of reconnection are almost straight close to the reconnection “point,” so it is possible to define an angle $\theta$ between the vortices (leftmost line diagram). We also define the intervortex distance $\delta$ as the minimum distance between the retracting vortices (center line diagram). The arrows on the lines represent the directions of circulation. Straight vortices reconnect as in the top rightmost diagram. This is the parallel reconnection. The way to understand this is to follow each vortex after reconnection: One can identify a vortex by joining any two segments, provided that the arrows point in the same direction; what matters is the direction of the arrows. This picture does not preclude an antiparallel orientation (bottom rightmost diagram) locally at reconnection but the present intermediate asymptotics picture does not possess that resolution.

Fig. 2.

The intervortex distance $\delta$ as a function of time after reconnection for 20 reconnection events. Each point represents a measurement. The trend is in broad agreement with the $\delta \propto \sqrt{\kappa t_a}$ scaling for which the dashed lines are a guide to the eye. The data are collected in a few instances for up to 2 s after reconnection, which is a factor of 10 longer than the data collection in refs. 27 and 28. We have inserted an example of the error bar, taken conservatively as the size of the pixel and the time between images.

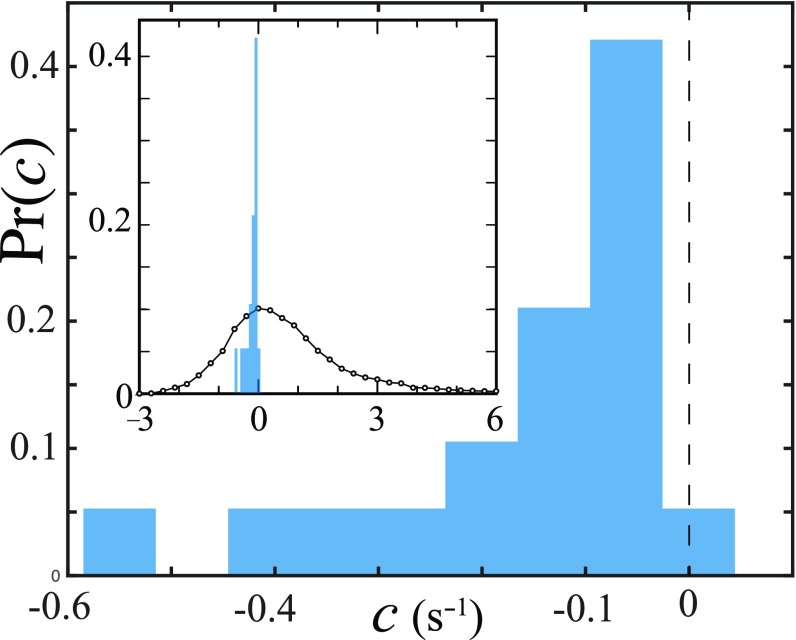
If we insist on fits of the type used in refs. 27 and 28, we find that the distribution of c (Fig. 3) peaks near 0, with a median value of −0.10 s⁻¹ and an average of −0.15 s⁻¹. This means that the deviation from the average is less than 10%. Moreover, all values of c are negative. This fact could be due to boundary conditions: The 1/2 scaling breaks down when the vortex comes to rest as the cusp relaxes into a straight vortex and when the boundary conditions progressively slow down its motion. This contrasts from refs. 27 and 28 in which the distribution peaked at 0 and was much broader with a slightly larger number of positive values than negative values (Fig. 3, Inset). This difference is most likely the result of very different conditions of the system: quiet in our case, turbulent in refs. 27 and 28. Finally, deviations from the 1/2 scaling of the intermediate asymptotic regime could be due to the curvature and/or the presence of neighboring vortices.

Fig. 3.

Normalized frequency distribution of the parameter $c$ representing the deviation from the 1/2-power scaling, $\delta =A\hspace{0.17em}\sqrt{\kappa t_a}\left(1+c{t}_a\right)$. The distribution consists only of negative values, peaking at slightly lower than 0, in striking contrast with the data from the pulsed counterflow experiments (28) (Inset, black curve) for which the distribution was much wider and there were more instances in which $c$ was positive than negative. Inset spike represents data in the main plot.

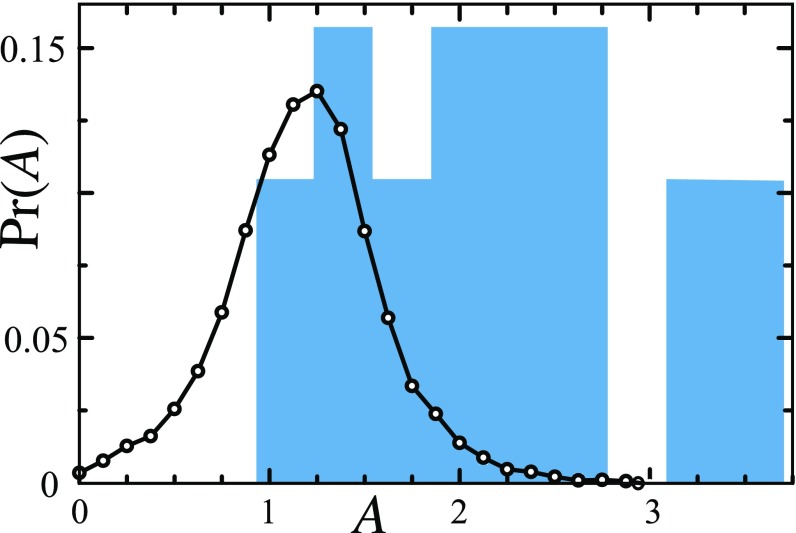
Although the statistics are limited, another important distinction is the distribution of the prefactor $A$. As is clear from Fig. 4, we observe four instances in which $A>3$ unlike any of the previous 20,000 observations in ref. 28 and, in general, higher values of $A$. Indeed, the average value $\overline{A}$ of $A$ is 2.14, compared with $\overline{A}=1.1$ in ref. 28 and with $\overline{A}=0.4$ in the simulations in ref. 29. The difference between the two experiments could be due to the very different conditions and geometries of the system, as already mentioned, and perhaps also to the reduced projection effects here. Previous experiments looked at shorter timescales after reconnection ($10^{-3}\hspace{0.17em}\mathrm{s}<t_a<0.2\hspace{0.17em}\mathrm{s}$) over which the particle pairs of interest were visible even while moving with a velocity component orthogonal to the plane of the laser sheet. The current experiments study longer timescales ($2\times 10^{-2}\hspace{0.17em}\mathrm{s}<t_a<2\hspace{0.17em}\mathrm{s}$), with particles distributed along the vortex lengths, visible only when aligned with the plane of the laser sheet.

Fig. 4.

Normalized frequency distribution of the prefactor A of the scaling $\delta =A\hspace{0.17em}\sqrt{\kappa t_a}\left(1+c{t}_a\right)$. The black curve represents the data from about 20,000 events in the pulsed counterflow experiments reported in ref. 28, while the histogram represents the 20 events currently under study. Unlike the pulsed counterflow data, the present measurements show events with A $>$ 3, corresponding to high intervortex velocity, and no events for A < 1.

The surprising fact that in previous experiments there were no reported reconnections with A $>$ 3 might also be caused by their technique for measuring the separation distance $\delta$ between particle pairs. If the separation was too rapid, the algorithm might not have detected the particles as a pair. Moreover, the bigger particles compared with the present ones might have slowed down the separation between vortices due to drag, reducing the effective A. We cannot observe the prefactor A before reconnection because of the way in which the vortices are arranged: The observations are for straight vortices approaching each other in the direction orthogonal to the field of view, so it is not possible to see the intervortex distance $\delta$ before reconnection. The reason for the difference from simulations in ref. 29 may well be that they were performed just for the reconnection of vortex rings.

Let us consider the localized induction approximation (LIA) for the vortices, first derived by Da Rios (37) and rediscovered multiple times (38, 39). The Da Rios equation for the position of the vortex $\mathbf{s}$, also related to the elastica (40–42) originally solved by Euler, is

$$\frac{d\mathbf{s}}{dt}\simeq \beta \frac{d\mathbf{s}}{d\sigma }\times \frac{d^2\mathbf{s}}{d{\sigma }^2},$$ [1]

where $\sigma$ is the parametric arc length and $\beta \simeq \kappa$. We neglect logarithmic corrections for the core size and the radius of curvature and examine the self-similar solutions described by Gutierrez et al. (43) by defining the dimensionless coordinate $\eta =\sigma /\sqrt{\beta t}$. A similarity solution is sought in terms of $\mathbf{s}\left(\sigma ,t\right)=\sqrt{\beta t}\mathbf{G}\left(\eta \right)$, and the resulting equation for $\mathbf{G}$ is

$$\frac{1}{2}\mathbf{G}-\frac{1}{2}\eta \mathbf{G}\prime =\mathbf{G}\prime \times {\mathbf{G}}^{″},$$ [2]

where the prime denotes the derivative with respect to $\eta$. The solutions are a one-parameter family of curves governed by the initial curvature $C_0$, which satisfies $C_0=A/4$. The parameter $C_0$ or $A$ uniquely determines the opening angle $\theta$ between the two branches of the retracting vortex. In fact, it is possible to write an analytical relationship (43) between the curvature and the opening angle as

$$A=4\sqrt{-\frac{2}{\pi }log\left(\sin \left(\theta /2\right)\right)}.$$ [3]

Note that the self-similar solutions are for individual curves and describe the relaxation of the cusps, but do not take into account the presence of other vortices.

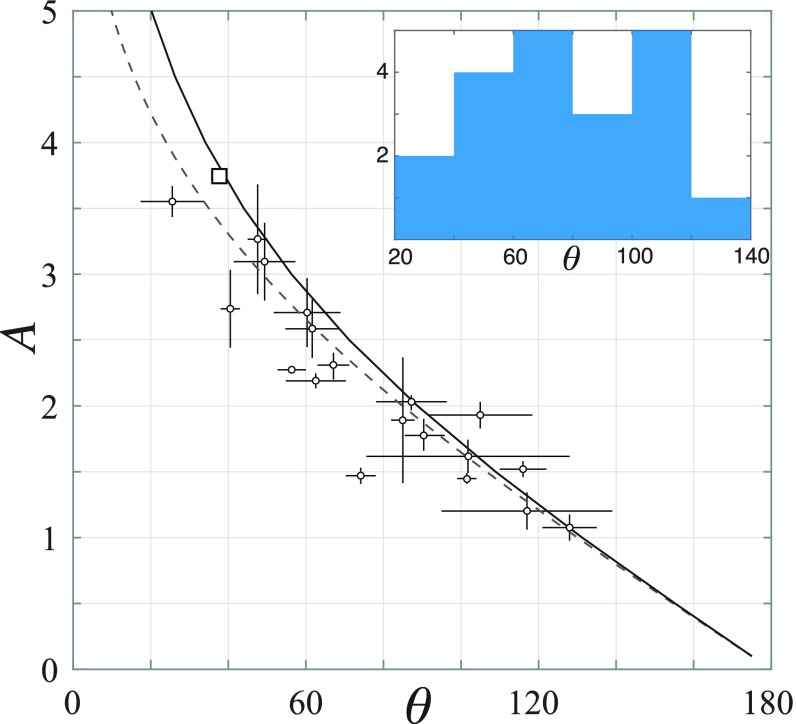
As already stated, our data were obtained around 1.9 K, at which there is still 40% of normal component, with the attendant damping effect due to mutual friction (44). To account for this effect, it is possible to include in the Da Rios equation the extra term $\alpha d^2\mathbf{s}/d{\sigma }^2$, as done by Lipniacki (45). From the tables in ref. 44 and our temperature range 1.9 K < T < 2 K we can estimate a mutual friction coefficient to be $0.25<\alpha <0.3$. No analytical relation between the prefactor $A$ and the angle $\theta$ exists for such a modified equation, but it is possible to compute one numerically. In Fig. 5 we present the data for $A$ as a function of $\theta$ as well as the two theoretical relationships with and without the mutual friction term. We calculated the $A-\theta$ relationship also for the self-similar solution of the full Biot–Savart law (46), but no appreciable difference was seen in comparison with LIA. We estimated the angle by measuring it manually. The horizontal error bars reflect the uncertainty in these measures and the inherent curvature of the vortices. The vertical error bar is the uncertainty on the nonlinear fit to obtain the prefactor $A$. It is clear from the plot that there is an overall agreement between the experimental data and the theory, but it is hard to decide whether the data are better fitted by the inclusion or omission of the mutual friction. In ref. 34, however, we showed that the overlap of the data with theory is better if mutual friction is included. We plotted the distribution of the angles in Fig. 5, Inset. As for prefactor A, we observed a relatively flat distribution in the middle with no reconnections for angles less than 20^○ and larger than 140^○, in contrast to the distribution predicted for mechanical and thermal turbulence; they peaked, respectively, for high and low $\theta$ (47).

Fig. 5.

Plot of the prefactor A as a function of the angle of reconnection. The circles represent the present data while the square represents the data in ref. 34. The dashed line represents the analytical relationship $A=4\sqrt{-\frac{2}{\pi }log\left(\sin \left(\theta /2\right)\right)}$ for the case $\alpha =0$, while the solid line represents the case for $\alpha =0.3$, appropriate to $T\simeq 1.9$.

In conclusion, we have examined the reconnection of almost straight reconnecting vortices. On a global scale these vortices reconnect in a parallel configuration and display a self-similar evolution. The local rearrangement of vortices at the reconnection “point” is not visible on this scale, and a locally antiparallel configuration is by no means precluded. To observe the local rearrangement into antiparallel configuration and deviations from the self-similar solution of LIA and Biot–Savart equations, it is necessary to make observations at much smaller scales on the order of the vortex core.

Our results are that deviations from the 1/2-power scaling of the intervortex distance as a function of reconnecting time are much smaller than in previous pulsed counterflow experiments (27, 28). We have shown that the relationship between the angle of reconnection and the prefactor $A$ follows the analytical formula deduced from the self-similar solution of LIA. We also observed reconnection events with A $>$ 3 (corresponding to $\theta$ < 50^○), higher than any of the events in the pulsed counterflow experiments. More broadly, in the intermediate asymptotic regime for which reconnecting vortices are almost straight, the behavior of reconnection is substantially different from that during the decay of a vortex tangle, where the vortices are curved and close together.

Materials and Methods

The experimental setup and visualization method is the same as in ref. 34 and is described in detail in ref. 33. It consists of an optical cryostat filled with liquid helium in which we inject a dilute mixture of atmospheric air in helium gas. The atmospheric air freezes into tracer particles that get trapped on the quantum vortices due to a Bernoulli pressure gradient. The particle size was estimated to be on the order of 0.5 μm, sometimes as small as few hundred nanometers, based on both optical (48) and terminal (33) velocity considerations. The particles are illuminated with a laser sheet 1 cm wide and a thickness with a full width at half maximum (FWHM) of 150 $\mathrm{\mu }$m generated with a 4-mW laser. The imaging setup consists of a Princeton Instruments Pro-EM, EM-CCD low-light camera running at a frame rate of 30–100 frames per second and a resolution of 512 × 512–512 × 128, on which is mounted a macro-lens (Micro-Nikkor 105 mm f/2.8 lens). The 8.2-mm $\times$ 8.2-mm field of view is inside a glass cell, 2 cm², that is used to stabilize the system. Note that no particular procedure was used to generate the vortices, which were present from transition or created by parasitic heat flux. However, we cooled on the order of a few hundred microkelvins per second and waited on the order of at least tens of minutes in the superfluid state to obtain the long, straight, and relaxed vortices in which we were interested. The original movies can be downloaded from https://zenodo.org/record/2543528#.XEId3lVKhph and questions concerning them can be addressed to the corresponding author.