Thermomagnetic recording fidelity of nanometer-sized iron and implications for planetary magnetism

Significance

Extraterrestrial rocks that contain particles of iron or kamacite are thought to carry paleomagnetic recordings from the time of the formation of the Solar System. Interpretation of these recordings has hitherto falsely assumed particles were uniformly magnetized. We have reexamined the magnetic recording reliability of these minerals using numerical models that account for the more complex magnetic structures that are likely to exist and show that iron and kamacite particles are exceptionally good and thermally stable recorders of ancient magnetic fields, dominated by the recording made when iron cools through its Curie point. Additional recordings for thermal events that occur substantially below the Curie temperature will be difficult to extract from iron-dominated samples.

Abstract

Paleomagnetic observations provide valuable evidence of the strength of magnetic fields present during evolution of the Solar System. Such information provides important constraints on physical processes responsible for rapid accretion of the protoplanetesimal disk. For this purpose, magnetic recordings must be stable and resist magnetic overprints from thermal events and viscous acquisition over many billions of years. A lack of comprehensive understanding of magnetic domain structures carrying remanence has, until now, prevented accurate estimates of the uncertainty of recording fidelity in almost all paleomagnetic samples. Recent computational advances allow detailed analysis of magnetic domain structures in iron particles as a function of grain morphology, size, and temperature. Our results show that uniformly magnetized equidimensional iron particles do not provide stable recordings, but instead larger grains containing single-vortex domain structures have very large remanences and high thermal stability—both increasing rapidly with grain size. We derive curves relating magnetic thermal and temporal stability demonstrating that cubes (>35 nm) and spheres (>55 nm) are likely capable of preserving magnetic recordings from the formation of the Solar System. Additionally, we model paleomagnetic demagnetization curves for a variety of grain size distributions and find that unless a sample is dominated by grains at the superparamagnetic size boundary, the majority of remanence will block at high temperatures ($\sim \mathrm{100}\hspace{0.17em}°$C of Curie point). We conclude that iron and kamacite (low Ni content FeNi) particles are almost ideal natural recorders, assuming that there is no chemical or magnetic alteration during sampling, storage, or laboratory measurement.

Magnetic remanences recorded in meteorites and lunar samples have been used to investigate solar nebular formation (1, 2), partial planetesimal differentiation (3, 4), and the possibility of an early lunar dynamo (5–7). The magnetic recorder, Ni-poor kamacite (FeNi) (essentially metallic iron), is commonly found in such planetary materials; and due to kamacite’s chemical instability, its presence is usually seen as an indicator of potentially pristine magnetic remanences. However, for a magnetic mineral to retain an original magnetic remanence, the magnetic carriers must also be thermally stable on geological timescales.

Most of our theoretical understanding of the thermal stability of iron particles’ remanences is based on single-domain (SD) theory, which assumes that ideal magnetic recorders are magnetically uniform (8). Using Néel’s theory for SD grains, Pullaiah et al. (9) determined a series of curves (henceforth referred to as “Pullaiah curves”) that describe the thermal response of the common terrestrial magnetic recorders magnetite and hematite. Paleomagnetists use such Pullaiah curves to estimate the temporal stability of natural magnetic remanences by linking measured laboratory unblocking temperatures to theoretical room-temperature relaxation times. These curves can be used in a variety of applications, e.g., magnetic dating (10, 11) and determining the likely primary nature of magnetic remanences. With the exception of Winklhofer et al. (12) and Fabian et al. (13), all previously published Pullaiah curves found in the literature, e.g., Pullaiah et al. (9) and Garrick-Bethell and Weiss (14), are based entirely on SD theory, which does not take into account more complex magnetic domain structures such as the flower and single-vortex (SV) states (15). We know such nonuniform structures are ubiquitous in the vast majority of iron particles found in planetary materials (16–18). In fact, near-equant iron SD particles are theoretically thermally unstable at room temperature; i.e., they are superparamagnetic (19–21) with relaxation times of seconds, not billions of years.

Given that the majority of magnetic remanence carriers in iron, and likely other minerals, are SV (22), the paleomagnetic recordings that they contain can be correctly understood only by a reevaluation of their thermomagnetic stability. Can such iron particles record and retain magnetic remanences over geological timescales and do Pullaiah curves for vortex states in natural kamacite significantly deviate from those of SD grains?

A pioneering study by Winklhofer et al. (12) used a constrained micromagnetic model to calculate Pullaiah curves for magnetite for nonuniform magnetic structures. However, such constrained models make assumptions about possible transition paths (23) and may not necessarily correctly estimate the energy barriers needed to construct Pullaiah curves. Additionally the work of Winklhofer et al. (12) was limited by computers of the time, i.e., to calculating low-resolution models with only a few points for each curve.

The aim of this study is to exploit new model developments (18, 24), which allow us to quantify the thermal stability of nonuniform magnetic structures, such as those found in kamacite. These developments allow us to use unconstrained numerical micromagnetic approaches that use a nudged elastic band (NEB) algorithm to determine the thermal stability of complex nonuniform magnetic domain states (25). We determine relaxation times and thermal stability in submicrometer grains of iron as a function of grain size, shape, and temperature. We use the micromagnetic modeling package MERRILL (Micromagnetic Earth Related Robust Interpreted Language Laboratory) (26) to calculate relaxation times when producing new Pullaiah curves for realistic ferromagnetic domain states, i.e., flower and single-vortex counterparts in both spheres and cubes of iron.

Results

Domain States and Remanences.

Although all three allotropes of iron available at atmospheric pressures have a cubic crystalline form, their occurrence in the terrestrial environment is rare because of the ease with which it oxidizes or alloys with other elements. In extraterrestrial settings, pure iron is often observed in spherical morphologies (27, 28). Remanence characteristics of magnetic crystals are significantly affected by the grain morphology, and so we examine both cubic and spherical grain shapes of iron. The evolution of domain structure with grain size determined from unconstrained 3D micromagnetic models follows the well-established evolution seen in other materials (21, 29, 30) whereby the smallest particles have relaxation times of order ${\mathrm{10}}^2$ s or less and are termed superparamagnetic (SP). As particle size increases, grains become stable SD, followed by a transition to an unstable SV state and then to a stable SV state. For equidimensional cubes and iron spheres at room temperature, the critical grain size $d_0$ marks the transition from SP to SD, $d_0^{\prime }$ that from stable SD to unstable SV, and $d_1^{\prime }$ that from unstable to stable SV.

In iron, the stable SD grain size range is almost entirely absent (20, 21) with the exception of a very narrow zone from 23 nm to $25\hspace{0.17em}\mathrm{n}\mathrm{m}$ where the local energy minimum (LEM) is an SD-like flower state which switches via vortex nucleation and annihilation. The critical grain size ($d_0^{\prime }$) for iron at which the transition from an SD to an SV state occurs is at $28\hspace{0.17em}\mathrm{n}\mathrm{m}$ equivalent spherical volume diameter (ESVD) for cubes, in agreement with the previous estimate of $24\hspace{0.17em}\mathrm{n}\mathrm{m}$ edge length by Muxworthy and Williams (21), and $25\hspace{0.17em}\mathrm{n}\mathrm{m}$ for spheres. However, SV grains at or just below the $d_0^{\prime }$ threshold are not thermally stable. Indeed, we find that the smallest stable SV domain states are at $32\hspace{0.17em}\mathrm{n}\mathrm{m}$ (ESVD) for cubes and $43\hspace{0.17em}\mathrm{n}\mathrm{m}$ for spheres.

The SV state can also be further classified according to the alignment of the vortex core relative to the crystalline anisotropy axis. In equidimensional grains the transition from SD to SV initially favors a vortex core aligned with the hard axis (HSV), which like its counterpart seen in magnetite (24) is only weakly stable. At larger grain sizes the easy-aligned vortex (ESV) state dominates over a large grain size range and ESV states remain the lowest-energy state up to at least $200\hspace{0.17em}\mathrm{n}\mathrm{m}$, which is the largest grain size modeled in this study. Experimental observations indicate the SV states can be nucleated in substantially larger grains still (18).

If SV states are to contribute substantially to the paleomagnetic signal in rocks, then each SV grain must contribute a significant net remanence. To this end we calculate the average net remanence at $20\hspace{0.17em}°\mathrm{C}$ as a function of grain size determined by averaging the domain state magnetizations from 100 solutions (with random initial magnetization) per grain size (Fig. 1). The most significant observation from Fig. 1A is that throughout the SV grain size range the remanence per particle increases monotonically for spheres. Given that the SD size range in iron is very restricted, it follows that SV grains provide both a large and a stable remanence and are therefore almost certainly the dominant source of remanence in lunar and meteoritic samples whenever spherical particles of iron or kamacite are the primary magnetic mineral.

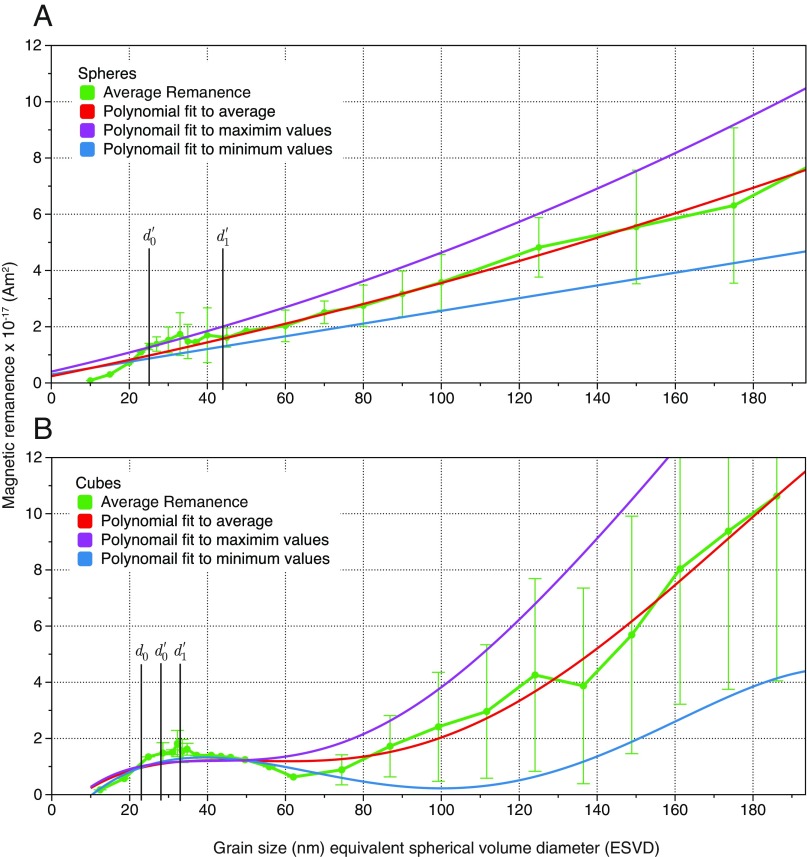
Fig. 1.

(A and B) Average magnetic remanence of iron as a function of grain size for (A) spheres and (B) cubes (green curve and error bars). The curves were determined from 100 LEM solutions each from a different random initial magnetic state. The magenta, red, and blue curves are best-fit polynomial for the average, plus one SD and minus one SD, respectively.

The behavior for cubes of iron is somewhat more complicated. Grains smaller than $d_0^{\prime }$ are in a near uniform domain sate, and so we expect the remanence of each grain to increase as $d^3$, which is what we observe. In this SD range, the remanence of cubes and spheres should have near identical values when plotted in ESVD units. Grains slightly larger than $d_0^{\prime }$ are in an unstable SV state, with the lowest-energy state having the vortex core paradoxically aligned with the hard crystalline axis (HSV). However, the energies of the easy-aligned vortex cores (ESV) are not predicted to be significantly higher than those of the hard-aligned vortex cores, and so both states are accessible, with a low-energy barrier between them. As a result, grains in this region are SP at room temperature so that $d_0^{\prime }<d_1^{\prime }$ with respect to thermal stability. The ESV and HSV states have different remanences due to the slight deformation of the vortex core in response to the crystalline anisotropy. Additionally for cubes, the core axis length varies with direction (cubic diagonals vs. edges). Because of this, the SD of remanence (${\sigma }_{\mathrm{r}}$) increases as seen at about $30\hspace{0.17em}\mathrm{n}\mathrm{m}$ grain size for both cubes and spheres.

Cubic grains larger than $33.5\hspace{0.17em}\mathrm{n}\mathrm{m}$ have only one stable state which is the ESV state, resulting in two distinct features of the remanence curve in Fig. 1B: first, the dramatic decrease in ${\sigma }_{\mathrm{r}}$ as expected (as the hard axis states are no longer easily accessible) and second, the decrease in average remanence value. The decrease is caused by the ESV core that carries the remanence aligning along the cube’s $⟨100⟩$ easy directions, which are shorter than those of the HSV $⟨111⟩$ aligned core by a factor of $\sqrt{3}$, and so a net decrease in remanence is expected. In cubes larger than 60 nm, ${\sigma }_{\mathrm{r}}$ increases dramatically with grain size, marking the transition from simple symmetrical SV domain states to more complex twisted vortex states (31), where both the grain shape and crystalline anisotropy play an increasingly important part in determining both the number and form of the domain states that can be nucleated. Although still dominated by vortex-like structures, the increasing multiplicity and asymmetry of domain states that can be nucleated beyond 60 nm can be thought of as the slow transition toward a multidomain (MD) state. During this transition, the vortex cores distort along the hard crystalline directions and eventually evolve into domain walls.

While we would not expect to see a decrease in remanence with grain size in spherical grains (because the core length is direction invariant), we might have expected to see a decrease in ${\sigma }_{\mathrm{r}}$ when the ESV state dominates. However, spheres, unlike cubes, do not have a shape that mirrors the crystalline anisotropy, and so preference of alignment of the vortex core along the easy crystalline axis is much weaker in spheres and their vortex cores often align in random directions in the HSV to ESV grain size range.

Despite the increasing variance of the remanence with grain size in both spheres and cubes, the curves shown in Fig. 1 indicate that in most lunar and meteoritic samples where iron or kamacite is the dominant magnetic mineral, the primary carrier of magnetic remanence will be SV domain states and that these provide both high remanence and high thermal and temporal stability, a result unexpected from SD theory.

Thermal and Temporal Stability.

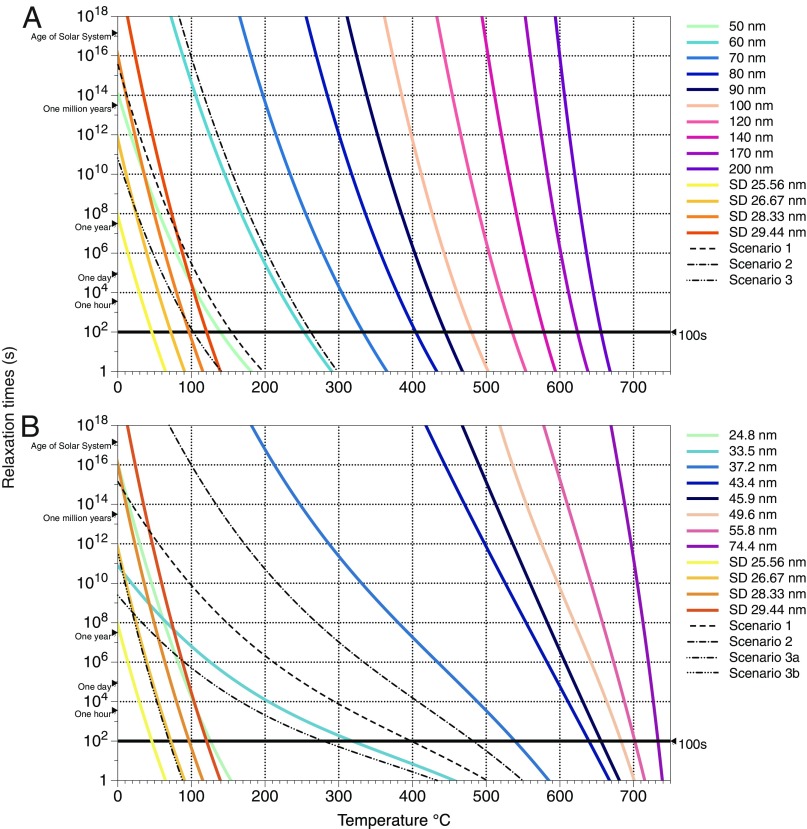
Using similar NEB calculations to those we have previously applied (18, 24, 30), we determined energy barriers between various LEM states and calculated Pullaiah curves with relaxation times for both cubic and spherical iron grains. Fig. 2A shows the relaxation times for small iron spheres up to 200 nm, and Fig. 2B shows the same for small iron cubes up to 75 nm ESVD. On each graph we have superimposed the relaxation times calculated analytically (Eq. 1) for ideal SD iron up to 30 nm (ESVD) using

$$\tau \left(T\right)={\tau }_0\exp \left(\frac{2}{3}\frac{v\left|K_1\left(T\right)\right|}{k_{\mathrm{B}}T}\right),$$ [1]

where $\tau$ is the relaxation time at temperature $T$ (in degrees kelvin), ${\tau }_0$ is the switching time, $v$ is the particle volume, $K_1$ is the temperature-parameterized magneto-crystalline anisotropy constant, and $k_{\mathrm{B}}$ is Boltzmann’s constant. These times are calculated purely based on the energy barrier that results from the cubic magneto-crystalline anisotropy; we neglect the microscopic coercivity due to the self-demagnetizing field because of the particle symmetry of both cubes and spheres.

Fig. 2.

(A and B) Pullaiah curves for small spherical (A) and cubic (B) grains of iron through the SD and SV grain size range that shows the relationship between the temporal and thermal stabilities of magnetization. Heating a sample and noting the temperature at which it loses its magnetization can therefore tell us the age of remanence acquisition. In B the sizes are ESVD. The dashed lines are the interpolated Pullaiah curves (using Eq. 8) that determine the blocking temperatures and maximum affected grain sizes for the remagnetization scenarios listed in Table 1.

There are a number of key observations to be made from Fig. 2 A and B. First, we observe that iron exhibiting SD domain structures, i.e., both flower-state micromagnetic models (24.8 nm model in Fig. 2B) and the analytical ideal-SD particle calculations (yellow-orange lines on left side in Fig. 2 A and B) are poor thermal recorders that behave superparamagnetically at relatively low temperatures in agreement with the literature [e.g., Kneller and Luborsky (19), Butler and Banerjee (20), and Muxworthy and Williams (21)]. The analytic calculations made for grain sizes from $25\hspace{0.17em}\mathrm{n}\mathrm{m}$ to $30\hspace{0.17em}\mathrm{n}\mathrm{m}$ are necessarily constrained to be in an SD state, and in reality these are all above the critical grain size and would exist only in SV domain states.

Second, we find that the smaller iron particles containing SV domain states are also relatively poor magnetic recorders. The stability decreases very quickly with grain size so that we observe SP behavior for grain sizes below $\sim 43\hspace{0.17em}\mathrm{n}\mathrm{m}$ and below $\sim 32\hspace{0.17em}\mathrm{n}\mathrm{m}$ ESVD in spheres and cubes, respectively (Fig. 2). There is a change in the gradient of the Pullaiah curves for SD and SV that reflects the different domain states and switching mechanisms. The result is that small SV grains have lower temporal, but higher thermal stability. In spheres the energy barrier between LEM states is traversed by simple rotation of the vortex structure so that the contribution from the exchange and self-demagnetizing energies to the energy barrier is zero, leaving magneto-crystalline anisotropy as the sole remaining term controlling thermal blocking in small iron spheres.

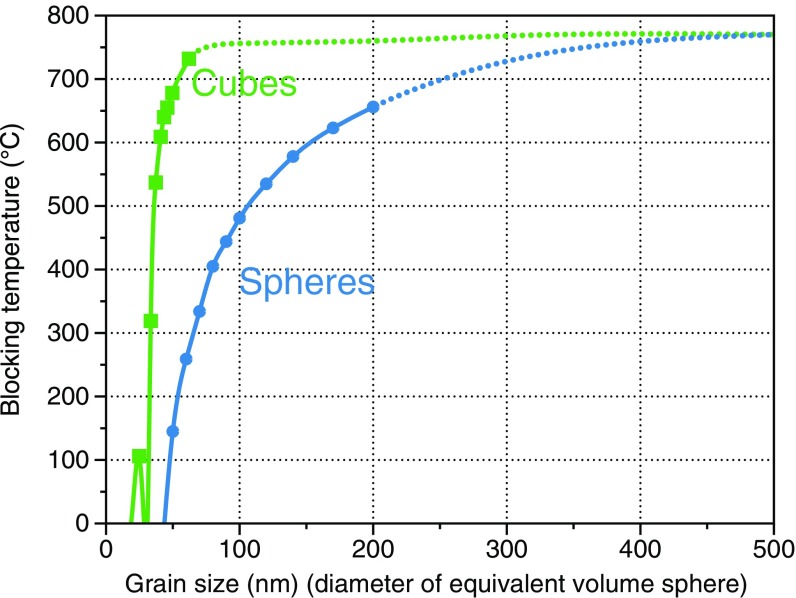
Small iron cubes are again more complex than spheres of the same nominal size. The primary mechanism by which SV states traverse energy barriers is by structure coherent rotation (SCR) (24). In this case the domain structure changes slightly during reversal owing to configurational anisotropy (32) caused by the interaction of domain structures with grain shapes. In SCR, in addition to the magneto-crystalline anisotropy, both the exchange and demagnetizing energies play a crucial role in controlling the height of the energy barrier between LEM states. The smallest iron cube that we modeled ($24.8\hspace{0.17em}\mathrm{n}\mathrm{m}$) contains a flower-domain state that behaves similarly to the 25.5-$\mathrm{n}\mathrm{m}$ ideal-SD case except that its relaxation gradient is slightly lower. The 33.5-$\mathrm{n}\mathrm{m}$ state is unstable, entering the superparamagnetic regime above $\sim 325\hspace{0.17em}°\mathrm{C}$. Domain states just below this (from $25\hspace{0.17em}\mathrm{n}\mathrm{m}$ to $31\hspace{0.17em}\mathrm{n}\mathrm{m}$) comprise multiple possible LEM structures, both easy axis and hard axis aligned vortices, with free energy values very near to each other and with relatively low energy barriers between domain states. At $33.5\hspace{0.17em}\mathrm{n}\mathrm{m}$ and beyond, the ESV state prevails and the barrier increases steadily with grain size. Thus, by $\sim 43\hspace{0.17em}\mathrm{n}\mathrm{m}$ we observe blocking temperatures of $\sim 640\hspace{0.17em}°\mathrm{C}$ (Fig. 3) and by $74.4\hspace{0.17em}\mathrm{n}\mathrm{m}$ temperatures of $\sim 745\hspace{0.17em}°\mathrm{C}$ (compared with $\sim 370\hspace{0.17em}°\mathrm{C}$ for similar-sized spheres).

Fig. 3.

Blocking temperatures for small cubic (green) and spherical (blue) grains of iron. The small peak observed at the start of the cubic blocking temperature curve corresponds to a narrow unstable zone of hard-axis aligned single vortices (HSV) that mark the transition between stable SD and stable SV domain states (24, 30). The dotted lines are extrapolations of blocking temperature beyond the size range for which full micromagnetic computations were performed.

We summarize the blocking temperatures in Fig. 3, in which the stark difference between the thermal behaviors of spheres and cubes can be seen. For cubes we observe an initial unstable region as the switching regime changes from SD, to flower, and then to SV. Once this zone is traversed, there is a very rapid increase in blocking temperature. Spheres on the other hand do not exhibit an unstable region at room temperature, and the increase in blocking temperature is relatively smooth, following a pattern similar to what would be expected for SD rotation.

Simulated Remanent Magnetization and Thermal Demagnetization.

Thermal demagnetization curves can be used to estimate the range of thermomagnetic responses from distributions of iron cubes and spheres. From these, we can assess the ability of meteorites and lunar samples to hold a recording of the intensity of one or more components of a paleomagnetic field.

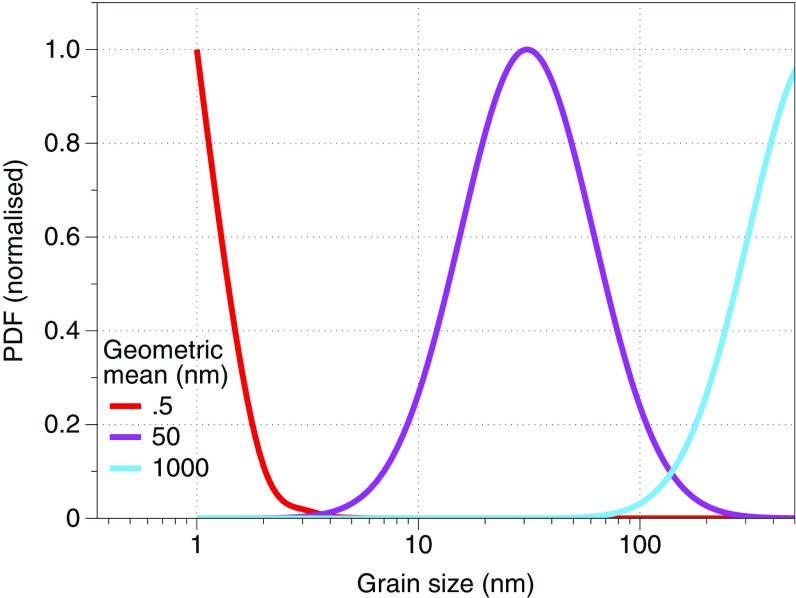
We constructed simulated remanent magnetizations (SiRMs) from the range of LEM domain states found from random initial states. The SiRM cannot be said to be a true thermomagnetic remanence (TRM) as we do not simulate cooling in an external field. In a true TRM the remanence is fixed by the fraction of the domain states that are aligned with the external field at their blocking temperature $T_{\mathrm{b}}$, although the remanence continues to grow below $T_{\mathrm{b}}$ with $M_{\mathrm{s}}\left(T\right)$. For uniaxial SD grains Neél (8, 33) calculated this fractional alignment as proportional to $\tanh \left(E_{\mathrm{m}}\left(v\right)/k_{\mathrm{B}}{T}_{\mathrm{b}}\right).$ Because a grain’s magnetic energy ($E_{\mathrm{m}}$) increases much faster with grain volume than $T_{\mathrm{b}}$, the equation implies that the fractional alignment will increase with grain size. We expect a similar relationship for SV grains, although this has not yet been fully established. In our model we make the simplification that the fractional alignment of the domain states is constant for all grain sizes and that remanences of each grain are all aligned parallel to each other (they are saturated). The remanence attributed to any one grain size is simply the average magnetization from 100 random initial states. The SiRM will still have many of the characteristics of a TRM in terms of the expected demagnetizing (zero field) blocking temperature spectrum. In calculating the SiRMs, the relative number of particles of each grain size was chosen from the probability density function of a log-normal distribution of grain sizes (see Fig. 5). The stepwise thermal demagnetization of the SiRM is then simply determined from which grains would remain blocked after heating to a given temperature according to the blocking temperature curves of Fig. 3.

Fig. 5.

Probability density functions for log-normal grain size distributions used to determine the simulated demagnetization curves in Fig. 4.

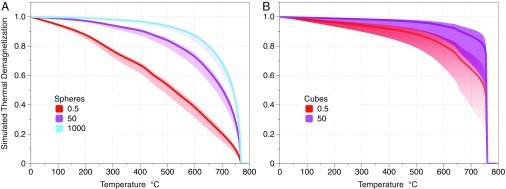
It is important to note that although we have extrapolated grain remanences and blocking temperatures for grains much larger than those for which we have full micromagnetic simulations, the resulting uncertainties in the shape of the thermal demagnetization of the SiRM curves will be restricted to the relatively small region corresponding to temperatures above the maximum calculated blocking temperatures of $730\hspace{0.17em}°\mathrm{C}$ for iron cubes and $656\hspace{0.17em}°\mathrm{C}$ for iron spheres. The predicted SiRM demagnetization curves are shown in Fig. 4 for a range of assumed log-normal distributions (Fig. 5). Each curve in Fig. 4 has a shaded region representing the $\pm {\sigma }_{\mathrm{r}}$ influence of the remanence curve uncertainties shown in Fig. 1.

Fig. 4.

(A and B) The simulated stepwise thermal demagnetization curves for different distributions of (A) spherical and (B) cubic grains of iron. The line and the shaded area on each graph show the predicted demagnetization curve for the best-fit polynomial to the mean remanence and one SD (Fig. 1).

The grain size distributions shown in Fig. 5 all have the same SD of ${\sigma }_d=\log \left(2\right)$, but with various geometric means (medians) from $\tilde{d}=0.5\hspace{0.17em}\mathrm{n}\mathrm{m}$ to $\tilde{d}=\mathrm{1,000}\hspace{0.17em}\mathrm{n}\mathrm{m}$. A distribution with a median of $0.5\hspace{0.17em}\mathrm{n}\mathrm{m}$ is clearly dominated by SP grains with a small percentage of stable SD and SV states. It is only these stable domain states that contribute to the remanence, and for this reason it is possible to distinguish remanence contributions from relatively large grains: For example, the relative population of stable ESV spheres at grain sizes $50\hspace{0.17em}\mathrm{n}\mathrm{m}$ compared with $400\hspace{0.17em}\mathrm{n}\mathrm{m}$ falls only by a factor of $\sim$10, so that these larger grains still make a significant contribution to the observed remanence. At the other extreme, the distribution with $\tilde{d}=\mathrm{1,000}\hspace{0.17em}\mathrm{n}\mathrm{m}$ is dominated by low-remanence MD grains (assumed zero in our model) and thus does not contribute to the observed sample magnetization.

Discussion

Discriminating Primary and Secondary Remanences.

As stated in the first two sections of Results, it has been known for some time that the SD grain size range for iron is vanishingly small (20, 21) so that the remanence is carried by the larger inhomogeneously magnetized particles, previously called “pseudosingle-domain” (PSD) grains. The exact nature of the remanence of PSD states remained poorly understood (34, 35), until the advent of unconstrained 3D micromagnetic modeling (36, 37) which identified vortex domain structures. These were suggested as the cause of “PSD” behavior by refs. 12 and 38. Only recently has it been possible to attempt a comprehensive estimate of their thermal stability (18, 24, 30). As a consequence, the interpretation of paleomagnetic signals has hitherto been done on the basis of SD theory even though it has long been acknowledged that SD particles are unlikely to be the dominant remanence carriers (22).

Nagy et al. (24) demonstrated that SV domain states provide surprisingly high temporal and thermal stability, even in excess of that of SD grains that were until recently generally regarded as “ideal” magnetic recorders. What we have shown in this paper in the case of iron is that not only do SV domain states have high thermal and temporal stability, but also the remanence grows steadily with size, so that SV states will likely dominate the observed remanence in lunar rocks and chondritic meteorites where iron or kamacite is the major magnetic mineral.

The remanence and blocking temperature calculations provide the means for constructing simulated remanence and stepwise thermal demagnetization curves which can provide an insight into the ability of assemblages of iron particles to accurately record a thermomagnetic remanence and to what extent this type of natural remanent magnetization (NRM) might be susceptible to secondary viscous remanent magnetization (VRM) and/or thermo-viscous (TVRM) overprinting.

We have constructed simulated remanence curves for a wide range of possible grain size distributions. The distribution of smallest grains ($\tilde{d}=0.5\hspace{0.17em}\mathrm{n}\mathrm{m}$) is dominated by grains at the SD–SV boundary ($d_0^{\prime }$) where only the finest SV particles contribute to the signal. Only in this case do we observe a relatively smooth decay of magnetization between room temperature and the Curie point. In all other grain distributions and for all cubic grains (which exhibit the sharpest increase in blocking temperature with grain size), the SiRM remanence remains blocked to within a few tens of degrees of the Curie point. In natural samples therefore we would normally expect most of the remanence to be blocked within $\hspace{0.17em}100\hspace{0.17em}°\mathrm{C}$ of the Curie point.

Experimental evidence in support of the prevalence of high–blocking-temperature demagnetization curves is difficult to find because of the ease with which iron oxidizes on heating and the difficulty in most laboratories to achieve the high temperatures required. In fact, many of the published thermal demagnetizing curves for iron show evidence of chemical alteration, with nonreversible heating curves and Curie points well below the expected value of $770\hspace{0.17em}°\mathrm{C}$. Indeed, they commonly display a $580\hspace{0.17em}°\mathrm{C}$ magnetite Curie point [e.g., Lawrence et al. (6), Wasilewski (28), Grommé et al. (39), and Helsley (40)]. However, Lawrence et al. (6) did have a single specimen with apparent blocking temperatures up to $770\hspace{0.17em}°\mathrm{C}$.

Because the average stability of SV domain states increases with grain size and for nonspherical grains, we would expect characteristic demagnetization curves in most lunar and meteoritic samples to be dominated by the high–unblocking-temperature particles. The implication is that most extraterrestrial material that is free from oxidation should be dominated by its primary remanence, with any secondary VRM or TVRM component accounting for a small fraction of the observed sample magnetization. This conclusion differs from that of Garrick-Bethell and Weiss (14) who used classical SD theory and obtained a much broader spectrum of blocking temperatures. They suggested that lunar rocks would be capable of recording secondary remanences arising from (i) shallow burial below the lunar surface, $-20\hspace{0.17em}°\mathrm{C}$ for 1 billion y; (ii) lunar surface exposure where it experienced diurnal solar heating, $100\hspace{0.17em}°\mathrm{C}$ for 300 $\mathrm{M}\mathrm{y}$, and finally (iii) Earth storage of lunar rocks at $20\hspace{0.17em}°\mathrm{C}$ for 10 y (14). Using our calculated Pullaiah curves (Fig. 2), we can predict the maximum temperature required to remove each of the VRM and TVRM secondary overprints shown in Table 1.

Table 1.

Laboratory heating needed to remove TVRMs from three different scenarios, along with the maximum-size grain each TVRM will remagnetize

			Temperature, $°\mathrm{C}$,required to remove overprint within $100\hspace{0.17em}\mathrm{s}$		Maximum grain size affected, $\mathrm{n}\mathrm{m}$
Scenario	TVRM scenario	Acquisition time and temperature, $°\mathrm{C}$	Spheres	Cubes	Spheres	Cubes
1	Burial below lunar surface	1 billion y $\left(3.15\times 10^{16}\hspace{0.17em}\mathrm{s}\right)$ at $-20\hspace{0.17em}°\mathrm{C}$	155	400	51	34.5
2	Diurnal heating on the lunar surface	300 million y $\left(9.46\times 10^{15}\hspace{0.17em}\mathrm{s}\right)$ at $100\hspace{0.17em}°\mathrm{C}$	265	485	61.2	35.4
3	Sample storage on Earth	10 y $\left(3.15\times 10^8\hspace{0.17em}\mathrm{s}\right)$ at $20\hspace{0.17em}°\mathrm{C}$	105	280 (i), 75 (ii)	$<d_1$	$<d_1$

Note that for scenario 3 the demagnetizing temperatures quoted are for two possible domain states: (i) flower and (ii) easy-aligned single vortex.

Our Pullaiah curves indicate that in theory it is possible that secondary overprints may dominate the thermal demagnetization curves, and thus the Arai plots of any Thellier-type paleointensity experiment, up to temperatures of about $485\hspace{0.17em}°\mathrm{C}$. However, these overprints occupy very different blocking temperature ranges in cubes and spheres, so that it may be impossible to separate different VRM components in samples which have a range of grain morphologies. More importantly, we can see from the simulated thermal demagnetization curves (Fig. 4) that, with the exception of the smallest grain size distribution with $\tilde{d}=0.5\hspace{0.17em}\mathrm{n}\mathrm{m}$, grains with blocking temperatures of less than $485\hspace{0.17em}°\mathrm{C}$ in cubes and $265\hspace{0.17em}°\mathrm{C}$ in spheres account for less than $0.05\%$ of the total NRM. Even for a grain distribution with $\tilde{d}=0.5\hspace{0.17em}\mathrm{n}\mathrm{m}$ a significant fraction of the NRM is overprinted only for spherical grains. The conclusions must therefore be that lunar and meteoritic samples could be exceptionally good paleomagnetic recorders, which are unlikely to acquire a significant overprint from a VRM or TVRM process relevant to the geological settings of lunar samples.

Paleointensities and Chemical Alteration.

We are left with the problem that many lunar samples demonstrate significant low-temperature components with nearly all being completely unblocked by $\sim 580\hspace{0.17em}°$C (39, 41, 42), and, assuming this alteration occurs via a grain surface process leaving a core-shell structure (43), then the residual iron particles will be of a smaller size and thus also lower blocking temperature. We note, however, that Strangway et al. (44) suggested that many lunar samples were likely to have been exposed to moderate magnetic fields on return from the moon and Lawrence et al. (6) demonstrated that such samples were unlikely to preserve a pristine TRM.

In the terrestrial environment, pure iron readily oxidizes so that thermal demagnetization experiments are extremely likely to fail even when attempted in vacuum or inert atmospheres (18). We suspect that many published thermal demagnetization curves or Arai plots for lunar and meteoritic samples will be contaminated by chemical alteration.

The question remains as to whether it is possible to extract reliable paleointensities from these samples which have a high magnetic recording fidelity, but are exceptionally susceptible to thermochemical alteration. The answer is likely to reside in nonheating methods, but such techniques have been attempted several times with limited success (45–47). Such methods usually either rely on SD theory (48) or require construction of a transfer function between coercivities and blocking temperature (based on a derived “calibration factor”). This transfer function depends on the exact mineralogy and grain size distribution and critically on the magnetic domain structure that the grains contain. Hitherto a purely phenomenological approach has been taken where calibration factors have been assigned to certain rock types. These approaches can only ever be first-order approximations with poorly defined uncertainties given a lack of rigorous theoretical understanding of the underlying physical processes involved.

Conclusions

Butler and Banerjee (20) concluded that the proportion of stable naturally occurring magnetically single-domain, iron grains is extremely small. Although their purely analytical results systematically underestimated the critical grain size for the SD/SV transition region (21), this conclusion remains valid. We have shown here that SV domain states offer both high magnetic remanence and high magnetic stability and offer the possibility of holding a thermomagnetic recording over periods from the beginning of the Solar System. Thermomagnetic demagnetization curves are predicted to be dominated by high blocking temperatures with at least $80\%$ of the remanence remaining until within $100\hspace{0.17em}°\mathrm{C}$ of the Curie point. This also implies that most meteoritic and lunar samples where iron or kamacite is the dominant magnetic mineral should contain a high-fidelity recording of an ancient magnetic field and be largely resistant to secondary TVRM overprints.

However, the high-fidelity recording of iron particles remains tantalizingly out of reach using normal laboratory observations due to the ease with which iron particles thermochemically alter. Nonheating paleointensity methods may be the only way to access the paleomagnetic recordings in iron particles, and micromagnetic calculations such as those outlined in this study could eventually establish a complete theory to derive accurate transfer functions between coercivities and blocking temperatures for SV grains. This would significantly increase the reliability of nonheating paleointensity methods. The exposure of many lunar samples to moderate magnetic fields after sampling, however, remains a problem.

Materials and Methods

Calculation of Blocking Temperatures and Relaxation Times.

Numerical micromagnetic modeling (26, 49, 50) is used to calculate the magnetization, $\overrightarrow{m}\left(\overrightarrow{x}\right)=\left(m_x\left(x,y,z\right),m_y\left(x,y,z\right),m_z\left(x,y,z\right)\right)$, of a magnetic material denoted by $\mathrm{\Omega }$ with $\left(x,y,z\right)\in \mathrm{\Omega }$. This technique divides the total energy, $E_{\mathrm{t}\mathrm{o}\mathrm{t}}$, resulting from the magnetization into four components: the exchange $E_{\mathrm{e}}$, demagnetizing $E_{\mathrm{d}}$, magneto-crystalline aniosotrpy $E_{\mathrm{a}}$, and external (Zeeman) $E_{\mathrm{z}}$ energies, according to the equations

$$E_{\mathrm{e}}=A\left(T\right){\int }_{\mathrm{\Omega }}\left[{\left(\nabla m_x\right)}^2+{\left(\nabla m_y\right)}^2+{\left(\nabla m_z\right)}^2\right]\hspace{0.17em}d\overrightarrow{x},$$ [2]

$$E_{\mathrm{d}}=-\frac{M_{\mathrm{s}}\left(T\right)}{2}{\int }_{\mathrm{\Omega }}{\overrightarrow{H}}_{\mathrm{d}}\cdot \overrightarrow{m}\hspace{0.17em}d\overrightarrow{x},$$ [3]

$$E_{\mathrm{a}}=K_1\left(T\right){\int }_{\mathrm{\Omega }}\left[m_x^2{m}_y^2+m_x^2{m}_z^2+m_y^2{m}_z^2\right]\hspace{0.17em}d\overrightarrow{x},$$ [4]

$$E_{\mathrm{z}}=-M_{\mathrm{s}}\left(T\right){\int }_{\mathrm{\Omega }}{\overrightarrow{H}}_z\cdot \overrightarrow{m}\hspace{0.17em}d\overrightarrow{x},$$ [5]

where $A\left(T\right)$, $M_{\mathrm{s}}\left(T\right)$, and $K_1\left(T\right)$ are the temperature-dependent exchange, saturation magnetization, and magneto-crystalline anisotropy constants, respectively (below), with $H_{\mathrm{d}}$ the demagnetizing field and $H_{\mathrm{z}}$ the externally applied Zeeman field. The total energy $E_{\mathrm{t}\mathrm{o}\mathrm{t}}$ is the sum of Eqs. 2–5.

Magnetization configurations ($\overrightarrow{m}$) that minimize $E_{\mathrm{t}\mathrm{o}\mathrm{t}}$ correspond to stable magnetization structures. In general, it is not possible to find analytical expressions for $\overrightarrow{m}$ that minimize $E_{\mathrm{t}\mathrm{o}\mathrm{t}}$, and so the region $\mathrm{\Omega }$ is subdivided into tetrahedral elements and $\overrightarrow{m}$ is spatially sampled at the $n$ points comprising tetrahedra vertices. $E_{\mathrm{t}\mathrm{o}\mathrm{t}}$ then describes a 3$n$ dimensional energy landscape with respect to the three components of the magnetization; the task of micromagnetic algorithms is then to find magnetization structures that correspond to LEMs of this landscape. The total energy itself is calculated as the sum of partial energy contributions over each element, where the magnetization is assumed to vary linearly. The size of the elements is controlled by the exchange length ${\ell }_{\mathrm{e}\mathrm{x}}$ (31, 51), and below this size (taken as the average length of the side of a tetrahedral element) magnetization fields resemble uniform domains and no longer capture complex magnetization structure. Eq. 5 outlines the expression used for exchange length with exchange $A\left(T\right)$ and saturation magnetization $M_{\mathrm{s}}\left(T\right)$ outlined below as

$${\ell }_{\mathrm{e}\mathrm{x}}=\sqrt{\frac{A\left(T\right)}{{\mu }_0{M}_{\mathrm{s}}{\left(T\right)}^2/2}},$$ [6]

where ${\mu }_0$ is the permeability of free space. Numerical values of $A\left(T\right)$ and $M_{\mathrm{s}}\left(T\right)$ are detailed in ref. 26.

Relaxation Time and Blocking Temperatures.

The NEB method (25, 52–54) is used to calculate energy barriers between any two LEM states (18, 24, 30). The magnetization $\overrightarrow{m}$ at a given temperature results in a high-dimensional energy surface using Eqs. 1–4. Some configurations of $\overrightarrow{m}$ correspond to wells in the energy landscape, which are stable magnetization structures. The blocking temperatures may then be approximated by calculating the energy barrier between these LEM states determined by the NEB method. To calculate blocking temperatures and relaxation times we use the Neél–Arrhenius (8) relation that equates the magnitude of an energy barrier with the relaxation time

$$\tau \left(T\right)={\tau }_0\exp \left(\frac{\mathrm{\Delta }E}{k_{\mathrm{B}}T}\right),$$ [7]

where ${\tau }_0$ is the atomic reorganization time taken to be $\approx 10^{-9}$ (55), $\mathrm{\Delta }E$ is the size of the energy barrier required to transition from one LEM state to another in joules, $k_{\mathrm{B}}$ is Boltzmann’s constant, and $T$ is the temperature in degrees kelvin. Note that the relaxation times will be reduced by the degeneracy of the minimum energy paths by which the domain can switch. For a cubic crystalline symmetry this may be of the order of 4, but will also depend upon the grain symmetry. Given the uncertainly in ${\tau }_0$ and that in determining the exact degeneracy, we have chosen simply to state the relaxation time for a single energy barrier; it should be noted that the actual relaxation times observed might be lower by a factor of typically 1–8.

Once relaxation times $\tau \left(T\right)$ have been calculated for the complete temperature range (from $293\hspace{0.17em}°\mathrm{K}$ to $\mathrm{1,038}\hspace{0.17em}°\mathrm{K}$), it is a simple task to calculate the blocking temperature by selecting a reference relaxation time, typically a laboratory timescale (we take ${\tau }_{\mathrm{r}\mathrm{e}\mathrm{f}}=100\hspace{0.17em}\mathrm{s}$ in this study), and interpolating $T$ to the temperature that corresponds to $\tau \left(T\right)={\tau }_{\mathrm{r}\mathrm{e}\mathrm{f}}$.

Pullaiah Curve Interpolation.

The following function was used to obtain the scenarios in Table 1 (dashed curves in Fig. 2) by interpolating between any two curves representing given sizes $S_1$ and $S_2$ on a Pullaiah diagram,

$$P\left(T\right)=P_1\left(T\right)+\left(\frac{S-S_1}{S_2-S_1}\right)\left(P_2\left(T\right)-P_1\left(T\right)\right),$$ [8]

where $S$ is a chosen size between $S_1$ and $S_2$; $P_1\left(T\right)$ and $P_2\left(T\right)$ are the polynomials representing the Pullaiah curves at size $S_1$ and $S_2$, respectively; and $P\left(T\right)$ is the interpolated line between $P_1\left(T\right)$ and $P_2\left(T\right)$.