Abstract
The response of colloidal particles to a light-controlled external temperature field can be harnessed for opto-thermophoretic manipulation of the particles. The thermoelectric effect is regarded as the driving force for thermophoretic trapping of particles at the light-irradiated hot region, which is thus limited to ionic liquids. Herein, we achieve opto-thermophoretic manipulation of colloidal particles in various non-ionic liquids, including water, ethanol, isopropyl alcohol and 1-butanol, and establish the physical mechanism of the manipulation at the molecular level. We reveal that the non-ionic driving force originates from a layered structure of solvent molecules at the particle-solvent interface, which is supported by molecular dynamics simulations. Furthermore, the effects of hydrophilicity, solvent type, and ionic strength on the layered interfacial structures and thus the trapping stability of particles are investigated, providing molecular-level insight into thermophoresis and guidance on interfacial engineering for optothermal manipulation.
Graphical Abstract

INTRODUCTION
Manipulation of colloidal particles under external fields such as electric fields,1–3 magnetic fields,4 and light fields5–8 have spurred a myriad of scientific research and applications. Optical manipulation techniques are intriguing due to the versatile non-contact control of various colloidal particles, including quantum dots,9 dielectric particles,10 and metal particles.11–13 However, optical tweezers require rigorous optics and high optical power. Plasmonic tweezers have emerged as a manipulation technique with low-power and simple optics.14–17 However, plasmonic tweezers often rely on immobilized metal nanostructures, which lack the capability for dynamic manipulation.18
Recent years have witnessed tremendous efforts in exploiting thermophoretic forces for optical-based manipulation.19–24 Confinement and control of single nanoparticles have been achieved with dynamic temperature fields by Cichos’s group.21–22 Non-invasive thermophoretic transport of molecules including DNAs and vesicles has been recently of particular interest to the community of optothermal manipuation.19–20, 23–24 In response to an optically controlled temperature gradient ∇T, colloidal particles undergo thermophoresis and migrate to either the cold or the hot region with a drift velocity u = −DT∇T, where DT is the thermophoretic mobility. Opto-thermophoretic tweezers enable versatile low-power manipulation of colloidal particles and living cells.25–29 The key to opto-thermophoretic trapping is realization of a negative sign of DT that drives colloidal particles from the cold to hot region. However, the system-specific thermophoretic drift of colloidal particles has not been fully understood, resulting in variable manipulation scenarios depending on various parameters such as temperature, ionic strength of solutions, surface chemistry of particles and solute concentrations.30–31
Thermoelectricity is considered as a driving force for particle migration and opto-thermal manipulation.32–36 It is induced by thermal diffusion and spatial separation of dissolved ions in an ionic liquid under a temperature gradient field. Wurger et al. proposed a general opto-thermal system, in which surface “thermocharge” accumulation under a local temperature field leads to a thermoelectric field that can be used to concentrate or deplete colloidal particles at the thermal hot spot.34 However, previous studies of thermophoresis in the fluidic systems of low ionic strength and low acidity reveal the existence of non-ionic effects.37–39 Putnam et al. observed an intrinsic negative DT for carboxyl particles in LiCl electrolyte at a low ionic strength, which arises from local excess enthalpy at the particle-solvent interface.37 Piazza et al. observed a negative DT for proteins at a low temperature, which is attributed to hydrophobic interactions at the protein-solvent interface.38 We have recently reported the cold-to-hot migration of colloidal particles under light-generated temperature gradient field in water.27, 40 However, the applicability of the opto-thermophoretic tweezers to different solvents has remained unknown.
Herein, we report opto-thermophoretic manipulation of colloidal particles in various non-ionic liquids, including water, ethanol, isopropyl alcohol (IPA) and 1-butanol, and establish the working principle of opto-thermophoretic tweezers at the molecular level. Our experiments and molecular dynamics (MD) simulations reveal that thermophoretic trapping is driven by the entropy at the particle-liquid interface, with a minor effect from the dispersion force. The trapping stability of particles can be improved by tuning the particle hydrophilicity, solvent type and ionic strength that determine the layered structure of solvent molecules at the particle surface. We have further achieved opto-thermophoretic trapping, rotation and translation of silver nanowires (AgNWs) at a low optical power. This work demonstrates the applicability of opto-thermophoretic tweezers to a broad range of colloidal systems.
METHODS
Materials and Sample Preparation
The optothermal substrates were prepared by depositing 4.5 nm Au thin films on glass coverslips with thermal deposition (Denton thermal evaporator, base pressure: 10−5 Torr) followed by thermal annealing at 550 °C in air for 2 hours. The polystyrene (500 nm, 1 μm and 2 μm in diameter) and silica spheres (1 μm and 2 μm in diameter) were purchased from Bangs Laboratories. De-ionized water from a Milli-Q water purification system (resistivity 18.2 MΩ·cm at 25 °C) was used. Methanol, ethanol, isopropyl alcohol and 1-butanol with ACS grade were purchased from Fisher Scientific. As-purchased polystyrene and silica sphere solutions were dried at 25 °C and 80 °C for overnight using a convection oven, which were re-dispersed in different solvents with a volume ratio of 1:1000 (particle:solvent).
Hydrophobic modification of silica spheres was achieved by transferring the particles to a 50 mL RB flask with 5 mL toluene followed by addition of 3.5 mmol g−1 (w.r.t. SiO2) of (pentaflurotrimethyl)triethoxysilane and 5 mL toluene. This reaction mixture was refluxed for 2 hours and cooled down using an ice-water bath, which was dried at 100 °C for 12 h. The zeta potential of the silica spheres in water was measured using a Zetasizer Nano ZS (Malvern Instruments).
Ag nanowires (AgNWs) were synthesized using a previously reported method.41 AgNO3 (204 mg, 1.2 mM, Alfa Aesar, 99.9+%) and CuCl2.2H2O (6.5 mg, 0.038 mM, Aldrich) were used as metal precursors. 1,4-butanediol (1,4-BD, Pfaltz & Bauer, 99%) and poly-vinylpyrrolidone (PVP, 100 mg, average M.W. 58000, Alfa Aesar) were used as solvent and capping agent respectively. Using syringe pump, we injected the two precursors separately at a rate of 100 mL/h into the reaction mixture being held at 185 °C. A total reaction time of 900 s yielded AgNWs. Product purification and separation were done using two cycles of dissolution (ethanol) and selective precipitation (hexanes; at 5500 rpm for 5 minutes). The prepared AgNWs were dispersed in IPA for the trapping experiments.
Optical Setup
A 532 nm laser beam (Coherent, Genesis MX STM-1 W) was expanded to a diameter of ~ 5 mm with a beam expander (Thorlabs, GBE05-A) and projected onto a computer-controlled digital micro-mirror device (DMD) to create a dynamic one-dimensional optothermal potential on the substrate. The optical images reflected from the DMD were relayed onto the substrate through a 1000 mm doublet lens, a 200 mm doublet lens, an infinity-corrected tube lens, and a 40× objective lens (Nikon, NA 0.75) in an inverted optical microscope (Nikon Ti-E). The DMD and lens were removed from the setup and a 100X oil lens (Nikon, NA 0.5–1.3) was used to measure the trapping stiffness. We employed a color CCD camera (Nikon) and a fast monochromic CCD camera (Andor) to record optical images and to track particles, respectively. A 532 nm notch filter was inserted between the objective and the cameras to block the laser beam.
Computational Fluid Dynamic Simulations
The temperature gradient field created by a laser beam focused at the substrate-solvent interface was computed with a finite-element solver (COMSOL Multiphysics). For simplicity, a two-dimensional axisymmetric model comprised of a glass substrate, an Au film, and the solvent was established. Pre-defined conjugate heat transfer and Laminar flow models were used to simulate the heat transfer and fluid dynamics. A Gaussian distribution heat source was placed at the substrate-solvent interface to model the optical heating from the laser beam. Room temperature was set at all other boundaries.
Molecular Dynamics Simulations
The structure of the silica surface was obtained from Heinz and coworkers at https://bionanostructures.com/interface-md/, and corresponds to the surface of silica nanostructures > 200 nm in diameter at pH 7.42 The structure included ionization at the surface with 0.84 SiO-Na+ per nm2, and the silica slab and associated sodium ions were modelled using the INTERFACE force field by Heinz et al..43 The coordinates and force-field parameters were converted from version 1.5 from the aforementioned website with the supplied msi2namd2 program, followed by conversion to gromacs format using psf2top.py (https://github.com/resal81/PyTopol). Water and methanol were modeled with the SPC/E water model and CHARMM36 force field, respectively.44–45 Some core silicon atom types (SI1, SI4, SI7) were frozen to prevent deformation and provide a stationary reference. All system construction, simulation and analysis were carried out using GROMACS 5.0.7.46 The system was constructed by solvating the 3.4 × 3.5 × 1.9 nm3 silica slab and associated Na+ ions in either 1800 water or 750 methanol, resulting in a periodic box of 3.4 × 3.5 × 5.8 nm3. A steepest descent energy minimization was performed, and the followed simulations used a 2 fs time step and constraint of bonds between hydrogens and other heavy atoms using the LINCS algorithm.47 Electrostatic interactions were calculated using the particle mesh Ewald method of summation with a cutoff value of 1.2 nm.48 The “v-rescale” thermostat was used to maintain a system temperature of 298K.49 The system was equilibrated by NVT simulation for 200 ps prior to a production run of 60 ns. Trajectories were visualized using UCSF-Chimera50 and analysis was performed using GROMACS built-in packages.
RESULTS AND DISCUSSION
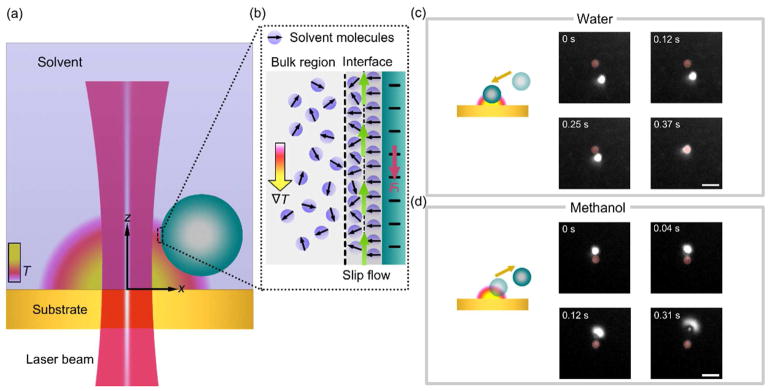
The working principle of opto-thermophoretic tweezers is illustrated in Figs. 1a & b. A laser beam is focused onto an opto-thermal substrate (see Methods Section) to create a temperature gradient field at the substrate-solvent interface. Colloidal particles with surface charges are suspended in non-ionic polar solvents. Under the temperature gradient field, a colloidal particle migrates from the cold to hot region and gets trapped at the laser beam center with the balance of the entropy-driven force Fi, optical gradient force, optical scattering force and particle-substrate interaction.
Figure 1. Working principle of opto-thermophoretic tweezers.
(a) Schematic illustration of thermophoretic trapping of a colloidal particle at the hot region of an opto-thermal substrate upon irradiation by a laser beam. (b) Schematic illustration of a layered structure of solvent molecules at the particle-solvent interface. The interfacial-entropy-driven force Fi (red arrow) originates from an induced slip flow (green arrows) under a temperature gradient field ∇T, driving the particle from the cold to hot region for its trapping at the laser beam. (c) Schematics and optical images of trapping of a 1 μm polystyrene (PS) sphere in water due to the dominance of the interfacial entropy-driven force Fi. (d) Schematic and optical images of anti-trapping (i.e., repulsion from the light-irradiated hot region) of a 1 μm PS sphere in methanol due to the dominance of dispersion force Fd (See Figure S1). A laser beam with a diameter of 2 μm and a power intensity of 0.16 mW/μm2 was irradiated onto the opto-thermal substrate (indicated by red circles in the optical images of c & d). A 20 μm thick chamber that contains the colloidal solution was stacked on top of the substrate. Scale bars in the optical images of (c–d) are 5 μm.
Migration of the particle due to the entropy-driven force Fi can be described by Anderson’s model where the thermophoretic drift velocity u is expressed as37, 51
| (1) |
where DT is the thermophoretic mobility, ∇T is the temperature gradient, η is the viscosity of the solvent, T is the temperature, κ and κP are the thermal conductivities of the solvent and the particle respectively, and is the slip-velocity coefficient with h(z)as the local excess enthalpy density at a distance z from the particle surface (compared with that at an infinite distance). When the local excess enthalpy density is mainly due to polarization of solvent molecules under the interfacial electrical field, h(z)can be evaluated as , where ε is the dielectric constant of solvent as a function of z and E(z) is the local electrical field.37 We approximate , ε(z) as εb, and at the particle-solvent interface as an effective value τ, where ζ is the surface potential of the particle, λ is the effective decay length of the local electrical field and εb is the dielectric constant of the solvent in the bulk region. Therefore, the thermophoretic drift velocity u is given by
| (2) |
We can see that one of the parameters that determine the particle migration direction is τ, which is related to the structures of the solvent molecule at the particle-solvent interface.52–55 As described in the BDM model proposed by Bockris, Devanathan, and Muller,52 solvent molecules adsorb onto the charged surface of a colloidal particle to form layered structures at the particle-solvent interface. As shown in Fig. 1b, the molecules in the first layer have their orientation aligned with the electric field from the surface charges, while those in the second layer are partially oriented toward the particle surface. The molecules in the third layer and beyond (i.e., bulk region) become disordered.
Under an externally applied temperature gradient, the orientation of the interfacial molecular dipoles at the hot side of the particle becomes disordered due to the increased entropy, leading to a higher permittivity and thus a higher electric energy density. Interestingly, the increased permittivity at the higher temperature leads to a positive τ in Equation (2), rendering the thermophoretic motion of the particle from the cold to the hot region to achieve opto-thermophoretic trapping. As illustrated in Fig. 1b, the permittivity gradient induces a slip flow,31 which leads to the interfacial-entropy-driven force Fi (red arrow) and drags the particle to the hot region.
There is also a dispersion force Fd, which arises from the density gradient of the solvent under the temperature gradient (Fig. S1).31 In contrast to the interfacial-entropy-driven force, the dispersion force drives particles from the hot to cold region. Common solvents expand upon heating with one exception (i.e., water below 5 °C). The colder solvent with a higher density experiences a stronger van der Waals attraction from the particle, leading to a slip flow that drives the particle towards the cold region, as illustrated in Fig. S1. According to Wurger’s hydrodynamic model,31 the thermophoretic drift velocity due to the dispersion force is written as
| (3) |
where β is the thermal expansivity of the solvent, H is the Hamaker constant of the particle-solvent interactions, d0 is a molecular length scale, and η is the viscosity of the solvent.
For a charged colloidal particle under a temperature gradient ∇T, the thermophoretic migration can also be contributed by temperature-gradient-induced distortion of the Debye layer.56 A temperature gradient will deform the Debye layer, leading to an electric force acting on the surface charges of the colloidal particle and a solvent-friction force on the surface of the colloidal particle. The two forces are typically a factor smaller than that caused by the temperature dependence of the internal electrostatic energy at the interface (equation (2)). We thus exclude their contributions on the thermophoretic migration as the polar solvents in our experiments have relatively large dielectric constant εb (spans from 20ε0 to 80ε0). Thermo-osmotic flow also coexists with the thermophoretic migration once a temperature gradient is created at the substrate-solvent interface. Thermo-osmotic flow that is parallel to the substrate surface has a negative effect in trapping, which is significant for a very thin Debye layer compared to the particle size.31, 57 We neglect the thermo-osmosis effect for a low ionic strength of the polar solvents and a large Debye screening length (in the order of μm) of the charged substrate surface.
As an example, we use polystyrene (PS) spheres in water as an example to compare the effects of the dispersion force and the interfacial-entropy-induced force on the thermophoresis of the colloidal particles. Since the ionic sulfate groups grafted on the surface of PS spheres make a rough interface, the van der Waals interactions between the particle and water is weak and the molecular length scale d0 should be estimated based on the size of the ionic sulfate groups rather than the size of the solvent molecules. With d0 ~ 1 nm, H ~ 2 × 10−20 J, β ~ 2.56 × 10−4 K−1 and η ~1.08 × 10−3 cP at 25 °C, DT induced by the dispersion force is 0.35 μm2 K−1 s−1. With ζ ~ 50 mV and τ ~2,58 DT induced by the interfacial-entropy-induced force gives a value of −3 μm2 K−1 s−1, which is one order of magnitude higher than that caused by the dispersion force. The opposite signs of DT indicate that the dispersion force drives the particle from the hot to the cold region while the interfacial-entropy-induced force drives the particle from the cold to the hot region. It should be noted that the dispersion force can dominate over the entropy-driven force for colloidal particles in solvents with a high thermal expansivity β and a low viscosity η (e.g., methanol).
To experimentally explore the roles of the entropy-induced force and dispersion force in opto-thermophoretic manipulation of colloidal particles, we studied kinetics of 1 μm PS particles under a light-generated temperature gradient field in water and methanol, respectively. We carried out real-time tracking of the particles with a fast CCD camera, as shown in Fig. 1c and Fig. 1d. A laser beam with a diameter of 2 μm and a power intensity of 0.16 mW/μm2 was focused onto the optothermal substrate to create a localized temperature gradient field (Fig. S2). The particle solutions were contained in a 20 μm thin chamber above the substrate to reduce thermal convection.59 Upon irradiation of the laser beam, a particle in water was rapidly delivered towards and trapped at the beam center (Fig. 1c). In contrast, a particle in methanol was repelled away from the beam center and the substrate upon the irradiation of the laser beam (Fig. 1d and Video S1). It should be noted that particle migration was driven by the temperature gradient field rather than the optical gradient force. Our weakly focused laser beam, which has a diameter of 2 μm, generates a small optical gradient force compared to the opto-thermophoretic force.
We further measured the drift velocities of the particles under the temperature gradient field in water and methanol (Fig. S3). For 1 μm PS particles, we obtained an absolute value of ~ 10 μm s−1 in both solvents. Considering an average in-plane temperature gradient of 4 K μm−1 (Fig. S2), we calculated the drift velocity of 12 μm s−1 in water (Equation 2), which is close to the experimental value. Wurger’s hydrodynamic model gives a drift velocity of −12 μm s−1 in methanol, which indicates that the dispersion force drove the anti-trapping of the particle due to the weak entropy-induced force. We also measured the drift velocities of 2 μm PS particles in water and methanol (Fig. S3 and Video S2). The drift velocity for 2 μm PS particles in methanol is slightly smaller than that of 1 μm PS particles in methanol. The smaller velocity is attributed to the weaker average temperature gradient field and negligible hydrodynamic boundary effect due to repulsion of the particle away from the substrate.40, 60
To identify the mechanisms and driving forces of colloidal thermophoresis, molecular dynamics simulations have been applied to study thermophoretic migration behaviors for a small number of systems.61–62 To validate the mechanism behind entropy-driven force in opto-thermophoretic tweezers at the molecular level, we carried out molecular dynamics (MD) simulations to investigate the structure of solvent molecules at the particle interface. As similar trapping and anti-trapping of silica spheres under a temperature gradient field in water and methanol was observed with the case of PS spheres, we used a well-established model of the silica surface to simulate the interfacial solvent structure. Snapshots of the simulation boxes after 80 ns NVT simulation are shown in Figs. 2a & b, together with the number density profiles (Fig. 2c) and orientational polarization profiles (Fig. 2d). As shown in Fig. 2c, the number density for both water and methanol molecules exhibits an oscillatory behavior, suggesting the formation of layered structures of solvent molecules, i.e., layers (peaks) and sublayers (dips), at the silica-solvent interfaces.63–64 The slight out-of-phase of the two curves is due to the different molecule sizes between water and methanol. The number density becomes relatively uniform as it approaches the bulk phase with increased distance from the silica surface.
Figure 2. Molecular dynamics simulation of silica-water and silica-methanol interfaces.
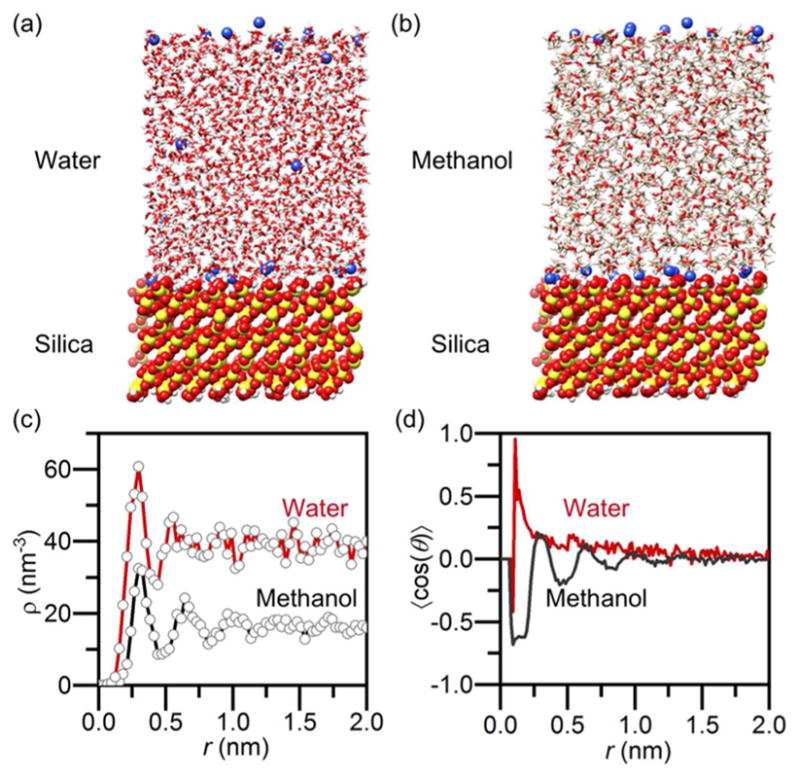
Snapshots of the simulation box with (a) water and (b) methanol in contact with a silica surface at pH 7.5. (c) Number density profiles of water molecules (red) and methanol molecules (black) at the interface. (d) Orientational polarization profiles (relative to axis perpendicular to the silica surface) of water molecules (red) and methanol molecules (black) at the interface respectively. In (c–d), the origin of the r-axis is set to the silica surface.
The orientational polarization profile < cos(θ)>, which represents the degree of ordering in the solvent layers, was obtained by calculating the normalized cosine of the angle between the molecular dipoles and the normal of the silica surface, as plotted in Fig. 2d. In water, the orientation of dipoles decays exponentially as distance from the interface increases, with the dipole orientation becoming random in the bulk region. This justifies our permittivity gradient model in evaluating the thermophoretic mobility DT in equation 2. Beyond the electrostatic charge-dipole interactions, hydrogen bonding at the interface also plays a critical role in the structuring of the solvent molecules, which is termed as a “solvation layer”.54, 65 In methanol, the polarization profile exhibits damped oscillations, which is due to the formation of an antiparallel bilayer structure.64 Within the layered solvent structure, the first layer of well-oriented methanol molecules (r ~ 0.25 nm) interacts with the silica surface via hydrogen-bonding and presents a hydrophobic surface, inducing an opposite polarization in the second layer (r ~ 0.5 nm). This layered structure accounts for the weak entropy-driven force in methanol because the cancellation effect of the antiparallel layers leads to a significantly diminished slip flow at the particle-methanol interface. Though surface defects need to be considered for realistic surfaces of silica spheres, the surface defects will not affect the formation of layered structures but increase the population and dynamics of the molecules at the interface, in other words, it will amplify the interfacial effect for thermophoretic trapping.64
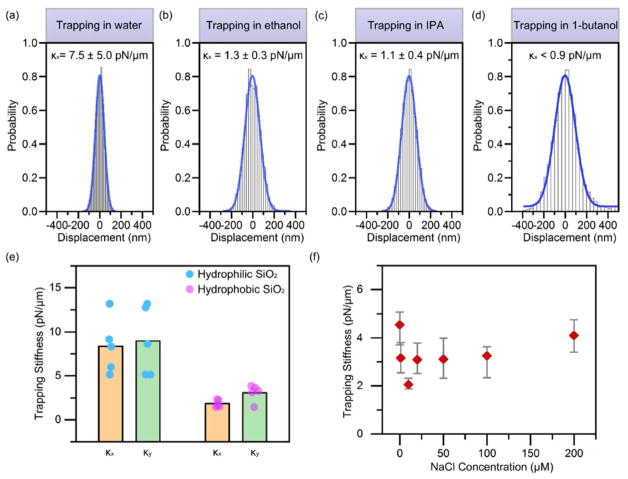
According to our established working mechanism, the entropy-driven force must dominate over the dispersion force to enable opto-thermophoretic trapping of colloidal particles. We can choose suitable polar solvents to meet this requirement. For ethanol, IPA and 1-butanol where d0 ~ 2 nm and H ~ 1 × 10−20 J, DT contributed by the dispersion force is ~ 0.55, ~ 0.26 and ~ 0.11 μm2 K−1 s−1, respectively, which is smaller than the contribution from the entropy-driven force (in the order of μm2 K−1 s−1). Thus, we expect that opto-thermophoretic trapping of particles can be achieved in these solvents, which has been verified experimentally. As examples, we demonstrated opto-thermophoreic trapping of 500 nm PS spheres in water, ethanol, IPA and 1-butanol. Moreover, the trapping stability in these solvents was studied by tracking the position fluctuations of the particles under the temperature gradient field. The histograms of the particle displacement are presented in Figs. 3a–d (x direction) and Fig. S4 (y direction). Gaussian fitting was used to measure the variance σ of the Brownian motion and to extract the trapping stiffness The trapping stiffness in water has the largest value of 7.5 ±5.0 pN/μm. The particle trapping in 1-butanol is not stable where the position fluctuation reaches a non-harmonic region that is outside the laser beam. Since the trapping stiffness κ ∝ DT,67 the trapping stability is influenced by the term in Equation (2), the values of which are summarized in Table S1. 1-butanol leads to a trapping stiffness one order of magnitude smaller than water due to its small dielectric constant and large viscosity. The ratio of the trapping stiffness in ethanol to that in water is less than the value predicted by Equation (2) (Table S1), which can be attributed to the smaller τ 64 and the larger dispersion force in ethanol. The trapping stiffness in IPA is comparable to that in ethanol where strong particle-solvent interactions with extended interfacial structures occur.68 The consistency between the experiments and the models of the particle-trapping in the various solvents further validates the mechanism of the entropy-driven force in opto-thermophoretic tweezers.
Figure 3. Effects of solvent, particle hydrophilicity and ion concentration on opto-thermophoretic trapping of colloidal particles.
(a–d) Measured histograms of particle displacement and the corresponding trapping stiffness (x direction) for 500 nm PS spheres in water, ethanol, IPA and 1-butanol. (e) Measured trapping stiffness for 1 μm hydrophilic and hydrophobic silica (i.e., SiO2) particles in water. The dots indicate the values of different particles. The columns indicate the average values. (f) Measured trapping stiffness for 1 μm PS spheres in IPA as a function of NaCl concentration. A focused laser beam with a diameter of ~ 520 nm and an optical power of ~ 0.5 mW was illuminated onto the optothermal substrate with a thin chamber of (a–d, f) 20 μm in depth and (e) 120 μm in depth. Standard deviations (a–d) and error bars (f) of the trapping stiffness were obtained by tracking 5–6 different particles.
We have further demonstrated fine tuning of opto-thermophoretic trapping of colloidal particles by controlling surface chemistry of the particles or ionic strength of the solvents. Both surface chemistry and ionic strength can modify the interfacial molecule layers and thus the entropy-driven force. Fig. 3e shows the trapping stiffness of 1 μm hydrophilic and hydrophobic silica (SiO2) particles in water. To increase the hydrophobicity, the as-purchased hydrophilic silica particles were coated with (pentaflurotrimethyl)triethoxysilane, which reduced the concentration of silanol groups on the particle surfaces and extended the hydrophobic areas. The surface charge was not changed by the coating, as shown by zeta-potential measurements (Fig. S5). A lower trapping stability was observed for the hydrophobic particles. This is because the poor adsorption of water molecules on the hydrophobic surfaces weakened the layered structure and thus reduced the entropy-driven force.63 It should be noted that the optical gradient force is much weaker than the entropy-driven force, which is verified by the release of a trapped hydrophilic silica particle when translating it from the optothermal substrate to the glass substrate (Video S3). We used 120 μm chambers to avoid spontaneous adhesion of silica particles to the substrate. Though a stronger convection at thicker chambers may lower the trapping stability,40 hydrophilic particles will maintain a higher trapping stiffness than that of hydrophobic ones for a stronger entropy-driven force. Fig. S6 shows the measured trapping stiffness of 500 nm PS spheres in water as a function of NaCl concentration. The trapping stiffness decreased when the NaCl concentration was increased, and could not be achieved any more once the NaCl concentration was increased to 400 μM. We believe that the increased ionic strength, and thus the ion-molecule interactions, destabilized the layered structure at the particle-solvent interface.27 In addition, a thermoelectric effect that led to DT~ 2 μm2 K−1 s−1 occurred,31, 69 setting an upper limit of ionic concentration for opto-thermophoretic tweezers. However, as the saturated NaCl concentration in IPA is much lower than that in water, trapping stability is maintained across the entire NaCl concentration range in IPA, as shown in Fig. 3f.
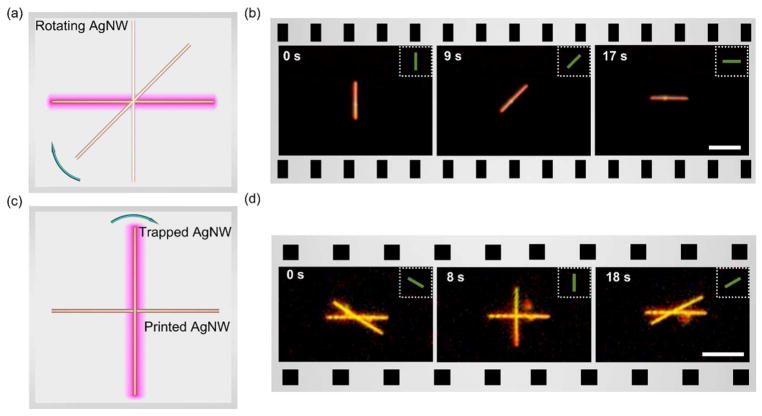
Lastly, we demonstrated the opto-thermophoretic manipulation of Ag nanowires (AgNWs). The AgNWs have a length in the range of 2–12 μm and a width in the range of 50–300 nm (see Fig. S7). Optical manipulation of metal nanostructures is challenging due to enhanced optical absorption and scattering, which dramatically increases the optical radiation force. We dispersed the AgNWs in IPA where the entropy-driven force could overcome the optical scattering force to achieve opto-thermophoretic trapping of the AgNWs. We further achieved the opto-thermophoretic transport and rotation of AgNWs at a low optical power using a one-dimensional optothermal potential, as shown in Fig. 4a and Video S4. The controlled rotation of a single AgNW above the other AgNW immobilized on the substrate was also demonstrated (Fig. 4b), showing the potential of opto-thermophoretic tweezers for assembly of nanowires into functional components and devices.
Figure 4. Opto-thermophoretic manipulation of AgNWs in IPA.
(a) Schematic illustration and (b) time-resolved dark-field optical images of rotation of a AgNW with one-dimensional optothermal potential. (c) Schematic illustration and (d) time-resolved dark-field optical images of rotation of a AgNW over another AgNW printed on the substrate. Insets in (b) and (d) show the orientations of the 10 μ1 μm2 line-shaped laser beam with an optical power of 0.67 mW. Scale bars: (b) 10 μm and (d) 5 μm.
CONCLUSIONS
We have established the working mechanism of opto-thermophoretic tweezers for colloidal particles in non-ionic liquids at the molecular level. Specifically, opto-thermophoretic trapping is driven by the entropy at the particle-liquid interface with a minor effect from dispersion forces. The entropy-driven force arises from the structured solvent layers at the particle-solvent interfaces, which is supported by all-atom MD simulations. Parameters such as particle hydrophilicity, particle surface charge, solvent type and ionic strength can be adjusted to control the interfacial structure of the solvent molecules in order to improve the trapping stability of colloidal particles. With their low-power operation and simple optics, opto-thermophoretic tweezers will find applications in colloidal science, materials science, cell biology, and nanofabrication.
Supplementary Material
Acknowledgments
X.P., L.L., E.H.H. and Y.Z. acknowledge the financial supports of the Army Research Office (W911NF-17-1-0561) and the National Institute of General Medical Sciences of the National Institutes of Health (DP2GM128446). P.K. and S.H. acknowledge the financial supports of the National Science Foundation (CHE-1505135) and the Welch Foundation (F-1738). We thank the Texas Advanced Computing Center at The University of Texas at Austin for providing HPC resources that have contributed to the research results reported within this paper. URL: http://www.tacc.utexas.edu. We also thank Z. Mao, W. Cai and Y. Liu for helpful discussions.
Footnotes
X.P. and Y.Z. conceived the idea. X.P. and L.L. prepared the materials, worked on the trapping experiments, and collected the data. E.H.H. conducted the MD simulations. P. K. and S.H. did the surface modifications of silica particles and synthesized the AgNWs. Y.Z. supervised the project. All authors participated in the discussions of the results and wrote the manuscript. The authors declare no competing financial interests.
The following files are available free of charge.
Supplementary Videos, Supplementary Figures and Supplementary Table (PDF).
References
- 1.Chiou PY, Ohta AT, Wu MC. Massively Parallel Manipulation of Single Cells and Microparticles Using Optical Images. Nature. 2005;436:370. doi: 10.1038/nature03831. [DOI] [PubMed] [Google Scholar]
- 2.Uppalapati M, Huang YM, Jackson TN, Hancock WO. Microtubule Alignment and Manipulation Using AC Electrokinetics. Small. 2008;4:1371–1381. doi: 10.1002/smll.200701088. [DOI] [PubMed] [Google Scholar]
- 3.Ohta AT, Garcia M, Valley JK, Banie L, Hsu HY, Jamshidi A, Neale SL, Lue T, Wu MC. Motile and Non-Motile Sperm Diagnostic Manipulation Using Optoelectronic Tweezers. Lab Chip. 2010;10:3213–3217. doi: 10.1039/c0lc00072h. [DOI] [PubMed] [Google Scholar]
- 4.Snezhko A, Aranson IS. Magnetic Manipulation of Self-Assembled Colloidal Asters. Nat Mater. 2011;10:698. doi: 10.1038/nmat3083. [DOI] [PubMed] [Google Scholar]
- 5.Grier DG. A Revolution in Optical Manipulation. Nat Photonics. 2003;424:810–816. doi: 10.1038/nature01935. [DOI] [PubMed] [Google Scholar]
- 6.Spesyvtseva SES, Dholakia K. Trapping in a Material World. ACS Photonics. 2016;3:719–736. [Google Scholar]
- 7.Jing P, Wu J, Liu GW, Keeler EG, Pun SH, Lin LY. Photonic Crystal Optical Tweezers with High Efficiency for Live Biological Samples and Viability Characterization. Scientific Reports. 2016;6:19924. doi: 10.1038/srep19924. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Yang X, Liu Y, Oulton RF, Yin X, Zhang X. Optical Forces in Hybrid Plasmonic Waveguides. Nano Lett. 2011;11:321–328. doi: 10.1021/nl103070n. [DOI] [PubMed] [Google Scholar]
- 9.Jauffred L, Richardson AC, Oddershede LB. Three-Dimensional Optical Control of Individual Quantum Dots. Nano Lett. 2008;8:3376–3380. doi: 10.1021/nl801962f. [DOI] [PubMed] [Google Scholar]
- 10.Pauzauskie PJ, Radenovic A, Trepagnier E, Shroff H, Yang P, Liphardt J. Optical Trapping and Integration of Semiconductor Nanowire Assemblies in Water. Nat Mater. 2006;5:97–101. doi: 10.1038/nmat1563. [DOI] [PubMed] [Google Scholar]
- 11.Yan Z, Sweet J, Jureller JE, Guffey MJ, Pelton M, Scherer NF. Controlling the Position and Orientation of Single Silver Nanowires on a Surface Using Structured Optical Fields. ACS Nano. 2012;6:8144–8155. doi: 10.1021/nn302795j. [DOI] [PubMed] [Google Scholar]
- 12.Blattmann M, Rohrbach A. Plasmonic Coupling Dynamics of Silver Nanoparticles in an Optical Trap. Nano Lett. 2015;15:7816–7821. doi: 10.1021/acs.nanolett.5b02532. [DOI] [PubMed] [Google Scholar]
- 13.Lehmuskero A, Johansson P, Rubinsztein-Dunlop H, Tong L, Käll M. Laser Trapping of Colloidal Metal Nanoparticles. ACS Nano. 2015;9:3453–3469. doi: 10.1021/acsnano.5b00286. [DOI] [PubMed] [Google Scholar]
- 14.Juan ML, Righini M, Quidant R. Plasmon Nano-Optical Tweezers. Nat Photonics. 2011;5:349–356. [Google Scholar]
- 15.Righini M, Zelenina AS, Girard C, Quidant R. Parallel and Selective Trapping in a Patterned Plasmonic Landscape. Nat Phys. 2007;3:477–480. [Google Scholar]
- 16.Berthelot J, Acimovic SS, Juan ML, Kreuzer MP, Renger J, Quidant R. Three-Dimensional Manipulation with Scanning Near-Field Optical Nanotweezers. Nat Nanotechnol. 2014;9:295–299. doi: 10.1038/nnano.2014.24. [DOI] [PubMed] [Google Scholar]
- 17.Huft PR, Kolbow JD, Thweatt JT, Lindquist NC. Holographic Plasmonic Nanotweezers for Dynamic Trapping and Manipulation. Nano Lett. 2017;17:7920–7925. doi: 10.1021/acs.nanolett.7b04289. [DOI] [PubMed] [Google Scholar]
- 18.Ndukaife JC, Kildishev AV, Nnanna AGA, Shalaev VM, Wereley ST, Boltasseva A. Long-Range and Rapid Transport of Individual Nano-Objects by a Hybrid Electrothermoplasmonic Nanotweezer. Nat Nanotechnol. 2015;11:53. doi: 10.1038/nnano.2015.248. [DOI] [PubMed] [Google Scholar]
- 19.Duhr S, Braun D. Why Molecules Move Along a Temperature Gradient. Proc Natl Acad Sci U S A. 2006;103:19678–19682. doi: 10.1073/pnas.0603873103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Reichl MR, Braun D. Thermophoretic Manipulation of Molecules inside Living Cells. J Am Chem Soc. 2014;136:15955–15960. doi: 10.1021/ja506169b. [DOI] [PubMed] [Google Scholar]
- 21.Braun M, Cichos F. Optically Controlled Thermophoretic Trapping of Single Nano-Objects. ACS Nano. 2013;7:11200–11208. doi: 10.1021/nn404980k. [DOI] [PubMed] [Google Scholar]
- 22.Braun M, Bregulla AP, Günther K, Mertig M, Cichos F. Single Molecules Trapped by Dynamic Inhomogeneous Temperature Fields. Nano Lett. 2015;15:5499–5505. doi: 10.1021/acs.nanolett.5b01999. [DOI] [PubMed] [Google Scholar]
- 23.Smith CLC, Thilsted AH, Pedersen JN, Youngman TH, Dyrnum JC, Michaelsen NA, Marie R, Kristensen A. Photothermal Transport of DNA in Entropy-Landscape Plasmonic Waveguides. ACS Nano. 2017;11:4553–4563. doi: 10.1021/acsnano.6b08563. [DOI] [PubMed] [Google Scholar]
- 24.Talbot EL, Kotar J, Parolini L, Di Michele L, Cicuta P. Thermophoretic Migration of Vesicles Depends on Mean Temperature and Head Group Chemistry. Nat Commun. 2017;8:15351. doi: 10.1038/ncomms15351. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Jiang HR, Wada H, Yoshinaga N, Sano M. Manipulation of Colloids by a Nonequilibrium Depletion Force in a Temperature Gradient. Phys Rev Lett. 2009;102:208301. doi: 10.1103/PhysRevLett.102.208301. [DOI] [PubMed] [Google Scholar]
- 26.Fukuyama T, Fuke A, Mochizuki M, Kamei K, Maeda YT. Directing and Boosting of Cell Migration by the Entropic Force Gradient in Polymer Solution. Langmuir. 2015;31:12567–12572. doi: 10.1021/acs.langmuir.5b02559. [DOI] [PubMed] [Google Scholar]
- 27.Lin L, Peng X, Mao Z, Wei X, Xie C, Zheng Y. Interfacial-Entropy-Driven Thermophoretic Tweezers. Lab Chip. 2017;17:3061–3070. doi: 10.1039/c7lc00432j. [DOI] [PubMed] [Google Scholar]
- 28.Lin L, Zhang J, Peng X, Wu Z, Coughlan ACH, Mao Z, Bevan MA, Zheng Y. Opto-Thermophoretic Assembly of Colloidal Matter. Science Advances. 2017;3:e1700458. doi: 10.1126/sciadv.1700458. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Kang Z, Chen J, Wu SY, Chen K, Kong SK, Yong KT, Ho HP. Trapping and Assembling of Particles and Live Cells on Large-Scale Random Gold Nano-Island Substrates. Scientific Reports. 2015;5:9978. doi: 10.1038/srep09978. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Piazza R. Thermophoresis: Moving Particles with Thermal Gradients. Soft Matter. 2008;4:1740–1744. [Google Scholar]
- 31.Wurger A. Thermal Non-Equilibrium Transport in Colloids. Rep Prog Phys. 2010;73:126601. [Google Scholar]
- 32.Morthomas J, Wurger A. Thermoelectric Effect on Charged Colloids in the Huckel Limit. Eur Phys J E: Soft Matter Biol Phys. 2008;27:425–434. doi: 10.1140/epje/i2008-10410-8. [DOI] [PubMed] [Google Scholar]
- 33.Wurger A. Transport in Charged Colloids Driven by Thermoelectricity. Phys Rev Lett. 2008;101:108302. doi: 10.1103/PhysRevLett.101.108302. [DOI] [PubMed] [Google Scholar]
- 34.Majee A, Wurger A. Thermocharge of a Hot Spot in an Electrolyte Solution. Soft Matter. 2013;9:2145–2153. [Google Scholar]
- 35.Eslahian KA, Majee A, Maskos M, Wurger A. Specific Salt Effects on Thermophoresis of Charged Colloids. Soft Matter. 2014;10:1931–1936. doi: 10.1039/c3sm52779d. [DOI] [PubMed] [Google Scholar]
- 36.Aboubakry L, Arghya M, Alois W. Nanoscale Seebeck Effect at Hot Metal Nanostructures. New J Phys. 2017;20:025001. [Google Scholar]
- 37.Putnam SA, Cahill DG. Transport of Nanoscale Latex Spheres in a Temperature Gradient. Langmuir. 2005;21:5317–5323. doi: 10.1021/la047056h. [DOI] [PubMed] [Google Scholar]
- 38.Iacopini S, Piazza R. Thermophoresis in Protein Solutions. EPL. 2003;63:247. [Google Scholar]
- 39.Cong H, Chen J, Ho HP. Trapping, Sorting and Transferring of Micro-Particles and Live Cells Using Electric Current-Induced Thermal Tweezers. Sens Actuators, B. 2018;264:224–233. [Google Scholar]
- 40.Lin L, Peng X, Wei X, Mao Z, Xie C, Zheng Y. Thermophoretic Tweezers for Low-Power and Versatile Manipulation of Biological Cells. ACS Nano. 2017;11:3147–3154. doi: 10.1021/acsnano.7b00207. [DOI] [PubMed] [Google Scholar]
- 41.Skrabalak SE, Wiley BJ, Kim M, Formo EV, Xia Y. On the Polyol Synthesis of Silver Nanostructures: Glycolaldehyde as a Reducing Agent. Nano Lett. 2008;8:2077–2081. doi: 10.1021/nl800910d. [DOI] [PubMed] [Google Scholar]
- 42.Emami FS, Puddu V, Berry RJ, Varshney V, Patwardhan SV, Perry CC, Heinz H. Force Field and a Surface Model Database for Silica to Simulate Interfacial Properties in Atomic Resolution. Chem Mater. 2014;26:2647–2658. [Google Scholar]
- 43.Heinz H, Lin TJ, Kishore Mishra R, Emami FS. Thermodynamically Consistent Force Fields for the Assembly of Inorganic, Organic, and Biological Nanostructures: The Interface Force Field. Langmuir. 2013;29:1754–1765. doi: 10.1021/la3038846. [DOI] [PubMed] [Google Scholar]
- 44.Huang J, MacKerell AD. Charmm36 All-Atom Additive Protein Force Field: Validation Based on Comparison to NMR Data. J Comput Chem. 2013;34:2135–2145. doi: 10.1002/jcc.23354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Berendsen HJC, Postma JPM, van Gunsteren WF, Hermans J. Intermolecular Forces. In: Pullman B, editor. Proceedings of the Fourteenth Jerusalem Symposium on Quantum Chemistry and Biochemistry; Jerusalem, Israel. April 13–16: 1981; Dordrecht: Springer Netherlands; 1981. [Google Scholar]
- 46.Abraham MJ, Murtola T, Schulz R, Páll S, Smith JC, Hess B, Lindahl E. Gromacs: High Performance Molecular Simulations through Multi-Level Parallelism from Laptops to Supercomputers. SoftwareX. 2015;1:19–25. [Google Scholar]
- 47.Hess B, Bekker H, Berendsen HJC, Fraaije JGEM. Lincs: A Linear Constraint Solver for Molecular Simulations. J Comput Chem. 1997;18:1463–1472. [Google Scholar]
- 48.Darden T, York D, Pedersen L. Particle Mesh Ewald: An N·Log(N) Method for Ewald Sums in Large Systems. J Chem Phys. 1993;98:10089–10092. [Google Scholar]
- 49.Bussi G, Donadio D, Parrinello M. Canonical Sampling through Velocity Rescaling. J Chem Phys. 2007;126:014101. doi: 10.1063/1.2408420. [DOI] [PubMed] [Google Scholar]
- 50.Pettersen EF, Goddard TD, Huang CC, Couch GS, Greenblatt DM, Meng EC, Ferrin TE. UCSF Chimera—a Visualization System for Exploratory Research and Analysis. J Comput Chem. 2004;25:1605–1612. doi: 10.1002/jcc.20084. [DOI] [PubMed] [Google Scholar]
- 51.Anderson JL. Colloid Transport by Interfacial Forces. Annu Rev Fluid Mech. 1989;21:61–99. [Google Scholar]
- 52.Bockris JOM, Devanathan MAV, Muller K. On the Structure of Charged Interfaces. Proc R Soc London, Ser A. 1963;274:55–79. [Google Scholar]
- 53.Marrink SJ, Berkowitz M, Berendsen HJC. Molecular Dynamics Simulation of a Membrane/Water Interface: The Ordering of Water and Its Relation to the Hydration Force. Langmuir. 1993;9:3122–3131. [Google Scholar]
- 54.Turov VV, Mironyuk IF. Adsorption Layers of Water on the Surface of Hydrophilic, Hydrophobic and Mixed Silicas. Colloids Surf, A. 1998;134:257–263. [Google Scholar]
- 55.Macias-Romero C, Nahalka I, Okur HI, Roke S. Optical Imaging of Surface Chemistry and Dynamics in Confinement. Science. 2017;357:784–788. doi: 10.1126/science.aal4346. [DOI] [PubMed] [Google Scholar]
- 56.Dhont JKG, Briels WJ. Single-Particle Thermal Diffusion of Charged Colloids: Double-Layer Theory in a Temperature Gradient. Eur Phys J E: Soft Matter Biol Phys. 2008;25:61–76. doi: 10.1140/epje/i2007-10264-6. [DOI] [PubMed] [Google Scholar]
- 57.Bregulla AP, Würger A, Günther K, Mertig M, Cichos F. Thermo-Osmotic Flow in Thin Films. Phys Rev Lett. 2016;116:188303. doi: 10.1103/PhysRevLett.116.188303. [DOI] [PubMed] [Google Scholar]
- 58.Churaev NV, Derjaguin BV, Muller VM. Surface Forces. Springer Science & Business Media; New York: 2013. [Google Scholar]
- 59.Donner JS, Baffou G, McCloskey D, Quidant R. Plasmon-Assisted Optofluidics. ACS Nano. 2011;5:5457–5462. doi: 10.1021/nn200590u. [DOI] [PubMed] [Google Scholar]
- 60.Wurger A. Hydrodynamic Boundary Effects on Thermophoresis of Confined Colloids. Phys Rev Lett. 2016;116:138302. doi: 10.1103/PhysRevLett.116.138302. [DOI] [PubMed] [Google Scholar]
- 61.Han M. Thermophoresis in Liquids: A Molecular Dynamics Simulation Study. J Colloid Interface Sci. 2005;284:339–348. doi: 10.1016/j.jcis.2004.09.067. [DOI] [PubMed] [Google Scholar]
- 62.Tetsuro T, Hirotaka I, Itsuo H, Satoyuki K. Negative Thermophoresis of Nanoparticles Interacting with Fluids through a Purely-Repulsive Potential. J Phys : Condens Matter. 2017;29:475101. doi: 10.1088/1361-648X/aa9350. [DOI] [PubMed] [Google Scholar]
- 63.Bonthuis DJ, Gekle S, Netz RR. Dielectric Profile of Interfacial Water and Its Effect on Double-Layer Capacitance. Phys Rev Lett. 2011;107:166102. doi: 10.1103/PhysRevLett.107.166102. [DOI] [PubMed] [Google Scholar]
- 64.Karnes JJ, Gobrogge EA, Walker RA, Benjamin I. Unusual Structure and Dynamics at Silica/Methanol and Silica/Ethanol Interfaces—a Molecular Dynamics and Nonlinear Optical Study. J Phys Chem B. 2016;120:1569–1578. doi: 10.1021/acs.jpcb.5b07777. [DOI] [PubMed] [Google Scholar]
- 65.Raghavan SR, Walls HJ, Khan SA. Rheology of Silica Dispersions in Organic Liquids: New Evidence for Solvation Forces Dictated by Hydrogen Bonding. Langmuir. 2000;16:7920–7930. [Google Scholar]
- 66.Florin EL, Pralle A, Stelzer EHK, Hörber JKH. Photonic Force Microscope Calibration by Thermal Noise Analysis. Appl Phys A: Solids Surf. 1998;66:S75–S78. [Google Scholar]
- 67.Helden L, Eichhorn R, Bechinger C. Direct Measurement of Thermophoretic Forces. Soft Matter. 2015;11:2379–2386. doi: 10.1039/c4sm02833c. [DOI] [PubMed] [Google Scholar]
- 68.Naruke Y, Kosaka S, Nakano T, Kikugawa G, Ohara T. A Molecular Dynamics Study on Mass Transport Characteristics in the Vicinity of SiO2–Water/IPA Interfaces. Int J Heat Mass Transfer. 2015;84:584–591. [Google Scholar]
- 69.Reichl M, Herzog M, Götz A, Braun D. Why Charged Molecules Move across a Temperature Gradient: The Role of Electric Fields. Phys Rev Lett. 2014;112:198101. doi: 10.1103/PhysRevLett.112.198101. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.