A Modified Random Survival Forests Algorithm for High Dimensional Predictors and Self-Reported Outcomes

Abstract

We present an ensemble tree-based algorithm for variable selection in high dimensional datasets, in settings where a time-to-event outcome is observed with error. The proposed methods are motivated by self-reported outcomes collected in large-scale epidemiologic studies, such as the Women’s Health Initiative. The proposed methods equally apply to imperfect outcomes that arise in other settings such as data extracted from electronic medical records. To evaluate the performance of our proposed algorithm, we present results from simulation studies, considering both continuous and categorical covariates. We illustrate this approach to discover single nucleotide polymorphisms that are associated with incident Type II diabetes in the Women’s Health Initiative. A freely available R package icRSF (R Core Team, 2018; Xu et al., 2018) has been developed to implement the proposed methods.

1 Introduction

Rapid advances in biomedical technology have resulted in a rich array of data from large prospective studies such as the Women’s Health Initiative (WHI), including extensive behavioral, genotypic, metabolomic and phenotypic information. These databases are invaluable resources for elucidating the factors governing the etiology of complex disorders - but in order to use them most effectively, robust methods for accounting for measurement error in high dimensional datasets need to be developed. In large, prospective studies like the WHI, the prevalence and incidence of many diseases such as diabetes are determined by self-administered questionnaires, which are cost-effective and logistically feasible; however, self-reports are imperfect for estimating disease prevalence and incidence. In this paper, we propose a novel algorithm for assessing variable importance in high dimensional datasets (p ≫ n) in which a time to event outcome is observed with error, such as through self-reports.

Consider the onset of a silent event such as Type 2 diabetes, that can only be detected by administering a diagnostic test. If a perfect diagnostic test is administered repeatedly, the onset of the disease can be inferred to lie in the interval between the last negative and first positive diagnostic test - that is, the time to event is interval censored. However, due to cost considerations, imperfect diagnostic tests or self-reported outcomes are often used in-lieu of perfect diagnostic tests, especially in large-scale epidemiologic studies that follow hundreds of thousands of subjects. Recent studies indicate that the sensitivity of self-reported diabetes outcomes in the WHI can range from 45%–60% with a specificity of 99% (Margolis et al., 2014). In these settings, analytical approaches that ignore the error in the observed time to event outcome can result in loss of power and an increased rate of false discovery (Gu et al., 2015). Self-reported outcomes are frequently collected in large, observational studies and will likely become increasingly more frequent as more cost effective study designs are considered.

A rich literature exists for analyzing outcomes measured with error. Previous work in this area includes methods for error-prone outcomes with application to data collected from laboratory-based diagnostic tests, including likelihood based methods and through the Hidden Markov Model framework (Balasubramanian and Lagakos (2003); Jackson et al. (2003)). However, while all these methods account for mis-measured outcomes, none of them are applicable to high dimensional datasets. Estimating variable importance in high dimensional data settings has been an active area of research. Several algorithms have been proposed specifically for time to event outcomes. L_p shrinkage methods have been extended to accommodate time to event outcomes, by replacing the observed data likelihood by the Cox partial likelihood. Other approaches include the use of hierarchical clustering to reduce the dimensionality of the covariate space, such as the tree harvesting approach. Variance based methods such as supervised principal components have also been proposed. A comprehensive review of methods for the analysis of high dimensional data applicable to time to event outcomes can be found in (Witten and Tibshirani, 2010). Random Survival Forests (Ishwaran et al., 2008) (RSF) is an ensemble tree-based algorithm for variable selection in high dimensional datasets, in the presence of right-censored time to event outcomes. RSF enjoys all the properties of Random Forests (Breiman, 2001) including computational efficiency and good prediction performance with low generalization error. This algorithm is particularly useful in settings where the covariate space is characterized by complex inter-relationships including the presence of interaction effects with respect to the survival outcome.

In this paper, we propose an extension of the RSF algorithm (Ishwaran et al., 2008) for variable selection in high dimensional data settings while simultaneously accounting for a time to event outcome that is measured with error. Our work is motivated by self-reported outcomes that are routinely collected in large-scale epidemiologic studies, such as the WHI (Anderson et al., 1998). The methods equally apply to settings in which an imperfect, laboratory-based diagnostic test is utilized to assess the occurrence of a silent event. Examples of such data include outcomes extracted from electronic medical records which can be imperfect. The proposed algorithm incorporates a formal likelihood framework that accommodates sequentially administered, error-prone self-reports or laboratory based diagnostic tests (Gu et al., 2015). The original RSF algorithm is modified to account for error-prone outcomes by incorporating a new splitting criterion based on a likelihood ratio test statistic. A new permutation based metric for variable importance is proposed. In Section 2, we introduce notation, form of the likelihood and present the modified RSF algorithm. In Section 3, we present simulation studies evaluating the performance of our proposed algorithm to the original RSF algorithm. Here we separately consider the setting of continuous covariates and categorical covariates such as in genome-wide association studies (GWAS). In Section 4, we apply the proposed methods to a dataset of 88,277 Single Nucleotide Polymorphisms (SNPs) on a subset of 9,873 women in the WHI Clinical Trial and Observational Study SNP Health Association Resource (SHARe). The goal of these analyses is to discover the subset of SNPs that are associated with incidence of type II diabetes. We present a discussion of future directions and potential limitations of the proposed methods in Section 5. The methods illustrated in this paper have been implemented in an R software package icRSF, which is available at the Comprehensive R Archive Network (CRAN) website (R Core Team, 2018; Xu et al., 2018).

2 Methods

In Section 2.1, we present notation and the form of the likelihood for time to event outcomes, in the presence of error-prone, self-reported outcomes. In Section 2.2, we describe the steps in the modified RSF algorithm and in Section 2.3, we describe the likelihood ratio test based splitting criterion and associated variable importance metric.

2.1 Notation, Likelihood and Estimation

Let X refer to the random variable denoting the unobserved time to event for an individual, with associated survival, density and hazard functions denoted by S(x), f(x) and λ(x), for x ≥ 0 respectively. The time origin is set to 0, corresponding to the baseline visit at which all subjects enrolled in the study are assumed to be event-free. In other words, Pr(X > 0) = 1. Without loss of generality, we set X = ∞ when the event of interest does not occur. Let N denote the number of subjects and n_i denote the number of visits for the i^th subject during the follow-up period. At each visit, we assume that each subject would self report their disease status as either positive or negative. For example, at each semi-annual (WHI-CT) or annual contact (WHI-OS), all participants were asked, “Since the date given on the front of this form, has a doctor prescribed any of the following pills or treatments?” Choices included “pills for diabetes” and “insulin shots for diabetes”. Thus, incident treated diabetes was ascertained, and was defined as a self-report of a new physician diagnosis of diabetes treated with oral drugs or insulin.

For the i^th subject, we let R_i = {R_i1,· · ·, R_ini} and t_i = {t_i1, · · ·, t_ini} denote the 1 × n_i vectors of self-reported, binary outcomes and corresponding visit times, respectively. In particular, R_ik is equal to 1 if the k^th self-report for the i^th subject is positive (indicating occurrence of the event of interest such as diabetes) and 0 otherwise. We assume that self-reports are collected at pre-scheduled visits up to the time of the first positive self-report - thus, the vectors of test results (R_i), visit times (t_i) and the number of self-reports collected per subject (n_i) are random. Let τ₁, · · ·, τ_J denote the distinct, ordered visit times in the dataset among N subjects, where 0 = τ₀ < τ₁ < ... < τ_J < τ_J+1 = ∞ - thus, the time axis can be divided into J + 1 disjoint intervals, [0, τ₁), [τ₁, τ₂), · · ·, [τ_J, ∞).

The joint probability of the observed data for the ith subject can be expressed as:

$$\begin{gathered} g({\mathbf{R}}_{\mathbf{i}},{\mathbf{t}}_{\mathbf{i}},n_i)=\sum _{j=1}^{J+1}Pr({\tau }_{j-1}<X_i\le {\tau }_j)\text{Pr}({\mathbf{R}}_{\mathbf{i}},{\mathbf{t}}_{\mathbf{i}},n_i\mid {\tau }_{j-1}<X_i\le {\tau }_j) \\ =\sum _{j=1}^{J+1}{\theta }_j\text{Pr}({\mathbf{R}}_{\mathbf{i}},{\mathbf{t}}_{\mathbf{i}},n_i\mid {\tau }_{j-1}<X_i\le {\tau }_j) \end{gathered}$$

where θ_j = Pr(τ_j−1 < X ≤ τ_j), τ₀ = 0 and τ_J+1 = ∞.

To simplify the form of the expression above, we make the assumption that given the true time of event X_i, an individual’s n_i self-reports are independent. That is,

$$Pr({\mathbf{R}}_{\mathbf{i}}\mid X_i,{\mathbf{t}}_{\mathbf{i}})=\prod _{k=1}^{n_i}Pr(R_{ik}\mid X_i,t_{ik})$$

This assumption implies that the observed values of other self-reported outcomes do not provide additional information about the distribution of a particular self-reported outcome from that provided by the actual time of the event. We note that this assumption is analogous to the common assumption in measurement error regression models that the conditional distribution of the response variable, given the covariate and its proxy, is the same as the conditional distribution given only the covariate. It can be shown that the joint probability of the observed data for the ith subject can be simplified as:

$$\begin{gathered} g({\mathbf{R}}_{\mathbf{i}},{\mathbf{t}}_{\mathbf{i}},n_i)=\sum _{j=1}^{J+1}{\theta }_j\left[\prod _{k=1}^{n_i}Pr(R_{ik}\mid {\tau }_{j-1}<X_i\le {\tau }_j,t_k)\right] \\ =\sum _{j=1}^{J+1}{\theta }_j{C}_{ij} \end{gathered}$$ (1)

where $C_{ij}=[{\prod }_{k=1}^{n_i}Pr(R_{ik}\mid {\tau }_{j-1}<X_i\le {\tau }_j,t_k)]$ (Gu et al., 2015). We assume that the probability of a positive self-report at the kth visit (R_ik = 1) conditional on the interval containing the true event time and visit time can be expressed as:

$$Pr(R_{ik}=1\mid {\tau }_{j-1}<X_i\le {\tau }_j,t_k)=\{\begin{array}{cc}{\phi }_1,& t_k\ge {\tau }_j\\ 1-{\phi }_0,& t_k\le {\tau }_{j-1}\end{array}$$

Here, φ₁ and φ₀ denote the sensitivity and specificity of self-reports, respectively. Thus the terms C_ij, for j = 1, · · ·, J + 1 in equation (1) can be expressed as a product involving the constants φ₁ and φ₀. Thus, in the absence of covariates, the log likelihood for a random sample of N subjects can be expressed as:

$$\begin{gathered} l(\mathit{\theta })=log(L(\mathit{\theta }))=\sum _{i=1}^{N}log(\sum _{j=1}^{J+1}{C}_{ij}{\theta }_j) \\ =\sum _{i=1}^{N}log(\sum _{j=1}^{J+1}{D}_{ij}{S}_j) \end{gathered}$$

where $S_j=Pr(X>{\tau }_{j-1})={\sum }_{l=j}^{J+1}{\theta }_l$. Here, the vector of interval probabilities can be expressed as θ = T_rS, where T_r is the (J +1)×(J +1) transformation matrix and D_N×(J+1) = C × T_r. For the special case where self-reports are perfect (φ₁ = φ₀ = 1), the likelihood above reduces to the non-parametric likelihood for interval censored observations given in Turnbull (1976).

In most settings, including the WHI, it is of interest to evaluate the association of a vector of covariates with respect to the time to event of interest. Let Z denote the P × 1 vector of covariates with corresponding P × 1 vector of regression coefficients denoted by β. To incorporate the effect of covariates, we assume the proportional hazards model, λ(x|Z = z) = λ₀(x)e^z′β, or equivalently, S(x|Z = z) = S₀(x)^ez′β.

To derive the form of the log-likelihood based on the assumption of the proportional hazards model, we first re-parameterize the log likelihood in terms of the of the survival function, S = (1 = S₁, S₂, · · ·, S_J+1)^T, where S_j = p(X > τ_j−1). Since $S_j={\sum }_{l=j}^{J+1}{\theta }_l$, the vector of interval probabilities can be expressed as θ = T_rS, where T_r is the (J + 1) × (J + 1) transformation matrix. Let C = [C_ij] denote the N × (J + 1) matrix of the coefficients, C_ij, and let the N × (J + 1) matrix D be defined as D_N×(J+1) = C × T_r. Then, the log-likelihood function for the one-sample setting can be expressed as

$$l(\mathbf{S})=\sum _{i=1}^{N}log(\sum _{j=1}^{J+1}{D}_{ij}{S}_j),$$ (2)

where S₁ = 1 and S₂, S₃, · · ·, S_J+1 are the unknown parameters of interest.

Let 1 = S₁ > S₂ > ... > S_J+1 denote the baseline survival functions (i.e. corresponding to Z = 0), evaluated at the left boundaries of the intervals [0, τ₁), [τ₁, τ₂), · · ·, [τ_J, ∞). Then, for subject i, with corresponding covariate vector z_i, $S_j^{(i)}={(S_j)}^{e^{{\mathbf{z}}_i^{\prime }\mathit{\beta }}}$. Thus, the log-likelihood function for a random sample of N subjects in equation (2) can be extended to incorporate covariates as

$$l(\mathbf{S},\mathit{\beta })=\sum _{i=1}^{N}log(\sum _{j=1}^{J+1}{D}_{ij}{(S_j)}^{e^{{\mathbf{z}}_i^{\prime }\mathit{\beta }}}).$$ (3)

The elements of the D matrix are functions of the observed data including the visit times, the corresponding self-reported results (t_i, R_i for i = 1, · · ·, n_i), and the constants φ₀, φ₁. Assuming that φ₀, φ₁ are known, the maximum likelihood estimates of the unknown parameters β₁, · · ·, β_P, S₂, · · ·, S_J+1 can be obtained by numerical maximization of the log-likelihood function in equation (3), subject to the constraints that 1 > S₂ > S₃ >· · ·> S_J+1 > 0. Statistical inference regarding the parameters of interest (β₁, · · ·, β_P, S₂, · · ·, S_J+1) can be made by using asymptotic properties of the maximum likelihood estimators (Cox and Hinkley (1979)). The estimated covariance matrix of the maximum likelihood estimates can be obtained by inverting the Hessian matrix. Hypothesis tests regarding the unknown parameters can be carried out using the likelihood ratio or Wald test.

2.2 Modified Random Survival Forests (RSF)

We describe the key steps involved in implementing the modified RSF algorithm for error-prone self-reported outcomes. The details regarding the splitting criterion and estimation of variable importance are described in Section 2.3.

1. Draw b = 1, · · ·, B bootstrap samples of size N from the original data. As is typical of the bootstrap procedure, we expect that on average $\frac{1}{3}$ of the data will be excluded - this subset is denoted as the out-of-bag (OOB) sample.

2. Corresponding to each bootstrap sample, grow a survival tree. At each node of the tree, randomly select a user-defined number of candidate variables, p^* < P. Among the subset of p^* variables, select the variable and corresponding value of split that maximizes the likelihood ratio test splitting criterion (see Section 2.3). Split the parent node into two daughter nodes based on the selected variable and its splitting value.

3. Grow the tree to full size until the number of subjects in the terminal node is equal to or fewer than a user defined parameter, M. An additional, the user can specify a p value threshold (e.g. 0.1), such that splitting of nodes will stop if none of the randomly selected variables satisfy a likelihood ratio test p value less than the threshold indicating no association with outcome. In this process, the tree separates dissimilar subjects into distinct terminal nodes - thus, each terminal node will include a homogenous subset of subjects with respect to the distribution of the time to event of interest.

4. For each tree corresponding to each bootstrap sample (b = 1, · · ·, B), calculate the OOB log likelihood, l_b. The value of the OOB log likelihood is used to calculate a permutation based variable importance metric (See Section 2.4 for details). Use the variable importance metric to rank variables from most to least important with regard to its association with the time-to-event outcome.

2.3 Node Splitting Criterion and Variable Importance

Here we describe our proposed criterion for splitting nodes in a survival tree and an associated measure of variable importance.

1. Criterion for splitting nodes

As in CART, survival trees are binary trees grown by recursive splitting of parent nodes. At each node of a tree, subjects are assigned to one of two daughter nodes by a split on a variable Z and associated threshold c, such that the resulting daughter nodes have maximal difference in outcome. Assume that a specific node includes N^* subjects and that p^* < P variables are randomly selected as candidate variables for splitting the node into two daughter nodes. The process of splitting this parent node into two daughter nodes is based on identifying the variable and its splitting value that maximizes the likelihood ratio test statistic criterion described below:

For each candidate variable Z_k and a corresponding splitting value c_k, we defined a new random variable $Z_k^{\ast }=1$ if Z_k < c_k and $Z_k^{\ast }=0$, otherwise. We obtain the maximized value of the log likelihood for all N^* subjects, based on the PH model including $Z_k^{\ast }$ as the single covariate, with corresponding regression coefficient ${\beta }_k^{\ast }$ (Equation (3)). We compare this full model to the null model (without $Z_k^{\ast }$) and obtain the value of the likelihood ratio test statistic for testing the null hypothesis $H_0:{\beta }_k^{\ast }=0$. The random variable corresponding to the best split (denoted $Z_m^{\ast }$ with associated regression coefficient ${\beta }_m^{\ast }$) is found by searching over all p^* candidate covariates and all possible splitting values to find that which maximizes the likelihood ratio test statistic. We note that for continuous covariates, this step is implemented by searching over a user-defined grid of possible splitting values.

Comparison to original RSF

The proposed splitting criterion differs significantly from that in the RSF algorithm - the randomSurvivalForest R software package includes three variations of the log rank splitting rule as well as a conservation of events splitting rule (Ishwaran and Kogalur, 2007). While these approaches are appropriate for right censored event times, they do not allow for error in the outcome as is characteristic of self-reports.

2. Criterion to stop splitting

Each tree is grown until the number of subjects in a node is fewer than a user specified threshold and/or none of the randomly selected p^* variables have a p value less than a user defined threshold (e.g. 0.1) corresponding to their univariate association with the time to event outcome in a Cox PH model.

3. Variable importance

At each node, the unknown parameters ( ${\beta }_m^{\ast }$, S₂, S₂, . . . , S_J+1) are estimated by maximizing the log likelihood shown in Equation (3) that incorporates the covariate $Z_m^{\ast }$. For every survival tree in the ensemble, a value of log-likelihood based on the OOB sample (l_b, for b = 1, · · ·, B) is calculated as follows: Subject i in the OOB sample of tree b is dropped down the tree and assigned a terminal node. Let l_ib denote the log likelihood contribution for subject i in the OOB sample for tree b. The value of l_ib is calculated based on the log likelihood in Equation (3), using parameters ( ${\widehat{\beta }}_m^{\ast }$, Ŝ₂, Ŝ₂, . . . , Ŝ_J+1) obtained at the immediate parent of the terminal node to which subject i is assigned. The log-likelihood for tree b (l_b) is obtained as the sum of the log-likelihood contributions of all subjects in the OOB sample - that is, l_b = Σ_i∈OOBl_ib.

We obtain a measure of variable importance for each variable Z_k by permuting its values, while all other variables remain as in the original dataset. Following a random permutation of variable Z_k, the value of the OOB log-likelihood l̃_bk is calculated, for every tree b = 1 · · · B based on the OOB sample. The variable importance for Z_k is calculated as:

$${\mathit{VIMP}}_k=\sum _{b=1}^{B}max\left\{(l_b-{\stackrel{\sim }{l}}_{bk}),0\right\}$$ (4)

Average values of VIMP_k are reported for each covariate k, by averaging over multiple permutations of Z_k. Larger values of VIMP_k indicate that the covariate Z_k has strong association with the outcome. In Section 3.1 of the Supplement, we illustrate the performance of the proposed variable importance metric in a simulated dataset.

Comparison to original RSF

In the original RSF algorithm, variable importance for each variable x is obtained as the difference between the average prediction error of the ensemble based on randomized x assignments from the prediction error of the original ensemble. Prediction error is calculated from the Harrell’s concordance index corresponding to the cumulative hazard function estimated for each subject in the dataset.

3 Simulation

To motivate the proposed algorithm, we illustrate the degradation in the variable selection performance of the original RSF algorithm, with increasing error in the self-reported outcomes (See Supplement, Section 2). In Sections 3.1 – 3.3, we present results from three simulation studies considering different variable types to compare the performance of our proposed modified RSF algorithm to the original RSF algorithm proposed by Ishwaran, H. et al. (2008).

Simulation set-up

Each simulated dataset included N = 100 subjects and P = 100 covariates, of which the first five (Z₁, · · ·, Z₅) were assumed to be true biomarkers. We assumed that the true time to event followed an exponential distribution and that the set of five biomarkers influenced the outcome through a proportional hazards model. We note that the exponential distribution assumption is only used to set the values of the parameters S₂, · · ·, S_J+1 and is not an assumption of the proposed approach. Let λ₀ denote the hazard corresponding to the reference group (corresponding to Z₁ = · · · = Z₅ = 0). Under the proportional hazards model, the hazard for a subject with arbitrary values of the covariates Z₁, · · ·, Z₅ is given by λ_{Z1,Z2,Z3,Z4,Z5} = λ₀e^{β₁Z₁+β₂Z₂+β₃Z₃+β₄Z₄+β₅Z₅}. The regression coefficients β₁, · · ·, β₅ were all assumed to be equal and set to 2. The hazard function for the reference group λ₀ was varied such that the cumulative incidence rates during the four year follow-up period were 0.1 and 0.3, respectively. We assumed that the duration of follow-up was 4 years and that there were annual visits at which self-reported outcomes were collected. We considered four settings of (sensitivity, specificity) for self-reported outcomes: (1.00, 1.00), (0.75, 1.00), (0.61, 0.995), (1.00, 0.9) as well as two study designs - the first, in which there were no missed visits; the second, in which no further visits are scheduled following the first positive self-report. For each subject i, binary self-reported outcomes at each visit at years 1–4 (R_i1, · · ·, R_i4) were simulated by assuming specific values for the sensitivity and specificity of self-reports. For example, assume that the time-to-event for subject i is X_i = 2.5 years, the sensitivity and specificity of self-reported outcomes are φ₁ = 0.9 and φ₀ = 0.7, respectively. Then, the self-reported outcomes at visits 1–4 are simulated according to P(R_i1 = 1 | X_i = 2.5, t_i1 = 1) = P(R_i2 = 1 | X_i = 2.5, t_i2 = 2) = 1 − φ₀ and P(R_i3 = 1 | X_i = 2.5, t_i3 = 3) = P(R_i4 = 1 | X_i = 2.5, t_i4 = 4) = φ₁.

The datasets were analyzed using the original RSF, using the R package randomForest-SRC (Ishwaran and Kogalur, 2015) and the modified RSF algorithm assuming a 1000 trees and user defined threshold no fewer than 10 subjects in a terminal node. The 100 variables were ranked from most to least important based on: (1) variable importance from RSF; and (2) variable importance from modified RSF. The top five ranking variables by each metric were considered as “discovered biomarkers”. The average proportion of datasets in which each of the five true biomarkers was discovered (p̂) and its associate standard error ( $SE=1.96\ast \sqrt{\frac{\widehat{p}(1-\widehat{p})}{100}}$) was calculated for each metric.

3.1 Simulation: Continuous covariates

The 100 covariates per subject were simulated as independent, Gaussian random variables with mean 0 and unit variance. Table 1 presents the average proportion of datasets in which the five true biomarkers were ranked among the top five variables, by each variable importance metric. We present results for both study designs, that is (1) No missing data; and (2) Missing all data following the first positive self-report.

Table 1. Simulation - Continuous covariates.

The average proportion of datasets (±SE) in which the five true biomarkers are ranked among the top five according to three measures of variable importance, namely (1) original RSF algorithm (p_RSF ); and (2) variable importance from the modified RSF algorithm (p₁). 1 − S_J+1, φ₁, φ₀ denote the cumulative incidence in the reference group, sensitivity and specificity, respectively.

1 − Sj+1	φ1	φ0	No missing data		Missing all data following first positive self-report
			pRSF	p1	pRSF	p1
0.10	1.00	1.00	0.736(±0.0441)	0.812(±0.0391)	0.736(±0.0441)	0.786(±0.0410)
	0.75	1.00	0.716(±0.0451)	0.748(±0.0434)	0.716(±0.0451)	0.768(±0.0422)
	0.61	0.995	0.636(±0.0481)	0.684(±0.0465)	0.636(±0.0481)	0.712(±0.0453)
	1.00	0.90	0.518(±0.0500)	0.760(±0.0427)	0.518(±0.0500)	0.586(±0.0493)
0.30	1.00	1.00	0.792(±0.0406)	0.828(±0.0377)	0.792(±0.0406)	0.850(±0.0357)
	0.75	1.00	0.764(±0.0425)	0.794(±0.0404)	0.764(±0.0425)	0.794(±0.0404)
	0.61	0.995	0.686(±0.0464)	0.708(±0.0455)	0.686(±0.0464)	0.736(±0.0441)
	1.00	0.90	0.620(±0.0485)	0.814(±0.0389)	0.620(±0.0485)	0.670(±0.0470)

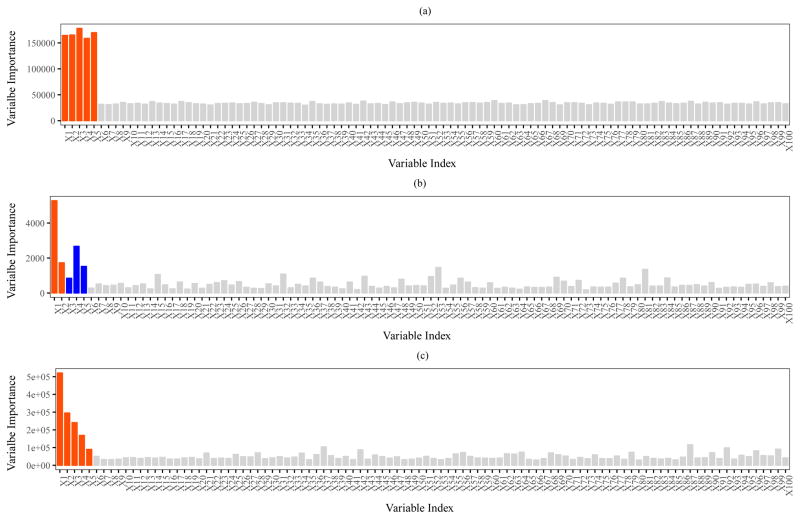
When there is no missing data and when specificity is close to perfect (φ₀ = 0.99, 1.00), the proportion of datasets in which the true biomarkers are discovered by RSF is comparable to that by the modified RSF algorithm. Figure 1(a) shows a bar plot of the average variable importance (across 100 datasets) by modified RSF, for the setting in which 1 − S_J+1 = 0.10, φ₁ = 0.61, φ₀ = 0.995 and no missed visits,. The average variable importance for each of the five true biomarkers is more than six times larger than that of a covariate not associated with outcome (noise).

Figure 1. Variable importance from modified Random Survival Forests.

Barplot of variable importance for each of 100 covariates, considering the setting in which 1 − S_J+1 = 0.10, φ₁ = 0.61, φ₀ = 0.995 and there are no missed visits. (a) Continuous covariates - average variable importance over 100 simulated datasets is shown, where the first five (shown in red) represent the true biomarkers. (b) GWAS data - variable importance for a representative simulation is shown (results are not averaged as the identity of the true biomarkers varies between simulations). ’Blue’ indicates true biomarkers with MAF ∈ (0.35, 0.5] and ‘red’ indicates true biomarkers with MAF ∈ (0, 0.35]. (c) Omics data - average variable importance over 100 simulated datasets is shown, where the first five (shown in red) represent the true biomarkers.

On the other hand, when specificity is low, our proposed algorithm achieves significantly better performance when compared to RSF. For example, when the cumulative incidence is 10%, sensitivity is 1.00 and specificity is 0.90, each of the top five biomarkers is discovered by the original and modified RSF algorithms with probabilities 0.52 (SE = ±0.05) and 0.76 (SE = ±0.04), respectively. A similarly improved performance by the modified RSF algorithm was observed when the cumulative incidence was larger (1 − S_J+1 = 0.30). However, when we assumed that no follow-up data are collected following the first positive self-report, the modified RSF algorithm did not achieve any statistically significant improvement in variable selection performance when compared to the original RSF algorithm. This highlights the loss of information that occurs when data collection ceases following the first positive self-report, in settings where the specificity is less than perfect. In all settings considered, the average probability of being “discovered” for one of the 95 non-biomarkers did not exceed 0.03 (SE = ±0.02) and was comparable between both the original and modified RSF algorithms.

3.2 Genome-wide Association Study (GWAS)

To incorporate the structure of data observed in a GWAS study, we fixed the 100 × 100 design matrix of covariates to equal a randomly sampled subset of the GWAS data in the WHI Clinical Trials and Observational Study SHARe. We randomly selected 100 out 10,832 subjects and 100 out of 909,622 SNPs available in the dataset. Of the 100 selected SNPs, 53 SNPs had Minor Allele Frequencies (MAF) values ≤ 0.35 and 47 had MAF (0.35, 0.50]. For computational efficiency, each SNP was converted into a binary variable by coding the ’AA’ genotype as 0 and the ‘ Aa’ and ‘ aa’ genotypes as 1. In each simulation, five of the 100 SNPs were randomly selected to be the true biomarkers with β = 1. Tables 2 and 3 present the average proportions of simulated datasets in which the five true biomarkers were ‘discovered’, for the settings of (1) No missing data and (2) Missing all data following the first positive self-report, respectively. In each table, we separately report the results for biomarkers (SNPs) with MAF in the ranges (0.00, 0.35] and (0.35, 0.50].

Table 2. Simulation - Genome-wide association study (GWAS).

The average proportion of datasets (±SE) in which the five true biomarkers are ranked among the top five according to two measures of variable importance, namely (1) original RSF algorithm (p_RSF), and (2) variable importance from the modified RSF algorithm (p₁). 1 − S_J+1, φ₁, φ₀ denote the cumulative incidence in the reference group, sensitivity and specificity, respectively. The results are stratified by Minor Allele Frequency categories of (0, 0.35] and (0.35, 0.5]. We assume the setting of no missed visits.

1 − Sj+1	φ1	φ0	No missing data
			MAF ∈ (0, 0.35]		MAF ∈ (0.35, 0.5]
			pRSF	p1	pRSF	p1
0.10	1.00	1.00	0.578(±0.0494)	0.560(±0.0496)	0.725(±0.0447)	0.701(±0.0458)
	0.75	1.00	0.575(±0.0494)	0.566(±0.0496)	0.702(±0.0457)	0.710(±0.0454)
	0.61	0.995	0.487(±0.0500)	0.511(±0.0500)	0.594(±0.0491)	0.657(±0.0475)
	1.00	0.90	0.339(±0.0473)	0.556(±0.0497)	0.435(±0.0496)	0.703(±0.0457)
0.30	1.00	1.00	0.619(±0.0486)	0.623(±0.0485)	0.737(±0.0440)	0.754(±0.0431)
	0.75	1.00	0.607(±0.0488)	0.578(±0.0494)	0.688(±0.0463)	0.692(±0.0462)
	0.61	0.995	0.529(±0.0499)	0.526(±0.0499)	0.571(±0.0495)	0.654(±0.0476)
	1.00	0.90	0.427(±0.0495)	0.563(±0.0496)	0.533(±0.0499)	0.767(±0.0423)

Table 3. Simulation - Genome-wide association study (GWAS).

The average proportion of datasets (±SE) in which the five true biomarkers are ranked among the top five according to two measures of variable importance, namely (1) original RSF algorithm (p_RSF ), and (2) variable importance from the modified RSF algorithm (p₁). 1 − S_J+1, φ₁, φ₀ denote the cumulative incidence in the reference group, sensitivity and specificity, respectively. The results are stratified by Minor Allele Frequency categories of (0, 0.35] and (0.35, 0.5]. We assume that all visits following the first positive self-report are missing.

1 − Sj+1	φ1	φ0	Missing all data following first positive self-report
			MAF ∈ (0, 0.35]		MAF ∈ (0.35, 0.5]
			pRSF	p1	pRSF	p1
0.10	1.00	1.00	0.578(±0.0494)	0.586(±0.0493)	0.725(±0.0447)	0.704(±0.0456)
	0.75	1.00	0.575(±0.0494)	0.569(±0.0495)	0.702(±0.0457)	0.706(±0.0456)
	0.61	0.995	0.487(±0.0500)	0.510(±0.0500)	0.594(±0.0491)	0.635(±0.0481)
	1.00	0.90	0.339(±0.0473)	0.313(±0.0464)	0.435(±0.0496)	0.463(±0.0499)
0.30	1.00	1.00	0.619(±0.0486)	0.600(±0.0490)	0.737(±0.0440)	0.753(±0.0431)
	0.75	1.00	0.607(±0.0488)	0.580(±0.0494)	0.688(±0.0463)	0.710(±0.0454)
	0.61	0.995	0.529(±0.0499)	0.528(±0.0499)	0.571(±0.0495)	0.672(±0.0469)
	1.00	0.90	0.427(±0.0495)	0.465(±0.0499)	0.533(±0.0499)	0.605(±0.0489)

As expected, across all settings both algorithms were better able to discover biomarkers that have a higher MAF when compared to biomarkers with lower MAF. As in the simulations with the continuous covariates, when no follow-up data are collected following the first positive self-report, the modified RSF algorithm and the original RSF algorithm achieve similar performance with respect to the probability of discovering true biomarkers. Figure 1(b) shows a bar plot of the variable importance metric by modified RSF for a representative simulated dataset, for the setting in which 1 − S_J+1 = 0.10, φ₁ = 0.61, φ₀ = 0.995 and no missed visits - the variable importance metrics were not averaged across simulations as the identity of the five true biomarkers varied randomly between simulated datasets. ’Blue’ indicates true biomarkers with MAF ∈ (0.35, 0.50] and ‘red’ indicates true biomarkers with MAF ∈ (0.00, 0.35]. As expected, true biomarkers with MAF ∈ (0.35, 0.50] were more likely to rank higher than true biomarkers with MAF ∈ (0.00, 0.35].

However, when there is no missing data and when specificity is less than perfect (φ₀ = 0.90), we observed significantly improved performance by the modified algorithm when compared to the original algorithm. For example, when the cumulative incidence of events is 10%, φ₀ = 0.90 and φ₁ = 1.00, and biomarkers have MAF in the range (0, 0.35], each biomarker is discovered by the original and modified RSF algorithms with probabilities 0.34 (SE = ±0.047) and 0.56 (SE = ±0.050), respectively. When biomarkers have MAF in the range (0.35, 0.50], each biomarker is discovered by the original and modified RSF algorithms with probabilities 0.44 (SE = ±0.050) and 0.70 (SE = ±0.046), respectively.

3.3 Cardiovascular Disease Omics Study

We incorporated data from a cardiovascular disease ‘omics’ study that was conducted to discover prognostic biomarkers in blood plasma for near-term cardiovascular events. Subjects were selected from the CATHGEN project, which collected peripheral blood samples from consenting research subjects undergoing cardiac catheterization at Duke University Medical Center from 2001 through 2011. 68 cases were selected from among individuals who had a major adverse cardiac event (MACE) within two years following the time of their sample collection. In a 1:1 matched study design, 68 controls were selected from individuals who were MACE-free for the two years following sample collection and were matched to cases on age, gender, race/ethnicity and severity of coronary artery disease. High-content mass spectrometry and multiplexed immunoassay-based techniques were employed to quantify 625 proteins and metabolites from each subject’s serum specimen. Comprehensive metabolite profiling of the individual samples was based on a combination of four platforms employing mass spectrometry (MS) based techniques to profile lipids, fatty acids, amino acids, sugars and other metabolites. Proteomic analysis was based on a combination of targeted methods using a quantitative multiplexed immunoassay technique as well as a comprehensive protein profiling strategy based on tandem mass spectrometry. A detailed description of the mass spectrometry based platforms and proteomics analysis can be found in a previous publication (Guo and Balasubramanian, 2012).

To incorporate the structure of observed data, we selected a random subset of 100 out the 625 covariates for all 136 subjects - of these, 5 were selected to represent the set of ‘true’ biomarkers, each with β = 1. Each of the 100 covariates were standardized to render them with mean 0 and unit variance. The $\left(\begin{array}{c}100\\ 2\end{array}\right)$ pairwise Pearson correlations between covariate pairs ranged from −0.54 to 1.0 (IQR [−0.07, 0.16]), exhibiting the complex dependence structure commonly observed in ‘omics’ datasets (Figure 4 of Supplement). The pairwise correlations between the five true biomarkers ranged from −0.22 to 0.20. Each of the five biomarkers also exhibited varying marginal distributions, as seen in Figure 5 of the Supplement. Table 1 in the Supplement presents the average proportions of simulated datasets in which the five true biomarkers were ‘discovered’, for the settings of (1) No missing data and (2) Missing all data following the first positive self-report, respectively. As in previous simulations, when no follow-up data are collected following the first positive self-report, the modified RSF algorithm and the original RSF algorithm achieved similar performance. When there is no missing data and when specificity is less than perfect (φ₀ = 0.90), we observed significantly improved performance by the modified RSF algorithm when compared to the original RSF algorithm. For example, when the cumulative incidence of events is 10%, φ₀ = 0.90 and φ₁ = 1.0, the average probability of being discovered by the original and modified RSF algorithms were 0.46 (SE = ±0.05) and 0.70 (SE = ±0.05), respectively. Figure 1(c) shows a bar plot of average variable importance, when 1 − S_J+1 = 0.10, φ₁ = 0.61, φ₀ = 0.995 and there are no missed visits. The bars corresponding to the first five variables shown in red correspond to the true biomarkers. Average variable importance for the five biomarkers varied considerably, reflecting the differences in the shapes of their marginal distributions.

4 Application: Women’s Health Initiative Clinical Trials and Observational Study SHARe

Data from the WHI Clinical Trial and Observational Study SHARe, which includes data on 909,622 SNPs on 10,832 African American and Hispanic women. Prevalent and incident Type 2 diabetes were determined by self-reports collected at annual (WHI Observational Study) or semi-annual (WHI Clinical Trials) visits. Incident treated diabetes was ascertained by a positive self-report of a new physician diagnosis of diabetes treated with oral drugs or insulin. No further information was collected with regard to a new diabetes diagnosis following the first positive self-report. We illustrate the application of our proposed algorithm using this dataset to identify SNPs associated with incident diabetes. The data used in this analysis can be obtained by submitting a research use statement and associated supplemental documentation as described in the Women’s Health Initiative Clinical Trial and Observational Study SHARe dbGaP website. See WHI SHARe dbGaP.

Data pre-processing

Individuals who self-reported diabetes at baseline were excluded (N=959). The analysis dataset included 9,873 subjects from the following race/ethnicity groups - African Americans (N=6,704), Hispanic Americans (N=3,169). We included follow-up until 2013, resulting in a median duration of follow-up of 12 years including 108,197 person-years of total follow-up. During the course of follow-up, 20.34% of women self-reported incident diabetes.

We follow a multi-step procedure to filter the GWAS dataset that included 909,622 SNPs. First, SNPs that meet at least one of the following criteria were excluded from our analysis: 1) greater than 1% of missing values (68,176 SNPs); 2) MAF below 5% (63,019 SNPs); 3) a Hardy-Weinberg equilibrium test p-value less than 0.05 (467,735 SNPs). We carried out a set of univariate analyses to test the association of each remaining SNP with incident diabetes, while adjusting for population substructure. To quantify the extent of genetic variability that is explained by race/ethnicity, we carried out a principal components analysis and extracted the top two principal components that accounted for 1.88% and 0.48% of the total variability, respectively (Price et al., 2006). The association of each SNP with incident diabetes was evaluated by fitting a model based on the likelihood in equation (3) (Gu et al., 2015). P values from a likelihood ratio test were calculated and SNPs with p > 0.20 were excluded from analysis (222,415 SNPs). Following these filtering procedures, we included 88,277 SNPs in our analysis.

Methods

The analysis dataset included 88,277 SNPs on 9,873 subjects. The analyses were run by allowing three levels for each SNP, that is, ‘ AA’, ‘Aa’, ‘aa’. All missing entries are imputed assuming the major allele. The analysis adjusted for the top two principal components to correct for population stratification and included the following potential confounders: smoking status, alcohol intake, age, education, WHI study, BMI, recreational physical activity, dietary energy intake, family history of diabetes, and hormone therapy use. The baseline characteristics of the 9,873 subjects is described in Table 2 in the Supplement. (Gu et al., 2015). The ranking of individual SNPs was assessed by the following methods:

1. Univariate Cox Proportional Hazards (PH) model: Statistical significance of each SNP is assessed individually, while adjusting for population stratification and other confounders. The time to event was calculated as the time between the enrollment date and the date of the first positive self-report (observed event), or the date of last contact (censored observation). The SNPs were ranked according to the Wald test p-value of the null hypothesis of no association between the SNP and incident diabetes.

2. RSF: This multivariable analysis was based on the original RSF algorithm (Ishwaran et al., 2008) using the R package randomForestSRC (Ishwaran and Kogalur, 2015). The input to the algorithm included the set of 88,277 SNPs as well as the top two principal components (to adjust for population stratification) and potential confounders. The time to event outcome is defined as in the Cox PH model. A survival forest of 1000 trees was built with a node splitting criterion based on the log rank test. SNPs were ranked according to a variable importance metric obtained as the difference in the cumulative hazard function before and after permutation.

3. Modified RSF: This multivariable analysis was based on the proposed algorithm using the R package icRSF (R Core Team, 2018; Xu et al., 2018) based on the input of the set of 88,277 SNPs as well as the top two principal components (to adjust for population stratification) and potential confounders. The sensitivity and specificity of self-reported diabetes were assumed to be 0.61 and 0.995, respectively (Margolis et al., 2014; Gu et al., 2015). A survival forest of 1000 trees was built and the minimum terminal node size was fixed at 5 subjects. SNPs were ranked according to a variable importance metric obtained as the difference in the OOB log-likelihood before and after permutation.

Results

Figure 6 in the Supplement shows a bar plot of the variable importance of each SNP (1 through 88,277) resulting from the analysis based on the proposed algorithm - the horizontal dashed line indicates the variable importance threshold separating the top 10 SNPs from the rest. SNPs that were found to rank among the top 10 most important by at least one of the above analyses are shown in Table 4. Each SNP is annotated with its host gene (if known) and the left and right flanking genes. A total of 27 SNPs were identified in the top 10 by at least one of the three strategies, while simultaneously adjusting for population stratification and potential confounding by other factors. We examined the degree of linkage disequilibrium (LD) between all pairs of the 27 SNPs in Table 4 - only 1 pair of SNPs was found to have r² values of 0.05 or larger.

Table 4.

Rankings of individual SNPs in the WHI Clinical Trial and Observational Study SHARe from the following analyses: (1) Univariate Cox PH model; (2) RSF; (3) modified RSF. Each analysis simultaneously adjusted for all potential confounding variables as well as the top two principal components to account for population stratification. SNPs are ordered from most (rank= 1) to least important (rank > 1000) with regard to their association with time to incident Type 2 diabetes.

SNP	Gene	Left Gene	Right Gene	Cox PH	RSF	modified RSF
rs10777370		DCN	BTG1	102	> 1000	1
rs639724		LOC100130372	LOC284749	> 1000	31	2
rs16983007				715	> 1000	3
rs7187364	WWOX	LOC645947	LOC729251	615	> 1000	4
rs2805429	RYR2	MT1P2	LOC100130331	4	> 1000	5
rs10733596	SNX30	C9orf80	SLC46A2	246	> 1000	6
rs16997235				26	4	7
rs17087990		ATXN8OS	DACH1	151	> 1000	8
rs17627111	ESRRG	USH2A	GPATCH2	> 1000	> 1000	9
rs10126793				15	20	10
rs16917265		C9orf80	SNX30	1	1	47
rs16991792	LOC731957	SYN3	LARGE	7	> 1000	248
rs1277957		EFNB1	PJA1	> 1000	2	392
rs10859620	HERC3	LOC100129137	NAP1L5	30	9	> 1000
rs1457586	ZNF385D	VENTXP7	LOC728516	2	156	> 1000
rs17300926				6	528	> 1000
rs17555633	SLIT3	LOC728095	CCDC99	> 1000	3	> 1000
rs7707956		EDIL3	LOC391807	> 1000	5	> 1000
rs2365943	PTPRG	FHIT	LOC100128936	> 1000	6	> 1000
rs9345756		ADH5P4	NUFIP1P	> 1000	7	> 1000
rs7762347		LOC100131805	LOC100129616	> 1000	8	> 1000
rs6553479		LOC402192	LOC100131470	> 1000	10	> 1000
rs2805434	RYR2	MT1P2	LOC100130331	3	> 1000	> 1000
rs137299	LOC731957	SYN3	LARGE	5	> 1000	> 1000
rs286588		MRPS35P1	MRPS36P1	8	> 1000	> 1000
rs11769851		tcag7.955	LOC442727	9	> 1000	> 1000
rs1317548	CDC123	NUDT5	CAMK1D	10	> 1000	> 1000

Three SNPs (rs16997235, rs10126793, rs16917265) were ranked among the top 50 by all three strategies. Three SNPs (rs639724, rs2805429, rs10859620) were ranked among the top 50 by two strategies. In addition, several SNPs among the top 10 by the modified RSF algorithm were not detected among the top 1000 by the other two approaches. For example, the top SNPs identified by the modified RSF algorithm (rs10777370, rs7187364, rs16983007) had ranks above 1000 by RSF. The left gene of SNP rs10777370 (DCN) and host gene of rs7187364 (WWOX) have both previously been implicated as a risk allele for Type 2 diabetes (Bolton et al., 2008; Sakai et al., 2013). The host gene of rs17627111 (ESRRG) has been previously shown to be associated with type 2 diabetes in African Americans (Murea et al., 2011). Several other genes that either contain or flank the SNPs identified among the top 10 by at least one analysis have been previously found to be implicated in Type 2 diabetes (Table 3 in the Supplement).

5 Discussion

In this paper, we propose an ensemble tree based algorithm for variable selection in high dimensional datasets, in settings where a time to event outcome is observed with error. The models developed in this paper are motivated by imperfect, self-reported outcomes of incident type 2 diabetes collected in the Women’s Health Initiative. The proposed methods apply to other settings in which the event of interest is diagnosed using an imperfect laboratory-based diagnostic test that is given at prescheduled times during follow-up. For the special case in which the diagnostic tests are perfect, the likelihood incorporated into the algorithm reduces to the Turnbull non-parametric estimator for interval censored outcomes (Turnbull, 1976).

We presented results from simulations, considering different data types and a variety of settings with regard to cumulative incidence of event during the study and sensitivity/specificity of the self-report (or imperfect diagnostic test). We compared the performance of our proposed algorithm to RSF (Ishwaran et al., 2008), which assumes that outcomes are observed without error. We considered datasets in which continuous variables are measured as well as datasets typically seen in GWAS studies. When studies collect self-reports or test results according to a predetermined schedule and when specificity is less than perfect, our proposed algorithm has a significantly better performance with regard to variable selection when compared to the original RSF algorithm. In studies where collection of self-reports or diagnostic test results ceases after the first positive result, our modified algorithm no longer performs better than RSF. We applied the proposed algorithm to data from the WHI Clinical Trial and Observational Study SHARe. Several genes associated with top ranking SNPs were found to be related to the risk of type 2 diabetes in the literature (Table 3 in the Supplement).

The proposed algorithm assumes that the values of sensitivity and specificity of the self-reported outcomes/diagnostic tests are constant. In some applications, these could depend on demographic variables and change over time. In other settings, the sensitivity/specificity parameters could be unknown and require estimation. For these applications, it would be useful to extend the proposed methods. Another direction for future work includes variable selection algorithms for recurrent events (e.g. stroke) identified by self-reports or error-prone procedures. In this setting, one could consider an observed data likelihood based on a Hidden Markov Model framework. In this setting, the observed data correspond to different states that are assumed to be subject to misclassification of the true underlying disease state of the individual (Macdonald and Zucchini, 1997; Jackson, 2011).