Abstract
Spatial attention is the cognitive function that coordinates the selection of visual stimuli with appropriate behavioral responses. Recent studies have reported that phase-amplitude coupling (PAC) of low and high frequencies covaries with spatial attention, but differ on the direction of covariation and the frequency ranges involved. We hypothesized that distinct phase-amplitude frequency pairs have differentiable contributions during tasks that manipulate spatial attention. We investigated this hypothesis with electrocorticography (ECoG) recordings from participants who engaged in a cued spatial attention task. To understand the contribution of PAC to spatial attention we classified cortical sites by their relationship to spatial variables or behavioral performance. Local neural activity in spatial sites was sensitive to spatial variables in the task, while local neural activity in behavioral sites correlated with reaction time. We found two PAC frequency clusters that covaried with different aspects of the task. During a period of cued attention, delta-phase/high-gamma (DH) PAC was sensitive to cue direction in spatial sites. In contrast, theta-alpha-phase/beta-low-gamma-amplitude (TABL) PAC robustly correlated with future reaction times in behavioral sites. Finally, we investigated the origins of TABL PAC and found it corresponded to behaviorally relevant, sharp waveforms, which were also coupled to a low frequency rhythm. We conclude that TABL and DH PAC correspond to distinct mechanisms during spatial attention tasks and that sharp waveforms are elements of a coupled dynamical process.
Keywords: Phase-amplitude coupling, Sharp waves, Cued attention, Reaction time
Introduction
Spatial attention defines a set of cognitive mechanisms that select behaviorally relevant visual information while filtering out behaviorally irrelevant information (Posner 1980). Attention facilitates visuomotor coordination through modulation of neural activity in visual (Corbetta et al. 1990; Mangun and Hillyard 1988; Moran and Desimone 1985), parietal and prefrontal regions during visuomotor tasks (Corbetta et al. 1993; di Pellegrino and Wise 1993; Snyder, Batista, and Andersen 1997). Phase amplitude coupling (PAC) has been proposed as a mechanism underlying attention (Esghaei, Daliri, and Treue 2015; Landau et al. 2015; Schroeder and Lakatos 2009; Szczepanski et al. 2014). PAC quantifies the relationship between the phase of a low frequency signal and the amplitude envelope of a high frequency signal. It has been hypothesized that low-frequency oscillations serve as temporal reference frames for higher frequency (>20 Hz) activity (Bonnefond, Kastner, and Jensen 2017; Canolty and Knight 2010; Lakatos et al. 2008; Mizuseki et al. 2009). These hypotheses are supported by evidence that stimulus perception depends on the phase of ongoing oscillations (Mathewson et al. 2011). However, these hypotheses have been challenged by evidence that non-sinusoidal, sharp waveforms containing multi-spectral components, result in spurious PAC between low and high frequencies (Gerber et al. 2016; Jensen, Spaak, and Park 2016).
Two relevant PAC experiments on cued spatial attention resulted in opposing conclusions. In a human cued target-detection task with distractors, Szczepanski et al. found delta-theta-phase/high-gamma amplitude (2–5 Hz to 100–150 Hz) PAC correlated with reaction time (RT) in cortical sites associated with the dorsal attention network. Correlations were stronger when subjects attended within the receptive hemifield of recording sites (Szczepanski et al. 2014). The authors suggest that PAC enhances spatial attention given positive interactions between PAC, cueing direction and reaction time. In contrast, Esghaei et al. found decreased PAC between low (1–8Hz) and high (30–120 Hz) frequencies when monkeys attended to the receptive field of area MT (Esghaei, Daliri, and Treue 2015). The authors conclude that PAC suppresses attention given its negative covariation with cueing direction.
Beyond differences in recording methodologies, task paradigms and species, each group focused on different low-frequency ranges (e.g. 2–5 Hz for Szczepanski et al. and 1–8 for Esghaei et al.) that may engage distinct neural circuitry. Delta (1–3 Hz) in primary sensory cortices has been shown to reflect rhythmically presented stimuli when attended (Lakatos et al. 2008). Theta (4–7 Hz) and alpha (8–13 Hz) have been associated with sustained attention (Clayton, Yeung, and Cohen Kadosh 2015; Sadaghiani and Kleinschmidt 2016) and inhibition (Mehta, Lee, and Wilson 2002; Rihs, Michel, and Thut 2007). Additional evidence suggests that delta and alpha play opposing roles in selective attention (Lakatos et al. 2016). Finally, recent investigations into the origins of PAC revealed that distinct PAC frequency pairs correspond to waveforms that explain different cognitive processes in a memory task (Vaz et al. 2017). Given these findings, we wondered whether specific PAC frequency pairs corresponded to distinct cognitive elements of a spatial attention task.
In this study, we investigated PAC phenomena during a spatial attention task, and hypothesized that specific PAC frequency pairs correspond to distinct cognitive functions. Additionally, we investigated how non-sinusoidal, sharp waveforms contributed to PAC. Using methods defined by Tort et al. to measure PAC with the modulation index, we used a non-parametric cluster-based statistical approach to find behaviorally relevant PAC frequencies (Maris and Oostenveld 2007; Tort et al. 2010). We functionally classified cortical sites based on their sensitivity to spatial properties of stimuli or behavioral performance. We found that theta-alpha-phase/beta-low-gamma-amplitude (TABL) PAC scaled with reaction time while delta-phase/high-gamma-amplitude was related to cueing direction. Furthermore, we found that non-sinusoidal, sharp waveforms contributed to TABL PAC and developed computationally inexpensive methods to detect them. However, we found that sharp waveforms were behaviorally relevant and coupled to a low frequency oscillation. Our findings show that the functional characteristics of PAC depend critically on low frequency phase and that sharp waves are elements of a coupled dynamical process.
Materials and methods
Subjects and data acquisition
The study included six human participants, of both sexes, with treatment-resistant epilepsy who were undergoing invasive electrocorticography (ECoG) to detect seizure foci. None had vision or attention deficits. The data from three subjects were analyzed with different methods in a previous experiment (Daitch et al. 2013) the remaining data were not previously analyzed. A computer monitor was placed 20 inches away from the subject’s eyes. ECoG data was recorded in the subject’s hospital room from platinum clinical electrodes with 2.3 mm diameter and 10 mm spacing (PMT Corporation, Chanhassen, Minnesota). The raw ECoG signals were sampled at 1200 Hz and amplified with clinical bioamplifiers (Guger Technologies, Schiedlberg, Austria). We developed custom scripts for use with the BCI2000 software platform for task presentation and data acquisition (www.bci2000.org, Schalk et al. 2004).
Experimental design
Subjects participated in a modified Posner spatial cueing task previously described by Daitch et al. (Daitch et al. 2013). Subjects were cued with a centrally located arrow that pointed either left or right and appeared for 500 ms. After cue offset and an additional delay, the target appeared for 160 ms. An equivalent number of left and right targets were presented in random order. A target appeared at the cued location on 80% of trials (valid) and at the un-cued location on 20% of trials (invalid). All subjects engaged in sessions where the timing between cue offset and target was fixed. Fixed trials had a cue-target interval of 500 ms. Five of the six subjects alternated between sessions with fixed and variable cue-target interval. In variable sessions, the interval between cue offset and target onset varied between 500, 1000 and 1500 ms with equal probability. Variable trials were included to rule-out the possibility that coupling was due entirely to rhythmic task timing. Once we ruled this possibility out, only fixed trials were used because they were more appropriate for direct comparison.
Subjects were instructed to fixate centrally throughout the task and to respond as fast as possible to two targets, the letters “L” and “T”, with left and right button-presses respectively. The experimenter reminded subjects of instructions periodically. Eye movements of three of six subjects were tracked using the EyeLink 1000 (SR Research, Ottawa, Ontario, Canada) in order to verify central gaze fixation in a previous study (Daitch et al. 2013). Eye tracking for all subjects was not possible due to interference caused by bandages covering regions surrounding the eyes. The experimenter watched subjects and noted trials with excess movement or breaks in visual fixation, so they could be removed from analyses. Additional recordings taken prior to the task, at the start of each recording session, served as a baseline period. We focused our study on how PAC during the cue period relates to spatially and behaviorally defined sites. We define the cue period as the period between the onset of the cue and the onset of the target. Sites were functionally classified by neural activity during the target period, which is defined as the first 400 ms after the target appears. We used a 400 ms target-locked window to avoid differences in signal that were unrelated to visuospatial attention.
In the target period we classified cortical sites as “spatial” or “behavioral” based on local neural activity that discriminated spatial task variables or behavioral responses. Spatial sites had high-gamma power that discriminated target location (i.e. contralateral vs ipsilateral to recording sites) or target validity (i.e. valid vs invalid). We classified behavioral sites based on significant two-tailed Spearman correlation between high-gamma power in the target period and RT. We removed cortical sites with both spatial and behavioral classifications from further analysis due to their limited number.
Digital signal processing
We performed all digital signal analysis with custom scripts in MATLAB (The MathWorks Inc, Natick, MA). A custom graphical user interface was developed to visually inspect temporal and spectral properties of every channel. Channels with abnormal amplitude (e.g. > ±1000 mV) or power spectra (e.g. harmonic noise) were flagged. Time periods containing transient artifacts across groups of channels were flagged. All flagged channels and time periods were removed from further analysis. We performed spectral decomposition using Morlet wavelet convolution and estimated phase and amplitude envelopes from the resulting complex signals. All signals were then down-sampled to 300 Hz. All wavelet-derived properties (i.e. phase, amplitude and power) were generated from the whole signal, before trials were extracted, to avoid edge effects.
Two sets of wavelet libraries were used for phase amplitude coupling. We created these libraries to satisfy mathematical constraints on phase-amplitude coupling measurements. Specifically, the bandwidth of the frequency-for-amplitude (Fa) must be twice the frequency-for-phase (Fp) of interest (Aru et al. 2015). The two wavelet libraries were constructed as follows.
Frequency for amplitude wavelets
We used the full width at half-maximum (FWHM) of the Morlet wavelet as a lower bound estimate for bandwidth. We designed Fa wavelets to have a FWHM of 20 Hz and used 21 wavelets with center frequencies ranging from 20 Hz to 150 Hz in 5Hz increments.
Frequency for phase wavelets
We designed narrow-band Fp wavelets for phase specificity. Higher frequency resolution was employed for phase signals to distinguish between delta, theta and alpha rhythms. We used 20 Fp wavelets ranging from 1 Hz to 20 Hz with 1Hz spacing and FWHM of 0.8 Hz.
Quantifying phase-amplitude coupling with the modulation index
We measured PAC using the modulation index (MI) (Tort et al. 2010), which quantifies the magnitude of coupling. MI also provides a common measurement to compare different forms of PAC (e.g. unimodal vs bimodal) across different frequencies. MI was calculated as the Kullback-Leibler divergence between the uniform distribution (i.e. pure entropy) and the observed probability density P(j), which describes the normalized mean amplitude at a given binned phase (see P(j) below). Pairwise calculation of MIs for two sequences of frequencies produces a comodulogram. MI is calculated as follows:
Where DKL is the Kullback-Leibler divergence, P is the observed phase-amplitude probability density function, Q is the uniform distribution and N is the number of phase bins. P follows the equation:
where is the mean fA amplitude signal at phase bin j of the phase signal . We divided phase into 18 bins of 20-degree intervals. For a review of PAC methods refer to (Tort et al. 2010).
To identify PAC frequency pairs of interest, we sorted trials by RT and divided them into quartiles (Fig. 2E–G). We used signals from the fastest and slowest quartiles to generate P(j) distributions of normalized amplitude per binned phase, from which we calculated the MI. We verified the precision of our methods with simulations using methods defined in the appendix of Tort et al. (Tort et al. 2010)(Supplemental Fig. 1B–F). Specific parameters or MATLAB scripts used for simulations are available upon request.
Fig. 2.
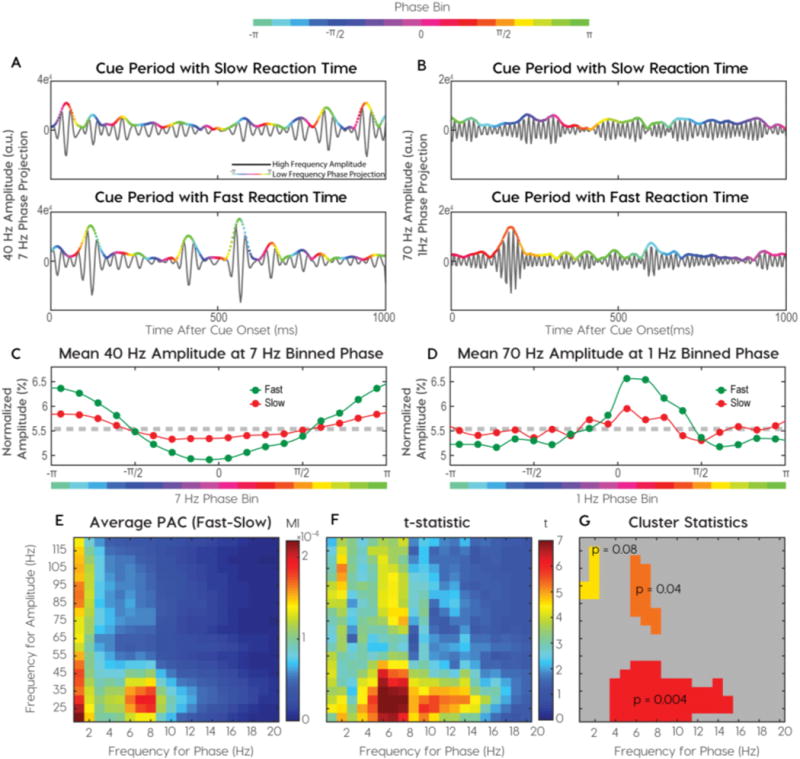
Identification of distinct phase-amplitude coupling clusters. (A–B) Single trial examples of more coupling on fast trials than slow trials. (A) Beta (25Hz) amplitude couples to alpha phase (8Hz) and (B) gamma (70 Hz) amplitude couples to delta (1 Hz) phase. High-frequency amplitude envelopes are colored with low-frequency phase. (C–D) The phase-amplitude probability densities for two frequency pairs in a single subject. (C) Normalized beta amplitude at binned alpha phase and (D) Normalized gamma amplitude at binned delta phase. (E–G) Descriptive and inferential statistics across cortical sites from all subjects (E) Mean modulation indices calculated for pairwise frequencies. (F) An identical threshold was applied to t-statistics for observed and permuted distributions. Suprathreshold, adjacent t-statistics were summed and observed clusters were compared to maximum clusters in permutation distributions. (G) Three candidate clusters along with their chance probabilities.
Statistical analysis
We employed a non-parametric cluster-based approach to time-series and two-dimensional comodulograms for three reasons. First, the distributions of time-series and comodulogram were not normal, preventing the use of usual statistical comparisons like paired t-tests. Second, the large number of samples creates a multiple comparisons problem that could be addressed with a clustering approach. Finally, the non-parametric cluster-based approach we employed controls the family-wise error rate at a critical alpha-level (Maris and Oostenveld 2007). The null hypothesis for all permutation tests was no difference between the signals or comodulograms being compared.
Band limited power and PAC time series comparisons
Statistical inference testing of band-limited power and PAC time series followed methods described by Maris and Oostenveld (Maris and Oostenveld 2007). Cluster candidates were generated using t-statistics to test the null hypothesis that there was no difference between categories at each sample. If a sample t-statistic exceeded an alpha level of 5% then the null hypothesis was rejected for the sample and it was considered a cluster candidate. Temporally adjacent cluster candidates were grouped into a single cluster and their t-statistics were summed to produce a clustering statistic. The clustering statistic of the observed data was tested against a permutation distribution. To produce the permutation distribution, trial labels (e.g. valid vs invalid) are shuffled and randomly reassigned 10,000 times. For each shuffle, cluster candidates and clustering statistics were generated as described above. The maximum clustering statistic from each shuffle was used to create the permutation distribution. We calculated p-values for observed clusters using the formula p = (r+1)/(n+1), where r is the number of shuffled clustering statistics greater than the observed clustering statistic and n is the total number of shuffled sets used (North, Curtis, and Sham 2002). We corrected for multiple comparisons across cortical sites with the False Discovery Rate (FDR) correction method.
Phase-amplitude coupling comparison
We adapted a two-dimensional non-parametric permutation test to make cluster-based statistical inferences on comodulograms based on the difference between fast and slow trials. First, we generated 1500 shuffled distributions for each cortical site by randomly reassigning RTs to trials, sorting, dividing into quartiles, and calculating the absolute difference in comodulograms for fast and slow trial quartiles as follows:
We use the pooled variance in each frequency pair in the distribution of to determine the cutoff threshold specific to each frequency pair. Adjacent supra-threshold frequency-pairs were grouped together in clusters and t-statistics were summed. We tested the null hypothesis that the shuffled data was no different from the observed data using a two-dimensional cluster based permutation test where diagonals were not considered neighbors (Maris and Oostenveld 2007). Due to the absolute value used to calculate , p-values for these permutation tests were calculated on a one-tailed distribution at an alpha of 5%. This was used for determining frequencies of interest in the comodulogram.
PAC time series were calculated using MI calculations in a 500 ms sliding window with 50 ms increments. While this window only includes half a 1 Hz cycle, we empirically confirmed that the large amount of data (>250 s) used in these analyses ensured that all phases of the 1 Hz cycle were represented in the MI calculation. Differences between PAC time-series for spatial and behavioral site categories were calculated with the one-dimensional cluster-based permutation test described above.
Inter-trial coherence and preferred phase statistics
Inter-trial coherence is the magnitude of the mean phase across trials. It reflects the phase consistency across trials for every time point and frequency. Preferred phases were calculated as the maximum phase-bin in the phase-amplitude probability density plot (see P(j) above). Preferred phases were calculated separately for each cortical site. The non-uniformity of preferred phases was determined with the Rayleigh test and the equivalence of the circular means for spatial and behavioral sites was calculated with the Kuiper test (Berens 2009).
Sharp waveform detection
To detect the presence of sharp waves we employed methods from QRS detection in ECG analyses (Benitez et al. 2000; Mitz et al. 2017). We used the squared first differential of the ECoG Signal to identify periods of rapid change. The Hilbert transformation is then applied to the squared differential of the ECoG signal. The instantaneous amplitude (i.e. the absolute value) of the resultant analytic signal is the amplitude envelope of the squared differential (Fig. 6C, black trace). We set a threshold of one standard deviation from the mean. Any candidate sharp wave that did not surpass this threshold for more than 16 ms was rejected. Finally, we calculated the amplitude change, or height, of each candidate sharp wave and rejected the bottom 80% to ensure that the most prominent waveforms were being isolated.
Fig. 6.
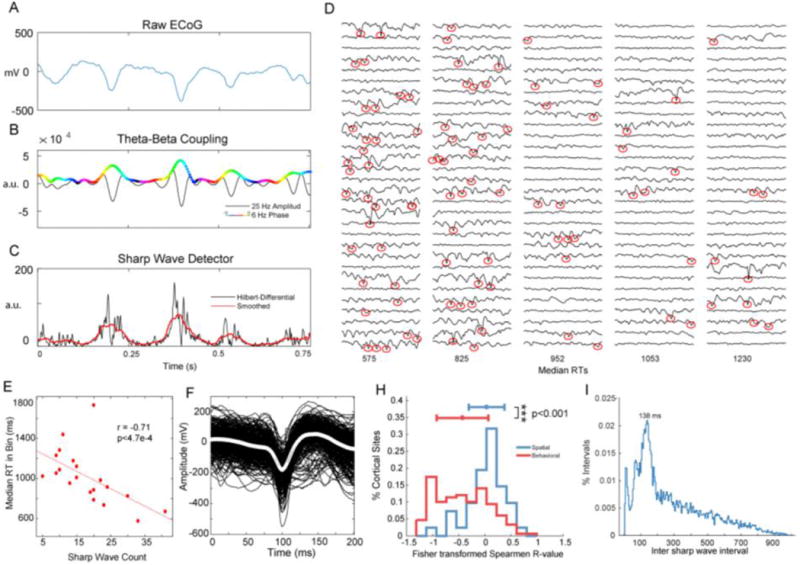
Transient waves are behaviorally relevant and coupled to 7.2 Hz phase. (A) Raw ECoG Signal shows three sharp waves that correspond to (B) theta (6Hz)-phase, beta (25 Hz)-amplitude coupling with a 180-degree phase preference. (C) Hilbert transform of the differential of the raw ECoG signal amplifies rapid (i.e. sharp) changes in the ECoG signal. A threshold on the Hilbert-Differential identified transient waves. (D) Single trials sorted by RT and grouped into 30-trial bins with median RTs below each column. Red circles highlight identified sharp waves, which were more likely to occur on trials with fast reaction times. (E) Correlation between the number of sharp waves in an RT-bin and RT. (F) The averaged waveform for the cortical site in (D) and (E). (H) The distribution of correlation coefficients for spatial and behavioral sites. (I) Distribution of inter-sharp wave intervals peaked at 138 ms, corresponding to 7.2 Hz.
Results
Reaction time reflects task performance
We employed a spatial cueing task to induce and measure covert shifts in spatial attention. Participants fixated on a central crosshair throughout the task. At the beginning of each trial a central arrow, or “cue”, pointed towards the most likely location of a subsequent “target”. Two target locations were possible. We defined these locations as “contralateral” or “ipsilateral”, depending on whether it was on the same side, or the opposite side, of the recording sites. The cue predicted the location of the target in 80% of trials (i.e. valid trials). In 20% of trials the target appeared opposite to where the cue pointed (i.e. invalid trials). In our version of the task participants were required to discriminate “L” from “T” targets that were randomly rotated (Fig. 1, top). Across six participants, 26 of 5370 trials were removed due to transient artifacts across all channels found through visual inspection. Of the remaining data, 5100 of 5344 trials were completed with 92.2% correct responses. We used trials with correct responses for further analyses. Invalid trials incurred higher RTs than valid trials (medians (ms): valid = 831, invalid = 927, rank sum: 7.2e6, approximate z-value: −9.8, p = 1.6e-22). No differences in reaction time occurred between trials with contralateral and ipsilateral cues (medians (ms): contralateral = 860, ipsilateral = 863, rank sum: 5.1e6, approximate z-value: −1.7, p = 0.08). Higher RTs on invalid trials confirmed that the task induced lateralized shifts in visual attention. We focused our physiological analyses on two periods in the task, the “cue period” and the “target period”. We define the “cue period” as the time between cue onset and target onset and the “target period” as the first 400 ms after target onset. Cued shifts in attention occurred during the cue period. The target location and identity is revealed during the target period, allowing subjects to locate the target, identify it, and subsequently respond appropriately.
Fig. 1.
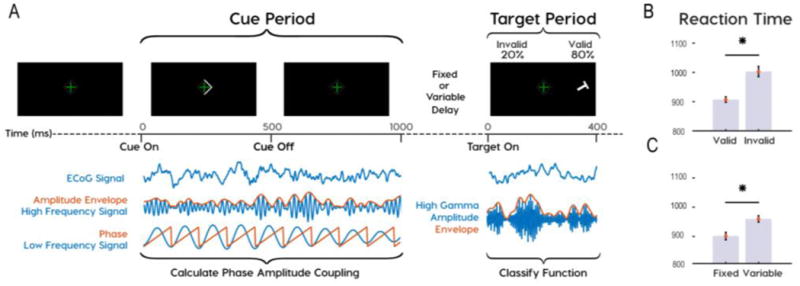
Task design showing analysis periods and behavioral results. (A) Subjects participated in a Posner cued attention task, with the most probable target location indicated by an arrowhead presented at fixation prior to target onset. Phase amplitude coupling (PAC) was analyzed during the cue period. Functional classifications were based on high-gamma amplitude during the target period. Subjects responded to “L” and “T” targets with left and right mouse clicks. (B) Reaction times were greater for invalid than valid trials and (C) for variable than fixed delays.
Distinct clusters of PAC correlate with RT
We identified behaviorally relevant PAC frequencies by comparing the cue periods preceding fast and slow RTs. After sorting trials by RT, we binned them into quartiles and analyzed differences in cue period PAC between the fastest and slowest quartiles. We found PAC differences in multiple frequency pairs (Fig. 2A, B). For visualization purposes, color-coded low-frequency phases are projected on the high-frequency amplitude envelope (Supplemental Fig. 1B, D). The modulation index (MI) quantified PAC intensity, or the non-uniformity of the phase-amplitude probability density plot (Fig. 2C, D). We calculate the MI for each frequency pair to generate a comodulogram. The absolute difference between slow and fast comodulograms averaged over all cortical sites and subjects, revealed coupling between delta-phase and theta-alpha-phase to higher frequency (>20Hz) amplitude envelopes (Fig. 2E).
Cluster-based permutation testing determined the significance of PAC while controlling for false positives. Permutation distributions were generated by shuffling reaction times between trials and calculating absolute differences in comodulograms between the slowest and fastest quartiles in shuffled datasets. Significant phase-amplitude frequency clusters outlined adjacent frequency pairs with significant t-statistics (Fig. 2F). Three clusters of frequency pairings explained RT variance: 1) theta-alpha-phase/beta-low gamma-amplitude (TABL) (Fig. 2G, red), 2) delta-phase/high-gamma-amplitude (DH) (Fig. 2G, yellow), and 3) alpha-phase/high-gamma-amplitude (AH) (Fig. 2G, orange). We focused on comparing DH with TABL PAC for three reasons. First, they have unique phase and amplitude frequencies, unlike alpha-high gamma PAC. Second, the magnitudes of DH and TABL PAC during cued attention were the least correlated across all electrodes (Spearman Correlations RDH-TABL = 0.107, RTABL-AH = 0.518, RDH-AH = 0.471). Third, TABL and DH PAC have been shown to underlie distinct mechanisms in human memory (Vaz et al. 2017). Therefore, we hypothesized that DH and TABL were most likely to show different functional characteristics during the spatial attention task.
To verify precision in measuring frequency-specific PAC we modeled PAC with simulated signals using procedures from Tort and colleagues (Tort et al. 2010) (Supplemental Fig. 1A–E). We also performed the cluster-permutation test for each cortical site and found clusters in the same locations as those shown in Fig. 2g. Subject-specific differences were apparent in averaged comodulograms shown alongside electrode locations on an averaged brain plots (Supplemental Fig. 3). Five of six subjects displayed robust TABL PAC. Most subjects had less DH PAC magnitude compared to TABL PAC. Interestingly, TABL PAC did not appear on single trials and only emerged when we calculated phase-amplitude distributions on multiple (>15) trials (Supplemental Fig. 2). To explore differences in TABL and DH PAC we returned to disparities in the motivating literature. While both Esghaei et al. and Szczepanski et al. found that PAC depended on spatial task variables, only the latter found that PAC correlated with RT (Esghaei, Daliri, and Treue 2015; Szczepanski et al. 2014). Therefore, we explored whether DH and TABL PAC uniquely depended on spatial variables or task performance (i.e. RT) by classifying cortical sites by function and comparing PAC across functional classes.
Functional classification of spatial and behavioral cortical sites
We classified cortical sites based on high-gamma (75–150 Hz) power as it has been shown to correlate with local neuronal activity (Ray and Maunsell, 2011). We classified neural activity in the target period for two reasons. First, this period had the most robust discriminatory neural responses. Second, all the information required for a correct response was made available in the target period. Therefore, all classifications relied on high-gamma power in the first 400 ms after target onset.
We defined “spatial” cortical sites based on neural activity discriminating target location or validity. Due to the contralateral organization of visual receptive fields, contralateral targets typically produced larger neural responses than ipsilateral targets. Invalid targets, occurring on 20% of trials, typically produced larger changes in high-gamma power than valid targets. We justified grouping validity sensitive sites with location sensitive sites because calculating a target’s validity requires the target’s location as an operand. Thus, we classified a cortical site as “spatial” when its high-gamma power discriminated either contralateral from ipsilateral targets (Fig. 3A) or valid from invalid targets (Fig. 3C), cluster permutation test threshold p < 0.05, FDR corrected). In contrast, we defined “behavioral” cortical sites based on discriminatory neural activity pertaining to RT. We call these sites behavioral because the RT of correct responses is the measured behavior in the task. Behavioral cortical sites had significant Spearman correlations between mean post-target high-gamma power and RT (Spearman correlation threshold p < 0.05, FDR corrected). Mean high-gamma and RT had log-normal distributions so we represent this as a correlation of the log of both values in (Fig. 3D).
Fig. 3.
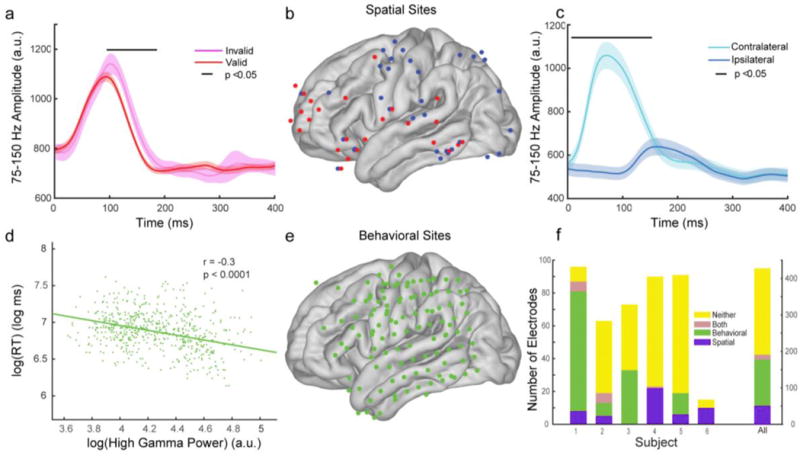
Functional classification of “spatial” and “behavioral” cortical sites. Spatial cortical sites have high gamma (75–150Hz) activity that discriminates spatial parameters of the task. Exemplary mean high gamma power, with standard error bars, from two spatial cortical sites discriminating (A) valid from invalid targets and (C) targets that appear contralateral from targets that appear ipsilateral to recording sites. (B) Distribution of spatial cortical sites from all subjects where red dots discriminate validity and blue dots discriminate location. Behavioral cortical sites had high gamma activity that correlated with reaction times (RTs). (D) Exemplary correlation from one behavioral cortical site. (E) The cortical surface distribution of behavioral sites from all subjects. (F) Breakdown of electrode classifications for each participant (left vertical axis) and for all participants (right vertical axis).
We found 51 spatial and 127 behavioral sites. We removed the 13 sites classified to both groups and 237 classified to neither group, from further analyses (Fig. 3F). Spatial cortical sites were found primarily over visual cortex, parietal cortex, motor cortex and frontal cortex, with the distribution of dorsal parietal and posterior frontal sites roughly matching the dorsal attention network (Corbetta and Shulman 2002) (Fig. 3B). Behavioral cortical sites were found over motor cortex, parietal cortex, and temporal cortex (Fig. 3E). We compared these two functional classes to investigate functional properties of TABL and DH PAC.
Phase and magnitude differentiate PAC clusters across functional classes
We first characterized differences in the phase preferences and coupling magnitudes of DH and TABL PAC. We defined preferred phases as the low-frequency phase bin with the greatest high-frequency amplitude. Preferred phases are independent of coupling magnitude, and if no coupling exists then preferred phases will be uniformly distributed on average. We calculated the preferred phase using all cue periods, then calculated the circular mean across all cortical sites within a functional class. We repeated this analysis for pseudo-trials generated from the rest period recorded prior to the task to ensure that coupling did not exist during rest. Pseudo-trials had identical length to the cue period, but were sampled randomly from the rest period.
During rest, preferred phases were uniformly distributed in both functional classes and frequency pairs (Rayleigh test, TABL PAC: spatial z = 1.5, p = 0.86; behavioral z = 0.97, p = 0.38; DH PAC: spatial z = 0.03, p = 0.97; behavioral z = 2.86, p = 0.06; Fig. 4A, red). In contrast, all sites had preferred phases during the cue period. (Rayleigh test, TABL PAC: spatial z = 28, p = 1e-12; behavioral z = 41, p = 6e-20; DH PAC: spatial z = 37, p = 3e-9; behavioral z = 71, p = 4e-32, Fig. 4A, blue). Furthermore, the mean DH PAC phase preferences differed across spatial and behavioral sites (spatial mean = 237, std = 67, behavioral mean = 321, std = 69, Kuiper test, k = 1.1e5, p = 0.001, Fig. 4A, top). However, TABL PAC consistently showed a 180-degree phase preference in all sites (spatial mean = 184, std = 42, behavioral mean = 178, std = 53; Kuiper test, k = 1.7e4, p = 0.10, Fig. 4A, bottom). Phase preferences were not affected by cue direction or reaction time. Therefore, the preferred phases of DH and TABL PAC during the cue period showed consistent differences.
Fig. 4.
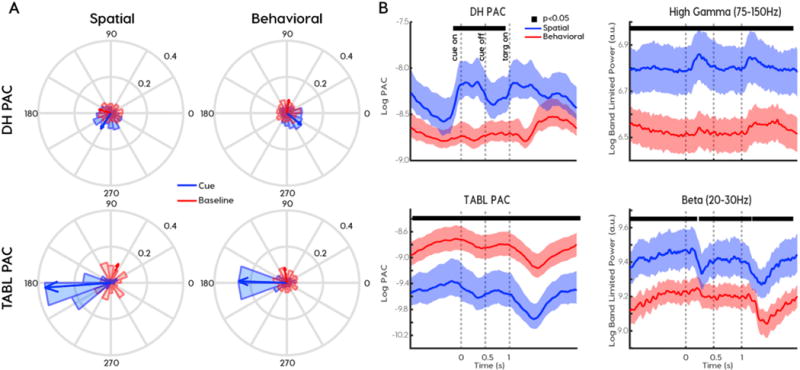
Phase preferences and relative PAC magnitude distinguish coupling frequencies and functional classes. (A) Preferred phases differed for delta to high-gamma (DH) PAC (top row) and theta-alpha to beta-low-gamma TABL PAC (bottom row) across spatial (left column) and behavioral (right column) cortical sites. Coupling emerged in the cue period (blue) relative to baseline pseudo-trials (red). Arrows indicate the circular mean of preferred phases across all subjects and cortical sites. (B) The relationship between PAC magnitude (left column) and the corresponding frequency-for-amplitude power (right column) reverses across behavioral (red) and spatial (blue) cortical sites. Solid black lines at top of graph indicates clusters of samples where spatial and behavioral signals were significantly different at p < 0.05.
We hypothesized that spatial sites were more active than behavioral sites during the cue period. To verify this, we compared high-gamma variance and inter-trial coherence (ITC) across functional classes. High-gamma power and variance were greater in spatial sites than in behavioral sites (power: cluster permutation test p < 0.001 (Fig. 4B, top right), variance: rank sum, p < 0.001 (Supplementary Fig. 4A). ITC measures the coherence over trials in both phase and amplitude. Again, spatial sites had greater ITC in the 1–10 Hz frequency range during the cue period (Supplemental Fig. 4B, C). Taken together, neural activity in spatial sites were more modulated by spatial cueing than behavioral sites were in both low and high frequencies. DH PAC paralleled these indexes of neural modulation and was higher in spatial sites than in behavioral sites (cluster permutation test, p < 0.001, Fig. 4B, top left). Furthermore, DH PAC peaked after cue onset and target onset, much like high gamma power. In contrast, TABL PAC was greater in behavioral sites than in spatial sites (cluster permutation test, p < 0.001, Fig. 4B, bottom left). This was not due to high beta or low-gamma power, both of which were greater in spatial sites (cluster permutation test, p < 0.001, Fig. 4B, bottom right). It was also not due to greater alpha activity in behavioral sites (Supplemental Fig. 4E). Finally, this was not due to baseline differences. When we applied the same analysis to psuedotrials created from a baseline period recorded prior to the attention task, we found there were no significant differences in PAC or power across the functional classes. We interpreted the increased high-gamma in spatial sites to reflect previously described increases in firing rates of visual areas during attention tasks, which have been shown to occur even in the absence of stimuli (Kastner and Ungerleider 2000). Therefore, high TABL PAC corresponded to reduced neural modulation across the functional categories.
To summarize, TABL PAC and DH PAC showed a reversal in their relationship to power. TABL PAC was greater in behavioral sites, despite reduced power, variance and ITC. In contrast, DH PAC positively covaried with every measure of neural modulation we measured. Since there were no observed differences in PAC or power at baseline, this reversal was best explained by the task. Along with differences in phase preference, magnitude differences provided additional evidence that DH and TABL PAC dynamics depended on functional classifications.
Distinct PAC frequency pairs correspond to cortical function
We investigated PAC differences across spatial conditions (i.e. contralateral vs ipsilateral cues) and behavioral responses (i.e. RT) (Fig. 5A). We quantified differences using previously defined clusters (Fig. 2G). On contralateral trials, we found increased DH PAC in spatial cortical sites and no change in behavioral sites (sign test, spatial: z-value 2.6, p = 0.009, behavioral: z-value = −1.8, p = 0.07; Fig. 5C). The difference between classes was significant (rank sum, z-value = −3.4, p = 7e-4, corrected). TABL PAC showed no changes across ipsilateral and contralateral cueing conditions and there were no differences between classes (sign test, spatial: z-value 1.05, p = 0.29, behavioral: z-value = 0.94, p = 0.34, rank sum, z-value = 0.15, p = 0.9, Fig. 5B). This suggested DH PAC was specific to spatial variables in spatial sites.
Fig. 5.
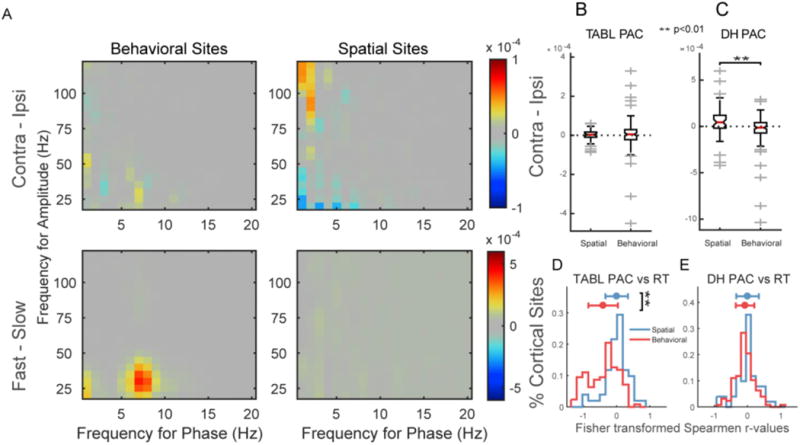
PAC magnitude differences across task conditions distinguish between phase frequencies and functional classes. (A) Shows positive comodulogram differences for behavioral (left) and spatial (right) sites when subtracting contralateral from ipsilateral trials (top) and fast from slow trials (bottom). These changes were quantified using previously identified PAC clusters. (B) No ipsi-contra differences were observed as a product of lateralized cued attention in theta/alpha-beta/low gamma (TABL) PAC at either spatial or behavioral sites. (C) Delta-high gamma (DH) PAC increases on contralateral vs. ipsilateral trials in spatial sites relative to behavioral sites. (D) TABL PAC was more negatively correlated with RT in behavioral than spatial sites. DH PAC showed no differences between behavioral and spatial sites (E).
To understand which functional class drove differences between fast and slow trials we correlated DH and TABL PAC with RT for all sites in each functional class. Spatial sites showed no significant trend in correlations (t-test, DH vs RT ≠ 0: p = 0.80, TABL vs RT ≠ 0: p = 0.97, two-tailed) and there were no differences between Fisher transformed r-value distributions (t-test, DH vs RT ≠ TABL vs RT: p = 0.90, two-tailed, Fig. 5E). In contrast, TABL PAC was more negatively correlated with RT in behavioral sites (t-test, DH vs RT ≠ TABL vs RT: p < 1e-11, two-tailed, Fig. 5D). To summarize, during the cue period DH PAC in spatial sites varied with cue direction and TABL PAC in behavioral sites correlated with RT.
Coupled sharp waves correspond to TABL PAC
DH PAC has been described in prior attention literature (Esghaei, Daliri, and Treue 2015; Lakatos et al. 2008; Szczepanski et al. 2014), but TABL PAC has not been previously shown in attention tasks. It has, however, been shown to correlate with encoding and retrieval in memory tasks (Vaz et al. 2017). Additionally, non-sinusoidal or “sharp” wave-forms have been shown to produce coupling in the range of TABL PAC (Gerber et al. 2016; Vaz et al. 2017). We hypothesized that if sharp waveforms resulted in TABL PAC, then they too will correlate with RT in behavioral sites. Furthermore, we hypothesized that if these sharp waveforms were part of a coupled dynamical process, then the interval between sharp waveforms would not be random. To address these questions and characterize sharp waveforms, we developed methods that are less computationally expensive than traditional PAC measurements.
On visual inspection of the raw ECoG we found that non-sinusoidal, sharp waveforms temporally co-occurred with TABL PAC (Fig. 6A, B). We reasoned that the “sharpness” of the waveform could be used to detect these events and employed techniques previously used for QRS wave detection in electrocardiogram analyses (Benitez et al. 2000; Mitz et al. 2017). This method uses the Hilbert transform of the ECoG signal’s first differential to identify rapid (i.e. sharp) changes in the signal (Fig. 6C). We applied this sharp wave detection to individual trials and displayed the results of an exemplar recording site in 30-trial RT bins (Fig. 6D). We found that trials with fast responses (i.e. low RTs) were more likely to have sharp waveforms than trials with slow responses (Fig. 6E). In aggregate, sharp waveform correlations with RT were significantly more negative in behavioral sites than in spatial sites (rank sum p < 0.001, Fig. 6H), similarly to TABL PAC (Fig. 5D). Alongside the correlations for specific channels we used the minimum of the detected sharp wave to time-lock waveforms and observe their shapes. We observed that detected sharp waveforms had a 50 ms width, similar to transient neocortical beta rhythms that have been previously described in multiple species (Sherman et al. 2016) (Fig. 6F).
On visual inspection it appeared as if these sharp waveforms were themselves coupled to a low frequency oscillation, so we analyzed the intervals between sharp waves. For every trial with more than one sharp wave we recorded the interval between adjacent sharp waves. The distribution of these inter-sharp-wave intervals was not log-normal or Poisson (chi-square goodness-of-fit both p < 0.0001), which would be expected if intervals were randomly spaced. Instead, a peak of 138 ms suggested that sharp waveforms coupled to a 7.2 Hz oscillation (Fig. 6I).
In summary, TABL PAC associated with sharp waveforms that could be detected with computationally inexpensive methods. However, these sharp waves had a 50 ms width, corresponding to a transient beta wave, and the distribution of sharp wave intervals suggested that they occurred regularly within a theta-alpha range oscillation. Thus, sharp wave morphometry and the intervals between sharp waveform events are contributors to the detected TABL PAC. While characterization of these transient waveforms may require additional nuance, their correlations with RT across functional classes matched that of TABL PAC, suggesting a common origin.
Discussion
This study expands our understanding of phase amplitude coupling (PAC) in several ways. First, we identified an interaction between theta-alpha-phase and beta-low-gamma amplitude (TABL PAC) during spatial cueing that correlated with future reaction times (RTs) and is novel to the attention literature. Second, we characterized differences between TABL PAC and delta-phase, high-gamma-amplitude coupling (DH) PAC. Specifically, we found DH PAC positively covaried with contralaterally cued attention in spatial sites while TABL PAC correlated with RT in behavioral sites. Unlike DH PAC, TABL PAC negatively covaried with multiple indices of neural modulation and maintained a consistent 180-degree preferred phase during the task. Third, we identified sharp wave correlates of TABL PAC using novel methods, which showed how sharp waveforms during cued attention correlated with future RT. Finally, we showed that behaviorally relevant sharp waveforms are also coupled with low frequency oscillations. Taken together, this study highlights the unique contributions of distinct PAC frequency clusters in a spatial attention task.
Methodological considerations for frequency-specificity in PAC analyses
The complexity of PAC analyses (Aru et al. 2015), evidence for spurious PAC (Jensen, Spaak, and Park 2016; Kramer, Tort, and Kopell 2008), and the novelty of TABL PAC in spatial attention tasks warrants a discussion of methods. We employed the modulation index (MI) to measure the intensity of PAC due to its advantages over other methods (for a review, see Tort et al., 2010). Sufficient data length was critical to resolving TABL PAC. This was due to the relative sparsity of transient waveforms leading to TABL PAC on single trials. Additionally, coupling between two frequencies (e.g. Fp and Fa) can only occur in the presence of two additional frequencies: the sum and the difference of the original two frequencies (i.e. Fa + Fp and Fa−Fp, see Supplemental Fig. 1A arrows). To account for this, we developed wavelet libraries independently for phase and amplitude signals. Wide band-width amplitude filters were required to measure PAC in higher phases (Aru et al. 2015; Dvorak and Fenton 2014). Conversely, narrow band-widths allowed phase-specificity when filtering phase signals, since broadband phase estimates may include separable PAC components that cancel each other out.
In addition to signal processing and measurement considerations, we used reaction time to identify behaviorally relevant PAC frequency clusters. Furthermore, instead of shuffling phase and amplitude signals relative to each other, we shuffled trials between behavioral categories (e.g. fast and slow RT quartiles) to generate chance distributions. This guaranteed that our statistical inferences were made from distributions with physiologically observed phase-amplitude relationships. We then employed a non-parametric cluster-based permutation test for statistical inferences. These methods resolved behaviorally relevant PAC frequency clusters spanning frequency bands previously associated with attentional processes (Busch, Dubois, and VanRullen 2009; Buzs aki 2005; Senkowski et al. 2006; Thut et al. 2006).
Sharp waveforms are dynamically coupled
We propose that sharp waveforms are a behaviorally relevant, special case of PAC. This is an alternative to suggestions that non-sinusoidal sharp waveforms cause spurious PAC (Gerber et al. 2016; Kramer, Tort, and Kopell 2008). We demonstrated transient beta (50 ms) waves that occurred at 138 ms intervals, suggesting a coupled dynamical process. Similar waveforms have been shown across species (Sherman et al. 2016) and have relevance to human memory tasks (Vaz et al. 2017). Sharp waveforms have high frequency components coupled to certain phases of low frequency rhythms, which is fits the definition of PAC. Persistent nesting of sinusoidal oscillations is another special case of PAC, not the only possibility. PAC approaches identify frequency interactions between high and low frequencies that can lead to a better understanding of underlying dynamics. Because PAC analyses are computationally expensive and sensitive to noise, we used our PAC findings to inform a computationally inexpensive sharp wave detection approach, which better described individual trials.
A theoretical framework and implications for PAC in attention
Two hypotheses are relevant to PAC and cued spatial attention (for an extensive review see (Bonnefond, Kastner, and Jensen 2017). The communication through coherence (CTC) hypothesis proposes that excitability windows of two communicating brain regions are temporally aligned by low frequency oscillations to promote information transfer (e.g. spikes) across regions (Bastos, Vezoli, and Fries 2015; Fries 2005). In contrast, the gating by inhibition (GBI) hypothesis proposes that low frequencies periodically suppress information in a neuronal population (Jensen and Mazaheri 2010).
Although we do not have evidence to assess the CTC hypothesis, we found evidence for a suppressive role for TABL PAC, which fits with the GBI hypothesis. First, multiple indices of neural modulation suggested spatial sites were more active than behavioral sites during spatial cueing, yet TABL PAC was greater in behavioral than spatial sites. Furthermore, TABL PAC consistently demonstrated a 180-degree phase preference, which meant that high frequency activity preferred the trough of the low frequency oscillation. This pattern of coupling has been shown in “pulsed-inhibition” or “gating by inhibition” models of alpha oscillatory activity (Jensen and Mazaheri 2010; Mathewson et al. 2011), where the peak of alpha oscillatory amplitude periodically suppresses higher frequency activity. Finally, the transient waves that cause TABL PAC have been shown in multiple species and studies to relate to decreased information relay (Miller et al. 2012; Sherman et al. 2016). Taken together these results support a suppressive function of TABL PAC during our spatial attention task.
Conclusions
Spatial attention enhances neural responses to attended stimuli and by filtering out unwanted information (Kastner and Ungerleider 2000). Prior studies differed on whether PAC contributes to selection (Szczepanski et al. 2014) or filtering (Esghaei, Daliri, and Treue 2015). Here we show evidence that the functional properties of PAC depend critically on phase frequency. DH PAC facilitates lateralized spatial attention while TABL PAC contributes to behavioral performance, potentially through suppressive gating of activity. Furthermore, we demonstrate that sharp waves producing TABL PAC are themselves coupled to low frequency oscillations. While the function of these sharp waves remains unclear, PAC remains a useful tool in understanding the neural correlates of human attention.
Supplementary Material
Acknowledgments
Research reported in this publication was supported by the Washington University Institute of Clinical and Translational Sciences grant UL1TR000448, sub-award TL1TR000449, from the National Center for Advancing Translational Sciences (NCATS) of the National Institutes of Health (NIH). The content is solely the responsibility of the authors and does not necessarily represent the official view of the NIH.”
PI: Bradley Evanoff, MD, MPH.
Project Title: Washington University Institute of Clinical and Translational Sciences.
Also, the Washington University Institute of Clinical and Translational Sciences is supported by CTSA Grant UL1 TR002345.
Abbreviations
- PAC
Phase amplitude coupling
- TABL
Theta-Alpha / Beta-Low Gamma
- DH
Delta / High Gamma
- RT
Reaction time
- MI
Modulation index
Appendix A. Supplementary data
Supplementary data related to this article can be found at https://doi.org/10.1016/j.neuroimage.2018.03.003.
References
- Aru Juhan, et al. Untangling cross-frequency coupling in neuroscience. Current Opinion in Neurobiology. 2015;31:51–61. doi: 10.1016/j.conb.2014.08.002. September 2014. [DOI] [PubMed] [Google Scholar]
- Bastos Andre M, Vezoli Julien, Fries Pascal. Communication through coherence with inter-areal delays. Current Opinion in Neurobiology. 2015;31:173–180. doi: 10.1016/j.conb.2014.11.001. [DOI] [PubMed] [Google Scholar]
- Benitez DS, Gaydecki PA, Zaidi A, Fitzpatrick AP. A new QRS detection algorithm based on the Hilbert transform. Computing in Cardiology. 2000 Feb;27:379–382. [Google Scholar]
- Berens Philipp. CircStat: a MATLAB toolbox for circular statistics. Journal of Statistical Software. 2009;31(10):1–21. [Google Scholar]
- Bonnefond Mathilde, Kastner Sabine, Jensen Ole. Communication between brain areas based on nested oscillations. Eneuro. 2017 Apr;4 doi: 10.1523/ENEURO.0153-16.2017. ENEURO. 0153-16.2017 http://eneuro.sfn.org/lookup/doi/10.1523/ENEURO.0153-16.2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Busch Niko a, Dubois Julien, VanRullen Rufin. The phase of ongoing EEG oscillations predicts visual perception. The Journal of neuroscience: the official journal of the Society for Neuroscience. 2009;29(24):7869–7876. doi: 10.1523/JNEUROSCI.0113-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buzsáki György. Theta rhythm of navigation: link between path integration and landmark navigation, episodic and semantic memory. Hippocampus. 2005;15(7):827–840. doi: 10.1002/hipo.20113. [DOI] [PubMed] [Google Scholar]
- Canolty Ryan T, Knight Robert T. The functional role of cross-frequency coupling. Trends in cognitive sciences. 2010;14(11):506–515. doi: 10.1016/j.tics.2010.09.001. http://www.pubmedcentral.nih.gov/articlerender.fcgi?artid=3359652&tool=pmcentrez&rendertype=abstract. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clayton Michael S, Yeung Nick, Kadosh Roi Cohen. The roles of cortical oscillations in sustained attention. Trends in Cognitive Sciences. 2015;19(4):188–195. doi: 10.1016/j.tics.2015.02.004. [DOI] [PubMed] [Google Scholar]
- Corbetta Maurizio, et al. Attentional modulation of neural processing of shape, color, and velocity in humans published by: american association for the advancement of science stable. Science. 1990;248(4962):1556–1559. doi: 10.1126/science.2360050. http://www.jstor.org/stable/2874769. [DOI] [PubMed] [Google Scholar]
- Corbetta Maurizio, Miezin Francis M, Shulman Gordon L, Petersen Steven E. A PET study of visuospatial attention. The Journal of Neuroscience. 1993;13(3):1202–1226. doi: 10.1523/JNEUROSCI.13-03-01202.1993. http://www.ncbi.nlm.nih.gov/pubmed/8441008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Corbetta Maurizio, Shulman Gordon L. Control of goal-directed and stimulus-driven attention in the brain. Nature reviews. Neuroscience. 2002;3(3):201–215. doi: 10.1038/nrn755. [DOI] [PubMed] [Google Scholar]
- Daitch Amy L, et al. Frequency-specific mechanism links human brain networks for spatial attention. Proceedings of the National Academy of Sciences of the United States of America. 2013;110(48):19585–19590. doi: 10.1073/pnas.1307947110. http://www.pubmedcentral.nih.gov/articlerender.fcgi?artid=3845177&tool=pmcentrez&rendertype=abstract. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dvorak Dino, Fenton André A. Toward a proper estimation of phase-amplitude coupling in neural oscillations. Journal of Neuroscience Methods. 2014;225:42–56. doi: 10.1016/j.jneumeth.2014.01.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Esghaei Moein, Reza Daliri Mohammad, Treue Stefan. Attention decreases phase-amplitude coupling, enhancing stimulus discriminability in cortical area MT, 82. Frontiers in neural circuits. 2015 Dec;9 doi: 10.3389/fncir.2015.00082. http://journal.frontiersin.org/article/10.3389/fncir.2015.00082/abstract. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fries Pascal. A mechanism for cognitive dynamics: neuronal communication through neuronal coherence. Trends in Cognitive Sciences. 2005;9:474–480. doi: 10.1016/j.tics.2005.08.011. [DOI] [PubMed] [Google Scholar]
- Gerber Edden M, et al. Non-sinusoidal activity can produce cross-frequency coupling in cortical signals in the absence of functional interaction between neural sources. PLoS ONE. 2016;11(12):1–19. doi: 10.1371/journal.pone.0167351. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jensen Ole, Mazaheri Ali. Shaping functional architecture by oscillatory alpha activity: gating by inhibition. Frontiers in human neuroscience. 2010 Nov;4:186. doi: 10.3389/fnhum.2010.00186. http://www.pubmedcentral.nih.gov/articlerender.fcgi?artid=2990626&tool=pmcentrez&rendertype=abstract. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jensen Ole, Spaak Eelke, Park Hyojin. Discriminating valid from spurious indices of phase-amplitude coupling. Eneuro. 2016;3(6) doi: 10.1523/ENEURO.0334-16.2016. http://eneuro.sfn.org/lookup/doi/10.1523/ENEURO.0334-16.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kastner Sabine, Ungerleider Leslie G. Mechanisms of visual attention in the human cortex. Annual review of neuroscience. 2000;23:315–41. doi: 10.1146/annurev.neuro.23.1.315. [DOI] [PubMed] [Google Scholar]
- Kramer Mark A, Tort Adriano BL, Kopell Nancy J. Sharp edge artifacts and spurious coupling in EEG frequency comodulation measures. Journal of Neuroscience Methods. 2008;170(2):352–357. doi: 10.1016/j.jneumeth.2008.01.020. [DOI] [PubMed] [Google Scholar]
- Lakatos Peter, et al. Science. 5872. Vol. 320. New York, N.Y: 2008. Entrainment of neuronal oscillations as a mechanism of attentional selection; pp. 110–113. [DOI] [PubMed] [Google Scholar]
- Lakatos Peter, et al. Global dynamics of selective attention and its lapses in primary auditory cortex. Nature Neuroscience. 2016;19(12):1707–1717. doi: 10.1038/nn.4386. http://www.nature.com/doifinder/10.1038/nn.4386. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Landau Ayelet Nina, Marianne Schreyer Helene, Van Pelt Stan, Fries Pascal. Distributed attention is implemented through theta-rhythmic gamma modulation. Current Biology. 2015;25(17):2332–2337. doi: 10.1016/j.cub.2015.07.048. [DOI] [PubMed] [Google Scholar]
- Mangun GRR, Hillyard SAA. Spatial gradients of visual attention: behavioral and electrophysiological evidence. Electroencephalography and Clinical Neurophysiology. 1988;70(5):417–428. doi: 10.1016/0013-4694(88)90019-3. http://linkinghub.elsevier.com/retrieve/pii/0013469488900193. [DOI] [PubMed] [Google Scholar]
- Maris Eric, Oostenveld Robert. Nonparametric statistical testing of EEG- and MEG-data. Journal of Neuroscience Methods. 2007;164:177–190. doi: 10.1016/j.jneumeth.2007.03.024. [DOI] [PubMed] [Google Scholar]
- Mathewson Kyle E, et al. Pulsed out of awareness: EEG alpha oscillations represent a pulsed-inhibition of ongoing cortical processing. Frontiers in Psychology. 2011 May;2:1–15. doi: 10.3389/fpsyg.2011.00099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mehta MR, Lee AK, Wilson MA. Role of experience and oscillations in transforming a rate code into a temporal code. Nature. 2002;417(6890):741–746. doi: 10.1038/nature00807. [DOI] [PubMed] [Google Scholar]
- Miller Kai J, et al. Human motor cortical activity is selectively phase-entrained on underlying rhythms. PLoS Computational Biology. 2012;8(9) doi: 10.1371/journal.pcbi.1002655. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitz Andrew R, et al. Using pupil size and heart rate to infer affective states during behavioral neurophysiology and neuropsychology experiments. Journal of Neuroscience Methods. 2017;279:1–12. doi: 10.1016/j.jneumeth.2017.01.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mizuseki Kenji, Sirota Anton, Pastalkova Eva, Buzsáki György. Theta oscillations provide temporal windows for local circuit computation in the entorhinal-hippocampal loop. Neuron. 2009;64(2):267–280. doi: 10.1016/j.neuron.2009.08.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moran Jeffrey, Desimone Robert. Selective attention gates visual processing in the extrastriate cortex published by: american association for the advancement of science stable. Science. 1985;229(4715):782–784. doi: 10.1126/science.4023713. http://www.jstor.org/stable/1696121. [DOI] [PubMed] [Google Scholar]
- North BV, Curtis D, Sham PC. A note on the calculation of empirical P values from Monte Carlo procedures. American journal of human genetics. 2002;71(2):439–441. doi: 10.1086/341527. http://www.pubmedcentral.nih.gov/articlerender.fcgi?artid=379178&tool=pmcentrez&rendertype=abstract. [DOI] [PMC free article] [PubMed] [Google Scholar]
- di Pellegrino Giuseppe, Wise Steven P. Visuospatial versus visuomotor activity in the premotor and prefrontal cortex of a primate. The Journal of neuroscience: the official journal of the Society for Neuroscience. 1993;13(3):1227–1243. doi: 10.1523/JNEUROSCI.13-03-01227.1993. http://www.ncbi. nlm.nih.gov/pubmed/8441009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Posner MI. Orienting of attention. The Quarterly journal of experimental psychology. 1980;32(1):3–25. doi: 10.1080/00335558008248231. [DOI] [PubMed] [Google Scholar]
- Ray Supratim, Maunsell John HR. Different origins of gamma rhythm and high-gamma activity in macaque visual cortex. PLoS Biology. 2011;9(4) doi: 10.1371/journal.pbio.1000610. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rihs Tonia A, Michel Christoph M, Thut Gregor. Mechanisms of selective inhibition in visual spatial attention are indexed by alpha-band EEG synchronization. The European journal of neuroscience. 2007;25:603–610. doi: 10.1111/j.1460-9568.2007.05278.x. [DOI] [PubMed] [Google Scholar]
- Sadaghiani Sepideh, Kleinschmidt Andreas. Brain networks and alpha-oscillations: structural and functional foundations of cognitive control. Trends in Cognitive Sciences. 2016;20(11):805–817. doi: 10.1016/j.tics.2016.09.004. [DOI] [PubMed] [Google Scholar]
- Schalk Gerwin, et al. BCI2000: a general-purpose brain-computer interface (BCI) system. IEEE transactions on bio-medical engineering. 2004;51:1034–1043. doi: 10.1109/TBME.2004.827072. [DOI] [PubMed] [Google Scholar]
- Schroeder Charles E, Lakatos Peter. Low-frequency neuronal oscillations as instruments of sensory selection. Trends in Neurosciences. 2009;32(1):9–18. doi: 10.1016/j.tins.2008.09.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Senkowski Daniel, Molholm Sophie, Gomez-Ramirez Manuel, Foxe John J. Oscillatory beta activity predicts response speed during a multisensory audiovisual reaction time task: a high-density electrical mapping study. Cerebral Cortex. 2006;16(11):1556–1565. doi: 10.1093/cercor/bhj091. [DOI] [PubMed] [Google Scholar]
- Sherman Maxwell A, et al. Neural mechanisms of transient neocortical beta rhythms: converging evidence from humans, computational modeling, monkeys, and mice. Proceedings of the National Academy of Sciences. 2016;113(33):E4885–E4894. doi: 10.1073/pnas.1604135113. http://www.pnas.org/lookup/doi/10.1073/pnas.1604135113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Snyder Lawrence H, Batista AP, Andersen Richard A. Coding of intention in the posterior parietal cortex. Nature. 1997;386(6621):167–170. doi: 10.1038/386167a0. [DOI] [PubMed] [Google Scholar]
- Szczepanski Sara M, et al. Dynamic changes in phase-amplitude coupling facilitate spatial attention control in fronto-parietal cortex. PLoS Biology. 2014;12(8):e1001936. doi: 10.1371/journal.pbio.1001936. http://dx.plos.org/10.1371/journal.pbio.1001936. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thut Gregor, Nietzel Annika, Brandt Stephan A, Pascual-Leone Alvaro. Alpha-band electroencephalographic activity over occipital cortex indexes visuospatial attention bias and predicts visual target detection. The Journal of neuroscience: the official journal of the Society for Neuroscience. 2006;26:9494–9502. doi: 10.1523/JNEUROSCI.0875-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tort Adriano BL, Komorowski Robert, Eichenbaum Howard, Kopell Nancy. Measuring phase-amplitude coupling between neuronal oscillations of different frequencies. Journal of neurophysiology. 2010;104(2):1195–1210. doi: 10.1152/jn.00106.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vaz Alex P, et al. Dual origins of measured phase-amplitude coupling reveal distinct neural mechanisms underlying episodic memory in the human cortex. NeuroImage. 2017 Dec;148:148–159. doi: 10.1016/j.neuroimage.2017.01.001. 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


