Abstract
Purpose
On‐board magnetic resonance imaging (MRI) greatly enhances real‐time target tracking capability during radiotherapy treatments. However, multislice and volumetric MRI techniques are frame rate limited and introduce unacceptable latency between the target moving out of position and the beam being turned off. We present a technique to estimate continuous volumetric tissue motion using motion models built from a repeated acquisition of a stack of MR slices. Applications including multislice target visualization and out‐of‐slice motion estimation during MRI‐guided radiotherapy are demonstrated.
Methods
Eight healthy volunteer studies were performed using a 0.35 T MRI‐guided radiotherapy system. Images were acquired at three frames per second in an interleaved fashion across ten adjacent sagittal slice positions covering 4.5 cm using a balanced steady‐state–free precession sequence. A previously published five‐dimensional (5D) linear motion model used for MRI‐guided radiotherapy gating was extended to include multiple slices. This model utilizes an external respiratory bellows signal recorded during imaging to simultaneously estimate motion across all imaged slices. For comparison to an image‐based approach, the manifold learning technique local linear embedding (LLE) was used to derive a respiratory surrogate for motion modeling. Manifolds for every slice were aligned during LLE in a group‐wise fashion, enabling motion estimation outside the current imaged slice using a motion model, a process which we denote as mSGA. Additionally, a method is developed to evaluate out‐of‐slice motion estimates. The multislice motion model was evaluated in a single slice with each newly acquired image using a leave‐one‐out approach. Model‐generated gating decision accuracy and beam‐on positive predictive value (PPV) are reported along with the median and 95th percentile distance between model and ground truth target centroids.
Results
The average model gating decision accuracy and PPV across all volunteer studies was 93.7% and 92.8% using the 5D model, and 96.8% and 96.1% using the mSGA model, respectively. The median and 95th percentile distance between model and ground truth target centroids was 0.91 and 2.90 mm, respectively, using the 5D model and 0.58 and 1.49 mm using the mSGA model, averaged over all eight subjects. The mSGA motion model provided a statistically significant improvement across all evaluation metrics compared to the external surrogate‐based 5D model.
Conclusion
The proposed techniques for out‐of‐slice target motion estimation demonstrated accuracy likely sufficient for clinical use. Results indicate the mSGA model may provide higher accuracy, however, the external surrogate‐based model allows for unbiased in vivo accuracy evaluation.
Keywords: motion modeling, MRI, radiotherapy
1. Introduction
Respiratory motion during radiotherapy reduces the accuracy of radiation delivery. Passive methods that consider motion as a component of uncertainty and active methods that address motion by compensation have been used to mitigate such impact.1 Methods of active respiratory motion compensation include breath hold techniques, abdominal compression, gantry or multileaf collimator (MLC) target tracking,2 and radiotherapy gating.3 Radiotherapy gating can be based on internal or external motion surrogates4, 5 or on tumor motion measured directly in images.6
Magnetic resonance image (MRI)‐guided radiotherapy is an emerging technology that enables respiratory motion compensation based on images that have excellent soft‐tissue contrast.7, 8 The ViewRay MRIdian (ViewRay, Inc. Oakwood Village, OH) is a commercially available device that performs radiotherapy gating based on target position measured directly in real‐time MR images. MRIdian gating images can be acquired in a single sagittal slice at four frames per second (FPS), or across three sagittal slices at 2 FPS.9 The time between image frames contributes to the gating latency, or overall latency between when a target moves across a gating boundary and when the beam state changes. Unfortunately, current fast MRI techniques are unable to acquire volumetric images or two‐dimensional (2D) images across multiple slice positions quickly enough to avoid introducing unacceptable gating latency. For that reason, at our institution single slice target tracking is used. This approach suffers from poor ability to capture out‐of‐slice target motion, target deformation, and limited visualization of dynamic relationships between adjacent mobile anatomical structures, such as the pancreas, duodenum, and stomach.
Surrogate‐based motion models provide mathematical frameworks that can be used to estimate anatomical motion using a respiratory surrogate. Motion models have been used in the context of MRI‐guided radiotherapy to estimate motion in a three‐dimensional volume from a single imaging slice,10, 11 orthogonal imaging planes,12, 13 or sequentially acquired adjacent sagittal slices,14 as well as to predict motion to reduce gating latency.15, 16 We recently developed a model‐interpolated gating (MI gating) technique to reduce the image frame rate required for accurate gating using a continuously updated biomechanically inspired motion model and external respiratory surrogate.17 In this manuscript, we present an extension of our technique that allows estimation of target motion across multiple slice positions for MRI‐guided radiotherapy gating. Additionally, we compare the external surrogate‐based model to an image‐based alternative. Image‐based surrogates present two advantages: (a) the use of an external respiratory surrogate is associated with additional setup effort and potential for operator error, which could be avoided using an image‐based surrogate and (b) image‐based surrogates are potentially more representative of internal anatomical motion, increasing the accuracy of modeling. Our method was adapted from a simultaneous group‐wise manifold alignment (SGA) motion model developed by Baumgartner et al.,14 and modified to improve computational efficiency to make clinical implementation feasible. Additionally, we propose a method to evaluate the accuracy of out‐of‐slice motion estimation using this model. We term our method modified SGA (mSGA) for distinction.
2. Materials and methods
2.A. Motion modeling techniques
2.A.1. Motion modeling: 5D model
Motion modeling was performed using a 5D linear motion model, originally developed in the context of computed tomography imaging.18, 19, 20, 21 The MRI‐based 5D motion modeling process was described in detail our recent publication17 and is briefly summarized as follows. A respiratory pneumatic bellows (Lafayette Instrument, Lafayette, IN, USA) signal was recorded simultaneously during imaging studies on an external computer using LabVIEW (Austin, TX). Registration‐derived deformation vector fields were fit along the respiratory bellows surrogate to the 5D linear motion model:
| (1) |
where is the model‐estimated tissue position, is the initial tissue position and and are parameters which correlate tissue position to the surrogate amplitude v (voltage amplitude) and surrogate velocity f (time derivative of voltage). In the present study, the model was fit at each imaged slice position using the 10 most recently acquired images. We explored the use of more images for model fitting, varying the number of training images from 10 to 50 in intervals of 10, but determined that using the 10 most recently acquired images resulted in the most accurate motion modeling. This result agrees with our findings in our previous work.17
Our previous publication evaluated the accuracy of this model's ability to generate gating decisions between images acquired at a slow frame rate (≤1 FPS) in a single slice. This technique could enable gating based on pulse sequences that require long delays between image acquisitions (e.g., T2 weighted imaging). The present work uses a 2D multislice image acquisition that repeatedly acquires a set of 10 images across adjacent slice positions in a little over 3 s. In this way a multislice model‐based representation of the subject's anatomy in a region of interest (ROI) about the target is built, continuously updated and validated with each newly acquired image. A schematic depicting the 5D modeling workflow is shown in Supporting Information Fig. S1.
2.A.2. Simultaneous group‐wise manifold alignment (SGA) image surrogate
Locally linear embedding (LLE), originally described by Roweis and Saul, learns a nonlinear manifold structure using series of locally linear fits.22 Baumgartner et al.23 showed that LLE can be used to extract a motion surrogate from images acquired across various respiratory phases by learning how the images relate to one another. In LLE, each high dimensional data point is approximated by the weighted sum of its nearest neighbors. In the present application the high dimension data point is a 2D image and the nearest neighbor images are identified by sum of squared pixel‐wise intensity differences. The weights are found by minimizing the embedding error given by
| (2) |
where a high‐dimensional data vector (e.g., of voxel image data) is a high‐dimensional neighbor of is the reconstruction weight associated with neighbor and K is the number of nearest neighbors. Specifically, least squares minimization is performed under the constraint that all weights sum to one as described by Roweis and Saul.24 Then, a set of vectors of reduced dimensionality d is found such that the weighting and nearest neighbors identified in the high dimensional space are preserved. This is performed by fixing the reconstruction weights W ij defined in the high‐dimensional space and minimizing the cost function
| (3) |
where is the low‐dimensional data vector corresponding to (i.e., where d is the selected final dimensionality of the manifold) and is the low‐dimensional neighbor corresponding to . This method preserves the locally linear relationships of the high‐dimensional data, while providing a low‐dimensional representation of the dataset.
In addition, SGA incorporates an interslice penalty term to establish a correspondence between adjacent slices by aligning the surrogates during LLE. The two high‐dimensional datasets for adjacent slices are denoted as X 1 , X 2 where an image in each set is expressed as , , respectively. The corresponding sets of low‐dimensional embeddings are Y 1 , Y 2 with individual data points , . The combined cost function to find the aligned low‐dimensional embeddings of two adjacent imaging slices simultaneously is defined as
| (4) |
where Φ1( Y 1 ) and Φ2( Y 2 ) are the intradataset costs for each set of images given by the standard LLE cost function [Eq. (3)] and μ is a parameter which controls the interdataset cost weighting Φ12( Y 1 , Y 2 ) in the total cost function.
The interdataset cost function is given by
| (5) |
where N is the total number of images in each dataset, i 1 and i 2 are the index in each image set and U is a Gaussian similarity kernel which defines the relative penalty associated with each grouping of surrogate values. The similarity kernel weightings are given by
| (6) |
where σ is a kernel parameter and is the normalized square root of sum of squared voxel‐wise intensity differences between the images (i.e., Euclidean distance). The connections between the images across slice positions were sparsified while maximizing the total similarity in terms of the normalized Euclidean distance such that each high‐dimensional data point was connected to only one other data point at the adjacent slice position. This sparsification was performed with an algorithm proposed to solve the assignment problem.25 Including the interdataset penalty term discouraged images that had low sum of squared voxel‐wise intensity differences from having different surrogate values.
The method above outlines SGA for two image sets. In our study, we acquired images across a stack of ten adjacent slices. We extended the SGA procedure to compute the low‐dimensional embedding for all slice positions simultaneously. Specifically, SGA manifold learning was performed by minimizing the cost function
| (7) |
where the subscript i indicates the relative position of the image slices. Occasionally, a slice‐dependent translational shift remained between some of the manifolds. This discrepancy was removed by extracting a rotation and translation between the manifolds using Procrustes method.26 This extension resulted in a smaller out‐of‐slice motion error estimated using the back‐propagated surrogate described below.
Prior to performing SGA, the images were processed with a 6 × 6 averaging convolution filter to reduce the influence of noise and a ROI was manually selected for SGA to exclude bowel regions which exhibited nonrespiratory motion‐related changes due to digestive processes. We explored the use of the deformation vector fields (DVF)s in place of the images during the mSGA modeling process (i.e., SGA surrogate generation), but observed that the images produced the most accurate modeling results.
2.A.3. Modified SGA (mSGA) weighted nearest neighbor motion model
Motion modeling using manifold learning was performed by combining the DVFs obtained from image registration and the nonparametric out‐of‐sample extension for LLE proposed by Saul and Roweis.27 The goal of the out‐of‐sample extension is to provide a generalization of the learned manifold to estimate a new low‐dimensional data point from a new image (i.e., estimate a surrogate value for a newly acquired image). This extension is performed by identifying the K nearest neighbors in the training dataset X , computing reconstruction weights W using constrained least squares minimization of the error defined in Eq. (2), and computing the weighted sum of the low‐dimensional embeddings in X . This process is summarized by
| (8) |
where is the low‐dimensional embedding corresponding to each nearest neighbor and, W j is the same reconstruction weight associated with each neighbor identified in the high‐dimensional space. Since adjacent slice manifolds are aligned by SGA, the nearest low‐dimensional neighbors in the adjacent slices are directly identified. The nearest neighbor surrogate weights are computed from members of the adjacent slice using least‐squared minimization of a cost similar to Eq. (2) in the low‐dimensional manifold. In order to obtain motion information, the new DVF is estimated using these weights W j and the DVFs corresponding to the images in X . This is expressed by
| (9) |
where is the DVF corresponding to each nearest neighbor. Since each slice is aligned with its adjacent slices, this process can be repeated until a motion estimate is obtained in every slice, as illustrated in Fig. 1).
Figure 1.
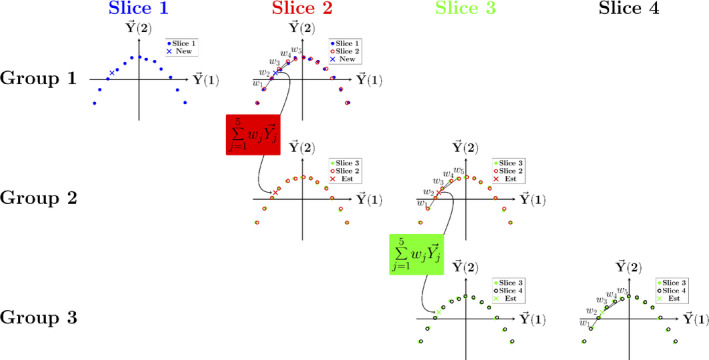
Schematic representation of surrogate propagation from an image acquired at slice 1 (blue “x”) across to slice 4. The surrogate is estimated in each slice as a weighted sum of the five most similar surrogate values in the aligned adjacent slice (slice 2). Since the same images are included in the next group (group 2), the weights can be used to estimate the surrogate in the next group of aligned manifold surrogates (connection between Group 1 and 2). The process is repeated until reconstruction weights are obtained in every slice. [Color figure can be viewed at wileyonlinelibrary.com]
The mSGA model is used to estimate motion in every slice for each newly acquired image until 10 new images are available at each slice position. The model is then updated using the most recent set of images at each slice position. The model is not updated each time a new image is acquired due to computation time constraints. The SGA surrogate generation and mSGA modeling process is summarized in Supporting Information Fig. S2.
2.B. Evaluation study
2.B.1. Imaging protocol
All imaging studies were performed under an IRB‐approved research protocol using the ViewRay MRIdian.9, 28 Briefly, MRIdian combines three 60Co treatment heads with a 0.35 T split bore MRI. All MRI software and hardware were provided by Siemens Medical Systems (Erlangen, Germany) with the exception of the gradient and surface coils which were designed by ViewRay. All imaging was performed using research mode, in which the MRI system is operated independently from the radiotherapy system. A balanced steady‐state–free precession sequence was used to conduct eight healthy volunteer studies following informed consent.29 Images were obtained at approximately 3 FPS with a 400 × 400 mm2 field of view, 2 × 2 mm2 in‐plane resolution, 556 Hz/Px bandwidth, 4.5 mm slice thickness, 1.38 ms echo time, 3.26 ms repetition time, 60° flip angle, generalized autocalibrating partially parallel acquisition acceleration30 factor of 2, partial Fourier factor of 6/8. Ten adjacent sagittal slice positions were imaged in an interleaved fashion repeatedly until 200 images were acquired at each slice position. Additionally, volunteers were instructed to hold their breath at a normal exhale breathing phase while a breath hold image was obtained at each slice location (approximately 3.3 s in duration).
2.B.2. Image registration
Image registration‐derived DVFs were used in two ways in this study: for building/fitting the mSGA and 5D models and to deform contours for ground truth target tracking. Image registration was performed using a multi‐level b‐spline deformable registration with mutual information as a similarity metric using the elastix registration software.31, 32, 33 The influence of noise on image registration accuracy was reduced by using a bilateral filter prior to registration. Reference images for registration were obtained from natural exhale breath hold images in cooperative volunteers (3) or selected from free‐breathing images when a natural exhale breath hold phase was unavailable (2) or when the range of motion was large (3) and using a mid‐exhale breathing phase improved registration accuracy. The range of motion in the volunteer studies with large motion was 25.6, 48.0, and 52.9 mm.
Registration accuracy was evaluated by performing a landmark evaluation in a similar manner to that described in our previous publication where the same anatomical features tracked as radiotherapy targets served as landmarks.17 The location of the landmark in the first 50 images acquired at each slice position, as well as the location in the reference image used in registration was manually identified. The distance of the landmark from the location in the reference image and from the mean landmark position in the registered images served to evaluate registration accuracy and consistency, respectively.
2.B.3. Model gating evaluation
The model gating studies were conducted offline using software developed in the MATLAB programming environment (Mathworks, Natick, MA). For each volunteer, a normal anatomical feature subject to respiratory motion that spanned multiple slices (e.g., a blood vessel in the liver) was used to simulate a radiation therapy target. Contours of the target were manually drawn in the set of reference images used for image registration. The target contour was expanded automatically by a 3‐mm gating margin and generated at the end exhale breathing phase to form a gating boundary. When greater than 10% of the target contour moved outside this boundary, a “beam‐off” gating decision was made. The 10% threshold was used because the same threshold is used in clinical gating at our institution.
The model was evaluated in the same imaging slice corresponding to each newly acquired image. Only the portion of the model describing the currently imaged slice was used to generate a gating decision. Model‐derived gating decisions (“beam‐on” and “beam‐off”) were compared to the ground truth gating decisions obtained from imaging. All model gating studies were prospective and utilized a leave‐one‐out approach. Only previously acquired images were used to fit the model and the current surrogate value was used to generate model gating decisions. Since the mSGA model fitting duration takes a substantial amount of time, the model was updated after 10 new images were acquired at each slice position. The 5D model on the other hand can be updated more rapidly, thus the model was updated after a new image was acquired at each slice position. Model‐derived gating decisions were quantitatively evaluated by computing the gating accuracy and positive predictive value (PPV). Gating accuracy was defined as the proportion of total gating decisions that were correct. Gating PPV was defined as the proportion of “beam‐on” model gating decisions that were correct. Additionally, the positions of the model‐tracked and image‐tracked target centroids were compared. The median and 95th percentile distances between these centroids are reported. The gating results using the mSGA and 5D motion models were compared using a paired t‐test between the gating evaluation metrics obtained with each model.
In the comparison procedure described above, the same image was used for gating accuracy evaluation and for mSGA surrogate generation. In a practical clinical implementation, the model would presumably be used to form gating decisions from volumetric or multislice motion, rather than motion only in the currently imaged slice. Therefore, a full evaluation of the accuracy of the model must include the motion propagation step. Since only one imaging slice can be acquired at each time point, the accuracy of motion propagation outside the currently imaged slice could not be measured directly against a ground truth. Instead, the surrogate was propagated to each of the nine unimaged slice positions and then back in reverse to generate “back‐propagated” surrogates. These back‐propagated surrogates were used with the model at the currently imaged slice to compute the same evaluation metrics as described above. We report the average result across back‐propagated surrogates from all nine other slices. Back‐propagating the surrogate implies that the motion information is transferred twice the number of slices required for motion modeling (e.g., motion estimation in the adjacent slice only requires transferring the motion information across one slice, but back‐propagation requires that the surrogate to be propagated again back to the original slice). Propagation error may compound with the number of times the surrogate has been propagated. Additionally, propagation error also depends on the specific relationships between each group of images. Therefore, back‐propagation to and from every slice was included in the evaluation (as opposed to only the slices nearest to the current imaging slice).
2.B.4. mSGA model parameter selection
The mSGA requires the selection of five parameters: the number of training images, final dimensionality of the surrogate d, interdataset penalty term μ, similarity kernel parameter σ, and number of nearest neighbor images K. The possible ranges of parameters were constrained to ensure computation times consistent with a real‐time system. All parameters were selected empirically by performing a number of gating studies and evaluating the effect of each parameter on gating accuracy and PPV. The final selected parameters used in our study were 50 training images, d of 3, μ of 1, σ of 1, and 25 K nearest neighbor images.
3. Results
3.A. Registration accuracy
The accuracy and consistency of deformable image registration was similar to that in our previous studies.17 Across all volunteer studies the median registration accuracy and consistency was 1.26 and 0.71 mm, respectively.
3.B. Model evaluation
The average model gating accuracy across the eight volunteer studies was 93.7% for the 5D model, 96.8% for the mSGA model, and 93.4% with the back‐propagated surrogate and mSGA model. The corresponding PPVs were 92.8%, 96.1%, and 92.3%, respectively. The median and 95th percentile distance between the model‐tracked and image‐tracked target centroids were 0.91 and 2.90 mm for the 5D model, 0.58 and 1.49 mm for the mSGA model, and 0.97 and 2.76 mm for the back‐propagated surrogate and mSGA model, respectively, averaged across all volunteer studies. Figure 2 shows the individual results of each model evaluation obtained across all volunteer studies.
Figure 2.
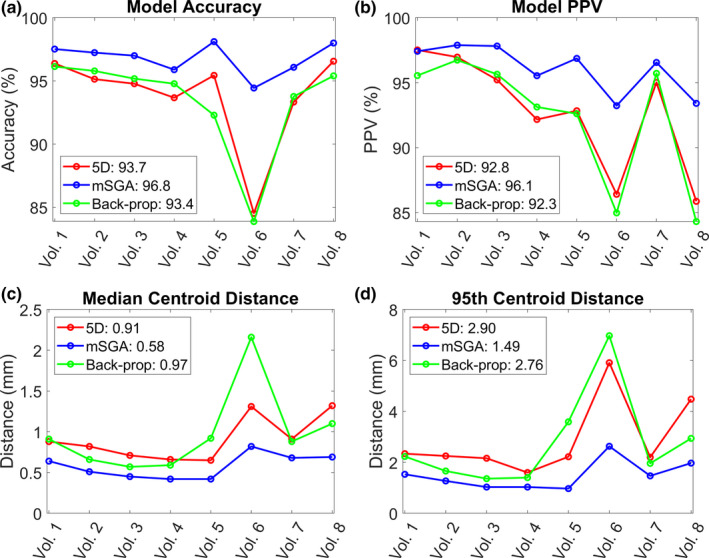
The model gating decision accuracy (a), positive predictive value (b), and median (c) and 95th percentile (d) distance between the model‐tracked and image‐tracked target centroids for each volunteer study and motion model. The average value across all volunteer studies using each model is shown in the legend. [Color figure can be viewed at wileyonlinelibrary.com]
A paired t‐test revealed that the mSGA model outperformed the 5D model by yielding statistically significant differences across all evaluation metrics. However, there were no statistically significant differences comparing the back‐propagated surrogate and mSGA model to the 5D model.
An example of the proportion of the target in the gating margin and distance between the image‐tracked and model‐tracked gating target centroids are shown for a portion of volunteer study 8 in Fig. 3.
Figure 3.
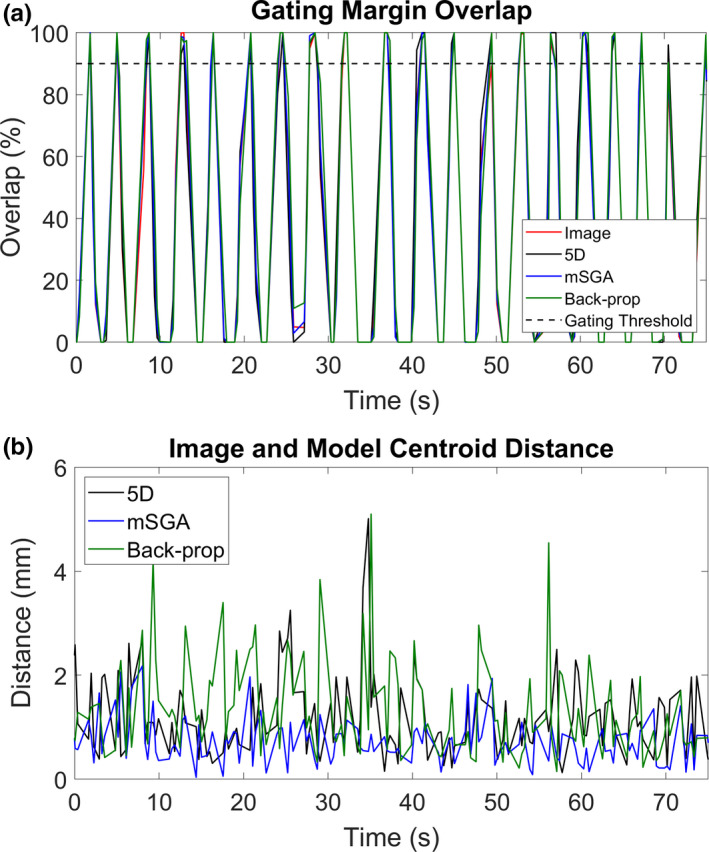
Proportion of the target within the gating margin derived from the images directly and using each model (a) and distances between the image‐tracked and model‐tracked target centroids (b) for a portion of volunteer study 8. [Color figure can be viewed at wileyonlinelibrary.com]
4. Discussion
The inability to visualize and respond to three‐dimensional (3D) motion is a limitation of current MRI‐guided radiotherapy technology.34 In this work, we evaluated a technique to perform radiotherapy gating based on a motion model and a series of 2D images acquired across 10 slice positions. An example comparison between tracking a target in the acquired image and using the mSGA model is shown in Fig. 4. This figure also shows how the model can be used to enable multislice target visualization in the axial and coronal planes. A video corresponding to this example can be found in the Supporting Information associated with this manuscript.
Figure 4.
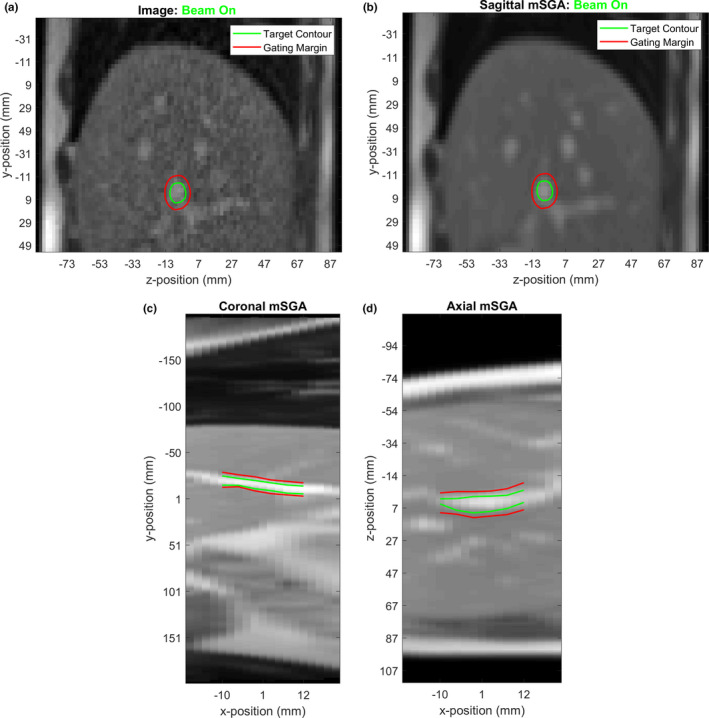
An example of an acquired image and image‐tracked target (a), the corresponding mSGA model‐generated image and model‐tracked target at the same slice position (b) and the coronal (c) and axial (d) model‐generated images and cross section of the model‐tracked target volume. Model‐generated images were obtained by combining the first 50 images used to fit the model using the registration information, then deforming them according to the motion obtained from the model. [Color figure can be viewed at wileyonlinelibrary.com]
In the present manuscript, we use in vivo studies to estimate the accuracy of the proposed multislice tracking technique as applied to respiratory gating. The present work does not quantify the benefit of multislice gating in terms of dosimetric accuracy relative to single‐slice gating. Such potential benefits could be estimated using a simulation to provide 3D ground truth motion. Additionally, simulations could be used to assess the proposed back‐propagated surrogate out‐of‐slice motion error evaluation. However, simulation studies are subject to limitations and are beyond the scope of the present manuscript. These studies should be the topic of future work.
Two motion models were evaluated: mSGA based on the work of Baumgartner et al.,14, 23 and the 5D model. Our technique applied with both of these models is likely sufficiently accurate for clinical use. One of the key differences between the two models is the use of an image‐based or external surrogate. Use of an external surrogate introduces an additional setup step and is associated with the possibility of human error. However, because the external surrogate is acquired completely independently of the images, each newly acquired image represents an opportunity for an unbiased test of the model against ground truth information. In the case of mSGA, since the surrogate and the ground truth are obtained from the same image, a completely unbiased ground truth test is not possible. We evaluated the accuracy of the model in the currently imaged slice, and estimated model accuracy outside the currently imaged slice using the back‐propagated surrogate. We observed that error was both slice specific and dependent on the distance of propagation as shown in Supporting Information Fig. S3. This indicates that propagation error is specific to the relationship between the images in each group of adjacent slices and increases with the number of propagations. The mSGA model without surrogate back‐propagation was statistically significantly more accurate than the 5D model across all evaluation metrics. However, none of the gating statistics derived from the 5D model and the mSGA model using the back‐propagated surrogate were statistically significantly different. Notably, the motion models performed worst in volunteer study 6. Breathing pattern changes (e.g., chest vs abdominal breathing) were observed during this volunteer's study, as well as an extremely deep inspiration breath that may have been associated with stretching during the study (the volunteer was observed stretching during another study in the same imaging session).
Although the mSGA was found to be more accurate, use of the 5D model may still be sufficiently accurate and holds some advantages. The use of an external surrogate with the 5D model means that every newly acquired image can be used for an unbiased evaluation of model accuracy prior to model updating. The mSGA model uses each newly acquired image for surrogate generation, and thus a strictly unbiased evaluation of model accuracy is not possible in vivo. Second, the respiratory bellows is continuously available (sampled at 100 Hz), reducing gating latency. Additionally, use of the respiratory bellows could enable other imaging studies to be acquired during gated treatments.17 Third, the 5D model requires fewer images for model fitting reducing fitting time and potentially allows for more rapid adjustment to breathing pattern changes. In our study, ten images acquired at each slice position were used to fit the 5D model, whereas 50 were used for mSGA modeling. As mentioned previously, using more images to fit the 5D model reduced the accuracy of motion modeling. An implementation of the technique with the clinical imaging protocol (4 FPS) would require 25 and 125 s of imaging prior to gated treatment with the 5D and mSGA models, respectively. Fourth, the 5D model is less computationally demanding than the mSGA model. In our MATLAB‐based, largely single‐threaded implementation, refitting the 5D model required 8.1 ms and a model gating decision for the entire gating target volume was obtained in 42 ms on average across all volunteer studies. For the mSGA model, model refitting occurred after ten new images were acquired at each slice position and took 4.7 s. A gating decision for the target volume was obtained on average in 60 ms with the mSGA model. Model gating accuracy and PPV can be improved further using the mSGA model with more training images, more nearest neighbors, and more frequent model refitting. For example, increasing the number of training images to 100 images, using 50 nearest neighbors to fit the mSGA model, and updating the model after a new image is acquired at each slice position did not increase the average gating accuracy, but increased the average PPV from 96.1% to 96.8% and reduced the median and 95th percentile centroid distance from 0.58 to 0.51 mm and from 1.49 to 1.24 mm, respectively, across all volunteer studies. However, the computation time associated with larger datasets could cause practical challenges in a clinical implementation of the technique (model fitting took on average 34 s and target volume gating decisions required 81 ms).
The results reported in this work are subject to some limitations. In this study, ten adjacent slice positions were imaged. This region spans 4.5 cm laterally, which may be too large or too small for some tumors. Since motion propagation error compounds with the distance that the motion is propagated, the results may be worse for tumors that span more than 4.5 cm laterally. Conversely, for smaller tumors, it is possible that the motion propagation would be more accurate than the results we report in this work. In our study, we imaged regions subject to substantial respiratory motion. The selected regions excluded the heart as well as the lateral periphery of the volunteers. The models may perform differently in regions subject to differing effects of respiratory motion.
The mSGA model evaluated in this report differs from and expands upon the work reported by Baumgartner et al.23 in a few key ways. The group‐wise simultaneous manifold alignment technique was originally developed for retrospective sorted slice‐based four‐dimensional (4D) MRI, and was later applied to positron emission tomography (PET) motion correction. Specifically, motion‐corrupted PET acquisitions were simulated and motion corrections were derived from registrations of the selected 4D MRI images obtained using the manifold learning technique.35 The method was further developed by Baumgartner et al.14 enabling motion estimates to be obtained across many slice positions using a weighted sum of deformation vector fields. The group evaluated their model using a simulation study as well as an in vivo study that compared an acquired navigator to a navigator derived from a 3D volume generated from their motion model. In our work, we developed a method to evaluate the accuracy of motion modeling outside the currently imaged slice using the back‐propagated surrogate. Additionally, we modified SGA to address computational challenges relevant to a clinical implementation of the technique. First, we elected to refit the model using only the most recent set of training images in order to avoid increasing the computation time as the study progressed. Second, we updated the model only after 10 images were acquired. Since model refitting requires an appreciable amount of time in our largely single‐threaded MATLAB implementation, the radiation beam may need to be held while the model is updated (approximately 4 s). The model update duration could be reduced by a parallel computation of the sum of squared distance between the images, as well as by changing the algorithm used to sparsify the connections between images across slice positions. Specifically, instead of solving the assignment problem across slice positions from scratch each time the model is updated, the previous optimization result could be incorporated to speed up the new optimization. This could be performed using an alternative algorithm to speed up computation time.36, 37 Finally, we acquired the current image‐based surrogate using the out‐of‐sample extension for LLE rather than refitting the manifold weights as performed by Baumgartner et al.
The MRI‐guided radiation therapy provides the opportunity to conduct radiotherapy gating by tracking targets in images acquired during treatment. However, the current imaging technology is not able to acquire 3D images or images across multiple locations without introducing unacceptable gating latency. As a result, only a portion of the tumor is typically tracked in a single slice. Several approaches have been developed to address this limitation. Harris et al.,10, 11 and separately Stemkens et al.,12 created a motion model based on an initial 4D‐MRI and estimated 3D motion by fitting the model to 2D cine images. This approach is limited by the fact that motion estimation outside the imaged slice(s) is constrained to the initial model which is not updated and may not accommodate changes in breathing patterns, irregular breaths, digestive motion, or pose changes. Furthermore, the cine images are used to instantiate the modeled positions and thus cannot be used for real‐time ground truth comparison. Li et al.38 estimated high‐spatial resolution 3D cine images by registering and deforming an initial high‐spatial resolution breath hold image to 3D cine images with 5 mm isotropic resolution acquired at 2 Hz. The utility of this technique is limited by the time necessary to perform 3D deformable registration (at least several seconds according to the authors). Furthermore the 0.5‐s 3D cine acquisition period would introduce prohibitive gating latency and the 5‐mm spatial resolution of the cine imaging would potentially limit the accuracy of target tracking. Seregni et al.13 developed a feature tracking model with temporal prediction and, separately, an internal to external correlation model similar to the 5D model. Using interleaved orthogonal 2D images acquired every 0.25 s, they demonstrated an ability to increase the effective frame rate of feature tracking which would potentially reduce gating latency. A key difference of our technique is that it involves reducing the imaging frame rate in any given slice well below what is necessary for direct image radiotherapy gating (i.e., 1 frame every 3 s or slower). We have shown in our previous work17 that a reduced frame rate could expand the set of pulse sequences that can be used for gating, and in the present report demonstrate the use of multiple cyclically imaged sagittal slices can be used to build a multislice motion model.
5. Conclusion
We have demonstrated a technique for multislice real‐time motion estimation for MRI‐guided radiotherapy based on a continuously updated motion model and a cyclic 2D multislice image acquisition. The accuracy of the technique has been demonstrated in a simulated radiotherapy gating experiment with in vivo images acquired at 0.35 T. Two specific motion models were evaluated: the mSGA model, which potentially maximizes motion estimation accuracy using an image‐based surrogate, and the external surrogate‐based 5D motion model, which enables continuous unbiased ground truth evaluation, maximizing clinical confidence during treatment.
Conflicts of Interest
James Lamb has previously received speaking and consulting fees from ViewRay. James Lamb, John Ginn, and Daniel Low have submitted a provisional patent related to this work.
Supporting information
Fig. S1. A schematic representation of the 5D modeling workflow.
Fig. S2. A schematic representation of the mSGA modeling workflow.
Fig. S3. The slice position dependence of gating accuracy (a), gating positive predictive value (b), distance between the model‐tracked and image‐tracked target centroids (c), and proportion of the model‐tracked target overlapping the image‐tracked target (d) using the mSGA model and back‐propagated surrogate in volunteer study 1. The slice number indicates the position of the imaged slice relative to all other slices. The evaluation slice is the location where the model and image gating statistics are compared. The origin slice refers to the location where the back‐propagated surrogate originates. For example, the dark blue line (Origin Slice #1) is located at one of the lateral ends of the imaged volume and is the furthest imaged slice from evaluation slice 9. Note that only a subset of the 10 imaged slices were “evaluation slices” since the tracked target did not span all imaged positions. Increasing error associated with propagation distance is indicated by a relatively small median distance between modeled and tracked target centroids for nearby slice positions compared to distant slice positions. The proportion of the model‐tracked contour overlapping the image‐tracked contour is also larger for nearby slice positions compared to distant slice positions. Slice‐specific model gating performance is indicated by the fact that model gating performance may improve or worsen as the volume is traversed (e.g., moving from evaluation slice #3 to evaluation slice #9).
Video S1. A video showing the image‐tracked target in the sagittal images acquired across multiple slice positions during a healthy volunteer study. The model generated images and model‐tracked target corresponding to each acquired image are shown in the sagittal, coronal and axial planes.
Acknowledgments
This work was supported in part by a National Institutes of Health grant (2T32EB2101‐41).
References
- 1. Keall PJ, Mageras GS, Balter JM, et al. The management of respiratory motion in radiation oncology report of AAPM Task Group 76. Med Phys. 2006;33:3874–3900. [DOI] [PubMed] [Google Scholar]
- 2. Sawant A, Venkat R, Srivastava V, et al. Management of three‐dimensional intrafraction motion through real‐time DMLC tracking. Med Phys. 2008;35:2050–2061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Loo BW Jr., Kavanagh BD, Meyer JL. Motion management and image guidance for thoracic tumor radiotherapy: clinical treatment programs. Front Radiat Ther Oncol. 2011;43:271–291. [DOI] [PubMed] [Google Scholar]
- 4. Wagman R, Yorke E, Ford E, et al. Respiratory gating for liver tumors: use in dose escalation. Int J Radiat Oncol Biol Phys. 2003;55:659–668. [DOI] [PubMed] [Google Scholar]
- 5. vanvan der Voort Zyp NC , Prevost JB, Hoogeman MS, et al. Stereotactic radiotherapy with real‐time tumor tracking for non‐small cell lung cancer: clinical outcome. Radiother Oncol. 2009;91:296–300. [DOI] [PubMed] [Google Scholar]
- 6. Fu D, Kahn R, Wang B, et al. Xsight lung tracking system: a fiducial‐less method 26 for respiratory motion tracking. Robot Radiosurg Treat Tumors Move Respir. 2007;1:265. [Google Scholar]
- 7. Yun J, Wachowicz K, Mackenzie M, Rathee S, Robinson D, Fallone BG. First demonstration of intrafractional tumor‐tracked irradiation using 2D phantom MR images on a prototype linac‐MR [published online ahead of print 2013/05/03]. Med Phys. 2013;40:051718. [DOI] [PubMed] [Google Scholar]
- 8. Lamb JM, Ginn JS, O'Connell DP, et al. Dosimetric validation of a magnetic resonance image gated radiotherapy system using a motion phantom and radiochromic film [published online ahead of print 2017/04/25]. J Appl Clin Med Phys. 2017;18:163–169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Mutic S, Dempsey JF. The ViewRay system: magnetic resonance‐guided and controlled radiotherapy [published online ahead of print 2014/06/17]. Semin Radiat Oncol. 2014;24:196–199. [DOI] [PubMed] [Google Scholar]
- 10. Harris W, Ren L, Cai J, Zhang Y, Chang Z, Yin FF. A technique for generating volumetric cine‐magnetic resonance imaging. Int J Radiat Oncol Biol Phys. 2016;95:844–853. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Harris W, Yin F‐F, Wang C, Zhang Y, Cai J, Ren L. Accelerating volumetric cine MRI (VC‐MRI) using undersampling for real‐time 3D target localization/tracking in radiation therapy: a feasibility study. Phys Med Biol. 2017;63:01NT01. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Stemkens B, Tijssen RH, de Senneville BD, Lagendijk JJ, van den Berg CA. Image‐driven, model‐based 3D abdominal motion estimation for MR‐guided radiotherapy. Phys Med Biol. 2016;61:5335–5355. [DOI] [PubMed] [Google Scholar]
- 13. Seregni M, Paganelli C, Lee D, et al. Motion prediction in MRI‐guided radiotherapy based on interleaved orthogonal cine‐MRI. Phys Med Biol. 2016;61:872–887. [DOI] [PubMed] [Google Scholar]
- 14. Baumgartner CF, Kolbitsch C, McClelland JR, Rueckert D, King AP. Autoadaptive motion modelling for MR‐based respiratory motion estimation. Med Image Anal. 2017;35:83–100. [DOI] [PubMed] [Google Scholar]
- 15. Bourque AE, Carrier J‐F, Filion É, Bedwani S. A particle filter motion prediction algorithm based on an autoregressive model for real‐time MRI‐guided radiotherapy of lung cancer. Biomed Phys Eng Expr. 2017;3:035001. [Google Scholar]
- 16. Sharp GC, Jiang SB, Shimizu S, Shirato H. Prediction of respiratory tumour motion for real‐time image‐guided radiotherapy. Phys Med Biol. 2004;49:425–440. [DOI] [PubMed] [Google Scholar]
- 17. Ginn JS, O'Connell D, Thomas DH, Low DA, Lamb JM. Model‐interpolated gating for magnetic resonance image–guided radiation therapy. Int J Radiat Oncol Biol Phys. 2018;102:885–894. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Low DA, Parikh PJ, Lu W, et al. Novel breathing motion model for radiotherapy. Int J Radiat Oncol Biol Phys. 2005;63:921–929. [DOI] [PubMed] [Google Scholar]
- 19. O'Connell DP, Thomas DH, Dou TH, et al. Comparison of breathing gated CT images generated using a 5DCT technique and a commercial clinical protocol in a porcine model. Med Phys. 2015;42:4033–4042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Dou TH, Thomas DH, O'Connell DP, Lamb JM, Lee P, Low DA. A method for assessing ground‐truth accuracy of the 5DCT technique. Int J Radiat Oncol Biol Phys. 2015;93:925–933. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Thomas D, Lamb J, White B, et al. A novel fast helical 4D‐CT acquisition technique to generate low‐noise sorting artifact–free images at user‐selected breathing phases. Int J Radiat Oncol Biol Phys. 2014;89:191–198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Roweis ST, Saul LK. Nonlinear dimensionality reduction by locally linear embedding. Science. 2000;290:2323–2326. [DOI] [PubMed] [Google Scholar]
- 23. Baumgartner CF, Kolbitsch C, McClelland JR, Rueckert D, King AP. Groupwise simultaneous manifold alignment for high‐resolution dynamic MR imaging of respiratory motion. Inf Process Med Imaging. 2013;23:232–243. [DOI] [PubMed] [Google Scholar]
- 24. Saul LK, Roweis ST. An introduction to locally linear embedding. unpublished Available at: http://www cs toronto edu/˜roweis/lle/publications html; 2000.
- 25. Munkres J. Algorithms for the assignment and transportation problems. J Soc Industrial Appl Math. 1957;5:32–38. [Google Scholar]
- 26. Goodall C. Procrustes methods in the statistical analysis of shape. J R Stat Soc Series B (Methodol). 1991;53:285–339. [Google Scholar]
- 27. Saul LK, Roweis ST. Think globally, fit locally: unsupervised learning of low dimensional manifolds. J Mach Learn Res. 2003;4:119–155. [Google Scholar]
- 28. Ginn JS, Agazaryan N, Cao M, et al. Characterization of spatial distortion in a 0.35 T MRI‐guided radiotherapy system. Phys Med Biol. 2017;62:4525–4540. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Scheffler K, Lehnhardt S. Principles and applications of balanced SSFP techniques. Eur Radiol. 2003;13:2409–2418. [DOI] [PubMed] [Google Scholar]
- 30. Griswold MA, Jakob PM, Heidemann RM, et al. Generalized autocalibrating partially parallel acquisitions (GRAPPA). Magn Reson Med. 2002;47:1202–1210. [DOI] [PubMed] [Google Scholar]
- 31. Klein S, Pluim JPW, Staring M, Viergever MA. Adaptive stochastic gradient descent optimisation for image registration. Int J Comput Vis. 2008;81:227. [DOI] [PubMed] [Google Scholar]
- 32. Shamonin DP, Bron EE, Lelieveldt BP, Smits M, Klein S, Staring M. Fast parallel image registration on CPU and GPU for diagnostic classification of Alzheimer's disease. Front Neuroinform. 2013;7:50. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Klein S, Staring M, Murphy K, Viergever MA, Pluim JP. elastix: a toolbox for intensity‐based medical image registration. IEEE Trans Med Imaging. 2010;29:196–205. [DOI] [PubMed] [Google Scholar]
- 34. van Herk M, McWilliam A, Dubec M, Faivre‐Finn C, Choudhury A. Magnetic resonance imaging‐guided radiation therapy: a short strengths, weaknesses, opportunities, and threats analysis. Int J Radiat Oncol Biol Phys. 2018;101:1057–1060. [DOI] [PubMed] [Google Scholar]
- 35. Baumgartner CF, Kolbitsch C, Balfour DR, et al. High‐resolution dynamic MR imaging of the thorax for respiratory motion correction of PET using groupwise manifold alignment. Med Image Anal. 2014;18:939–952. [DOI] [PubMed] [Google Scholar]
- 36. Mills‐Tettey GA, Stentz A, Dias MB. The dynamic Hungarian algorithm for the assignment problem with changing costs. Technical Report CMU‐RI‐TR‐07‐27, Robotics Institute, Pittsburgh, PA, July 2007. Available from: https://www.ri.cmu.edu/publications/the-dynamic-hungarian-algorithm-for-the-assignment-problem-with-changing-costs/
- 37. Toroslu IH, Üçoluk G. Incremental assignment problem. Inf Sci. 2007;177:1523–1529. [Google Scholar]
- 38. Li G, Wei J, Kadbi M, et al. Novel super‐resolution approach to time‐resolved volumetric 4‐dimensional magnetic resonance imaging with high spatiotemporal resolution for multi‐breathing cycle motion assessment. Int J Radiat Oncol Biol Phys. 2017;98:454–462. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Fig. S1. A schematic representation of the 5D modeling workflow.
Fig. S2. A schematic representation of the mSGA modeling workflow.
Fig. S3. The slice position dependence of gating accuracy (a), gating positive predictive value (b), distance between the model‐tracked and image‐tracked target centroids (c), and proportion of the model‐tracked target overlapping the image‐tracked target (d) using the mSGA model and back‐propagated surrogate in volunteer study 1. The slice number indicates the position of the imaged slice relative to all other slices. The evaluation slice is the location where the model and image gating statistics are compared. The origin slice refers to the location where the back‐propagated surrogate originates. For example, the dark blue line (Origin Slice #1) is located at one of the lateral ends of the imaged volume and is the furthest imaged slice from evaluation slice 9. Note that only a subset of the 10 imaged slices were “evaluation slices” since the tracked target did not span all imaged positions. Increasing error associated with propagation distance is indicated by a relatively small median distance between modeled and tracked target centroids for nearby slice positions compared to distant slice positions. The proportion of the model‐tracked contour overlapping the image‐tracked contour is also larger for nearby slice positions compared to distant slice positions. Slice‐specific model gating performance is indicated by the fact that model gating performance may improve or worsen as the volume is traversed (e.g., moving from evaluation slice #3 to evaluation slice #9).
Video S1. A video showing the image‐tracked target in the sagittal images acquired across multiple slice positions during a healthy volunteer study. The model generated images and model‐tracked target corresponding to each acquired image are shown in the sagittal, coronal and axial planes.


