Keeping Track of Where We Are: Spatial Working Memory in Navigation

Abstract

Spatial working memory (WM) seems to include two types of spatial information, locations and relations. However, this distinction has been based on small-scale tasks. Here, we used a virtual navigation paradigm to examine whether WM for locations and relations applies to the large-scale spatial world. We found that navigators who successfully learned two routes and also integrated them were superior at maintaining multiple locations and multiple relations in WM. However, over the entire spectrum of navigators, WM for spatial relations, but not locations, was specifically predictive of route integration performance. These results lend further support to the distinction between these two forms of spatial WM and point to their critical role in individual differences in navigation proficiency.

Classic conceptualizations of working memory (WM) typically involve a typology of sub-types of WM, such as the phonological loop, the visuospatial sketchpad, and the episodic buffer (Baddeley & Hitch, 1974). More recently, however, even finer gradations have become apparent. Within the spatial domain, it is possible to maintain an absolute spatial coordinate of an object (i.e., a spatial location) or the relative position of an object (i.e., a spatial relation). In fact, recent evidence suggests that maintaining spatial locations is supported by distinct neural correlates from those involved in maintaining spatial relations (Ackerman & Courtney, 2012; Blacker & Courtney, 2016; Blacker, Ikkai, Lakshmanan, Ewen, & Courtney, 2016; Ikkai, Blacker, Lakshmanan, Ewen, & Courtney, 2014). Using functional magnetic resonance imaging (fMRI), Ackerman and Courtney (2012) found that relation WM was supported by activity in anterior portions of prefrontal and parietal regions, whereas location WM was associated with activity in more posterior portions of these same regions. Moreover, Blacker et al. (2016) demonstrated with electroencephalography (EEG) that maintaining a spatial relation in WM was associated with an increase in posterior alpha power compared to maintaining a spatial location. Posterior alpha power has been interpreted as representing a suppression of irrelevant sensory information (e.g., Kelly, Lalor, Reilly, & Foxe, 2006) and thus may suggest that maintaining a spatial relation involves suppression of the initial sensory code (i.e., the spatial locations). Further, Blacker et al. (2016) found that maintaining a spatial relation in WM was associated with increased connectivity in the alpha frequency band between frontal and posterior regions, compared to maintaining a spatial location. Together, this work suggests that locations and relations are distinct types of spatial information that are held in WM via distinct and potentially competing neural mechanisms.

However, the stimuli used in these experiments are small-scale displays in which spatial locations and spatial relations have rather narrow meanings. How widely can these results be generalized to real-world tasks involving space, such as navigation? Further, can these distinct types of spatial WM account for the vast individual differences that are seen in navigation ability? Previous work investigating the relationship between WM and navigation has focused on the classic conceptualization of types of WM, finding that good and poor navigators use distinct verbal and spatial WM processes when acquiring spatial knowledge (Weisberg & Newcombe, 2016; Wen, Ishikawa, & Sato, 2011). For example, Wen et al. (2011) found that individuals with a good sense of direction, as measured by self-report, encoded landmarks and routes verbally and spatially and integrated the two types of information; whereas individuals with a poor sense of direction only encoded landmarks verbally and relied on visual cues only in processing route knowledge. The authors concluded that the two groups differed on their acquisition of landmark, route, and survey knowledge due to differential reliance on verbal, visual and spatial WM. However, within spatial WM, a further differentiation between spatial locations and spatial relations might reveal new evidence about individual differences in navigation as well as testing the generality of the new distinction in types of spatial WM. In a small-scale space, knowing a location may mean knowing the absolute coordinates of a location (e.g., in Cartesian coordinates or retinotopic space), whereas knowing a relation may mean knowing that location A is above and to the right of location B. In a large-scale, navigable space, knowing a location means knowing that the post office is at 334 Walnut St., whereas knowing a relation means knowing that the post office is north of the pub and west of the library. To the extent that processing locations and processing relations involve distinct cognitive processes, we predicted that WM for these two types of spatial information, as measured in a small-scale context, should both be relevant, possibly differentially relevant, in predicting navigation performance in a large-scale virtual environment.

We utilized a desktop virtual environment, which is immersive even though shown on a computer screen, and which participants treat as a large-scale, 3-D space. We chose this virtual environment because it has previously enabled demonstration of individual differences along multiple dimensions of navigation ability (Weisberg & Newcombe, 2016; Weisberg, Schinazi, Newcombe, Shipley, & Epstein, 2014). In this paradigm, participants learn eight buildings along two separate routes and then travel along two connecting routes to see how the whole environment is laid out. Performance on a pointing task reveals three clusters of participants: a cluster who perform poorly overall; a cluster of participants who perform well overall; and a cluster of participants who perform well when they are required to point to landmarks on that same route, but poorly when pointing to landmarks along a different route. This clustering pattern is supported by a taxometric analysis (Meehl & Yonce, 1994, 1996), has replicated across several studies (Weisberg & Newcombe, 2016; Weisberg et al., 2014), and displays convergent and divergent validity in the form of correlations with a self-reported sense of direction scale and verbal ability measure, respectively. Using this group-based approach, Weisberg and Newcombe (2016) found that participants who performed poorly overall on the virtual navigation pointing task had significantly worse verbal and spatial WM performance, as measure by the Operation Span and Symmetry Span tasks, respectively (Unsworth, Heitz, Schrock, & Engle, 2005), compared to the other two groups. In addition to examining WM for spatial locations and relations using a novel task, we also included an examination of Symmetry Span performance in the current study to facilitate comparison to Weisberg and Newcombe’s (2016) previous work.

Here we also considered the role of WM load, which previous studies on WM and navigation have not explored. While much of the previous work on the distinction between WM for location and relation information has been limited to maintaining one location or one relation (Blacker et al., 2016; Ikkai et al., 2014), navigating almost always requires that multiple pieces of spatial information be maintained. Previous work has demonstrated that individual differences in WM performance are more evident when load is high (Cusack, Lehmann, Veldsman, & Mitchell, 2009; Linke, Vincente-Grabovetsy, Mitchell, & Cusack, 2011). Thus, we anticipated that high load WM trials would predict navigation performance, but low load would not.

In summary, we hypothesized that WM for both spatial locations and spatial relations contribute to individual differences in navigation performance, but differentially to different aspects of the virtual environment navigation task. Finally, we predicted that these differences would be most evident at higher WM load.

Method

Participants

Seventy-five adults (42 female; age M=21, SD=2.1) participated for either monetary compensation (n=27) or class extra credit (n=48). All participants had normal or corrected-to-normal vision, and gave written informed consent approved by the Institutional Review Boards of Johns Hopkins University and Temple University. All participants were recruited from the Johns Hopkins University community and were tested at a single site on the Johns Hopkins Homewood campus.

Video Game Experience Questionnaire

Given previous work demonstrating a visuospatial WM advantage for action video game players (Blacker & Curby, 2013; Blacker, Curby, Klobusicky, & Chein, 2014) and a link between Tetris training and enhanced spatial skills (Feng, Spence, & Pratt, 2007; Terlecki, Newcombe, & Little, 2008; for a meta-analysis on spatial skills training see, Uttal et al., 2013), we had participants complete a video game experience questionnaire. For each of the following genres, participants listed how many hours per week on average over the past year they played each genre of game and listed the games from that genre they played in the past year: action, fighting, strategy, fantasy, sports, other.

Tasks

All experimental tasks were displayed on a 22” Dell monitor with participants seated approximately 50cm from the monitor.

Virtual Spatial Intelligence and Learning Center Test of Navigation

(Virtual Silcton; Schinazi, Nardi, Newcombe, Shipley, & Epstein, 2013; Weisberg et al., 2014). Virtual Silcton is a behavioral navigation paradigm administered via desktop computer, mouse, and keyboard. Participants learned two routes in separate areas of the same virtual environment by traveling along a road indicated by arrows (Figure 1). They learned the names and locations of four buildings along each of these routes. Then, they traveled along two routes that connect the sets of buildings from the first two routes. Participants could take as much time as they liked during learning, but were required to travel from the beginning to the end and back to the beginning of each route.

Figure 1.

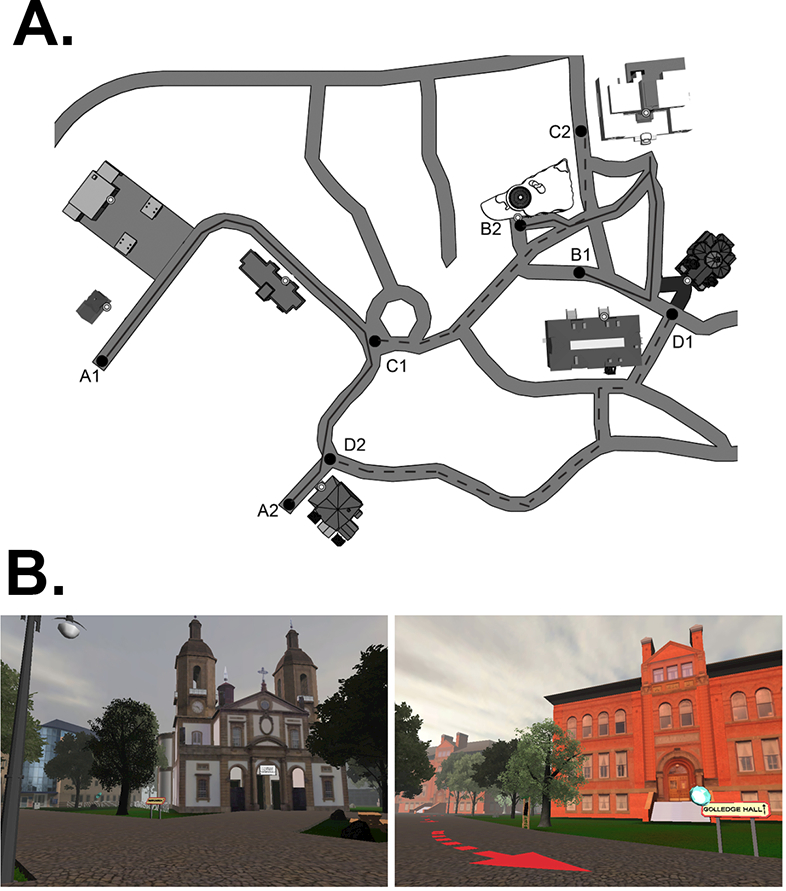
A) An aerial view map depicts the layout of buildings, main routes, and connecting routes for the virtual environment. Note that the spatial arrangement of buildings was identical to a real world environment (used in Schinazi et al, 2013). The letter-number combinations indicate starting and ending points along each of the routes learned. All participants began each route at 1, travelled the entire route to 2, and walked back to 1. Participants always learned the main routes (solid lines) first, but route A and route B were counter-balanced between participants. Then participants learned both connecting routes (dashed lines), and route C and route D were similarly counter-balanced. B) First-person point of view of the virtual environment.

Participants were tested on how well they learned directions among the buildings within one of the first two routes, and among buildings that are between the first two routes. In the onsite pointing task, participants were placed next to each building and the name of one of the other buildings appeared at the top of the screen. Participants then used a computer mouse to rotate their view until a crosshair on the screen lined up with their perceived direction of the named building. The participant then clicked to indicate their answer, and the prompt at the top of the screen changed to one of the other buildings. Once all buildings were pointed to while standing next to the first building, participants were transported to the next building, and they pointed to all of the buildings from there. Participants were not given any feedback on their pointing performance. The dependent variable was the absolute error between the participant’s pointing judgment and the actual direction of the building, corrected to be less than 180°, and averaged separately for Within-route and Between-route trials.

Working Memory Measures

Experimental stimuli were controlled by MATLAB (The MathWorks, Natick, MA) using Psychophysics Toolbox extensions (Brainard, 1997; Pelli, 1997).

Symmetry Span Task

Participants completed the automated Symmetry Span task (Kane et al., 2004), which has been shown to be a sensitive measure of individual differences in visuospatial WM. Participants recalled sequences of 2–5 red-square locations while performing an interleaved symmetry judgment task (Figure 2). The dependent measure for Symmetry Span was the partial score¹, which is the sum of red squares recalled in the correct location and serial order, regardless of whether the entire trial was recalled correctly. This score will henceforth be referred to as the Symmetry Span Score. We chose to include Symmetry Span in the task battery due to its’ established reliability and sensitivity to individual differences. Also, while our main predictions do not involve the results of the Symmetry Span task, we include these methods and results to aid comparison to previous studies and to comply with complete reporting of all study tasks.

Figure 2.

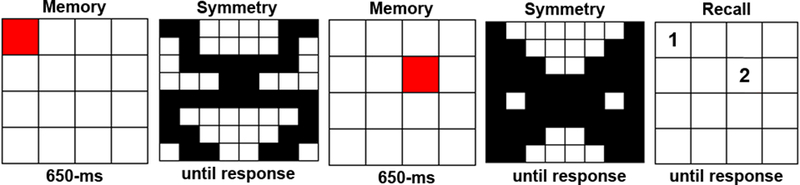
Example Symmetry Span trial. Participants are asked to remember the order and location of red squares while performing an interleaved symmetry judgment task where they were asked to decide if the image was symmetrical along its vertical axis.

Spatial Locations and Relations Task

Participants also completed a novel WM task that required participants to either maintain spatial relations or spatial locations (Figure 3). This task was modeled after the tasks used in previous studies (Ackerman & Courtney, 2012; Blacker & Courtney, 2016; Ikkai et al., 2014).

Figure 3.

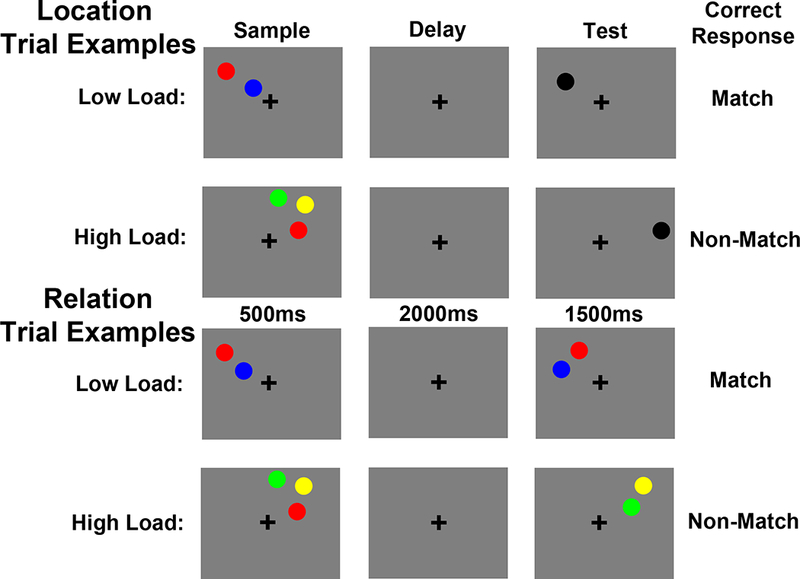
Trial examples for the Spatial Relations and Locations WM task. Under low load, Location trials required participants to imagine a line between two sample circles, hold the location of that line in memory across a delay and then decide if a test circle fell in that location or not. Under high load, Location trials required participants to maintain the locations of three circles in memory and then decide if a test circle fell in one of those locations or in a completely new location. Under low load, Relation trials required participants to maintain the vertical relationship (above/below) of two sample circles and then decide if two test circles were in the same relationship. Under high load, Relation trials required participants to maintain the three vertical relationships between three sample circles and then decide if one of those pairs were presented in the same relationship at test. See the online article for the color version of this figure.

All stimuli were presented on a 50% gray background. A trial began with a 500ms fixation cross, presented in the middle of the screen. Next, a 500ms verbal cue indicated whether the trial would be a “Relation” or a “Location” trial. A sample array was then presented for 500ms, which contained 2 or 3 colored circles (each subtending 0.79°×0.66° of visual angle). The color of each circle was chosen randomly without replacement from red, green, yellow and blue. Each circle in an array was presented between 2.0–3.0° of visual angle apart, but within the same quadrant of visual space. After a 2000ms delay period, a test array was displayed for 1500ms. Participants entered their response during this 1500ms test array. The test array remained on the screen for the entire 1500ms regardless of when they responded. Finally, a 100ms feedback display was presented where the fixation cross turned green for a correct response, red for an incorrect response, and blue if the response was slower than 1500ms.

For both trial types, there was a low load (i.e., sample array contained 2 colored circles) and a high load (i.e., sample array contained 3 colored circles) condition. For Location trials (Figure 3), under low load, participants were instructed to imagine a line segment from one circle to the other circle and maintain the location of that line in memory over the delay period. These instructions were used to encourage participants to encode the exact spatial coordinates of one concrete object (i.e., the imaginary line segment), while maintaining the same number of circles (i.e., 2) on the screen for Location and Relation trials. At test, participants were asked to decide whether or not the black test circle fell on that imaginary line segment. For match trials, the black test circle fell in the exact center of the two previously presented sample circles (i.e., in the center of the remembered imaginary line segment). For non-match trials, the black test circle fell between 2.7×2.2° and 3.5×2.9° of visual angle from the position of that center point between the sample circles.

For Location trials, under high load, participants were instructed to remember the absolute locations of the three sample circles. At test, participants were asked to decide whether or not the black test circle was in one of the three sample locations or in a completely new location. For match trials, the black test circle fell in the identical location as one of the sample circles and for non-match trials it fell between 2.7×2.2° and 3.5×2.9° of visual angle from any of the three sample locations.

While the low and high load Location trials consisted of different instructions to the participant, the key factor is that under low load participants were asked to maintain one spatial location (i.e., the location of the imaginary line segment) and under high load participants were asked to maintain three spatial locations (i.e., the locations of the three sample circles). The imaginary line manipulation in the low load trials was necessary to equate the number of sample circles displayed for Location and Relation trials. Further, previous work using this task has shown that the load manipulation for Location trials activates brain regions that are typically found with load increases in other types of visuospatial WM (Blacker & Courtney, 2016), such as posterior parietal cortex (e.g., Todd & Marois, 2004) and frontal eye fields (e.g., Leung, Seelig, & Gore, 2004).

For Relation trials (Figure 3), under low load, participants were instructed to encode and maintain the relative vertical positions of the two sample circles (e.g., red is above blue). Upon test, participants indicated whether or not the circles in the test array had the same relative vertical positions as the sample circles. For Relation trials, under high load, participants were instructed to encode and maintain the three possible vertical relationships between the sample circles (e.g., green is above yellow, yellow is above red, red is below green). As with low load, at test, participants indicated whether or not the circles in the test array had the same relative vertical positions as the sample circles. Note, which of the three relationships was tested was unpredictable, which forced participants to maintain all three relationships during the delay period. The horizontal relationship was never task-relevant in Relation trials.

There are a few crucial aspects of the task design worth elaborating on. First, regardless of trial type, under low load, participants were asked to encode and maintain one piece of information: either one spatial location (Location trials) or one spatial relation (Relation trials) and under high load, participants were asked to encode and maintain three pieces of information: either three spatial locations or three spatial relations. Second, trial type was pseudorandomly presented so participants could not predict what trial type they would see until the cue. Load was uncued, so the participants were unaware of the load until the sample array appeared. Third, the sample array circles were always presented in one quadrant of the display and the test array circles were always presented in the same quadrant as the sample circles. For all trial types, participants pressed one button for a “match” response and another for a “non-match” response and these response key mappings were counterbalanced across participants. Participants completed 256 trials total.

Results

Video Game Experience

In our current sample, we had little variation in video game experience, with most participants reporting little to no experience. In the action video game literature, individuals are typically considered action gamers if they report 5+ hrs/week of action games (e.g., Green & Bavelier, 2007); however, in our sample only 4 out of 75 met that criterion. Considering all genres of games, 18 participants reported 5+ hrs/week of video game play. Unsurprisingly, we found no evidence of video game experience being a significant predictor of performance on the navigation or WM tasks.

Virtual Silcton Performance

For the Virtual Silcton onsite pointing task, the absolute value of the angular difference between a participant’s answer and the correct angle was calculated for each trial and then averaged across trials to yield the overall error score for each participant. Guessing would yield an average error score of 90°. Participants learned the locations of the buildings significantly better than chance, one-sample t(74)=34.20, p<0.001. No individual participant’s average pointing error was above the 90° threshold (maximum=68.71°) and the group mean pointing error was 36.74° (SD=13.49).

We separated trials on whether the target building was on the route in which the participant was currently standing (Within-route) or on the other main route (Between-route). Dividing the trials in this manner resulted in 24 Within trials and 32 Between trials. A paired-samples t-test on Within versus Between trial types revealed a significant difference, t(74)=12.89, p<0.001, such that error on Within trials (M=24.55°, SD=13.36) was significantly lower than error on Between trials (M=45.88°, SD=16.50). There was a significant correlation between participants Between-route and Within-route pointing performance, R(75)=0.56, p<0.001, consistent with previous studies (Weisberg & Newcombe, 2016; Weisberg et al., 2014).

Symmetry Span and Virtual Silcton

Weisberg and Newcombe (2016) demonstrated that complex span WM performance was related to navigation performance. In that study, 3 groups of navigators were identified using a two-step cluster analysis, using participants’ Between- and Within-route pointing error. In that study, when constraining the number of groups to three, clustering was robust across method (k-means or two-step), and whether clustering was done within samples (five separate studies) or across samples. Taxometric analyses also support the categorical division of participants into groups. Here we chose to use the same group approach to aid in comparison between this current study and the previous work. Moreover, because the previous cluster approach used data from almost 300 participants, we used the group cut-off scores for those data to divide our participants into these same groups of navigators. Still, because the data on which participants are clustered are continuous, we conducted group-based ANOVAs and correlations to test our critical hypotheses.

An individual with a Between-route pointing average <37° was considered an “Integrator” (N=24). An individual with a Between-route pointing average ≥37° and a Within-route pointing average <28° was considered a “Non-Integrator” (N=23), whereas an individual with a Within-route pointing average of ≥28° was considered an “Imprecise Navigator” (N=28). Figure 4 shows these three groups in the current study and also illustrates that as expected no individuals were “good” at Between-route pointing and “bad” at Within-route pointing (i.e., the empty upper left quadrant of Figure 4). For each of our WM measures, we computed all possible pairwise comparisons between these three groups, correcting for multiple comparisons by using a Bonferroni correction with a critical value of 0.05/3=0.017 for post-hoc contrasts.

Figure 4.

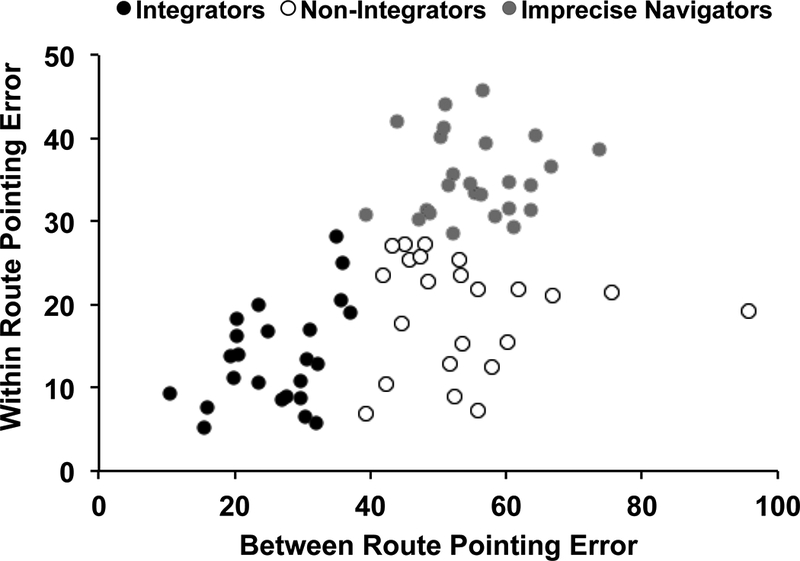
Scatterplot for Between- and Within-route pointing error, which yields three distinct groups of navigators based on the group boundaries used by Weisberg and Newcombe (2016).

One participant did not complete the Symmetry Span task. The 3 groups had significantly different Symmetry Span Scores, F(2,71)=4.25, p<0.05, partial η²=0.11. Post-hoc contrasts revealed that Integrators performed significantly better than Imprecise Navigators, t(50)=3.00, p<0.01, d=0.85, but no other comparisons approached significance, ps>0.05. As shown in Figure 5A, Non-Integrators scored in between Integrators and Imprecise Navigators on the Symmetry Span task, which suggests a more linear relationship between pointing and Symmetry Span performance, as compared to Weisberg and Newcombe (2016). Therefore, we tested a correlation between Symmetry Span Score and Within- and Between-route pointing separately. Symmetry Span Score and Between-route pointing were significantly negatively correlated, R=−0.24, p<0.05. Symmetry Span Score and Within-route pointing were marginally correlated, R=−0.22, p=0.057. Both correlations showed that better WM performance was associated with less error on the pointing task (Figure 5B). Next we extended these previous findings by using a novel WM task to measure individual differences in WM for spatial locations and relations separately, to test whether these different types of spatial WM differentially relate to navigation ability.

Figure 5.

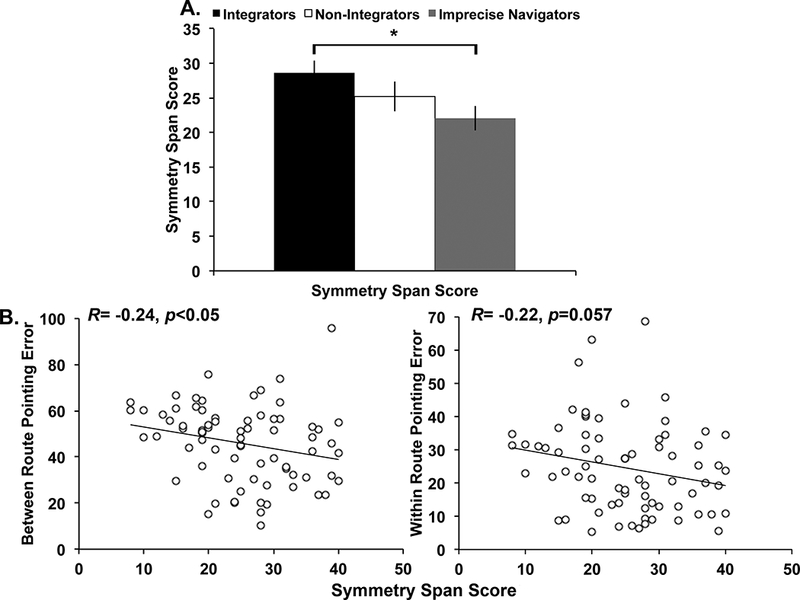
(A) Symmetry Span Scores by navigator group. The main effect of group was significant, p<0.05. (B) Scatterplots showing the relationship between Symmetry Span Score and Between (left) and Within (right) route pointing error. *p<0.05. Error bars represent standard error of the mean.

WM for Relations and Locations

As discussed in the Introduction, we predicted differences in our effects based on WM load and therefore sought to consider those separately. However, to be complete in our reporting, we first tested a 2 (trial type: location, relation) × 2 (load: low, high) × 3 (group: Integrators, Non-Integrators, Imprecise Navigators) repeated-measures ANOVA (Figure 6). The main effect of trial type, F(1,72)=15.89, p<0.001, partial η²=0.18, and load, F(1,72)=334.539, p<0.001, partial η²=0.82, emerged with accuracy being higher for location trials and low load trials, respectively. Importantly, the main effect of group was also significant, F(2,72)=6.20, p<0.005, partial η²=0.15. Post-hoc contrasts revealed that Integrators had significantly higher accuracy than Non-Integrators, t(45)=3.08, p<0.05, d=0.92, and Imprecise Navigators, t(50)=3.56, p<0.05, d=1.02. Performance was not different between Non-Integrators and Imprecise Navigators, p>0.05. Further, group did not significantly interact with load or trial type Fs≤2.32, ps≥0.11. Figure 6 reveals that Integrators outperformed both Non-Integrators and Imprecise Navigators on all trial types and loads. The trial type × load interaction was significant, F(1,72)=25.02, p<0.001, partial η²=0.26, whereby the accuracy difference between low and high load was greater for Relation trials than Location trials.

Figure 6.

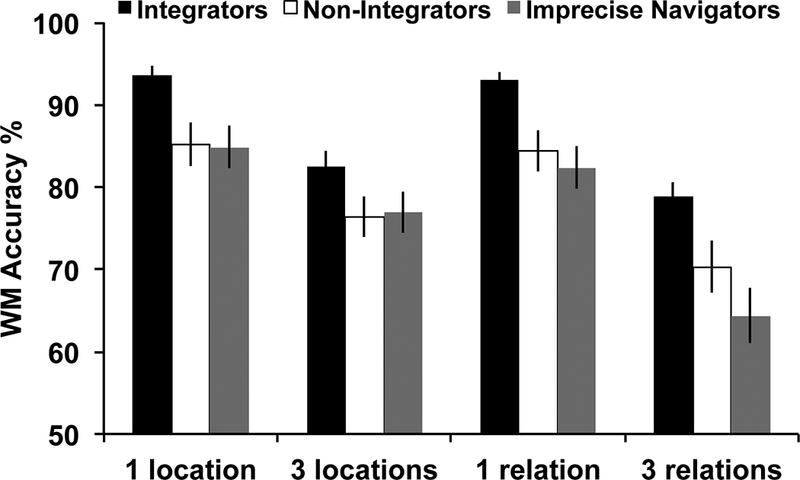
WM task accuracy for each trial type and load by navigator group. Post-hoc contrasts showed that Integrators had significantly higher accuracy than the Non-Integrators and Imprecise Navigators. Error bars represent standard error of the mean.

Critically, there was also a significant 3-way interaction between group × trial type × load, F(2,72)=3.12, p=0.050, partial η²=0.08. Figure 6 illustrates that the trial type x load interaction is being driven by a drop in performance at high load for Non-Integrators and Imprecise Navigators, whereby performance appears lower for 3 Relations than 3 Locations. We explored this 3-way interaction with separate follow-up 2 (trial type) × 3 (group) ANOVAs for each load.

For low load, the main effect of group was significant, F(2,72)=6.62, p<0.005, partial η²=0.15. Given the trial type × load interaction above in the omnibus ANOVA, we were interested in which groups demonstrated significantly different performance for Location vs. Relation trials within each load. All three groups showed no significant difference between performance on 1 Location and 1 Relation accuracy, all ps>0.05. Finally, neither the main effect of trial type nor the trial type x group interaction reached significance, Fs≤1.60, p≥0.21.

For high load, the main effects of group, F(2,72)=5.13, p<0.01, partial η²=0.13, and trial type, F(1,72)=26.66, p<0.001, partial η²=0.27, were significant. Further the trial type × group interaction reached significance, F(2,72)=3.65, p<0.05, partial η²=0.09. Again we were interested in which groups demonstrated significantly different performance for Location vs. Relation trials within high load. Integrators did not differ in their performance on 3 Relations vs. 3 Locations, t(23)=1.71, p>0.05, but both Non-Integrators, t(22)=2.63, p<0.05, d=0.45, and Imprecise Navigators, t(27)=4.50, p<0.05, d=0.85, showed significantly higher accuracy on 3 Locations compared to 3 Relations. While Integrators maintained their performance across both trial types at high load, the other two groups showed a deficit for maintaining 3 Relations in WM compared to 3 Locations.

As with the Symmetry Span task, we also investigated whether there was a linear relationship between WM performance and pointing error. The primary goal of the current study was to identify what type of visuospatial WM differentiates individuals who are good at both within and between route integration. We anticipated that WM for spatial relations would be associated with route integration performance above and beyond that of WM for simple spatial locations. To this end, we examined partial correlations between the Virtual Silcton pointing task and WM for spatial relations while controlling for WM for spatial locations and vice versa. We focused our correlation analyses here on high load trials for two reasons: 1) the separate load ANOVAs above illustrated that the groups only differed in their performance under high load and 2) previous work has shown that higher WM loads are more sensitive to individual differences (Cusack et al., 2009; Linke et al., 2011). There was a trend-level partial correlation between relation WM accuracy and Between-route pointing, while controlling for location WM accuracy, R=−0.20, p=0.08 (Figure 7A). Similarly, there was a significant partial correlation between relation WM accuracy and Within-route pointing, while controlling for location WM accuracy, R=−0.25, p<0.05 (Figure 7B). However, location WM accuracy was not significantly correlated with Within- or Between-route pointing error, ps≥0.40, when controlling for relation WM accuracy. This difference between relation and location WM, as it relates to navigation performance, suggests that relation WM, but not location WM, is critical in predicting individual differences in route integration.

Figure 7.

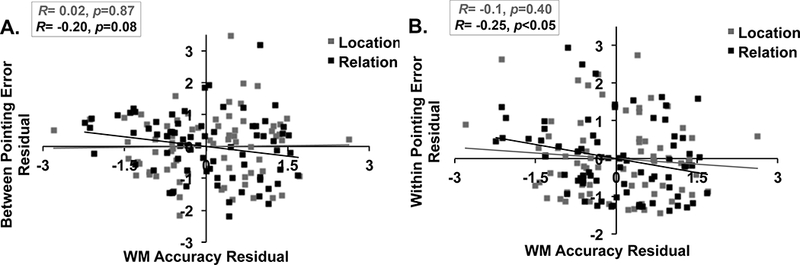
Scatterplots showing partial correlation results between spatial Relation and Location WM task and Virtual Silcton Pointing Task. (A) Relation WM (controlling for Location WM) was marginally correlated with Between-route pointing, but Location WM (controlling for Relation WM) was not. (B) Relation WM (controlling for Location WM) was significantly correlated with Within-route pointing, but Location WM (controlling for Relation WM) was not.

Our results here show that there was a significant relationship between both Symmetry Span performance and pointing error, as well as relation WM performance and pointing error. To examine the relative predictive contribution of these two WM tasks, we followed up with a linear regression analysis. A simple linear regression was calculated to predict overall pointing error (i.e., mean of between- and within-route) based on Symmetry Span score and high load relation WM accuracy. A significant regression equation was found, F(2,71)=4.75, p<0.05, with an R² of 0.12. The analysis showed that Symmetry Span score did not significantly predict pointing error, β= −0.21, p=0.31, whereas relation WM accuracy did predict pointing error, β= −22.91, p<0.05. These results show that relation WM performance was a better predictor of individual differences in navigation performance compared to a complex span WM task like Symmetry Span.

Discussion

Spatial information is not a unitary construct, but is logically and neurally divisible into components (Hegarty & Waller, 2005; Newcombe & Shipley, 2015). Here, our data suggest that WM for spatial locations and relations differentially predict spatial navigation performance. Specifically, WM for multiple spatial relations correlates with the ability to point to buildings located on two separate routes of a virtual environment, but WM for spatial locations does not. Whereas previous research on WM has shown divisions in spatial WM for small-scale displays (e.g., Ackerman & Courtney, 2012), this is the first time that such a division has been investigated in large-scale space. Showing that divisions in spatial WM in small-scale displays generalize to a large-scale environment suggests the importance of the location-relation distinction.

Why might WM for multiple spatial relations be especially important for spatial navigation? Recent EEG evidence has shown that WM for spatial relations involves suppression of the sensory code (Blacker et al., 2016; Ikkai et al., 2014). Learning the buildings within one route involves learning the location of each building through sensory representations (e.g., vestibular and visual) of traveling along the route. Participants travel directly between the building along the same route, and so location information can be encoded with respect to the route itself. But when asked about buildings from two different routes, the sensory code of traveling along the connecting route does not provide relevant information, since this has not been experienced directly. The sensory code of the connecting route should therefore be suppressed, and abstracted into a general spatial relation between two sets of buildings. Indeed, previous work on the route integration paradigm showed that the best navigators were also the best at recalling which building belonged to which route, suggesting that they were relating the two sets of buildings together, instead of coding the locations of each building within the environment (Weisberg & Newcombe, 2016).

It is particularly telling that relational WM for the high load condition is predictive of overall pointing performance. In addition to high load conditions yielding greater individual differences overall (Cusack et al., 2009; Linke et al., 2011), this finding could point to a strategy difference between Integrators and the other two groups. The Integrators may be encoding and maintaining relations, in both the WM task and the navigation task, in which case they need to learn fewer pieces of information. Using abstracted relations instead of sensory-based locations may serve as a chunking process that allows for higher accuracy with increased information load (e.g., Bor, Duncan, Wiseman, & Owen, 2003; Miller, 1956). Non-Integrators and Imprecise Navigators on the other hand, may be attempting to learn the spatial locations of all the objects, and draw inferences about the relations from a sensory reconstruction of the stimulus. In the low load condition, the difference between learning the location vs. the relation is minimal. Only in the high load condition do these computational differences multiply.

Note that these findings involve a different distinction than the contrast between egocentric and allocentric spatial processing often used in the navigation literature. In an egocentric reference frame, locations are represented with respect to the perspective of a perceiver, whereas in an allocentric reference frame, locations are represented within a framework independent of the perceiver’s position (Klatzky, 1998). The distinction between location and relation information cross-cuts this distinction. The relation WM task uses what Klatzky calls “point-to-point bearings”, which can be derived from either an egocentric or an allocentric reference frame. Thus, the participants could use either type of reference frame to derive the relationship(s), but they could not use an individual object representation in either reference frame to successfully perform the task.

While our data suggest that the difference between WM for spatial locations and relations extends to a large-scale spatial environment, one potential limitation may be our use of a desktop display for the virtual navigation task. An important future direction will be to examine this distinction when an individual is physically navigating a real large-scale space. For example, previous work has shown that in addition to visual information, the podokinetic information gained during physical navigation contributes to the formation of a cognitive map (Chrastil & Warren, 2013). Determining how spatial WM ability interacts with the bodily cues that are present in physical navigation should be explored.

The link here between WM for spatial relations and individual differences in route integration ability may have broader implications for developing ways to improve these critical spatial skills through training. For example, a body of research has shown that WM can be improved through training and/or non-invasive brain stimulation (e.g., Blacker et al., 2014; Jaeggi, Buschkuehl, Jonides, & Perrig, 2008; Jones, Stephens, Alam, Bikson, & Berryhill, 2015; Richmond, Wolk, Chein, & Olson, 2014). However, currently no study has specifically examined whether relational WM is malleable with training or whether improving relational WM would show transfer to navigation performance. This notion represents a critical future direction.

As noted above, replicating and extending these findings is an important future direction of this work. The effect sizes we report, especially for our critical interactions, are small. We chose our present sample size to match that used by Weisberg and Newcombe (2016; Study 1). In part, that sample size was chosen to provide adequate representation of each pointing group. The group differences in Virtual Silcton have now been shown to be robust in sample sizes of 50 or more across several studies (Weisberg & Newcombe, 2016; Weisberg et al., 2014). Less, however, is known about the effect sizes between these groups on other cognitive tasks. Indeed, in the Symmetry Span task, which is the overlapping WM task between this study and the previous one, we found comparable effect sizes. Given these small effect sizes, our current study may be underpowered, especially for interactions. A larger replication of this work would be informative.

In sum, we have shown that the best navigators have superior WM for both spatial locations and spatial relations, especially when load is high. Further, across the entire range of navigators, WM for spatial relations is predictive of route integration ability. This evidence supports the distinction between these two types of spatial information processing and their generality across varying spatial scales, as well as shedding light on individual differences in navigation.