Are Linear Speed and Jumping Ability Determinants of Change of Direction Movements in Young Male Soccer Players?

Abstract

The study was undertaken to investigate the relationships between linear speed, change of direction, and explosive power in the lower limbs of young soccer players. We aimed to determine the variables associated with effective change-of-direction speeds (time) based on the 30-m ZigZag (cutting maneuver) under 60° (CODS¹), and 30 m sprint divided into forward-backward-forward movement (CODS²). Sixty young soccer players (age: 17.4 ± 0.7 years, height: 1.76 ± 0.06 m, weight: 68.1 ± 8.9 kg) from soccer sport clubs were included. The participants performed 30-m change-of-direction sprints and 30-m backward and forward sprints. For the maximum speed evaluation, a straight-line 30-m sprint test was performed. Counter-movement jumps and standing broad jumps were used to assess jumping ability. Pearson’s linear correlation and a multiple stepwise linear regression model were used to adjust for variations related to the influence of functional speed and explosive power variables, which were analyzed based on the CODS¹ and CODS² data. Our results showed that 30-m CODS² and standing broad jumps were associated with CODS¹. The variation for the 30-m change-of-direction maneuvers under 60° could be explained by the results of 30-m forward-backward-forward change-of-direction. The standing broad jump explained 10% variation for the performances in change-of-direction sprint decrements and 9% variation for the 5-m change-of-direction with the best times, whereas straight-line sprinting was related to forward-backward-forward change-of-direction. The 10-m sprint explained 50% variation of the performances in the first 10-m forward running in the CODS² and 12% variation for 10-m backward-forward change-of-direction. The 30-m sprint explained 36% variation for 30-m forward-backward-forward change-of-direction. The 30-m sprint and overall body mass also explained 58% variation for 10-m forward-backward change-of-direction. For coaching purposes, we report that forward-backward-forward and cutting maneuver change-of-direction movements are independent and highly useful skills. This information can help to provide better training prescriptions.

Key points.

• The aim of this study was to determine variables explaining the effectiveness of the COD speed in two different variation; 30 m zigzag (cutting maneuver) under 60°, and 30 m sprint divided into forward-backward-forward movement in youth soccer.

• The results showed that change of direction of movement (forward/backward/forward) and standing broad jump were associated with change od direction speed under 60°. Whereas straight-line sprinting was related to change of direction movement (forward/backward/forward).

• The results of this study provide further evidence to suggest that COD¹ (CODS over 45° to 60°), COD² (forward/backward/forward sprint) and straight-line sprinting represent three different physical qualities in soccer players. Therefore, we should determine these abilities via separate assessments.

• It is also important that the above-mentioned skills must be developed through a different type of conduction training.

Introduction

In recent years, soccer has been characterized by dynamic changes in the physical activity of players during the game. There are continuous, but unpredictable, changes occurring at different intensities throughout the match. Players must perform different types of speed-related movements (in place or moving), rapid movements of different parts of the body (e.g. the lower limbs), and must respond to various, potentially unpredictable situations occurring during the match. Speed-related movements include: the individual attack, returning to a defensive position, or, in one-on-one interactions, passing the defender, and unpredictable movements by the attacker to surprise the defender. In most cases these actions are preceded by starts from different positions and different directions.

Speed, as a motor function and ability in soccer, is based on running at a maximum sprint speed for less than a 30-m distance (96% of sprints during a soccer match), accelerating for less than 10-m (49% of sprints occurring during the match), and sprints with change of direction (COD) movements (every 2-4 seconds). CODs involve movements in different directions (left, right, forward, backward) and at different angles (Comfort et al., 2014; Little and Williams, 2005; Sporis et al., 2009; Stolen et al., 2005). Akenhead et al. (2013) found that the English Premier League soccer player, on average, sprints (>5.8 ms^-2) for 2% of the overall distance traveled in the match, engages in high-speed running (>6.78 ms^-2) for 5% of the total distance traveled in the match, covers 10% of the total distance in acceleration motions, and spends 8% of the match in stopping movements. In turn, professional players from the English FA Premier League can perform on average more than 8 CODs per minute during a match. Therefore, an effective soccer player (the attacker or defender) should have the ability to move at high speeds in a straight line, or most frequently, while performing COD movements or changes of running pace (Carling et al., 2008; Hachana et al., 2014). In contrast to short sprint episodes, multiple accelerations over short distances, frequent stop-movements, and repeated COD movements all require different repositioning techniques that are key with respect to soccer playing ability. Most often, these movements occur as a reaction to stimuli that the players are constantly experiencing throughout the game (Gonçalves et al., 2015; Šimonek et al., 2016).

The impact of COD on a soccer players’ movements as their physical activity increases during the match remains a topic of current research and analysis, as researchers seek to identify the determinants of these movements. Numerous soccer studies have focused on the relationship between sprints, CODs, and jumping abilities; however, the results have been inconsistent. Some studies showed a strong correlation between these variables, while others showed poor relationships. In a study by Little and Williams (2005) on a group of 106 English soccer players, it was found that between COD speed (evaluated using the Zigzag test), starting speed (acceleration), and maximum speed achieved, there were statistically significant correlations. However, the determination coefficients between the tests were low (from 0.119 to 0.388). Based on these findings, the authors concludes that COD speed and straight sprints are characteristic and independent motor skills among soccer players (Little and Williams, 2005). Similarly, strong and moderate correlations between acceleration, maximum speed, and results of the Zigzag agility test were reported by Köklü et al. (2015), based on their investigation of 16-year-old soccer players.

The relationship between COD movements and vertical and horizontal jumps has also been explored. In the studies of Struzik et al. (2017), they investigated 12-year-old soccer players. They found no significant links between counter-movement jumps (CMJ) and CODs during sprints. Rouissi et al. (2017) found no significant correlation between standing broad jump (SBJ) and COD performance. In contrast, Young and Farrow (2006) and Lockie et al. (2014) indicated that leg power was an essential component of COD speed. It is believed that team players who achieve higher jump results will probably achieve faster times in multidirectional speed tests. The relationship between speed and jumping ability has also been investigated. However, according to Marques and Izquierdo (2014), the relationship between speed and strength of the lower limbs should be interpreted with caution.

Since the majority of COD runs in soccer matches occur at angles between 1° and 90°, which are specific to soccer, it is important to determine COD speeds at these angles (Faude et al., 2012; Hader et al., 2015). In addition, the defending player often moves away from the attacker for a short distance using controlled backward running followed by forward sprinting (Hammami et al., 2016). A high-level of skill is required to combine COD movements, changes of movement type, and re-accelerations. The backward, run as an unorthodox movement, occurred over 5.3% (± 2.4%) of the total match time, according to one study (Krustrup et al., 2009). Some researchers suggest that speed, COD and strength of the lower limbs should be measured and evaluated using separate tests (Buchheit et al., 2012; Cardoso de Araujo et al., 2018; Sheppard and Young, 2006; Silva-Junior et al., 2011). In turn Castagna et al. (2003) indicated that a strong differentiation between forward, backward, and sideways motion exists. Presumably, COD movements should be measured with various tests in which the subject would perform forward, backward, and sideways motions.

There are a small number of studies that have used multiple regression models to identify associations between sets of variables such as vertical and horizontal jumps (e.g., CMJ, SBJ), linear speed (e.g., 10-m sprint, 30-m sprint), COD sprints, and other patterns of movements in young soccer players. Determining the models of these variables will provide increased knowledge of the key determinants of motor behavior in young soccer players. It is helpful to evaluate motor ability levels using a battery of tests to optimize the training process (Northeast et al., 2017). Such models may contribute to a more effective selection and specification of the game performed by each player through enhanced physical preparation and skill acquisition (Köklü et al., 2015). Therefore, the purpose of these studies was to investigate the relationship between linear speed (straight-line sprinting) and jumping ability (lower extremity explosive power measured through horizontal and vertical jumping) on COD performance measures (COD-speed) in young soccer players. We aimed to determine the variables that can explain the effectiveness of COD speed using the 30-m ZigZag (cutting maneuver) under 60° and the 30-m sprint divided into forward-backward-forward movement. This is the first study defining the performance of change-of-directions under 60° based on times measured at 5m, 10m, 15m, 20m, 25m and 30m in the test. Additionally, the first research on the determination of performance change-of-direction forward-backward and backward-forward during the 30-meter distance was conducted.

We used a multiple regression model to identify associations between the set of variables to be developed that could determine the efficiency of COD movement patterns. We hypothesized that there is a strong relationship between the results of straight-line sprinting and jumps and the two tests defining COD speed in young soccer players.

Methods

To determine COD-speed (Ruscello et al., 2013), the 30-m sprint test in two different patterns was applied. The first test, the30CODS¹, comprised six 5-m sections, wherein the CODs were less than 60°. In practice, this test is often recognized as a ZigZag. A 60° cutting maneuver, as recognized by Faude et al. (2012), is specific to moving the soccer ball during the match. Another test, the 30CODS², involved 15-m forward sprinting, stopping, 5-m backward sprinting, stopping, and then 10-m forward sprinting. This is a modified form of the sprint with backward and forward running (SBF) test. This test was also chosen for its specificity with regard to soccer practices and matches. For the maximum speed measurements, 30-m sprint tests were performed. To determine the total time and the time required for each 5-m segment of a particular test, the 30-m COD¹ sprinting test, 30-m COD² sprinting test, and the 30-m sprint test were performed with the Fusion Smart Speed System (Fusion Sport, Coopers Plains, QLD, Australia). The jumping ability of each player, based on the CMJs and SBJs, was determined using the Optojump System (Microgate Engineering, Bolzano, Italy)

Soccer players at different competitive levels were recruited to better generalize the results of the study. The research was conducted during the soccer season to avoid additional confounding variables. It included a wide battery of tests comprising maximal speed (30-m sprint), COD movements, and horizontal and vertical jumping tests (CMJs and SBJs), which are commonly used in soccer training. The experiment was carried out in the Chair of Ball Games Research Laboratory in the University School of Physical Education in Wroclaw, with an ISO 9001:2009 certification, in collaboration with the Lower Silesia Sport Federation in Wroclaw, Poland. The study was conducted over one afternoon.

Participants

We included 60 male soccer players from the Lower Silesian sports clubs, who participated in the Central League of Junior Championships in Poland. The mean age of the participants was 17.4 years (± 0.7 year), mean height was 176.3 cm (± 6.1 cm), and mean body weight was 68.1 kg, (± 8.9 kg). The average length of training experience of the players was 78.3 months (± 29.8). The general characteristics of the players are shown in Table 1. Before the tests, each participant was informed about the aims of the research and the benefits and risks of the investigation. In the case of minors, parents/guardians were informed about the purpose of the study and the benefits and risks of the investigation. The same procedure was carried out with the coaches. They were also aware that the study was approved by the Senate’s Research Bioethics Commission at the University and that the procedures complied with the Declaration of Helsinki concerning human experimentation. The parents/guardians of the participants younger than 18 years provided written consent, and participants older than 18 years provided their own written consent for participation after being thoroughly informed about the study as described above.

Table 1.

Physical characteristics of the participants (n=60) and descriptive data (mean, ± SD; 95% CIs, %CV) for each variable of interest.

Measurement	Variables	Mean ± SD	-95%Cl	+95%Cl	%CV
	Age (y)	17.4. ±0.7	17.3	17.6	4.03
	Height [cm]	176.3. ±6.1	174.7	177.8	3.43
	Body mass [kg]	68.2. ±8.9	65.8	70.4	13.03
	Training experience (months)	78.3. ±29.8	64.0	92.7	38.00
Sprint (30S)	10-m Sprint [s]	2.495. ±0.104	2.468	2.522	4.16
	30-m Sprint [s]	5.019. ±0.179	4.973	5.065	3.57
	5-m vSprint [ms-1]	8.63. ±0.52	8.49	8.76	6.00
Change-of-direction sprint (30CODS¹)	30-m CODS¹ [s]	10.786. ±0.528	10.649	10.922	4.90
	5-m bCODS¹[s]	1.682. ±0.097	1.657	1.707	5.74
	CODS¹dec [%]	6.93. ±2.65	6.25	7.62	38.22
Change-of-direction sprint (30CODS²)	10-m CODS² (forward run) [s]	2.517. ±0.126	2.484	2.550	5.02
	30-m CODS² [s]	8.037. ±0.327	7.953	8.122	4.07
	F&BCOD [s] (forward & backward run)	3.092. ±0.203	3.04	3.144	6.56
	B&FCOD [s] (backward & forward run)	3.633. ±0.28	3.561	3.706	7.71
Jumping ability	CMJ [cm]	42.47. ±4.49	41.31	43.63	10.58
	SBJ [cm]	230.45. ±13.70	226.91	233.99	5.94

30S = 30-m Sprint test; 5-m vSprint = peak sprint speed for each 5 m in the 30S; 30CODS¹ = 30-m COD¹ Sprinting test; 30-m CODS¹ = the final time in the 30CODS¹; 5-m bCODS¹ = the best time at 5-m in the 30CODS¹; CODS¹dec = the percent sprint decrement in the 30CODS¹; 30CODS² = 30-m Backward and Forward Sprint Test; 10-m CODS² = 10-m starting speed time in the 30CODS²; 30-m CODS² = the final time in the 30CODS²; F&B_COD = time of COD from forward movement to backward movement (10-m distance) in the 30CODS²; B&F_COD = time of COD from backward movement to forward movement (10-m distance) in the 30CODS²; CMJ = height of the countermovement jump; SBJ = distance of the standing broad jump. The values are expressed as mean and standard deviation (SD) with 95% confidence interval (95% CI) and terms of coefficient of variation (% CV)

Procedures: Assessment of functional speed ability

30-m Sprint Test (30S): In each case, the participant took a high starting position behind the starting line with his preferred forward leg in position. The toes of the forward leg were close to the starting line and the rear foot was placed on a SMART JUMP mat (a reactive mat that captures false starts; a part of the Fusion Smart Speed System [Fusion Sport]) 30 cm from the starting line. When a specified light beam started flashing (the trial start time), the athlete began running as fast as possible to a cone that was placed 2 m beyond the final gate, which was located 30 m from the starting line. The fastest time of 3 trials was used in the data analysis. The participants were given a 3-min rest break between each of the trials, which was sufficient for the athlete to fully recover. The sprint times measured were: total 30-m sprint time, 10-m starting time, and peak sprint speed at each 5 m (5-m vSprint). The intraclass correlation coefficient (ICC) for the times recorded by the participants was 0.80 (95% Cl; 0.72-0.87) and the CV (coefficient of variation) was 6.11%.

30 m COD¹ Sprinting Test (30CODS¹): The participants performed a 30-m sprint with a COD every 5 m at an angle of 60° (Ruscello et al., 2013). The test procedure was similar to the actual 30-m sprinting test. Changes of sprinting direction were performed by the participants moving around a 1-m high cone at the following distances from the starting line: 2.5 m, 7.5 m, 12.5 m, 17.5 m, 22.5 m, and 27.5 m (Figure 1). The first COD was to the right. Three 5-m sprint tests were used for the analysis, in which the changes of running direction went from a COD to the right followed by three 5-m sections, each including left turns. The ICC for the times recorded by the participants was 0.92 (95% Cl; 0.88-0.95) and the CV was 7.4%. The results analysis included the final times (30-m CODS¹), the best times at 5-m (5-m bCODS¹), and the percentage of sprint decrements during the CODs (CODS¹dec). CODS¹dec was converted using the formula proposed by Girard et al. (2011):

Figure 1.

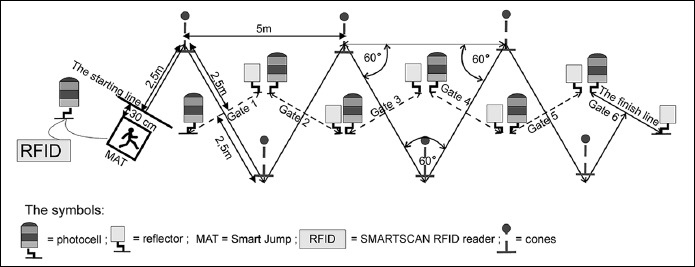
Thirty-meter COD¹ Sprinting test (30CODS¹) diagram.

Best time (5-m bCODS¹) was recorded as the best time at 5-m in the 30m CODS¹ test.

30 m COD² Sprinting Test (30CODS²): The 30CODS² test (30-m forward/backward/forward sprint) is a modified SBF test (9-3-6-3-9 sprint with backward and forward running). The SBF test was previously described in the literature by Hammami et al. (Hammami et al., 2017). The test was carried out using the same distances as in the 30S and 30CODS¹ and was divided into the following sections: a 15-m forward run, a 5-m backward run, and a 10-m forward run (Figure 2). The COD of the run was determined by crossing the lines of each section with both feet. The run was required to proceed in a straight line, or as straight as possible so as to limit the loss of time-trial (the execution time for the entire test). The following timing parameters were used to analyze the results: the 10-m starting speed time (10-m CODS²), the 10-m COD time (F&B_COD) which was the time of COD from forward to backward (measured between 10-m and 20-m of the entire 30-m distance), the 10-m COD time (B&F_COD), which was the time of COD from backward to forward (measured between 15-m and 25-m of the entire 30-m distance), and the 30-m final time (30-m CODS²). The ICC for the times recorded by the participants was 0.94 (95% Cl; 0.91 – 0.96) and the CV was 5.67%.

Figure 2.

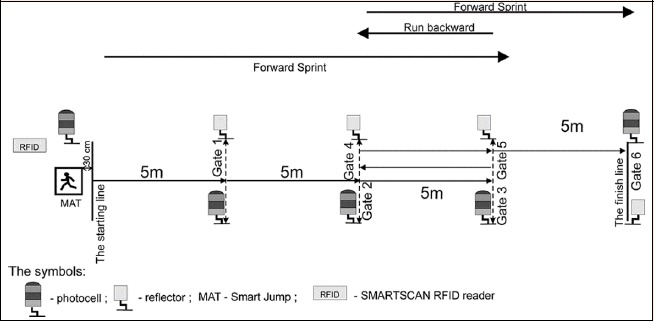
Thirty-meter COD² Sprinting test (30CODS²) diagram.

Assessment of lower extremity explosive power

Counter-Movement Jump (CMJ): Players performed a vertical height jump with arm swing on a hard flat surface. We used an optical measurement system (Optojump; Microgate Engineering, Bolzano, Italy) to measure the height (cm) of the jumps. The participants performed three jumps and the best (the highest) was recorded for the analysis.

CMJs were performed starting from a standing position. Participants were instructed to keep their hands on their hips during the jump. Each player was instructed to jump as high as possible. Each jump was performed as an initially rapid preparatory downward eccentric action (Dello Iacono et al., 2016).

The height of each jump (CMJ) was calculated using the flight time. A minimum of 2 minutes of recovery was provided between each repetition and 5–6 min between each jump modality. The ICC for the scores recorded by the participants was 0.93 (95% Cl; 0.88 – 0.96) and the CV was 8,5%.

Standing Broad Jump (SBJ): From an erect position with the feet placed in parallel and with legs bent at the knee as close to a 90° angle as possible, the player performed the SBJ. He was instructed to jump as far as possible and land on both feet without falling backwards. The test result was measured from the start line to the rear heel edge, or whichever part of the body that was closest to the starting line after the jump (Rouissi et al., 2017). The jumping distance was measured to the nearest 1.0 cm. Three trials were executed by each participant and the longest distance was recorded for analysis. A minimum of 2 minutes of recovery was provided between each trial. The ICC for the scores recorded by the participants was 0.92 (95% Cl; 0.87 – 0.96) and the CV was 6,71%.

Overall, the test procedures did not specify the methods of starting and changing. The direction of the race was dependent on the individual’s preferences and the unique skills and abilities of the players.

Statistical analysis

The data were processed using Statistica 13.0 for Microsoft Windows (Microsoft Corp., Redmond, WA, USA). Data are first presented as means ± standard deviations (SD), and 95% confidence intervals (Cl). The distribution of each variable was examined for the assumption of normality using the Kolmogorov-Smirnov test. Correlations were determined using Pearson’s product moment-correlation coefficient (r). The magnitudes of the correlation coefficients were stratified into groups comprising: trivial (r < 0.1), small (0.1 < r < 0.3), moderate (0.3 < r < 0.5), large (0.5 < r < 0.7), very large (0.7 < r < 0.9), nearly perfect (r> 0.9) and perfect (r = 1.0) (26). A multiple stepwise regression analysis (forward and backward stepwise methods) was used to adjust the influence of the functional speed and the variations in the explosive power variables analyzed in the 30CODS¹ and 30CODS². In the multiple stepwise regression models, only independent variables were used and linear correlations with dependent variables were statistically significant (p <0.05). In addition, between the independent variables, a relationship between nearly perfect and very large correlation coefficients was not observed (non-co-linearity of variables). In addition, based on a residual regression analysis, the residuals were distributed normally.

Results

Table 1 shows descriptive the means±SDs and 95% CIs of the maximum and minimum scores. Several significant correlations of different strengths were found in the studies (Table 2). A nearly perfect correlation was observed between the 30-m CODS¹ and 5-m bCODS¹ (r = 0.91, p <0.001). The 30-m CODS² was significantly correlated (p <0.001) with the 10-m CODS² (r = 0.75), F&B_COD (r = 0.71), B&F_COD (r = 0.80), 10-m sprint (r = 0.56) and the 30-m sprint (r = 0.60). The F&B_COD was significantly correlated with the B&F_COD (r = 0.72, p <0.001). A significantly (P <0.001) large and very large correlation existed between t_10CODM and the 10-m sprint (r = 0.71) and the 30-m sprint (r = 0.65). The 30m sprint was significantly correlated (p <0.001) with the 10-m sprint (r = 0.86) and the 5-m vSprint (r = -0.77). A significantly large correlation existed between the 10-m sprint and the 5-m vSprint (r = -0.53, p <0.001). In addition, significantly large correlations were found between CMJ and SBJ (r = 0.57, p <0.001).

Table 2.

Results of Pearson’s correlation analysis (r) in young Polish soccer players.

Variables	10-m Sprint	30-m Sprint	5-m vSprint	30-m CODS¹	5-m bCODS¹	CODS¹dec	10-m CODS²	30-m CODS²	F&BCOD	B&FCOD	CMJ	SBJ	m	v
10-m Sprint	-	.86***	-.53***	.11	.18	-.19	.71***	.56***	.21	.35**	-.01	-.21	.05	.04
30-m Sprint	.86***	-	-.77***	.18	.22	-.16	.65***	.60***	.27*	.32**	-.16	-.24	-.02	-.11
5-m vSprint	-.53***	-.77***	-	-.08	-.16	.20	-.45***	-.49***	-.22	-.25	.35**	.33**	-.002	.17
30-m CODS¹	.11	.18	-.08	-	.91***	-.14	.21	.29*	.08	.20	-.16	-.20	.09	.15
5-m bCODS¹	.18	.22	-.16	.91***	-	-.54***	.25	.29*	.09	.17	-.18	-.30*	.03	.03
CODS¹dec	-.19	-.16	.20	-.14	-.54***	-	-.18	-.11	-.05	.002	.10	-.31*	.11	.22
10-m CODS²	.71***	.65***	-.45***	.21	.25	-.18	-	.75***	.30*	.38**	-.01	-.24	-.05	.23
30-m CODS²	.56***	.60***	-.49***	.29*	.29*	-.11	.75***	-	.71***	.80***	-.001	-.25	-.22	-.05
F&BCOD	.21	.27*	-.22	.08	.09	-.05	.30*	.71***	-	.72***	016	.15	-.42***	-.05
B&FCOD	.35**	.32*	-.25	.20	.17	.002	.38*	.80***	.72***	-	.02	-.15	-.21	-.004
CMJ	-.01	-.16	.35**	-.16	-.18	.10	-.01	-.001	.16	.02	-	.57***	-.21	.24
SBJ	-.21	-.24	.33*	-.20	-.30*	-.31*	-.24	-.25	.15	-.15	.57***	-	.16	.23
m	.05	-.02	-.002	.09	.03	.11	-.05	-.22	-.42***	-.21	-.21	.16	-	.66***
V	.04	-.11	.17	.15	.03	.22	.23	-.05	-.05	-.004	.24	.23	.66***	-

10-m Sprint = 10-m starting speed time in the 30-m Sprint test (30S); 30-m Sprint = the final time in the 30S; 5-m vSprint = peak sprint speed for each 5 m in the 30S; 10-m CODS² = 10-m starting speed time in the 30-m Backward and Forward Sprint Test (30CODS²); 30-m CODS² = the final time in the 30CODS²; F&B_COD = time of COD from forward movement to backward movement (10-m distance) in the 30CODS²; B&F_COD = time of COD from backward movement to forward movement (10-m distance) in the 30CODS²; 30-m CODS¹ = the final time in the 30-m COD Sprinting test (30CODS¹); 5-m bCODS¹ = the best time at 5-m in the 30CODS¹; CODS¹dec = percent sprint decrement in the 30CODS¹; CMJ = height of the Counter-Movement Jump; SBJ = distance of the Standing Broad Jump; r = Pearson correlation coefficient

* p<0.05

** p<0.01

*** p<0.001.

Other significant moderate or small correlations between variables were also observed (Table 2).

A multiple stepwise regression was developed and independent variables were used to determine the variance of the CODS² properties (Table 3).

Table 3.

Multiple regression calculations (forward and backward stepwise model) for the 30CODS² test.

Dependent variable	nv	Independent variables	r	R2	R2 variation	F value	p
10-m CODS²	3	10-m Sprint	0.71	50%	50%	58.653	<0.001
Prediction equation: 10-m CODS² = 0.361+0.864 x “10 m Sprint”
30-m CODS²	5	30-m Sprint	0.60	36%	36%	32.561	<0.001
Prediction equation: 30-m CODS²= 2.538+1.096 x “30 m Sprint”
F&BCOD	2	Body mass	0.42	17%	17%	12.239	<0.001
		Body mass + 30-m sprint	0.49	24%	7%	5.288	0.025
Prediction equation: F&BCOD = 2.230 +0.23 x “30-m sprint” -0.009 x “Body mass”
B&FCOD	2	10 m Sprint	0.35	12%	12%	8.091	0.006
Prediction equation: B&FCOD = 1.274+0.946 x “10-m Sprint”

n_v = number of significant variables used in the regression model or interaction between variables; 10-m Sprint = 10-m starting speed time in the 30-m Sprint test (30S); 30-m Sprint = final time in the 30S; 10-m CODS² = 10-m starting speed time in the 30-m Backward and Forward Sprint Test (30CODS²); 30-m CODS² = the final time in the 30CODS²; F&B_COD = time of COD from forward movement to backward movement (10-m distance) in the 30CODS²; B&F_COD = time of COD from backward movement to forward movement (10-m distance) in the 30CODS²; r = Pearson correlation coefficient; R² = coefficient of determination; p = significance level; 95% CI = confidence interval.

The 10-m sprint variable explained 50% (p < 0.001) variation for the performances in the 10-m CODS², while the 30-m sprint variable explained 36% (p < 0.001) variation for the performances in the 30-m CODS²_. The 30-m sprint variable explained 51% (p < 0.001) variation of the performances in F&B_COD, whereas body mass was explained by an additional 7% (p = 0.003) variation. On the other hand, the variable for COD under 180° from backward sprint to forward spring was explained by a 10-m Sprint variable (12%, p = 0.006).

Reconstructed regression models were calculated to determine the most robust predictors of COD¹ (by 60°). The regression models created for the variables were explained (from 8% to 10%) by only one in the group of variables that were analyzed in this study. The variation for 5-m bCODS¹ was explained only by the SBJ (9%, p = 0.018). However, the variation for properties of the 30-m CODS¹ variable based on the general time required for COD at a 60° angle was explained only by the 30-m CODS² variable (8%, p = .026). The SBJ variable explained the 10% variation (p = .015) in the performances of CODS¹dec (Table 4).

Table 4.

Multiple regression calculations (forward and backward stepwise model) for the 30CODS¹ test.

Dependent variable	nv	Independent variables	r	R2	R2 variation	F value	p
30-m CODS¹	2	30-m CODS²	0.29	8%	8%	5.192	0.026
Prediction equation: 30-m CODS¹ = 7.067+0.463 x “30-m CODS²”
5-m bCODS¹	2	SBJ	0.30	9%	9%	5.897	0.018
Prediction equation: 5-m bCODS¹ = 2.176-0.002 x “SBJ”
CODS¹dec	2	SBJ	0.31	10%	10%	6.264	0.015
Prediction equation: CODS¹dec = 31.986-14.892 x “SBJ”

n_v = number of significant variables used in the regression model or interaction between variables; 30-m CODS¹ = the final time in the 30-m COD¹ Sprinting test; 5-m bCODS¹ = the best time at 5 m in the 30CODS¹; CODS¹dec = the percent sprint decrement in 30CODS¹; 30-m CODS² = the final time in the 30CODS²; SBJ = distance of the Standing Broad Jump; r = Pearson correlation coefficient; r² = coefficient of determination; p = significance level.

Discussion

The fundamental goal of this study was to investigate the effects of linear speed and jumping ability (lower extremity explosive power) on COD agility performance measures, such as the 30-m CODS¹ and 30-m CODS². We noted that important relationships existed between the 30-m CODS² and the 30-m sprint. In both trials, the forward movement was the most common. However, the overall result of the 30CODS¹ test was strongly associated with the total time for the 30CODS² test and the best time at a distance of 5-m in the CODS¹ test. The results of the SBJ were negatively related to the results of the speed decrease or best time at a distance 5-m in the 30CODS¹ test and were positively relation to jump height in the CMJ. Also noteworthy is the lack of a significant relationship between CMJ height and other variables (exception: relation to 5-m vSprint). The relationships between the jumps and the 30CODS¹ test and 30CODS² indicate the need to carefully interpret these relationships. Similar recommendations were suggested by Marques and Izquierdo (2014).

The above relationships confirmed the results of other research. Köklü et al. (2015) studied 16-17-year-old soccer players (n=16) and found a moderate correlation between the Zigzag test without using a ball (COD under 100° angle) and the 10-m sprint. Similarly, the ZigZag agility test without the ball strongly correlated with 30-m sprint times (Little and Williams (2005), who analyzed England’s professional soccer players found significant correlations between the 10-m Sprint and the ZigZag test (r = 0.346), and between the 20-m Sprint and the ZigZag test (r = 0.458). Sporiš et al. (2011) analyzed soccer players from the Serbian U-16 national team and also found correlations between the 30-m Sprint and the ZigZag test (r = 56, p < 0.01).

A secondary goal was to examine the potential for developing a multiple regression model that could identify associations between a set of variables to determine the efficiency of COD movement patterns. Based on the multiple regression models that have been created, it has been shown that the 30CODS¹ test time is most closely related to the test results for CODs from forward to reverse and vice versa. This proves the specifics of both tests in which the direction of the run changes. However, a prediction equation for the 30CODS¹dec test and the 5-m bCODS¹ are the most related to the results of the SBJ. Therefore, the type of test should be considered (e.g., CMJ or SBJ) when looking for relationships between COD movements and jump indicators. Based on the analysis of the relationship between COD² and the linear 30-m sprint, the pattern of backward movement performed between 15 and 20 m allows for the determination of the specific skills needed during a soccer match. During the 30CODS² test (from 10-m to 20-m), the participants changed their manner of running from forward (deceleration) to backward (re-acceleration). In addition, at 15 m, the players again slowed down the forward sprint and then accelerated in the second forward sprinting. This requires high-level motor abilities, which are of primary importance among all the skills (technical proficiencies) needed for COD.

It should be stressed that in numerous research papers the relationships between variables such as jumping, sprinting, or COD motions were calculated using simple linear correlations, as noted by Braz et al. (2017). This analytical method allows only two variables to be compared. Only with the forward stepwise method has it been possible to determine the extent of the influence of a set of variables on the effect of a motor action (as a dependent variable). In this study, we found that the 30CODS¹ test result was only 8% explained by the 15-5-10-m sprint test with backward and forward movement (30CODS² test). This shows that this COD pattern (forward/backward) is different from the CODS¹ at 60° angles; however, the results of the 30CODS¹ test and the 30CODS² are dependent upon each other. It can be assumed that variables other than acceleration, straight line sprints, or jumps will determine the results of 30CODS¹ tests in young soccer players. Furthermore, based on the prediction equation for CODS, shortening of the 30CODS² test time by 0.1 s may be important to reduce the 30CODS¹ test time by 0.05 s. Gains in repeated COD performance probably reflect mainly neuronal adaptations and enhanced coordination, which comprise the selective activation of motor units, better synchronization, selective activation and relaxation of muscle groups, and an increased recruitment of motor units (Pyne et al., 2008).

In studies conducted on Brazilian professional soccer players, Braz et al. (2017) investigated the relationship between sprints with and without COD. Based on the multiple regression models, 10-m and 20-m sprint variables showed low explanatory power (≤5%) for COD sprints. Little and Williams (2005) investigated male professional soccer players from the English League teams. They found that the ZigZag agility test was correlated with the 10-m speed test and the flying 20-m test for maximum speed (P<0.001). However, determinants showed that even in the most correlated tests, acceleration and maximum velocity accounted for only 39% of the common variance and should be analyzed separately for soccer players. Thomas and Nelson (2001) argued that if the common variation between two variables was less than 50%, they were specific or somewhat independent.

In the current study, SBJ explained only 9% variance in the regression models for the 5-m bCODS¹ and 10% for the CODS¹dec. Prediction equations were prepared for the shortest time at 5-m and the drop-in speed during the 30-m CODS¹ test. A 1 cm increment in SBJ can mean shortening the time of the fastest 5-m CODS¹ and reducing the CODS¹dec by 15%. Hence, the jump associated with horizontal power is related to the rate of COD at which acceleration occurs (Lockie et al., 2014). On the other hand, the CMJ variable did not explain the variance in the regression models of the 30-m CODS¹ at 60°. In a study of 16-17-year-old soccer players by Köklü et al. (2015), a strong correlation was found between CMJ and ZigZag agility (angle100°) without the ball (r = -0.769, p = 0.01). Similar to that, Braz et al. (2017) conducted experiments on Brazilian professional soccer players and noticed significant correlations between CMJ and the ZigZag test. On this basis, multiple regression models were prepared and the results indicated that vertical jump variables including CMJ did not help explain the ZigZag test results (r² = 11%).

The differences between the studies that determined correlations between jump or speed and COD speed can be explained in several ways. One is that the players have different levels of physical abilities and skills. Another may be related to the distance used in the sprint tests. In studies conducted with young athletes (Lloyd et al., 2013), it was shown that linear speed, strength and power in the lower limbs, anthropometric variables, asymmetry, and perception and decision-making processes may be important contributors to high agility outcomes. Furthermore, rounded and sharp patterns of COD techniques might influence athletic performances, according to Condello et al. (2013). In the literature, other factors including age, level of competitiveness, frequency, and volume of training in the sport, also affected COD speed in soccer players. Köklü et al. (2015) found that 16-year-old soccer players showed moderate to strong correlations between acceleration, maximum speed, and agility (10-m Sprint – 30-m Sprint, r = 0.714; 10-m Sprint - ZigZag, r = 0.567; 30-m Sprint - CMJ, r = 0.599; 30-m Sprint - ZigZag, r = 0.744; CMJ - ZigZag, r = 0.769, respectively).

Some limitations of this study should be acknowledged. First, the tests were conducted indoors to standardize the environmental conditions and the floor surface. Soccer matches are played on natural grass and the difference between the surfaces can affect the way the subjects move. A second limitation is that, although reliability was assessed in the modified tests (30CODS¹, 30CODS²), it is not known whether they have construct validity relative to the standards of play. Third, of the limited data available, comparisons between studies are further limited by the different methodologies used to asses COD ability (i.e. T-test, Illinois agility, 505, ZigZag test). Fourth, differences in the length of the lower limbs and body asymmetry have not been accounted for in this study, but these may be important to the speed and manner of COD. However, there are a small number of studies that have reported the determinants of COD movements at 60° angles and CODs of running forward to backward.

Conclusion

The results of the proposed predictive models for COD, the changes in the form of movement patterns (forward/backward), and the correlation between speed, agility and jump variables presented in this work indicate the constant need to determine these patterns and correlations. Studies have indicated that COD speed (at specified angles) should be analyzed separately from changes in the form of movement patterns because other variables can explain the results of tests determining their level. Variables determining COD were primarily explained by the variables that determined jumping ability. On the other hand, variables that determined speed changes in the form of movement patterns (forward/backward and vice versa) were explained by speed variables. Therefore, our hypothesis that there is a strong dependency between the results of straight-line sprinting and two agility tests used in young soccer players was proved only partially.

The results of this study provide further evidence to suggest that COD speed (CODS¹ under 45° to 60°), CODS² (forward/backward/forward sprint) and straight-line sprinting (30S) represent three different physical qualities in soccer players and probably in other team sport athletes, such as basketball and handball players. Therefore, we should determine these abilities via separate assessments. It is also important that the above-mentioned skills must be developed through a different type of conduction training. Jumping ability demonstrated a strong correlation with 30-m CODS¹, whereas straight-line sprinting was more associated with the 30-m CODS² (forward/backward/forward). Moreover, this study provided data on speed, COD and jumping among youth soccer players in Poland. Practitioners can use this information for comparative purposes, although further research will be necessary to compare the competition standards.

Biographies

Marek POPOWCZAK

Employment

Department of Team Sport Games, University School of Physical Education in Wroclaw, Poland

Degree

Ph.D.

Research interests

Talent identification in team sports, motor ability development

E-mail: marek.popowczak@awf.wroc.pl

Andrzej ROKITA

Employment

Department of Team Sport Games, University School of Physical Education in Wroclaw, Poland

Degree

PhD, Assoc. Prof.

Research interests

The use of the “EDUball” educational ball in primary schools. Talent identification in team sports.

E-mail: andrzej.rokita@awf.wroc.pl

Kamil ŚWIERZKO

Employment

Department of Team Sport Games, University School of Physical Education in Wroclaw, Poland

Degree

MSc

Research interests

Talent identification in team sports, motor abilities

E-mail: kamil.swierzko@gmail.com

Stefan SZCZEPAN

Employment

Department of Swimming, University School of Physical Education in Wroclaw, Poland

Degree

Ph.D.

Research interests

Motor learning, motor skill acquisition processes, augmented feedback, swimming science.

E-mail: stefan.szczepan@awf.wroc.pl

Ryszard MICHALSKI

Employment

Department of Track and Field and Gymnastic, University School of Physical Educationvin Wroclaw, Poland

Degree

PhD

Research interests

Track and field, motor development

E-mail: ryszard.michalski@awf.wroc.pl

Krzysztof MAĆKAŁA

Employment

Department of Track and Field and Gymnastic, University School of Physical Education in Wroclaw, Poland

Degree

PhD

Research interest

Theory and methodology of athletics, motor ability development, biomechanical analysis of sprinting

E-mail: krzysztof.mackala@awf.wroc.pl