Abstract
Recognizing factors associated with mortality in patients admitted to the ICU with acute exacerbation of chronic obstructive pulmonary disease could reduce healthcare costs and improve end-of-life care. Previous studies have identified possible predictive variables, but analysis is lacking on the combined effect of demographic factors and comorbidities. Using the MIMIC-III database, this study examined factors associated with mortality in a model incorporating comorbidities, comorbidity indices, and demographic factors. After determining associations between predictive variables and mortality through univariate and multivariate binomial logistic regression, three predictive models were developed: (1) univariate GLM-derived logistic, (2) Mean Gini-derived logistic (MGDL), and (3) random forest. The MGDL model best predicted mortality with an AUROC of 0.778. Variables with the greatest relative importance in determining mortality included the Charlson Comorbidity Index, Elixhauser Index, male, and arrhythmia. The results support the potential of using the MGDL model and need for further work in exploring demographic factors.
Introduction
Acute exacerbation of chronic obstructive pulmonary disease (AECOPD) accounts for nearly 3.5% of all hospitalizations with an associated cost per hospitalization that has risen from $22,187 in 2002 to $38,455 in 2010.1 Given an estimated 514,000 hospitalizations due to AECOPD in 20082, total spending on AECOPD is roughly 20 billion dollars per year. Chipping away at this staggering figure could reduce costs tremendously, which would benefit from an understanding of which factors predict mortality in these patients. Consequently, these predictive factors could be targeted through public health measures for decreasing the cost burden of AECOPD.
Moreover, finding AECOPD predictive factors could enable physicians to understand which admitted patients may have a higher risk for mortality. An improved prediction of mortality could not only improve plan of care, but also drive further more informed conversations regarding end-of-life (EOL) care. Physicians often avoid EOL discussions for fear of hurting their relationship with patients.3-5 However, these discussions have been shown to reduce costs associated with overly involved EOL medical care and improve overall satisfaction and quality of life.5-8 Recognizing a patient with factors linked to higher mortality could help facilitate additional EOL discussion.
Studies have examined how demographic factors and comorbidities increase risk for developing COPD,9-10 and the way that acute measures, such as serum albumin and arterial pCO2, can predict mortality.11-13 Literature reviews have found factors including disease duration, older age, low pH, and low Glasgow Coma Scale score to be significantly associated with a higher risk of mortality in COPD patients.14-15 Others have developed predictive models to forecast readmission, illness severity, and risk of one-year mortality in patients with COPD.16-19 Tabak et al. used coefficients from a logistic regression model including age, sex, laboratory results, vital signs, and comorbidities to predict mortality in AECOPD patients.20
There is a lack of large-scale analyses on the combined ability of comorbidities and demographic information to predict mortality in ICU patients admitted with AECOPD. Moreover, previous studies have not considered such combined features using machine learning approaches for developing mortality prediction models for AECOPD patients. Using publicly accessible electronic health record (EHR) data, this study examined which factors were significantly associated with mortality in a model that incorporated comorbidities, comorbidity indices, and demographic factors. Univariate and multivariate Generalized Linear Model (GLM) analyses were used to determine associations between predictive variables and mortality. Multiple predictive models were then developed using logistic regression and machine learning. The predictive capacity of the developed models were assessed according to their sensitivity, specificity, and Area Under the Receiver Operating Characteristic (AUROC) curve.
Methods
Data Source
Data were obtained from the Medical Information Mart for Intensive Care III (MIMIC-III) database, a publicly accessible collection of over 58,000 intensive care unit (ICU) admissions at the Beth Israel Deaconess Medical Center from 2001 to 2012.21 Admissions to the ICU due to AECOPD were determined using the AECOPD ICD-9-CM code 491.21, resulting in three data sets for each corresponding admission: (1) demographic and demographic variables including insurance status, marital status, ethnicity, time of admission, and time of death; (2) additional demographic variables of gender (1 if male, 0 if female) and date of birth; and, (3) a series of comorbidities for each admission represented by a binary 1 or 0 variable. The first and second data sets were combined into a single demographic table, and age at admission was calculated by subtracting date of birth from the time of admission.
Predictors and Outcome
All data cleaning and analyses were performed using the Julia programming language (v0.5),22 utilizing the DataFrames.jl package (v0.8.5) to create the data tables.
To measure the effect of socioeconomic status (SES), insurance status as categorized by MIMIC-III was used: (1) Medicare, (2) Private, (3) Medicaid, (4) Government, and (5) Self Pay. Insurance was used as a proxy for SES under the general assumption that Medicaid and Self Pay represent low-income patients, Private and Government represent higher-income patients, and Medicare represents elderly patients. Five variables were created, one for each of these statuses, with a possible value of 1, if that person had that type of insurance, or 0. Since each person had only one kind of insurance, every admission had a value of 1 for only one of these five insurance variables.
There were four primary ethnicities designated in MIMIC-III: (1) White, (2) Black/African American, (3) Hispanic/Latino, and (4) Asian. Any ethnicity outside these four was placed in an “other” category. As before, each variable was given a value of 1 or 0, and each admission had a value of 1 for only one of the five ethnicity variables. With regards to marital status, there were five possible categories: (1) Married, (2) Single, (3) Divorced, (4) Widowed, or (5) Separated. Patients were classified under one of these binary variables or a sixth, “unknown marital status,” variable.
Nine age bins were derived using guidelines provided by the National Cancer Institute’s Surveillance, Epidemiology, and End Results Program (SEER) Database: (1) 49 and under, (2) 50-54, (3) 55-59, (4) 60-64, (5) 65-69, (6) 70-74, (7) 75-79, (8) 80-84, and (9) 85 and older.23
Comorbidity predictors were obtained from the third data set containing a series of comorbidities for each admission represented by a binary 1 or 0 variable. Extracted comorbidities were found in the Elixhauser and Charlson Comorbidity indices using previously created code and literature on which ICD-9-CM codes fell under each of these conditions.24-25 To investigate the correlation between these comorbidity indices and mortality, an age-adjusted Charlson comorbidity score26-27 and an Elixhauser comorbidity score28 were calculated for each patient and included as predictive variables. These indices are a combination of comorbidities that can be used to predict mortality and a patient’s level of morbidity.
The outcome variable was mortality during the ICU admission. Using the time of death variable, a “DEATH” indicator variable was created with a value of either 0 (if the death time was null, implying that the patient did not die during the admission), or 1 if the patient died. Some patients had multiple admissions to the ICU. For these patients, only the most recent admission was used, and a separate variable representing number of readmissions was created.
Statistical Analysis
Using the GLM.jl package (v0.6.1), univariate GLMs were fitted to measure the univariate significance of association between each of the predictors and mortality. Those with significant associations were then placed in a multivariate regression against mortality in order to determine which variables maintained a significant predictive association with mortality after taking into account their interactions with other variables.
After significant associations were determined through univariate binomial logistic regression models, multiple predictive models were developed to predict mortality. A multivariate binomial logistic regression model was created using the variables that were significantly associated with mortality through univariate logistic regression. Variables that did not improve the predictive strength of the model (as measured using AUROC) were removed.
The ability of machine learning to improve the predictive capacity of the model was then examined through two methods. First, using R29 and the RCall.jl package (v0.6.4), relative variable importance was calculated using Mean Gini decrease,30 a tool chosen because it bridges machine learning and logistic regression. It utilizes random forests to create a predictive model and then derives the relative contribution of each feature in predicting the outcome. From this, the 25 features with greatest relative importance (additional variables did not improve the predictive strength of the model and were not included) were incorporated into a logistic model. Variables that did not improve the predictive strength of the model were removed. Second, using the DecisionTree.jl package (v0.5.1), a random forest model consisting of an ensemble of 500 trees was used. Trees were made using a random 70% selection of all training samples and 10 of the 65 possible features. Meta-parameters were selected using five-fold cross-validation. Trees were grown to a maximum depth of 10. The model then selected which trees had best classification accuracy.
Each of the chosen models was developed on a training set comprised of 70% of the total dataset; testing was then done on the remaining 30% of the dataset. Each prediction made by the models was initially given as a decimal value representing likelihood of mortality. If this likelihood fell below a given threshold, it was deemed to be a survival, and if it fell above that threshold, it was deemed a mortality. The threshold was varied from 0 to 1 at increments of 0.02 and calculated sensitivity and specificity of the predictions made by the model at each threshold. Using these sensitivities and specificities and the AUC.jl package (v0.1), an AUROC value for each model was calculated.
Results
MIMIC-III contained 1,198 admissions due to AECOPD. These admissions represented 943 unique subjects with an average of 0.27 readmissions per patient. Summary statistics on this population are shown in Table 1. Of the 467 males and 476 females admitted, 156 patients died.
Table 1.
Summary statistics on patients admitted to the ICU with AECOPD
| Variable | Summary Statistics | Variable | Summary Statistics |
|---|---|---|---|
| Age | 0-49: 23 (2.4%) 50-54: 43 (4.6%) 55-59: 57 (6.0%) 60-64: 96 (10.2%) 65-69: 158 (16.8%) 70-74: 130 (13.8%) 75-79: 162 (17.2%) 80-84: 161 (17.1%) 85 and up: 113 (12.0%) |
Insurance Status | Medicare: 776 (82.3%) Private: 104 (11.0%) Medicaid: 48 (5.1%) Self-pay: 2 (0.2%) |
| Ethnicity | White: 727 (77.1%) Black/African-American: 89 (9.4%) Hispanic/Latino: 18 (1.9%) Asian: 13 (1.4%) Other/Unknown: 96 (10.2%) |
||
| Gender | Male: 467 (49.5%) Female: 476 (50.5%) |
Marital Status | Married: 355 (37.6%) Divorced: 79 (8.4%) Single: 209 (22.2%) Widowed: 243 (25.8%) Separated: 9 (1%) Unknown: 48 (5.1%) |
| Charlson Comorbidity Index | 6.216 +/- 2.654 | ||
| Elixhauser Comorbidity Index | 5.036 +/- 1.968 | ||
| Number of Readmissions | 0.270 +/- 0.995 | Death | Lived: 787 (83.5%) Died: 156 (16.5%) |
Results of univariate binomial logistic regression analysis of all the predictive variables against mortality is shown in Table 2. Note that in order to correct for the risk of Type-I error inflation that occurred because of the multiple testing, a Bonferroni correction was applied. The significance level of 0.05 was divided by the number of predictors, 64, to create a new significance level of 0.0008. Those with a significant association at this level, indicated in red, were then placed in a multivariate binomial logistic regression. Table 3 shows the result of this analysis. Arrhythmias, coagulopathy, and Charlson Comorbidity Index (CCI) were all significantly associated (p < 0.05) with mortality.
Table 2.
Univariate GLM analysis of each of the independent predictors against mortality. Predictors with significant association (p < 0.0008) are shown in red.
| Variable | Coefficient | P-value | Variable | Coefficient | P-value | |
|---|---|---|---|---|---|---|
| Congestive Heart Failure | -0.2199 | 0.2183 | Renal Disease | 0.1637 | 0.4492 | |
| Arrhythmia | 0.8 | <1e-5 | Drug Abuse | -0.9227 | 0.1281 | |
| Valve Disorder | 0.1503 | 0.5328 | Dementia | -7.9501 | 0.8767 | |
| Pulmonary Circulation Disorder | -0.5449 | 0.0592 | Number of Readmissions | 0.027 | 0.7791 | |
| Peripheral Vascular Disease | 0.1683 | 0.5255 | Charlson Comorbidity Index | 0.1486 | <1e-5 | |
| Hypertension | -0.3043 | 0.0928 | Elixhauser Score | 0.0613 | 0.1625 | |
| Hypertension with Complications | 0.1811 | 0.4391 | Insurance Status | |||
| Paralysis | -0.3326 | 0.6615 | Medicare | 0.5825 | 0.0289 | |
| Other neurologic disorder | 0.3049 | 0.2654 | Private | -0.6833 | 0.0475 | |
| Diabetes | -0.3517 | 0.1081 | Medicaid | -0.1569 | 0.7078 | |
| Diabetes with Complications | -0.3432 | 0.4403 | Government | -0.8755 | 0.4016 | |
| Hypothyroidism | -0.3758 | 0.2248 | Self Pay | -7.9501 | 0.8767 | |
| Renal Failure | 0.1637 | 0.4492 | Ethnicity | |||
| Liver Disease | 0.7848 | 0.0115 | White | -0.0116 | 0.9556 | |
| Ulcer | -0.8754 | 0.4016 | Black/AA | -0.3717 | 0.2658 | |
| AIDS | -8.955 | 0.8543 | Hispanic/Latino | -1.2302 | 0.2315 | |
| Lymphoma | 0.2361 | 0.7169 | Asian | 0.8219 | 0.1758 | |
| Metastases | 0.8267 | 0.0102 | Male | -0.0079 | 0.9643 | |
| Tumor | 0.8035 | 0.0008 | Marital Status | |||
| Rheumatoid Arthritis + Collagen Vascular Disease | 0.0929 | 0.9837 | Married | 0.2973 | 0.0941 | |
| Coagulopathy | 0.9406 | 0.0002 | Divorced | -0.1103 | 0.7354 | |
| Obesity | -0.7624 | 0.604 | Single | -0.3627 | 0.111 | |
| Weight Loss | 0.5243 | 0.1277 | Widowed | -0.1737 | 0.4004 | |
| Fluid and Electrolyte Disorder | 0.2425 | 0.1669 | Separated | 0.3696 | 0.6466 | |
| Blood Loss Anemia | -0.1784 | 0.7444 | Age | |||
| Deficiency Anemia | -0.6564 | 0.2182 | 0-49 | -1.4943 | 0.1405 | |
| Alcohol Abse | -0.6876 | 0.1165 | 50-54 | -1.0046 | 0.0964 | |
| Moderate/Severe Liver Disease | 0.421 | 0.5258 | 55-59 | -1.3236 | 0.0265 | |
| Psychoses | -1.416 | 0.0503 | 60-64 | -0.4676 | 0.1605 | |
| Depression | -0.7696 | 0.015 | 65-69 | -0.8204 | 0.0054 | |
| Myocardial Infarction | 0.423 | 0.0374 | 70-74 | 0.3293 | 0.1637 | |
| Cerebrovascular Disease | 0.3093 | 0.3094 | 75-79 | 0.1667 | 4574 | |
| Mild Liver Disease | 0.7684 | 0.0161 | 80-84 | 0.6839 | 0.001 | |
| Hemiplegia or Paraplegia | -0.6906 | 0.5117 | 85 and up | 0.4757 | 0.05 |
Table 3.
Multivariate GLM analysis of all variables found to be significant in univariate analysis against mortality. Significant predictors (p < 0.05) are shown in red.
| Variable | Coefficient | P-Value |
|---|---|---|
| Arrhythmia | 0.7015 | 0.0001 |
| Tumor | 0.3402 | 0.2379 |
| Coagulopathy | 0.8211 | 0.0018 |
| CCI | 0.1055 | 0.0044 |
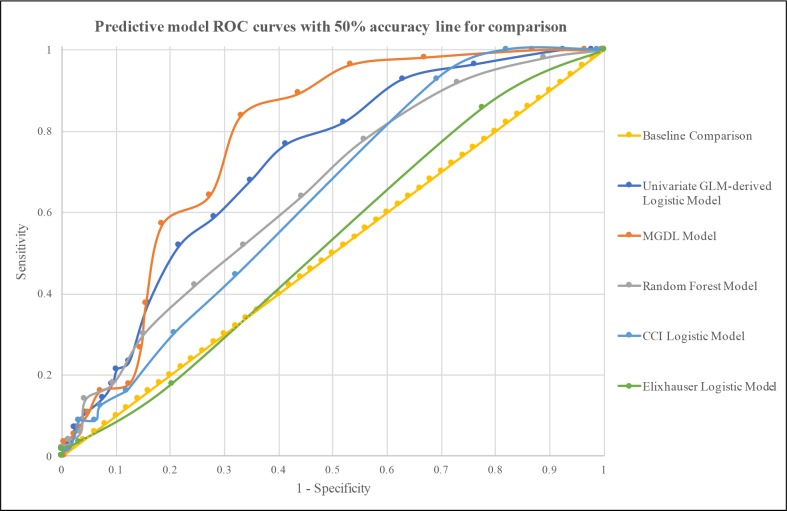
In the next phase of this study, predictive models were developed to predict mortality in patients admitted to the ICU with AECOPD. The first predictive model was a logistic regression model comprised of variables found to be significantly associated with mortality through univariate logistic regression. Rather than using the significance level of 0.0008, p < 0.05 was chosen as the level of significance for initial inclusion of variables because the Bonferroni correction can be conservative and we did not want to fail to include any important predictors due to the conservative estimate. To improve the sensitivity and specificity of this model, the Elixhauser score was included and variables that decreased the predictive capacity of the model were removed. This resulted in the inclusion of the parameters shown in Table 4. By varying the threshold for accepting a prediction as indicative of mortality, the ROC curve shown in Figure 1 was created. The AUROC for this curve was 0.719, and notable sensitivity/specificity combinations included sensitivity of 68% and specificity of 65% at a threshold of 0.14, and sensitivity of 77% and specificity of 59% at a threshold of 0.12.
Table 4.
Predictors included in the first and second predictive model.
| Model 1 Predictors: Predictors from univariate GLM analysis |
Model 2 Predictors: Predictors from Mean Gini Decrease analysis |
|---|---|
| CCI | CCI |
| Elixhauser Score | Elixhauser Score |
| Pulmonary Circulation Disease | Arrhythmia |
| Fluid + Electrolyte Disorder | |
| Myocardial Infarction | Hypertension |
| Arrhythmia | Congestive Heart Failure |
| Liver Disease | Number of Readmissions |
| Metastases | Coagulopathy |
| Tumor | White Ethnicity |
| Coagulopathy | Age 80-84 |
| Psychological Disease | Valve Disease |
| Depression | Widowed Marital Status |
| Insurance: Medicare | Neurological Disease |
| Age 65-69 | Age 70-74 |
| Age 80-84 | Peripheral Vascular Disease |
Figure 1.
ROC curves for the predictive models. Along with the three main models, a baseline linear curve and logistic models of each of the comorbidity indices are provided for comparison.
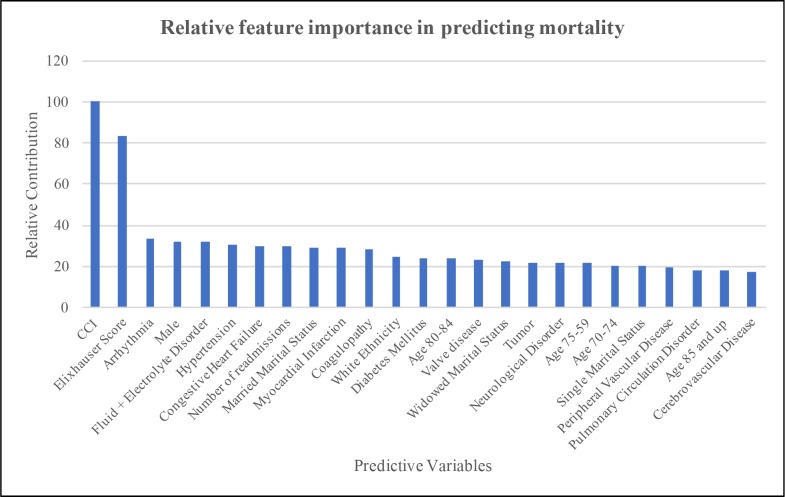
The results of the Mean Gini Decrease analysis are shown in Figure 2. The numerical values show the relative contribution of each variable compared to the highest contributor. Using a baseline contribution of 100 by CCI, which had the greatest relative contribution towards predicting mortality, the Elixhauser Score had a relative contribution of 83.1% that of the CCI. Arrhythmia had a relative contribution of 33.8% that of the CCI. After removal of any variables that did not improve the predictive capacity of the predictive model, a Mean Gini-derived logistic (MGDL) model was created using the parameters shown in Table 4. From this model, an ROC curve (Figure 1) with an AUROC of 0.778 was derived. Notable sensitivity/specificity combinations included sensitivity of 84% and specificity of 67% at a threshold of 0.14, and sensitivity of 64% and specificity of 73% at a threshold of 0.16.
Figure 2.
Results of Mean Gini Decrease analysis for Relative Feature Importance.
Logistic regression models composed of just the comorbidity indices are provided for comparison (Figure 1). A logistic predictive model with just the CCI had an AUROC of 0.622; with only the Elixhauser, it had an AUROC of 0.540. The ROC curve generated by the random forest model (Figure 1) yielded an AUROC of 0.652. Notable sensitivity/specificity combinations included sensitivity of 64% and specificity of 56% at a threshold of 0.08 and sensitivity of 52% and specificity of 66.5% at a threshold of 0.10.
Discussion
Understanding which variables can contribute to mortality in patients admitted to the ICU with AECOPD may be used to inform the development of targeted public health measures and potentially enhance discussions around EOL care. In this study, three models that included comorbidities, comorbidity indices, and demographic factors were developed, of which the MGDL predictive model performed best. The univariate GLM-derived logistic model did not perform as well, which may be due to the way that the models were constructed. The MGDL model determined which features had the greatest relative contribution towards predicting mortality after taking into account all their interactions, which was not taken into account in univariate analysis. It should be noted, though, that both of these logistic predictive models outperformed logistic models of either comorbidity index alone (Figure 1).
Previous literature suggests that of the comorbidities contained in the CCI and Elixhauser Comorbidity Index, those most commonly associated with exacerbations of COPD are anxiety, depression, and cardiovascular disease.33 Of these, only cardiovascular-related conditions had a high enough feature importance to be included independently in the MGDL model. Neurologic disorders and electrolyte disorders were included in the MGDL model, and coagulopathy was included in both the first and second model. While the connection between these and mortality due to AECOPD is interesting, conclusions cannot be drawn without further studies.
In addition to some of the variables that comprise them, the CCI and Elixhauser Comorbidity Index were included in the predictive models because both indices improved the predictive strengths of these models when included. In fact, in the MGDL model, increases in CCI had the largest impact on mortality. Increases in CCI scores have been correlated with worse outcomes in ICU patients as well as increasing age in the literature. One study described how univariate analysis of respiratory ICU patients in Beijing, China showed that CCI was correlated with a higher risk of death.31 This has been validated using retrospective claims data as well.32 Stavems et al. developed a model composed of CCI score, age, sex, and type of admission.32 Our data did not provide information on the type of admission, but a logistic regression model comprising sex and the age-adjusted CCI score on our dataset had an AUROC of 0.5669, suggesting that our model may be better suited for this set of patients. Though they improved the predictive strength of the MGDL model, the CCI and Elixhauser Comorbidity Index certainly do have limitations, as they may contain certain comorbidities not useful for AECOPD and lack some that are. Various modifications have been made to these indices for different health conditions34-35, and further modification may improve the predictive strength of the MGDL model.
With an AUROC of 0.778, the MGDL model performed well.36 Duenk et al. used logistic regression to develop the Pro-Pal COPD tool to identify COPD patients in potential need of palliative care. Using demographic factors, questionnaire results, and comorbidities, their model performed very well, with an AUC of 0.82. As compared to the 155 patient sample used in the development of the Pro-Pal COPD tool, the MGDL model was developed on a larger sample of patients and does not require some of the questionnaire results used by the Pro-Pal COPD tool that might not be readily available in the EHR. Tabak et al. also developed a model to predict mortality in AECOPD patients using demographic factors, lab results, vitals, and comorbidities. Their model had an AUROC ranging from 0.830-84 and was trained on a large cohort of nearly 70,000 patients.20 In comparison to the Tabak model, though, the MGDL model does not require lab results or vital signs. The model can predict mortality from a person’s medical history, information that can be obtained right when a patient enters the hospital.
Though developed on data from ICU patients, the MGDL model offers the opportunity to augment patient care in a variety of settings. The threshold in the MGDL model can be varied to leverage the model in different scenarios. At a threshold of 0.10, the model has a sensitivity of 96.4% and a specificity of 46.7%. Such a high sensitivity could be useful as a first-pass screening in the Emergency Department, where the goal is to minimize any missed severe cases. On the other hand, if the goal is to allocate a fixed number of resources to patients at the highest risk, then minimization of false positives is key. In this case, the threshold of the model could be raised to 0.18, creating a specificity of 81.5% and sensitivity of 57.1%. If a situation necessitated both good sensitivity and specificity, a threshold of 0.14 offers a sensitivity of 84% and specificity of 67%. At each of these thresholds, the model better predicts mortality than either the Elixhauser Score or CCI alone.
When discussing the performance of these different predictive models, it is important to keep in mind the end goal of a predictive model: to improve patient care. In order to do so, the results of any model will need to be incorporated into a decision support tool that can notify a provider if a patient is at a particularly high risk of dying. At this point, decision support tools in practice are dominated by basic “if this, then that” functions while logistic regression models and even more complex models have yet to be incorporated broadly.37 In incorporating these machine learning models, training time must be considered. Furthermore, one needs to consider the consequences of implementing a machine learning model versus a logistic regression based model. Previous work has shown that decision support tools are most effective when they provide advice or information to patients along with providers.38 This could theoretically be problematic in certain machine learning models in which justification for a certain prediction or weighting of variables is not provided. With a logistic regression, variables are assigned weights; providers and patients could therefore be informed about specific risk factors that led to a prediction.
Future work will look to improve the predictive strength of this model. The MIMIC-III database provides an opportunity to study, on a larger scale, conditions commonly encountered in the ICU; however, it does have some limitations in terms of data availability. For example, smoking history, which is a known impactful comorbidity for AECOPD,39 was not included because it was not immediately available as structured data in the MIMIC-III database. Incorporation of this element could be quite informative and next steps include using natural language processing techniques to extract smoking history from clinical notes.40-41 Future work will also involve validating this model with other large patient samples (e.g., using data from other EHR systems and institutions).
Future analysis will continue to examine the importance of demographic factors. Many of the demographic factors examined in this study were not significant predictors of mortality. In particular, SES did not play a significant role in predicting mortality. Yet, SES has repeatedly been shown to play a role in health outcomes in various fields. It may be the case that insurance status is not an effective proxy for SES. However, if insurance is in fact an effective representation of SES, then perhaps there is a different explanation behind the lack of significance of SES. It may be the case that SES is related to a patient’s development of COPD, but once the patient is admitted to the ICU, SES no longer plays a role in predicting mortality; instead, comorbidities and age become more important predictors. Future work will further explore this relationship by examining other representations of SES available in other databases.
In addition to demographic factors, future work will examine the impact of including in-hospital lab values to the MGDL model. The MGDL model offers significant utility in clinical settings where these values may not be readily available, but usually by the time a patient reaches the ICU, basic lab values have already been obtained. Given that these values have been included in several models, including the Tabak model, incorporating these values may increase the predictive strength of the MGDL model, making it more useful for the ICU setting.
Finally, previous models predicting mortality in AECOPD patients have primarily been developed using logistic regression.18,20 Mortality prediction for COPD patients have been developed using machine learning techniques such as Classification and Regression Tree (CART) analysis.11 Therefore, logistic regression and random forests were chosen to develop the predictive models for this study. Random forests were chosen as the particular machine learning algorithm because they offered decreased training time and more manageable meta-parameters. Future work, though will compare other machine learning models to the logistic regression and random forest models used in this study. Support vector machines (SVM) have been used to analyze genes related to severity of COPD.42 Outside of COPD, though, other machine learning techniques have been used to predict mortality. Stylianou et al. used artificial neural networks (ANN) and naïve Bayes, in addition to random forests and SVM, to predict mortality after burn injury.43 We have begun analysis with these models and will continue to explore them in the future.
Conclusion
Hospitalizations due to AECOPD account for significant healthcare costs; better predictions of mortality in ICU patients with AECOPD could reduce those costs and improve EOL care. Three models incorporating comorbidities, comorbidity indices, and demographic factors were developed to predict mortality in these patients. Of the three models, the MGDL model performed best with an AUROC of 0.778. In order to realize the maximum potential of predictive models, they must be implemented in care. The MGDL model offers the opportunity to enhance care in a variety of settings, and its threshold can be varied to provide the optimal sensitivity and specificity combination given the clinical setting. Future work will look to validate this model in other large patient samples, include more demographic factors, and perform analysis with additional machine learning models.
Acknowledgments
The authors thank Michael Superdock for his help with model development as well as Dilum Aluthge and Ishan Sinha for their help with data cleaning and analysis. This work was funded in part by the Scholarly Concentration Program in The Warren Alpert Medical School of Brown University as well as National Institutes of Health grants R01LM011364 and U54GM115677. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.
References
- 1.Jinjuvadia C, Jinjuvadia R, Mandapakala C, Durairajan N, Liangpunsakul S, Soubani AO. Trends in Outcomes Financial Burden and Mortality for Acute Exacerbation of Chronic Obstructive Pulmonary Disease (COPD) in the United States from 2002 to 2010. Copd. 2017;14(1):72–9. doi: 10.1080/15412555.2016.1199669. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Wier LM, Elixhauser A, Pfuntner A, Au DH. Rockville (MD): Agency for Healthcare Research and Quality (US); 2006. Overview of Hospitalizations among Patients with COPD 2008: Statistical Brief #106. Healthcare Cost and Utilization Project (HCUP) Statistical Briefs. [PubMed] [Google Scholar]
- 3.Buiting HM, Rurup ML, Wijsbek H, van Zuylen L, den Hartogh G. Understanding provision of chemotherapy to patients with end stage cancer: qualitative interview study. BMJ supportive & palliative care. 2011;1(1):33–41. doi: 10.1136/bmj.d1933. [DOI] [PubMed] [Google Scholar]
- 4.Lamont EB, Christakis NA. Prognostic disclosure to patients with cancer near the end of life. Annals of internal medicine. 2001;134(12):1096–105. doi: 10.7326/0003-4819-134-12-200106190-00009. [DOI] [PubMed] [Google Scholar]
- 5.Walczak A, Butow PN, Tattersall MH, Davidson PM, Young J, Epstein RM, et al. Encouraging early discussion of life expectancy and end-of-life care: A randomised controlled trial of a nurse-led communication support program for patients and caregivers. International journal of nursing studies. 2017;67:31–40. doi: 10.1016/j.ijnurstu.2016.10.008. [DOI] [PubMed] [Google Scholar]
- 6.Detering KM, Hancock AD, Reade MC, Silvester W. The impact of advance care planning on end of life care in elderly patients: randomised controlled trial. BMJ (Clinical research ed) 2010;340:c1345. doi: 10.1136/bmj.c1345. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Heyland DK, Allan DE, Rocker G, Dodek P, Pichora D, Gafni A. Discussing prognosis with patients and their families near the end of life: impact on satisfaction with end-of-life care. Open medicine : a peer-reviewed, independent, open-access journal. 2009;3(2):e101–10. [PMC free article] [PubMed] [Google Scholar]
- 8.Zhang B, Wright AA, Huskamp HA, Nilsson ME, Maciejewski ML, Earle CC, et al. Health care costs in the last week of life: associations with end-of-life conversations. Archives of internal medicine. 2009;169(5):480–8. doi: 10.1001/archinternmed.2008.587. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Fumagalli G, Fabiani F, Forte S, Napolitano M, Balzano G, Bonini M, et al. INDACO project: COPD and link between comorbidities lung function and inhalation therapy. Multidisciplinary respiratory medicine. 2015;10(1):4. doi: 10.1186/2049-6958-10-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Montserrat-Capdevila J, Godoy P, Marsal JR, Barbe F, Galvan L. Risk factors for exacerbation in chronic obstructive pulmonary disease: a prospective study. The international journal of tuberculosis and lung disease : the official journal of the International Union against Tuberculosis and Lung Disease. 2016;20(3):389–95. doi: 10.5588/ijtld.15.0441. [DOI] [PubMed] [Google Scholar]
- 11.Asiimwe AC, Brims FJ, Andrews NP, Prytherch DR, Higgins BR, Kilburn SA, et al. Routine laboratory tests can predict in-hospital mortality in acute exacerbations of COPD. Lung. 2011;189(3):225–32. doi: 10.1007/s00408-011-9298-z. [DOI] [PubMed] [Google Scholar]
- 12.Hoiseth AD, Omland T, Hagve TA, Brekke PH, Soyseth V. NT-proBNP independently predicts long term mortality after acute exacerbation of COPD - a prospective cohort study. Respiratory research. 2012;13:97. doi: 10.1186/1465-9921-13-97. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Marcun R, Sustic A, Brguljan PM, Kadivec S, Farkas J, Kosnik M, et al. Cardiac biomarkers predict outcome after hospitalisation for an acute exacerbation of chronic obstructive pulmonary disease. International journal of cardiology. 2012;161(3):156–9. doi: 10.1016/j.ijcard.2012.05.044. [DOI] [PubMed] [Google Scholar]
- 14.Singanayagam A, Schembri S, Chalmers JD. Predictors of mortality in hospitalized adults with acute exacerbation of chronic obstructive pulmonary disease. Annals of the American Thoracic Society. 2013;10(2):81–9. doi: 10.1513/AnnalsATS.201208-043OC. [DOI] [PubMed] [Google Scholar]
- 15.Steer J, Gibson GJ, Bourke SC. Predicting outcomes following hospitalization for acute exacerbations of COPD. QJM : monthly journal of the Association of Physicians. 2010;103(11):817–29. doi: 10.1093/qjmed/hcq126. [DOI] [PubMed] [Google Scholar]
- 16.Chen CZ, Ou CY, Wang WL, Lee CH, Lin CC, Chang HY, et al. Using post-bronchodilator FEV(1) is better than pre-bronchodilator FEV(1) in evaluation of COPD severity. Copd. 2012;9(3):276–80. doi: 10.3109/15412555.2012.654529. [DOI] [PubMed] [Google Scholar]
- 17.Diamantea F, Kostikas K, Bartziokas K, Karakontaki F, Tsikrika S, Pouriki S, et al. Prediction of hospitalization stay in COPD exacerbations: the AECOPD-F score. Respiratory care. 2014;59(11):1679–86. doi: 10.4187/respcare.03171. [DOI] [PubMed] [Google Scholar]
- 18.Duenk RG, Verhagen C, Bronkhorst EM, Djamin RS, Bosman GJ, Lammers E, et al. Development of the ProPal-COPD tool to identify patients with COPD for proactive palliative care. International journal of chronic obstructive pulmonary disease. 2017;12:2121–8. doi: 10.2147/COPD.S140037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Montserrat-Capdevila J, Godoy P, Marsal JR, Barbe F, Galvan L. Risk of exacerbation in chronic obstructive pulmonary disease: a primary care retrospective cohort study. BMC family practice. 2015;16:173. doi: 10.1186/s12875-015-0387-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Tabak YP, Sun X, Johannes RS, Hyde L, Shorr AF, Lindenauer PK. Development and validation of a mortality risk-adjustment model for patients hospitalized for exacerbations of chronic obstructive pulmonary disease. Medical care. 2013;51(7):597–605. doi: 10.1097/MLR.0b013e3182901982. [DOI] [PubMed] [Google Scholar]
- 21.Johnson AE, Pollard TJ, Shen L, Lehman L-WH, Feng M, Ghassemi M, et al. Scientific Data. 2016. MIMIC-III, a freely accessible critical care database. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Bezanson J, Edelman A, Karpinski S, Shah VB. Julia: A Fresh Approach to Numerical Computing. SIAM Review. 2017;59(1):65–98. [Google Scholar]
- 23.Standard Populations - 19 Age Groups National Cancer Institute SEER: NIH. [Available from: https://seer.cancer.gov/stdpopulations/stdpop.19ages.html.
- 24.Etheleon. Elixhauser-quan.sql. github.com/MIT-LCP/mimic-code2017.
- 25.Quan H, Sundararajan V, Halfon P, Fong A, Burnand B, Luthi JC, et al. Coding algorithms for defining comorbidities in ICD-9-CM and ICD-10 administrative data. Medical care. 2005;43(11):1130–9. doi: 10.1097/01.mlr.0000182534.19832.83. [DOI] [PubMed] [Google Scholar]
- 26.Chang CM, Yin WY, Wei CK, Wu CC, Su YC, Yu CH, et al. Correction: Adjusted Age-Adjusted Charlson Comorbidity Index Score as a Risk Measure of Perioperative Mortality before Cancer Surgery. PloS one. 2016;11(6):e0157900. doi: 10.1371/journal.pone.0157900. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Charlson ME, Pompei P, Ales KL, MacKenzie CR. A new method of classifying prognostic comorbidity in longitudinal studies: development and validation. Journal of chronic diseases. 1987;40(5):373–83. doi: 10.1016/0021-9681(87)90171-8. [DOI] [PubMed] [Google Scholar]
- 28.Elixhauser A, Steiner C, Harris DR, Coffey RM. Comorbidity measures for use with administrative data. Medical care. 1998;36(1):8–27. doi: 10.1097/00005650-199801000-00004. [DOI] [PubMed] [Google Scholar]
- 29.Team RC. 2013. R: A language and environment for statistical computing. Vienna, Austria: R Foundation for Statistical Computing. [Google Scholar]
- 30.James G, Witten D, Hastie T, Tibshirani R. New York: Springer; 2013. An introduction to statistical learning with applications in R. [Google Scholar]
- 31.He H, Sun Y, Sun B, Zhan Q. 2016. Application of a parametric model in the mortality risk analysis of ICU patients with severe COPD. The clinical respiratory journal. [DOI] [PubMed] [Google Scholar]
- 32.Stavem K, Hoel H, Skjaker SA, Haagensen R. Charlson comorbidity index derived from chart review or administrative data: agreement and prediction of mortality in intensive care patients. Clinical epidemiology. 2017;9:311–20. doi: 10.2147/CLEP.S133624. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Smith MC, Wrobel JP. Epidemiology and clinical impact of major comorbidities in patients with COPD. International journal of chronic obstructive pulmonary disease. 2014;9:871–88. doi: 10.2147/COPD.S49621. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Quan H, Li B, Couris CM, Fushimi K, Graham P, Hider P, et al. Updating and validating the Charlson comorbidity index and score for risk adjustment in hospital discharge abstracts using data from 6 countries. American journal of epidemiology. 2011;173(6):676–82. doi: 10.1093/aje/kwq433. [DOI] [PubMed] [Google Scholar]
- 35.Volk ML, Hernandez JC, Lok AS, Marrero JA. Modified Charlson comorbidity index for predicting survival after liver transplantation. Liver transplantation : official publication of the American Association for the Study of Liver Diseases and the International Liver Transplantation Society. 2007;13(11):1515–20. doi: 10.1002/lt.21172. [DOI] [PubMed] [Google Scholar]
- 36.Goldstein BA, Navar AM, Pencina MJ, Ioannidis JP. Opportunities and challenges in developing risk prediction models with electronic health records data: a systematic review. Journal of the American Medical Informatics Association : JAMIA. 2017;24(1):198–208. doi: 10.1093/jamia/ocw042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.O’Sullivan D, Fraccaro P, Carson E, Weller P. Decision time for clinical decision support systems. Clinical medicine (London, England) 2014;14(4):338–41. doi: 10.7861/clinmedicine.14-4-338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Roshanov PS, Fernandes N, Wilczynski JM, Hemens BJ, You JJ, Handler SM, et al. Features of effective computerised clinical decision support systems: meta-regression of 162 randomised trials. BMJ (Clinical research ed) 2013;346:f657. doi: 10.1136/bmj.f657. [DOI] [PubMed] [Google Scholar]
- 39.Dusemund F, Baty F, Brutsche MH. Significant reduction of AECOPD hospitalisations after implementation of a public smoking ban in Graubunden Switzerland. Tobacco control. 2015;24(4):404–7. doi: 10.1136/tobaccocontrol-2013-051290. [DOI] [PubMed] [Google Scholar]
- 40.Uzuner O, Goldstein I, Luo Y, Kohane I. Identifying patient smoking status from medical discharge records. Journal of the American Medical Informatics Association : JAMIA. 2008;15(1):14–24. doi: 10.1197/jamia.M2408. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Wang Y, Chen ES, Pakhomov S, Arsoniadis E, Carter EW, Lindemann E, et al. Automated Extraction of Substance Use Information from Clinical Texts. AMIA Annual Symposium proceedings AMIA Symposium. 2015;2015:2121–30. [PMC free article] [PubMed] [Google Scholar]
- 42.Hua L, Zhou P. [Combining protein-protein interactions information with support vector machine to identify chronic obstructive pulmonary disease related genes]. Molecular Biology. 2014;48(2):333–43. [PubMed] [Google Scholar]
- 43.Stylianou N, Akbarov A, Kontopantelis E, Buchan I, Dunn KW. Mortality risk prediction in burn injury: Comparison of logistic regression with machine learning approaches. Burns: journal of the International Society for Burn Injuries. 2015;41(5):925–34. doi: 10.1016/j.burns.2015.03.016. [DOI] [PubMed] [Google Scholar]