Abstract
Most existing studies used logistic regression to establish scoring systems to predict intensive care unit (ICU) mortality. Machine learning-based approaches can achieve higher prediction accuracy but, unlike the scoring systems, frequently cannot provide explicit interpretability. We evaluated an interpretable ICU mortality prediction model based on Recurrent Neural Networks (RNN) with long short-term memory(LSTM)units. This model combines both sequential features with multiple values over the patient’s hospitalization (e.g. vital signs or laboratory tests) and non-sequential features (e.g. diagnoses), while identifying features that most strongly contribute to the outcome. Using a set of 4,896 MICU admissions from a large medical center, the model achieved a c-statistic for prediction of ICU mortality of 0.7614 compared to 0.7412 for a logistic regression model that used the same data, and identified clinically valid predictors (e.g. DNR designation or diagnosis of disseminated intravascular coagulation). Further research is needed to improve interpretability of sequential features analysis and generalizability.
1. Introduction
Identification of patients at high risk of death in the ICU is important for guiding treatment decisions, quality assurance and resource utilization management. A number of scoring systems have been developed for this purpose, including Acute Physiology and Chronic Health Evaluation (APACHE) such as APACHE III1 and APACHE IV2; Simplified Acute Physiology Score (SAPS) such as SAPS II3, SAPS III4, and Mortality Probability Model (MPM) such as MPM I5, MPM II6 and MPM III7. Most of these studies used logistic regression, an interpretable prediction model, to identify predictive features and corresponding weights to establish these scoring systems8.
Recently, there has been an increasing interest in applying more advanced machine learning models to ICU mortality prediction9. One technique that holds a particular promise is recurrent neural networks (RNN) that has been successful in analyses of sequential data. Several previously published studies on ICU mortality prediction extracted sequential features from Electronic Medical Records (EMR) and used RNN to build prediction models. Che et al.10 developed a deep learning model GRU-D in one of the early attempts to predict ICU mortality using neural networks. GRU-D was based on Gated Recurrent Unit (GRU), a type of recurrent neural network. It takes two representations of missing patterns, i.e., masking and time interval, and effectively incorporates them into a deep model architecture, so that it not only captured the long-term temporal dependencies in time series, but also utilized the missing patterns to achieve better prediction results. Aczon et al.11 viewed the clinical trajectory of a patient as a dynamic system, and developed a recurrent neural network to analyze outcomes of patient care in a Pediatric Intensive Care Unit (PICU) of a major tertiary care center. Harutyunyan et al.12 considered several clinical problems, including modeling risk of mortality, forecasting length of stay, detecting physiologic decline and phenotype classification, and formulated a heterogeneous multitask problem where the goal was to jointly learn multiple clinically relevant prediction tasks based on the same time series data. To address this problem, they proposed an RNN architecture that leverages the correlations between the various tasks to learn a better predictive model. Jo et al.13 presented a joint end-to-end neural network architecture that combines long short-term memory (LSTM) and a latent topic model to simultaneously train a classifier for mortality prediction and analyze latent topics indicative of mortality from the text of clinical notes.
Although the existing studies utilizing RNNs achieved higher accuracy of ICU mortality prediction compared with the traditional scoring systems based on logistic regression, they cannot provide explicit interpretability as scoring system can, and therefore lack face validity. Additionally, most of the existing studies on RNN mainly considered the sequential features (e.g. vital signs or laboratory test results) extracted from EMR data, but did not describe methods for combined analyses of non-sequential (e.g. patient demographics, diagnoses and procedures) features together with sequential features.
In this paper, we describe an interpretable ICU mortality prediction model based on Logistic Regression and RNN with LSTM units14. The distinguishing features of this model are as follows.
The model allows to combine sequential features that include multiple values over the course of the patient’s ICU stay (e.g. a sequence of pulse measurements) and non-sequential features that only have a single value in the dataset, such as diagnoses or procedures recorded prior to the prediction time point.
The model is interpretable. It uses different RNNs with LSTM units to encode different sequential features into different representation vectors. It can provide the top ten positive or negative features and the corresponding weights to indicate significances of different features.
2. Methods
In this section, we first describe the ICU mortality prediction problem, and then propose our interpretable prediction model. Additionally, we introduce our data source and features used for prediction. Finally, we discuss evaluate of the ICU mortality prediction model.
2.1. Problem Description
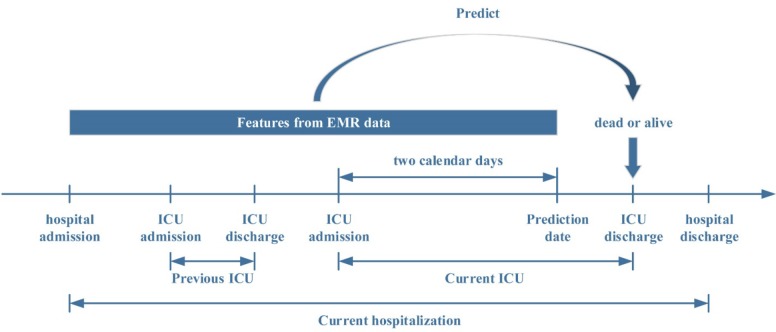
The goal of the model we developed was to identify patients hospitalized in the ICU at high risk for death during the ICU stay based on the EMR data accumulated by the end of the two calendar days into the ICU admission (Figure 1). We chose the prediction time point as two calendar days into the ICU admission because the initial empiric assessment showed that not enough data may accumulate at earlier time points to allow for a sufficiently accurate mortality risk estimate.
Figure 1.
ICU mortality prediction problem
2.2. Interpretable Prediction Model
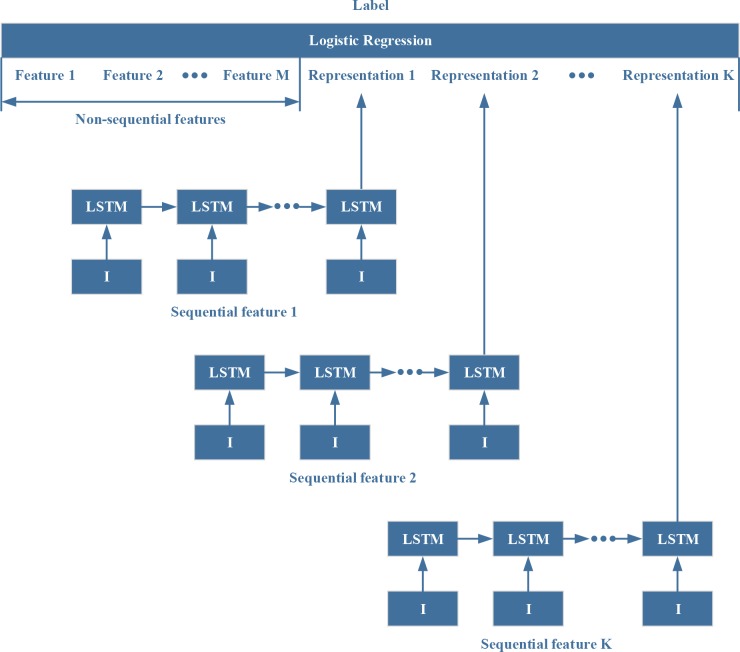
The features from EMR data can be divided into two types: 1) non-sequential features that reflect static information at the time the prediction is made (e.g. whether a particular diagnosis had been recorded during the hospital stay prior to the prediction time point); and 2) sequential features, that represent patient characteristics where the rate and direction of change add clinically relevant information to static value (e.g. blood oxygen content that is low but rising may be indicative of a better prognosis than the same blood oxygen content value that is falling). We assume that there are N ICU admissions. For the n-th ICU admission, there are Mnon-sequential features, denoted as , and K sequential features, denoted as , where and T is the length of sequence. The prediction results are denoted as .
We use K RNNs with LSTM units14 to encode the K sequential features into K vectors. For the k-th LSTM unit, the input gate can be represented as
| (1) |
Where is input vector corresponding to is output vector of LSTM, is cell vector of LSTM, is weights from input vector to input gate, is weights from output vector to input gate, is weights from cell vector to input gate, is bias for input gate, and f(·) is sigmoid function.
The forget gate can be represented as
| (2) |
Where is weights from input vector to forget gate, is weights from output vector to forget gate, is weights from cell vector to forget gate, and is bias for forget gate.
The output gate can be represented as
| (3) |
Where is weights from input vector to output gate, is weights from output vector to output gate, is weights from cell vector to output gate, and is bias for output gate.
The cell vector of this LSTM could be calculated as
| (4) |
Where is weights from input vector to cell vector, is weights from output vector to cell vector, is bias for cell vector, g(·) is tanh function, and ⊙ is Hadamard product.
The output vector can be calculated as
| (5) |
Thus, the probability of death can be represented as
| (6) |
Where wz is the weights for non-sequential features, is the weights for sequential features, and b is bias for Logistic Regression (Figure 2).
Figure 2.
ICU Mortality Prediction Model
For interpretability, we can use the weights in to represent the significance of the corresponding features, and rank the features based on these weights in order to find out the top ten positive features and the top ten negative features that have contributed most strongly to the prediction of ICU mortality.
The LSTM update complexity per unit per time step is O(W), where W is the number of weights including and .
2.3. Data Source
EMR data were collected at Asan Medical Center (AMC), an academic tertiary care hospital with approximately 2,700 beds that admits c. 100,000 adult patients per year. Medical ICU (MICU) that served as the source of data for this project is composed of 28 beds and is separate from the cardiac care unit (CCU). Over 900 patients per year are admitted to the MICU.
AMC implemented Asan Medical Information System (AMIS) to become a paperless hospital beginning in 1989. AMIS includes a computerized physician order entry system (CPOE), a picture archiving communication system (PACS), an electronic medical record system, a data warehouse (DW) and an enterprise resource planning (ERP) system. During the study period (2010 to 2017) period, all laboratory data, vital signs and nursing assessments for MICU patients were recorded in the EMR.
2.4. Feature Description
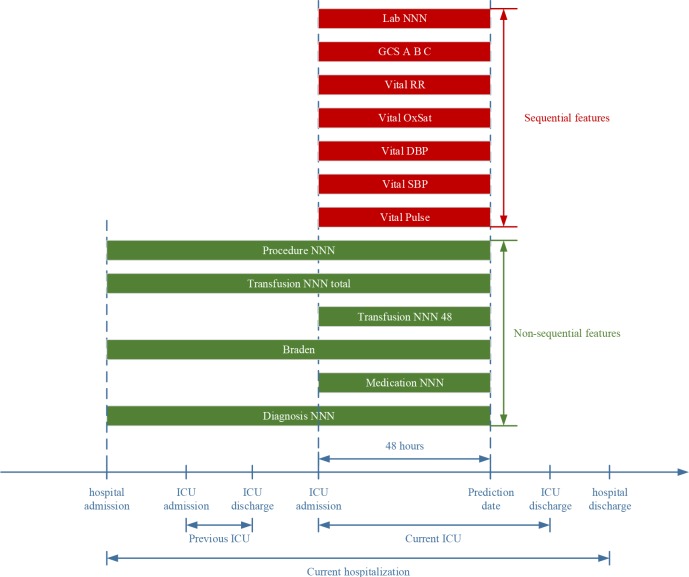
The features we used in the ICU mortality prediction model include both sequential features and non-sequential features, as illustrated in Figure 3. The non-sequential features include patient demographics, diagnoses, medications, Braden score (risk of development of decubitus ulcers), blood transfusions and procedures. The sequential features include vital signs, Glasgow Coma Scale (GCS), and laboratory test results. We included laboratory test results that were typically included in the commonly used ICU mortality risk scoring systems, based on their availability in the dataset.
Figure 3.
Time Frame for Data Acquisition for Feature Categories
Non-sequential features:
1) Demographics features included patient sex and age.
Sex was represented as a binary feature (male / female)
Age was represented as a categorical feature. We divided patient age into nine levels: “<20”, “21-30”, “31-40”, “41-50”, “51-60”, “61-70”, “71-80”, “81-90”, and “> 90”.
2) Diagnoses features were derived from the International Classification of Diseases version 10 (ICD-10) codes entered by clinicians treating the patient during the hospitalization. International Classification of Diseases, as the short-form of International Statistical Classification of Diseases and Related Health Problems, is the international standard diagnostic ontology for epidemiology, health management and clinical purposes. This system is designed to map health conditions to corresponding generic categories together with specific variations, assigning for these a designated code, up to six characters long. Each diagnosis feature was a binary variable that represented whether the patient had a specific diagnosis recorded from hospital admission to the first two calendar days after ICU admission.
3) Medications features represented the information on medications administered during ICU admission. Each medication feature was a binary variable that indicated whether this medication was given to the patient during the first two calendar days after ICU admission.
4) Braden Scale is a scoring system that evaluates the patient’s risk of developing a pressure ulcer. It consists of six categories: sensory perception, moisture, activity, mobility, nutrition, and friction/shear. The total score can range from 6 to 23 with a lower score indicating a higher risk.
5) Transfusion features indicated the amount of blood products transfused during the hospitalization. The analytical dataset included two transfusion features:
Transfusion-48-NNN: Amount of a particular blood product (e.g. packed red blood cells or platelets) transfused during the first two calendar days after ICU admission.
Transfusion-Total-NNN: Amount of a particular blood product transfused from hospital admission to the first two calendar days after ICU admission.
6) Procedures features were represented medical, surgical, and diagnostic procedures. Each procedure feature was a binary variable that indicated whether the patient had this specific procedure recorded from hospital admission to the first two calendar days after ICU admission.
Sequential features:
1) Vital Signs, including pulse, systolic blood pressure (SBP), diastolic blood pressure (DBP), arterial blood oxygen saturation (OxSat) and respiratory rate (RR)
2) GCS is a commonly used scoring system for assessing the individual’s level of consciousness, including:
GCS-A: Eye response.
GCS-B: Verbal response.
GCS-C: Motor response.
3) Laboratory tests included: arterial blood gas pH (pH-ABGA), arterial blood gas partial pressure of oxygen (pO2), serum sodium, serum creatinine, serum albumin, white blood cell count (WBC), hemoglobin (Hb), and serum lactic acid.
In the RNN-LSTM model, each of the sequential features was represented by the sequences of 48 values corresponding to the 48 hours in the first two calendar days after ICU admission. If there was more than one value available during a particular hour, the mean of the values during that hour was calculated. If there was no value reported during a particular hour, missing value was set. We used mean and standard deviation to transform real values into categorical values; missing values were assigned to a special category. In the comparison logistic regression model, each sequential feature was represented by two variables: a) the mean of the values reported during the first two calendar days after ICU admission and b) the slope of a line fitted through the values reported during the first two calendar days after ICU admission using least squares. In this way, both RNN-LSTM and logistic regression model represented the trends of sequential features.
2.5. Model Implementation
The RNN-LSTM-based prediction model was implemented via TensorFlow15, a widely used python library for Deep Neural Networks. Logistic regression as implemented in the scikit-learn16 python package was selected as the comparison. One hot encoding (or Dummy variables) was used to transform categorical features into binary features. The number of binary features equals to the number of possible unique values of categorical features. This approach was utilized for the age variable in both RNN-LSTM and the logistic regression model, and for all sequential features in the RNN-LSTM model. The batch size for the RNN-LSTM model was set to 100. The number of neurons in hidden layer was selected from [16, 32, 64], using hyperparameter optimization. We used cross entropy as the objective function, and used L2 regularization to avoid overfitting. We used Adam (an algorithm for first-order gradient-based optimization of stochastic objective functions, based on adaptive estimates of lower-order moments) to train the neural networks. The initial learning rate was set to 0.01.
2.6. Evaluation of ICU Mortality Prediction Accuracy
In this paper, we compared the RNN-LSTM-based prediction model with a logistic regression model. We divided the dataset into training dataset (90%) and test dataset (10%). In the training dataset, we used 5-fold cross-validation to optimize RNN-LSTM model parameters, including the coefficient for L2 regularization, and the dimension of hidden layer. In the comparison logistic regression model, 5-fold cross-validation was used to optimize the coefficient for L2 regularization.
C-statistic was used to evaluate the discriminative ability of the ICU mortality prediction model. As the first step, we generated the Receiver Operating Characteristic (ROC) curve by plotting the true positive rate (TPR) against the false positive rate (FPR) at various threshold settings. We subsequently calculated the c-statistic as the Area under the ROC Curve (AUC).
3. Results:
3.1. Experiment Description
The analytical dataset included 4,896 ICU admission records. Each record has 6,102 features (Table 1). Over 11% of patients died during their ICU stay (Table 2). Some of the data categories (e.g. GCS) were not available for a significant number of patients.
Table 1.
Feature Summary
| name | type | number | |
|---|---|---|---|
| Non-sequential | Sex | Binary | 1 |
| Age | Categorical | 1 | |
| Diagnosis | Binary | 866(20%) | |
| Medication | Binary | 194(20%) | |
| Braden | Integer | 1 | |
| Transfusion 24 | Integer | 3 | |
| Transfusion total | Integer | 3 | |
| Procedure | Binary | 18 | |
| Sequential | Vital-Pulse | Real | 48 |
| Vital-DBP | Real | 48 | |
| Vital-SBP | Real | 48 | |
| Vital-OxSat | Real | 48 | |
| Vital-RR | Real | 48 | |
| GCS-A | Real | 48 | |
| GCS-B | Real | 48 | |
| GCS-C | Real | 48 | |
| Lab-pH-ABGA | Real | 48 | |
| Lab-pO2 | Real | 48 | |
| Lab-Sodium | Real | 48 | |
| Lab-Creatinine | Real | 48 | |
| Lab-Albumin | Real | 48 | |
| Lab-WBC | Real | 48 | |
| Lab-Hb | Real | 48 | |
| Lab-Lactic-acid | Real | 48 |
Table 2.
Patient Characteristics
| Variable | Value | Data not Available |
|---|---|---|
| Study Patients, N | 4896 | N/A |
| Age, mean (SD) | 62.75 (14.66) | 0 |
| Female, N (%) | 1693 (34.58%) | 0 |
| Died during the ICU stay, N (%) | 548 (11.19%) | 0 |
| Three most common diagnoses: | Do Not Resuscitate | |
| Pneumonia, unspecified | N/A | |
| Sepsis, unspecified | ||
| Three most common procedures: | Endotracheal intubation | |
| Central Line Insertion | N/A | |
| Dialysis catheter placement | ||
| Three most common medications | Remifentanil | |
| albumin (inj) | N/A | |
| norepinephrine (inj) | ||
| Braden score (decubitus ulcer risk), mean (SD) | 12.88 (2.56) | 409 |
| Blood transfusion over the entire hospital stay, mean (SD) | 13.33 (30.90) | N/A |
| Blood transfusion over first two calendar days of the ICU | 9.02 (11.03) | N/A |
| admission, mean (SD) | ||
| Pulse, mean (SD) | 97.30 (25.01) | 0 |
| Systolic blood pressure, mm Hg, mean (SD) | 117.34 (30.17) | 0 |
| Diastolic blood pressure, mm Hg, mean (SD) | 63.26 (17.04) | 0 |
| Oxygen saturation, %, mean (SD) | 88.54 (26.17) | 0 |
| Respiratory rate, mean (SD) | 21.59 (6.33) | 0 |
| Glasgow coma scale A | 2.53 (1.23) | 2983 |
| Glasgow coma scale B | 4.44 (1.03) | 4274 |
| Glasgow coma scale C | 4.19 (2.10) | 3006 |
| Arterial blood gas: pH, mean (SD) | 7.39 (0.11) | 38 |
| Arterial blood gas: pO2, mean (SD) | 98.16 (48.03) | 37 |
| Serum sodium, mEq/L, mean (SD) | 138.22 (6.98) | 439 |
| Serum creatinine, mg/dL, mean (SD) | 1.85 (1.59) | 546 |
| Serum albumin, g/dL, mean (SD) | 2.30 (0.53) | 883 |
| White blood cell count, mean (SD) | 13.25 (17.49) | 454 |
| Hemoglobin, g/dL, mean (SD) | 9.58 (2.02) | 454 |
| Lactic acid, mmol/L, mean (SD) | 3.96 (4.00) | 4562 |
The number of unique features in some of the data categories was very large. For example, there were 4333 diagnoses features and 974 procedures features. Empirically we found that including all of them to train prediction models led to overfitting of the models to the training dataset, decreasing the AUC for the test dataset. We therefore used Pearson correlation coefficient to select the top 20% most predictive features in these two categories, including top 10% positively correlated features and top 10% negatively correlated features.
3.2. Accuracy comparison
RNN-LSTM model consistently outperformed the comparison logistic regression model (Table 3), both during the cross-validation on the training dataset and on the test dataset. Across the cross-validation runs, the AUC of the RNN-LSTM on average exceeded logistic regression by 3.25%. On the test dataset, the AUC of the RNN-LSTM model was higher than logistic regression by 2.02%.
Table 3.
Accuracy of ICU Mortality Prediction (ROC AUC)
| Training dataset (5-fold Cross-validation) | Test dataset | ||||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | average | ||
| Logistic Regression | 0.7804 | 0.7665 | 0.7662 | 0.7803 | 0.7819 | 0.7751 | 0.7412 |
| RNN-LSTM model | 0.8010 | 0.8045 | 0.8177 | 0.7957 | 0.8193 | 0.8076 | 0.7614 |
3.3. Interpretability
Using the weights in the RNN-LSTM model, we have identified 20 features that were most strongly associated with either ICU mortality (Table 4) or ICU survival (Table 5). Diagnoses and medications were the strongest contributors to identification of patients at high risk of death, with the Do Not Resuscitate status (indicating that no heroic measures should be undertaken for saving the patient’s life if their heart stops) being the strongest predictor. No sequential features were strongly predictive of ICU mortality. On the other hand, a number of sequential features -both laboratory tests and vital signs - were strongly predictive of ICU survival. Age was non-linearly associated with ICU mortality: patients in the oldest age group (> 90) had a high risk of mortality (weight 0.30406), while a younger age group (71-80) was associated with an increased chance of survival (weight -0.38747).
Table 4.
Top 10 Features Most Strongly Associated with ICU Mortality
| No. | Feature | Category | Sequential | Weight |
|---|---|---|---|---|
| 1 | Do Not Resuscitate | Diagnoses | No | 0.925982 |
| 2 | Prednisolone | Medications | No | 0.405208 |
| 3 | Disseminated intravascular coagulation | Diagnoses | No | 0.376092 |
| 4 | Gastroesophageal reflux with esophagitis | Diagnoses | No | 0.370576 |
| 5 | Heart failure | Diagnoses | No | 0.362328 |
| 6 | Fentanyl | Medications | No | 0.357122 |
| 7 | Peramivir | Medications | No | 0.355913 |
| 8 | Chronic kidney disease, stage 4 | Diagnoses | No | 0.353353 |
| 9 | Adenosine | Medications | No | 0.345557 |
| 10 | Acidosis | Diagnoses | No | 0.317825 |
Table 5.
Top 10 Features Most Strongly Associated with ICU Survival
| No. | Feature | Category | Sequential | Weight |
|---|---|---|---|---|
| 1 | Arterial blood gas pH | Labs | Yes | -0.74865 |
| 2 | Oxygen saturation | Vitals | Yes | -0.70677 |
| 3 | Pulse | Vitals | Yes | -0.67069 |
| 4 | Respiratory rate | Vitals | Yes | -0.63233 |
| 5 | Delirium | Diagnoses | No | -0.46512 |
| 6 | Drug rash | Diagnoses | No | -0.42524 |
| 7 | Aspiration pneumonitis | Diagnoses | No | -0.42105 |
| 8 | Liver transplant | Diagnoses | No | -0.41801 |
| 9 | Aspiration pneumonia | Diagnoses | No | -0.41251 |
| 10 | Age (71-80) | Demographic | No | -0.38747 |
4. Discussion
In this large study of nearly 5,000 ICU admissions, we found that a deep learning model able to take advantage of sequential nature of some of the data was able to achieve higher accuracy in identification of patients at high risk of death compared to the most commonly used approach, logistic regression. This finding demonstrates the importance of sequential analysis of clinical data. Many patients may have abnormal laboratory or physical findings that have achieved a stable level, and not be gravely ill. On the other hand, a rapid change in a key physiologic parameter may signal impending clinical deterioration, even if the absolute value is not [yet] in a critical zone.
Another important aspect of our study is human interpretability of the analytical findings. Many modern machine-learning techniques use complex data transformations that are difficult for human observers to examine, in order to arrive at the outcome. Consequently, face validity of the resulting models is difficult to confirm, and their limitations harder to appreciate, leading to an overall lower trust in their conclusions17. This has led to a strong interest in Explainable AI (XAI) systems that are able to provide human understandable reasons for their actions18. The model we have developed is a step in this direction. Many of the features the model has identified as strong contributors to prediction of ICU mortality, such as a Do Not Resuscitate designation or a diagnosis of disseminated intravascular coagulation, are clinical indicators of severe illness and / or poor prognosis. Other prognostic factors identified by the model, such as association of the liver transplant diagnosis with better chances of survival, may be due to the specific clinical workflow at the study institution, where all patients who are about to undergo a liver transplant are admitted to the MICU, and most of these patients go on to do well.
Our study also demonstrates some of the limitations of implementation of Explainable AI in analyses of sequential data. While our model flagged several sequential features as important predictors of ICU survival, identifying the actual patterns of these features (increase, decrease or a more complex shape) was not trivial. This therefore remains an important direction of future research.
The present study also had several other limitations. A single institution served as the source of data for the study; our findings may therefore not be generalizable to other clinical or geographic settings. The data came from a medical ICU and our findings may not be applicable to other ICU categories. Several data elements, including Glasgow Coma Scale and lactate levels, were missing for the majority of the patients; this may have led to a decrease in the model’s prediction accuracy. Inclusion of a greater range of laboratory tests or vital signs (e.g. urine output, weight) may also have been helpful. Finally, we did not compare our method with a clinically used system (e.g. APACHE or SAPS).
In conclusion, we have demonstrated that an RNN-LSTM-based system can exceed the accuracy of a “traditional” logistic regression model while maintaining a degree of transparency that allows clinicians to examine its face validity. Research is needed to further enhance explainability and predictive accuracy of the system.
Acknowledgements
This work was supported in part by a grant 2017-502 from the Asan Institute for Life Science, Asan Medical Center, Seoul, Republic of Korea.
References
- 1.Knaus WA, Wagner DP, Draper EA, et al. The APACHE III prognostic system: risk prediction of hospital mortality for critically III hospitalized adults. Chest. 1991;100(6):1619–1636. doi: 10.1378/chest.100.6.1619. [DOI] [PubMed] [Google Scholar]
- 2.Zimmerman JE, Kramer AA, McNair DS, Malila FM. Acute Physiology and Chronic Health Evaluation (APACHE) IV: hospital mortality assessment for today’s critically ill patients. Crit Care Med. 2006 May;34(5):1297–1310. doi: 10.1097/01.CCM.0000215112.84523.F0. [DOI] [PubMed] [Google Scholar]
- 3.Le Gall JR, Lemeshow S, Saulnier F. A new Simplified Acute Physiology Score (SAPS II) based on a European/North American multicenter study. JAMA. 1993 Dec 22-29;270(24):2957–2963. doi: 10.1001/jama.270.24.2957. [DOI] [PubMed] [Google Scholar]
- 4.Moreno RP, Metnitz PG, Almeida E, et al. SAPS 3--From evaluation of the patient to evaluation of the intensive care unit. Part 2: Development of a prognostic model for hospital mortality at ICU admission. Intensive Care Med. 2005 Oct;31(10):1345–1355. doi: 10.1007/s00134-005-2763-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Lemeshow S, Teres D, Pastides H, Avrunin JS, Steingrub JS. A method for predicting survival and mortality of ICU patients using objectively derived weights. Crit Care Med. 1985 Jul;13(7):519–525. doi: 10.1097/00003246-198507000-00001. [DOI] [PubMed] [Google Scholar]
- 6.Lemeshow S, Teres D, Klar J, Avrunin JS, Gehlbach SH, Rapoport J. Mortality Probability Models (MPM II) based on an international cohort of intensive care unit patients. JAMA. 1993 Nov 24;270(20):2478–2486. [PubMed] [Google Scholar]
- 7.Higgins TL, Teres D, Copes WS, Nathanson BH, Stark M, Kramer AA. Assessing contemporary intensive care unit outcome: an updated Mortality Probability Admission Model (MPM0-III) Crit Care Med. 2007 Mar;35(3):827–835. doi: 10.1097/01.CCM.0000257337.63529.9F. [DOI] [PubMed] [Google Scholar]
- 8.Vincent JL, Moreno R. Clinical review: scoring systems in the critically ill. Crit Care. 2010;14(2):207. doi: 10.1186/cc8204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Sharma A, Shukla A, Tiwari R, Mishra A. Mortality Prediction of ICU patients using Machine Leaning: A survey. Paper presented at: Proceedings of the International Conference on Compute and Data Analysis.2017. [Google Scholar]
- 10.Che Z, Purushotham S, Cho K, Sontag D, Liu Y. arXivpreprint arXiv:1606.01865. 2016. Recurrent neural networks for multivariate time series with missing values. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Aczon M, Ledbetter D, Ho L, et al. arXiv preprint arXiv:1701.06675. 2017. Dynamic Mortality Risk Predictions in Pediatric Critical Care Using Recurrent Neural Networks. [Google Scholar]
- 12.Harutyunyan H, Khachatrian H, Kale DC, Galstyan A. arXiv preprint arXiv:1703.07771. 2017. Multitask Learning and Benchmarking with Clinical Time Series Data. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Jo Y, Lee L, Palaskar S. arXiv preprint arXiv:1709.02842. 2017. Combining LSTM and Latent Topic Modeling for Mortality Prediction. [Google Scholar]
- 14.Graves A. Supervised sequence labelling with recurrent neural networks. Springer; 2012. Supervised sequence labelling; pp. 5–13. [Google Scholar]
- 15.Abadi M, Barham P, Chen J, et al. TensorFlow: A System for Large-Scale Machine Learning. Paper presented at: OSDI2016. [Google Scholar]
- 16.Pedregosa F, Varoquaux G, Gramfort A, et al. Journal of machine learning research. 2011. (Oct) Scikit-learn: Machine learning in Python; pp. 2825–2830. [Google Scholar]
- 17.Gunning D. Defense Advanced Research Projects Agency (DARPA), nd Web. 2017. Explainable artificial intelligence (xai) [Google Scholar]
- 18.IJCAI 2017 Workshop on Explainable Artificial Intelligence (XAI) 2017. http://home.earthlink.net/~dwaha/research/meetings/ijcai17-xai/. Accessed 03/05/2018.