Privacy-preserving biomedical data dissemination via a hybrid approach

Abstract

Sharing medical data can benefit many aspects of biomedical research studies. However, medical data usually contains sensitive patient information, which cannot be shared directly. Summary statistics, like histogram, are widely used in medical research which serves as a sanitized synopsis of the raw health dataset such as Electrical Health Records (EHR). Such synopsized representation is then be used to support advanced operations over health dataset such as counting queries and learning based tasks. While privacy becomes an increasingly important issue for generating and publishing health data based histograms. Previous solutions show promise on securely generating histogram via differential privacy, however such methods only consider a centralized solution and the accuracy is still a limitation for real world applications. In this paper, we propose a novel hybrid solution to combine two rigorous theoretical models (homomorphic encryption and differential privacy) for securely generating synthetic V-optimal histograms over distributed datasets. Our results demonstrated accuracy improvement over previous study over real medical datasets.

Introduction

The use of electronic health records (EHRs) has witnessed a dramatic increase [1], [2]. The development of health data collection and sharing also provides medical researchers more comprehensive resources. For example, researchers may want to learn the distribution of certain variables of a disease, but each local institution may not have enough samples to support such data analysis task. In this case, cross institutional collaboration are often requires. However, due to institutional policy and privacy concerns, EHR data with sensitive patient information may not be shared directly to other institutions. Many big data networks such as Electronic Medical Records and Genomics (eMERGE) Network [3], the the patient-centered SCAlable National Network for Effectiveness Research (pSCANNER) clinical data research network (CDRN) [4], the Scalable Architecture for Federated Translational Inquiries Network (SAFTINet) [5], and PopMedNet [6] have been established to facilitate biomedical research and collaboration. However, medical data contains large volume of sensitive personal information, thus the privacy issue accompanied with medical data sharing became a critical challenge. Existing studies have shown that it is possible to recover sensitive individual information, such as personal identity [7], disease condition [8], [9], through improper published medical data. Leaking these sensitive information may result in many negative impacts on research participants, which include, but are not limited to, the discrimination of employment or certain type of insurance [10], loss of willingness of participating research studies. If the leaked information including genomes of participants, there may be further implication on their blood relatives [11], as they may share similar genotypes. Many studies have demonstrated the vulnerability of directly sharing summary statistics, such as Homer’s attack [12] and likelihood ratio test [13] based on allele frequency, or Beacon attack [14] and its extension [15], [16] based on the presence of alleles to identify membership in a pool. Another study [17] has also demonstrated that even the intermediate statistics in building a logistic regression model may leak sensitive information. Therefore, it is essential to develop new protection techniques to facilitate biomedical data sharing.

Differential privacy (DP) has been used as one of promising techniques in many previous studies to safeguard statistical data sharing [18]. Roughly speaking, DP ensures that the change of one record (e.g., insertion, deletion, or modification) in a dataset will not increase the risk of the released differential private information. To achieve DP, perturbations [19] are usually introduced onto the input data to mask out potential sensitive information. With the help of DP, the computational results will be indistinguishable whether one particular record is in the dataset or not. Many studies have utilized DP technique to protect interactive query answering, regression model learning, synthetic data dissemination and histogram release [20]–[27]. For example, DPCube [26] is a DP based privacy-preserving V-optimal histogram release framework which relies on a 2-phase KD-tree partitioning strategy. DPCube framework adds noise to the data at the end of each phase to protect the privacy of the released histogram. Despite the limitation of two-step noise adding, DPCube is designed as a centralized model which assumes all data are available in a single repository. However, health data collected by single institute might be underrepresented, since a single institute may have limited samples (especially for rare disease). , However, different medical institutions may reluctant to directly share their own medical data to the others or untrusted third parties. To tackle above challenge, homomorphic encryption (HME) [28] may provide an alternative solution by supporting the computation over encrypted data across different institutions. In general, HME is a form of cryptosystem, by which one can perform computation directly over encrypted data. The outcomes obtained from homomorphic operations, if decrypted, can match the result of same operation carried out on plaintext. Based on above HME properties, each institute can securely outsource their private data onto an untrusted cloud environment [29]. Hence, the cloud could perform secure upper level computation over encrypted data from multiple institutions to form the aggregated results [30], [31]. During the past few years, the performance and capability of HME has been improvement significantly [32]–[35]. Many HME based secure computation applications have been proposed, such as secure machine learning and predictive model design [36], [37], homomorphic computation of Edit distance [38], [39], logistic regression for GWAS [35] and statistical testing for GWAS[40] etc. Although, HME techniques provide a strong protection of the data privacy and security during computation process, potential information leakage from the outcomes may also result in potential privacy risks [12]-[16]. Thus, built upon HME, we will resort to DP to develop a hybrid framework to facilitate privacy-preserving dissemination of statistical results (in particularly the release of differentially private histogram) across different institutions. A histogram is an estimate representation of the distribution for numerical data, which partition quantitative variables disjointly with count of points into each partitions [41]. The histograms are usually applied by medical institutions to summarize their collected health data to provide efficient query or other statistical operations [42].

According to aforementioned problems, it is necessary to build a medical data histogram releasing model which is optimized for the dual objectives of privacy and decentralization. While in one hand, such model can generate a synthetic histogram from distributed medical datasets (i.e. cross-institutional health records), and in the other hand can guarantee the privacy for both released data and the corresponding releasing process. Inspired by such idea, we developed a hybrid framework that combines HME and DP in this paper, which can securely generate a cross-institutional synthetic V-optimal histogram over encrypted medical data from multiple institutions and then release privacy-preserving V-optimal histogram via DP based perturbation operations. The main contributions of our proposed hybrid methods are as follows:

• We present the one of the first designs of a hybrid framework that combines HME and DP for securely generating privacy-preserved V-optimal histogram over distributed datasets.

• We proposed a secure interactive V-optimal histogram generating algorithm based on HME scheme. This algorithm could use multiple collections of encrypted medical data to efficiently generate a synthetic cross-institutional V-optimal histogram based on HME scheme.

• We proposed an innovative secure collaborative computing model involving untrusted cloud service provider and a trusted third party. While in this design, the cloud service provider will contributes to the majority of histogram computation via secure HME evaluation and the trusted third party act as an assistant to the cloud service provider to collaboratively conduct certain lightweight histogram generating process as well as HME private/public key management.

• We evaluated several applications using the released histograms, including counting queries and classification analysis. Our proposed hybrid framework has been evaluated over real biomedical data[43], and experimental results demonstrated efficiency and accuracy advantage of our proposed HME and DP-based hybrid framework.

Methods

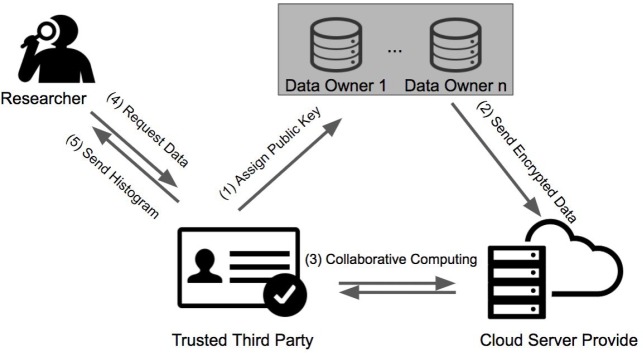
In this section, we present the proposed privacy-preserving V-optimal histogram generating and publishing framework. Figure 1 provides an overview of the proposed framework, which contains three major entities, including Data Owners (DOs), Cloud Service Provider (CSP)and a Trusted Third Party (TTP).Each entity is responsible to perform its corresponding tasks as explained in details below. In addition, we assume a semi-honest trust model, where each entity follows the protocol, but with the curiosity to derive additional sensitive information based on their received data.

• Cloud Service Provider (CSP): An untrusted entity which provides outsourced storage and most outsourced computing power. By relying on HME operations, it can securely calculate on encrypted medical data received from different data owners (DOs). In addition, for certain HME non-favorable operations (e.g, comparison), the CSP will resort to the TTP’s assistance, where we will introduce randomly distort on the intermediate results (but without affecting the underlying comparison outcomes) before sending them to the TTP to maximize the privacy and security protection. Finally, CSP will generate differentially private histogram by adding homomorphically encrypted Laplacian noise. .

• Trusted Third Party (TTP): A trusted institution which performs three critical steps: (1) Generating one pair of private key and public key and disseminating public key to both Cloud Service Provider and Data Owners . (2) During the computation, TTP will assist the Cloud Service Provider to perform certain comparison operations over perturbed inputs from CSP. This refers to a secure interactive HME protocol, where TTP applies its private key to decrypt these noise inputs followed by a comparison operation. We assume the CSP and TTP are not colluded, thus TTP cannot learn the underlying sensitive information based the noise inputs (please refer to the later section for more details). (3) In final stage, TTP will decrypt the differentially private histogram obtained from CSP, which can be released for further analysis by biomedical researchers.

• Data Owners (DOs): Institutions or hospitals that possess medical datasets upon which they would like to collaborate, while still preserving data privacy and data utility. They will work with CSP by summarizing local data and send the encrypted version to CSP

• Researchers: who are interested in using the released histogram to conduct certain pilot studies.

Figure 1:

The overview of the proposed privacy-preserving V-optimal histogram releasing framework

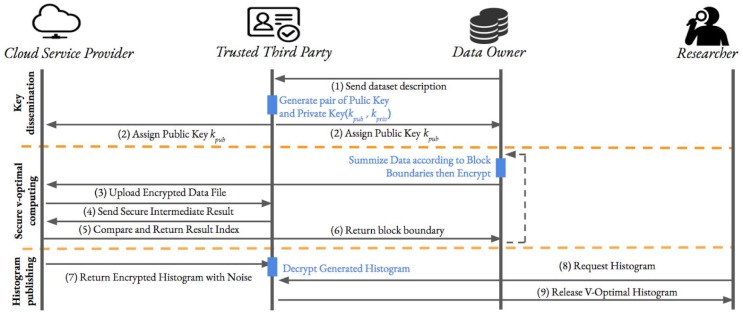
In our design, the workflow of our framework (see Figure 2) contains three major steps: Key Dissemination, Secure histogram generating, and DP Histogram Releasing. In the remaining part of this session, we will elaborate our method.

Figure 2.

The workflow of the proposed framework

Step 1. Key Dissemination: In our design we use HEAAN [44] as the fundamental HME library to implement the proposed framework. Thus, according to the design of HEAAN, the parameters such as polynomial modulus, coefficient modulus, plaintext modulus and scale factor need to be initialized at the beginning to create the security and public key pairs, where the parameter selection for our HEAAN based HME environment will be discussed in Results section). . We use kpriv and kpub to denote the generated private key and public key, respectively. The public key kpub will be disseminated to all DO for private medical data provisioning and CSP for further secure HME computation, respectively. While for private kpriv, it will be kept in the storage space of TTP which is then used for facilitating the interactive HME process and decrypting the final differentially private histogram.

Step 2. Secure Histogram Generating: DOs will use the received public key k_pub to encrypt their private medical data. We assume the medical data collected by each institute is a record type dataset, where each row represent one medical record for an individual patient and columns are medical attributes. We use a data matrix X = (x₁, x₂, x₃, …, x_n), X∈ R^mn to denote the collected medical data, for each x_i ∈R^m in X represent one medical record for an individual patient. We use x^j, $x_i^j$ to represent the j-th feature of whole medical data, and the j-th feature for i-th record, respectively. In our framework, we design an interactive computing mode between DOs and CSP, which requires multiple data exchanges back-and-forth within these two roles. In such a way, the private medical data from each DO is not a one-time upload to the cloud, but according to the instructions of the cloud, provision the corresponding data in batches. The data provisioning method in our framework is then discussed as follow(as illustrated in Algorithm 1): each time before data provision, each DO would receive an instruction message from CSP, which is denoted by < P^k, x^j >where P^k is a partition instruction that is need to be used for partition the data into k subsets. Once DOs received such instruction message from CSP, they first follow P^k to partition the data into X₁, X₂, X_k subset data. They for each subset data X_σ, generate a provisioning histogram H_σ according to Algorithm 2. Note that for generating the provision histogram with some specific features, we assume that there exists predefined range for each features among all DOs. For instance, for age feature, it is usually has a range between 0-110. And the number of bins β, which used for generating provisioning histogram is also considered as a predefined parameter. The histogram H_σ obtained from provisioning step is then denoted as $H_{\sigma }=(c_1{}^{\sigma },c_2{}^{\sigma },c_3{}^{\sigma },\dots ,c_{\beta }{}^{\sigma })$, where $c_t{}^{\sigma }$ indicate the count for t-th bin of the generated histogram. Such histogram is then been encrypted and sent to CSP for further HME computation. One navie way to perform encryption is to encrypt each count $c_t{}^{\sigma }$ in H_σ as one ciphertext, which would require β * k ciphertexts been uploaded onto CSP. By taking the advantage of CRT-batching schemes, we can encrypt H_σ as one ciphertext as well as applying same arithmetic operations to each element $c_t{}^{\sigma }$ stored in different slots. Instead of being accessible, the entire structure is encapsulated within a single unit which greatly reduces the space and computational complexity.

Algorithm 1. Private Medical Data Provision

Inputs: Instruction < Pk, xj > Provision Histogram Bin Number β , Data X

Outputs: Provisioning Medical Data ε(H)

1: | Divide X into k subsets according to Pk , denoted by X1, X2, X3, ... , Xk

2: | for Xσ , i = 1, 2, ..., k do

3: | Hσ = gen_prov_histogram (Xσ, xj, β)

4: | end for

5: | Encrypt H = Hσ , i = 1, 2, 3,..., k) as ε(Hσ) = ε(H1 , H2 ,..., Hk)

6: | return ε(H)

Algorithm 2. Provisioning Histogram Generation, gen_prov_histogram ()

Inputs: Data X, feature xj , bin number β

Outputs: Provisioning Histogram H

1: | Get the predefined range for feature xj

2: | Divide the entire range of feature xj into β intervals

3: | Count how many records in X fall into each interval according to feature xj

6: | Return Generated Histogram H

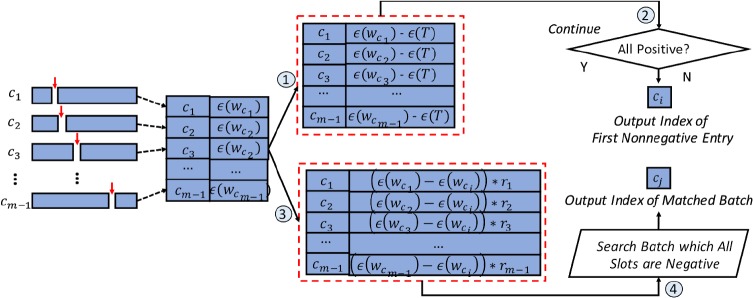
After receiving all encrypted data from each DO, CSP will aggregate them into one ciphertext crt_all (i.e., a secure global uniform histogram through homomorphic addition operations). Then CSP will partition crt_all from different positions. For example, as shown in Figure 3, we have m-1 ways to separate crt_all corresponding to m elements stored in the ciphertext, where each partition is presented as $<cr{t}_k^1,cr{t}_k^2>$ and k = 1,2,…, m – 1. In our protocol, we calculate the minimum weighted variance $w={\displaystyle \sum _{j=1}^{m-1}{k}_j{V}_j}$ to determined if such partition is the best way to splitting the feature or current feature need further splitting. For each pair of ciphertext, CSP securely calculates the variance of this pair $<V(cr{t}_k^1),V(cr{t}_k^2)>$ and adding $w_{c_k}=w(V(cr{t}_k^1))+w(V(cr{t}_k^2))$. Particularly, if any $w_{c_k}$ is less than a threshold which sets according to characteristic of individual features, the cutting process should be stopped. Otherwise, CSP generates a new matrix which store the value of $sub{w}_{c_k}=w_{c_s}-w_{c_t}(\text{s}=1,2,\dots ,\text{k, and t}=\text{s, s+1, s+2, }\dots \text{, k)}$. Before sending the $sub{w}_{c_k}$ to TTP, CSP will multiply a random number r_u (u = 1,2, …,k) with each $sub{w}_{c_k}$ to prevent information leakage. When TTP receive $sub{w}_{c_k}$ from CSP, TTP will using k_priv to decrypt the result and find the first $sub{w}_{c_k}$ which all values in slots are negative. Then, return the index of $sub{w}_{c_k}$ back to CSP, CSP will use this index to inform DO how to splitting the feature in next loop.

Figure 3.

Minimum Weighted Variance Cut Selection for achieving secure V-optimal histogram generation via collaborative computation between CSP and TTP

Step 3. DP Histogram Releasing: CSP keeps running the secure partition until all features of raw medical data has been considered in partition process. When secure V-optimal histogram generated, it could not be directly decrypted and shared, since it reflects the real distribution of raw data and could lead to privacy leakage. In the next step, we need apply differential privacy protection to the histogram by adding encrypted Laplace noises (generated by DOs) to the count of each bins, where the sensitive of histogram computation is 1 [26]. While implementing the Laplace mechanism, we need to carefully select the the privacy budget ε. When εis too large, DP noise might not provide enough protection for the released data. When εgoes too small, the perturbed histogram may ends up too much noise that would lead to the meanessless results. The impact of privacy budget on the performance of the proposed framework will be discussed in the experimental results section (see Figure 3). Then, the CSP returns this encrypted and DP-perturbed histogram to TTP. Finally, TTP decrypts DP-perturbed histogram and releases it to researchers for conducting pilot studies.

Results

In order to evaluate the quality of the differentially private histogram produced by our hybrid method, we conducted two experiments.. For the complexity analysis, we analyzed the running time of the proposed hybrid model for generating V-optimal histograms and profiled total running time for each key step for our approach. For the utility analysis, we evaluated two metrics using the released V-optimal histogram, which are classification and count query performance, respectively, to show the benefit of our proposed approach. A Diabetes 130-US hospitals dataset retrieved from the UCI Data Repository [43] with 55 features and 100K instances are used to evaluate our proposed framework. In order to generate smaller scale experiment data, we first strip all categorical features from the dataset and remain the numerical features, then we use MATLAB build-in feature selection function sequentialfs() to select the top 3 features and discard all the other features. The class was represented by re-admission attribute with two possible values 0 and 1 indicating if the corresponding individual has been or not been re-admitted for a same clinical group. In order to simulate the distributed setting of medical data, we evenly split aforementioned data into three parts to simulate data held by three different institutions. . For all experiments, we used 80-bit security level, where our parameter settings allow for 4096 slots within each ciphertext.. All results were obtained on a Ubuntu 16.04 Server with 3.60GHz CPU and 48GB memory, on which we implemented all histogram process and related applications.

Table 1 illustrated the efficiency evaluation experiment results, where we compared running time of different key steps in the proposed framework. We can see that DO and TTP only took little effort during the whole process, while all heavy work were completed by the CSP. The communication cost between three parties is moderate as it only consumed a few MBs, although we can still observe a large overhead of homomorphic encrypted data. ,

Table 1.

Running time and communication cost for securely generating V-optimal Histogram

Running Time (Seconds)	Data Encryption	CSP	Decryption	Total
	0.180	661.735	0.011	661.926
Communication Size (MB)	Raw Data	Provisioned Data	Histogram Plantext	Histogram Ciphertext
	2.30	4.332	0.001	0.722

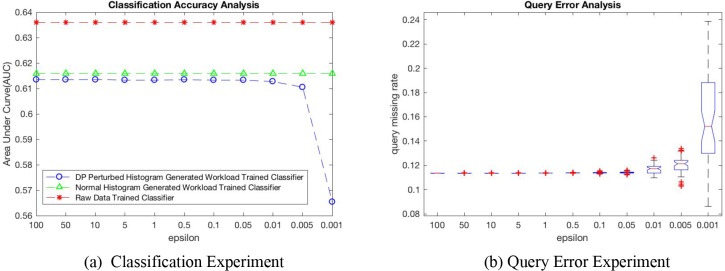
We evaluate the utility of the DP-perturbed histogram for training a logistic regression model. As the released histogram is an representation of the distribution for origin data, we can generate synthetic datasets through sampling process. In this experiment, we use three datasets (i.e., D1: dataset sampled based DP-perturbed V-optimal histogram, D2: dataset sampled based on the noise-free V-optimal histogram, as well as D3: the raw dataset) to evaluate the performance in terms of area under the ROC curve (AUC). The testing datasets were sample from the raw datasets with a sampling rate of 20%. Figure 3(a) shows the classification accuracy using aforementioned three datasets with respect to varying privacy budget ε ;∈ (0.001, 100). The original classifier trained by dataset D3 provides the best baseline accuracy at 0.636 in terms of the AUC. Our classifier trained by dataset D1 achieves slightly worse but comparable accuracy than the baseline due to the additive noise. While the accuracy gap between D1 and D2 trained classifiers is even smaller with an average of 1.5%. Another observation through the classification results, when the∈is larger than 0.01, there are no significant performance changes in terms of AUC. However, we observed significant performance loss when the privacy budget is less than 0.01. This is because when∈is smaller than 0.01, the total noise added to the data is pretty large, which further affects the AUC for trained classifier model.

We also evaluate the utility of the histogram for count query. In this evaluation, according to a randomly generated query requests set, we compared the query results from DP V-optimal histogram with different privacy budget ε against the query results from the raw data. The missing rate represents the relative difference of count query results (i.e., $|n_{dp}-n_{raw}|/n_{raw}$) from raw data (i.e., n_raw) and DP-perturbed histogram (i.e., n_dp). Figure 3(b) shows the data missing rates with different privacy budgets in boxplots of 50 independ queries.When the privacy budget is less than 0.01, the noise become overwhelming the real distribution of histogram and ruin the query result. In this experiment, ε = 0.05 provides a good trade-off between the accuracy and privacy.

Discussion and limitations

Security Model: As aforementioned, we assume a semi-honest security model in this project, where each entity faithfully follow the protocol, but may try to gain additional information about the underlying sensitive information. We assume there is no collusion among different parties. In this proposed framework, the private secrets are the medical data from each DO. . We consider the following potential leakage situations to show that our model is secure and privacy-preserving.

1. Leakage of DO’s data to CSP: . The private medical data will remain encrypted and protected by HME all the time when it been outsourced on to CSP. While during the computation process, CSP is only able to conduct HME evaluations over ciphertexts and produces encrypted results. Therefore, it’s impossible for CSP without the private key to have the ability to access the raw data.

2. Leakage of DO’s data to TTP The TTP in our framework only contributes to find the the index of minimum weighted variance of different t partitions through the v-optimal histogram releasing process and the publishing of final DP-perturbed histogram. TTP has the private key and is able to decrypt the intermediate data passed by CSP. While the V-optimal histogram generating algorithm is optimized by us to guarantee the privacy and security for the releasing process, and the data passed to TTP has been obfuscated with random noise. Thus even TTP holds the private and is able to decrypt the ciphertext, the private information of DO still cannot be revealed by the TTP. In addition, the histogram received by TTP from CSP has already been protected by DP operations. Thus, decrypting such information at the TTP will not increase any additional privacy risks beyond the DP guarantee. t

3. Leakage of one DO’s data to other DOs: The medical data are assumed to be collected by each DO individually, and the private medical data is not allowed to be shared with other DOs. While in our framework, the encryption key (i.e., public key) is generated by TTP, and then disseminated to DOs. While only TTP holds the private key, which could decrypt ciphertext, and we assume there is no collusion. Once the medical data is encrypted by each DO, then none of the other DO has the ability to decrypt them, which in other word guarantees the data for each DO cannot be revealed to the other DOs.

4. DO data leakage to Public: TTP publishes a differentially private histogram to public. Under DP protection, we can ensure that no risk is insured when data from individual patients is included, excluded or modified in a particular dataset, which provides a strong privacy protection for histogram data dissemination.

Limitations: The proposed framework has several limitations: First, current HME techniques still face the challenges that when the dataset size scales up, the computation complexity for secure evaluation over encrypted ciphertext increases sharply. With the rapid growing of computational cost along with data scale, the scalability would be a bottleneck of the proposed approach.. In this paper, we only proposed a preliminary implementation for combining HME and DP to generate V-optimal histogram, no additional optimization techniques are considered. However, according to our current design, there would be several ways for optimizing the HME based histogram generating process. For instance we can apply large size CRT-batching [44] to wrap multiple instances into one large ciphertext and use batching based HME operation to boost the computation process. Multiprocessing design [45], [46] or distributed computing [30], [47] framework could be another alternative way for such solution. Second, in our current design, we still need an trusted third part to assist cloud service for some portion of the computing tasks, while an ideal design is to eliminate such trusted third party and only to remain DO and CSP in the framework. To achieve such framework design, we should investigate more into the HME based histogram releasing algorithm design. We may be able to construct secure circuits for generating histogram, where each gate is evaluated homomorphically, in such a way, all histogram releasing related computation could be done under HME scheme. Finally, we still observed a storage overhead for homomorphically encrypted medical data. Under our HME parameter settings, the ciphertext would increases to several orders of magnitudes in comparison to that of raw medical data. To address this problem, advanced data provisioning method or compression techniques should be investigated. The limitations stated above warrant the further investigation of advanced crypto techniques to facilitate privacy-preserving biomedical data dissemination.

Conclusion

In this paper, we proposed a hybrid privacy-preserving framework based on HME and DP to securely generate privacy-reserving V-optimal histogram through distributed medical datasets. The proposed method uses HME to guarantee the security and data privacy through histogram computation process, and use DP-based perturbation to release the privacy-preserving histogram. An interactive secure histogram generating algorithm is also proposed in this paper. According to such design, HME based CSP contributes to the majority of histogram generating process, while a TTP is introduced as an assistant to facilitate a small portion of the whole computation task. By introducing random noise, we ensure the collaborative computing process between CSP and TTP is also secured. Through experiments, we evaluate the performance results of our proposed model, which demonstrated the advantages. . Classification and count query experiments are conducted to evaluate the quality of generated DP perturbed histogram. While in the classification experiment, logistic regression models trained based on sampled data from the DP-perturbed histogram shows slightly accuracy degradation (an average 4.9% accuracy down in terms of AUC) compared with the models trained on raw data, and the count query experiment also shows acceptable error rate (an average of 0.113) between queries via histogram data and raw data. In general, our proposed framework can efficiently generate a privacy-preserving V-optimal histogram through distributed collected medical datasets, in which all steps of the computations are evaluated securely without revealing any private intermediary information, the published histogram also preserved considerable privacy for medical data under differential privacy guarantee.

Funding

This work is supported by NIH grants R00HG008175, R01GM114612, R01GM118574, U01EB023685.

Figure 3.

(a) Accuracy performance in terms of AUC for training logistic regression models using data sampled from DP-based V-optimal histogram, V-optimal histogram from raw data, and raw data; and (b) count queay missing rate with different privacy budgets ε varying between 0.001 to 100.