Abstract
The forces and torques governing effective 2-D translation and rotation of the laryngeal cartilages (cricoid, thyroid, and arytenoids) are quantified on the basis of more complex 3-D movement. The motions between these cartilages define the elongation and adduction (collectively referred to as posturing) of the vocal folds. Activations of the five intrinsic laryngeal muscles, the cricothyroid, thyroarytenoid, lateral cricoarytenoid, posterior cricoarytenoid, and interarytenoid are programmed as inputs, in isolation and in combination, to produce the dynamics of 2-D posturing. Parameters for the muscles are maximum active stress, passive stress, activation time, contraction time, and maximum shortening velocity. The model accepts measured electromyographic signals as inputs. A repeated adductory – abductory gesture in the form ∣ hi-hi-hi-hi-hi ∣ is modeled with electromyographic inputs. Movement and acoustic outputs are compared between simulation and measurement.
Keywords: vocal folds, posturing, biomechanics, voice onset
ASA-PACS: 43.70 bk, aj
I. INTRODUCTION
Vocal fold dynamics for speaking and singing can be treated in two parts: (1) large and relatively slow deformations occurring when the vocal folds are positioned for voicing, coughing, and breathing by moving laryngeal cartilages with muscle forces, and (2) small and relatively fast deformations occurring when the tissue is driven into self-sustained oscillation by aerodynamic and acoustic pressures. These two parts are referred to, respectively, as vocal fold posturing and vocal fold vibration. Posturing is further subdivided into adducting (or abducting) the medial surfaces of the vocal folds and elongating (or shortening) of the vocal folds. This posturing occurs in a nonperiodic (but ultimately always cyclic) fashion at frequencies of 1 – 10 Hz. Vocal fold vibration, on the other hand, occurs at 100 – 1000 Hz.
Although vocal fold posturing and vocal fold vibration are thus thought to be separate mechanical processes, many parameters of vibration (e.g., fundamental frequency, amplitude of vibration, and voice onset time) are dependent on posturing. For example, adduction of the vocal processes of the arytenoid cartilages has been shown to affect the intensity of the voice (Titze and Sundberg, 1992; Murry et al., 1998), is involved in fundamental frequency regulation (Hirano et al., 1970; Honda, 1983), voice initiation (Cooke et al., 1997), devoicing or vocal offset (Yoshioka, 1981), and ventilation or glottal aspiration (Tomori et al., 1998). Some voice disorders have been attributed to insufficiencies of voice onset and offset (e.g., Peters et al., 1986, Werner-Kukuk and von Leden, 1970, Gallena et al., 2001). Adequacy of vocal fold posturing has been used to quantify vocal improvement as a result of therapy (Boone, 1994, Gallena et al., 2001) and singing training (Miller, 1994).
Speech simulation at the biomechanical level requires a mathematical description of vocal fold posturing. Because many of the empirical data come from electromyography of the laryngeal muscles, the control variables are designed to be simulated muscle activations. The model described in this paper accepts these simulated muscle activations as inputs. The outputs are movement variables of the arytenoid cartilages and (if vocal fold vibration is included) the acoustic pressures and flows in the vocal tract.
Vocal fold adduction, abduction and elongation are not simple one-dimensional movements because the entire medial surface of the vocal folds is non-uniformly deformed. Anterio-posterior and inferio-superior variations are typical. Also, the 3-D nature of arytenoid cartilage movement (a rocking motion) affects the dynamics of posturing, as described years ago by Frable (1961), Maure and Dickson (1971), von Leden and Moore (1961), Sellars and Keen (1978). More recently, Selbie et al. (1998) studied the cricoarytenoid joint facets in great detail. It was shown that rocking occurs along the long axis of the cricoid facet, which has curvatures in all directions. A matching set of opposite curvatures was found on the arytenoid facet, so that the joint resembled a tongue-in-groove architecture. Selbie et al. showed that arytenoid cartilage motion was highly constrained and that rotation about a vertical axis perpendicular to the plane of the glottis was not possible, but that such rotation was “apparent” when the 3-D motion was projected onto a horizontal plane (the plane of the glottis). Their results suggest that, for the modeling presented in this paper, translational displacements and rotations of the cricoarytenoid joint should be viewed only as “effective” 2-D displacements, based on direction cosines determined from the actual 3-D motions.
A three-dimensional continuum model of vocal fold posturing (Hunter, et al. 2004) showed that the range and speed of adduction and abduction were not only dependent on individual laryngeal muscle properties, but also on the rotational and translational mechanics of passive (connective) tissue. Because of the complexity of three dimensional continuum mechanics, however, only adduction/abduction of the arytenoid cartilages was addressed; elongation from cricothyroid joint motion was not included in the former 3-D model, but will be addressed here for a parsimoniously constructed 2-D case.
Vocal fold posturing requires at least an x and a y displacement of the vocal processes relative to the glottal midplane. The x-displacement (medial-lateral) is for adduction and the y-displacement (ventro-dorsal or anterior-posterior) is for elongation. Although the three-dimensional rocking of the arytenoid cartilages over articular surfaces results in x, y, and z motions of the vocal processes, the important motion for our modeling is in the x-y plane (Hunter and Titze, 2004). Therefore, it is possible to capture the main features of vocal fold elongation and adduction in the transverse plane, as will be demonstrated in this paper.
For application to phonetics, the primary question of interest is: Can the biomechanical model predict the time-course of adduction-abduction and vocal fold elongation with muscle activations derived from natural speech?
II. MECHANICS OF TWO-DIMENSIONAL POSTURING
We have begun the mathematical implementation of two-dimensional modeling by first determining the lines of action of all intrinsic laryngeal muscle fibers in a three-dimensional space. The intrinsic muscles are the cricothyroid (CT), thyroarytenoid (TA), lateral cricoarytenoid (LCA), posterior cricoarytenoid (PCA) and interarytenoid (IA). Figure 1 shows a sketch of these muscles. Because the muscles are not uniform in shape, many small muscle fiber bundles needed to be identified and dissected in previous work for a given muscle (Cox et al., 1999 for canine and human CT and TA; Mineck, et al., 2000 for canine LCA, PCA, and IA). With the use of a three-dimensional digitizer (Microscribe-3D), the point of origin (x1j,y1j,z1j) and the point of insertion (x2j,y2j,z2j) of the j-th fiber bundle of each muscle were measured in a Cartesian coordinate system. This allowed the length lj of each muscle fiber bundle to defined
| (1) |
as well as the x and y direction cosines, αj and βj,
| (2) |
| (3) |
Figure 1.
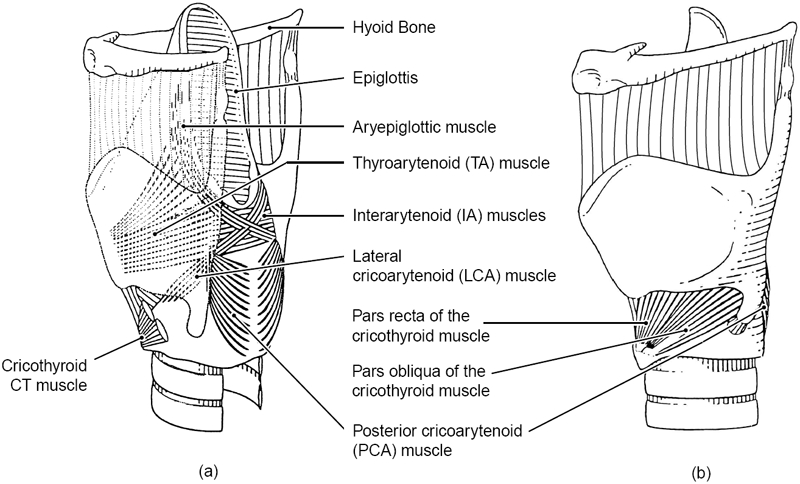
Framework of the larynx with intrinsic musculature. (a) posterio-lateral view, (b) lateral view.
From these measures, the composite x and y direction cosines for the entire muscle force were computed as follows:
| (4) |
| (5) |
where Aj is the cross-sectional area of a given muscle fiber bundle (typically on the order of 1/mm × 1/mm; Cox et al. 1999). Figure 2 shows a sketch of the lines of action of the forces, and Table 1 lists anatomically measured direction cosines α and β for four of the muscles (Mineck et al., 2000; Berry et al., 2003; Titze, 2006). The direction cosines of the CT muscle will be discussed separately because it does not attach to the arytenoid cartilage and is therefore a component of a separate mechanical system. Also in the table are the directional moment arms γ, to be discussed later.
Figure 2.
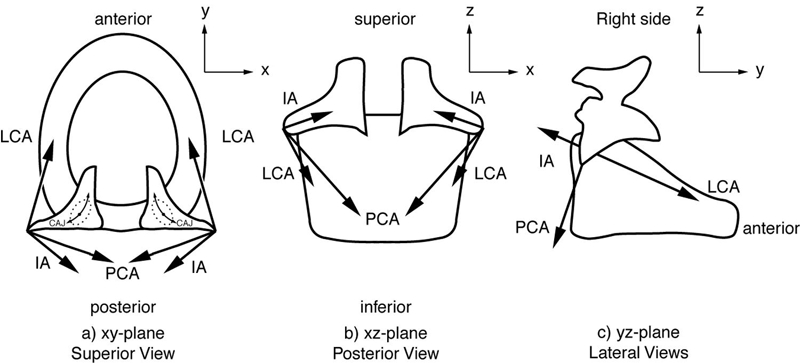
Lines of action of the forces of the laryngeal muscles.
Table 1.
Direction cosines and directional moment arms for canine CAJ dynamics (averaged over 8 larynges, left and right side). After Cox et al. (1999), and Mineck et al. (2000). γ is positive for counter-clockwise “equivalent rotation” of the right arytenoid cartilage.
| Muscle | α | B | γ (mm) |
|---|---|---|---|
| PCA | -0.1 | -0.8 | -5.49 |
| LCA | -0.198 | 0.886 | 3.915 |
| TA | 0.015 | 0.990 | 0.8 |
| IA | -0.697 | -0.644 | -3.30 |
It must be pointed out that, at this stage of modeling, our data sets represent a mixture of canine and human species. Biomechanical data are mainly from canines and anatomical data are mainly from humans. Hence, our results can only be considered as representative of human biomechanics to the extent that the canine is a reasonable model. Work is continuing to complete data tables for both species (Titze, 2006). Fortunately, human ligament stress-strain curves were included. Hence, the vocal fold length changes (to be discussed) are a fairly good approximation to human length changes.
Figure 3 shows a transverse section through the right vocal fold, arytenoid cartilage, and thyroid cartilage, with the cricoid cartilage sketched underneath (ring-shaped). The two-dimensional lines of action of the muscle forces are shown. TA1 represents the vocalis portion of the TA muscle, while TA2 represents the muscularis portion. The overall action of the TA is the vector sum of the two. Also shown are vector forces for the IA, PCA, and LCA.
Figure 3.
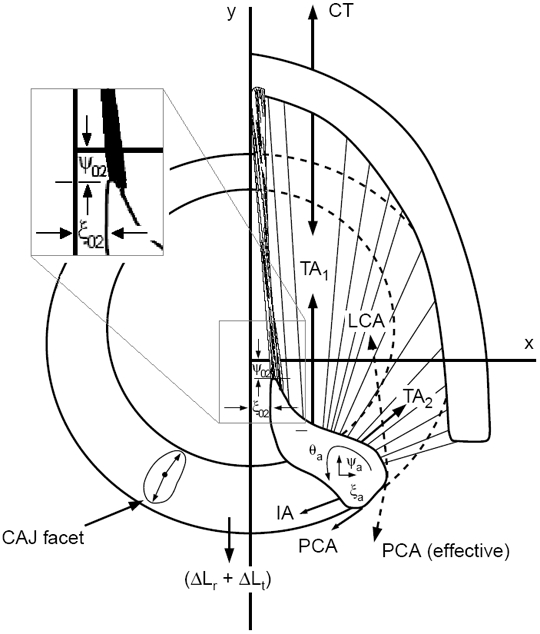
Forces acting on the arytenoid cartilages for cricoarytenoid movement.
It has been observed by experimenting with excised larynges (Titze, 2006) that the LCA muscle has the primary function of creating the “effective 2-D rotation” of the vocal processes of the arytenoid cartilages (counterclockwise for the right cartilage), which brings the tip of the vocal processes into or near the glottal midplane. In Figure 3, the symbols ξ02 and ψ02 describe the position of the vocal process. The IA muscle has the primary function of adducting the arytenoid cartilage near the posterior wall, thereby closing the posterior gap. Abduction is controlled by the PCA muscle, which is the antagonist to the LCA for rotation. TA1 is primarily used for length reduction, but TA2 is an adductor that creates “effective” counterclockwise rotation of the arytenoid cartilages, similar to the LCA.
Equations of Motion for Cricoarytenoid Joint Movement
For quantitative modeling, the elastic and viscous forces governing “effective” cricoarytenoid joint (CAJ) translation and rotation need to be known, together with the muscular forces. The x-motion of the arytenoid cartilage around the CAJ is
| (6) |
where αi is the direction cosines for the i-th muscle, ξa is the x-displacement of the arytenoid cartilage from the center of the cricoarytenoid joint (CAJ), Ma is the mass of the arytenoid cartilage, kx is the “effective” translational stiffness, dx is the damping coefficient, and Fi is the i-th tissue force (i = 1 for the LCA muscle, i = 2 for the IA muscle, i = 3 for the PCA muscle, i = 4 for the CT muscle, i = 5 for the combined TA muscles, i = 6 for the vocal ligament, and i = 7 for the vocal fold mucosa). Since CT is not acting directly on the arytenoid cartilage, F4 in Equation 6, but becomes non-zero for vocal fold elongation to be discussed later.
In a similar fashion, the equations of motion for “effective” y-displacements and rotation of the arytenoid cartilage are written as
| (7) |
| (8) |
where ψa is the y-displacement and θa is the rotation around the cricoarytenoid joint, βi is the i-th directional cosine for y-displacement (Table 1), γi is the i-th directional moment arm from Table 1, ky and κ are respective translational and rotational stiffnesses, Ia is the moment of inertia of the arytenoid cartilage, and dr is the rotational damping coefficient. These inertial, elastic, and viscous damping constants of the CAJ are largely nonlinear and have been determined empirically in various excised larynx experiments (Titze, 2006).
Equations of Motion for Cricothyroid Joint Movement
Dynamical equations for vocal fold elongation have been published previously (Titze et al., 1988) and are reviewed here only for completeness. For a rotational strain εr of the cricothyroid joint (CTJ), which is defined as vocal fold elongation normalized to a resting vocal fold length L0,
| (9) |
where Ir is the moment of inertia associated with the CTJ rotation, F4 and F5 are the CT and TA forces, respectively, as defined above, w is the moment arm for the CT torque, h is the moment arm for the TA torque, and tr is the rotational time constant for viscous damping, defined as a damping coefficient dr divided by the rotational stiffness kr (Titze, 2006). Similarly, the second-order equation for translational strain εi around the CTJ joint was found to be
| (10) |
where Mt is the mass associated with CTJ translation and tt is the translational time constant for viscous damping.
All the forces Fi in Equations 6 – 8 and forces F4 and F5 in Equations 9 – 10 are governed by two constitutive first-order equations based on the traditional Kelvin model (Fung, 1980),
| (11) |
| (12) |
where Ai is the cross-sectional area of the muscle, Ei is Young’s modulus, εi is the strain in the muscle, tsi is a series time constant, tpi is a parallel time constant, σi is the active internal stress, tai is the internal activation time constant, ai is the normalized activity level (ranging between 0.0 and 1.0), and σai is the active isometric stress (Titze, 2006).
The total strain for vocal fold elongation (or TA elongation) becomes the sum of an adductory strain εa (due to arytenoid cartilage motion on the cricoid cartilage), the rotational strain εr, and the translational vocal fold strain εi,
| (13) |
where εa is the adductory strain yet to be determined.
Determination of the Adductory Strain
With reference to Figure 3, the x-axis is placed at the tip of the vocal process in the cadaveric position, and the y-axis is placed at the midsagittal plane in the glottis. If we define xCAJ and yCAJ to be the coordinates of the center of the CAJ (as measured from the origin of our coordinate system), and if we define to be the cadaveric (resting) x-position of the vocal process, then the x-displacement of the vocal process tip (ξ02) is geometrically defined as
| (14) |
and the y-displacement of the vocal process tip (ψ02) is
| (15) |
It is now possible to define the adductory strain that couples the differential equations in the foregoing sections. Recalling that the vocal process rests at y = 0 for the cadaveric position, the total strain is
| (16) |
The adductory strain εa is now obtained from Equation 16 by substituting ψ02 from Equation 15,
| (17) |
This adductory strain couples the differential equations of motion for adduction and elongation. Since the stress in every tissue of the vocal fold is affected by the overall vocal fold strain ε, this coupling can be very important in vocal fold posturing.
Solution of the Combined Differential Equations
The following is a summary of how the posturing problem is solved:
Define as fourth-order Runge-Kutta dependent variables the forces Fi and active stresses σi (Equations 11 and 12) of all five intrinsic muscles, the vocal ligament, and the vocal fold mucosa. (12 variables in all; the ligament and mucosa do not have active stresses).
Further define as Runge-Kutta dependent variables εr, , εt, , ξa, , ψa, , θa, , (10 variables).
Define the derivatives of all of the above 22 variables as further independent variables, leading to a total of 44 first order differential equations to be solved simultaneously.
Define all the mechanical constants as outlined in the text and in Titze (2006).
Define muscle activations as inputs (constant or time-varying).
Inside the Runge-Kutta loop, calculate all strains and strain rates, the active and passive forces of all muscles, the passive forces of the ligament and mucosa, the stiffnesses, and the first-order derivatives as defined in step three.
Plot the time course of the displacement as desired.
III. RESULTS
A pictorial representation of simulated “effective” two-dimensional posturing is shown in Figure 4. Seven pictures are shown. For each picture, the outside semicircular border is the thyroid cartilage and the paired objects on the inside are the arytenoid cartilages. The black portion is the glottis. The upper left picture is for the cadaveric position (no muscle forces applied). The next five pictures are for 100% contraction of each of the five intrinsic muscles of the larynx in isolation, with the line of action of the muscle force shown by arrows. The bottom picture is for a coordinated vocal fold adduction that involves several muscles simultaneously. Note the CT action pulls the arytenoid cartilages backwards, LCA action “effectively” rotates the tips of the vocal processes towards the glottal midline, PCA action creates the opposite rotation, TA action shortens and adducts the vocal folds, and IA action adducts the posterior glottis.
Figure 4.
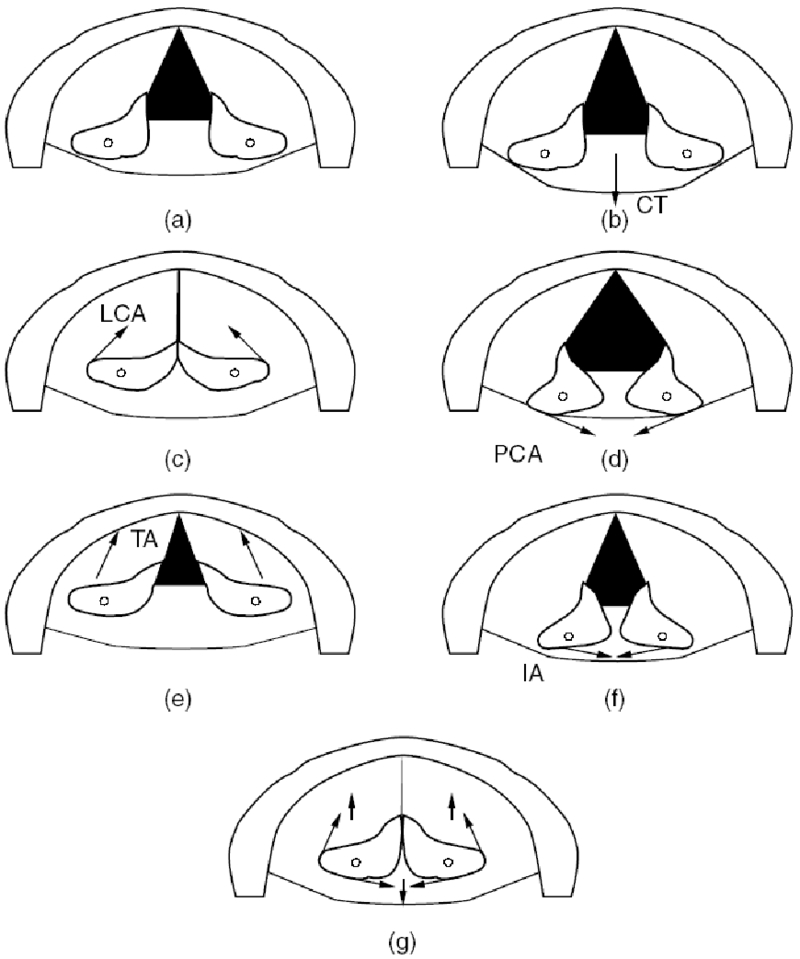
Two-dimensional arytenoid cartilage posturing with specified muscle activations, (a) cadaveric (b) 100% CT, (c) 100% LCA, (e) 100% TA, (f) 100% IA, and (g) 20% CT, 50% LCA, 0% PCA, 20% TA, 90% IA.
Corresponding time variations for the vocal process of the arytenoid cartilage are shown in Figure 5. Part (a) shows the variation of ξ02 and part (b) shows the variation of ψ02. Recall that these are the x and y displacements, respectively, of the tips of the vocal processes of the arytenoid cartilages. Response time from cadaveric position to maximum glottal opening with 100% PCA is 50 ms. Response time from cadaveric position to glottal closure (ξ02 = 0) with 100% LCA is 75 ms.
Figure 5.
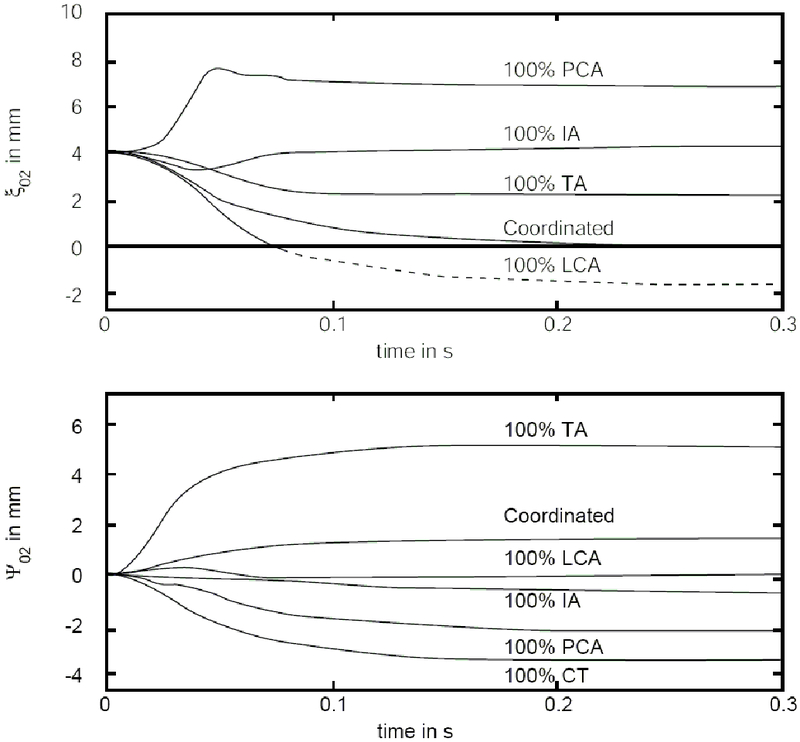
Time course of posturing variables, (a) adduction variable ξ02, and (b) elongation variable ψ02.
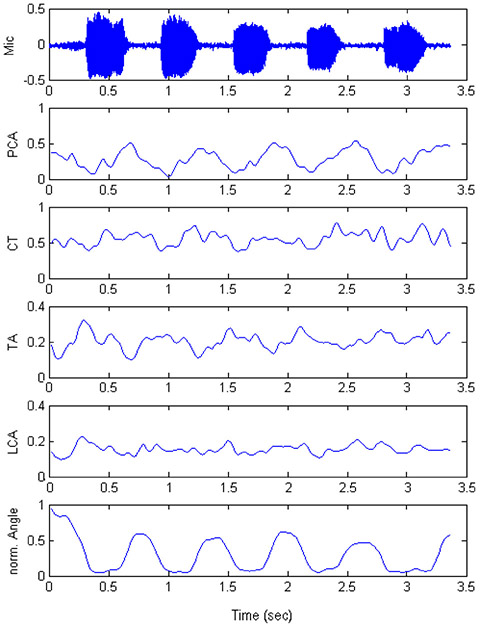
Figure 6 shows measured EMG data from Poletto et al. (2004) for the utterance | hi-hi-hi-hi-hi |. In the top trace we see the microphone signal, followed by the right PCA activity (normalized to 1.0), the right CT activity, the left TA activity, the left LCA activity, and the approximation angle (also normalized to 1.0). Note that the peak of the PCA activity occurs at the beginning of voice offset and that the peaks of TA and LCA activities occur just prior to voice onset. Thus, the adductors TA and LCA toggle with the abductor PCA to produce voicing and devoicing, roughly in equal intervals. For this subject, variation in LCA was less significant than variation in TA. CT activity correlated roughly with PCA activity, suggesting that CT is a mild abductor for devoicing.
Figure 6.
(after Poletto, et al. 2004). Data from production of | hi-hi-hi-hi-hi |. The head mounted microphone is shown in the top row. The following four rows are the rectified and smoothed EMG signals for the four muscles: PCA, CT, TA, and LCA. Normalized glottal angle is shown in the bottom row.
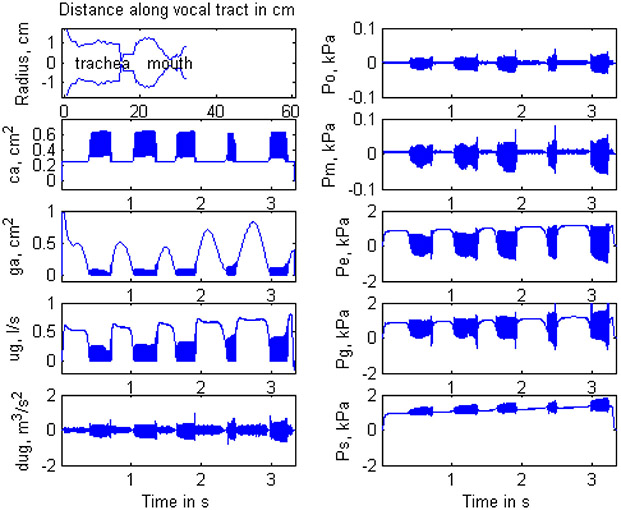
The four EMG signals were introduced as inputs to the 2-D posturing model in an attempt to simulate the utterance | hi-hi-hi-hi-hi |. Computer outputs are shown in Figure 7. On the left panel, from top to bottom, we show the vocal tract configuration for the vowel | i |, followed by vocal fold contact area ca, glottal area ga, glottal flow ug, and glottal flow derivative dug. On the right panel, again from top to bottom, we see oral output pressure Po (the simulated microphone signal corresponding to the top trace of Figure 6), pressure in the mouth Pm (just behind the lips), pressure input to the vocal tract at the epilarynx tube Pe, intraglottal pressure Pg, and subglottal pressure Ps. In the Poletto et al. (2004) data set, no subglottal pressure was reported. We assumed a lung pressure that varied from 1.0 kPa at the beginning of the utterance to 1.5 kPa at the end. This was necessary to maintain voicing in light of a slightly overall rising of PCA from beginning to end and a slight falling of TA from beginning to end. Also, no IA activity was reported by Poletto et al. (2004). We held IA activity constant at 0.35 (35% of maximum) to potentially close the posterior gap.
Figure 7.
Waveform outputs of the simulator. Left column: vocal tract outline, contact area, glottal area ga, flow ug, flow derivative dug. Right column: pressure out Po, pressure behind lips Pm, pressure at epiglottis Pe, pressure at glottis Pg, and subglottal pressure Ps. The upper right is the pressure at the mouth which can be played back as simulated voice (compare to row one of Figure 6).
Note that the simulated glottal area ga in Figure 7 (left panel, in the middle) has a peak value ranging from 0.5 – 0.8 cm2 across the four devoicing periods. Knowing that in our simulation the glottis was triangular and that the glottal length was 1.0 cm, the mean glottal angle at maximum opening ranged from 60° – 80°, comparable to the 60° angle measured by Scherer (1995). Using high-speed endoscopy, Hunter (2001) showed the maximum glottal angle in a repeated sniff-/i/ task to be 51±20° for three subjects. In three studies of the range of motion of the arytenoid (reviewed in Hunter and Titze, 2005), maximum glottal angle (using a 1 cm glottis) can be calculated to be 56±2°. Also in Hunter and Titze, two other models of vocal fold posturing were discussed to underestimate arytenoid motion (a maximum glottal angle of about 33°). Thus, the data presented in this paper are within the range described in the literature, although on the high end.
CONCLUSION
To our knowledge, this study was the first successful attempt to simulate a speech-like utterance with EMG signals as the sole inputs to a biomechanical vocal fold model. The simulation reproduced the dynamic posturing gestures for voicing and devoicing in the utterance | hi-hi-hi-hi-hi |. Both the maximum excursion of the vocal process and the time course of adduction-abduction agreed reasonably well with measured data. The internal mechanical properties of laryngeal muscles (contraction times, maximum active stress, shortening velocity, etc.) were solely responsible for this time course and extent of movement. But it must be reiterated that biomechanical data sets from both human and canine species were used, making the results applicable to humans only to the extent that the canine model is accurate.
We conclude that a two-dimensional model of vocal fold posturing, based entirely on the mechanics of “effective rotation and translation” of cricothyroid and cricoarytenoid joints and contraction of five intrinsic laryngeal muscles, can be used to simulate the dynamics of adduction and abduction in speech. But it requires careful resolution of both force and displacement vectors from 3-D to 2-D with the use of direction cosines, given that the true motion is a rocking rather than gliding and rotating. Also, the “effective 2-D viscoelastic parameters,” such as spring constants and damping ratios, must be viewed as being unique to the 2-D geometry. Further refinements of effective movement arms of the forces, joint stiffnesses, and maximum active forces in the muscles would be helpful to establish more precise ranges of motion and the exact response times for the posturing gestures. More importantly, future 3-D investigations such as the one by Hunter et al. (2004) should address the simultaneity of the dynamics of length change (and corresponding F0 variations) in conjunction with adductory-abductory posturing. This would ultimately make 2-D approaches obsolete and make 3-D models useful in speech simulation.
Acknowledgement
This work was supported by Grant RO1 DC04436 from the National Institute on Deafness and Other Communication Disorders.
REFERENCES
- Berry D, Montequin D, Titze I & Hoffman H (2003). An investigation of cricoarytenoid joint mechanics using simulated muscle forces. J. Voice 17(1), 47–62. [DOI] [PubMed] [Google Scholar]
- Cox K, Alipour F, & Titze I (1999). Geometric structure of the human and canine cricothyroid and thyroarytenoid muscles for biomechanical applications. Annals of Otology, Rhinology & Laryngology, 108(12): 1151–1158. [DOI] [PubMed] [Google Scholar]
- Boone D, McFarlane SC (1994). The voice and voice therapy. (5th ed.). Englewood Cliffs, NJ: Prentice Hall, (Chapter 66). [Google Scholar]
- Cooke A., Ludlow CL, Hallett N, & Selbie WS. (1997). Characteristics of vocal fold adduction related to voice onsets. J. Voice 11 (1):12–22,. [DOI] [PubMed] [Google Scholar]
- Frable MA (1961). Computation of motion at the cricoarytenoid joint. Arch Otolaryngol, 73, 73–78. [DOI] [PubMed] [Google Scholar]
- Fung YC (1981) Biomechanics: Mechanical Properties of Living Tissues. New York: Springer Verlag. [Google Scholar]
- Gallena S,. Smith PJ, Zeffiro T & Ludlow CL. (2001). Effects of levodopa on laryngeal muscle activity for voice onset and offset in Parkinson disease. Journal of Speech, Language, and Hearing Research 44 (6):1284–1299. [DOI] [PubMed] [Google Scholar]
- Hirano M, Vennard W, & Ohala J. (1970). Regulation of register, pitch and intensity of voice: An electromyographic investigation of intrinsic laryngeal muscles. Folia Phoniatr. (Basel) 22 (1):1–20. [DOI] [PubMed] [Google Scholar]
- Honda K (1983). Variability analysis of laryngeal muscle activities In: Vocal fold physiology: biomechanics, acoustics and phonatory control, (Titze IR and Scherer Ronald C., eds) Denver, CO: The Denver Center for the Performing Arts, p. 127–137. [Google Scholar]
- Hunter EJ (2001). “Three-dimensional biomechanical model of vocal fold posturing,” Ph.D. dissertation, University of Iowa. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hunter EJ, Titze IR & Alipour F (2004). A three-dimensional model of vocal fold adduction/abduction. J.Acoust.Soc.Am. 115 (4):1747–1759. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hunter EJ, & Titze IR (2005). Review of range of arytenoid cartilage motion. Acoustic Research Letters Online [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller R (1994). The mechanics of singing: coordinating physiology and acoustics in singing In: Vocal arts medicine: the care and prevention of professional voice disorders. (Benninger M, Jacobson B, Johnson A, eds.). New York: Thieme, (Chapter 62). [Google Scholar]
- Mineck CW, Tayama N, Chan R & Titze IR (2000). Three-dimensional anatomic characterization of the canine laryngeal abductor and adductor musculature. Ann.Otol.Rhinol.Laryngol. 109 (5):505–513. [DOI] [PubMed] [Google Scholar]
- Murry T, Xu Jie Jie & Woodson GE (1998). Glottal configuration associated with fundamental frequency and vocal register. J. Voice 12 (1):44–49. [DOI] [PubMed] [Google Scholar]
- Peters HF, Boves L & van Dielen IC (1986). Perceptual judgment of abruptness of voice onset in vowels as a function of the amplitude envelope. Journal of Speech and Hearing Disorders 51 (4):299–308. [DOI] [PubMed] [Google Scholar]
- Poletto CJ, Verdun LP, Strominger R, & Ludlow CL (2004) Correspondence between laryngeal vocal fold movement and muscle activity during speech and nonspeech gestures. J.Appl.Physiol. 97 (3):858–866. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Selbie WS, Zhang L, Levine WS, & Ludlow CL (1998). Using joint geometry to determine the motion of the cricoarytenoid joint. J. Acoust. Soc. Am, 103, 1115–1127. [DOI] [PubMed] [Google Scholar]
- Selbie WS, Gewalt SL, & Ludlow CL (2002). Developing an anatomical model of the human laryngeal cartilages from magnetic resonance imaging. J. Acoust. Soc. Am, 112 (3 Pt 1), 1077–1090. [DOI] [PubMed] [Google Scholar]
- Sellars IE, Keen EN (1978). The anatomy and movements of the cricoarytenoid joint. The Laryngoscope, 88, 667–674. [DOI] [PubMed] [Google Scholar]
- Scherer R, (1995). Laryngeal function during phonation In: Diagnosis and Treatment of Voice Disorders, edited by Rubin J, Sataloff R, Korovin G, and Gould W, New York: IGAKU-SHOIN, 1995, p. 93–104. [Google Scholar]
- Titze IR, Jiang J & Druker DG (1988). Preliminaries to the body-cover model of pitch control. J.Voice 1 (4):314–319. [Google Scholar]
- Titze IR & Sundberg J (1992). Vocal intensity in speakers and singers. J.Acoust.Soc.Am. 91 (5):2936–2946. [DOI] [PubMed] [Google Scholar]
- Titze IR, Solomon NP, Luschei ES, & Hirano M (1994). Interference between normal vibrato and artificial stimulation of laryngeal muscles at near vibrato rates. J. Voice, 8(3), 215–225. [DOI] [PubMed] [Google Scholar]
- Titze IR (2006). The Myoelastic-Aerodynamic Theory of Phonation. Denver, CO: National Center for Voice and Speech. [Google Scholar]
- Tomori Z, Benacka R & Donic V (1998). Mechanisms and clinicophysiological implications of the sniff- and gasp-like aspiration reflex. Respir.Physiol 114 (1):83–98. [DOI] [PubMed] [Google Scholar]
- Von Leden H, Moore P (1961). The mechanics of the cricoarytenoid joint. Arch Otolaryngol, 73, 63–72. [DOI] [PubMed] [Google Scholar]
- Werner-Kukuk E & von Leden H (1970). Vocal initiation: High speed cinematographic studies on normal subjects. Folia Phoniatr.(Basel) 22 (2):107–116. [PubMed] [Google Scholar]
- Yoshioka H (1981). Laryngeal adjustments in the production of the fricative consonants and devoiced vowels in Japanese. Phonetica 38 (4):236–251. [DOI] [PubMed] [Google Scholar]