Evaluation of the accuracy and precision of the Diffusion parameter EStImation with Gibbs and NoisE Removal pipeline

Abstract

This work evaluates the accuracy and precision of the Diffusion parameter EStImation with Gibbs and NoisE Removal (DESIGNER) pipeline, developed to identify and minimize common sources of methodological variability including: thermal noise, Gibbs ringing artifacts, Rician bias, EPI and eddy current induced spatial distortions, and motion-related artifacts. Following this processing pipeline, iterative parameter estimation techniques were used to derive diffusion parameters of interest based on the diffusion tensor and kurtosis tensor. We evaluated accuracy using a software phantom based on 36 diffusion datasets from the Human Connectome project and tested the precision by analyzing data from 30 healthy volunteers scanned three times within one week. Preprocessing with both DESIGNER or a standard pipeline based on smoothing (instead of noise removal) improved parameter precision by up to a factor of 2 compared to preprocessing with motion correction alone. When evaluating accuracy, we report average decreases in bias (deviation from simulated parameters) over all included regions for fractional anisotropy, mean diffusivity, mean kurtosis, and axonal water fraction of 9.7%, 8.7%, 4.2%, and 7.6% using DESIGNER compared to the standard pipeline, demonstrating that preprocessing with DESIGNER improves accuracy compared to other processing methods.

1. INTRODUCTION

Diffusion MRI (dMRI) is a technique to non-invasively visualize the structure of microstructural tissue properties (Beaulieu, 2002; Jones, 2010; Le Bihan et al., 1986). A common drawback to dMRI, despite its use in clinical applications in brain (Moseley et al., 1990; Warach et al., 1995) and body (Haider et al., 2007; Kiselev, 2017; Koh and Collins, 2007), is the sparse signal relative to noise or artifacts. There is a need for robust dMRI processing pipelines to provide clinicians and researchers with confidence in diffusion outcome measurements. Such a pipeline should adequately identify and correct for thermal noise and for the various imaging artifacts typically present in dMRI, as described here in more detail.

Human dMRI data collected on clinical scanners suffers from low SNR typically due to a combination of strong diffusion gradients and long echo times (TE=60–120ms). The low SNR limits the precision and, albeit less intuitive, the accuracy of diffusion parameter estimators (Aja-Fernandez et al., 2008; Veraart et al., 2011). Improved precision with the same hardware can only be achieved by lengthening the scan time, which is often clinically infeasible since precision increases slowly, as a square root of scan time. Otherwise, increasing SNR can be achieved by lowering the spatial resolution, which results in loss of anatomical detail; by shortening the echo time, which is often not possible due to hardware limitations; or by smoothing, which inherently decreases the effective resolution due to partial volume effects. Furthermore, since the noise level couples with the expected signal due to the generally non-Gaussian nature of the MRI noise in magnitude MR images (Gudbjartsson and Patz, 1995), one needs to employ an accurate noise model either in the parameter estimation framework (Sijbers and den Dekker, 2004) (e.g., maximum likelihood estimators), or correct the signal (e.g., using the method of moments), prior to any parameter fitting (Aja-Fernandez et al., 2008; Koay and Basser, 2006).

In addition to limited SNR, human dMRI data may also suffer from a plethora of particular artifacts that stem from various sources. Long scan times intensify motion-based and physiological artifacts (Le Bihan et al., 2006), strong gradients can cause eddy current artifacts (Andersson and Skare, 2002; Andersson and Sotiropoulos, 2016) and these gradients coupled with magnetic field inhomogeneity and EPI read-out lead to geometric distortions (Andersson et al., 2003). In addition, radio frequency pulse inhomogeneity can lead to spatial signal bias (Smith et al., 2004) and insufficient spatial sampling can cause Gibbs ringing (Barker G, 2001; Tournier et al., 2011; Veraart et al., 2016a). Gibbs ringing artifacts are of particular relevance in dMRI. They are produced when high-contrast boundaries are sampled with an insufficient spatial sampling frequency. This artifact has been identified as the source of inaccuracies in the parameterization of the dMRI data, including negative radial diffusivity or kurtosis values (Perrone et al., 2015; Veraart et al., 2016a), often referred to as the so-called “black voxels” in kurtosis maps (Kellner et al., 2016; Perrone et al., 2015; Veraart et al., 2016a).

To address the need of a processing pipeline that amends the low SNR and artifacts mentioned above, we developed the DESIGNER pipeline to restore the quality and integrity of dMRI data while preserving spatial resolution (Ades-Aron, 2016). The main DESIGNER steps are: (i) MP-PCA denoising (Veraart et al., 2016c) based on identifying Marchenko-Pastur distribution of noise-only principal components. This approach improves SNR (by factor of 2–4) without longer scan time or reduced spatial resolution. (ii) Rician bias correction based on the estimated noise level (Veraart et al., 2016b). (iii) Gibbs correction based on shifting the zero-crossings of the sinc function in k-space (Kellner et al., 2016). (iv) Corrections for EPI distortions, motion, and field inhomogeneity (Smith et al., 2004). (v) Parameter estimation. In this work, this pipeline combines preprocessing and analyses steps in a specific order, and then, as an example, estimates diffusion signal’s cumulants (diffusion and kurtosis tensors), as well as White Matter Tract Integrity (WMTI) metrics (Fieremans et al., 2011) for quantification of the axonal water fraction (AWF). However, this approach is compatible with parameter estimation for any signal representation and/or biophysical model of choice as the last step.

DESIGNER is currently available online in a fully integrated open-source framework implemented in both MatLab (The MathWorks, Inc.) and Python and can be found at: www.github.com/NYU-DiffusionMRI/Diffusion-Kurtosis-Imaging.

The outline of this work is as follows. We first characterize the nature of thermal noise and a number of specific artifacts relevant to dMRI. Next, we show how each component of DESIGNER is tailored to either remove noise, or model and correct artifacts. Finally, we demonstrate the robustness of the pipeline in terms of accuracy relative to an unbiased high-SNR reference dataset and parameter precision in human data.

The accuracy and precision of the DESIGNER pipeline were evaluated using simulated and test-retest dMRI datasets. Accuracy was evaluated by synthesizing a reference dMRI signal based on averaging the dMRI signals from 36 subjects randomly taken from the Human Connectome Project data set. Precision was evaluated in terms of the scan-rescan reproducibility of diffusion metrics in normal human volunteers. We report that the DESIGNER pipeline demonstrated higher accuracy and stability over the standard dMRI analysis approaches as compared to a typical processing pipeline with or without smoothing.

2. METHODS

2.1. DESIGNER pipeline

The flowchart shown in Figure 1 describes the order of operations of DESIGNER and compares it to a typical processing pipeline used in dMRI. The most distinct feature of the designer pipeline is the specificity in image quality improvement, including thermal noise reduction and Gibbs ringing correction. We will show that such targeted approaches outperform more brute force techniques, e.g. spatial smoothing, which are adopted by several dMRI analysis pipelines (Cui et al., 2013; Tabesh et al., 2011).

Figure 1:

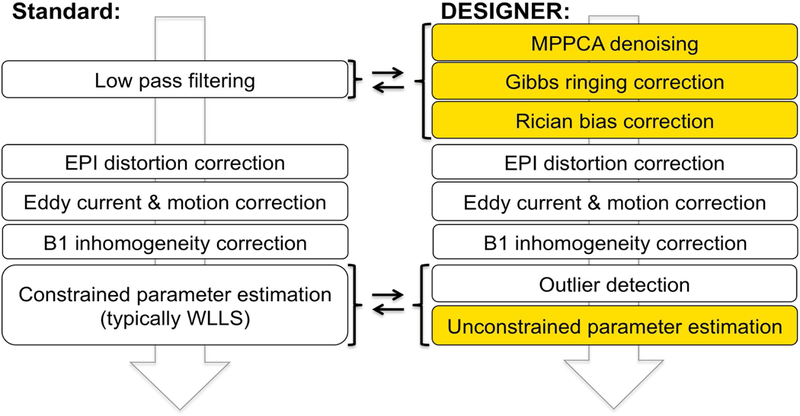
Overview of processing pipelines for dMRI: commonly used (left) and DESIGNER (right). The main difference is that smoothing has been replaced with MP-PCA denoising (by exploiting the redundancy of signal in the dMRI datset), followed by Gibbs artifact correction, and Rician bias correction. These steps (in this order) improve performance of the downstream artifact correction methods such as EPI/eddy distortion and motion corrections, and in our DKI example, can be followed by an unconstrained WLLS DKI fit due to an improved quality of the fit input.

Our basic metric of the efficacy of denoising and Gibbs ringing removal is the power spectrum, E(k) = |ϵ(k)|²/A, of normalized residuals ϵ(x) = (S_post (x) − S_pre (x))/σ within a slice, where S is the original signal, S_post is the post correction signal, S_pre is the pre correction signal, and σ is standard deviation of noise, ϵ(k) = ∫ d²x ϵ(x) e^−ikx, and A is the slice area (the number of voxels). We study this power spectrum as a function of the radial k = |k| within a slice, after angular-averaging over the shell-like bins. For the perfectly spatially-uncorrelated residuals, the power spectrum normalized in this way is a unit line E(k) = 1 for all k. We apply this metric to each step and show results for MPPCA and Gibbs correction steps.

We now describe each pipeline step in detail.

2.1.1. Denoising using MP-PCA

Data is first processed using our recently introduced MP-PCA technique for noise estimation and reduction (Veraart et al., 2016b; Veraart et al., 2016c). This technique is enabled by exploiting data redundancy in the PCA domain using properties of the eigenspectrum of random covariance matrices. It is important that the denoising step is the first stage of the pipeline as it relies on noise being uncorrelated both spatially and among the successive acquisitions (in the dMRI case, in the q-space). Performing this step after processing steps that use interpolation to reconstruct images would result in correlated noise and failure of the basic assumptions underlying the random matrix theory-based approach to PCA denoising. MP-PCA removes only thermal noise without compromising anatomical features, requires about 1 minute processing time for the whole brain, and provided an accurate estimate of the noise level that is needed for Rician bias correction in a later stage. MP-PCA software has been implemented in MatLab (https://www.nitrc.org/projects/mppca/) and as a C++ library function, as part of the open-source MRtrix package (Tournier et al., 2012).

Here, we evaluate the performance of MP-PCA in terms of accuracy and precision, whereby we also investigate the effect of spatial redundancy by selecting different kernel windows and varying SNR-levels, as described below.

2.1.2. Gibbs Ringing Artifact Correction

The MR image is reconstructed from finite sampling of the signal following the inverse Fourier transform. High-contrast boundaries such as the border between CSF and gray/white matter may produce an image artifact in the form of Gibbs rings due to insufficient sampling of the high frequency information. Diffusion parameters are significantly affected by Gibbs ringing, both qualitatively (Barker G, 2001; Perrone et al., 2015) and quantitatively, as our recent analytical calculations show (Veraart et al., 2016a). Consequently, correction techniques like Gegenbauer reconstruction (Amartur and Haacke, 1991) or extrapolation methods (Amartur et al., 1991; Archibald and Gelb, 2002) aim at recovering missing frequencies based on the analytical information available. We apply an alternative approach where the truncation in k-space can be modeled as a convolution with a sinc-function in image space. Hence, the severity of the artifacts depends on how this sinc-function is sampled. The method implemented here re-interpolates the image based on local subvoxel shifts to sample the ringing pattern at the zero-crossings of the oscillating sinc-function (Kellner et al., 2016). This sinc-function is found by computing the total variation in the neighborhood of each voxel in each orthogonal direction in an image defined on a square lattice and computing the shift in voxel position which minimizes the oscillation. The final voxel value is found by interpolating the shifted image based on the original image grid. This way, the artifact can be effectively and robustly removed with a minimal amount of filtering.

2.1.3. Rician Bias Correction

The noise in dMRI images is governed by a Rician or non-central χ distribution that creates a positive bias in low SNR (especially SNR < 2) images (Gudbjartsson and Patz, 1995). This bias may affect the fitting of a diffusion model at high b data (e.g., b ≳ 2000 s/mm²) (Gudbjartsson and Patz, 1995). We use MP-PCA denoising to estimate an unbiased standard deviation σ of the noise at each voxel (Veraart et al., 2016b) from low b (typically, up to b = 1000 s/mm²) data, and use the analytical paradigm described by (Koay and Basser, 2006) to estimate the expected value of true signal voxel intensity η:

$${\eta }^2={\langle M\rangle }^2+(\xi (\theta )-2){\sigma }^2$$

where M is the measured magnitude signal intensity, and ξ(θ) is a correction factor with $\theta \equiv \frac{\eta }{\theta }\equiv SNR$ (Koay and Basser, 2006). At SNR>2, ξ(θ ) goes to 1 and we make use of the approximation: $\eta =\sqrt{{\langle M\rangle }^2-{\sigma }^2}$ to calculate the correct signal intensity.

2.1.4. EPI + Eddy Current and Motion Correction

Strong and rapidly switching diffusion gradient fields cause scaling and shear effects in the phase-encoding direction, as well as image translations that vary with slice position. To account for geometric distortions, eddy currents, and motion artifacts, FSL’s TOPUP (Andersson et al., 2003) and single target eddy (Andersson and Sotiropoulos, 2016) are used to model slice dependent geometric shearing, and correct for motion differences by registering to a high SNR b = 0 image respectively. DESIGNER improves the accuracy of EPI and eddy current correction by preceding this correction with MP-PCA denoising. Here, we evaluate the extent of accuracy improvement in motion correction using two motion correction tools – eddy and TORTOISE (C. Pierpaoli, 2010). The DWI phantom fully described in the next section was used to evaluate the improvement in accuracy in motion correction that results from MPPCA denoising. We generated 6 random sinusoids to add continuous rotation and translation to the phantom, we then added noise at SNR=15 and denoised with MPPCA. Motion correction was performed on the noiseless phantom, noisy phantom, and denoised phantom. The mutual information was computed between each volume of the original phantom and each corresponding volume of the three test datasets.

2.1.5. B₁ Bias Field Correction

The signal intensity of MR image data can be spatially biased due to radiofrequency (RF) field inhomogeneities caused by high-density receiver coils. This is often referred to as a B₁ bias field. This variability in signal through tissue of the same type can affect the tensor fitting to diffusion data. In particular, in the case of multiple b-shell acquisitions spread over different scan series, the inhomogeneity spectrum can vary and propagate major artifacts to model parameters. For each DWI series, we estimate the bias field based on the mean b = 0 image and apply the field correction to all related volumes. This correction is performed using the FAST (Smith et al., 2004; Zhang et al., 2001) tool in FSL.

2.1.6. Outlier Detection

The two types of outlier correction implemented here include the eddy signal dropout (“repol”) tool (Andersson et al., 2016), as well iterative parameter estimation during tensor estimation. least-squares regression models assume that signal variability is due to thermal noise rather than artifacts such as ghosting or chemical shifts. While signal variability produced by thermal noise is approximately Gaussian distributed with SNR > 2, variability produced by artifacts, in general, cannot be modeled. Due to the likely presence of outliers in dMRI data, it is important to use an estimator that is not sensitive to artifacts. The method of outlier detection and rejection (Collier et al., 2015) employs iteratively reweighted linear least-squares (IRWLLS) regression to identify potential outliers, whereby the residuals of the fit determine the weighting applied to the next iteration, ensuring that outlying directions with larger residuals will receive correspondingly lower weights during the estimation of the tensor (Collier et al., 2015).

The steps described here outline the major components of DESIGNER. After the completion of these steps, a model can be fit to signal using a diffusion parameter estimator. Placing positivity constraints on diffusion or kurtosis parameters is a reasonable assumption for most biological applications of dMRI, however the disadvantage is that such constraints inevitably bias the estimated values. In the classical approach, these constraints are required. With DESIGNER, we typically obtain fairly stable and unbiased results even without constraints. In addition, constrained nonlinear fitting is often time consuming, especially as compared with linear fitting for DTI and DKI, and is prone to fitting outlier data points to boundary condition values.

The DESIGNER pipeline provides the advantage of targeting noise and artifacts as separate entities, increasing both accuracy and precision of estimated parameters. We will now describe our methods for evaluating accuracy and precision.

2.2. Accuracy

2.2.1. Diffusion brain software phantom used to assess accuracy

We measured the accuracy of DESIGNER by creating a diffusion brain phantom using data from the Human Connectome Project (Van Essen et al., 2013). 36 dMRI images with voxel size 1.25x1.25x1.25mm³, acquired in a matrix of 145x174x145 were used to create an artificial dMRI brain phantom. These datasets were corrected for EPI and motion artifacts on an individual basis prior to phantom construction.

We first computed the nonlinear warp from a b = 0 image of each dataset to the b = 0 image of a single HCP subject using Elastix (Klein et al., 2010). 6^th order spherical harmonic representations were then computed for b = 1000, 2000, and 3000 s/mm² shells of each dataset and then transformed to a common space by applying the warp computed based on b = 0 images. Spherical harmonics were rotated based on the Jacobian of each warp field in order to keep them correctly aligned after nonlinear transformation. Finally, transformed spherical harmonics for each shell were averaged and projected in 30 unique directions generated by finding the lowest Coulomb energy for 30 repelling charges on a sphere (Jones et al., 1999). This procedure allowed us to generate a new set of dMRI images with the same resolution but much higher SNR by averaging over both subjects and over diffusion directions. High SNR benchmark parametric maps of FA, MD, MK, and AWF were computed for the HCP phantom based on an unconstrained linear least-squares fit.

2.2.2. Evaluating accuracy of DESIGNER on the software phantom

The above software phantom was used as a reference by which to benchmark the efficacy of different steps of DESIGNER. By adding noise with known variance to a ground truth anatomical image, we can directly measure the value and SNR improvement gained after the implementation of each correction routine. Ideally this phantom would have no noise or artifacts that could potentially bias results; however, with 36 HCP datasets, we were able to produce a phantom with at most 1/6 the noise of the individual HCP images and SNR > 100.

Gibbs artifacts were added to the phantom through convolution of the diffusion signal with a sinc-function that has the same frequency as that caused by image truncation in k-space and then down-sampled by a factor of two. 50 realizations of noise at an SNR of 15 were also added to all shells (b = 0, 1000, 2000, 3000 s/mm²) of the phantom dMRI images to simulate thermal noise in 50 independent acquisitions. For all 50 noise realizations of the phantom, images were processed (see Figure 1) by using (A) standard pipeline and (B) DESIGNER and then compared to the high SNR reference values. In addition, we also varied the SNR level from 5 to 50 by injecting Rician noise at varying a into each volume and tested the effect of the window kernel for performing MP-PCA in the posterior limb of the internal capsule (PLIC) by either a) choosing a window of randomly sampled voxels through the whole brain, or b) choosing a window of voxels that belong exclusively to the single anatomic region of interest.

Furthermore, an ROI analysis was performed to test the accuracy of DESIGNER compared to standard pipelines in different white matter regions. For this analysis, the JHU (Hua et al., 2008) white matter atlas was used to delineate different regions. ROI values over the HCP phantom will be compared to the voxel-wise average of 50 noise realizations after processing with both DESIGNER and the standard pipeline.

2.3. Precision

2.3.1. Dataset used to assess to precision

We tested the precision of DESIGNER pipeline by collecting data in N = 30 subjects (22/8 males/females, average age 25.8±6.4 range 18–41 years) who were imaged with MRI three times within a 5-day period. All subjects provided informed consent prior to participation. The study was reviewed and approved by the 59^th Medical Wing, USAF, Institutional Review Board. Commencing seven days prior to the first MRI and continuing throughout the study duration all subjects were alcohol free, drug/medication free, and tobacco free. To minimize diurnal physiological fluctuations, the daily time of repeat scans within the same subject was consistent for all three scans.

The human dMRI was performed on a 3T Trio (Siemens, Erlangen Germany) and consisted of 12 shells of b-values (b = 250, 500, 600, 700, 800, 900, 1000, 1250, 1500, 1750, 2000, 2500 s/mm²; bipolar gradient duration δ = 47 ms, gradient separation Δ = 54 ms), and GRAPPA=2 acceleration. Thirty-two isotropically distributed diffusion-weighted directions were collected per shell, in addition to a total of sixteen b = 0 images. The imaging data were collected using a single-shot, echo-planar, single refocusing spin-echo, diffusion-weighted sequence with a spatial resolution of 1.7x1.7x4.6 mm and seven slices prescribed in sagittal orientation to sample the midsagittal band of the corpus callosum. The sequence control parameters were TE/TR=120/1500 ms with the FOV=200 mm.

2.3.2. Evaluating precision of DESIGNER

Test-retest reproducibility data was used to estimate the precision of the parameter measurements. This dataset pays specific attention to the corpus callosum, which is a white matter tract that has been well studied in diffusion literature. The chosen orientation allowed us to get a clear sample of the genu and splenium of the corpus callosum without needing to worry about confounders like partial volume effects. Due to the unusual acquisition of this dataset, the original reproducibility data was down sampled in q-space to b = 500, 1500, and 2500 s/mm² with 30 directions per shell in order to better represent a typical clinical DKI scanning protocol, although with thick slices to help compensate for long TE and short TR. This data has an SNR of 12–15 at b=0 in brain tissue, comparable to some clinical diffusion protocols. Images were processed (see Figure 1) using both (i) the standard pipeline with a smoothing kernel of 1.25 x the voxel size and constrained tensor fitting, and (ii) DESIGNER.

Parametric maps including FA, MD, MK, and AWF (Fieremans et al., 2011) were computed using an unconstrained fit prior to alignment to the JHU-ICBM-FA-1mm template (Hua et al., 2008) and are used to illustrate the precision of the two pipelines. Technically, AWF derivation from kurtosis tensor was designed only for highly-aligned WM tracts. As applied to the whole brain, it loses its meaning as water fraction inside axons; here, we use this metric merely for the demonstration purpose of model parameter estimation. Not surprisingly, its performance improves, roughly, similarly to that of kurtosis tensor components. The metric used to assess precision is the coefficient of variability: σ_n/μ_n where σ_n is the standard deviation in the n^th parameter over the three time points, and μ_n is its mean over the three time points. CoV can be favorably biased in the case where there are very few samples (Sokal and Rohlf, 1981), in order to compensate for the small number of test-retest datasets, we compute the unbiased $\text{CoV}=\left(1-\frac{1}{4t}\right){\sigma }_t/{\mu }_t$ where t is the sample size.

We registered the three datasets in each subject to the first time-point using the within-subject FA images using a six-degree of freedom rigid body registration using FSL-FLIRT (Smith et al., 2004) software. A nonlinear warp was computed from the FA of each subject to the JHU-ICBM-FA-1mm template (Hua et al., 2008) and applied to the parametric maps. σ_n/μ_n were compared at each voxel of the brain in order to generate variability maps and show which areas in demonstrate comparatively higher precision. For this analysis, the JHU (Hua et al., 2008) white matter atlas was used to delineate different regions in the corpus callosum and FSL-FAST was used to select total CSF, GM, and WM regions in template space. Mean and standard deviation of σ_n/μ_n were measured voxel-wise, over ROIs in the corpus callosum, and over total tissue type ROIs in order to summarize the precision of each pipeline.

3. RESULTS

3.1. Effects of Individual Processing Steps

3.1.1. Denoising using MP-PCA

Figure 3a shows an example axial slice taken from the HCP phantom (with added noise as described in Sec. 2.3.2) through the human brain at b = 1000 s/mm², where the image has been denoised using MP-PCA and using spatial smoothing using a Gaussian kernel (FWHM = 1.25 x 1 voxel for each axis). We found that smoothing partially removes anatomic signal while MP-PCA removes only signal related to thermal noise, which can be seen in the residual maps below. Power spectra of residuals (PSR) normalized to noise variance (Fig. 2) for MPPCA show a constant energy equal to unity for all k meaning that mostly noise is being removed (independently at each k space frequency), however smoothing removes high frequency components of the image giving very large energy spectrum values. It is qualitatively evident that MP-PCA outcomes are less blurred as compared to smoothed images. Residual maps show that the smoothed dataset has lower tissue specificity; the presence of anatomy in residuals of Fig. 3a implies blurring of signal at these locations. It is more difficult to distinguish separate anatomy in the smoothed dataset compared to the denoised dataset because of partial volume effects introduced by the smoothing operation.

Figure 3:

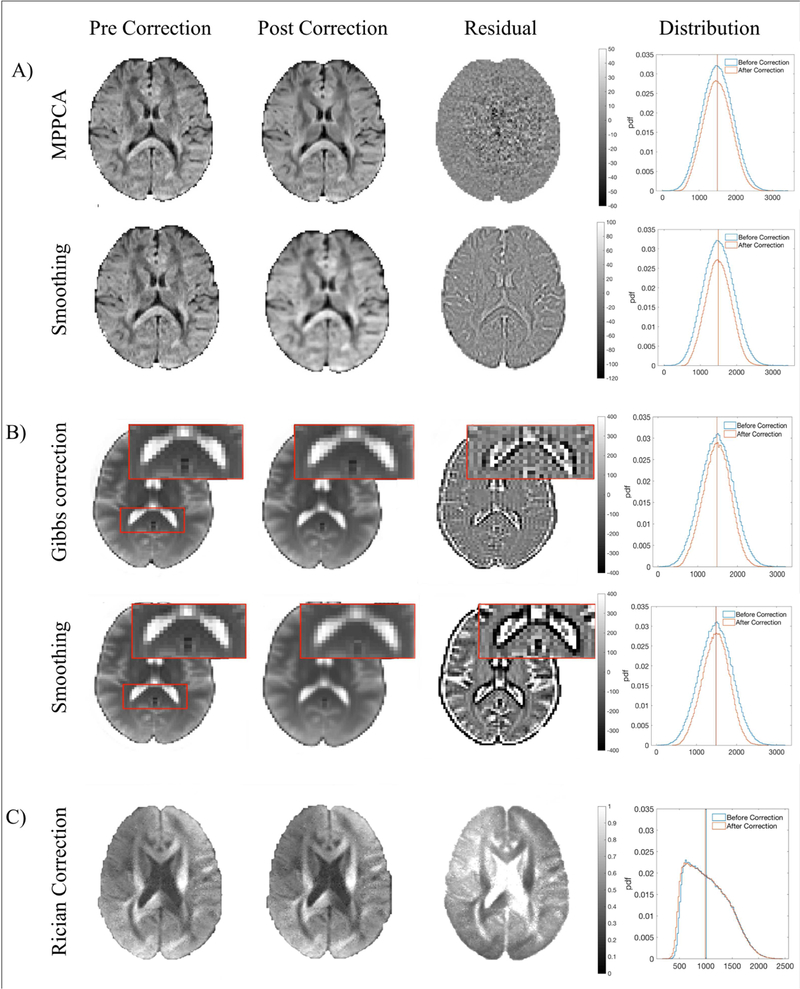
Effects of DESIGNER steps on HCP phantom. A) Effects of MP-PCA denoising (first row) versus smoothing (second row) on a b = 1000 s/mm² image. Residuals show that MP-PCA remove only noise while smoothing removes additional signal. B) Effect of the Gibbs artifact correction on a b = 0 image with Gibbs artifacts evident in in the splenium of the corpus callosum before and after artifact correction, smoothing removes extra anatomy in addition to artifacts. C) Effect of the Rician bias correction on a b = 2000 s/mm² image and the distribution of signal in the posterior limb of the internal capsule before and after correction.

Figure 2:

Energy spectrum of residuals for b = 1000 s/mm² human data that was Processed with DESIGNER. Residual maps were normalized by σ to give unitless energy values, therefore an energy of one implies that only noise with a standard deviation of σ was removed from the original image.

We also compared the noise reduction due to MP-PCA to noise reduction due to fitting a model to the same data. A fit of an exact physical model by maximizing the likelihood of the a priori known data distribution, e.g. Rician, provides the best possible “denoising” and noise bias correction automatically. Figure 4a (left) shows that the distribution of MD values from a set of 1000 voxels randomly selected over the entire brain are the same with and without MP-PCA applied to the data (without introducing any imaging artifacts). Conversely, ROI homogeneity (Fig. 4a, right) allows MP-PCA to sometimes remove more noise than even an ideal model fitting would enable. (In an extreme case of all ROI voxels having the same ground truth parameters, there would be a single informative principal component for the whole ROI, irrespective of the model complexity, and the remaining components carry only the noise, which MP-PCA removes.)

Figure 4:

A) The distribution of MD deviation from the ground truth in an ROI of randomly distributed voxels over the entire brain when denoising is applied prior to fitting and when no denoising is applied, compared to the distribution of MD in an ROI of the PLIC. This example illustrates that a correct signal model/representation works as well as denoising (i.e., in the perfect model case denoising should not yield extra benefit if the fitting is unbiased and no imaging artifacts are introduced). B) Variability of Diffusivity scales linearly with noise variance (PLIC of HCP phantom). The residual variance extrapolated to zero noise level provides an estimate for the inherent biological variability.

We similarly found that MP-PCA denoising of an anatomically coherent region will minimize the variability in diffusivities irrespective of underlying SNR. We found that the number of significant principal components increases from 2 to 6 as phantom SNR increases from 5 to 50 (Figure 4b). We also confirmed that the normalized variance of mean diffusivity estimated from the HCP phantom depends linearly on the added noise variance σ² (i.e., 1/SNR²), in agreement with the Central limit theorem:${\sigma }_D^2={\sigma }_{D,0}^2+\alpha {\sigma }^2$. The slope α is greatest (2.67) for diffusivity estimated without any denoising, equivalent to independent voxel-wise model fit (as discussed above). Any improvement in precision (reduction in α) will be associated with the spatial redundancy. Smoothing captures this redundancy within the local Gaussian kernel, hence its α is notably lower (0.61); however, denoising with MP-PCA reduces α even further to 0.14, by maximizing the spatial redundancy effect.

In addition, we found that by varying the SNR it is possible to isolate biological variability inherent to tissue in the HCP dataset in the PLIC from the variability that comes from added noise. From the intercept value ${\sigma }_{D,0}^2$ (extrapolating ${\sigma }_D^2$ to σ = 0), we found that in the ideal (noise free) phantom data, there is 4.47% relative variability of mean diffusivity in this region. Interestingly, we found 4.7% variability in the same phantom region in MD derived from the original phantom, meaning that the phantom is very close to the ideal noise free scenario.

3.1.2. Gibbs Artifact Correction

PSR for Gibbs correction (Fig. 2) increases along with k, meaning that the correction has an effect primarily in high contrast regions. Residuals depicted in Figure 3b (brain images also from HCP phantom) demonstrate the effect of Gibbs artifact correction. Ideal residuals should show only periodic lines (period = 2 voxels) emanating from the boundaries between tissue types. Even though both the Gibbs correction used here and smoothing effectively remove artifacts, smoothing additionally removes relevant anatomic detail. This is particularly evident in the splenium of the corpus callosum, where ringing originating from the white matter-ventricle boundary causes an overestimation of white-matter intensities that are not smoothed away. Power spectra of residuals in Figure 2 show that minimal additional signal was removed in addition to the high frequency ringing artifacts.

3.1.3. Rician Bias Correction

Power spectrum results for Rician correction exist only at low k, which makes sense since the Rician bias correction shifts intensities of the entire DWI downwards by σ. The effects of Rician bias correction on the HCP phantom and the relevant residual map through the corpus callosum in a b = 2000 s/mm² image are shown in Figure 3c. This correction is most visible as a bias in raw tissue intensity, as illustrated by the histogram of b = 2000 s/mm² intensities in the posterior limb of the internal capsule and the negative shift in signal after bias correction.

3.1.4. EPI + Eddy Current and Motion Correction

PSR values for eddy current and motion correction have a very high amplitude at low frequencies because the operation is performed on the entire image rather than in specific regions. We find increased accuracy of motion correction (particularly at low SNR) using TORTOISE (C. Pierpaoli, 2010) and FSL-eddy (Smith et al., 2004) after data has been denoised. In Supplementary Figure 1 we plot of the mutual information between the HCP phantom and the same phantom after adding rotation, translation, and Rician distributed noise. We performed motion correction and MPPCA denoising on the phantom to measure the dependence of motion correction on image SNR. It is visible from Supplementary Figure 1 that denoising increases the accuracy of motion correction at low b-values (SNR=2.7) by a factor of 2.

3.1.5. Outlier Detection and Correction

Figure 5 shows a b = 1000 s/mm² image containing a ghosting artifact, voxels that were shown to have large residuals during the fit, and a parametric map in which the effect of the artifact has been diminished. The bottom row shows the results of a fit routine using constrained linear least squares (CLLS) regression and how artifacts can potentially corrupt parametric maps if unaccounted. Designer and IRWLLS cleanly removes the ghosting artifact depicted in Fig. 4.

Figure 5:

IRWLLS detection of outlier voxels due to a chemical shift in an example b = 1000 s/mm² image. These voxels are reweighted during fitting to produce the corrected parametric maps.

3.2. Comparison of DESIGNER with Standard Pipelines

3.2.1. Accuracy

We found that DESIGNER provides the most accurate results, particularly in high contrast regions where there exists greater potential for partial volume effects, indicating that processing techniques that include smoothing decrease the overall contrast of diffusion parameters, which may bias the results of statistical analyses.

Figure 6 shows that smoothing tends to bias parametric maps based on histograms of signal over white matter, gray matter, and CSF in the HCP phantom. Parameters derived after processing with DESIGNER hold true to the ground truth signal distribution, and smoothing causes changes in the distribution shape due to partial volume effects. DESIGNER keeps extremely close to the same mean and median values as the ground truth, while other pipelines have large discrepancies. We also show the distribution of parameter values after minimal preprocessing with only EPI and eddy current correction to demonstrate that processing the signal prior to tensor fitting removes the bias caused by thermal fluctuations.

Figure 6:

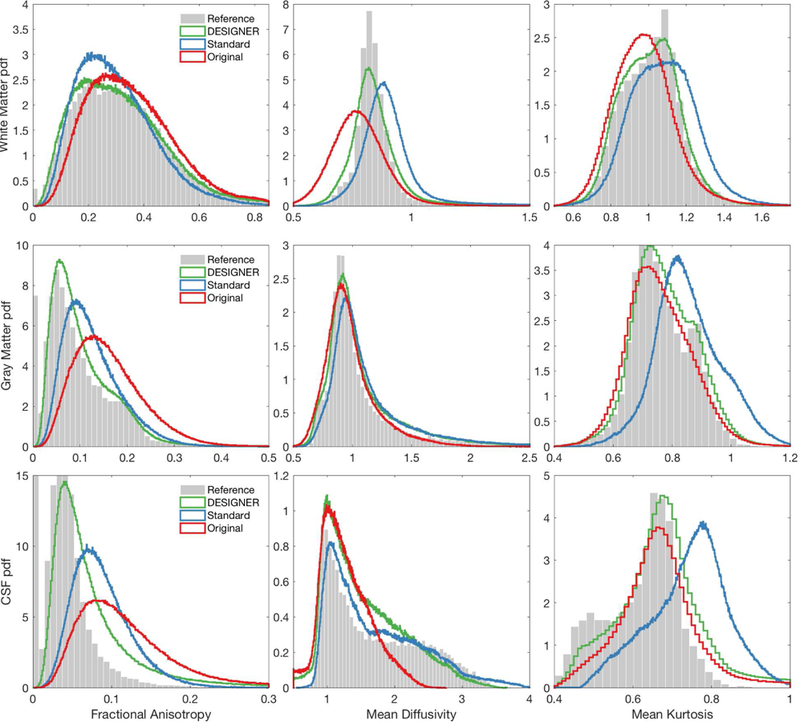
Bias inherent to each pipeline and comparison to the ground truth. These images are based on ROIs of total white matter, gray matter, and CSF of the HCP brain phantom. Histograms are of FA, MD, MK, and AWF from left to right respectively. The distribution of parameters processed with DESIGNER hold more closely to that of the ground truth compared to processing using smoothing or no denoising methods.

Diffusion parameters show decreased contrast when smoothed compared to DESIGNER. Figure 7 shows the decrease in contrast present in FA, MD, MK, and AWF in actual subjects, rather than in the simulated brain phantom. In the zoomed box shown in the figure, the difference in MK is particularly evident.

Figure 7:

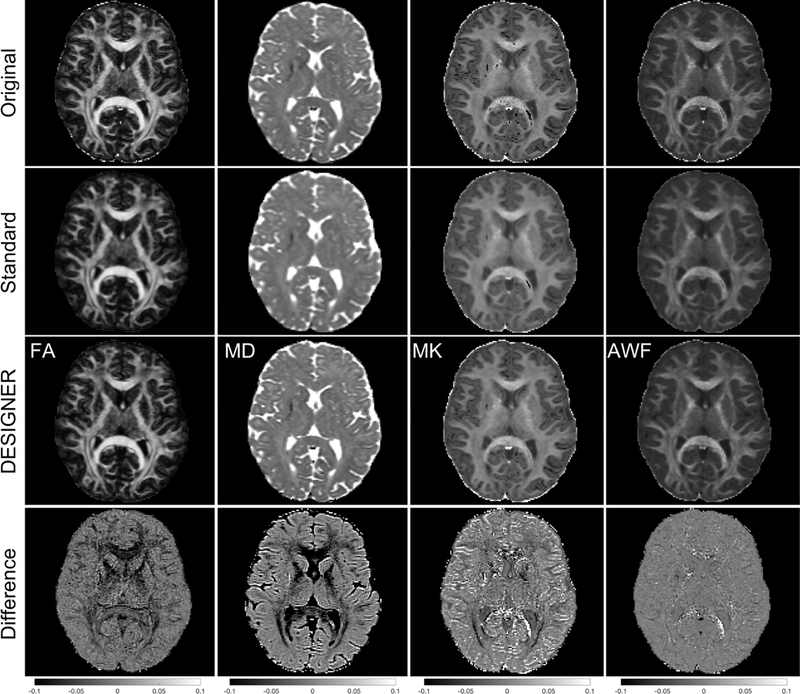
Example, real-subject dataset - difference in contrast for FA, MD, MK, and AWF for DESIGNER, a standard pipeline (eddy current, motion correction, and smoothing), the original pipeline with (eddy current and motion correction), and the difference between DESIGNER and original processing.

Results of an ROI analysis based on JHU-ICBM regions (Hua et al., 2008) indicate that on average, DESIGNER provides more accurate values than the pipeline that uses smoothing. A two-tailed t-test, comparing the mean value of DESIGNER and standard pipeline to that of the ground truth gave corresponding results. FA showed statistical difference from reference data in 0/48 and 42/48 regions with on average 3.36% and 12.84% relative difference from the reference for DESIGNER and standard pipeline, respectively. MD showed statistical difference from reference in 3/48 and 46/48 regions with average 1.56% and 10.22% relative difference from the reference for DESIGNER and standard pipeline, respectively. MK showed statistical difference from reference data in 10/48 and 35/48 regions with on average 1.42% and 5.57% relative difference from the reference for DESIGNER and standard pipeline, respectively. Finally, AWF showed statistical difference from reference data in 9/48 and 43/48 regions with on average 1.65% and 9.22% relative difference from the reference for DESIGNER and standard pipeline, respectively. These data are tabulated in supplementary material, and Figure 8 provides boxplots that show the differences between groups for FA, MD, MK, and AWF.

Figure 8:

Boxplots that show FA, MD, MK, and AWF values in 23 ROIs from the JHU White Matter atlas. ROIs over the left and right hemispheres have been averaged since there are very few differences across hemispheres that pertain to this analysis. Boxplots for HCP phantom data come from an ROI of the original phantom after averaging 50 noise realizations, boxplots of DESIGNER and standard pipelines represent the ROI after preprocessing and averaging over noise realizations.

3.2.2. Precision

The inherent variability of each pipeline is indicated in Figure 9 by voxel-wise mean σ_n/μ_n maps over all 30 subjects in standard space. When no post-processing is applied to raw data, there is up to 40% variability between the three scans, and σ_FA/μ_FA was 22% for the standard pipeline with smoothing, and 20% for DESIGNER. This means that DESIGNER achieves at least as good reproducibility as smoothing with FWHM = 1.25 x 1 voxel, albeit without the loss of anatomical detail, and without parameter biases due to partial volume. We also found that variability in data processed with only EPI and motion correction can be greater than that of DESIGNER by up to a factor of 2. Table 1 shows mean and standard deviation CoV values in gray matter, white matter, and CSF for each diffusion parameter.

Figure 9:

Comparison of mean σ_n/μ_n over all 30 subjects for three cases: From left to right, the images show within subject variability when no processing is applied, when DESIGNER is applied, and when the standard processing pipeline with smoothing (1.25xVS) is applied. The coefficient of variation is lowest in parametric maps processed with DESIGNER compared to processing with both topup+eddy and with smoothing.

Table 1:

Mean and standard deviation σ_n/μ_n values for FA, MD, MK, and AWF over all CSF, white matter, and gray matter, over all sets of subjects. We compare the coefficient of variation in white matter in 4 cases – no smoothing, smoothing at a FWHM of 1.2 x voxel size, smoothing at 1.25 x voxel size, and DESIGNER.

		fa	md	mk	awf
Designer	CSF	0.193 ± 0.165	0.101 ± 0.185	0.097 ± 0.186	0.080 ± 0.147
	WM	0.203 ± 0.143	0.114 ± 0.175	0.100 ± 0.176	0.084 ± 0.108
	GM	0.202 ± 0.142	0.113 ± 0.172	0.100 ± 0.172	0.084 ± 0.106
1.25 X VS	CSF	0.207 ± 0.175	0.141 ± 0.209	0.094 ± 0.193	0.079 ± 0.163
	WM	0.218 ± 0.163	0.167 ± 0.208	0.094 ± 0.181	0.083 ± 0.142
	GM	0.217 ± 0.160	0.168 ± 0.203	0.093 ± 0.177	0.082 ± 0.137
0 X VS	CSF	0.262 ± 0.174	0.164 ± 0.207	0.147 ± 0.231	0.105 ± 0.156
	WM	0.271 ± 0.158	0.188 ± 0.206	0.141 ± 0.218	0.107 ± 0.132
	GM	0.271 ± 0.157	0.189 ± 0.201	0.137 ± 0.214	0.107 ± 0.128

An ROI analysis over local white matter regions found that the CoV varies depending on the white matter regions analyzed. The corpus callosum was found to show the least variability compared to other white matter regions for FA, MD, and AWF, while MK showed greater variability due to the influence of outliers. We found that DESIGNER showed the lowest CoV (fa 0.020 ± 0.057) in the genu compared to smoothing (md 0.021 ± 0.057) and no post-processing md (0.027 ± 0.072) and these results are representative of the whole corpus callosum.

It is expected that a certain degree of smoothing can achieve reduction in the noise that matches that of the MP-PCA denoising. At the same level of precision, the advantage of using DESIGNER is an improved accuracy, as shown in Section 3.2.1.

4. DISCUSSION

The accuracy and precision analyses demonstrate that using DESIGNER to process diffusion images improves the quality of diffusion parameters compared to existing dMRI analysis approaches. DESIGNER maximizes the accuracy of diffusion metrics by modeling and correcting for several artifacts common in diffusion data collected with clinical scanners. When comparing HCP phantom parameters processed using DESIGNER and standard pipelines, we found that DESIGNER helps retain SNR and image contrast comparable to that of the reference values and that spatial smoothing lead to lower contrast. The distribution of FA, MD, MK, and AWF values were most similar to reference values and suffered from fewer outliers (particularly in MK) following DESIGNER processing. Smoothing led to systematic underestimation of FA and overestimation of MD values due to induced partial voluming with gray matter or CSF. Finally, we found in an ROI analysis that even in small white matter regions DESIGNER holds to the same distribution and ground-truth values, while the standard pipeline sees many significant differences. We also observed that pipeline accuracy depends on spatial location in the brain. We used a voxel wise, FWE corrected one-sample t-test to assess differences between the parameters obtained from the noisy versions of the phantom processed with each of the pipelines. We found that pure white matter regions are more accurate independent of pipeline choice, however DESIGNER does the best job preserving parameter accuracy in regions with ambiguous tissue types. These results are shown in Supplementary Figure 3.

DESIGNER maximizes the precision and reliability of DTI, DKI and white matter microstructural modeling parameters by reducing the effect of random noise on parametric maps. We observed that the use of the standard pipeline based on smoothing with 1.25 x voxel size FWHM lead to higher variability and/or lower precision than that of DESIGNER, whereas smoothing with greater than the proposed FWHM had lower variability but also lower anatomic specificity. We also found that variability tends to vary depending on spatial location in brain tissue and on the diffusion parameter in question. The white matter tends to have the most stable CoV values compared to other regions, likely due to spatially varying physiological noise and how tissue is distributed in the brain. In addition to physiological noise, the number of outliers created during tensor estimation and the degree of smoothing affect the magnitude of CoV values, which is one reason why FA (due to eigenvalue repulsion) and MK (low radial diffusivity outlier effects) tend to have higher CoV values. While increasing the amount of smoothing may in principle increase the precision of results without limit, it also results in misleading statistical outcomes. Therefore, any pipeline should be evaluated both with respect to accuracy and precision.

We also show here that the benefits of spatial redundancy depend on the window kernel for MP-PCA denoising. When the underlying data matrix includes different tissue types, such that the underlying tissue parameters within the data matrix are sufficiently different, the lack of spatial redundancy might lower the benefit of the denoising step if the diffusion and noise model are known a priori. Indeed, to take this idea to a logical extreme by applying MP-PCA to a random set of voxels (Fig. 4a left), we see very similar variability between MP-PCA and tensor fitting alone. This is because at b-values in the range of 1000–3000 s/mm², the cumulant expansion (DTI, DKI) provides adequate representation of the signal’s functional form, whereas spatial redundancy is cancelled by the random voxel selection. Alternatively, when denoising is applied on a coherent set of voxels from a local ROI (e.g., PLIC in Fig. 4a right), we see a very strongly decreased variance in the distribution of MD, indicating that we have removed notably more thermal noise than what would have been possible through voxel-wise DTI or DKI tensor fitting alone, with or without MP-PCA applied prior to that. The subsequent steps of DESIGNER applied after MP-PCA denoising benefit greatly from this boost to image SNR (see supplementary Figure 1: increased accuracy in motion correction after MPPCA denoising). Future work might focus on adaptive denoising kernels to fully exploit spatial redundancy, thereby enabling consistently improved precision of parameter estimators such as the maximum likelihood estimator.

In addition to improved accuracy and precision, DESIGNER also improves ther performance of individual artifact correction techniques. In particular, the estimation of motion or distortion parameters is very challenging in case of low SNR and prone to local minima, and residual image misalignments or artifacts will lower the accuracy and precision of diffusion parameter estimators. As shown in supplementary Figure 1, preceding motion correction with the denoising step provides for more stable correction and therefore likely benefits all subsequent processing steps.

DESIGNER is not necessarily tied to diffusion tensor or diffusion kurtosis imaging. We reasonably expect that the reduction of noise and artifacts in DWI datasets will also increase the accuracy and precision of any kind of biophysical model parameter estimation (e.g. based on the recently introduced rotational invariants (Novikov et al., 2018b) as well as estimating parameters of popular signal representations, e.g. based on spherical harmonics, and subsequently the accuracy of fiber tractography results as well. In the future, we intend to show that this pipeline is capable of reducing the amount of spurious fibers generated during tractography.

One limitation of this study is that even though DESIGNER reduces the amount of image smoothing, it is not fully smoothing-free, especially due to steps involving image interpolation which include Gibbs correction and eddy current correction. While it is impossible to avoid all sources of partial volume effects in signal processing, we believe we may have come as close as practically possible. We expect that the DESIGNER pipeline will help bridge the gap between diffusion microstructural imaging and clinical practice, by improving robustness, reproducibility, accuracy and precision, as well as by enabling separation of acquisition/modeling and biological variability (Novikov et al., 2018a). One of the fundamental reasons for the development of DESIGNER is to enable the further clinical feasibility of diffusion imaging in general, and DESIGNER accomplishes this is by boosting confidence in statistical analyses through corresponding confidence in parameter accuracy.

DESIGNER is currently available online and can be found at: www.github.com/NYU-DiffusionMRI/Diffusion-Kurtosis-Imaging/designer (https://www.nitrc.org/projects/mppca/). The current implementation is dependent on MRtrix preprocessing toolbox (Tournier et al., 2012) (v. 3.0, www.mrtrix.org) and FMRIB’s diffusion toolbox (Andersson and Sotiropoulos, 2016) (eddy, FSL v. 5.0.10, www.fmrib.ox.ac.uk/fsl), as well as tensor estimation software (Veraart et al., 2013).

5. CONCLUSIONS

DESIGNER enables the robust estimation of parametric diffusion maps with improved accuracy and without compromising precision compared to standard processing routines based on spatial smoothing. The specific pre-processing steps used in DESIGNER (MP-PCA denoising, Gibbs artifact correction, Rician bias correction, EPI + eddy current and motion correction, IRWLLS fitting) alleviate the need for smoothing. Our results suggest that diffusion parameter estimation benefits most from noise and artifact specific processing techniques, and that further effort should be spent in analyzing specific sources of noise and artifacts in MRI and accounting for them individually, rather than by one-size-fits-all smoothing which potentially damages datasets.