Increased expression diversity buffers the loss of adaptive potential caused by reduction of genetic diversity in new unfavourable environments

Abstract

Mechanisms underlying adaptation to rapid environmental change are issues in evolutionary biology. It is widely accepted that reduction in genetic diversity when suddenly exposed to an unfavourable environment limits the adaptive potential of populations. With growing empirical evidence that expression diversity is likely to increase in the new environment, the role that expression diversity plays in adaptation needs to be theorized. Here, we first established a negative exponential relationship between expression diversity and genetic diversity using a phenomenological differential equation. We then derived a complex trade-off relationship between the changes of expression and genetic diversity, which followed a combination of exponential functions. Furthermore, we found the increase in expression diversity could buffer the loss of adaptive potential as genetic diversity decreased to a certain extent. These theoretical deductions were validated by transcriptomic data of Miscanthus lutarioriparius grown in two experimental fields and supported by good fit and random simulation. These results suggest that increased expression diversity may compensate the loss of genetic diversity and allow the populations to maintain a certain level of phenotypic variation to cope with sudden environmental change. This may buffer the quick diminishing of adaptive potential and consequently increases the change of adaptation to the new environment.

1. Introduction

How life adapts to the environment is one of the most fundamental questions in evolutionary theory [1,2]. More importantly, how life adapts to rapid environmental change is becoming increasingly paramount in the Anthropocene with human activity leading to drastic environmental change [3]. Thus far, the only mechanism known to cause the evolution of adaptations is natural selection acting directly on variation at the genetic and phenotypic levels [4]. Genetic diversity is considered the primary driver responsible for adaptation to new unfavourable environments [1,4]. Though neutral or slightly deleterious alleles [5,6] and cryptic genetic variation [7,8] in the previous environment may facilitate adaptation to the new environment, genetic diversity usually decreased in the new unfavourable environment [9]. With the loss of genetic diversity, population-level phenotypic variation due to phenotypic plasticity [10] or epigenetic modifications [11] may increase in response to environmental changes and may offset the loss of genetic diversity to some extent, thus potentially enhancing the population's ability to adapt to the new environment.

Recent transcriptome techniques indicated that gene expression variation may provide another potential target for natural selection [12,13]. However, the role of expression diversity for early adaptation to rapid environmental change in wild remains unclear. Here, we analysed the RNA-seq data from 80 Miscanthus lutarioriparius individuals from two distinct environments [14]. We first established a theoretical model that describes the relationship between expression diversity and genetic diversity in one environment. Then we used empirical population transcriptomic data to fit the model well in both sites. Finally, we developed a phenomenological buffer hypothesis that the increased expression diversity that governs phenotypes could buffer the loss of adaptive potential due to the reduced genetic diversity.

2. The buffer model of adaptive potential

(a). Theoretical relationship between expression diversity and genetic diversity

To understand the relationship between changes in genetic and expression diversity, we begin by making this theoretical assumption:

$$\frac{\mathrm{d}{E}_d}{\mathrm{d}\pi }=f\hspace{0.17em}(E_d,\pi ),$$ 2.1

where the derivative of expression diversity (E_d) with respect to genetic diversity (π) is considered to be some function of E_d and π once a population is exposed to a new and unfavourable environment. Although it is not possible to capture the exact shape of f(E_d, π) in equation (2.1), it is still safe to assume that f(E_d, π) has two continuous derivatives on $E_d,\pi \in [0,\hspace{0.17em}\mathrm{\infty })$, which can be expanded into a Taylor series about E_d = 0, π = 0. That is, $f\hspace{0.17em}(E_d,\hspace{0.17em}\pi )=f\hspace{0.17em}(0,\hspace{0.17em}0)+f_{E_d}(0,\hspace{0.17em}0)E_d+f_{\pi }(0,\hspace{0.17em}0)\pi +o(E_d,\hspace{0.17em}\pi )$, where o(E_d, π) is the high-order infinitesimal. If we take the first two terms as an approximate, equation (2.1) becomes

$$\frac{\mathrm{d}{E}_d}{\mathrm{d}\pi }=c_1+c_2{E}_d+c_3\pi .$$ 2.2

Solving equation (2.2), we obtain the relationship between E_d and π

$$E_d=a{\mathrm{e}}^{b\pi }+c\pi +d.$$ 2.3

where a, b, c and d are constants.

Here we built up the differential equation (2.1) as a theoretical starting point to deduce the relationship between expression diversity (E_d) and genetic diversity (π). The phenomenological assumption is that the derivative of E_d with respect to π in a site is some function of E_d and π, i.e. f(E_d, π), however, the details of the shape of f(E_d, π) are extremely difficult to establish, likely to vary from one gene to another, and any assumptions regarding its form are ultimately somewhat speculative. We tried to reduce the problem by assuming that f(E_d, π) naturally incorporated the general effect of E_d and π on the change of E_d with changed π, and has two continuous derivatives on E_d and π, respectively. Thus we safely avoided giving the exact shape of f(E_d, π) and made the problem solvable. According to the Taylor expansion which is widely used for linearization of complex issues in equation (2.2), we obtained the theoretical relationship between expression diversity and genetic diversity in equation (2.3).

We fitted the theoretical relationships between E_d and π using population transcriptomic data from 80 M. lutarioriparius individuals grown in the two distinct environments JH (Jiangxia) and QG (Qingyang) (see the electronic supplementary material). Using nonlinear least-squares estimates method, the fitted relationship was derived as $E_{{\hspace{0.17em}}_d}^J=0.52{\mathrm{e}}^{-1435\pi }+0.36$ in JH (R² = 0.367, p < 0.001, figure 1a) and $E_{{\hspace{0.17em}}_d}^Q=0.47{\mathrm{e}}^{-1076\pi }+0.49$ in QG (R² = 0.435, p < 0.001, figure 1b), where $E_d^J\hspace{0.17em}\mathrm{and}\hspace{0.17em}{E}_d^Q$ represent E_d in JH and QG, respectively. Note that all fitted coefficients in the two formulae were significant, except for the coefficients c. These fitting results are satisfactory given the great variation of E_d in real transcriptomic data due to relative high goodness of fit, so support equation (2.3) and its assumption equation (2.1).

Figure 1.

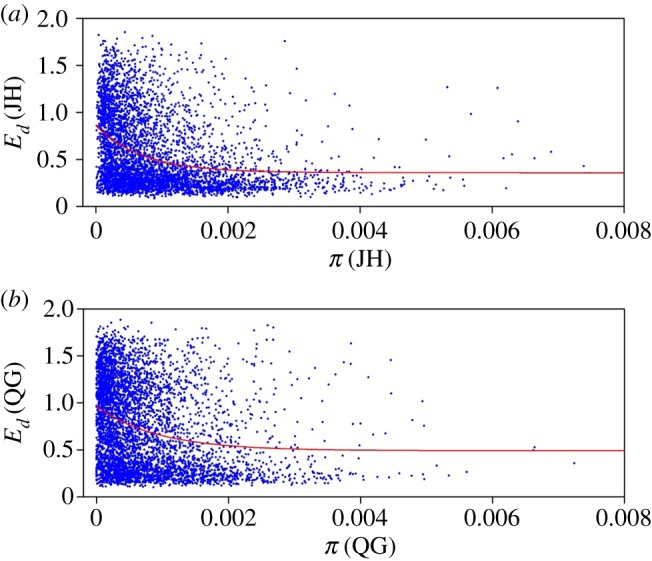
(a) The relationship between genetic diversity and expression diversity for genes with SNPs in the native habitat JH with the fitting formula as $E_{{\hspace{0.17em}}_d}^J=0.52{\mathrm{e}}^{-1435\pi }+0.36$ (R² = 0.367, p < 0.001) and (b) in the new unfavourable site QG with the fitting formula as $E_{{\hspace{0.17em}}_d}^Q=0.47{\mathrm{e}}^{-1076\pi }+0.49$ (R² = 0.435, p < 0.001). (Online version in colour.)

Recent studies have reported reduced expression variation and genetic diversity during the domestication [15,16], which seemed to be in disagreement with our results. In fact, the increase in E_d observed here was at the early stage of adaptation of M. lutarioriparius to the new unfavorable environment rather than the long-term domestication outcome. During the early adaptation, the increase of E_d was most probably as a result of the release of cryptic genetic variation and environmental interactions [17,18]. For example, some alleles may be favoured and the others may be deleterious after initial introduction to the domestic habitat [5].

We then derive the relationship between the change of ΔE_d and Δπ when the population is exposed to the new and unfavourable environment. We calculate $\mathrm{\Delta }{E}_d=E_d^Q-E_d^J=a^Q{\mathrm{e}}^{b^Q\pi }-a^J{\mathrm{e}}^{b^J\pi }+(c^Q-c^Q)\pi +(d^Q-d^J)$. Assuming that π is the linear function of Δπ, $\pi =w_1\mathrm{\Delta }\pi +w_2$, we simplified the ΔE_d formula and obtained

$$\mathrm{\Delta }{E}_d=k_1{\mathrm{e}}^{m\mathrm{\Delta }\pi }+k_2{\mathrm{e}}^{n\mathrm{\Delta }\pi }+k_3\mathrm{\Delta }\pi +k_4,$$ 2.4

where k₁, k₂, k₃, k₄, m and n are constants. We used ΔE_d and Δπ of transcriptomic data in two sites fitted by the nonlinear least-squares estimates method and obtained $\mathrm{\Delta }{E}_d=0.54{\mathrm{e}}^{6897\mathrm{\Delta }\pi }-0.85{\mathrm{e}}^{11782\mathrm{\Delta }\pi }+0.46$ (R² = 0.164, p < 0.01, electronic supplementary material, figure S1). Note that all fitted coefficients in the formula were significant, except for the coefficients k₃. We also used two other methods to prove that equation (2.4) was robust (see the electronic supplementary material, figure S3).

(b). The buffer effect of expression diversity on decrease in genetic diversity

It is widely accepted that the ability of a population to adapt to a new unfavourable environment decreases with the loss of genetic diversity. Assume that the adaptive potential of such a population, F, is a linear function of Δπ, i.e. $F=F_0+h\mathrm{\Delta }\pi$, where F₀ represents the initial adaptability once exposed to the new environment and h is a coefficient and represents the decrease rate of the adaptive potential with the decrease of genetic diversity. Because Δπ is negative, the worse the new environment compared to the native habitat, the bigger or quicker the loss of adaptive potential.

Because gene expression diversity is considered as a potential target of natural selection, we can incorporate ΔE_d into adaptive potential and assume that ΔE_d and Δπ are additive, which gives $F^{\mathrm{\prime }}=F_0+h\mathrm{\Delta }\pi +r\mathrm{\Delta }{E}_d$, where r is a coefficient and represents the increase rate of the adaptive potential with the increase of expression diversity. Owing to the positive ΔE_d and negative Δπ, F′ is larger than F. That is, the decrease in adaptive potential due to the loss of genetic diversity can be slowed down or lessened in degree by the increase in expression diversity during the unfavourable environmental changes. We define this as a buffer effect and formulate it as

$$B=F^{\mathrm{\prime }}-F=(F_0+h\mathrm{\Delta }\pi +r\mathrm{\Delta }{E}_d)-(F_0+h\mathrm{\Delta }\pi )=r\mathrm{\Delta }{E}_d,$$ 2.5

which shows the adaptive potential with E_d could withstand the environmental pressure to some extent for some time such as a cold winter or a dry season. Although the duration of withstanding environmental pressures is limited, expression diversity could buffer the initial decline of adaptive potential and open up novel opportunities for adaptation to the unfavourable environment.

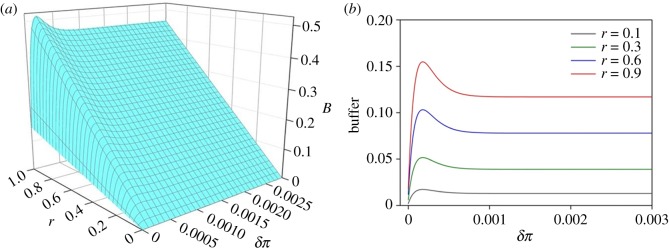
To better depict the buffer effect, we used transcriptomic data to specifically illustrate how the buffer effect explicitly varies with ΔE_d and r. According to equation (2.5) and the fitted ΔE_d formula, we obtained $B=r(0.54{\mathrm{e}}^{6897\mathrm{\Delta }\pi }-0.85{\mathrm{e}}^{11782\mathrm{\Delta }\pi }+0.46)$. By standardizing the coefficient between adaptive potential and the change of E_d, r is set from 0 to 1. Figure 2a showed that the buffer effect will increase with the decrease of π when Δπ is slight. This means that the buffer effect does function with a very small reduced genetic diversity. Second, the buffer effect will descend to and approach the stable value with the decrease of π when Δπ exceeds a certain threshold, which indicates that the buffer ability of expression diversity on adaptive potential is not infinite. Third, the buffer effect will reach its maximum value when Δπ takes a certain value, which means that the buffer may play an essential role in the new unfavourable environment when genetic diversity slightly decreases.

Figure 2.

(a) The relationship between buffer size (B), coefficient (r) and the degree of reduction in genetic diversity (δπ). (b) The buffer size under given parameters of four different coefficients r, i.e. the increase rate of the adaptive potential with the increase of expression diversity. (Online version in colour.)

The coefficient r determined the maximum buffer effects when genetic diversity slightly decreases (figure 2b), which suggested that extreme environments might facilitate a local adapted population to release its adaptive potential [19]. Many studies have demonstrated that the environment encountered affected the level of phenotypic plasticity under selection [20,21]. Though stressful or novel environments are predicted to release cryptic genetic variation, adaptive potential may vary under different environments. A decanalizing effect against environmental perturbation will appear as a positive relationship with environmental variance. This means that the adaptive potential available for adaptation might be correlated with the extent of stress caused by the new unfavourable environment [22].

3. Conclusion

The ability of populations to adapt to rapid environmental change by the combination of climate change and human activity depends on both adaptive genetic and phenotypic responses. However, the extent to which expression diversity contributes to evolutionary potential of wild populations, and the relationship between expression diversity and genetic diversity responses to environmental changes remains unresolved and is a key research priority. This study proposed the buffer hypothesis based on the trade-off between the change of expression diversity and genetic diversity, which seemed to be a possible mechanism of adaptive potential among the genes in the new unfavourable environment. Of course, this is inevitably only a first approximation and does not mean that the buffer processes embodied in the model will necessarily give rise to the patterns of variation of expression and genetic diversity that are observed. If they do not, the fit of model and data suggest that at worst the actual processes are quite well characterized by the buffer hypothesis.

Data accessibility

Population transcriptomic data of Miscanthus lutarioriparius are available from the NCBI sequence read archive (project ID: SRP066219, https://www.ncbi.nlm.nih.gov/bioproject/PRJNA301483).

Authors' contributions

T.S. conceived the ideas and designed the research. W.L. developed the hypothesis and theoretical model. K.L.F. and Q.X. collected and analysed the transcriptomic data with help from C.C.T. and J.Y. W.L. and T.S. wrote the manuscript. K.L.F., Q.X., C.C.T. and J.Y. contributed to manuscript revisions. All authors approved the final version of the manuscript and agree to be accountable for all aspects of the work.

Competing interests

The authors declare no competing interests.

Funding

The work was supported by grants from the Key Research Program of the Chinese Academy of Sciences (KFZD-SW-112-01-08), the National Natural Science Foundation of China (nos. 31400284, 31500186), the National Key Research and Development Program of China (no. 2016YFC0500905), Youth Innovation Promotion Association, CAS (no. Y829281G02), the Project for Autonomous Deployment of the Wuhan Botanical Garden (no. 55Y755271G02).