Abstract
The principles governing the functional organization and development of long-range network interactions in the neocortex remain poorly understood. Using in vivo wide-field and 2-photon calcium imaging of spontaneous activity patterns in mature ferret visual cortex, we find widespread modular correlation patterns that accurately predict the local structure of visually-evoked orientation columns several millimeters away. Longitudinal imaging demonstrates that long-range spontaneous correlations are present early in cortical development prior to the elaboration of horizontal connections, and predict mature network structure. Silencing feed-forward drive through retinal or thalamic blockade does not eliminate early long-range correlated activity, suggesting a cortical origin. Circuit models containing only local, but heterogeneous, connections are sufficient to generate long-range correlated activity by confining activity patterns to a low-dimensional subspace via multi-synaptic short-range interactions. These results suggest that local connections in early cortical circuits can generate structured long-range network correlations that guide the formation of visually-evoked distributed functional networks.
Introduction
The cortical networks that underlie behavior exhibit an orderly functional organization at local and global scales, which is readily evident in the visual cortex of carnivores and primates1–6. Here, neighboring columns of neurons represent the full range of stimulus orientations and contribute to distributed networks spanning several millimeters2,7–11. Anatomical studies that have probed the organization of horizontal connections in visual cortex suggest that network interactions could exhibit considerable functional specificity9–11. But the fine scale structure of network interactions, and the degree to which the activity of a given cortical locus is reliably coupled with the spatiotemporal patterns of activity elsewhere in the network, have yet to be determined. Likewise, the sequence of events that leads to the development of mature network interactions is largely unexplored since these occur at early stages in development when visual stimuli are ineffective in evoking reliable neuronal responses12,13.
Previous studies have suggested that spontaneous activity patterns may be a powerful tool for probing network structure independent of stimulus-imposed organization, and one that is applicable especially early in development14–18. This approach is further supported by the finding that under anesthesia individual spontaneous events can resemble visually-evoked activity patterns for stimuli known to engage distributed functional networks19,20.
We therefore sought to exploit the sensitivity and resolution of in vivo calcium imaging to probe patterns of spontaneous activity in the mature and developing ferret visual cortex. We first show that in the mature cortex, correlated spontaneous activity exhibits precise local and long-range similarities to modular, orientation selective responses. By employing longitudinal imaging in the developing cortex, we next show this long-range correlated activity predicts future evoked responses and is generated within intracortical circuits prior to the emergence of long-range horizontal connectivity. Lastly, we demonstrate that a circuit model containing only local connections is sufficient to generate long-range correlated activity in close agreement with our empirical data. Together, these results demonstrate that patterns of spontaneous activity recapitulate the precise local and global organization of cortical networks activated by visual stimuli, and suggests large-scale network structure arises early in development through local interactions.
Results
Large-scale modular networks revealed by correlated spontaneous activity
In the awake visual cortex imaged near the time of eye-opening, wide-field epifluorescence imaging reveals highly dynamic modular patterns of spontaneous activity that cover millimeters of cortical surface area (Fig. 1a,b; Supplementary Video 1). Spontaneous activity patterns consist of a distributed set of active domains which become active either near simultaneously or in a spatiotemporal sequence spreading across the field of view within a few hundred milliseconds.
Figure 1: Correlated spontaneous activity in awake ferret visual cortex reveals large-scale modular distributed functional networks.
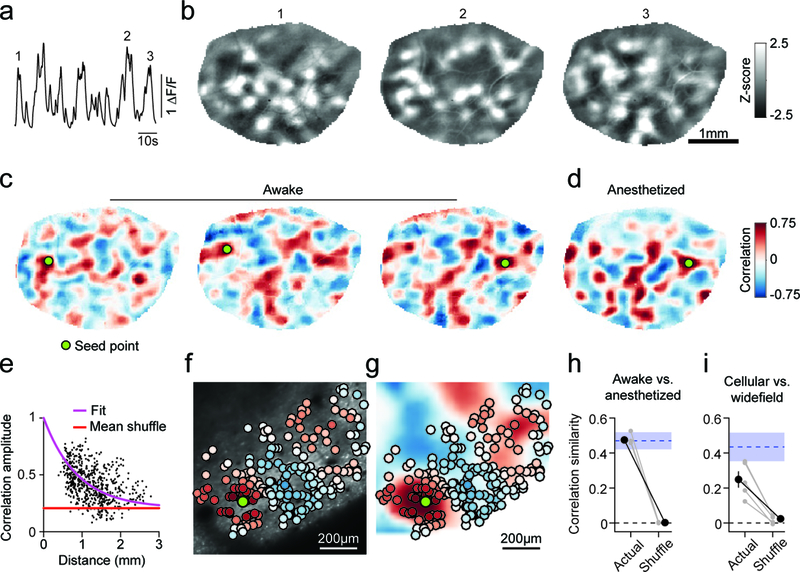
a. Timecourse of spontaneous activity measured with wide-field epifluorescence in an awake ferret (mean across pixels in ROI). b. Representative z-scored images of spontaneous events at times indicated in (a). c. Spontaneous activity correlation patterns (Pearson’s correlation) shown for 3 different seed points (green circle). Correlation patterns span millimeters, can show both rapid changes between nearby seed points (left and middle) and long-range similarity for distant seed points (middle and right). d. Correlation patterns are highly similar in the awake and anesthetized cortex. e. Correlation values at maxima as a function of distance from the seed point showing that correlation amplitude remains strong over long distances. f-g. Spontaneous activity is modular and correlated at the cellular level (f) and shows good correspondence to spontaneous correlations obtained with wide-field imaging (g). h. Correlations measured under anesthesia are statistically similar to those in the awake cortex (n=5, grey: individual animals, black: mean ± SEM). Blue shaded region indicates within-state similarity (mean ± SEM). i. Cellular correlations are significantly similar to wide-field correlations (n=5, grey: individual animals, black: mean ± SEM). Blue region indicates within-modality similarity (mean ± SEM).
The strikingly regular modular structure of spontaneous activity patterns suggests a high degree of correlation in the activity of neurons making up this distributed network. To evaluate this correlation structure, we first detected individual large-scale spontaneous events within ongoing spontaneous activity (see Methods), which occurred frequently in the awake cortex (inter-event interval: 2.13 (1.33 – 6.53) seconds; duration 1.13 (0.73 – 1.73) seconds; median and IQR; n=5 animals, Supplementary Fig. 1a,b). The spatial structure of activity was relatively stable with minor fluctuations over the course of an event, and exhibited frame-to-frame cross-correlations near 0.5 for a two-second window centered on the peak activity (Supplementary Fig. 2). The frequency and duration of spontaneous events is reminiscent of synchronous states observed in LFP recordings from awake animals, appearing distinct from both the desynchronized activity often observed during active attention, as well as the oscillatory activity seen in slow-wave sleep and with certain types of anesthesia21.
Spontaneous activity correlation patterns were then computed from detected events by choosing a given seed point and computing its correlation in spontaneous activity with the remaining locations within the field of view. Correlation patterns for a given seed point show a striking widespread modular organization, with patches of positively correlated activity separated by patches of negatively correlated activity (Fig. 1c). Correlation patterns exhibited significant long-range structure, with statistically significant correlations persisting for more than 2 mm (Fig. 1e; p<0.01 vs. surrogate for example shown, p<0.01 for 10 of 10 animals imaged following eye-opening). The consistency of the correlation patterns is evident in the fact that nearby seed points placed in regions that are negatively correlated exhibit dramatically different spatial correlation patterns (Fig. 1c, left and middle), while seed points placed millimeters away in regions that are positively correlated show quite similar spatial correlation patterns (Fig. 1c, middle and right). Moving the seed point across the cortical surface revealed a large diversity of correlation patterns (Supplementary Video 2), consistent with principal component analysis revealing that the overall number of relevant global variance components in spontaneous activity patterns is typically larger than ten (Supplementary Fig. 3; 13±3 PCs required to explain 75% variance, mean ± standard deviation, n=10).
To determine the impact of brain state and anesthesia on the spatial patterns of correlated spontaneous activity, we followed awake imaging sessions with imaging under light anesthesia (0.5–1% isoflurane). Notably, although spontaneous activity in the awake cortex was more dynamic than under anesthesia, (Supplementary Fig. 4a,c; Supplementary Video 3), the spatial patterns of spontaneous activity, both in extent, modularity, and correlation structure were remarkably similar across states (Fig. 1d,h; Supplementary Fig. 4; p=0.031 one-sided Wilcoxon signed-rank test (T+(4)=15, n=5), with 5 of 5 experiments from 3 animals individually significant at p<0.001 vs. shuffle). Given this strong similarity, awake and anesthetized recordings were pooled in subsequent analyses, and anesthetized recordings were performed exclusively in some experiments.
We next performed 2-photon imaging with cellular resolution in conjunction with wide-field imaging in the same animal, finding strong and spatially organized spontaneous activity at the cellular level. The duration of events was similar to that observed with wide-field imaging (0.88 (0.54–1.32) seconds, median and IQR), and within an event the pattern of active cells was largely consistent across time (frame-to-frame correlations >0.5 for one second around the peak frame within an event, p<0.01 vs. random epochs, bootstrap test). Cellular spontaneous events exhibited similar durations to events detected in wide-field data (Supplementary Fig. 1; Supplementary Video 4). bThe modular organization of spontaneous activity and the spatial correlation patterns observed in populations of individual layer 2/3 neurons was well-matched to those found with wide-field imaging, demonstrating that the network structures revealed with wide-field epifluorescence imaging reflect the spatial activity patterns of individual neurons in superficial cortex (Fig. 1f-g, i; p=0.031 one-sided Wilcoxon signed-rank test (T+(4)=15, n=5), with 4 of 5 experiments from 3 animals individually significant at p<0.05 vs. shuffle). Together these results indicate that neurons in layer 2/3 of visual cortex participate in long-range modular networks whose correlation structure appears robust to changes in brain state.
Long-range correlations reflect fine-scale structure of orientation columns
As individual spontaneous events can resemble patterns of activity evoked by oriented stimuli19,20, we sought to determine whether this correlated spontaneous activity, representing an average over many events and therefore potentially revealing the underlying network architecture, accurately reflects the fine-scale structure of modular networks representing stimulus orientation. We first compared the patterns of spontaneous correlations to the spatial layout of visually-evoked orientation domains in animals imaged 5 or more days after eye-opening, when orientation selectivity is robust (Fig. 2a). We observed seed points for which the spontaneous correlation pattern closely matched the layout of orientation domains, even at remote distances from the seed point (Fig. 2b, Supplementary Fig 5, mean similarity of orientation vs. spontaneous: rOP = 0.42 ± 0.03; mean ± SEM; n=8). We also found a significantly weaker but above chance similarity of spontaneous correlations to the ocular dominance map (Supplementary Fig 5, mean similarity of OD vs. spontaneous: rOD = 0.18 ± 0.04; mean ± SEM; n=3; p<0.0001 vs. surrogate for 3 of 3 animals tested; p=0.02, Mann-Whitney). The strong long-range similarity to orientation preference for certain seed points suggests that the orientation tuning at such seed points can be predicted from the tuning at remote locations that are correlated in spontaneous activity. To test this idea, we computed the sum over tuning curves at distant locations weighted by their spontaneous correlation with the seed point and compared this prediction to the seed point’s actual tuning curve (Fig. 2c, top left). Correlated spontaneous activity predicted the preferred orientation in a small circular patch of radius 0.4mm with a high level of accuracy. Notably, orientation predictions remained highly accurate even when only considering correlations in regions more than 2.4 mm away from the circle’s center point (Fig. 2c-f, p<0.0001 vs. surrogate for all exclusion radii, with 8 of 8 individual animals significant at p<0.05 across all exclusion radii), demonstrating a high degree of long-range fidelity in the structure of spontaneously active networks and those evoked through oriented visual stimuli.
Figure 2: Tuning properties can be predicted from correlated network elements several millimeters away.
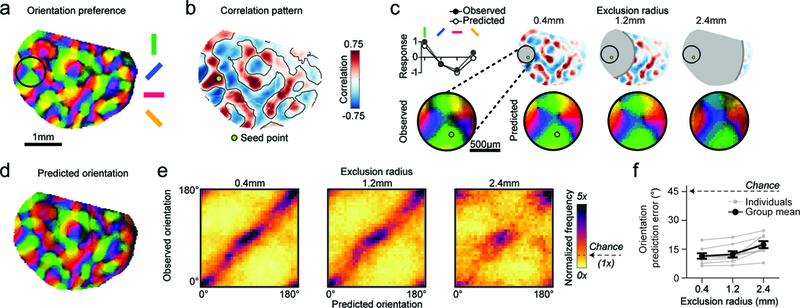
a. Orientation preference map. b. Spontaneous correlation pattern (Pearson’s correlation) for indicated seed point. Contour lines from vertical selective domains from (a) reveal that spontaneous correlations closely resemble the layout of orientation preference map. c. Local orientation tuning for region within black circle in (a) can be accurately predicted from the aggregate orientation tuning of distant cortical locations, weighted by long-range correlations. (Top left) Observed and predicted tuning for single pixel shown below. (Bottom left) Observed orientation tuning. (Right) Accurate orientation predictions based on increasingly distant regions of spontaneous correlations (excluding pixels within either 0.4, 1.2, or 2.4 mm from the seed point). d. The prediction based on correlations >1.2 mm away (excluding all correlations <1.2 mm from seed point) matches the actual preferred orientation within the entire field of view (see (a)). e. Across animals, the precision of predicted orientation tuning remains high, even when based on restricted regions more than 2.4mm away from the site of prediction (see (c)) f. Prediction error as function of exclusion radius (45º is chance level). For e, f: n = 8 animal experiments with 5 days or more of visual experience (gray); group data in f is shown as mean ± SEM (black).
Orientation preference displays pronounced heterogeneity in rate of change across the cortical surface, most notably at pinwheel centers2,7,22; thus a more stringent test of the relation of the spontaneous activity to the fine structure of the orientation map is to ask whether spontaneous correlation patterns exhibit an analogous heterogeneity in their rate of change that correlates with the orientation preference map. Moving the seed point across the cortex shows regions of gradual change in correlation structure punctuated by abrupt shifts in the large-scale pattern (Supplementary Video 2). By computing the rate of change of the correlation pattern as the seed point was moved (see Methods), we observed peaks of large change over relatively small distances (Fig. 3a-b). A systematic mapping across the cortical surface revealed a set of lines, which we termed spontaneous fractures (Fig. 3c). Moving the seed point across any of these fractures led to strong changes in the global correlation pattern, while correlations changed much less when the seed point was moved within the regions between the fractures. Notably, the layout of spontaneous fractures was stable even when only correlations with remote locations (>2.4 mm from seed point) were used to predict the local rate of change (Fig. 3c,f; correlation between fracture patterns for full area vs. >2.4mm: r=0.88±0.04, mean ± SEM, n=8). Strikingly, the layout of spontaneous fractures followed closely the heterogeneity in the rate of change in preferred orientation (Fig. 3d), which also formed an intricate network of lines across the cortical surface, and often both appeared in tight register with one another (Fig. 3e; p = 0.0078, Wilcoxon signed-rank test (T+(7)=35, n=8), with 8 of 8 individual animals significant at p<0.001 vs. shuffle), as highlighted by the positions of pinwheel centers (Fig. 3c,d). Thus spontaneous fractures are local manifestations of dramatic large-scale diversity in distributed network structure and emphasize that both the fine- and large-scale organization of correlated spontaneous activity are precisely matched with the structure of the visually-evoked orientation network.
Figure 3: Tight relation between global spontaneous correlation and fine-scale structure of orientation columns after eye-opening (EO).
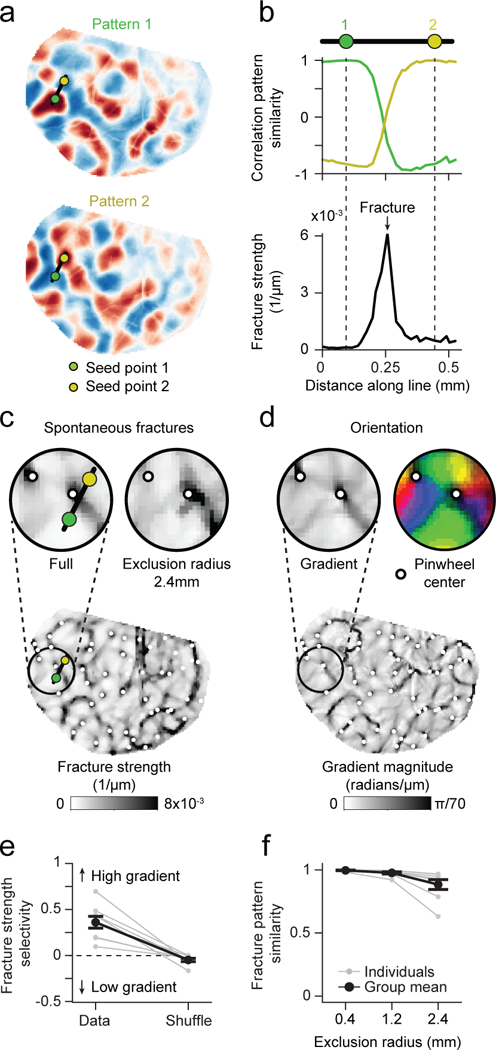
a-b. Fractures in correlated networks. Advancing the seed-point along the black line in (a) reveals a punctuated rapid transition in global correlation structure expressed by a high rate of change in the correlation pattern between adjacent pixels (b, bottom). c. Locations with high rate of change form a set of lines across the cortical surface, which we termed spontaneous fractures. d. The layout of spontaneous fractures precisely coincides with the high-rate of change regions in the orientation preference map. e. Correlation fractures show selectivity for regions of high orientation gradient. f. Fracture location is independent of local correlation structure and remains stable when only long-range correlations are included (see Fig. 2c). For e, f: n = 8 animal experiments with 5 days or more of visual experience (gray); group data in e, f is shown as mean ± SEM (black).
Distributed functional networks exist in the early cortex
Having established that the spontaneous correlation structure faithfully captures key aspects of the distributed networks evoked by visual stimulation, we sought to exploit the correlation structure to gain insights into the nature of these networks at earlier stages of development and determine how they evolve to the mature state. Surprisingly, even at post-natal day 21, 10 days prior to eye opening (and the earliest time point examined), we observed robust spontaneous activity, which exhibited modular patterns that extended for long distances across the cortical surface (Fig. 4a; Supplementary Video 5) and with a temporal structure similar to that found in older animals (Supplementary Fig. 2c-e). Likewise, we found strong correlation patterns that displayed pronounced peaks even several millimeters away from the seed point (Fig. 4b), consistent with electrophysiological recordings23.
Figure 4: Early spontaneous activity exhibits long-range correlations.
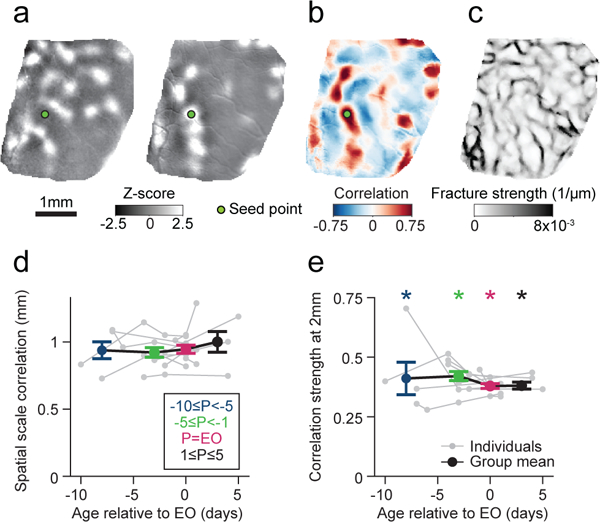
a. Representative z-scored images of early spontaneous activity at P23, seven days prior to EO. b-c. Early spontaneous activity shows hallmarks of mature spontaneous activity, including long-range correlated activity (Pearson’s correlation) (b) and pronounced spontaneous fractures (c). d. The spatial scale of correlations in spontaneous activity (decay constant fit to correlation maxima as function of distance from seed point) is already large early on and changes little across ages. Data points were grouped into four age bins. P denotes postnatal age relative to EO. e. The magnitude of long-range correlations for maxima 2 mm from the seed point is statistically significant at all ages examined (p<0.0001 vs. surrogate data). For d, e: n=10 chronically recorded animals; e: asterisks indicate p<0.0001, actual vs surrogate data; d,e: group data is shown as mean ± SEM.
Indeed, the spatial scale of spontaneous correlations changed marginally with age and already 10 days prior to eye opening it was nearly as large as 5 days after eye opening (Fig. 4d,e; correlation spatial scale: p = 0.86, Kruskal Wallis H-test (Χ2(3)=0.78, n=29); correlation strength at 2 mm: p<0.0001 vs. surrogate for all groups; across groups: p = 0.42, Kruskal Wallis H-test (Χ2(3)=2.82, n=27)). Moreover, spontaneous fractures were already pronounced at the earliest time points, indicating the presence of locally highly organized long-range functional networks in the early cortex (Fig. 4c). These observations are surprising in light of the limited development of long-range horizontal connections at this early age. Anatomical studies in ferret visual cortex show that layer 2/3 pyramidal cell axons exhibit only about two branch points at P2224, extend only up to 1mm from the cell body25, and are still lacking spatial clusters of synaptic terminals, which are distributed across several millimeters in the mature cortex26, but only start to become evident at about P26–2725,27.
Early spontaneous correlations predict mature tuning preference
Our finding that modular activity, long-range correlations, and fractures—all the features that define the modular distributed network—are evident at this early age could suggest that the basic structure of the network may already be similar to its mature state. If so, then we should be able to predict the structure of the mature visually evoked network from the spontaneous activity correlation patterns at these early time points. To test this possibility, we employed chronic recordings starting as early as postnatal day 21, and 10 days prior to eye opening, and mapped all imaging data from each animal onto a common reference frame via an affine transformation, allowing us to track the structure of spontaneous correlations across development (Fig. 5a). We assessed the ability to predict local tuning from remote correlated locations—similar to Fig. 2f, but now applied across age—to predict the visually evoked orientation map from early spontaneous activity. We found that predictions remained fairly accurate up to 5 days prior to eye opening and were above chance even for the youngest age group, showing that even at this early stage, signatures of the future visually-evoked network are apparent (Fig. 5b,c; EO −10 to −5: p<0.0001 vs. surrogate, 4 of 5 individual data points significant vs. surrogate at p<0.05). At the same time, it is clear that there is extensive refinement of the distributed network over this time period (Fig. 5a; Supplementary Fig. 6), such that the ability of the spontaneous correlation patterns to predict the visually-evoked orientation patterns increases significantly with age (Fig. 5c; p=0.0004, Kruskal Wallis H-test (Χ2(3)=18.08, n=31); EO −10 to −5 vs. EO: p=0.004, Wilcoxon rank-sum (U(10)=0.0, n=12)). It is also clear that the refinement during this period involves a rearrangement in the spatial organization of spontaneous fractures (Supplementary Fig. 6c, f).
Figure 5: Spontaneous activity prior to eye-opening predicts future evoked responses.
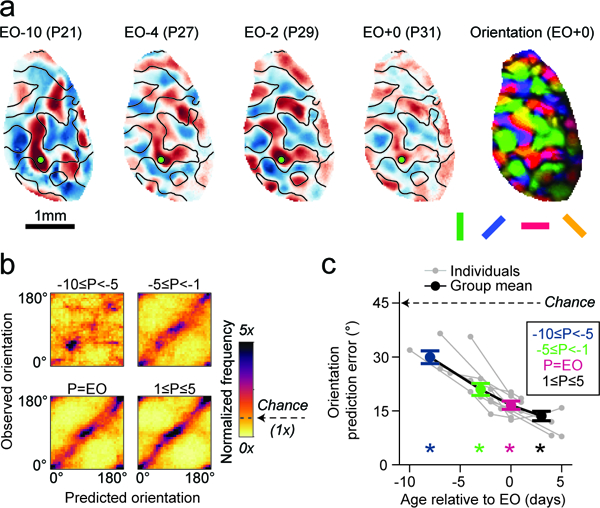
a. Longitudinal imaging of a chronically-implanted animal reveals that early spontaneous correlation patterns exhibit signatures of the mature orientation map (right), despite considerable reorganization in correlation structure. Contour lines indicate horizontal selective domains measured at EO. b. The structure of spontaneous correlations can predict the future mature orientation preference map organization as early as 10 days before eye opening. c. Spontaneous correlation structure predicts orientation preference significantly better than chance, even at the youngest ages examined. For b, c: n=11 chronically recorded animals; c: asterisks indicate p<0.0001, actual vs surrogate data; c: group data is shown as mean ± SEM.
Long-range correlations persist in early cortex despite silencing feed-forward drive
Having demonstrated that modular distributed networks are present prior to the maturation of horizontal connectivity, and predict the system of orientation columns in the mature cortex, we next considered the potential circuit mechanisms capable of generating such large-scale distributed networks in the early cortex. Spontaneous retinal waves are a prominent feature of the developing nervous system28, which exhibit highly organized structure and have been shown to propagate into visual cortex29. To assess a potential contribution of retinal waves to activity patterns in the early cortex, we performed intraocular infusions of TTX, in conjunction with wide-field imaging of spontaneous activity in the cortex. Despite completely abolishing light-evoked responses (response amplitude, pre: 0.357 ± 0.061 ΔF/F, post: 0.023 ± 0.028 ΔF/F, mean ± SEM, bootstrap test vs. baseline: pre-inactivation: p<0.008, post: 0.365, n=3, P22–25), we continued to observe large-scale spontaneous events, and the spatial correlation structure was significantly more similar to the pre-inactivation structure than would be expected by chance (Supplementary Fig. 7, similarity vs. shuffle, p<0.001 for 3 of 3 animals, bootstrap test).
To address the possibility that coordinated thalamic activity drives large-scale correlations in the early cortex30, we infused muscimol into the LGN to silence feed-forward inputs to the cortex at P22–25 (Fig. 6a). Muscimol completely blocked light-evoked responses (Fig. 6b, response amplitude, pre: 0.720±0.105, post: 0.005±0.006, mean ± SEM, bootstrap test vs. baseline: pre-inactivation: p=0.0087, post: p=0.2584, n=3), and dramatically decreased the frequency of spontaneous events in the cortex (Fig. 6c, < 1 event / minute, with a 713 ± 82 % increase in the inter-event-interval, mean ± SEM, n=3). However, the events remaining after geniculate inactivation still showed widespread modular activity patterns spanning millimeters, and exhibited spatial correlation structures similar to those observed prior to inactivation (Fig. 6d-f, similarity vs. shuffle: p<0.001 for 3 of 3 individual experiments, bootstrap test), consistent with prior experiments where silencing was induced via optic nerve transection23. In addition, we find that the spatial layout of correlation fractures is also similar following LGN inactivation (fracture similarity: 0.164 ± 0.015, p=0.04, bootstrap test, n=3 animals), suggesting that the fine-scale structure of correlation patterns is also generated within cortical circuits. Notably, the spatial extent of correlations was unchanged following muscimol (Fig. 6g, control: 1.04 ± 0.12; inactivation: 1.13 ± 0.20 mm, mean ± SEM), demonstrating that feedforward drive cannot account for the spatial structure and extent of correlated spontaneous activity in the early cortex. These results suggest that the modular, large-scale distributed networks present in the early visual cortex are intrinsically generated within cortical circuits, rather than being inherited from feed-forward pathways.
Figure 6: Long-range correlations in spontaneous activity persist in the absence of feed-forward input.
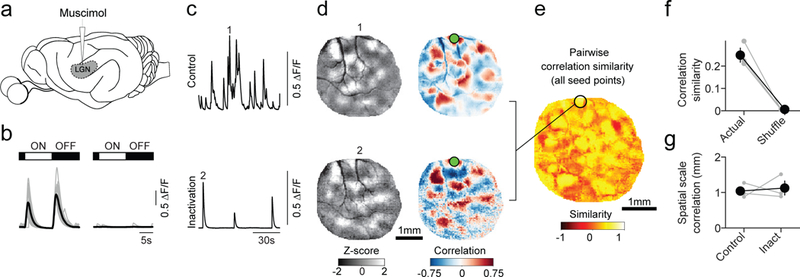
a. Cortical spontaneous activity was measured before and following LGN inactivation via targeted muscimol infusion. b. Cortical responses (averaged across all pixels in ROI) to full-field luminance changes before (left) and after (right) LGN inactivation. Scale bars: 5 sec, 0.5 ΔF/F. c. Time-course of spontaneous activity for mean of all pixels before (top) and after (bottom) inactivation. Scale bars: 30 sec, 0.5 ΔF/F. d. Representative spontaneous events (left) and correlation patterns (Pearson’s correlation) (right) before (top) and after (bottom) inactivation. e. Similarity of correlation structure in representative experiment before and after inactivation for all cortical locations. f. Correlation structure was significantly more similar before and after inactivation than shuffled data (p<0.001 vs. shuffle, for 3 of 3 individual experiments, n=3 animals, bootstrap test). Error bars: mean ± SEM. g. The spatial scale of spontaneous correlations remains long-range following LGN inactivation (n=3 animals). Error bars: mean ± SEM. Scale bars: 1 mm (d,e).
Heterogeneous circuit models produce large-scale organization from local connections
However, as these large-scale cortical networks are present prior to the maturation and elaboration of long-range horizontal connectivity, these results also present a conundrum. To explore how a developing cortex lacking long-range connectivity could generate long-range correlated patterns of activity, we examined dynamical network models of firing rate units31, variants of which have been used previously to model spontaneous activity in the mature visual cortex32–35. In such models, modular patterns of activity can form via lateral suppression and local facilitation. Such an interaction is often assumed to result from lateral connections that are identical at each position in cortex, circularly symmetric, and follow a ‘Mexican-hat’ profile36,37. However, despite producing modular patterns of activity, the resulting patterns produced by such connectivity exhibit an unrealistic regular hexagonal structure (Supplementary Fig. 8). Furthermore, due to the symmetries of this connectivity, sampled activity patterns produce correlation patterns that are nearly identical across seed points and decay more rapidly with distance, failing to show long-range structure (Supplementary Fig. 8) and correlation fractures (see below), indicating that this mechanism alone cannot account for the widespread and diverse correlation patterns we observe in vivo.
Instead the rich structural diversity observed in empirical correlation patterns suggests that local network interactions might not be homogeneous across cortex. Moreover, if local connections vary, this can bias the interactions between nearby domains, such that some show a stronger tendency to be co-active than others. Such biases can propagate across the network via multi-synaptic connections and induce correlations even between remote locations (Fig. 7a). Thus, local, but heterogeneous synaptic connections may ‘channel’ the spread of activity across cortex, potentially explaining the pronounced correlations found between remote network elements.
Figure 7: Circuit mechanisms for long-range correlations in early visual cortex.
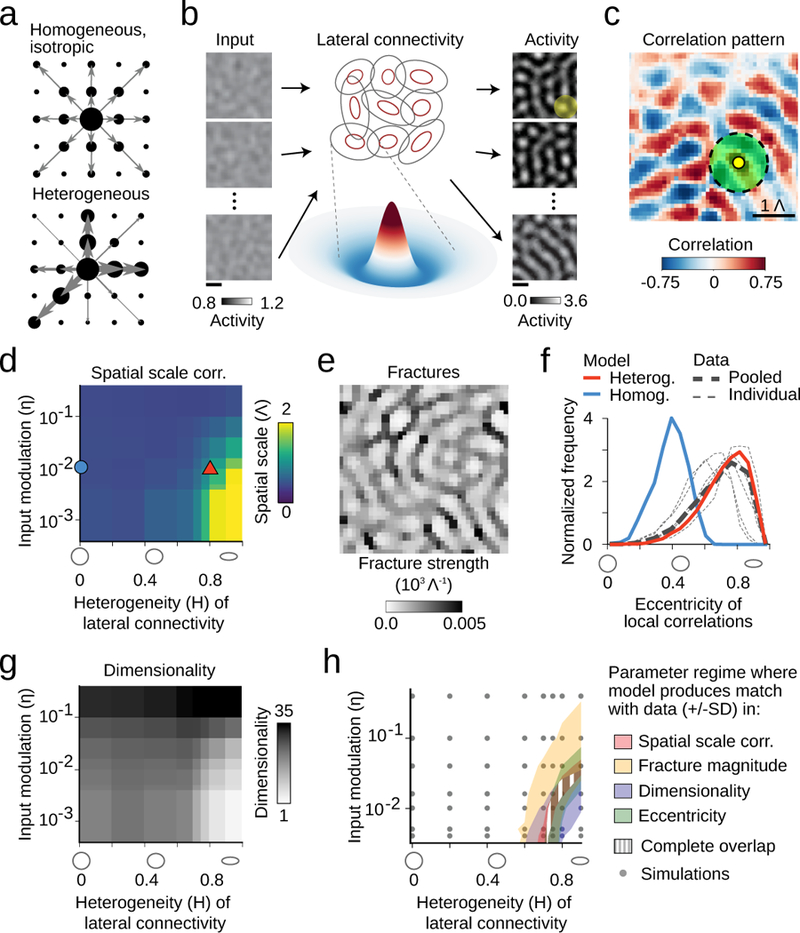
a. Homogenous local connections (arrow) induce moderate correlations (black dots) with all nearby domains (black dots), whereas heterogeneity introduces biases, strengthening some correlations (large dots) more than others (small dots). b. A dynamical circuit model of spontaneous activity in the early cortex: a constant input modulated spatially by filtered noise is fed into a recurrent network with short-range, heterogeneous Mexican-hat (MH) connectivity. It produces a set of modular output patterns with typical spatial scale Λ determined by the MH size (average MH size (2SD of its negative part) illustrated by the green circle). c. In the heterogeneous regime, the model shows long-range correlations in agreement with experiment (heterogeneity H=0.8; input modulation (SD of noise component) η=0.01; n=100 output patterns, 16% of modelled region shown) (top). d. The spatial scale of correlations increases with increasing heterogeneity in the lateral connections and also with decreasing input modulation. Red triangle in (d): parameters used in (c). Blue circle in (d): isotropic, homogeneous connectivity, inconsistent with the range of correlations in experiment (compare d, and Fig. 4d and Supplementary Fig. 8). e. Pronounced fracture pattern in the heterogeneous regime (same parameters as in c). f. Match of empirical data to model predictions of local correlation eccentricity (same parameters as in c). g. Dimensionality of n=100 output patterns produced by the model decreases with increasing heterogeneity and decreasing input modulation. h. In the parameter regime where the model spontaneous patterns approach the empirically observed dimensionality, their short- and long-range correlation structure is in quantitative agreement with the experimental data. Shaded regions show parameter regimes in the model in which different properties lie within the range (mean ± SD) of the experimental values (using 1Λ=1 mm, linear interpolation between simulations). Scale bars: domain spacing 1Λ (b,c,e).
To test the idea that heterogeneous local connections can produce long-range correlations, we modeled cortical spontaneous activity using a dynamical rate network31–35, in which model units (representing a local pool of neurons) receive recurrent input from neighboring units weighted by an anisotropic Mexican-hat function, whose longer axis varies randomly across the cortical surface (Fig. 7b; Methods). To this network, we supplied a constant drive, modulated spatially by a Gaussian random field with only local correlations (Fig. 7b, left; Methods). For sufficiently strong connections, the network activity evolves towards a modular pattern with roughly alternating patches of active and non-active domains (Fig. 7b, right). In the regime of strongly heterogeneous connectivity and moderate input modulation (see Methods, eq. 21), the model produces pronounced long-range correlations (Fig. 7c-d; Supplementary Fig. 9a,b) and correlation fractures (Fig. 7e, Supplementary Fig. 9c,d), both in quantitative agreement with experiment (Fig. 7h). The model also predicts that the spatial structure of correlated activity should be fairly robust against large changes in input drive strength (Fig. 7g), which is consistent with our empirical observations following the inactivation of the retina and LGN (Fig. 6a-g, Supplementary Fig. 7). In contrast, these properties do not match experimental data if lateral connections are homogeneous and isotropic (Fig. 7f,h, left region in diagram).
If local network connections are actually heterogeneous across cortex, we wondered if this could leave a signature on the local structure of correlated activity, rendering the correlation peak around the seed point anisotropic and variable across space. Indeed, fitting an ellipse to the correlation peak in the model and assessing the degree of eccentricity (Supplementary Fig. 9g; Methods) demonstrates a high degree of anisotropy in the local correlation structure. Notably, our experimental data displays a similar degree of eccentricity in the local correlation peaks and matches closely to the values observed in the heterogeneous model regime (Fig. 7f; Supplementary Fig. 9g,h).
Moreover, if heterogeneous connections constrain the layout of activity patterns then some patterns should occur more frequently while others are suppressed32,33,38, effectively reducing the dimensionality of the space spanned by the patterns. To test this prediction, we assessed the dimensionality of this activity space in both model and experiment (see Methods, eq. 16). We find that whereas when the dimensionality of the input patterns to the model is high (by construction), the dimensionality of the output patterns in the heterogeneous regime is much smaller and similar to experimental data (Fig. 7g, h; Supplementary Fig. 9e,f).
Intriguingly, these results might imply an intimate connection between low dimensionality, long-range correlations, anisotropic local correlations and pronounced fractures. To test this idea, we studied the correlation structure in a minimal statistical model of an ensemble of spatially extended, modular activity patterns that are maximally random, but confined to a subspace of predefined dimensionality k (Supplementary Fig. 10; Methods). Indeed, when the dimensionality is relatively low, this simple statistical model not only produces long-range correlations, but also anisotropic local correlations and a network of pronounced correlation fractures (Supplementary Fig. 10c). These results raise the possibility that low-dimensionality could be an organizing principle that is sufficient to explain the observed features of correlated spontaneous activity. This suggests that any mechanism that reduces the dimensionality of spontaneous activity could have similar effects on its correlation structure, including alternative forms of heterogeneity in connectivity or in cellular properties.
So far we have assumed modular activity patterns are generated by Mexican-hat shaped connectivity. Although there is some evidence for Mexican-hat structures in early ferret visual cortex36, the presence of an anatomical Mexican-hat has yet to be established. To address this, we generated an excitatory / inhibitory two-population model in which the range of lateral excitation exceeds that of inhibition—an arrangement consistent with recordings in mature cortical slices37 (Supplementary Fig. 8; Methods). Consistent with refs. 39,40, we found that a Mexican-hat is not strictly required for the formation of modular patterns, which can arise even if the range of lateral excitation exceeds that of inhibition (Supplementary Fig. 8). Importantly, both the Mexican-hat and the excitatory / inhibitory two-population model show a similar increase in the spatial range of correlations as the heterogeneity in the lateral connections is increased (Supplementary Fig. 11), suggesting that the effects of local heterogeneity depend only weakly on the specific form of network interactions generating modular activity. Thus, our computational models describe a plausible mechanism for how the early cortex, even in the absence of long-range horizontal connections, could produce spontaneous activity that is correlated over large distances.
Discussion
Evidence in support of a fundamental modular structure for distributed network interactions in visual cortex has been derived from previous studies documenting the orientation specificity of long-range horizontal connections9–11, and in the similarity of spontaneous activity imaged with voltage sensitive dye to the modular patterns of activity evoked with grating stimuli19,20. Our analysis of spontaneous activity in mature visual cortex extends these observations by showing the remarkable degree of precision that is evident in the correlated activity of long-range network interactions, such that the activity patterns of small populations of neurons accurately predict the structure of local functional architecture over broad regions of cortex covering millimeters of surface area. Even the finest-scale topographic features of orientation maps—the so-called fractures or pinwheel centers—are accurately reflected in the long-range network interactions evident from correlated spontaneous activity. These results, together with the stability of large-scale correlation patterns across awake and anesthetized states, demonstrates an exceptional degree of functional coherence in cortical networks, a coherence that transcends the columnar scale and likely insures reliable distributed neural representations of sensory input.
Patterns of spontaneous activity also allowed us to characterize the state of distributed network structure early in development. Given the strong association of modular activity patterns with the modular arrangement of long-range horizontal connections in mature cortex9–11, we were surprised to find robust long-range modular patterns of correlated activity as early as 10 days prior to eye opening, when horizontal connections are immature24,25,27. We emphasize that the correlated patterns of activity at this developmental stage are not identical to the patterns found in the mature cortex, instead undergoing significant refinement in this period prior to eye opening. Indeed, developmental changes in the patterns of correlated activity are likely to reflect ongoing maturation of multiple features of circuit organization including the emergence of long-range horizontal connections. Nevertheless, the presence of such long-range modular correlation patterns in the absence of a well-developed horizontal network in layer 2/3 challenges the necessity of long-range monosynaptic connections for generating distributed modular network activity27,41.
Furthermore, our retinal and thalamic inactivation experiments bolster previous work23, and definitively establish that early correlated patterns of spontaneous activity cannot be attributed to patterns of activity arising from retina or LGN. The finding that modular correlation patterns distributed over distances comparable to those found with intact feedforward inputs indicates that immature cortical circuits have the capacity to generate long-range modular patterns. It is important to emphasize that these observations do not rule out a causal role for feedforward inputs in establishing modular cortical network structure. Patterns of retinal and geniculocortical activity could play a critical role in guiding the development of these cortical activity patterns (e.g. 42–44), but they are clearly not required for their expression.
Together, these results present a challenging puzzle: long-range correlated activity in the early cortex is generated through intracortical circuits in the absence of long-range horizontal connectivity. Our dynamical model suggests a powerful solution by showing that long-range correlations can arise as an emergent property in heterogeneous circuits via multi-synaptic short-range interactions that tend to favor certain spatially extended activity patterns at the expense of others. By confining the space of possible large-scale activity patterns to a low-dimensional subspace, long-range order is established in the form of distributed coactive domains, explaining our observation of long-range spontaneous correlations in the early visual cortex. These results also suggest that the high degree of local precision that is evident in mature distributed network interactions could derive from the origin of network structure in early local interactions that seed the subsequent emergence of clustered long-range horizontal connections via Hebbian plasticity mechanisms.
Online Methods
Animals
All experimental procedures were approved by the Max Planck Florida Institute for Neuroscience Institutional Animal Care and Use Committee and were performed in accordance with guidelines from the US National Institutes of Health. 24 female ferret kits were obtained from Marshall Farms and housed with jills on a 16 h light/8 h dark cycle. See Supplementary table 1 for complete list of all animals used in each figure. No statistical methods were used to pre-determine sample sizes, but our sample sizes are similar to those reported in previous publications (e.g. refs 6,13,45).
Viral injections
Viral injections were performed as previously described6,45,46. Briefly we expressed GCaMP6s47 by microinjecting AAV2/1.hSyn.GCaMP6s.WPRE.SV40 (obtained from University of Pennsylvania Vector Core) into visual cortex approximately 6–10 days prior to imaging experiments. Anesthesia was induced with either ketamine (12.5 mg/kg) or isoflurane (4–5%), and maintained with isoflurane (1–2%). Atropine (0.2mg/kg) and bupivacaine were both administered, and animal temperature was maintained at approximately 37°C with a homeothermic heating blanket. Animals were also mechanically ventilated and both heart rate and end-tidal CO2 were monitored throughout the surgery. Using aseptic surgical technique, skin and muscle overlying visual cortex were reflected and a small burr hole was made with a hand-held drill (Fordom Electric Co.). Approximately 1μL of virus contained in a pulled glass pipette was pressure injected into the cortex at two depths (~200 μm and 400 μm below the surface) over 20 minutes using a Nanoject-II (World Precision Instruments). This procedure reliably produced robust and widespread labelling of visual cortex, with GCaMP6 expression typically extending over an area >3 mm in diameter (Supplementary Fig. 12).
Cranial window surgery
To allow repeated access to the same imaging field, chronic cranial windows were implanted in each animal 0–2 days prior to the first imaging session. Animals were anesthetized and prepared for surgery as described above. Using aseptic surgical technique, skin and muscle overlying visual cortex were reflected and a custom-designed metal headplate was implanted over the injected region with MetaBond (Parkell Inc.). Then both a craniotomy (~5mm) and a subsequent durotomy were performed, and the underlying brain stabilized with a 1.4 mm thick 3 mm diameter stacked glass coverslip46. The headplate was hermetically sealed with a stainless steel retaining ring (5/16” internal retaining ring, McMaster-Carr) and glue (VetBond, 3M). Unless the animal was immediately imaged after a cranial window surgery, the imaging headplate was filled with a silicone polymer (Kwik-kast, World Precision Instruments) to protect it between imaging experiments.
Wide-field epifluorescence and two-photon imaging
Wide-field epifluoresence imaging was achieved with a Zyla 5.5 sCMOS camera (Andor) controlled by μManager48. Images were acquired at 15Hz with 4 × 4 binning to yield 640 × 540 pixels. Two-photon imaging was performed with a B-Scope microscope (ThorLabs) driven by a Mai-Tai DeepSee laser (Spectra Physics) at 910 nm. The B-Scope microscope was controlled by ScanImage (Vidreo Technologies) in a resonant-galvo configuration with single-plane images (512 × 512 pixels) being collected at 30 Hz.
In animals imaged after eye opening, phenylephrine (1.25–5%) and tropicamide (0.5%) were applied to the eyes to retract the nictitating membrane and dilate the pupil, and the cornea was protected with regular application of eye drops (Systane Ultra, Alcon Laboratories). The silicon polymer plug overlying the sealed imaging chamber was then gently peeled off. Whenever the imaging quality of the chronic cranial window was found to be suboptimal for imaging, the chamber was opened under aseptic conditions, regrown tissue or neomembrane was removed and a new coverslip was inserted. In some cases, prior to imaging, animals were paralyzed with either vecuronium or pancuronium bromide (0.2 mg/kg/h in lactated Ringer’s, delivered IV).
For imaging experiments in awake animals, animals were habituated to head fixation beginning at least 2 days before imaging. Habituation consisted of exposure to the fixation apparatus for brief periods after which animals were returned to their home cage. For imaging, animals were head fixed and wide-field and two-photon imaging was performed as above. In experiments where both awake and anesthetized imaging were performed, awake imaging was always performed first, followed by anesthesia induction as described above. Awake recordings of spontaneous activity were performed in a darkened room and eye position not monitored.
For anesthetized, longitudinal imaging experiments, anesthesia was induced with either ketamine (12.5 mg/kg) or isoflurane (4–5%), and atropine (0.2mg/kg) was administered. Animals were intubated and ventilated, and an IV catheter was placed in the cephalic vein. In some imaging sessions, it was not possible to catheterize the cephalic vein; in these cases, an IP catheter was inserted. Anesthesia was then maintained with isoflurane (0.5–0.75%).
Following imaging, animals were recovered from anesthesia and returned to their home cages. During recovery, neostigmine was occasionally administered to animals that were paralyzed (0.01–0.1μL/kg per dose).
Visual stimulation
Visual stimuli were delivered on a LCD screen placed approximately 25–30cm in front of the eyes using PsychoPy49. For evoking orientation responses, stimuli were full-field sinusoidal gratings at 100% contrast, at 0.015–0.06 cycles per degree, drifting at 1 or 4 Hz, and presented at each of eight directions of motion, for 5s, repeated 8–16 times. In addition, “blank” stimuli of 0% contrast were also presented. Stimuli were randomly interleaved and were presented for 5s followed by a 5–10s gray screen. Spontaneous activity was recorded in a darkened room, with the visual stimulus set to a black screen.
Analysis software
Data analysis was performed in Python, ImageJ, and Matlab (The Mathworks).
Signal extraction for wide-field epifluorescence imaging
To correct for mild brain movement during imaging (especially in the awake state), we registered each imaging frame by maximizing phase correlation to a common reference frame. Furthermore, all imaging experiments acquired during a single day were registered into one reference frame. The ROI was manually drawn around the cortical region with high and robust visually evoked activity. The baseline F0 for each pixel was obtained by applying a rank-order filter to the raw fluorescence trace with the rank between 15 to 70 and the time window between 10 and 30s (values chosen for each imaging session individually, depending on the strength of spontaneous activity). The rank and time window were chosen such that the baseline followed faithfully the slow trend of the fluorescence activity. The baseline corrected spontaneous activity was calculated as (F-F0)/F0 = ΔF/F0.
The baseline for each pixel for the visually evoked activity was obtained by taking the averaged last 1s of the inter-stimulus interval immediately before stimulus onset. The grating evoked response was then calculated as being the average of the fluorescence ΔF/F0 over the full stimulus period (5s).
Event detection
To detect spontaneously active events, we first determined active pixels on each frame using a pixel-wise threshold set to 4–5 standard deviations above each pixel’s mean value across time. Active pixels not part of a contiguous active region of at least 0.01mm2 were considered ‘inactive’ for the purpose of event detection. Active frames were taken as frames with a spatially extended pattern of activity (>80% of pixels were active). Consecutive active frames were combined into a single event starting with the first high activity frame and then either ending with the last high activity frame or, if present, an activity frame defining a local minimum in the fluorescence activity. In order to assess the spatial pattern of an event, we extracted the maximally active frame for each event, defined as the frame with the highest activity averaged across the ROI. Importantly, calculating the spontaneous correlation patterns (see below) over all frames of all events preserves their spatial structure (Supplementary Fig. 13).
Imaging sessions in which less than 10 spontaneous events were detected were excluded from further analysis. This threshold was chosen based on randomly sampling (with replacement) a varied number of activity patterns, which revealed that spontaneous correlation patterns (see below) for subsamples of >10 events were highly similar (second-order correlation >=0.5) to those obtained from all events (Supplementary Fig. 14).
Spontaneous correlation patterns
To assess the spatial correlation structure of spontaneous activity, we applied a Gaussian spatial high-pass filter (with SD of Gaussian filter kernel shigh=195μm) to the maximally active frame in each event and down-sampled it to 160 × 135 pixels. The resulting patterns, named spontaneous patterns A in the following, were used to compute the spontaneous correlation patterns as the pairwise Pearson’s correlation between all locations x within the ROI and the seed point s
| 1 |
Here the brackets < > denote the average over all events and σx denotes the standard deviation of A over all N events i at location x. Note that the spatial structure of spontaneous activity was already evident without filtering (Supplementary Fig. 15). High-pass filtering allowed us to extract this spatial structure, but our results did not sensitively depend on the filtering. For instance, weaker high-pass filtering using a kernel with shigh=520μm resulted in a highly similar correlation structure (data not shown).
Shuffled control ensemble and surrogate correlation patterns
We compared the real ensemble of spontaneous activity patterns from a given experiment with a control ensemble, obtained by eliminating most of the spatial relationship between the patterns. To this end, all activity patterns were randomly rotated (rotation angle drawn from a uniform distribution between 0° and 360° with a step size of 10°), translated (shifts drawn from a uniform distribution between ±450 μm in increments of 26 μm, independently for x- and y-direction) and reflected (with probability 0.5, independently at the x- and y-axis at the center of the ROI), resulting in an equally large control ensemble with similar statistical properties, but little systematic interrelation between patterns. Surrogate correlation patterns were then computed from these ensembles as described above.
Spatial range of correlations
To assess the spatial range of spontaneous correlations (Figs. 1e and 3d), we identified the local maxima (minimum separation between maxima 800 μm) in the correlation pattern for each seed point and fitted an exponential decay function
| 2 |
to the values of these maxima as a function of distance x to the seed point (Fig. 1e; Supplementary Fig 9a). Here ξ is the decay constant, named ‘spatial scale correlation’ in Fig. 4d and 7c-f. The baseline c0 accounts for spurious correlations due to a finite number of spontaneous patterns and was estimated as the average value at maxima in the surrogate correlation patterns described above.
To assess the statistical significance of long-range correlations ~2 mm from the seed point, we compared the median correlation strength for maxima located 1.8–2.2 mm away against a distribution obtained from 100 surrogate correlation patterns. For individual animals, the p-value was taken as the fraction of median correlation strength values from surrogate data greater than or equal to the median correlation strength for real correlation patterns. For 2 of 12 animals, the statistical significance of long-range correlations could not be assessed, due to insufficient coverage in rotated and translated surrogate activity patterns caused by an irregularly shaped ROI. These animals were excluded from analysis of long-range correlation strength.
Comparison of awake and anesthetized correlations
Correlation similarity across awake and anesthetized states was computed for each seed-point as the Pearson’s correlation coefficient of the spontaneous correlations for that seed point across states. For each seed-point, correlations within 400 μm were excluded from analysis. These “second-order correlations” (shown for each seed point in Supplementary Fig. 4f) were then averaged across all seed points within the ROI. To determine the significance of these second-order correlations across state, we shuffled corresponding seed points across states 1000 times, and again computed correlation similarity. Likewise, to gain an estimate of the expected similarity for a well-matched correlation structure, we computed the similarity of each state to itself. Correlation patterns were first separately computed for half of the detected events, and then the two patterns were compared as above.
Comparison of wide-field and cellular correlations
2-photon images were corrected for in plane motion via a 2D cross correlation-based approach. For awake imaging, periods of excessive motion were discarded and excluded from further analysis. Cellular regions of interest (ROIs) were drawn using custom software (Cell Magic Wand, 50) in ImageJ and imported into Matlab via MIJ 51. Fluorescence was averaged over all pixels in the ROI and traces were converted to ΔF/F06, where the baseline fluorescence, F0, was computed from a filtered fluorescence trace. The raw fluorescence trace was filtered by applying a 60 s median filter, followed by a first-order Butterworth high-pass filter with a cut-off time of 60 s.
To compute spontaneous correlations (Fig. 1f, g), we first identified frames containing spontaneous events, which were defined as frames in which > 30% of imaged neurons exhibited activity > 2 standard deviations above their mean. The stability of activity during an event was computed as the cross-correlation of each frame with the peak activity frame, and was compared to a distribution of 100 randomly chosen intervals of the same length. Cellular activity on all event frames was then Z-scored using the mean and standard deviation of each frame, and correlation patterns for each cell were computed as the pairwise Pearson’s correlation coefficient, using the activity of all neurons on all active frames.
To compare the correlation structure obtained at the cellular level with that obtained via wide-field imaging (Fig. 1g) we first aligned the 2-photon field of view (FOV) to the wide-field image using blood vessel landmarks and applied an affine transformation to obtain the pixel coordinates of each imaged neuron in the wide-field frame of reference. Correlation similarity was obtained as above by computing the second-order correlation between the cellular correlation structure and that of the corresponding wide-field pixels, using all cells >200μm from the seed point. Shuffled second-order correlations were obtained by randomly rotating and translating the 2P FOV within the full wide-field ROI, 1000 times. To estimate the maximum expected degree of similarity, we computed a second-order correlation within the cellular correlation structure itself by determining the similarity of correlation structures computed using only 50% of detected events (dashed line and blue bar in Fig. 1i).
Orientation preference and ocular dominance maps
The orientation preference maps (Fig. 2a, 5a (right)) were calculated based on the trial-averaged responses evoked by binocularly presented moving grating stimuli of eight directions equally spaced between 0 and 360 degree. Responses were Gaussian band-pass filtered (SD: slow=26μm, shigh=195μm) and orientation preference was computed by vector summation:
| 3 |
where wk(x) is the tuning curve at location x, i.e. the trial-averaged response to a moving grating with direction ϕk at location x. The preferred orientation at x is 0.5 arg(z(x)).
Orientation pinwheel centers (Fig 2i, j) were estimated as described in Refs. 52,53. The Matlab routine provided by Schottdorf et al. (Ref. 53). was used. Orientation contour lines (Fig. 2b, 5a) are the zero-levels of the 0°−90° difference map, obtained by using the matplotlib.pyplot.contours routine. Surrogate orientation preference maps were obtained by phase shuffling the original maps in the Fourier domain52.
Ocular dominance maps were calculated based on the trial-averaged responses evoked by presenting moving grating stimuli of eight directions equally spaced between 0 and 360 degree either to the contralateral or ipsilateral eye. The trial averaged response to each orientation and ocular condition was Gaussian band-pass filtered as described above for the orientation map. Contralateral and ipsilateral response maps were computed by respectively averaging together the trial-average responses to the stimuli presented either to the contralateral or ipsilateral eye. The ocular dominance map was computed as a difference of the contralateral and ipsilateral response maps.
Similarity of correlation patterns to the orientation and ocular dominance maps
To quantify how similar patterns of correlated spontaneous activity are to known functional maps in visual cortex, we computed the average pairwise similarity of the spontaneous correlation patterns either to the ocular dominance map or the orientation preference map (Supplementary Fig. 5). The assessment of similarity of each correlation pattern to the ocular dominance map is the magnitude of their pairwise coefficient:
| 4 |
where OD(y) is the ocular dominance map at location y and C(x, y) is the spontaneous correlation pattern between seed location x and location y and corr denotes Pearson’s correlation coefficient. Correspondingly, the similarity of each correlation pattern to the orientation map is computed as the magnitude of the pairwise correlation coefficient to the real and imaginary components of the vector-summed orientation map z:
| 5 |
Prediction analysis and exclusion areas
To test whether orientation tuning can be predicted from the tuning at remote locations with correlated spontaneous activity (Fig. 2c), we estimated the tuning curve at seed point s=(sx,sy) by the sum over tuning curves wk at different locations weighted by their spontaneous correlation C with the seed point:
| 6 |
where k denotes the orientation of the stimulus. The sum was taken over locations x outside a circular area centered at the seed point with radius 0.4, 1.2 or 2.4mm. For this calculation, both wk and C are z-scored. To assess the goodness of the prediction, we calculated the angular difference between the predicted and the actual preferred orientation (Fig. 2f). Low values indicate a high match, whereas 45° indicates chance level.
Statistical significance (Fig. 2f) was determined by repeating this analysis for 100 surrogate orientation preference maps, obtained by phase shuffling in the Fourier domain52. For individual animals, the p-value was taken as the fraction of values equal or smaller than the value for the real orientation map. To pool across animals within an exclusion radius (Fig. 2f), we then generated 10,000 surrogate group medians by randomly drawing from the distributions of surrogate data points (one per animal), and the p-value was taken as the fraction of group medians equal or smaller than the median value for the actual data.
Spontaneous fractures
Fracture strength was defined as the rate by which the correlation pattern changes when changing the seed point location over some small distance (Fig. 3b (bottom), Fig. 3c). It was computed as:
| 7 |
where Fdx (Fdy) denotes the x(y)-component of the rate of change of the correlation pattern at seed point s. We approximated this rate of change by the (second-order) correlation between two correlation patterns with seed points at adjacent pixels a distance d apart:
| 8 |
| 9 |
where corrx denotes Pearson’s correlation coefficient calculated over all locations x and ey is a unit vector in y-direction. The subtraction from 1 in the numerator ensures F=0 at seed point locations, around which the correlation pattern does not change, while high values of F indicate high changes. We used d=26 μm, the spatial resolution of the correlation patterns.
We defined fracture magnitude (Supplementary Fig. 9c,d, Supplementary Fig. 10f (bottom), Supplementary Fig. 11b) as the difference between F, averaged over the fracture lines, and its average in regions >130μm apart from the nearest fracture line. To extract the fracture lines from F we first applied a spatial median filter with a window size of 78μm to remove outliers. We then applied histogram normalization, contrast enhancement by using Contrast Limited Adaptive Histogram Equalization (CLAHE, clip limit=20, size of neighborhood 260×260 μm2), and a spatial high-pass filter (Gaussian filter, SD shigh=390 μm). The resulting values were binarized (threshold=0), and the resulting two-dimensional binary array eroded and then dilated (twice) to remove single not-contiguous pixels. We skeletonized this binary array to obtain the fracture lines.
We quantified the co-alignment between spontaneous fractures and high orientation gradient regions by the fracture selectivity (Fig. 3e), defined as the difference between F at high orientation gradient locations (xhigh, >π/5 radians/pixel) and locations far from high orientation gradients (xlow, >150μm from xhigh):
| 10 |
where the brackets denote average over locations xhigh and low xlow, respectively. A value of FS of 1 indicates co-alignment between the spontaneous fractures and the orientation gradient, whereas a value near 0 indicates no such alignment. To assess significance (Fig. 3e) we repeated this analysis for 1000 surrogate orientation preference maps, obtained by phase shuffling in the Fourier domain. The p-value is the fraction of values equal or larger than the value for the orientation map.
In order to test whether spontaneous fractures reflect the correlation structure over remote distances and not only in their local neighborhood (Fig. 3c (top), Fig. 3f), we computed F as above, but excluding a circular region with radius 0.4, 1.2 or 2.4 mm, centered at the seed point s. We then computed the Pearson’s correlation coefficient with the original F.
Registration for longitudinal imaging
To compare spontaneous correlation patterns across days in longitudinally imaged animals, we transformed all imaging data into a common reference frame (Supplementary Fig. 6a). This transformation corrected for small displacement and expansion of cortical tissue over the imaging period, presumably due to cortical growth. We used an affine transformation, thereby taking into account rotation, scaling, translation and shear mapping of the cortex:
| 11 |
| 12 |
| 13 |
The parameter of the transformation matrix T and of the displacement vector h were found by minimizing the distance between landmarks determined for each day of experiment. Landmarks were found by marking radial blood vessels (i.e. blood vessels oriented orthogonally to the imaging plane) by visual inspection. The following expression was minimized (least square fit) to find transformation parameters from day t to the reference day tref (eye opening):
| 14 |
with N landmarks (between 10 to 30) in both coordinate systems at coordinates xtref,i in the reference coordinate system, and the coordinates xt,i at day t.
Analysis of spontaneous correlation across development
To compare spontaneous correlation patterns across development, we calculated a second-order correlation (Supplementary Fig. 6d,e) between the correlation patterns on a given day and the reference day (eye opening) with the same seed point. Changes in correlation fractures over development were quantified as the second order correlation of fracture patterns (Supplementary Fig. 6f). In both cases, an estimate of the expected degree of similarity was computed by first separately computing correlations and their corresponding fracture patterns for half of the detected events, and then computing the second-order correlations as above.
To determine whether correlation patterns early in development can predict mature orientation preferences (Fig. 5c), we computed orientation tuning predictions as above, using the correlation pattern on a given day to weight tuning curves measured following eye opening, with an exclusion radius of 400 μm. The predicted orientation preference map was compared to the actual map as described above (“Prediction analysis and exclusion areas”) for both individual animals and group medians.
To assess the statistical significance of long-range correlation strength at 2 mm across development, we compared correlation maxima to those of surrogate correlation patterns as described above (“Spatial range of correlations”). To pool across experiments within an age group, we then generated 10,000 surrogate group medians by randomly drawing from the distributions of surrogate data points (one per experiment), and the p-value was taken as the fraction of group medians greater than the median value for the actual data.
Retinal and LGN inactivation experiments
For retinal inactivation experiments, a cranial window was implanted over visual cortex as described above. After imaging spontaneous activity under light isoflurane anesthesia (0.5–1%) as described above, visually evoked responses were recorded in response to full-field luminance steps6. Isoflurane levels were then increased and intraocular infusions of TTX were performed into each eye. For each intraocular injection, a small incision was made just posterior to the scleral margin using the tip of a 30-gauge needle attached to a Hamilton syringe. Each eye was then injected with 2–2.5 μL of 0.75 mM TTX solution (Tocris Bioscience) to reach an intraocular dose of 21.45 μM that is roughly comparable the dosage used previously in the ferret54. Following infusion of TTX, isoflurane levels were reduced, and the animal returned to a stable light anesthetic plane. The efficacy of TTX was tested by the absence of visually evoked responses to full-field luminance steps. Following confirmation of retinal blockade, spontaneous activity was imaged as above. Following collection of spontaneous activity, retinal blockade was again confirmed through the absence of cortical responses to visual stimuli.
For LGN inactivation experiments, surgical preparation was as described above. A head-post was implanted near bregma, a craniotomy was made over visual cortex, and sealed with a coverslip affixed directly to the skull with cyanoacrylate glue and dental cement. A second craniotomy was then made over the approximate location of the LGN (Horsley-Clarke coordinates: AP −1mm, LM 6mm). The LGN was typically located at a depth of 5–8.5mm, and its spatial position mapped by identifying units responsive to a full-field luminance stimulus through systematic electrode penetrations. Once the LGN position was determined, spontaneous activity in visual cortex was recorded as above, followed by visually-evoked responses to luminance steps. A micropipette filled with muscimol (25–100 mM, Tocris Biosciences) was lowered into the center of the LGN, and infusions of ~0.5 μL were made at three depths along the dorsal-ventral extent of the penetration using a nanoliter injector (Nanoject). The efficacy of thalamic inactivation was confirmed by the abolishment of visually evoked activity prior to and following imaging of spontaneous activity in the cortex.
Spontaneous activity was analyzed as described above, with one exception: the 10 event threshold for inclusion (see above) was not applied to the LGN inactivation experiments as in 1 of 3 cases <10 events were recorded following LGN inactivation. Comparisons between pre- and post- inactivation patterns made using second-order correlations as described above for comparisons of awake and anesthetized activity.
Local correlation structure
To describe the shape of the peak of a correlation pattern around its seed point (Fig. 7f,g; Supplementary Fig. 9g), we fitted an ellipse (least-square fit) with orientation φ, major axis ς1 and minor axis ς2 to the contour line at correlation=0.7 around the seed point. The eccentricity ε of the ellipse is defined as:
| 15 |
Its value is 0 for a circle, with increasing values indicating greater elongation of the ellipse.
Dimensionality of spontaneous activity
We estimated the dimensionality deff of the subspace spanned by spontaneous activity patterns (Supplementary Fig. 10a) by (see Ref 55):
| 16 |
where λi are the eigenvalues of the covariance matrix for the N locations (pixels) within the ROI (Supplementary Fig. 9e). These values were compared to the dimensionality of surrogate spontaneous activity patterns by taking the median value of 100 surrogate ensembles generated for each animal as described above (in “Shuffled control ensemble and surrogate correlation patterns”).
Statistical Model
To generate a statistical ensemble of spatially extended, modular patterns with predefined dimensionality k (Supplementary Fig. 10), we first synthesized k two-dimensional Gaussian random fields52 with spectral width matched to that of the experimentally observed spontaneous activity patterns (size 100×100 pixel; spatial period Λstat 10 pixel). Interpreting these k patterns as vectors vj (j=1,…,k) in the high-dimensional pixel space, we orthonormalized them based on a Householder reflection. From these k orthonormal basis vectors v, we generated activity patterns Ai (i=1, … 10,000) by linear combinations with coefficients ζ drawn independently from a Gaussian distribution with 0 mean and SD equal to 1:
| 17 |
Over this ensemble we computed the correlation patterns analogously to the analysis of the experimental data. From these we computed the fracture strength and magnitude (Supplementary Fig. 10f, (bottom)) and the local maxima at a distance of 4Λstat from the seed point to estimate the strength of long-range correlations (Supplementary Fig. 10f, (top)).
Dynamical Model
The model addresses the question whether short-range lateral connections can give rise to patterns of spontaneous activity that are (i) modular, exhibit (ii) long-range correlations and (iii) pronounced spontaneous fractures. Feature (i) can be explained by the Turing-mechanism, which for simplicity we implemented employing a ‘Mexican hat’ connectivity (local excitation, lateral inhibition), but other network motives can be used as well (Extended Data Supplementary Notes). The model shows that heterogeneity in the lateral connections is sufficient to explain features (ii) and (iii). Heterogeneity was implemented using elongated Mexican hats whose properties vary randomly across cortex.
We modeled the early spontaneous activity by a two-dimensional firing rate network (Fig. 7) obeying the following dynamics
| 18 |
| 18a |
where r(x,t) is the average firing rate in a local pool of neurons at location x, τ is the neuronal time constant, M(x,y) are the synaptic weights connecting locations x and y, I(x) is the input to location x, and γ a factor controlling the overall strength of synaptic weights. The connectivity M is assumed to be short-range and follows a Mexican hat structure. Moreover, the Mexican hats are anisotropic, modeled as the difference of two elongated Gaussians, whose axis of elongation and scale vary discontinuously across space:
| 19 |
| 19a |
| 19b |
Here σ1 and σ2 (≤ σ1) denote the SDs of the smaller Gaussian in the direction of its major and minor axis, respectively. For the larger Gaussian both SDs are scaled by a factor κ≥1. The level sets of the Gaussians are ellipses whose larger (smaller) axis is p roportional to σ1 (σ2) and so the eccentricity ε (eq. 15) measures the degree of elongation of the Mexican hat. The angle φ determines the orientation of the elongated Mexican hat. The dependence of these parameters on cortical space x is suppressed in eq. 19 for brevity. M is normalized such that the magnitude of its maximal eigenvalue is equal to 1. For all simulations we set κ=2, τ=1 and γ=1.02 and used random initial conditions r(x,t=0) drawn from a uniform distribution between 0 and 0.1.
We introduced the heterogeneity parameter H to parameterize and systematically vary the heterogeneity of elongated Mexican hats across cortical space x. The eccentricity ε was drawn from a normal distribution with mean <ε> and standard deviation σε both depending linearly on H (<ε>=H, σε=0.13 H). The size of σ1 was drawn from a normal distribution with SD 0.1<σ1>H and mean <σ1>=1.8. The orientation φ of the Mexican hat axis was drawn from a uniform distribution between 0° and 180°. These three parameters were drawn independently at each location.
In the case of isotropic Mexican hat connectivity (σ1=σ2) the eigenvectors of M are plane waves and the spectrum is peaked at the wavenumber k=2π/Λ, and thus the typical spatial scale Λ of the pattern is given by
| 20 |
This defines the spatial scale Λ used as reference in Fig. 7b,c. For comparison between model and data we identified 1Λ with 1mm, which is roughly the spatial scale of spontaneous patterns observed in experiment.
The input drive I is assumed constant in time for simplicity, consistent with our observation that in the early cortex spontaneous patterns were often fairly static during a spontaneous event (Supplementary Figure 2 and Video 5). I is modulated in space using a band-pass filtered Gaussian random field G with spatial scale Λ, zero mean and unit SD52:
| 21 |
We varied the input modulation η between 0.004 and 0.4 in Figs. 4k,l the regime over which we observed a smooth transition from an input-dominated system to a system dominated by the recurrent connections.
To model a spontaneous event, we integrated eq. 18 until a near steady state of the dynamics was reached. The results in Fig. 7c-h were obtained for an integration time of 500τ, but already a much shorter integration over 50τ resulted in similar solutions and nearly the same level of long-range correlations and dimensionality. Different spontaneous events were obtained by using different realizations of input drive I and initial conditions (same connectivity M). To generate Figs. 7d,g,h and Supplementary Figs. 9b,d,f,h and 11 we furthermore averaged over 10 realizations of connectivity M for each parameter setting.
We numerically integrated the dynamics using a 4th order Runge-Kutta method in a square region of size 100 × 100 using periodic boundary conditions. The time step was dt=0.15τ and the spatial resolution 10 pixel per Λ.
The simulations were performed on the GPUs GeForce GTX TITAN Black and GeForce GTX TITAN X. The code was implemented in Python and Theano (version 0.8.1).
Model of excitatory and inhibitory neural population
To investigate whether modular activity and long-range correlations can be generated without Mexican hat connectivity, we generated an excitatory / inhibitory two-population model. Building on previous work39,40, the model consists of an excitatory and an inhibitory neural population and neurons are linked via local lateral connections (with Gaussian profiles). We consider a regime, in which the range of connections formed by excitatory neurons is more than 30% larger than that of inhibitory neurons.
Spontaneous activity in the early visual cortex is modelled by the following dynamics:
| 22 |
| 23 |
| 24 |
where ue(x,t) (ui(x,t)) is the average firing rate of an excitatory (inhibitory) unit at location x in a two-dimensional model cortex. τ is the neuronal time constant and assumed to be the same for excitatory and inhibitory units. Mmn(x,y) are the synaptic weights connecting location y in population n to location x in population m (m,n є {e,i}, with e being the excitatory and i the inhibitory population). The sum goes over all locations y within the network. γ is a factor controlling the overall strength of synaptic weights. Both excitatory and inhibitory units cover space uniformly and with equal density. Jm(x) is the input to location x in population m.
The connectivity matrix M consists of the four synaptic weight matrices Mmn(x,y) that are assumed to be short-range and modelled by isotropic Gaussians:
| 25 |
| 26 |
Here σmn denotes the SD and amn the strength of the Gaussian that connects population n to m. The amn were normalized such that the maximal eigenvalue of M is equal to 1. Note that the Gaussian connectivity profile is isotropic and identical for all units. Thus, the network connectivity exhibits rotation and translation symmetry.
To model a spontaneous event, we assumed an input drive constant in time and space with a value Je(x) = Ji(x) =J = 1. We set τ=1, γ=1.02 and used random initial conditions ue(x,t=0), ui(x,t=0) drawn from a Gaussian distribution with zero mean and unit SD rectified at zero. The parameters for the connectivity were set to aee=22.2, aie=aei=21.6, aii=20.8, σee=σie=1.9, σei=1.4, σii=0.6. (Changing these values by 10% produced qualitatively similar results.)
We integrated the network dynamics until a near steady state of the dynamics was reached. The results in Supplemental Figs. 8d-h, 11 were obtained for an integration time of 500τ. Different spontaneous events were obtained by using different initial conditions (same connectivity M and input J). We numerically integrated the dynamics using a 4th order Runge-Kutta method in a square region of size 80 × 80 using periodic boundary conditions and a time step dt=0.15τ. As above, the simulations were performed on the GPUs GeForce GTX TITAN Black and GeForce GTX TITAN X. The code was implemented in Python and Theano (version 0.8.1).
In our numerical simulations, hexagonal activity patterns occurred for a broad range of connectivity parameters. For specific choices of parameter combinations, we could even obtain this type of solution when setting σii to a similar value as σei, so that the range of connectivity from inhibition to excitation is similar to that from inhibition to inhibition, and adjusting the strengths aii and aei such that the inhibition to excitation is comparable or slightly stronger than inhibition to inhibition56,57. In other regimes, we also observed uniform or oscillatory solutions.
Notably, the activity patterns produced by this isotropic model reflect the symmetries of the underlying dynamics and thus consist of all translated and rotated versions of a hexagonal pattern, thereby leading to a correlation structure inconsistent with experimental data (Extended Data Figs. 8h, 11b). To address the impact of heterogeneity in the two-population model, we introduce heterogeneity by making the Gaussian connectivity matrices Mmn anisotropic and by varying the strength of elongation, and the orientation and size of its axis across space (discontinuously, as in the one-population Mexican hat model):
| 27 |
| 28 |
| 29 |
| 30 |
Here, Mmn(x,y) is the connectivity from location y in population n to location x in population m. The quantities σmn 1 and σmn 2 denote the SD of the Gaussian in the direction of its major and minor axis, respectively. The angle φ determines the orientation of the elongated Gaussian. The dependence of these parameters on cortical space x is suppressed for clarity. amn denotes the connectivity strength.
To study systematically the effect of heterogeneity, we define a heterogeneity parameter H and use eccentricity ε to measure the degree of elongation of the Gaussians, as before (see Methods eq. 15). To construct a network, at each location x the eccentricity was drawn from a normal distribution with mean <ε> and standard deviation <σε> both depending linearly on H (<ε>=H, <σε>=0.025H). The σ1mn were drawn from normal distributions with average values σee=σie=1.9, σei=1.4, σii=0.6, respectively, and identical SD equal to 0.003H. The orientation φ of the Gaussian was drawn from a uniform distribution between 0° and 180°. All parameters were drawn independently at each location x and were, apart from the offsets σ1mn, identical for all four Gaussians Mmn(x,y). Finally, each synthesized matrix M was normalized such that the real part of its principle eigenvalue was equal to 1.
To model a spontaneous event, we applied to both the excitatory and the inhibitory population an input drive
| 31 |
that was constant in time and randomly modulated across space, where Gm is Gaussian white noise band-pass filtered around the spatial scale Λ, which is the dominant scale of activity patterns for the homogeneous isotropic case (H=0). The realization of the Gaussian noise Gm was different for the excitatory and inhibitory populations. Different spontaneous events were obtained by using different realizations of input drive Jm and different initial conditions (same connectivity M). We systematically varied the input modulation strength η between 0.0004 and 0.4. All other parameters and the numerical implementation were identical to the homogeneous isotropic model described in the previous section.
Statistical analysis
Non-parametric statistical analyses were used throughout the study. All tests were two-sided unless otherwise noted. Wilcoxon signed-rank, Kruskal Wallis H-test, Wilcoxon rank-sum tests were used were indicated above. Bootstrapping and surrogate approaches were used to estimate null distributions for other test statistics as described above. Sample sizes were chosen to be similar to prior studies using similar methodologies in non-murine species (e.g. Refs: 6,12,13,26,45). All animals in each experiment were treated equivalently, and no randomization or blinding was performed.
Supplementary Material
Acknowledgements
We would like to thank D. Ouimet and V. Hoke for technical and surgical assistance, P. Hülsdunk for assistance registering and motion-correcting imaging data, as well as members of the Fitzpatrick and Kaschube laboratories for helpful discussions. This research was supported by US National Institutes of Health grants EY011488 and EY026273 (D.F.), Bernstein Focus Neurotechnology grant 01GQ0840, (M.K.), BMBF project D-USA-Verbund: SpontVision, FKZ 01GQ1507 (M.K.), the International Max Planck Research School for Neural Circuits in Frankfurt, as well as the Max Planck Florida Institute for Neuroscience.
Footnotes
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Competing financial interests
The authors declare no competing financial interests.
Code availability
The code for data analysis and simulations can be made available upon request to the corresponding author.
Reporting summary
Additional details on experimental design and reagents are described in the Life Sciences Reporting Summary.
References
- 1.Hubel DH & Wiesel TN Receptive fields and functional architecture of monkey striate cortex. J Physiol 195, 215–243, (1968). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Blasdel GG & Salama G Voltage-sensitive dyes reveal a modular organization in monkey striate cortex. Nature 321, 579–585, (1986). [DOI] [PubMed] [Google Scholar]
- 3.Weliky M, Bosking WH & Fitzpatrick D A systematic map of direction preference in primary visual cortex. Nature 379, 725–728, (1996). [DOI] [PubMed] [Google Scholar]
- 4.Issa NP, Trepel C & Stryker MP Spatial frequency maps in cat visual cortex. J Neurosci 20, 8504–8514, (2000). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Kara P & Boyd JD A micro-architecture for binocular disparity and ocular dominance in visual cortex. Nature 458, 627–631, (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Smith GB, Whitney DE & Fitzpatrick D Modular Representation of Luminance Polarity in the Superficial Layers of Primary Visual Cortex. Neuron 88, 805–818, (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Bonhoeffer T & Grinvald A Iso-orientation domains in cat visual cortex are arranged in pinwheel-like patterns. Nature 353, 429–431, (1991). [DOI] [PubMed] [Google Scholar]
- 8.Ohki K, Chung S, Ch’ng YH, Kara P & Reid RC Functional imaging with cellular resolution reveals precise micro-architecture in visual cortex. Nature 433, 597–603, (2005). [DOI] [PubMed] [Google Scholar]
- 9.Gilbert CD & Wiesel TN Columnar specificity of intrinsic horizontal and corticocortical connections in cat visual cortex. J Neurosci 9, 2432–2442, (1989). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Malach R, Amir Y, Harel M & Grinvald A Relationship between intrinsic connections and functional architecture revealed by optical imaging and in vivo targeted biocytin injections in primate striate cortex. Proc Natl Acad Sci U S A 90, 10469–10473, (1993). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Bosking WH, Zhang Y, Schofield B & Fitzpatrick D Orientation selectivity and the arrangement of horizontal connections in tree shrew striate cortex. J Neurosci 17, 2112–2127, (1997). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Chapman B & Stryker MP Development of orientation selectivity in ferret visual cortex and effects of deprivation. J Neurosci 13, 5251–5262, (1993). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Chapman B, Stryker MP & Bonhoeffer T Development of orientation preference maps in ferret primary visual cortex. J Neurosci 16, 6443–6453, (1996). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Smith SM, Vidaurre D, Beckmann CF, Glasser MF, Jenkinson M, Miller KL, Nichols TE, Robinson EC, Salimi-Khorshidi G, Woolrich MW, Barch DM, Ugurbil K & Van Essen DC Functional connectomics from resting-state fMRI. Trends Cogn Sci 17, 666–682, (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Matsui T, Murakami T & Ohki K Transient neuronal coactivations embedded in globally propagating waves underlie resting-state functional connectivity. Proc Natl Acad Sci U S A 113, 6556–6561, (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Carrillo-Reid L, Miller JE, Hamm JP, Jackson J & Yuste R Endogenous sequential cortical activity evoked by visual stimuli. J Neurosci 35, 8813–8828, (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Luczak A, Bartho P & Harris KD Spontaneous events outline the realm of possible sensory responses in neocortical populations. Neuron 62, 413–425, (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Mohajerani MH, Chan AW, Mohsenvand M, LeDue J, Liu R, McVea DA, Boyd JD, Wang YT, Reimers M & Murphy TH Spontaneous cortical activity alternates between motifs defined by regional axonal projections. Nat Neurosci 16, 1426–1435, (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Kenet T, Bibitchkov D, Tsodyks M, Grinvald A & Arieli A Spontaneously emerging cortical representations of visual attributes. Nature 425, 954–956, (2003). [DOI] [PubMed] [Google Scholar]
- 20.OHashi K, Fekete T, Deneux T, Hildesheim R, van Leeuwen C & Grinvald A Interhemispheric synchrony of spontaneous cortical states at the cortical column level. Cereb Cortex 28, 1794–1807, (2018). [DOI] [PubMed] [Google Scholar]
- 21.Harris KD & Thiele A Cortical state and attention. Nat Rev Neurosci 12, 509–523, (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Ohki K, Chung S, Kara P, Hubener M, Bonhoeffer T & Reid RC Highly ordered arrangement of single neurons in orientation pinwheels. Nature 442, 925–928, (2006). [DOI] [PubMed] [Google Scholar]
- 23.Chiu C & Weliky M Spontaneous activity in developing ferret visual cortex in vivo. J Neurosci 21, 8906–8914, (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Borrell V & Callaway EM Reorganization of exuberant axonal arbors contributes to the development of laminar specificity in ferret visual cortex. J Neurosci 22, 6682–6695, (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Durack JC & Katz LC Development of horizontal projections in layer 2/3 of ferret visual cortex. Cereb Cortex 6, 178–183, (1996). [DOI] [PubMed] [Google Scholar]
- 26.White LE, Coppola DM & Fitzpatrick D The contribution of sensory experience to the maturation of orientation selectivity in ferret visual cortex. Nature 411, 1049–1052, (2001). [DOI] [PubMed] [Google Scholar]
- 27.Ruthazer ES & Stryker MP The role of activity in the development of long-range horizontal connections in area 17 of the ferret. J Neurosci 16, 7253–7269, (1996). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Arroyo DA & Feller MB Spatiotemporal Features of Retinal Waves Instruct the Wiring of the Visual Circuitry. Front Neural Circuits 10, 54, (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Ackman JB, Burbridge TJ & Crair MC Retinal waves coordinate patterned activity throughout the developing visual system. Nature 490, 219–225, (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Yang JW, An S, Sun JJ, Reyes-Puerta V, Kindler J, Berger T, Kilb W & Luhmann HJ Thalamic network oscillations synchronize ontogenetic columns in the newborn rat barrel cortex. Cereb Cortex 23, 1299–1316, (2013). [DOI] [PubMed] [Google Scholar]
- 31.Wilson HR & Cowan JD A mathematical theory of the functional dynamics of cortical and thalamic nervous tissue. Kybernetik 13, 55–80, (1973). [DOI] [PubMed] [Google Scholar]
- 32.Goldberg JA, Rokni U & Sompolinsky H Patterns of ongoing activity and the functional architecture of the primary visual cortex. Neuron 42, 489–500, (2004). [DOI] [PubMed] [Google Scholar]
- 33.Blumenfeld B, Bibitchkov D & Tsodyks M Neural network model of the primary visual cortex: from functional architecture to lateral connectivity and back. J Comput Neurosci 20, 219–241, (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Murphy BK & Miller KD Balanced amplification: a new mechanism of selective amplification of neural activity patterns. Neuron 61, 635–648, (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Gálan RF On how network architecture determines the dominant patterns of spontaneous neural activity. PLoS One 3, e2148, (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Dalva MB Remodeling of inhibitory synaptic connections in developing ferret visual cortex. Neural Dev 5, 5, (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Levy RB & Reyes AD Spatial profile of excitatory and inhibitory synaptic connectivity in mouse primary auditory cortex. J Neurosci 32, 5609–5619, (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Renart A, Song P & Wang XJ Robust spatial working memory through homeostatic synaptic scaling in heterogeneous cortical networks. Neuron 38, 473–485, (2003). [DOI] [PubMed] [Google Scholar]
- 39.Ali R, Harris J & Ermentrout B Pattern formation in oscillatory media without lateral inhibition. Phys Rev E 94, 012412, (2016). [DOI] [PubMed] [Google Scholar]
- 40.Kang K, Shelley M & Sompolinsky H Mexican hats and pinwheels in visual cortex. Proc Natl Acad Sci U S A 100, 2848–2853, (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Shouval HZ, Goldberg DH, Jones JP, Beckerman M & Cooper LN Structured long-range connections can provide a scaffold for orientation maps. J Neurosci 20, 1119–1128, (2000). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Cang J, Renteria RC, Kaneko M, Liu X, Copenhagen DR & Stryker MP Development of precise maps in visual cortex requires patterned spontaneous activity in the retina. Neuron 48, 797–809, (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Chapman B & Godecke I Cortical cell orientation selectivity fails to develop in the absence of ON-center retinal ganglion cell activity. J Neurosci 20, 1922–1930, (2000). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Huberman AD, Speer CM & Chapman B Spontaneous retinal activity mediates development of ocular dominance columns and binocular receptive fields in v1. Neuron 52, 247–254, (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
Methods references
- 45.Smith GB, Sederberg A, Elyada YM, Van Hooser SD, Kaschube M & Fitzpatrick D The development of cortical circuits for motion discrimination. Nat Neurosci 18, 252–261, (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Smith GB & Fitzpatrick D Viral Injection and Cranial Window Implantation for In Vivo Two-Photon Imaging. Methods Mol Biol 1474, 171–185, (2016). [DOI] [PubMed] [Google Scholar]
- 47.Chen TW, Wardill TJ, Sun Y, Pulver SR, Renninger SL, Baohan A, Schreiter ER, Kerr RA, Orger MB, Jayaraman V, Looger LL, Svoboda K & Kim DS Ultrasensitive fluorescent proteins for imaging neuronal activity. Nature 499, 295–300, (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Edelstein A, Amodaj N, Hoover K, Vale R & Stuurman N Computer control of microscopes using microManager. Curr Protoc Mol Biol Chapter 14, Unit 14 20, (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Peirce JW PsychoPy--Psychophysics software in Python. J Neurosci Methods 162, 8–13, (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Wilson DE, Smith GB, Jacob AL, Walker T, Dimidschstein J, Fishell G & Fitzpatrick D GABAergic Neurons in Ferret Visual Cortex Participate in Functionally Specific Networks. Neuron 93, 1058–1065, (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Sage D, Dimiter P, Tinevez J-Y & Schindelin J in Image J User & Developer Conference (2012). [Google Scholar]
- 52.Kaschube M, Schnabel M, Löwel S, Coppola DM, White LE & Wolf F Universality in the evolution of orientation columns in the visual cortex. Science 330, 1113–1116, (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Schottdorf M, Keil W, Coppola D, White LE & Wolf F Random Wiring, Ganglion Cell Mosaics, and the Functional Architecture of the Visual Cortex. PLoS Comput Biol 11, e1004602, (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Cramer KS & Sur M Blockade of afferent impulse activity disrupts on/off sublamination in the ferret lateral geniculate nucleus. Brain Res Dev Brain Res 98, 287–290, (1997). [DOI] [PubMed] [Google Scholar]
- 55.<j/>Abbott LF, Rajan K & Sompolinsky H in The Dynamic Brain: An Exploration of Neuronal Variability and Its Functional Significance (ed Ding Mingzhou and Glanzman Dennis) Ch. 4, 65–82 (Oxford University Press, Inc., 2011). [Google Scholar]
- 56.Pfeffer CK, Xue M, He M, Huang ZJ & Scanziani M Inhibition of inhibition in visual cortex: the logic of connections between molecularly distinct interneurons. Nat Neurosci 16, 1068–1076, (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Somogyi P, Kisvarday ZF, Martin KA & Whitteridge D Synaptic connections of morphologically identified and physiologically characterized large basket cells in the striate cortex of cat. Neuroscience 10, 261–294, (1983). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


