Abstract
The aim of this study is to develop and evaluate a novel imaging method (SSF, Spatial gradient Sparse in Frequency domain) for the reconstruction of activation sequences of ventricular arrhythmia from noninvasive body surface potential map (BSPM) measurements. We formulated and solved the electrocardiographic inverse problem in the frequency domain, and the activation time was encoded in the phase information of the imaging solution. A cellular automaton heart model was used to generate focal ventricular tachycardia (VT). Different levels of Gaussian white noise were added to simulate noisecontaminated BSPM. The performance of SSF was compared with that of WMN (weighted minimum norm) inverse solution. We also evaluated the method in a swine model with simultaneous intracardiac and body surface recordings. Four reentrant VTs were observed in pigs with myocardial infarction generated by left anterior descending artery occlusion. The imaged activation sequences of reentrant VTs were compared with those obtained from intracardiac unipolar electrograms. In focal VT simulation, SSF increased the correlation coefficient (CC) by 5% and decreased localization errors (LEs) by 2.7 mm on average under different noise levels. In the animal validation with reentrant VT, SSF achieved an average CC of 88% and an average LE of 6.3 mm in localizing the earliest and latest activation site in the reentry circuit. Our promising results suggest SSF provides noninvasive imaging capability of detecting and mapping macroreentrant circuits in 3-dimensional ventricular space. SSF may become a useful imaging tool of identifying and localizing the potential targets for ablation of focal and reentrant ventricular tachycardia.
Keywords: Cardiac Imaging, Inverse Problem, Myocardial Infarction, Reentrant Ventricular Tachycardia, Spatial Gradient Sparse, Swine Model, Ventricular Arrhythmia
I. Introduction
Ventricular arrhythmias are defined as abnormal heart rhythms (arrhythmias) that originate from the lower chambers of the heart (ventricles). In the present study, we classify ventricular arrhythmias into two categories based on their periodicity. Referring to the international consensus document on VT/VF ablation [1], a periodic arrhythmia can be VT, non-sustained VT or sustained VT (Duration Classification), can be monomorphic VT, an episode from multiple monomorphic VT, a segment of pleomorphic VT or ventricular flutter (Morphology of QRS complexes Classification), and can be clinical VT, incessant VT, repetitive monomorphic VT or an episode of VT storm (Clinical Characteristics Classification). The common property is a segment of relatively stable VT originating from the same origin or generated by the same reentrant circuit. The body surface ECGs of periodic arrhythmias listed above can be the direct input to our proposed imaging algorithm. On the other hand, VTs with dynamically changing QRS configurations and VF which has a totally chaotic morphology are aperiodic and cannot be the direct input to our imaging algorithm. This is because we lose the time resolution by formulating and solving the problem in the frequency domain. Single heartbeat such as premature ventricular complexes (PVC) could also be the input since a VT train can be generated by concatenating the same heartbeat multiple times. In summary, our proposed imaging algorithm may not be directly applied when the VTs are generated by continuing changing reentrant circuits or when VF occurs. Given the low incidences of the above cases, our proposed imaging technique is aimed at reconstructing activation sequences in a majority of ventricular arrhythmias.
Catheter ablation is one of the therapeutic options to treat ventricular arrhythmias. Before applying radiofrequency energy in the arrhythmogenic area, endocardial mapping is usually performed to identify the target of ablation depending on the mechanism of the arrhythmia. For focal VTs, the target of ablation is the point with the earliest activation. Activation mapping techniques can create a three-dimensional (3D) activation time colored map by assigning an activation time to each spatial point. For reentrant VTs, entrainment mapping is usually considered as a supplement to activation mapping. For reentrant VTs related to scar from prior myocardial infarction (scar-related VTs), substrate mapping is useful in determining the anatomical substrates that could lead to VTs by creating a 3D amplitude map of local electrograms. Regions with low potentials (<1.5 mV) are considered pathological [2], [3]. Pace mapping could be used to locate the origins of focal VTs and reentrant VTs, but it is less precise than activation mapping. The aforementioned endocardial mapping techniques are invasive and limited by both time and the inability to assess activations in midmyocardial and epicardial regions. Cardiac electrical imaging technique is a promising approach that can noninvasively reconstruct activation sequences or action potentials of the whole heart. By detecting the earliest activated location, it allows the physician to know the arrhythmia mechanism and the potential area of ablation before inserting a catheter into the heart, thus improving the effectiveness and efficiency of catheter ablation and reducing overall procedure time. By reconstructing action potentials, it could also identify regions with low potentials and estimate the extent of myocardial infarction.
Noninvasive cardiac electrical imaging involves solving the inverse problem of electrocardiography. In the past decades, a number of efforts have been made in this field, which can be classified based on different aspects. 1) The input could be body surface potentials [4]–[35] or endocardial potentials [36], [37]. Using body surface potentials as input is predominant because of a larger covering area with more electrodes. Using endocardial potentials does not belong to noninvasive cardiac electrical imaging technique by a narrower definition. 2) The source model could be a single moving dipole model [5], [11], [21] or equivalent distributed source model [6], [9], [14], [32]. 3) The solution space could be twoThe solution space could be two-dimensional [4], [6], [9], [12], [13], [22], [28], [34], [38] or three-dimensional [24], [39], [25], [29], [17], [18], [26], [16], [20], [23], [27], [31], [40], [33], [32], [35]. Since He and coworkers⣙ early work to solve ECG inverse imaging in 3D heart [7], [8], [10], [41], several approaches have been taken to address the challenge of imaging cardiac electrical activity in 3D space or throughout the myocardium. Such approach is desirable since cardiac electrical propagation is inhomogeneous and varies across the myocardium, and arrhythmias may originate from epicardial or endocardial sites or from a mid-myocardial wall. 4) The information to formulate a constraint in order to deal with the ill-posed property of the inverse problem could be physiological knowledge [8], [39] or physical knowledge [6], [14], [32]. Physiological knowledge such as the prior knowledge of cardiac electrical activity, fiber orientation and statistical knowledge from body surface potentials could help a lot in solving the inverse problem and achieving a global optimum. But it is also limited by incorporating into the physiological knowledge when the state of the heart is complicated or could not be evaluated accurately. Physical knowledge includes the geometry of the heart and the physical relationship between cardiac sources and body surface electrodes. It is robust in the sense of its applicability. 5) The unit of solution could be time (activation sequence) [9], [15], [32], [42] or potential (endocardial or epicardial potential [4], [6], [28] and transmural potential [17], [24], [35], [39]). The activation time of each myocardial cell is defined as the time of arrival of the depolarization phase of action potential, which is of clinical interest since it depicts the electrical activation sequence in the heart. The region with the earliest activation time is considered as the origin of an arrhythmia. Activation sequence reflects electrical propagation pathways of ventricular arrhythmias. On the other hand, more parameters could be derived from the reconstructed potentials and usually the amplitude of the potential is a marker for identifying infarction or slow-conduction zone [34], [35]. 6) The norm of the constraint could be L2-norm [6], [28], [42], L1-norm [29], [32] or a norm in between [25]. L2-norm is based on the minimization of energy resulting from the consensus that a stable state usually possesses the least energy. L1-norm is usually associated with sparsity. Sparsity could appear either in space or in time depending on which property is pursued. To solve the inverse problem, a problem with L2-norm constraints is easy to solve and is guaranteed with a global optimum. However, a problem with L1-norm or other norms is hard to find an optimum and requires some special algorithms to search the solution space and find a solution. The solution will be smooth if it is L2-norm, and sparse if it is L1-norm. A norm between 1 and 2 will result in a smoothness in between these two.
Reconstructing cardiac activation sequences is a type of inverse imaging in which the aims are to find the site with the earliest activation time. Approaches combining time and frequency domain analysis have shown promise in brain source imaging [43], [44]. In addition to combining different dimensions, solving the inverse problem in the frequency domain [45], [46] has shown merits in imaging brain oscillation.
In the present study, we have developed a physical-knowledge-based method on projected edge dipole model (derived from equivalent distributed dipole model) to reconstruct activation sequences for periodic arrhythmias from body surface potentials noninvasively. We conducted a series of computer simulations to evaluate the developed method in imaging ventricular arrhythmias. We also conducted animal studies to validate the approach in a swine model with infarction using simultaneously recorded intracardiac electrograms.
II. Methods
A. Forward Modeling and Equivalent Current Density on Edge in a Tetrahedron Model
The equivalent current density , defined as in (1), can serve as a cardiac current source for computing the field potential [14], [32].
| (1) |
where Gi is the intracellular effective conductivity tensor and øm is the transmembrane potential. Based on the bidomain theory [47], the electrical field of assumed quasi-static condition is governed by:
| (2) |
where Gi and Ge are the intracellular and extracellular effective conductivity tensors, øe is the extracellular potential, and øm is the transmembrane potential.
The whole ventricular myocardium is divided into N distributed current sources. At each current source’s location, an orthogonal triple dipole represents the local vector field of equivalent current density with an arbitrary direction. By applying the boundary element method (BEM) [48], [49], (2) can be linearized into a discrete matrix form:
| (3) |
where Φ is an M × 1 vector of body surface potentials at M electrodes, J is a 3N × 1 vector of equivalent current density at N orthogonal triple dipoles, and L is an M × 3N transfer matrix where L = (L1L2 … LN) with Li as an M ×3 matrix representing the electric lead field between M electrodes and 3 moments of ith dipole.
During normal cardiac activation, a myocardial cell is activated periodically. Its transmembrane potential, along with magnitude of the equivalent current density, fluctuates at a given frequency. Incorporating this periodicity into our imaging scheme requires directly constrain the magnitude of an orthogonal triple dipole, thereby increasing the complexity of solving the inverse problem and limiting the possible transformation that could be applied to the formulation. Therefore, we propose a new tetrahedron model in which the edge center represents the equivalent current density.
A Delaunay triangulation was used to transform the N distributed dipoles into tetrahedrons. The long edges that connect two dipoles farther than the threshold of the distance were detected and deleted since their centers were not confined to the ventricular myocardium. The threshold was estimated by calculating distances between each dipole and all the other dipoles. After removing tetrahedrons with long edges, the edges that do not belong to any remaining tetrahedrons were further deleted. Therefore, a clean tetrahedron model was created and it was plotted for a manual check to ensure there was no cavity in the model, otherwise a looser threshold would be chosen to generate a new tetrahedron model.
Since the edge centers serve as the new current sources, the transfer matrix needs to be updated as well. For the kth edge that connects ith dipole and jth dipole, the lead field between this edge and mth body surface electrode is defined as:
| (4) |
where Lemk is the edge lead field between mth electrode and kth edge, is the spatial vector between two dipoles, Lmi is a 1 × 3 vector of the dipole lead field between mth electrode and ith dipole and Lmj is the dipole lead field between mth electrode and jth dipole. Because in (4) the absolute value of vector projection is used, the direction of does not matter and Lemk is a non-negative value.
For a tetrahedron model, (3) is rewritten as:
| (5) |
where Φ is an M × 1 vector of body surface potentials at M electrodes, JE is a K ×1 vector of equivalent current density at Kedge centers, and LE is an M × K transfer matrix.
B. Spatial Gradient Sparse in Frequency Domain and Activation Time
A periodic signal is characterized by its main oscillating frequency and phase in the frequency domain. When the whole ventricular myocardium is activated in sequence, there is a delay in the time domain and a phase shift in the frequency domain. Based on the linearity of (5) and the time shift property of Fourier transform, (5) can be transformed into the frequency domain, and the phase of each edge current source corresponds to its activation time.
Apply Fourier transform to (6) and substitute into main oscillating frequency ω0:
Thus, in the frequency domain, (5) is expressed as:
| (8) |
where F∅ (ω0) is an M×1 complex vector and is a K×1 complex vector. Because there is one main oscillating frequency in the heart that dominates the propagation of activation, ω0 is omitted in the following equations and is determined by detecting the frequency with the maximum power in the power spectrum excluding the direct current component.
Suppose we extract amplitude and phase from the main frequency ω0, in the time domain Jei(t −ti) can be expressed as Aicos(ω0t − ti), and its Fourier transform will be:
| (9) |
| (10) |
From (10), the phase of the complex vector is proportional to the time delay in the activation sequence.
Starting from the earliest activated site to the latest activated site, the time delay ti ranges from 0 to T (cycle length of the periodic cardiac activity), and the phase shift is from 0 to 2π. A phase of π corresponds to a point of minimum deflection (activation time) for a sine wave. So, the phase of the earliest activated site is π. The phase of other regions that are activated later will have a phase between π and 3 π depending on where they are in the cycle. Since the phase range of π to 3 π is equivalent to a phase range of −π to π, the phase from the earliest activated site to the latest activated site is from −π to π. In reentrant VT, a sudden change between − π and π exists because the earliest site is close to the latest site. In focal VT, this sudden change appears after flipping (−π to 0 being flipped to 0 to −π, 0 to π being flipped to π to 0). Mathematically, this sudden change between −π and π always exists. On the other hand, in the time domain, the heart is divided into the activated region and the region to be activated at any time point during activation. In the frequency domain, the phase jump is a reflection of the state of the heart within a certain period of time (a time segment of signals used for analysis). Physiologically, it is a relatively stable marker. In 3-dimensional space, this results in a spatial gradient sparse of phase in the myocardium that could be utilized as a constraint in the reconstruction of activation time.
| (6) |
| (7) |
C. Weighted Spatial Gradient Sparse Reconstruction
Equation (8) formulates a forward problem that connects distributed edge current sources with body surface potentials in the frequency domain. Given body surface measurements and the lead field, solving the equivalent current density cannot be done by a direct matrix inversion because this is a highly ill posed problem with a strict null space. The effects of sources deep into the myocardium cannot be distinguished from the effects produced by sources near the surface without the addition of prior knowledge. Regularization needs to be added to obtain a unique and stable solution, and the constraint terms are usually based on the physiological property of the heart [7], [39] or the physical property of the cardiac model [32], [42]. A solution that achieves the minimum energy is considered as feasible and stable, hence it is widely used in cardiac electrical imaging [6], [15]. In our proposed method, a weighted spatial gradient sparse is applied:
| (11) |
| (12) |
| (13) |
W is a depth weighting matrix to balance deep sources in the heart model, G is a numerical first order gradient matrix, R is a set including all the neighboring current sources’ indices of a current source, and r is the number of elements in set R. Neighboring sources are determined by calculating spatial distances between one source and all other sources and sorting them in an ascending order. λ is the regularization parameter, which can be determined by L-curve method [50], [51]. r determines how wide the smooth region will be in the final solution, and λ balances between the residual term and the spatial sparse term. They are both data-driven. For noisy data, a small r and λ will be very sensitive to the noise. Therefore, a larger r and λ is desirable for experimental data and a smaller r and λ is suitable for simulation data (their range is usually from 1 to 10). Also, r should not be too large to lose the sparse property in the solution.
It is notable that the spatial gradient sparse constraint is applied to which is a complex vector, not to the phase of . This is because the mathematical expression of phase is nonlinear and will result in a non-convex problem that is hard to solve and that requires special algorithms to deal with. However, (11) - (13) formulates a convex problem that can be solved with CVX, a MATLAB package specialized in solving convex programs [52], [53]. It is also notable that the spatial gradient is applied inside L1-norm, not outside. So that the constraint term won’t be 0 between neighboring nodes who have the same amplitude but different phases. When is obtained, phase is calculated, and linearly rescaled to a range of 0 to T for reentrant VTs. In the application of focal VT, phase is first flipped back to the range of − π to π, then is linearly rescaled to 0 to T. Activation time is obtained by multiplying the phase with the cycle length T (estimated from the butterfly plot of body surface ECGs) divided by 2 π, and the 3D activation sequence is thereby constructed.
The proposed method is named SSF (Spatial gradient Sparse in the Frequency domain) for later references in this paper. This method uses the same forward model for the forward and inverse calculations. The current formulation is a spatial weighted form of Total Variation [29], [54] in the frequency domain. Before we came to current formulation, other potential formulations were considered. First, L2-norm on the constraint term rendered a reentry pattern into a focal pattern in reentrant VT since the distance between the earliest and the latest activation site is so large (>50 mm) that it is not reasonable to consider it as a reentry pattern anymore. For focal VT, L2-norm constraint in frequency domain was able to reconstruct activation sequences with a larger localization error and a smaller correlation coefficient compared with SSF. Second, the weighting matrix W reduces the spatial bias towards superficial nodes and penalizes superficial nodes. Since we want to apply a constraint on spatial gradient, a depth weighting matrix in the constraint term is critical. Lastly, standard total variation in time domain cannot be applied to reconstruct the activation sequence of a reentrant VT since it is very difficult to pick up the correct time segment of a reentrant VT beat. It has the same limitation as WMN method in time domain.
D. Computer Simulation of Focal Ventricular Tachycardia
To simulate a focal ventricular tachycardia (VT) train, a realistic anisotropic ventricle model was used [10]. In brief, a cellular automaton heart model incorporating generalized anisotropy (including myocardial fiber orientations and conduction velocities) was constructed from CT images of a human subject and was discretized into 30,083 cardiac automatons with a side length of 1.5 mm. The action potential was set individually, and the equivalent current density was calculated by multiplying the myocardial conductivity tensor with the spatial gradient of the instantaneous action potential [42]. The cellular automatons were grouped into 3,887 dipoles according to their segment number. This yields a single beat activation model with a time resolution of the generated current density of 1 millisecond. Finally, the tetrahedron model was built upon this dipole model, and the equivalent current density on each edge was calculated by a spatial projection of the two dipoles’ components that are connected with this edge.
Single-site pacing simulation protocol was applied to mimic focal VTs. In total, 12 pacing sites were selected based on the anatomical structure of the ventricles, namely in the basal posterior (BP), basal septum (BS), basal left wall (BLW), basal right wall (BRW), basal anterior (BA), middle septum (MS), middle posterior (MP), middle left wall (MLW), middle right wall (MRW), middle anterior (MA), apical anterior (AA) and apical posterior (AP) regions. For each single-site pacing simulation, the time courses of all current densities on edges were plotted to determine the beginning and end of a single-beat activation. The time segment of the activation was extracted and concatenated 100 times to form a chain. The whole series of current density was filtered by a zero-phase bandpass filter between 1 Hz and 10 Hz. Since VT is defined as a heart rate higher than 120 bpm, down-sampling to the filtered VT train was done to represent a heart rate of 120 bpm.
The piece-wise homogeneous boundary element model of a heart-torso model was built by using a commercial software (Curry 6.0, Neuroscan, North Carolina, USA) based on the torso and lungs segmented from a standard high-resolution male torso MRI images (ViP V2.0 IT’IS Foundation, Zürich, Switzerland). 208 body surface electrodes, which were recorded from a human subject, were placed on the front and back of this standard male body surface, and were registered with the heart-torso model. The lead field between dipoles and electrodes was transformed to the lead field between edge sources and electrodes. The body surface potentials of a focal VT train were generated by multiplying the VT train of current density with the lead field.
Gaussian white noise of various SNR levels (5, 10, 20 and 40 dB) were added to the forward calculated body surface potentials to simulate ECG signals collected in a clinical setting. Fourier transform of the final simulated body surface potentials of the focal VT train on all electrodes was used to calculate the power across different frequencies. The main oscillating frequency was determined from the total power spectrum (sum of power spectrums of all electrodes). Equation (11) to (13) were used to solve the inverse problem in the frequency domain, and the activation sequence was reconstructed accordingly. The schematic diagram of the above computer simulation is presented in Fig. 1.
Fig. 1.
Schematic diagram of computer simulation. VT = ventricular tachycardia.
Besides evaluating SSF on a simulated focal VT train by concatenating 100 times of the same activation time segment of current densities, effects of frequency variation and the size of pacing were also investigated. For frequency variation simulation study, pacing at basal left wall (BLW) at a Gaussian noise level of 20 dB was selected. We used MATLAB to randomly generate 100 different cycle lengths that fall into a normal distribution. The mean value of cycle length is the original simulated cycle length that corresponds to a frequency of 2 Hz. The standard deviation parameter sigma was set to 0, 1, 5, 8, 10 or 20 each time. Then the current densities of the focal VT train with frequency distribution were multiplied with lead field and Gaussian noise were added to generate body surface potentials at 20 dB SNR. SSF was applied to reconstruct the activation sequences. For each sigma, simulation was done 10 times to obtain an average performance of SSF since the distribution of cycle length was randomly generated.
The effect of the size of pacing was evaluated by pacing simultaneously at 1, 5, 10, 20 or 40 neighboring sites in space around the original single pacing site. We changed the size of pacing for each original single pacing site (12 pacing sites throughout the ventricles). We also evaluated with different SNRs (5, 10, 20 and 40 dB).
E. Application to Reentrant Ventricular Tachycardia in a Swine Model
1). Experimental Procedure:
To apply the proposed method to reentrant VT, four female pigs (57.8 ± 4.0 kg) with late myocardial infarction (MI) were studied under a protocol with simultaneous body surface potential mapping and 3D intracardiac mapping [55], [56]. The study protocol was approved by the Institutional Animal Care and Use Committee at University of Alabama at Birmingham.
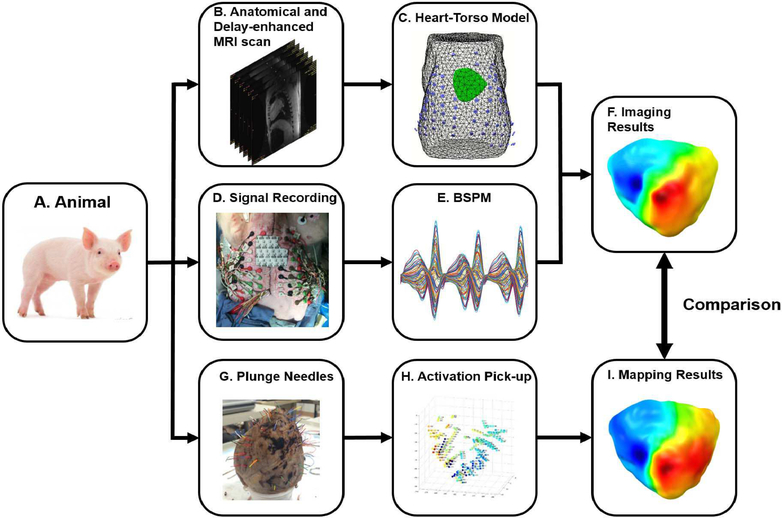
The study flowchart is shown in Fig. 2. Left anterior descending (LAD) coronary artery occlusion for 150 minutes was performed. A month later serial echocardiography studies were performed and nine weeks after MI, anatomical MRI and delay-enhanced MRI images were obtained to construct the swine heart-torso model and to identify myocardial fibrosis regions respectively (Panel B in Fig. 3).
Fig. 2.
Swine study flowchart. LAD = left anterior descending coronary artery.
Fig. 3.
Schematic diagram of swine study. A: experimental animal. B: Anatomical and delay-enhanced MRI for the construction of heart-torso model and the identification of infarction area. C: Heart-torso model with body surface electrodes registered with the body surface. D: Simultaneous body surface recording and intracardiac recording. E: BSPM, the recorded body surface potential maps. F: Imaging results by using the proposed imaging method. G: Excised heart with color-coded bristles replacing plunge-needle electrodes. H: Discrete activation times from each unipolar channel. I: Interpolated intracardiac activation time map.
On the day of mapping, 10 weeks after MI, pigs were anesthetized and 128 body surface electrodes were placed on the front chest and back of the pig to record body surface potentials at a sampling rate of 1 kHz. The locations of body surface electrodes were digitized using an electromagnetic 3D digitizer (Fastrak, Polhemus Inc., Colchester, VT, USA). A 7F EP catheter was inserted into the RV (via the femoral vein) for pacing. After several minutes of signal recording with adequate signal quality, the heart was exposed via median sternotomy. Up to 70 transmural plunge-needle electrodes were inserted throughout the left ventricle (LV), the right ventricle (RV), and the septum, with greater electrode density in and around the MI. Each plunge-needle electrode was made of epoxy fiberglass strands (0.7 mm diameter in the heart and 0.6 mm diameter before the right angle) with 50-μm diameter silver electrodes with the most epicardial electrode 1 mm beneath the surface. RV plunges contained 3 electrodes 2 mm apart (depth of 5 mm), LV plunges contained 6 electrodes 2 mm apart (depth of 11 cm), and septal plunges contained 6 electrodes 3.5 mm apart (depth of 18.5 mm). The sternotomy incision was then closed so that unipolar electrograms were recorded simultaneously with body surface potentials in a closed-chest condition (Panel D in Fig. 3). Rapid single-site pacing and burst pacing was done to induce reentrant VT (as previously defined [57] in the swine heart.
After the mapping study, the heart was excised with all the plunge-needle electrodes in situ and was pressure perfused in formalin for at least 12 hours. Each plunge-needle was replaced by color-coded plastic brush bristles (Panel G in Fig. 3) that were localized by careful digitization as described in [58].
2). Data Analysis:
The ventricle geometry and torso were segmented from anatomical MRI images by a commercial software (Curry 6.0, Neuroscan, North Carolina, USA) and the body surface electrodes were registered to the torso surface based on several anatomical landmarks (Panel C in Fig. 3). The BEM model was built to relate body surface electrodes with distributed cardiac sources. A segment of body surface potentials with reentrant VT (Panel E in Fig. 3) was used for imaging the reentrant circuit. Principle Component Analysis (PCA) was used for extracting the main components with SNR higher than 1 to further filter signals after a bandpass filter of 1 and 30 Hz. Finally, a 3D activation sequence was reconstructed by the proposed method (Panel F in Fig. 3).
Since intracardiac mapping results were used for the validation of the activation sequence, intracardiac electrograms of several reentrant VT beats were analyzed. After bandpass filtering the unipolar signals, the first derivative was calculated for each channel. The time with the maximum negative first derivative was automatically detected as the activation time. By combining the activation time with the positions of plunge-needle electrodes, the 3D activation time maps of reentrant VT beats were constructed (Panel H in Fig. 3). Finally, the plunge-needle electrodes were registered with the ventricle model, and the activation time was interpolated spatially to the ventricle model to obtain 3D intracardiac activation time maps (Panel I in Fig. 3).
F. Statistical Analysis
For computer simulation of focal VT, the evaluation was made between the simulated activation sequence and the imaging activation sequence. The correlation coefficient (CC) and relative error (RE) were computed to quantify the agreement of the overall activation pattern. Localization error (LE) was also computed to evaluate the targeting performance of the proposed method. In the time domain, we have proposed two methods to localize the origins of PVC or focal VT before: one was based on the WMN [42]; the other introduced temporal sparse into the formulation [32]. Considering the computational effort, we compared the imaging performance of the proposed method with that of the WMN on the same source model. For the WMN method, a single focal VT beat was used for the analysis. It was also evaluated with the simulated activation sequence to calculate imaging statistics. WMN was applied to 10 focal VT beats to get the average performance of pacing at each site with a certain noise level.
For animal experiment of reentrant VT, the evaluation was made between the measured intracardiac activation sequence and the imaged activation sequence.
CC, RE and LE are defined as follows:
| (14) |
| (15) |
| (16) |
where ATi and MTi represent the imaged and measured (or simulated) activation time at ith cardiac source, and are the average of the two activation sequences, and SI and SM are the spatial locations of imaged and measured earliest (or latest) activation time sites respectively.
III. Results
A. Computer Simulation of Focal Ventricular Tachycardia
Table 1 summarizes the imaging statistics of WMN and SSF under different noise levels. As SNR decreases, the performance of WMN declines. However, SSF manages to maintain good performance unaffected by the noise level.
TABLE I.
Imaging Statistics of Computer Simulation
| SNR | CC (%) | LE (mm) | RE (%) | |||
|---|---|---|---|---|---|---|
| Method | WMN | SSF | WMN | SSF | WMN | SSF |
| 40 dB | 88.17±10.83 | 91.67±7.30 | 6.0±2.8 | 4.5±2.2 | 23.67±6.08 | 19.42±5.38 |
| 20 dB | 87.50±10.50 | 91.67±8.07 | 7.0±2.9 | 4.9±2.4 | 20.58±5.48 | 21.67±5.07 |
| 10 dB | 84.92±11.52 | 90.83±8.91 | 7.9±3.2 | 5.3±2.7 | 19.92±4.98 | 19.00±4.51 |
| 5 dB | 83.08±12.10 | 89.92±9.95 | 10.2±3.1 | 5.6±3.2 | 18.83±4.99 | 18.75±4.75 |
CC = correlation coefficient, LE = localization error, RE = relative error, SNR = signal-to-noise ratio, SSF = spatial sparse in frequency domain method, WMN = weighted minimum norm method.
The average CC and LE of 12 single-site pacing simulations are also plotted in the top row of Fig. 4. As for RE, there is no significant difference between the two methods. The RE among different noise levels varies less in SSF than that of WMN. This is due to the way the activation time in SSF was calculated. The cycle length of a beat was first determined from the butterfly plot of body surface potentials. Then the phase of SSF with a range of 0 to 2π was multiplied by this cycle length to transfer it into activation time. Therefore, there was no time shrinkage in SSF. Two factors that influence the value of RE: the shape of distribution and the absolute error. SSF with no time shrinkage has less variation in the absolute error so it also varies little in the value of RE.
Fig. 4.
Comparison of imaging statistics between SSF and WMN in 12 single-site pacing simulation of focal VT. The top row shows the average CC and LE of all the 12 pacing sites. The second and bottom rows present four cases that SSF has improved the imaging performance significantly. The triangle mark denotes the WMN method, and the square mark denotes the SSF method. CC is plotted in orange lines and LE is shown in blue lines.
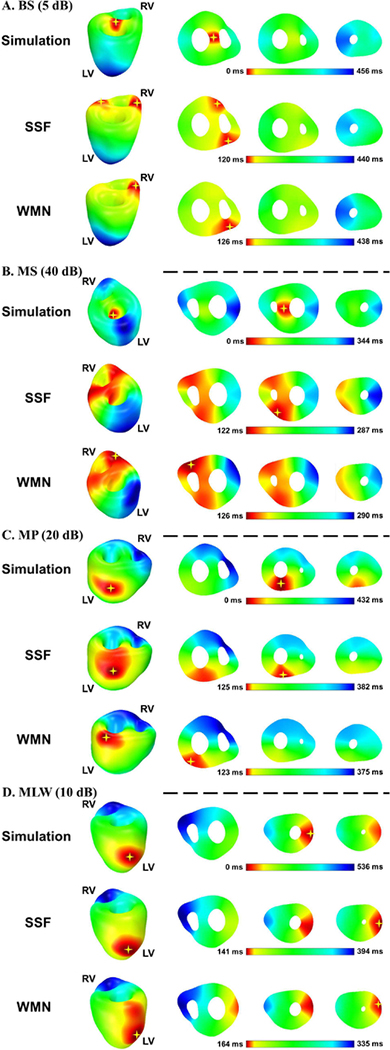
Among the 12 single-site pacing simulations, four cases were considered difficult and usually had low CCs and LEs: basal septum (BS), middle septum (MS), middle posterior (MP) and middle left wall (MLW). Their imaging statistics are shown in the middle and bottom rows in Fig. 4, and the 3D activation sequences are presented in Fig. 5. For the first two cases, the difficulty came from the pacing source lying in the middle region of the heart. On the body surface, the initiation part of the excitation is almost cancelled out by the cardiac electric propagation along two opposite directions. Therefore, the signal is very weak on the body surface, and is harder to visualize by the imaging process. This is why the activation time maps of BS and MS target the earliest activation sites to the sites that are slightly later in time than the true earliest activation site. WMN tended to assign a single source while SSF was able to obtain a balance in space as shown in the middle column of BS and MS in Fig. 5. While calculating the earliest activation site, this spatial balance led to a smaller LE and a higher CC. Since the LV is more remote from the front body surface than the RV anatomically in human, the pacing source in MP or MLW is considered as a deep source and would be harder to detect. This is where SSF outperformed WMN; both CC and LE were improved by using SSF. The imaging results are presented in the bottom two rows in Fig. 5. SSF and WMN share the same color bar in each panel. In general, SSF performed better than WMN, and SSF improved the performance the most in these four cases.
Fig. 5.
Activation time maps of four single-site pacing simulations. The pacing sites are displayed with SNR levels. In each panel, the 3D simulated activation sequence is depicted in the first row. The activation sequences reconstructed by SSF method and WMN method are listed in the second and third rows, respectively. The earliest region in each activation sequence is denoted by a yellow star. All maps are color coded from red to blue with red representing earliest and blue representing latest activation time. BS = basal septum, MLW = middle left wall, MP = middle posterior, MS = middle septum, LV = left ventricle, RV = right ventricle.
Simulation on frequency variation produces the results in Fig. 6. The left panel shows the average of CC and RE, and the right panel presents average LE and the number of simulation among 10 times that generates either a negative CC or a CC less than 50% (Bad simulation). The results of bad simulation were not included when calculating average of CC, RE and LE in Fig. 6. As the standard deviation of frequency distribution increases, the number of bad simulation increases as well. Starting from sigma = 8, there is at least a 40% probability for SSF being unable to reconstruct the activation sequences correctly. Even for sigma = 5, SSF could not obtain reasonable results one out of ten times. SSF is reliable when sigma < 5. The underlying reason is because of the frequency distribution in the power spectrum. When sigma is large, it is more unlikely to find a focused peak with the maximum power in the power spectrum as shown in Fig. 1 and Fig. 9. If the peak is split, the frequency with the maximum power could not represent the activity of the majority in the heart. This finding supports our statement in Introduction that SSF is good for reconstructing activation sequences in a relatively stable VT train without too much variation in cycle lengths.
Fig. 6.
Results of simulation on frequency variation. Pacing at BLW, SNR = 20 dB was selected to investigate the effect of frequency variation. CC = correlation coefficient, LE = localization error, RE = relative error.
Fig. 9.
ECG Lead II and frequency spectrum of four reentrant ventricular tachycardia in infarcted swine study. First column: ECG Lead II plots of analyzed time segments. Second column: Power spectrum of body surface potentials after bandpass filtering and PCA filtering. Third column: Signal-to-Noise Ratio (SNR) determined from the power spectrum.
Figure 7 summarizes simulation results when changing the pacing size and noise level. The mean value (the height) and the standard deviation (the color) of each bar were calculated by averaging among 12 pacing sites (size = 1) or segments (size > 1). Along the dimension of pacing size, smaller size usually generates higher CC, lower RE and smaller LE. Along the dimension of SNR, higher SNR usually produces higher CC, lower RE and smaller LE.
Fig. 7.
Effect of pacing size and SNR on the performance of SSF. The height of each bar represents the value of CC, RE or LE. The color on each bar corresponds to the standard deviation of CC, RE or LE. CC = correlation coefficient, LE = localization error, RE = relative error, SD = standard deviation.
B. Reentrant VT in a Swine Model
The physiological statistics of the four pigs are shown in Table 2 including the average infarct extent estimated from delay-enhanced MRI images Swine 1 had the highest ejection fraction and the smallest chamber dimensions post-MI due to having the smallest infarct of the group.
TABLE II.
Physiological Statistics of Swine
| Weight (kg) | EF (%) | EDV (ml) | ESV (ml) | AIE (%) | |
|---|---|---|---|---|---|
| Swine 1 | 53.4 | 48.6 | 89.6 | 46 | 8.17 |
| Swine 2 | 63.1 | 44.4 | 90.7 | 50.4 | 18.7 |
| Swine 3 | 57.9 | 30.9 | 134.7 | 93 | 17.2 |
| Swine 4 | 56.8 | 42.3 | 139.8 | 80.6 | 10.9 |
AIE = average infarct extent; EDV = end diastolic volume; EF = ejection fraction; ESV = end systolic volume.
Table 3 summarizes the imaging statistics. In total, 4 long stable reentrant VTs were recorded and analyzed. We did not observe any reentrant VT induced by programmed electrical stimulation (PES) in Swine 1, which may be due to its smaller average infarct extent. Two reentrant VTs in Swine 2, one in Swine 3 and one in Swine 4 were successfully induced by PES. They were recorded by the plunge-needle electrodes and the body surface electrodes simultaneously. We compared the imaged activation sequences with those obtained from the intracardiac unipolar electrograms. The average CC was 88.00±4.83 %, the average RE was 0.23±0.03, the average LE of the earliest activated site was 6.3 ± 1.9 mm and the average LE of the latest activated site was 6.3±3.4 mm. Two reentrant VTs in Swine 2 were more stable compared to the other two reentrant VTs, therefore a longer segment of body surface signals and 3D mapping data were used for analysis in Swine 2. The main oscillating frequency was estimated from the power spectrum of the analyzed body surface signals (Middle column in Fig. 9), and on average, ω0 was 5.12 Hz (equal to 307 beats per minute). The intracardiac mapping results of one of the reentrant VTs from swine 2 (S2RVT1) are presented in Fig. 8.
TABLE III.
Imaging Statistics of Reentrant VT of Swine
| Reentry | Needle | Channel | CC | RE | LE_E (mm) | LE_L (mm) | ω0 (Hz) | t (s) |
|---|---|---|---|---|---|---|---|---|
| S2RVT1 | 71 | 257 | 0.90 | 0.20 | 8.5 | 8.3 | 4.51 | 17.7 |
| S2RVT2 | 71 | 257 | 0.88 | 0.27 | 4.8 | 2.1 | 4.77 | 26.6 |
| S3 RVT | 50 | 198 | 0.81 | 0.25 | 7.1 | 9.8 | 5.92 | 3.55 |
| S4RVT | 61 | 230 | 0.92 | 0.21 | 4.6 | 5.1 | 5.29 | 2.27 |
CC = correlation coefficient; Channel = the number of unipolar channels; LEE = localization error of the earliest site; LE_L = localization error of the latest site; Needle = the number of plunge-needle electrodes; RE = relative error; RVT = reentrant ventricular tachycardia; t = the time length of analyzed reentrant ventricular tachycardia in body surface potentials; ω0 = the main oscillating frequency of reentrant ventricular tachycardia.
Fig. 8.
Intracardiac mapping results of S2RVT1. The analyzed reentrant ventricular tachycardia beat is framed in a red rectangle on the top left corner. Two loops that compose the figure 8 reentry circuit are depicted in the middle left row. The corresponding activation time map is shown in the bottom left row. Its cross section and sagittal view are listed on the right of the activation time map. The individual unipolar electrogram of each site in the circuit with activation time marked on top is shown at right. Ant = anterior view of the heart, LV = left ventricle, Pos = posterior view of the heart, RV = right ventricle.
The VT beat analyzed is framed in a red rectangle at top left. The two reentry loops that comprised a figure 8 reentry circuit are depicted in the left middle row with the unipolar electrogram of each channel presented on the right. The activation time is defined as the time with the maximum negative first derivative, which is marked by a red vertical line with its corresponding time in ms shown directly above. Activation from sites A-B-C-D-E-F-G and back to A forms an anterior top loop that passes through the LV, the septum and the RV. Reentrant loop A-H-I-J-K-G-A forms another lateral loop that circulates in the RV. Individual unipolar electrograms are shown at right. Conduction block is denoted by a black rectangle between sites A and G. The 3D color map of intracardiac activation time is at bottom left, with red representing earliest activation and blue representing latest activation. Here the anterior loop is denoted by two black dashed lines and the lateral loop is shown in the orange dashed curves. The cross-section view of this color map is at right with one sagittal view on the bottom left corner. The view of the anterior loop is exactly the same as that of the 3D color map.
Figure 9 provides plots of ECG Lead II and the total power spectrums (used to determine the main oscillating frequency) of the four reentrant VTs. The last column is the Signal-to-Noise Ratio (SNR) determined from the power spectrum. Signal refers to the power amplitude of the main oscillating frequency, namely the maximum power amplitude in the plot. It is marked with a red star in the figure. The noise is the largest amplitude of power excluding the main frequency and its harmonics (a wave with a frequency that is a positive integer multiple of the main frequency) which is indicated by the black arrow.
Figure 10 illustrates the imaging results of the four reentrant VTs. Each panel represents one reentrant VT. Within each panel, the measured 3D intracardiac activation time maps are listed in the first row. The corresponding imaged activation sequences are presented in the second row with color-coding from red to the blue. The yellow star denotes the earliest activated site and the orange star denotes the latest activated site. In the third row, the infarct area is shown in red inside the ventricular myocardium and the infarct extent was estimated from the delay-enhanced MRI images of the heart. Three rows share identical lightening and 3D view. Cross sectional views of the measured and infarction are exactly the same. The cross-section views of the imaged were chosen to show the earliest and the latest activated sites. The pathways of three of the four reentrant VTs were formed in the anterior border, and one was in the posterior border. Plunge-needle electrodes were more densely placed in the anterior side, while there were fewer electrodes in posteriorly. This explains why in Swine 3 the distance between the earliest and latest activation site in imaging results was longer than that in the measured results. In the other three reentrant VTs, the distances were similar between the imaged and measured results.
Fig. 10.
Imaging results of four reentrant ventricular tachycardia in the swine study. The first and the second rows are the measured intracardiac activation time maps and the reconstructed activation time maps. Activation time maps are color coded from red to blue with red indicating the earliest activated site and blue the latest. Yellow stars define the earliest site and orange stars stand for the latest site. The infarction extent of each pig is in the third row and the red object is the infarction. LV = left ventricle, RV = right ventricle, RVT = reentrant ventricular tachycardia.
IV. Discussion
A. Property of SSF
To our knowledge, SSF is the first 3D imaging method designed for imaging periodic ventricular arrhythmias especially for imaging activation sequences of reentrant VT. The constraint is formulated based on spatial gradient sparse in the frequency domain that leads to a higher spatial similarity between imaged and simulated (or measured) activation sequences.
SSF is built on a tetrahedron model that is transformed from the distributed rotating dipole model. In the time domain, the time segment of a reentrant beat used for analysis is difficult to determine since this is a reoccurring event within the whole ventricle. The starting time point of a beat in the butterfly plot of body surface potentials is not closely associated with the starting point of a reentrant circuit. This makes it difficult to image the activation sequence of a reentrant circuit using an imaging algorithm developed in the time domain. However, in the frequency domain, the activation sequence is encoded into phase. To express the phase of a cardiac source, a tetrahedron model with edges serving as the new cardiac sources can clearly define the amplitude and phase of the current density, which cannot be done in a rotating dipole model or a standard tetrahedron model. Both the standard tetrahedron model and the distributed rotating dipole model use an orthogonal triple of dipoles to represent the vector field of local equivalent current density with an arbitrary direction. Each axis (x, y and z) has a magnitude and a phase in the frequency domain. If we want to apply constraint on the phase, only the phase of the dipole’s magnitude represents the correct phase of the cardiac activity on this dipole. This means we need to transform the variable X to calculate its norm: , then apply the constraint on the phase of its Fourier transformation. In the formulation of optimization function, this increases the complexity of the expression of optimization function, let alone the spatial gradient sparsity constraint placed on top of it. It will be a non-convex optimization and increases the computational burden substantially. On the other hand, we have tried to solve the magnitude and phase on each axis individually, but because of the inability to constrain on the phase of dipole’s magnitude, this method did not work out. In summary, the new tetrahedron model makes it easier to express the phase of dipole’s magnitude and renders the optimization function to be a convex optimization problem.
The tetrahedron model and spatial gradient sparse in the frequency domain are the novel features of SSF. The statistics from the focal VT simulation demonstrated the robustness of SSF against noise and a better spatial balance than WMN when imaging deep sources by applying a spatial gradient sparsity constraint. It aims to find a solution that has the least gradient jump in the whole heart (the second term in (11)) while minimizing the difference between measured signals and calculated signals (the first term in (11)), thus reducing the area with earliest activation time. The statistics from the reentrant VT swine study demonstrated that SSF was able to reconstruct the global reentry circuit with good accuracy. By solving one objective function, SSF will obtain the activation time pattern in the heart without other post-processing methods, such as deriving activation time from the time course of equivalent current density or from the transmural potentials.
Based on the above discussion, the imaging approach we proposed—SSF (Spatial gradient Sparse in the Frequency domain)—is novel in five folds. 1) It takes the complex number resulting from Fourier transform as a whole and solves real and imaginary parts together. 2) It imposes a spatial-weighted total variation in the frequency domain as the constraint. 3) The activation time is extracted from the phase, so there is no need to apply peak criteria [42] in the time course to determine the activation time for each source. 4) A projected edge dipole model derived from the distributed rotating dipole model is built to make the proposed algorithm feasible. 5) This is the first time that a 3D reentrant circuit throughout the ventricles can be reconstructed noninvasively by an imaging method.
B. Application to Reentrant VT
Reentry involves the electrical circuit looping back upon itself, and it typically results either from an anatomical obstacle (i.e. scar) in the setting of structural heart disease or from functional conduction block in a normal heart. Within the infarction zone, the myocardium is either electrically inexcitable or with low conduction velocity. In a series of studies on reentrant ventricular arrhythmias in the late MI period in dogs [59]–[64], researchers have investigated this type of reentrant VTs from a variety of aspects, such as epicardial mapping of reentrant VTs and electrophysiologic-anatomic correlation of reentrant circuits. Infarction in these dogs was created by a ligation on the LAD artery, and experiments were done 3–5 days after the ligation. It has been shown that regardless of the anatomical localization of reentrant circuits (epicardial, intramural, or subendocardial), and their dimension or method (spontaneous or programmed premature stimulation), reentrant excitation typically occurs in a figure 8 configuration [61].
We tested SSF in a swine model in which the infarction was created by a LAD artery occlusion and the experiments were done 2 months after the occlusion. Based on the location of the infarction and the time duration since MI, our findings were very similar to those from the canine MI model. We observed a figure 8 configuration of reentrant VT circuits in the swine model both from 3D intracardiac mapping (Fig. 8) and from 3D imaging results (Fig. 10). The infarction zone is comprised of cells with partial depolarization, reduced action potential amplitude and decreased upstroke velocity [60]. The intracardiac electrograms in Fig. 8 show that the VT macroreentrant circuit consisted of myocardial regions with a wide range of action potential amplitudes (from 2 mV to 25 mV), and with a tract of surviving tissue that traverses the infarct [65].
Inside the infarcted area, there are surviving muscle fibers and strands of fibrous tissue [66] Reentry occurs at the border of the infarct and the larger subendocardial muscle mass [67]. This concept was further supported by comparing the locations of conduction block with the infarction extent in the ventricles as shown in Fig. 10. Since the intracardiac mapping results and infarction results shared the same cross section view, the earliest and latest activated sites in the reentrant circuit were located on the border of the infarct and the normal tissue, respectively.
C. Clinical Implication
To terminate reentrant VT via ablation, information such as the central common pathway, VT exit site, and lines of conduction block is needed. Efforts have been made to directly map the reentrant circuit by means of endocardial mapping [65], [67], epicardial mapping [59], [60] or entrainment mapping [68]. However, these approaches are limited by the low resolution and/or the inability to capture the macroreentry throughout the ventricles simultaneously. These invasive procedures also expose patients to prolonged procedure times that can increase peri-procedural risk. Previously, a noninvasive epicardial imaging technique was applied to infarcted canine hearts lying inside a human torso model [69]. It was able to reconstruct the reentry pathway and its key components based on the imaged epicardial potentials. However, the initiation of a reentry beat was detectable only when it reached the epicardium appearing as a breakthrough on the epicardial potential map. Most recently, epicardial and endocardial potentials were reconstructed in patients with reentrant VTs [34] although limiting to the heart surface. We reconstructed the reentrant circuit throughout the 3D myocardium in vivo and compared the results with those from simultaneous 3D intracardiac mapping. We have successfully recorded 4 reentrant VTs in swine and achieved an average CC of 88.00±4.83%, an average RE of 0.23±0.03, an average LE of earliest activated sites of 6.3±1.9 mm, and an average LE of latest activated sites of 6.3±3.4 mm. RF ablation at the exit, central and proximal sites in the reentry circuit (sites identified by this approach) results in a high incidence of termination [68]. Identification of the pathway and the VT exit site of a reentrant VT, which are clearly shown in the 3D imaged activation time maps, should reduce the searching area for ablation and the ablation time, and ultimately help in successful termination of reentrant VT.
D. Study Limitation
Our study is limited by the relatively low number of reentrant VTs studied, but our results were considered among all the VTs studied. Moreover, compared with the VT induction rate in infarcted dogs [60], we were able to induce reentrant VT in 75% of the infarcted swine studied. The reentrant VTs studied were monomorphic. We did not observe polymorphic VTs in the swine study. Therefore the performance of SSF in imaging polymorphic VT needs to be evaluated in the future. Additional testing of SSF could be done using other datasets that include a volume ventricle model and recordings of BSPM. The spatial resolution of measured activation sequences was limited by the number of plunge-needle electrodes in the myocardium, but the resolution was sufficient to define reentrant VT in all 4 of the infarcted swine. While the positions of plunge-needle electrodes were digitized in vitro, we have used this method with success in a number of prior studies. Even with these limitations, we have shown that SSF was able to reconstruct activation sequences of a reentrant VT noninvasively and depict the reentry circuit in the swine hearts.
V. Conclusions
We have proposed and developed a novel SSF cardiac electrical imaging approach that reconstructs activation sequences in focal and reentrant VTs by formulating and solving the inverse problem in the frequency domain. We evaluated the performance of SSF through focal VT simulation under a variety of noise levels and demonstrated that SSF achieved better results than WMN. We successfully applied SSF to reentrant VTs in a late MI swine model, for imaging the reentrant circuits in four reentrant VTs. The localization of the VT exit site was supported by previous works. In the future, we will test SSF thoroughly in more complicated cases, such as in animal and human hearts. Noninvasively detecting the central pathway and the exit site of a reentrant circuit would save VT patients from undergoing prolonged procedure and result in a smaller but more accurately delineated ablation region. Further investigation in animal models and in patients will evaluate its potential for defining arrhythmia mechanisms noninvasively in ways that could improve pharmacologic treatment of VT.
Acknowledgement
The authors thank Sharon Melnick and Shannon Salter for technical assistance, and Dr. Zhaoye Zhou for useful discussions.
This work was supported in part by NIH HL080093 and by the Institute for Engineering in Medicine of the University of Minnesota.
Contributor Information
Ting Yang, Biomedical Engineering Department, University of Minnesota, Minneapolis, MN 55455, USA..
Steven M. Pogwizd, Division of Cardiovascular Disease, School of Medicine, the University of Alabama at Birmingham, Birmingham, AL 0019, USA.
Gregory P. Walcott, Division of Cardiovascular Disease, School of Medicine, the University of Alabama at Birmingham, Birmingham, AL 0019, USA.
Long Yu, Biomedical Engineering Department, University of Minnesota, Minneapolis, MN 55455, USA..
Bin He, University of Minnesota and the Carnegie Mellon University, Pittsburgh, PA 15213, USA..
References
- [1].Natale A, Raviele A, Al-Ahmad A, Alfieri O, Aliot E, Almendral J, Breithardt G, Brugada J, Calkins H, Callans D, Cappato R, Camm JA, Bella PD, Guiraudon GM, Haïssaguerre M, Hindricks G, Ho SY, Kuck KH, Marchlinski F, Packer DL, Prystowsky EN, Reddy VY, Ruskin JN, Scanavacca M, Shivkumar K, Soejima K, Stevenson WJ, Themistoclakis S, Verma A, Wilber D, and for the Venice Chart members, “Venice Chart International Consensus Document on Ventricular Tachycardia/Ventricular Fibrillation Ablation,” J. Cardiovasc. Electrophysiol, vol. 21, no. 3, pp. 339–379, March 2010. [DOI] [PubMed] [Google Scholar]
- [2].Marchlinski FE, Callans DJ, Gottlieb CD, and Zado E, “Linear ablation lesions for control of unmappable ventricular tachycardia in patients with ischemic and nonischemic cardiomyopathy,” Circulation, vol. 101, no. 11, pp. 1288–1296, 2000. [DOI] [PubMed] [Google Scholar]
- [3].Arenal A, del Castillo S, Gonzalez-Torrecilla E, Atienza F, Ortiz M, Jimenez J, Puchol A, García J, and Almendral J, “Tachycardia-related channel in the scar tissue in patients with sustained monomorphic ventricular tachycardias,” Circulation, vol. 110, no. 17, pp. 2568–2574, 2004. [DOI] [PubMed] [Google Scholar]
- [4].Barr RC and Spach MS, “Inverse calculation of QRS-T epicardial potentials from body surface potential distributions for normal and ectopic beats in the intact dog.,” Circ. Res, vol. 42, no. 5, pp. 661–675, 1978. [DOI] [PubMed] [Google Scholar]
- [5].Gulrajani RM, Roberge FA, and Savard P, “Moving dipole inverse ECG and EEG solutions,” IEEE Trans. Biomed. Eng, no. 12, pp. 903–910, 1984. [DOI] [PubMed] [Google Scholar]
- [6].Oster HS, Taccardi B, Lux RL, Ershler PR, and Rudy Y, “Noninvasive electrocardiographic imaging,” Circulation, vol. 96, no. 3, pp. 1012–1024, 1997. [DOI] [PubMed] [Google Scholar]
- [7].Li G and He B, “Localization of the site of origin of cardiac activation by means of a heart-model-based electrocardiographic imaging approach,” IEEE Trans. Biomed. Eng, vol. 48, no. 6, pp. 660–669, 2001. [DOI] [PubMed] [Google Scholar]
- [8].He B, Li G, and Zhang X, “Noninvasive three-dimensional activation time imaging of ventricular excitation by means of a heart-excitation model,” Phys. Med. Biol, vol. 47, no. 22, p. 4063, 2002. [DOI] [PubMed] [Google Scholar]
- [9].Tilg B, Fischer G, Modre R, Hanser F, Messnarz B, Schocke M, Kremser C, Berger T, Hintringer F, and Roithinger FX, “Model-based imaging of cardiac electrical excitation in humans,” IEEE Trans. Med. Imaging, vol. 21, no. 9, pp. 1031–1039, 2002. [DOI] [PubMed] [Google Scholar]
- [10].He B, Li G, and Zhang X, “Noninvasive imaging of cardiac transmembrane potentials within three-dimensional myocardium by means of a realistic geometry anisotropic heart model,” IEEE Trans. Biomed. Eng, vol. 50, no. 10, pp. 1190–1202, 2003. [DOI] [PubMed] [Google Scholar]
- [11].Armoundas AA, Feldman AB, Mukkamala R, and Cohen RJ, “A single equivalent moving dipole model: an efficient approach for localizing sites of origin of ventricular electrical activation,” Ann. Biomed. Eng, vol. 31, no. 5, pp. 564–576, 2003. [DOI] [PubMed] [Google Scholar]
- [12].Greensite F, “Heart surface electrocardiographic inverse solutions,” Model. Imaging Bioelectrical Act. Princ. Appl. N. Y. Kluwer Acad. Publ, pp. 119–160, 2004. [Google Scholar]
- [13].Farina D, Jiang Y, Skipa O, Dossel O, Kaltwasser C, and Bauer WR, “The use of the simulation results as a priori information to solve the inverse problem of electrocardiography for a patient,” in Computers in Cardiology, 2005, 2005, pp. 571–574. [Google Scholar]
- [14].Liu Z, Liu C, and He B, “Noninvasive reconstruction of three-dimensional ventricular activation sequence from the inverse solution of distributed equivalent current density,” IEEE Trans. Med. Imaging, vol. 25, no. 10, pp. 1307–1318, 2006. [DOI] [PubMed] [Google Scholar]
- [15].Berger T, Fischer G, Pfeifer B, Modre R, Hanser F, Trieb T, Roithinger FX, Stuehlinger M, Pachinger O, Tilg B, and Hintringer F, “Single-Beat Noninvasive Imaging of Cardiac Electrophysiology of Ventricular Pre-Excitation,” J. Am. Coll. Cardiol, vol. 48, no. 10, pp. 2045–2052, November 2006. [DOI] [PubMed] [Google Scholar]
- [16].Dossel O, Bauer WR, Farina D, Kaltwasser C, and Skipa O, “Imaging of bioelectric sources in the heart using a cellular automaton model,” in Engineering in Medicine and Biology Society, 2005. IEEE-EMBS; 2005. 27th Annual International Conference of the, 2006, pp. 1067–1070. [DOI] [PubMed] [Google Scholar]
- [17].Nielsen BF, Cai X, and Lysaker M, “On the possibility for computing the transmembrane potential in the heart with a one shot method: An inverse problem,” Math. Biosci, vol. 210, no. 2, pp. 523–553, 2007. [DOI] [PubMed] [Google Scholar]
- [18].Nielsen BF, Lysaker M, and Tveito A, “On the use of the resting potential and level set methods for identifying ischemic heart disease: An inverse problem,” J. Comput. Phys, vol. 220, no. 2, pp. 772–790, 2007. [Google Scholar]
- [19].Liu C, Skadsberg ND, Ahlberg SE, Swingen CM, Iaizzo PA, and He B, “Estimation of Global Ventricular Activation Sequences by Noninvasive Three-Dimensional Electrical Imaging: Validation Studies in a Swine Model During Pacing,” J. Cardiovasc. Electrophysiol, vol. 19, no. 5, pp. 535–540, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20].Han C, Liu Z, Zhang X, Pogwizd S, and He B, “Noninvasive three-dimensional cardiac activation imaging from body surface potential maps: a computational and experimental study on a rabbit model,” IEEE Trans. Med. Imaging, vol. 27, no. 11, pp. 1622–1630, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [21].Lai D, Liu C, Eggen MD, Iaizzo PA, and He B, “Equivalent moving dipole localization of cardiac ectopic activity in a swine model during pacing,” IEEE Trans. Inf. Technol. Biomed, vol. 14, no. 6, pp. 1318–1326, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Sapp JL, Dawoud F, Clements JC, and Horáček BM, “Inverse solution mapping of epicardial potentials: quantitative comparison to epicardial contact mapping,” Circ. Arrhythm. Electrophysiol, p. CIRCEP–111, 2012. [DOI] [PubMed] [Google Scholar]
- [23].Han C, Pogwizd SM, Killingsworth CR, and He B, “Noninvasive reconstruction of the three-dimensional ventricular activation sequence during pacing and ventricular tachycardia in the canine heart,” Am. J. Physiol.-Heart Circ. Physiol, vol. 302, no. 1, pp. H244–H252, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Liu C, Eggen MD, Swingen CM, Iaizzo PA, and He B, “Noninvasive Mapping of Transmural Potentials During Activation in Swine Hearts From Body Surface Electrocardiograms,” IEEE Trans. Med. Imaging, vol. 31, no. 9, pp. 1777–1785, September 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Rahimi A, Xu J, and Wang L, “-Norm Regularization in Volumetric Imaging of Cardiac Current Sources,” Comput. Math. Methods Med, vol. 2013, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Nielsen BF, Lysaker M, and Grøttum P, “Computing ischemic regions in the heart with the bidomain model—first steps towards validation,” IEEE Trans. Med. Imaging, vol. 32, no. 6, pp. 1085–1096, 2013. [DOI] [PubMed] [Google Scholar]
- [27].Han C, Pogwizd SM, Killingsworth CR, Zhou Z, and He B, “Noninvasive cardiac activation imaging of ventricular arrhythmias during drug-induced QT prolongation in the rabbit heart,” Heart Rhythm, vol. 10, no. 10, pp. 1509–1515, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Erem B, Coll-Font J, Orellana RM, St’ovicek P, and Brooks DH, “Using transmural regularization and dynamic modeling for noninvasive cardiac potential imaging of endocardial pacing with imprecise thoracic geometry,” IEEE Trans. Med. Imaging, vol. 33, no. 3, pp. 726–738, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Xu J, Dehaghani AR, Gao F, and Wang L, “Noninvasive transmural electrophysiological imaging based on minimization of total-variation functional,” IEEE Trans. Med. Imaging, vol. 33, no. 9, pp. 1860–1874, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Zhou Z, Han C, Yang T, and He B, “Noninvasive Imaging of 3-Dimensional Myocardial Infarction From the Inverse Solution of Equivalent Current Density in Pathological Hearts,” IEEE Trans. Biomed. Eng, vol. 62, no. 2, pp. 468–476, February 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Han C, Pogwizd SM, Yu L, Zhou Z, Killingsworth CR, and He B, “Imaging cardiac activation sequence during ventricular tachycardia in a canine model of nonischemic heart failure,” Am. J. Physiol.-Heart Circ. Physiol, vol. 308, no. 2, pp. H108–H114, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Yu L, Zhou Z, and He B, “Temporal sparse promoting three dimensional imaging of cardiac activation,” IEEE Trans. Med. Imaging, vol. 34, no. 11, pp. 2309–2319, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Zhou Z, Jin Q, Chen LY, Yu L, Wu L, and He B, “Noninvasive Imaging of High-Frequency Drivers and Reconstruction of Global Dominant Frequency Maps in Patients With Paroxysmal and Persistent Atrial Fibrillation,” IEEE Trans. Biomed. Eng, vol. 63, no. 6, pp. 1333–1340, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Wang L, Gharbia OA, Horácˇek BM, and Sapp JL, “Noninvasive epicardial and endocardial electrocardiographic imaging of scar-related ventricular tachycardia,” J. Electrocardiol, vol. 49, no. 6, pp. 887–893, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Schulze WH, Chen Z, Relan J, Potyagaylo D, Krueger MW, Karim R, Sohal M, Shetty A, Ma Y, and Ayache N, “ECG imaging of ventricular tachycardia: evaluation against simultaneous non-contact mapping and CMR-derived grey zone,” Med. Biol. Eng. Comput, vol. 55, no. 6, pp. 979–990, 2017. [DOI] [PubMed] [Google Scholar]
- [36].He B, Liu C, and Zhang Y, “Three-dimensional cardiac electrical imaging from intracavity recordings,” IEEE Trans. Biomed. Eng, vol. 54, no. 8, pp. 1454–1460, 2007. [DOI] [PubMed] [Google Scholar]
- [37].Liu C, Iaizzo PA, and He B, “Three-dimensional imaging of ventricular activation and electrograms from intracavitary recordings,” IEEE Trans. Biomed. Eng, vol. 58, no. 4, pp. 868–875, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Wang Y, Cuculich PS, Zhang J, Desouza KA, Vijayakumar R, Chen J, Faddis MN, Lindsay BD, Smith TW, and Rudy Y, “Noninvasive electroanatomic mapping of human ventricular arrhythmias with electrocardiographic imaging,” Sci. Transl. Med, vol. 3, no. 98, p. 98ra84–98ra84, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Wang L, Zhang H, Wong KC, Liu H, and Shi P, “Physiological-model-constrained noninvasive reconstruction of volumetric myocardial transmembrane potentials,” IEEE Trans. Biomed. Eng, vol. 57, no. 2, pp. 296–315, 2010. [DOI] [PubMed] [Google Scholar]
- [40].Zhou Z, Han C, Yang T, and He B, “Noninvasive imaging of 3-dimensional myocardial infarction from the inverse solution of equivalent current density in pathological hearts,” IEEE Trans. Biomed. Eng, vol. 62, no. 2, pp. 468–476, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [41].He B and Wu D, “Imaging and visualization of 3-D cardiac electric activity,” IEEE Trans. Inf. Technol. Biomed, vol. 5, no. 3, pp. 181–186, 2001. [DOI] [PubMed] [Google Scholar]
- [42].Liu Z, Liu C, and He B, “Noninvasive reconstruction of three-dimensional ventricular activation sequence from the inverse solution of distributed equivalent current density,” IEEE Trans. Med. Imaging, vol. 25, no. 10, pp. 1307–1318, 2006. [DOI] [PubMed] [Google Scholar]
- [43].Gramfort A, Strohmeier D, Haueisen J, Hämäläinen MS, and Kowalski M, “Time-frequency mixed-norm estimates: Sparse M/EEG imaging with non-stationary source activations,” NeuroImage, vol. 70, pp. 410–422, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44].Castaño-Candamil S, Höhne J, Martínez-Vargas J-D, An X-W, Castellanos-Domínguez G, and Haufe S, “Solving the EEG inverse problem based on space–time–frequency structured sparsity constraints,” NeuroImage, vol. 118, pp. 598–612, 2015. [DOI] [PubMed] [Google Scholar]
- [45].Jensen O and Vanni S, “A new method to identify multiple sources of oscillatory activity from magnetoencephalographic data,” Neuroimage, vol. 15, no. 3, pp. 568–574, 2002. [DOI] [PubMed] [Google Scholar]
- [46].Yuan H, Doud A, Gururajan A, and He B, “Cortical imaging of eventrelated (de) synchronization during online control of brain-computer interface using minimum-norm estimates in frequency domain,” IEEE Trans. Neural Syst. Rehabil. Eng, vol. 16, no. 5, pp. 425–431, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [47].Miller WT and Geselowitz DB, “Simulation studies of the electrocardiogram. I. The normal heart.,” Circ. Res, vol. 43, no. 2, pp. 301–315, 1978. [DOI] [PubMed] [Google Scholar]
- [48].Barr RC, Pilkington TC, Boineau JP, and Spach MS, “Determining Surface Potentials from Current Dipoles, with Application to Electrocardiography,” IEEE Trans. Biomed. Eng, vol. BME-13, no. 2, pp. 88–92, April 1966. [DOI] [PubMed] [Google Scholar]
- [49].Gulrajani RM, “The forward problem of electrocardiography: Theoretical underpinnings and applications,” Model. Imaging Bioelectrical Act, pp. 43–79, 2005. [Google Scholar]
- [50].Hansen PC, “Analysis of discrete ill-posed problems by means of the L-curve,” SIAM Rev, vol. 34, no. 4, pp. 561–580, 1992. [Google Scholar]
- [51].Hansen PC and O’Leary DP, “The use of the L-curve in the regularization of discrete ill-posed problems,” SIAM J. Sci. Comput, vol. 14, no. 6, pp. 1487–1503, 1993. [Google Scholar]
- [52].Grant M, Boyd S, and Ye Y, CVX: Matlab software for disciplined convex programming. 2008.
- [53].Grant M and Boyd S, “Graph implementations for nonsmooth convex programs,” Recent Adv. Learn. Control, pp. 95–110, 2008. [Google Scholar]
- [54].Rudin LI, Osher S, and Fatemi E, “Nonlinear total variation based noise removal algorithms,” Phys. Nonlinear Phenom, vol. 60, no. 1–4, pp. 259–268, 1992. [Google Scholar]
- [55].Pogwizd SM and Corr PB, “Electrophysiologic mechanisms underlying arrhythmias due to reperfusion of ischemic myocardium.,” Circulation, vol. 76, no. 2, pp. 404–426, 1987. [DOI] [PubMed] [Google Scholar]
- [56].Pogwizd SM and Corr PB, “Reentrant and nonreentrant mechanisms contribute to arrhythmogenesis during early myocardial ischemia: results using three-dimensional mapping.,” Circ. Res, vol. 61, no. 3, pp. 352–371, September 1987. [DOI] [PubMed] [Google Scholar]
- [57].Pogwizd SM, Chung MK, and Cain ME, “Termination of Ventricular Tachycardia in the Human Heart: Insights From Three-dimensional Mapping of Nonsustained and Sustained Ventricular Tachycardias,” Circulation, vol. 95, no. 11, pp. 2528–2540, June 1997. [DOI] [PubMed] [Google Scholar]
- [58].Han C, Pogwizd SM, Killingsworth CR, and He B, “Noninvasive imaging of three-dimensional cardiac activation sequence during pacing and ventricular tachycardia,” Heart Rhythm, vol. 8, no. 8, pp. 1266–1272, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [59].El-Sherif N, Smith RA, and Evans K, “Canine ventricular arrhythmias in the late myocardial infarction period. 8. Epicardial mapping of reentrant circuits.,” Circ. Res, vol. 49, no. 1, pp. 255–265, 1981. [DOI] [PubMed] [Google Scholar]
- [60].Mehra R, Zeiler RH, Gough WB, and El-Sherif N, “Reentrant ventricular arrhythmias in the late myocardial infarction period. 9. Electrophysiologic-anatomic correlation of reentrant circuits.,” Circulation, vol. 67, no. 1, pp. 11–24, 1983. [DOI] [PubMed] [Google Scholar]
- [61].El-Sherif N, Gough WB, Zeiler RH, and Hariman R, “Reentrant ventricular arrhythmias in the late myocardial infarction period. 12. Spontaneous versus induced reentry and intramural versus epicardial circuits,” J. Am. Coll. Cardiol, vol. 6, no. 1, pp. 124–132, 1985. [DOI] [PubMed] [Google Scholar]
- [62].Gough WB, Mehra R, Restivo M, Zeiler RH, and El-Sherif N, “Reentrant ventricular arrhythmias in the late myocardial infarction period in the dog. 13. Correlation of activation and refractory maps.,” Circ. Res, vol. 57, no. 3, pp. 432–442, 1985. [DOI] [PubMed] [Google Scholar]
- [63].EL-SHERIF N, GOUGH WB, and RESTIVO M, “Reentrant ventricular arrhythmias in the late myocardial infarction period: 14. Mechanisms of resetting, entrainment, acceleration, or termination of reentrant tachycardia by programmed electrical stimulation,” Pacing Clin. Electrophysiol, vol. 10, no. 2, pp. 341–371, 1987. [DOI] [PubMed] [Google Scholar]
- [64].El-Sherif N, Gough WB, and Restivo M, “Reentrant ventricular arrhythmias in the late myocardial infarction period: mechanism by which a short-long-short cardiac sequence facilitates the induction of reentry.,” Circulation, vol. 83, no. 1, pp. 268–278, 1991. [DOI] [PubMed] [Google Scholar]
- [65].De Bakker JM, van Capflle FJ, Janse MJ, van Hemel NM, Hauer RN, Defauw JJ, Vermeulen FE, and de Wekker PFB, “Macroreentry in the infarcted human heart: the mechanism of ventricular tachycardias with a ‘focal’ activation pattern,” J. Am. Coll. Cardiol, vol. 18, no. 4, pp. 1005–1014, 1991. [DOI] [PubMed] [Google Scholar]
- [66].Fenoglio JJ Jr, Pham TD, Harken AH, Horowitz LN, Josephson ME, and Wit AL, “Recurrent sustained ventricular tachycardia: structure and ultrastructure of subendocardial regions in which tachycardia originates,” Josephson Sch. Leg. Important Contrib. Electrophysiol, vol. 68, no. 3, p. 187, 2015. [DOI] [PubMed] [Google Scholar]
- [67].De Bakker JM, Van Capelle FJ, Janse MJ, Wilde AA, Coronel R, Becker AE, Dingemans KP, Van Hemel NM, and Hauer RN, “Reentry as a cause of ventricular tachycardia in patients with chronic ischemic heart disease: electrophysiologic and anatomic correlation.,” Circulation, vol. 77, no. 3, pp. 589–606, 1988. [DOI] [PubMed] [Google Scholar]
- [68].Stevenson WG, Friedman PL, Sager PT, Saxon LA, Kocovic D, Harada T, Wiener I, and Khan H, “Exploring postinfarction reentrant ventricular tachycardia with entrainment mapping,” J. Am. Coll. Cardiol, vol. 29, no. 6, pp. 1180–1189, 1997. [DOI] [PubMed] [Google Scholar]
- [69].Burnes JE, Taccardi B, Ershler PR, and Rudy Y, “Noninvasive electrocardiogram imaging of substrate and intramural ventricular tachycardia in infarcted hearts,” J. Am. Coll. Cardiol, vol. 38, no. 7, pp. 2071–2078, 2001. [DOI] [PMC free article] [PubMed] [Google Scholar]