Peptide-Lipid Interaction Sites Affect Vesicles’ Responses to Antimicrobial Peptides

Abstract

This article presents coarse-grained molecular dynamics simulations of pore-forming antimicrobial peptide melittin and its interactions with vesicles composed of a mixture of zwitterionic and anionic phospholipids. Besides creating holes in the membrane, the adsorption of melittin also induces vesicle budding, which can develop into vesiculation at high peptide concentrations, as well as vesicle invagination, which can eventually result in a corrugated membrane surface. These rich morphology changes are mediated by the curvature of the vesicles and the peptide concentration. Highly curved vesicles favor the recruitment of melittins with a higher density of binding sites. The peptides mainly penetrate into the membrane surface in monomers via hydrophobic interaction. Lowly curved vesicles recruit melittins with a low density of binding sites. Surplus peptides are prone to form oligomers and shallowly adsorb on the surface of membrane via electrostatic interaction. The penetration of monomers induces membrane pore formation and positive membrane curvature, which promote vesicle budding. The adsorption of oligomers induces negative membrane curvature, which promotes vesicle invagination. This work demonstrates that antimicrobial peptides adopt multiple actions to destroy bacterial membranes.

Introduction

During cellular processes such as endocytosis and exocytosis, the cell membrane undergoes various morphological changes and leakage, which are governed by the interplay between proteins (or peptides) and lipid membranes. Antimicrobial peptides (AMPs) are one of the most common examples of peptides that modify the membrane structure. AMPs are small and positively charged peptides that pursue antimicrobial activities against bacteria, fungi, and other generalized targets (1, 2, 3). Although they have diverse molecular and secondary structures, it is widely accepted that the interaction of AMPs with the bacterial membrane is central to their toxicities (1, 2, 3, 4).

Numerous studies have illustrated that the mechanism of cell death induced by AMPs may involve both membrane disruption and processes that are not membrane disruptive (4). Membrane-disruptive peptides usually insert into the lipid headgroup region of the membrane and cause thinning of the chain region, which creates internal membrane tension at low peptide concentration. Upon reaching a critical concentration, the peptides start to form equilibrated pores to release the tension. Several pore models have been suggested, such as “barrel-stave,” “carpet,” and “toroidal” holes that allow leakage of cytoplasmic components (5, 6, 7, 8, 9). In contrast, nondisruptive peptides translocate across the membrane via transient pores and act on cytoplasmic targets (4).

Pore formation may not adequately explain the mechanism of AMPs. Various membrane shape changes induced by AMPs have been observed, such as local lipid accumulation with effective vesicle area reduction (8, 9, 10, 11), budding of giant phospholipid vesicles (12, 13, 14, 15), and tubular protrusion from supported phospholipid bilayers (16). Atomic force microscopy studies have also examined the effect of AMPs on the cell’s enveloping of Escherichia coli and revealed distinct membrane morphology changes, including surface corrugation (roughness) and surface-bound vesiculation (17, 18). Such highly dynamic changes in the membrane curvature are probably a consequence of different mechanisms of AMPs. Nevertheless, it is unclear whether the same or different chemical and physical effects determine these rich morphology changes and formation of membrane pores.

AMPs are small amphipathic peptides. Upon binding to the membrane, their small hydrophobic motifs are prone to insertion into the lipid headgroup and perturb the membrane. Continuum elastic models suggest that inducing local membrane curvature and pores are efficient ways to relax the inclusion-induced stress (19, 20). However, these models rely on assumptions about the local elastic properties, which are difficult to to be verified experimentally, and there is a lack of specific interactions between peptides and lipids (21).

Alternatively, molecular dynamics (MD) simulations can be used to obtain dynamic membrane models that feature the complicated interplay between peptides and lipids with molecular details. For example, all-atom (AA) MD simulations have been employed to model the pore formation and micellar disaggregation mechanisms of magainin (22), melittin (23), HIV-1 Tat (24), and cyclic peptides (25) interacting with a model phospholipid membrane. However, AAMD simulations are limited to systems that contain only a few hundred lipids and a couple of peptides at a nanosecond timescale. Peptide-induced cell death covers timescales ranging from nanoseconds to seconds and involves thousands of lipids. Coarse-grained (CG) models are therefore required to simulate these processes in larger systems and for longer times.

The CG MARTINI force field has been used to observe the spontaneous buckling and budding of a lipid bilayer induced by magainin 2, which were presumed to lead to very large transient pores that were larger than what was indicated by the equilibrium structures (26). We recently presented systematic CG dissipative particle dynamics (DPD) simulations of various types of antimicrobial peptides with different secondary structures interacting with a lipid bilayer membrane (27, 28, 29, 30). We found that peptides use multiple mechanisms to exert their membrane-disruptive activities, which involve stable pores, transient pores, and buckling. However, both the AAMD and CGMD simulations mainly focus on the planar bilayer with periodic boundary conditions. It remains unclear whether the buckling is related to the corrugation and vesiculation as found in experiments. Therefore, an appropriate model should include a vesicle interacting with peptides without the periodic boundary limitation. However, most CG methods (such as MARTINI and DPD) with an explicit solvent are still not efficient in simulating the long-time dynamics of large vesicles. To date, only the DPD method has been used by us to simulate a small vesicle containing 1200 lipid molecules and with a radius of 7 nm and its interaction with model AMPs (28). We found that the small vesicle was ruptured by the AMPs and resealed again. Nevertheless, the response of larger vesicles to AMPs still remains to be investigated.

“Dry MARTINI” is a recently developed solvent-free CG method that allows simulations on the dynamics of vesicles with diameters of up to 50 nm and a timescale of 1 μs (31). In this work, we use this method to study the interactions between the AMP melittins and phospholipid vesicles with different size. We demonstrate that vesicle curvature and peptide concentration are two important factors in modulating the peptide-binding sites and the forms of interactions between lipids and peptides, which in turn influence the shapes and leakage of the membrane. This work provides a complete picture of the responses of vesicles to pore-forming antimicrobial peptides and reveals the corresponding hidden mechanisms.

Methods

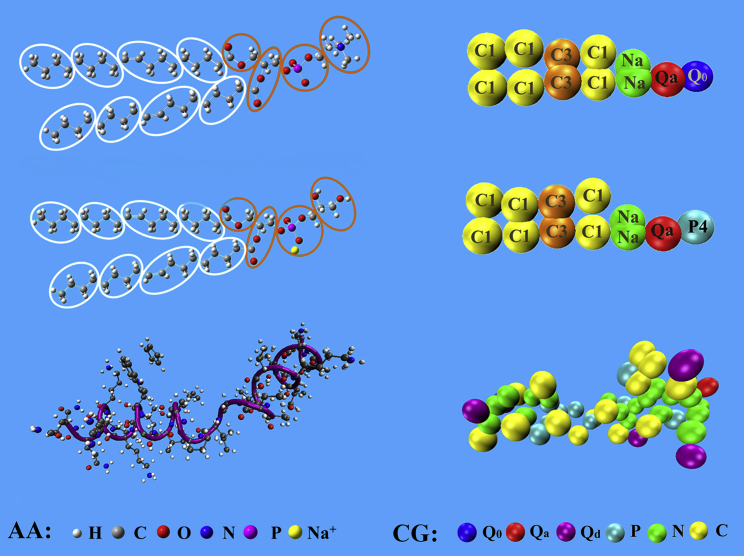
Solvent-free versions of CG Dry MARTINI simulations (31) were performed with version 5.0.4 of the GROMACS package (32, 33, 34, 35). As shown in Fig. 1, linearly connected interacting beads represent the CG models of dioleoyl phosphatidylcholine (DOPC) lipid, dioleoyl phosphatidylglycerol (DOPG) lipid, and melittin molecule in α-helix structure. Accordingly, a lipid molecule was modeled as a polymer connected by harmonic bonds, which consisted of four hydrophilic head beads and two tails. One or more side-chain beads attached to one backbone bead represented an amino acid residue. Harmonic bonds also connected the backbone beads of a peptide. The CG beads were sorted into charged (Q), polar (P), nonpolar (N), and apolar (C) types. Each type was further divided into sublevels based on their hydrogen donor capacities (d), hydrogen acceptor capacities (a), lack of hydrogen bond forming capacities (0), or by a number indicating the degree of polarity (from 1 for low polarity to 5 for high polarity). The nonbonded interactions between the beads were described by shifted Lennard-Jones 12-6 potentials and Coulomb interactions. The nonbonded interaction matrix underlying the MARTINI force field was reparametrized in Dry MARTINI to account for the omitted solvent degrees of freedom. The original publication of Dry MARTINI was only for lipids (31). Based on the types of CG beads (36, 37), the interaction parameters can be easily extended to peptide with same interaction levels given in (31). The potentials of mean force for moving the amino acid side-chain analogs and backbone bead of melittin obtained by Dry MARTINI (Fig. S1) are in satisfactory agreement with those obtained by wet MARTINI (36, 37) except for the side chain of residue TRP. In the MARTINI model, four overlapped beads (three C-type beads and one P1-type bead) represented the large ring structure of TRP. The implicit description for water may overestimate the hydrophilicity of this aromatic ring. Nevertheless, a melittin only contains one TRP residue, which might not significantly alter the melittin-lipid interactions. The same as in the normal wet MARTINI model, bonded interaction parameters were obtained from AAMD simulations, including bond stretching, angle bending, and dihedral angle distortions (31, 36, 37).

Figure 1.

CG models of DOPC lipid, DOPG lipid, and melittin molecule. To see this figure in color, go online.

Self-assembling from planar bilayers was used to prepare vesicles containing 1600, 3200, 4800, 6400, 8000, and 9600 lipids with radii of 8.5, 11.2, 13.2, 14.9, 16.4, and 17.6 nm, respectively. Each bilayer was composed of 70% zwitterionic DOPC and 30% anionic DOPG lipids. In this assembly process, Na⁺ ions were added to the system to keep it neutral. CGMD simulations were performed with the second-order stochastic dynamics integrator in GROMACS, with the friction in the Langevin equation having a time constant of τ_T = 4.0 ps. All simulations were conducted in a constant-number, constant-volume, and constant-temperature ensemble (NVT, V = 150 × 150 × 150 nm³, T = 298 K) with periodic boundary conditions. After a vesicle assembled, we calculated the density distribution of Na⁺ ions, as given in Fig. S2. It clearly shows that the counterions are denser near the anionic surfaces of the membrane, but the maximal density is only ∼4 times the bulk value. The release of counterions from the membrane surfaces allows the follow-up AMPs to bind to the membrane efficiently. Then, α-helical melittins were placed ∼1 nm away from the surface of the vesicle. The peptide concentration was denoted by the peptide/lipid molar ratio P/L and ranged from 1/100 to 10/100. Experiments showed that almost all of the melittins were able to bind to the vesicle in α-helical secondary structures in this range of P/L (38). At the same time, Na⁺ ions in the same amount of charge as the melittins were randomly removed from the exterior environment of the vesicle. A certain number of Cl⁻ ions were also added when the charges of peptides exceeded the amount of Na⁺ ions outside the vesicle. For each system, five independent samples were prepared. Each sample was simulated for 1 μs.

The surface tension of a vesicle of radius R was calculated by (39)

$${\sum }_V=-\left(\frac{1}{R^2}\right)\underset{0}{\overset{\infty }{\int }}dr{r}^2\left[P_T\left(r\right)-P_{rr}\left(r\right)\right],$$ (1)

where P_T(r) and P_rr(r) are the tangential and radial pressure tensors, respectively. The pressure tensor in spherical coordinates was transformed from Cartesian coordinates and was then implemented in the GROMACS package (32, 33, 34, 35).

To examine the lipid disordering and spontaneous membrane curvature induced by peptides, we simulated one peptide monomer, dimer, trimer, or tetramer binding onto a planar bilayer. The initial oligomer structures were obtained by assembling two, three, or four peptides in a cluster in a water box and performing an explicit-solvent CGMD simulation for 1 μs. The bilayer was composed of 512 lipids with the same DOPC:DOPG = 7:3 ratio as vesicles. Because at low P/L the assembled oligomer tended to dissociate into monomers when it approached the membrane surface, here we applied a rigid-body constraint to retain the oligomer structures.

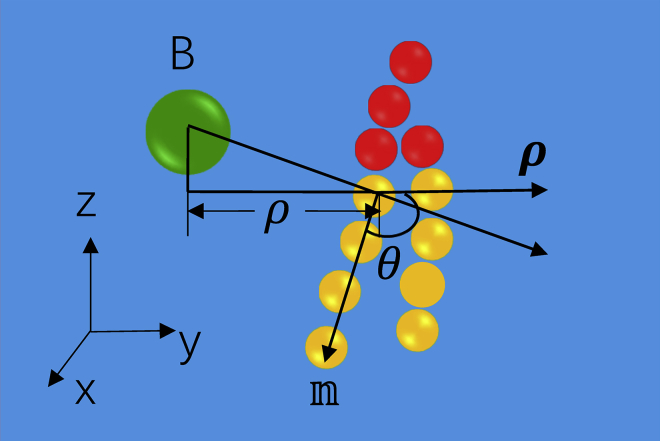
The tilt angle θ of a lipid near a peptide monomer was defined as the angle between the tail vector and a vector ρ from a peptide to a lipid, as shown in Fig. 2. Here, was a unit vector from the top hydrophobic tail bead proximal to the headgroup to the end hydrophobic tail bead, and ρ was a vector from a peptide backbone bead to the top tail bead projecting onto the bilayer plane (or xy plane). θ(ρ) was calculated by averaging over the peptide backbone beads, over the lipid molecules inside a ring with an inner radius of ρ − 0.5Δρ and outer radius ρ + 0.5Δρ, and over 500 samples. Δρ was set as 0.5 nm. For the peptide dimer-, trimer-, and tetramer-induced lipid tilting, θ(ρ) was estimated more roughly by setting the projecting vector between a lipid top tail bead and the center of mass of the oligomer as ρ. The mean tilt angle θ_M underneath a peptide monomer or oligomer was calculated by taking the average of θ(ρ) within a region before θ approaches the equilibrium value of 90°. To obtain the samples, a long trajectory of one peptide monomer or oligomer adsorbed on the bilayer was simulated for 1 μs. Then, 500 samples with a time separation of 1 ns were evenly chosen from the trajectory in the last 500 ns. These samples were also used for the calculation of bending rigidity and spontaneous curvature of the membrane.

Figure 2.

Sketch of the tilt angle of a lipid near a peptide monomer. B represents a peptide backbone bead. The planar bilayer normal is in the z direction. To see this figure in color, go online.

The spontaneous curvature C_s was obtained from the stress profile of a planar bilayer using the relation (40, 41, 42)

$$2\kappa C_s=-\underset{-\infty }{\overset{+\infty }{\int }}zs\left(z\right)dz,$$ (2)

provided that the membrane was initially tensionless and the binding of inclusions did not significantly fluctuate the membrane. The pressure tensor with tangential component P_T = P_xx = P_yy and normal component P_N determined the stress profile

$$s\left(\text{z}\right)=P_N-P_T\left(z\right)$$ (3)

and bilayer tension

$${\sum }_B=\underset{-\infty }{\overset{+\infty }{\int }}s\left(z\right)dz.$$ (4)

In Eq. 2, κ was the membrane bending rigidity, which can be obtained by fitting the spectra of lipid orientation fluctuation (43, 44). In the orientation fluctuation method, the bilayer was mapped to a coarser discrete grid with spacing h (∼1.3 nm). The lipid molecular orientations 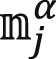(α = 1 and 2 denoting upper and lower monolayer and j denoting the jth tail) were first projected onto the xy plane and then mapped onto a two-dimensional real-space grid, which yielded n^α(r), representing the average value of projected belonging to lattice (m_x,m_y). Here, r = hm, and m = m_xi + m_yj. The Fourier transformation of the lipid orientation vector $\mathit{n}\left(\mathit{r}\right)=\frac{1}{2}\left[{\mathit{n}}^1\left(\mathit{r}\right)-{\mathit{n}}^2\left(\mathit{r}\right)\right]$ was

$${\hat{\mathit{n}}}_q=\frac{h^2}{L_x{L}_y}\sum _{\mathit{m}}\mathit{n}\left(\mathit{r}\right)e^{-i\mathit{q}\cdot \mathit{r}},$$ (5)

with $\mathit{q}=\left(\frac{2\pi m_x}{L_x},\frac{2\pi m_y}{L_y}\right)$, where $-\frac{L_x}{2h}\le m_x<\frac{L_x}{2h}$, and $-\frac{L_y}{2h}\le m_y<\frac{L_y}{2h}$. The thermal fluctuations in lipid orientation followed

(6)

Here, ${\hat{\mathit{n}}}_q^{\parallel }=\left[\mathit{q}\cdot {\hat{\mathit{n}}}_q\right]/q$ was the longitudinal component of ${\hat{\mathit{n}}}_q$. For a bilayer with modest size, fitting of Eq. 6. as a function of q gave the bending rigidity κ.

Results

Vesicle morphologies induced by AMPs

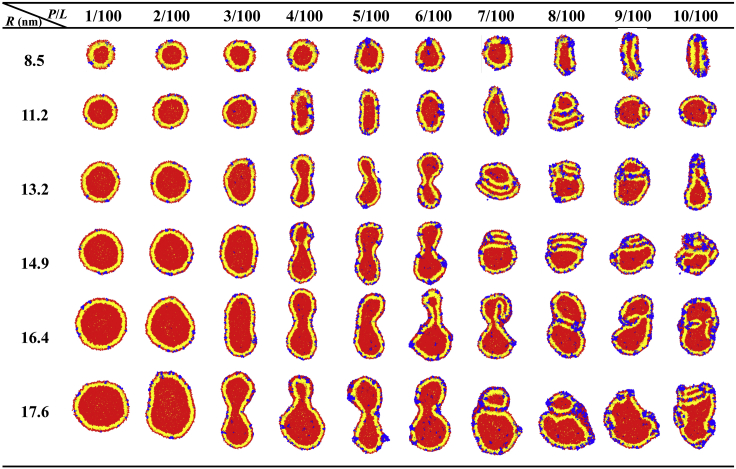
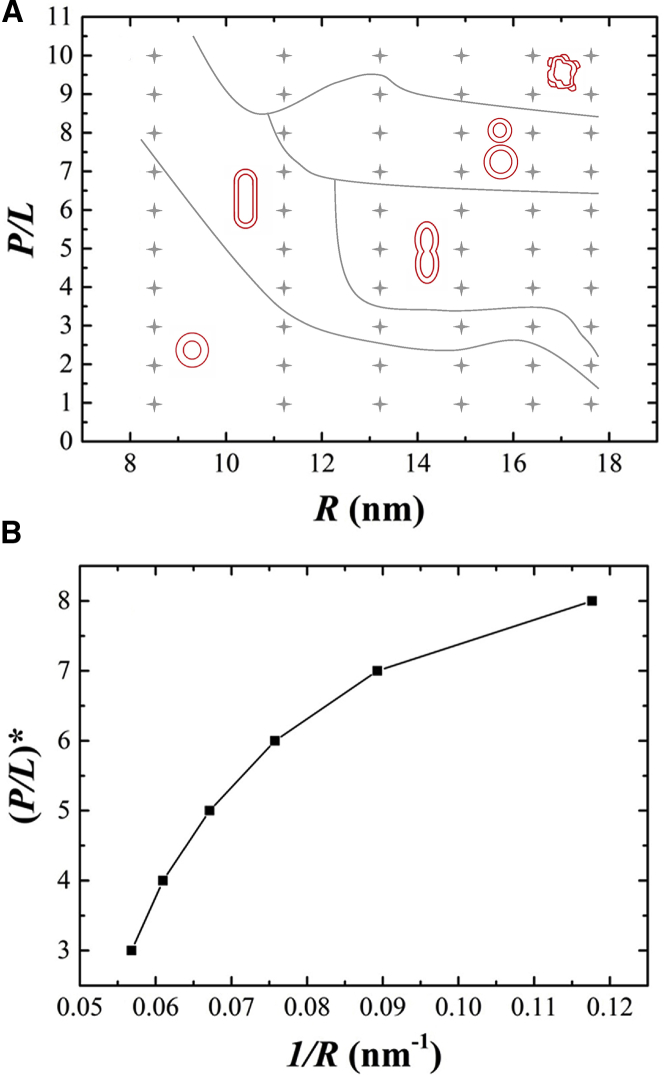
We simulated vesicles composed of 70% zwitterionic DOPC and 30% anionic DOPG lipids with a radius R ranging from 8.5 to 17.6 nm and interacting with melittins on their exterior surfaces. Fig. 3 presents typical images of simulations for 1 μs. Rich morphologies were observed, including intact spherical vesicles, prolate ellipsoidal vesicles, dumbbell vesicles, outside budded vesicle, and corrugated vesicles. These shape transformations strongly depend on the vesicle size or membrane curvature (for a spherical vesicle of radius R, its curvature is 1/R), as well as peptide concentration. The dependencies are illustrated in the rough phase diagram in Fig. 4 A.

Figure 3.

Cross-sectional snapshots of different-sized vesicles interacting with melittins at various peptide concentrations at a simulation time of 1 μs. Red, yellow, and blue beads represent the lipid headgroups, lipid tails, and peptides, respectively. To see this figure in color, go online.

Figure 4.

(A) Rough phase diagram of melittin-induced vesicle morphology (peptide/lipid molar ratio versus vesicle radius). The solid lines separating the regions are not actual phase boundaries but guides to the eye. (B) The critical peptide/lipid molar ratio (P/L)^∗, at which a vesicle retains a spherical shape, is shown as a function of vesicle curvature 1/R. To see this figure in color, go online.

For a tiny vesicle (R = 8.5 nm) with a large positive curvature, AMPs are adsorbed onto the vesicle surface but do not deform the spherical shape in a wide range of peptide concentrations (P/L from 1/100 to 7/100). The tiny vesicle can only be elongated when the peptide concentration is very high. If the size of the vesicle increases, the vesicles can be deformed by peptides at relatively low concentrations. Beyond simply being elongated, bigger vesicles buckle into dumbbell shapes as a result of the inclusion of peptides. At higher peptide concentrations, these dumbbells even transition to the formation of a daughter vesicle that connects to the mother vesicle. When the vesicles are exposed to even higher concentrations of peptides, they transform into irregular shapes with very rough and vague surfaces. Such rough surfaces contain lipid-wrapped peptide blebs and multilayered membrane corrugations. The phase diagram shows that there is a critical P/L value below which the vesicle remains in spherical shape; when the peptide concentration exceeds the critical value, the vesicles exhibit global shape changes. Fig. 4 B indicates that this critical ratio (P/L)^∗ increases monotonically as the vesicle curvature 1/R increases.

Membrane pore formation induced by AMPs

In association with the vesicle deformation, transmembrane pores that include one or more melittins were observed at sufficiently high peptide concentration (see Fig. 3). Interestingly, the pores in a larger vesicle start to form at a lower P/L ratio than those in a smaller vesicle. However, the pores in smaller vesicles are larger. For example, the critical pore forming P/L is 5/100 for a vesicle with a radius of R = 8.5 nm. The pore can accommodate up to five to six peptides (Fig. S3). For a vesicle with R = 17.6 nm, the critical P/L is as low as 3/100. A pore in such big vesicle only maximally contains two to three peptides (Fig. S3). More pores were observed when the concentration of peptide increased. However, for a larger vesicle, the number of pores reaches a maximal value at certain P/L (around 6/100 for R = 17.6 nm). Beyond this concentration, the AMPs induce fewer permeable pores but increase the surface area of the vesicle and cause corrugation. This means that surprisingly, a larger vesicle can survive at higher peptide concentrations.

Shape evolution of peptide-bound vesicles

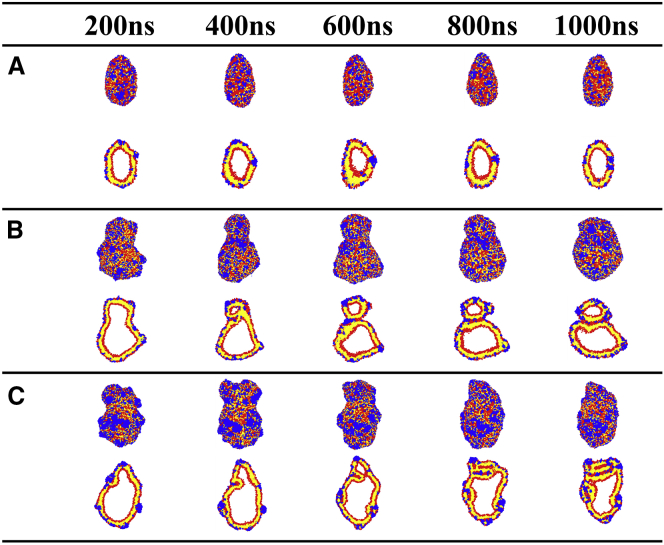
We investigated the kinetics of the peptide-induced vesicle transformation by tracking the time evolution of three typical vesicle shapes: a prolate ellipsoid, a mother vesicle with a bud, and a corrugated vesicle.

Figs. 5 A and S4 present a time sequence of snapshots of relatively small vesicles with radius of 11.2 nm interacting with melittins at a concentration of P/L = 6/100. Similar to the process of melittin perturbing a planar bilayer (27, 28, 29, 30), the peptides initially bind onto the vesicle in monomers with their helical axes oriented parallel to the surface of the membrane. Their hydrophilic faces extend into the solvent, whereas the hydrophobic faces are buried in the hydrocarbon core of the membrane. The binding of AMPs compresses the lipids on the outer leaflet, which induces local membrane fluctuation. The penetration of the peptides also thins the membrane and allows AMPs to insert and form small pores. An initial pore only contains one or two peptides. Later on, more peptides and lipid headgroups are able to enter this pore and enlarge it to an intermediate-sized, permeable, and stable hole. In this condition, the local membrane fluctuation is weak. After pore formation, the local compression is partially released, and the vesicle deforms into an ellipsoid.

Figure 5.

Time evolution of three typical vesicle shape transformations induced by melittins: (A) prolate ellipsoid, (B) mother vesicle with bud, and (C) corrugated vesicle. The upper panel shows the exterior view of a whole vesicle; the lower panel shows a cut slice of the vesicle. To see this figure in color, go online.

Fig. 5 B presents the budding evolution of a larger vesicle with radius of 17.6 nm interacting with melittins at a peptide concentration of P/L = 8/100. In this condition, the adsorption of peptide sufficiently increases the membrane area of the outer leaflet and induces strong local fluctuation. This local fluctuation cannot be efficiently released via pore formation because the pores are usually small in this case. Alternatively, the vesicle adopts dumbbell shape that buckles to release the peptide-induced local compression. As the neck of the dumbbell becomes narrow, the membrane starts to contact and fuse. Subsequently, a daughter vesicle connected to the mother vesicle forms.

Fig. 5 C presents the evolutions of a corrugated vesicle with a radius of 17.6 nm induced by melittins at concentration of P/L = 10/100. The lipids in such a large vesicle pack more tightly than lipids in a smaller vesicle. The vesicle can only recruit melittin monomers with a relatively low density of binding sites. The surplus AMPs are prone to associate into oligomers as they approach the vesicle surfaces. The bundled peptide oligomers do not penetrate deeply into the membrane. In contrast, they extract lipids to wrap them up and form blebs. Some blebs can even transform into tubular invaginations when more peptides are involved, which leads to very rough and blurred vesicle surfaces.

The clustering of the peptides was estimated by calculating the radial distribution function (RDF) between the center of mass of the peptides. Because the peptides distribute on the surfaces of vesicles, the RDF was defined as the relative area density of peptide in a ring on the surface of a spherical vesicle as a function of the chord length between peptides A and B (Fig. 6), i.e., $g\left(r\right)=\frac{{\sum }_{i\in \text{A}}{\sum }_{j\in \text{B}}\delta \left(r-r_{ij}\right)\times 4\pi R^2}{N_{\text{peptide}}\times \left(N_{\text{peptide}}-1\right)\times 2\pi rsin\theta \mathit{\Delta }r}$. Because the peptide-bound vesicles are not perfect spheres, this method only provides rough estimate of the correlation between the peptides. Fig. 6 B shows that at low peptide concentration (P/L < 3/100), the RDF profiles slowly grow to relatively flat curves, indicating that the peptides uniformly distribute on the surfaces of vesicles without forming clusters. At higher P/L ratios, the RDFs exhibit obvious peak structures at short distances, indicating that the peptides aggregate into oligomers. The number of peptides inside the peak shell represents the average size of the oligomers. Fig. 6 C shows that the size of oligomer increases with peptide concentration and vesicle radius. A few abnormal points at medium and high P/L in Fig. 6 C imply that the vesicle’s shape significantly deviates from a sphere.

Figure 6.

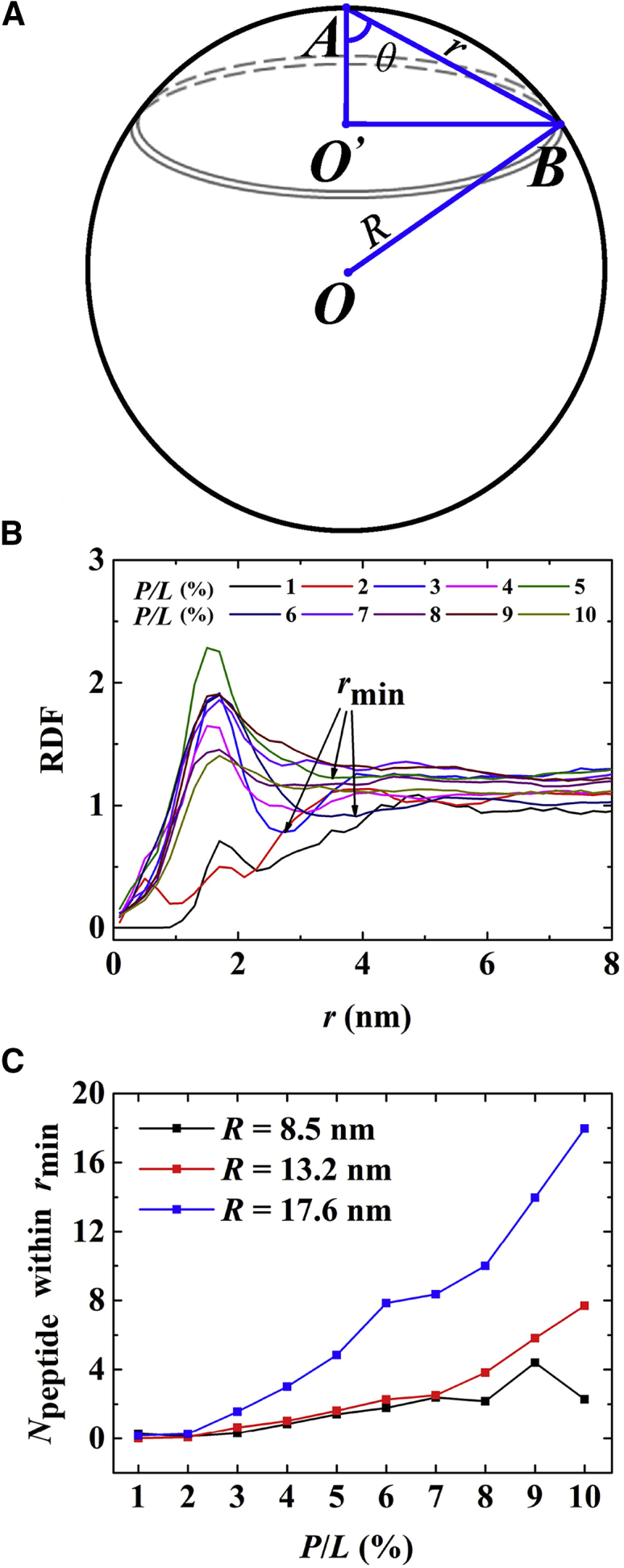
(A) Definition of the ring on the surface of a sphere for calculation of the RDF between melittins. (B) Typical RDFs of melittins with various concentration binding to vesicles with radius of 17.6 nm are shown. (C) The number of peptides in the first shell of RDF is shown as a function of P/L, which indicates the clustering of the peptides. To see this figure in color, go online.

Lipid tilting and spontaneous membrane curvature induced by peptide binding

To investigate the molecular mechanism of the complicated vesicle morphological transformation, we quantitatively examined the peptide-induced lipid disordering and spontaneous membrane curvature. A vesicle’s curvature has monotonic increasing relation with its membrane tension (Fig. S5). Thus, for a convenient and accurate calculation, the lipid disordering induced by peptides was estimated by simulating planar bilayers with a series of initial tension interacting with melittins (Fig. S6). The disordering was defined as the lipid tilt angle θ relative to the bilayer plane. The spontaneous membrane curvature was also obtained from planar bilayers. A detailed definition and calculation of the tilt angle and spontaneous membrane curvature were given in Methods.

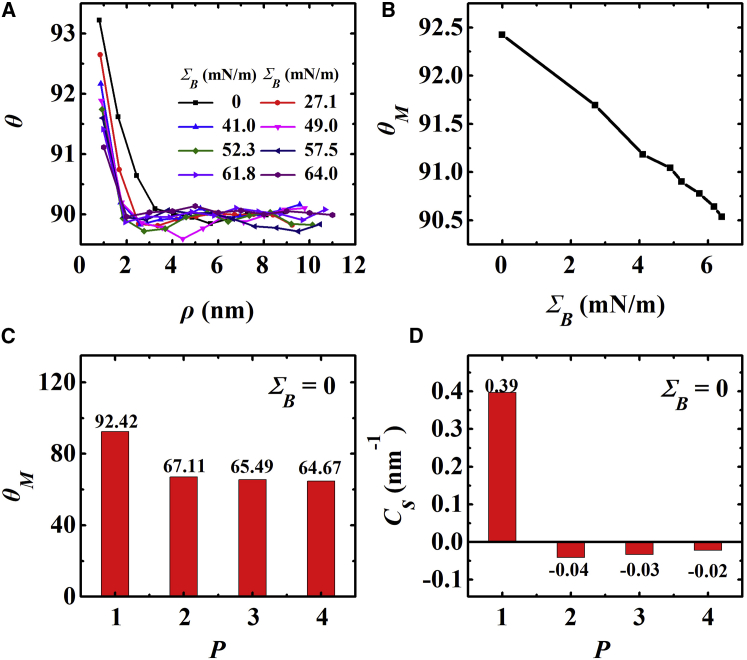
Fig. 7 A shows that the binding of a melittin monomer leads to the surrounding lipids tilting toward the hydrophobic portion of the peptide, i.e., θ > 90°. The lipids close to the peptide tilt more significantly than those lipids far from the peptide. Moreover, the average tilt angle θ_M for lipids underneath a peptide decreases if the membrane has higher tension (Fig. 7 B). In contrast, the binding of a melittin dimer, trimer, or tetramer leads to lipid tails splaying away from the peptide, i.e., θ_M < 90°, as shown in Fig. 7 C. In accord with the lipid tilting, the bending rigidity of the membrane decreases from 6.34 × 10⁻²⁰ J for a pure lipid bilayer to 5.73, 3.94, 3.45, and 3.88 × 10⁻²⁰ J for bilayers with binding of peptide monomer, dimer, trimer, and tetramer, respectively (see the spectra of lipid orientation fluctuation in Fig. S7). Note that we did not simulate melittin oligomers binding on a tensed membrane because the restrained bundle favors insertion into a tensed membrane. A lipid tilt angle larger than 90° (or smaller than 90°) implies that the peptide induces a positive (or negative) membrane curvature. This prediction is confirmed by the spontaneous curvatures obtained from the integration of the product of the membrane’s stress tensor (Fig. S8) and the bilayer normal coordinate (Eq. 2). As shown in Fig. 7 D, the binding of peptide monomer onto a bilayer composed of 512 lipids induces positive spontaneous curvature as large as 0.4 nm⁻¹, whereas dimer, trimer, and tetramer all induce negative curvatures with values less than 0.05 nm⁻¹.

Figure 7.

(A) Melittin-induced lipid tilt angle as a function of the distance between a melittin monomer and surrounding lipids. Data were obtained from lipid bilayers with different initial membrane tension. (B) The mean tilt angle for lipids underneath a peptide monomer as a function of initial membrane tension is shown. (C) The mean lipid tilt angle induced by the binding of melittin monomer, dimer, trimer, and tetramer on an initially tensionless bilayer is shown. (D) Spontaneous membrane curvature induced by the binding of melittin monomer, dimer, trimer, and tetramer on an initially tensionless bilayer is shown. To see this figure in color, go online.

Gómez-Llobregat et al. reported that the spontaneous membrane curvature induced by melittin monomer was 0.23 nm⁻¹ (45), less than the value obtained by us. In their method, they studied the membrane-curvature-dependent binding free energy by tracking positions and orientations of single melittin interacting with a buckled lipid bilayer. Then spontaneous curvature was obtained indirectly by fitting the binding free energy to a quadratic model. To estimate the position and orientation of the peptide, they assumed that the lipid bilayer only buckled in one direction and the melittin monomer was a rigid rod. In contrast, the calculation of spontaneous curvature in our method is direct and free of any approximation.

In a recent work, Paterson et al. performed dye leakage experiments of giant unilamellar vesicles (GUVs) exposed to melittin and magainin 2 by using a high-throughput microfluidic device (46). By generating extensive dye leakage data sets, they proposed that melittin acted as a negative-curvature-inducing wedge because they found that membrane containing positive-curvature lipids inhibited melittin-induced pore formation. Their conclusion was based on the assumption that melittin monomer was the active species disrupting the membrane. However, our simulations show that both melittin monomer and oligomer can modify the structure of the membrane; the monomer induces positive curvature, whereas the oligomer induces negative curvature. Our results imply that it is not sufficient to interpret the AMPs’ membrane-disruptive behavior by only considering the topology of a single peptide monomer; the aggregation of AMPs also plays an important role.

Discussion

The responses of phospholipid vesicles to the pore-forming AMPs predicted by our simulations show good agreement with experimental results. For example, optical and fluorescence microscopy measurements of magainin 2 (13), melittin (8, 9, 12, 14), mastoparan (10), cecropin-melittin hybrid antimicrobial peptide BP100 (11), and gomesin (15) revealed that the behavior of a vesicle depends on the concentration of peptide. At low peptide concentration, the adsorption of AMPs caused the leakage of water and ions from the vesicle but did not disrupt the liposomes or change the membrane structure. At medium concentration, the membrane became permeable to large molecules, and the vesicle was lysed. Before the pore formation, the shape of the vesicle changed. Formations of pear and pearl chain buds were found. At high concentration, the vesicle survived, but the membrane surface area increased, and lipids formed dense clusters. The simulation results are also qualitatively consistent with the high-resolution atomic force microscopy images of the cell envelope of E. coli treated by AMPs (17, 18). Similar to our observations, nanometer images showed that AMPs induced the formation of groove- and pore-like lesions on the surface of E. coli. At the highly curved apical ends, obvious collapse of cell structure was observed (17, 18). These agreements indicate that our CG simulations capture the main features of the peptide-vesicle complexes.

The advantage of the simulation methods is their facility to provide detailed structures of the membrane that are unresolved by optical methods, such as the structures of pores, blebs, and grooves. More importantly, our work also reveals the mechanisms of the rich membrane morphology changes at the molecular level. We found that peptide concentration, membrane curvature, and peptide binding sites have combining effects in regulating the interactions between melittins and vesicles. In the following, we will discuss these effects in detail and compare them with relevant experiments.

Effects of peptide concentration

The peptide concentration affects the forms of the AMPs interacting with vesicles, as well as the responses of the vesicle to the inclusion of peptides. At a relatively low peptide concentration, the electrostatic repulsion between cationic AMPs promotes their separation and individual interaction as monomers with the membrane. These amphiphilic monomers are prone to adsorb onto the membrane surface in a parallel state. The peptide inclusion disrupts the lipid packing and increases the membrane area through an amphipathic wedge-like mechanism, but it is not enough to cause global changes in membrane shape at relatively low concentrations. Only when the peptide concentration is above a critical value do the local disordered areas correlate and interplay, leading to global transformation of the vesicle shape. Some peptides, especially those in regions of high peptide-binding density, have the possibility of switching from a parallel binding state to a transmembrane insertion state and creating membrane pores.

At higher peptide concentrations, the number of AMP monomers that are bound to the membrane approaches saturation. Surplus peptides tend to associate into oligomer bundles via hydrophobic interactions. These oligomers have hydrophobic cores and hydrophilic and positively charged surfaces, as shown in Fig. S3 D. They mainly interact with the membrane via electrostatic attraction, extracting the lipids from the membrane to wrap over their surfaces rather than penetrating into the hydrophobic core of the membrane.

Recent experiments on epsin1-, AP180-, and green-fluorescent-protein-treated GUVs demonstrated that collision among crowded membrane-bound proteins generated pressures that could stretch, bend, and ultimately disrupt the membrane surface, leading to budding and fission (47, 48, 49). The efficiency of fission was found to be determined only by the membrane coverage by protein, regardless of the helix hydrophobicity of the proteins. According to those experimental results (47, 48, 49), the crowding of protein mainly modifies the thickness and spacing of the hydrophilic layer of the protein-binding leaflet, which might be equivalent to increasing the hydrophilicity of the leaflet or the effective sizes of the headgroups of lipids. The hydrophilic asymmetry between the two leaflets of the membrane eventually generates positive curvature. This mechanism may also be applicable to the rich vesicle shape transitions induced by melittin. However, a melittin molecule has a much smaller size than epsin1, AP180, or green fluorescent protein. The protein crowding mechanism might be subtle. In fact, we find out that at the critical (P/L)^∗ ratios at which vesicles start to deform (Fig. 4 B), the α-helical melittin monomers already occupy more than 30% of the membrane area, which exceeds the required area fraction of 10–25% to generate vesicle shape transition as predicted by continuum model (19). (Given the area per lipid of 0.7 nm² and area per peptide of 4 nm² (50), the area fraction occupied by peptide monomers is ∼2 × P/L × 4/0.7.) Therefore, we believe that amphipathic wedge-like insertion is the main mechanism adopted by melittin to induce positive membrane curvature and vesicle budding.

Effects of membrane curvature

The first role of membrane curvature is to recruit amphipathic helices. Positive curvature of a membrane induces lipid tilting and exposes hydrophobic cavities. In other words, changes in membrane curvature accentuate lipid-packing defects and generate membrane stresses. A smaller and highly curved vesicle favors the recruitment of melittins with a higher density of binding sites without exhibiting obvious shape deformation. This effect is similar to many peripheral proteins binding to curved membrane (51, 52, 53). The wedge-shaped peripheral proteins recognize the lipid-packing defects by preferentially adsorbing to a positively curved membrane though the insertion of an amphipathic sequence, which can effectively release the curvature-correlated stress. These facts also suggest that there is a critical curvature-dependent peptide concentration above which hydrophobic interactions may saturate. Surplus AMPs may then bind to the membrane through curvature-nonselective interactions, such as electrostatic interactions. Because melittin is not only a membrane-curvature-sensing peptide but also a curvature-inducing peptide (see the forthcoming discussion), as a rough approximation, we regard the maximal peptide/lipid molar ratio (P/L)^∗ at which a vesicle retains a spherical shape as the curvature-based saturation peptide concentration. We found that this critical saturation concentration is almost proportional to the vesicle curvature (Fig. 4 B). Above this critical concentration, AMPs tend to associate into clusters rather than penetrate into the membrane as monomers. This explains well why there are more peptide oligomers on the surfaces of larger vesicles at the same P/L > (P/L)^∗.

Another role of membrane curvature is to modulate the peptide penetration depth and the local tilting of lipids around the peptide and consequently the membrane shape transition. Upon binding to the membrane surface, melittin refolds into a helical structure with well-separated amphipathic portions. Like many peripheral proteins (51, 52), the penetration of melittin’s hydrophobic moiety affects the distribution of lipid-packing defects by creating voids underneath the peptides, which stresses the membrane. To resist the stressing, the lipids around the peptide tend to tilt their tails to fill the voids. In a flat or lowly curved membrane, the peptide penetration is shallow, but the void is large. The surrounding lipids have to tilt substantially to fill the voids (Fig. 6). As a result, the area of the outer leaflet expands more dramatically than the inner leaflet. To match the area/volume ratio, the vesicle is prone to transform into dumbbell or external budded state. The lipid tilting also prompts the bound peptide to insert vertically into the membrane. Thus, at a relatively low peptide concentration, transmembrane peptide insertion can occur in a large vesicle. Nevertheless, a large vesicle has fewer defects that allow only a low density of peptides to penetrate into the hydrophobic core of the membrane. Therefore, the induced membrane pores are usually small and composed of a few peptides.

In contrast, for a highly curved membrane, the peptide penetration is much deeper such that the peptide may even touch the lipids in the opposing leaflet. As a result, the areas of both leaflets expand, and the membrane thins dramatically. In this case, however, the peptide-induced voids in the membrane are small. It is not necessary for the bound peptides and surrounding lipids to tilt to a large degree. The parallel peptide-binding state is relatively stable. Peptide insertion and translocation can occur only when the peptide density is sufficiently high. Nevertheless, because the peptides have a higher density of binding sites on a small vesicle, once a pore forms, it permits more peptide insertions and easily triggers vesicle rupture.

The smallest small unilamellar vesicle that can be prepared in experiments has a radius of 17.5 nm (54, 55), the same as the largest vesicle we simulated here. However, many experimental techniques commonly investigate the action of AMPs on large unilamellar vesicles and GUVs as well as bacterial cells with radii between 50 nm and 50 μm (56), which are much larger than the vesicles that we can investigate by simulations. It might be hard to compare our results directly and quantitatively with the optical microscopy observations on the AMP-treated GUVs and E. coli because of the length-scale difference. However, the opening of pores, the outside vesicle budding, and the surface corrugation observed in our simulations resemble the experimental results very well. The resemblance suggests that the AMPs’ mechanisms revealed by our simulations can be extrapolated to small unilamellar vesicles, large unilamellar vesicles, and GUVs.

Effects of peptide-lipid interaction sites

Melittins can interplay with lipids via hydrophobic and electrostatic interactions. The hydrophobic force promotes the hydrophobic motif of a peptide to insert into the lipid tail core of the membrane, whereas the electrostatic force facilitates the binding of charged amino acids of the peptide to the lipid headgroup. Accordingly, a melittin monomer prefers to reside at the membrane’s hydrophilic/hydrophobic interface because of the combination of hydrophobic and electrostatic interactions. This kind of peptide-lipid interaction site induces an asymmetrical lipid distribution in which the lipids in the proximal leaflet are compressed while lipids in the distal leaflet expand. This leads to a positive membrane curvature, transmembrane peptide insertion, and peptide translocation. Nevertheless, if the number of peptides exceeds the binding sites admissible by the lipid-packing defects, the late approaching peptides tend to associate into oligomers, which have hydrophilic shells and hydrophobic cores. They reside on the membrane surface and interact with the lipid heads mainly by electrostatic attraction, like hydrophilic nanoparticles (Fig. S3 D). The electrostatic attraction drags the charged lipid headgroups to wrap the hydrophilic surfaces of the oligomers. This kind of peptide-lipid interaction site leads to negative membrane curvature and invagination. The combination of monomer-induced budding (exocytosis) and oligomer-induced invagination (endocytosis) eventually results in a corrugated vesicle surface.

The variety of peptide-lipid interaction sites also effectively explains the vesicles’ survival and the increase in surface area at high peptide concentrations. These phenomena were previously explained by the membrane-resealing model (12). According to this model, large holes could be created in the membrane at high peptide concentrations, which permitted a larger efflux than influx of both water and large molecules, eventually allowing the membrane to reseal. At the same time, the continuous insertion of melittins into the membrane increased the surface area. Our previous explicit-solvent simulation for a small vesicle verified this mechanism (28). However, the resealing model might only be applicable to small and highly curved vesicles, which favor the recruitment of melittin monomers with a higher density of binding sites. For large vesicles, our simulations show that the peptide concentration mainly affects the number of transmembrane pores but not their sizes. Moreover, an increase in the peptide concentration only enhances the number of pores in a certain range. Above a critical concentration at which peptides start to form oligomers, the number of pores even decreases.

Based on our simulations, the surprising survival phenomenon of a vesicle can be interpreted in terms of asymmetric lipid packing. As mentioned, the binding of melittin monomers compresses the packing of lipids on the proximal leaflet and stresses the packing of the lipids on the distal leaflet; now, if there are hydrophilic bead-like oligomers approaching the membrane, they will preferentially utilize this asymmetric lipid packing by forming stabilized blebs and invagination structures. Such endocytosis structures facilitate compact lipid packing on the leaflet proximal to the peptides along with loosened lipid packing on the leaflet distal to the peptides. The exocytosis- and endocytosis-induced grooved vesicle surface not only expands the membrane area but also makes it unnecessary for the vesicles to release the peptide-induced compression and stress by forming pores to translocate lipids and peptides across the membrane. The vesicles are therefore rescued because of their lower leakage. Nevertheless, for a bacterial cell exposed to a high concentration of melittins, the peptide-induced corrugated surfaces already destroy the integrity of the membrane, which is sufficient to cause a loss of cell activities.

Melittin-induced membrane area changes were also observed in micropipette aspiration experiments of GUVs (8, 9). Those experiments showed that the projection length of GUVs inside the micropipette initially increased, which was then followed by a considerable decrease. Such phenomena were initially interpreted as a membrane area increase at constant volume followed by a volume increase at constant area (8, 9). Lee et al. (8, 9) proposed that the former process was caused by the wedge effect of melittin that stretched the lipid bilayer, whereas the latter process was caused by the opening of stable pores that allowed outside glucose but not the inside sucrose to pass, resulting in an osmotic imbalance with influx of water. Later on, Riske’s group proposed an alternative mechanism (56). They suggested that the effective vesicle area reduction was caused by the local lipid accumulation, which was evidenced by the bright fluorescence spots appearing on the vesicle surface concomitant with the retraction of the projection length inside the micropipette in (9). The phospholipid clustering was also observed in GUVs treated with mastoparan (10) and cecropin-melittin hybrid antimicrobial peptide BP100 (11) at a high P/L ratio. Riske et al. further supposed that peptide-mediated local membrane adhesion induced membrane folding/wrinkling and led to accumulation of lipids (10, 11, 56). The outcomes of our simulations prove this folding/wrinkling mechanism. More importantly, our simulations directly reveal that the predominant adhesion mediator is peptide oligomer.

Conclusion

Our simulations on the interactions between antimicrobial peptide melittins and lipid vesicles revealed that melittins induce not only membrane pore formation but also vesicle budding, which can develop into vesiculation at high peptide concentrations, as well as vesicle invagination, which can eventually result in a corrugated membrane surface. These rich morphology changes are mediated by the curvature of vesicles and the peptide concentration. Highly curved vesicles favor the recruitment of melittins with a higher density of binding sites. The AMPs mainly penetrate into the membrane surface in monomers via hydrophobic interaction. In contrast, low-curvature vesicles recruit melittins with a low density of binding sites. Surplus AMPs are prone to form oligomers and shallowly adsorb on the surface of the membrane via electrostatic interaction. According to a detailed analysis of the lipid orientation around AMPs and the induced spontaneous membrane curvature, the adsorption of monomer induces membrane pore formation and positive membrane curvature, which promotes vesicle budding. On the other hand, the adsorption of oligomer induces negative membrane curvature, which promotes vesicle invagination. The combination of AMP-induced vesicle budding, invagination, and pore formation eventually results in the loss of membrane activity.

Author Contributions

L.G. and W.F. designed the research. Y.S. and M.W. performed the research. Y.S., M.W., L.F., S.Z., and S.W. analyzed data. Y.S. and L.G. wrote the manuscript.

Editor: Alemayehu Gorfe.