Multivariate Analysis of Structural and Diffusion Imaging in Traumatic Brain Injury

Abstract

Rationale and Objectives

Diffusion tensor (DT) and T1 structural magnetic resonance images provide unique and complementary tools for quantifying the living brain. We leverage both modalities in a diffeomorphic normalization method that unifies analysis of clinical datasets in a consistent and inherently multivariate (MV) statistical framework. We use this technique to study MV effects of traumatic brain injury (TBI).

Materials and Methods

We contrast T1 and DT image-based measurements in the thalamus and hippocampus of twelve TBI survivors and nine matched controls normalized to a combined DT and T1 template space. The normalization method uses maps that are topology-preserving and unbiased. Normalization is based upon the full tensor of information at each voxel and, simultaneously, the similarity between high-resolution features derived from T1 data. The technique is termed symmetric normalization for multivariate neuroanatomy (SyNMN). Voxel-wise MV statistics on the local volume and mean diffusion are assessed with Hotelling’s T² test with correction for multiple comparisons.

Results

TBI significantly (FDR p < 0.05) reduces volume and increases mean diffusion at coincident locations in mediodorsal thalamus and anterior hippocampus.

Conclusion

SyNMN reveals evidence that traumatic brain injury compromises the limbic system. This TBI morphometry study and an additional performance evaluation contrasting SyNMN with other methods suggest that the DT component may aid normalization quality.

1 Introduction

Traumatic brain injury (TBI) is the most frequent cause of death and disability in individuals ages 15 to 24 and is also prevalent in older adults (1). TBI, most commonly caused by automotive accidents and falls, occurs at a rate of approximately 1 in 600 per year in the general population (1), whereas up to 10% of soldiers returning from Iraq may suffer from some form of TBI (2). Even mild TBI may lead to significant behavioral changes (3) and is very likely to be under-reported, particularly by those who have experienced concussion (4; 5). In consequence, up to two percent of individuals in the U.S. live with TBI-related disability. Thus, focus on TBI as a public health concern is increasing, along with further development of sensitive tools for assessing axonal and cortical injury (3; 6), tracking recovery from these injuries (7) and predicting outcome (8; 9).

Traditional T1 imaging may be used to uncover in vivo effects of TBI in the cortex and deep gray matter structures. Neuronal atrophy, due to concussion, was detected with T1 imaging and linked to ongoing depression (5), while TBI related reductions in gray matter concentration have also been correlated with attention deficits (10). Hippocampal volume may be reduced by TBI (11; 12), along with the basal forebrain (12). The thalamus appears to undergo injury during or after TBI as assessed post-mortem (13), through finite element models of TBI (4; 14) and through large-deformation tensor-based morphometry of control and subject populations (6). An additional post-mortem report indicated involvement of the mediodorsal thalamus, which has connections to the prefrontal cortex (15). This finding has also been validated at the cellular level through neuropathology (16) and through histochemical staining and explicit neuronal counts (17). TBI effects in hippocampus have also been verified neuropathologically (18).

Despite the value of T1 imaging for examining cortical atrophy, increasing evidence suggests that traditional magnetic resonance imaging has limited ability to detect TBI-related damage outside the cortex or deep gray matter, where diffusion tensor imaging may be more valuable (19; 20; 21; 22). Thus, the diffusion tensor imaging modality is emerging as the preferred mechanism for revealing traumatic axonal injury through a variety of diffusion-related measures. DT quantifies the level of diffusion in a primary direction (the principal direction or the direction of parallel diffusion - presumably along a fiber cluster) and in secondary and tertiary directions (the radial diffusion, in the two directions perpendicular to the main fiber direction). The mean of these values is the mean diffusion (MD), also known as the apparent diffusion coefficient (ADC). MD may be a useful biomarker in both white and gray matter and has been shown to relate to cellular integrity (23; 24) and may serve as a surrogate measure for gray matter loss (25). The variance of these three diffusion measures is called the fractional anisotropy (FA). FA takes values in the range zero to one and is a measure of white matter integrity when underlying cellular structure exhibits a preferred diffusion direction (where FA is greater than approximately 0.25) (24). Changes in diffusion are hypothesized to relate to axonal swelling in TBI (20) or myelin loss (23). DT may also be used to locate (interruptions in) fiber tracts (24; 26).

DT studies have analyzed these diffusion-related measures to show that TBI leads to strong effects in the corpus callosum (27; 28; 29; 30; 31; 20; 32), which may imply a disruption of brain connectivity (33; 26). Brain regions related to motor function are also affected (22; 34), but may also recover over time (35). White matter pathology caused by TBI may also appear in a number of fascicles and may lead to to cognitive deficits (3). A few studies have suggested that mean diffusion implies cortical injury or pathology (36; 25; 37). Increases in mean diffusion due to mild cognitive impairment (MCI) have been directly related to reductions in cognitive performance (38). Only one DT study has shown evidence of thalamic injury (39) despite the ability of DTI to detect the subdivisions of thalamus into its nuclei (40; 41). Such divisions are not visible in T1.

Thus, TBI induces both cortical injury, usually assessed with T1 structural images, and also axonal injury, captured in diffusion tensor imaging. These emerging very high resolution T1 (sub-millimeter) and diffusion tensor modalities provide a unique opportunity for computing image-based brain maps from a more complete picture of the underlying neuroanatomy. Towards this end, we develop a normalization procedure that uses both T1 images of fine gray matter (computational structure) and DT images of detailed white matter (connective tissue) at the same time and at their own intrinsic resolution to guide whole brain normalization. This technique will enable our TBI study to leverage both modalities in a template-based whole brain population normalization framework. We are thus able to perform a multivariate scalar and tensor driven statistical contrast between a TBI and matched control population. To our knowledge, this type of consistent cross-modality study has not been previously performed in any population.

There is little related work, in medical image registration, on the topic of using more than one modality to guide normalization. In 1993, Miller, et al. published likely the first multivariate deformable normalization method (42) and applied this method to map between a 2D patient and template dataset. Similarly, Park, et al (43) developed a multiple channel elastic DT registration method for simultaneously mapping T2 and fractional anisotropy images. The full tensor is not used in Park’s normalization. Similarly, Studholme (44) proposes a method that uses a channel-by-channel approximation of DT and T1 mutual information. Tensor appropriate reorientation and interpolation are not used in the gradient optimization and each tensor component is treated separately, thus ignoring the physical relationship between tensor components. Miller’s recent work (45) is more typical of the approach currently used where individuals’ datasets are normalized only according to T1 structural images – other modalities are treated as secondary and carried along by the T1 mapping. Alternatively, normalization may be done only on the DT images (46; 47), which is known to enhance alignment of major fiber pathways with respect to T1 only mapping (48). However, this strategy is inadequate for indirectly mapping T1 images and cortex due to the low DT resolution and lack of detail in gray matter and cerebrospinal fluid. Thus, a combined strategy is needed.

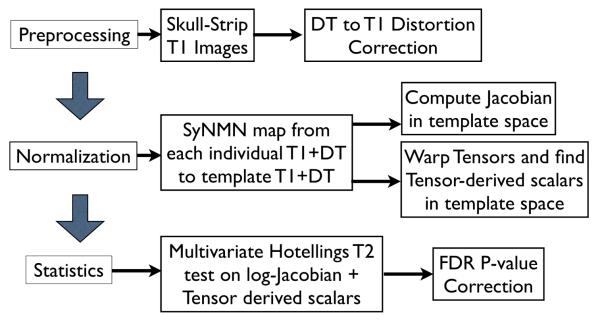
Combining information from DT and T1 constrains inter-subject mapping by complementary neuroanatomical attributes, thus leading to a fundamentally more meaningful map of neuroanatomy. The diffusion data in DT provides information in white matter areas that appear homogeneous in T1, while T1 images provide a clearer pictures of sulcal and gyral folds and gray, white and cerebrospinal fluid interfaces. The following sections of the paper will give an overview of the theory for our multivariate normalization technique, illustrate the practical benefit of the approach and apply the strategy to quantify TBI effects that are consistent across modalities. Thus, we show that this technique has the potential to yield new insight into the underlying mechanisms of brain injury by unifying the multiple modalities acquired in clinical scanning protocols through a common and consistent framework. An overview of the process, explained in detail below, is shown in figure 1.

Fig. 1.

An overview of the steps required in our multivariate processing for population analysis of tensor and scalar components. The Jacobian measures local volume of neuroanatomy, while tensor-derived scalars relate to the integrity of cellular structure. Multivariate tests enable relationships between these variables to enhance statistical power for detecting group differences.

2 Materials and Methods

2.1 Theory for MV Image Processing

Multivariate Datasets

Current clinical imaging protocols collect multiple modalities during a patient visit. Each modality captures complementary attributes of the subject’s health. Taken together and in the same coordinate system, the set of these images obtained in a single imaging session on the same subject can be considered as a single multivariate (or multi-spectral or multi-parametric) image. The MV image provides an array of measures that quantify the local neuroanatomy in space and time.

This integrative view of clinical imaging is ideal for setting up multivariate studies that look at these multiple measures as a whole. The approach is illustrated in figure 2 and figure 3. Consider an n-modality dataset, I_n = {I₁, … , I_n} and a second dataset, J_n, from a different individual or the same individual at a different time. A common approach to mapping between these individuals is to select one image modality as the reference, for example, I₁, typically a T1 structural image, and to find the image registration between it and J₁. However, this approach ignores modality dependent distortions and also does not take advantage of the additional information provided by the alternative pictures of the individuals’ anatomical-functional systems in modalities 2 → n.

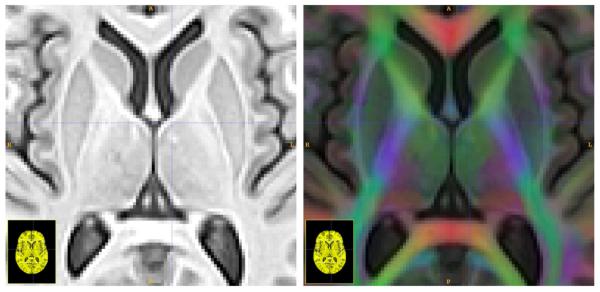
Fig. 2.

Here we see one slice from the template T1 (left) and T1 plus DT (right) after intra-modality distortion correction. The RGB channel intensity is weighted by the FA and indicates principal fiber direction going left-to-right (red) going bottom-to-top (green) and going in-and-out of the page (blue) which are superimposed on the T1 image in the right panel.

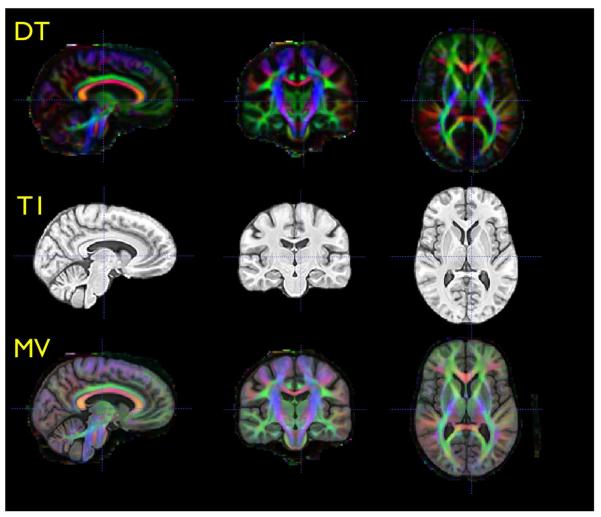
Fig. 3.

Triplanar views of the DT component of the template (top), the T1 component of the template (center) and the combined MV template (bottom). Inter– modality distortion correction, with a small deformation model, is necessary to bring these images into alignment.

Our alternative strategy, symmetric normalization for multivariate neuroanatomy, is illustrated in figure 4. While the technique is generalizable to arbitrary modalities, we specialize it, below, for the diffusion tensor and T1 modalities. Note that, for simplicity, we assume that the DT and T1 inter-modality, intra-subject distortion can be removed before proceeding to the multivariate SyNMN population normalization. In this study, we use the standard approach of eddy-current distortion correction (49) and subsequent inter-modality distortion with a small deformation between T1 and b0 images (25).

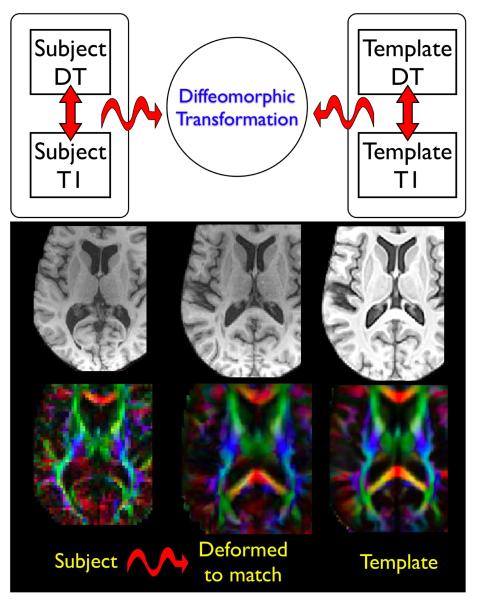
Fig. 4.

Two integrated MV datasets of individual anatomical structure and the mapping between the MV datasets via transformation, ϕ. Our methods are able to leverage both modalities to guide the computation of ϕ with maximal subject information. Curved arrows indicate intersubject transformations while straight arrows indicate intrasubject transformations. The TBI subject, at left, exhibits ventricular enlargement visible in both the DT and T1 modality. Note that the SyNMN technique is able to deform both modalities into the configuration shown in the center column, closely resembling the template in the right column. This map factors out diffeomorphic shape differences between the individual brain volumes.

Symmetric Diffeomorphic Registration

SyNMN uses diffeomorphisms (differentiable and invertible maps with differentiable inverse) as the underlying transformation model. Diffeomorphisms have the flexibility to capture both subtle intra-subject shape changes and the large deformations required when transforming, for instance, a TBI brain into a template space. Our diffeomorphisms are maps that take a position x in domain Ω back to Ω. A path (or set) of such maps, parameterized by t, may be written ϕ: x ∈ × t ∈ [0, 1] → Ω where, for each t we have a unique diffeomorphism. The maps smoothly deform images in such a way that neighbors remain neighbors, curves remain curves and boundaries between structures are respected. Furthermore, a small change in t gives a small change in the diffeomorphism as each new diffeomorphism is generated by integrating an ordinary differential equation dϕ(x, t)/dt = v(ϕ(x, t), t).

The deformation imposed by the transformation, ϕ, is given by the length of the diffeomorphic “curve” connecting ϕ(x, 0) and ϕ(x, 1). Taking the shortest path length gives a metric distance, which we term D_shape,

$$D_{\mathit{shape}}\left(\varphi \right(\mathbf{x},0),\varphi (\mathbf{x},1\left)\right)=\underset{\mathit{v}}{\min }{\int }_0^1\Vert \mathit{v}(\mathbf{x},t)\Vert \mathit{dt}.$$

Higher values for D_shape indicate larger deformation. Thus, the v at any time gives the tangent to the current diffeomorphism and is a vector field (50). The velocity is typically regularized by the Green’s Kernel of a linear operator, here chosen to be L = ▽²+Id, where Id is the identity. In scalar image registration, the v at each time is determined by the minimization and regularization of the similarity term relating two images, I and J. The map, ϕ(x, 1) warps the image I into the space of the image J via ϕ(x, 1)I = I(ϕ⁻¹(x, 1)).

We use a symmetric formulation for diffeomorphic image registration, referred to as symmetric normalization (SyN) (51), which does not require one to choose a “fixed” and “moving” image. Rather, both images deform smoothly along the shortest length path of diffeomorphisms connecting them. We now summarize the approach to symmetric normalization, but leave major details to external references (51). SyN performs image normalization by minimizing an image similarity term, D_similarity, and a transformation metric distance term, D_shape, within the space of diffeomorphisms (50). Thus, we find a series of maps, ϕ(x, t), that smoothly deform image I into the space of image J and, at the end-point, ϕ(x, 1), minimizes the following energy,

$$D_{\mathit{shape}}^2\left(\varphi \right(\mathbf{x},0),\varphi (\mathbf{x},1\left)\right)+D_{\mathit{similarity}}\left(\varphi \right(x,1),I,J).$$ (1)

The term D_similarity may contain the mutual information, intensity difference or other image matching criteria. As this method works directly within the diffeomorphic space, and is unbiased with respect to the data terms, we eliminate the need for ad hoc approaches to guaranteeing inverse consistency and transformation invertibility. Our optimization technique and transformation space guarantee these properties are held true by optimizing the energy term symmetrically and generating transformations through the appropriate ordinary differential equation (50). Note that, without loss of generality, SyN symmetrizes the normalization problem expressed in equation 1 by decomposing ϕ into two components ϕ₁ and ϕ₂ which are applied consistently to I and J.

We now provide the extension to SyN that includes a tensor similarity measure in the D_similarity term and incorporates tensor reorientation. This simple change to the theory requires much additional complexity in terms of implementation which is beyond the scope of the current paper. Nevertheless, we will describe the general issues, and our solutions, below.

Symmetric Diffusion Tensor Diffeomorphic Registration

Diffusion tensor data requires special handling because a transformation of the underlying space should preserve the tensor orientation. Miller, et al gave an algorithm that maps DT images based upon fiber orientation, which requires projecting each tensor (matrix) to a vector quantity, the principal eigenvector of the tensor (46). We have recently developed a method in which we are able to estimate small deformation optimization of a DT similarity metric while taking into account the reorientation (47). We detail our method for using this small deformation model to define velocity fields that may be integrated in time, through the SyNMN framework, to define large deformation diffeomorphisms.

First, define a diffusion tensor as D_i, a symmetric, positive definite 3 × 3 matrix. The deviatoric Euclidean distance between tensors gives a similarity metric that measures the orientation and shape of the tensor,

$${\Vert {\mathbf{D}}_1-{\mathbf{D}}_2\Vert }_{\mathit{DV}}=\sqrt{\mathrm{Tr}\left({({\mathbf{D}}_1-{\mathbf{D}}_2)}^2\right)-\frac{1}{3}{\left(\mathrm{Tr}\right({\mathbf{D}}_1)-\mathrm{Tr}({\mathbf{D}}_2\left)\right)}^2}.$$ (2)

The difficulty, traditionally, in optimizing this similarity measure with respect to a generic deformable transformation is that the deformation affects the tensor values themselves. Zhang, et al (47) developed an analytical method for parameterizing a deformation in terms of a local affine patch, thereby permitting one to compute analytical derivatives of the similarity measure above with respect to small deformations.

Now consider I_DT and J_DT, two DT images with pixel values I_DT(x) = D₁, J_DT(x) = D₂. Our goal is to compute the similarity between these two diffusion tensor images with respect to a pair of diffeomorphisms, ϕ₁ and ϕ₂. Then, at coordinate x, the DT image difference is,

$${\Vert I_{\mathit{DT}}\left({\varphi }_1\right(\mathbf{x}\left)\right)-J_{\mathit{DT}}\left({\varphi }_2\right(\mathbf{x}\left)\right)\Vert }_{\mathit{DV}}^2,$$ (3)

where we apply the transformations ϕ₁ and ϕ₂ to the DT images. Local deformations of the DT image should preserve orientation of white matter fibers in relation to the anatomy. Thus, to warp and reorient the DT images, we use the preservation of principle directions (PPD) method, as given by Alexander and Gee (52). PPD guarantees that tensors properly reorient under a warping. To see that this is valid in our framework, consider that a diffeomorphism, ϕ(x), is, by definition, a locally affine transformation. Then, in a small neighborhood, N, about x, we can approximate the diffeomorphism as an affine transformation, F. Hence, prior work on locally affine DT normalization (47) and reorientation under affine transformation (52) extends directly to diffeomorphisms. Prior work (47) on DT normalization also enables us to directly optimize the parameters of our mapping with respect to the deviatoric DT metric, using the same strategy.

DT images also require a special approach to interpolation, as interpolation should also respect the shape of the tensor space. A number of strategies have been proposed (53; 54), however we use the efficient log-Euclidean interpolation strategy (53) whenever warping, sub-sampling or interpolating tensors.

SyNMN with T1 and DT

As we discussed SyN with DT in the previous section, the additional extension to MV data requires the use of modality-dependent similarity criterion as well as a strategy for sensibly weighting information from each modality in the registration optimization. Define I₂ as consisting of {I_T1, I_DT} image modalities, assumed to exist in the same patient space and in the same rigid orientation. Furthermore, define D_{MV sim}(I₂, J₂) as the similarity criterion operating on a MV pair, I₂ and J₂.

The multivariate extension to SyN, SyNMN, thus minimizes an energy term similar to that given in equation 1,

$$D_{\mathit{shape}}^2\left(\varphi \right(\mathbf{x},0),\varphi (\mathbf{x},1\left)\right)+D_{\mathit{MV}\mathit{sim}}\left(\varphi \right(x,1),{\mathbf{I}}_2,{\mathbf{J}}_2).$$ (4)

Equation 4 retains the transformation models used in symmetric normalization and uses the same shape distance term, but also uses additional similarity metrics, contained in D_{MV sim}, for the additional DT component of the image. We define D_{MV sim} as, at a voxel,

$$\begin{array}{cc}\hfill D_{\mathit{MV}\mathit{sim}}({\mathbf{I}}_2,{\mathbf{J}}_2,\varphi )=& {\omega }_1\left(\mathbf{x}\right)\mathit{MI}\left(I_{T1}\right({\varphi }_1),J_{T1}({\varphi }_2\left)\right)+\hfill \\ \hfill & {\omega }_2\left(\mathbf{x}\right){\Vert I_{\mathit{DT}}\left({\varphi }_1\right)-J_{\mathit{DT}}\left({\varphi }_2\right))\Vert }_{\mathit{DV}}^2\hfill \end{array}$$ (5)

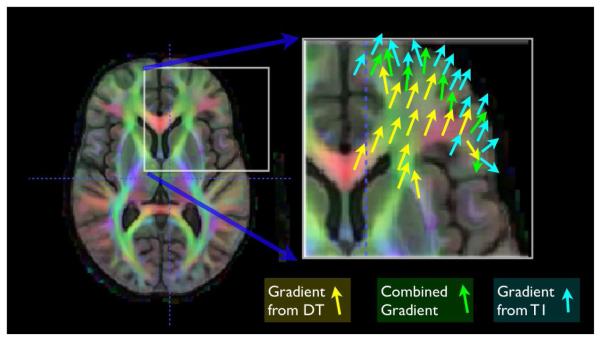
where MI is the mutual information (defined in the usual way) and the ω_i weights each similarity term as a function of the domain. If this term is optimized, we write I₂(ϕ₁(0.5)) ≈ J₂(ϕ₂(0.5)). Our previous work in curve matching (55) showed that weights which vary across the spatial domain allow results that may be superior to results found with constant weighting terms. These combined gradient functions, used at each iteration, are illustrated in figure 5. The sum of the weighting functions is always constrained to add to one. We also normalize each similarity derivative such that its maximum displacement, before weighting, is on the order of a single voxel. This latter step aids in making a fair combination of the different gradients.

Fig. 5.

The optimization of the DT and T1 combined similarity term leads to a combined gradient term. Within white matter, the majority of the gradient contribution comes from the DT component, while elsewhere the gradient is either from the T1 or a smooth combination of T1 and DT, at white matter and gray matter interfaces.

A reasonable choice for weighting functions will depend upon the relative signal of the input images. Here, we use a weight that prioritizes the DT component of the image where the FA is high (above 0.25) and prioritizes the T1 component elsewhere. The weighting function should also be smooth. Thus our weight function for the scalar term is given as ω₁(x) = G_σ ★ (1.0 – FA(x)) where FA(x) is the 0.25 thresholded FA of the template DT image and G_σ is a Gaussian smoothing kernel operating on the weight function. We smooth with a 1.5 voxel standard deviation to maintain locality. As the weighting is constrained to sum to one, we also have ω₂(x) = 1 – ω₁(x). This strategy of thresholding at 0.25 ensures that the tensor metric is leveraged only within white matter regions with strong tensor information and avoids using DT in noisy regions. Smoothing the thresholded data to create a weight function leads to a smooth optimization landscape.

Note that the SyNMN registration algorithm involves taking derivatives of the objective function D_{MV sim} and then regularizing in both space and time. Therefore, the critical gradients which we must compute are the derivatives of D_{MV sim} with respect to the current position of the diffeomorphism. Regularizing this derivative gives an estimate of the update to the diffeomorphism’s “velocity” which determines the transformation uniquely. The gradients of MI may be found in (56; 57) and for the DT norm in(47). Given these gradient terms, the mapping between any individual and template is found by a standard multi-resolution gradient descent strategy, as used in (51; 47) or (58). Thus, in this work, the principal efforts involved in combining DT with T1 do not concern, explicitly, the independent transformation model. The key difference is in the objective term and how the gradients for each term are combined in a standard gradient descent scheme. In practice, we also note that we never up-sample the DT to the T1 resolution. Rather, only the DT similarity metric gradient is up-sampled before it is combined with the T1 similarity metric gradient. We now apply this combined DT and T1 normalization to a TBI and control cohort.

2.2 Cohort and Image Dataset

The data was collected as part of a larger study investigating the neural correlates of attention deficits and treatment responses of various psychoactive drugs in the survivors of TBI (principal investigator: J.W.).

Cohort

Our cohort includes 12 individuals with TBI and nine healthy controls. The 12 subjects with TBI included 7 men and 5 women aged between 21 and 59 years (mean age = 35.0, SD = 12.1) with a mean education of 13.3 years (SD = 1.7). Eleven were right-handed, while seven were Caucasian, 3 African American, 1 Hispanic, and 1 Asian. Control participants included 6 men and 3 women aged between 23 and 46 years (mean age = 36.2, SD = 8.8) with a mean education of 14.5 years (SD = 2.0). All were right-handed, while four of them were Caucasians and 5 African Americans. The two groups did not differ significantly in terms of age, gender, ethnicity, handedness or years of education (tested with t-test or Fisher’s exact test, as appropriate). This group was also selected to contain no visible lesions within the T1 image.

Imaging parameters

DT images were collected with a single-shot, spin-echo, diffusion-weighted echo-planar imaging (EPI) sequence and a GRAPPA parallel imaging acquisition. The diffusion sampling scheme consisted of one image without diffusion gradients (b=0s/mm2), followed by 30 non-collinear and non-coplanar diffusion encoding directions isotropically distributed in space (b=1000s/mm2). Additional imaging parameters were: TR=7300ms, TE=91ms, number of averages=1, and 1.875 mm² in-plane and 2mm out-of-plane resolution.

High resolution T1-weighted anatomic images were obtained using 3D MPRAGE imaging sequence and the following acquisition parameters: TR = 1620 ms, TI = 950 ms, TE = 3 ms, flip angle = 15 degrees, 160 contiguous slices of 1.0 mm thickness, FOV = 192 × 256 mm², matrix = 192 × 256, 1NEX with a scan time of 6 min. The resulting voxel size was 1 mm³. All T1 images were skull-stripped by using SyN to map a brain mask from a template to each individual image.

3 Results

We differentiate the performance of SyNMN and SyN for normalizing this population in both a qualitative and quantitative setting. After establishing the validity of SyNMN with respect to SyN for normalizing both tensor and scalar modalities. We also evaluate performance on template-based hippocampus segmentation. We then proceed to a MV morphometric analysis of the data.

3.1 Performance Evaluation

In order to contrast performance, we normalize the full cohort of images with three strategies, to a previously computed data-derived T1 and DT template. We perform the population mapping with (1) SyN normalization; (2) DT only SyN normalization; and (3) SyNMN normalization as described in the previous section. We expect a mapping derived from only a single modality will not perform as well when applied to both modalities. While this seems an obvious point, no prior assessment has been done on a multivariate normalization approach. Furthermore, the current standard approaches use only a T1 image to normalize DT (48), or b0 images as in (39). Here, we illustrate and quantify the benefit of using both modalities at the same time.

Qualitative Assessment

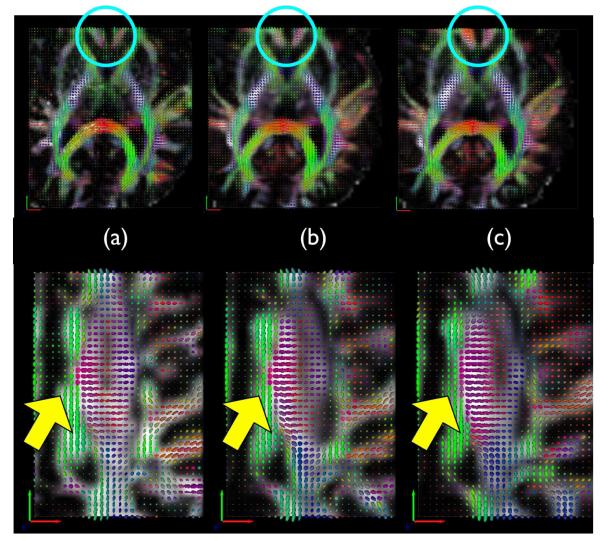
Figure 6 shows that using the DT component in SyNMN does indeed impact normalization quality of the tensor component. The SyNMN normalization solution respects the tensor orientation whereas the SyN solution is not guided by the tensor similarity metric and thus does not align tensors well. However, the T1 mapping, in both cases, are of high quality. This shows that the additional tensor data provides a meaningful anatomical guidance that constrains the map more precisely within white matter, as expected.

Fig. 6.

Column (a) shows a target DT image where as (b) shows a SyNMN mapping from an individual DT to the target DT. Column (c) shows the SyN result, which ignores the DT component. Better alignment of tensors with SyNMN are visible within the caudate at top and within the corticospinal tract along the bottom row. The lack of quality tensor alignment in the SyN result is not due to low quality normalization of T1 images, but rather due to the fact that the data visualized here is invisible in the T1 modality.

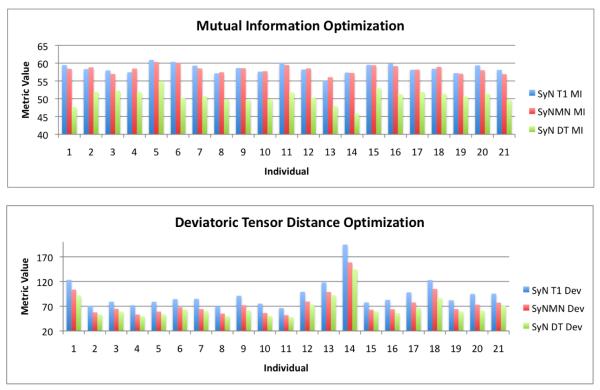
Quantitative Assessment of Optimization Performance

We quantify performance of the three strategies by comparing the deviatoric DT metric and the mutual information metric on the T1 images, after normalization, across the full dataset. We graph, for each individual, the integrated mutual information and deviatoric tensor distance metric, with the three algorithms, in figure 7. The average± standard deviation SyN-T1 focused mutual information/deviatoric DT distance metric is 58.5±1.35 / 93.45±28.6; for SyNMN, the values are 58.3±1.1 / 74.64±24.7; for SyN-DT focused, the values are 50.65±1.96 / 66.94±22.1. Note that mutual information should be maximized and the DT metric minimized. Metric values have been rescaled to lie approximately in the range zero to 100. The average DT metric is best reduced by DT alone registration whereas SyNMN produces a much better average DT metric than SyN alone, as expected. Similarly, SyN and SyNMN produce overall similar mutual information values, where SyN is (on average) slightly better. Thus, SyNMN has the ability to optimize both the DT term and the T1 term, as intended by design. Indeed, performance on DT approaches that of DT normalization alone and, in some cases, performance on T1 is better than that of SyN on T1 alone.

Fig. 7.

The bivariate performance, in our TBI dataset, of SyN-T1, SyN-DT and SyNMN are shown in the graphs above for mutual information and the deviatoric tensor distance. SyNMN provides a balanced optimization of both terms, across the dataset. For some cases, one may see that SyNMN outperforms SyN in the mutual information term.

3.2 Evaluation of Hippocampus Segmentation Quality

Having quantified the bivariate optimization ability of SyNMN, we now establish its neuroanatomical validity with respect to standard SyN T1 performance and Demons registration (59) performance, as provided in the Insight ToolKit (ITK), for template-based hippocampus segmentation. We do not evaluate the DT only performance, as hippocampus does not appear in clarity within DT. We labeled the left and right hippocampi in the template and the full dataset with an established labeling protocol described in (60). Each algorithm was then applied to map the template to the individual image, yielding a coordinate transformation from the template hippocampus to individual space. Both SyN and SyNMN are symmetric (or inverse consistent), and thus also provide an individual to template mapping. For evaluation, the labeled template hippocampus is warped to the individual space with linear interpolation and thresholded at 0.5. The resulting binary image may then be compared with the manual labeling in terms of Dice overlap. Table 1 shows the results, for each algorithm and each individual, in terms of the Dice overlap statistic. Figure 8 shows an example result for individual tbi 14.

Table 1.

Dice overlap between labeled hippocampi generated by expert manual segmentation and automatic segmentation by SyN with T1, SyNMN with DT and T1 data and the Demons method. Aggregate performance difference, for both left and right hippocampi, is assessed by pairwise T-test. SyN and SyNMN show similar performance.

Evaluation of Automated Hippocampus Segmentation
Subject	SyN Dice Left	SyN Dice Right	SyNMN Dice Left	SyNMN Dice Right	Demons Dice Left	Demons Dice Right
1	0.776	0.837	0.821	0.818	0.732	0.802
2	0.790	0.889	0.805	0.878	0.778	0.862
3	0.854	0.833	0.888	0.836	0.837	0.841
4	0.819	0.834	0.879	0.851	0.831	0.834
5	0.793	0.878	0.835	0.903	0.773	0.828
6	0.853	0.887	0.876	0.866	0.822	0.853
7	0.826	0.834	0.857	0.813	0.779	0.813
8	0.857	0.861	0.871	0.874	0.847	0.830
9	0.922	0.910	0.905	0.924	0.823	0.824
tbi 10	0.862	0.858	0.838	0.857	0.800	0.846
tbi 11	0.873	0.893	0.887	0.863	0.854	0.881
tbi 12	0.840	0.872	0.868	0.856	0.799	0.846
tbi 13	0.789	0.838	0.781	0.873	0.682	0.723
tbi 14	0.786	0.814	0.786	0.799	0.694	0.792
tbi 15	0.882	0.886	0.862	0.885	0.801	0.762
tbi 16	0.868	0.887	0.871	0.862	0.861	0.859
tbi 17	0.898	0.880	0.905	0.886	0.791	0.877
tbi 18	0.860	0.895	0.891	0.906	0.790	0.858
tbi 19	0.860	0.849	0.871	0.869	0.790	0.856
tbi 20	0.883	0.882	0.899	0.838	0.790	0.807
tbi 21	0.786	0.878	0.812	0.880	0.789	0.681
Average	0.845	0.866	0.860	0.864	0.794	0.823
T-Test vs Demons		6.49		6.9		0
P-Value vs Demons		8.57E-08		2.20E-08		1

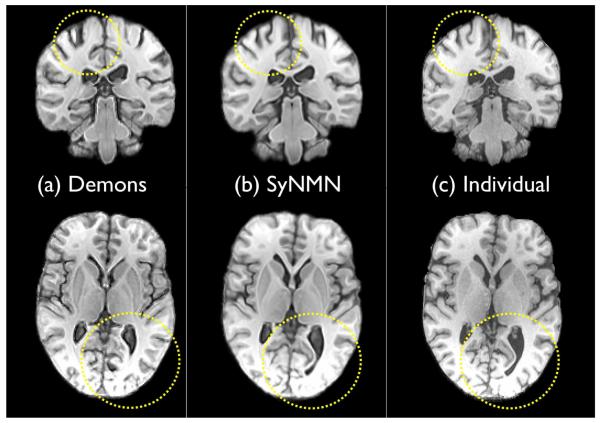
Fig. 8.

Two slices from the Demons mapping of template to individual are shown in (a); the SyNMN mapping of template to individual is in (b). The individual is in (c). Note that the Demons mapping is of overall high quality. However, the fine details (some outlined in yellow) are not as accurately mapped as in SyN and SyNMN. Detailed matching – and the ability to capture large deformation – is where the advantage of diffeomorphisms arise, in contrast to “elastic” types of methods. However, we cannot claim to have an optimal implementation of the Demons algorithm.

We assessed the significance of performance differences with a pair-wise T-test on all hippocampus overlap values. SyNMN outperformed the Demons method (T = 6.91, P < 8.6e – 8, significant) and SyN (T = 1.83, P < 0.075, not significant), in terms of Dice overlap. SyN also outperformed Demons (T = 6.49, P < 2.2e – 8, significant). Thus, SyNMN is able to improve DT alignment without compromising high-resolution neuroanatomical accuracy. We used default parameters for the Demons method and chose optimization criterion similar to those chosen for SyN/SyNMN: three levels of optimization occurred in a multi-resolution Gaussian pyramid; optimization proceeded until a maximum number of iterations or the similarity metric could no longer be improved. Maximum iterations were 100 at the coarsest level, 100 at the middle level and 50 at the finest level.

3.3 Multivariate Effects of TBI

Having established the ability of SyNMN as an optimizer and its neuroanatomical validity, we now contrast SyNMN-based morphometry with that of SyN-based morphometry. We perform a Hotelling’s T² test to assess differences in the control versus TBI population in the left and right thalamus and the left and right hippocampi. We test these two limbic system structures, hippocampus and thalamus, for three reasons: (1) these structures have been found to be affected by TBI in neuropathological studies and thus serve as good “gold standard” regions in which we expect to detect TBI effects; (2) these limbic structures are often overlooked in previous studies of TBI with diffusion tensor imaging; (3) restricting testing to these structures increases detection power for effects in this relatively small population. We assess the log-Jacobian measure of local structural volume, relative to brain size, and the mean diffusion together with the T² statistic. Hotelling’s T² distribution is the vectorial extension of the scalar Student’s T distribution. Hotelling’s test takes advantage of the joint distribution of our measurements in a two-dimensional description of the data. That is, if the log-Jacobian and mean diffusion parameters are studied separately (as marginals), then meaningful relationships between these variables will not be exploited and important differences may be missed. For instance, a subtle but consistent difference in both mean diffusion and structure size, at the same location, may not be significant under separate univariate tests. However, in some cases, a multivariate test would be able to find a significant difference in the pair of measures. This is because the T² test treats the data as an “ellipse” rather than two separate one-dimensional quantities and thus may provide better discrimination between groups. At the same time, a multivariate strategy uses half of the number of voxel-wise tests required if one were to perform separate tests on log-Jacobian and mean diffusion. Another advantage of Hotelling’s T² test is that it is affine invariant and extensible to any finite number of variables.

Given this design, our multivariate study assesses the probability of a control-patient difference in both mean diffusion and local structure sizes. The structural regions were labeled probabilistically by mapping between a set of labeled data and the template for this study. 2.5 mm smoothing was applied to the log-Jacobian and mean diffusion images before T² testing. We performed the same study with SyN, using the T1 structural images alone to guide the mapping. This involved using SyNMN but with the DT weight set to zero. The significance of our results were assessed with the theoretical probability distribution function for the T² test and then corrected for multiple comparisons by using the standard false discovery rate method.

We restricted the study to the thalamus and hippocampus because of existing evidence of TBI effects in these structures, because thalamus and hippocampus are both part of the limbic system and because of the complexity of contrasting results between two population studies across the whole brain. We chose a statistical threshold for our T² test at the FDR-corrected p < 0.05 level (61) and accepted clusters that exceed 50 contiguous voxels. These results are visualized in figure 9 on the template image.

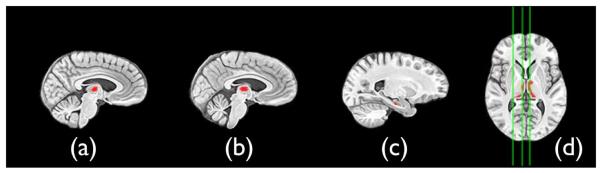
Fig. 9.

T² results after FDR correction at p < 0.05 indicate that the left and right mediodorsal thalamus and the hippocampus are affected by TBI. Sagittal slices (a) (b) and (c) are highlighted in the axial slice and indicate right mediodorsal thalamus, left mediodorsal thalamus and the left anterior hippocampus, respectively. The MV test, here, indicates that the mean diffusion is larger and the log-Jacobian smaller in the TBI subjects relative to controls. Similar results were gained with SyN. However, the hippocampus cluster did not survive FDR correction. Images are displayed in radiologic convention.

SyNMN resolved significant MV effects in the hippocampus and bilateral medial and dorsal (mediodorsal) thalamic nuclei. The T² test is strictly positive. However, inspection of the signs of the averages of the (Jacobian, mean diffusion) vector in both groups enables one to separate the outcome of each T² test into 2ⁿ categories where n indicates the number of components in the T² vector. Here, n = 2 and the test indicates that the mean diffusion is larger and the log-Jacobian smaller in the TBI subjects relative to controls. These provide evidence of simultaneous compromise of both cellular integrity, from the DT component, and structural atrophy, from the log-Jacobian component of the test. No effects were found to be significant in any of the other three possible combinations of mean diffusion and log-Jacobian. Neither the SyN derived T² nor the univariate statistics showed a significant effect in the hippocampus that exceeded the p < 0.05 FDR correction level. We hypothesize that this is because the T1 and DT normalization in hippocampus benefited from both components’ contribution to the mapping. Additionally, some power is gained by the T² test.

4 Discussion

Recall that SyNMN performance, as an optimizer and in template-based hippocampus segmentation, was comparable to univariate SyN. SyNMN also significantly outperformed a standard implementation of the Demons method for template-based hippocampus segmentation. Average Dice overlap values in the range of 0.86 are considered good for automated hippocampus segmentation, particularly when atrophy is present, as in TBI and epilepsy (62; 51). These results, with minimum Dice overlap in our dataset of 0.786 (near inter-rater overlap), indicate that our morphometric analysis is based on reasonable quality normalization.

Our morphometry findings in two limbic structures support previous postmortem neuropathologic studies of these structures in TBI (18; 13; 17). Our work thus provides in vivo evidence of effects that were seen post-mortem in pathology. We hypothesize that our findings reflect the same underlying TBI sequelae as those reported in (18; 13; 17). Our results also provide a neuroanatomical interpretation for the observed psychological impairments in TBI survivors, such as lowered motivation (3; 63; 64) and frequency of depression (65; 5; 2). The mediodorsal thalamus is connected directly to prefrontal regions and the anterior cingulate, both thought to mediate executive function and motivation (17), suggesting potential loss of input connections from the thalamus. McAllister has suggested the thalamus, and possibly hippocampus, as a common link between TBI and psychosis (66).

Our results are in partial agreement with two additional imaging studies. Salmond et al (39) performed a DTI study, with 16 patients and 16 controls, using normalization based on b0 images, that revealed significantly increased mean diffusion in the thalamus and hippocampus. Mean diffusion in the hippocampus was correlated with impairments in a learning and memory test. Localization accuracy in Salmond’s study is, however, relatively lower than in the present study, for two reasons. First, a low-dimensional normalization was used. Second, a large smoothing kernel (10mm) was applied to the mean diffusion maps. Tomaiuolo et al (11) and Salmond (12) also located effects in the hippocampus in TBI subjects using VBM. Thalamus may not have appeared as significantly affected by TBI in other DT studies for a variety of reasons. One is that thalamus may be masked out in white matter restricted studies. A second reason is that the large majority of DT studies in TBI look only at FA, which is low and variable in thalamus and hippocampus. Most of these studies do not consider mean diffusion.

A concern of many DT studies is the difficulty of assigning an underlying meaning to the observed differences in tensor-derived scalars. In the absence of other knowledge, this can be very challenging. However, in TBI, it is likely that axonal and/or neuronal injury underlie the apparent increase in mean diffusion (39). Post mortem studies highlight the presence of neuronal loss in both hippocampus and thalamus (15; 13). Our study thus indicates that DTI and mean diffusion may provide a surrogate in vivo measure reflecting underlying neuronal loss. In this respect, the mean diffusion and the log-Jacobian may represent complementary measures of a common phenomenon, although with very different technique. Additional post-mortem studies are required to verify this hypothesis. Moreover, it is also possible that increase in mean diffusion represents cell or tissue injury, without necessarily requiring significant volume loss.

An additional concern of bias arises when matching on DT and using DT-derived scalars in morphometry. The similarity metric that we use – the deviatoric tensor distance – factors out differences in tensor size. Because our metric ignores differences in mean diffusion, we are able to perform testing on mean diffusion without being concerned about bias. If mean diffusion impacted our similarity metric, our normalization results would be biased in a conservative direction – that is, fewer results would appear than if we did not base matching on this tensor feature.

To our knowledge, this study is the first to use spatially coincident DT and T1 measures in a MV statistical design. Other studies, such as (67), relate spatially distant measures across the brain. This technique is a natural extension of our current work, as would be using fiber tracking (68; 69; 70) to relate cortical and deep brain structure or white matter measures. Other shortcomings in this study are the small population size, wide range of ages (though subjects and controls are pairwise matched for age and education) and variable mechanisms of injury. Variable times between injury and imaging are also an issue. Even with these confounds, effects were consistent enough to appear at a relatively reasonable level of significance, after correction for multiple comparisons.

Despite potential technical challenges, both DT and T1 in normalization should provide fundamentally more meaningful transformations between or within individuals. However, more widespread application and detailed evaluation of the impact of DT on whole brain normalization is required to establish this principal, which we expect to be furthered naturally with increasing DT quality. The most common approach for multiple modality studies is to perform normalization with respect to one modality of structural image. SyNMN absorbs this model while permitting much greater flexibility through parameter selection and using full MV datasets. We showed that SyNMN impacts the statistical significance of a MV statistical study on a known patient population. In particular, SyNMN leads to a finding in the hippocampus that was not present in the T1 only results. For these reasons, we believe that SyNMN provides an ideal complement to multivariate datasets currently being collected and will improve normalization-based studies. However, many issues remain, including parameter selection, similarity metric choice and whole brain evaluation. One issue not explicitly dealt with here is the possibility of severe non-rigid deformation in the intrasubject T1 to DT mapping. As we use advanced thirty direction one repeat DT scans through parallel MR imaging, severe distortion is not present in our data. However, it is likely that data with such distortions may be dealt with by modifying the spatially varying weight function to use DT only where data is reliable. Although we restricted the current analysis to regions in which neuropathological ground truth is well-understood, we intend our future work to develop strategies for comparing whole brain results between univariate and multivariate normalization, potentially through an extended manual, neuroanatomical labeling protocol.

In conclusion, traumatic brain injury (TBI) leads to complex effects in white matter, the cortex and deep gray matter structures. We apply SyNMN, a new multivariate diffeomorphic mapping technique, to analyze the significant consequences of traumatic brain injury in two limbic system structures, the thalamus and hippocampus, both known, neuropathologically, to be affected in TBI. A key benefit of this new tool is the ability to find brain maps that are guided by both the fine cortical resolution available in T1 imaging and the unique window onto white matter fiber tracts and apparent diffusion provided by DT images. At the same time, this technique enables production of a new multivariate (or multiple modality) template space that enables simultaneous and consistent statistical analyses of DT and T1 derived measurements of the brain. We showed that this new multiple-modality view of brain normalization has benefits for neuroimaging analyses and may lead to new insights into the brain that span modalities. In particular, we study injury induced in TBI subjects by testing against a control population revealing notable loss of volume and increase in apparent diffusion coefficient/mean diffusion in the mediodorsal thalamus and anterior hippocampus. Thus, we show that multivariate normalization uncovers effects that are significant at the same neuroanatomical location across modalities yielding new insight into TBI and the value of MRI.