Abstract
Purpose:
To develop a DCE MRI method capable of high spatiotemporal resolution, 3D carotid coverage, and T1-based quantification of contrast agent concentration for the assessment of carotid atherosclerosis using a newly developed Multitasking technique.
Methods:
5D imaging with three spatial dimensions, one T1 recovery dimension, and one DCE time dimension was performed using MR Multitasking based on low-rank tensor (LRT) modeling, which allows direct T1 quantification with high spatiotemporal resolution (0.7 mm isotropic and 595 ms, respectively). Saturation recovery (SR) preparations followed by 3D segmented fast low angle shot (FLASH) readouts were implemented with Gaussian-density random 3D Cartesian sampling. Bulk motion removal scheme was developed to improve image quality. The proposed protocol was tested in phantom and human studies. In vivo scans were performed on fourteen healthy subjects and seven patients with carotid atherosclerosis. Kinetic parameters AUC, vp, Ktrans and ve were evaluated for each case.
Results:
Phantom experiments showed T1 measurements using the proposed protocol were in good agreement with reference value (R2 = 0.96). In vivo studies demonstrated that AUC, vp, and Ktrans in patient group were significantly higher than in control group (0.63 ± 0.13 vs 0.42 ± 0.12, P < 0.001; 0.14 ± 0.05 vs 0.11 ± 0.03, P = 0.034; 0.13 ± 0.04 vs 0.08 ± 0.02, P < 0.001, respectively). Results from repeated subjects showed good inter-scan reproducibility (ICC: vp, 0.83; Ktrans, 0.87; ve, 0.92; AUC, 0.94.).
Conclusion:
Multitasking DCE is a promising approach for quantitatively assessing the vascularity properties of the carotid vessel wall.
Keywords: dynamic contrast enhanced (DCE) MRI, carotid atherosclerosis, vasa vasorum, quantitative imaging, MR Multitasking
Introduction:
Carotid atherosclerosis is the primary pathological process underlying ischemic stroke, a leading cause of morbidity and mortality worldwide (1). Inflammation is widely known as the driving force behind the progression of atherosclerosis and plaque destabilization (2). There are multiple effects associated with inflammation that weaken plaque structural integrity, including inhibition of collagen production and dissolution of the fibrous matrix by means of matrix metalloproteinases, and cause plaque rupture and severe clinical events (3–5). Vasa vasorum neovascularization is one of the hallmarks of vascular inflammation, which provides the pathways for harnessing inflammatory cell types such as monocytes and macrophages to the vessel wall. In addition, elevated adventitial vasa vasorum permeability is associated with the increase of intimal thickness, endothelial dysfunction and inflammation of plaques (6–9).
Dynamic contrast enhanced (DCE) MRI has been used for quantitative assessment of the neovascular architecture and perfusion properties in carotid artery wall (4,10–17). It involves the rapid acquisition of T1-weighted (T1W) images before and during the injection of gadolinium (Gd)-based contrast agent. Dynamic signal enhancement curves are then extracted from a region of interest (ROI) and analyzed using a kinetic model to quantify fractional microvascular volume (vp), permeability (Ktrans) and fractional extravascular extracellular space (EES, ve)(10,16,17). Non-model-based parameters, such as area under the concentration versus time curve (AUC) have also been used as an auxiliary criterion of plaque progression prediction (18). The correlation between vp and Ktrans from DCE and the proinflammatory cardiovascular risk factors has been demonstrated (4). In an atherosclerotic rabbit model, Ktrans and AUC have been found to correlate with aortic plaque neovascularization (10).
Despite these encouraging results, the current application of DCE MRI in carotid vessel wall imaging still faces demanding technical challenges, including: 1) submillimeter in-plane spatial resolution (0.5–0.7mm), required for accurate contrast kinetic characterization without significant partial volume effects of vessel wall; 2) adequate anatomical coverage, required to cover the entire carotid vasculature; 3) high temporal resolution, required to accurately capture the contrast kinetics in blood (AIF or arterial input function); 4) accurate quantification of the contrast agent concentration in the tissue of interest. These requirements are conventionally in direct conflict with each other, forcing compromises to be made. For example, Kerwin et al. used high in-plane spatial resolution with 2D acquisitions while sacrificing anatomical coverage and temporal resolution (10). In addition, existing DCE protocols directly transform the change in pixel signal intensity to Gd concentration for kinetic modeling (10,14). Nonlinearity between T1W MRI signal and contrast agent concentration, particularly during peak enhancement, introduces potential errors in AIF calculation (11). Dynamic T1 mapping would allow direct quantification of contrast agent concentration, but the requirement to collect multiple images at different inversion/saturation recovery times for T1 fitting makes the above technical requirements even more difficult to satisfy.
In this work, we propose a T1 mapping-based DCE method that satisfies all the four technical requirements of carotid vessel wall imaging. The method is based on MR Multitasking(19), which uses a low-rank tensor (LRT) imaging model (20–24) to exploit the high correlation between images at different saturation recovery times and different contrast enhancement phases and thus achieves a vastly accelerated acquisition. The Multitasking framework was combined with 3D Cartesian sampling, allowing for faster reconstruction. Bulk motion detection and removal scheme were also implemented for the improvement of image quality. This new method enables 3D acquisition with high spatial resolution (0.7 mm isotropic), high temporal resolution (595 ms), and large coverage of the carotid arteries. Moreover, contrast concentration estimation is based on fully quantitative dynamic T1 mapping during the enhancement process for accurate kinetic modeling.
Methods:
Imaging model
The proposed Multitasking DCE technique is formulated as recovering a five-dimensional image a with three spatial dimensions (x,y,z) and two time dimensions (saturation recovery time TI and DCE time course t). There is strong correlation between images along and across time dimensions, which induces the images to be linearly dependent, and therefore low-rank. Therefore, we model the high-dimensional image a(x, TI, t) as a low-rank tensor . This tensor is partially separable (PS) (20) in the combination of space x = [x y z]T, TI, and t:
| (1) |
where the u’s, v’s, and w’s denote spatial, saturation recovery (SR), and DCE basis functions, respectively, L, M, and N denote model orders, and glmn are the elements of the core tensor , which governs the interaction between basis functions (25,26). In matrix notation, this can be expressed as
| (2) |
where the columns of U, V, and W contain the basis functions for each dimension, ⊗ denotes the Kronecker product, and the subscript (i) denotes the mode- i matricization (also known as unfolding or flattening) of the tensor (26). This low-rank model separates the image into spatial and temporal factors, decoupling the tradeoffs between spatial and temporal resolution and reducing the degrees of freedom in the image, thereby providing an avenue for accelerated acquisition.
Sequence design
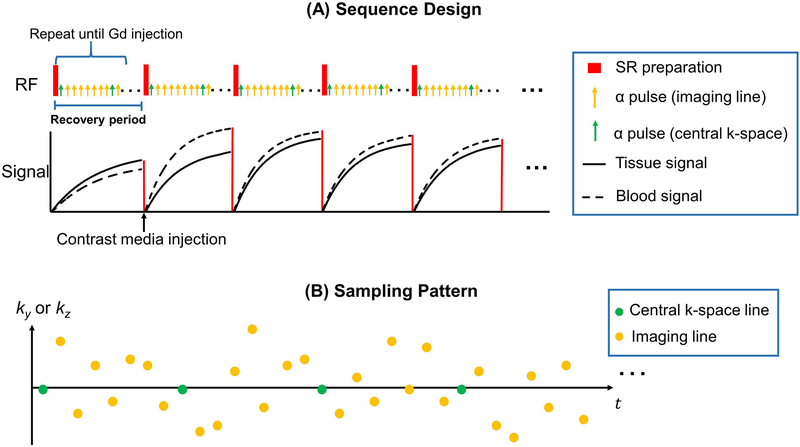
In this work, a non-selective saturation recovery preparation pulse followed by 3D segmented fast low angle shot readouts (SR-FLASH) with flow compensation was used as the basic sequence structure (Figure 1A). The FLASH readouts sample the entire recovery period in between SR prep pulses so that T1 can be quantified. Pre-contrast T1 values for the main tissues of interest (blood, vessel wall, and muscle) are relatively long (over 1000 ms). Classically, distinguishing T1 from proton density (PD) during parameter mapping would require a long recovery period, leading to low imaging speed and risking corruption of the signal evolution by the inflow of fresh blood. Fortunately for time-resolved DCE T1 mapping, a static PD map can be shared amongst the series of T1 maps at different contrast phases (including the peak contrast phase where T1 is shortest), allowing for much shorter recovery periods.
Figure 1.
(A): Pulse sequence diagram for the proposed 5D DCE and corresponding simulated signal evolution for vessel wall and blood. Non-selective saturation recovery preparation pulse is applied every TR followed by a series alpha pulses. A readout lines is collected every alpha pulse. This SR period is repeated to traverse the entire k-space seven times during the scan. The contrast media is injected when 144 SR periods was collected. (B): Simplified illustration of k-space sampling strategy. Cartesian acquisition with randomized reordering in ky and kz directions is implemented according to a variable-density Gaussian distribution. A center k-space line is acquired every 8 lines as the LRT subspace training data. Rest of the data forms the imaging data.
Sampling pattern
A 3D Cartesian sampling scheme was used for data acquisition, as shown in Figure 1B. Randomized Gaussian-density sampling in both the phase (ky) and partition (kz) encoding was used to incoherently undersample the k-space (27,28). In addition, the k-space center line (ky = kz = 0) was collected every 8 readout lines as training data (19,20). This training data is reorganized as a tensor and used to estimate the temporal basis functions, as will be described in the Image reconstruction section. This data should be collected frequently enough to capture the multi-dimensional dynamics, including saturation recovery and dynamic contrast enhancement. The temporal resolution of the training data is 88 ms. The rest of the k-space data are the imaging data, which contains high spatial resolution information to recover the spatial factor U.
Image reconstruction
There are various strategies for undersampled low-rank tensor reconstruction (19,23,24,29) that are generally compatible with the proposed method. This work used the strategy of MR Multitasking described in (19). This is a factored, explicit low-rank strategy, which reconstructs the image tensor by sequentially determining each of its factors. Briefly, image reconstruction is divided into three steps: 1) pre-determine the T1 recovery basis functions in V from a dictionary of SR signal curves; 2) estimate the DCE basis functions in W and the core tensor from the training data; and 3) recover the basis images in U by fitting the known tensor factors to the imaging data.
In the first step, because T1 relaxation is physically governed by the Bloch equations, a dictionary of feasible SR signal curves were generated ahead of time for a range of T1 values and B1 inhomogeneities. Specifically, the dictionary had 101 T1 values logarithmically spaced from 100 ms to 3000 ms, 17 flip angles from 4° to 12° with half-degree increments, and 21 saturation pulse angles linearly spaced from 60° to 120°. The T1 recovery factor V was directly extracted from the singular value decomposition (SVD) of this dictionary.
With V obtained, the core tensor and DCE factor W can be obtained from the training data as follows. Denoting the (k,TI,t)-space tensor of training data as , we solve the small-scale low-rank tensor completion problem:
| (3) |
where dtr is the collected training data, M(·) applies the training data sampling pattern, ‖·‖* denotes the nuclear norm, Dtr,(i) denotes the mode-i matricization of the tensor , and R(·) is an optional additional regularization functional (chosen as temporal total variation (TV) in the DCE time direction for this work (30–32)). Note that because is only defined over the limited region of k-space where training data are collected and because there are no Fourier transforms in Equation 3, this cost function can be minimized with low computational complexity. Given , now the core-tensor-weighted combined temporal factor, Φ =G(1)(W⊗V)T, can be quickly extracted, for example by truncating the SVD of or the higher-order SVD (HOSVD) (33) of . For this work, the λ was chosen based on the discrepancy principle (34) for one dataset, and then used for all datasets.
With a known temporal subspace spanned by the rows of Φ, image reconstruction then reduces to the recovery of the L images in U from the acquired imaging data d.
| (4) |
with undersampling operator Ω, Fourier transform F, coil sensitivity operator S, and optional regularization functional R(·). In this work, we employ a spatial TV regularizer to integrate compressed sensing into the low-rank framework (30,35).
Kinetic model
The extended Tofts model was used in this work in order to account for potential reflux in the 9.8 min scan (16). Contrast concentration curves of blood and the tissue of interest are extracted from left and right carotid arterial lumens and vessel wall, respectively. The relationship between contrast agent concentration and kinetic parameters are governed by the following equation:
| (5) |
Where Ct(t) and Cp(t) is the contrast agent concentrations in vessel wall tissue and plasma at time t, respectively, represents the integration of plasma concentration curves from injection to time t, vp is the fractional plasma volume, Ktrans is the transfer constant, and ve is the fractional EES. Considering the hematocrit of blood, the Cp(t) can be determined by the contrast agent concentration in blood Cb(t) by: Cp(t) = Cb(t)/(1−Hct), assuming the average hematocrit value (Hct) of 0.4 (15,36). With Equation 5 and the concentration curves over DCE time course t, vp, Ktrans and ve can be fitted using the function lsqnonlin (non-linear least-square solver) in MATLAB (R2015b, Mathworks, MA, USA).
The concentration curves Ct(t) andCb(t) required to fit for vp, Ktrans and ve can be calculated from dynamic T1 curves of blood and vessel wall T1,b(t) and T1,t(t) according to the following equations:
| (6) |
| (7) |
Where T1pre,b and T1pre,t represent the pre-contrast T1 values of blood and vessel wall, T1,b(t) and T1,t(t) are the T1 values at time t, and γ is the T1 relaxivity of contrast media administrated. T1 can be quantified from the signal directly as follows. At a specific DCE time point t, given T1(t), amplitude A, SR pulse parameter B, and FLASH readout interval TR, flip angle α, recovery time point n = 1, 2, …, Nτ (for Nτ = 52 readouts per SR period), the signal intensity is (37):
| (8) |
with the signal curves recovered from acquired data, A, B, T1(t), and α were fitted according to the Equation 8, also using MATLAB’s lsqnonlin. A computational simulation was conducted to test the accuracy of dynamic T1 estimation and kinetic parametric mapping of the Multitasking DCE, as shown in the Section C of the Supporting Information.
Abrupt motion removal
Abrupt movement of the subject, such as swallowing, is often inevitable during any scan that spans several minutes (38). Unaddressed abrupt bulk motion leads to blurring and other motion artifacts. Because the carotid vessel wall is thin, it is especially sensitive to motion artifacts that worsen the partial volume effect, leading to incomplete vessel wall visualization and errors in quantification.
In the LRT framework, images with abrupt motion are less correlated with the remainder of the images and so would have a high residual after temporal estimation. Prior to image reconstruction, the outlier time points corrupted by bulk motion can therefore be detected by determining which columns of Dtr (the Casorati matrix of raw training data) have a high residual after temporal subspace modeling. Calculating a “single-time” temporal factor matrix Φst (i.e., with only one time dimension indexing the readout number) from the SVD of Dtr, the training data residual is then:
| (9) |
Where is the residual matrix, is the matrix of training data, is the single-time temporal factor matrix, Nk denotes the number of data points in each readout, Nc is the number of coils, Nro represents the total number of training data readouts, and the superscript † denotes the pseudoinverse. The time-resolved sum-of-squares residual vector r can be calculated as having elements
| (10) |
Training data corresponding to high-residual time points were removed before evaluating Equation 3, and imaging data immediately surrounding those time points were removed before evaluating Equation 4.
The effect of motion removal was tested by comparing the signal-to-nosie ratio (SNR) of blood and vessel wall, the contrast-to-noise ratio (CNR) of vessel wall versus blood and the sharpness of blood/vessel wall boundary of the image with motion removal with the same frame without motion removal. The SNR of the tissue of interest was defined by:
| (11) |
With SIt is the signal intensity of the tissue of interest, and σbg is the standard deviation of the background signal. The CNR was defined by:
| (12) |
With SIt1 and SIt2 with are the signal intensity of the two tissues. The sharpness of the blood/vessel wall boundary was estimated using the rise-distance method (39).
Imaging experiments
The proposed protocol was implemented on a 3T clinical MR scanner (MAGNETOM Verio, Siemens Healthineers, Erlangen, Germany). Each SR period lasted 595 ms with 52 TIs, one every 11 ms. One readout line was collected per TI. The SR period was repeated 1008 times in a scan of 9.8 min, resulting in a total of 52×1,008 = 52,416 time points, each corresponding to a 3D image. The DCE bin temporal footprint was selected to be 1.2 s as two SR periods, except when evaluating the effect of different temporal resolutions/footprints. Detailed imaging parameters are summarized in Table 1.
Table 1:
Multitasking DCE sequence parameters.
| Imaging Parameters (in coronal orientation) | |||
|---|---|---|---|
| 150 mm × 150 mm | 26 mm | ||
| 208 × 208 × 36 | 0.7 mm isotropic | ||
| 595 ms | 52 | ||
| 11 ms | 6.8 ms | ||
| 8° | 9.8 min | ||
Phantom study
To validate the T1 mapping accuracy and reproducibility of the proposed Multitasking DCE, two experiments were performed on the same T1 phantom on separate days. The T1 values of the phantom ranged from 70 ms to 2000 ms, covering the pre- and post-contrast T1 values of the major tissue types of interest. Images with standard 2D inversion-recovery spin-echo (IR-SE) sequence with TR = 10000 ms and seven different inversion times (23, 100, 400, 900, 1600, 2200, 3000 ms) were also acquired at the center slice to provide the T1 reference. Other IR-SE imaging parameters were: FOV = 150×150 mm2, in-plane spatial resolution = 1.2 mm, slice thickness = 8 mm.
In vivo study
The in vivo study was approved by the ethics boards of our institutions. All subjects gave written informed consent before participating in this study. Fourteen healthy volunteers (aged 25 to 57 years, five females) were recruited for the study; to assess the reproducibility of the proposed method, seven of the volunteers were scanned twice, on different days, using the same protocol. Subjects were scanned using a 12-channel head coil and a 4-channel surface coil from the system vendor. During the imaging session, localizers and time-of-flight (TOF) MR angiography were acquired to identify the overall neck anatomy. Following these sequences, Multitasking DCE was performed. Gd contrast media (Gadavist, 0.1 mmol/kg, Bayer Schering Pharma) was injected intravenously 1.4 minute into the scan, when 144 SR periods were collected. The injection rate was 1 mL/s, followed by a 20 mL saline flush at the same rate. To provide an in vivo T1 reference, pre- and post-contrast single-slice MOLLI (40) at 1.17 mm in-plane spatial resolution were also acquired immediately before and after the DCE scan, respectively. Vessel wall was not visible on the MOLLI images due to low spatial resolution, but the T1 values of blood and muscle could be quantified and were adopted as the reference.
Furthermore, seven patients (aged 54 to 80 years, three females) with a history of carotid atherosclerosis were recruited. In addition to the abovementioned protocol, a series of conventional carotid plaque imaging protocols including pre-contrast T1W turbo-spin-echo (TSE), pre-contrast T2W TSE and post-contrast T1W TSE were collected to assist in plaque diagnosis.
Image analysis
For each subject in the control group, three slices (two below the carotid bifurcation and one above) with clear vessel wall delineation were selected for analysis. ROI of the vessel wall in normal subjects was manually selected using the T1W images at early TIs and the pre-contrast T1 maps, as shown in the Supporting Information Figure S1. For the paired measurements of the same subject on separate days, slices were matched manually and corresponding slices were selected for comparison. In the patient group, the anatomical location of the plaque is identified on the conventional images. Then the anatomical location of the plaque was manually defined on the corresponding Multitasking DCE images. Three slices around plaque area were selected for each subject. Pixel-wise mapping for vp, Ktrans, ve and AUC were obtained for each slice in MATLAB.
Reproducibility at different temporal resolution
In practice, too high temporal resolution may result in noisy concentration curves, while too low temporal resolution may cause blurring of the fast-changing dynamic information, particularly in the AIF. To evaluate the impact of temporal resolution on the kinetic parameter mapping, the reproducibility of kinetic parameters at different temporal resolutions were evaluated in the seven repeated subjects. Temporal resolutions from 595 ms to 7.2 s were retrospectively selected for image reconstruction.
Statistical analysis
Intra-group mean value and standard deviation of kinetic parameters for both the control and patient groups were calculated, and a two-way mixed ANOVA was performed in SPSS (Version 24, IBM, NY, USA) to address any correlation between samples arising from the use of three slices from each subject. For the mixed ANOVA, slice location was set as a within-subjects factor and the group (control or patient) was set as a between-subjects factor; a slice/group interaction term was included in the analysis. A p value of less than 0.05 was considered to be significant. Reproducibility analysis, including Bland-Altman analysis, coefficient of variation (CV) (16) and intraclass correlation coefficient (ICC) (41) of vp, Ktrans, ve and AUC were applied to the data collected from the seven repeated volunteers.
Results
Computational Simulation
Figure S4 in the Supporting Information is an illustration of the computational phantom. Figure S5 and Figure S6 show the result of the dynamic T1 fitting and kinetic parametric mapping, respectively. Table S1 lists the mean value and standard deviation of the ROI of the kinetic parametric mapping.
Phantom measurements
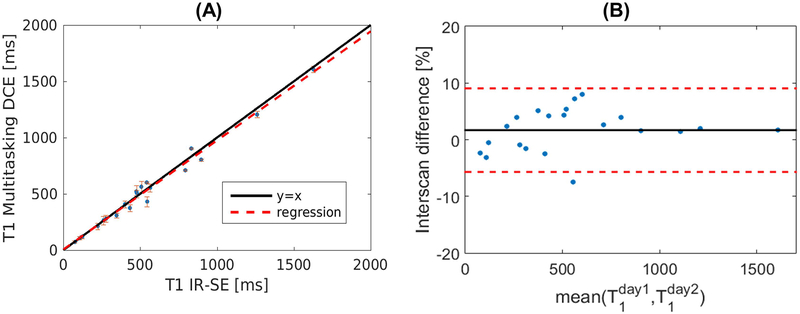
Figure 2A shows the result of T1 mapping comparison between Multitasking DCE and IR-SE reference in the phantom. The T1 values from Multitasking DCE were in good agreement with reference values (R2 = 0.96). Figure 2B illustrates the T1 mapping reproducibility of the proposed method in the phantom. The mean absolute interscan differences between separate scans are 1.68%. Results shows that T1 mapping of Multitasking DCE is reproducible. Figure S2 and S3 demonstrates the T1 mapping variability of Multitasking DCE.
Figure 2:
Phantom measurements. (A): Comparison of T1 quantification using the proposed Multitasking DCE versus a standard reference method (IR-spin echo). The solid black line represents y = x while the dashed red lines stands for the regression of the results from two methods (R2 = 0.96). The error bar shows the standard deviation for each measured T1. (B): The Bland–Altman plot shows reproducibility of the T1 measurement of the proposed protocol measured on two different days. Solid line and dashed lines indicate the means and standard deviation of the T1 values between different measurement, respectively.
In vivo measurements
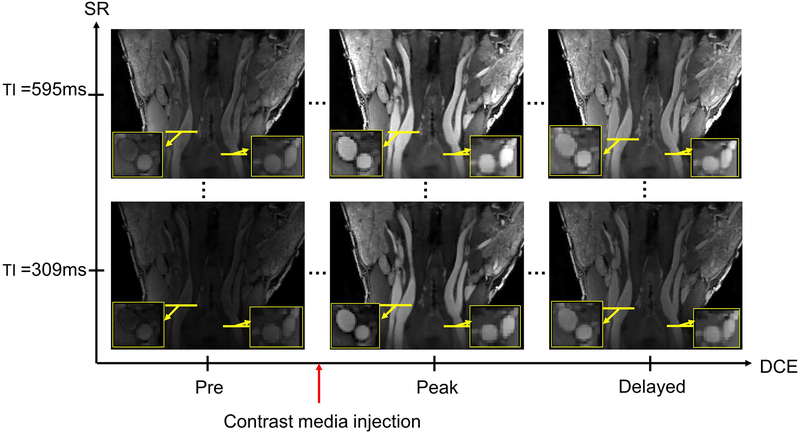
Figure 3 shows typical Multitasking DCE images. With isotropic spatial resolution, the image can be viewed from any orientation. In Figure 3, images are shown in both coronal orientation and transversal orientation. Coronal orientation provides an excellent view of entire carotid vessel along the direction of flow, while transversal orientation is useful for visualizing lumen and vessel wall condition. As previously mentioned, there are 1,008 DCE phases, each of which contains 52 SR times in the proposed protocol. Figure 3 shows SR = 309 ms and SR = 595 ms (the final SR time) for three representative DCE times: the pre-contrast, peak-enhanced, and wash-out. Table S2 in the Supporting Information lists the comparison of T1 values between Multitasking DCE and MOLLI reference for healthy subjects.
Figure 3:
Representative image set from a study of a normal subject using the proposed method. Multi-phase images are reconstructed with the LRT framework in the SR dimension (images at different TI times) and dynamic enhancement dimension (images at different time after injection). Zoomed-in images are the transversal view of the locations marked by yellow lines. Multiple SR phases allows T1 quantification and direct estimation of contrast concentration. Three key DCE phases are shown along horizontal axis, including pre-injection, peak enhancement, and washing out. DCE temporal footprint is 1.2 s.
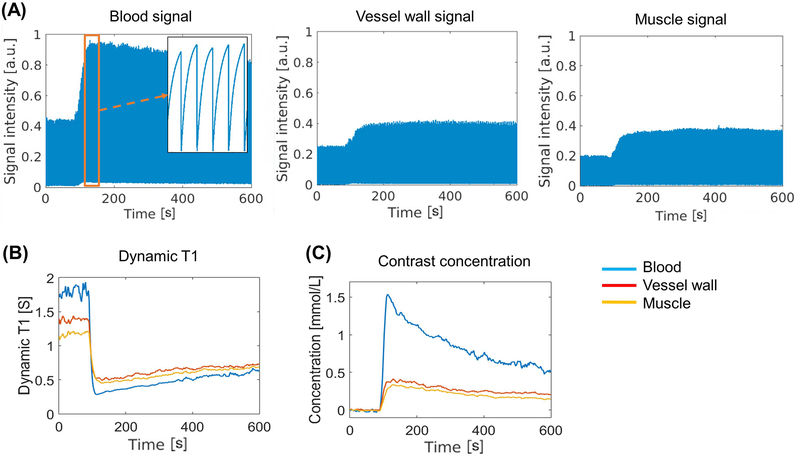
Figure 4 illustrates the typical process of the conversion from signal intensity to contrast agent concentration. Figure 4A displays the real-time signal intensity for blood, vessel wall and muscle, respectively. Figure 4B and 4C show the corresponding dynamic T1 mapping and calculated contrast agent concentration curves.
Figure 4:
(A): Real-time signal evolution of three representative tissues from a healthy subject. The zoom-in area in the image of blood signal shows the SR curves during the peak enhancement. (B) Dynamic T1 mapping based on the SR information. (C) Contrast agent concentration curves derived directly from the T1 mapping according to contrast media relaxivity.
Figure 5 shows example parametric maps. Figure 5A shows a case of a normal subject with thin vessel wall. Figure 5B and 5C show T1 weighted images and kinetic parameter maps from a patient with lipid-rich necrotic core and one with intra-plaque hemorrhage, respectively. The plaque composition was diagnosed clinically with the pre-contrast T1 TSE, T2 TSE and post-contrast T1 TSE images.
Figure 5:
Examples of kinetic parametric mappings. The gray-scale images are the post-contrast T1-weighted images in coronal view. The overlaid color maps on the zoomed-in area in transversal view are AUC, vp, Ktrans and ve maps. (A) is an example from a healthy subject with thin vessel wall. The location of the zoomed-in images in red and blue frames are marked by the red and blue lines in the coronal image in (A), respectively. (B) is from a 58-year old patient with lipid core. (C) is from a 69-year-old patient with intra-plaque hemorrhage. The location of zoomed-in area is marked by the red line in the coronal image in (B) and (C), respectively. The plaques were marked by white arrows on the AUC maps.
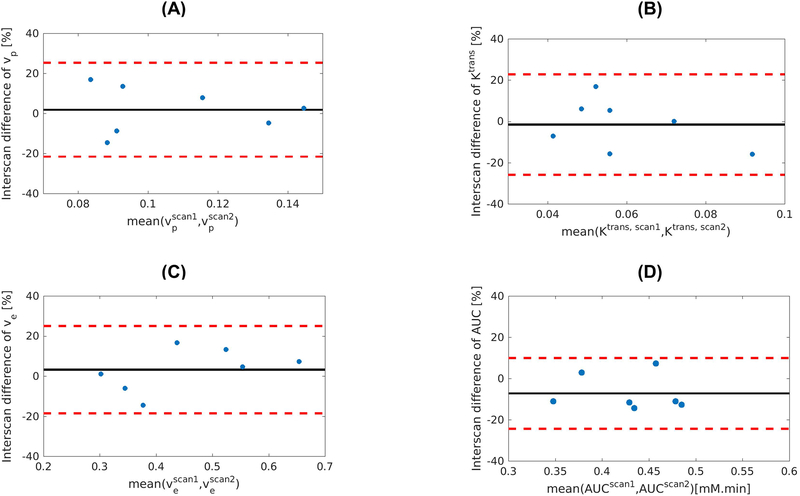
In Figure 6, Bland–Altman plots illustrate the reproducibility of the kinetic parameters vp, Ktrans, ve and AUC of the proposed method. The CV of vp, Ktrans, ve and AUC were 4.62%, 4.24%, 3.50%, and 2.16%, respectively. The ICC of vp, Ktrans, ve and AUC were 0.83, 0.87, 0.92, and 0.94, respectively.
Figure 6:
Reproducibility of the kinetic parameters vp, Ktrans, ve and AUC, as measured by mean absolute interscan difference. Seven healthy subjects received the second scan with the same protocol on a separate day. The Bland-Altman plots show good reproducibility of the kinetic parameters.
Table 2 lists the mean and standard deviation measurements of vp, Ktrans, ve and AUC in both the control group and patient group. The results for both groups were generally in agreement with published values from literature (13,15). The ANOVA showed that vp, Ktrans and AUC were significantly higher in the patient group than in the control group (P = 0.034, <0.001, <0.001, respectively). Detailed results for vp, Ktrans, ve and AUC from mixed ANOVA analysis are shown in Table S3. Table S4 lists the mean and standard deviation measurements of vp, Ktrans, ve and AUC of the adjacent muscle in both groups.
Table 2:
Kinetic modeling properties in healthy subjects (n = 14) and patients with known carotid atherosclerosis (n = 7). For vp, Ktrans and AUC the mean values of patient group were significantly higher than the mean value of healthy group.
| vp | Ktrans (min−1) | ve | AUC (mM·min) | |
|---|---|---|---|---|
| Control | 0.11 ± 0.03 | 0.08 ± 0.02 | 0.49 ± 0.10 | 0.42 ± 0.12 |
| Patient | 0.14 ± 0.05 | 0.13 ± 0.04 | 0.54 ± 0.08 | 0.63 ± 0.13 |
| P value | 0.034 | < 0.001 | 0.522 | < 0.001 |
Effects of motion removal
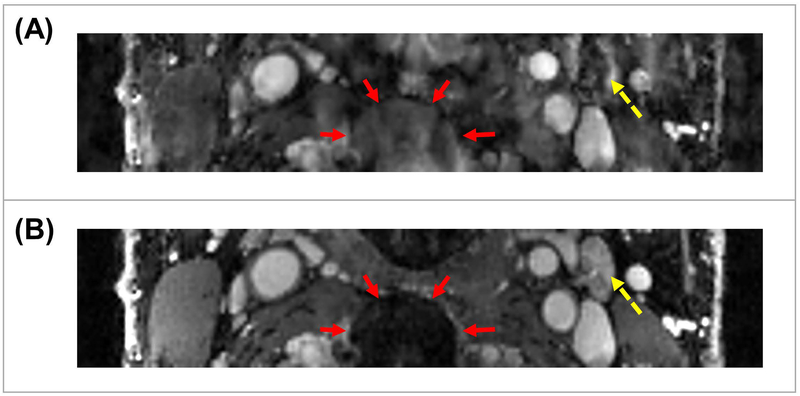
Figure 7 demonstrates the effects of motion removal. Figure 7A shows an example of a motion-corrupted image, while Figure 7B shows the same image after motion removal. The image quality parameters before motion removal is: SNRblood = 16.7, SNRvessel wall = 7.2, CNR = 9.5, sharpness = 2.68mm−1 (The signal intensity was normalized). After motion removal, the parameters are: SNRblood = 74.8, SNRvessel wall = 30.4, CNR = 44.4, sharpness = 4.71mm−1. All the parameters are substantially higher after motion removal, indicating better image quality and vessel wall delineation.
Figure 7:
Effects of motion removal in the proposed method. Abrupt motion is a common issue in DCE studies. Without motion removal, images may be corrupted by artifacts. Reconstructed images with motion removal shows sharper and superior delineation of different tissue types. (A) is an image corrupted by motion artifacts. The set of red arrows mark a blurry structure. The dashed yellow arrow marks a vessel with corrupted contrast. (B) is the image from the same subject after motion removal. The area marked by red arrows has much clearer structure. The vessel marked by dashed yellow arrow has more reasonable contrast and better delineation.
Reproducibility at different temporal resolution
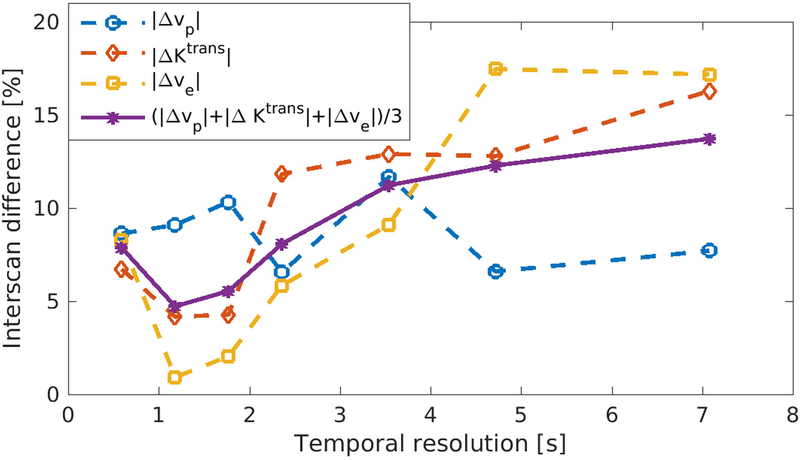
Figure 8 illustrates the mean absolute interscan differences of vp, Ktrans and ve at different reconstructed temporal resolutions. Measurements of Ktrans and ve were most reproducible at the temporal resolution of 1.2 s, yielding interscan difference 4.2% and 0.9%, respectively, while vp was most reproducible at the temporal resolution of 595 ms with 8.6% interscan difference. On average, the parameters were most reproducible at the temporal resolution of 1.2 s with the mean interscan difference (the mean value of the interscan difference of vp, Ktrans and ve) of 4.7%.
Figure 8:
Reproducibility at different temporal resolution. The reproducibility between two scans was evaluated at different temporal resolutions retrospectively. The chosen temporal resolutions were 595 ms, 1.2s, 1.8s, 2.4s, 3.6s, 4.8s, and 7.2s. When temporal resolution<1s, the average reproducibility was not as good because of the reduced SNR. When temporal resolution>3s, the reproducibility decreased due to the worse depiction of fast-changing dynamic information. The best reproducibility achieved when temporal resolution = 1.2s.
Discussion
In this study, we presented a novel Multitasking DCE MRI method for the carotid artery. We achieved high spatial resolution, high temporal resolution, and complete carotid coverage with fully quantified T1 dynamics in a single 10-min scan. The feasibility of the proposed method was demonstrated in phantoms and in vivo.
Compared with previous work on carotid vessel wall DCE, the proposed method has multiple advantages. First, this technique allows 3D acquisition with large anatomical coverage and isotropic resolution at 0.7 mm. The intima-media thickness of carotid vessel wall, which is often used to gauge disease status, is around 0.7 mm for healthy subjects (42). Although the intima-media thickness could increase in patients with atherosclerosis, previous findings showed that the imaging of carotid vessel wall requires a spatial resolution of at least 0.5–0.7 mm to capture the complex structure of plaque with limited partial volume artifacts and sufficient vessel wall/lumen delineation (10,43–45). In most of the existing DCE protocols, the in-plane resolution can meet this requirement; however, slice thickness is typically over 2 mm in order to maintain sufficient SNR in 2D acquisitions (12,15). Insufficient spatial resolution in the slice direction has two detrimental effects for vessel wall DCE. First, lesion delineation would be compromised, leading to possibly missing the lesion in the worst case scenario. Second, the partial volume effect which mixes vessel wall tissue and blood together would induce substantial errors in the dynamic modeling. In our method, the high isotropic spatial resolution would significantly reduce such effects. It also allows flexible reformats of the images from any orientation, rendering optimal lesion visualization, especially in cases where the lesion is highly irregular and heterogeneous. Combined with the large anatomical coverage, the proposed method allows a comprehensive assessment of the disease extent.
Secondly, the proposed method can achieve a temporal resolution up to 595 ms, which can potentially capture the faster dynamics during the contrast enhancement. With existing methods, it is very challenging to achieve high temporal and high spatial resolution simultaneously. For example, Kerwin et al. reported the temporal resolution of 15 s (14). Calcagno et al., which adopted a 3D sequence with 0.6 mm isotropic resolution, reported the temporal resolution of around 30 s (10). Reliable estimation of the perfusion properties of vessel wall requires the accurate sampling of both AIF and vessel wall signal at an adequate temporal resolution. Recent studies have shown that the acquisition of AIF, which is changing more rapidly than vessel wall signal, requires the temporal resolution on the order of 1 second (46,47). In this work, we sought to evaluate the effect of temporal resolution on the estimation of kinetic parameters, as demonstrated in Figure 8. The highest temporal resolution 595 ms did not provide the best reproducibility, possibly due to its reduced SNR. When temporal resolution was higher than 1.2s, reproducibility tended to decrease along with the decrease of temporal resolution. The mean absolute interscan difference reached the minimum when temporal resolution was at 1.2s, and was within 10% when temporal resolution was less than 3s, implicating that the temporal resolution around 1–3 s could be an attractive choice for carotid DCE MRI. The main limitation in the current evaluation of temporal resolution is that the sample size is relatively small. Future evaluation with larger group of subjects is needed.
Thirdly, quantification of the contrast concentration with the proposed method is based on dynamic T1 mapping and contrast media relaxivity, as opposed to a linear approximation of contrast concentration from T1-weighted signal intensity (as in most of the current methods). The assumption of linearity between signal intensity and contrast concentration is only valid when contrast agent concentration is low and may not hold true in tissues with high contrast agent uptake or in the plasma. Linear approximation of concentration curves from signal intensity would introduce extra error to the result (11). To our knowledge, the proposed protocol is the first 3D protocol enabling full quantification with dynamic T1 mapping.
The scan time in this work was set to be 9.8 min to collect sufficient data for the LRT reconstruction. In the recovery of the spatial coefficient U, insufficient data can result in decreased image quality and reduced accuracy of the parametric fitting. In the future, additional source of acceleration, such as partial Fourier acquisition may be adopted to further reduce the scan time.
The estimates of the kinetic parameters vp, Ktrans, ve of control and patient groups are in line with the values published in literatures (4,12–15). Among them, vp and Ktrans has been shown in a number of studies to correlate with the histological markers of inflammation (1). In this work, vp and Ktrans in the patient group are both significantly higher than in the control group, which is consistent with previous studies. However, the correlation between ve and inflammation biomarkers in carotid atherosclerosis has not been fully demonstrated yet. Besides, the estimate of ve can be largely influenced by the total scan time because it relies on the presence of significant reflux. Previous work showed that a 7-min imaging period after contrast agent administration is not enough to accurately estimate ve (16). Further investigations are needed to reveal the response of ve in the inflammation of carotid atherosclerosis.
The proposed method requires further validation with histology. The capability of the proposed protocol in quantitatively assessing vasa vasorum was evaluated through the reproducibility of the kinetic parameters of two scans with the same protocol on the same subject. In addition, the consistency of the kinetic parameter values in our study and previously published literature is a support for the potential clinical value of the proposed protocol. In future, histological verification would elucidate the potential advantages of the proposed method in the diagnostic performance, including sensitivity, specificity, etc. compared with more conventional DCE approaches.
A potential limitation of the proposed technique is the lack of a black blood phase for vessel wall identification. The sequence we used in this work combined SR preparation and FLASH readouts. With SR preparation, the signal for all tissue types was always positive during the recovery evolution. Any residual signal from the previous recovery period was reset to zero by the SR pulse, eliminating spin history issues during dynamic T1 mapping. In our study, the rim of the vessel wall was identified from the pre-contrast gray-scale images and the pre-contrast T1 maps generated with our method, taking advantage of the long T1 of blood (supplementary Figure S1). In the future, inversion recovery preparation could be used in place of SR preparation, which would additionally yield black blood images at the blood null point for any DCE phase, potentially allowing better vessel wall identification. However, additional factors should be taken into consideration with inversion recovery. The extension of the magnetization recovery time to accommodate the full IR period could be subject to inflow effects. Also, during the dynamic process, residual magnetization would be carried over to subsequent recovery periods, which would have to be accounted for during T1 mapping.
Conclusion
We have demonstrated that the proposed Multitasking DCE MRI of carotid arterial wall is feasible with dynamic T1 mapping to achieve high spatiotemporal resolution and entire carotid coverage at the same time. The proposed method showed accurate T1 quantification, and robustness to motion in studies on phantom and healthy subjects. Preliminary patient studies were promising, and further validation is warranted in a larger clinical population.
Supplementary Material
Acknowledgement
This project is partially supported by NHLBI R01 HL096119 (NW, YX, ZF, ZD, DL), American Heart Association 15SDG25710441 (ZF) and Chinese National Natural Science Fund 81541126 (WY). The authors would like to thank Heidi Gransar for the valuable guidance on the statistical analyses.
Footnotes
Senior authors contributed equally to this work
References
- 1.Yuan C, Oikawa M, Miller Z, Hatsukami T. MRI of carotid atherosclerosis. J Nucl Cardiol. 2008;15(2):266–275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Ross R Atherosclerosis—an inflammatory disease. N Engl J Med. 1999;340(2):115–126. [DOI] [PubMed] [Google Scholar]
- 3.Wasserman BA, Smith WI, Trout HH, Cannon RO, Balaban RS, Arai AE. Carotid artery atherosclerosis: in vivo morphologic characterization with gadolinium-enhanced double-oblique MR imaging—initial results. Radiology 2002;223(2):566–573. [DOI] [PubMed] [Google Scholar]
- 4.Kerwin WS, O’Brien KD, Ferguson MS, Polissar N, Hatsukami TS, Yuan C. Inflammation in carotid atherosclerotic plaque: A dynamic contrast-enhanced MR imaging study. Radiology 2006;241(2):459–468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Langheinrich AC, Kampschulte M, Buch T, Bohle RM. Vasa vasorum and atherosclerosis-Quid novi? Thromb Haemost. 2007;97(6):873–879. [PubMed] [Google Scholar]
- 6.Falk E Why do plaques rupture? Circulation 1992;86(6 Suppl):III30–42. [PubMed] [Google Scholar]
- 7.Gillard J Imaging of carotid artery disease: from luminology to function? Neuroradiology 2003;45(10):671–680. [DOI] [PubMed] [Google Scholar]
- 8.Saba L, Anzidei M, Sanfilippo R, Montisci R, Lucatelli P, Catalano C, Passariello R, Mallarini G. Imaging of the carotid artery. Atherosclerosis 2012;220(2):294–309. [DOI] [PubMed] [Google Scholar]
- 9.Naghavi M, Libby P, Falk E, Casscells SW, Litovsky S, Rumberger J, Badimon JJ, Stefanadis C, Moreno P, Pasterkamp G. From vulnerable plaque to vulnerable patient. Circulation 2003;108(14):1664–1672. [DOI] [PubMed] [Google Scholar]
- 10.Calcagno C, Lobatto ME, Dyvorne H, Robson PM, Millon A, Senders ML, Lairez O, Ramachandran S, Coolen BF, Black A, Mulder WJ, Fayad ZA. Three-dimensional dynamic contrast-enhanced MRI for the accurate, extensive quantification of microvascular permeability in atherosclerotic plaques. NMR Biomed. 2015;28(10):1304–1314. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Calcagno C, Mani V, Ramachandran S, Fayad ZA. Dynamic contrast enhanced (DCE) magnetic resonance imaging (MRI) of atherosclerotic plaque angiogenesis. Angiogenesis 2010;13(2):87–99. [DOI] [PubMed] [Google Scholar]
- 12.Calcagno C, Robson PM, Ramachandran S, Mani V, Kotys-Traughber M, Cham M, Fischer SE, Fayad ZA. SHILO, a novel dual imaging approach for simultaneous HI-/LOw temporal (Low-/Hi-spatial) resolution imaging for vascular dynamic contrast enhanced cardiovascular magnetic resonance: numerical simulations and feasibility in the carotid arteries. J Cardiovasc Magn Reson. 2013;15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Dong L, Kerwin WS, Chen HJ, Chu BC, Underhill HR, Neradilek MB, Hatsukami TS, Yuan C, Zhao XQ. Carotid Artery Atherosclerosis: Effect of Intensive Lipid Therapy on the Vasa Vasorum-Evaluation by Using Dynamic Contrast-enhanced MR Imaging. Radiology 2011;260(1):224–231. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Kerwin WS, Oikawa M, Yuan C, Jarvik GP, Hatsukami TS. MR imaging of adventitial vasa vasorum in carotid atherosclerosis. Magn Reson Med. 2008;59(3):507–514. [DOI] [PubMed] [Google Scholar]
- 15.Wu T, Wang J, Song Y, Deng X, Li A, Wei J, He L, Zhao X, Li R, Zhou Z, Wu W, Huang J, Jiao S, Yuan C, Chen H. Homologous HOmologous Black-Bright-blood and flexible Interleaved imaging sequence (HOBBI) for dynamic contrast-enhanced MRI of the vessel wall. Magn Reson Med. 2015;73(5):1754–1763. [DOI] [PubMed] [Google Scholar]
- 16.Gaens ME, Backes WH, Rozel S, Lipperts M, Sanders SN, Jaspers K, Cleutjens JPM, Sluimer JC, Heeneman S, Daemen MJAP, Welten RJTJ, Daemen JWH, Wildberger JE, Kwee RM, Kooi ME. Dynamic Contrast-enhanced MR Imaging of Carotid Atherosclerotic Plaque: Model Selection, Reproducibility, and Validation. Radiology 2013;266(1):271–279. [DOI] [PubMed] [Google Scholar]
- 17.Tofts PS, Brix G, Buckley DL, Evelhoch JL, Henderson E, Knopp MV, Larsson HB, Lee TY, Mayr NA, Parker GJ, Port RE, Taylor J, Weisskoff RM. Estimating kinetic parameters from dynamic contrast-enhanced T(1)-weighted MRI of a diffusable tracer: standardized quantities and symbols. J Magn Reson Imaging. 1999;10(3):223–232. [DOI] [PubMed] [Google Scholar]
- 18.Khalifa F, Soliman A, El‐Baz A, Abou El‐Ghar M, El‐Diasty T, Gimel’farb G, Ouseph R, Dwyer AC. Models and methods for analyzing DCE‐MRI: A review. Med Phys. 2014;41(12). [DOI] [PubMed] [Google Scholar]
- 19.Christodoulou AG, Shaw JL, Nguyen C, Yang Q, Xie Y, Wang N, Li D. Magnetic resonance multitasking for motion-resolved quantitative cardiovascular imaging. Nat Biomed Eng. 2018;2(4):215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Liang Z-P. Spatiotemporal imaging with partially separable functions. Proc IEEE Int Symp Biomed Imaging. 2007. p 988–991. [Google Scholar]
- 21.Yu Y, Jin J, Liu F, Crozier S. Multidimensional compressed sensing MRI using tensor decomposition-based sparsifying transform. PLoS One. 2014;9(6):e98441. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Trzasko JD, Manduca A. A unified tensor regression framework for calibrationless dynamic, multi-channel MRI reconstruction. In: Proceedings of the 21st Annual Meeting of ISMRM, Salt Lake City, Utah, USA. 2013. Vol. 603 2013. 21. [Google Scholar]
- 23.Christodoulou AG, Redler G, Clifford B, Liang Z-P, Halpern HJ, Epel B. Fast dynamic electron paramagnetic resonance (EPR) oxygen imaging using low-rank tensors. J Magn Reson. 2016;270:176–182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.He J, Liu Q, Christodoulou AG, Ma C, Lam F, Liang ZP. Accelerated High-Dimensional MR Imaging With Sparse Sampling Using Low-Rank Tensors. IEEE Trans Med Imaging. 2016;35(9):2119–2129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Tucker LR. Some mathematical notes on three-mode factor analysis. Psychometrika 1966;31(3):279–311. [DOI] [PubMed] [Google Scholar]
- 26.Kolda TG, Bader BW. Tensor decompositions and applications. SIAM Rev. 2009;51(3):455–500. [Google Scholar]
- 27.Monajemi H, Jafarpour S, Gavish M, Donoho DL, Ambikasaran S, Bacallado S, Bharadia D, Chen Y, Choi Y, Chowdhury M. Deterministic matrices matching the compressed sensing phase transitions of Gaussian random matrices. Proc Natl Acad Sci. 2013;110(4):1181–1186. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Wech T, Lemke A, Medway D, Stork LA, Lygate CA, Neubauer S, Köstler H, Schneider JE. Accelerating cine‐MR imaging in mouse hearts using compressed sensing. J Magn Reson Imaging. 2011;34(5):1072–1079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Liu J, Musialski P, Wonka P, Ye J. Tensor completion for estimating missing values in visual data. IEEE Trans Pattern Anal Mach Intell. 2013;35(1):208–220. [DOI] [PubMed] [Google Scholar]
- 30.Lingala SG, Hu Y, DiBella E, Jacob M. Accelerated dynamic MRI exploiting sparsity and low-rank structure: k-t SLR. IEEE Trans Med Imaging. 2011;30(5):1042–1054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Feng L, Axel L, Chandarana H, Block KT, Sodickson DK, Otazo R. XD‐GRASP: Golden‐angle radial MRI with reconstruction of extra motion‐state dimensions using compressed sensing. Magn Reson Med. 2016;75(2):775–788. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Adluru G, Awate SP, Tasdizen T, Whitaker RT, DiBella EV. Temporally constrained reconstruction of dynamic cardiac perfusion MRI. Magn Reson Med. 2007;57(6):1027–1036. [DOI] [PubMed] [Google Scholar]
- 33.De Lathauwer L, De Moor B, Vandewalle J. A multilinear singular value decomposition. SIAM J Matrix Anal Appl. 2000;21(4):1253–1278. [Google Scholar]
- 34.Morozov VA. On the solution of functional equations by the method of regularization. 1966. Russian Academy of Sciences. p 510–512. [Google Scholar]
- 35.Zhao B, Haldar JP, Christodoulou AG, Liang ZP. Image Reconstruction From Highly Undersampled (k, t)-Space Data With Joint Partial Separability and Sparsity Constraints. IEEE Trans Med Imaging. 2012;31(9):1809–1820. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Jaspers K, Aerts HJ, Leiner T, Oostendorp M, van Riel NA, Post MJ, Backes WH. Reliability of pharmacokinetic parameters: Small vs. medium‐sized contrast agents. Magn Reson Med. 2009;62(3):779–787. [DOI] [PubMed] [Google Scholar]
- 37.Look DC, Locker DR. Time saving in measurement of NMR and EPR relaxation times. Rev Sci Instrum. 1970;41(2):250–251. [Google Scholar]
- 38.Fan Z, Zuehlsdorff S, Liu X, Li D. Prospective self‐gating for swallowing motion: A feasibility study in carotid artery wall MRI using three‐dimensional variable‐flip‐angle turbo spin‐echo. Magn Reson Med. 2012;67(2):490–498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Higaki T, Tatsugami F, Fujioka C, Sakane H, Nakamura Y, Baba Y, Iida M, Awai K. Visualization of simulated small vessels on computed tomography using a model-based iterative reconstruction technique. Data Brief. 2017;13:437–443. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Xue H, Greiser A, Zuehlsdorff S, Jolly MP, Guehring J, Arai AE, Kellman P. Phase‐sensitive inversion recovery for myocardial T1 mapping with motion correction and parametric fitting. Magn Reson Med. 2013;69(5):1408–1420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.McGraw KO, Wong SP. Forming inferences about some intraclass correlation coefficients. Psychol Methods. 1996;1(1):30. [Google Scholar]
- 42.Bots ML, Hoes AW, Koudstaal PJ, Hofman A, Grobbee DE. Common carotid intima-media thickness and risk of stroke and myocardial infarction: the Rotterdam Study. Circulation 1997;96(5):1432–1437. [DOI] [PubMed] [Google Scholar]
- 43.Millon A, Mathevet J-L, Boussel L, Faries PL, Fayad ZA, Douek PC, Feugier P. High-resolution magnetic resonance imaging of carotid atherosclerosis identifies vulnerable carotid plaques. J Vasc Surg. 2013;57(4):1046–1051.e1042. [DOI] [PubMed] [Google Scholar]
- 44.van Wijk DF, Strang AC, Duivenvoorden R, Enklaar D-JF, van der Geest RJ, Kastelein JJ, de Groot E, Stroes ES, Nederveen AJ. Increasing spatial resolution of 3T MRI scanning improves reproducibility of carotid arterial wall dimension measurements. Magn Reson Mater Phy. 2014;27(3):219–226. [DOI] [PubMed] [Google Scholar]
- 45.Cai J, Hatsukami TS, Ferguson MS, Kerwin WS, Saam T, Chu B, Takaya N, Polissar NL, Yuan C. In vivo quantitative measurement of intact fibrous cap and lipid-rich necrotic core size in atherosclerotic carotid plaque. Circulation 2005;112(22):3437–3444. [DOI] [PubMed] [Google Scholar]
- 46.Henderson E, Rutt BK, Lee T-Y. Temporal sampling requirements for the tracer kinetics modeling of breast disease. Magn Reson Imaging. 1998;16(9):1057–1073. [DOI] [PubMed] [Google Scholar]
- 47.Li KL, Buonaccorsi G, Thompson G, Cain JR, Watkins A, Russell D, Qureshi S, Evans DG, Lloyd SK, Zhu X. An improved coverage and spatial resolution—using dual injection dynamic contrast‐enhanced (ICE‐DICE) MRI: A novel dynamic contrast‐enhanced technique for cerebral tumors. Magn Reson Med. 2012;68(2):452–462. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.