Abstract
Purpose:
Managing local SAR in parallel transmission requires ensuring that the peak SAR over a large number of voxels (>105) is below the regulatory limit. The safety risk to the patient depends on cumulative (not instantaneous) SAR thus making a joint design of all RF pulses in a sequence desirable. We propose the Iterative Minimization Procedure with Uncompressed Local SAR Estimate (IMPULSE), an efficient optimization formulation and algorithm that can handle uncompressed SAR matrices and optimize pulses for all slices jointly within a practical time frame.
Methods:
IMPULSE optimizes parallel transmit pulses for small-tip-angle slice selective excitation to minimize a single cost function incorporating multiple quantities (local SAR, global SAR, and per-channel power) averaged over the entire multislice scan subject to a strict constraint on excitation accuracy. Pulses for an 8-channel 7T head coil were designed with IMPULSE and compared to pulses designed using generic optimization algorithms and VOPs to assess the computation time and SAR performance benefits.
Results:
IMPULSE achieves lower SAR and shorter computation time compared to a VOP approach. Compared to the generic SQP algorithm, computation time is reduced by a factor of 5–6 by using IMPULSE. Using as many as 6 million local SAR terms, up to 120 slices can be designed jointly with IMPULSE within 45 seconds.
Conclusions:
IMPULSE can handle significantly larger number of SAR matrices and slices than conventional optimization algorithms, enabling the use of uncompressed or partially compressed SAR matrices to design pulses for a multislice scan in a practical time frame.
INTRODUCTION
High field MRI has several benefits, particularly those associated with increased polarization of nuclear spins (1,2); however, complications arise due to the increasingly complex interactions between the patient and the transmitted RF fields (3). inhomogeneity is problematic at field strengths greater than 3 Tesla and leads to flip angle inhomogeneity (FAI) and unwanted image shading (4). Additionally, as the Larmor frequency increases, interactions between the increasingly inhomogeneous electric field and human tissue can result in local specific absorption rate (SAR) hotspots that may cause unsafe tissue heating (5,6). These two effects can be counteracted by using a parallel transmit (pTx) RF coil with multiple independent transmit channels, allowing the current applied to each channel to be optimized in order to reduce FAI and suppress local SAR hotspots (7–12). Importantly, both and local SAR distributions can vary depending on the load and therefore the pTx waveform should ideally be optimized at the scanner for every patient.
Although pTx methods that achieve flip angle uniformity have been demonstrated experimentally with some reliability (13–15), accomplishing low FAI while managing the risk of tissue heating in a patient-specific manner has not been addressed optimally. Compared to , local SAR is more difficult to measure in-vivo; methods such as direct SAR mapping using thermoacoustics (16) or electric properties tomography (17) haven’t yet become reliable. For this reason, SAR is typically estimated using electromagnetic simulations with generic numerical tissue models (18) and a safety factor of about 1.5 is applied to account for uncertainties in the simulation compared to the physical coil and patient (19). With a patient-specific SAR estimate, obtained for example through simulation on a segmentation of a low resolution MRI of the patient (20) or predicted from measured maps with a convolutional neural network (21,22), a smaller safety factor would be possible.
The SAR matrix formalism (22) allows for computation of peak local SAR for arbitrary pTx pulses using a compact matrix notation and has been instrumental in allowing the incorporation of SAR into various pTx optimization approaches. Because of the size of the grid required for accurate electromagnetic simulation throughout the anatomy of interest, typically more than 105 nonzero matrices will be formed. Each of these matrices is complex-valued, square, Hermitian and has dimension equal to the number of independent transmit channels. Using generic optimization solvers, the time required for pTx pulse design becomes impractical when considering all these matrices; for this reason, the virtual observation point (VOP) compression method (23) was developed as a pre-processing step to allow a significant (order-of-magnitude) acceleration of on-scanner estimation of true peak local SAR (over the full set of SAR matrices) in a way that guarantees no underestimation and bounded overestimation. Since the compression from the full set of matrices to a much smaller set of VOP matrices can require significant computation time, VOPs are typically pre-computed on each body model following numerical simulation of and E fields produced by the transmit coil in that body model. For cases with large number of voxels(> 106) such as in the torso, in the head with <2mm voxel size, or when considering a population of tissue models rather than a single model, the time needed for VOP compression can be in the range of tens of minutes. Although the approach has been improved by Lee et al (24) who introduced a generalized compression technique for a tighter overestimation bound for the same number of VOP matrices and by Kuehne et al (25) who introduced an approach to reduce compression time for models with a large number of voxels, the overestimation and computation time could still be improved.
Most prior approaches to solving the SAR-aware pTx design problem formulate the optimization as a constrained minimization with normalized root mean square excitation error (NRMSE) as the objective, and using SAR, power, and/or temperature constraints (9,10,26). These efforts to tackle the pulse design problem used generic optimization tools to solve either a convex version of the problem (9) with fixed k-space trajectories or a nonconvex version (10) with the magnitude least squares (MLS) formulation (27) and variable k-space trajectories at the expense of longer optimization times. In all cases VOPs were needed to make the computation tractable. A fast algorithm that can optimize over all SAR matrices directly without a compression step would eliminate the computational burden and overestimation error associated with VOPs.
An additional consideration when managing SAR is that all RF pulses in an entire pulse sequence contribute to the single time-averaged SAR quantity that contributes to tissue heating and safety risk. Designing each individual pulse to eliminate SAR hotspots gives fewer degrees of freedom than considering all pulses in the sequence jointly which allows for a solution that produces hotspots in different locations for each excitation, resulting in a lower value of SAR after temporal averaging (28). This concept has been described previously as “SAR hopping” where the mean FAI over all slices is minimized while constraining the cumulative SAR (29,30). A drawback of this approach is that there is no control of the FAI at each individual slice and the proposed formulation could achieve very low FAI at one slice at the expense of unacceptably high FAI at another slice. Furthermore, the increase in the number of optimization variables by designing pulses for multiple slices can increase the computation time.
In view of the above concerns we propose a new minimum SAR (minSAR) formulation for the multislice small-tip pTx design problem and show an efficient optimization algorithm for solving it termed the Iterative Minimization Procedure with Uncompressed Local SAR Estimate (IMPULSE). We seek to minimize the cumulative SAR over a multislice scan while ensuring that the FAI at each slice is below some tolerance. Using a special class of optimization algorithm with favorable convergence properties (called a proximal algorithm), we show that this problem can be solved in a time frame suitable for on-scanner design while retaining the benefits of SAR hopping and having the additional advantage of not requiring compressed SAR matrices.
THEORY
minSAR pulse design formulation
Our goal is to find a sequence of channel weightings to apply to each spoke (8) of each excitation pulse in a multislice scan to achieve minimum SAR while satisfying a user-specified tolerance on the acceptable inhomogeneity (quantified by the NRMSE with respect to a target magnitude excitation profile). As part of this problem, we also seek to find the optimal number and location of spokes and the optimal target phase (according to MLS theory) to achieve minimum SAR. The value of the NRMSE tolerance will depend on the imaging application; for example, quantitative MRI such as relaxometry would likely have a lower NRMSE tolerance than applications that only involve qualitative assessments of images. This minimum SAR approach is valuable for applications where the SAR of the sequence can be trivially adjusted after the pulse design by modifying scan parameters such as flip angle, TR, or number of slices without affecting the flip angle inhomogeneity of the optimized pTx pulse. In this way, the headroom that is afforded by the minimum SAR pulse can be exchanged for reduced acquisition time, increased signal, increased coverage, or other improvements to the imaging sequence. Particularly in the case of designing multiple slices jointly, a significant advantage of the minSAR formulation over methods that minimize total excitation error over all slices is that it eliminates the possibility of some slices being unacceptably inhomogeneous with others being more homogeneous than necessary.
Mathematically, we wish to determine a complex valued matrix (an underbar denotes a channel weighting variable) where each column is a complex weight vector to apply to each of NC transmit channels at each of the NK spokes and each of the NS different RF pulses/slices throughout the entire scan. The objective COST (Eq. 1) is to maximize the allowable RF duty cycle or equivalently to minimize a cost function that encapsulates all local SAR, global SAR, and average power constraints in a single expression:
| [Eq. 1] |
where
NR is the total number of SAR terms equal to number of SAR voxels (local SAR) + 1 (global SAR) + number of channels (average power)
Bi denotes a column of B
Qr is a local SAR, global SAR, or average power matrix computed for some nominal duty cycle
χr is a scaling factor to harmonize the different constraint limits
In this way, COST(B) represents the amount by which the nominal duty cycle can be scaled while still ensuring that all of the NR constraints are satisfied. Note that a smaller value of COST corresponds to a lower SAR.
Due to the small-tip approximation (31,32), the excitation profile over the NX nonzero pixels in each slice can be represented as where is a vector formed by combining the NK columns of B corresponding to the spokes for slice s and is a system matrix that is a nonlinear function of the spokes locations, , (which are to be optimized) as well as the measured and B0 maps and pre-computed slice-select subpulse (Appendix A). The feasible set, , of acceptable pulses that satisfy the flip angle inhomogeneity for a given target magnitude profile, dmag,(s), and obey the peak power limits is
| [Eq. 2] |
which can be interpreted a union of ellipsoids combined with a magnitude constraint, , for the instantaneous power (Appendix B). Each ellipsoid is centered at the maximum homogeneity pulse, has orientation determined by the spokes location and target phase, and has size determined by the NRMSE tolerance. Note that unlike the terms in the COST function, these constraints are not time-averaged and must be satisfied for each slice.
With these definitions in place, the minSAR optimization problem is expressed compactly as:
| [Eq. 3] |
There are several unique aspects to the minSAR problem. The objective includes all uncompressed SAR terms and is piecewise quadratic making it convex but nondifferentiable. The constraint is nonconvex but the feasible set can be expressed in terms of ellipsoids and a hypersphere for which computing a projection happens to be very simple. Furthermore, the objective is influenced by all channel weightings in the pulse sequence whereas each only depends on a subset of them.
IMPULSE
We propose IMPULSE as an efficient optimization procedure, based on the alternating direction method of multipliers (ADMM) algorithm, that exploits the unique features of the minSAR problem. Most conventional algorithms for constrained optimization problems transform the problem into a set of optimality conditions that must be true at the optimal solution (a generalization of the fact that the gradient must be zero at the optimal point for unconstrained optimization). The solution to the optimality conditions is guaranteed to be optimal but can be difficult to compute particularly in cases where the objective or constraints involve many terms like the minSAR problem. In contrast, IMPULSE is a proximal algorithm which is a class of algorithms that offer the benefit of “good enough” convergence within a few iterations although converging to a strict tolerance level can take a much larger number of iterations. Since there are significant sources of error in the process used to estimate SAR (eg. inaccuracies in the numerical coil and body models compared to the physical coil and patient) this lenient convergence criteria is acceptable and prevents overfitting to inaccuracies in the SAR estimation.
The basic approach is to first convert the problem into an unconstrained problem with two different channel weight variables (called y and z here) using an augmented Lagrangian to enforce consistency between y and z:
| [Eq. 4] |
where is the indicator function for the feasible set (evaluates to zero when the variable is feasible and infinity otherwise), λ is a Lagrange multiplier that enforces similarity between y and z, and is the “augmentation” which further enforces consistency between y and z by applying an additional penalty on the deviation between them and contributes to the increased rate of convergence controlled by the penalty parameter ρ. The standard iterative method of minimizing a Lagrangian involves doing the following at each iteration: (1) minimize the expression with a fixed value of λ, (2) update λ based on the value of the Lagrange residual (y − z). The first step can be further decomposed into sequential subproblems: (a) minimization of Lρ with respect to y with fixed z and then (b) minimization of Lρ with respect to z with y fixed to the updated value from (a). Because of the augmentation term , these two subproblems can be solved efficiently: subproblem (a), which we call the SAR update, is an unconstrained (but nondifferentiable) minimization that can be performed efficiently even with uncompressed SAR matrices using a “cutting plane” method, and subproblem (b), which we call the FAI-update, is a projection onto which can be parallelized as NS independent projections onto the individual .
The IMPULSE algorithm can be described in terms of three variables and an iteration counter k:
Z(k): Output of the FAI update signifying a “feasible” set of channel weights that satisfies the FAI (NRMSE) tolerance
Y(k): Output of SAR-update signifying set of channel weights with reduced SAR compared to Z(k−1) but possibly violating the FAI tolerance
U: Running vector sum of the residual Y(k) − Z(k) for all prior iterations
The initial pulse matrix Z(0) is found using a SAR-unaware algorithm (8) where spokes are added until the FAI tolerance is met. Starting from this initial pulse (that satisfies the FAI tolerance but has high SAR), the three main steps that are performed at each iteration of the algorithm are:
Initialization: U(0) = 0, Z(0), iteration counter: k = 0
REPEAT:
- Step 1: SAR-update
Minimize SAR (over all excitations) characterized by the COST function while penalizing distance from Z − U controlled by the penalty parameter ρ[Eq. 5] - Step 2: FAI-update
Split the Y and U matrices into vectors y and u for individual slices s and for each slice project y + u onto the feasible set of pulses (ie find the weights that satisfy the FAI tolerance with minimum distance from y + u while updating spokes locations and target phase if needed)[Eq. 6] - Step 3: Residual update
Increment U by the residual between Y and Z for current iteration[Eq. 7]
UNTIL: ‖Y − Z‖ ≈ 0 and ‖Z(k) − Z(k−1)‖ ≈ 0
A complete flowchart of the IMPULSE algorithm is shown in Figure 1 and a visualization of the iterations for one slice is described in Figure 2. A full mathematical derivation of the algorithm is given in Supporting Document A.
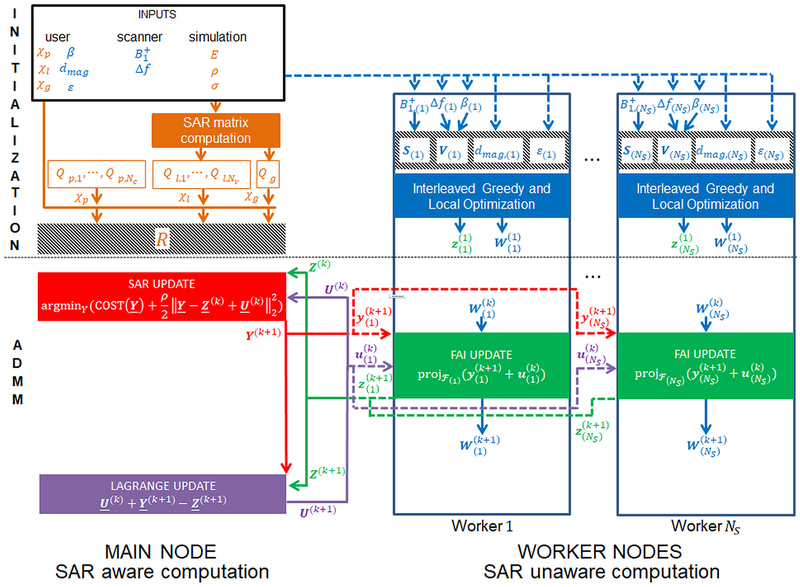
Figure 1:
Flowchart for the IMPULSE optimization algorithm. A main node receives inputs and divides work among NS worker nodes. The user inputs are χp, χl, χg corresponding to average per channel power, local SAR, and global SAR constraints and β (the slice select subpulse waveform), dmagc (the magnitude of the target excitation map for each slice), and ε (the tolerance on the NRMSE for each slice). Scanner inputs are the transmit sensitivity maps and Δf the off resonance maps for each channel and each slice. Simulation inputs are E, the electric field over the whole volume for each channel; ρ, the mass density of the tissue model; and σ, the conductivity of the tissue model. The variables in blue which affect the flip angle inhomogeneity of individual slices but not SAR are distributed (indicated by dashed line) to NS worker nodes corresponding to NS separate slices to be excited during the scan. During the initialization step, work proceeds on the main node and worker nodes in parallel. On the main node, SAR matrices are formed using the simulation input and these are transformed into the oracle matrix, R, after normalization by the constraints. On the worker nodes, the maps are flattened to form a matrix S which characterizes the effect of the transmit sensitivity maps on the flip angle, β and Δf are combined into a single matrix V which characterizes the phase accrual from off resonance, and the dmag and ε values are stored on each worker. In this way the pTx pulse design problem is defined completely by five variables: R which describes cumulative SAR and power information over all slices, and S, V, dmag, and ε which characterize the flip angle inhomogeneity of each slice. While oracle construction is happening on the main node, SAR unaware interleaved greedy and local optimization occurs on each of the worker nodes for each slice. Spokes are added until the NRMSE tolerance is satisfied. The output is a channel weighting vector z and a matrix W that describes the phase accrual from optimal spokes locations. These variables are initial values for the ADMM algorithm. First a SAR update is performed which serves to reduce the SAR of the pulse while still applying a penalty on the distance from z. The output Y will have lower SAR but could possibly violate the NRMSE tolerance. Then the Y variable is split across slices and distributed to the workers, each of which performs a FAI update where y is projected on to the feasible set to get a vector z that is guaranteed to satisfy the NRMSE tolerance but will have higher SAR. Then the z variables for each slice is sent back to the main node and a composite matrix Z is formed which is used to update the Lagrange multiplier U that serves to enforce consistency between the Y and Z variables. These three updates are performed iteratively until Y ≈ Z at which point the final pulse will have minimum SAR while also satisfying the NRMSE tolerance.
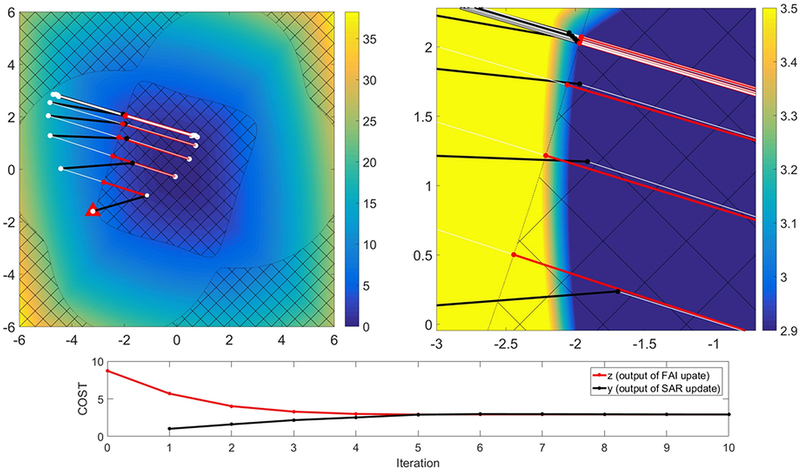
Figure 2:
Visualization of ADMM iterations in IMPULSE in 2 dimensions with two magnifications. The x and y coordinates correspond to real-valued channel weights for 2 channels. The background image is the value of COST for each of the weights. The hatched region corresponds to “unfeasible” channel weights that violate the FAI tolerance. The goal is to find the point in the feasible (unhatched) region that has minimum SAR. The red triangle indicates the weights resulting from the SAR-unaware interleaved greedy and local algorithm and is the initial value of the z variable which signifies a channel weight that satisfies the FAI tolerance. The initial value of y signifying the output of the SAR update is set to 0. The initial value of the u variable which signifies the residual between y and z is set to 0. The first step of the algorithm is to subtract the residual from z to get the quantity z-u which is indicated by the white dot which is initially in the center of the triangle. The next step is to find y by performing the SAR update which seeks to minimize SAR while penalizing deviation from the white dot. This quantity y is indicated by the black dot. The next step is to perform the FAI update which projects y (black dot) onto the feasible set (ie find the point in the feasible region that is closest to the black dot). Finally, the value of u (the residual) is updated by adding the difference between z and y for the current iteration (ie at each iteration the white vector equals the sum of all the previous red vectors). This completes one iteration of the algorithm. After 8 such iterations the algorithm converges as can be confirmed in the plot of the COST of y and z at each iteration. It can also be confirmed visually in the right figure that the final red dot is indeed the point in the feasible region with minimum SAR
Algorithm for SAR update
The sub-iterations of the SAR update in two dimensions are visualized in Figure 3 and the detailed algorithm is given in Table 1. The SAR update involves finding the sequence of channel weights Y that achieves the minimization in [Eq. 7]. The objective function contains a regularization or penalty term
| [Eq. 8] |
which penalizes deviation from the output of the FAI update (ie violation of the NRMSE tolerance). Since this regularization term will dominate the objective for Y far from Z(k) – U(k) (ie weights that significantly violate the NRMSE tolerance), replacing COST(Y) with a simpler piecewise linear approximator PLA(Y) that is accurate only for reasonably homogeneous pulses (those in the vicinity of Z(k) – U(k)) will still give a nearly exact solution to the SAR update. Specifically, this is accomplished by using an approach called a bundle or cutting plane method (Table 1) where PLA(Y), a piecewise linear lower bound to COST(Y), is constructed iteratively. At sub-iteration j,
| [Eq. 9] |
is minimized using a efficient finite-time algorithm called column-exchange describe in detail in (33). Based on the value and gradient of the true COST function at this minimum, a new tangent plane is added to PLA to refine the approximation of COST. The process is repeated until PLA(Y[j]) ≈ COST(Y) at the current iteration.
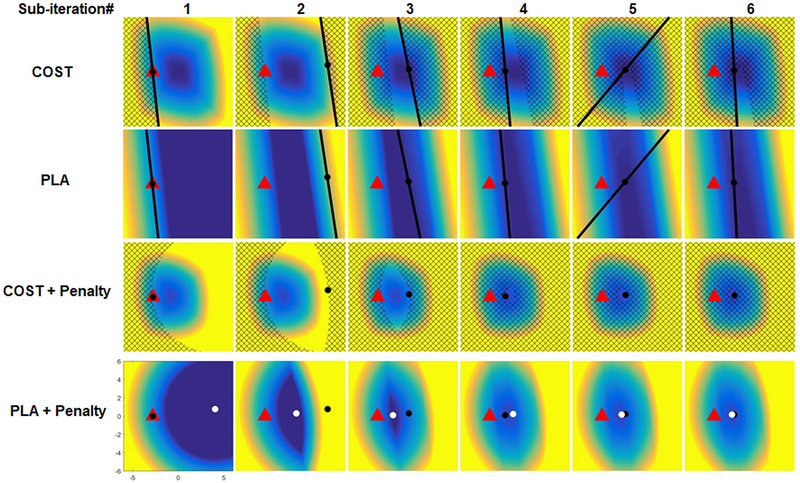
Figure 3:
Visualization of the sub-iterations of the SAR-update. The starting point (red triangle) is the quantity Z − U found by subtracting the cumulative residual U from the result of the FAI update Z(k) from the previous ADMM iteration. The goal is to minimize SAR while also penalizing distance from this red triangle. The current location, Y[j], for each sub-iteration of this SAR update is indicated with a black dot and this is initialized to the same location as the red triangle. The first step in the cutting plane algorithm is to find the gradient of SAR at Y[j] using the vectorized oracle and updating the piecewise linear approximation (PLA) of SAR by adding a cutting plane tangent to COST found using the gradient at Y[j]. The PLA (second row) is less than or equal to the true SAR (first row) at all locations and is exactly equal to the true SAR at Y[j]. The hatched region in the first row indicates locations where the PLA is greater than the true SAR at Y[j]. The next step is to add the penalty term which penalizes distance from the red triangle. The hatched region in the third row indicates the region where the PLA + Penalty is greater than the value of the true SAR + penalty at Y[j] (ie the region that cannot be a solution to the SAR update). The PLA + penalty term is minimized to give the Y[j+1] which is indicated by the white dot. This process is repeated and at each sub-iteration the hatched region in third row increases and the search area for potential solutions decreases until it converges to a single point.
Table 1:
Algorithm for SAR update
| Flatten Z(k), U(k) into vectors z(k), u(k) |
| GIVEN: z(k), u(k), y[j] = z(k) − u(k); j, G[j], w[j] from prior ADMM iterations |
| REPEAT: |
| 1. Update the matrix of normal vectors G[j] by appending the normal vector at y[j]. |
| 2. Update the vector of intercepts w[j] by appending the intercept at y[j]. |
| 3. Update pulse by minimizing the PLA + PENALTY function with the refined piecewise linear approximation: |
| 4. j = j + 1 |
| UNTIL: COST stops changing |
| Reshape y[j] into Y(k) |
The most demanding step in this procedure is the evaluation of the COST function and its subgradient in order to determine the tangent cutting planes at each iteration. This is performed efficiently with a “vectorized SAR oracle” (34) that computes SAR in a vectorized manner similar to the approach described by Hoyos-Idrobo (10); this vectorized SAR oracle is described in detail in Supporting Document B and Supporting Information Figure S1. The oracle is queried with a sequence of channel weightings and returns the value of COST and its subgradient. This is done efficiently by constructing a single large matrix that incorporates all local SAR, global SAR, and power terms as rows of the matrix such that both COST and its subgradient for a particular sequence of channel weightings can be found quickly through a single matrix multiplication. This vectorization eliminates “for loops” to exploit the built-in optimizations for single instruction multiple data (SIMD) of numerical computing packages (eg MATLAB) and also allows for simple GPU acceleration. For this reason the computation time of the oracle is approximately constant with both number of SAR terms and number of slices (Supporting Information Figure S2) and this is one of the reasons behind the efficiency of IMPULSE.
Algorithm for FAI update
The FAI update can be accomplished through iterative projections onto the ellipsoid ( in Eq. 2) formed by fixing the target excitation phase and spokes locations interleaved with an update of the phase and spokes locations after each projection using optimization transfer and variable exchange (27). The projection can be performed using a specialized algorithm for Euclidean projection of a point onto an ellipsoid (35). In the case were this projection causes the peak power constraint ( in Eq. 2) to be violated, the magnitude of the resulting channel weights is reduced to abide by the power limit and the projection is repeated until the closest point on the ellipsoid that satisfies the power limit is found. This entire process can be done in parallel for all slices. A visualization of the FAI update for one slice is given in Supporting Information Figure S3.
A concise high-level overview of the entire IMPULSE algorithm decomposed into each of the individual sub-algorithms is shown in Supporting Information Figure S8.
METHODS
We assessed the performance of the IMPULSE algorithm by designing pTx RF and gradient waveforms using an 8 channel head coil at 7T for axial brain slices. We demonstrated performance of IMPULSE on the brain using simulated field maps and experimentally on a spherical phantom using temperature measurements. Unless otherwise stated, the following parameters were used for the pTx pulse: number of spokes = 2, local SAR constraint = 10 W/kg, global SAR constraint = 3.2 W/kg, average power per channel = 10W, peak instantaneous power per channel = 600W, slice thickness = 1 mm, NRMSE tolerance = 5%. All computations were done using an Intel Xeon E5–2650 CPU (48 threads), and a Nvidia GTX 1080Ti GPU. IMPULSE was implemented in MATLAB using the Parallel Computing Toolbox and VOP compression was implemented in C++ with OpenMP and Eigen (see Supporting Document D, Supporting Information Figure S4, and Supporting Information Figure S5). A value of ρ = 0.006 was used for all simulations. Justification for this value is given in Supporting Document E and Supporting Information Figure S6. For an intuitive visualization of the effect of ρ on the convergence of the algorithm please see the Supporting Information Video files rho_small.avi (ρ = 0.001), rho_best.avi (ρ = 0.005), and rho_large.avi (ρ = 0.01).
Electromagnetic Field Simulations
For development of the IMPULSE algorithm, pTx pulses were designed using simulated and electric field maps found through full-wave FDTD simulations with an 8-channel pTx head coil model (Sim4Life, SPEAG, Zurich) tuned and matched using cosimulation (Advanced Design System) and the Duke head models from the Virtual Family (IT’IS, Zurich) (18). To get and E field maps, simulations were done with a harmonic excitation at 298 MHz (corresponding to the 7T Larmor frequency) with each channel of the coil excited independently. A 1.5 mm isotropic voxel size was used for the simulation, resulting in 6,371,811 nonzero voxels.
Reduction of SAR with IMPULSE
The ability of IMPULSE to reduce SAR compared to the SAR-unaware interleaved greedy and local algorithm was evaluated by designing pulses for two axial slices spaced 2 cm apart centered around the isocenter of the coil on Duke both with SAR hopping (using the described IMPULSE algorithm) and without SAR hopping (by running IMPULSE on two slices separately in parallel). The resulting SAR maps were evaluated for the two pulses for all three methods.
The use of uncompressed SAR matrices with IMPULSE was compared with the conventional approach of using VOPs solved using the sequential quadratic programming (SQP) algorithm. We found the SQP algorithm performed slightly better than the active-set algorithm for our minSAR problem although Hoyos-Idrobo et al (10) reported superior performance with the active-set algorithm. The two methods were compared by measuring the time for pulse design optimization and calculating the resulting SAR after optimization. VOPs computed with both ε = 2.5% and ε = 15% for the overestimation parameter in the VOP compression (23) were used and the time needed for the compression was quantified. These values represent tight and loose overestimation bounds, respectively, and allowed quantification of the SAR performance vs computation time penalty for these two extreme cases. L-curves of SAR vs NRMSE (1–10%) were generated for all three methods (IMPULSE and VOPs with two different ε). Reported values of SAR were computed accurately using the full set of uncompressed matrices even in cases where VOPs were used for optimization.
The performance of IMPULSE on a large number of slices was quantified by designing pulses for 120 slices spaced evenly over 12 cm. Three different formulations of the minSAR optimization problem (Table 2) were compared: a simple convex problem was solved using an interior-point algorithm with the CVX solver (36), a nonconvex problem solved with the SQP algorithm (fmincon), and the same nonconvex problem with IMPULSE.
Table 2:
Three formulations/algorithms for minSAR optimization
| SLICES DESIGNED JOINTLY? | NO | YES | YES |
| OPTIMIZE SPOKE LOCATIONS? | NO | YES | YES |
| OPTIMIZE TARGET PHASE? | NO | YES | YES |
| SAR ESTIMATE | VOP | UNCOMPRESSED | UNCOMPRESSED |
Experiments
An 8-Tx, 32-Rx 7T coil (Nova Medical) was used for experiments. Single slice pTx pulses were designed for the central axial slice of a 170mm spherical phantom with εr = 80 and σ = 0.91 S/m. A spoiled gradient echo (SPGR) sequence was used with TR = 4000ms, TE = 8ms, and flip angle of 30 degrees. Flip angles were deduced by exciting at variable flip angles and fitting the measured signal values to the SPGR signal equation; the effects of T1 and T2* can be ignored because of long TR and short TE. Pulses designed with the interleaved greedy and local algorithm were compared to IMPULSE. For SAR estimation, the electric fields were simulated using FEKO (Altair Engineering, Troy MI) with coil and phantom models mimicking the experiments including positioning of the phantom within the coil. The SAR maps were verified using a fiberoptic temperature probe (FISO FOT-L-NS-967A) placed at a location within the phantom corresponding to the greatest change in the simulated SAR hotspot between the two pulse design methods. To maximize the temperature increase in order to improve the accuracy of the measurement, identical pulses were applied as for imaging but the TR of the sequence was decreased to 100 ms.
RESULTS
Reduction of SAR with IMPULSE
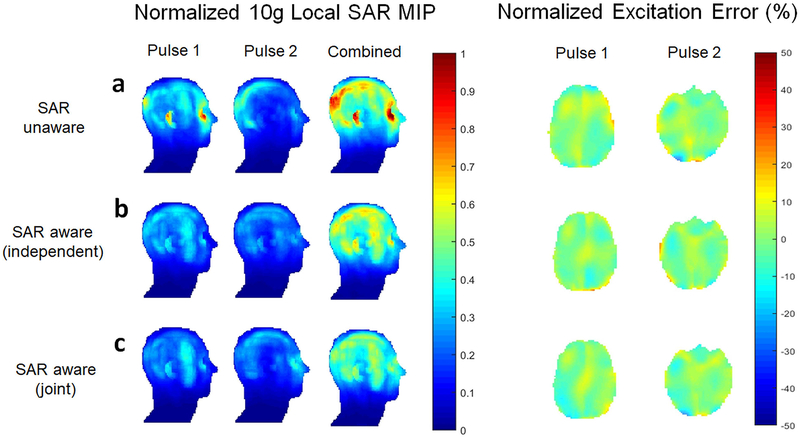
The reduction of peak local SAR with IMPULSE is demonstrated in Figure 4. Significant SAR reduction (2×) is achieved through the use of IMPULSE vs a SAR-unaware (interleaved greedy and local) algorithm (a). Further SAR reduction is obtained by designing the two pulses for the two slices jointly (c) instead of independently (b). Compared to the SAR unaware algorithm, with IMPULSE peak local SAR is reduced by 42% when slices are designed independently and 52% when designed jointly.
Figure 4:
SAR reduction through the use of SAR aware algorithm (IMPULSE) vs (a) SAR-unaware (interleaved greedy and local) algorithm. Further SAR reduction is obtained by designing the two pulses for the two slices jointly (c) instead of independently (b). Note that with the independent design the peak local SAR for each pulse is less than the corresponding peak local SAR for each pulse with the joint design but the total SAR of the two pulses is lower with the joint design than with the independent design because the SAR distributions are optimized to reduce constructive summation.
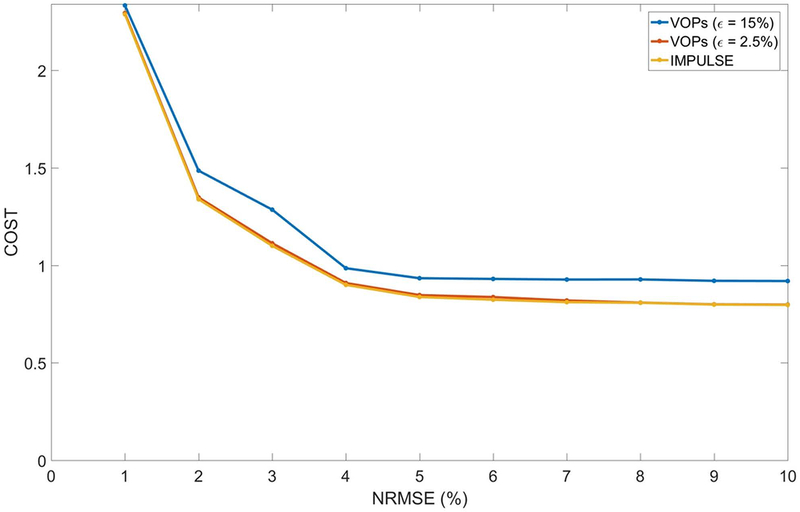
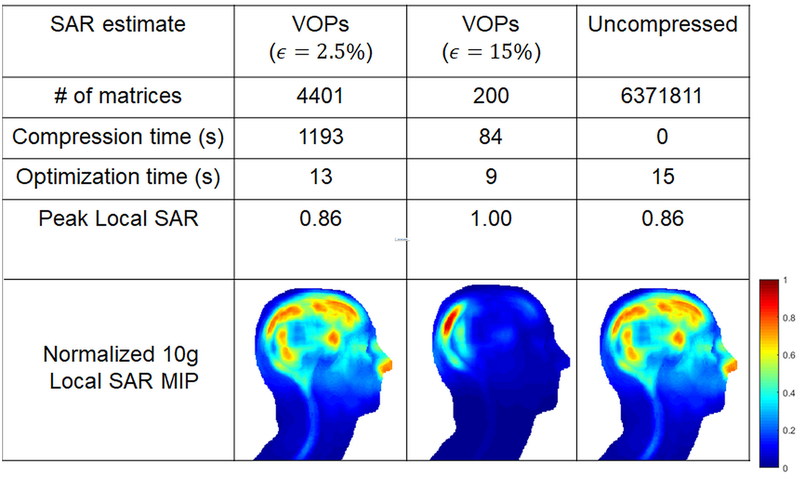
Figure 5 shows the L-curves for IMPULSE and using VOPs with two overestimation parameters to excite a single slice and Figure 6 shows the computation times along with SAR maps for each method of SAR estimation. With a strict overestimation parameter (2.5%), there is negligible SAR penalty compared to using uncompressed matrices, but the computation time for VOP compression is long (1193 s). Since the VOP method sequentially assigns clusters, there is no obvious way to reduce this computation time through parallelization. For a more relaxed overestimation parameter (15%), the compression time is decreased to 84 seconds, but still longer than the optimization time with IMPULSE (15 seconds), and the SAR penalty compared to IMPULSE increases approximately 15%. The benefits of IMPULSE over using VOPs are reinforced in Figure 6 which shows representative SAR maps (maximum intensity projection through the whole head/neck) that indicate that a more intense hotspot results with this relaxed parameter. The table in Figure 6 shows that IMPULSE achieves the fastest total computation time while also achieving the lowest peak local SAR.
Figure 5:
L-curves of SAR vs NRMSE using uncompressed SAR matrices (IMPULSE) and using VOPs with overestimation parameter of 2.5% and 15%. Over a range of NRMSE values (1 −10%), IMPULSE achieves similar SAR performance to use of VOPs with 2.5% estimation. Compared to VOPs with a 15% overestimation error the SAR with IMPULSE is 10–15% less.
Figure 6:
Tabulation of optimization times, compression times, and total number of matrices for pTx optimization done with VOPs using ϵ=2.5% and ϵ=15% and with uncompressed SAR matrices. Using VOPs with ϵ=2.5% comes with a significant penalty in compression time of 1193 seconds. Optimized SAR MIPs are shown and a significant SAR hotspot is seen when using ϵ=15%.
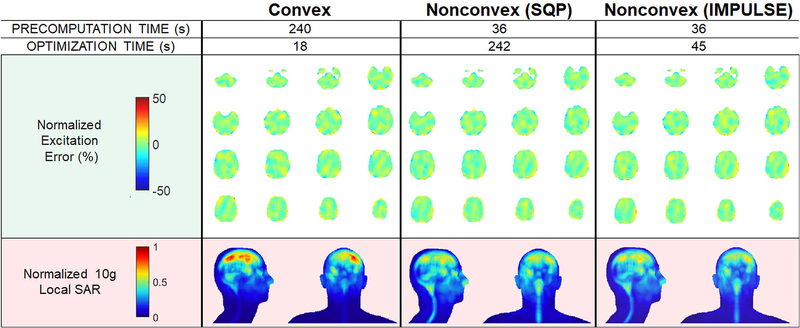
Figure 7 shows computation times, SAR maps, and flip angle maps for 16 of the 120 slices (maps of all slices are in Supporting Document F and Supporting Information Figure S7). When a convex algorithm is used to design the pulses for the multislice case, the peak local SAR is high but the duration of the optimization is short (18 seconds). By solving the more complete nonconvex problem including optimization of spokes locations using the SQP solver, the peak local SAR can be reduced by 37%; however, this inefficient algorithm requires a long optimization time of 242 seconds. Using IMPULSE to solve the nonconvex problem reduces the optimization time to 45 seconds with similar SAR performance. Because IMPULSE eliminates the time for VOP compression, the only precomputation needed is that for SAR matrix / oracle construction which takes 36 seconds.
Figure 7:
SAR reduction and computation time savings when designing 120 slices for the Duke body model using IMPULSE compared to prior methods. IMPULSE results in significantly lower SAR compared to solving a convex formulation of the minSAR problem while being more computationally efficient than a generic SQP solver in solving the nonconvex formulation.
Experiments
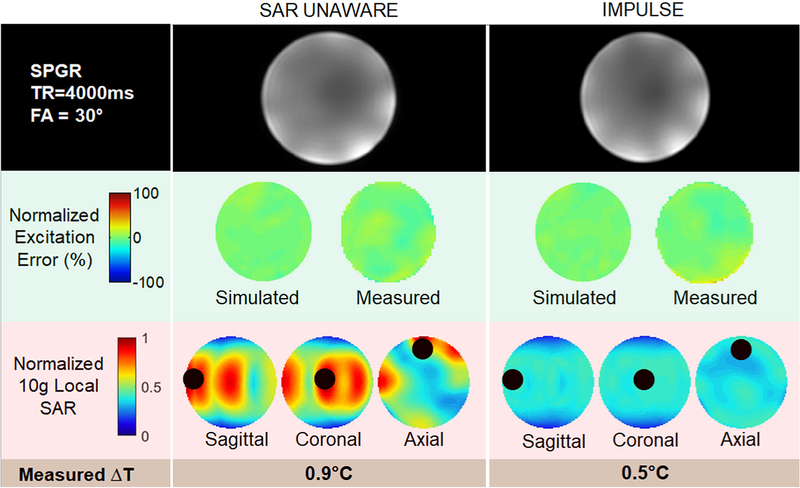
As shown in Figure 8, using a pTx pulse design with the SAR-unaware algorithm, a uniform excitation pattern (5% NRMSE) is achieved. However, this also results in a significant SAR hotspot at the center portion of the anterior surface of the phantom. When the pulse is designed with IMPULSE, 5% NRMSE is achieved with a 72% reduction in peak local SAR. Simulated flip angle maps matched closely with the measured maps (measured NRMSE = 6.13% for SAR unaware and 6.87% for IMPULSE). Local SAR simulations were supported by the temperature measurements which indicated a similar reduction of temperature at the hotspot location (indicated by a dark circle) using IMPULSE.
Figure 8:
Experimental data showing the ability of IMPULSE to produce a uniform flip angle map but also eliminate SAR / temperature hotspots unlike the SAR unaware pTx design method. Simulated peak local SAR is reduced by 72% and measured temperature at the hotspot location (marked by a dark circle) is 0.4 degrees Celsius lower while achieving nearly identical flip angle inhomogeneity (both simulated and measured).
DISCUSSION
We have introduced a complete formulation of the SAR-aware pTx pulse optimization problem which minimizes the total SAR of the RF pulse sequence in a patient-specific way. This minSAR formulation allows specification of a tolerance on the acceptable NRMSE in the excitation profile (which incorporates multiple sources of nonconvexity) while minimizing the cumulative SAR of the pulse sequence subject to that constraint. This formulation is applicable in situations where SAR can be adjusted after the pulse design by changing parameters (such as flip angle or TR) to force SAR to be equal to the regulatory limit, thereby fully utilizing SAR headroom. SAR is characterized as a single convex expression combining the terms corresponding to average per channel power, global SAR, and local SAR (which is expressed using all SAR matrices and is therefore a better representation of the patient than using a compressed set of VOPs). Additionally, the formulation incorporates the design of all RF pulses in the sequence into a single joint optimization which enables SAR hopping with only minor penalty in computation time compared to designing a pulse for a single slice.
This minSAR problem, while seemingly quite difficult to solve, actually has an efficient solution which we have termed IMPULSE. The key feature of IMPULSE is the decomposition of the overall optimization problem into SAR-dependent and FAI-dependent subproblems, each of which happens to have a very efficient solution. The SAR update involves minimizing a single convex but nondifferentiable (specifically, piecewise quadratic) function representing patient-specific SAR with a regularization term that penalizes the distance from the previous value of the channel-weighting vector (and thus restricts how much the NRMSE tolerance is violated after the SAR update). The efficiency of the presented method for the SAR update is due to (1) the SAR expression having a particular form such that its value and subgradient can be found quickly using a vectorized oracle and (2) the regularization term producing a sharp minimum such that the unconstrained minimization can be solved with a cutting plane algorithm over just a few iterations (each of which query the oracle just once). Importantly, both these factors are independent of the number of terms in the SAR expression for the following reasons: (1) the computation time for the oracle is approximately constant with respect to the number of terms (i.e. local SAR matrices) because of its vectorized nature (Supporting Information Figure S3) and (2) the regularization term effectively restricts the search region over which the value of the minimum is possible enabling convergence within a few iterations. In this way the cutting plane method allows for optimizing over the full set of SAR matrices in an efficient way without having to precompute a compressed set of matrices. The FAI-dependent subproblem, despite being nonconvex, can also be solved efficiently because (unlike with the SAR update which evaluates cumulative SAR over the entire pulse sequence) the optimization for the FAI update can be split across slices since the NRMSE for one slice is independent from the NRMSE of every other slice. This allows the FAI-update to be trivially parallelized and the time saved through parallelization can be used to address the nonconvexities of the problem (finding the optimal target phase distribution and spokes locations).
There are a few limitations to the IMPULSE algorithm that must be considered when using it in practice. Firstly, the ρ parameter that controls the amount of regularization in the SAR update will control the tradeoff between the time to convergence and the suboptimality of the solution (Supporting Document E). Based on the application and the acceptable duration for the pulse optimization, the value of ρ that achieves minimum SAR in that duration can be chosen. Another limitation, as with any optimization algorithm, is that there is no guarantee of global optimality. The results using IMPULSE are within 7% of the solution found with MATLAB using an SQP algorithm while requiring significantly less computation time (IMPULSE: 45 seconds, SQP: 242 seconds, time for SQP optimization to reach same value as IMPULSE: 143 seconds). Describing the global optimality of IMPULSE is a difficult theoretical problem and therefore beyond the scope of this paper, but it is important to note that the ADMM algorithm has been shown to have desirable global convergence properties (37).
A significant feature of IMPULSE that could serve as a solution to the patient-tissue model mismatch problem in SAR estimation is that it enables more sophisticated methods of SAR estimation without significant increase in computation time. Here we used a single high resolution head model to demonstrate the capabilities of IMPULSE to handle a large number of voxels but in practice a lower resolution model would likely be sufficient. In this case, it would be possible to incorporate information from an entire population of models. A simple approach would be to select the K models from the population that most closely match the patient (38) and add the local and global SAR terms for these models to the COST expression. As shown in Supporting Document B, the computation time for the oracle, when using a GPU, is approximately constant for up to 107 SAR terms meaning that the optimization time will not increase significantly for K up to about 50 head models if each has 200,000 voxels. In order to use this approach with VOPs, precomputing the compression for all possible combinations would be prohibitively expensive for even moderate values of K and performing the compression online in a patient-specific way would likely be prohibitively time consuming for values of K greater than about 5 based on the scaling behavior of the VOP compression with number of voxels (Supporting Information Figure S5). For values of K that exceed the upper limit even for IMPULSE, another option would be to perform a partial VOP compression to reduce the total number of voxels to a manageable range. This would be both less time consuming and more accurate than a complete compression to a few hundred SAR matrices and thus practical for real-time implementation.
There are several other obvious potential extensions to the IMPULSE algorithm described here. Design of large tip angles would be easily possible with the additive angle method (39), although this would increase the computation time. SAR matrices could be replaced with temperature matrices (26) which are mathematically equivalent but estimate temperature directly, thus allowing for a more lenient constraint than SAR. It is also possible to perform SMS-pTx design by allowing for the target excitation vector to include multiple slices (40).
CONCLUSION
IMPULSE represents a novel pulse design algorithm that offers the ability to design pTx pulses without a SAR compression step. This results in significant savings in precomputation time and improvements in SAR performance. IMPULSE also efficiently accomplishes SAR hopping and optimizes spokes locations both of which lead to additional SAR reduction. Most importantly, all these benefits are possible while still limiting the optimization time to a duration that is practical for on-scanner pulse design even with today’s computing hardware.
Supplementary Material
ACKNOWLEDGEMENTS
The authors acknowledge Alessandro Sbrizzi for valuable discussion and the following funding sources: GE Healthcare, NIH SIO RR026351–01AI, NIH P41 EB015891 and NIH 1 U01 EB025144–01
APPENDIX
A. Constructing System Matrix
is a matrix whose columns are nonzero entries of flattened maps
describes phase accrual from traversing k-space (depends on number and location of spokes):
describes phase accrual from off-resonance (depends on number but not location of spokes)
γ is the gyromagnetic constant
Δf is the off-resonance map computed
x and y are locations of pixels in design grid for slice s
kx and ky spokes locations for slice s
is the slice-select subpulse waveform with discretization Δt
⋄ represents broadcasted elementwise multiplication eg.
⊕ represents the broadcasted elementwise Kronecker product eg.
B. Expression for Feasible Set
The feasible set of b(s) that satisfy the NRMSE constraint for a specified target magnitude profile dmag,(s) and tolerance ϵ(s) is
(27).
This expression involving magnitudes (a nonlinear operation) is difficult to optimize, so using the fact that
for all φ(S)
and
for at least one value of φ(s) (in particular )
it must be true that
Here the set for fixed φ(s) is simply an ellipsoid so is a (nonconvex) union of ellipsoids. Similarly, allowing to vary in addition to φ(s) gives the larger set of acceptable channel weightings
which is the union of ellipsoids for all combinations of φ(s) and . In addition to the NRMSE tolerance channel weightings must also satisfy a peak power constraint where the maximum allowable voltage at a channel is limited by the hardware peak power limit and the reference impedance Z0.
REFERENCES
- 1.Duyn JH. The future of ultra-high field MRI and fMRI for study of the human brain. Neuroimage 2012;62:1241–1248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Ugurbil K, Adriany G, Andersen P. Ultrahigh field magnetic resonance imaging and spectroscopy. Magn Reson Imaging 2003;21:1263–1281. [DOI] [PubMed] [Google Scholar]
- 3.Vaughan JT, Garwood M, Collins CM. 7T vs. 4T: RF power, homogeneity, and signal-to-noise comparison in head images. Magn Reson Med 2001;46:24–30. [DOI] [PubMed] [Google Scholar]
- 4.Collins CM, Liu W, Schreiber W, Yang QX, Smith MB. Central brightening due to constructive interference with, without, and despite dielectric resonance. J Magn Reson Imaging 2005;21(2):192–196. [DOI] [PubMed] [Google Scholar]
- 5.Jin J, Chen J. On the SAR and field inhomogeneity of birdcage coils loaded with the human head. Magn Reson Med 1997;38:953–963. [DOI] [PubMed] [Google Scholar]
- 6.Wang Z, Lin J, Mao W, Liu W, Smith M, Collins C. SAR and temperature:simulations and comparison to regulatory limits for MRI. J Magn Reson Imaging 2007;26:437–441. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Graesslin I, Vernickel P, Bornert P, Nehrke K, Mens G, Harvey P, Katscher U. Comprehensive RF safety concept for parallel transmission MR. Magn Reson Med 2015;74:589–598. [DOI] [PubMed] [Google Scholar]
- 8.Grissom WA, Khalighi MM, Sacolick LI, Rutt BK, Vogel MW. Small-tip-angle spokes pulse design using interleaved greedy and local optimization methods. Magn Reson Med 2012;68:1553–1562. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Guerin B, Gebhardt M, Cauley S, Adalsteinsson E, Wald LL. Local specific absorption rate (SAR), global SAR, transmitter power, and excitation accuracy trade-offs in low flip-angle parallel transmit pulse design. Magn Reson Med 2014;71:1446–1457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Hoyos-Idrobo A, Weiss P, Massire A, Amadon A, Boulant N. On variant strategies to solve the Magnitude Least Squares optimization problem in parallel transmission RF pulse design and under strict SAR and power constraints. IEEE Trans Med Imaging 2014;33:739–748. [DOI] [PubMed] [Google Scholar]
- 11.Saekho S, Yip C-P, Noll DC, Boada FE, Stenger VA. A Fast-kz 3D Tailored RF Pulse for Reduced B1 Inhomogeneity. Magn Reson Med 2006;55:719–724. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Zhu Y Parallel excitation with an array of transmit coils. Magn Reson Med 2004;51(4):775–784. [DOI] [PubMed] [Google Scholar]
- 13.Eggenschwiler F, O’Brien KR, Gruetter R, Marques JP. Improving T2-weighted imaging at high field through the use of kT-points. Magn Reson Med 2014;71:1478–1488. [DOI] [PubMed] [Google Scholar]
- 14.Massire A, Vignaud A, Robert B, LeBihan D, Boulant N, Amadon A. Parallel-transmission-enabled three-dimensional T2-weighted imaging of the human brain at 7 Tesla. Magn Reson Med 2015;73:2195–2203. [DOI] [PubMed] [Google Scholar]
- 15.Schmitter S, Wu X, Ugurbil K, Van de Moortele P-F. Design of parallel transmission radiofrequency pulses robust against respiration in cardiac MRI at 7 Tesla. Magn Reson Med 2015;74:1291–1305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Winkler SA, Picot PA, Thornton MM, Rutt BK. Direct SAR mapping by thermoacoustic imaging: A feasibility study. Magn Reson Med 2016;0:0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Zhang X, Liu J, He B. Magnetic Resonance Based Electrical Properties Tomography: A Review. IEEE reviews in biomedical engineering 2014;7:87–96. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Christ A, Kainz W, Hahn E. The virtual family—development of surface-based anatomical models of two adults and two children for dosimetric simulations. Phys Med Biol 2010;55:23–38. [DOI] [PubMed] [Google Scholar]
- 19.Boulant N, Gras V, Amadon A, Luong M, Ferrand G, Vignaud A. Workflow proposal for defining SAR safety margins in parallel transmission. ISMRM annual meeting Paris 2018. p 295. [Google Scholar]
- 20.Torrado-Carvajal A, Hernandez-Tamames JA, Herraiz JL, Eryaman Y, Rozenholc Y, Adalsteinsson E, Wald LL, Malpica N. A multi-atlas and label fusion approach for patient-specific MRI based skull segmentation. 22nd Annual Meeting ISMRM Milan 2014. [DOI] [PubMed] [Google Scholar]
- 21.Meliado EF, Raaijmakers A, Savenije M, Sbrizzi A, Maspero M, Lujiten P, van den Berg C. On-line Subject-Specific Local SAR Assessment by Deep Learning. 26th Annual Meeting ISMRM Paris 2018. p 293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Graesslin I, Homann H, Biederer S, Bornert P, Nehrke K, Vernickel P, Mens G, Harvey P, Katscher U. A specific absorption rate prediction concept for parallel transmission MR. Magn Reson Med 2012;68:1664–1674. [DOI] [PubMed] [Google Scholar]
- 23.Eichfelder G, Gebhardt M. Local specific absorption rate control for parallel transmission by virtual observation points. Magn Reson Med 2011;66:1468–1476. [DOI] [PubMed] [Google Scholar]
- 24.Lee J, Gebhardt M, Wald L, E A. Local SAR in Parallel Transmission Pulse Design. Magn Reson Imaging 2012;67(6):1566–1578. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Kuehne A, Waiczies H, Niendorf T. Massively accelerated VOP compression for population-scale RF safety models. 25nd Annual Meeting ISMRM Honolulu p 0478. [Google Scholar]
- 26.Boulant N, Wu X, Adriany G, Schmitter S, Ugurbil K, Van de Moortele P-F. Direct control of the temperature rise in parallel transmission by means of virtual observation points: simulations at 10.5T. Magn Reson Med 2016;75:249–256. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Setsompop K, Wald LL, Alagappan V, Gagoski BA, Adalsteinsson E. Magnitude Least Squares Optimization for Parallel Radio Frequency Excitation Design Demonstrated at 7 Tesla With Eight Channels. Magn Reson Med 2008;59(4):908–915. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Graesslin I, Weller J, Schweser F, Annighoefer B, Biederer S, Katscher U, Nielsen T, Harvey P, Bornert P. SAR Hotspot Reduction by Temporal Averaging in Parallel Transmission. ISMRM 17th Annual Meeting Hawaii 2009. p 176. [Google Scholar]
- 29.Gras V, Vignaud A, Mauconduit F, Luong M, Amadon A, LeBihan D, Boulant N. Signal-domain optimization metrics for MPRAGE RF pulse design in parallel transmission at 7 tesla. Magn Reson Imaging 2016;76(5):1431–1442. [DOI] [PubMed] [Google Scholar]
- 30.Guerin B, Adalsteinsson E, Wald LL. Local SAR reduction in multi-slice pTx via “SAR hopping” between excitations. ISMRM annual meeting Melbourne 2012. p 642. [Google Scholar]
- 31.Grissom WA, Yip CY, Zhang Z, Stenger VA, A FJ, Noll DC. Spatial domain method for design of RF pulses in multicoil parallel excitation. Magn Reson Med 2006;56:620–629. [DOI] [PubMed] [Google Scholar]
- 32.Pauly J, Nishimura D, Macovski A. A k-space analysis of small-tip-angle excitation. J Magn Reson 1989;81(1):43–56. [DOI] [PubMed] [Google Scholar]
- 33.Kiwiel K A method for solving certain quadratic programming problems arising in nonsmooth optimization. IMA JNumerAnal 1986;6:137–152. [Google Scholar]
- 34.Pendse MR, Rutt BK. A Vectorized Formalism for Efficient SAR Computation in Parallel Transmission. 23nd Annual Meeting ISMRM Toronto 2015. p 379. [Google Scholar]
- 35.Kiseliov YN. Algorithms of projection of a point onto an ellipsoid. Lithuanian Math J 1994;34(2):141–159. [Google Scholar]
- 36.Grant M, Boyd S. CVX: Matlab software for discipliend convex programming. 2013. [Google Scholar]
- 37.Wang W, Yin W, Zeng J. Global convergence of ADMM in non-convex nonsmooth optimization. UCLA CAM Rep 2015:15–62. [Google Scholar]
- 38.Pendse MR, Rutt BK. Multi-body-model Method for Design of Mismatch-insensitive SAR-aware Parallel Transmit RF Pulses. 23nd Annual Meeting ISMRM Toronto 2015. p 3217. [Google Scholar]
- 39.Grissom WA, Yip CY, Wright SM, Fessler JA, Noll DC. Additive angle method for fast large-tip-angle RF pulse design in parallel excitation. Magn Reson Med 2008;59:547–560. [DOI] [PubMed] [Google Scholar]
- 40.Pendse MR, Rutt BK. IMPULSE-SMS: Local SAR and peak power optimized pTx pulse design for simultaneous multislice imaging at high fields. 24th Annual Meeting ISMRM Singapore 2016. p 1017. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.