Evaluation and Clinical Application of a Commercially Available Iterative Reconstruction Algorithm for CBCT-Based IGRT

Abstract

Purpose:

We have quantitatively evaluated the image quality of a new commercially available iterative cone-beam computed tomography reconstruction algorithm over standard cone-beam computed tomography image reconstruction results.

Methods:

This iterative cone-beam computed tomography reconstruction pipeline uses a finite element solver (AcurosCTS)-based scatter correction and a statistical (iterative) reconstruction in addition to a standard kernel-based correction followed by filtered back-projection-based Feldkamp-Davis-Kress cone-beam computed tomography reconstruction. Standard full-fan half-rotation Head, half-fan full-rotation Head, and standard Pelvis cone-beam computed tomography protocols have been investigated to scan a quality assurance phantom via the following image quality metrics: uniformity, HU constancy, spatial resolution, low contrast detection, noise level, and contrast-to-noise ratio. An anthropomorphic head phantom was scanned for verification of noise reduction. Clinical patient image data sets for 5 head/neck patients and 5 prostate patients were qualitatively evaluated.

Results:

Quality assurance phantom study results showed that relative to filtered back-projection-based cone-beam computed tomography, noise was reduced from 28.8 ± 0.3 HU to a range between 18.3 ± 0.2 and 5.9 ± 0.2 HU for Full-Fan Head scans, from 14.4 ± 0.2 HU to a range between 12.8 ± 0.3 and 5.2 ± 0.3 HU for Half-Fan Head scans, and from 6.2 ± 0.1 HU to a range between 3.8 ± 0.1 and 2.0 ± 0.2 HU for Pelvis scans, with the iterative cone-beam computed tomography algorithm. Spatial resolution was marginally improved while results for uniformity and HU constancy were similar. For the head phantom study, noise was reduced from 43.6 HU to a range between 24.8 and 13.0 HU for a Full-Fan Head and from 35.1 HU to a range between 22.9 and 14.0 HU for a Half-Fan Head scan. The patient data study showed that artifacts due to photon starvation and streak artifacts were all reduced, and image noise in specified target regions were reduced to 62% ± 15% for 10 patients.

Conclusion:

Noise and contrast-to-noise ratio image quality characteristics were significantly improved using the iterative cone-beam computed tomography reconstruction algorithm relative to the filtered back-projection-based cone-beam computed tomography method. These improvements will enhance the accuracy of cone-beam computed tomography-based image-guided applications.

Introduction

Onboard cone-beam computed tomography (CBCT) has been widely used to position patients receiving radiation therapy. However, the image quality of CBCT is inferior to that of fan-beam (planning) CT,^1–3 as increased radiation scatter in the patient and wide area detector lead to greater noise and poorer contrast. Thus, high levels of scattered radiation present a fundamental limitation to CBCT image quality.^4–6 In addition to hardware approaches that physically reduce detected levels of scatter, many different software approaches have been developed to compensate for CBCT-based scatter.^5,7-26 Recently, graphics processor unit (GPU)-based parallel computation methods have become popular,^27-29 and along with advanced CBCT reconstruction techniques, fast computation has become available in the clinic.^17,30-35 Here, we report on evaluation of a new commercially available iterative reconstruction system, to determine whether a software-only method improves the quality of CBCT images, for the purposes of more accurate CBCT-based image-guided radiotherapy.

Methods and Materials

The standard CBCT reconstruction pipeline on a TrueBeam linear accelerator kV imaging system (Varian Medical Systems, Palo Alto, California) removes scatter using a kernel-based correction¹² followed by filtered back-projection reconstruction, based on the Feldkamp-Davis-Kress (FDK) algorithm.³⁶ Varian Medical Systems has recently developed a new commercially available software includes a physics-based scatter correction (for pelvis only) and an iterative reconstruction algorithm and can be briefly summarized into the following 6 major steps³⁷: (1) The reconstruction results of the conventional FDK algorithm with kernel-based scatter correction algorithm are used as the first pass for reconstruction results; (2) a patient couch model is added to account for scatter through the patient couch; (3) material densities are converted from CT numbers as mixtures of water and bone; (4) both primary projection and scatter images are computed using a finite element solver (AcurosCTS) to model the behavior of photons as they pass (and scatter) through volumetric images from the first-pass reconstruction results³⁸; (5) scatter is corrected by subtracting scatter images from the projection images; and (6) the second-pass reconstruction consists of a statistical reconstruction method that takes the Poisson distribution of quantum noise into account and applies edge preserving image regularization.^39,40 This new approach is referred to as iterative_CBCT to differentiate from standard FDK reconstruction (FDK_CBCT). The iterative_CBCT reconstruction has 5 noise reduction factors to choose from, corresponding to increasing magnitudes of noise reduction level: very low, low, medium, high, and very high.

Catphan Phantom Study

The Catphan 504 phantom (The Phantom Laboratory Inc, Greenwich, New York) was scanned on a Truebeam linac using 3 CBCT acquisition modes: standard full-fan half-rotation Head (Full-Fan Head), half-fan full rotation Head (Half-Fan Head), and standard half-fan full-rotation pelvis (Pelvis). X-ray tube settings for head CBCT modes were 100 kVp and 15 mA; for pelvis mode, the settings were 125 kVp and 60 mA. For all 3 modes, pulse length was 20 milliseconds and rotation speed was 6 degrees/s. Each scan was repeated 3 to 6 times. Raw projection data were stored and reconstructed off-line using the standard (FDK) and iterative_CBCT reconstruction algorithms with the same set of machine calibration data. The Truebeam console reconstruction system utilizes the FDK reconstruction algorithm along with a postprocessing smoothing filter (Standard) and ring correction factor (Medium), and these same postprocessing methods were applied to the iterative_CBCT reconstructor. In this way, all postprocessing parameters, other than the reconstruction algorithm, were the same between the FDK and the iterative_CBCT reconstruction systems. For each set of data, the iterative_CBCT data set was reconstructed 5 times, corresponding to the 5 available noise reduction factor options. All reconstructed Catphan images were analyzed using a commercially available software package: the Catphan QA program (Image Owl, Inc, Greenwich, New York). This software quantitatively evaluates the following imaging metrics⁴¹:

1. Noise: defined as the standard deviation of measured HU values in a central region in a CTP 486 module of the Catphan 504 phantom. This module is a solid uniform cylinder with a designed CT number within 20 HU at standard scanning protocols. The central region has a diameter 40% of the module diameter.

2. Low contrast: Based on the smallest detected diameter of inserts at 1% contrast, inserts have different diameters (2-9 and 15 mm) in a CTP 515 module of the Catphan 504 phantom. For each target size, 2 rows of circle region of interests (ROIs) were generated in the background (BKG) inside and outside the inserts. The average HU was calculated for every circle and the standard deviation was calculated from the set of average HU numbers. The insert of a certain diameter is detectable if 4 times the standard deviation of average HU numbers is <1% contrast (=10 HU) as follows:

   $$4\times \text{SD}\le 10\text{HU}.$$ 1
3. Uniformity: based on average HU value of 4 peripheral cylinders (I_n, n = 1, …, 4) compared with that of a central cylinder (I_ctr) in the CTP 486 module of the Catphan 504 phantom;

   $$\text{Uniformity}=\text{max}\left\{|I_{\text{n}}-I_{\text{ctr}}|\right\}, n=1,\dots ,4$$ 2
4. HU constancy: maximum absolute difference between measured CT numbers (I_n, n = 1, …, 3) from expected CT numbers ($I_{\text{n}}^{\text{expect}},\text{n}=1,\dots ,3$) for 3 known inserts in the CTP 404 module of the Catphan 504 phantom. These inserts are air (−1000 HU), LDPE (−100 HU), and acrylic (120 HU).

   $$\text{HU constancy}=\text{max}\left\{|I_{\text{n}}-I_{\text{n}}^{\text{expect}}|\right\}, \text{n}=1, \dots ,3$$ 3

5. Spatial resolution: based on the modulation transfer function (MTF) of 2 embedded ball bearings, with average frequencies listed at 50% and 10% MTF levels separately in the CTP 528 module of the Catphan 504 phantom.

The contrast-to-noise ratio (CNR) was also evaluated for the Catphan phantom within the Eclipse treatment planning system (Varian Medical Systems). The CNR calculation was based on a cylinder with a diameter of 15 mm and a length of 40 mm at 1% contrast level in the CTP 515 module of the Catphan 504 phantom. An ROI cylinder was contoured at the center of the 15 mm 1% contrast insert. A BKG cylinder was contoured adjacent to the insert. These contoured volumes were propagated to all image sets using rigid image registration. Average HU values (I_ROI and I_BKG) and standard deviations (N_ROI and N_BKG) were calculated within the ROI and BKG contours, respectively, and the CNR was calculated by the following equation^42,43:

$$\text{CNR}=\frac{I_{\text{ROI}}-I_{\text{BKG}}}{N_{\text{BKG}}}$$ 4

Stereotactic End-to-End Verification Phantom Study

An anthropomorphic head phantom (stereotactic end-to-end verification phantom (STEEV), Computerized Imaging Reference Systems, Inc, Norfolk, Virginia) was also used to verify noise reduction of the iterative_CBCT reconstructor. This phantom is constructed of tissue-equivalent materials to simulate soft tissues and bones. An in-house-developed water tube and an acrylic rod were inserted into the phantom. To evaluate noise level and CNR in the STEEV phantom, images were acquired using Full-fan Head and Half-fan Head protocols. On each image set, 2 cylinders (10 mm diameter and 25 mm length) were contoured in the water tube and acrylic rod. One additional reference cylinder with identical dimensions was contoured between the water and acrylic contours in the adjacent BKG. Images were reconstructed by FDK and iterative_CBCT with different noise reduction parameters. Noise and CNR were calculated from the ROIs in the water and acrylic inserts for each set of images.

Clinical Patient CBCT Data Set Study

We also qualitatively evaluated image data sets of 10 patients with cancer (5 head/neck [H&N] and 5 prostate) and computed noise within targets and selected organs at risk. All patients have been enrolled in an image quality study approved by internal review board. One CBCT projection data set was selected for every patient and reconstructed using the standard FDK_CBCT and iterative_CBCT reconstruction algorithms with the Medium noise reduction factor. Treatment planning contouring was performed by a radiation oncologist as was visual assessment of the images reconstructed by the FDK_CBCT and iterative_CBCT systems. For analysis, the following structures were selected for patients with H&N cancer: gross tumor volume or target, spinal cord and brainstem, right parotid gland, and left parotid gland. For patients with prostate cancer, the prostate gland and bladder were selected for analysis. The CBCT image data sets, reconstructed with the FDK and iterative_CBCT reconstructors, were rigidly registered to the simulation CT data sets in Eclipse/ARIA (Varian Medical Systems). The noise for each contour (represented by the HU standard deviation) was compared between CBCT data sets reconstructed with both algorithms. Noise reduction ratio was calculated as the noise ratio of iterative_CBCT images over FDK_CBCT images for each contour.

Results

Catphan Phantom Study

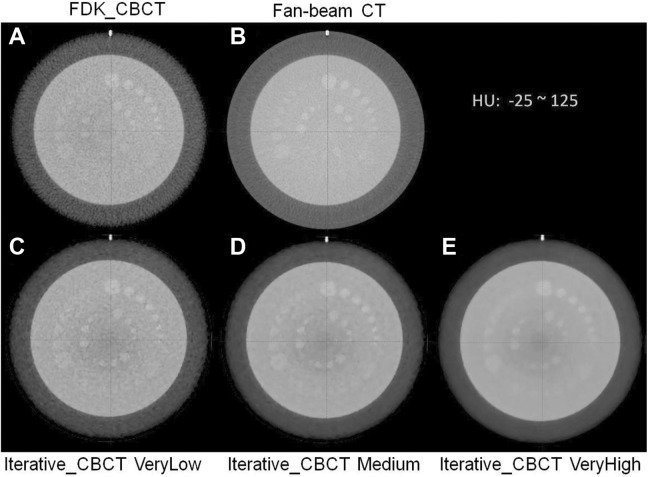
Figure 1 displays the Catphan (CTP 515 module) low-contrast images reconstructed using the FDK and iterative_CBCT algorithms for the Pelvis acquisition modes. Image noise is reduced when the noise reduction level is enhanced. Table 1 lists quantitative results of the Catphan 504 scans using 3 CBCT modes by the FDK and iterative_CBCT reconstruction methods with 5 noise reduction factors. Using the iterative_CBCT reconstructor, relative to results of the FDK reconstruction, noise was reduced from 28.8 ± 0.3 HU to a range between 18.3 ± 0.2 HU and 5.9 ± 0.2 HU for Full-Fan Head scans, from 14.4 ± 0.2 HU to a range between 12.8 ± 0.3 HU and 5.2 ± 0.3 HU for Half-Fan Head scans, and from 6.2 ± 0.1 HU to a range between 3.8 ± 0.1 HU and 2.0 ± 0.2 HU for Pelvis scans. For images reconstructed with the FDK_CBCT algorithm, inserts (at 1% contrast level) with diameters of 9, 7, and 3 to 4 mm were detected for Full-Fan Head, Half-Fan Head, and Pelvis scans, respectively. On the other hand, for the iterative_CBCT reconstruction algorithm, inserts with diameter of 6, 3, and 1 mm (at 1% contrast level) were detected in images using Full-Fan Head, Half-Fan Head, and Pelvis acquisition modes, respectively. The CNR was improved from 0.6 ± 0.0 to a range between 0.9 ± 0.0 and 2.8 ± 0.1 for Full-Fan Head scans, from 1.2 ± 0.1 to a range between 1.2 ± 0.1 and 4.6 ± 0.8 for Half-Fan Head scans, and from 2.4 ± 0.0 to a range between 3.5 ± 0.1 and 13.1 ± 2.0 for Pelvis scans.

Figure 1.

Comparison of low-contrast results: current FDK_CBCT (A), CT (B), and iterative_CBCT reconstructed with different noise reduction factors: VeryLow (C), Medium (D), and VeryHigh (E). HU window: [−25, 125 HU]. CBCT indicates cone-beam computed tomography; FDK, Feldkamp-Davis-Kress.

Table 1.

Image Quality Results of Catphan Phantom Studies.^a

Protocols	Noise Reduction Factor	Noise, HU	Low Contrast, mm	CNR	MTF, lp/cm		Uniformity, HU	HU Constancy, HU
					50%	10%
CT		4.7	2	3.16	3.4	5.7	2.4	11
Head Full-Fan CBCT	FDK_CBCT	28.8 (0.3)	9	0.6 (0.0)	4.1 (0.4)	7.2 (0.4)	3.8 (2.0)	8.7 (1.5)
	VeryLow	18.3 (0.2)	9	0.9 (0.0)	4.1 (0.3)	7.0 (0.2)	6.8 (0.7)	13.3 (3.1)
	Low	16.2 (0.2)	9	1.0 (0.0)	4.0 (0.3)	6.9 (0.2)	6.8 (0.7)	13.7 (3.5)
	Medium	13.3 (0.2)	8-9	1.2 (0.0)	4.0 (0.3)	6.9 (0.3)	6.9 (0.9)	14.3 (4.0)
	High	9.7 (0.2)	7-8	1.6 (0.0)	3.9 (0.2)	6.8 (0.2)	6.9 (1.2)	13.7 (3.1)
	VeryHigh	5.9 (0.2)	6	2.8 (0.1)	3.9 (0.1)	6.8 (0.2)	6.7 (1.4)	13.3 (1.5)
Head Half-Fan CBCT	FDK_CBCT	14.4 (0.2)	7	1.2 (0.1)	2.7 (0.3)	5.3 (0.2)	14.1 (2.6)	12.5 (1.3)
	VeryLow	12.8 (0.3)	7	1.2 (0.1)	3.1 (0.2)	5.1 (0.2)	3.2 (1.3)	17.5 (2.2)
	Low	11.4 (0.3)	7	1.4 (0.2)	3.0 (0.2)	5.1 (0.1)	3.1 (1.3)	17.7 (0.8)
	Medium	9.5 (0.3)	6	1.8 (0.2)	3.0 (0.1)	5.1 (0.2)	3.4 (1.0)	17.8 (1.3)
	High	7.3 (0.4)	4-5	2.6 (0.4)	2.9 (0.1)	5.1 (0.2)	3.3 (0.2)	17.7 (0.8)
	VeryHigh	5.2 (0.3)	3	4.6 (0.8)	2.8 (0.1)	5.2 (0.1)	2.6 (0.1)	17.2 (1.0)
Pelvis CBCT	FDK_CBCT	6.2 (0.1)	3-4	2.4 (0.0)	2.6 (0.0)	4.9 (0.1)	3.6 (1.0)	4.3 (1.2)
	VeryLow	3.8 (0.1)	2-4	3.5 (0.1)	2.9 (0.0)	4.8 (0.0)	8.1 (3.1)	1.8 (0.8)
	Low	3.1 (0.1)	2-4	4.8 (0.3)	2.9 (0.0)	4.8 (0.0)	7.9 (3.1)	2.0 (1.0)
	Medium	2.5 (0.1)	2	7.0 (0.6)	2.8 (0.0)	4.9 (0.1)	7.8 (3.2)	2.0 (1.0)
	High	2.2 (0.1)	1	10.0 (1.4)	2.7 (0.0)	5.0 (0.1)	7.5 (3.2)	1.8 (0.8)
	VeryHigh	2.0 (0.2)	1	13.1 (2.0)	2.6 (0.0)	5.1 (0.1)	6.9 (2.9)	1.8 (0.8)

Abbreviations: CBCT indicates cone-beam computed tomography; CNR, contrast to noise ratio; CT, computed tomography; FDK, Feldkamp-Davis-Kress; MTF, modulation transfer function.

^a Noise, low contrast detection, CNR defined by Equation 4, 50% and 10% MTF level, uniformity defined by Equation 2, and HU constancy defined by Equation 3 are listed for 3 CBCT mode reconstructed by 2 reconstructors, FDK_CBCT and iterative_CBCT with 5 noise reduction factors, VeryLow, Low, Medium, High, and VeryHigh. Standard deviations are in parentheses.

Increasing noise reduction level slightly decreases both MTF 50% and 10% for all 3 CBCT modes except MTF 10% for Pelvis scan results. The MTF 50% decreases from 3.1 to 2.8 lp/cm for Half-Fan Head results with noise reduction enhanced from very low to very high, but MTF 10% results stayed relatively constant. The level of noise reduction does not substantially impact the uniformity and HU constancy, as any observed differences in these metrics between the reconstruction methods are lower in magnitude than the image noise level.

STEEV Phantom Study

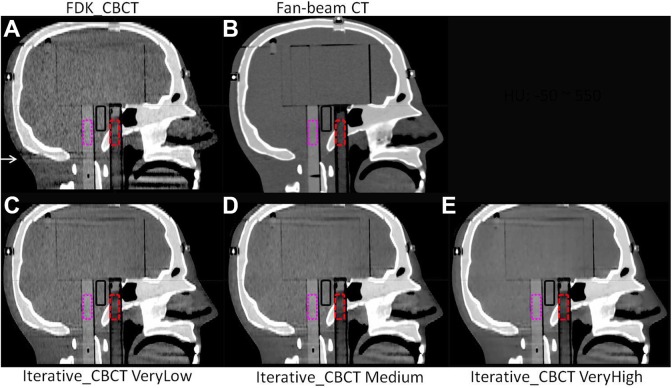
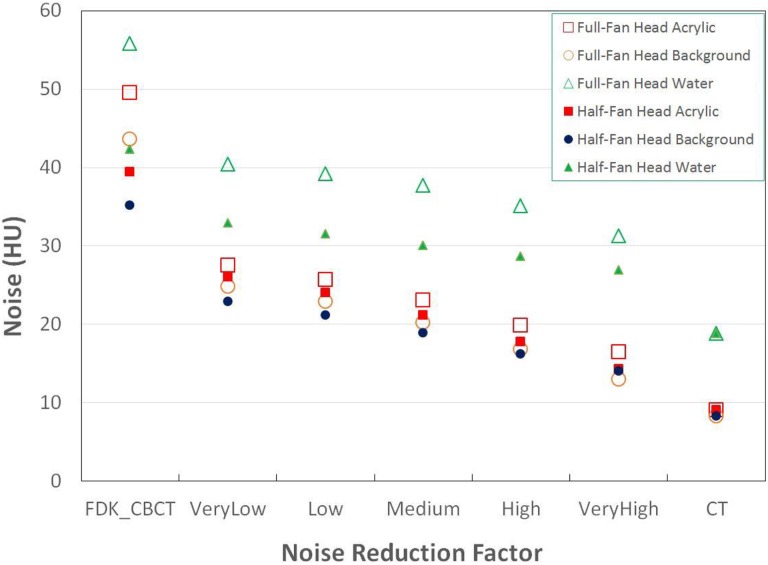
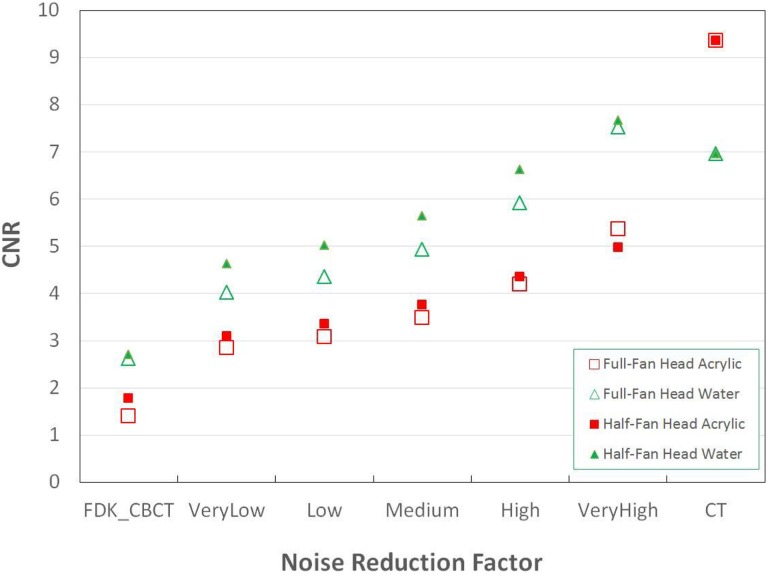
STEEV phantom Half-Fan CBCT images are shown in Figure 2. Of note, streak artifacts are minimized with increasing noise reduction, particularly below the bottom of the skull, as noted by the arrow in Figure 2. This region with artifact indicative of missing data in the FDK reconstruction has been corrected with the iterative_CBCT reconstructor. Noise levels are illustrated in Figure 3, demonstrating that noise is reduced close to the noise level of CT images. The head phantom study showed that noise was reduced from 43.6 HU to a range between 24.8 and 13.0 HU for a Full-fan Head and from 35.1 HU to a range between 22.9 and 14.0 HU for a Half-fan Head scan. The CNR results are also compared in Figure 4. The CNR is increased with the noise reduction and approaches to that of CT images.

Figure 2.

STEEV phantom Half-Fan Head images reconstructed by FDK_CBCT (A), iterative_CBCT with VeryLow (C), Medium (D), and VeryHigh (E) noise reduction factors compared with CT images (B). The contour defined by the water tube is shown in the red dashed lines; acrylic rod contour is shown in the pink dotted lines; contours in the background are also shown in black solid lines. HU window: [−50, 550 HU]. CBCT indicates cone-beam computed tomography; CT, computed tomography; FDK, Feldkamp-Davis-Kress; STEEV, stereotactic end-to-end verification.

Figure 3.

STEEV phantom noise of acrylic, background, and water contours in Full-Fan Head and Half-Fan Head results by different reconstructions, FDK_CBCT, iterative_CBCT with very low, low, medium, high, and very high noise reduction factors. Noise of CT results is displayed at the right. CBCT indicates cone-beam computed tomography; CT, computed tomography; FDK, Feldkamp-Davis-Kress; STEEV, stereotactic end-to-end verification.

Figure 4.

STEEV phantom CNR based on acrylic and water contours in Full-Fan Head and Half-Fan Head results with different reconstructions, FDK_CBCT, iterative_CBCT with very low, low, medium, high, and very high noise reduction factors. CT results are displayed at the right. CBCT indicates cone-beam computed tomography; CNR, contrast to noise ratio; CT, computed tomography; FDK, Feldkamp-Davis-Kress; STEEV, stereotactic end-to-end verification.

Clinical Patient CBCT Data Set Study

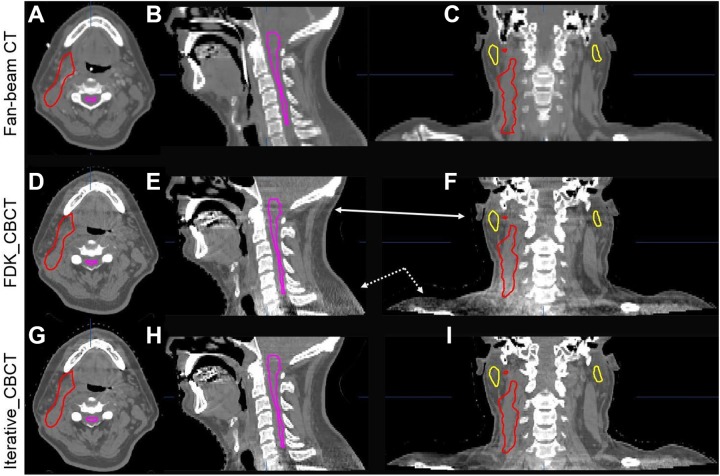
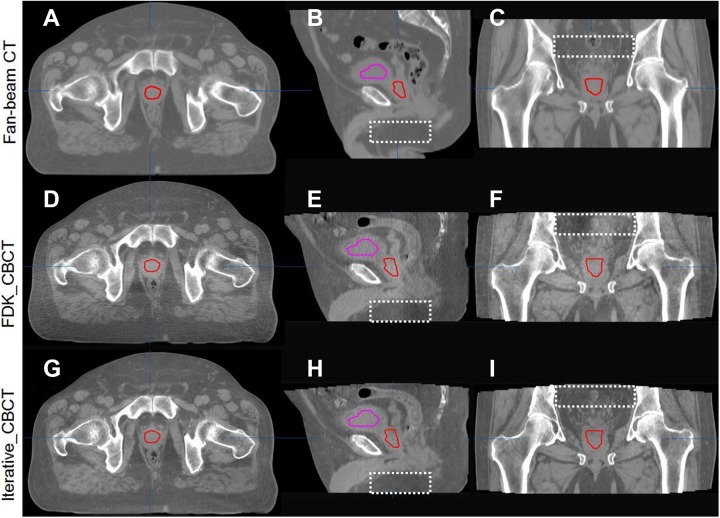
Figure 5 shows a sample H&N image data set in axial, coronal, and sagittal views reconstructed by FDK_CBCT and iterative_CBCT with Medium noise reduction factor compared against planning CT (CT) images. Upon review of 5 H&N image data sets, a radiation oncologist noted mitigation of streak artifacts in H&N region (as noted in the coronal and sagittal views of Figure 5) and better visualization of the laryngopharyngeal region, fat/muscle boundaries, and level 2 lymph nodes, with the iterative_CBCT reconstructions (Figure 5). After reviewing 5 prostate image data sets, the radiation oncologist noted significant improvement in image quality and reduction in streak artifacts as evidenced in Figure 6. Much clearer definition of the prostate and normal organ boundaries was also observed for the pelvic scan using the iterative_CBCT reconstruction algorithm.

Figure 5.

Comparison of CT images (upper row, A-C) and CBCT images reconstructed by FDK_CBCT (middle row, D-F), and iterative_CBCT algorithm with Medium noise reduction factor (lower row, G-I) and for a head/neck patient. HU window: [−400, 600 HU]. Artifacts (arrows on the coronal and sagittal views) are mitigated in the iterative_CBCT reconstructions. Contours of spinal cord, left and right parotid glands, and target are displayed. CBCT indicates cone-beam computed tomography; CT, computed tomography; FDK, Feldkamp-Davis-Kress.

Figure 6.

Comparison of CT images (upper row, A-C) and CBCT images reconstructed by FDK_CBCT (middle row, D-F), and iterative_CBCT algorithm with Medium noise reduction factor (lower row, G-I) and for a prostate patient. HU window: [−400, 600 HU]. Contours of the bladder and prostate are displayed. The images reconstructed with the iterative_CBCT algorithm show qualitative improvement in noise, reduced HU discontinuities as indicated by dashed rectangular in the sagittal and coronal views. CBCT indicates cone-beam computed tomography; CT, computed tomography; FDK, Feldkamp-Davis-Kress.

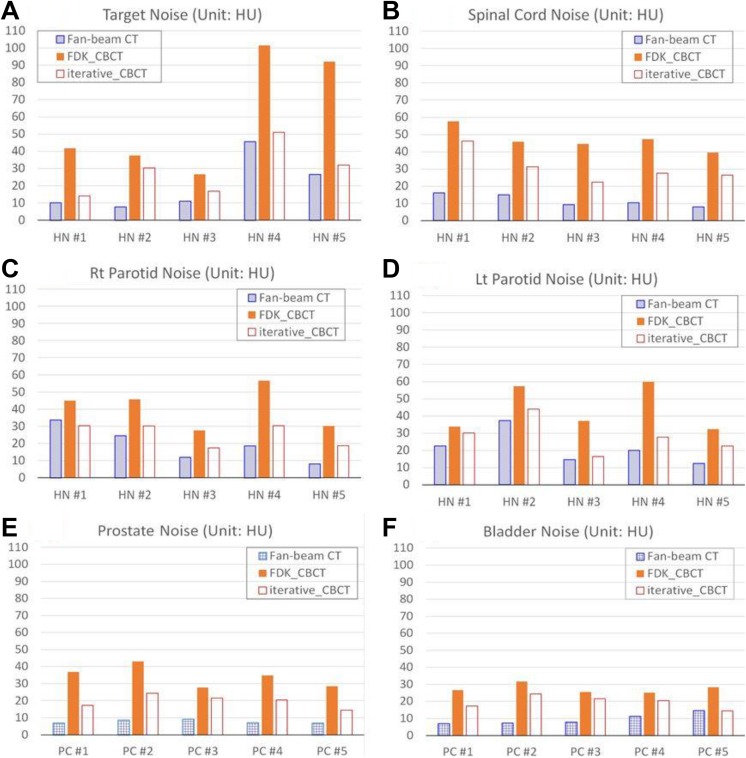
Noise analysis was performed for the 5 H&N and 5 prostate image data sets, and the results of noise levels are illustrated in Figure 7. Noise reduction ratio was calculated for each contour. Averaged over 5 patients with H&N cancer, noise was reduced to 53% ± 20% (33%-81%), 65% ± 11% (50%-80%), 62% ± 5% (54%-68%), and 65% ± 20% (44%-89%) for the target, spinal cord/brain stem, right parotid, and left parotid, respectively. On average, image noise was reduced by 61% ± 15% for all 5 patients with H&N cancer. For the 5 patients with prostate cancer, noise was reduced to 52% ± 12% (47%-78%) for the prostate gland and 66% ± 18% (45%-91%) for the bladder. On average, image noise was reduced by 62% ± 15% for all 5 patients with prostate cancer.

Figure 7.

Organ noise of 5 H&N patients and 5 prostate patients in CT, FDK_CBCT, and iterative_CBCT images. (A) Target noise of 5 H&N patients; (B) spinal cord noise of 5 H&N patients; (C) right parotid noise of 5 H&N patients; (D) left parotid noise of 5 H&N patients; (E) prostate noise of 5 prostate patients; and (F) bladder noise of 5 prostate patients. CBCT indicates cone-beam computed tomography; CT, computed tomography; FDK, Feldkamp-Davis-Kress; H&N, head and neck.

Discussion

This commercially available iterative_CBCT algorithm presented here is different from other approaches focused on improving image quality of low-dose CBCT scans^17,28,31,44 in that it uses the same raw projection data from standard Truebeam CBCT acquisitions and applies software-only methods to improve low-contrast detection and soft-tissue visibility.^40,45,46 Consistent with results in the literature,^{7-10,13,17,23,30-33,47-49} iterative reconstruction uses physical constraints, such as regularization penalty terms to improve image quality by reducing image noise and enhancing CNR. This iterative reconstruction algorithm reduces noise and enhances low-contrast detection while maintaining spatial resolution relative to the standard (FDK-based) approach.

Either scatter correction or iterative reconstruction will improve image quality. This iterative_CBCT employs the statistical iterative reconstruction for all scan modes but only applies Acuros-based scatter correction for Pelvis scan modes. The Acuros-based scatter correction is more accurate than a general mode used in FDK_CBCT because it calculates the photon absorption based on models of the imaging hardware (X-ray source beam shape and spectrum, model of the detector, antiscatter grid) and a model of the patient (derived from a prereconstructed 3-dimensional volume containing material and density information).¹² This is obtained by deterministically solving the Boltzmann transport equation. As a result, patient image quality and soft-tissue contrast improvement were greater for patients with prostate cancer compared to patients with H&N cancer with the iterative_CBCT algorithm.

Some improvement, albeit not substantial, was noted in the HU uniformity and constancy for the phantom scans with the iterative_CBCT versus standard reconstructor. It should be noted that both uniformity and HU constancy of the reconstruction had been calibrated using the same Catphan phantom based on standard FDK_CBCT reconstruction as the baseline. Table 1 shows slightly off-calibrated on uniformity and HU constancy for iterative_CBCT reconstruction although the differences (<5 HU) are very minimal. The Varian recommended tolerances for both uniformity and HU constancy are 40 HU. It is likely that the iterative_CBCT reconstruction results will be improved when the calibration is performed using iterative_CBCT as the baseline.

Computation time is an important consideration for clinical applications. The algorithm uses the same projection data as standard CBCT scans. Traditionally, this would require enormous computation time for either iterative reconstruction or specified scatter correction. With an optimized GPU-based parallel computation, only additional 10 to 20 seconds is needed for typical cases with H&N cancer without Acuros scatter correction, and only additional 20 to 30 seconds is needed after CBCT acquisition for volumetric reconstruction for typical pelvis geometries with Acuros scatter corrections. Such reconstruction speed is similar to current standard FDK-based reconstruction in the clinic, which takes several seconds to reconstruct CBCT images after acquisition. This suggests that the iterative_CBCT reconstructor running on a GPU-based processor is fast enough for online reconstruction for routine clinical applications.

The CT (fan-beam CT) results are compared to CBCT results for phantom studies and patient studies. The CT image resolution of 0.60 mm differs from that for Full-Fan CBCT images (0.51 mm) and Half-Fan CBCT images (0.91 mm). The image resolution has a downstream effect on MTF and noise level, thereby impacting low-contrast detection and CNR. The CNR value is determined not only by the noise level but also by the contrast. Both Head CBCT protocols use 100 kVp and Pelvis CBCT protocol uses 125 kVp while CT uses 120 kVp X-ray tube setting. Higher X-ray energy results in relatively less contrast. The average HU number differences between the ROI and the BKG in the Catphan are 15.3 ± 1.1, 12.4 ± 0.4, and 13.2 HU for all Head CBCT images, Pelvis CBCT images, and CT images, respectively. The nominal value should be 10 HU. The improved contrast for the CT images, in addition to reduced inherent scattering with fan-beam versus cone-beam acquisition, favors CT from a quantitative phantom analysis perspective.

The iterative_CBCT reconstruction has 5 options for noise reduction, and our results show that higher noise reduction level leads to less noise, better low-contrast detection, and higher CNR. However, we also noticed that any imperfections in the CBCT imager calibration may be magnified with higher levels of noise reduction. At the same time, oversmoothed images were observed for some patient image sets reconstructed with VeryHigh noise reduction. The selection of noise reduction should be made with consideration of all factors relevant to the patient imaging, including noise, low-contrast detectability, and image sharpness.

Conclusions

Statistical reconstruction in combination with advanced scatter correction substantially improves CBCT image quality by increasing CNR, maintaining uniformity and HU constancy, and reducing streak artifacts. Based on investigation of phantom and patient data sets for H&N and pelvic anatomies, we have demonstrated that the iterative_CBCT reconstruction algorithm improves visual perception of soft tissues that are necessary for accurate visualization in the routine clinical practice. The presented enhancements are expected to improve the accuracy of soft tissue-based, image-guided localization using CBCT and aid in contouring and dose calculation for future online adaptive radiation therapy.

Abbreviations

BKG

background

CBCT

cone-beam computed tomography

CNR

contrast to noise ratio

CT

computed tomography

FDK

Feldkamp-Davis-Kress

GPU

graphics processor unit

H&N

head and neck

MTF

modulation transfer function

QA

quality assurance

ROI

region of interest

STEEV

stereotactic end-to-end verification