Thermodynamic Integration and Steppingstone Sampling Methods for Estimating Bayes Factors: A Tutorial

Abstract

One of the more principled methods of performing model selection is via Bayes factors. However, calculating Bayes factors requires marginal likelihoods, which are integrals over the entire parameter space, making estimation of Bayes factors for models with more than a few parameters a significant computational challenge. Here, we provide a tutorial review of two Monte Carlo techniques rarely used in psychology that efficiently compute marginal likelihoods: thermodynamic integration (Friel & Pettitt, 2008; Lartillot & Philippe, 2006) and steppingstone sampling (Xie, Lewis, Fan, Kuo, & Chen, 2011). The methods are general and can be easily implemented in existing MCMC code; we provide both the details for implementation and associated R code for the interested reader. While Bayesian toolkits implementing standard statistical analyses (e.g., JASP Team, 2017; Morey & Rouder, 2015) often compute Bayes factors for the researcher, those using Bayesian approaches to evaluate cognitive models are usually left to compute Bayes factors for themselves. Here, we provide examples of the methods by computing marginal likelihoods for a moderately complex model of choice response time, the Linear Ballistic Accumulator model (Brown & Heathcote, 2008), and compare them to findings of Evans and Brown (2017), who used a brute force technique. We then present a derivation of TI and SS within a hierarchical framework, provide results of a model recovery case study using hierarchical models, and show an application to empirical data. A companion R package is available at the Open Science Framework: https://osf.io/jpnb4.

Formal cognitive models that attempt to explain cognitive processes using mathematics and simulation have been a cornerstone of scientific progress in the field of cognitive psychology. When presented with several competing cognitive models, a researcher aims to select between these different explanations in order to determine which model provides the most compelling explanation of the underlying processes. This is not as simple as selecting the model that provides the best quantitative fit to the empirical data: Models that are more complex have greater amounts of flexibility and can over-fit the noise in the data (Myung, 2000; Myung & Pitt, 1997). Therefore, some method of selecting between models is required that balances goodness-of-fit with model complexity. This need has led to serious discussions about the right approach to model selection. Finding principled methods that are able to successfully select the best model can be difficult (e.g., Evans, Howard, Heathcote, & Brown, 2017), especially for cognitive process models, which are often functionally complex (Evans & Brown, 2017).

Traditionally, model selection has relied on finding the set of model parameter values that maximize some goodness-of-fit function and then penalizing that fit with some measure of model complexity based on the number of parameters in the model (e.g., Busemeyer & Diederich, 2010; Lee, 2001; Lewandowsky & Farrel, 2011; Shiffrin, Lee, Kim, & Wagenmakers, 2008; Wasserman, 2000); then different models can be compared because they are put on equal footing via the added penalty term. However, such methods take an overly simplistic approach to model selection by ignoring a model’s functional form and assuming that all parameters make an equal contribution to a model’s flexibility (Myung & Pitt, 1997). Alternatively, a Bayesian framework provides a principled way to account for the flexibility contained in a complex process model beyond a mere parameter count (Annis & Palmeri, 2017; Shiffrin et al., 2008). Several non-Bayesian methods have been proposed for accounting for the flexibility of a model’s functional form (e.g., Grünwald, Myung, & Pitt, 2005; Ly, Marsman, Verhagen, Grasman, & Wagenmakers, 2017; Myung, Navarro, & Pitt, 2006). We only concern ourselves with Bayesian approaches in this tutorial.

We start with Bayes’ rule applied to parameter estimation. This aims to find the joint posterior distribution of the parameter vector θ given the observed data vector D. This probability, p(θ∣D), via Bayes’ rule is:

$$p(\mathit{\theta }\mid \mathit{D})=\frac{p(\mathit{D}\mid \mathit{\theta })p(\mathit{\theta })}{p(\mathit{D})},$$ (1)

where p(θ) is the prior probability of the parameters, p(D∣θ) is the likelihood of the parameters given the data, and p(D) is a normalizing constant called the marginal likelihood. In its full form, the marginal likelihood is equal to the integral over all possible values of the model parameters, thereby making Bayes’ rule:

$$p(\mathit{\theta }\mid \mathit{D})=\frac{p(\mathit{D}\mid \mathit{\theta })p(\mathit{\theta })}{\int p(\mathit{D}\mid {\mathit{\theta }}^{\prime })p({\mathit{\theta }}^{\prime })d{\mathit{\theta }}^{\prime }},$$ (2)

Because there is usually a vector of parameters in a cognitive model, calculating the marginal likelihood involves calculating a multiple integral; note that within the multiple integral, this vector is explicitly denoted by θ′ rather than θ to make clear that these are different values from one another, but from now on, we will simply refer to the vector of parameters using θ alone. Outside of a handful of simple examples, such integrals cannot be solved analytically and cannot be estimated using standard numerical methods. In the case of Bayesian parameter estimation, where the goal is to calculate the posterior, this challenge is largely avoided by Markov Chain Monte Carlo (MCMC) methods (e.g., Brooks, Gelman, Jones, & Meng, 2011); MCMC circumvents any need to estimate the marginal likelihood because the integral cancels out via a ratio of posteriors used in many MCMC algorithms. As we see below, in the case of Bayesian model selection, the marginal likelihood, the denominator of Equation 2, is of key interest and so the integral must be estimated.

Because we are interested in model comparison, it can be useful to make the model we are working with explicit in that the probabilities are all conditional on the model being assumed; outside of model selection, the model is often assumed implicitly. Now, Bayes’ rule can be rewritten to include an explicit notation of model M:

$$p(\mathit{\theta }\mid \mathit{D},M)=\frac{p(\mathit{D}\mid \mathit{\theta },M)p(\mathit{\theta }\mid M)}{p(\mathit{D}\mid M)}.$$ (3)

A common form of Bayesian model selection involves another application of Bayes’ rule, but now to determine the posterior probability of each model, M_k, given the data, D, and to select model k with the highest probability:

$$p(M_k\mid \mathit{D})=\frac{p(\mathit{D}\mid M_k)p(M_k)}{p(\mathit{D})},$$ (4)

The denominator is another normalizing constant, but this one marginalizes across all possible models, not any particular model (and is not the same as the denominator in Equation 1 since that one conditionalized on a particular model implicitly). Because alternative models are discrete objects, this turns into a summation over models, rather than an integral:

$$p(M_k\mid \mathit{D})=\frac{p(\mathit{D}\mid M_k)p(M_k)}{{\sum }_{j=1}^{M}p(\mathit{D}\mid M_j)p(M_j)},$$ (5)

where p(M_k∣D) is the posterior probability of model k, p(M_k) is the prior probability of model k, p(D∣M_k) is the marginal likelihood (this is the same marginal likelihood that is the denominator in Equations 1-3), and ${\sum }_{j=1}^{M}p(\mathit{D}\mid M_j)p(M_j)$ is a normalizing factor, which is constant across models, and therefore, can be ignored in relative model comparison. In the case of two models, the ratio of posterior probabilities gives the posterior odds:

$$\frac{p(M_1\mid \mathit{D})}{p(M_2\mid \mathit{D})}=\frac{p(\mathit{D}\mid M_1)}{p(\mathit{D}\mid M_2)}\times \frac{p(M_1)}{p(M_2)},$$ (6)

which is a function of the prior odds, $\frac{p(M_1)}{p(M_2)}$, and the Bayes factor, $\frac{p(\mathit{D}\mid M_1)}{p(\mathit{D}\mid M_2)}$; note that the use of an odds ratio eliminates the need to calculate the denominator in Equations 4-5. It is common to perform Bayesian model selection in the absence of any explicitly stated prior on models. In that case, the goal of Bayesian model selection is to compute the Bayes factor, which weighs the evidence provided by the data in favor of one model over another (Jeffreys, 1961) and is given by the ratio of the marginal likelihoods for each model:

$$B_{12}=\frac{p(\mathit{D}\mid M_1)}{p(\mathit{D}\mid M_2)}=\frac{\int p(\mathit{D}\mid {\mathit{\theta }}_{M_1},M_1)p({\mathit{\theta }}_{M_1}\mid M_1)d{\mathit{\theta }}_{M_1}}{\int p(\mathit{D}\mid {\mathit{\theta }}_{M_2},M_2)p({\mathit{\theta }}_{M_2}\mid M_2)d{\mathit{\theta }}_{M_2}},$$ (7)

where θ_M1and θ_M2 are the parameter vectors for M₁ and M₂, respectively. Computing the marginal likelihoods requires estimating integrals that cannot be solved using standard techniques.

The Bayes factor marginalizes over the entire parameter space, thereby taking into account the complexity of the model resulting from its entire functional form. There are many off-the-shelf software packages (e.g., JASP Team, 2017; Morey & Rouder, 2015) that can estimate Bayes factors for a range of standard statistical models, such regression and ANOVA (e.g., Rouder & Morey, 2012; Rouder, Morey, Speckman, & Province, 2012). For more complex or non-linear models, such as those developed by cognitive modelers, off-the-shelf software packages generally do not exist. Instead, methods for estimating Bayes factors must be applied by modelers themselves.

Methods that have previously been applied to cognitive models include the Savage-Dickey ratio test (e.g., Wagenmakers, Lodewyckx, Kuriyal, & Grasman, 2010), product space methods (Lodewyckx et al., 2011), the grid approach (Lee, 2004; Vanpaemel & Storms, 2010), and bridge sampling (Gronau, Sarafoglou, et al., 2017; Meng & Wong, 1996), a generalization of Chib’s method (Chib, 1995; Chib & Jeliazkov, 2001). Table 1 gives an overview of the practical considerations for these methods. Although the Savage-Dickey ratio has proved popular due to being computationally inexpensive and easy to implement, it is only applicable to instances where one model is nested within another model (that is, one model is a special case of a more general model), limiting its scope.

Table 1.

Comparison of practical considerations for commonly used methods of computing Bayes factors.

Method	Easy for beginners	Easy to compare many models	Applicable to non- nested models	Requires minimal posterior samples	Requires a single MCMC run	Scales with dimensions
Grid approach	Y	Y	Y	NAd	NAe	N
Arithmetic mean	Ya	Y	Y	NAd	NAe	N
Savage-Dickey ratio	Y	N	N	Y	Y	Y
Product space	N	N	Y	N	Y	Y
Bridge sampling	Yb	Y	Y	N	Y	Y
TI/SS	Yc	Y	Y	Y	N	Y

^aWhile the arithmetic mean approach is conceptually simple and is not difficult to implement naïvely, in practical situations it usually requires the use of specialized hardware and software that might be foreign to the beginner.

^bAlthough Bridge Sampling would likely be difficult for beginner users to implement, Gronau, Singmann, and Wagenmakers (2017) have created a package would is broadly applicable to most situations. TI/SS require setting tuning parameters such as the number of temperatures and the temperature schedule. While prior research has shown certain tuning parameters to work well, this nevertheless adds complexity to the approach for the beginner.

^dThis method does not require posterior samples.

^eThis method does not require MCMC.

For non-nested model comparison, methods such as the product space method can be used. This method requires the embedding of the two competing models within a supermodel that contains an indicator variable that selects one of the models on each iteration of the MCMC chain. The proportion of times a particular model is selected is the posterior probability of the model. The product space method can suffer from mixing issues in which a chain fails to jump between models efficiently. This results in the need for very long MCMC runs, or for the use of more sophisticated algorithms to get the sampler to make efficient jumps (Lodewyckx et al., 2011). The grid approach suffers from the curse of dimensionality in which the computational expense increases exponentially with the number of parameters, making this approach impractical for models with more than a few parameters.

The bridge sampling method is very promising compared to many past methods used in cognitive modeling, requiring samples from the posterior, the definition of and sampling from an additional proposal distribution, and the definition of a bridge function. It has been successfully applied to several situations involving high-dimensional models and has an R package that only requires the user to provide posterior samples, which bypasses the need for the user to define a proposal distribution or bridge function (Gronau, Singmann, & Wagenmakers, 2017). However, as discussed by Gronau et al. (2017), the accuracy of the bridge sampling algorithm is highly dependent on an accurate representation of the joint posterior distribution, which implies that a large number of posterior samples are often required, especially in the case of complex cognitive models.

Because our main aim is to provide a tutorial and application of two additional methods of estimating marginal likelihoods, we do not discuss the above methods any further and refer readers interested in different methods for estimating the marginal likelihood to reviews by Friel and Wyse (2012) and Liu et al. (2016).

Specifically, in this article, we outline two recent advancements in methods for computing Bayes factors that also show promise: thermodynamic integration (TI; Friel & Pettitt, 2008) and steppingstone sampling (SS; Xie et al., 2011). These methods are part of the general class of Monte Carlo methods (Brooks et al., 2011) that rely on drawing random samples from a distribution in order to compute an estimate of an integral. TI and SS have been used in fields such as biology (Lartillot & Philippe, 2006), phylogenetics (e.g., Xie et al., 2011), ecology (e.g., P. Liu et al., 2016), statistics (e.g., Friel & Pettitt, 2008), and physics (e.g., Ogata, 1989), but to the best of our knowledge they have not previously been applied to problems of selecting between models in psychology. Importantly, TI and SS compute the Bayes factor through a mathematically rigorous, but conceptually and practically simple extension of MCMC techniques. We believe that the simplicity of these methods, along with our tutorial and online code, will help allow more psychology researchers who are familiar with MCMC techniques to calculate Bayes factors for comparing models, while also adding alternative methods for users of other methods to explore.

We provide an introduction to the techniques and demonstrate their viability with one widely applicable cognitive model of decision making, the Linear Ballistic Accumulator model (LBA; Brown & Heathcote, 2008). We provide an R package (R Core Team, 2017) for implementing TI and SS, available at the Open Science Framework: https://osf.io/jpnb4. TI and SS are fairly easy to implement within existing code that samples from the posterior, and therefore, the descriptions from our article should be straightforward to implement within any programming language used for cognitive modeling and Bayesian inference.

From here, our article takes the following format: We begin with a brief overview of the process of estimating the marginal likelihood necessary to compute the Bayes factor, with an initial focus on conceptually simple, but computationally expensive “brute force sampling” methods for illustration. Next, we detail the TI and SS methods, including both conceptual explanations and detailed mathematical derivations. After this, we present example applications of TI and SS with LBA, comparing these to recent applications of brute force methods with LBA by Evans and Brown (2017). Lastly, we apply the TI and SS methods to hierarchical models, which have become prominent in cognitive modelling and for which brute force sampling methods are impossible to use in practice; we present applications of TI and SS in a hierarchical framework with LBA, applied to both simulated and observed data. Although TI and SS are completely general and apply to any Bayesian model, we know of no prior derivations of TI or SS in a hierarchical framework.

While we illustrate the marginal likelihood estimates using TI and SS, as well as estimates obtained using brute force sampling, it is important to note that for the LBA model, and indeed for most cognitive models, there is no known ground truth for the Bayes factor because the marginal likelihoods cannot be calculated analytically. While the estimates we provide, and the comparisons to brute force sampling, do not validate these methods, TI and SS have been validated using models with analytically-available marginal likelihoods. For example, Friel and Wyse (2012) used two Gaussian linear non-nested regression models with gamma priors that had analytically-available marginal likelihoods to compare several estimation methods, including Chib’s method (Carlin & Chib, 1995), annealed importance sampling (Neal, 2001), nested sampling (Skilling, 2006), harmonic mean (Newton & Raftery, 1994), and TI. They found that TI performed better than nested sampling and the harmonic mean and performed similarly to Chib’s method and annealed importance sampling. A similar approach was used by Liu et al. (2016), who used a Gaussian model with an analytically-available marginal likelihood, comparing nested sampling, harmonic mean, arithmetic mean (Kass & Raftery, 1995), and TI. They found that TI produced highly accurate, low variance estimates of the analytically available marginal likelihood. The SS method has also been validated by Xie et al. (2011), using a Gaussian model with an analytically-available marginal likelihood to compare SS to TI and the harmonic mean. They found that SS and TI produced accurate estimates of the marginal likelihood and outperformed the harmonic mean.

Basic Monte Carlo Methods for Estimating Marginal Likelihoods

Monte Carlo integration techniques take advantage of the relationship between expected values and their corresponding integral representations. Consider first the definition of the expected value of the random variable, θ:

$$\mathbf{E}[\mathit{\theta }]=\int \mathit{\theta }p(\mathit{\theta })d\mathit{\theta },$$ (8)

where p(θ) is the probability of θ. The law of large numbers tells us that the arithmetic average of n samples drawn with probability p(θ) converges on the expected value as n approaches infinity. Thus, with a sufficient number of samples (and finite variance), we can estimate the expected value with an average:

$$\mathbf{E}[\mathit{\theta }]\approx \frac{1}{n}\sum _{i=1}^n{\mathit{\theta }}_i.$$ (9)

where θ_i, is sampled from p(θ). This can be generalized to the expected value of a function f applied to θ as:

$$\mathbf{E}[f(\mathit{\theta })]=\int f(\mathit{\theta })p(\mathit{\theta })d\mathit{\theta }$$ (10)

$$\approx \frac{1}{n}\sum _{i=1}^{n}f({\mathit{\theta }}_i).$$ (11)

where θ_i~p(θ) as above.

We are now in a position to use Monte Carlo methods for solving many integrals. Imagine being tasked with solving an integral that can be expressed in the general form of Equation 10, where f(θ) is some arbitrary function and p(θ) defines a probability distribution from which samples can be drawn. The integral can be estimated by taking random samples from p(θ), passing those randomly sampled θ values through f(θ), and taking the arithmetic average. What began as the definition of expected value becomes a way to solve an integral – an integral that may be impossible to solve analytically or using standard numerical methods.

This logic forms one of the simplest Monte Carlo techniques to estimate an integral: the arithmetic mean estimator. In the context of estimating the marginal likelihood under Bayes, it is computed by drawing random samples, θ_i, from the prior distribution, p(θ), computing the likelihood, p(D∣θ_i), for each sample, and then taking the arithmetic mean:

$$p(\mathit{D})=\int p(\mathit{D}\mid \mathit{\theta })p(\mathit{\theta })d\mathit{\theta }$$ (12)

$$=\mathbf{E}[p(\mathit{D}\mid \mathit{\theta })]$$ (13)

$$\approx \frac{1}{n}\sum _{i=1}^{n}p(\mathit{D}\mid {\mathit{\theta }}_i),$$ (14)

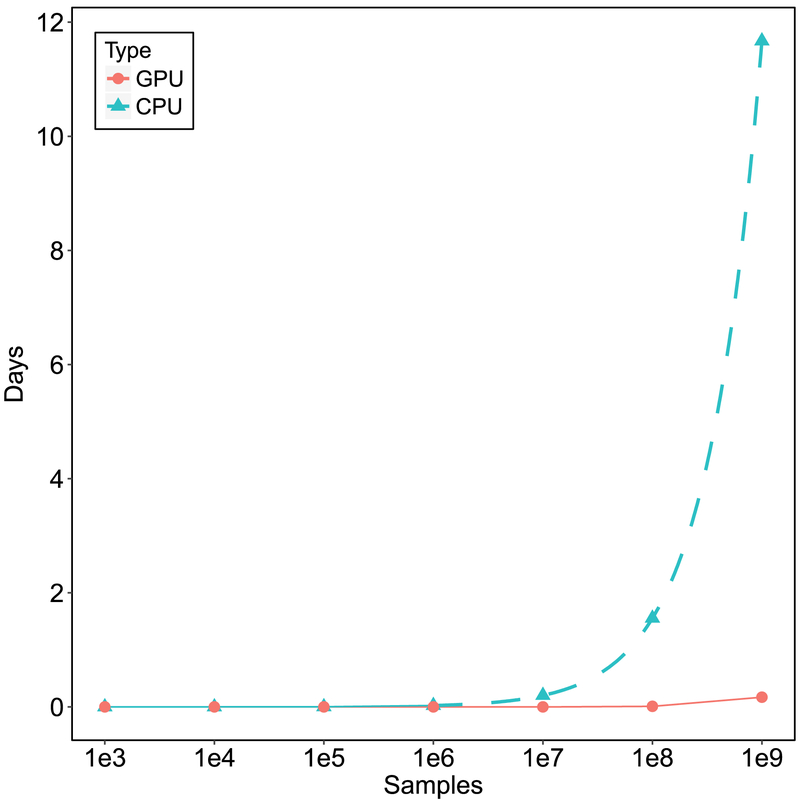
where θ_i~p(θ) (note again that we assume conditionalizing on model M implicitly rather than explicitly). The arithmetic mean estimator requires samples to be drawn from prior. Unfortunately, the likelihood is often highly peaked compared to the prior, meaning that relatively few random samples (from the prior) will be drawn within the highest-density areas of the likelihood function. This will generally lead to underestimation of the marginal likelihood unless a very large number of samples are used. Although this issue can theoretically be solved with a huge number of samples, the computational burden placed on a CPU quickly becomes overwhelming with the significant increases in the number of samples often required (e.g., see Figure 1).

Figure 1.

Estimated number of days to collect the corresponding sample size using a brute-force Monte Carlo approach to estimating the marginal likelihood with a GPU vs. a CPU. The points represent actual data and the dotted line represents the predictions. Evans and Brown (2017) found sample sizes of approximately 1e8 are sufficient for accurate estimates of marginal likelihoods for single participant LBA models with 6 parameters. For hierarchical models, more may be needed.

Evans and Brown (2017) provided a method for alleviating some of the computational burden arising from the need for very large numbers of samples when calculating the arithmetic mean by using graphical processing unit (GPU) technology to quickly compute, in parallel, a large number of samples from the prior. For instance, they found that sample sizes of approximately 100,000,000 were necessary to approach reasonable estimates of the marginal likelihood for one 6-parameter cognitive model for a single participant; on their hardware, a process that would take a couple days for CPU computing (Figure 1) was possible within minutes using GPU computing. However, the GPU method of Evans and Brown (2017) has limitations: First, the method can be difficult to implement technically, and requires relatively expensive GPU hardware on high-end desktop workstations to reap the full computational benefits, meaning that it may not be feasible for the average user.¹ Second, and perhaps more important, the GPU method does not entirely circumvent the curse of dimensionality, whereby ever-growing numbers of samples are needed for ever-more-complex models. For example, when using hierarchical models, which model the data of multiple participants simultaneously using both parameters for individuals as well as parameters for the group, the number of brute-force samples required to gain a precise and stable approximation of the marginal likelihood becomes exponentially greater. Even using GPU methods, it is unlikely to be able to achieve reasonable sampling within any reasonable amount of time.

One method of increasing the efficiency of the sampling process is importance sampling. Importance sampling was one of the first Monte Carlo methods used to estimate marginal likelihoods in the statistics literature (Newton & Raftery, 1994). Instead of sampling from the prior, as is done with the arithmetic mean estimator, importance sampling involves sampling from another distribution, called the importance distribution, and then re-weighting the samples to obtain an unbiased estimate.

Here, we illustrate an estimation of p(D) using importance sampling. This derivation requires defining an importance distribution, g(θ), a proper probability distribution (from which random samples can be drawn) that more closely resembles the shape of the likelihood, usually with heavier tails than the posterior. In the case of estimating the marginal likelihood, the importance sampling equation is:

$$p(\mathit{D})=\int p(\mathit{D}\mid \mathit{\theta })p(\mathit{\theta })d\mathit{\theta }$$ (15)

$$=\int \frac{p(\mathit{D}\mid \mathit{\theta })p(\mathit{\theta })}{g(\mathit{\theta })}g(\mathit{\theta })d\mathit{\theta }.$$ (16)

Note that we have not changed the marginal likelihood, but have only multiplied it by 1, g(θ)/g(θ).

Before we represent this integral as an expected value, the importance sampling equation for the marginal likelihood is commonly written with a denominator equal to the integral of the prior, using the same importance distribution, g(θ). This intermediate step is performed so the equation simplifies to a convenient representation. Again, this does not change the marginal likelihood as we are only dividing it by 1:

$$p(\mathit{D})=\frac{\int \frac{p(\mathit{D}\mid \mathit{\theta })p(\mathit{\theta })}{g(\mathit{\theta })}g(\mathit{\theta })d\mathit{\theta }}{\int \frac{p(\mathit{\theta })}{g(\mathit{\theta })}g(\mathit{\theta })d\mathit{\theta }}.$$ (17)

Now we can plug in just about any appropriate importance distribution we choose. If we set the importance distribution, g(θ), equal to the prior, p(θ), we obtain the arithmetic mean estimator shown earlier:

$$p(\mathit{D})=\frac{\int \frac{p(\mathit{D}\mid \mathit{\theta })p(\mathit{\theta })}{p(\mathit{\theta })}p(\mathit{\theta })d\mathit{\theta }}{\int \frac{p(\mathit{\theta })}{p(\mathit{\theta })}p(\mathit{\theta })d\mathit{\theta }}$$ (18)

$$=\frac{\mathbf{E}\left[\frac{p(\mathit{D}\mid \mathit{\theta })p(\mathit{\theta })}{p(\mathit{\theta })}\right]}{\mathbf{E}\left[\frac{p(\mathit{\theta })}{p(\mathit{\theta })}\right]}$$ (19)

$$\approx \frac{1}{n}\sum _{i=1}^{n}p(\mathit{D}\mid {\mathit{\theta }}_i).$$ (20)

where θ_i~p(θ).

When the posterior, p(θ∣D), is used as the importance distribution, we obtain the harmonic mean estimator (Newton & Raftery, 1994):

$$p(\mathit{D})=\frac{\int \frac{p(\mathit{D}\mid \mathit{\theta })p(\mathit{\theta })}{p(\mathit{\theta }\mid \mathit{D})}p(\mathit{\theta }\mid \mathit{D})d\mathit{\theta }}{\int \frac{p(\mathit{\theta })}{p(\mathit{\theta }\mid \mathit{D})}p(\mathit{\theta }\mid \mathit{D})d\mathit{\theta }}$$ (21)

$$=\frac{{\mathbf{E}}_{\mathit{\theta }\mid \mathit{D}}\left[\frac{p(\mathit{D}\mid \mathit{\theta })p(\mathit{\theta })}{p(\mathit{\theta }\mid \mathit{D})}\right]}{{\mathbf{E}}_{\mathit{\theta }\mid \mathit{D}}\left[\frac{p(\mathit{\theta })}{p(\mathit{\theta }\mid \mathit{D})}\right]}$$ (22)

$$\approx \frac{1}{\frac{1}{n}{\sum }_{i=1}^n\frac{1}{p(\mathit{D}\mid {\mathit{\theta }}_i)}}.$$ (23)

where θ_i~p(θ∣D) and the subscript θ∣D in E_θ∣D emphasizes that the expected value is taken with respect to the posterior distribution of θ.

The marginal likelihood estimate produced from the harmonic mean estimator is “computationally free” because it is obtained using the same samples from which posterior inferences can be drawn (via MCMC). It is also a more efficient estimator than the prior importance distribution, as its density is more peaked in the high likelihood areas. However, this efficiency comes at the cost of bias. Because the harmonic mean estimator uses the posterior as its importance distribution, it tends to ignore low likelihood regions, such as those comprising the prior, leading to overestimates of the marginal likelihoods (Xie et al., 2011). In addition, the harmonic mean can also, theoretically, have infinite variance (Lartillot & Philippe, 2006; Newton & Raftery, 1994). In the section describing steppingstone sampling, we will show how this importance sampling scheme is improved.

Thermodynamic Integration and Steppingstone sampling

In this section, we detail the thermodynamic integration and steppingstone sampling methods of estimating the marginal likelihood. Our goal is to provide sufficient details for an interested user to implement these methods for complex cognitive models.

Thermodynamic Integration (TI)

Conceptual introduction.

The thermodynamic integration (TI) approach involves drawing samples from Bayesian posterior distributions whose likelihood functions are raised to different powers (called temperatures, t) that range between 0 and 1. We will show how this computational “trick” provides a way of estimating the marginal likelihood of the original target posterior distribution.

Posteriors (Equation 1) whose likelihoods are raised to the power of 0 obviously are equivalent to the prior, and posteriors whose likelihoods are raised to the power of 1 obviously constitute the full posterior distribution. Raising the likelihood to a power between 0 and 1, therefore, results in a posterior distribution having some mixture of the prior and posterior. After sampling from each posterior, the log-likelihood (ln p(D∣θ), not raised to a power) under each sample is computed. The mean log-likelihood under each power posterior constitute points along a curve. The area under this one-dimensional curve, which can be estimated using ordinary numerical integration techniques, equals the log marginal likelihood. One can then transform the log marginal likelihood into the marginal likelihood and use this value to compare with another model in a Bayes factor. Note that we present all results using the log marginal likelihood as it is often easier to depict graphically, given that the marginal likelihood is usually a very large number. Likewise, we present Bayes factors on the log scale as well.

Mathematical details.

The key to the TI approach is to raise the likelihood in the posterior to a power, t. The following derivations will ultimately represent the log marginal likelihood as a one-dimensional integral with respect to t, which can then be solved using standard numerical methods.

Before proceeding with these derivations, we first define a new posterior distribution that is a function of both D and t (assuming model M implicitly):

$$p(\mathit{\theta }\mid \mathit{D},t)=\frac{p(\mathit{D}\mid \mathit{\theta }{)}^{t}p(\mathit{\theta })}{p(\mathit{D}\mid t)}.$$ (24)

This is called the power posterior, note this is only equivalent to the posterior in Equations 1-3 when temperature t = 1. The power posterior has the following marginal likelihood, which we refer to as the power marginal likelihood:

$$p(\mathit{D}\mid t)=\int p(\mathit{D}\mid \mathit{\theta }{)}^{t}p(\mathit{\theta })d\mathit{\theta },t\in [0,1].$$ (25)

Let us step through how this simple transformation can be capitalized upon to estimate a marginal likelihood, p(D).

We begin by recasting the log marginal likelihood as the difference between the log power marginal likelihoods at t = 1 and t = 0:

$$\text{ln}p(\mathit{D})=\text{ln}p(\mathit{D}\mid t=1)-\text{ln}p(\mathit{D}\mid t=0).$$ (26)

Given that p(D∣t = 0) ends up simply being the integral of the prior distribution, which integrates to 1 (assuming the requisite proper priors), its log equals zero. And we note again that p(D∣t = 1) is equal to the target marginal likelihood. So this step is just rewriting the log of the marginal likelihood in a different form, but a form that will be useful below.

We then introduce the following identity:

$$\text{ln}p(\mathit{D}\mid t=1)-\text{ln}p(\mathit{D}\mid t=0)={\int }_0^1\frac{d}{dt}\text{ln}p(\mathit{D}\mid t)dt.$$ (27)

This just follows from the definition of a definite integral over the bounds of t. We now have a one-dimensional integral with respect to t. However, the integrand contains a derivative, which we would like to represent in a more convenient form.

The remainder of the derivation involves computing this derivative and representing the result as an expected value that can be estimated using MCMC. To begin with, taking the derivative with respect to t, we find the following:

$$\frac{d}{dt}\text{ln}p(\mathit{D}\mid t)=\frac{1}{p(\mathit{D}\mid t)}\frac{d}{dt}p(\mathit{D}\mid t)$$ (28)

This again leaves us with another derivative to compute. We first replace p(D∣t) with its integral definition from Equation 25. Then, the derivative and integral commute (by the Leibniz integral rule²), moving the $\frac{d}{dt}$ inside the integral, which becomes a partial $\frac{\partial }{\partial t}$ because the interior term also depends on θ:

$$\frac{d}{dt}p(\mathit{D}\mid t)=\int \frac{\partial }{\partial t}p(\mathit{D}\mid \mathit{\theta }{)}^{t}p(\mathit{\theta })d\mathit{\theta }.$$ (29)

The next step just solves the derivative using the fact that $\frac{\partial }{\partial t}{a}^t=a^t$ ln a.

$$\int \frac{\partial }{\partial t}p(\mathit{D}\mid \mathit{\theta }{)}^{t}p(\mathit{\theta })d\mathit{\theta }=\int p(\mathit{D}\mid \mathit{\theta }{)}^t\text{ln}p(\mathit{D}\mid \mathit{\theta })p(\mathit{\theta })d\mathit{\theta }.$$ (30)

Substituting back into Equation 28 we obtain the following:

$$\frac{d}{dt}\text{ln}p(\mathit{D}\mid t)=\frac{1}{p(\mathit{D}\mid t)}\int p(\mathit{D}\mid \mathit{\theta }{)}^t\text{ln}p(\mathit{D}\mid \mathit{\theta })p(\mathit{\theta })d\mathit{\theta }.$$ (31)

After rearranging we have:

$$\frac{d}{dt}\text{ln}p(\mathit{D}\mid t)=\int \frac{p(\mathit{D}\mid \mathit{\theta }{)}^{t}p(\mathit{\theta })}{p(\mathit{D}\mid t)}\text{ln}p(\mathit{D}\mid \mathit{\theta })d\mathit{\theta }.$$ (32)

Notice that the integrand is now composed of one term that is the power posterior and another term that is the log-likelihood. We can represent this as an expected value, referred to in the literature (e.g., Friel, Hurn, & Wyse, 2014; Friel & Wyse, 2012) as the expected log posterior deviance:

$$\int \frac{p(\mathit{D}\mid \mathit{\theta }{)}^{t}p(\mathit{\theta })}{p(\mathit{D}\mid t)}\text{ln}p(\mathit{D}\mid \mathit{\theta })d\mathit{\theta }={\mathbf{E}}_{\mathit{\theta }\mid \mathit{D},t}[\text{ln}p(\mathit{D}\mid \mathit{\theta })].$$ (33)

Because the integral in Equation 33 can be written in terms of an expected value and because we can sample from the power posterior using standard MCMC techniques, we can estimate the integral using the Monte Carlo integration methods described earlier.

Finally, substituting the above into Equations 26 and 27, we find that the log marginal likelihood is equal to the integral with respect to t of the expected posterior deviance from 0 to 1:

$$\text{ln}p(\mathit{D})={\int }_0^1{\mathbf{E}}_{\mathit{\theta }\mid \mathit{D},t}[\text{ln}p(\mathit{D}\mid \mathit{\theta })]dt.$$ (34)

While this is yet another integral, it is just a one-dimensional integral over t, which can be estimated using standard numerical integration techniques. While the derivation may seem complicated, the resulting algorithmic implementation is actually quite simple.

Implementation.

Approximating the integral in Equation 34 is straightforward: Draw samples from power posteriors across a range of temperatures, compute the mean log-likelihood under each temperature, and numerically integrate over the resulting curve to produce an estimate of the log marginal likelihood of the target posterior distribution. Thankfully, random sampling from the power posterior is possible using a standard Metropolis-Hastings algorithm (Brooks et al., 2011; Hastings, 1970), and standard numerical integration techniques are readily applied to the one-dimensional problem.

The algorithm for generating the random samples from the power posterior needed to estimate the log marginal likelihood with TI (and later, SS) is outlined in Box 1. The inner loop, over i, is a standard MCMC (Metropolis-Hastings) sampler with the exception that samples are drawn from a posterior whose likelihood is raised to a particular temperature. The outer loop, over j, cycles through the various temperatures, t. This procedure therefore results in an array of MCMC chains, with each chain at a different temperature between 0 and 1. In practice, this procedure can be run with multiple chains so that convergence can more easily be assessed at each temperature.

Box 1. Pseudo-code algorithm for estimating the marginal likelihood using TI or SS, where each power posterior is run independently. K is the number of temperatures, and N is in the number of iterations in the chain at each temperature.

$$\begin{array}{cc}\hfill & 1:\text{Given}t=\{0,\dots t_j\dots ,1\}\text{and an initial}{\theta }_{1,j}\hfill \\ \hfill & 2:\mathbf{for}1\le j\le k\mathbf{do}\hfill \\ \hfill & 3:\mathbf{for}2\le i\le n\mathbf{do}\hfill \\ \hfill & 4:\text{Propose}{\theta }^{\ast }\text{from proposal density}q({\theta }^{\ast }\mid {\theta }_{i-1,j})\hfill \\ \hfill & 5:\text{Accept}{\theta }^{\ast }\text{with probability}\hfill \\ \hfill & \alpha =\text{min}\left(1,\frac{p(\mathit{D}\mid {\theta }^{\ast }{)}^{t_j}p({\theta }^{\ast })q({\theta }_{i-1}\mid {\theta }^{\ast })}{p(\mathit{D}\mid {\theta }_{i-1}{)}^{t_j}p({\theta }_{i-1})q({\theta }^{\ast }\mid {\theta }_{i-1})}\right).\hfill \\ \hfill & 6:\text{Store}{\theta }_{i,j}\leftarrow {\theta }^{\ast }\text{with probability}\alpha ,\text{otherwise store}{\theta }_{i,j}\leftarrow {\theta }_{i-1,j}\hfill \\ \hfill & 7:\mathrm{end}\mathrm{for}\hfill \\ \hfill & 8:\mathrm{end}\mathrm{for}\hfill \\ \hfill & 9:\text{Using}\theta ,\text{estimate}p(\mathit{D})\text{with TI}(\text{Equation 35 or 39})\text{or}\text{SS}(\text{Equation 51})\hfill \end{array}$$

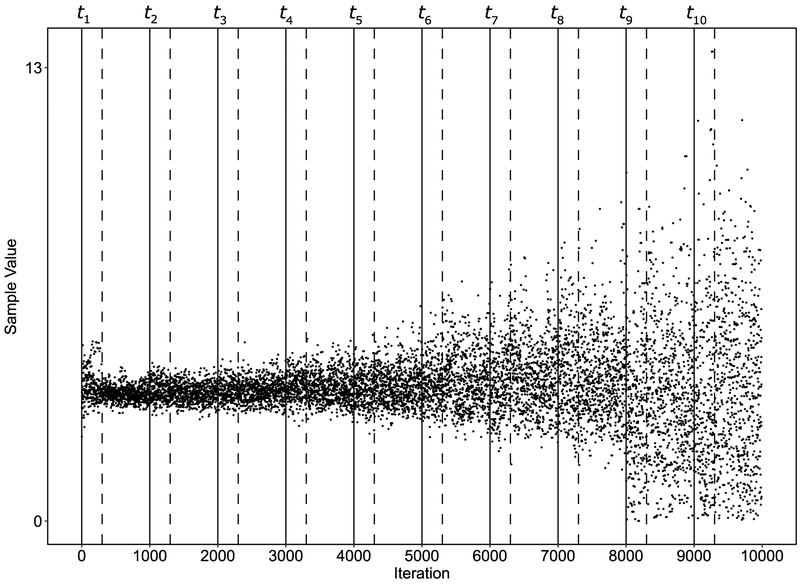
In addition to running each power posterior independently, a single, long MCMC run can also be used. This is referred to by Lartilot and Philippe (2006) as the quasistatic method. Box 2 shows the pseudo-code for the quasistatic method. The quasistatic method (Box 2) and independent method (Box 1) begin exactly the same for the first temperature rung, but unlike the independent method, the quasistatic method does not re-initialize the chain at each subsequent temperature. Rather, the chain continues, using the previous sample to compute the acceptance probability of the current proposal. This is equivalent to using the final sample from temperature t_j as the initial sample at temperature t_j + 1. The quasistatic method can be run from t = 0 to t = 1 (i.e. an annealing schedule), or in reverse from t = 1 to t = 0 (i.e. a melting schedule). Figure 2 shows the evolution of MCMC chains produced by the quasistatic algorithm. After an initial burn-in period whose end is denoted by the first dotted line, samples are initially drawn at temperatures of 1. These are pure posterior samples. After drawing n samples from the posterior at t = 1, the temperature changes to the next temperature rung in the schedule (depicted at the second solid line at 1000 iterations). At this temperature, another burn-in period begins and is followed by 700 sampling iterations. This process continues until the temperature is reduced down to 0, the final temperature rung in the schedule. Since the quasistatic method avoids having to burn-in from random starting points for each temperature, it can often achieve higher accuracy in fewer samples than running each power posterior independently. The intuition behind the quasistatic method is that good samples for temperature t_j are also reasonable for t_j+1, whenever the latter does not differ much from the former.

Box 2. Pseudo-code algorithm for estimating the marginal likelihood using the quasistatic method. The resulting MCMC chain is a single, long MCMC chain in that the all current samples are dependent on their previous samples, even at points in which the chain changes temperatures. k is the number of temperatures, and n is in the number of iterations in the chain at each temperature.

$$\begin{array}{cc}\hfill & 1:\text{Given}t=\{0,\dots t_j\dots ,1\},\text{an initial}{\theta }_{1,1},\text{and}i=2\hfill \\ \hfill & 2:\text{for}1\le j\le k\mathbf{do}\hfill \\ \hfill & 3:\mathbf{for}1\le h\le n\mathbf{do}\hfill \\ \hfill & 4:\text{Propose}{\theta }^{\ast }\text{from porposal density}q({\theta }^{\ast }\mid {\theta }_{i-1,j})\hfill \\ \hfill & 5:\text{Accept}{\theta }^{\ast }\text{with probability}\hfill \\ \hfill & \alpha =\text{min}\left(1,\frac{p{(\mathit{D}\mid {\theta }^{\ast })}^{t_j}p({\theta }^{\ast })q({\theta }_{i-1}\mid {\theta }^{\ast })}{p{(\mathit{D}\mid {\theta }_{i-1})}^{t_j}p({\theta }_{i-1})q({\theta }^{\ast }\mid {\theta }_{i-1})}\right).\hfill \\ \hfill & 6:\text{Store}{\theta }_{i,j}\leftarrow {\theta }^{\ast }\text{with probability}\alpha ,\text{otherwise store}{\theta }_{i,j}\leftarrow {\theta }_{i-1,j}\hfill \\ \hfill & 7i\leftarrow i+1\hfill \\ \hfill & 8:\mathbf{end}\mathbf{for}\hfill \\ \hfill & 9:\mathbf{end}\mathbf{for}\hfill \\ \hfill & 10:\text{Using}\theta ,\text{estimate}p(\mathit{D})\text{with TI}(\text{Equation 35 or 39})\text{or SS}(\text{Equation 51})\hfill \end{array}$$

Figure 2.

The evolution of several superimposed MCMC chains running under different temperatures. Black lines represent the location of each temperature index along the chains. The dashed lines represent the burn-in period after initializing each temperature. The initial temperature is 1 (posterior sampling) and the final temperature is 0 (prior sampling). The samples become increasingly spread out as the posterior transitions to the prior.

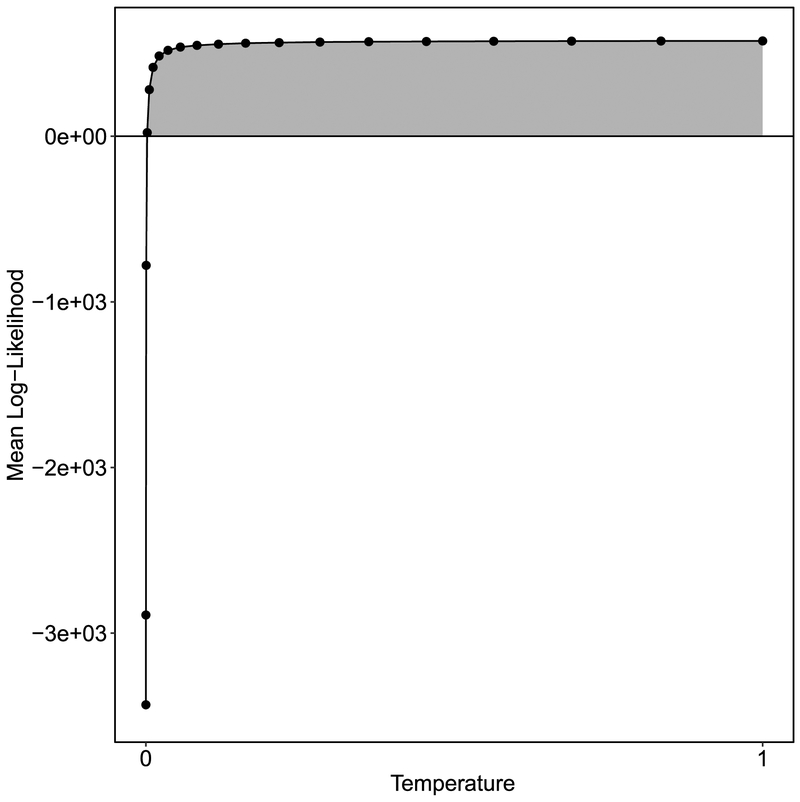
After the chain of samples at each temperature are collected per the algorithm in Box 1 or Box 2, the mean log-likelihood is computed given samples from each power posterior. This involves computing the log likelihood, ln p(D∣θ_i), under each sample θ_i, and then calculating the average across samples within each t. That average approximates E_θ∣D,t[ln p(D∣θ)]. We then plot E_θ∣D,t[ln p(D∣θ)] as a function of t. An example of one such curve is shown in Figure 3. The estimate of the integral in Equation 34 is simply the area under this curve, which can be estimated using any variety of standard numerical integration techniques. For example, Friel and Pettitt (2008) suggest the simple trapezoidal rule:

$$\text{ln}p(\mathit{D})\approx \sum _{j=2}^k\frac{t_j-t_{j-1}}{2}\left[\frac{1}{n}\sum _{i=1}^n\text{ln}p(\mathit{D}\mid {\mathit{\theta }}_{i,j})+\frac{1}{n}\sum _{i=1}^n\text{ln}p(\mathit{D}\mid {\mathit{\theta }}_{i,j-1})\right].$$ (35)

where t forms the set of temperatures (sometimes referred to as the temperature schedule with each temperature, indexed by j, referred to as a rung), k is the total number of temperatures, and n is the number of samples. Also, note that the two terms in Equation 35 are from rungs j and j-1 and that they may have differing numbers of samples. Following Friel and Pettitt (2008), the Monte Carlo variance associated with the estimate can also be obtained in two steps. The first step is to compute the TI estimate using the trapezoidal rule under each sample:

$$T{I}_i=\sum _{j=2}^k\frac{t_j-t_{j-1}}{2}[\text{ln}p(\mathit{D}\mid {\mathit{\theta }}_{i,j})+\text{ln}p(\mathit{D}\mid {\mathit{\theta }}_{i,j-1})],i=\{1,\dots ,n\}.$$ (36)

Figure 3.

The mean log-likelihood computed under samples drawn from a posterior raised to the corresponding temperature. The area under the curve, shown in grey, is the estimate of the marginal likelihood produced from the thermodynamic integration method. Note the Monte Carlo standard error bars are not plotted because they too small to be displayed.

This results in a vector TI, where each element, TI_i, is the TI estimate corresponding to the MCMC sample, i. The sample mean, ${\widehat{\mu }}_{TI}$, is the average over TI. In the second step, the variance of ${\widehat{\mu }}_{TI}$ is given by:

$$\text{Var}({\widehat{\mu }}_{TI})=\frac{1}{n}\text{Var}(\mathbf{T}\mathbf{I}).$$ (37)

One could then compute the standard error or construct a 95% confidence interval if desired.

There are two major sources of error in the TI approach: The sampling error associated with MCMC and the error associated with the discretization of k temperatures. In general, the error associated with MCMC sampling can be reduced by increasing the number of samples per power posterior or using a more efficient sampler (for discussions, see Brooks et al., 2011; Turner, Sederberg, Brown, & Steyvers, 2013). The discretization introduces error in the TI estimate of the log marginal likelihood as well. The development of methods that aim to decrease the discretization error is an active area of research (e.g., Friel, Hurn, & Wyse, 2014; Hug, Schwarzfischer, Hasenauer, Marr, & Theis, 2016; Oates, Papamarkou, & Girolami, 2016). Research has shown that there are ways to increase the accuracy of the TI estimate via changes in temperature schedule. One method is simply to increase the number of temperature rungs, which increases the stability of the integral, but obviously comes at the cost of an increased computational workload. We found that in many situations a curve with 30-35 or more points worked well, and this may be a good place for an interested user to begin with their model. There is currently no known solution to picking the optimal number of rungs and therefore it is left to the judgment of the researcher.

A visual examination of the thermodynamic curve after finding the mean log-likelihood under each power posterior can serve as a sanity check. The curve should be smooth; it is a strictly increasing function of temperature (Friel et al., 2014). If a higher temperature point has a lower marginal likelihood then it indicates there is something wrong with the MCMC sampling procedure that was used (e.g., possibly that more sampling is needed, or a longer burn-in process is required).

An additional method to reduce error is to change the distribution of the temperature rungs. One of the first papers that introduced TI (Lartillot & Phillippe, 2006) simply used an evenly spaced temperature schedule. Since then, temperature schedules leading to more efficient estimation of the marginal likelihood have been devised. Such methods commonly place more rungs near small values of t, where the expected likelihood, E_θ∣D,t ln p(D∣θ), tends to change more rapidly. A commonly used scheduling framework is one that sets t_j to the (j-1)th quantile of a Beta(α, 1) distribution (Xie et al., 2011):

$$t_j={\left(\frac{j-1}{k-1}\right)}^{1∕\alpha },$$ (38)

where k is the total number of temperatures, j = {1, 2, … , k}, and α is a tuning parameter that modulates the skew of the distribution over t. When α = 1, the temperatures are uniformly distributed over the interval. As α decreases towards zero, temperatures become positively skewed, α values of 0.30 (Xie et al., 2011) and 0.25 (Friel & Pettitt, 2008) have been shown to be suitable for a range of models such as (but not limited to) linear regression models, hidden Markov random field models, and continuous-time Markov chain models. In general, this moderate skew towards the prior works well because most of the rungs are going to be located in places in which the curve changes rapidly. Figure 3 illustrates what the distribution of 20 temperature rungs looks like when α = 0.30.

Attempts to improve the numerical integration method have also been made (e.g., Friel et al., 2014; Hug et al., 2016). For example, Friel et al. (2014) used a corrected trapezoidal rule that takes into account the second derivative (i.e., the variance) of the log-likelihood:

$$\begin{gathered} \text{ln}p(\mathit{D})\approx \sum _{j=2}^k\frac{t_j-t_{j-1}}{2}\left[\frac{1}{n}\sum _{i=1}^n\text{ln}p(\mathit{D}\mid {\mathit{\theta }}_{i,j})+\frac{1}{n}\sum _{i=1}^n\text{ln}p(\mathit{D}\mid {\mathit{\theta }}_{i,j-1})\right] \\ -\sum _{j=2}^k\frac{{\left(t_j-t_{j-1}\right)}^2}{12}\left[\text{Var}(\text{ln}p(\mathit{D}\mid {\mathit{\theta }}_{i,j}))-\text{Var}(\text{ln}p(\mathit{D}\mid {\mathit{\theta }}_{i,j-1}))\right]. \end{gathered}$$ (39)

Friel et al. showed that the correction term improves the estimate with nearly zero additional computational cost, only requiring the variance the log-likelihoods under the power posterior samples at each temperature rung. Note that the corrected trapezoidal rule is based on the variance of the entire power posterior sample and therefore we do not consider its Monte Carlo variance.

Steppingstone Sampling (SS)

Conceptual introduction.

Steppingstone sampling (SS; Xie et al., 2011) proceeds in largely the same way as TI: sample from power posteriors at a variety of temperatures and then use the resulting samples to compute the estimate of the marginal likelihood. The only practical difference between TI and SS is the formula used to compute the estimate. The SS estimator uses a variant of importance sampling. The basic idea is to use adjacent, slightly more diffuse power posteriors as importance distributions. For example, the power posterior with a temperature of 0.1 is a slightly more diffuse power posterior than the one at 0.2 and therefore performs well as an importance distribution. More formally, for each power marginal likelihood, p(D∣t_j), an estimate is obtained using p(D∣t_j–1) as an importance distribution. Each estimate, p(D∣t_j), is then combined using the SS estimator to obtain an estimate of the marginal likelihood, p(D).

Mathematical details.

The SS approach exploits the following identity:

$$p(\mathit{D})=\frac{p(\mathit{D}\mid t=1)}{p(\mathit{D}\mid t=0)}=\prod _{j=1}^k\frac{p(\mathit{D}\mid t_j)}{p(\mathit{D}\mid t_{j-1})},$$ (40)

where p(D∣t_j) takes the same form as the power marginal likelihood from TI, given in Equation 25. It is probably easiest to demonstrate why this identity holds with an example. Consider k = 3 and temperatures that are evenly spaced, then:

$$p(\mathit{D})=\frac{\int p(\mathit{D}\mid \mathit{\theta }{)}^{\frac{1}{3}}p(\mathit{\theta })d\mathit{\theta }}{\int p(\mathit{D}\mid \mathit{\theta }{)}^{\frac{0}{3}}p(\mathit{\theta })d\mathit{\theta }}\frac{\int p(\mathit{D}\mid \mathit{\theta }{)}^{\frac{2}{3}}p(\mathit{\theta })d\mathit{\theta }}{\int p(\mathit{D}\mid \mathit{\theta }{)}^{\frac{1}{3}}p(\mathit{\theta })d\mathit{\theta }}\frac{\int p(\mathit{D}\mid \mathit{\theta }{)}^{\frac{3}{3}}p(\mathit{\theta })d\mathit{\theta }}{\int p(\mathit{D}\mid \mathit{\theta }{)}^{\frac{2}{3}}p(\mathit{\theta })d\mathit{\theta }}.$$ (41)

Now cancel out common terms in the numerator and denominator, which results in:

$$p(\mathit{D})=\frac{\int p(\mathit{D}\mid \mathit{\theta })p(\mathit{\theta })d\mathit{\theta }}{\int p(\mathit{\theta })d\mathit{\theta }}.$$ (42)

The denominator is simply the integral of the prior. Given a proper prior, this will integrate to 1 and we will be left with the marginal likelihood, p(D).

The procedure then estimates each of the k ratios using importance sampling. The importance distribution for each power posterior, p(D∣t_j), is p(D∣t_j–1), the reason being that the distribution at the lower adjacent temperature, p(D∣t_j–1), is slightly more diffuse than p(D∣t_j) and therefore serves as a useful importance distribution. The following derivations will generate estimates of all p(D∣t_j) using this importance sampling framework. Then, these ratios will be substituted into Equation 40 to obtain the SS estimator of p(D).

Recall the definition of the power marginal likelihood raised to the temperature, t_j:

$$p(\mathit{D}\mid t_j)=\int p(\mathit{D}\mid \mathit{\theta }{)}^{t_j}p(\mathit{\theta })d\mathit{\theta }.$$ (43)

We can rewrite this in an importance sampling framework using the power posterior raised to temperature t_j–1 as the importance distribution:

$$p(\mathit{D}\mid t_j)=\int \frac{p(\mathit{D}\mid \mathit{\theta }{)}^{t_j}p(\mathit{\theta })}{p(\mathit{\theta }\mid \mathit{D},t_{j-1})}p(\mathit{\theta }\mid \mathit{D},t_{j-1})d\mathit{\theta }.$$ (44)

In order to help to simplify the equation later, we perform an intermediate step before representing it as an expected value. To do this, we divide by the integral of the prior, again using the power posterior raised to the previous temperature as the importance distribution:

$$p(\mathit{D}\mid t_j)=\frac{\int \frac{p(\mathit{D}\mid \mathit{\theta }{)}^{t_j}p(\mathit{\theta })}{p(\mathit{\theta }\mid \mathit{D},t_{j-1})}p(\mathit{\theta }\mid \mathit{D},t_{j-1})d\mathit{\theta }}{\int \frac{p(\mathit{\theta })}{p(\mathit{\theta }\mid \mathit{D},t_{j-1})}p(\mathit{\theta }\mid \mathit{D},t_{j-1})d\mathit{\theta }}.$$ (45)

This trick was also performed earlier for the harmonic mean derivation. It is only done to ensure the final representation is in a mathematically convenient form. Remember, this is equivalent to dividing by 1, given proper priors. We then represent the numerator and denominator as expected values:

$$\frac{\int \frac{p(\mathit{D}\mid \mathit{\theta }{)}^{t_j}p(\mathit{\theta })}{p(\mathit{\theta }\mid \mathit{D},t_{j-1})}p(\mathit{\theta }\mid \mathit{D},t_{j-1})d\mathit{\theta }}{\int \frac{p(\mathit{\theta })}{p(\mathit{\theta }\mid \mathit{D},t_{j-1})}p(\mathit{\theta }\mid \mathit{D},t_{j-1})d\mathit{\theta }}=\frac{{\mathbf{E}}_{\mathit{\theta }\mid \mathit{D},t_{j-1}}\left[\frac{p(\mathit{D}\mid \mathit{\theta }{)}^{t_j}p(\mathit{\theta })}{p(\mathit{\theta }\mid \mathit{D},t_{j-1})}\right]}{{\mathbf{E}}_{\mathit{\theta }\mid \mathit{D},t_{j-1}}\left[\frac{p(\mathit{\theta })}{p(\mathit{\theta }\mid \mathit{D},t_{j-1})}\right]}.$$ (46)

To obtain a computable approximation, the ratio of expected values can be approximated with the following ratio of averages over a large number of random samples:

$$\frac{{\mathbf{E}}_{\mathit{\theta }\mid \mathit{D},t_{j-1}}\left[\frac{p(\mathit{D}\mid \mathit{\theta }{)}^{t_j}p(\mathit{\theta })}{p(\mathit{\theta }\mid \mathit{D},t_{j-1})}\right]}{{\mathbf{E}}_{\mathit{\theta }\mid \mathit{D},t_{j-1}}\left[\frac{p(\mathit{\theta })}{p(\mathit{\theta }\mid \mathit{D},t_{j-1})}\right]}\approx \frac{\frac{1}{n}{\sum }_{i=1}^n\frac{p{\left(\mathit{D}\mid {\mathit{\theta }}_{i,j-1}\right)}^{t_j}p({\mathit{\theta }}_{i,j-1})p(\mathit{D}\mid t_{j-1})}{p(\mathit{D}\mid {\mathit{\theta }}_{i,j-1}{)}^{t_{j-1}}p({\mathit{\theta }}_{i,j-1})}}{\frac{1}{n}{\sum }_{i=1}^n\frac{p({\mathit{\theta }}_{i,j-1})p(\mathit{D}\mid t_{j-1})}{p{\left(\mathit{D}\mid {\mathit{\theta }}_{i,j-1}\right)}^{t_{j-1}}p({\mathit{\theta }}_{i,j-1})}}.$$ (47)

After simplifying we find the following:

$$p(\mathit{D}\mid t_j)\approx \frac{1}{n}\sum _{i=1}^n\frac{p(\mathit{D}\mid {\mathit{\theta }}_{i,j-1}{)}^{t_j}}{p(\mathit{D}\mid {\mathit{\theta }}_{i,j-1}{)}^{t_{j-1}}}{\left[\frac{1}{n}\sum _{i=1}^n\frac{1}{p(\mathit{D}\mid {\mathit{\theta }}_{i,j-1}{)}^{{}^{t_{j-1}}}}\right]}^{-1}.$$ (48)

where θ_j–1,i~p(θ∣D, t_j–1) In a similar fashion, it is straightforward to show (see the Appendix for the full derivation):

$$p(\mathit{D}\mid t_{j-1})\approx {\left[\frac{1}{n}\sum _{i=1}^n\frac{1}{p(\mathit{D}\mid {\mathit{\theta }}_{i,j-1}{)}^{{}^{t_{j-1}}}}\right]}^{-1},$$ (49)

where θ_i~p(θ∣D, t_j–1). Lastly, substituting the estimators of p(D∣t_j) and p(D∣t_j–1) into Equation 40, we have the steppingstone estimator:

$$\widehat{\text{SS}}=\prod _{j=1}^k\frac{1}{n}\sum _{i=1}^n\frac{p(\mathit{D}\mid {\mathit{\theta }}_{i,j-1}{)}^{t_j}}{p(\mathit{D}\mid {\mathit{\theta }}_{i,j-1}{)}^{t_{j-1}}},$$ (50)

where θ_{j–1, i}~p(θ∣D, t_j–1).

Implementation.

As noted in Box 1 and 2, the same samples (minus the samples from the power posterior at t = 1, p(θ∣D, t = 1)) used for TI can be used to produce samples for the steppingstone estimate as well. The only difference is how those samples are used to estimate the marginal likelihoods.

Xie et al. (2011) showed that Equation 50 can be numerically unstable in practice and that stability is improved by taking the log of the estimator and factoring out the largest log-likelihood:

$$\begin{gathered} \text{ln}p(\mathit{D})\approx \text{ln}\widehat{\text{SS}} \\ =\sum _{j=1}^{k-1}\text{ln}\left[\frac{1}{n}\sum _{i=1}^n\text{exp}((\text{ln}p(\mathit{D}\mid {\mathit{\theta }}_{i,j})-L_{max,j})(t_{j+1}-t_j))\right]+(t_{j+1} \\ -t_j)\ast L_{max,j}, \end{gathered}$$ (51)

where L_max,j is the maximum log-likelihood under the power posterior sample at temperature t_j. Note the SS estimator does not require samples from the posterior, p(θ∣D, t = 1), as the maximum temperature is k – 1. This is because the importance sampling distribution for the power posterior at t_j is the adjacent power posterior at t_j∣1. It is also important to note that the log version of SS is not an unbiased estimator of ln p(D). However, this bias dramatically decreases as the number of temperature rungs increases (see Xie et al., 2011), and in the present work, we did not find this aspect of the SS estimator to be problematic.

Since SS relies on the entire posterior sample (the maximum sample from the set must be computed), the variance for SS is computed slightly differently than TI. The first step involves computing exponentiated form of the k-1 SS ratios:

$$r_j=\frac{1}{n}{\left(L_{max,j}\right)}^{t_{j+1}-t_j}\sum _{i=1}^n{\left(\frac{p(\mathit{D}\mid {\mathit{\theta }}_{i,j})}{L_{max,j}}\right)}^{t_{j+1}-t_j},j=\{1,\dots ,k-1\}.$$ (52)

The result is then used to compute the variance of the log SS estimate (Xie et al., 2011):

$$\text{Var}(\text{ln}\widehat{\text{SS}})=\frac{1}{n^2}\sum _{j=1}^{k-1}\sum _{i=1}^n{\left(\frac{p(\mathit{D}\mid {\mathit{\theta }}_{i,j}{)}^{t_{j+1}-t_j}}{r_j}\right)}^2.$$ (53)

The Linear Ballistic Accumulator

In this section, we illustrate how to compute the marginal likelihood (and hence Bayes factors) with TI and SS for a cognitive model of decision making called the Linear Ballistic Accumulator model (LBA; Brown & Heathcote, 2008). There are three main reasons for choosing the LBA to demonstrate TI and SS. First, the LBA is a general model, widely applicable to a variety of tasks involving a decision. Second, there are many demonstrations of TI and SS using more standard statistical models (validating these methods relative to a ground-truth analytic solution), but we are unaware of any demonstrations using a psychologically-motivated cognitive model. This is important, as there are often unique issues associated with cognitive models due to their correlated structure (e.g., Turner et al., 2013). Third, the LBA, like many cognitive models, is not included in off-the-shelf software packages that compute marginal likelihoods and Bayes factors for statistical models like regression and ANOVA (e.g., JASP Team, 2017; Rouder & Morey, 2012; Rouder et al., 2012). For models like the LBA, general methods of marginal likelihood estimation, such as TI and SS, must be applied.

We first describe the LBA and its parameters. Next, we describe how we use simulated data from the LBA as a test bed for TI and SS. Here, we use the same simulated data sets as Evans and Brown, which allows us to compare the marginal likelihood estimates obtained via TI and SS to those obtained by them using a brute force GPU-based method.

The LBA is a member of a broader class of sequential sampling models (Ratcliff & Smith, 2004), which assume that decision making is a process of accumulating evidence for various choice alternatives over time. To make a decision, people sample noisy evidence for each alternative at some rate (the “drift rate”), until the accumulated evidence for one of the alternatives reaches some threshold level of evidence (the “response threshold”), whereby an overt response is triggered. Specifically, the LBA assumes that a stimulus is perceptually encoded for some time, τ_e. After encoding, evidence for each response alternative, r_i, begins to accumulate in independent accumulators each having their own response thresholds, b_i. The rate at which evidence accumulates in the ith accumulator is the drift rate, d_i. The drift rates are sampled across trials from a normal distribution with mean v_i and standard deviation, s_i. The starting point of the evidence accumulation process also varies across trials and across accumulators and is assumed to be drawn from a uniform distribution on the interval (0, A), where A < b_i. The distance between A and the threshold b is the relative threshold, k. A response is made when the first accumulator reaches its threshold and the motor response is completed with time, τ_r (where τ_e + τ_r = τ).

The simulated data set of Evans and Brown (2017) was essentially a simulation of data from a single participant from an experiment with two conditions, where the participant completed 600 trials per condition and the response time and accuracy of each response was recorded; we repeated those simulations here. Evans and Brown referred to this as a “simple” data set, as the data were generated with identical parameter values for both conditions (1 and 2), meaning that there should be no significant difference between the data simulated in these two conditions. The data-generating parameters for the simple model were as follows: A = 1, b = 1.4, v_c = 3.5, v_e = 1, s_c = 1, s_e = 1, τ = .3, where the subscripts c and e correspond to correct and incorrect responses, respectively.

We fitted two versions of LBA to this simulated data set (the same as Evans and Brown): A “simple” model where no parameters were free to vary between the two conditions (i.e., a model that matches the process that generated the simulated data), and a “complex” model, where conditions 1 and 2 had different values for the correct drift rate, response threshold, and non-decision time.

Formally, for the simple model, the vector of choice response times, RT, follows the LBA likelihood:

$$\mathit{R}\mathit{T}\sim LBA(k,A,v_c,v_e,s_c,s_e,\tau ),$$

where v_c and v_e are the mean drift rates for correct and incorrect responses, respectively, and s_c and s_e are the corresponding standard deviations (with s_c = 1, as in Evans and Brown). The priors for both models were the same as those used by Evans and Brown, with the simple model having the following priors:

$$\begin{gathered} k\sim TN(0.4,0.4,0,\infty ) \\ A,v_e,s_e\sim TN(1,1,0,\infty ) \\ {v}_c\sim TN(3,3,0,\infty ) \\ \tau \sim TN(0.3,0.3,0,\infty ), \end{gathered}$$

where TN(a, b, c, d) is the truncated normal with mean a, standard deviation b, lower bound c, and upper bound d. For the complex model, the likelihood of choice response times is given by:

$$\mathit{R}{\mathit{T}}_j\sim LBA\left(k_j,A,v_{c,j},v_e,s_c,s_e,{\tau }_j\right),$$

where j indexes the condition. The complex model has the following priors:

$$\begin{gathered} k_j\sim TN(0.4,0.4,0,\infty ) \\ A,v_e,s_e\sim TN(1,1,0,\infty ) \\ {v}_{c,j}\sim TN(3,3,0,\infty ) \\ {\tau }_j\sim TN(0.3,0.3,0,\infty ) \end{gathered}$$

In addition, each model contained a contaminant process (as in Evans and Brown, common in some applications of decision making models), whereby the probability density of the model was made up of 98% of the standard LBA process, and 2% of a distribution assumed to be due to random contaminants, which was a uniform distribution between 0 and 5 seconds.

Examples

In this section, we provide examples of TI and SS using the LBA. We compare them to the arithmetic mean estimator. The arithmetic mean estimator is a very inefficient estimator that requires an enormously large numbers of samples to obtain a sufficient level of accuracy; given a large enough sample size it will eventually converge to the true marginal likelihood. Evans and Brown used GPU technology to obtain massive numbers of samples in a relatively short period of time (see Figure 1). We subsequently refer to these as the brute force GPU estimates or simply GPU estimates.

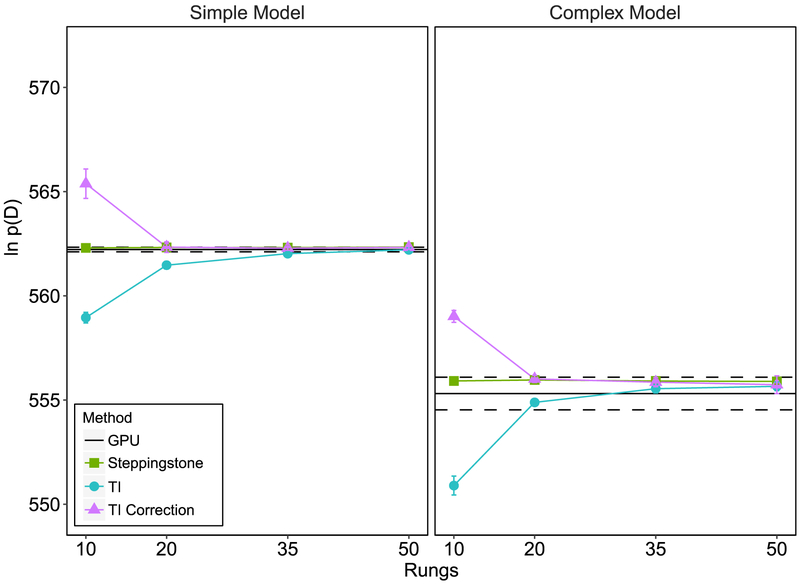
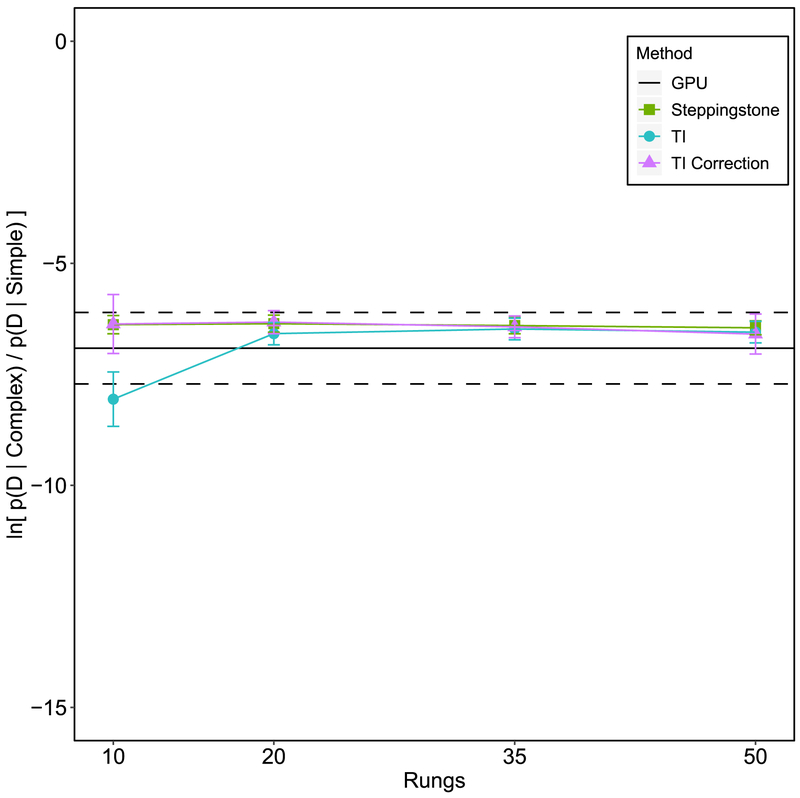
Figure 4 shows the resulting log marginal likelihood estimates. The solid line represents mean GPU estimate from Evans and Brown and the dotted line represents the standard deviation, based on 10 independent runs³. For the TI approach, we used 4 different temperature rung quantities: 10, 20, 35, and 50, and an α value of 0.3. We computed the TI estimate of the log marginal likelihood using both the standard trapezoidal rule (Equation 35) and the trapezoidal rule with the correction term (Equation 39). Posterior samples were drawn using DE-MCMC sampling (Turner et al., 2013) although any MCMC sampler can be used. After a burnin of 300 iterations, we drew a total of 700 samples for each temperature rung. We repeated this procedure 10 times. The means and standard deviations of the log marginal likelihood estimates (based on 10 independent replications) are shown in Figure 4 as a function of the number of temperature rungs and model type. The results for the simple model, in which no parameters varied across conditions, are plotted on the left panel and the results for the complex model are plotted on the right. The mean GPU estimate of the log marginal likelihood computed by the brute force method is shown as a solid black line and the standard deviation is shown as a dotted black line. As expected, we observed decreases in the difference between the arithmetic mean estimate and both types of TI with increases in the number of temperature rungs used. The estimated variance of the individual TI estimates (Equation 37) was very low, ranging from .002 to .02 for the simple model and from .0003 to .02 for the complex model. The TI correction method reached a stable estimate at 10 rungs for the simple and complex model, while the ordinary TI estimate reached stability at 35 to 50 rungs.

Figure 4.

The estimated log marginal likelihood, ln p(D), plotted as a function of the number of temperature rungs, estimation method, and model type. The solid black lines and dashed black lines, show the estimated mean and standard deviation of ln p(D), respectively, from Evans and Brown (2017) who used a brute force GPU method. All means and standard deviations are based on 10 independent replications of the respective method. All error bars represent standard deviations.

We tested the SS method using the same samples and data from the TI simulation study described earlier. Figure 4 shows the SS estimate becomes stable at approximately 10 rungs for the simple and complex model. It converges to the same marginal likelihood as both forms of TI. The estimated variance of the SS estimates (Equation 53) were very low, ranging from .002 to .006 for the simple model and from .003 to .01 for the complex model. Lastly, Figure 5 shows it produces stable Bayes factors at approximately 10 rungs, similar to that of the TI correction method. Both TI and SS correctly favor the simple model over the complex model, matching the conditions that generated the simulated data.

Figure 5.

Evidence for and against the complex model plotted in terms of the log Bayes factor as a function of the number of temperature rungs. All error bars represent standard deviations.

Figure 5 shows the estimated evidence yielded by each method for the complex model over the simple model in terms of the Bayes factor (depicted on the log scale for plotting purposes). Positive values indicate evidence in favor of the complex model (and against the simple model), and negative values indicate evidence against the complex model (and in favor of the simple model). The data were generated from the simple model, meaning that values less than 0 indicate correct model selection (i.e. evidence against the complex model), with log Bayes factors of magnitude from 1 to 3 indicating positive evidence, those from 3 to 5 representing strong evidence, and those greater than 5 indicating very strong evidence (Kass and Raftery, 1995)⁴.

Marginal Likelihoods for Hierarchical Models

So far, we have focused on models of a single subject. The simultaneous modeling of multiple subjects through hierarchical models has become a large area of interest for models of cognition as they allow for the simultaneous estimation of subject-level and group-level parameters. Hierarchical models often contain hundreds of parameters. Given that on current GPU hardware, it takes roughly 2 days to collect 10¹⁰ samples, we might reasonably anticipate that for a high-dimensional hierarchical model, orders of magnitude more samples might be needed, requiring months or years of GPU computation to converge on accurate estimates.

We must turn to methods like TI and SS to have any chance of estimating marginal likelihoods for such models. Fortunately, TI and SS are completely general and readily apply to hierarchical models. We show how these approaches can be applied to hierarchical models by deriving estimators within a hierarchical framework. The upshot is we do not need to alter any of the core mechanisms of TI or SS. The only difference is that we use subject-level samples from a hierarchical model instead of the subject-level samples from a single-subject model.

Interestingly, the derivations show we can ignore group-level parameters in the actual computation of the marginal likelihood even though group-level parameters clearly influence the marginal likelihood through the subject-level parameters. This is due to the structure of hierarchical models in which the data are conditionally independent of the group-level parameters. To provide some intuition as to why this is true, we will first describe hierarchical models in general and give a derivation of one of the simplest estimators of the marginal likelihood, the arithmetic mean estimator. Next, we will show the derivations of TI and SS for hierarchical models.

Mathematical Details for Hierarchical Models

In hierarchical models , subject-level parameters are sampled from a population whose parameters are unknown quantities. For example, we might assume that subject-level parameters are sampled from a normal distribution with unknown mean and variance. From a Bayesian perspective, these unknown quantities can be treated as random variables in the same way that subject-level parameters are treated as random variables. Therefore, in addition to the subject-level parameter vector, θ, we can introduce a group-level parameter vector, ϕ, producing a hierarchical model of the following form:

$$\begin{gathered} {\mathit{D}}_s\sim p({\mathit{D}}_s\mid {\mathit{\theta }}_s) \\ {\mathit{\theta }}_s\sim p({\mathit{\theta }}_s\mid \mathit{\varphi }) \\ \mathit{\varphi }\sim p(\mathit{\varphi }), \end{gathered}$$ (54)

where the subscript, s, denotes the subject index. This hierarchical model has the joint posterior joint posterior, p(θ, ϕ∣D).

Given this hierarchical model structure, we now proceed to deriving the arithmetic mean estimator. To begin, we first define the joint posterior according to Bayes’ rule (dropping the s subscript for simplicity):

$$p(\mathit{\theta },\mathit{\varphi }\mid \mathit{D})=\frac{p(\mathit{D}\mid \mathit{\theta },\mathit{\varphi })p(\mathit{\theta },\mathit{\varphi })}{\int \int p(\mathit{D}\mid \mathit{\theta },\mathit{\varphi })p(\mathit{\theta },\mathit{\varphi })d\mathit{\theta }d\mathit{\varphi }}.$$ (55)

Note that the log-likelihood, ln p(D∣θ, ϕ), is the log-likelihood summed over all participants, ln p(D∣θ, ϕ) = ∑_s ln p(D_sθθ_s, ϕ). It is often difficult to work with the posterior in this form because we must define a joint prior distribution over θ and ϕ. We can simplify this formulation by using a basic rule of probability, p(a, b) = p(a∣b)p(a) and rewriting the posterior as:

$$p(\mathit{\theta },\mathit{\varphi }\mid \mathit{D})=\frac{p(\mathit{D}\mid \mathit{\theta },\mathit{\varphi })p(\mathit{\theta }\mid \mathit{\varphi })p(\mathit{\varphi })}{\int \int p(\mathit{D}\mid \mathit{\theta },\mathit{\varphi })p(\mathit{\theta }\mid \mathit{\varphi })p(\mathit{\varphi })d\mathit{\theta }d\mathit{\varphi }}.$$ (56)

This simplifies matters, but we are still left with a likelihood that depends on the joint distribution over θ and ϕ. Given the structure of hierarchical models, we can drop ϕ from the likelihood because the data are conditionally independent of the group-level parameters. This independence is clear in the original formulation of the hierarchical model where we state that D_s ~ p(D_s∣θ_s). Then, we can write the posterior as:

$$p(\mathit{\theta },\mathit{\varphi }\mid \mathit{D})=\frac{p(\mathit{D}\mid \mathit{\theta })p(\mathit{\theta }\mid \mathit{\varphi })p(\mathit{\varphi })}{\int \int p(\mathit{D}\mid \mathit{\theta })p(\mathit{\theta }\mid \mathit{\varphi })p(\mathit{\varphi })d\mathit{\theta }d\mathit{\varphi }}.$$ (57)

Having formulated the posterior in this way, we can write its marginal likelihood as the following expected value:

$$\int \int p(\mathit{D}\mid \mathit{\theta })p(\mathit{\theta }\mid \mathit{\varphi })p(\mathit{\varphi })d\mathit{\theta }d\mathit{\varphi }={\mathbf{E}}_{\mathit{\theta },\mathit{\varphi }}[p(\mathit{D}\mid \mathit{\theta })].$$ (58)

and approximate this expected value with an average:

$${\mathbf{E}}_{\mathit{\theta },\mathit{\varphi }}[p(\mathit{D}\mid \mathit{\theta })]\approx \frac{1}{n}\sum _{i=1}^{n}p(\mathit{D}\mid {\mathit{\theta }}_i),$$ (59)

where θ_i~p(θ∣ϕ_i) and ϕ_i~p(ϕ) [which is equivalent to (θ_i, ϕ_i)~p(θ, ϕ)]. Note again, the log-likelihood, ln p(D∣θ), is the log-likelihood summed over all participants,ln p(D∣θ) = ∑_s ln p(D_s∣θ_s). This is the arithmetic mean estimator of the marginal likelihood for the hierarchical model. To obtain the samples from the joint prior distribution, ϕ_i is first sampled from p(ϕ). The resulting sample is then used to sample θ_i, from p(θ∣ϕ_i). Equivalently, if the joint prior distribution is defined, then pairs, (θ_i, ϕ_i), can be sampled from p(θ, ϕ). Then, for each θ_i, the likelihood, p(D∣θ_i), is computed and the average is taken to obtain the estimate of the marginal likelihood. Importantly, while the subject-level parameter vector, θ, enters directly into the computation of the marginal likelihood, the group-level parameter vector, ϕ does not. Rather, ϕ constrains which values of θ are more likely, and therefore has an indirect but, nonetheless, important influence on the estimation of the marginal likelihood. Analogously, the group-level parameter vector enters into marginal likelihood estimations in such an indirect manner for TI and SS, as shown below.

For TI, given the group-level parameter vector, ϕ, and the subject-level parameter vector, θ, the power marginal likelihood is:

$$p(\mathit{D}\mid t)=\int \int p(\mathit{D}\mid \mathit{\theta }{)}^{t}p(\mathit{\theta }\mid \mathit{\varphi })p(\mathit{\varphi })d\mathit{\theta }d\mathit{\varphi },t\in [0,1].$$ (60)

Recall from the original TI derivation that we can take the log of p(D∣t) and rewrite it as the difference in the log marginal likelihood at t = 1 and t = 0. We can then represent this difference as an integral:

$$\text{ln}p(\mathit{D}\mid t)=\text{ln}p(\mathit{D}\mid t=1)-\text{ln}p(\mathit{D}\mid t=0)={\int }_0^1\frac{d}{dt}\text{ln}p(\mathit{D}\mid t)dt.$$ (61)

Taking the derivative with respect to t we have:

$$\frac{d}{dt}\text{ln}p(\mathit{D}\mid t)=\frac{1}{p(\mathit{D}\mid t)}\frac{d}{dt}p(\mathit{D}\mid t).$$ (62)

We must now solve the derivative of p(D∣t) with respect to t. The derivative commutes with the double integral and becomes a partial derivative with respect to t:

$$\frac{d}{dt}p(\mathit{D}\mid t)=\frac{d}{dt}\int \int p(\mathit{D}\mid \mathit{\theta }{)}^{t}p(\mathit{\theta }\mid \mathit{\varphi })p(\mathit{\varphi })d\mathit{\theta }d\mathit{\varphi }$$ (63)

$$=\int \int \frac{\partial }{\partial t}p(\mathit{D}\mid \mathit{\theta }{)}^{t}p(\mathit{\theta }\mid \mathit{\varphi })p(\mathit{\varphi })d\mathit{\theta }d\mathit{\varphi }.$$ (64)

$$=\int \int p(\mathit{D}\mid \mathit{\theta }{)}^t\text{ln}p(\mathit{D}\mid \mathit{\theta })p(\mathit{\theta }\mid \mathit{\varphi })p(\mathit{\varphi })d\mathit{\theta }d\mathit{\varphi }$$ (65)

The partial derivative is computed by factoring out the terms that do not depend on t, p(θ∣ϕ) and p(ϕ), and using the rule, $\frac{\partial }{\partial t}{a}^t=a^t$ ln a. The derivative of the log of p(D∣t) is then:

$$\frac{d}{dt}\text{ln}p(\mathit{D}\mid t)=\frac{1}{p(\mathit{D}\mid t)}\int \int p(\mathit{D}\mid \mathit{\theta }{)}^t\text{ln}p(\mathit{D}\mid \mathit{\theta })p(\mathit{\theta }\mid \mathit{\varphi })p(\mathit{\varphi })d\mathit{\theta }d\mathit{\varphi }.$$ (66)

After rearranging, we see the integrand is the product of the power posterior and the likelihood:

$$\frac{d}{dt}\text{ln}p(\mathit{D}\mid t)=\int \int \frac{p(\mathit{D}\mid \mathit{\theta }{)}^{t}p(\mathit{\theta }\mid \mathit{\varphi })p(\mathit{\varphi })}{p(\mathit{D}\mid t)}\text{ln}p(\mathit{D}\mid \mathit{\theta })d\mathit{\theta }d\mathit{\varphi }.$$ (67)

This can be written as the expected likelihood with respect to the joint power posterior of θ and ϕ:

$$\frac{d}{dt}\text{ln}p(\mathit{D}\mid t)={\mathbf{E}}_{\mathit{\theta },\mathit{\varphi }\mid \mathit{D},t}[\text{ln}p(\mathit{D}\mid \mathit{\theta })].$$ (68)

Substituting this back into the original identity for ln p(D∣t) we see it is equal to the integral over t of the expected likelihood with respect to the joint posterior of θ and ϕ:

$$\text{ln}p(\mathit{D}\mid t)={\int }_0^1{\mathbf{E}}_{\mathit{\theta },\mathit{\varphi }\mid \mathit{D},t}[\text{ln}p(\mathit{D}\mid \mathit{\theta })]dt.$$ (69)

Thus, all that is required for hierarchical TI is to draw subject-level samples from the joint power posterior, p(θ, ϕ∣D, t). The resulting subject-level samples, θ_i, are then used to compute the mean likelihood under each temperature, t. The integral can then be approximated using the trapezoidal rule (Equation 35 or 39).

The SS derivation in the hierarchical framework relies on the same identity as the non-hierarchical case (Equation 40):

$$p(\mathit{D})=\prod _{j=1}^k\frac{p(\mathit{D}\mid t_j)}{p(\mathit{D}\mid t_{j-1})}.$$ (70)

The numerator and denominator are derived within the importance sampling framework using the power posterior at temperature t_j–1 as the importance distribution. Then, for p(D∣t_j) we have:

$$p(\mathit{D}\mid t_j)=\int \int \frac{p{(\mathit{D}\mid \mathit{\theta })}^{t_j}p(\mathit{\theta }\mid \mathit{\varphi })p(\mathit{\varphi })}{p(\mathit{\theta },\mathit{\varphi }\mid \mathit{D},t_{j-1})}p(\mathit{\theta },\mathit{\varphi }\mid \mathit{D},t_{j-1})d\mathit{\theta }d\mathit{\varphi }.$$ (71)

We then divide by the joint prior and use the power posterior at temperature t_j–1 as the importance distribution. This is done so the equation simplifies properly and is equivalent to dividing by one.

$$p(\mathit{D}\mid t_j)=\frac{\int \int \frac{p{(\mathit{D}\mid \mathit{\theta })}^{t_j}p(\mathit{\theta }\mid \mathit{\varphi })p(\mathit{\varphi })}{p(\mathit{\theta },\mathit{\varphi }\mid \mathit{D},t_{j-1})}p(\mathit{\theta },\mathit{\varphi }\mid \mathit{D},t_{j-1})d\mathit{\theta }d\mathit{\varphi }}{\int \int \frac{p(\mathit{\theta }\mid \mathit{\varphi })p(\mathit{\varphi })}{p(\mathit{\theta },\mathit{\varphi }\mid \mathit{D},t_{j-1})}p(\mathit{\theta },\mathit{\varphi }\mid \mathit{D},t_{j-1})d\mathit{\theta }d\mathit{\varphi }}.$$ (72)

We then represent the numerator and denominator as expected values with respect to the joint posterior:

$$\begin{gathered} \frac{\int \int \frac{p{(\mathit{D}\mid \mathit{\theta })}^{t_j}p(\mathit{\theta }\mid \mathit{\varphi })p(\mathit{\varphi })}{p(\mathit{\theta },\mathit{\varphi }\mid \mathit{D},t_{j-1})}p(\mathit{\theta },\mathit{\varphi }\mid \mathit{D},t_{j-1})d\mathit{\theta }d\mathit{\varphi }}{\int \int \frac{p(\mathit{\theta }\mid \mathit{\varphi })p(\mathit{\varphi })}{p(\mathit{\theta },\mathit{\varphi }\mid \mathit{D},t_{j-1})}p(\mathit{\theta },\mathit{\varphi }\mid \mathit{D},t_{j-1})d\mathit{\theta }d\mathit{\varphi }} \\ =\frac{{\mathbf{E}}_{\mathit{\theta },\mathit{\varphi }\mid \mathit{D},t_{j-1}}\left[\frac{p{(\mathit{D}\mid \mathit{\theta })}^{t_j}p(\mathit{\theta }\mid \mathit{\varphi })p(\mathit{\varphi })}{p(\mathit{\theta },\mathit{\varphi }\mid \mathit{D},t_{j-1})}\right]}{{\mathbf{E}}_{\mathit{\theta },\mathit{\varphi }\mid \mathit{D},t_{j-1}}\left[\frac{p(\mathit{\theta }\mid \mathit{\varphi })p(\mathit{\varphi })}{p(\mathit{\theta },\mathit{\varphi }\mid \mathit{D},t_{j-1})}\right]}. \end{gathered}$$ (73)

The numerator and denominator are then approximated by the following averages:

$$\begin{gathered} \frac{{\mathbf{E}}_{\mathit{\theta },\mathit{\varphi }\mid \mathit{D},t_{j-1}}\left[\frac{p{(\mathit{D}\mid \mathit{\theta })}^{t_j}p(\mathit{\theta }\mid \mathit{\varphi })p(\mathit{\varphi })}{p(\mathit{\theta },\mathit{\varphi }\mid \mathit{D},t_{j-1})}\right]}{{\mathbf{E}}_{\mathit{\theta },\mathit{\varphi }\mid \mathit{D},t_{j-1}}\left[\frac{p(\mathit{\theta }\mid \mathit{\varphi })p(\mathit{\varphi })}{p(\mathit{\theta },\mathit{\varphi }\mid \mathit{D},t_{j-1})}\right]} \\ \approx \frac{\frac{1}{n}\sum _{i=1}^n\frac{p{\left(\mathit{D}\mid {\mathit{\theta }}_{i,j-1}\right)}^{t_j}p({\mathit{\theta }}_{i,j-1}\mid {\mathit{\varphi }}_{i,j-1})p({\mathit{\varphi }}_{i,j-1})}{p{(\mathit{D}\mid {\mathit{\theta }}_{i,j-1})}^{t_{j-1}}p\left({\mathit{\theta }}_{i,j-1}\mid {\mathit{\varphi }}_{i,j-1}\right)p({\mathit{\varphi }}_{i,j-1})}p(\mathit{D}\mid t_{j-1})}{\frac{1}{n}\sum _{i=1}^n\frac{p({\mathit{\theta }}_{i,j-1}\mid {\mathit{\varphi }}_{i,j-1})p({\mathit{\varphi }}_{i,j-1})}{{(\mathit{D}\mid {\mathit{\theta }}_{i,j-1})}^{t_{j-1}}p\left({\mathit{\theta }}_{i,j-1}\mid {\mathit{\varphi }}_{i,j-1}\right)p({\mathit{\varphi }}_{i,j-1})}p(\mathit{D}\mid t_{j-1})}. \end{gathered}$$ (74)

After simplifying:

$$p(\mathit{D}\mid t_j)\approx \frac{1}{n}\sum _{i=1}^n\frac{p{(\mathit{D}\mid {\mathit{\theta }}_{i,j-1})}^{t_j}}{p{(\mathit{D}\mid {\mathit{\theta }}_{i,j-1})}^{t_{j-1}}}{\left[\frac{1}{n}\sum _{i=1}^n\frac{1}{p{(\mathit{D}\mid {\mathit{\theta }}_{i,j-1})}^{t_{j-1}}}\right]}^{-1},$$ (75)

where (θ_i, ϕ_i)~p(θ, ϕ∣D, t_j–1). The derivation for p(D∣t_j–1) is similar. These are then substituted into the SS identity (Equation 75). Thus, all that is necessary for hierarchical SS is to sample from the joint posterior and use the subject-level samples to compute the mean likelihood at each temperature.

Example

We fit 4 different hierarchical models to a dataset of 10 simulated subjects, with 2 experimental conditions, and 300 trials per condition. One of the interesting properties of Bayes factors is that they allow one to find evidence for the null in way that traditional approaches to model selection cannot. To this end, a data set was simulated with no difference in parameters over conditions. We used two models that are commonly of theoretical interest: one model that assumed different drift rates for each condition, and one model that assumed different thresholds for each condition. In addition, we used a simple model, one with no parameters varying over conditions, and a complex model, with drift rate, threshold, and non-decision time all varying over conditions. These simple and complex models can be considered the hierarchical counterparts to the simple and complex single-subject models described previously. The drift-rate model and the threshold-model are both special cases of the complex model; the simple model is a special case of all models. The full mathematical description of the models can be found in Appendix B. We fit the models to each of the dataset using 3 different rung values (10, 20, or 35) for 10 independent replications⁵. We note again that given the large number of samples that the brute-force method required to give a stable estimate of the marginal likelihood in the single-subject model with 9 parameters, we do not believe that it would be computationally feasible to obtain a marginal likelihood estimate for hierarchical models, which all contain between 72 and 108 parameters, using this method.

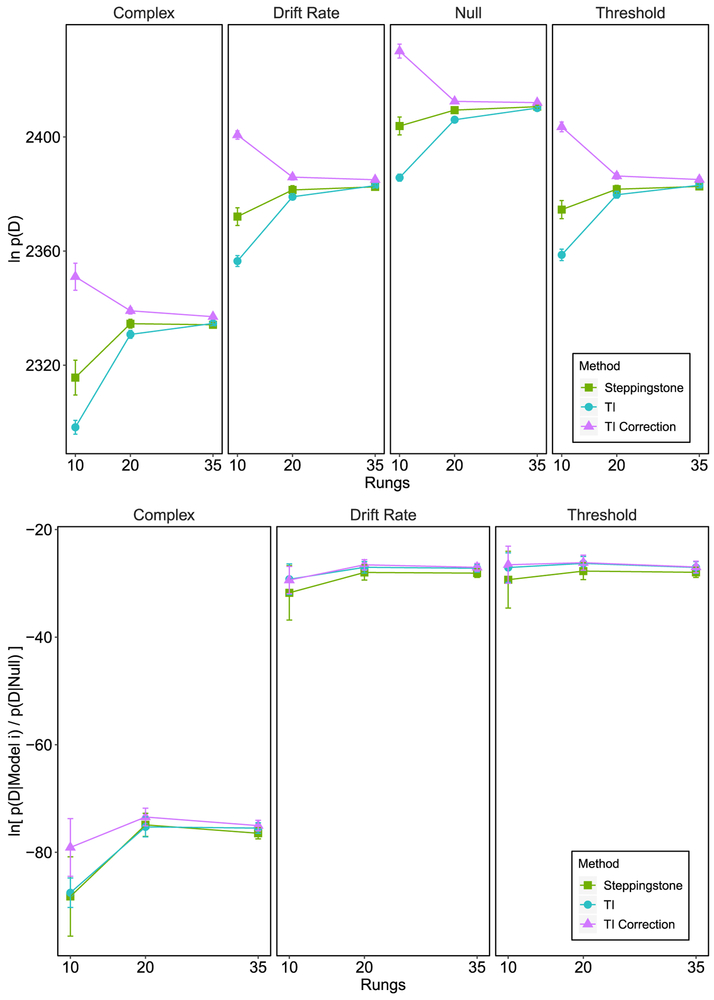
The resulting marginal likelihoods produced by fitting each model on the simulated dataset for each method is plotted in the top panels of Figure 6. For the SS and TI methods across all rungs, the marginal likelihood is highest for the null model and penalizes the complex model more so than the models with a single parameter varying across conditions. The SS estimator appears to become stable with a lower number of rungs than either ordinary TI or corrected TI. Both TI methods become stable between 20 and 35 rungs. The estimated variance of the individual SS and TI estimates (Equation 53 and 37, respectively) were very low, ranging from .01 to 1.03 for SS and from .003 to .03 for TI. The bottom panel of Figure 6 plots the evidence against the complex, drift rate, and threshold models in terms of the log Bayes factor. SS and TI all decisively provide evidence against each of the models across all rungs. Unlike the raw marginal likelihoods, the Bayes factor appears to become stable at lower rung numbers for SS and TI. This suggests that although the marginal likelihoods were not stable at lower rung numbers, their ratios changed at a fairly constant rate across rungs.

Figure 6.

The top panel plots the marginal likelihood obtained for each model under the different methods given a null data set. The bottom panel plots the Bayes factor in terms of the null model across temperature rungs and methods. Negative Bayes factors represent evidence against the corresponding model when compared to the null model. All error bars represent standard deviations.

Next, we fit each of the models to a simulated dataset in which drift rate varied across conditions. The top panel of Figure 7 plots the marginal likelihood under each model. For SS and TI, the marginal likelihood for the drift rate model is the highest⁶. The complex model marginal likelihood was relatively high compared to the threshold and null models. This was most likely due to the complex model containing a drift rate that varies across conditions. Stable estimates were achieved between 10 and 20 rungs for all methods. The estimated variance of the individual SS and TI estimates (Equation 53 and 37, respectively) were very low, ranging from .004 to 1.39 for SS and from .003 to .03 for TI. The evidence against each model when compared to the drift rate model is plotted in terms of the log Bayes factor in the bottom panels of Figure 7. SS and TI both attained stable and decisive Bayes factors at 10 rungs. Note, that we do not know whether the Bayes factors stabilized at the correct value as we have no ground truth. Our conclusions are only based on the fact that we know which model generated the data and can reasonably expect that model to have the highest Bayes factor compared to other models.

Figure 7.

The top panel plots the marginal likelihood obtained for each model under the different methods given a data set in which drift rate varied across conditions. The bottom panel plots the Bayes factor in terms of the drift rate model across temperature rungs and methods. Negative Bayes factors represent evidence against the corresponding model when compared to the drift rate model. All error bars represent standard deviations.

Application to Empirical Data

Lastly, we applied the methods to the empirical data set of Rae, Heathcote, Donkin, Averell, and Brown (2014), which was also used by Evans and Brown (2017) to test their GPU brute-force method. Empirical data can be more prone to noise than standard simulated data, which may negatively impact our ability to obtain a consistent estimate of the marginal likelihood within a reasonable number of samples. Indeed, Evans and Brown found that when applying their method to this data set, the estimated marginal likelihoods became extremely variable, to the point where the variance in the estimates were higher than the resulting Bayes factor, making any inferences extremely questionable. We aim to see whether the methods will have similar problems of large increases in variability when applied to empirical data, or whether our estimates will remain relatively stable. For brevity, we keep this section purely focused on the conclusions of the method (i.e., which model the Bayes factors favor), and the consistency in the estimates across multiple independent sampling runs.

Rae et al. (2014) presented participants with a perceptual discrimination task containing conditions that either emphasized speed or accuracy. Rae et al. were interested in whether the emphasis on response caution in the accuracy condition would result in changes to response threshold only or to changes in response threshold and drift rate. Rae et al. found decreases in response caution, as well as the difference between correct and error drift rates (i.e., a decrease in the quality of incoming evidence) in the speed condition compared to the accuracy condition.

We fit the same two models as those described in Evans and Brown to the Rae et al. data, a threshold-only model and a drift rate + threshold model, as well as two additional models, a simple model in which no parameters vary over conditions (equivalent to the simple hierarchical model described in the previous section) and a drift-rate-only model (equivalent to the hierarchical drift rate model described in the previous section). We used 7 cores each running 5 temperature rungs for a total 35 temperature rungs for 10 independent replications (except for the drift + threshold model in which one of the replications was removed from the analysis due to a stuck chain). We used the same DE-MCMC sampling and burn-in scheme outlined in the previous section (see footnote 3).

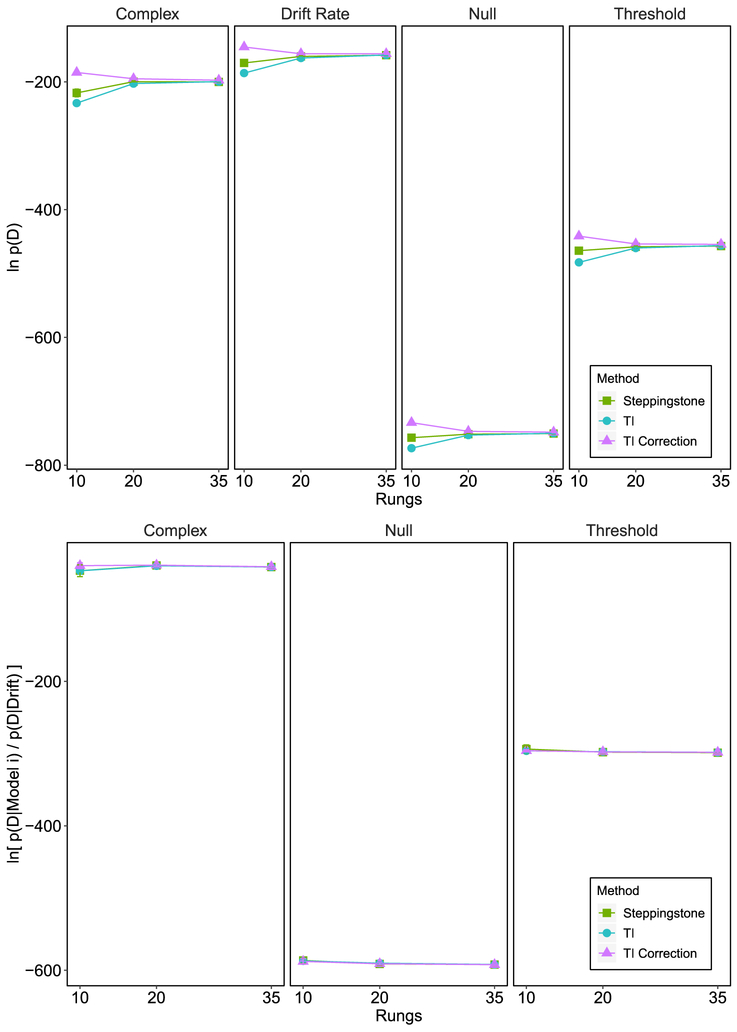
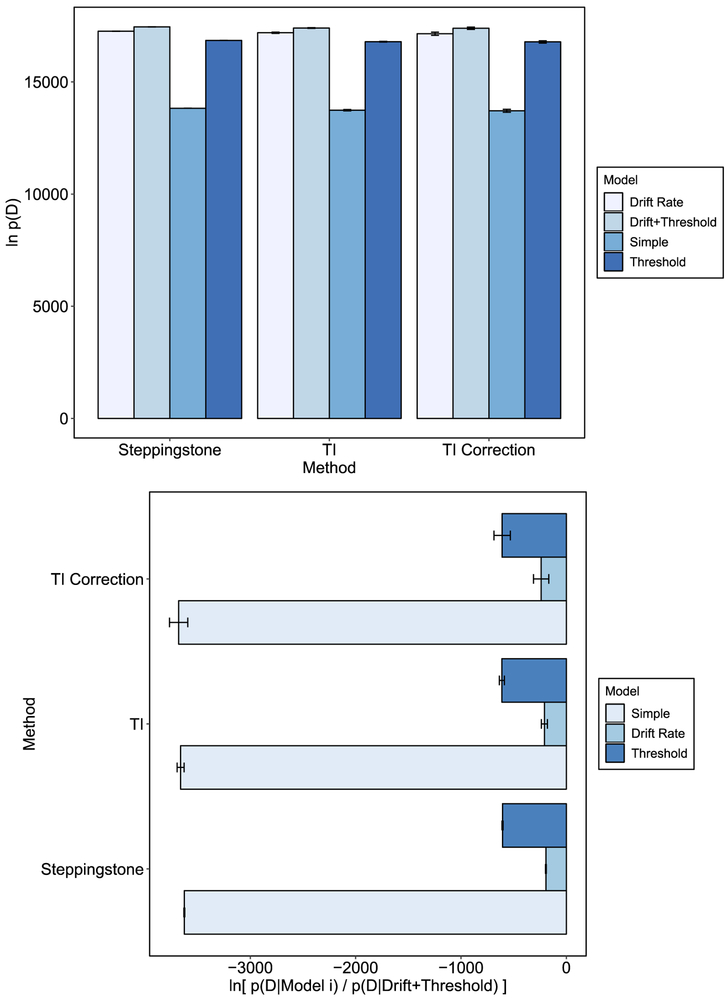
The marginal likelihood under each model is plotted in Figure 8 as a function of the method used. SS and TI are in agreement. All of the methods yielded the same rank ordering of the models in which the drift + threshold model had the highest marginal likelihood. For the TI correction method there was more variability in the estimates than was the case for the standard TI method. We believe the increased variance in the TI correction method was due to it being more sensitive to the convergence of the chains than other methods. For a given power posterior, if a chain or a group of chains converge more slowly than other chains or become stuck, the change in log-likelihood variance between the current power posterior and the next power posterior might be very large. According to Equation 39, if this change is errantly large, it will lead to an overcorrection of the trapezoidal rule. Indeed, we found this to be the case for one of the replications of the drift + threshold model (removed from the current analysis and replaced). The other methods, that only rely on the mean log-likelihoods show much less sensitivity to convergence. Therefore, we recommend careful examination of convergence when using the TI correction method, possibly running longer MCMC chains in order to ensure convergence. This issue is likely to be specific to our DE-MCMC sampling method in which dozens of chains are used and must all appropriately converge. There are variants of DE-MCMC that ensure better convergence, such as migration (e.g., Turner et al., 2013), but we chose to use a standard DE-MCMC sampler for simplicity and generalizability. For MCMC methods that use fewer chains and converge appropriately, this might be less of an issue.

Figure 8.

The top panel plots the marginal likelihood for each model under the different methods given the Rae et al. data set. The bottom panel plots the Bayes factor obtained for each method and model. Negative evidence represent evidence against the corresponding model when compared to the drift rate + threshold model. All error bars represent standard deviations.

The bottom panel of Figure 8 shows the evidence against all the other models in terms of the drift + threshold model. The log Bayes factor gives decisive evidence against all the simpler models across all methods. Thus, our results are consistent with those of Rae et al. who concluded that a response caution emphasis produces changes in threshold as well as drift rate. Our results are also more conclusive than those of Evans and Brown, whose GPU method yielded relatively noisy estimates compared to the ones here, produced by TI and SS. Our results also produced marginal likelihoods that were far larger than those produced by the GPU. Given that all methods converged on similar marginal likelihoods, this might suggest the GPU method as implemented by Evans and Brown method may suffer from underestimation of the marginal likelihood, due to the vast number of samples required for an accurate estimate of the arithmetic mean within hierarchical models.

General Discussion

The ability to appropriately select between competing cognitive models is important for theory development. At the heart of any good model selection procedure is the proper balance between goodness-of-fit and model complexity. The Bayes factor is one well-principled and agreed upon method of performing model selection. In order to compute the Bayes factor, it is often necessary to obtain the marginal likelihood for each model, a quantity that marginalizes – integrates – over the entire parameter space.

One of the simplest approaches is the grid approach (Lee, 2004; Vanpaemel & Storms, 2010). It is one of the easiest methods for beginners to implement, allows easy comparisons of sets of nested or non-nested models, and does not require the use of MCMC. However, the grid approach is computationally intractable for all but the most simplest possible models. See Table 1 for a summary comparison of practical considerations for many different techniques.

Recent methodological advancements, as well as the increasing availability of powerful computing platforms, have led to efficient methods for estimating the marginal likelihood using Monte Carlo techniques. Monte Carlo techniques for integration take advantage of representing the marginal likelihood integral as an expected value and then approximating that expected value via sampling procedures (random number generation). One of the simplest, and widely known, Monte Carlo estimators is the arithmetic mean estimator (see Table 1). The method does not require MCMC; an estimate of the marginal likelihood can be obtained by sampling from the prior distribution and computing the average likelihood over those samples, making the approach easy for beginners. In order to compare nested or non-nested models, the method can be run for each model independently. A limitation of this technique is that the likelihood is highly peaked relative to the prior and therefore extremely small likelihoods tend to dominate, resulting in an underestimation of the marginal likelihood if there is an insufficient sample size. Even for relatively simple models, hundreds of millions of samples are often needed for accurate estimates. Obtaining this many samples sizes for even the simplest model can take days to obtain using standard CPU hardware. Evans and Brown took advantage of the massively parallel computing power of GPU’s to reduce the sampling time from days to minutes or hours. But for more complex models, especially hierarchical models, even the speedup from using GPU’s cannot overcome the inherent limitations with the arithmetic mean approach. Additionally, the GPU approach has the potential to be technically challenging, making it less accessible to many beginner users.

Methods that scale well with dimensionality of the model and have been used widely in psychology include the Savage-Dickey method (Wagenmakers et al., 2010), the product space method (Lodewyckx et al., 2011), and bridge sampling (Gronau, Sarafoglou, et al., 2017) (see Table 1). The commonly used Savage-Dickey ratio provides a relatively simple method of estimating Bayes factors and is easy for beginners to implement. In addition, it only requires a single MCMC run to collect posterior samples. The major drawback is that it is limited to comparisons between nested models. The product space method, which can been used to compare non-nested models, suffers from being difficult to implement effectively, especially for beginners (requiring methodological “tricks”), and is difficult to compare many models (often only two models are compared). It is also not uncommon for very long MCMC runs to be required for convergence. Bridge sampling has been implemented within an R package (Gronau, Singmann, et al., 2017) making it easy to use for beginners to use. It is also possible to compare many nested and non-nested models by simply running the method separately for each model. While bridge sampling only requires samples from the posterior from a single MCMC run, the accuracy of the marginal likelihood estimate is dependent on an accurate representation of the joint posterior distribution, which implies a large number of posterior samples are often required.

Our article provides a tutorial overview of two relatively recent techniques for estimating the marginal likelihood: thermodynamic integration (TI; Friel & Pettitt, 2008; Lartillot & Philippe, 2006) and steppingstone sampling (SS; Xie et al., 2011); see Table 1 for their comparison to other methods. Like the arithmetic mean approach, both are Monte Carlo techniques. Both rely on sampling from posteriors whose likelihood is raised to different powers, or temperature rungs, ranging from 0 to 1. Because of the minimal amount of additional coding necessary, TI and SS should be easy for a beginner to implement who has existing code. After sampling from the posteriors under different temperatures, the TI estimate or the SS estimate can be computed using these samples. In TI, the mean likelihood under each power posterior form points along a curve, and the area under that curve is estimated using ordinary numerical integration. SS combines the ideas of importance sampling and power posteriors. For both methods, as the number of rungs increases, the estimates converge to the marginal likelihood. The distribution of the temperature rungs is an important choice for efficient estimation of the marginal likelihood; distributions that place more temperature rungs closer to 0 tend to produce better estimates (Friel et al., 2014; Xie et al., 2011).

Potential users of TI and SS should note that these techniques are not without certain disadvantages. Table 1 notes that a computational drawback of using TI and SS is their reliance on collecting samples from posteriors raised to many different powers; this aspect of TI and SS is unlike other approaches such as bridge sampling (Gronau, Sarafoglou, et al., 2017), Chib’s method (Chib, 1995), or the product space method (Lodewyckx et al., 2011). In the present work, we found that with our particular dataset and models, we needed approximately 20-35 power posteriors to obtain stable estimates of the marginal likelihood. For some models, such as those that might take days or weeks to estimate a single posterior, TI and SS might be impractical given that dozens of power posteriors are needed (unless parallel hardware is available). Whether TI and SS will be feasible for a particular model and a particular dataset will need to be evaluated on a case-by-case basis.

Another disadvantage of TI and SS is that they rely on the user to choose the number of temperature rungs and the temperature schedule, which might introduce additional complexity for the beginner. Although temperature schedules that moderately skew the rungs near the prior have been shown to work well and 20-35 rungs worked well for our particular models, these hyperparameters should be selected with care by the user and may require some pilot work to determine. This is in contrast to other techniques, such as bridge sampling, Chib’s method, or the product space method, that operate more like black boxes. So TI and SS should also not be viewed as the only solution to computing Bayes factors. There are myriad techniques that might be more or less suitable to the user’s particular domain. For excellent broad reviews of techniques to compute marginal likelihoods see Friel and Wyse (2012) and Liu et al. (2016).

While it is important to not conflate logical consistency with automaticity when using TI and SS, it is just as important to not conflate these concepts when using Bayesian model selection in general. Priors matter, especially in Bayesian model selection (e.g., Gershman, 2016; Kass & Raftery, 1995; C. C. Liu & Aitkin, 2008; Vanpaemel, 2010, 2011; Vanpaemel & Lee, 2012) and both TI and SS are sensitive to the prior, unlike other techniques such as the harmonic mean (Xie et al., 2011). Therefore, it is the researcher’s responsibility to define appropriate priors when performing Bayesian model selection (see Lee & Vanpaemel, 2017 for a practical discussion). This is in contrast to posterior estimation where the priors matter less in the case of large datasets. Just as the priors on the model parameters influence the Bayes factor, priors on the models themselves, p(M), influence the posterior probability of the model and must also be carefully specified if the posterior probability of the model is desired.

Here, we used the Linear Ballistic Accumulator (LBA; Brown & Heathcote, 2008) model of choice response time to illustrate TI and SS techniques, performing many of the same comparisons used by Evans and Brown using the GPU method. Although TI and SS contain robust mathematical properties that should lead to proper estimation of the posterior distribution, this accurate approximation is also dependent upon how successful the method of sampling is at estimating the posterior distribution. We compared their estimated marginal likelihood values to those obtained by Evans and Brown in the case of a simple 6 parameter LBA model. In this case, Evans and Brown were able to sample until they reached the asymptote of an marginal likelihood approximation (practically no variance), suggesting that this was an accurate estimate of the marginal likelihood. Crucially, we found that both TI and SS converged to these same marginal likelihood values. Note, this does not validate the methods because there is no ground truth and we have merely compared TI and SS to another estimation method.

We provided an explicit formalization of these methods within a hierarchical framework. Hierarchical models have recently become quite popular within cognitive modelling, as they provide the benefits of group-level inference and constraint, while still estimating separate parameters for each individual participant. Although the methods were originally derived to apply to any Bayesian model, we specifically derived each method for hierarchical models by explicitly assuming group-level and subject-level priors. For the methods to work under hierarchical models, it is necessary to obtain joint posterior samples from the hierarchical model and then to use the subject-level samples to compute the likelihoods for each method. Importantly, this extension allows Bayes factors to be calculated that compare different models of the population effects, rather than only assessing these effects within individual subjects.

• We provide a tutorial on estimating marginal likelihoods through thermodynamic integration and steppingstone sampling

• For each method we provide a conceptual explanation, the mathematical details, and a description of how to implement them

• We use the Linear Ballistic Accumulator as a running example to illustrate how to apply the method, and to display the accuracy of the method in complex psychological models

• We extend the methods to hierarchical models, and apply them to empirical data from the rapid decision-making literature

Appendix A

The steppingstone estimator writes the marginal likelihood as a product of ratios of marginal likelihoods at adjacent temperatures:

$$p(\mathit{D})=\frac{p(\mathit{D}\mid t=1)}{p(\mathit{D}\mid t=0)}$$ (A1)

$$=\frac{p(\mathit{D}\mid t_K)}{p(\mathit{D}\mid t_{K-1})}\frac{p(\mathit{D}\mid t_{K-1})}{p(\mathit{D}\mid t_{K-2})}\dots \frac{p(\mathit{D}\mid t_{K-(K-2)})}{p(\mathit{D}\mid t_{K-(K-1)})}\frac{p(\mathit{D}\mid t_1)}{p(\mathit{D}\mid t_0)}$$ (A2)

$$=\prod _{j=1}^K\frac{p(\mathit{D}\mid t_j)}{p(\mathit{D}\mid t_{j-1})}.$$ (A3)

The marginal likelihood at temperature t_j is estimated via importance sampling using the posterior at temperature t_j–1 as the importance distribution:

$$p(\mathit{D}\mid t_j)=\frac{\int \frac{p{(\mathit{D}\mid \mathit{\theta })}^{t_j}p(\mathit{\theta })}{p(\mathit{\theta }\mid \mathit{D},t_{j-1})}p(\mathit{\theta }\mid \mathit{D},t_{j-1})d\mathit{\theta }}{\int \frac{p(\mathit{\theta })}{p(\mathit{\theta }\mid \mathit{D},t_{j-1})}p(\mathit{\theta }\mid \mathit{D},t_{j-1})d\mathit{\theta }}.$$ (A4)

This can then be represented in terms of expected values:

$$\frac{\int \frac{p{(\mathit{D}\mid \mathit{\theta })}^{t_j}p(\mathit{\theta })}{p(\mathit{\theta }\mid \mathit{D},t_{j-1})}p(\mathit{\theta }\mid \mathit{D},t_{j-1})d\mathit{\theta }}{\int \frac{p(\mathit{\theta })}{p(\mathit{\theta }\mid \mathit{D},t_{j-1})}p(\mathit{\theta }\mid \mathit{D},t_{j-1})d\mathit{\theta }}=\frac{{\mathbf{E}}_{\mathit{\theta }\mid \mathit{D},t_{j-1}}\left[\frac{p{(\mathit{D}\mid \mathit{\theta })}^{t_j}p(\mathit{\theta })}{p(\mathit{\theta }\mid \mathit{D},t_{j-1})}\right]}{{\mathbf{E}}_{\mathit{\theta }\mid \mathit{D},t_{j-1}}\left[\frac{p(\mathit{\theta })}{p(\mathit{\theta }\mid \mathit{D},t_{j-1})}\right]}.$$ (A5)

The expected values are approximated by averages:

$$\frac{{\mathbf{E}}_{\mathit{\theta }\mid \mathit{D},t_{j-1}}\left[\frac{p{(\mathit{D}\mid \mathit{\theta })}^{t_j}p(\mathit{\theta })}{p(\mathit{\theta }\mid \mathit{D},t_{j-1})}\right]}{{\mathbf{E}}_{\mathit{\theta }\mid \mathit{D},t_{j-1}}\left[\frac{p(\mathit{\theta })}{p(\mathit{\theta }\mid \mathit{D},t_{j-1})}\right]}\approx \frac{\frac{1}{n}\sum _{i=1}^n\frac{p{(\mathit{D}\mid {\mathit{\theta }}_{i,j-1})}^{t_j}p({\mathit{\theta }}_{i,j-1})p(\mathit{D}\mid t_{j-1})}{p{(\mathit{D}\mid {\mathit{\theta }}_{i,j-1})}^{t_{j-1}}p({\mathit{\theta }}_{i,j-1})}}{\frac{1}{n}\sum _{i=1}^n\frac{p({\mathit{\theta }}_{i,j-1})p(\mathit{D}\mid t_{j-1})}{p{(\mathit{D}\mid {\mathit{\theta }}_{i,j-1})}^{t_{j-1}}p({\mathit{\theta }}_{i,j-1})}}.$$ (A6)

After canceling like terms and simplifying, we have the following estimator of p(θ∣t_j):

$$\frac{\frac{1}{n}\sum _{i=1}^n\frac{p{\left(\mathit{D}\mid {\mathit{\theta }}_{i,j-1}\right)}^{t_j}p({\mathit{\theta }}_{\mathit{i},j-1})p(\mathit{D}\mid t_{j-1})}{{p(\mathit{D}\mid {\mathit{\theta }}_{i,j-1})}^{t_{j-1}}p\left({\mathit{\theta }}_{i,j-1}\right)}}{\frac{1}{n}\sum _{i=1}^n\frac{p({\mathit{\theta }}_{\mathit{i},j-1})p(\mathit{D}\mid t_{j-1})}{p{(\mathit{D}\mid {\mathit{\theta }}_{i,j-1})}^{t_{j-1}}p({\mathit{\theta }}_{i,j-1})}}=\frac{p\left(\mathit{D}\mid t_{j-1}\right)\frac{1}{n}\sum _{i=1}^n\frac{p{(\mathit{D}\mid {\mathit{\theta }}_{i,j-1})}^{t_j}}{p{(\mathit{D}\mid {\mathit{\theta }}_{i,j-1})}^{t_{j-1}}}}{p\left(\mathit{D}\mid t_{j-1}\right)\frac{1}{n}\sum _{i=1}^n\frac{1}{p{(\mathit{D}\mid {\mathit{\theta }}_{i,j-1})}^{t_{j-1}}}}.$$ (A7)

$$=\frac{\frac{1}{n}\sum _{i=1}^n\frac{p{(\mathit{D}\mid {\mathit{\theta }}_{i,j-1})}^{t_j}}{p{(\mathit{D}\mid {\mathit{\theta }}_{i,j-1})}^{t_{j-1}}}}{\frac{1}{n}\sum _{i=1}^n\frac{1}{p{(\mathit{D}\mid {\mathit{\theta }}_{i,j-1})}^{t_{j-1}}}},$$ (A8)

where θ_j–1,i~p(θ∣D, t_j–1).

The marginal likelihood at temperature t_j–1 is also estimated via importance sampling with the importance distribution also set to the posterior at temperature t_j–1:

$$p(\mathit{D}\mid t_{j-1})=\frac{\int \frac{p{(\mathit{D}\mid \mathit{\theta })}^{t_{j-1}}p(\mathit{\theta })}{p(\mathit{\theta }\mid \mathit{D},t_{j-1})}p(\mathit{\theta }\mid \mathit{D},t_{j-1})d\mathit{\theta }}{\int \frac{p(\mathit{\theta })}{p(\mathit{\theta }\mid \mathit{D},t_{j-1})}p(\mathit{\theta }\mid \mathit{D},t_{j-1})d\mathit{\theta }}.$$ (A9)

We can represent this in terms of expected values:

$$\frac{\int \frac{p{(\mathit{D}\mid \mathit{\theta })}^{t_{j-1}}p(\mathit{\theta })}{p(\mathit{\theta }\mid \mathit{D},t_{j-1})}p(\mathit{\theta }\mid \mathit{D},t_{j-1})d\mathit{\theta }}{\int \frac{p(\mathit{\theta })}{p(\mathit{\theta }\mid \mathit{D},t_{j-1})}p(\mathit{\theta }\mid \mathit{D},t_{j-1})d\mathit{\theta }}=\frac{{\mathbf{E}}_{\mathit{\theta }\mid \mathit{D},t_{j-1}}\left[\frac{p{(\mathit{D}\mid \mathit{\theta })}^{t_{j-1}}p(\mathit{\theta })}{p(\mathit{\theta }\mid \mathit{D},t_{j-1})}\right]}{{\mathbf{E}}_{\mathit{\theta }\mid \mathit{D},t_{j-1}}\left[\frac{p(\mathit{\theta })}{p(\mathit{\theta }\mid \mathit{D},t_{j-1})}\right]}.$$ (A10)

The expected values are approximated by averages:

$$\frac{{\mathbf{E}}_{\mathit{\theta }\mid \mathit{D},t_{j-1}}\left[\frac{p{(\mathit{D}\mid \mathit{\theta })}^{t_{j-1}}p(\mathit{\theta })}{p(\mathit{\theta }\mid \mathit{D},t_{j-1})}\right]}{{\mathbf{E}}_{\mathit{\theta }\mid \mathit{D},t_{j-1}}\left[\frac{p(\mathit{\theta })}{p(\mathit{\theta }\mid \mathit{D},t_{j-1})}\right]}\approx \frac{\frac{1}{n}\sum _{i=1}^n\frac{p{\left(\mathit{D}\mid {\mathit{\theta }}_{i,j-1}\right)}^{t_{j-1}}p({\mathit{\theta }}_{\mathit{i},j-1})p(\mathit{D}\mid t_{j-1})}{p{(\mathit{D}\mid {\mathit{\theta }}_{i,j-1})}^{t_{j-1}}p({\mathit{\theta }}_{i,j-1})}}{\frac{1}{n}\sum _{i=1}^n\frac{p({\mathit{\theta }}_{\mathit{i},j-1})p(\mathit{D}\mid t_{j-1})}{p{(\mathit{D}\mid {\mathit{\theta }}_{i,j-1})}^{t_{j-1}}p({\mathit{\theta }}_{i,j-1})}}.$$ (A11)

After canceling like terms and simplifying we have the following estimator of p(D∣t_j–1):

$$\frac{\frac{1}{n}\sum _{i=1}^n\frac{p{\left(\mathit{D}\mid {\mathit{\theta }}_{i,j-1}\right)}^{t_{j-1}}p({\mathit{\theta }}_{\mathit{i},j-1})p(\mathit{D}\mid t_{j-1})}{p{(\mathit{D}\mid {\mathit{\theta }}_{\mathit{i},j-1})}^{t_{j-1}}p({\mathit{\theta }}_{i,j-1})}}{\frac{1}{n}\sum _{i=1}^n\frac{p({\mathit{\theta }}_{\mathit{i},j-1})p(\mathit{D}\mid t_{j-1})}{p{(\mathit{D}\mid {\mathit{\theta }}_{i,j-1})}^{t_{j-1}}p({\mathit{\theta }}_{i,j-1})}}=\frac{\frac{1}{n}\sum _{i=1}^{n}p(\mathit{D}\mid t_{j-1})}{p(\mathit{D}\mid t_{j-1})\frac{1}{n}\sum _{i=1}^n\frac{1}{p{(\mathit{D}\mid {\mathit{\theta }}_{i,j-1})}^{t_{j-1}}}}$$ (A12)

$$=\frac{\frac{1}{n}\mathit{np}(\mathit{D}\mid t_{j-1})}{p(\mathit{D}\mid t_{j-1})\frac{1}{n}\sum _{i=1}^n\frac{1}{p{(\mathit{D}\mid {\mathit{\theta }}_{i,j-1})}^{t_{j-1}}}}$$ (A13)

$$=\frac{1}{\frac{1}{n}\sum _{i=1}^n\frac{1}{p{(\mathit{D}\mid {\mathit{\theta }}_{i,j-1})}^{t_{j-1}}}}.$$ (A14)

where θ_j–1,i~p(θ∣D, t_j–1). Substituting and p(D∣t_j) into Equation A9 we have the steppingstone estimator:

$$p(\mathit{D})=\prod _{j=1}^K\frac{p(\mathit{D}\mid t_{\mathit{j}})}{p(\mathit{D}\mid t_{\mathit{j}-1})}$$ (A15)

$$\approx \prod _{j=1}^K\left[\frac{\frac{1}{n}\sum _{i=1}^n\frac{p{(\mathit{D}\mid {\mathit{\theta }}_{i,j-1})}^{t_j}}{p{(\mathit{D}\mid {\mathit{\theta }}_{i,j-1})}^{t_{j-1}}}}{\frac{1}{n}\sum _{i=1}^n\frac{1}{p{(\mathit{D}\mid {\mathit{\theta }}_{i,j-1})}^{t_{j-1}}}}{\left[\frac{1}{\frac{1}{n}\sum _{i=1}^n\frac{1}{p{(\mathit{D}\mid {\mathit{\theta }}_{i,j-1})}^{t_{j-1}}}}\right]}^{-1}\right]$$ (A16)

$$\approx \prod _{j=1}^K\frac{1}{n}\sum _{i=1}^n\frac{p{(\mathit{D}\mid {\mathit{\theta }}_{i,j-1})}^{t_j}}{p{(\mathit{D}\mid {\mathit{\theta }}_{i,j-1})}^{t_{j-1}}}.$$ (A17)

Appendix B

In this appendix, we describe additional mathematical/simulation details of the hierarchical models used to test TI and SS. When testing TI and SS with simulated data sets, we used a total of 4 models, referred to as Simple, Complex, Drift Rate, and Threshold. All models assume choice response times are distributed according to the LBA. We fixed the standard deviation corresponding to the accumulator for correct responses to 1. For each model, the likelihood of the vector of choice response times for subject i in condition j, RT_i,j, is given below:

$$\begin{gathered} \text{Simple}:{\mathit{RT}}_{i,j}\sim \mathit{LBA}(A_i,k_i,{\tau }_i,v_i^c,v_i^e,s_i^e,s_i^c) \\ \text{Complex}:{\mathit{RT}}_{i,j}\sim \mathit{LBA}(A_i,k_{i,j},{\tau }_{i,j},v_{i,j}^c,v_i^e,s_i^e,s_i^c). \\ \text{Drift Rate}:{\mathit{RT}}_{i,j}\sim \mathit{LBA}(A_i,k_i,{\tau }_i,v_{i,j}^c,v_i^e,s_i^e,s_i^c) \\ \text{Threshold}:{\mathit{RT}}_{i,j}\sim \mathit{LBA}(A_i,k_{i,j},{\tau }_i,v_i^c,v_i^e,s_i^e,s_i^c) \end{gathered}$$

The priors on subject-level parameters for the Simple model are provided below with all truncated normal distributions having a lower bound of 0 and an upper bound of ∞:

$$\begin{gathered} A_i\sim \mathit{TN}({\mu }^A,{\sigma }^A) \\ {k}_i\sim \mathit{TN}({\mu }^k,{\sigma }^k) \\ {\tau }_i\sim \mathit{TN}({\mu }_{\tau },{\sigma }_{\tau }) \\ {v}_i^c\sim \mathit{TN}({\mu }_{v_c},{\sigma }_{v_c}) \\ {v}_i^e\sim \mathit{TN}({\mu }^{v_e},{\sigma }^{v_e}) \\ {s}_i^e\sim \mathit{TN}({\mu }^{s_e},{\sigma }^{s_e}). \end{gathered}$$

The priors on subject-level parameters for the Complex model are:

$$\begin{gathered} A_i\sim \mathit{TN}({\mu }^A,{\sigma }^A) \\ {k}_{i,j}\sim \mathit{TN}({\mu }_j^k,{\sigma }_j^k) \\ {\tau }_{i,j}\sim \mathit{TN}({\mu }_j^{\tau },{\sigma }_j^{\tau }) \\ {v}_{i,j}^c\sim \mathit{TN}({\mu }_j^{v_c},{\sigma }_j^{v_c}) \\ {v}_i^e\sim \mathit{TN}({\mu }^{v_e},{\sigma }^{v_e}) \\ {s}_i^e\sim \mathit{TN}({\mu }^{s_e},{\sigma }^{s_e}). \end{gathered}$$

The priors on subject-level parameters for the Drift Rate model are:

$$\begin{gathered} A_i\sim \mathit{TN}({\mu }^A,{\sigma }^A) \\ {k}_i\sim \mathit{TN}({\mu }^k,{\sigma }^k) \\ {\tau }_i\sim \mathit{TN}({\mu }^{\tau },{\sigma }^{\tau }) \\ {v}_{i,j}^c\sim \mathit{TN}({\mu }_j^{v_c},{\sigma }_j^{v_c}) \\ {v}_i^e\sim \mathit{TN}({\mu }^{v_e},{\sigma }^{v_e}) \\ {s}_i^e\sim \mathit{TN}({\mu }^{s_e},{\sigma }^{s_e}). \end{gathered}$$

The priors on subject-level parameters for the Threshold model are:

$$\begin{gathered} A_i\sim \mathit{TN}({\mu }^A,{\sigma }^A) \\ {k}_{i,j}\sim \mathit{TN}({\mu }_j^k,{\sigma }_j^k) \\ {\tau }_i\sim \mathit{TN}({\mu }^{\tau },{\sigma }^{\tau }) \\ {v}_i^c\sim \mathit{TN}({\mu }^{v_c},{\sigma }^{v_c}) \\ {v}_i^e\sim \mathit{TN}({\mu }^{v_e},{\sigma }^{v_e}) \\ {s}_i^e\sim \mathit{TN}({\mu }^{s_e},{\sigma }^{s_e}). \end{gathered}$$

The priors on group-level parameters were the same across models and conditions:

$$\begin{gathered} {\mu }^A,{\sigma }^A,{\mu }^{v_e},{\sigma }^{v_e},{\mu }^{s_e},{\sigma }^{s_e}\sim \mathit{TN}(1,1) \\ {\mu }^{\tau },{\sigma }^{\tau }\sim \mathit{TN}(.3,.3) \\ {\mu }^{v_c},{\sigma }^{v_c}\sim \mathit{TN}(3,3) \\ {\mu }^k,{\sigma }^k\sim \mathit{TN}(.4,.4). \end{gathered}$$