Slow slip events in the roots of the San Andreas fault

By analyzing GPS time series, we have detected an averaged M_w 4.9 slow slip event in the roots of the San Andreas fault.

Abstract

Episodic tremor and accompanying slow slip are observed at the down-dip edge of subduction seismogenic zones. While tremors are the seismic signature of this phenomenon, they correspond to a small fraction of the moment released; thus, the associated fault slip can be quantified only by geodetic observations. On continental strike-slip faults, tremors have been observed in the roots of the Parkfield segment of the San Andreas fault. However, associated transient aseismic slip has never been detected. By making use of the timing of transient tremor activity and the dense Parkfield-area global positioning system network, we can detect deep slow slip events (SSEs) at 16-km depth on the Parkfield segment with an average moment equivalent to M_w 4.90 ± 0.08. Characterization of transient SSEs below the Parkfield locked asperity, at the transition with the creeping section of the San Andreas fault, provides new constraints on the seismic cycle in this region.

INTRODUCTION

The discovery of deep-seated slow slip events (SSEs) was enabled by the establishment of continuous global positioning system (GPS) measurements at the Nankai and Cascadia subduction zones (1, 2). Soon after, tectonic tremors that are temporally and spatially correlated with SSEs were discovered in Japan (3), leading to the recognition of the coupled phenomenon called episodic tremor and slip (ETS) (4, 5). ETS mostly occurs below the transition from brittle to ductile fault zone properties (6), where increasing temperatures and pore pressures due to metamorphic dehydration reactions (7) inhibit fast ruptures. Long-lived tremor signals, in contrast with classical earthquakes, are made of a large number of low-frequency earthquakes (LFEs) that are thought to be due to the activation of small seismic asperities by surrounding slow slip (8). Strain rate transients due to SSEs correlated with tremor bursts are observed for transient durations ranging from minutes to months (9). However, because of geodetic detection limitations, SSEs are not always observed at locations and times of tectonic tremors (10). Recent studies have shown that using the timing of tremor bursts to stack multiple episodes in GPS time series helps to extract an averaged slow slip signal (11). Using transient tremor activity to guide the detection of the SSE’s geodetic signal, (12) demonstrated that many smaller SSEs are occurring during the periods between large SSEs.

On continental strike-slip faults, shallow transient creep events have been captured using strainmeters, creepmeters, and InSAR (interferometric synthetic aperture radar) measurements [e.g., (13–16)]. However, spontaneous SSEs at the down-dip edge of the seismogenic zone on strike-slip plate boundaries have not been observed yet with geodetic measurements. Persistent tremor and LFE activity at the deep transition zone have been detected along two segments of continental strike-slip faults in the world: a section of the San Andreas fault (SAF) near Parkfield (17) and on the Alpine Fault in New Zealand (18, 19). The Parkfield segment of the SAF might be different from most strike-slip faults because it overlies the remnants of a subduction zone where serpentine is still actively dehydrating (20). With these processes happening, it is a good analog of young and warm subduction zones, where most of the ETS are occurring. Numerous studies of LFEs on that segment have characterized their temporal behavior since 2003, defining 88 families with a range of temporal behavior from continuous to episodic (21). Here, we extract the first geodetic signature of transient slip associated with LFE bursts on that segment by taking advantage of the redundancy of information provided by more than 10 years of continuous time series from a dense GPS network, 68 stations within 100 km from Parkfield, California (Fig. 1).

Fig. 1. Tectonic context and GPS network.

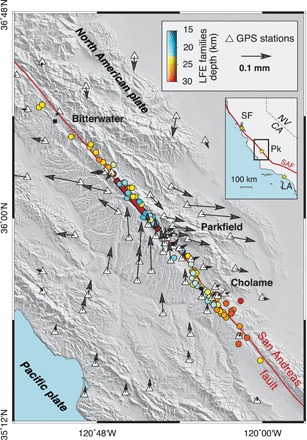
The right-lateral strike-slip SAF that delimited the Pacific plate from the North American plate is represented by the red line. The circles represent the LFE families color coded by their depths. The white triangles show the network of GPS stations. The black arrows indicate the predicted static surface displacements due to an SSE of M_w 4.9 occurring from 14- to 18-km depth, with the surface projection of the model dislocation shown by the thick red bar. The black squares indicate the cities. LA, Los Angeles; SF, San Francisco; CA, California; NV, Nevada; Pk, Parkfield.

We postprocessed the GPS time series to correct for signals due to earthquakes, postseismic relaxation, seasonal oscillations, and common mode errors (see Materials and Methods). In individual residual time series, only noise can be seen, with an SD of about 1 mm (fig. S1). To account for the timing of LFE bursts, we select the families with strongly episodic behavior, which produce clear transient accelerations in the cumulative LFE count. We assemble them into two groups in which families have episodic transients over the same time periods: the NW (northwest) Parkfield group and the Cholame group (Fig. 2A and fig. S2). To define the central transient event times, we use the maximums in daily LFE counts (Fig. 2B; see Materials and Methods). We then stack 500-day windows of GPS time series aligned on the central event times to increase the signal-to-noise ratio of possible transient slip events. While the stacked GPS time series have a much reduced SD of ~0.15 mm, no transient events can be observed in the individual time series. To detect transient events at the noise level of individual time series, we use a geodetic matched filter technique [see Materials and Methods; (22)] based on calculating the correlation between synthetic templates from a mechanical dislocation model and the residual GPS time series. By discretizing the fault plane into many patches and computing the corresponding synthetic templates and correlations at each station, we can extract the locations that maximize the correlation. We applied this method to the 500-day GPS time series stacked over 20 LFE bursts for the NW Parkfield group (Fig. 3) and 65 bursts for the Cholame group (fig. S2) during the period 2006–2016.

Fig. 2. Temporal behavior of the episodic LFE families of the NW Parkfield group.

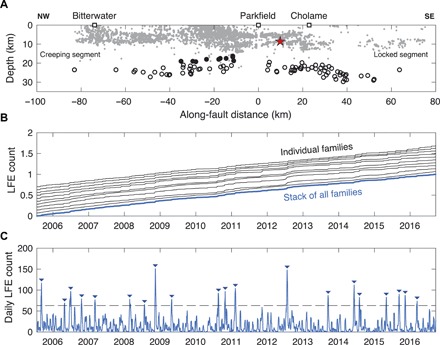
(A) The circles represent the location of all the LFE families. The filled circles represent the families of the NW Parkfield group. The gray dots indicate the relocated microseismicity from 1984 to 2011 (47). The hypocenter of the M_w 6.0 Parkfield earthquake is shown by the red star. (B) Cumulative number of LFEs per family (normalized by the total number and offset for clarity) of the NW Parkfield group and summed over the families (blue curve). (C) Daily count of LFEs in the group. The inverse triangles identify the 20 dates of LFE bursts used to align and stack windows of GPS time series. The dashed line indicates the threshold used to select the transient times. SE, southeast.

Fig. 3. Correlation results from the geodetic matched filter analysis for the NW Parkfield group.

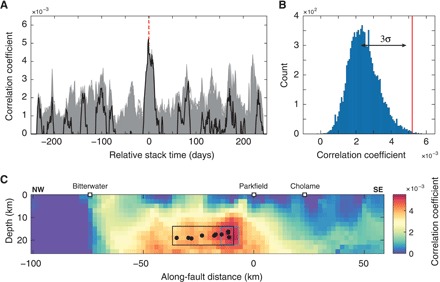
(A) Positive part of the correlation functions for all the patches (gray curves). The black curve highlights the correlation function with the highest amplitude. The red dashed line indicates the zero relative stack time. (B) Histogram of the 10,000 maximums of correlation after stacking GPS windows using 20 random dates instead of the LFE burst dates. The red line indicates the amplitude of the observed correlation at the relative stack time zero in (A). The black arrowhead line indicates the 3σ of a Gaussian distribution fit. (C) Amplitude of the correlation at zero relative stack time for each dislocation patch on the fault. The highest correlation values are clustered around the black solid circles showing the location of the LFE families in the NW Parkfield group. The black rectangle and blue square are the SSE rupture areas used to estimate the M_w of the transient event.

RESULTS

Geodetic matched filter analysis

The resulting correlation functions from the application of the geodetic matched filter for the NW Parkfield group are showing oscillations with maximum correlation coefficients of ~4 × 10⁻³ (Fig. 3A). The maximum correlation coefficient (5.3 × 10⁻³) is located at the relative stack time zero, where we would expect it in case of a detectable transient geodetic signal associated with the LFE bursts. The maximum correlation amplitudes are coming from patches colocated with the LFE families whose bursts we used to align and stack the GPS time series (Fig. 3C). To determine whether such an amplitude is significant relative to the correlation amplitudes produced by noise, we repeat the same correlation analysis 10,000 times, but taking 20 random times to stack the GPS time series instead of the times of the LFE bursts. Doing so, the distribution of the maximum amplitudes of correlation at zero relative stack times is centered on 2.3 × 10⁻³. The amplitude obtained by using the actual LFE burst times exceeds 3σ from this distribution. Counting the number of occurrences that exceed the amplitude obtained using the LFE bursts, we can say that the probability to have an amplitude of 5.3 × 10⁻³ by random chance is 0.01 or that the confidence level of having made a detection due to a transient slip on the fault is 99.9%. This value is conservative in the sense that it only takes into consideration the amplitude of the correlation, without considering the location of fault patches producing the maximum correlations with respect to the locations of the LFE families used. Accounting for that second parameter is not straightforward, but it would further decrease the probability of having such a correlation amplitude by random chance as the large correlation amplitudes in the noise are often located close to the surface, the largest correlation coefficient due to noise being dominated by single stations close to the fault. The same correlation analysis for the Cholame segment does not result in a positive detection (fig. S2) because the amplitude of slip associated with these more frequent tremor bursts, if any, is too small to be detected by the geodetic matched filter. Moreover, the spatial distribution of the GPS stations favors lower amplitude detections in NW Parkfield compared with Cholame, as the stations are densely populated where NW Parkfield deep SSEs would produce high-amplitude surface displacement. We also searched for the transient signals detected by GPS in NW Parkfield in strainmeter time series, but given the noise level at periods of ~10 days, we did not succeed in significantly extracting the signal due to the slow slips (fig. S5).

Average geodetic moment

To estimate the geodetic moment associated with the average SSE that we have detected in NW Parkfield, we modeled the GPS time series stacked over the 20 LFE bursts and over the north and east components of each station. The stacking over the components is weighted by the predicted displacement from unit slip on the peak correlation patch, also called Green’s function. Such a weighting gives the right sign for all the components and gives more weight for stations that are recording higher amplitudes. This final stacked time series is modeled by a linear term plus a 10-day transient centered on zero (Fig. 4A). The SSE duration is fixed on the basis of the average duration of the LFE transients (Fig. 4C), since we cannot precisely retrieve the duration from the GPS data alone—the data being equally well explained with transient durations from 3 to 20 days. Since adding a transient event to a time series fitting model adds free model parameters in comparison to a linear fit, we compared the performance of models with and without a transient event, accounting for the number of parameters in each model. We estimated the Akaike information criterion (AIC) for both models on 81-day stacked GPS time windows and computed the difference between the two criterions, ΔAIC (see Materials and Methods). The negative ΔAIC values at relative stack time zero (Fig. 4D) indicate that a model with a transient better explains the stacked GPS time series, and positive values on the sides show that if the window is not centered on the LFE bursts, the stacked GPS time series is better explained by a linear term only. The amplitude of the transient offset is well constrained and can be related to the geodetic moment (M₀ = μ × slip × area, where μ = 30 GPa is the assumed shear modulus) and the corresponding moment magnitude (M_w) of the average SSE. To estimate the M_w, we have to assume an SSE rupture area. The most logical choice is to select an area that outlines the LFE families that are activated by the transient slips (black contour, Fig. 3C). Using this rectangular area of 208 km², a uniform slip of 3.6 mm per event produces M_w 4.9 SSEs. Because of the trade-off between the rupture area and the amplitude of slip, the choice of a rupture area mainly affects the amplitude of slip, giving similar estimates of M_w. For example, with a much smaller area (48 km²) that contains only the patches with maximum correlation (blue contour, Fig. 3C), the estimated M_w is 4.85 for a uniform slip of 12 cm. Since the estimated transient offset and corresponding M_w are an average of 20 events, we performed jackknife tests to estimate the influence of individual events on the stack (see Materials and Methods; figs. S3 and S4). But, given the uncertainty on the measure of the transient offset means while removing events in the stack, we cannot assess the weight of individual events in the average. However, these tests provide an uncertainty on the average magnitude over the 20 events, which is between 4.84 and 4.98 (Fig. 4B and fig. S3). These deep-seated events of M_w ~4.9 produce a surface displacement pattern with maximum amplitudes of 0.1 mm (Fig. 1), which is the smallest transient event surface expression ever recorded by GPS to our knowledge. While no published estimates of the moment released by LFEs in Parkfield are available, the amplitude of body waves produced by the shallowest LFEs is consistent with M_w 1 events or smaller (23). Taking an upper bound of 1500 events per burst, the geodetic moment for the average SSE is at least 400 times larger than the seismic moment, which is consistent with estimates made for Cascadia SSEs (24).

Fig. 4. Model of the average SSE.

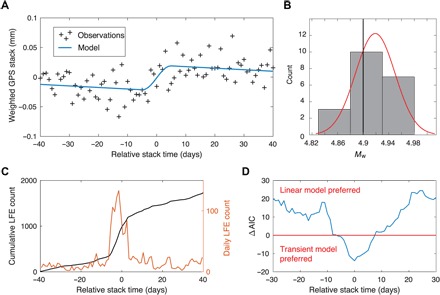
(A) Weighted stack of the GPS postprocessed time series. The blue curve shows the best fitting model with a linear term plus a 10-day transient event centered on zero. (B) Histogram showing the M_w estimates from the jackknife test. The red line is a Gaussian fit of the histogram. The black line shows the M_w estimated with all the events and assuming the black rectangle shown in Fig. 3C as a rupture area. (C) Cumulative number of LFEs in black, averaged over the 20 bursts of LFEs. The orange curve represents the corresponding daily count of LFEs. (D) Difference of the AICs for models including transient events and linear models. The models are computed on 81-day sliding time windows with centered transient events. Negative values mean that the model with a transient is preferred for a given relative stack time.

DISCUSSION

The long-term slip rate on the SAF is 34 mm/year [e.g., (25)]. The slip during the bursts thus corresponds to 21% of the tectonic loading if we consider the rupture area that contains all the LFE families (black rectangle on Fig. 3C). Note that the smaller area (blue rectangle on Fig. 3C) is not realistic because transient SSEs would release twice the loading rate. Since the number of LFEs during the transient events of the episodic NW Parkfield families represents about 25% of their total number, LFEs might be reliable creepmeters (i.e., the LFE rate can be used as a proxy for the slip rate), as suggested by (26). Using that assumption, we can estimate the rupture area as a function of the coupling ratio (fig. S5). At depths of the analyzed transient events (14 to 18 km), interseismic geodetic coupling models find coupling ratios ranging from 0 to 0.5 [e.g., (27, 28)]. A coupling ratio of 0 corresponds to a rupture area that closely outlines the LFE families (slightly smaller than the black rectangle in Fig. 3C), while a coupling ratio of 0.5 corresponds to a larger rupture area of 360 km².

To define generic properties of slow slip phenomena, including SSEs and tremors, a scaling law that differs from the one for classical earthquakes has been proposed by (29). Earthquakes have a seismic moment proportional to the cube of their duration. Considering tremor, LFEs and SSEs, (29) propose that the seismic moment is proportional to the duration of slow slip ruptures. Many numerical simulations based on different assumptions are able to reproduce SSEs with proportionality between their moment and their duration to the power 1 to 3 (30–33). The average ETS that we have characterized at NW Parkfield has a duration of ~10 days, for a geodetic moment of 10^16.35 N m. The scaling law in (29) predicts that an event of geodetic moment 10^16.35 N m should have a duration shorter than 1 day. However, the upper left quadrant of the moment released versus duration representation may be limited by geodetic measurement detection capabilities, rather than an actual absence of events. Since the stacking technique over multiple events and components used in the present study lowers the detection threshold at periods of 10 days, we are able to access an area with lower moment released than the ones already described. This observation could in particular be explained by the model in (34), in which SSEs and earthquakes have similar scalings, shifted by their rupture speeds.

In elastodynamic seismic cycle models, strike-slip faults with variable along-depth frictional properties are loaded from below their base by aseismic slip at the long-term rate [e.g., (35, 36)]. In the transition zone, in between the deep steadily slipping area where no stress accumulates and the shallow locked patches where most of the stress builds up, stress accumulates during short periods of time in between transient events (37). As seismic emissions detected by surface seismometers correspond to only a small fraction of the total moment released by SSEs in the transition zone, it is crucial to have precise estimates of the moment release from geodetic observations. The discovery and characterization of the series of M_w 4.9 SSEs provide an important constraint for the next generation of Parkfield seismic cycle models. The development of models that can reproduce this slip behavior during the interseismic period should provide new insights about the transition zone rheology, which might lead to an improved understanding of the loading of the shallower seismic patch that ruptured with unusually regular intervals, between 12 and 38 years apart, from 1857 to 2004 (38).

MATERIALS AND METHODS

GPS postprocessing

The 68 GPS stations used in this study have been installed by several different entities in the early 2000s and eventually all merged into the Plate Boundary Observatory (PBO) (Fig. 1). We used the PBO combined solution, also referred to as level 2b product (39). The daily position time series d(t) were computed using the North American tectonic plate reference frame (NAM08). Stations in the area of interest with abnormal noise amplitude have been excluded from the analysis. To extract the different tectonic components of the time series, we modeled the position x(t) as

$$\mathit{x}(\mathit{t})=\mathit{x}({\mathit{t}}_{\mathrm{r}})+\mathit{v}(\mathit{t}-{\mathit{t}}_{\mathrm{r}})+{\displaystyle \sum _{\mathit{i}}}{\mathit{a}}_{\mathit{i}}\mathit{H}(\mathit{t}-{\mathit{t}}_{\mathit{i}})+{\displaystyle \sum _{\mathit{i}}}{\mathit{b}}_{\mathit{i}}\text{log}(1+\frac{\mathit{t}-{\mathit{t}}_{\mathit{i}}}{{\mathit{T}}_{\mathit{i}}})$$ (1)

where x(t_r) is a constant offset, with t_r being the reference time, v(t − t_r) is the secular velocity, the a_i are the coseismic offsets occurring at time t_i, and b_i are the amplitudes of the postseismic transients starting at time t_i with relaxation times T_i (40). H(t) is the Heaviside function. In the period of time of our analysis, we modeled two earthquakes and related postseismic relaxation, the 22 December 2003 M_w 6.6 San Simeon earthquake and the 28 September 2004 M_w 6.0 Parkfield earthquake. After correcting the time series for x(t), the residuals represent mainly annual and longer-period oscillations. Since we are searching for short-term—few-days long—transient events, we corrected for these long wavelength signals, mainly due to seasonal loading, by removing a 150-day moving average window l(t). We finally corrected for the common mode of the residuals by applying a probabilistic principal components analysis to the whole network (41) that accounts for gaps in the time series. The common mode corresponds to the first principal component c(t). From 2006 to 2016, a period during which the number of stations is stable, this method gave a very similar result as when estimating the common mode by averaging all the time series for a given component. To validate that we are only removing a common mode and no short-term tectonic signal, we have also computed the common modes for both sides of the fault independently. The extracted common modes are identical on both sides at the 0.2-mm level, indicating that no short-term tectonic transient has been removed (a tectonic signal would have produced an opposite displacement on both sides of the fault). The final residual time series used in this study are r(t) = d(t) − x(t) − l(t) − c(t). An example of the GPS postprocessing procedure is presented in fig. S1 for the north component of the station CAND.

LFE catalog

We used the LFE catalog released by (21), in which LFEs are assembled in 88 families. We have selected two groups of families that present clear transients in the time series of the cumulative number of events. North of Parkfield, where the temporal behavior presents a clear along-depth gradation from continuous at depth to episodic more shallowly, we assembled the 10 families located at depths above 20 km (Fig. 2A). In the Cholame segment, south of Parkfield, the episodic versus continuous behavior is more heterogeneous, so we have analyzed only the 10 families defined as episodic by (26) based on (42) MFD75 criterion (fig. S2). In these two groups, the several-day-long transients are happening over the same periods of time on independent families (Fig. 2 and fig. S2), the propagation between families being observed at much shorter time scales, with speeds higher than 10 km h⁻¹ within sub-bursts of LFEs (43). To pick the timing of LFE bursts, we computed the daily count of LFEs in the two groups and applied a moving average window of duration equal to the duration of the prominent tremor bursts (10 days for the NW Parkfield group and 2 days for the Cholame group). This smoothing avoids multiple detections on a single transient event. We then picked the maximums of these daily count time series, which are the times that we are using to align the events.

Geodetic matched filter

To detect and locate transient activity related to a slip on a fault in GPS time series, we used the geodetic matched filter developed in (22). This method correlates synthetic surface displacement time series due to a dislocation model of transient slip on a fault patch with postprocessed GPS time series. We discretized the SAF plane around Parkfield into 1040 4-km² patches. For each patch, we computed the Green’s function coefficients g_i, which relate unit strike-slip on a given patch to surface displacement at each station and for each horizontal component i, in a homogeneous elastic half-space using the analytical formulation of (44). The rise time function for synthetic slip templates is given by $\mathit{s}(\mathit{t})=\frac{1}{2}[1-\text{cos}(\frac{\mathrm{\pi }\mathit{t}}{\mathit{T}}\left)\right]$, where T is the transient duration. In the results presented in this paper, T = 30 days. The templates are eventually defined by w_i(t) = g_is(t).

We then performed the fully normalized correlations between the synthetic templates and the GPS time series stacked over many LFEs bursts ds(t). For a given patch, we compute

$${\mathit{C}}_{\mathit{i}}(\mathit{t})=\frac{{\displaystyle {\sum }_{\mathit{k}=1}^{\mathit{T}}}{\stackrel{.}{\mathit{w}}}_{\mathit{i}}({\mathit{t}}_{\mathit{k}})\stackrel{.}{\mathit{d}}{\mathit{s}}_{\mathit{i}}({\mathit{t}}_{\mathit{k}}+\mathrm{\tau })}{\sqrt{{\displaystyle {\sum }_{\mathit{k}=1}^{\mathit{T}}}{\stackrel{.}{\mathit{w}}}_{\mathit{i}}^2({\mathit{t}}_{\mathit{k}}){\displaystyle {\sum }_{\mathit{k}=1}^{\mathit{T}}}\stackrel{.}{\mathit{d}}{\mathit{s}}_{\mathit{i}}^2({\mathit{t}}_{\mathit{k}}+\mathrm{\tau })}}$$ (2)

where the overdots are the temporal derivatives, and τ corresponds to the move out for a given i. T is the template length in samples, equivalent to its duration in days. To obtain the final correlation function C_f(t) for a given patch, we computed the weighted stack, with N being the number of GPS stations

$${\mathit{C}}_{\mathit{f}}(\mathit{t})=\frac{{\displaystyle {\sum }_{\mathit{i}=1}^{2\mathit{N}}}|{\mathit{g}}_{\mathit{i}}|{\mathit{C}}_{\mathit{i}}(\mathit{t})}{{\displaystyle {\sum }_{\mathit{i}=1}^{2\mathit{N}}}|{\mathit{g}}_{\mathit{i}}|}$$ (3)

At any given time, the amplitudes of C_f can be mapped on the fault plane to locate the highest correlations.

Time series model performances

One way to compare the performances of models with different numbers of free parameters that explain a dataset is to compute the statistical AIC (45). This widely used statistical criterion has notably been used as a detection criterion to detect transient events in GPS time series [e.g., (46)]. In our study, we used this criterion to compare linear models with models including a transient event to explain the weighted stack of GPS time series. This criterion is defined as

$$\text{AIC} ={\mathit{k}}_{\mathrm{d}} \text{ln}(2\mathrm{\pi })+{\mathit{k}}_{\mathrm{d}} \text{ln}{\displaystyle \sum _{\mathit{j}=1}^{{\mathit{k}}_{\mathrm{d}}}}\frac{{({\mathit{O}}^{\mathit{j}}-{\mathit{M}}^{\mathit{j}})}^2}{{\mathit{k}}_{\mathrm{d}}}+{\mathit{k}}_{\mathrm{d}}+2{\mathit{k}}_{\mathrm{p}}$$ (4)

where O is the dataset, M is the corresponding model, k_d is the number of data samples, and k_p is the number of free parameters. In our tests, we used k_d = 81, which corresponds to a 81-day stacked GPS time window. For the linear models, k_p = 2, and for the models including a transient, k_p = 3, since the transients were forced to be in the middle of the selected time window, and the duration was fixed to 10 days (based on the average duration of the LFE transients) because we cannot constrain the duration with the GPS data alone. To compare linear models (AIC_l) with models including a transient event (AIC_t), we computed the difference between the two criteria ΔAIC = AIC_t − AIC_l. A positive value of ΔAIC means that the data are best explained with a linear model, while a negative value means that a model including a transient is preferred.

Jackknife tests

To quantify the influence of individual events on the stack of 20 transients, we performed a jackknife test. We computed the distributions of estimated transient offsets for all possible combinations of events while removing p events, for p = 1 to p = 18. The number of combinations is $\frac{\mathit{n}!}{(\mathit{n}-\mathit{p})!\mathit{p}!}$, where n = 20 is the total number of events. The mean of all the distributions is stable (3.93 × 10⁻² mm) because the n events equally contribute to each distribution. The SD decreases with increasing number of stacked events m = n − p (fig. S4B). In the range where the number of realizations is sufficient for a precise measure of the SD, this decrease is well explained by a 1/m least squares fit, which can be explained as the combination of the signal-to-noise ratio increasing as $1/\sqrt{\mathit{m}}$ and standard error of the mean decreasing as $1/\sqrt{\mathit{m}}$.

When doing the same analysis with n = 19, the 20 mean offsets vary by up to 15% from the mean with n = 20 (fig. S4C). This dispersion is higher than the theoretical variation expected for an insignificant event (zero offset) being removed, which should be 5.3% from the mean with n = 20. This shows that the noise fluctuations are dominant with respect to the amplitude variations of individual events in the stack of the 20 events, preventing any characterization of individual events’ contribution in the stack. We also do not observe a correlation between the 20 mean offsets for n = 19 and the number of LFEs per burst. However, the SD for m = 19 and n = 20 gives us an estimate of the uncertainty for the transient offset and for the corresponding M_w of the average event (Fig. 4B and fig. S3).

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/5/2/eaav3274/DC1

Fig. S1. GPS postprocessing.

Fig. S2. Correlation analysis for the Cholame segment.

Fig. S3. Jackknife tests with one event removed.

Fig. S4. Jackknife tests.

Fig. S5. Strainmeter time series analysis.

Fig. S6. LFEs as creepmeters.

References (48, 49)