Characterizing the effects of sex, APOE ɛ4, and literacy on mid-life cognitive trajectories: Application of Information-Theoretic model averaging and multi-model inference techniques to the Wisconsin Registry for Alzheimer’s Prevention Study

Abstract

Objective:

Prior research has identified numerous genetic (including sex), education, health and lifestyle factors that predict cognitive decline. Traditional model selection approaches (e.g., backward or stepwise selection) attempt to find one model that best fits the observed data, risking interpretations that only the selected predictors are important. In reality, several predictor combinations may fit similarly well but result in different conclusions (e.g., about size and significance of parameter estimates). In this paper we describe an alternative method, Information-Theoretic (IT) model averaging, and apply it to characterize a set of complex interactions in a longitudinal study on cognitive decline.

Method:

Here we used longitudinal cognitive data from 1256 late-middle aged adults from the Wisconsin Registry for Alzheimer’s Prevention study to examine the effects of sex, Apolipoprotein E (APOE) ɛ4 allele (non-modifiable factors), and literacy achievement (modifiable) on cognitive decline. For each outcome, we applied IT model averaging to a set of models with different combinations of interactions among sex, APOE, literacy, and age.

Results:

For a list-learning test, model-averaged results showed better performance for women vs men, with faster decline among men; increased literacy was associated with better performance, particularly among men. APOE had less of an association with cognitive performance in this age range (~40–70).

Conclusions:

These results illustrate the utility of the IT approach and point to literacy as a potential modifier of cognitive decline. Whether the protective effect of literacy is due to educational attainment or intrinsic verbal intellectual ability is the topic of ongoing work.

Introduction

Signs of cognitive decline often begin a decade or more before diagnosis of dementia due to late-onset Alzheimer’s disease (AD), a neurodegenerative disease associated with greatly impaired cognition and daily functioning (Price et al., 2009; Price & Morris, 1999). After age, presence of one or more Apolipoprotein E (APOE) ɛ4 alleles is the strongest predictor of risk of late onset AD (Strittmatter & Roses, 1996; Tang et al., 1996), particularly among non-Hispanic Caucasians (Tang et al., 1998). Several studies report earlier and faster declines in memory or executive function among APOE ɛ4 carriers than non-carriers (i.e., APOE by age interactions), with detectable accelerations in decline beginning around age 60 (Caselli et al., 2009; Chang et al., 2014; Wisdom, Callahan, & Hawkins, 2011). Studies also indicate that the rate of ɛ4-associated cognitive decline and AD risk are moderated by sex with ɛ4-carriage increasing rate of decline and risk more in women than in men (Altmann, Tian, Henderson, & Greicius, 2014; Beydoun et al., 2012; Koran, Wagener, & Hohman, 2017; Mielke, Vemuri, & Rocca, 2014; Mortensen & Høgh, 2001; Neu et al., 2017; Payami et al., 1996; Riedel, Thompson, & Brinton, 2016). Higher literacy levels (as measured by word reading tasks) have been shown to mitigate age- and/or APOE-related cognitive decline in non-demented elders (Kaup et al., 2015; Manly, Touradji, Tang, & Stern, 2003).

No studies, to our knowledge, have investigated the combined influences of sex, APOE genotype, and literacy on early to late middle-age cognitive trajectories in an integrated analytic framework. However, the number of configurations in which these and other covariates could be associated with a given outcome is quite large, and this presents a problem of what model configuration to choose. Traditional model selection approaches, such as forward, backward, or stepwise selection, attempt to find a model that best fits the observed data. One issue that can arise from such methods is concluding that only the selected predictors are important while assuming those not selected are unimportant (Anderson & Burnham, 2002). In reality, several models may fit the data similarly well but result in different conclusions, and inference from a single model chosen after a selection procedure can lead to overly optimistic results and conclusions (Claeskens and Hjort 2008). Information-theoretic (IT) modeling techniques offer a way to characterize complex sets of interactions and make multi-model inference while avoiding the pitfalls of predictor selection methods (Anderson & Burnham, 2002; Claeskens & Hjort, 2008).

The IT framework evaluates “a small set of science hypotheses, all of which are plausible” (p. 202, (Anderson & Burnham, 2002)). The IT approach has its roots in biological ecology research (Burnham, Anderson, & Huyvaert, 2011; Hegyi & Garamszegi, 2011; Richards, 2005; Richards, Whittingham, & Stephens, 2011; Symonds & Moussalli, 2011), and aims to use the relative strength of information among all considered models instead of selecting a single model. The methods start with formulating a reasonably sized collection of models with the same outcome, but different covariate structures (such as different main effects, interactions, etc.). Each model should test hypotheses that are scientifically reasonable to include. After fitting all of these models to the data, results are combined across models in proportion to the relative strength of information each model provides. These relative strengths are quantified through the theory of the corrected Akaike Information Criterion (AICc), which estimates the relative differences among these models with respect to their Kullback-Leibler divergence, a measure of the distance between a proposed model and the “true” model (see Figure 1, Burnham et al., 2011; Hurvich & Tsai, 1989). This allows models fitting similarly well to contribute relatively equal amounts of influence on the resulting parameter estimates, while models that fit poorly have little or no influence on results.

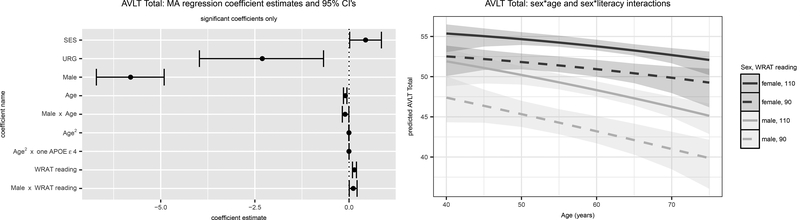
Figure 1. AVLT Total: Significant Model-Averaged Terms (Left) and Predicted Values (Right).

Results are for the outcome, AVLT Total. The left panel depicts parameter estimates and 95% confidence intervals (CI’s) for CI’s that do not overlap 0. The right panel depicts predicted values and 95% confidence limits using the model averaged parameter estimates for both sexes and high vs low literacy. SES=Socioeconomic status; URG = Underrepresented groups; WRAT = Wide Range Achievement Test (3rd edition).

The aims of this study were to describe the IT model averaging method and apply it to characterize how sex, literacy, and APOE genotype influence age-related trajectories for several neuropsychological tests in a longitudinal sample enriched for risk of developing AD (Wisconsin Registry for Alzheimer’s Prevention (WRAP)). In secondary analyses, we compare the IT model averaging results with traditional model selection methods.

Methods

WRAP study and participants

WRAP is a longitudinal cohort study enriched for AD-risk via over-enrollment of participants with a parental history of AD (for details, see (Johnson et al., 2017)); primary aims of the study include identifying predictors associated with cognitive decline and estimating their associations. All participants were free of dementia at baseline. At the time of these analyses, there were 1549 enrolled WRAP participants (baseline age mean(sd)= 53.7(6.6); parental history of AD n(%)= 1125(72.6%)). To be included in these analyses, participants had to be free at baseline of Mild Cognitive Impairment (MCI) and any of four neurological conditions (stroke, Parkinson’s disease, multiple sclerosis, epilepsy), have completed at least 2 study visits, and have complete data in the predictors needed for the analyses (n=1256 eligible; n’s excluded: MCI, n=4; neurological disorder, n=59; <2 visits, n=226; incomplete predictors, n=4; see Table 1 for additional details). This study was conducted in compliance with ethical principles for human subjects research defined in the Declaration of Helsinki, including approval by the University of Wisconsin Institutional Review Board.

Table 1:

Sample characteristics

	Overall	Female	Male	p-value*
N	1256	873 (69.5%)	383 (30.5%)
Age (mean (sd))	53.67 (6.55)	53.56 (6.57)	53.92 (6.51)	0.238
URG (N (%))	85 (6.8)	61 (7.0)	24 (6.3)	0.715+
ESL (N (%))	21 (1.7)	16 (1.8)	5 (1.3)	0.636+
Follow-up years (mean (sd))	9.10 (2.60)	9.04 (2.63)	9.22 (2.53)	0.34
Number of visits (N (%))
2	135 (10.7)	102 (11.7)	33 (8.6)	0.124+
3	265 (21.1)	180 (20.6)	85 (22.2)
4	432 (34.4)	310 (35.5)	122 (31.9)
5	424 (33.8)	281 (32.2)	143 (37.3)
APOE ε4 count (N (%))
0	767 (61.1)	523 (59.9)	244 (63.7)	<0.001+
1	438 (34.9)	303 (34.7)	135 (35.2)
2	51 (4.1)	47 (5.4)	4 (1.0)
SES (N (%))
1	39 (3.1)	26 (3.0)	13 (3.4)	<0.001^
2	122 (9.7)	99 (11.3)	23 (6.0)
3	267 (21.3)	202 (23.1)	65 (17.0)
4	241 (19.2)	171 (19.6)	70 (18.3)
5	587 (46.7)	375 (43.0)	212 (55.4)
RAVLT total (mean (sd))	51.10 (7.95)	52.61 (7.30)	47.64 (8.30)	<0.001
RAVLT delayed recall (mean (sd))	10.46 (2.82)	10.96 (2.60)	9.33 (2.99)	<0.001
Trails A (mean (sd))	26.81 (8.55)	26.28 (8.24)	28.02 (9.11)	0.001
Trails B (mean (sd))	62.06 (24.61)	60.21 (22.16)	66.28 (29.03)	<0.001
Boston Naming 60 (mean (sd))	57.02 (3.09)	56.87 (3.19)	57.35 (2.84)	0.002
CFL fluency (mean (sd))	43.37 (11.07)	43.99 (10.75)	41.94 (11.65)	0.002
Digit Span backward (mean (sd))	7.09 (2.22)	7.00 (2.17)	7.31 (2.32)	0.024
Digit Span forward (mean (sd))	10.51 (2.18)	10.40 (2.11)	10.76 (2.31)	0.006
Stroop color word, (mean (sd))	108.12 (20.63)	109.86 (19.58)	104.09 (22.42)	<0.001
4-Test IICV (mean (sd))	0.73 (0.33)	0.73 (0.33)	0.73 (0.33)	0.803

^*Note: Comparisons made with Mann-Whitney, unless noted with or # of participants omitted from model averaging for that outcome due to <2 visits with that outcome’s data: AVLT Total and Delay, 7; Trails A and B, 6; Digit span forward and backward, 7; Stroop CW, 21; BNT, 10; CFL, 10; 4 Test IICV, 9.

⁺Fisher’s exact

^{^}Chi-squared

Abbreviations: URG = Underrepresented groups; ESL = English is a Second Language; SES = Socioeconomic Status; IICV = Intraindividual Cognitive Variability.

Study protocol and outcomes

At each study visit, participants completed comprehensive cognitive assessments, detailed health and lifestyle questionnaires, and provided blood samples for current and future analyses. The first follow-up visit occurred approximately 4 years after baseline, with subsequent visits occurring approximately every 2 years (for details, see (Johnson et al., 2017)). We analyze ten outcomes in this study that have been shown to be sensitive to AD-related cognitive changes (one intraindividual variability (IICV) measure and nine cognitive measures available since baseline of the WRAP study). The nine measures used are: the Rey Auditory Verbal Learning and Memory Test (Schmidt, 1996), sum of learning trials (“AVLT Total”) and long delay recall trial (“AVLT Delay”); Trail Making Test (“Trails A” and “Trails B”, (Lezak, Howieson, Bigler, & Tranel, 2012)); Stroop Color-Word Interference Test (Trenerry, Crosson, DeBoe, & Leber, 1989), number of correct items in two minutes; Controlled Oral Word Association Test (Benton, Hamsher, & Sivan, 1994), total words in 60 seconds for each letter: C, F, L (“CFL”); the Boston Naming Test (“BNT”, (Kaplan, Goodglass, & Weintraub, 2001)), total correct and Digit span forward and backward total items correct (Wechsler, 1997).

Given recent results in WRAP and other studies suggesting that higher intraindividual cognitive variability (IICV) across tests at a given visit predicts increased risk of subsequent decline or AD pathology (Anderson et al., 2016; Gleason, Norton, Anderson, Wahoske, Washington, Umucu, Koscik, Dowling, Johnson, & Carlsson, 2017; Holtzer, Verghese, Wang, Hall, & Lipton, 2008; Koscik et al., 2016), we also characterized how IICV varied by sex, literacy, APOE, and age in our sample. Specifically, we calculated “4-Test IICV” as the standard deviation of z-scores of AVLT Total and Delay, Trails B, and the Wide Range Achievement Test (3^rd ed., “WRAT”) reading recognition subtest standard score (Wilkinson, 1993); AVLT Delay, Trails B, and WRAT were Box-Cox transformed prior to z-scoring (AVLT Delay had a constant of 1 added to all scores before transformation) The WRAT Reading score when used in middle-aged and older adults is accepted as a stable proxy for premorbid verbal abilities and quality of education (Ashendorf, Jefferson, Green, & Stern, 2009; Manly et al., 2003; Olsen, Fellows, Rivera-Mindt, Morgello, & Byrd, 2015). Baseline WRAT reading and IICV were not correlated (Spearman rho=.022, p=.44) even though WRAT is a component of the IICV calculation.

Key Predictors and Covariates

Key predictors in this study include age (years), sex (Male/Female), APOE ɛ4 allele count (i.e., 0, 1, 2 (for details on genotyping methods, see (Darst et al., 2017))), and WRAT. For subjects without baseline WRAT, the value at their second visit was used. Additional covariates included race/ethnicity (non-Hispanic Caucasian vs underrepresented group, URG), if English was the subject’s native language (ESL), and socioeconomic status (SES; 1 = <$20k; 2 = $20k-<$40k; 3= $40k-<$60k; 4=$60k-<$80k, and 5=$80k or more). Missingness in SES was present in 54 (4.3%) participants. To recover these subjects for analyses, their baseline SES values were imputed through proportional odds regression using baseline values of age, sex, race/ethnicity, the Center for Epidemiological Studies of Depression (CES-D) total score (Radloff, 1977), literacy, and years of education as predictors.

Data analysis

We followed the steps outlined for the IT-modeling approach detailed below.

1. Specifying the model set.

Based on research indicating potential interactions between literacy and sex, APOE ɛ4 count (0=reference group) or age (on cognitive outcomes), we developed a set of 28 research-supported hypothesized models representing increasingly complex relationships among sex, literacy, APOE ɛ4 status, and age-related cognitive decline (Table 2). We then proceeded with steps 2–7 for each of our outcomes.

Table 2:

Model set fixed effects structure

Model #	Model hierarchy	SES and SES^2	ESL	URG	Sex	Age	WRAT	APOE	Age^2	Sex * Age	Sex * Age^2	WRAT * Age	WRAT * Age^2	APOE * Age	APOE * Age^2	Sex * WRAT	Sex * APOE	Sex * WRAT * Age	Sex * WRAT * Age^2	Sex * APOE * Age	Sex* APOE * Age^2
1	baseline model	x	x	x	x	x
2	M1 + WRAT	x	x	x	x	x	x
3	M1 + APOE	x	x	x	x	x		x
4	M1 + Age^2	x	x	x	x	x			x
5	M1 + WRAT + APOE	x	x	x	x	x	x	x
6	M1 + WRAT + Age^2	x	x	x	x	x	x		x
7	M1 + APOE + Age^2	x	x	x	x	x		x	x
8	M1 + WRAT + APOE + Age^2	x	x	x	x	x	x	x	x
9	M1 + Sex * Age	x	x	x	x	x				x
10	M9 + Sex * Age^2	x	x	x	x	x			x	x	x
11	M2 + WRAT * Age	x	x	x	x	x	x					x
12	M11 + WRAT * Age^2	x	x	x	x	x	x		x			x	x
13	M3 + APOE * Age	x	x	x	x	x		x						x
14	M13 + APOE * Age^2	x	x	x	x	x		x	x					x	x
15	M9 + WRAT * Age	x	x	x	x	x	x			x		x
16	M9 + APOE * Age	x	x	x	x	x		x		x				x
17	M11 + APOE * Age	x	x	x	x	x	x	x				x		x
18	M15 + APOE * Age	x	x	x	x	x	x	x		x		x		x
19	M2 + Sex * WRAT	x	x	x	x	x	x									x
20	M3 + Sex * APOE	x	x	x	x	x		x									x
21	M9 + Sex * WRAT	x	x	x	x	x	x			x						x
22	M9 + Sex * APOE	x	x	x	x	x		x		x							x
23	M19 + Sex * APOE	x	x	x	x	x	x	x								x	x
24	M21 + Sex * APOE	x	x	x	x	x	x	x		x						x	x
25	M1 + Sex * WRAT * Age	x	x	x	x	x	x			x		x				x		x
26	M1 + Sex * WRAT * Age^2	x	x	x	x	x	x		x	x	x	x	x			x		x	x
27	M1 + Sex * APOE * Age	x	x	x	x	x		x		x				x			x			x
28	M1 + Sex * APOE * Age^2	x	x	x	x	x		x	x	x	x			x	x		x			x	x

Note: Models represent several possible hypothesized associations between sex, age, WRAT, and APOE. For example, Model 1 includes within person random effects (intercept and age-related slope) and SES, ESL, URG, sex and age. Model 1 terms are included in all other models. Given the potential for differences in age-related trajectories, Models 9, 11, and 13 examine whether sex, WRAT, or APOE influence age-related change in a linear way while models 10, 12, and 14 examine non-linear (i.e., quadratic) differences.

2. Fit each model and check model assumptions.

All models used a mixed effects structure, with the fixed effects for each model in the set as specified by Table 2, and subject specific intercepts and age-related slopes as random effects. For outcomes of AVLT Delay and BNT, logistic regression mixed models were used to address the discrete nature and ceiling effects in the data; other outcomes used standard linear mixed effects models. For all models, SES was treated as continuous, age and SES were centered to their baseline means, and their associated quadratic terms calculated from these centered values. Each model was fit to the data by maximum likelihood, and model diagnostics were performed on the model with the most parameters and the “best fitting” model (lowest AICc value). Diagnostics included checking for homoscedastic and appropriately distributed residuals, outliers, normally distributed random effects, correlation between random effects and residuals, and overdispersion (for logistic regressions). CFL and IICV were square-root transformed to address residuals issues. Stroop Color Word was removed from subsequent analysis due to several residuals violations not addressed with reasonable transforms.

Even after reasonable transformations, the following issues persisted. Small correlations between the random effects and residuals were noted (≤ ~|0.3|). CFL also had several large positive residual outliers associated with a single subject. A sensitivity analysis for CFL removed this subject and re-performed the entire algorithm; because results did not change in any meaningful way, CFL results presented here include this subject.

3. Extract model statistics.

For each model in the set, the extracted model statistics included the number of model parameters (k, including number of both fixed and random effects terms), Akaike’s Information Criterion-corrected (AICc), and the log likelihood statistic. AICc is based on the Kullback-Leibler (K-L) divergence, which is a measure of information loss when model ‘g’ is used to approximate the true data generating model, model ‘f’ (Burnham & Anderson, 2003). For data with n observations and fitted regression model ‘g’ with k parameters, the formula for AICc is (K. P. Burnham & Anderson, 2002):

$$AICc=-2\ln \left(p(y|\widehat{\theta })\right)+\frac{2kn}{n-k-1}$$

where y is the observed data, $\widehat{\theta }$are the maximum likelihood estimates of the k parameters from model ‘g’, and ‘p()’ the likelihood function for model ‘g’.

4. Calculate Δ_j’s.

The minimum AICc across the model set was used to calculate the difference between the best fitting model (i.e., that with the minimum AICc) and model j. For model j:

$${\Delta }_j=(AICcofmodelj)-(minimumAICcvalueinset),forj=1,2,\dots Jmodelsintheset$$

5. Calculate model weights.

Δ_j’s for each model are used to calculate the Akaike weights (w_j’s) of all models in the set. Heuristically, w_j represents the likelihood that model j is the K-L best model in the set. The w_j’s helps quantify model uncertainty and are used to combine information across the set of models. w_j is calculated as:

$$w_j=\frac{exp\left(-{\mathrm{\Delta }}_j/2\right)}{{\displaystyle {\sum }_{k}exp}\left(-{\mathrm{\Delta }}_k/2\right)}$$

6. Combine results across models.

Regression coefficient results from each model are multiplied by their corresponding weight (w_j), and all weighted results are then summed together for the final model averaged result. When a regression parameter does not appear in a particular model, it is set to zero in that model. Thus, for the i^th regression parameter in one model, the model averaged i^th regression parameter is:

$${\overline{\widehat{\beta }}}_i={\displaystyle \sum _j{\omega }_j}{\widehat{\beta }}_{i(j)},where{\widehat{\beta }}_{i(j)}=0if{\beta }_{i}doesnotappearinmodelj$$

7. Confidence intervals and inference using model averaged results.

To facilitate multi-model inference, model-averaged estimates were evaluated using 95% CI’s obtained through non-parametric bootstrapping. For each outcome, the data used to fit the model sets was first stratified at the subject level by the total number of visits (2, 3, 4, or 5) per subject. Within each stratum, subjects were selected, with replacement, back to the number of subjects within that stratum, thus preserving the original number of subjects, observations/subject, and distribution of follow-up visits. Each bootstrap replicate went through steps 2–6; 10,000 bootstrap replicates were performed for each outcome. Bootstrap quantiles were used to calculate CI’s (using linear interpolation when necessary). Standard CI interpretation methods were used for inference about regression parameters (i.e., CI’s that did not overlap with 0 were considered significant at the α=0.05 level). This process was used for both regression parameters and predicted outcomes.

Bootstrap rationale.

While Burnham and Anderson propose analytical methods for model-averaged inference and CI’s, these methods are predicated upon assumptions of a limiting normal distribution for the model-averaged estimate (Burnham & Anderson, 2002). Clauskens and Hjort have shown that, unless one assumes the model weights (w_j’s) used are fixed and not random quantities, there is no guarantee of a limiting normal distribution (Claeskens & Hjort, 2008). Thus, we utilized bootstrapping methods similar to those proposed by Burnham and Anderson (Burnham & Anderson, 2002).

Secondary analyses.

Comparison of modeling methods.

To illustrate how results from the above approach differ from some traditional approaches, we selected three tests and compared IT model averaged results with results obtained via single regression models determined by a best fitting model approach and by a backwards elimination approach. In both methods, the same general mixed effects model structure and use of maximum likelihood fits were used. For the best fitting approach, the model selected was that out of the candidate set which had the minimum AICc value. For backwards elimination, the starting model included all terms that appeared in any of the models within the candidate set, and the criteria for elimination was which covariate reduced AICc by the largest amount, while preserving the hierarchy of higher order terms. Elimination stopped when removal of any remaining term did not reduce AICc. For both methods, CI’s and inference from the resulting single models utilized the asymptotic normal properties of regression estimates.

Type I error assessment.

No family-wise error rate correction was performed; however, an assessment of the interaction findings in relation to type I error rates was done. For each outcome, 17 unique interaction coefficients defined by the model set were examined (eleven two-way and six three-way) for a total of 99 two-way and 54 three-way interactions across the nine outcomes. For each of these coefficient groupings, the binomial distribution was used to examine how often one would expect to detect at least the number of significant coefficients found in these analyses (at the 0.05 level), assuming the global null hypothesis that all coefficients are truly zero, and (naively) the results collection is mutually independent.

Software used.

All analyses were performed using R version 3.4.0. Proportional hazard models were fit using ‘polr’ in the MASS package; mixed effect regression models were fit using ‘lmer’ and ‘glmer’ in the lme4 package; AICc-based model statistics were calculated using ‘aictab’ in the AICcmodavg package; bootstrapping was performed utilizing HTCondor version 8.6.3.

Results

Sample Characteristics

Baseline sample characteristics are shown in Table 1 overall and by sex. Mean(sd) age at baseline and last visit were 53.7(6.6) and 62.8(6.8), respectively. Men and women did not differ in terms of age, years of follow-up, proportion of URG or ESL, and IICV. The sexes differed on APOE ɛ4 count, SES, and all cognitive tests at baseline. Women performed better than men at baseline on all tests except BNT and Digit Span. Those who were excluded due to having completed only one visit did not differ from the analysis group in terms of age, sex, or IICV but did have lower SES and baseline cognitive scores, and higher proportions URG (36%) and ESL (10.8%).

Model-averaged Results

Model averaged coefficients and corresponding 95% CI’s for all non-intercept terms are shown in Tables 3 (AVLT Total, AVLT Delay, log₁₀Trails A and log₁₀Trails B, and CFL) and 4 (Digit Span forward and backward, BNT, and 4-Test IICV). In each table, 95% CI’s that exclude 0 are identified by bold-face; gray shading denotes CI’s containing 0. AICc’s and weights for all outcomes and models in the set are presented in Supplemental Table 2. Results are summarized below using model numbers (and the first time a model number is referenced in the results, the corresponding highest order term(s) beyond those included in Model 1 are included in parentheses); for each outcome, results are supported by a two-panel figure (left-panel depicts 95% CIs that exclude 0 and right-panel depicts predicted outcomes by age and selected predictors using model-averaged estimates).

Table 3:

Model averaged parameters for all model terms AVLT Total, AVLT Delay, log₁₀Trails A, log₁₀Trails B, and Square-root CFL

Model term	log10 Trails A	log10 Trails B	AVLT Total	AVLT Delayed	Sqrt CFL
SES	−0.008 (−0.015, −0.002)	−0.013 (−0.02, −0.006)	0.442 (0.018, 0.86)	0.056 (0.001, 0.114)	0.047 (−0.001, 0.095)
SES^2	0.005 (2.78E–05, 0.01)	0.005 (−0.001, 0.012)	−0.261 (−0.537, 0.013)	−0.012 (−0.048, 0.024)	−0.003 (−0.039, 0.032)
URG	0.063 (0.035, 0.091)	0.099 (0.067, 0.131)	−2.301 (−3.973, −0.677)	−0.177 (−0.386, 0.035)	−0.003 (−0.194, 0.183)
Male	0.034 (0.022, 0.053)	0.037 (0.021, 0.051)	−5.799 (−6.709, −4.908)	−0.64 (−0.773, −0.537)	−0.173 (−0.277, −0.024)
Age	2.67E–04 (−3.72E–04, 0.001)	0.003 (0.002, 0.004)	−0.096 (−0.148, −0.057)	−0.006 (−0.011, 0.001)	0.014 (0.01, 0.017)
ESL	−0.002 (−0.06, 0.054)	−0.009 (−0.064, 0.049)	−0.988 (−3.959, 1.905)	−0.176 (−0.539, 0.254)	−0.014 (−0.396, 0.379)
Male x Age	−1.51E–04 (−0.002, 0.001)	1.01E–04 (−0.001, 0.002)	−0.104 (−0.178, −0.005)	−0.01 (−0.021, −0.001)	−0.001 (−0.01, 0.003)
one APOE ε4	2.69E–05 (−0.007, 0.009)	0.001 (−0.001, 0.014)	−0.033 (−1.186, 0.052)	−0.002 (−0.134, 0.046)	0.009 (−0.023, 0.146)
two APOE ε4	−2.03E–05 (−0.028, 0.007)	4.36E–04 (−0.008, 0.022)	−0.081 (−2.456, 0.015)	−0.014 (−0.401, 0.003)	−0.012 (−0.23, 0.043)
Male x one APOE ε4	2.41E–06 (−0.011, 0.017)	4.39E–05 (−0.001, 0.007)	3.41E–04 (−0.996, 0.925)	0.003 (−0.029, 0.222)	−0.029 (−0.368, −1.25E–06)
Male x two APOE ε4	1.28E–04 (−0.01, 0.075)	1.89E–05 (−0.01, 0.008)	0.118 (−2.439, 9.44)	0.005 (−0.368, 1.23)	−0.004 (−0.845, 0.84)
Age x one APOE ε4	2.11E–07 (−5.73E–05, 0.002)	5.76E–08 (−1.82E–06, 9.14E–05)	−7.57E–06 (−0.004, 0.001)	−2.25E–05 (−0.006, 0.001)	2.05E–07 (−3.72E–04, 4.92E–04)
Age x two APOE ε4	−1.12E–06 (−0.003, 7.38E–06)	1.89E–07 (−2.48E–06, 1.95E–04)	−2.79E–05 (−0.013, 0.002)	−1.42E–04 (−0.031, 0.001)	−9.33E–06 (−0.007, 7.55E–06)
Age^2	4.96E–06 (−1.48E–06, 1.32E–04)	6.74E–05 (1.16E–06, 1.43E–04)	−0.001 (−0.007, −5.22E–06)	1.06E–06 (−5.95E–05, 3.71E–04)	−2.32E–05 (−0.001, 1.03E–06)
Male x Age^2	−8.76E–06 (−2.29E–04, −1.03E–08)	1.12E–05 (−5.02E–05, 1.38E–04)	1.04E–04 (−0.004, 0.005)	−2.37E–06 (−0.001, 1.29E–05)	2.96E–05 (−3.24E–06, 0.001)
Age^2 x one APOE ε4	3.62E–09 (−7.51E–06, 8.92E–05)	5.41E–14 (−1.65E–20, 1.50E–07)	−3.80E–21 (−6.02E–12, −6.18E–32)	−6.12E–19 (−2.74E–08, 4.51E–11)	−1.66E–38 (−4.99E–27, 6.95E–28)
Age^2 x two APOE ε4	8.71E–09 (−1.30E–05, 2.01E–04)	−1.02E–13 (−2.00E–07, 2.03E–13)	−6.14E–21 (−4.74E–12, 4.94E–17)	−2.54E–18 (−2.36E–07, 3.84E–12)	−2.93E–38 (−1.90E–26, 6.40E–28)
Male x Age x one APOE ε4	−7.52E–07 (−0.005, −1.89E–11)	−1.01E–14 (−7.53E–07, −3.29E–28)	1.53E–21 (−2.83E–13, 3.13E–12)	9.58E–18 (−1.22E–09, 6.91E–07)	6.76E–37 (−6.22E–29, 1.24E–24)
Male x Age x two APOE ε4	2.77E–06 (3.53E–10, 0.014)	1.16E–14 (−4.73E–08, 1.13E–07)	1.94E–20 (−2.38E–14, 2.35E–10)	2.95E–17 (−2.89E–08, 1.75E–06)	4.95E–36 (−1.74E–29, 1.79E–23)
WRAT reading	0.001 (2.76E–06, 0.002)	−0.002 (−0.003, −0.001)	0.142 (0.091, 0.197)	0.018 (0.01, 0.025)	0.024 (0.018, 0.03)
Male x WRAT reading	−0.002 (−0.004, −7.27E–06)	−0.001 (−0.003, 3.36E–05)	0.113 (0.005, 0.213)	0.007 (−1.94E–04, 0.02)	0.012 (0.001, 0.023)
Age x WRAT reading	−3.70E–06 (−1.12E–04, 2.54E–05)	−6.60E–06 (−1.07E–04, 7.96E–05)	−5.13E–05 (−0.004, 0.004)	−4.21E–05 (−0.001, 2.04E–04)	4.55E–05 (−4.26E–06, 0.001)
Age^2 x WRAT reading	−2.63E–08 (−6.09E–06, 5.25E–06)	2.74E–06 (−2.96E–07, 1.61E–05)	−2.34E–06 (−2.92E–04, 2.64E–04)	−1.66E–07 (−3.77E–05, 1.99E–06)	2.12E–06 (−5.98E–08, 6.13E–05)
Male x Age x WRAT reading	−1.85E–06 (−1.24E–04, 1.03E–04)	6.46E–07 (−1.31E–04, 1.31E–04)	0.001 (−0.003, 0.009)	6.11E–05 (−5.62E–05, 0.001)	−3.18E–05 (−0.001, 1.03E–04)
Male x Age^2 x WRAT reading	2.27E–08 (−7.72E–06, 8.58E–06)	−3.08E–06 (−2.16E–05, 1.22E–07)	−2.70E–05 (−0.001, 3.34E–04)	1.28E–07 (−6.11E–06, 3.61E–05)	−2.32E–06 (−7.99E–05, 1.35E–06)
Male x Age^2 x one APOE ε4	−1.06E–08 (−2.30E–04, 6.12E–07)	−1.10E–16 (−6.63E–09, 1.58E–10)	3.71E–22 (−8.99E–16, 1.21E–12)	−3.42E–19 (−7.80E–08, 2.43E–11)	−1.19E–37 (−5.49E–25, −1.24E–49)
Male x Age^2 x two APOE ε4	−4.06E–08 (−0.001, 3.08E–05)	1.26E–15 (−9.45E–13, 8.32E–08)	−2.84E–21 (−4.52E–11, 6.42E–20)	−6.96E–18 (−4.33E–06, 2.47E–13)	2.66E–37 (−2.49E–28, 3.36E–25)

Note: “E” represents “x10^”; e.g. 1.23E–04 = 1.23×10^−4

95% CI’s that do not overlap 0 (are significant) are identified by bold-face font; gray shading denotes CIs that overlap 0.

Memory.

For AVLT Total, Model 21 (highest order terms: sex*age, sex*WRAT) was best-fitting, contributing a weight of .562 to model averaging; Model 26 (sex*WRAT*age²) contributed .183 and Model 25 (sex*WRAT*age) contributed .139 (weights in supplemental Table 2); all other model weights were under .05. Significant interactions included ɛ4 count 1*age², sex*age, and sex*literacy (left-panel, Figure 1). Figure 1 (right-hand panel) depicts AVLT Total model-averaged predicted performance for the latter two interactions since the estimated beta for the interaction with age and ɛ4 count 1 was ostensibly 0 (i.e., at 10 years below the average age, estimated AVLT performance is .0329 points higher for those with 0 vs 1 ɛ4 allele while at 10 years above the average age, estimated AVLT performance is .0331 points higher for those with 0 vs 1 ɛ4 allele). There’s a larger gap in AVLT Total scores for high vs low literacy in men than in women (i.e., worse scores at lower literacy levels) and men show faster AVLT Total age-related decline than women.

The best fitting model for AVLT Delay was also Model 21 (weight=.531), followed by Model 15 (WRAT*age, sex*age, weight=.123) and Model 25 (.119). Variability in AVLT Delay was explained largely by SES, sex, literacy and age, with age-related AVLT Delay decline steeper for men than women (see Supp. Fig. 1A for S trajectories).

Executive function/ Working Memory.

The best fitting models for log₁₀ Trails B were Models 6 (WRAT + age²; weight=.330), 26 (weight=.297), 12 (WRAT*age²; weight=.124), and 19 (sex*WRAT; weight=.109). Variability in log₁₀ Trails B was explained by SES, URG status, sex, literacy, age (linear and quadratic), and a 3-way interaction with sex*APOE ɛ4 count 1*age (left-hand panel, Figure 2A). Though significant, the estimated beta for the sex*age*APOE interaction was again close to 0. Predicted age-related trajectories show slower times for men than women and lower vs higher literacy (right-hand panel, Figure 2A; no predicted values are shown for men and APOE ɛ4 count=2 due to the small cell size (n=4)).

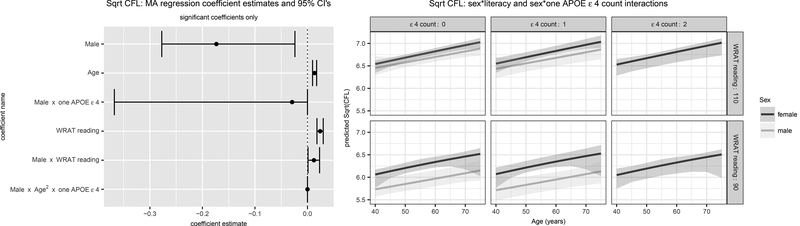
Figure 2. Trails B and CFL Significant Model-Averaged Terms (Left) and Predicted Values (Right).

Results in Figure 2A are for Trails B (log10 transformed) and in Figure 2B are for CFL (square-root transformed). For each, the left panel depicts parameter estimates and 95% confidence intervals (CI’s) for CI’s that do not overlap 0. The right panel depicts predicted values and 95% confidence limits using the model averaged parameter estimates for both sexes, high vs low literacy, and APOE ɛ4 allele count. SES=Socioeconomic status; URG = Underrepresented groups; WRAT = Wide Range Achievement Test (3rd edition).

The best fitting models for Digit Span Backward were Models 6 (weight=.583), 12(.168), 26(.117), and 8 (WRAT + APOE + age²; weight=.104). Variability in Digit Span Backward was explained by quadratic age, literacy, and sex with greater sex differences at higher literacy levels (Supp. Figure 1B).

Attention.

The best fitting models for log₁₀ Trails A were Models 19 (weight=.574), 21 (.248), and 25 (.064). Supplemental Figure 1C depicts significant beta estimates and their CI’s (left panel) and predicted values vs age, stratifying by sex and literacy (high vs low; right panel). Predicted values indicate that women of high literacy perform worse on log₁₀ Trails A than women of low literacy while the opposite is true for men. Although the interactions of sex*quadratic age, and sex*age*APOE ɛ4 counts of 1 or 2 were statistically significant, all had estimated betas extremely close to 0 (Table 4; Supp. Fig. 1C).

Table 4:

Model averaged parameters and 95% CI’s for all model terms and CFL, BNT, Digit Span Forwards, Digit Span Backwards, and 4 Test IICV

Model term	Boston Naming	Digit Span Forwards	Digit Span Backwards	Sqrt 4 test IICV
SES	0.012 (−0.052, 0.075)	−0.001 (−0.116, 0.111)	0.031 (−0.08, 0.145)	−0.003 (−0.013, 0.006)
SES^	−0.053 (−0.095, −0.001)	−0.05 (−0.121, 0.024)	−0.032 (−0.105, 0.048)	0.001 (−0.006, 0.008)
URG	−0.695 (−0.888, −0.487)	−0.346 (−0.794, 0.1)	−0.26 (−0.719, 0.194)	−0.021 (−0.056, 0.016)
Male	0.225 (0.122, 0.353)	0.344 (0.102, 0.628)	0.22 (−0.041, 0.425)	0.022 (1.97E-04, 0.043)
Age	0.014 (0.009, 0.02)	−0.014 (−0.025, −0.006)	0.004 (−0.004, 0.018)	0.001 (2.79E-04, 0.002)
ESL	−0.672 (−0.983, −0.351)	−0.236 (−1.068, 0.604)	0.012 (−0.796, 0.849)	0.007 (−0.057, 0.073)
Male x Age	−1.29E–05 (−0.011, 0.001)	−1.59E–04 (−0.016, 0.016)	−0.001 (−0.03, 0.004)	2.10E–04 (−0.002, 0.002)
one APOE ε4	−8.14E–08 (−0.209, 0.005)	0.001 (−0.042, 0.21)	−0.007 (−0.192, 0.046)	−3.21E–14 (−4.89E–08, 3.58E–11)
two APOE ε4	0.024 (−0.004, 0.437)	−0.002 (−0.268, 0.201)	0.011 (−0.125, 0.399)	9.65E–15 (−5.56E–09, 2.23E–08)
Male x one APOE ε4	−1.06E–07 (−0.008, 8.98E–08)	−0.005 (−0.597, 3.04E–04)	−4.96E–05 (−0.058, 0.003)	2.64E–18 (−7.61E–14, 8.71E–12)
Male x two APOE ε4	−1.16E–07 (−0.007, 2.82E–04)	−0.005 (−1.054, 0.292)	−3.87E–04 (−0.243, 9.44E–05)	−6.43E–18 (−1.29E–11, 1.19E–12)
Age x one APOE ε4	1.39E–10 (−1.23E–07, 5.44E–06)	4.99E–07 (−8.04E–05, 1.57E–04)	−2.01E–05 (−0.019, 1.01E–07)	2.79E–15 (−4.45E–12, 6.67E–09)
Age x two APOE ε4	−2.89E–11 (−4.74E–06, 2.76E–06)	−4.76E–07 (−2.38E–04, 2.25E–04)	1.72E–05 (−0.001, 0.016)	1.07E–14 (−1.20E–13, 2.41E–08)
Age^2	−0.001 (−0.002, −0.001)	−0.001 (−0.002, −2.19E–05)	−0.001 (−0.003, −5.34E–05)	1.69E–04 (1.39E–05, 2.73E–04)
Male x Age^2	1.68E–06 (−5.65E–07, 0.001)	3.14E–04 (−1.75E–05, 0.003)	1.74E–04 (−4.14E–06, 0.003)	−2.03E–04 (−3.78E–04, −1.23E–05)
Age^2 x one APOE ε4	−4.22E–53 (−1.58E–40, 3.89E–45)	3.68E–48 (−2.02E–39, 2.70E–37)	−4.83E–47 (−1.31E–36, 9.17E–40)	1.36E–27 (−5.71E–27, 3.12E–18)
Age^2 x two APOE ε4	−2.89E–52 (−2.67E–40, 6.78E–44)	−3.50E–48 (−8.37E–38, 5.21E–38)	−8.24E–47 (−1.58E–36, 1.02E–38)	1.30E–27 (−9.95E–21, 1.21E–18)
Male x Age x one APOE ε4	9.19E–52 (−6.53E–53, 8.76E–39)	8.40E–48 (−5.94E–42, 2.10E–35)	−6.06E–48 (−3.05E–36, 2.26E–39)	−3.26E–27 (−2.33E–17, 9.20E–25)
Male x Age x two APOE ε4	−2.59E–51 (−7.83E–39, 8.47E–42)	−2.61E–47 (−1.42E–35, 3.11E–38)	4.18E–48 (−2.58E–38, 7.81E–36)	−1.06E–26 (−8.36E–17, 2.84E–23)
WRAT reading	0.046 (0.038, 0.051)	0.073 (0.053, 0.083)	0.079 (0.059, 0.087)	−0.003 (−0.004, −0.002)
Male x WRAT reading	2.60E–05 (−1.06E–05, 0.018)	0.014 (3.42E–04, 0.051)	0.003 (2.05E–05, 0.043)	0.007 (0.005, 0.009)
Age x WRAT reading	9.30E–05 (−2.52E–05, 0.001)	1.62E–04 (−3.61E–04, 0.002)	−1.03E–04 (−0.001, 0.001)	3.28E–04 (2.05E–04, 4.61E–04)
Age^2 x WRAT reading	−1.48E–06 (−2.56E–05, 2.95E–05)	2.75E–05 (1.70E–07, 1.60E–04)	6.62E–06 (−4.67E–05, 1.05E–04)	4.44E–06 (−5.00E–06, 1.50E–05)
Male x Age x WRAT reading	2.61E–07 (−4.02E–04, 0.001)	−3.42E–04 (−0.003, 1.45E–04)	−1.35E–04 (−0.003, 2.30E–04)	1.43E–04 (−6.86E–05, 3.42E–04)
Male x Age^2 x WRAT reading	−5.76E–08 (−6.12E–05, 1.94E–05)	−1.95E–05 (−2.06E–04, 4.47E–05)	−4.03E–06 (−1.41E–04, 7.72E–05)	−6.68E–06 (−2.05E–05, 7.43E–06)
Male x Age^2 x one APOE ε4	8.12E–53 (−1.04E–53, 7.22E–40)	1.19E–49 (−8.64E–40, 9.43E–38)	−2.76E–49 (−9.82E–38, 1.01E–39)	−2.78E–28 (−2.07E–18, 1.01E–25)
Male x Age^2 x two APOE ε4	1.10E–52 (−4.00E–44, 5.31E–40)	−4.20E–49 (−2.62E–37, 7.14E–39)	−1.92E–48 (−1.38E–36, 1.55E–40)	−1.64E–29 (−1.13E–20, 1.08E–18)

Note: “E” represents “x10^”; e.g. 1.23E–04 = 1.23×10^−4

95% CI’s that do not overlap 0 (are significant) are identified by bold-face font; gray shading denotes CIs that overlap 0.

The best fitting models for Digit Span Forward were Models 6 (weight=.307), 26 (.234), 19 (.163), and 12 (.124). Variability in Digit Span Forward was explained by sex, age (linear and quadratic) and literacy; significant interactions included sex*literacy and literacy*quadratic age. The latter beta estimate was near zero; sex differences in the outcome are negligible at low literacy levels while men outperform women at high literacy levels (Supp. Figure 1D).

Language.

The best fitting models for CFL were Models 19 (weight=.416) and 21 (.251). Variability in CFL was explained by age, sex, literacy, and interactions sex*APOE count 1, sex*literacy, and sex*APOE count 1*quadratic age, although the three-way beta estimate was essentially 0 (Figure 2B). Women did better overall and sex differences were smaller in ɛ4 count=0 than count=1. All improved with age. The best fitting models for BNT were Models 6 (weight=.630), 12 (.239), and 8 (.128). Variability in BNT was explained by SES, URG status, sex, age, ESL status, and literacy level with higher literacy, SES, male sex and older age associated with better performance, while URG and ESL status were associated with lower BNT scores (Supp. Figure 2).

Intraindividual variability.

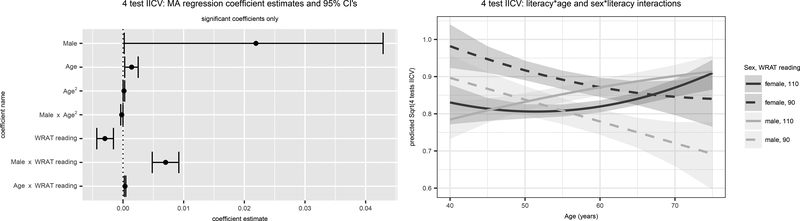
The best fitting model for 4-Test IICV was Model 26 (weight=0.959); all other models contributed <0.05 to the parameter weights. Variability in 4-Test IICV was accounted for by sex, age, and literacy, with significant sex* age², sex*literacy, and literacy*age interactions (Figure 3). At lower levels of literacy, women show higher 4-Test IICV than men and IICV declines with age; in contrast, IICV increases with age at higher literacy levels and is at times higher among men than women (Figure 3).

Figure 3. 4-Test Intraindividual Cognitive Variability Significant Model-Averaged Terms (Left) and Predicted Values (Right).

Results are for the outcome, 4-Test IICV. The left panel depicts parameter estimates and 95% confidence intervals (CI’s) for CI’s that do not overlap 0. The right panel depicts predicted values and 95% confidence limits using the model averaged parameter estimates for both sexes and high vs low literacy. SES=Socioeconomic status; URG = Underrepresented groups; WRAT = Wide Range Achievement Test (3rd edition).

Model comparisons.

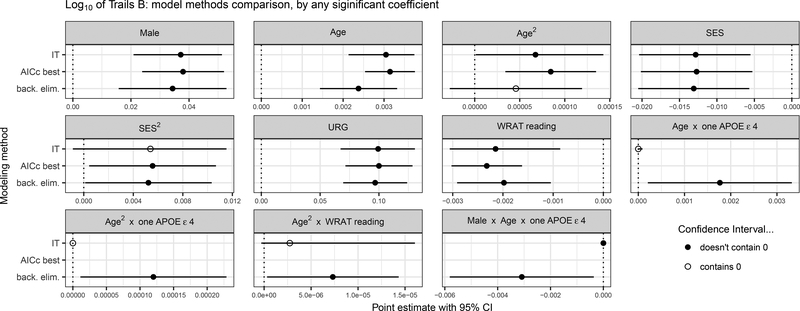
In secondary analyses of 3 outcomes (AVLT Total, AVLT Delay, and Trails B), we compared estimated betas and 95% CI’s between the IT, best fit, and backward selection approaches for coefficients that were significant in any of the methods, per outcome. Results differed most across model selection approaches for Trails B, with 6 of 11 terms inconsistently significant across methods (see Figure 4 for point estimates and CI’s for the three approaches for Trails B and Supplementary Figure 4 for AVLT Total and Delay).

Figure 4. Trails B Significant Results by IT, Best Fit, and Backward Selection Methods.

Parameter estimates and 95% CI’s are depicted for each of three modeling methods (IT, AICc Best Fit, and Backward Elimination) for parameters that were significant by at least one of the three methods. CI’s that overlap 0 (i.e., not significant) are shown in blue. Results varied across methods for all the interaction terms. IT=Information Theoretic model averaging method; AICc best = AICc best fit model selection method; back. Elim.= backward elimination model selection method; SES=Socioeconomic status; URG = Underrepresented groups; WRAT = Wide Range Achievement Test (3rd edition).

Type I error assessment.

Fourteen (14.1%) of 99 unique two-way interactions were significant, corresponding to a probability of 0.00012 under the global null. Four (7.4%) of 54 unique three-way interactions were significant, corresponding to a 0.132 probability under the global null.

Discussion

In this study, we used information-theoretic (IT) model averaging techniques to characterize how sex, APOE ɛ4 carrier status, and literacy modify age-related cognitive and IICV trajectories in a sample that was middle-aged and free of clinical impairment at baseline assessment. We observed age-related declines for all cognitive outcomes except the two language-related measures (CFL and BNT). Age-related declines in IICV were associated with lower literacy levels while IICV tended to increase with age among participants with higher literacy. Significant but small quadratic age effects were observed for a few outcomes. APOE ɛ4 count showed significant but small modifying effects on age-related trajectories on four outcomes. Sex and literacy were consistently significant predictors of measures of memory, executive function, working memory, language and intra-individual cognitive variability with effects showing stronger performance in women (vs men) and higher (vs lower) literacy.

Compared to those with no APOE ɛ4 alleles, carriage of one or two ɛ4 alleles is associated with greater risk of AD (Neu et al., 2017) and faster or earlier cognitive decline in certain domains. For example, in a sample of cognitively normal adults (mean baseline age ~60 years, followed an average of ~5 years), Caselli and colleagues reported accelerated age-related decline on AVLT Delay among APOE ɛ4 carriers (vs non-carriers) beginning prior to age 60 (Caselli et al., 2009). Predicted annual rate of AVLT Delay change, however, was very small for carriers and non-carriers in age-ranges similar to our sample (e.g., 50–59, 0.07 vs 0.08 and 60–69, 0.04 vs −0.03 for non-carriers vs carriers, respectively). In a metaanalyses, Wisdom and colleagues also reported significant yet small differences in age-related decline among APOE ɛ4 carriers relative to non-carriers (Cohen’s d estimated effect sizes <.20; (Wisdom et al., 2011)). Results in our sample showed similar significant, yet small age-modifying effects of one APOE ɛ4 allele (vs 0) for AVLT Total, Trails A and B, and CFL. These patterns, when considered along with data showing that APOE ɛ4 effects on later life cognitive trajectories are mediated by underlying neuropathology (Yu, Boyle, Leurgans, Schneider, & Bennett, 2014), underscore the importance of thoroughly characterizing neuropathology in late-middle age to better understand how APOE ɛ4 confers increased risk of AD dementia.

Previous research has also shown sex differences in risk of MCI (Roberts et al., 2012) and AD (e.g., Altmann et al., 2014), and rates of decline (e.g., McCarrey, An, Kitner-Triolo, Ferrucci, & Resnick, 2016; Mortensen & Høgh, 2001), with other studies showing evidence of potential sex*ɛ4 interactions (Payami et al., 1996). In our sample, sex*age interactions showed lower scores and faster decline in men for both AVLT measures. These results are consistent with other studies such as those reported for the Mayo Clinic Study of Aging in which men had worse memory (including , decline) and lower hippocampal volume compared to women (Jack, Wiste, Weigand, et al., 2015). Sundermann and colleagues posited that the paradoxical higher rates of MCI in men and higher rates of AD in women may be explained at least partially by two things: first, the “female advantage in verbal memory” may constitute a form of cognitive reserve for women which delays declines in verbal memory until older ages or until AD biomarkers are present; and second, the use of norms that don’t adjust for sex may result in over-identification of men or delayed identification of women with MCI (Sundermann et al., 2017, 2016).

Literacy level as measured by word reading tasks is considered a proxy for verbal intellectual ability and quality of education; lower literacy has been associated with faster memory decline in non-demented elders (e.g., Manly et al., 2003). Higher literacy levels have also been shown to be associated with resilience to APOE ɛ4-related cognitive decline (Kaup et al., 2015; Vemuri, Lesnick, Przybelski, et al., 2014). In our sample, literacy did not modify effects of APOE ɛ4 or age on cognition. These results were consistent, however, with other studies showing main effects only for predictors such as literacy or educational attainment (e.g., Berggren, Nilsson, & Lövdén, 2018, Lenehan, Summers, Saunders, Summers, & Vickers, 2015) and suggest that performance differences in late middle-age associated with these measures “reflect the persistence of earlier-life differences in cognitive functioning, and not differential rates of cognitive decline” (p. 11, Tucker-Drob, Johnson, & Jones, 2009). We did observe several sex*literacy interactions showing the pattern that the benefits of higher literacy associated were stronger for men than women for AVLT Total, Trails A, CFL and Digit Span; these results also underscore the importance of using norms that adjust for key demographic features.

4-Test IICV had several moderating effects. At lower literacy/premorbid verbal ability levels predicted IICV declined faster with age among men compared to women. In contrast, predicted IICV increased with age at higher literacy levels (and for both sexes), suggesting probable worsening in memory and/or executive function relative to premorbid verbal abilities. This pattern corresponds to other studies that have shown that higher IICV (calculated using variables similar to those we used) predicts MCI, AD or AD pathology ((E. D. Anderson et al., 2016; Gleason, Norton, Anderson, Wahoske, Washington, Umucu, Koscik, Dowling, Johnson, Carlsson, et al., 2017; Holtzer et al., 2008; Koscik et al., 2016)). The former pattern suggests that future studies could examine whether the risk-indicating value of IICV varies across underlying characteristics such as sex and literacy.

Traditional model selection methods such as stepwise regression are prone to overfitting the data, producing overconfident estimates with standard errors that do not account for the degrees of freedom in the search process (Hastie, Trevor, Tibshirani, Robert, & Friedman, Jerome, 2009). Shrinkage methods, such as Lasso (Taylor & Tibshirani, 2015), can help select important predictors with respect to the outcome, but parsimonious models and predictive accuracy are the typical goal, and statistical inference can be difficult (Hastie, Tibshirani, & Wainwright, 2015). While new post-selection inference techniques exist for certain models, they have not been developed for mixed models (Lee, Sun, Sun, & Taylor, 2016) and extensions of Lasso to mixed modeling environments have not yet been developed for inference (Schelldorfer, Bühlmann, & Van de Geer, 2011). Bayesian model averaging combines information from posterior distributions of parameters of interest across several models, weighting each by its posterior model probability (Hoeting, Madigan, Raftery, & Volinsky, 1999). However, it is important in Bayesian methods to formulate reasonable prior distributions for all parameters and model probabilities, and this can be prohibitive when the set of models under consideration is large (Claeskens & Hjort, 2008), Chen and colleagues (Chen, Ibrahim, Shao, & Weiss, 2003) have developed an automatic method that requires few hyperparameters to be directly specified, but their method depends upon the existence of a comparable independent dataset that can be used for elicitation. By using the IT approach in this paper, we obtained the robustness benefits of model averaging without the overhead of Bayesian methods, while still yielding familiar statistical outputs that support inferences (i.e. point estimates, CI’s).

Our secondary analyses suggest that the IT approach may guard against over-identifying and overestimating effects compared to traditional methods. First, in our comparison of the IT approach with best fit and backwards elimination approaches, main effects estimates between the three methods were generally very similar, though the IT method tended to have the widest confidence intervals. Relationships between the three methods were more complex for quadratic effects and interactions. Backwards elimination commonly “found” interactions that best fit did not, while IT tended to attenuate the estimated interaction coefficient ostensibly to zero. Second, the high numbers of significant two-way interaction effects detected in the IT method were well above those expected from random chance under the global null, lending confidence to conclusions about significant IT model-averaged effects. For all 4 significant three-way interactions, the IT method estimates have very tight CI’s that are extremely close to zero, especially compared to estimates that were found by backwards elimination, suggesting that IT methods might further guard against overconfident results.

The generalizability of our results is limited by cohort characteristics, including that our sample is relatively young, highly educated, enriched for AD risk, has few males homozygous for ɛ4 and has limited follow-up on participants from URG’s. In addition, use of APOE ɛ4 count is just one of many possible ways of parameterizing APOE-associated risk. The IT approach is computationally intensive and is not appropriate for every analysis scenario involving model selection, particularly those with few model terms. Like any model selection or averaging approach, IT model averaging methods are not without potential pitfalls. For example, some question whether weights assigned to models can reasonably extend to weights on specific model parameters between the models (Cade, 2015). Post-selection inference, model averaging and associated methods such as Lasso are still areas of active research and vetting through application. Applying these methods to additional data sets including simulated data sets with pre-specified characteristics (i.e. significant effects) will help inform when the more complex approaches yield most benefit in terms of predictive or inferential accuracy.

Conclusions

Data increasingly suggest that there are multiple risk factors that influence the path to Alzheimer’s dementia. Simple model selection approaches (e.g., building up models and comparing more complex to less complex nested models) will continue to be useful ways to handle relatively simple sets of model comparisons. However, as researchers seek to consider multiple risk factors simultaneously, more complex methods that are appropriate for mixed effects models and which avoid the pitfalls of methods like stepwise selection are needed. The IT model averaging approach offers a framework that allows results from multiple plausible hypotheses to provide weighted model-averaged parameter estimates and CI’s which can then be used to make inferences about parameters and to estimate outcomes.

The results from the WRAP sample suggest that age-related trajectories are modified more by sex and literacy levels than by APOE ɛ4 allele count in this age range. These patterns may be important to consider when interpreting standard scores that ignore sex or literacy in their calculations. Future applications of the IT methodology will examine the interplay of sex and literacy with other potential cognitive trajectory-modifying variables such as polygenic risk, AD biomarkers, or lifestyle factors (e.g., exercise or diet).