Assessing the Clinical Impact of Risk Models for Opting Out of Treatment

Abstract

Decision Curves are a tool for evaluating the population impact of using a risk model for deciding whether to undergo some intervention, which might be a treatment to help prevent an unwanted clinical event or invasive diagnostic testing such as biopsy. The common formulation of Decision Curves is based on an opt-in framework. That is, a risk model is evaluated based on the population impact of using the model to opt high-risk patients into treatment in a setting where the standard of care is not to treat. Opt-in Decision Curves display the population Net Benefit of the risk model in comparison to the reference policy of treating no patients. In some contexts, however, the standard of care in the absence of a risk model is to treat everyone, and the potential use of the risk model would be to opt low-risk patients out of treatment. Although opt-out settings were discussed in the original Decision Curve paper, opt-out Decision Curves are under-utilized. We review the formulation of opt-out Decision Curves and discuss their advantages for interpretation and inference when treat-all is the standard.

Introduction

We consider a setting with a well-defined patient population and some treatment or intervention directed at an unwanted clinical event. An example is estrogen-receptor-positive and node-positive breast cancer, typically treated with both hormonal therapy and adjuvant chemotherapy to help prevent relapse and reduce mortality. If a patient could look into the future and know that she would not relapse without adjuvant chemotherapy, she could forego chemotherapy, avoiding its expense and toxicity. A risk prediction instrument calculates, for each patient, her risk of relapse without adjuvant chemotherapy. An important question is whether the prediction instrument should be incorporated into the decision concerning chemotherapy, so that patients at low risk following hormonal therapy could forego chemotherapy.

Decision Curves are a tool for evaluating risk models for making decisions about an intervention based on risk [1]. The intervention can be a medical treatment, as in the example above, or may be a diagnostic test (such as biopsy) or intensive monitoring. Following conventions, we refer to all interventions as “treatment.” We recently reviewed Decision Curve methodology, offered guidance on the appropriate use of Decision Curves, and cautioned against misinterpretations [2]. An important aspect of using Decision Curves to best effect is identifying the relevant reference policy. The most relevant reference policy depends on whether standard practice, absent a prediction tool, is to recommend for or against treatment. The Decision Curves featured most prominently in the original paper [1] evaluate using a risk model to identify high-risk patients who should opt into treatment; the reference policy is treat-none. Reviews and extensions to Decision Curve analysis have exclusively discussed these opt-in Decision Curves [2–4]. In an informal survey of the literature, we were unable to find instances of Decision Curves using treat-all as the reference, even when treat-all is the standard ([5–7]).

This report reviews the formulation of opt-out Decision Curves when the potential use of a risk model is to opt low-risk patients out of treatment, and advocates for their use in such contexts.

Decision Curves for Opt-Out Treatment Policies

The setting is a clinical context where there is a decision to be made about undergoing a specified treatment related to an unwanted clinical event. In a patient population the current policy is treat-all, and there is interest in using a risk model to opt low risk patients out of treatment.

We follow existing notation [2, 8] and emphasize that key assumptions underlying Decision Curves apply in both the opt-out and opt-in contexts [2]. Patients who will go on to experience the clinical event (cases) have expected benefit B>0 from the treatment (where B accounts for the totality of good and bad effects of the treatment). Similarly, patients who will not experience the event (controls) have expected cost (or burden) of the treatment, C>0. Decision Curves incorporate a classical decision theory result: given benefits B and cost C, the optimal risk threshold R for deciding treatment is

$$R=\frac{C}{C+B}=\frac{\frac{C}{B}}{1+\frac{C}{B}}\leftrightarrow \frac{C}{B}=\frac{R}{1-R}$$ (1)

All Decision Curves assume that R reflects the relative size of C and B at (1). Decision Curves are useful in settings where C/B, and hence R, is unknown, with the presumption that once consensus on C/B is achieved, then R will be chosen accordingly.

When current policy is treat-all, all controls experience the cost C of treatment. The potential advantage of an opt-out policy to the patient population would accrue from controls whose predicted risks are below R; such patients avoid the cost C. The expected gain of using the risk model is TNR_R∙(1-ρ)∙C, where TNR_R is the true negative rate for risk threshold R and ρ is the proportion of cases in the population. The disadvantage of an opt-out policy in a treat-all context arises from cases who are no longer treated, quantified by FNR_R∙ρ∙B, where FNR_R is the false negative rate for threshold R.

One can consider B to be in units of C because only the relative size of B and C matters. Applying the relationship between (B, C) and R at (1), the Net Benefit of a risk-based opt-out treatment policy to the patient population is:

$$N{B}^{opt-out}=(1-\rho )TN{R}_R-\rho \frac{1-R}{R}FN{R}_R$$

We emphasize that this expression is accurate only in so far as the risk threshold R faithfully represents the cost:benefit ratio C/B. The opt-out Decision curve plots NB^opt-out versus the risk threshold R.

As with opt-in Decision Curves, interpreting the scale of opt-out Decision Curves is challenging because Net Benefit is in units of C. Observe that the maximum possible value of the opt-out Net Benefit is 1−ρ, which would be achieved by a perfect risk model that opts all controls and no cases out of treatment (TNR=1, FNR=0) [9]. Dividing NB^opt-out by 1 – ρ yields an expression that is benchmarked against the perfect model and has been called standardized Net Benefit. Here is the standardized opt-out Net Benefit, sNB^opt-out, presented along with its counterpart for the opt-in context:

$$sN{B}^{opt-out}=TN{R}_R-\frac{\rho }{1-\rho }\frac{1-R}{R}FN{R}_R$$

$$sN{B}^{opt-in}=TP{R}_R-\frac{1-\rho }{\rho }\frac{R}{1-R}FP{R}_R$$

Just as sNBopt-in is interpretable as the TPR appropriately discounted by the FPR [4], sNBopt-out can be viewed as the TNR appropriately discounted by the FNR. Similarly, just as sNBopt-in is interpretable as the fraction of maximum-possible opt-in Net Benefit, sNBopt-out is the fraction of maximum-possible opt-out Net Benefit.

In an opt-out context (current standard is treat-all), the treat-none policy has TNR=FNR≡1 and so the only component of the opt-out Net Benefit for treat-none that requires estimation is the prevalence. Treat-all has TNR=FNR≡0 and so its Net Benefit is 0 without uncertainty. This is directly analogous to the opt-in setting, where treat-none by definition has 0 Net Benefit and the Net Benefit of treat-all is subject to uncertainty in the prevalence.

We note that Net Benefit metrics can also be computed for prediction instruments other than risk models. For example, for binary decision rules, true and false positive or negative rates do not depend on the risk threshold, but the cost:benefit ratio C/B in Net Benefit expressions can still be interpreted on a risk threshold scale.

Relationship with Relative Utility Curves

Relative Utility quantifies the clinical utility of a risk model relative to perfect prediction [9, 10]. Relative Utility curves are hill-shaped, cresting at R=ρ. If a risk model is well-calibrated, then its Relative Utility curve plots 𝑠𝑁𝐵^{𝑜𝑝𝑡―𝑖𝑛} for R>ρ and 𝑠𝑁𝐵^{𝑜𝑝𝑡―𝑜𝑢𝑡} for R<ρ. The logic is to use treat-all as the reference when it is superior to treat-none and vice versa. We prefer to make Decision Curves for a plausible range of R using a consistent reference policy, rather than switching the reference policy at ρ and plotting two different types of Net Benefit.

If a risk model is not well-calibrated, the methodology for relativity utility curves uses a threshold adjustment to achieve the intended risk level, whereas Decision Curve methodology evaluates a risk model “as is.” Although [2] stated general equivalence of the metrics, standardized Net Benefit equals relative utility only for risk models that are calibrated (in the moderate sense, as defined in [11]).

Example

Slankamenac et al [6] propose a risk model for acute kidney injury (AKI) after liver resection. The authors describe that typically all liver resection patients are monitored in intensive care following surgery and suggest that patients at low risk could opt out of this treatment, citing R in 5–20%. For illustration, we simulated data to mimic the results in [6] and assume R=10%.

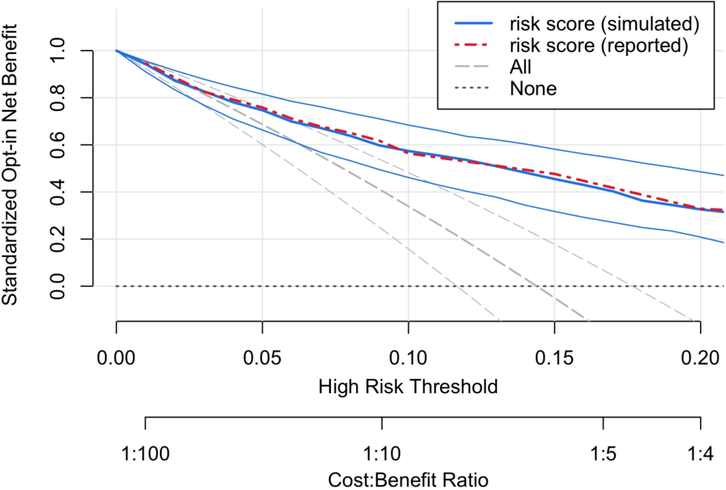
All Decision Curves should be read vertically, starting with a clinically justifiable risk threshold and comparing the Net Benefit of treatment policies at that threshold [2, 12]. Figure 1 shows an opt-in Decision Curve. For R=10%, the risk model has sNB^opt-in ≈57% and treat-none has sNB^opt-in≡0 because it is the reference policy. Figure 1 shows evidence that a risk-based treatment policy is superior to treat-none, but this is not directly relevant to policy evaluation in a context that currently treats all patients. To evaluate the risk model, 57% must be compared to 34%, the sNB^opt-in of treat-all. The contrast is awkward because the Net Benefit of each policy is relative to a third policy, treat-none. Furthermore, it is not possible from the display to evaluate the evidence that the risk-based treatment policy offers higher Net Benefit to the population than current policy.

Figure 1.

Opt-in Decision Curve analysis of the risk model in our simulated data. For comparison, the Net Benefit values reported in the original paper are also shown (see Table 6 in [6]). The standardized Net Benefit of each treatment policy is displayed compared to the treat-none policy, which has Net Benefit 0. The 95% confidence intervals shown in the plot are useful for comparing either the risk model or treat-all with treat-none. However, these confidence intervals cannot be used to compare the risk model with treat-all. For this context, where treat-all is current policy, it is more appropriate to display the standardized Net Benefit of risk-based treatment compared to this reference (Figure 2).

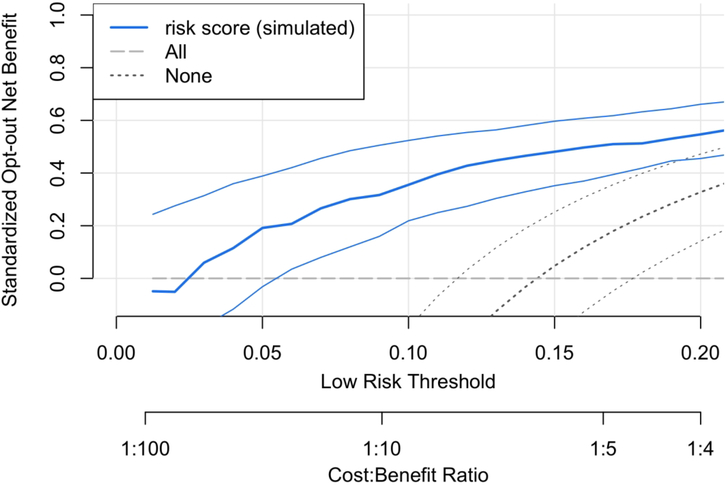
Using the same data, Figure 2 shows the opt-out Decision Curve. Now, treat-all is the reference and has constant 0 Net Benefit. Because the reference policy matches current policy, Figure 2 is more readily interpretable for the application. For the risk thresholds R=5%−20%, we estimate that using the model to opt low-risk patients out of treatment offers 20%−55% of the Net Benefit of perfect prediction. For R=10%, sNB^opt-out = 36%; the risk model achieves 36% of the Net Benefit of perfect prediction instead of treat-all.

Figure 2.

Opt-out Decision Curve analysis corresponding to Figure 1. Treat-all is the reference policy, and a risk model could be used to opt low-risk patients out of treatment. The analysis shows that the risk model offers an estimated 20%−55% of the maximum possible Net Benefit to the patient population for R=5%−20% compared to perfect prediction. For a pre-specified risk threshold, this opt-out Decision Curve allows an assessment of the evidence in favor of using the risk model over treat-all because the confidence intervals displayed are for risk-based treatment relative to treat-all. This is not possible using the opt-in Decision Curves in Figure 1.

An additional advantage of using opt-out Decision Curves in opt-out contexts is that they facilitate an evaluation of the evidence for recommending treatment based on the risk model. For R=10%, Figure 2 shows that the data provide strong evidence that a risk-based treatment policy is superior to treat-all because the confidence interval for the opt-out standardized Net Benefit excludes 0. Such an evaluation is not possible in Figure 1. A user provided with Figure 1 might be tempted to examine the evidence for the risk model compared to. treat-all by examining overlap in confidence intervals at R=10%. This is incorrect practice in general [13], and would lead to the incorrect conclusion in this instance.

Last, we note that when R<P and treat-all is currently policy, it may be preferable to omit the curve for treat-none from the Decision Curve display to simplify the plot and focus attention on the best candidate treatment policies. (Similarly, when R>P and treat-none is current policy, one might choose to omit the curve for treat-all.)

Software

The original Decision Curve software (www.decisioncurveanalysis.org) includes functionality for estimating opt-out decision curves, as does the R package rmda. The R package rmda has additional functionality to produce confidence intervals for curves, and emphasizes the linkage between cost/benefit and risk threshold with its labeling of the horizontal axis.

Discussion

The most commonly employed Decision Curves use an opt-in formulation, in which the Net Benefit of a treatment policy is calculated compared to treat-none and a risk model is evaluated for opting high risk patients into treatment. Opt-in and opt-out Decision Curves produce the same ordering of treatment policies; thus, for ranking policies based on point estimates the choice does not matter. The difficulty with using opt-in Decision Curves in an opt-out context arises with interpretation and quantifying uncertainty. We encourage the use of opt-out Decision Curves in situations where they are more meaningful than their opt-in counterpart.

It has been argued that when policy-makers must set treatment policy, they should select the policy that appears to perform best regardless of the strength of the evidence that a new policy is better than existing policy [3, 14]. This viewpoint leads to a focus on the ranking of point estimates of model performance, less interest in the quantification of performance metrics such as Net Benefit, and disinterest in measures of uncertainty such as confidence intervals. We acknowledge the controversy, but maintain the importance of both assessing the magnitude of the most relevant Net Benefit metric (opt-in vs. opt-out), as well as quantifying uncertainty when using samples of data to inform policy. The data example in this report illustrates an approach using confidence intervals, but we do not intend to prescribe how measures of uncertainty must be used in every situation.

We note there may be meaningful costs or harms from measuring one or more of the predictors in a risk model. The common version of Net Benefit discussed here does not account for such costs. The test tradeoff, developed for relative utility curves[8], can be used to discount the Net Benefit to account for the costs of using the model [12]. An interesting question arises if the current policy is treat-all when treat-none would have higher Net Benefit (R>ρ); or if the current policy is treat-none when treat-all would have higher Net Benefit (R<ρ). Should the reference policy be the current policy or the (superior) uniform alternative? The Decision Curve with respect to the current policy will be of interest to examine the Net Benefit of risk-based decision-making over current policy. However, a compelling proposal to switch to a risk-based policy should show that the risk model outperforms the better of treat-all and treat-none. Therefore, we think both types of Decision Curves will be of interest in this situation.